Summary
Memory models often emphasize the need to encode novel patterns of neural activity imposed by sensory drive. On the other hand, prior learning and innate architecture likely restrict neural plasticity. Here, we test how incorporation of synthetic hippocampal signals is constrained by pre-existing circuit dynamics. We optogenetically stimulated small groups of CA1 neurons as mice traversed a chosen segment of a linear track, mimicking the emergence of place fields. Stimulation induced persistent place field remapping in stimulated and non-stimulated neurons. Emergence of place fields could be predicted from sporadic firing in the new place field location and the temporal relationship to peer neurons prior to the optogenetic perturbation. Circuit modification was reflected by altered spike transmission between connected pyramidal cells and inhibitory interneurons, which persisted during post-experience sleep. We hypothesize that optogenetic perturbation unmasked sub-threshold place fields. Plasticity in recurrent/lateral inhibition may drive learning through rapid association of existing states.
eTOC
McKenzie, Huszar et al. show that optogenetic depolarization of CA1 pyramidal neurons induces place fields to emerge in locations with weak pre-existing drive. Stimulation also alters synaptic coupling strength between pyramidal cells and interneurons. Reorganization of feedback/lateral inhibition may be one mechanism for long-lasting changes in hippocampal neural computation.
Introduction
Neural systems face a fundamental tension between maintaining existing structure and changing to accommodate new information. Several potential solutions have been raised to deal with this stability-plasticity dilemma. At one extreme, novel patterns of neural activity are imposed solely by “outside-in” sensory drive. In such models, the storage of these new activity patterns occurs through synaptic plasticity, a process which potentially interferes with stability of previously stored knowledge (Bittner et al., 2017; Carrillo-Reid et al., 2016; McClelland, 2013). At the other extreme, neuronal circuits could generate and maintain a preconfigured stable dynamic, sometimes referred to as an attractor, manifold, or neural schema (Hopfield, 1982; McKenzie et al., 2014; Tse et al., 2007), with a large reservoir of patterns available for matching with novel experiences (Battaglia et al., 2005; Dragoi and Tonegawa, 2011; Edelman, 1993; Golub et al., 2018; Luczak et al., 2009; Mizuseki and Buzsaki, 2013). Where biological memory systems fall along this “inside-out/outside-in” continuum is a subject of debate.
The hippocampus is thought to contribute to episodic memory through rapid association of the constellation of sensory inputs that define a moment (Alme et al., 2014; Hasselmo and Wyble, 1997; Kumaran and McClelland, 2012; Liu et al., 2014; McNaughton and Nadel, 1990; Rolls, 1990; Tayler et al., 2013). According to this learning framework, the pattern of hippocampal neurons active at the time of learning generates an index for that episode (Teyler and DiScenna, 1986), and effectively binds the cortical regions carrying the multimodal episodic content (Tanaka et al., 2014). In support of models emphasizing rapid encoding of inputs, when single neurons are depolarized in a predetermined spatial position, robust firing persists in that location in the absence of external drive (Bittner et al., 2015; Bittner et al., 2017; Diamantaki et al., 2018; Diamantaki et al., 2016). This new spatial ‘code’ is thought to be due to the association of that neuron with excitatory afferent signals naturally tuned to the stimulated location (Bittner et al., 2017; Dragoi et al., 2003), thus suggesting that any hippocampal neuron can be associated with any spatial location.
Neural communication in general, and the hippocampal index model in particular (Buzsaki and Tingley, 2018; Teyler and DiScenna, 1986), is thought to depend upon the synchronous activity of groups of neurons. Little is known about how pre-existing connectivity and self-organized dynamics affect the encoding of novel experiences. Here, we address these problems by pairing focal optogenetic stimulation of small groups of CA1 pyramidal neurons with a segment of familiar space. Stimulation induced persistent place field remapping. Novel place fields emerged in both stimulated and non-stimulated neurons, and could appear outside of the stimulation zone. The new place field location could be predicted by the correlation structure of neural activity prior to the optogenetic perturbation, suggesting that the incorporation of arbitrary signals was constrained by pre-existing circuit dynamics. Circuit modification was reflected by altered coupling between connected pyramidal cell – inhibitory interneuron pairs as well as changes in ‘synapsembles’(Buzsaki, 2010), which persisted during post-experience sleep. We hypothesize that optogenetic perturbation caused plasticity in recurrent/lateral inhibition to convert sub-threshold inputs into bona fide place fields.
RESULTS
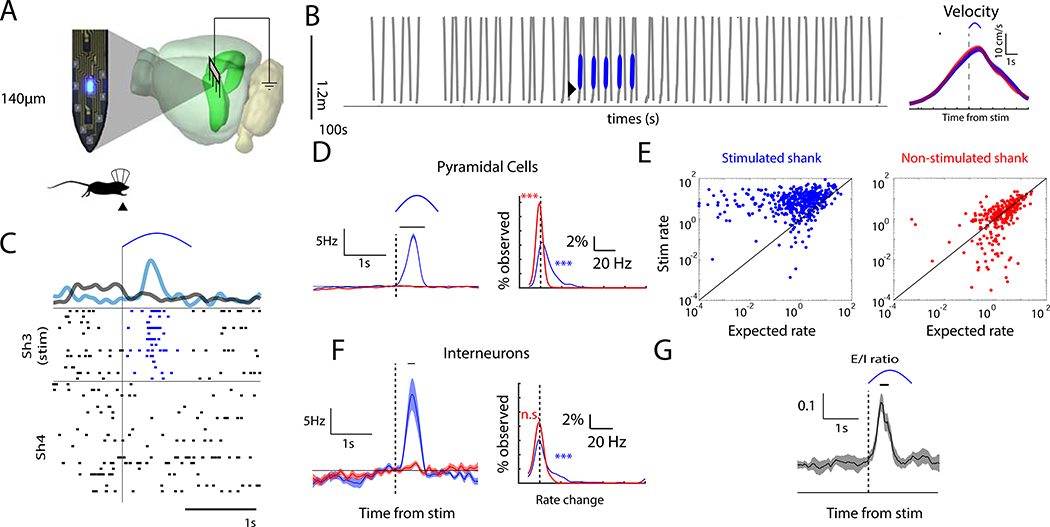
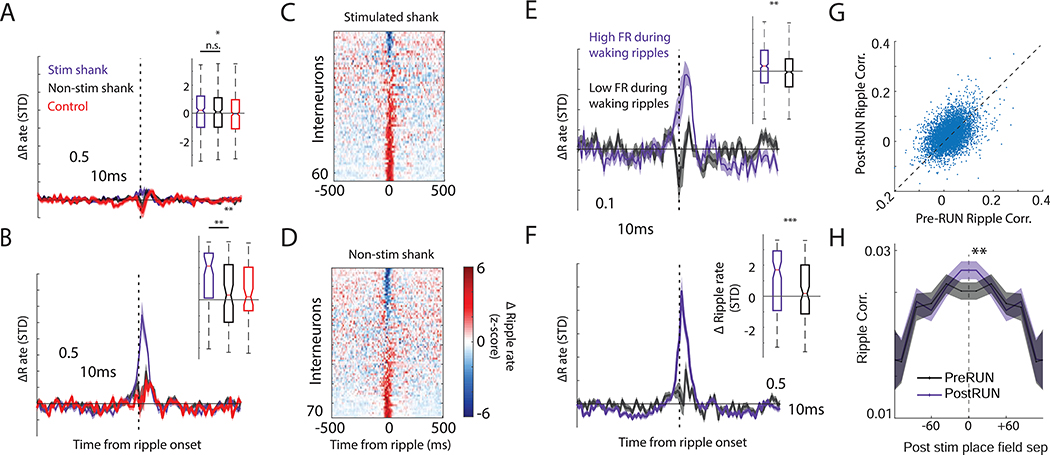
μLED stimulation drives spiking in nearby CA1 pyramidal cells and interneurons
The postulated ability for hippocampal circuits to imprint a random, novel pattern (Rolls, 1990) was tested in transgenic mice in which channelrhodopsin2 (ChR2) was expressed in excitatory pyramidal (PYR) neurons (N = 5 CaMKIIα-Cre:: Ai32 mice). μLED silicon probes were implanted in dorsal CA1 to record neural activity during sleep and behavior as mice ran on a linear track for water reward. Prior to any stimulation, neurons were recorded for at least one hour while mice stayed in their homecage (REST1), followed by running laps on a linear track (RUN1), another 1–4 hour long recording in the homecage (REST2), and then a final recording session on the track (RUN2) to test long-term place field stability. Stimulation was achieved through μLED illumination (Figure 1A, Figure S1) (Wu et al., 2015), which was delivered as mice ran on a linear track (1.2 m) for water reward (Figure 1B). After ten baseline trials (pre-Stim), stimulation (Stim = 1 second half sine wave) was given for two to ten trials (see Supplemental Table 1) at a fixed position and running direction that changed daily. Immediately following stimulation, at least another 10 trials were given (post-Stim) to test place field stability. During “Control” sessions, identical test conditions were given, however, no μLED stimulation was provided on the linear track. During stimulation sessions, μLED optogenetic stimulation induced highly focal drive in CA1 pyramidal neurons recorded on the stimulated shank (Figure 1C-E, Figure S1; N = 631; median increase above expected rate = 4.67 ± 0.37 Hz, Wilcoxon signed-rank test p < 10−7; effect size = 1.14, 95% highest density interval (HDI) effect size that excludes zero; 84.0% neurons on stimulated shank numerically increased rate above expected baseline). Induced firing was calibrated, prior to track running, to be within the physiological range normally seen at the center of a place field (McClain et al., 2019) Pyramidal cells on the neighboring shanks (≥ 250μm away; N = 529) showed a small but significant decrease in expected firing (Figure 1C-E; median rate difference = 0.02 ± 0.09 Hz, Wilcoxon signed-rank test p < 10−14; effect size = 0.29, 95% HDI effect size that excludes zero; 61.2% pyramidal cells on non-stimulated shank numerically decreased rate below expected baseline). The small decrease in the non-stimulated shanks was potentially due to recruitment of local lateral inhibition. Indeed, inhibitory interneurons recorded on the stimulated shank were also driven (Figure 1F; N = 126; median rate difference = 2.29 ± 2.83 Hz, Wilcoxon signed-rank test p < 10−5; effect size = 0.60, 95% HDI effect size that excludes zero; 69.1% interneurons on stimulated shank numerically increased rate above expected baseline), likely through monosynaptic drive from the optogenetically stimulated pyramidal cells (English et al., 2017). The overall increase in excitatory firing was higher than that observed for inhibitory cells. Considering the multi-unit activity of all recorded pyramidal cells and all interneurons, the excitatory/inhibitory ratio (E/I ratio) increased transiently during stimulation before returning to baseline (Figure 1G). As shown by previous studies (English et al., 2017; Stark et al., 2015), we found that focal optogenetic stimulation engaged small networks of pyramidal cells and interneurons during track running.
Figure 1. Location-specific optogenetic depolarization drives neural activity within a 125 μm radius.
(A) Schematic of a single shank from a μLED silicon probe. (B) Left, Mice (CaMKIIα − Cre :: Ai32) ran laps on a linear track (1.2m) retrieving water reward at each end. Breaking an infrared-beam (triangle) triggered 1s half-sine blue light via μLED probes implanted in area CA1. Right, the mean velocity of mice passing through the stimulation site before (red) and during (blue) optogenetic perturbation. Black bar indicates significant difference at p < 0.01 (C) Example sweep showing that light delivery drove pyramidal cells (rows = neurons) on the stimulated shank (Sh3). (D) Left, mean firing rate change of pyramidal cells recorded on the stimulated shank (blue, N = 631 cells) and non-stimulated shanks (red, N = 529 cells) around stimulation, relative to expected firing at that position. Bar indicates p < 0.001 comparing firing rate on stimulated versus non-stimulated shanks. Right, distribution of observed firing rate changes across neurons. Dashed line = no change. *** p < 0.001 comparing change in rate from zero. (E) For each neuron recorded on the stimulated shank (left) and non-stimulated shanks (right), the evoked firing rate as a function of the expected rate in that location based off of pre-Stim firing fields. (F) Same analysis as Panel D, for interneurons. (G) The mean excitatory/inhibitory ratio (E/I ratio) across sessions increases during stimulation. Bar indicates p < 0.001 comparing E/I ratio post-stimulation to the median E/I during the 2s prior to stim. See also Figure S1 and Figure S2.
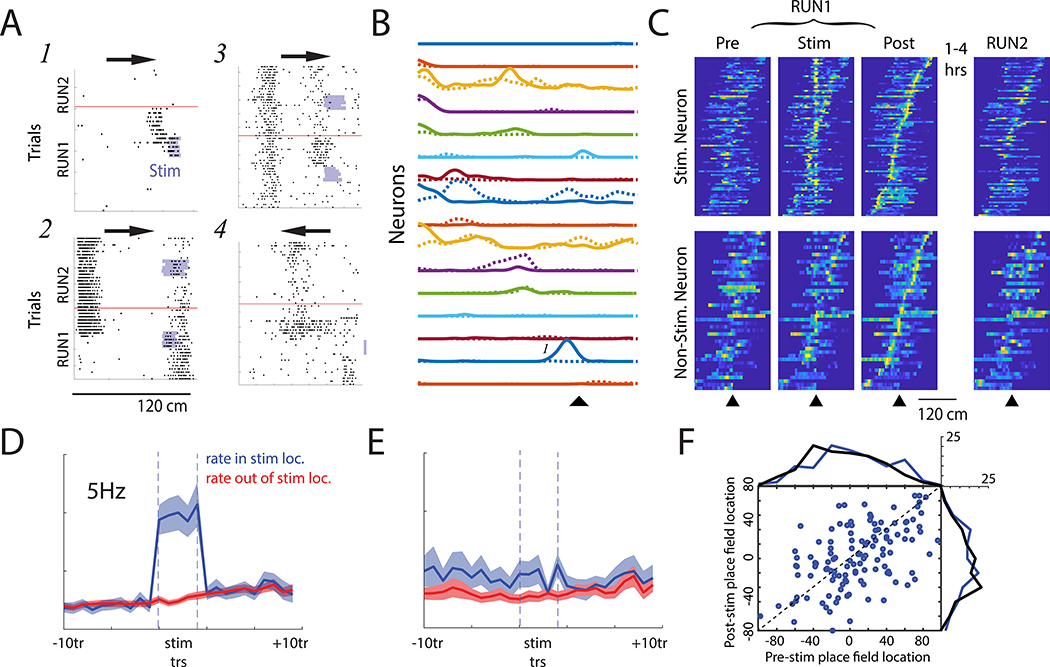
Focal optogenetic stimulation induces partial remapping of place fields
We next tested for the stability of optogenetically-induced place fields (Rickgauer et al., 2014; Stark et al., 2012). In contrast to prior studies that manipulated single neurons with current injection (Bittner et al., 2015; Bittner et al., 2017; Diamantaki et al., 2018; Diamantaki et al., 2016), we found that novel place fields emerged and disappeared both within and outside of the stimulation zone (Figure 2; Figure S2). Further, for CA1 neurons that ‘remapped’ (see STAR Methods), the locations of the place fields post-stimulation were not clustered around the stimulation zone on the track (Figure 2C-F), showing a reorganization of the place representation, at least within the small volume of the recorded CA1 circuit.
Figure 2. Optogenetically-induced place cell remapping is neither confined to stimulated neurons, nor the stimulation zone.
(A) Stimulation induced place field remapping after focal light delivery (light blue). Arrows show running direction. RUN1 and RUN2 sessions are separated by a horizontal red line. (1) Novel place field near the stimulation site. (2) Rate reduction of spiking within an existing place field and induction of a novel place field at a non-stimulated site. (3) Induced novel place field at stimulation location and persistence of an existing place field. (4) Induction of a novel place field observed on inbound runs, despite stimulation delivered during outbound traversals. (B) All place fields for an example stimulation session before (dashed) and after (solid) optogenetic stimulation. ▲ marks stimulation location. In the same session, some neurons shifted fields, some showed rate decreases, and some rate increases. Place field marked ‘1’ is the same as that shown in Panel A1. (C) Normalized place fields for all remapping neurons recorded on the stimulated and non-stimulated shanks. Place fields are centered on the stimulation location and plotted using spikes recorded before stimulation (pre), during stimulation trials (stim), directly after stimulation (Post), and during a follow-up track session after homecage recordings (RUN2). Place fields sorted by post-Stim peak firing location. (D) Mean firing rate of stimulated neurons within (blue) and outside (red) of the stimulation site before, during (between dashed lines), and after stimulation trials. Bar indicates p < 0.001 comparing firing rate on stimulated location versus the median rate in non-stimulated locations. (E) Same as Panel D for neurons recorded on the non-stimulated shank. (F) Place field location recorded prior to stimulation versus the Post-Stim location for remapping (blue) neurons. The distribution of place field centers pre- and post-Stim are shown for the remapping neurons (blue) and the stable (black) neurons for reference. Place field locations are centered on the Stim location. Note that place fields could remap to any location on the track and that there was no Post-stim over-representation of the stimulation site. See also Figure S2.
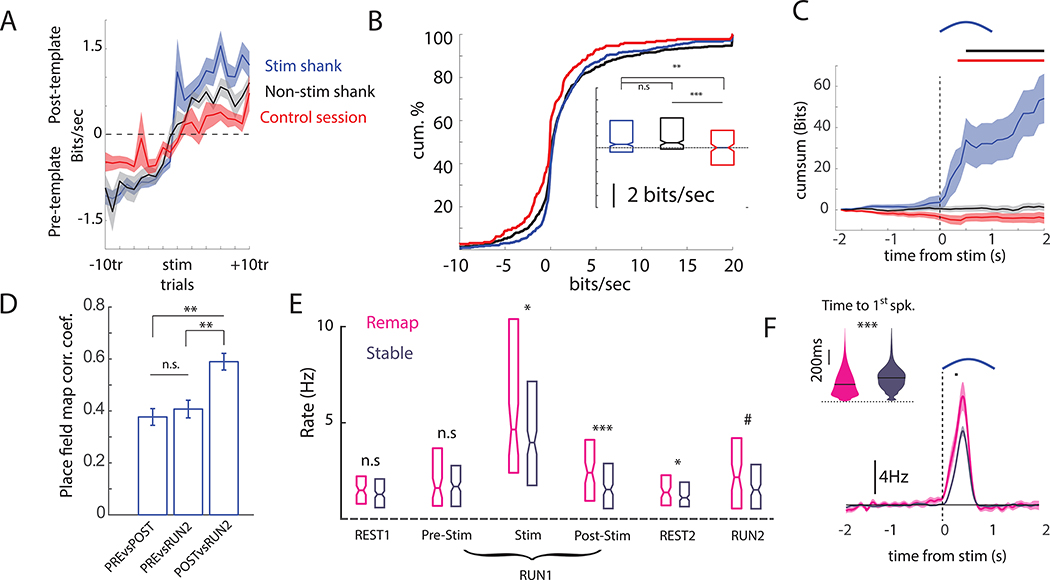
Two approaches were taken to quantify the illustrated remapping. First, the log-likelihood (LL) of an observed spike train was assessed given two conditional intensity functions, one derived from that neuron’s place field recorded prior to stimulation trials (pre-template LL) and another from place fields recorded after the last stimulation trial (post-template LL). The degree to which the log-likelihoods differed, the LL-ratio (post-template LL – pre-template LL; Harris et al., 2003), was used to quantify remapping. Using this LL-ratio metric, spatial tuning of neurons recorded on both stimulated and non-stimulated shanks (neighboring shanks for which the μLED was not activated) showed greater reorganization immediately after the stimulation trials as compared to the spatial tuning observed during Control sessions that lacked track stimulation (Stim vs Control: Mann-Whitney U Test, p < 10−6, effect size = 0.37, 95% HDI effect size that excludes zero; NonStim vs Control: Mann-Whitney U Test, p < 10−7, effect size = 0.40, 95% HDI); remapping did not differ between stimulated and non-stimulated shanks on stimulation sessions (Figure 3A,B). Similar results were obtained with a different remapping metric that uses Pearson correlation to compare trial-by-trial rate maps with the average place field maps recorded before and after stimulation (Figure S3). Trial-by-trial estimates of place field drift also revealed greater remapping after optogenetic stimulation regardless of whether the trials were separated by short or long intervals (Figure S3).
Figure 3). Focal optogenetic depolarization induces rapid remapping and persistent rate changes.
(A) Remapping was quantified as the log-likelihood difference between two models of single-cell spiking: one based on place fields recorded prior to stimulation (Pre-template), and another based on post-stimulation place fields (Post-template). The difference in log-likelihoods after stimulation gives gain/loss of information (Bit/sec) carried by the spike train about the post-stimulation place fields relative to pre-stimulation. Comparisons are made between neurons recorded on the stimulated shank and non-stimulated (neighboring) shanks in optogenetic session and identical Control session without optogenetic stimulation (B) The summed post-stimulation log-likelihood ratio (post – pre) was calculated for each neuron. The cumulative distribution of LL-ratios is given for neurons recorded on the stimulated shank (blue), non-stimulated shanks (black), and in Control sessions (red). Box plots show descriptive summaries for each group. (C) The mean ± SEM cumulative sum of the log-likelihood differences centered on stimulation for remapping cells. Soon after stimulation (400ms), neurons on the stimulated shank began to show spiking that was more consistent with post-stimulation place fields. Black bar indicates p < 0.01 comparing stimulated shank versus non-stim shank. Red bar indicates p < 0.01 comparing stimulated shank versus Control. (D) The place field stability (Pearson R) for remapping cells. Post-stim rate maps were more similar to RUN2 than the pre-stim rates. (E) The firing rates for remapping and stable cells during different segments of stimulation sessions. Remapping cells showed higher induced rates and higher rates in all post-stimulation epochs compared to stable cells. (F) The subset of neurons on the stimulated shank that remapped (pink) showed higher firing rates and shorter latencies to spike after stimulation (inset), as compared to stimulated neurons that maintained stable spatial firing fields (purple). Rate differences are calculated relative to the expected firing rates at those times given the pre-Stim place fields. Bar indicates p < 0.01 comparing firing rate of remapping versus stable cells. # p < 0.1, * p < 0.05, ** p < 0.01, *** p< 0.001. Shaded error bars = S.E.M. See also Figure S3.
The log-likelihood approach provides a moment-to-moment estimate of whether the observed spike train is better described by the pre- or post-stimulation fire rate maps. We used this metric to quantify how quickly new spatial firing fields emerged after stimulation. For stimulated neurons that remapped (N = 84, 12.3% of all stimulated pyramidal cells, see STAR Methods for remapping criteria), the spiking immediately after stimulation was better predicted by post-stim place fields (Figure 3C), suggesting that the place fields in these neurons emerged immediately. On the other hand, spiking of simultaneously recorded remapping neurons on the non-stimulated shanks (N = 44, 10.3% of all non-stimulated pyramidal cells) was equally well described by the pre- and post-stimulation place fields (Figure 3C) in the moments around stimulation, suggesting a distinct, slower process driving this firing field reorganization.
For those neurons that remapped, post-stimulation place fields signaled more spatial information (median information score = 4.94 ± 0.12 bits) than simultaneously recorded neurons with stable fields (median information score = 4.53± 0.10 bits; Mann-Whitney U-test, p = 0.002; effect size = 0.35, 95% HDI effect size that excludes zero), and comparable information as neurons recorded in Control sessions (median information score = 5.09 ± 0.17 bits, Mann-Whitney U-test, p = 0.49). Consistent with this observation, Bayesian decoding of the animal’s position during pre-stimulation trials using pre-stimulation place fields (median decoding error = 15.1 ± 0.92 cm) was as accurate as location decoding during post-stimulation trials using post-stimulation place fields (median decoding error = 15.4 ± 1.0 cm; N = 27 sessions, Mann-Whitney U-test, p = 0.87).
A second recording session (RUN2), revealed that the remapping could be stable after 1–4 hours in the homecage (Figure 1C, Figure 3D). Cells that remapped showed post-stimulation place fields that were more similar to those recorded during the second recording session (median corrPOSTvsRUN2= 0.59 ± 0.03) than to those place fields recorded prior to stimulation (Mann-Whitney U-test corrPREvsRUN2 vs corrPOSTvsRUN2, p = .0003; effect size = 0.40, 95% HDI that excludes zero), despite the shorter time difference between the first and last stimulation (median = 6 min), as compared to the interval between RUN1 and RUN2 (median = 3 hrs 7min). This stability after the homecage interval suggests that the observed remapping was not due to drift in place field coding or systematic recording instability. However, remapped place fields were not as stable as those observed in Control sessions (median corrPOSTvsRUN2= 0.75 ± 0.03 Mann-Whitney U-test corrPREvsRUN2 vs corrPOSTvsRUN2, p < 10−5; effect size = 0.63, 95% HDI that excludes zero). We also found no difference in spike sorting quality between the remapping and non-remapping sub-populations, as measured by L-ratio (p = 0.85) and isolation distance (Mann-Whitney U-test p = 0.24). These results show moderate long-term stability of optogenetically induced remapping in CA1 which was less stable than that observed during Control sessions.
Next, we examined potential physiological features that would reveal insights into why some neurons remapped and others did not. Comparing stimulated remapping cells versus stable cells, we did not find any differences in the radial position of the neuron (i.e. deep vs. superficial, p = 0.23), nor in overall firing rate or burstiness during pre-Rest or pre-Stim RUN periods (Figure 3E, all p > 0.20). Remapping neurons recorded on the stimulated shank tended to fire at a higher rate during stimulation and during subsequent post-Stim RUN trials (Figure 3D,E; Figure S3). Higher firing persisted during REST2 and was marginally higher during RUN2 (Figure 3D,E). Therefore, remapping was preferentially observed in neurons that responded to light with early spiking and a high firing rate, while relative stability was observed in neighboring neurons.
Prior studies have found that back-propagating action potentials and dendritic plateau potentials cause new place fields to emerge in the position in which those strong dendritic events occurred (Bittner et al., 2015; Bittner et al., 2017; Milstein et al., 2020). It is possible that the complex spike burst is an extracellular correlate of the plateau potential. We found that the first pass through a new place field (first trial with > 3Hz firing) was associated with bursting (spikes with ~5ms inter-spike interval; Figure S3F), a defining feature of a complex spike burst, though bursts were not more prominent on the first trial (12.2±0.02% spikes in a burst) as compared to later trials (11.1±0.01% spikes in a burst), irrespective of the rate threshold used to define the first place field pass. The geometry of the implanted silicon probes (Figure 1A) also allowed for an analysis of the backpropagating spikes over the radial axis of CA1, albeit to a limited extent (<200 μm). We therefore tested whether the spikes that appeared on the first pass of a new place field differed from the mean waveform recorded for each unit in which a new field emerged. This analysis revealed no differences in spike waveforms (Figure S3). However, because of the limitations in detecting spike features from more distal apical dendrites with extracellular methods, these results do not exclude the possibility of important distal dendritic events. We next tested whether the running speed on the first trial predicted subsequent place field width (width at half the peak firing rate), as has been observed with spontaneous and artificial plateau potentials (Bittner et al., 2017). We found no correlation (Pearson corr. coef. = 0.10, p = 0.27) between first trial running speed and subsequent place field width, irrespective of the firing rate criteria used to define a new field (1 – 10Hz tested).
Pre-stimulation dynamics predict post-stimulation remapping
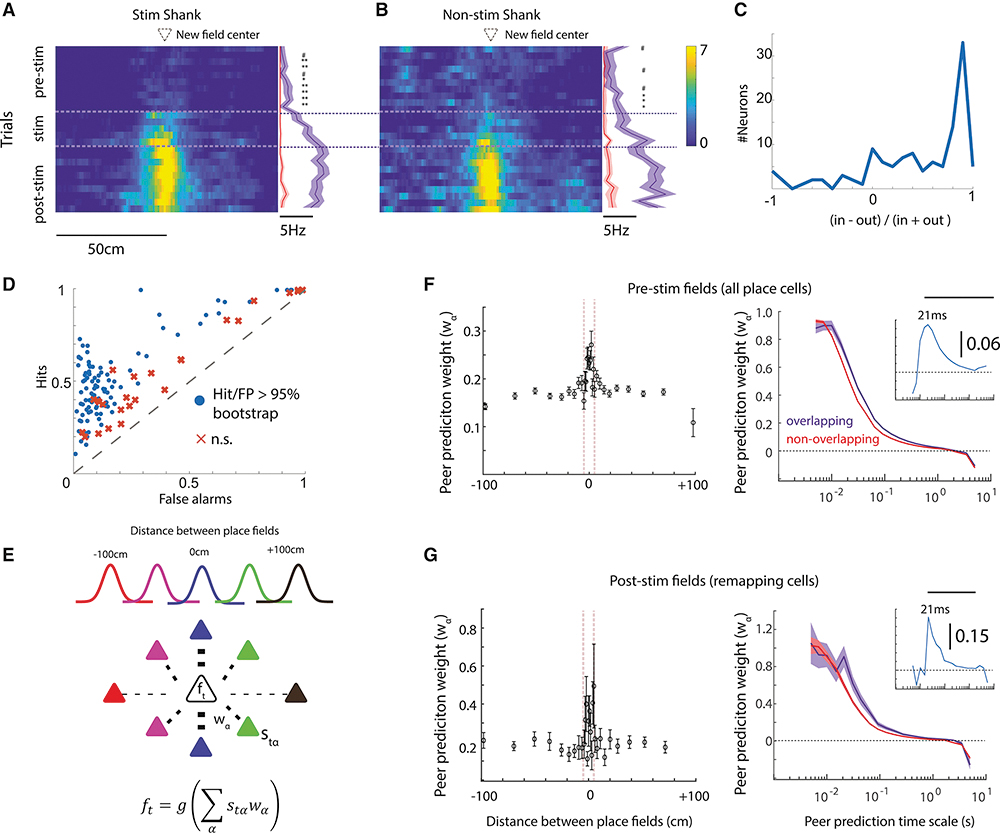
Since place fields did not emerge preferentially around the stimulation site on the track, we next examined whether any systematic firing patterns can explain the findings. We first tested whether, prior to stimulation, neurons fired differently in the location that would later become the center of the remapped place field. During pre-Stim trials, firing rates in the future place field were already elevated relative to the median rate recorded outside of the future place field for both neurons on the stimulated shank (Figure 4A,C) (N = 84, Mann-Whitney U-test, p < 0.05 from Trial 2–10; effect size 0.41 – 0.7, 95% HDI that excludes zero), and those recorded on the non-stimulated shanks (Figure 4B,C) (N = 42 neurons, Mann-Whitney U-test, p <0.05 from Trial 8–10; effect size 0.39 – 0.53, 95% HDI that excludes zero) even if such sporadic spiking did not translate to a quantitatively detectable place field. The pre-existing elevated spiking suggested that remapping unveiled the presence of pre-existing weak drive to these neurons at the location of the future place field.
Figure 4). Relationship between pre-stimulation neural activity and post-stimulation remapping.
(A) For remapping neurons recorded on the stimulated shank, the median firing rate in the center of the induced place field (blue) was already higher prior to optogenetic stimulation than in other regions of the track (red). (B) Firing rate in the future place field prior to stimulation was also higher for neurons recorded on the non-stimulated shank. In-field vs out-of-field rate: # p< 0.1, * = p < 0.05, ** p < 0.01 (C) The distribution across remapping neurons of the difference-over-sum of the in-future-field firing rates versus the out-of-field firing rates measured prior to stimulation. In-future-field rates were defined as spikes measured when the mouse was ±5 cm around the future place field peak; out-field rates were the mean firing rates measured at all other locations on the track. (D) The classification performance of the RUSBoost algorithm across neurons (points = neuron) to predict whether the pattern of neural activity in a given place, on a given trial, was recorded in the location of the future place field, or within another location on the track. Neurons compared against classifier performance with place-shuffled data. (E) Method for relating pre-stimulation activity to subsequent place field distribution. Using data recorded during REST1, the binned firing rate of each target cell (ft) was predicted using the weighted (wα) binned rate (stα) of other simultaneously recorded pyramidal cells. These weights were then related to the distance between place fields of the target cell and each peer predictor. (F) Left, On average, for all pairs of neurons with overlapping pre-stimulation place fields (peaks within 5 cm) higher peer prediction weights were observed during REST1 as compared to pairs whose fields were further apart (spikes binned at 44-ms). Right, Higher peer prediction strengths for pyramidal pairs with overlapping place fields were observed across a range of binning time scales. Bar indicates p < 0.01 comparing peer prediction weights for pairs of neurons with overlapping versus non-overlapping place fields. Inset, difference between peer-prediction weights for neurons with overlapping versus non-overlapping place fields at each time bin. (G) Same as Panel D, though comparing post-stimulation place fields and limiting the analysis to just neuron pairs in which either the target or peer predictor remapped. Shaded error bars = S.E.M.
Next, we tested whether we could invert the analysis and predict where the place field would be located given the trial-by-trial pattern within and outside of the future place field. Since the majority of data recorded prior to stimulation occurred outside of the new place field, the classification labels (‘future field pattern’ vs ‘not future field pattern’) were heavily unbalanced. To confront this issue, we adopted the RUSBoost binary classification algorithm (Seiffert et al., 2008) to predict whether each location would become a new place field based on a feature space defined by each neuron’s trial-by-trial firing rate within that location, and the proportion of spikes emitted in bursts (ISI < 7ms) in that location. Half of the pre-stimulation trials were used to train the classifier, which was able to classify whether spiking patterns occurred in a future place field significantly better than chance in 78.9% of remapping neurons (Figure 4D). When only firing rate or only the percentage of spikes in a burst were used to classify location as future place fields, the firing rate only model was associated with a significantly higher positive likelihood ratio (hit/false positive; paired Mann-Whitney U-test, p < 10−9). As expected, some neurons showed much higher classification performance than others, given the moderate effect size of pre-stimulation firing rate in predicting place field location.
Previous studies have reported that the pattern of spiking activity prior to a first-time experience is predictive of the future spatial layout of place fields in novel environments (Dragoi and Tonegawa, 2011; Farooq and Dragoi, 2019; Grosmark and Buzsaki, 2016). If new place fields in the current experiment were constrained by pre-existing dynamics, we reasoned that spontaneous activity during immobility/sleep in the homecage before track running would be predictive of how neurons remap with artificial stimulation. We adopted a generalized linear modeling approach where the spiking of a target neuron was predicted by a conditional intensity function defined by the weighted sum of the activity of neighboring pyramidal cells (Figure 4E) (dubbed as ‘peer prediction’) (Harris et al., 2003). We first tested whether this method could reveal evidence of dormant place fields prior to stimulation, where higher peer prediction weights are expected for those neurons that have overlapping place fields. As hypothesized, neurons with nearby place fields (peaks within 5 cm) showed higher peer prediction weights during REST1 (N = 7,770 pairs, median prediction weight = 0.27 ± 0.01) as compared to pairs of neurons whose fields were further apart (Figure 4F) (N = 64,836 pairs; median prediction weight = 0.23 ± 0.003, Mann-Whitney U-test, p < 10−9 at 30ms temporal bin; effect size = 0.13, 95% HDI that excludes zero). Next, we tested whether higher peer prediction weights (using REST1 data) were also observed for pairs of cells in which one, or both, remapped such that the post-Stim place fields were nearby. As was observed for the relationship between peer prediction weights and pre-Stim place fields, prediction weights were also significantly higher for pairs of neurons the remapped to nearby locations (Figure 4G) (N = 200 pairs; median = 0.19 ± 0.007), as compared to neurons that remapped but had place fields greater than 5 cm apart (N = 2,098 pairs; median = 0.11 ± 0.01; Mann-Whitney U test, p < 10−5; effect size = 0.20, 90% HDI that excludes zero). These results suggest that pre-existing circuit dynamics that constrain neuronal activity patterns during sleep also bias place field remapping by optogenetic perturbation.
Optogenetic stimulation changes interneuron and pyramidal cell firing patterns during post-RUN sharp-wave ripples
Because hippocampal sharp wave ripples (SPW-R; Figure S1B) are believed to play a key role in circuit plasticity (Buzsaki, 2015), we tested whether optogenetic induction of place fields are related to changes in neuronal participation in SPW-Rs from REST1 to REST2 and whether these changes differ from those seen in Control sessions where light stimulation was not given. Stimulated pyramidal neurons showed slightly higher rate increases within ripples as compared to changes seen in neurons (N = 291) recorded in Control sessions (p = 0.02; effect size = 0.13, 95% HDI that excludes zero) but not from neurons recorded on non-stimulated shanks (Figure 5A; N = 220; Mann-Whitney U-test, p = 0.46; effect size = 0.04). In contrast, interneurons driven synaptically on the stimulated shank (N = 63) showed a larger increase in SPW-R recruitment as compared to those (N = 77) recorded on the non-stimulated shank (Figure 5 B-D)(Mann-Whitney U-test, p = 0.005; effect size = 0.49, 95% HDI that excludes zero), and compared to Control sessions (N = 70; Mann-Whitney U-test, p = 0.005; effect size = 0.45, 95% HDI that excludes zero).
Figure 5. Optogenetic stimulation alters pyramidal cell and interneuron firing during ripple events.
(A) Pyramidal cells recorded on the stimulated shank (blue) did not show a change in ripple recruitment, REST1 vs REST2, any more than simultaneously recorded non-stimulated neurons (black), and marginally (p = 0.02) more than those recorded in Control sessions (red). (B) Unlike directly stimulated pyramidal cells, interneurons recorded on the stimulated shank showed increased ripple recruitment during REST2 SPW-Rs. (C, D) Normalized peri-ripple time histograms for interneurons recorded on the stimulated shank (C) and non-stimulated shanks (D). Interneurons are sorted by ripple-associated firing rate change. (E) Pyramidal cells that fired during waking ripples on the track (purple = upper 50%) showed greater gain in ripple participation (comparing ripple-related spiking during REST1 and REST2 in the homecage; median ± SEM) compared to those that participated less during waking ripples (black = lower 50%). Inset: Rate changes during ripples. (F) Interneurons that fired more often during waking ripples on the track showed high gain in ripple participation from pre-RUN to post-RUN rest/sleep. (G) The pairwise ripple co-modulation during REST1 was strongly correlated with REST2 ripple co-modulation (Pearson r = 0.42, p = 2.1−265). (H) The distance between post-stimulation place fields is correlated with the pairwise correlation in ripple activity for ripples recorded both prior to, and after, track running. Only pairs of neurons with fields within 20cm showed a significant (p = 0.007) gain in ripple co-modulation. * p < .05, ** p <.01, *** p < .001. Shaded error bars = S.E.M.
Typically, interneuron firing is excluded from SPW-R replay analyses. Therefore, we tested whether interneurons that are naturally recruited during the running task persist in their firing during the following homecage recording session. We also tested pyramidal cell reactivation as a positive control. Since interneurons lack well-defined firing fields, and typically have higher rates overall, we focused on the firing observed during waking SPW-Rs recorded on the track. As expected, CA1 pyramidal cells that were more strongly recruited into waking SPW-Rs (N = 703 neurons, threshold for ripple recruitment = 2.5Hz, derived from median split of waking ripple activity for Stim and Control session) showed an increase in firing from REST1 to REST2 (Figure 5E) (paired Mann-Whitney U-test, p < 10−8; effect size = 0.18, 95% HDI that excludes zero). This increase was greater than that observed for pyramidal cells (N = 672 neurons) that were less recruited into waking SPW-R (Figure 5E; unpaired Mann-Whitney U-test, p < 10−5; effect size = 0.21, 95% HDI). Similarly, interneurons that fired more during waking SPW-R (N = 127; threshold for ripple recruitment = 15.8Hz) also showed a REST2 versus REST1 gain in homecage SPW-R firing (Figure 5F; paired Mann-Whitney U-test, p = .0002; effect size = 0.44, 95% HDI that excludes zero), that was greater than that observed in interneurons that were only weakly recruited during waking SPW-R (Figure 5F; N = 119; unpaired Mann-Whitney U-test, p = 0.003; effect size = 0.34, 95% HDI that excludes zero). Therefore, synaptic drive of interneurons during both optogenetic stimulation and natural drive during waking SPW-Rs was predictive of subsequent sleep SPW-R recruitment.
In addition, we tested for reactivation of the optogenetically induced remapped spatial representations. We focused on those same pairs in which one or both neurons shifted place fields after stimulations. The degree of co-fluctuation (Spearman R) during SPW-Rs prior to track running strongly correlated with co-fluctuations after stimulation (Figure 5G; REST2 vs REST1 co-fluctuation, Pearson r = 0.42, p < 10−265). To factor out this significant baseline stability, multiple regression analysis was used to measure how the distance between post-stimulation place fields predicted REST2 SPW-R coupling, accounting for the REST1 baseline. The absolute distance between place fields post-stimulation negatively correlated with co-activity during post-RUN SPW-R (Figure 5H; t-stat = − 3.08, p = 0.002), showing enhanced SPW-R coupling for neurons whose place fields became nearby after optogenetically-induced remapping.
The degree of co-fluctuation (Spearman R) during SPW-Rs prior to track running also negatively correlated with the distances between post-stimulation place fields (Figure 5H; t-stat = −3.6, p = 0.001). These results held even after regressing out the distance between place fields prior to stimulation (t-stat = −2.7, p = 0.007). Our results are consistent with the peer prediction analysis showing that neurons with nearby post-Stim place fields have pre-existing stronger correlations prior to track stimulation.
These results demonstrate that the optogenetic perturbation can induce long-lasting changes in both pyramidal cell and interneuron firing during post-RUN SPW-Rs. Overall, these findings are consistent with the observation that the sequential order of place fields in both novel experiences (Dragoi and Tonegawa, 2011) and after artificial perturbation predict prior internal circuit dynamics.
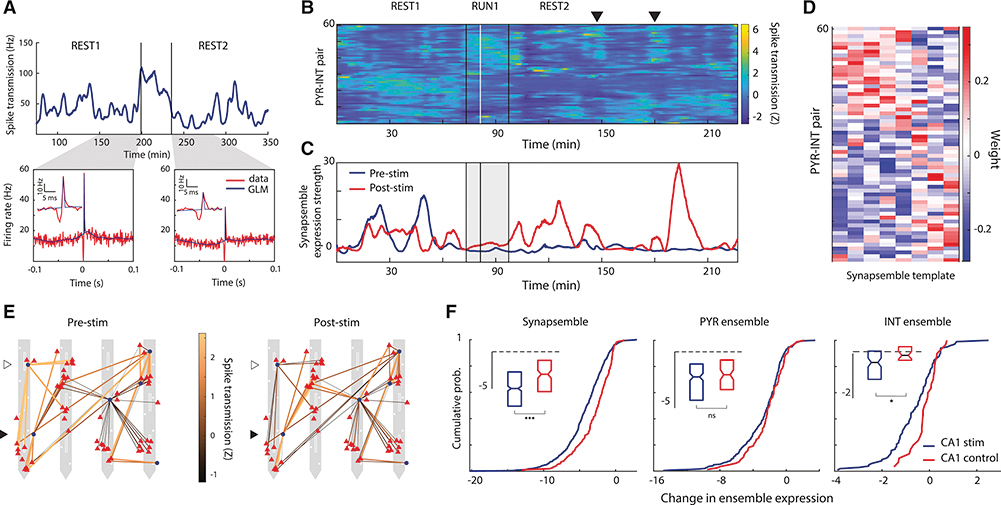
Optogenetic stimulation alters excitatory ➔ inhibitory synaptic coupling
We hypothesized that the changes in SPW-R participation of synaptically activated interneurons and the place field remapping, particularly of non-stimulated cells, was due to a reorganization of local CA1 circuitry, mainly affecting lateral inhibition. To explore this hypothesis, we examined spike transmission between pairs of monosynaptically connected pyramidal cells and interneurons (PYR-INT) (English et al., 2017; Fujisawa et al., 2008). To track how spike transmission changed over time, we developed a generalized linear model (GLM; see STAR Methods) to measure long timescale changes in the influence of the presynaptic drive to the postsynaptic interneuron while regressing out changes in the postsynaptic firing rate (Figure 6A; Figure S4). We found that putative synaptic coupling strength, as approximated by our spike transmission measure (see STAR Methods), varied 64.7±0.5% around the mean over the recording session (Figure 6A,B, Figure S4). These temporal fluctuations were independent of the presynaptic rate (Spearman R = 0.0124, p = 0.077, N = 1,771 pairs), but correlated with the postsynaptic rate (R = 0.38, p < 0.001, N = 1,771 pairs), potentially reflecting a confounding effect of postsynaptic excitability (Figure S5A-B). Yet, spike transmissions across neuron pairs sharing the same postsynaptic interneuron were only moderately correlated with each other (R = 0.24, p < 0.001, N = 12,581 convergent pairs), suggesting that the temporal dynamics of PYR-INT spike transmission cannot be fully explained by firing rate fluctuations of either presynaptic or postsynaptic neurons alone (Figure S5C).
Figure 6. Optogenetic stimulation reorganized spike transmission between PYR cells and INTs.
(A) Top. spike transmission (Hz) between an example PYR-INT pair reflecting a GLM-based estimate of the increase in postsynaptic rate due to the presynaptic spikes (see STAR methods). Bottom, observed and GLM-predicted cross-correlograms for the example PYR-INT pair, computed in 50-min homecage rest/sleep sessions before and after track running (see STAR methods). Insets highlight the peak at a finer timescale.
(B) Z scored spike transmission time series between 61 PYR-INT pairs in a single session. Black vertical lines, start and end of track running. White line, first optogenetic stimulation trial. The triangle highlights a recurring spike transmission ensemble.
(C) Time-resolved expression strengths of two PYR-INT spike transmission ensembles (synapsembles. see STAR methods) detected during pre-stim (blue) and post-stim (red) epochs.
(D) Templates of PYR-INT ensembles detected before optogenetic stimulation.
(E) Mean Z scored spike transmission functional connectivity maps during periods of high ensemble expression (>10) for pre-stim and post-stim synapsembles 3hown in (C). PYR ccll3 (red triangles) and INT3 (blue circles) arc superimposed on the recording sites (white squares) of a 4 shank pLED probe. Some INTs had a majority of connections that started strona and became weak after stimulation (empty triangle), while others showed the reverse pattern (filled triangle).
(F) Left: stimulation induced larger changes in synapsemble expression (blue, n = 543) than expected from unperturbed control sessions (red. n = 153: p < 0.001; Mann-Whitney U test). Synapsembles were detected before or after optogenetic stimulation, and the change in synapsemble expression was assessed as the difference in mean expression strength during time periods surrounding optogenetic stimulation: the halfway point on the track was used in control sessions. Insets show the same data as whisker plots. Center: the same ensemble analysis was also performed using smoothed firing rates of PYR cells (center: blue, n = 248: red. n = 83: p = 0.128: Mann-Whitney U test) and INTs (right: blue, n = 101; red. n = 30: p < 0.05: Mann-Whitney U test) that were included in putative monosynaptic connections, ‘p < 0.05. ***p < 0.001.
See also Figures S4-S6.
Spike transmission probability between simultaneously recorded PYR-INT pairs tended to co-fluctuate with pairs that increased and decreased at common moments (Figure 6B). To quantify how spike transmission across PYR-INT pairs is coordinated and changes as a result of optogenetic stimulation, we extracted patterns of significant coactivity using a combination of PCA and ICA (see STAR Methods) to define a vector of weights for the contribution of each PYR-INT pair to each ‘synaptic state’ (Figure S4), referred to here as ‘synapsembles’ (Buzsaki, 2010) (Figure 6 B-E). Each synapsemble was detected prior to or after stimulation, and its expression strength was tracked throughout the entire daily session (see STAR Methods). Compared to synapsembles in Control sessions (N = 153), optogenetic perturbation was associated with significant changes in synapsemble expression strengths (N = 543, p < 0.001, Mann-Whitney U-test; effect size = 0.44, 95% HDI that excludes zero, Figure 6F). These results also held when controlling for differences in baseline synapsemble expression strengths between optogenetic perturbation and Control conditions (Figure S5D).
Based on these analyses, we reasoned that changes in synapsemble expression ought to be accompanied by changes in cell ensembles defined by spiking. To investigate this possibility, we repeated the above analysis for presynaptic PYRs and postsynaptic INTs whose spike trains were smoothed to fluctuate at timescales equivalent to those of spike transmission (see STAR Methods). While we found no differences in PYR ensemble expression (p = 0.128, Mann-Whitney U-test, Figure 6F), INT ensembles were significantly reorganized following optogenetic stimulation (p = 0.012, Mann-Whitney U-test; effect size = 0.48, 95% HDI that excludes zero; Figure 6F).
To further investigate the nature of this plasticity, we tested an alternative statistical model to capture changes in spike transmission (see STAR Methods). In particular, spike transmission was constrained to fluctuate according to the Tsodyks-Markram dynamical model for short-term plasticity (Tsodyks and Markram, 1997), while long-term coupling strengths were held constant. The synapsemble analysis was repeated for this short-term plasticity model, and as observed in the long-term model, synapsembles reorganized more in the optogenetic stimulation sessions as compared to Controls (Figure S6). Therefore, multiple mechanisms could account for the observed changes in the coupling of pyramidal cells to interneurons in the minutes and hours after stimulation.
DISCUSSION
We report that optogenetic activation of a small group of pyramidal neurons resulted in remapping of place fields both at, and away from, the stimulation site and in both directly stimulated and non-stimulated neurons. New place fields tended to emerge in places already associated with sparse pre-existing activity. In addition, neurons with newly expressed place fields had pre-existing correlated firing with partner cells whose place fields were co-tuned following optogenetic stimulation. Optogenetically-induced place field remapping was accompanied by a reorganization of pyramidal cell–interneuron coupling and altered SPW-R membership of both pyramidal cells and interneurons, which persisted in the hours after perturbation. We hypothesize that reorganization of hippocampal circuits is both constrained and guided by pre-existing connectivity and internally organized physiological states.
Constraints on place field remapping
Interpretations of previous experiments on artificially induced place fields fall into two extremes. At one end is the assumption that association of any arbitrary environmental input with the appropriate plasticity manipulation in the hippocampus can give rise to new place fields (‘omnipotent blank slate’ model). Interpretations at the other extreme assume that perturbations simply uncover pre-existing or dormant place fields and success of artificial perturbations is, therefore, limited (‘preconfigured dynamic’ view). In support of the arbitrary place field induction interpretation, studies have shown that single neurons reliably form new place fields at any position on the running belt where those cells are injected with strong intracellular current, resulting in a large dendritic ‘plateau potential’ (Bittner et al., 2015; Bittner et al., 2017). These experiments (see also (Sheffield et al., 2017)) gave rise to a model in which CA1 pyramidal cells receive inputs from an array of upstream neurons (presumably in CA3) that represent all parts of the covered space evenly, and the plateau-related “instructive signal” is broadcast to all input synapses. Any input that occurs within a multi-second time window around the plateau potential can get strengthened, but more so when the synapses are active before a plateau rather than during or after a plateau (Bittner et al., 2017; Milstein et al., 2020). In support of the plateau potential experiments, juxtacellular stimulation of hippocampal pyramidal neurons (Diamantaki et al., 2018) and granule cells (Diamantaki et al., 2016) in freely moving subjects also induced place cell remapping to the stimulation site in a fraction of cases, especially when stimulation drove intense spiking (Diamantaki et al., 2018).
In contrast, our optogenetic perturbation experiments, along with previous studies on natural place field dynamics (Dragoi and Tonegawa, 2011; Grosmark and Buzsaki, 2016; Samsonovich and McNaughton, 1997), support the ‘pre-configured’ framework. Under our experimental conditions, neurons with induced place fields had dormant place fields and were weakly associated with pre-existing neuronal assemblies. These relationships were strengthened after optogenetic stimulation, as was revealed by their gain in SPW-R-related firing. What appeared to be a freshly learned novel place field (i.e., newly added ‘information’ to hippocampal circuits) may be more appropriately described as a matching process between existing internally organized neuronal trajectories and constellations of external inputs (Dragoi and Tonegawa, 2011; Farooq et al., 2019; Guo et al., 2020; Mizuseki and Buzsaki, 2013; Villette et al., 2015; Buzsaki 2010).
Other lines of evidence suggest that new place fields emerge upon a background of weak prior drive. The first place-field perturbation study used long-term potentiation (LTP) of the CA3-CA1 Schaffer collaterals under the hypothesis that each CA1 neuron receives input from an array of CA3 neurons that covered the available space equally (Dragoi et al., 2003). LTP perturbation induced novel place fields and made existing place fields disappear, analogous to plateau potential studies in single neurons (Milstein et al., 2020). However, new fields tended to emerge in low firing rate neurons in locations associated with pre-existing dormant activity; strong existing place fields could not be modified. In line with these findings, spatially uniform depolarization of silent CA1 pyramidal cells led to the reversible emergence of a spatially tuned subthreshold response and place-field spiking (Lee et al., 2012), indicating that a neuron driven by a preconfigured network in which it is embedded can selectively match to a particular external event. A related study showed that in a novel environment subthreshold fields pre-existed in the locations where place fields subsequently emerged without prior plateau potentials (Cohen et al., 2017).
Place fields can emerge rapidly in familiar and novel environments (Frank, 2004), precluding a scenario in which receptive fields emerge due to incremental plasticity with repetitive pairings of pre- and postsynaptic activity (Isaac et al., 2009). A recent behavioral study made the remarkable observation that prior to spontaneous emergence of a novel place field in a familiar environment, the exploring rat displayed prominent head scanning at that very place on the preceding trial (Monaco et al., 2014). Though plateau potentials may have occurred during such head scanning, the authors also found dormant place field firing prior to head scanning (their Fig. 2), allowing the interpretation that head scanning, like optogenetic perturbation, strengthened the membership with an assembly that already signified that place.
There are important differences between our study and others that have linked plateau potentials to arbitrary remapping. In our study, groups of neurons were depolarized with focal optogenetic stimulation, rather than single neurons driven with strong intrasomatic current injection. Our optogenetic stimulation excited and synchronized a small group of pyramidal cells (estimated 10–50 neurons by μLED (Wu et al., 2015) and effectively discharged local inhibitory cells (English et al., 2017). In turn, the resulting recruitment of feedback inhibition could have prevented regenerative dendritic depolarization, underlying plateau potentials (Grienberger et al., 2017; Lovett-Barron et al., 2012; Sheffield et al., 2017). Single-neuron versus multi-neuron drive may or may not be important because remapping to the stimulation site was not observed when single CA1 neurons were depolarized by holographic two-photon stimulation in a head-fixed situation (Rickgauer et al., 2014) that was similar to that employed in the plateau potential studies (Bittner et al., 2015; Bittner et al., 2017; Milstein et al., 2020). In all optical preparations, targeted stimulation of specific neurons causes the place field remapping in both the targeted and non-targeted populations, with place fields appearing at locations not associated with the artificial drive (Rickgauer et al., 2014; Robinson et al., 2020), similar to what was observed here and in previous reports (Stark et al., 2012). Finally, we have observed that a newly induced place field can persist alongside an existing field of the same neuron, in line with findings that a minority of pyramidal neurons can have two or multiple place fields (Mizuseki and Buzsaki, 2013). In contrast, a plateau-induced novel place field makes the spiking at the original place field disappear (Milstein et al., 2020).
We hypothesize that the magnitude of artificial perturbation in single neurons may explain the differences among these seemingly contradicting studies. Firing rates and synaptic strengths of neurons upstream to the recorded CA1 cells are strongly skewed (Mizuseki and Buzsaki, 2013), thus the assumption of equal representation of each position on the track may not hold. Such preconfigured, skewed synaptic weight distributions may explain why dormancy of place cells predicted the expression of novel place fields. Yet, we submit that if postsynaptic perturbation is strong, even very weak, pre-existing connections can be strengthened sufficiently and give rise to a novel place field. Thus, while the dormant-to-overt place field conversion may be the physiological mechanism for novel place field induction, strong dendritic events may also trigger arbitrary position-related place field expression. Importantly, this interpretation does not negate the possibility that plateau potentials reflect a physiological mechanism by which place fields are induced in the intact brain (Bittner et al., 2015). Yet, out findings demonstrate that this process in vivo may be more of unmasking of preexisting connections and strengthened partnership with assembly peers. This unmasking mechanism of place field emergence might be analogous to the ‘rate remapping’ observation, where ‘ghosts’ of place fields in one apparatus can often be recognized, which predict bona fide place fields in another apparatus (Leutgeb et al., 2005; Honi et al., 2020).
Mechanisms of perturbation-induced remapping
Dormant activity in the induced place field recorded prior to optogenetic perturbation predicted the pattern of remapping, irrespective whether the neuron was directly stimulated or not. The immediate changes during stimulation were likely brought about by rapid redistribution of recurrent and lateral inhibition (Trouche et al., 2016) and some of the immediate changes persisted several hours post-stimulation. Alongside place field remapping, optogenetic stimulation also recruited interneurons into ripples, affected the correlation structure among interneurons, and the pattern of coupling between monosynaptically connected PYR➔INT pairs. We hypothesize that the primary component of this local circuit reorganization is long-term plasticity in inhibitory signaling.
Although plastic changes may take place at multiple levels of CA1 local connectivity, one potential locus of this plasticity is the PYR to INT synapse, which is known to undergo activity dependent plasticity (Buzsaki and Eidelberg, 1982; Kullmann and Lamsa, 2011; Lau et al., 2017; Le Roux et al., 2013; Lu et al., 2007; Nissen et al., 2010). To study PYR-INT plasticity, we quantified the change in spike transmission probability (Csicsvari et al., 1998; English et al., 2017), a measure shown to be highly correlated with single pyramidal neuron-induced EPSPs in PV-expressing interneurons in vivo (Galarreta and Hestrin, 2001; Jouhanneau et al., 2018). A population measure of PYR-INT spike transmission (‘synapsembles’) showed a significant rearrangement following optogenetic stimulation, possibly driving the remapping in the place fields of pyramidal cells. We also observed significant synapsemble reorganization in a statistical model lacking slow time scale fluctuations, where changes in spike transmission only depended on the recent (seconds) history of presynaptic spiking (Ghanbari et al., 2020). We acknowledge that these indirect measures of synaptic plasticity need to be confirmed by future intracellular experiments. Yet, the current data are compatible with the hypothesis that interneurons played an important role (Dupret et al., 2013; Schoenenberger et al., 2016). As further support for the involvement of inhibition, we also demonstrated that interneuron firing rate ensembles, though not pyramidal ensembles, were reorganized following optogenetic stimulation. In addition, interneurons on the stimulated shank showed a large gain in SPW-R-related firing, compared to interneurons on non-stimulated shanks or in control sessions. Finally, interneurons which were highly active during waking SPW-Rs on the track showed a larger gain in SPW-Rs from pre-RUN sleep to post-RUN sleep in the home cage compared to interneurons with low waking SPW-R activity. Overall, our analysis of ensemble activity points to the critical role of inhibitory neurons in both short-term and long-term remapping of place fields. The molecular identity of the interneuron type(s) that played a critical role in our experiments need to be explored in future experiments.
In addition, the relationship between induced and spontaneous reorganization of hippocampal circuits need also be addressed in future studies. A growing body of literature has shown that, even when task demands and sensory stimuli remain fixed, the spatial code of the hippocampus “drifts” (Bladon et al., 2019; Cai et al., 2016; Mankin et al., 2012; Ziv et al., 2013) as reflected by different neural firing patterns observed in the same location at different times. It is possible that some of this drift may be related to reorganization of local feedback circuits. However, other mechanisms have also been postulated, such as fluctuations in intrinsic excitability (Cai et al., 2016) and varying readout of decaying cortical activity signaling some event that happened in the past (Bright et al., 2020). Rapid, task-dependent changes in the place coding has also been described (Jackson and Redish, 2007; Jezek et al., 2011; Kelemen and Fenton, 2010), which likely requires inhibitory neurons to coordinate groups of pyramidal neurons and allow for rapid transitions to other ensembles when task demands change, or when learning about a novel environment (Cohen et al., 2017; Frank, 2004; Sheffield et al., 2017). We hypothesize that our artificial stimulation affected this inhibitory recurrent circuitry to produce place field reorganization.
Conclusion
In summary, we hypothesize that moderate perturbations can unmask subthreshold, pre-existing place fields. Overall, perturbation studies are compatible with the general framework that incorporation of novel information within brain circuits is constrained and guided by a backbone of a pre-existing repertoire of states (Battaglia et al., 2005; Dragoi and Tonegawa, 2011; Farooq et al., 2019; Golub et al., 2018; Luczak et al., 2009; Mizuseki and Buzsaki, 2013). Such preconfigured dynamics may reflect regularities captured across prior learning experience - the neural schema (McKenzie et al., 2014; Tse et al., 2007) – in combination with the self-organized scaffold assembled across development (Farooq and Dragoi, 2019; Li et al., 2012; Xu et al., 2014).
STAR Methods
RESOURCE AVAILABILITY
Lead Contact
Further information and requests for resources and data should be directed to and will be fulfilled by the Lead Contact, György Buzsáki (Gyorgy.Buzsaki@nyumc.org)
Materials Availability
No new materials were generated in these studies.
Data and Code Availability
The datasets generated during the current study are available in the Buzsaki lab repository, https://buzsakilab.nyumc.org/datasets/McKenzieS/.
Custom lab software is available at https://github.com/buzsakilab/buzcode and MATLAB scripts for the current project will be made available upon reasonable request.
EXPERIMENTAL MODEL AND SUBJECT DETAILS
Homozygous CaMKIIα-Cre line T29–1 transgenic mice (Jackson Laboratory #005359) were crossed with homozygous Ai32 mice (Jackson Laboratory #012569) to express channelrhodopsin2 (ChR2) in neurons expressing male and female CaMKIIα in F1 hybrid mice (N = 5; 3 male; 25–40g, 30–50 weeks of age). After implantation, animals were housed individually on a reversed 12/12 h day/night schedule. Following one week of recovery, mice were recorded 5–7 days/week for two months before being euthanized with pentobarbital cocktail (Euthasol®, transcardial 300 mg/kg) and perfused with formalin (10%). All experiments were conducted in accordance with the Institutional Animal Care and Use Committee of New York University Medical Center.
METHOD DETAILS
Task
Mice were trained to run laps on a linear track (120 cm long, 4cm wide) to retrieve water reward (5–1μL) at each end. Before implantation, water access was restricted and was only available as reward on a linear track and ad libitum for 30 minutes at the end of each day. After mice reliably ran 50 trials in under an hour (~1 week daily training), free water access was restored for at least two days, and surgery was scheduled.
For a typical recording session, a one hour baseline recording was conducted in the mouse’s home cage (REST1), followed by a calibration of light intensity for optogenetic stimulation. Then mice ran 25–30 trials in a morning session (RUN1), followed by 1–4 hours of homecage recording (REST2) and another 25 trials in an afternoon/evening session (RUN2), followed by redelivery of the calibrating light pulses in the homecage and ad libitum water access. On Control sessions, the calibration pulses were given though no stimulation was delivered on the track.
To deliver optogenetic stimulation at a fixed location and running direction, an infrared sensor was placed at a random location on the track. Sensors were also placed at each end to control water delivery. An Arduino circuit detected beam breaks to activate solenoids to deliver water and to send a TTL pulse to a DAQ (CED Power 1401 Cambridge, UK) which delivered voltage control signals to the integrated μLEDs.
In every subject tested we noticed that there would be days in which mice would stop running past the unmarked stimulation site after stimulation and defecate despite being very familiar with the recording protocol. This occurred in 10–15% of recording sessions and these sessions were excluded. In the remaining sessions, mouse behavior did not appear to be affected by the stimulation (Figure 1).
Surgery
Mice were anesthetized with 1.5–2% isoflurane (2 L/min) and provided with a local anesthetic to the incision site (bupivicaine at .05 mg/kg, 2.5 mg/ml, S.C.). The skull was cleaned with saline and hydrogen peroxide and ground wires (bare stainless steel) were positioned intracranially over the cerebellum. The skull was then coated with Optibond (Kerr Dental, Brea, CA) and a craniotomy (~1.5 × 0.5 mm) was performed at AP −2.2, ML −2.0 (left hemisphere), 45° angle from the midline. The dura was removed and the probe was implanted ~0.5mm into the cortex. The probe and custom driver were cemented to the skull with C & B Metabond Quick Adhesive Cement (Parkell) and Unifast Trad acrylic (GC America). The craniotomy was capped with a mixture of mineral oil (one part) and dental wax (three parts), and a Faraday cage was constructed using copper mesh and connected to the cerebellar ground wire. Following surgery, an opioid analgesic was injected (Buprenex at 0.06 mg/kg, 0.015 mg/ml, IM) and given as needed for the next 1–3 days.
Recording and stimulation
Neural data was acquired using 32 site, 4-shank μLED probes (Wu et al., 2015); Neurolight, MI). Data were amplified and digitized at 30kHz with Intan amplifier boards (RHD2132/RHD2000 Evaluation System, Intan). μLEDs were controlled with voltage (2–3.5 V generating 1–20 μW of total light power) provided by a CED Power 1401 programmed with Spike2 (CED) which delivered light pulses (pre and post run) or 1s long sine waves (when the track IR beam was crossed). The animal’s position was monitored with a Basler camera (acA1300–60gmNIR, Graftek Imaging) sampling at 30Hz to detect head-mounted blue and red LEDs. Position was synchronized with neural data with TTLs signaling shutter position as well as a blinking LED (0.5 Hz) mounted 1 m above the maze.
Blue light (centered emission at 460 nm) was delivered on one or two μLEDs (always 1 μLED/shank, emission surface area = 150 μm2). To minimize artifact, the control voltage was held just under the forward voltage (2V). For calibrating light intensity, pulses (100ms, 1–1.5s variable inter-stimulus intervals) were delivered at 5 amplitudes (20 pulses/amplitude). The total radiant flux of the minimum pulse amplitude was typically around 1 – 5 μW, and the radiant flux of maximum amplitude, that was also used during track stimulation, was around 15–20 μW. This maximum intensity in the homecage was calibrated to be just subthreshold of a population oscillation, which was never observed on the track, likely since inhibitory tone is higher, as this highest stimulation level evoked a weaker response during the theta state (Figure S1). On the track, 1 s half sine waves were delivered when mice crossed an IR beam. Track stimulation only occurred in one running direction and, unless otherwise noted, was most frequently given for a block of 5 trials (see Supplemental Table 1).
QUANTIFICATION AND STATISTICAL ANALYSIS
Unit isolation
Spikes were extracted and classified using Kilosort (Pachitariu et al., 2016). Global principal components were calculated (three per channel,8 channels/shank) and spikes were extracted from the highpass filtered wideband signal (3rd order Butterworth filter, passband: 0.5 – 15kHz). Manual unit curation was done using Klusters. Spike sorting quality was assessed with L-Ratio (Schmitzer-Torbert et al., 2005), Isolation distance (Schmitzer-Torbert et al., 2005), inter-spike interval violation, and visual inspection of cross-correlations suggestive of erroneous splitting of single units.
Cell type classification
Spike waveform (width and asymmetry), autocorrelation properties, and mean firing rate (mean inter-spike interval) were used to classify neurons into excitatory cells and interneurons. The autocorrelation was parameterized with a double exponential model:
| 1 |
| 2 |
| 3 |
Units were defined by: rate, autocorrelation peak above baseline β1, spike width, and spike asymmetry. Then k-means clustering (k = 2) was performed on the z-score normalized feature matrix which separated excitatory cells from putative interneurons (including fast spiking and regular spiking interneurons). The validity of the cluster labels was confirmed through the cross-correlation (CCG) analysis, revealing increased synchrony at synaptic time-scales (see Synapsemble Analysis).
Ripple detection
The local field potential (LFP) was extracted by low-pass filtering the 30 kHz raw data (sinc filter with a 450 Hz cut-off band) and then downsampling to 1250 Hz. For ripple detection, the LFP was bandpass-filtered (3rd order Butterworth, passband: 130–200 Hz), squared, and z-score normalized. Events with peak power > 5 standard deviation (SD), sustained power > 2 SD, and duration between 30–200 ms were detected. When available, such events were also detected on a non-hippocampal, ‘noise’ channels and events common to both (e.g., EMG artifacts) were excluded. Stimulation periods were also excluded. Ripple onset was the first moment when the bandpassed signal increased >2 SD.
Ripple co-fluctuation Analysis
Ripple start and stop times were taken as the moments when ripple-band power rose above and fell below 2 SD of baseline. Rate per ripple was simply the number of spikes per neuron divided by the duration of the ripple event. Pairwise co-fluctuations were quantified through analysis of the Spearman correlation of ripple rates pre- (CorrPreRUN) and postRUN (CorrPostRUN). Multiple regression analyses were used to predict:
Post-RUN ripple correlations,
| 4 |
while accounting for pre-stimulation place fields
| 5 |
And preRUN ripple correlations,
| 6 |
while accounting for pre-stimulation place fields
| 7 |
Place Field Remapping Analysis
The two-dimensional location of the mouse was linearized by projecting actual position onto the straight line of the track. A Kalman filter (2nd order; locally quadratic) was used to derive a Bayesian MAP estimate of instantaneous speed and only moments with speed >1.5 cm/sec were considered for place field analysis. Position was binned (100 bins, each 1.2 cm) and the spike count and occupancy at each binned position was convolved with a Gaussian kernel (σ =5 spatial bins = 4.2 cm). Rate maps were calculated as the smoothed spike counts divided by the smoothed occupancy. Rate maps were calculated separately for inbound and outbound journeys and for each of four conditions: fpre_stim(x), fstim_trial(x), fpost_stim(x), fRUN2(x).
To calculate a trial-by-trial estimate of remapping, two methods were adopted. First, a statistical modelling approach was taken to assess the likelihood of the observed spike train derived from a Poisson process with a conditional intensity function defined by place field templates observed either before or after stimulation. The place maps were constructed from a training set of all trials except for the one for which the log-likelihood of the spike train was evaluated. The position x(t)at each moment during this test trial, and the place fields fpre_stim(x), fpost_stim(x) constructed from the training set were used to produce an estimated intensity at each time according to each place field template, fpre_stim(t) = fpre_stim(x(t)) and fpost_stim(t) = fpost_stim(x(t)). The log-likelihood of the spike train tswas calculated following Harris et al. (Harris et al., 2003), under two place field models:
| 8 |
| 9 |
Where ts is the time of each spike and .
The degree to which remapping occurred was quantified with the log-likelihood ratio normalized by the duration of the trial for the evaluated spike train T,
| 10 |
LLratio gives how much information is conveyed by the spike train about the post-stimulation rate map relative to the pre-stimulation rate map in bits per second. The cumulative sum of the LLratio without the normalization provides a running estimate of the total amount of information conveyed by the spike train with respect to one place field map or the other.
There were three classes of remapping neurons, those for which fields emerged, those for which fields disappeared, and those for which fields shifted. In all cases remapping neurons must have had average post-stim LLratio > 0.75 bit/sec. Shifting neurons must have had a spatial information score (Olypher et al., 2002) of more than 2 bits/spike for place fields before and after stimulation and the peak firing must have been at least 10cm apart; there was no rate threshold. For disappearing fields, the peak rate before stimulation must have been > 5 Hz and the peak rate after stimulation must have been < 5Hz with a pre-stim spatial information score >2 bits/spike. Similarly, for appearing fields, the peak rate after stimulation must have been > 5 Hz and the peak rate before stimulation must have been < 5Hz with a post-stim spatial information score > 2 bits/spike. Stable neurons were defined as those with an LLratio < 0.75 bit/sec, place field peaks that stayed within 10cm, and fields either before or after stimulation with >2bits/spike; no peak rate criteria were adopted. The main findings were robust against selection of spatial information score and LLratio, as well as for a correlation based remapping metric described below.
A second method to quantify remapping was also adopted that uses more standard correlation of place field templates. Here, two templates were calculated, one for place field maps prior to stimulation (premap) and another for post-stimulation place field maps (postmap). Both templates were correlated (Pearson’s correlation coefficient) with single trial rate maps (premap corr/postmap corr), always excluding the correlated trial from the data from which the template was defined (i.e. the premap template is derived from data from trials 2–10 when correlated with trial 1). The mean difference between the template matches prior to stimulation, Δcorr_prestim gives a measure for predictiveness of poststimulation spatial tuning in generating the prestimulation rate maps. The mean difference between the template matches post stimulation, Δcorr_poststim provides the converse measure, the predictability of prestimulation place field tuning for post stimulation activity. To avoid firing rate thresholds, we opted to include any place field map that showed trial-to-trial spatial reliability (mean premap corr. > 0.25 for trials before stimulation and mean postmap corr. > 0.25 for trials after stimulation). Trial-by-trial correlations were done in a similar manner where each trial’s firing rate map was correlated with each other and the rate of decorrelation (drift) was measured with or without intervening optogenetic simulation (Figure S4). Inhibitory cells were excluded from place field analyses.
Bayesian Decoding
Bayesian decoding was conducted following Zhang et al. (Zhang et al., 1998). The decoding time bin was 100 ms. Cross validation was accomplished by constructing place fields that excluded activity recorded on the trial for which position was estimated. Only sessions in which more than 20 pyramidal cells were simultaneously recorded were considered.
Predicting new field locations with RUSBoost
We adopted the RUSBoost binary classification algorithm (Seiffert et al., 2008) to predict whether neural activity observed at each location on the track was recorded in the future place location. RUSBoost is designed to handle the class imbalance problem in data with discrete class labels, which we faced, as we defined latent place field locations as 10 cm segments of the track centered on the post-stim place field peak. The RUSBoost algorithm uses a combination of RUS (random under-sampling) and the standard boosting procedure AdaBoost, to better model the minority class by removing majority class samples. RUSBoost was implemented with MATLAB 2020a’s fitcensemble algorithm to create 100 classification trees (without shrinkage) from the training set. The learned mapping was then used to predict whether withheld data was recorded in a future place field or not. The features that defined a location were the cell’s single-pass firing rate as observed for each 10 cm segment of the track, and the proportion of spikes observed in a burst. Ten random 50/50 splits of the pre-stimulation data were performed for the cross validation and the reported hit and false positive rates reflect the mean across independent cross-validations. A control bootstrap distribution was generated by shuffling the position labels for the held-out data (100 shuffles). The positive likelihood ratio (hits divided by false alarms) was used to compare whether neurons did better than the bootstrap distribution (> 95% bootstrap) and whether bursts or firing rates were more predictive.
Peer prediction Analysis
To predict the activity of one target cell from the population of peer cells, we used the generalized linear model approach of Harris et al. (Harris et al., 2003). Spike trains of the target and peers were binned with different resolutions (20 bin widths, logarithmically spaced from 5–5000 ms). Ten-fold cross validation was used to build a training set with 90% of the data and a test set with the remaining 10%. The predicted intensity at a time t was given by
| 11 |
The link function g(η) was defined as
| 12 |
The prediction weights wα were chosen to maximize the regularized log-likelihood on the training set:
| 13 |
Where nt is the number of spikes observed in that time bin.
The minimization was carried out using MATLAB 2018b’s fmincon function using the default Interior Point Algorithm and upper and lower weight bound of ±100.
Synapsemble Analysis
A wealth of in-vitro data suggests that the strength of synaptic coupling (e.g., magnitude of the evoked PSP) changes following different pairing protocols. Our goal was to capture related changes in our dataset by estimating long-term changes in spike transmission between monosynaptically connected pyramidal cells and interneurons (as defined by (English et al., 2017); Figure S4). In order to do this, we model the postsynaptic spike train using a generalized linear model (GLM) with the following two features: (1) a coarsened, slowly-evolving version of the postsynaptic rate (baseline term) and (2) a transient boost following the presynaptic spike whose magnitude varies with time on a long timescale (coupling term). The features are summed and passed through an exponential nonlinearity to yield the instantaneous postsynaptic rate λpost(t). The exponentiated coupling term can therefore be interpreted as a multiplicative, presynaptically-induced gain acting on an otherwise slowly evolving postsynaptic rate (the exponentiated baseline term). This separation of timescales assumption conveniently dodges the issue of capturing all parameters modulating the postsynaptic rate (e.g., theta, behavioral state). The conditional intensity function takes the following form:
| 14 |
where Pre and Post are the pre- and postsynaptic spike trains binned at dt = 0.8 ms, ensuring that each bin has at most one spike. Δ is the mode time lag between the pre- and postsynaptic spikes estimated from the raw CCG. C(Post) is the coarsened baseline rate obtained by counting postsynaptic spikes in 15 ms wide bins, expressing these as rates, and linearly interpolating at times corresponding to the centers of the dt-sized bins that were used to bin spikes. Note that in the absence of a presynaptic spike immediately preceding t (i.e., Pre(t − Δ) = 0), the predicted rate is equal to C(Post(t)). We model the slow changes in synaptic coupling Xc • k with a linear combination of cubic B-splines with equally spaced knots 8. For each pair of neurons, the spacing of the knots (every 400 – 1000 seconds, in increments of 100) is selected by cross-validation using 100 second even/odd data splits. More specifically, the data are divided into 100 second data segments, such that odd segments are used for training, and even segments for testing. Because the parameters k are only constrained when Pre(t − Δ) = 1, we fit the model in these bins exclusively. We use an LBFGS algorithm to minimize the convex negative log-likelihood with analytically computed gradients.
In order to explore the specific dynamics that govern changes in spike transmission, we made use of an extended GLM in which the coupling term takes the form of a dynamical model for short-term plasticity (Ghanbari et al., 2020; Tsodyks and Markram, 1997):
| 15 |
where λpost(ti + Δ) is the postsynaptic rate at monosynaptic lag Δ following the i-th presynaptic spike. At all other times, λpost = C(Post). A is the constant coupling strength, and wi is a scale factor that depends on the history of presynaptic spiking through the Tsodyks-Markram (TM) model (Tsodyks and Markram, 1997), a nonlinear dynamical system to capture short term plasticity:
| 16 |
| 17 |
| 18 |
R captures the dynamics of presynaptic resources whose recovery time course, set by timescale τd, determines the degree of short-term depression. u describes the utilization of resources that describe short-term facilitation through its timescale of decay τf, magnitude of facilitation f, and presynaptic release probability U. For each PYR-INT pair, we fit the most parsimonious model by comparing the Akaike information criterion of the following candidate models: no plasticity (w = 1), depression only (τf = 0, f = U), facilitation (τd = 0, f = U), 3-parameter TM (f = U), and the full model. For details of the optimization procedure, see (Ghanbari et al., 2020).
For each model (long- and short-term coupling), the instantaneous spike transmission – i.e., postsynaptic rate injected by a presynaptic spike – was estimated by taking the difference between the coarsened postsynaptic rate and that predicted by the full model:
| 19 |
In order to obtain a smoothly varying estimate of spike transmission (i.e., even at times when the presynaptic neuron is not spiking), λdiff was convolved using a Gaussian kernel with a standard deviation of 120 seconds. In order to get a bin-by-bin estimate of spike transmission (in Hz) per presynaptic spike, we normalized the resulting time series by the presynaptic spike train convolved in the same manner.
In order to find ensembles reflecting higher order coactivations among the spike transmission time series (i.e., synapsembles), we performed an unsupervised statistical analysis based on ICA (Lopes-dos-Santos et al., 2013; Peyrache et al., 2009; van de Ven et al., 2016). Briefly, spike transmission time series were represented as a matrix z, which was z-scored and downsampled to 10 Hz. The number of synapsembles in each session was based on the N principal components of the correlation matrix whose variances exceeded an analytical threshold based on the Marcenko-Pastur distribution describing variances expected for uncorrelated data. The high-dimensional activity matrix was projected onto the subspace spanned by these N principal components, and ICA was performed to extract synapsembles (each corresponds to an independent component). The expression strength of each synapsemble was computed as,
| 20 |
where Pi is the projection matrix (outer product, diagonal set to zero) of the i-th independent component. As such, A(t) quantifies the moment-to-moment similarity between an independent component (synapsemble template) and the instantaneous spike transmission pattern across all PYR-INT pairs.
In order to quantify synapsemble rearrangements across a relevant time point T, we defined the change in synapsemble expression as the difference between mean expression strength around T. For stimulation sessions, T was the first stimulation event on the track, while for controls, we selected the halfway point of the track running session. In each case, differences in mean expression strengths were based on time intervals that included entire homecage periods flanking the track period. Synapsembles were detected either in the period before or following T. A negative value for the change in expression strength reflects that the synapsemble is re-expressed less prominently following T (if it was detected prior) or before T (if it was detected after).
This analysis pipeline was also conducted for ensembles of presynaptic pyramidal neurons (PYR ensembles) or postsynaptic interneurons (INT ensembles). For each session, spike trains of neurons that figured in PYR-INT connections were binned at dt = 0.8 ms, and convolved with a Gaussian whose full-width at half maximum matched the timescale of the corresponding spike transmission time series as estimated from cross-validation in the long-term model. The resulting firing rate time series were z-scored, and the above described ensemble analysis was performed to estimate changes in rate ensembles around T.
GFP Control
Two adult male Tg(Camk2α-cre)T29–1Stl mice (The Jackson Laboratory; #005359; (Tsien et al., 1996) were anesthetized and injected with a Cre-dependent adeno-associated virus (AAV) expressing EYFP (Addgene viral prep # 27056-AAV5; http://n2t.net/addgene:27056; RRID:Addgene_27056) delivered through a glass pipette (Sutter Instruments). Injections targeted right dorsal CA1 (−2 mm AP, 1.7 mm ML w.r.t bregma; 1.2 mm depth), and 300 nL of AAV-Ef1a-DIO EYFP (titer ≥ 1×1013 vg/mL) was injected at a flow rate of 50 nl/min (World Precision Instruments, UMP3 UltraMicroPump). Three weeks following virus injection, animals were re-anesthetized for head plate implantation. The skull was exposed, and a custom designed 3D printed head plate was attached with C & B Metabond Quick Adhesive Cement (Parkell). A single steel screw was implanted over the cerebellum as ground and reference. Lastly, a craniotomy was drilled over the site of the virus injection, and sealed with silicone adhesive (World Precision Instruments, Kwik-Sil) until the day of recording.
Over the course of one week, mice were habituated to head fixation while running on a custom designed running wheel. On the day of recording, Kwik-Sil was removed to expose the craniotomy, and a μLED-equipped silicon probe was slowly lowered into the brain until sharp-wave ripples were detectable on all four shanks. Following 10–20 minutes, a 1h recording session was performed, during which light was delivered, one μLED at a time, to shanks with high single unit activity. 100ms square pulses with 1s inter-pulse intervals with 5 driving currents chosen to span the full range of light intensities used in mice expressing ChR2. μLEDs were driven using an open-source μLED current controller (https://github.com/YoonGroupUmich/osc1lite). Following the acute experiment, mice were perfused as described, and EYFP expression was verified using light microscopy (Olympus).
Effect size estimates
We follow the recommendation of (Calin-Jageman and Cumming, 2019) and the methods developed by Kruschke (Kruschke, 2013) to report effect sizes. We include an additional Bayesian statistical test for each comparison and report the highest density interval (HDI) of the effect size that lies outside of zero. For comparisons with underlying skewed distributions, we model the data, y, as having derived from a skewed, non-centered Student’s t-distribution.
In JAGS notation:
| 21 |
Where,
| 22 |
| 23 |
| 24 |
The choice of tau, mu, and df that best fits the data is found through Markov Chain Monte Carlo (MCMC) with weakly informed priors as in (Kruschke, 2013). Inter-subject differences were modeled by fitting means that were a linear combination of effects driven by random-effects for individual mice, muMOUSE, and the condition-specific effect of interest muCOND (e.g. COND = stim vs Control).
For normal data, a similar approach was taken, though assuming
| 25 |
The distribution of credible parameters was identified for each group under comparison and the effect size calculated with three MCMC chains, 1000 burn-in steps and five thinning steps (to avoid auto-correlations in the Markov process).
Supplementary Material
KEY RESOURCES TABLE.
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Chemicals, Peptides, and Recombinant Proteins | ||
| Dental Adhesive | Kerr Dental | Optibond |
| Dental Resin | Dentsply | Triad-Gel |
| Experimental Models: Organisms/Strains | ||
| CaMKII-Cre mice | https://www.jax.org | 005359; RRID: IMSR_JAX:005359 |
| Ai32 Mice | https://www.jax.org | 012569; RRID: IMSR_JAX:012569 |
| AAV-Ef1a-DIO EYFP | https://www.addgene.org/27056/ | 27056-AAV5; RRID:Addgene_27056 |
| Software and Algorithms | ||
| MATLAB 2018b | MathWorks | http://www.mathworks.com |
| Klustakwik | (Harris et al., 2000) | http://klustakwik.sourceforge.net/ |
| Kilosort | (Pachitariu et al., 2016) | https://github.com/cortex-lab/KiloSort |
| Neurosuite | (Hazan et al., 2006) | http://neurosuite.sourceforge.net |
| FMA Toolbox | Michael Zugaro, College de France | http://fmatoolbox.sourceforge.net |
| Recording and online analysis software | Cambridge Electronic Design | Spike2 |
| Recording software | Intan Technologies | http://intantech.com/ |
| Other | ||
| μLED Silicon Probes | (Wu et al., 2015); NeuroLight/Plexon | N/A |
| RHD2000 USB Interface Board | Intan Technologies | C3100 |
| 32 Channel Digital Amplifier | Intan Technologies | C3314 |
| Power1401 Microprocessor | Cambridge Electronic Design | Power1401-A3 |
Highlights.
μLED optogenetic stimulation induces remapping in CA1 neurons
Stimulated and non-stimulated neurons show comparable place field reorganization
Fields emerge in places with weak pre-existing drive, not at site of depolarization
Stimulation changes coupling between pyramidal cells and neighboring interneurons
Acknowledgements
We would like to thank Zachery Saccomano, Abed Ghanbari, for providing software used in the present study and Yunchang Zhang and Sinan Kokuuslu for their help with data collection. We would like to thank Manuel Valero, Thomas Hainmueller, Antonio Fernandez-Ruiz, and Shy Shoham for useful feedback on the manuscript prior to publication. This work was supported by NIMH K99MH118423, NIMH R00MH118423, NIH MH 122391, NSF PIRE grant (#1545858), U19 NS107616 and U19 NS104590.
Footnotes
Declaration of Interests
The authors declare no competing interests.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Alme CB, Miao C, Jezek K, Treves A, Moser EI, and Moser M-B (2014). Place cells in the hippocampus: Eleven maps for eleven rooms. Proceedings of the National Academy of Sciences 111, 201421056–201421056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Battaglia FP, Sutherland GR, Cowen SL, Mc Naughton BL, and Harris KD (2005). Firing rate modulation: a simple statistical view of memory trace reactivation. Neural Netw 18, 1280–1291. [DOI] [PubMed] [Google Scholar]
- Bittner KC, Grienberger C, Vaidya SP, Milstein AD, Macklin JJ, Suh J, Tonegawa S, and Magee JC (2015). Conjunctive input processing drives feature selectivity in hippocampal CA1 neurons. Nature Neuroscience 18, 1133–1142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bittner KC, Milstein AD, Grienberger C, Romani S, and Magee JC (2017). Behavioral time scale synaptic plasticity underlies CA1 place fields. Science 357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bladon JH, Sheehan DJ, De Freitas CS, and Howard MW (2019). In a Temporally Segmented Experience Hippocampal Neurons Represent Temporally Drifting Context But Not Discrete Segments. J Neurosci 39, 6936–6952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bright IM, Meister MLR, Cruzado NA, Tiganj Z, Buffalo EA, and Howard MW (2020). A temporal record of the past with a spectrum of time constants in the monkey entorhinal cortex. Proc Natl Acad Sci U S A 117, 20274–20283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buzsaki G (2015). Hippocampal sharp wave-ripple: A cognitive biomarker for episodic memory and planning. Hippocampus 25, 1073–1188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buzsaki G (2010). Neural syntax: cell assemblies, synapsembles, and readers. Neuron 68, 362–385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buzsaki G, and Eidelberg E (1982). Direct afferent excitation and long-term potentiation of hippocampal interneurons. Journal of Neurophysiology 48, 597–607. [DOI] [PubMed] [Google Scholar]
- Buzsaki G, and Tingley D (2018). Space and Time: The Hippocampus as a Sequence Generator. Trends Cogn Sci 22, 853–869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cai DJ, Aharoni D, Shuman T, Shobe J, Biane J, Song W, Wei B, Veshkini M, La-Vu M, Lou J, et al. (2016). A shared neural ensemble links distinct contextual memories encoded close in time. Nature 534, 115–118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calin-Jageman RJ, and Cumming G (2019). Estimation for Better Inference in Neuroscience. eNeuro 6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carrillo-Reid L, Yang W, Bando Y, Peterka DS, and Yuste R (2016). Imprinting and recalling cortical ensembles. Science 353, 691–694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen JD, Bolstad M, and Lee AK (2017). Experience-dependent shaping of hippocampal CA1 intracellular activity in novel and familiar environments. Elife 6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Csicsvari J, Hirase H, Czurko A, and Buzsaki G (1998). Reliability and state dependence of pyramidal cell-interneuron synapses in the hippocampus: an ensemble approach in the behaving rat. Neuron 21, 179–189. [DOI] [PubMed] [Google Scholar]
- Diamantaki M, Coletta S, Nasr K, Zeraati R, Laturnus S, Berens P, Preston-Ferrer P, and Burgalossi A (2018). Manipulating Hippocampal Place Cell Activity by Single-Cell Stimulation in Freely Moving Mice. Cell Rep 23, 32–38. [DOI] [PubMed] [Google Scholar]
- Diamantaki M, Frey M, Preston-Ferrer P, and Burgalossi A (2016). Priming Spatial Activity by Single-Cell Stimulation in the Dentate Gyrus of Freely Moving Rats. Curr Biol 26, 536–541. [DOI] [PubMed] [Google Scholar]
- Dragoi G, Harris KD, and Buzsaki G (2003). Place representation within hippocampal networks is modified by long-term potentiation. Neuron 39, 843–853. [DOI] [PubMed] [Google Scholar]
- Dragoi G, and Tonegawa S (2011). Preplay of future place cell sequences by hippocampal cellular assemblies. Nature 469, 397–401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dupret D, O’Neill J, and Csicsvari J (2013). Dynamic reconfiguration of hippocampal interneuron circuits during spatial learning. Neuron 78, 166–180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edelman GM (1993). Neural Darwinism - Selection and Reentrant Signaling in Higher Brain-Function. Neuron 10, 115–125. [DOI] [PubMed] [Google Scholar]
- English DF, McKenzie S, Evans T, Kim K, Yoon E, and Buzsaki G (2017). Pyramidal Cell-Interneuron Circuit Architecture and Dynamics in Hippocampal Networks. Neuron 96, 505–520 e507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farooq U, and Dragoi G (2019). Emergence of preconfigured and plastic time-compressed sequences in early postnatal development. Science 363, 168–173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farooq U, Sibille J, Liu K, and Dragoi G (2019). Strengthened Temporal Coordination within Pre-existing Sequential Cell Assemblies Supports Trajectory Replay. Neuron 103, 719–733 e717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frank LM (2004). Hippocampal Plasticity across Multiple Days of Exposure to Novel Environments. Journal of Neuroscience 24, 7681–7689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fujisawa S, Amarasingham A, Harrison MT, and Buzsaki G (2008). Behavior-dependent short-term assembly dynamics in the medial prefrontal cortex. Nature Neuroscience 11, 823–833. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galarreta M, and Hestrin S (2001). Spike transmission and synchrony detection in networks of GABAergic interneurons. Science 292, 2295–2299. [DOI] [PubMed] [Google Scholar]
- Ghanbari A, Ren N, Keine C, Stoelzel C, Englitz B, Swadlow HA, and Stevenson IH (2020). Modeling the Short-Term Dynamics of in Vivo Excitatory Spike Transmission. J Neurosci 40, 4185–4202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golub MD, Sadtler PT, Oby ER, Quick KM, Ryu SI, Tyler-Kabara EC, Batista AP, Chase SM, and Yu BM (2018). Learning by neural reassociation. Nat Neurosci 21, 607–616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grienberger C, Milstein AD, Bittner KC, Romani S, and Magee JC (2017). Inhibitory suppression of heterogeneously tuned excitation enhances spatial coding in CA1 place cells. Nature neuroscience 20, 417–426. [DOI] [PubMed] [Google Scholar]
- Grosmark AD, and Buzsaki G (2016). Diversity in neural firing dynamics supports both rigid and learned hippocampal sequences. Science 351, 1440–1443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo W, Zhang J, Newman J, and Wilson M (2020). Latent learning drives sleep-dependent plasticity in distinct CA1 subpopulations. bioRxiv [Google Scholar]
- Harris KD, Csicsvari J, Hirase H, and Dragoi G (2003). Organization of cell assemblies in the hippocampus. Nature 424, 552–556. [DOI] [PubMed] [Google Scholar]
- Harris KD, Henze DA, Csicsvari J, Hirase H, and Buzsaki G (2000). Accuracy of tetrode spike separation as determined by simultaneous intracellular and extracellular measurements. J Neurophysiol 84, 401–414. [DOI] [PubMed] [Google Scholar]
- Hasselmo ME, and Wyble BP (1997). Free recall and recognition in a network model of the hippocampus: simulating effects of scopolamine on human memory function. Behavioural Brain Research 89, 1–34. [DOI] [PubMed] [Google Scholar]
- Hazan L, Zugaro M, and Buzsaki G (2006). Klusters, NeuroScope, NDManager: a free software suite for neurophysiological data processing and visualization. J Neurosci Methods 155, 207–216. [DOI] [PubMed] [Google Scholar]
- Hopfield JJ (1982). Neural networks and physical systems with emergent collective computational abilities. Proceedings of the National Academy of Sciences of the United States of America 79, 2554–2558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Isaac JTR, Buchanan KA, Muller RU, and Mellor JR (2009). Hippocampal place cell firing patterns can induce long-term synaptic plasticity in vitro. The Journal of neuroscience : the official journal of the Society for Neuroscience 29, 6840–6850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jackson J, and Redish AD (2007). Network dynamics of hippocampal cell-assemblies resemble multiple spatial maps within single tasks. Hippocampus 17, 1209–1229. [DOI] [PubMed] [Google Scholar]
- Jezek K, Henriksen EJ, Treves A, Moser EI, and Moser M-B (2011). Theta-paced flickering between place-cell maps in the hippocampus. Nature 478, 246–249. [DOI] [PubMed] [Google Scholar]
- Jouhanneau JS, Kremkow J, and Poulet JFA (2018). Single synaptic inputs drive high-precision action potentials in parvalbumin expressing GABA-ergic cortical neurons in vivo. Nat Commun 9, 1540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelemen E, and Fenton AA (2010). Dynamic grouping of hippocampal neural activity during cognitive control of two spatial frames. PLoS Biology 8, e1000403–e1000403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kruschke JK (2013). Bayesian estimation supersedes the t test. J Exp Psychol Gen 142, 573–603. [DOI] [PubMed] [Google Scholar]
- Kullmann DM, and Lamsa KP (2011). LTP and LTD in cortical GABAergic interneurons: Emerging rules and roles. Neuropharmacology 60, 712–719. [DOI] [PubMed] [Google Scholar]
- Kumaran D, and McClelland JL (2012). Generalization through the recurrent interaction of episodic memories: a model of the hippocampal system. Psychological Review 119, 573–616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lau PY-P, Katona L, Saghy P, Newton K, Somogyi P, and Lamsa KP (2017). Long-term plasticity in identified hippocampal GABAergic interneurons in the CA1 area in vivo. Brain Structure and Function 222, 1809–1827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le Roux N, Cabezas C, Böhm UL, and Poncer JC (2013). Input-specific learning rules at excitatory synapses onto hippocampal parvalbumin-expressing interneurons. The Journal of Physiology 591, 1809–1822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee D, Lin BJ, and Lee AK (2012). Hippocampal Place Fields Emerge upon Single-Cell Manipulation of Excitability During Behavior. Science 337, 849–853. [DOI] [PubMed] [Google Scholar]
- Leutgeb S, Leutgeb JK, Barnes CA, Moser EI, McNaughton BL, and Moser M-B (2005). Independent codes for spatial and episodic memory in hippocampal neuronal ensembles. Science 309, 619–623. [DOI] [PubMed] [Google Scholar]
- Li Y, Lu H, Cheng PL, Ge S, Xu H, Shi SH, and Dan Y (2012). Clonally related visual cortical neurons show similar stimulus feature selectivity. Nature 486, 118–121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu X, Ramirez S, and Tonegawa S (2014). Inception of a false memory by optogenetic manipulation of a hippocampal memory engram. Philosophical Transactions of the Royal Society of London Series B, Biological sciences 369, 20130142–20130142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lopes-dos-Santos V, Ribeiro S, and Tort AB (2013). Detecting cell assemblies in large neuronal populations. J Neurosci Methods 220, 149–166. [DOI] [PubMed] [Google Scholar]
- Lovett-Barron M, Turi GF, Kaifosh P, Lee PH, Bolze F, Sun X-H, Nicoud J-F, Zemelman BV, Sternson SM, and Losonczy A (2012). Regulation of neuronal input transformations by tunable dendritic inhibition. Nature Neuroscience 15, 423–430. [DOI] [PubMed] [Google Scholar]
- Lu JT, Li CY, Zhao JP, Poo MM, and Zhang XH (2007). Spike-timing-dependent plasticity of neocortical excitatory synapses on inhibitory interneurons depends on target cell type. J Neurosci 27, 9711–9720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luczak A, Bartho P, and Harris KD (2009). Spontaneous events outline the realm of possible sensory responses in neocortical populations. Neuron 62, 413–425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mankin EA, Sparks FT, Slayyeh B, Sutherland RJ, Leutgeb S, and Leutgeb JK (2012). Neuronal code for extended time in the hippocampus. Proceedings of the National Academy of Sciences of the United States of America 109, 19462–19467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McClain K, Tingley D, Heeger DJ, and Buzsaki G (2019). Position-theta-phase model of hippocampal place cell activity applied to quantification of running speed modulation of firing rate. Proc Natl Acad Sci U S A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McClelland JL (2013). Incorporating rapid neocortical learning of new schema-consistent information into complementary learning systems theory. Journal of Experimental Psychology General 142, 1190–1210. [DOI] [PubMed] [Google Scholar]
- McKenzie S, Frank AJ, Kinsky NR, Porter B, Riviere PD, and Eichenbaum H (2014). Hippocampal Representation of Related and Opposing Memories Develop within Distinct, Hierarchically Organized Neural Schemas. Neuron 83, 202–215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McNaughton BL, and Nadel L (1990). Hebb-Marr networks and the neurobiological representation of action in space. In, Gluck M, and David Rumelhart, eds. (Hillsdale, NJ: Lawrence Erlbaum Associates, Inc; ), pp. 1–63. [Google Scholar]
- Milstein AD, Li Y, Bittner K, Grienberger C, Soltesz I, Magee J, and Romani S (2020). Bidirectional synaptic plasticity rapidly modifies hippocampal representations independent of correlated activity. bioRxiv [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mizuseki K, and Buzsaki G (2013). Preconfigured, skewed distribution of firing rates in the hippocampus and entorhinal cortex. Cell Rep 4, 1010–1021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monaco JD, Rao G, Roth ED, and Knierim JJ (2014). Attentive scanning behavior drives one-trial potentiation of hippocampal place fields. Nature neuroscience 17, 725–731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nissen W, Szabo A, Somogyi J, Somogyi P, and Lamsa KP (2010). Cell Type-Specific Long-Term Plasticity at Glutamatergic Synapses onto Hippocampal Interneurons Expressing either Parvalbumin or CB1 Cannabinoid Receptor. Journal of Neuroscience 30, 1337–1347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olypher AV, Lansky P, and Fenton AA (2002). Properties of the extra-positional signal in hippocampal place cell discharge derived from the overdispersion in location-specific firing. Neuroscience 111, 553–566. [DOI] [PubMed] [Google Scholar]
- Pachitariu M, Steinmetz N, Kadir S, Carandini M, and Kenneth H (2016). Kilosort: realtime spike-sorting for extracellular electrophysiology with hundreds of channels. bioRxiv. [Google Scholar]
- Peyrache A, Khamassi M, Benchenane K, Wiener SI, and Battaglia FP (2009). Replay of rule-learning related neural patterns in the prefrontal cortex during sleep. Nat Neurosci 12, 919–926. [DOI] [PubMed] [Google Scholar]
- Rickgauer JP, Deisseroth K, and Tank DW (2014). Simultaneous cellular-resolution optical perturbation and imaging of place cell firing fields. Nat Neurosci 17, 1816–1824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rolls ET (1990). Theoretical and neurophysiological analysis of the functions of the primate hippocampus in memory. Cold Spring Harbor Symposia on Quantitative Biology 55, 995–1006. [DOI] [PubMed] [Google Scholar]
- Robinson NTM, Descamps LAL, Russell LE, Buchholz MO, Bicknell BA, Antonov GK, Lau JYN, Nutbrown R, Schmidt-Hieber C, and Hausser M (2020). Targeted Activation of Hippocampal Place Cells Drives Memory-Guided Spatial Behavior. Cell. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Samsonovich A, and McNaughton BL (1997). Path integration and cognitive mapping in a continuous attractor neural network model. The Journal of Neuroscience 17, 5900–5920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanders H, Wilson MA, and Gershman SJ (2020). Hippocampal remapping as hidden state inference. Elife 9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmitzer-Torbert N, Jackson J, Henze D, Harris K, and Redish AD (2005). Quantitative measures of cluster quality for use in extracellular recordings. Neuroscience 131, 1–11. [DOI] [PubMed] [Google Scholar]
- Schoenenberger P, O’Neill J, and Csicsvari J (2016). Activity-dependent plasticity of hippocampal place maps. Nat Commun 7, 11824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seiffert C, Khoshgoftaar T, Van Hulse J, and Napolitano A (2008). RUSBoost: Improving Classification Performance when Training Data is Skewed. 19th International Conference on Pattern Recognition IEEE, 1–4. [Google Scholar]
- Sheffield MEJ, Adoff MD, and Dombeck DA (2017). Increased Prevalence of Calcium Transients across the Dendritic Arbor during Place Field Formation. Neuron 96, 490–504 e495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stark E, Koos T, and Buzsaki G (2012). Diode probes for spatiotemporal optical control of multiple neurons in freely moving animals. Journal of Neurophysiology 108, 349–363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stark E, Roux L, Eichler R, and Buzsaki G (2015). Local generation of multineuronal spike sequences in the hippocampal CA1 region. Proc Natl Acad Sci U S A 112, 10521–10526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanaka, Kazumasa Z, Pevzner A, Hamidi, Anahita B, Nakazawa Y, Graham J, and Wiltgen, Brian J (2014). Cortical Representations Are Reinstated by the Hippocampus during Memory Retrieval, pp. 347–354. [DOI] [PubMed] [Google Scholar]
- Tayler KK, Tanaka KZ, Reijmers LG, and Wiltgen BJ (2013). Reactivation of neural ensembles during the retrieval of recent and remote memory. Current Biology 23, 99–106. [DOI] [PubMed] [Google Scholar]
- Teyler TJ, and DiScenna P (1986). The hippocampal memory indexing theory. Behav Neurosci 100, 147–154. [DOI] [PubMed] [Google Scholar]
- Trouche S, Perestenko PV, van de Ven GM, Bratley CT, McNamara CG, Campo-Urriza N, Black SL, Reijmers LG, and Dupret D (2016). Recoding a cocaine-place memory engram to a neutral engram in the hippocampus. Nature Neuroscience 19, 564–567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tse D, Langston RF, Kakeyama M, Bethus I, Spooner PA, Wood ER, Witter MP, and Morris RGM (2007). Schemas and memory consolidation. Science 316, 76–82. [DOI] [PubMed] [Google Scholar]
- Tsien JZ, Chen DF, Gerber D, Tom C, Mercer EH, Anderson DJ, Mayford M, Kandel ER, and Tonegawa S (1996). Subregion- and cell type-restricted gene knockout in mouse brain. Cell 87, 1317–1326. [DOI] [PubMed] [Google Scholar]
- Tsodyks MV, and Markram H (1997). The neural code between neocortical pyramidal neurons depends on neurotransmitter release probability. Proc Natl Acad Sci U S A 94, 719–723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van de Ven GM, Trouche S, McNamara CG, Allen K, and Dupret D (2016). Hippocampal Offline Reactivation Consolidates Recently Formed Cell Assembly Patterns during Sharp Wave-Ripples. Neuron 92, 968–974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Villette V, Malvache A, Tressard T, Dupuy N, and Cossart R (2015). Internally Recurring Hippocampal Sequences as a Population Template of Spatiotemporal Information. Neuron 88, 357–366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu F, Stark E, Ku P-C, Wise, Kensall D, Buzsaki G, and Yoon E (2015). Monolithically Integrated μLEDs on Silicon Neural Probes for High-Resolution Optogenetic Studies in Behaving Animals. Neuron 88, 1136–1148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu HT, Han Z, Gao P, He S, Li Z, Shi W, Kodish O, Shao W, Brown KN, Huang K, et al. (2014). Distinct lineage-dependent structural and functional organization of the hippocampus. Cell 157, 1552–1564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang K, Ginzburg I, McNaughton BL, and Sejnowski TJ (1998). Interpreting neuronal population activity by reconstruction: unified framework with application to hippocampal place cells. Journal of Neurophysiology 79, 1017–1044. [DOI] [PubMed] [Google Scholar]
- Ziv Y, Burns LD, Cocker ED, Hamel EO, Ghosh KK, Kitch LJ, El Gamal A, and Schnitzer MJ (2013). Long-term dynamics of CA1 hippocampal place codes. Nature Neuroscience 16, 264–266. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The datasets generated during the current study are available in the Buzsaki lab repository, https://buzsakilab.nyumc.org/datasets/McKenzieS/.
Custom lab software is available at https://github.com/buzsakilab/buzcode and MATLAB scripts for the current project will be made available upon reasonable request.