Effects of Accounting for Interval-Censored Antibody Titer Decay on Seroincidence in a Longitudinal Cohort Study of Leptospirosis

Abstract

Accurate measurements of seroincidence are critical for infections undercounted by reported cases, such as influenza, arboviral diseases, and leptospirosis. However, conventional methods of interpreting paired serological samples do not account for antibody titer decay, resulting in underestimated seroincidence rates. To improve interpretation of paired sera, we modeled exponential decay of interval-censored microscopic agglutination test titers using a historical data set of leptospirosis cases traced to a point source exposure in Italy in 1984. We then applied that decay rate to a longitudinal cohort study conducted in a high-transmission setting in Salvador, Brazil (2013–2015). We estimated a decay constant of 0.926 (95% confidence interval: 0.918, 0.934) titer dilutions per month. Accounting for decay in the cohort increased the mean infection rate to 1.21 times the conventionally defined rate over 6-month intervals (range, 1.10–1.36) and 1.82 times that rate over 12-month intervals (range, 1.65–2.07). Improved estimates of infection in longitudinal data have broad epidemiologic implications, including comparing studies with different sampling intervals, improving sample size estimation, and determining risk factors for infection and the role of acquired immunity. Our method of estimating and accounting for titer decay is generalizable to other infections defined using interval-censored serological assays.

Abbreviations

MAT

microscopic agglutination test

Infections with a high proportion of asymptomatic, mild, or misdiagnosed cases are not accurately represented by reported cases and require serological investigation (1). For example, patients with fevers of acute onset and/or unknown origin are often preliminarily diagnosed with well-recognized, highly endemic pathogens based on clinical presentation. However, when samples are subjected to serological analysis, lesser-known or emerging infections can account for many of these illnesses (2–6). Incidence rates are a crucial epidemiologic tool for investigation of an infection’s burden, transmission dynamics, and trends, all of which guide public health interventions. It is therefore critical that paired serology be used to produce accurate incidence rates for these underreported infections, such as hantavirus, rickettsial disease, leptospirosis, and influenza, dengue, and Zika viruses (1–7).

Paired serology defines infections based on 2 samples from an individual (1). It is commonly used in longitudinal cohort studies. To conduct paired serology, 2 serum samples are obtained from an individual at different times. These samples are then subjected to a serological test, and the test values are compared to determine whether there is evidence that an infection has occurred. By long-standing convention, recent infections are defined according to 2 definitions: a seroconversion or a 4-fold rise in antibody titer (1). A seroconversion is defined when an individual with an initial antibody response below the test threshold has a positive result in the second. A 4-fold rise is defined when an individual has an initial response above the detection threshold and a second result at least 4 times the first (for example, a titer of 50 followed by one of 200). This 4-fold rise is equivalent to a 2-dilution change in a serial dilution test. The 4-fold rise criterion stems from the variability in the performance and interpretation of serological assays, which implies that a 2-fold rise (a single dilution change) could represent measurement error, not infection (1). In longitudinal studies, these definitions are applied irrespective of the interval between samples.

Antibody decay is a known phenomenon (8–10) that would be expected to occur in the interval between samples but is not accounted for by conventional interpretations of paired sera; as a result, they might underestimate infection rates when applied to studies with long intersample intervals. Failing to account for the decay in an individual’s antibody levels after the initial sample is taken means that the second sample is compared with an artificially high baseline value when applying the seroconversion or 4-fold rise criteria. This decreases the likelihood that an infection will be declared. It has been demonstrated that the conventional interpretations underestimate infections at the population level (1, 11), and some authors have suggested using a 2-fold rise in titer to define infections when estimating population-level attack rates (1, 11). However, this does not address individual-level measurement error and could therefore overestimate infection rates.

Interpretation of paired serology can be further complicated by 2 features shared by a number of pathogens. The first is the use of interval-censored serological assays, such as the hemagglutination-inhibition assay used for influenza diagnostics (1) or the dengue plaque reduction neutralization test (12). These tests do not produce a continuous numeric result but instead indicate an interval into which a sample’s titer falls. The second is the potential for reexposure in longitudinal cohorts. Reexposure can boost titers, masking titer decay. One method of handling this is to model longitudinal data allowing for both infection and titer decay simultaneously (8, 9, 11, 13, 14), but the 2 processes can be statistically unidentifiable, preventing accurate estimation of either (15).

One pathogen for which seroincidence studies have been crucial is leptospirosis, a bacterial zoonosis. Pathogenic spirochetes of the genus Leptospira cause approximately 1 million severe cases and almost 60,000 deaths per year (16). Humans become infected through direct contact with an infected mammalian host or contact with soil or water contaminated by infected animal urine (17). Severe manifestations, including pulmonary hemorrhage and Weil’s disease, represent only a small fraction of infections (17). The majority are asymptomatic or produce mild disease with nonspecific symptoms such as fever and myalgia (17) and are frequently misdiagnosed as better-known infections like malaria or dengue fever (3–6). The burden of leptospirosis is thus severely underestimated by reported cases, and seroincidence studies have been critical for understanding leptospiral dynamics and risk factors for infection (18, 19). As with other diseases, serological studies of leptospirosis are complicated by interval-censored titers and the potential for reexposure.

To characterize the effect of allowing for titer decay between serological samples, we reanalyzed data from a longitudinal cohort study of leptospirosis in an endemic urban slum setting. We first estimated the titer decay rate using historical data from a well-characterized point-source outbreak of leptospirosis with no reexposure (10). We then applied this decay rate to the cohort data. However, instead of directly comparing observed titers, we defined infections by comparing the second titer with a decayed version of the first. Although we focused on leptospirosis, the methods developed are readily adaptable to other infectious diseases.

METHODS

Estimating the rate of Leptospira antibody titer decay

There are numerous seroincidence studies of human leptospirosis (10, 20–27), but we identified only one that conducted longitudinal follow-up where reexposure was unlikely. This study, by Lupidi et al. (10), followed 18 patients who experienced clinical disease after a point-source outbreak of leptospirosis caused by a dead hedgehog that contaminated an Italian town’s drinking water in 1984. These patients were followed longitudinally, with samples taken “by the third or fourth week after the onset of disease” and at 9, 18, 36, and 54 months after infection. The outbreak serovar was identified as a member of serogroup Australis but was not conclusively identified, so the authors reported data for 3 serovars within this serogroup. At the time of the outbreak, seroprevalence rates for Australis serovars in this area of Italy were low (28), and seroprevalent cases were epidemiologically distinct from outbreak cases (28, 29), so reexposure among outbreak cases was unlikely.

Samples were tested using the microscopic agglutination test (MAT), the gold standard serodiagnostic test for leptospirosis (30). The MAT is conducted by combining serially diluted patient serum samples with a standard amount of a Leptospira reference strain, and then examining the mixture under darkfield microscopy. The cutoff for a positive result is 50% agglutination of the bacteria by the patient sample, and the result is given as the reciprocal of the highest dilution at which this endpoint is reached. This procedure is repeated for an epidemiologically relevant battery of reference strains. Dilutions used in this study were 1:50, 1:100, 1:320, 1:1,000, 1:3,200, 1:10,000, and 1:32,000. Data were extracted from Figure 1 of the published report (10).

Figure 1.

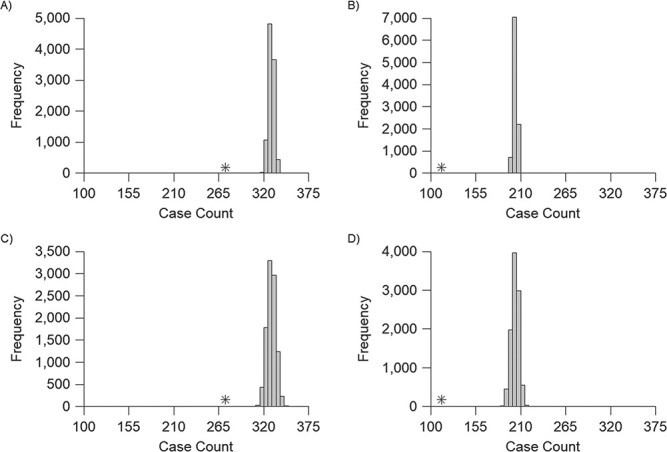
Comparison of infections defined using conventional and modified interpretations of paired serology among participants in a longitudinal cohort study conducted in Pau da Lima, Brazil, 2013--2015. In each panel, the case count using conventional interpretations of paired serology, which do not account for titer decay, is marked by an asterisk. Histograms show the number of infections defined in each of 10,000 imputations allowing for titer decay over all 6-month periods (A, C) or all 12-month periods (B, D). A and B use the point estimate of the decay rate, and C and D use a decay rate sampled from the distribution of the estimate.

To model titer decay, we first defined an unobservable variable W to be a patient’s true antibody level at the time of measurement. The result of a dilution assay like the MAT is an observed number of dilutions K = 0, 1, 2, etc., at which the sample meets the agglutination threshold. These dilutions represent an interval-censored version of W. Specifically, the observed dilution K = k is equivalent to d_k < W < d_k + 1, where the d_k are known constants based on the dilution factor. We then specified a model in which the expected value of W at time t since infection is m(t) = at^γexp(−βt). The constant a is a scaling factor that varies between individuals and serovars to account for heterogeneity in antibody decay (31–33). The parameter γ allows for an initial increase in antibody response postinfection if γ > 0. The parameter β represents the rate of exponential decay in antibody response following the initial rise, if any (34, 35); for example, when γ = 0, a value β = 0.2 would indicate that the expected response at time t + 1 is exp(−0.2) = 0.819 times the expected antibody response at time t. Additional technical details of the model and model-fitting are given in Web Appendix 1 (available at https://doi.org/10.1093/aje/kwaa253).

Effect of accounting for Leptospira titer decay in longitudinal cohort data

We then applied the estimated decay rate to data from an ongoing longitudinal cohort study in an urban slum in Salvador, the third largest city in Brazil. A previous, annually sampled cohort in this site had a crude seroincidence rate of 37.8 infections per 1,000 person-years (18) and a reinfection rate of 71.7 per 1,000, indicating frequent reexposure. This study also identified the peridomestic environment as a high-risk setting for leptospirosis (18, 19, 36). To better understand leptospiral dynamics and risk factors, we conducted a second longitudinal cohort study in which participants were sampled every 6 months (37). To be eligible, residents had to sleep at least 3 nights per week in the study site, be at least 5 years old, and consent to participate. This study was approved by the Yale University Ethics Committee (protocol 1,006) and Brazilian National Committee for Ethics in Research (protocol 963/2008). All participants provided written informed consent. Consent was also obtained from parents or guardians of participants who were minors. The study enrolled 2,421 of 3,716 eligible residents (37). We used the first 5 biannual samples, taken in 2013–2015, to quantify the effect of accounting for titer decay. We analyzed individuals with complete follow-up for each of the four 6-month and two 12-month intervals during this period. Table 1 shows the number of individuals for each interval and the corresponding seroincidence rates. In this study, samples were analyzed using successive 2-fold MAT dilutions, 1:50, 1:100, 1:200, …, 1:12,800. We restricted our analysis to the single serovar that causes 90% of infections in this setting (L. interrogans serovar Copenhageni) (19).

Table 1.

Comparison of Infections Defined Using Conventional and Modified Interpretations of Paired Sera Among Participants in a Longitudinal Cohort Study Conducted in Pau da Lima, Salvador, Brazil, 2013–2015

Interval	CompleteFollow-ups	Conventional Interpretation			Accounting for Titer Decay a
		SC	FFT	Infection Rate b	SC Median (IQR)	FFT Median (IQR)	Infection Rate b Median (IQR)
6 months
Period 1	1,593	48	16	40.2	58 (57, 60)	14 (13, 15)	45.8 (45.2, 46.5)
Period 2	1,485	87	9	64.6	99 (98, 101)	7 (6, 8)	71.4 (70.7, 72.7)
Period 3	1,601	36	11	29.4	43 (42, 44)	21 (20, 22)	40.0 (39.4, 40.6)
Period 4	1,399	52	14	47.2	68 (66, 70)	19 (17, 20)	62.2 (60.8, 62.9)
12 months
Year 1c	1,444	69	3	49.9	109 (107, 110)	11 (10, 11)	82.4 (81.7, 83.1)
Year 2d	1,292	36	5	31.7	64 (61, 67)	20 (20, 21)	65.8 (63.5, 67.3)

Abbreviations: IQR, interquartile range; FFT, 4-fold titer rise; SC, seroconversion.

^a The values for the interpretation allowing for titer decay are based on 10,000 imputations using a decay rate sampled from its distribution.

^b Per 1,000 population.

^c Periods 1 and 2.

^d Periods 3 and 4.

We used multiple imputation to apply titer decay to the cohort data. We first imputed a value for the titer at the beginning of a follow-up interval (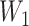) using a uniform distribution on the log-scale. For example, an observed number of dilutions , corresponding to a titer of 1:100, was randomly assigned a value of in the interval between 2 (inclusive) and 3 (exclusive). Colleagues with extensive MAT experience did not feel there was evidence to justify a nonuniform imputation distribution. We then applied the estimated decay rate over the interval between the samples to generate an expected titer at the end of the interval (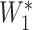), using the formula 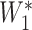= 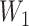× 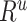, where R = exp(−β) and u is the intersample interval in months. We then recensored 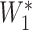to obtain an imputed number of dilutions 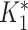by rounding down to the nearest whole number. This reflects the MAT procedure in which samples that do not meet the threshold at a given dilution are assigned a lower titer, effectively rounding them down. Finally, we defined infections by comparing 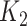with 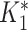instead of the conventional 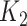to 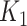. As an illustrative example, consider an individual with 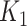= 3 (a titer of 1:200), and 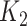= 4 (1:400) taken 6 months apart. Conventional interpretations would not define an infection in the intersample interval. Our method first imputes a value of 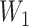between 3 (inclusive) and 4 (exclusive), for example 3.25. We then calculate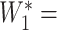 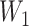× 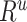= 3.25 × 0.926⁶ = 2.05. This value of 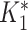is rounded down to 2 (a titer of 1:100) and compared with the 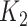of 4, resulting in an infection defined using the 4-fold rise criterion allowing for titer decay. See Web Figure 1 for a visual example. We repeated this procedure 10,000 times to estimate variation due to the imputation process. As a sensitivity analysis, we also repeated the procedure 10,000 times sampling the decay rate from the sampling distribution of its estimate instead of using the point estimate R.

Two concerns need to be mentioned. One is that titer kinetics in clinical cases in a naive population (Lupidi et al. (10)) might differ from those in a leptospirosis-endemic setting where individuals might have some level of immunity that would affect their titer decay rate (14, 38). We took 2 steps to ensure that applying the estimated decay rate to the cohort data was valid. First, we sampled 16 cohort participants within a 6-month interval, creating intervals of approximately 4, then 2, months. We visually compared the titer kinetics of these individuals with those of the individuals in Lupidi et al. (10). Second, to examine the sensitivity of our results to the decay rate, we repeated the above procedure using decay rates both faster and slower than the one estimated from the Lupidi et al. data. The decay constant was calculated by 1 − (1 − R). To calculate alternative decay rates, we added a multiplier M to the equation: 1 − (1 − R)M. We used M = 2 (to calculate a decay rate twice as fast as estimated), 1/2, and 1/4 (to estimate decay rates one-half and one-quarter as fast as estimated, respectively). The second concern is whether titer kinetics are similar when different Leptospira serovars cause infections. This cannot currently be addressed because no comparable longitudinal data without reexposure exist for L. interrogans serovar Copenhageni.

RESULTS

MAT titers from Lupidi et al. (10) varied by serovar and individual and were well modeled by exponential decay (Web Table 1 and Web Figure 2). The 3 serovars had significantly different intercepts, with the highest for serovar Lora, then Bratislava, then Australis (see Web Table 2 for parameter estimates). Our final model of exponential decay over time in months, with an intercept affected by serovar and individual, had an estimated decay rate R of 0.926 dilutions per month (95% confidence interval: 0.918, 0.934).

The parameter representing the initial titer rise was not statistically significant, so we excluded it (Web Table 1). Our inability to characterize initial titer rise in the Lupidi et al. (10) data is likely due to the lack of samples during the first month after infection, when the rise would occur. We attempted to resolve the initial titer rise by imputing the missing time of the first sample for each individual based on their titer trajectory, but this did not increase the precision of our estimates. The fixed 6-month periods between serosurveys in the Pau da Lima cohort also prevented us from characterizing initial titer rise from that data.

There was no visual evidence that titer decay in participants in the Brazilian cohort differed significantly from that of cases in Lupidi et al. (10) (Web Figure 3), so we applied the estimated decay rate to the longitudinal cohort data. Summaries of infections defined using both conventional interpretations and allowing for titer decay are presented in Table 1. Infections are reported for each of the four 6-month intervals as well as the two 12-month intervals. The imputation variance—captured by the interquartile range of infection counts across the 10,000 iterations—was small, indicating that each imputation produces comparable results. Results are reported for the analysis using a titer decay rate sampled from its distribution. Results using the decay rate point estimate are qualitatively similar, with narrower confidence intervals (Figure 1).

Accounting for titer decay increased the number of infections. While the mean 6-month infection rate under the conventional definition was 45.3 infections per 1,000 follow-ups, when allowing for decay the mean rate became 54.8/1,000. The difference was even more pronounced when considering 12-month sampling intervals, for which the mean infection rate went from 40.8/1,000 to 74.1/1,000 when accounting for titer decay (calculated from Table 1 values). Sensitivity analysis showed that even a decay rate only one-fourth as fast as that estimated from the Lupidi et al. data (10) would still result in more infections than the conventional definition (Table 2).

Table 2.

Sensitivity Analysis Demonstrating the Effect of Decay Rate on the Number of Infections Defined Using Paired Serology Among Participants in a Longitudinal Cohort Study Conducted in Pau da Lima, Brazil, 2013–2015

Titer Decay Rate	Total Infections a Per 6-Month Period, Median (IQR)
	Period 1	Period 2	Period 3	Period 4
Conventional (no decay)	64	96	47	66
0.981 (R/4)	66 (65–67)	98 (97–99)	51 (50–53)	69 (68–71)
0.962 (R/2)	69 (68–70)	100 (99–101)	56 (55–58)	73 (72–75)
0.926 (R)	73 (72–74)	106 (105–108)	64 (63–65)	87 (85–88)
0.857 (2R)	82 (81–83)	120 (120–121)	77 (76–78)	101 (100–101)

Abbreviations: IQR, interquartile range; R, estimated decay rate.

^a Total infections consists of seroconversions plus 4-fold rises.

DISCUSSION

We used likelihood-based estimation to model the decay of interval-censored leptospirosis antibody titers, and then applied that decay rate to longitudinal cohort data to more accurately measure seroincidence. Our model of leptospiral MAT titer decay demonstrated that accounting for decay substantially increased infection rates. We took steps to ensure that our decay estimate was reasonable but showed that even accounting for a considerably slower-than-estimated decay rate identified more infections than the conventional interpretation.

Our findings have important implications for epidemiologic study design and interpretation. The biannual incidence rate of leptospirosis in our study site was 1.21 times the rate estimated by conventional interpretations, representing a substantial increase in burden. We also identified that the intersample interval has important implications for interpretation. Leptospirosis incidence was underestimated by conventional definitions with both 6- and 12-month intervals, but the effect was much stronger with the longer interval. In our case, the estimated annual incidence rate was 1.82 times the value calculated with conventional interpretations. This calls into question the validity of direct comparisons among longitudinal studies with different sampling intervals. For other pathogens, the validity of such comparisons depends on the relative timescales of antibody decay and intersample intervals. Longitudinal cohort studies aim not only to calculate burden but also to determine risk factors for infection, and these previously unidentified infections could modify the risk factors identified from our data (18, 19, 36). Accurate burden and risk factor information is critical for public health practitioners working to prevent infection as well as researchers working to understand infection dynamics and trends. In addition, improved understanding of individual sequences of infection events could help evaluate whether preexisting antibody titers lower the risk of a subsequent infection. This has important implications for vaccine development (39). Finally, cohort study design could be influenced by these results, because a higher incidence rate will lower sample-size requirements.

Our method for quantifying decay and seroincidence has several benefits. The modeling framework is relatively simple and can be applied to other data sets and pathogens with minimal modifications. Beyond the paired samples to be analyzed, the method requires a single data set without reexposure to estimate the titer decay rate. While more data sets would increase the accuracy and generalizability of the estimated decay rate, we demonstrated that even a single data set can provide useful information. In addition, our method preserves the 4-fold rise criterion to avoid the misclassification possible when using a 2-fold rise as the infection standard at the individual level (1). Finally, our method takes into account the actual time elapsed between samples, making it flexible to variation in the intersample interval both within and between studies.

While we applied this method to leptospirosis, it is suitable for application to other infections. For example, brucellosis (40) and scrub typhus (a rickettsial infection) (41) are underreported infections commonly diagnosed using paired serology. If antibody decay rates can be calculated in the absence of reexposure, those rates can then be applied to longitudinal cohort studies to generate more accurate burden measures. However, data sets without reexposure can be lacking for endemic infections with a high force of infection. Another consideration when applying this method is the number of strains circulating. In our system, a single leptospirosis serovar causes most infections (19, 37). In areas where a single dengue virus serovar circulates, our method would apply. However, in the presence of multistrain dynamics, including cross-reactivity and -immunity—common for dengue virus and influenza—modifications would be required. In these more complex situations, models account for these dynamics by simultaneous estimation of titer increase, titer decay, and infection (8, 9, 11, 13, 14). To eliminate potential statistical identifiability issues (15) and simplify these models, our titer decay model could be incorporated as a deterministic process.

This study has the following limitations. The MAT is subjective and results vary by performer and laboratory. However, this is a common feature of dilution assays. Our method mimics the MAT procedure and accounts for some variability through the imputation process. We used a single historical data set to fit our model. To our knowledge, this is the only published data set of longitudinal human MAT follow-up in which reexposure is unlikely. Reexposure cannot be conclusively ruled out, but the low seroprevalence rate to outbreak strains (28), epidemiologic differences between outbreak and seroprevalent cases (28, 29), and lack of increased titers during longitudinal follow-up of outbreak cases (10) all make reexposure improbable. Individual starting titers varied, potentially due to differences in immune factors or the infecting dose. Separating these 2 factors is a major challenge in serological studies and one we cannot overcome with this data. The small data set (n = 18) limited us to considering a relatively simple exponential decay model. In particular, the timing of the samples limited our ability to account for any noninstantaneous initial rise in titer following infection.

Interval-censored serological assays are used to define infection with a range of pathogens (1, 9, 30), but we demonstrated that conventional interpretations of paired sera with long intersample intervals can substantially underestimate infection rates. Titer decay is therefore an important phenomenon to account for when interpreting paired serology conducted with long intersample intervals. Modeling the decay of interval-censored titers in the absence of reexposure allowed us to estimate a titer decay rate that we used to understand transmission in a more complex setting. Our method is flexible and generalizable to other infectious diseases defined using interval-censored assays.