Supporting Generalization in Non-Human Primate Behavior by Tapping into Structural Knowledge: Examples from Sensorimotor Mappings, Inference, and Decision-Making

Abstract

The complex behaviors we ultimately wish to understand are far from those currently used in systems neuroscience laboratories. A salient difference are the closed loops between action and perception prominently present in natural but not laboratory behaviors. The framework of reinforcement learning and control naturally wades across action and perception, and thus is poised to inform the neurosciences of tomorrow, not only from a data analyses and modeling framework, but also in guiding experimental design. We argue that this theoretical framework emphasizes active sensing, dynamical planning, and the leveraging of structural regularities as key operations for intelligent behavior within uncertain, time-varying environments. Similarly, we argue that we may study natural task strategies and their neural circuits without over-training animals when the tasks we use tap into our animal’s structural knowledge. As proof-of-principle, we teach animals to navigate through a virtual environment - i.e., explore a well-defined and repetitive structure governed by the laws of physics - using a joystick. Once these animals have learned to ‘drive’, without further training they naturally (i) show zero- or one-shot learning of novel sensorimotor contingencies, (ii) infer the evolving path of dynamically changing latent variables, and (iii) make decisions consistent with maximizing reward rate. Such task designs allow for the study of flexible and generalizable, yet controlled, behaviors. In turn, they allow for the exploitation of pillars of intelligence - flexibility, prediction, and generalization -, properties whose neural underpinning have remained elusive.

1. Introduction: The Neurosciences of Tomorrow

It is undoubtedly an exciting time in systems neuroscience. Techniques for neural recording and perturbation are improving at a remarkable pace (Sejnowski et al, 2014; Jun et al., 2017), and the development of rigorous behavioral training procedures is permitting for psychophysics in smaller animals akin to those classically undertaken in primates (Burgess et al., 2017; IBL et al., 2020). Further, novel approaches for tracking freely moving animals (Foster et al., 2014; Berger et al., 2018, 2020; Michaiel et al., 2020; Bala et al., 2020; Pereira et al., 2020; Wu et al, 2020; Mao et al., 2020) is encouraging researchers to measure and leverage in their analyses additional degrees of freedom (e.g., eye, arm, and full-body movements), as opposed to artificially restricting these potential sources of explainable variance (Musall et al., 2019). Continued steps in this direction promise to further (re)shape our field, one that is and will be largely defined by novel technologies allowing for the dissection of circuit-based correlates of complex behavior.

It is exactly for this promise, however, that more than ever it has become imperative to question the behaviors we study, and how we study them (Carandini, 2012; Gomez-Marin et al., 2014; Krakauer et al., 2017; Pitkow & Angelaki, 2017). Two-alternative forced choice (2-AFC; Fechner, 1889), match-to-sample (e.g., Blough, 1959), and go-no go (Donders, 1868) tasks, among others, have been a longstanding fixture and the major workhorse of systems neuroscience. These paradigms are routinely as reductionist as possible, typically providing 1 bit of information per trial, and tightly controlling the stimuli presented and the timing of these. This rigid experimental control arguably allows for carefully disentangling potential confounding variables (or at least the subset anticipated by experimentalists), yet tends to dissociate perception from action, guides the state-space of potential actions (i.e., actions as “reports” and not as information-sampling; Gottlieb & Oudeyer, 2018), and fixes the utility of samples we draw from the environment. Extensive behavioral training in experimental animals adds to the limited purview of the standard protocol, by not only teaching animals how to accomplish the task at hand, but effectively imposing an immutable task structure, suppressing natural behavioral strategies and their underlining neural circuitry.

Of course, we have learned a lot about brain function with this reductionist approach. Over the last few decades we have detailed the filters that exist at sequential stages of sensory processing, with, for example, edge detectors in primary visual cortex (e.g., Hubel & Wiesel, 1959) and motion detectors (Tanaka et al., 1986) synapses away. These insights have inspired the development of artificial intelligence (see Hassabis et al., 2017), and gratifyingly, the latter is in turn refining our understanding of the building blocks of the brain (e.g., Walker et al., 2019; see Bao et al., 2020 for an emblematic example within the field of pattern recognition). Nevertheless, we have made less progress in understanding how distinct neural nodes communicate with one another, how they operate within dynamic, uncertain, and natural environments, how we infer the causal structures that govern sensory data generation, and more formally, how established models of signal detection (Green & Swets, 1966), decision-making (Gold & Shadlen, 2007), value-based operations (Dayan & Niv, 2008), and motor behaviors (Shadmehr et al., 2010) all cohabitate and inform one another.

We believe, however, that our ultimate goal as neuroscientists should be to understand how the brain accomplishes precisely those behaviors we understand (and study) the least: behaviors that are typical of everyday life, and not those that routinely populate our experimental labs. These complex behaviors unfold dynamically, and do not respect the boundaries or temporal order we have traditionally placed between perception and action (Fig. 1). In this light, the framework of reinforcement learning (Sutton & Barto, 1998, 2018) and control dynamics (Chow & Jacobson, 1971; Todorov & Jordan, 2002; Madhav & Cowan, 2020) seem particularly well suited to inform the neurosciences of tomorrow, one with a natural closed loop between action and perception, time-varying uncertainty and beliefs, and a large state space of potential actions. Of course, these frameworks - where artificial agents learn from interacting with the environment, as humans do - are already a major player in theoretical neuroscience (e.g., Lee et al., 2012) and excellent empirical efforts (see Gershman & Uchida, 2019, for a recent review) are detailing their neural implementation. Similarly, authors (Botvinick et al., 2020) have eloquently written about a new wave of artificial intelligence (e.g., deep reinforcement learning) that is poised to inform next-generation neuroscience. Here, it is not our intention to discuss reinforcement learning and control broadly, nor to illustrate how these frameworks may guide data analyses (see Inverse Reinforcement Learning, Ng & Russell, 2000, Choi & Kim, 2011; Inverse Rational Control; Daptardar et al., 2019; Wu et al., 2020; Kwon et al., 2020). Instead, we very specifically distill a number of the conceptual contributions from this framework, and attempt to translate these to experimental choices that may accelerate the study of brain function by allowing animals to express intelligent behavior akin to that of human everyday life. Most importantly, we provide a concrete example of an experimental ecosystem that allows for such generalization, demonstrating generalization to three distinct and fundamental computations.

Figure 1:

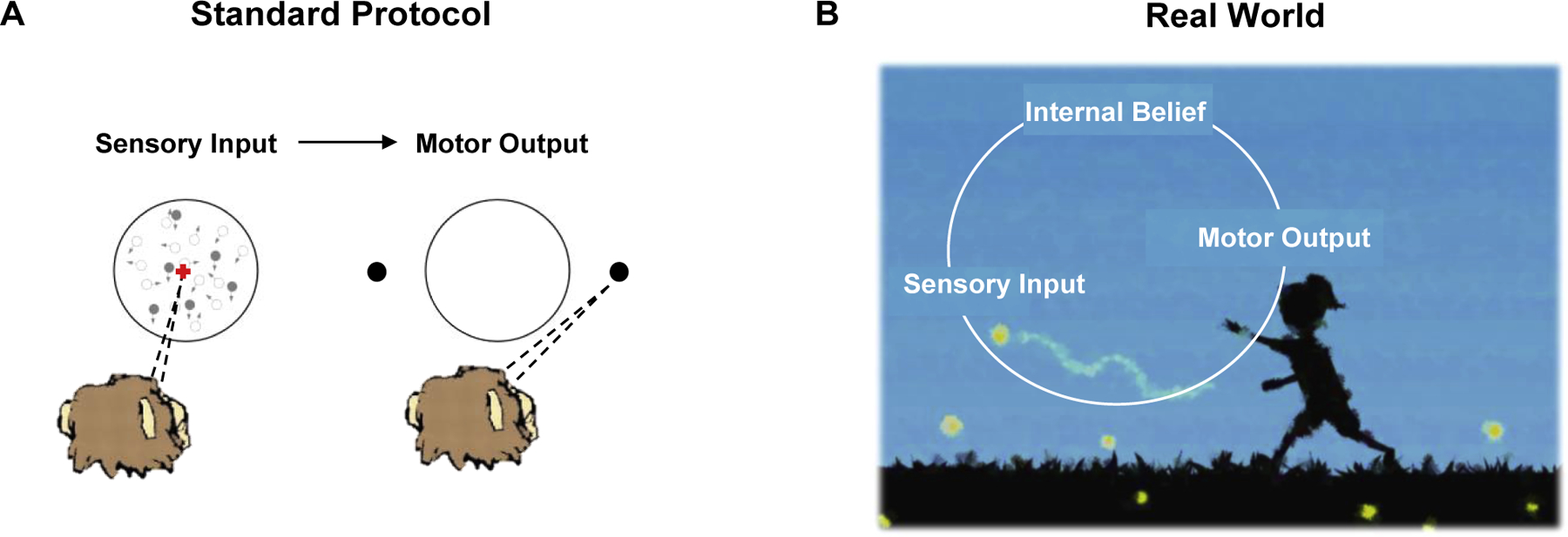
Conceptual Framework. (A) In standard two alternative-forced choice protocols, animals are asked to fixate, and are then presented with sensory stimuli they cannot control or modify. Next, at a different time, they are allowed to make a decision by motor output within an impoverished state space (e.g., only two choices available). (B). In the real world, we must first decide whether to engage in a particular task or not (e.g., catching a firefly), and then, we must operate within a sensory-motor loop, where actions may change the landscape of sensory evidence, and this evidence updates our internal models, which in turn may or may not change our actions.

1. 1. How Should Agents Interact with Their Surrounding? Continuous Active Sensing and Planning

In the terminology of reinforcement learning, we may state that the objective of agents in the world is to maximize their long-term cumulative reward by finding the best policy - the set of actions permitting to transition between states that ultimately will maximize utility. The value of a particular action can be expressed by the well-known Bellman Equation (Bellman, 1957) with a reward-discounting factor for future actions. It can also be expressed as the sum of the action’s immediate and future values, each depending on the agent’s current beliefs (Kaelbling et al., 1998). The immediate value of an action can be computed as the reward expected under the current posterior distribution provided by an ideal observer (Geisler, 2003; Yang et al., 2016). On the other hand, and most pertinent to the discussion of complex, dynamic, and flexible behavior, the future value depends on two factors. First, how an action steers the observer toward reward by successively changing states. And second, how it leads to new observations - putatively more informative than the current - and hence changing the quality of observations and beliefs (Kaelbling et al., 1998). Thus, as argued by Yang et al., 2016, this framework highlighting the need to estimate the value of future information, and how one may maximize it, emphasizes the utility of active, dynamic learning and sensing, where exploitation of current knowledge and exploration for new information are balanced and dependent not only on an ideal observer, but also on an ideal planner. Further, while most problems in reinforcement learning are currently operationalized within a coarsely discretized space, in the limit reinforcement learning and sensing must unfold in a continuous space. Thus, this framework similarly emphasizes the need for an internal and predictive model, a simplified version of the complex physics of the external environment. This model is what the brain - a controller - leverages in order to act on continuous external environments. Maximizing utility, therefore, involves building not only an approximation of the external environment, but also generating hypotheses as to the role our motor outputs play in changing the world, as well as keeping track of the associated uncertainties. As such, active sensing and the need to generate internal and probabilistic models of the external world and ourselves within it, must be key ingredients in guiding next generation experimental design (see Piktow & Angelaki, 2017 for a similar argument).

In addition to the theoretical advantages afforded by bridging across traditional areas of research that have largely been studied in isolated silos (i.e., observations, policies, and actions), an emphasis on active sensing may very well place neural circuits within the dynamical system most amenable to their study - their natural state. Most primate studies, for instance, currently require an observer to fix its gaze, thereby artificially separating perception from action. This compartmentalization may seem a sensible first order approach to describe the distinct components forming behavior, and this intent likely drove the development of what are today classic paradigms in the study of brain function. However, in natural conditions, and thus throughout evolution, perception and action do not occur serially. In fact, eye movements not only dictate the content and relative resolution of visual input, but perhaps most importantly, they dictate the relative timing of sensory input. Critically, this natural “rhythm” (Leopold & Park, 2020) of the visual system seemingly guides its functioning. Recent work in this line, for instance, has highlighted that the excitability of neurons in primary visual cortex (V1; Barczak et al., 2019) and the anterior nuclei of the thalamus (Leszczynski et al., 2020) are enhanced at saccade offset, and have suggested that this effect is mediated by a phase-reset of neural oscillations caused by eye movements (Lakatos et al., 2008; Rajkai et al., 2008). As such, physical movements of the eyes may disproportionally and temporarily favor a given channel of communication (e.g., V1 to MST) by oscillatory phase re-setting and alignment (see Jutras et al., 2013, for related evidence). That is, the visual system may be built to process “volleys” of visual input that are precisely timed to motor output, a reality of naturalistic neural processing and an omission in most laboratory studies of the visual system.

1.2. What Type of Task? Cognitive Maps, Structural Knowledge, and Learning Sets

Beyond the focus reinforcement learning shines on active sensing and planning, as well as on natural behaviors, this framework hints toward the types of tasks, experimental designs, and environments that may be the most amenable to the expression of intelligent behavior.

Experimentally, the capacity for flexibility and generalization - both pillars of intelligence - may express as the ability to exploit previously learned structures to solve novel tasks differing in their instantiation but following a similar logic. That is, flexibility is provided by general knowledge of a task or space structure (i.e., “structural knowledge”) and may be studied by training agents on one task, and then studying their behavior in an adjacent one. In this regard, recent simulations with artificial agents learning through experience and endowed with a deep recurrent neural network showed that if these agents are trained on a set of inter-related tasks with the same structure, they can generalize their behavior to other tasks with a similar structure without changing synaptic weights (Wang et al., 2018). Exposure to not one, but an array of similar tasks, was accompanied by development of structured representations in the dynamics of neural activity. In other words, “meta-reinforcement learning” (Wang et al., 2018) allowed for generalization based on activity dynamics.

These observations suggest that placing animals within an environment or a task with strong structural regularities may allow them to use their acquired cognitive maps (Tolman, 1948) and draw inferences. The example of two-dimensional space is particularly interesting as tasks where agents move through an environment may not only require animals to tap into structural knowledge acquired through evolution and development - aiding experimenters in the study of intelligent behavior - but may also leverage well known spatial codes - catalyzing our ability to understand the underlying physiology. For example, there is a set of vectors from which it is possible to linearly compute the distance between any pair of states, and thus all possible futures from the current state (Baram et al., 2018; Stachenfeld et al., 2017). These vectors adopt grid-like properties in two-dimensional spaces (Dordek et al., 2016; Stachenfeld et al., 2017). Interestingly, a recurrent neural network agent provided with self-motion input as it explores an open field via path integration will develop hexagonal grid-like cells (Banino et al., 2018). This grid-like representation provides an effective basis for agents to show shortcut behavior and locate goals in changing environments (Banino et al., 2018). Thus, the salient experimental description of grid cells has found a functional rationale of its properties through reinforcement learning; it is a (spatial) representation amenable for inference and behavioral generalization. Tim Behrens and colleagues (2018) have further proposed that place- and grid-like codes may underpin not only navigation through space, but more generally exploration of abstract, graphical, tree-like structures even when devoid of specific sensory information.

Taking a step back, the literature from reinforcement learning suggests that complex behaviors are scaffolded on the ability to actively engage with the environment, and to plan for the future. Further, it suggests that under the appropriate training regimes agents may learn abstract features from the structure of the task itself (e.g., “taking one step forward and then rightward is equal from taking one rightward and then forward”). Perhaps mostly importantly, these structural features may allow for generalization across tasks with similar structures and support inferential behavior (Wang et al., 2018, Behrens et al., 2018). With these principles in mind, we sought to develop an experimental ecosystem that would tap into our animals’ structural knowledge, and thus allow for the study of flexible, yet controlled, behaviors. In the following we present an example task and ecosystem, and demonstrate that it supports generalization to other behaviors - thus opening the door to future studies of the neural underpinning of intelligent behavior.

2. An Example Ecosystem for Natural Yet Controlled Behavior: Catching Fireflies

Non-human primates forage for food in their natural habitat (Pianka, 1997), and thus we attempted to incorporate into an intuitive foraging/path integration task many of the elements detailed above; a dynamic environment with closed loop action and sensing, the need to make plans and predictions over long periods of time, and a latent task-relevant variable that these animals had to track and could give us a lens into their internal models (Lakshminarasimhan et al., 2020). Furthermore, we aimed to includes these elements while remaining grounded in known sensory neurophysiology (e.g., the presence of motion sensors) and a vast literature on sensing optic flow and self-motion (e.g., Britten, 2008; Hou & Gu, 2020). Importantly, the variable dictating whether animals receive reward or not is latent (i.e., distance to a memorized target), forcing animals to make predictions and inferences regarding their environment and actions. These predictions are then confirmed or denied by the delivery or omission of reward. We first describe this basic task - what we call the “Firefly Task” - but wish to emphasize that, while animals need to be trained on this basic task (i.e. they need to be taught how to use a joystick to navigate in a virtual environment, in other words, they have to learn to “drive”), the real power of this framework is in exploring sub-tasks derived from their structural knowledge and learning set (Harlow, 1949) -- behavioral variants on which animals are never trained but share a common structure (see three examples in the next section).

Under free-viewing conditions, we trained animals to navigate via the integration of optic flow to the location of a briefly presented (300 ms) visual target - a “firefly” (Fig. 2, see Lakshminarasimhan et al., 2018, 2020; Noel et al., 2020). Animals stop within a reward boundary surrounding the (invisible) firefly to get juice reward (Fig 2., blue circle). In close similarity to classic protocols in systems neuroscience (i.e., random dot kinematograms, Newsome & Pare, 1988), the sensory stimulus is an array of briefly flashing elements. Again in similarity to classic random dot studies, observers must integrate these velocity signals into something useful. At difference from the traditional motion stimuli, however, here the animal’s virtual movement guides the velocity of optic flow, thus employing a closed action-perception loop. Additionally, instead of integrating disparate and singular velocity signals into an abstract global motion percept, here the visual motion stimuli are integrated into an estimate of self-position, akin to what subjects experience naturally throughout life. Thus, this behavior taps into structural knowledge acquired through evolution and development, thereby allowing exploitation of internal models of how two-dimensional space and the laws of physics work. These two ingredients, i.e., (i) closed-loop action-perception behavior that is rooted in (ii) structural knowledge, are the crucial differences between the Firefly Task and traditional 2-AFC tasks, and exactly what is needed to be able to study neural correlates of flexible (as opposed to over-trained), yet controlled, behaviors.

Figure 2:

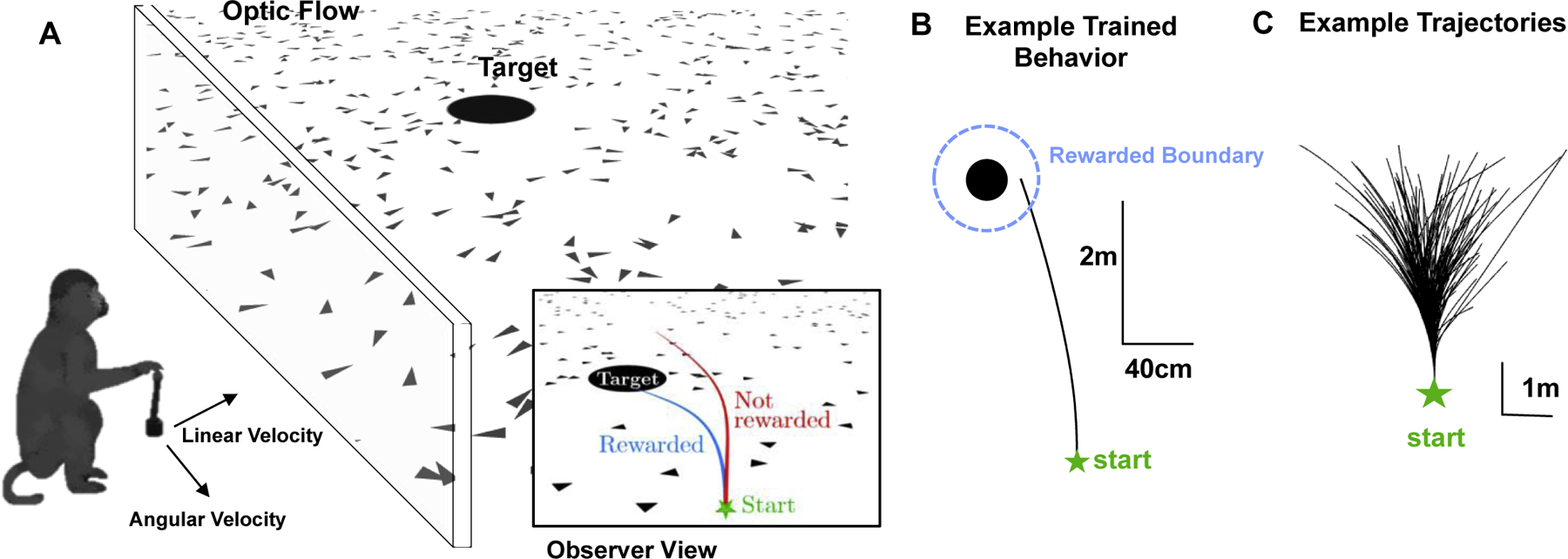
Path Integration Toward an Unseen Target in Virtual Reality - Teaching Non-Human Primates How to Report. (A) The animal has linear and angular velocity control via a joystick, allowing it to navigate and explore a two-dimensional space made up of a target (the firefly - black disk) and triangular elements that are presented only briefly and thus serving as optic flow. (B) Example trial where the monkey navigates straight to the target and is rewarded if it stops within a reward zone (reward zone is never explicitly shown to the animals). (C) A collection of example trajectories.

In the Firefly Task, individual trials last on the order of 2 to 4 seconds, and the output of each trial is a two-dimensional data-rich trajectory allowing for robust model fitting (Lakshminarasimhan et al., 2018; Noel et al., 2020) and the prolonged tracking of eye-movements. In this regard, the resulting data from the Firefly Task is akin to that obtained during other naturalistic tasks, such as two (e.g., Ames et al., 2019) or three (e.g., Young et al., 2019) dimensional reaches. It provides time-varying behavioral output on a time-scale that in principle should allow for hundreds or thousands of spikes, and hence accurate decoding from neural signals (as exemplified by the ever more robust decoders built in and for brain-machine interfaces; e.g., Chaudhary et al., 2016).

While steering the animal is constantly making predictions about the relative position of itself to the target, given that its goal is to stop when this (unseen) distance has reached zero (i.e., at the firefly position). Remarkably, and in sharp contrast to numerous studies probing optic flow processing during obligatory eye fixation, eye-movements during free-viewing steering reflect the animals’ belief of the firefly position, the critical latent variable required to successfully complete each trial and receive reward (Lakshminarasimhan et al., 2020). These findings suggest that during naturalistic navigation, eye movements are an integral component of the closed-loop strategy of prediction and action, and is not to be regarded as a nuisance variable, but instead measured and leveraged.

All together, training on the Firefly Task takes ~3 months, and in teaching these animals to “catch fireflies”, we demand from them to detect and remember the firefly location, and to integrate self-motion velocity signals into an estimate of self-position. Most importantly, we teach them that there is a two-dimensional space they can explore and exploit for rewards by navigating using a joystick. By construction, this space couldn’t be simpler (i.e., two-dimensions devoid of landmarks), but is also impossible to fully ‘visit’ - in fact, it is infinite. This means that animals must use what they know about the structure of the environment to continue exploring new spaces. In essence, we train the animals to naturally forage by “driving” within the virtual environment and we extract “reports” from their trajectories and stopping behavior. Critically, in the next section we test our hypothesis that the use of naturalistic action-perception tasks that tap into the subjects’ structural knowledge allow for the study of flexible behaviors. We show that macaques can generalize to task variants they were never trained to do. All the following data was collected within the same week (at exception from Figure 6, added during review) and is from the very first session these animals encountered the novel experimental scenarios. There was no explicit training.

Figure 6:

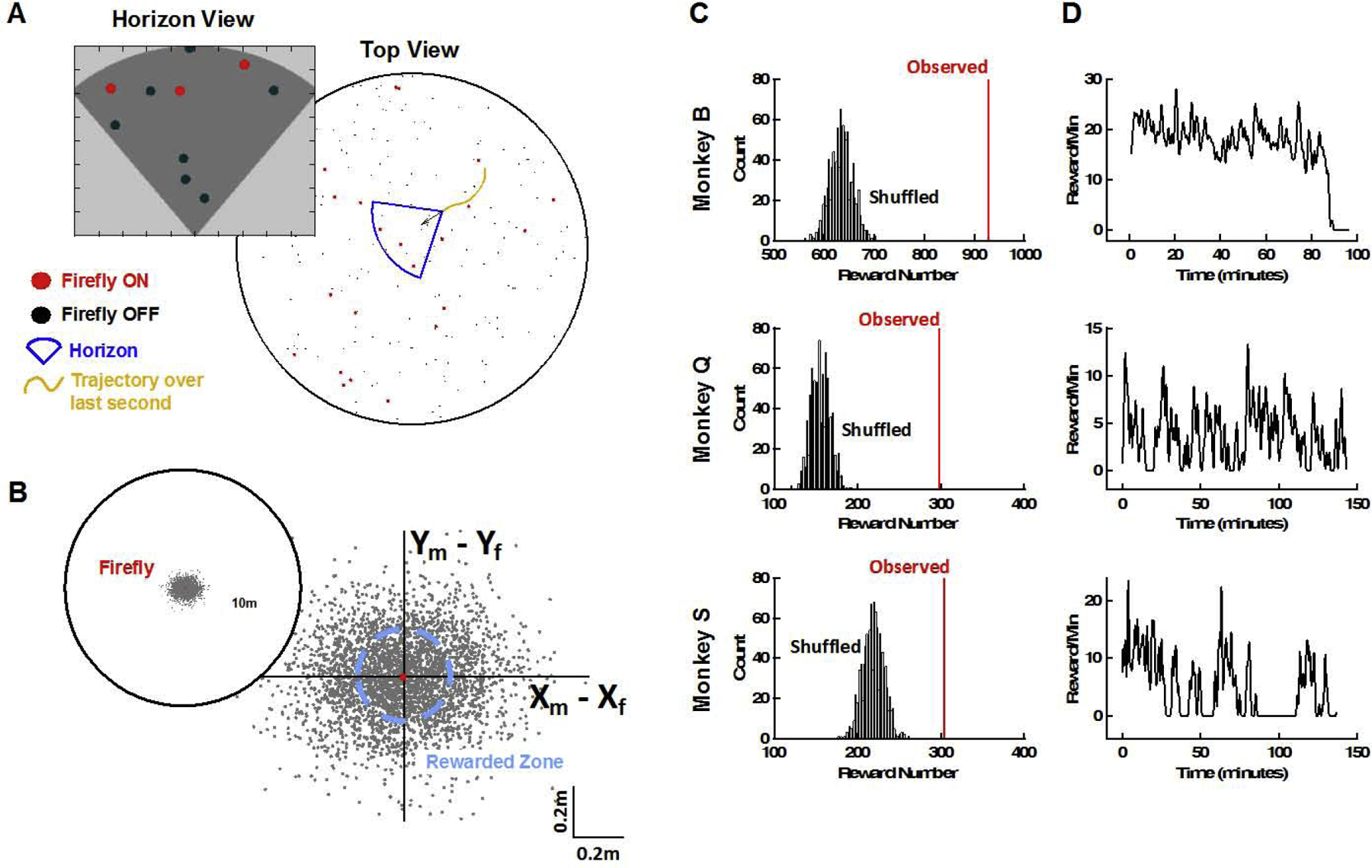
Naturalistic Foraging within a Multi-Firefly Scenario. (A) Two-hundred fireflies were present within a large virtual environment, and flashed at random times (red = firefly on, black = firefly off, blue and inset show the horizon of what was visible during the example frame, yellow trajectory shows movement over the last second). (B) Monkey stopping location referenced to the nearest firefly. (C) Observed (red) and null distribution (black, shuffled) of total rewards within the session. (D) Rewards per minute for the three different monkeys (B, Q, S) within the first session they were exposed to the environment with hundreds of fireflies.

3. Examples of Expressive Behavior in Non-Human Primates

3. 1. Rapid Adaptation to Novel Sensorimotor Mappings

In a first manipulation we examined whether, and how quickly, animals could adapt to novel sensorimotor mappings within the known experimental ecosystem. During their entire training period on the Firefly Task, animals experienced a single sensorimotor mapping. Moving the joystick forward by the maximal physical amount possible corresponded to a linear velocity of 200 cm/s. Moving the joystick laterally by the maximal physical amount possible corresponded to an angular velocity of 90 deg/s. Then, without any training we exposed animals to varying gains (uniform distribution between 1–2x, 1x corresponding to the trained gain described above, Fig. 3A) for blocks of approximately 50 trials and recorded their behavior.

Figure 3:

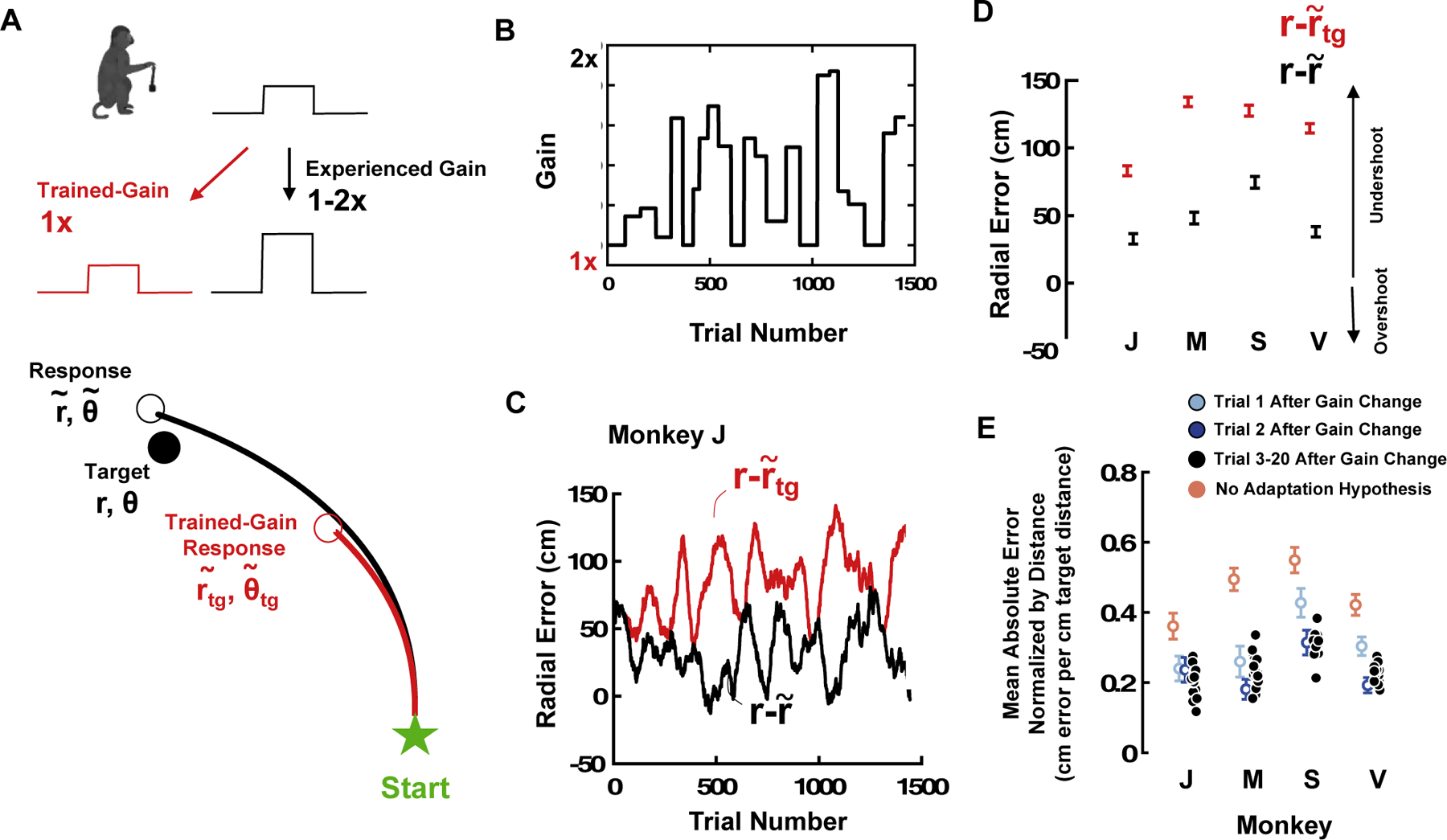
Gain Manipulation. (A) Animals were trained with a unique sensorimotor mapping (Trained-Gain, 1x) and then experienced gains that changed approximately every 50 trials and tiled the space from 1x (trained, red) to 2x (black). We compared the true error subjects made (lower panel, black, difference from r to $\tilde{r}$) vs. the error they would have made if using the gain they were accustomed to (lower panel, red, difference from r to $\widetilde{r_{tg}}$). (B and C) An example monkey (Monkey J) was able to quickly adjust its sensorimotor mappings, as shown by the fact that during the entire session the real gain (C, black) was smaller than what would have been predicted from the trained gain (C, red). The lack of covariance between gain changes and error suggests that the animal’s performance was not driven by changes in gain. The vertical shaded areas are time-periods of gain = 1x. (D) Average real radial error (black) and predicted if there were no sensorimotor adaptation (red) for all monkeys. (E) Examining the radial error on each trial as a function of trial number since gain change suggested that two monkeys (J and M) showed zero-shot learning, while another two (S and V) showed 1-shot learning. Y-axis is cm error per radial distance of targets (in cm; normalization is required given that error scales with distance and the distance of targets on first, second, etc., trial after gain change varied). Errors bars are +/− 1 S.E.M., red is the error predicted if animals would have used the gain they were trained with (1x), light blue is the average error on the first trial of a particular gain manipulation, dark blue is the second trial, and black are the rest (3–20).

To quantify the monkeys’ performance we computed the radial distance from origin and angle from straight-ahead, both for the target firefly (r and θ) and the endpoints of the monkey trajectory ($\tilde{r}$ and $\tilde{\theta }$, Fig. 3A). Then, to determine whether the animals adaptively remapped sensorimotor contingencies to match the gain presented vs. the gain they were trained on, we rescaled real velocity profiles to the trained gain and estimated what the monkey’s final endpoints would have been if they were using the gain settings they were used to ($\widetilde{r_{tg}}$ and $\widetilde{{\tilde{\theta }}_{tg}}$). Fig. 3A shows a representative trajectory differentiating between the real trajectory taken by the subject (Fig. 3A, black curve, r and θ) and the re-scaled version of this trajectory to match the gain monkeys were trained with (Fig. 3A, red curve, $\widetilde{r_{tg}}$ and $\widetilde{{\tilde{\theta }}_{tg}}$).

For illustration purposes, we plot the entire time-course of both the gain manipulation (Fig. 3B, 1x corresponds to the trained gain) and the radial error for a representative subject (Fig. 3C, Monkey J, gray shaded periods in Fig. 3B and C are periods of gain = 1x). This monkey tends to undershoot the radial distance ($r-\tilde{r}>0$, black curve, Fig 3C), and this pattern would have been exacerbated if the monkey had used the original gain it was trained with (red curve, Fig. 3C). Interestingly, while there are fluctuations in the animal’s performance as a function of trial number, these fluctuations (black curve, Fig. 3C) do not correlate with changes in the gain (p = 0.65). That is, the monkey’s targeting and stopping error is not driven by alterations in the gain. When collapsing across trials, this observation was true for all animals tested (Fig. 3D, Monkeys J, M, S, and V), showing a smaller stopping error than what would have been predicted if the animals did not appropriately adjust for the gain manipulation.

Lastly, to highlight the time-course of sensorimotor adaptation we computed the mean absolute error in radial distance normalized by the target radial distance. This was done as radial error scales with radial target distance (Lakshminarasimhan et al., 2018, 2020; Noel et al., 2020). Further, this ratio (error/target) was expressed as a function of number of trials from the latest change in gain. In Fig. 3E, the mean error on first trials since gain change is shown in light blue, the mean error on second trials is shown in dark blue, and the rest of trials (3–20) are shown in black. Further, the average error that would have occurred if the animals did not adjust for gain manipulations, and instead used the gain they were trained with, is shown in red (“no adaptation hypothesis”). Monkeys J and M were able to fully adapt during the first trial (light blue), as their mean error on the first trial is no different from the rest of trials since gain change (dark blue and black) and reduced from the no adaptation hypothesis. Monkeys S and V, on the other hand, showed an intermediate behavior from zero-shot to 1-shot learning, as their mean error on the first trial since gain change was reduced from what would be expected under the no adaptation hypothesis, but they did show continued improvement from trial 1 (light blue) to trial 2 (dark blue) after gain change. These animals did not improve further after the second trial.

3. 2. Tracking an Independently Evolving Latent Variable

As a more stringent test of the ability of these animals to express novel and interesting behaviors, to generalize beyond the simple task they were trained to do, we presented them with moving fireflies. That is, while their entire experience had ever consisted of static targets, without a single session of training we asked these animals to detect motion in the target that was independent from their own self-motion, to infer the direction and velocity of this motion based on a brief presentation (300ms), and finally to extrapolate intersection points between self and the unseen target, before stopping at the target location.

As in the trained behavior and as in the sensorimotor manipulation detailed above, fireflies initially appeared at a random location within a standard radial and angular range (i.e., 1–4m radial and −30 to +30° angular). On 90% of trials the firefly flashed briefly (300 ms, “ON-OFF trials”), and on the remaining 10% of trials the firefly was continuously shown (“ON trials”). Differently from before, however, on 50% of trials (distributed randomly, and both for trials where the firefly disappeared and not) fireflies moved at 80 cm/s, laterally either leftward (25% of trials) or rightward (25% of trials) until the trial ended. This modification from the trained task meant that animals not only had to “pursue” the unseen firefly, but they also had to update their expectation regarding the possible target end-positions based on the location and velocity presented during the visible period (Fig. 4A). They had to update their view of what is possible within the purview of the experiment. Given that fireflies were only briefly presented, the monkeys had to and did adjust their trajectories to minimize their distance to the moving targets after the latter had disappeared (see Fig. 4B for an example trial). That is, not only did they have to keep track of a latent variable that dynamically evolved due to their own self-motion, but they also had to infer whether an unseen target was itself moving, and if so, in which direction and with what speed.

Figure 4:

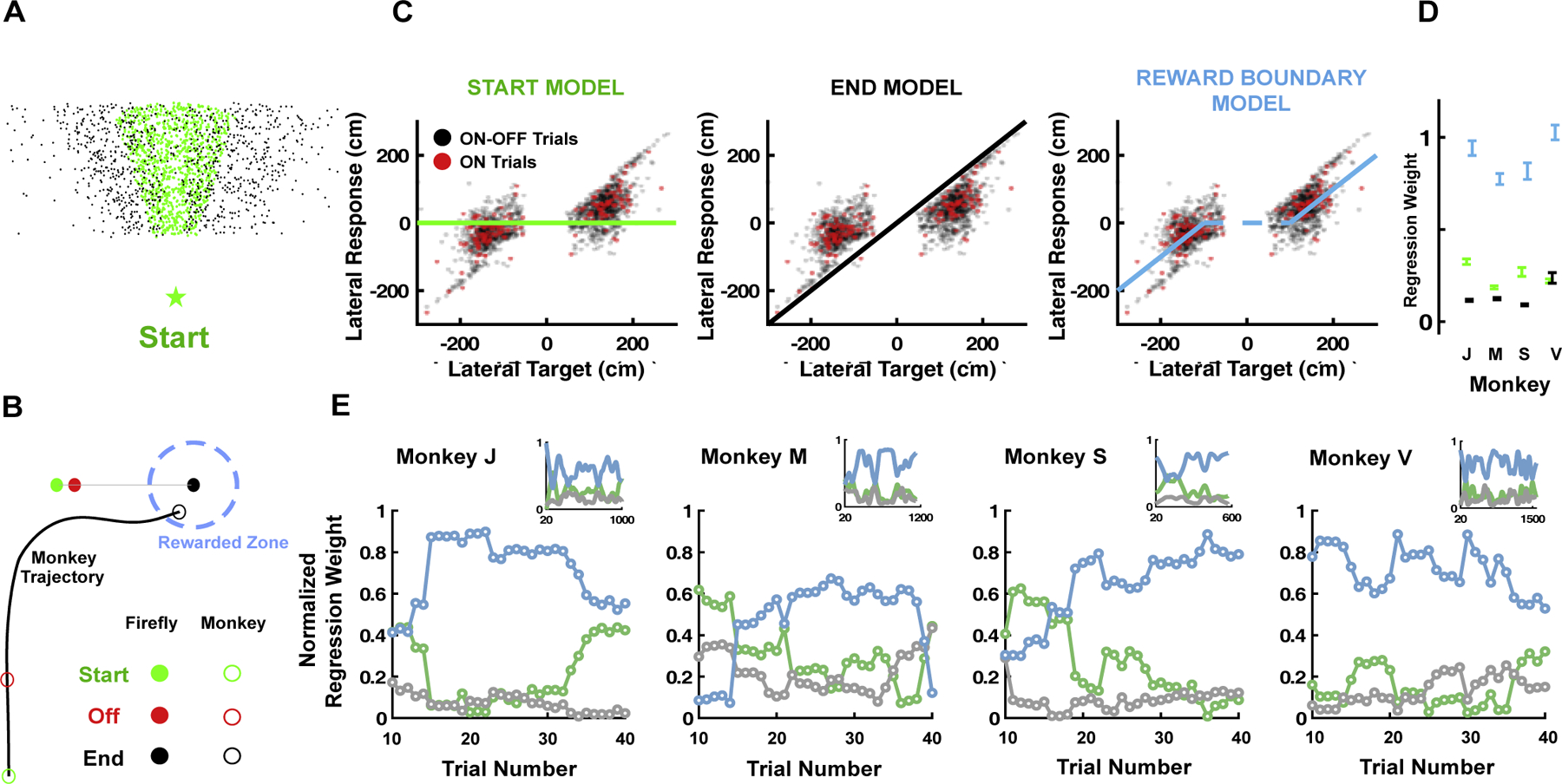
Moving firefly. (A) Location of firefly targets at the beginning (green) and end (black) of trials. (B) An example trajectory. The firefly moves rightward for 300 ms, and then disappears (green to red filled circles). In this time, the monkey moves forward without adjusting its lateral movement (green to red empty circles). Then, the firefly keeps moving, and while not seen, the monkey moves rightward (red to black empty circles) and stops within the reward boundary. (C). Lateral response (in cm) as a function of the lateral position of the target. Trials are re-coded such that if the monkey had navigated to the lateral position of the target at trial onset, its responses would lie along y = 0 (green). If the monkey had perfectly gone to the end position of the target, it’s responses would like along y = x (black, “end model”). If the monkey navigates to the closest reward boundary edges (which depends on the direction of motion of the firefly), its responses would lay along the blue curve. (D) All monkeys inferred that the firefly kept moving after disappearing and followed the reward boundary. Error bars are +/− 1 S.E.M. (weights are not normalized to 1 here and can take either positive or negative values). (E) Normalized weight (sum to 1, in order to compare relative weighting of the different models) of the start (green), end (black) and reward boundary (blue) models as determined by multiple regression within a moving window of 20 trials (x-axis start at trial 10 indicating the center of the moving window). Already in the first window examined Monkeys J and V are following the moving firefly. After ~20 trials all animals are. Inset show the entire session with weights smoothed with a 100 trials kernel. Multiple regression analyses within a window is necessary (vs. single trial) as when targets are near, they do not move much laterally, rendering impossible the distinction among different models.

The example trial (Fig. 4B) shows that in this occurrence the animal was successfully able to make an inference as to the future position of the latent target and was able to minimize its distance to the target before stopping. To scrutinize this ability more systematically, we re-coded all trials such that the target’s initial lateral position was equal to zero. Then, we plotted the corresponding lateral end position of the animal as a function of the corresponding lateral end position of the firefly (see Fig. 4C for all trials in an example monkey). This visualization allows entertaining three hypotheses. First, if the monkey steered to the initial position of the target its responses would lie horizontally along y = 0 (Fig. 4C, green line). Second, if the monkey perfectly steered to catch up with the final position of the moving target, its responses would like along y=x (Fig. 4C, black line). Lastly, if the animal steered to the closest reward boundary, its position would lie along the blue line (“reward boundary” model, Fig. 4C).

Fig. 4C shows all experimental trials from monkey J. Remarkably, the animal was able to infer the motion of the target and predict its future location by navigating toward the closest reward boundary. This is the optimal behavior, making the least effort possible while still maximizing reward. This behavior becomes even more striking when considering the subset of trials where the firefly always stayed on, “ON trials” (Fig. 4C, red dots, ~10% of total trials). In these trials there is no uncertainty as to the evolving position of the target, yet the animal still seemed to navigate to the closest reward boundary. Note that the reward boundary is never visually presented during the experiment, yet it was learned over the course of training.

To summarize the animals’ behavior, we expressed their steering lateral end-position as a function of a weighted sum of the target’s initial and end lateral position, as well as the position of the closest reward boundary. The multiple linear regression suggested that for all animals (Monkeys J, M, S, V), and both on experimental trials where the firefly disappeared (“ON-OFF Trials”) and for trials where the position of the target was continuously presented (“ON trials”), the reward boundary position best accounted for the monkeys’ behavior (Fig. 4D, “ON-OFF Trials” shown). A similar regression in a moving window of 20 trials showed that animals were very quick at adapting to this previously unseen scenario. After approximately 20 trials, all animals navigated to the closest boundary of the moving target (Fig. 4E, x-axis indicates the center of the moving window, and only ON/OFF trials with moving fireflies are taken into account). In fact, Monkeys J and V show this behavior within the first 20 trials - the first time-point examined. Further, while there were natural fluctuations in performance and thus in the weight attributed to the different models (start, end, reward boundary) across the entire session (Fig. 4E, insets) there was no apparent and consistent change in the relative weight attributed to the different models.

In summary and quite remarkably, monkeys did not need specialized training to pursue a dynamic latent variable, even when the entirety of their experience suggests that these targets do not move. This behavior requires animals to update their purview of possibilities (from targets not being able to move to dynamic targets), requires them to appropriately determine the direction and velocity of target movement above and beyond their own self-movement, and requires them to extrapolate the current position of the unseen target. As argued above, demonstration that non-human primates can do this task, in a controlled experimental setting, and with no specific training, goes a long way in showing the extent of their intelligent behavior - they can concurrently navigate through space, keep in mind the location of an evolving target (requiring navigation through a cognitive map), and collapse these two representations into an estimate of the relative distance between the two.

3. 3. Natural Decisions - Choice of Target

As a third example of the utility of tapping into structural knowledge inherent for naturalistic tasks, we demonstrate that once animals have learned to “report by driving”, we may also study naturalistic decision-making with no further training. This sort of decision-making is typically studied in laboratories by training animals to perform a predefined motor response (e.g. a saccade) to report an arbitrary stimulus category (e.g. a grating tilted clockwise relative to vertical; e.g., Glimcher, 2001; Romo & Salinas, 2003; Shadlen & Kiani, 2013). These standard tasks are purposely kept as simple as possible in order to isolate decision-making signals uncorrupted by signals such as memory, attention, and other. Further, these protocols typically involve additional manipulations, such as noise-levels and the magnitude of rewards and punishments, in order to isolate different components of the decision process, i.e., uncertainty, sensitivity, cost and reward functions, decision criteria, and confidence (see e.g., Chandrasekaran et al., 2017). Yet, for how successful this field has been, it may turn out that traditional studies are poorly informative on normal, real-life, cognition. Indeed, in natural situations we do not typically train for months on end in preparation for making a similar decision over- and-over again. Instead, here we show that provided that monkeys are familiar with the structure of an environment and how to navigate within it, they can make decisions to optimize their reward rate from the very first session where they are presented with multiple alternatives. Initially, we deliberately keep the task as simple as possible (2 alternatives, no punishment, equal rewards) to demonstrate the ability to draw psychometric curves and gauge optimal behavior with no training. Then we present a modified version where animals navigate a space of hundreds of choices with no trial structure.

To adapt the basic Firefly Task to a decision-making task we first displayed 2 targets simultaneously (see Fig. 5A). The 2 targets were identical and independently drawn from a distribution of potential locations (uniform between −35 and +35°, and between 100 and 400 cm in radial distance). Fig. 5B shows example trajectories. Without any further training beyond the single Firefly Task, the animals intuitively and deliberately selected one of the 2 targets; that which would increase their reward volume in the long term. This was assessed by comparing the distribution of endpoint distances to the nearest target (i.e., putatively “selected” target) to a baseline distribution generated from keeping endpoints fixed but permuting firefly locations across trials. The area under the curve when comparing these 2 cumulative distributions was 0.68, 0.74 and 0.78 for animals J, M, V. These values are largely above chance level and demonstrate that the animals understood they had to choose between one of the 2 targets and did not stop randomly. All animals demonstrated a clear preference for the closest target, and to lesser extent for the target that deviated less from straight-ahead (Fig. 5C).

Figure 5:

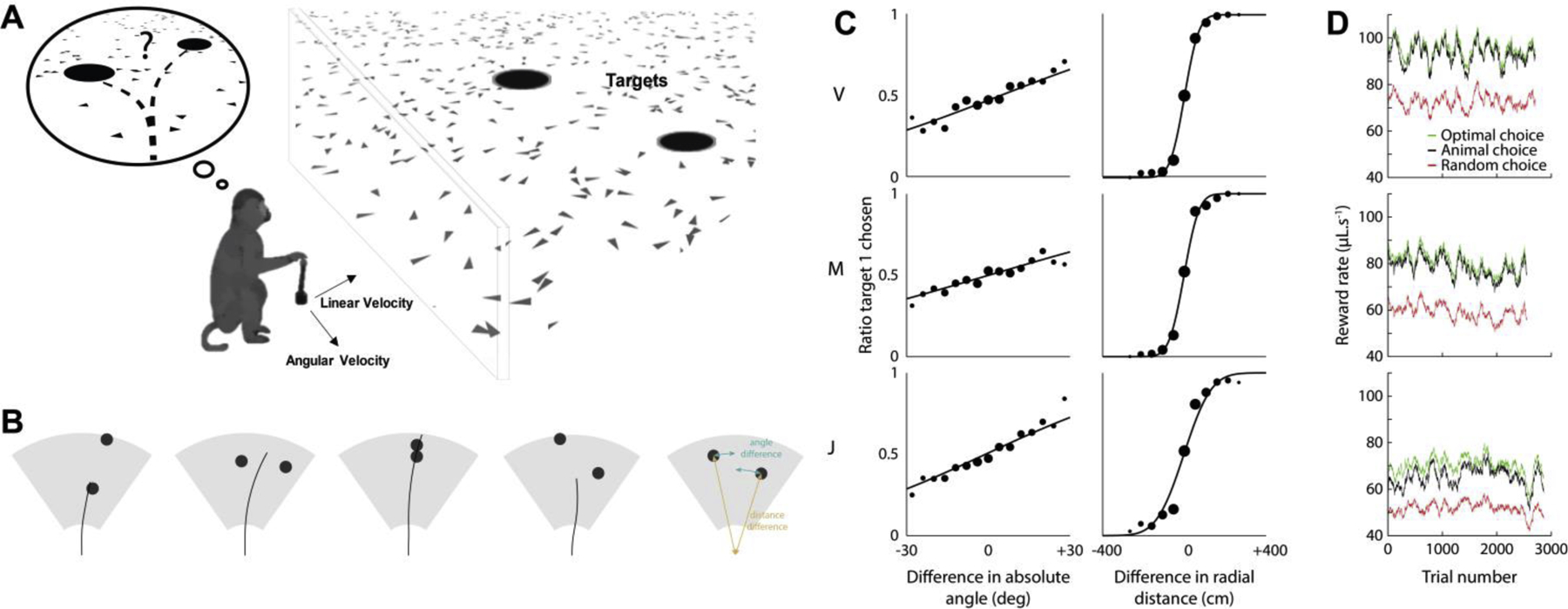
Binary decision-making via transfer learning in a naturalistic task (A) Depiction of the task. Two targets were displayed transiently and simultaneously to the animals. They were free to choose which one to catch. (B) Example of trajectories seen from top. The targets were drawn from independent distributions spanning the gray field in front of the animals. Black disks represent the positions at which the target appeared. The black line is the trajectory the monkeys followed, starting at the bottom. The last field depicts 2 variables the monkeys use to choose which target to catch: deviation from straight-ahead (difference in absolute angles) and relative distance (difference in radial distances). (C) Ratio of trials where the monkeys chose a specific target (target 1 vs. target 2) as a function of the difference between the absolute angle of the targets (left column) and difference between the radial distance of the targets (right column) for 3 monkeys (rows). All animals demonstrated a clear preference for closer and more straight-ahead targets. (D) Running average of the reward rate associated with optimal choice (green), animal’s choice (black) and random choice (red) as a function of trial number from introduction to the task.

Critically, animals were not trained to exhibit these preferences, they spontaneously preferred some target locations over others, even though any target would have led to the same reward. We assumed that monkeys try to maximize reward rates and can thus compare the monkey’s choices to that of an optimal agent. For each position of the target field, we computed travel time and the probability to successfully catch the target from data. The value associated with each target is the reward delivered by this target multiplied by the probability of catching the firefly (expected reward), divided by travel time (cost). An optimal agent would choose the target associated with the highest value. Fig. 5D shows the sliding average reward rate in μL.s-1 for the optimal choice (green), the monkey’s choice (black), and for a random choice (red). Monkeys were near optimal from the very first trials they were exposed to the task.

After demonstrating the ability to study the relatively simple case of 2 alternative choices under the firefly task, we questioned whether macaques would generalize - still within the very first session - to a much more complex scenario, one with multiple options and where the number of targets is constantly changing (ranging form 0 to 7 concurrently visible fireflies, with many more that could be in the vicinity but invisible, Fig. 6A inset, shows 10 in total with 3 visible). We embedded these animals within a large virtual environment (10 meters in diameter) that would repeat to infinite (see Supplementary Videos S1 & S2). This space was inhabited by 200 fireflies flashing at random times (Fig. 6A, red = firefly on, black = firefly off, blue = horizon, what is currently visible from an egocentric perspective). When we visualize the stopping locations of an example subject, we can observer that 43% of the times an animal stopped (linear velocity < 5cm/s), it did so within the boundaries of a reward zone (Fig. 6B). To quantitatively assess whether animals were deliberately stopping at the location of fireflies, we computed their total number of rewards (Fig. 6C, Observed), as well as the total number of rewards they would have received under different (rotated, 1000 permutations) configurations of firefly locations (Fig. 6C, Shuffled). All monkeys received significantly more rewards (all p<10⁻³) than they would have if simply stopping randomly. Further, we examined their reward rate per minute (Fig. 6D), and while we observed interesting idiosyncratic fluctuations (note Monkey S decided not to forage for ~30min), animals did not consistently improve with time, suggesting they were perfectly capable of navigating this large space of potential targets from the get go. Altering between voluntarily exploiting our environment vs. resting (Fig. 6D, bottom panel) is commonplace in our daily lives, yet seldomly falls within the purview of our traditional experiments (but see Milton et al., 2020 for a recent exception).

4. Outlook

While we have learned a considerable amount about individual neural nodes via traditional tasks, here we advocate for the study of naturalistic behaviors with continuous time, closed-loop sensorimotor contingencies, and dynamic latent variables. Tapping into these naturalistic behaviors, we may leverage our animals’ knowledge of how “the world works”, which in turn may allow for the study of intelligent behavior. Of course, distilling an algorithmic understanding of these behaviors will not be easy, but we believe that a focus on natural behaviors will ultimately accelerate our understanding of intelligence that allows for generalization and flexibility (see Dennis et al., 2020, for a recent and similar call for natural behaviors in rodents). In turn, we may study a given brain area or neural circuitry under a variety of task demands, as opposed to within a single over-trained behavior. Understanding the computations of a given brain area not within the context of one, but of many tasks, is likely to bring us one step closer to understanding brain function.

As a proof-of principle, here we show that if monkeys are trained to navigate (from an ego-centric point of view) and stop at the location of a rewarded target in two-dimensional space, they can additionally show a number of derived and interesting behaviors. More precisely, without any specific training, these animals were able to show within trial or at most 1-shot learning of a novel and constantly changing sensorimotor mapping between motor output and sensory consequences. Further, they were also able to intuitively understand that the firefly was moving and would keep moving even after disappearing. Remarkably, the animals were able to continuously estimate the likely position of the unseen firefly and appropriately navigate to its reward boundary already within the very first session they encountered moving fireflies. This shows both the astonishing intelligence of these experimental animals, being able to traverse a large space of potential actions and states while concurrently estimating how other agents are moving through their own space of potential actions and states, but also emphasizes our duty as experimentalist to allow them to show this behavior. As a contrast, in a similar task where monkeys had to capture a moving target with a virtual agent (i.e., allocentric point of view similar to “Pac-Man” vs. the more naturalistic egocentric point of view utilized here), it seemingly took ~ 24 hours of experimentation for these animals to reach stable behavior (Yoo et al., 2019), and in that case the target was always visible. Lastly, we were able to show that within a binary decision-making task monkeys instinctively maximize their expected reward per unit time, by choosing to navigate to targets associated with a higher reward rate. Further, decision-making naturally generalized to the case of hundreds of fireflies in a world with no trial structure. The presented examples of decision making did not include all aspects of state-of-the-art decision making studies, where observers are typically asked to deliberate on noisy and often ambiguous sensory stimuli. However, within the framework of the firefly task we could easily manipulate the contrast of fireflies, as well as the reliability and congruency of optic flow vis-à-vis self-motion. The general strategy of training animals on a “reporting mechanism” - stopping at the firefly location - can be used to study a large set of naturalistic behaviors given that animals naturally attempt to maximize their reward rate.

In addition to the strong advantages afforded by this approach in the study of behavior - note that all data presented here (except Figure 6), 4 animals in 3 different tasks, was collected within 1 week - we also believe naturalistic tasks (and stimuli; e.g., Chandrasekaran et al., 2013; see Sonkusare et al., 2019, Matusz et al., 2018) may ultimately facilitate the interpretation of neural responses. As shown within the framework of active sensing (Schroeder et al., 2010), for example, in natural behaviors sensory input will occur at specific timings, and this may allow the nervous system to operate as it intends to, to appropriately coordinate among different functional units. By eliminating active sensing and instead presenting sensory stimuli at pre-programmed intervals, it is possible that in the majority of empirical efforts to date attempting to relate neurons to behavior we have caused an internal cacophony (i.e., sensory input arriving at all sorts of uncoordinated times vis-à-vis internal dynamics), one we do not see or understand, but one that does not let the brain operate in the regime it has evolved for. Similarly, either implicitly or explicitly, many consider population responses to be low dimensional (see the panoply of tools available to express neural responses in low dimensions; Cunningham & Yu, 2014). However, it is probable that this is a feature of our stimuli and the behaviors we study, and not of our brain (Stringer et al., 2019). In essence, if we allow the brain to operate in a higher dimensional space, we may be able to ascribe more “noise” to task-dependent or information-sampling manifolds, to “signal” (Gao & Ganguli, 2015).

Now, it is true that the study of natural behaviors comes at the expense of needing more sophisticated behavioral tracking (Bala et al., 2020; Pereira et al., 2020; Wu et al, 2020) and data analysis tools (see Huk et al., 2018, for an insightful perspective on this topic). For example, one of the pillars of data analyses in neurophysiology, i.e., averaging across trials, breaks down in naturalistic tasks with continuous action-perception loops. On the bright side, it is unlikely that the brain computes averages. Further, powerful techniques for the efficient estimation of single-units tuning functions are already underway (Balzani et al., 2020; Dowling et al., 2020), and a number of techniques for inferring the latent dynamics of populations of neurons exists, even at the single trial level and when requiring time-warping (e.g., GPFA; Yu et al., 2009; LFADS: Sussilo et al., 2016; Pandarinath et al., 2018; PSID: Sani et al., 2020; Williams et al., 2020). Further, while in the current piece we have not discussed nor leveraged a reinforcement learning perspective for model-based data analyses (see Choi & Kim, 2011; Daptardar et al., 2019; Kwon et al., 2020; Wu et al., 2020), it is our hope that already starting to study natural and generalizable behaviors in systems neuroscience will precisely demand for developments in this area. The holy grail in artificial intelligence is the development of generalized intelligence, where networks and the weight of their synapses do not have to be updated when goals or environments change. Arguably, early work in reinforcement learning was not capable of this type of generalization because of the simplistic scenarios under which agents were trained, and due to their shallow neural networks. More recently, we have seen the advent of “deep reinforcement learning”, where, just as primates, artificial agents (i) learn from the environment (hence “reinforcement learning”), and (ii) are equipped with deep neural networks (hence “deep”). This new approach to artificial intelligence is already showing promise in allowing for some generalization (Wang et al., 2018), and promises to catalyze a new symbiotic relationship with neuroscience (Botvinick et al., 2020). Just as in artificial intelligence researchers are attempting to make their in-silico networks more akin to that of biological neural networks (at least in size), in neuroscience we ought to take example of the sorts of behaviors studied in reinforcement learning and present in our daily lives. As we demonstrate here, monkeys are clearly capable of transfer learning (Constantinescu et al., 2016), of generalizing across tasks and quickly extrapolating what they were taught to novel situations. Understanding how they do so will likely catalyze a new phase in artificial intelligence (Hassabis et al., 2017; Higgins et al., 2016, Rusu et al., 2016).

Highlights.

• Ultimately we wish to understand how brains operate within a naturalistic, closed action-perception loop

• Reinforcement Learning and Control Theory naturally wade across traditional subfields of neuroscience

• We develop an experimental ecosystem inspired by the frameworks above, and tapping into structural knowledge

• Macaques naturally generalize to novel sensorimotor mappings, cases of inferences, and multi-option decision-making