Threshold accumulation of a constitutive protein explains E. coli cell-division behavior in nutrient upshifts

Significance

The mechanism leading to cell division in the bacterium Escherichia coli is unknown, but we know that it results in adding a roughly constant size every cell cycle, regardless of size at birth. While most available studies try to infer information on cell division from steadily dividing cells in constant nutrient conditions, this study leverages a high-resolution device to monitor single-cell growth division upon nutrient changes. Comparing these data with different mathematical models, we are able to discriminate among fundamentally different mechanisms of cell-division control, and we show that the data support a model where an unregulated protein accumulates to a threshold and triggers division.

Abstract

Despite a boost of recent progress in dynamic single-cell measurements and analyses in Escherichia coli, we still lack a mechanistic understanding of the determinants of the decision to divide. Specifically, the debate is open regarding the processes linking growth and chromosome replication to division and on the molecular origin of the observed “adder correlations,” whereby cells divide, adding roughly a constant volume independent of their initial volume. In order to gain insight into these questions, we interrogate dynamic size-growth behavior of single cells across nutrient upshifts with a high-precision microfluidic device. We find that the division rate changes quickly after nutrients change, much before growth rate goes to a steady state, and in a way that adder correlations are robustly conserved. Comparison of these data to simple mathematical models falsifies proposed mechanisms, where replication–segregation or septum completions are the limiting step for cell division. Instead, we show that the accumulation of a putative constitutively expressed “P-sector divisor” protein explains the behavior during the shift.

To divide, a cell needs to coordinate the allocation and duration of multiple processes, including metabolism, maintenance of cellular compartments, and faithful replication and segregation of chromosomes (1–5). Hence, an accurately timed decision to divide may have primary importance for survival and fitness. Achieving this accuracy likely requires a combination of upstream scheduling and downstream control, many aspects of which are only partially known (2, 6–8).

Classic work has addressed cell-size control based on population measurements (5), drawing conclusions that are increasingly challenged by recent findings (7, 9–12). In particular, we do not know if there is one fixed rate-limiting process setting division, and, in this case, if it is related to chromosome synthesis and segregation or to cell-surface-related processes. Recent work on the behavior of single cells has identified clear phenomenological patterns by which cells decide to divide. These can be characterized as correlation patterns between size-growth variables, such as added or multiplicative growth (13–17). Nearly all of the available work has focused on steady-state (balanced growth) single-cell data and established that cell size is not the only variable entering the decision to divide (18) and that cells follow a remarkably simple and robust pattern for setting division (13, 19–21), characterized by low or no correlations between the added size over one cell cycle and the size at birth (near-“adder” correlations). However, we still largely ignore both the time hierarchy (or more complex scheduling plan) and the molecular players at the basis of the observed near-adder behavior.

More generally, models founded on different mechanisms for division control can give rise to equivalent predictions in steady growth. Steady conditions only allow the exploration of correlations (or, more generally, joint distributions) between quantities involved in cell-size control (15). For instance, the evidence of the adder behavior comes from the observation of a lack of correlation between added size and initial size at the single-cell level (20). In order to discriminate between alternative mechanisms, one needs to go beyond correlations and to explore causal relationships between the variables involved in size control. Exploring the dynamics of size control in nonsteady conditions, e.g., during a nutrient shift, has the potential to allow one to disentangle alternative models based on different causal relationships.

Near-adder behavior, also observed between consecutive initiations (9, 22), may derive from accumulation and trigger of an “initiator” protein-setting replication initiation (16, 23, 24). The initiation of replication is known to be affected by a critical ATP-bound DnaA. While some molecular mechanisms involved in DNA opening and replisome assembly have been identified, it is still not known how they contribute to setting the timing of initiation of DNA replication in different growth conditions or how they can contribute to cell-cycle progression in single cells (10, 25, 26). In particular, additional players and processes, such as the alarmone ppGpp and DNA supercoiling, are implicated (27, 28), and DnaA itself might not even be rate-limiting for replication initiation in all growth conditions (29). The further assumption that chromosome replication–segregation limits cell division would explain the observed near-adder correlations between divisions (16), but this is also the subject of intense debate, as there is still no agreement on whether the initiation process itself may be rate-limiting for cell division (7–9, 16, 22, 30, 31). Independently from the chromosome cycle, cell division (and its adder correlations) could be set by the accumulation of a putative “divisor” factor, possibly related to the FtsZ division ring (9, 32) or to the synthesis of the septum (31). Finally, both the division and initiation processes could be scheduled upstream by yet-unidentified central cell-cycle regulators (2, 10), and downstream control processes could condition cell division to the completion of a set of necessary processes (7, 8).

In order to shed more light on cell-division dynamics, one needs to access conditions where nutrient-imposed growth rate and division rate are decoupled, and look at the behavior of single cells. To this end, we followed the growth-division dynamics of cells undergoing nutrient upshifts in a high-resolution microfluidic device. In this device, cells can be kept in steady-state growth and go from minimal M9 medium with glucose to the same medium supplemented with casamino acids. In these shifts, the change of amino acid levels was shown to alter the amount of free ppGpp, affecting translation and transcription of ribosomal promoters (33). However, the division-rate dynamics and the division-control behavior of single cells remain to be characterized. Our results identify the time scales involved in the changes of growth- and division-related variables and characterize the correlation patterns between cell-size growth and timing of cell division emanating from the mechanisms of division control. Second, we compare the data with mathematical models to support and/or falsify different underlying mechanistic models, such as initiation-limited division, accumulation of a putative divisor protein, and slaving of changes in division rate to changes in growth rate.

Results

Long-Term Single-Cell Tracking through a Nutritional Shift.

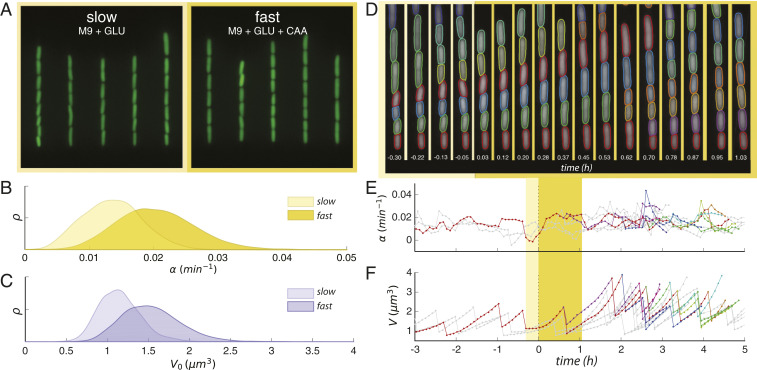
Robust environmental control was achieved by cultivating the Escherichia coli cells in a “mother machine” microfluidic device (34, 35). Fresh growth medium was fed into the device, and cells were observed through a timed switch from stringent (M9 + 0.4% glucose, doubling time = $57\pm 26$ min) to rich medium (M9 + 0.4% glucose +0.5% casamino acids, doubling time = $37\pm 13$ min). Cells must allocate energy resources toward the biosynthesis of amino acids while in stringent medium. When this metabolic limitation is relieved by the introduction of casamino acids into the external environment, cells grow and divide more quickly (36). Sample images from these respective “slow” and “fast” steady-growth states are shown in Fig. 1A. Consistent with Schaechter’s growth laws (37) and Woldringh’s original experiments (38), the increase in mean exponential growth rate $⟨{\alpha }_{\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{t}}⟩$ between steady states ($0.0137\pm 0.0052\hspace{0.17em}{\mathrm{m}\mathrm{i}\mathrm{n}}^{-\mathrm{1}}$ to $0.0203\pm 0.0062\hspace{0.17em}{\mathrm{m}\mathrm{i}\mathrm{n}}^{-\mathrm{1}}$; Fig. 1B) saw a requisite increase in mean birth volume $⟨V_0⟩$ ($1.15\pm 0.26\hspace{0.17em}\mu {\mathrm{m}}^{\mathrm{3}}$ to $1.53\pm 0.36\hspace{0.17em}\mu {\mathrm{m}}^{\mathrm{3}}$; Fig. 1B).

Fig. 1.

Robust and long-term single-cell tracking through a nutritional upshift. (A) Snapshots of trapped cells in microfluidic device under stringent (Left) and rich nutrient conditions (Right) (false-colored). (B) Steady-state distributions of growth rate ${\alpha }_{cc}$ in the two growth media. (C) Steady-state distributions of birth volumes $V_0$ for the sample populations in B. (D) Sample segmentation and tracking before and after the growth medium switch is implemented; time since switch is shown in hours. (E) Tracking the change of instantaneous growth rate following the switch for cells shown above. Yellow regions indicate time range spanned by segmented images; plotted line color corresponds to the cell above with the same color segmented boundary. (F) Volume tracking of the same cell lines. Interdivision time $\tau$ is identified as the interval between dramatic volume decreases.

The device configuration achieved high throughput without sacrificing spatiotemporal resolution, thereby enabling us to assess the system’s response to environmental perturbation at both population and single-cell levels. Thousands of single cells were segmented and tracked for several generations before and after the nutritional shift (Fig. 1 D–F). Cell shape and size were measured from the segmented cell boundary (Materials and Methods and SI Appendix) and used to determine individual growth rate and interdivision time. Specifically, the instantaneous growth rate of a single cell exhibiting exponential growth (34) is defined as ${\alpha }_{\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{t}}=\frac{1}{V}\frac{dV}{dt}$ (Fig. 1E); cell-division events can be found at the sudden and dramatic decreases in the volume of a tracked cell, yielding interdivision time $\tau$ (Fig. 1F).

Nonadiabatic Transition between Steady-Growth States.

In order to average equally and compare all of the different cell-cycle quantities (interdivision time, growth rate from cycle-wide exponential fit, and added volume), we associated their values to the time of division, then performed a sliding average. While different choices are possible, this is conservative with respect to quickly changing variables, and, technically, it ensures that the sliding averages do not start changing before the actual time of the nutrient shift. For instantaneous quantities, such as the growth rate and the production rates of the promoters, we also considered averages of the instantaneous (discrete) derivatives computed on single cells along lineages. These “instantaneous” averages are the appropriate choice in some instances, for example, as input to the quantitative models.

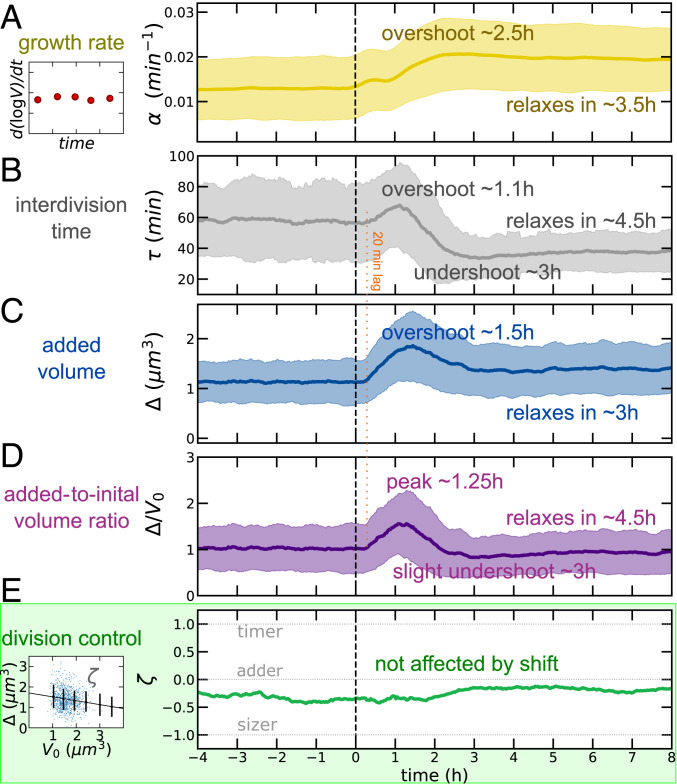
Fig. 2 shows how the mean cell growth, cell division, and cell-size parameters followed a very complex dynamics across the nutrient upshift, characterized by multiple time scales and trends, whereby the same quantity can both increase and decrease in different time windows.

Fig. 2.

Near-adder behavior is conserved through a nutrient upshift, despite complex dynamics of growth and division processes. Medium shift is indicated at dotted vertical line. (A) Mean growth rate (defined by a derivative of single-cell growth curves, as illustrated by the sketch in Left) as a function of time in the experiment. The solid line indicates observable mean, and shaded regions indicate SD for all time series. (B) Interdivision time transiently increases before reaching its new (lower) steady value across the upshift. (C and D) Mean added volume shows an overshoot over more than 2 h after the shift; the mean ratio of added to initial size is one at steady states. (E) The division control shows near-adder behavior robustly across the shift. The adder plot (added size vs. initial cell size, as illustrated by the sketch on Left) quantifies division control by the slope $\zeta$ (−1 for sizer, 1 for timer, and 0 for adder) (39). Data refer to averages over biological replicates using the P5ter promoter strain (Materials and Methods).

Fig. 2A shows the trend of mean growth rate vs. time in our data. Classically, it is assumed that cells display “rate maintenance” during an upshift, rapidly adopting the increased nutrient-imposed growth rate, but continuing at the preshift interdivision time for about one generation (40, 41), indicating a divergence from the relation $⟨{\alpha }_{\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{t}}⟩⟨\tau ⟩=\log 2$. The combination of an increasing growth rate under constant interdivision time is thought by some to establish the increased volume characteristic of rich medium (38, 42). Indeed, some degree of deviation is necessary for cells to achieve the ultimately increased volume dictated by bacterial growth laws (SI Appendix and ref. 10). Here, we found behavior far more complex than simple rate maintenance. In the minimal medium, cells had a growth rate of $0.0138\pm 0.0056\hspace{0.17em}\stackrel{-1}{min}$. Upon upshift, the growth rate increased gradually in agreement with early models of the upshift response (38), though initially it exceeded the new equilibrium value, reaching a maximum of $0.0219\pm 0.0076\hspace{0.17em}\stackrel{-1}{min}$ at $t=2.6\hspace{0.17em}\mathrm{h}$ before settling to $0.0204\pm 0.0059\hspace{0.17em}\stackrel{-1}{min}$.

Interdivision time exhibited a three-phase response (Fig. 2B), initially increasing from its preshift value of $57\pm 26\hspace{0.17em}min$ to $67\pm 28\hspace{0.17em}min$ at $t=1.1\hspace{0.17em}\mathrm{h}$, before quickly undershooting to a $34\pm 14\hspace{0.17em}min$ minimum 2 h later. The equilibrium interdivision time was established after approximately $4.5\hspace{0.17em}\mathrm{h}$ in the nutrient-rich growth medium to a value of $37\pm 13\hspace{0.17em}min$ (Fig. 2B). These noncomplementary responses of growth and division processes can be summarized by the trajectory in the plane $⟨{\alpha }_{\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{t}}⟩$ vs. $1/⟨\tau ⟩$ “growth space” (SI Appendix, Fig. S1A) ; we see that the nutritional upshift prompted the system to veer away from the “adiabatic” trajectory $⟨{\alpha }_{\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{t}}⟩⟨\tau ⟩=\log 2$ (dotted line), achieving a maximum of 0.968 at $t=1.3\hspace{0.17em}\mathrm{h}$. That is, directly following the upshift, cells grew to a final volume that is, on average, up to 2.63 times their birth volume. The population $⟨{\alpha }_{\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{t}}⟩⟨\tau ⟩$ then decreased and actually undershot $\log 2$ at $t=3\hspace{0.17em}\mathrm{h}$ (green segment), indicating that cells slightly reduced their size transiently in relation to their mothers before reaching equilibrium. SI Appendix, Fig. S1 B–E compare the trend of mean initial volume, cell width, growth rate, and interdivision time. Cell width relaxed very slowly to the new condition (31). Mean growth rate $⟨\alpha ⟩$ and mean interdivision/doubling time $⟨\tau ⟩$ at steady state are related through the equation $⟨{\alpha }_{\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{t}}⟩⟨\tau ⟩=\log 2$ (11, 43). However, the data show clearly that the system does not obey this relation in the process of adapting to a different nutrient condition (SI Appendix, Fig. S1F; we also note that in order to change mean size, this relation needs to be transiently broken).

Finally, we considered size changes across the shift. Simple calculations (13, 14, 20) show that at the steady state of balanced exponential growth, regardless of the mechanism of size control, the average added size $\mathrm{\Delta }$ and the average initial size have $V_0$ to be equal in order to produce two daughter cells that are the same size as the mother, but the two quantities need to be decoupled outside of steady-growth conditions, for example, in environments with changing nutrient conditions. Following the nutritional upshift at $t=0$, mean birth volume $V_0$ and mean added volume $\mathrm{\Delta }$ initially overshot their increased equilibrium values in the new growth medium (Fig. 2C and SI Appendix, Fig. S1A). Specifically, birth volume peaked at roughly 111% of its new equilibrium ($1.71\pm 0.44\hspace{0.17em}\mu {\mathrm{m}}^3$), reached at $t\simeq 2.5\hspace{0.17em}\mathrm{h}$, and plateaued to $1.54\pm 0.34$ for $t\ge 5\hspace{0.17em}\mathrm{h}$ (SI Appendix, Fig. S1A). Similarly, added volume attained a maximum of 123% of its equilibrium value, reaching $2.00\pm 0.78\hspace{0.17em}\mu {\mathrm{m}}^3$ at $t\simeq 1.5\hspace{0.17em}\mathrm{h}$ compared to its new plateau value of $1.63\pm 0.60\hspace{0.17em}\mu {\mathrm{m}}^3$ reached for $t\ge 4.5\hspace{0.17em}\mathrm{h}$ (SI Appendix, Fig. S1). Growth rate varied slowly, but it immediately changed its trend after the shift. Instead, interdivision time and added volume appeared to show a common delay of about 20 min (Fig. 2 B–D). The delay was even longer (about 1 h; SI Appendix, Fig. S1) for initial volume.* The mean ratio of added to mean volume needs to be unitary at stationarity, and this is verified in the data (Fig. 2D). During the transition, this quantity followed a fairly symmetric peak to about 1.5 times its value in about 2.5 h.

Near-Adder Behavior Is Conserved during the Upshift.

Recent studies have demonstrated the emergence of near-adder behavior in bacterial cells, but the underlying biophysical and molecular mechanisms remain elusive (13, 20, 30, 43). The size-control strategy employed to adjust to a new growth environment is similarly mysterious, since the existing adder observations have largely been confined to steady-state conditions. Our data provide the opportunity to extend the analysis of the robustness and the determinants of adder behavior out of steady-state growth.

Adder size control can be tested by plotting the added size against the initial size of dividing cells (39) and evaluating the slope. We define this parameter as $\zeta$. When $\zeta =0$, one has a perfect adder, i.e., cells add a size-independent volume to their initial size. The limits $\zeta =1$ and $\zeta =-1$ correspond to a timer (no control) and a sizer (absolute size threshold). Fig. 2E shows a strikingly robust trend of the measured near-adder behavior across the shift, despite all of the different time scales involved in the geometry changes. To further characterize the adopted size-control strategy and assess the contributions of the growth rate and interdivision time dynamics toward the overall size control, we also deployed an analysis developed in previous studies (15, 17) (SI Appendix, Fig. S2), whereby these contributions are inferred from the single-cell correlation patterns. This analysis confirmed a near-adder behavior that is uninterrupted by the environmental shift, affected by complementary dynamics between the timing- and growth-related components of size control.

Nutrient-Shift Data Are Qualitatively Incompatible with Some Proposed Models for Cell-Division Control.

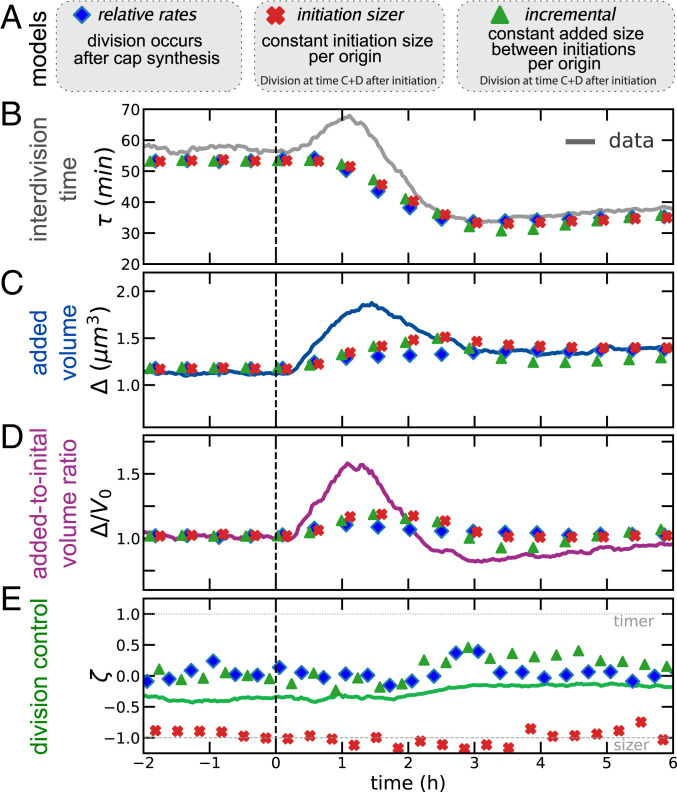
We first tested whether some previously proposed models could reproduce the complex behavior of division-related variables that we observed across the shift. To this end, we considered different models available in the literature (Fig 3A). Specifically, we ran single-cell simulations of the models proposed by Harris and Theriot (31) (“relative-rates” model), Ho and Amir (16) (“incremental” model), and the classic idea of “initiation sizer” (which we implemented here with size-uncoupled C + D period; ref. 7), using both modeled (Materials and Methods) and sampled growth-rate distributions across the shift (in the latter simulations, each cell was assigned an exponential growth rate extracted from the measured ones in each particular time bin).

Fig. 3.

The nonsteady data across the nutrient shift falsify commonly assumed models for division dynamics. (A) Summary of the models tested. (B–D) Dynamics of interdivision time (B) added size (C) and across the shift (D) cannot be re-created by existing size-control models. In particular, all of the tested models are too slow in reproducing the added-size dynamics and do not reproduce the initial increase in interdivision times. (E) The behavior of division control across the shift is steady across the shift for all three models considered. Data refer to averages over biological replicates using the P5ter promoter strain (Materials and Methods).

The models are described in more detail in Materials and Methods (see also SI Appendix). The relative-rates model assumes that chromosome replication–segregation is never limiting for cell division (9, 12) and that completion of synthesis of cap material (produced at the rate of surface synthesis) triggers division. A variant of the model may entail that target added size is proportional to width squared (31), and similar models assume that ring synthesis is limiting (32), but such variants are not crucial for our scopes. Both the incremental model and the initiation sizer model assume that replication–segregation are limiting for cell division. We did not consider the more complex scenario of concurrent time scales (7, 8) because of the unknown extra parameters used in this framework. The incremental model assumes that the chromosome is always limiting for cell division, and an interinitiation adder (per origin) based on the cell current growth rate. By contrast, the initiation sizer model assumes a critical size per origin at initiation.

None of the considered envelope- or chromosome-limited models for cell division predict correctly the division time dynamics (Fig 3B). Specifically, no model predicts that the interdivision time in the data initially increases, before decreasing to its new steady state. Considering interdivision timing dynamics across the shift, under increasing ${\alpha }_{\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{t}}$, in these models, interdivision time can only decrease upon increase of growth rate; hence, the models cannot reproduce the over/undershoot we observed for interdivision timing. Considering the dynamics of added size and initial size (Fig. 3 C and D), all models showed a delayed dynamics compared to the experimental data and cannot predict the observed early overshoot in added volume. Büke et al. (44) observe that the added size responds abruptly to changes in the ppGpp level, aided by transiently accelerated divisions upon a downshift, while growth adjusts on longer time scales. Confirming this observation, in our upshift data, the (counterintuitive) initial increase of interdivision time was accompanied by the increase of the added size on a faster time scale than the growth rate. Note, however, that in our shifts, the dynamics of ppGpp levels may follow a two-time-scale dynamics (45, 46).

A Threshold Accumulation Model of a Signal Produced at the Same Rate as a Protein Expressed from a Terminus-Proximate Constitutive Promoter Explains the Shift-Division Dynamics.

We figured that, instead, one may need a model where division dynamics is coupled to the mechanistic action of a biological circuit able to sense the physiological state of the cell. We therefore sought to define a mechanistic model where a protein under physiological control could act as the trigger defining cell division. In particular, we focused on a class of “threshold accumulator” models that have been proposed several times in the literature, both for replication and for cell division (1, 9, 23, 24, 32). We supposed that the fast and complex changes in division rate and added size observed during our shifts could be due to a coupling between the changes in biosynthetic “sectors” (47) occurring during the shift and cell-division dynamics. The literature offers models that describe proteome sector dynamics and biosynthesis in nonsteady regimes (33), and recent attempts were put forward to link these sectors with cell division (48–51). However, the descriptions differ, and current data do not allow us to select a specific one. Thus, rather than committing to a specific choice, we decided to take an experimentally driven approach to define our model.

Following the literature, we agnostically assumed that an effector molecule that is produced at a rate proportional to volume triggers division once a critical amount is reached (the above-mentioned threshold accumulation hypothesis). Steady-state data from our experiments provide validation of the fact that protein production is proportional to cell volume (SI Appendix, Fig. S3) and, thus, that a volume-specific rate $r$ is a good descriptor of protein synthesis from our promoters (52). Finally, a well-known sufficient requirement to obtain near-adder correlations from an accumulator model is that the trigger molecule is reset to zero upon birth (1, 31, 32). This last point can be achieved biologically if the divisor molecule is structural, e.g., cell-surface material that is integrated into the cell cap upon division (31).

Assuming a putative divisor protein is produced with rate $rV$, proportional to volume (here, $r$ has units of inverse volume and time), $dN/dt=rV$. There is a critical amount $N^{*}$ that, once reached, triggers division, $N\left(\tau \right)=N^{*}$, and at cell birth, the number of molecules are reset to zero $N\left(0\right)=0$. Solving for $N$, under steady growth, one obtains

$$N\left(t\right)=\frac{r}{{\alpha }_{\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{t}}}{V}_0\left(e^{{\alpha }_{\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{t}}t}-1\right),$$ (1)

and, as a consequence,

$$\begin{array}{cc}\hfill N^{*}& =\frac{r}{{\alpha }_{\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{t}}}{V}_0\left(e^{{\alpha }_{\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{t}}\tau }-1\right)\hfill \\ \hfill & =\frac{r}{{\alpha }_{\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{t}}}\left(V_f-V_0\right)\hfill \\ \hfill & =\frac{r}{{\alpha }_{\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{t}}}\mathrm{\Delta }.\hfill \end{array}$$ (2)

Our strains carried fluorescent reporters for ribosomal and constitutive promoters inserted in the chromosome close to either the origin or the terminus of replication (Materials and Methods and refs. 53 and 54), and we used their experimentally measured dynamics to define the putative production rate of the putative “adder protein.” The constitutive reporter “P5” is based on a strong exogenous promoter with consensus −10 and −35 sequences lacking any transcription factor regulation, as well as lacking a GC-rich ppGpp discriminator region at the transcription initiation site that would render it sensitive to inhibition by ppGpp. Conversely, the ribosomal reporter “P1” is derived from the P1 promoter of the ribosomal RNA operon rrnB and, therefore, contains a GC-rich discriminator region at the transcription start site. The upstream end of the promoter has been omitted, thus deleting the binding sites for any transcriptional regulators (Materials and Methods). Thus, we define “constitutive” here as lacking transcription factor regulation, as well as lacking a ppGpp discriminator region. In order to determine the role of ppGpp in the regulation of gene expression and of a possible trigger factor during a growth-shift adaptation, we compared the production rate of GFP in our strains having chromosomal reporters for ribosomal (P1) and constitutive (P5) promoters and measured the average volume-specific rate, $r\left(t\right)$, across the shift.

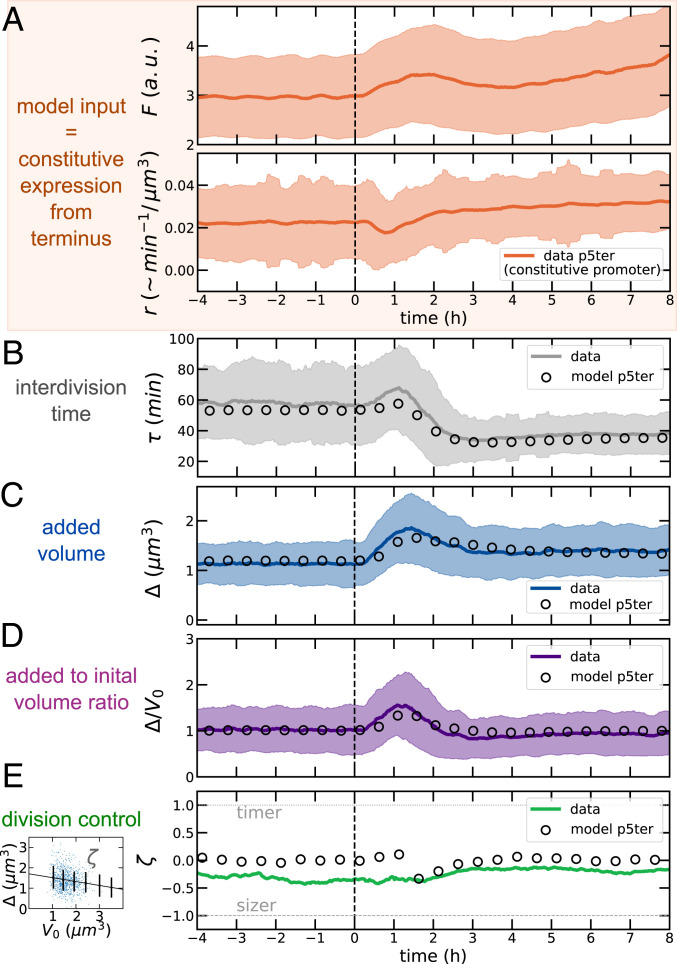
A comparison of Eq. 2 with steady-state data for all promoters indicates that $N^{*}$ was about the same in both conditions, before and after the shift (SI Appendix, Fig. S4). We therefore reverted for simplicity to a model where $N^{*}$ was constant (the data do not allow us to quantify this number in absolute terms due to the arbitrary unit of fluorescence measurement). We then ran simulations using as input from experimental data (hence, with no free parameters) both the measured production rate $r\left(t\right)$ (for the four strains with reporters) and the growth rate ${\alpha }_{\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{t}}\left(t\right)$ (Fig. 4A). Fig. 4 B–D shows that using similar dynamics to the terminus-proximate constitutive promoter P5ter gives very satisfactory agreement with the data and captures all of the complex changes of both interdivision time and (added and initial) cell-size dynamics. For consistency, we also verified that both model and data complied to an expected constraint involving strength of size control, mean size, and growth variables (SI Appendix, Fig. S5).

Fig. 4.

A putative divisor protein expressed from a constitutive promoter explains the shift data. (A) As model input, we used the measured instantaneous growth rates and volume-specific production rate $r$ (obtained from derivatives along lineages) from our promoters (in this case, the P5 constitutive promoter inserted close to the replication terminus). Note that this quantity has units ${\mathrm{m}\mathrm{i}\mathrm{n}}^{-1}$/$\mu {\mathrm{m}}^3$, minus a constant conversion factor from fluorescence to molecule number. The panel also shows the absolute fluorescence $F$ from the same promoter. A.u., arbitrary units. (B–D) The model predicts faithfully the size dynamics. (E) The model reproduces the observed robustness of near-adder size control. Other model variants using the production rates of different reporters fail to reproduce the observed size dynamics (SI Appendix, Figs. S6–S8). Data refer to average over biological replicates using the P5ter promoter strain (see Materials and Methods and SI Appendix, Figs. S6–S8 for the other strains).

While the robustness of the near-adder behavior across the shift was captured by all of the models based on four strains used here (Fig. 4E and SI Appendix, Figs. S6–S8), the only model that can reproduce the cell size and division time dynamics is the one based on the P5ter promoter. Conversely, the alternative models (based on ribosomal promoter P1 close to both replication origin and terminus, as well as on the same P5 promoter close to the origin) fail to reproduce the size and division time dynamics, reinforcing the idea that the agreement of the data with the model based on the P5ter promoter is not a coincidence (SI Appendix, Figs. S6–S8). Finally, compared to the models described in Fig. 3, this accumulator model requires only one free parameter ($N^{*}$, calibrated to match the initial size before the shift). Hence, in this case, the steady-state size after the shift is a prediction, which the model performs accurately (validating the idea of a constant critical threshold for the putative adder protein).

The Production Rate of the Accumulator Model Can Be Reverse-Engineered from Division Data and Behaves as a Constitutive Promoter.

An independent reverse argument on the same model leads to the same conclusions, without using the promoter-expression data as model input. This argument assumes that $N^{*}$ is constant after the shift and determines the volume-specific rate that the putative adder molecule needs to have in order to reproduce the data. Solving for $r$ in Eq. 2 gives a requirement on the volume-specific transcription rate in steady growth. In Materials and Methods, we generalize Eq. 2 out of balanced exponential growth, when the instantaneous growth rate ${\alpha }_{\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{t}}\left(t\right)$ and the volume-specific rate of expression $r\left(t\right)$ are time-dependent. The full equation cannot be analytically inverted to infer $r_{\mathrm{r}\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{e}}\left(t\right)$ from the instantaneous growth-rate ${\alpha }_{\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{t}}\left(t\right)$ and the added size $\mathrm{\Delta }\left(t\right)$. Nevertheless, the numerical solution matches very well the following expression

$$r_{\mathrm{r}\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{e}}\left(t-\tau /2\right)\simeq \frac{{\alpha }_{\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{t}}{N}^{*}}{\mathrm{\Delta }\left(t\right)}=\frac{{\alpha }_{\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{t}}\left(t\right)N^{*}}{V_0\left(t\right)\left(e^{{\alpha }_{\mathrm{c}\mathrm{c}}\left(t\right)\tau \left(t\right)}-1\right)}.$$ (3)

The delay comes from the fact that the integrated production rate over the cell cycle causes the (future) added size at the division time. This effect is fully captured by the expression presented in Materials and Methods.

SI Appendix, Fig. S9 shows the behavior of $r_{\mathrm{r}\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{e}}$ in the transient period after the shift, which initially decreases, and then reaches a higher plateau than found before the shift. This behavior closely resembles the dynamics of the P5 constitutive promoter. The precise value of $N^{*}$ does not affect this “down-up” dynamics and just sets a quantitative vertical offset in the plot shown in SI Appendix, Fig. S9; it is important for this reverse argument, however, that $N^{*}$ remains constant after the shift. Comparing SI Appendix, Fig. S9 with Fig 4A confirms that constitutive expression meets the requirements set by our shift data for the accumulated divisor factor. We also note that the model clearly works well in a fit where the threshold is different before and after shift, and, in this case, the best-fit parameter values are such that $N^{*}$ (preshift) $\simeq N^{*}$ (postshift), which confirms that the value of the threshold remains constant or nearly constant.

The model obtained by the reverse argument shows an even more faithful agreement with data (SI Appendix, Fig. S10). We also applied this model to an upshift experiment between the same two nutrient conditions at 30 °C (SI Appendix, Fig. S11), finding that the inferred rate by the reverse model shows the same pattern over the shift, initially decreasing, then increasing with an overshoot, before reaching a plateau. Finally, we used the reverse model for more detailed comparisons with data. First, we analyzed the shift dynamics by a discrete time variable representing the number of generations separating each lineage from the shift. The overshoots visible in Fig. 2 persist when the same data are plotted by aligning the cell generations before and after nutrient shift and are captured by both the positive and the reverse model (SI Appendix, Fig. S12). Second, we performed a detailed analysis of the generation seeing the shift and the subsequent one (SI Appendix, Figs. S13–S15). This analysis shows that the division behavior of the generation seeing the shift depends on the cell-cycle time at the time the nutrient level changes. The model reproduces well the cell-cycle behavior of the generation seeing the shift and the subsequent ones in terms of interdivision time and added size. However, a careful analysis also reveals discrepancies that are likely due to ingredients not present in our model (and not monitored in our data), such as the interplay of the shift time and the processing of the chromosome during the cell cycle (2, 7). Specifically, in the model, cells that see the nutrient shift late in their cell cycle do not modify their cycle duration compared to the preshift conditions, while in the data, these cells delay their division (SI Appendix, Fig. S15).

Discussion

This work has two main components.

First, it examines a well-defined upshift where the carbon source remains the same, and the cell adapts to the presence of the added amino acids, in real time and in single cells, extending classic results obtained when single-cell tracking was not possible (38). The response to the shift is unexpectedly complex, challenging old conclusions from population analysis. Most variables, including growth rate, show a two- or three-phase dynamics, with trend changes, overshoots, and undershoots before they fully relax; growth rate is slow to achieve full relaxation to its nutrient-imposed value; interdivision time and added size start changing early on, in parallel to growth rate itself (and not slaved to this variable). A near-adder correlation is maintained throughout the shift despite the complex response. We are aware that much of this complexity will need deeper theoretical and experimental investigations to be fully unraveled, but our dataset could set an important reference for forthcoming studies. Here, we decided to restrict our focus on the division-control dynamics and validation of competing cell-division models. Nutrient shift experiments at the single-cell level have been performed and analyzed by Harris and Theriot (31) and by two studies performed in parallel to this one (44, 55). Among these studies, only this study and the study by Büke et al. (44) focused on the coordination of division dynamics with growth. Theoretically, nutrient-shift simulations using a threshold accumulation model have been performed by Ojkic et al. (32), with a relative-rates model where FtsZ-ring synthesis limits division.

Second, the unexpected kinetics during the shift are qualitatively incompatible with several current models for control of cell size in single cells. This holds irrespective of the details. Thus, a new way of looking at the cell-division decision upon a shift in growth conditions is required. We explore experimentally the possibility that division could be triggered by the accumulation of a critical amount of a constitutively expressed (i.e., presumptively not growth-rate regulated, or not directly) molecule. As we show, the production levels for such a molecule explain the unexpected division kinetics, provided the molecule is expressed from an unregulated promoter located near the terminus.

Near-adder size-control behavior is robust across the shift, despite large changes in the cell-cycle parameters, as well as in the correlations between initial size and growth rate in this transient regime. This feature is surprising on biological grounds, and, as we show, it is a common feature of the current phenomenological models, where it is built on the assumption that either the interinitiation or the interdivision process invariably should reproduce adder correlations (for the case of an initiation sizer, we observe the same constant behavior, with a different value of the size-control parameter). This common assumption is essentially post hoc when looking at steady-state data, but its applicability to transient data indicates that its validity might be broader. Hence, we take the robustness of the size-control parameter across the shift as a validation (beyond expectation) of the widespread approach to modeling size control.

However, not all models can reproduce the complex temporal changes observed in the key cell-cycle parameters monitored here, and specifically of interdivision time, initial size, and added size. Standard frameworks describing cell-size control (13, 14) are “hierarchical,” in the sense that (constant, or fluctuating) nutrients are thought to affect growth rate, and size and division rate, in turn, adjust to the growth rate (44). However, division rate may sense nutrients directly (44) and become decoupled from the different cell-growth processes connected to the nutrient-imposed growth rate (bulk mass biosynthesis, elongation, and volume change). It is worth noting that, as soon as the nutrient condition is changed, both added size and interdivision time show changes before growth rate begins to change and reach a new steady state before growth rate does, thus invalidating a view where the cell cycle “senses” growth rate and adapts the interdivision time accordingly. A scenario where both the division and the biosynthesis machinery are able to sense and react to nutrient changes appears more plausible. As we further show, the standard view where cell division is slaved to the chromosome replication–segregation cycle appears to be at odds with the observed time scales and qualitative changes in cell-cycle parameters across the shift. Both results are in accordance with a parallel study on downshifts induced by increased ppGpp (44). Beyond the tested models, the same limitations may be common to most models available in the literature (which were not designed to describe shifts), as a consequence of the hidden assumption whereby these models describe division rate as a consequence of growth rate, treated as an input parameters (5).

Finally, using the data from four GFP reporter strains with either a ribosomal or a constitutive promoter inserted at two different locations along the genome, we could test the hypothesis that the adder molecule is a protein under the control of these kinds of promoters (whose expression is differently dependent on growth rate). We believe that, giving our current limited knowledge on the cross-talks between growth- and cell-cycle physiology, this “empirical” approach to forward models is preferrable to more theoretical routes postulating the behavior of different proteome sectors across shifts (48–51). Comparing the predictions of the four possible models that can be generated from our data, we show that the data are in agreement with a model where a putative adder protein is under the control of a constitutive promoter located close to the replication terminus of the E. coli chromosome. This model predicts efficiently the behavior of interdivision time, initial size, and added size of cells across the shift. Conversely, if we reverse-engineer the production rate of an accumulator model in order to reproduce our division data, we find that it matches the expression pattern of the terminus-proximate constitutive promoter.

Crucially, the specific production rate of a constitutive promoter transiently decreases immediately after the upshift, while the one of a ribosomal promoter transiently increases, in agreement with the rapid decrease in ppGpp upon addition of amino acids to cells grown in their absence (36). Note, however, that in this study, we do not investigate why the observed promoters show this complex behavior, which is a separate question (33). Presumably, cells are spending their resources producing more ribosomes to take advantage of the richer medium to such a level that constitutive promoters are fractionally down-regulated. We also note that surface and mass synthesis decouple during nutrient shifts (55).

The conclusion that a threshold accumulation process sets division is common in the recent literature (to the point that isolating competing hypotheses is an open challenge). A recent study combining experiments and theory concludes that in order to reproduce the observed trends across conditions, this molecule should be under growth-rate control and able to sense the mean duration of the replication or segregation period of the chromosome in a given condition (10). Several theoretical studies have speculated on the possible interactions between biosynthetic “sectors” and cell-division control (48–51). In particular, based on the analysis of steady-state growth-division data, two studies (48, 49) have suggested that the molecule affecting the adder behavior may be a protein of the “P sector” of the proteome, i.e., a constitutive promoter, in full agreement with the conclusions reached here.

It has been speculated that the divisor molecule could be FtsZ itself (9, 32). In agreement with our findings, FtsZ expression is not ppGpp-dependent (56). Additionally, its expression rate is inversely proportional to the replication–segregation period duration (9, 10, 48). However, the subcellular localization dynamics and activity of this protein are complex (57). Additionally, the dynamics of width across the shift in our data (SI Appendix, Fig. S1) is very slow compared to the changes in division rate and added size. Hence, our data seem at odds with a scenario whereby the FtsZ ring (or the septum) are always rate-limiting for cell division, which predicts a direct link between cell diameter and division rate (31, 32).

A parallel single-cell study has implicated the alarmone ppGpp (44), the key player of a network sensing nutrient levels and setting the growth rate through transcriptional control of ribosomal promoters, in the direct regulation of division rate. This result is based on the observation that the added size and interdivision time change faster than the growth rate in a downshift induced by upregulation of ppGpp synthesis. This observation opens the question of whether ppGpp could have direct or indirect interactions with the divisome.

In our shifts, the carbon source does not change, and available ppGpp levels are expected to decrease due to the increased levels of amino acids in the new medium (45), so the nutrient change could be paralleled to an effective rapid decrease in ppGpp levels, similarly to the case studied by Büke et al. (44) (in our case, we also expect that the transcription of genes for AA biosynthesis is shut off, freeing resources for the increased expression of genes involved in the transport of AA and biosynthesis of cellular components). Based on our data and modeling analysis, we speculate that the control of ppGpp on cell division could be exerted through an indirect effect of the change in ppGpp on the transcription of a constitutive promoter, supporting the idea that the more direct ppGpp–divisome interaction proposed by Büke et al. might not be necessary.

Our data and model show that this transcriptional effect can explain the fast time-scale changes observed in the shift. ppGpp binds directly to RNA polymerase (RNAP) and destabilizes its interaction with the promoter, with a strong effect on the transcription-initiation rate of ribosomal promoters, where the RNAP–promoter complex is particularly weak (45, 58). A rapid decrease in ppGpp could thus result in an increase in the amount of RNAP that is used to transcribe ribosomal genes, decreasing the amount of RNAP that is available for the transcription of other promoters, such as the P5 promoter used here. Hence, a change in ppGpp levels has, in principle, the power of changing the production rate of most gene categories on relatively fast time scales (36, 47). Our analysis shows that this action could be sufficient to modulate division rate very quickly across an upshift, and faster than effecting the observed changes in overall growth rate. As a rationale for this, we hypothesize that a change in the overall biosynthetic rate requires production of many ribosomes, whereas a sufficiently low threshold of a putative adder protein could make the effects of a change in its production rate on the cell-division rate very quick to observe.

To conclude, we propose a more generic and formal interpretation of our main results, which may help guide future analyses aiming to identify molecular players of cell division. The accumulator model can reproduce the data if two crucial prescriptions are included. First, the production rate has to transiently decrease during the upshift, then increase, in order to capture the behavior of the division rate. Hence, the divisor molecule must be something that responds in a precise way to changes in ppGpp levels, without using biosynthesis as a readout. Second, since the terminus-proximate location of the promoter appears to play a role, any putative molecular accumulator circuit leading to cell division should be able to count terminus copies or something correlated.

Materials and Methods

Experimental Details.

Strains and culture conditions.

The six strains assayed here each contain one of three promoters controlling GFP expression from the gfpmut2 gene (59) at either a genomic position close to the origin or the terminus of replication, with E. coli K-12 BW25113 serving as the background. The former is at genome coordinate 4,413,507 bp, between the two convergent genes aidB and yjfN, while the latter is at 1,395,706 bp, between the two convergent genes ynaJ and uspE. The two promoters used here correspond to the following: The first contains a shortened version of the well-characterized ribosomal RNA operon promoter rrnBP1 (60, 61), here called P1, which includes the sequence from −69 to +6 relative to the transcription start site. The binding sites for Fis and the higher-affinity H-NS binding site are thus omitted from this construct. The rrnBP1 promoter has a GC-rich discriminator region at the transcription-initiation site, which makes the open complex sensitive to changes in negative supercoiling and to inhibition by ppGpp (61). The second promoter used here is a constitutive promoter, P5, derived from the phage T5, that has consensus −10 and −35 sequences and no discriminator region. Per strain, one of the above promoters was placed at one of two chromosomal locations: either close to the origin of replication at ori-3 (4,413,507 bp, nearest gene aidB); or the replication terminus at ter-3 (1,395,706 bp, nearest gene ydaA). A kanamycin-resistance cassette (KanR) is divergently expressed from each promoter-gfpmut2 cassette. Bacteria were always kept at 37 °C. Growth medium had M9 minimal medium (BD Difco) and 0.4% glucose as the carbon source; the upshift consisted of switching M9–glucose with M9–glucose supplemented with 0.5% casamino acids (Sigma-Aldrich Company Ltd.; OmniPur). Overnight cultures were diluted 500:1 in new, slow-growth medium and returned to the incubator for 3 to 4 h, i.e., until the cells reached their exponential phase. One milliliter of culture was then pipetted into two 2-mL prewarmed Eppendorf tubes and centrifuged at 4,000 rpm and 37 °C for 4 min. The supernatant was pipetted off, and each pellet was resuspended in 40 to 50 $\mu$L of fresh slow-growth medium by vortexing. These condensed cultures were then injected into prewarmed, passivated, and rinsed polydimethylsiloxane (PDMS) chips as described below.

Device fabrication and loading.

PDMS-based (Sylgard by Dow Corning) microfluidic devices were constructed to support the long-term growth of E. coli under a nutrient upshift from slow to fast growth medium and bonded onto glass coverslips (Menzel-Gläser; 22 × 60 mm), as described in ref. 35. PDMS was cast over the master template to yield the negative-relief mother machine pattern to be fixed to the coverslip. Before loading bacteria into the device, each chip was treated with a solution of bovine serum albumin (BSA; Sigma-Aldrich Company Ltd.) to minimize bacterial interactions and binding to the glass or PDMS components. Devices were pipetted with 5 $\mu$L of 10% BSA and incubated at 37 °C for 45 to 60 min. Passivated chips were rinsed with fresh medium. Bacteria in exponential phase were then similarly pipetted into the device. The chip was then mounted on a spin coater (Electronic Micro Systems, model 4000), such that the line connecting both injection sites intersected the axis of rotation. Each sample was spun at 3,250 rpm for 10 min, and bacteria were pulled into the microchannels by the resulting centripetal force. Chips were inspected under 40× magnification to confirm that a substantial fraction of microchannels contained bacteria. In the case of poor trapping, the sample was spun again under the same settings.

Microfluidic circuit and growth medium switch.

Two 20-mL syringes (Becton Dickinson UK Ltd.; Plastipak) were prepared with each growth medium and mounted on separate syringe pumps (KD Scientific; Legato 110). A membrane filter (Sigma-Aldrich Company Ltd.; MF-Millipore, 0.22-$\mu$m pore size) was placed between the syringe and the dispensing tip (Intertronics; stainless steel, straight blunt, 1/2″, 23 gauge), ensuring that only sterile growth medium entered the microfluidic device. A Y-junction was formed with three pieces of Tygon tubing (Cole Parmer; 0.020″ × 0.060″ outside diameter [OD]; 40-, 40-, and 20-cm lengths) and a PEEK Y-connector (Kinesis; for 1/16″ OD tubing, flangeless fittings). The two 40-cm tubing segments were attached to the syringe-dispensing tips, and the 20-cm tubing segment was connected to the input injection site of the chip by using the stainless-steel shaft of a 90° dispensing tip (Intertronics; stainless steel, 90° bend blunt, 22 gauge). Prior to attaching the 90° connector to the chip, the fast-growth medium was pumped through the tubing at 100 $\mu$L/min until about 0.5 mL had drained from the connector end. The same was then repeated by using the slow-growth medium. The syringe pump controlling the slow-growth medium was then set to 10 $\mu$L/min, and the input connector tip was inserted into the chip. The two syringe pumps were programmed to alternate so that the slow-growth medium fed the device first, while the fast-growth medium pump was delayed. In most cases, a complete upshift experiment lasted between 18 and 24 h, with roughly equal time spent in each growth medium. While the chip was plugged in, the infusion flow rate was set to 10 $\mu$L/min, irrespective of growth medium. This corresponds to a flow velocity in the main feeding channel of approximately 166.7 mm/s. There was a brief delay of roughly 4 min before the new medium reached the device, which was accounted in our definition of the shift time. This corresponds to the 20-cm distance that the fluid must travel from the Y-connector junction to the chip. We also performed an experimental test of the time to fill a channel and the device itself, by flowing (fluorescent) Luria–Bertani medium (SI Appendix, Fig. S16). It takes less than 5 min (one frame) to completely fill a channel with medium. The mixing of the two media outside the channels is negligible, judging from the fluorescence, as expected from such a low-Reynolds-number flow. Additionally, we tested directly in the data that the growth rate averaged on the channels at the two outermost sides of the device shows a small delay, of about 5 min (SI Appendix, Fig. S16).

Optical microscopy and image acquisition.

Images were acquired under 60× magnification by using an inverted microscope (Nikon Eclipse Ti-E; oil objective, numerical aperture 1.45). The camera (Andor iXon DU-897 electron-multiplying charge-coupled device, Oxford Instruments Industrial Products Ltd.) captured 16-bit images at 512- × 512-pixel resolution, with the length of 1 pixel equal to 0.1067 $\mu$m. The motorized stage and camera were programmed to cycle between at most 40 fields of view, each spanning roughly eight microchannels, every 5 min, recording three images per field of view: one brightfield (red or green illumination; excitation PD01 and PM01, LUXEON Z light-emitting diode [LED], Lumileds; multiband FF01-392/474/554/635 optical filter, Semrock), one fluorescence (blue, PB01), and one blank without illumination. The exposure time for all images was 0.286 s, corresponding to the camera’s maximum shutter speed. All LEDs were set at their respective minimum forward currents to minimize potential interference with the cells due to overexposure. The entire apparatus was left to acquire images continuously through the growth-medium switch, with sufficient data before and after the switch event. The coverslip of the microfluidic device was fixed onto a custom aluminum thermoelectric cooler that was then fitted on the microscope stage. The stage and objective temperatures were always set to 37 °C. The input tubing was woven through inlet holes to ensure that fluid entering the chip was the appropriate temperature.

Data Analysis Details.

Segmentation and tracking algorithms.

We developed bugpipe, a custom-built MATLAB package to process mother machine-based images and handle the resulting cell data. In brief, for each background-subtracted fluorescence image, the segmentation algorithm proceeds in the following steps: 1) find regions of interest (ROIs), i.e., the channels trapping each cell line; 2) within each ROI, threshold and isolate cells in the background; 3) find cell boundaries and further process any “fused” cells; and 4) remove artifacts based on size. Simple background subtraction was performed by subtracting the respective dark frame from each fluorescence image. The tracking procedure that links individual cells between consecutive frames takes advantage of the geometric constraints imposed by the microchannel format of the microfluidic chip. Namely, that in the absence of cell divisions, a cell’s rank within a channel is conserved between frames. The tracking procedure operates by: 1) microchannel matching between frames, 2) sorting cells in-channel based on distance from the dead-end, and 3) determining markers for cell division to adjust the rank-based pairing as necessary. The package was designed with separate functions for segmentation, tracking, and data-handling procedures. This grants flexibility for the user if, say, only big-data manipulation tools are needed. Detailed information on bugpipe is available in SI Appendix. The bugpipe package and its complete documentation is available at https://github.com/panlilio/bugpipe. The data analyzed here refer to three repeats of the entire upshift experiment for the P5ori promoter, two repeats for the P5ter and P1ori promoters, and one repeat for the P1ter promoter.

Modeling Details.

We considered four alternative models to describe cell-size control in steady growth and during the nutrient shift. These models (with one exception) are known to reproduce the adder correlations in steady growth and can be parameterized to reproduce the empirical relation between size and growth rate across condition, known as Schaechter’s law (10, 37).

We generalized these models to nonsteady conditions under nutrient shifts. This generalization required nonstraightforward decisions. Here, we employed a data-driven strategy and used the experimental trajectory of the average growth rate $\overline{\alpha }\left(t\right)$, and of other quantities, if applicable, as input of the model. The model output that we tested against the experiments were the trajectories of division time, added size, initial size, and strength of division control during the shift.

In order to take into account for the nonsteady values of the single-cell growth rate ${\alpha }_{\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{t}}$, we consider the following dynamics

$$\frac{d{\alpha }_{\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{t}}\left(t\right)}{dt}=-\frac{1}{T_{\alpha }}\left({\alpha }_{\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{t}}\left(t\right)-\overline{\alpha }\left(t\right)\right)+\sqrt{\frac{{\sigma }_{\alpha }}{T_{\alpha }}}\xi \left(t\right),$$ (4)

where $\xi \left(t\right)$ is a Gaussian white noise with zero mean and an SD equal to one. Under constant values of $\overline{\alpha }\left(t\right)$ ($\overline{\alpha }\left(t\right)=\overline{\alpha }$), this equation corresponds to a Gaussian stationary distribution of the ${\alpha }_{\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{t}}\left(t\right)$ with mean $\overline{\alpha }$ and SD ${\sigma }_{\alpha }$. In this case, the parameter $T_{\alpha }$ sets the autocorrelation time of the single-cell growth rates. When instead $\overline{\alpha }\left(t\right)$ varies, $T_{\alpha }$ sets the typical time that it takes for a single cell to respond to the forcing imposed by $\overline{\alpha }\left(t\right)$. It is easy to show that the average growth rate is equal to

$$⟨{\alpha }_{\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{t}}\left(t\right)⟩={\int }_0^{\infty }ds\hspace{0.17em}\frac{1}{T_{\alpha }}\exp \left(-\frac{s}{T_{\alpha }}\right)\overline{\alpha }\left(t-s\right).$$ (5)

In order to simplify the inference of $\overline{\alpha }\left(t\right)$, we assumed $T_{\alpha }$ to be small compared to a cell cycle and to the typical time of change of $\overline{\alpha }\left(t\right)$ during the nutrient shift. Under this assumption, we set $\overline{\alpha }\left(t\right)=⟨{\alpha }_{\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{t}}\left(t\right)⟩$. For numerical purposes, we set $T_{\alpha }=1$ min. We also verified that our simulations gave the same results extracting the values of ${\alpha }_{\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{t}}$ from the experimental values in each time bin.

Initiation-sizer model.

The model assumes that initiation starts at a constant cell size per origin of replication (“initiation mass”), i.e., $⟨V_B⟩=O{V}^{*}$, where $V_B$ is the size of the cell at initiation, and $O$ is the number of origins, while $V^{*}$ is a constant size (independent of the condition) (43). Division happens at a time $⟨t_{C+D}⟩$ after initiation. In steady growth, the model reproduces Schaechter’s law and a sizer-like division control. This model is different (simpler) from the one used in ref. 30, which includes nontrivial correlations (see refs. 7 and 8 for a thorough discussion). Single-cell growth-rate trajectories were modeled as explained above. We set the two other free parameters of the model ($V^{*}$ and $⟨t_{C+D}⟩$) to reproduce the initial average size at the two steady-growth conditions before and after the shift. In particular, in steady growth, it is known (10, 30) that $⟨V_0⟩=V^{*}\exp \overline{\alpha }⟨t_{C+D}⟩$, which can be easily inverted to determine $V^{*}$ and $⟨t_{C+D}⟩$ using the values of $⟨V_0⟩$ and $\overline{\alpha }$ before and after the shift. Both the initiation and time-to-division are stochastic, where $⟨V_B⟩$ and $⟨t_{C+D}⟩$ are averages. We assume Gaussian noise on $\log V_B$ and $t_{C+D}$ with equal magnitude, set to reproduce the coefficient of variation of the initial size [which is independent of the condition (21, 39)].

Incremental model (16).

The model assumes that cells add, on average, a constant size per origin ${\mathrm{\Delta }}^{*}=⟨{\mathrm{\Delta }}_I⟩/O$ between initiations of replication. As in the initiation-sizer model, division takes place at a size-independent time $⟨t_{C+D}⟩$ after initiation. Single-cell growth-rate trajectories were modeled as explained above. The two free parameters of the model (${\mathrm{\Delta }}^{*}$ and $⟨t_{C+D}⟩$) are set to reproduce the initial average size at the two steady-growth conditions before and after the shift using the relationship $⟨V_0⟩={\mathrm{\Delta }}^{*}\exp \overline{\alpha }⟨t_{C+D}⟩$. Both the initiation and time-to-division are stochastic, where the $\log {\mathrm{\Delta }}_I$ and $t_{C+B}$ are independent Gaussian random variables with equal SD, set to match variability of initial size.

Relative-rates model.

This model assumes that septum-formation is the rate-limiting process for cell division (31). Synthesis of the target surface material $S$ happens at a rate proportional to the volume $dS/dt=\beta V$, and $S$ is reset to zero at every cell division. $\beta \left(t\right)$ along the shift is obtained from measured cell surface (from width and length, assuming the shape to be a spherocylinder) in our data. Division is triggered when $S\left(t\right)$ reaches a critical threshold $S^{*}$. Depending on the assumption (31), the threshold could be constant or proportional to the septum area $\pi w^2$, with $w$ being the width of a cell. We chose the former. Since the two models differ in the threshold $S^{*}$, while $\beta \left(t\right)$ is the same, they cannot both reproduce the average added size postshift. The former version (constant $S^{*}$) correctly predicts the average added size in steady state after the shift, while the latter does not. Neither version can reproduce the overshoots in our data. The rates $\beta \left(t\right)$ before, during, and after the shift are determined from the empirical value of the width $w\left(t\right)$. The rates $r$ before and after the shift are the two free parameters and are determined to reproduce the empirical values of the size before and after the shift. Noise is introduced in the value of $S^{*}\left(t\right)$, which has lognormal fluctuations set to match the variability of initial size.

Constitutive/ribosomal divisor accumulator model.

This model assumes that the accumulation of some protein triggers division. Synthesis of the divisor protein $N$ happens at a rate proportional to the volume $dN/dt=rV$, and $N$ is reset to zero at every cell division. Division is triggered when $N$ reaches a critical threshold $N^{*}$. We assume that $r\left(t\right)$ is proportional to the experimental volume-specific rate of expression of a constitutive or ribosomal promoter from our data, which we use as an empirical input of the model, together with the growth rate [both quantities are evaluated as instantaneous (discrete) derivatives]. The only free parameter of the model is the threshold $N^{*}$, which we assume to be constant during the shift and condition-independent. We set $N^{*}$ to match the average size at birth before the shift. Note that, contrarily to the other models described above, we do not set any free parameter to reproduce the initial size after the shift, which is therefore another prediction of the model. Stochasticity is introduced in the value of $N^{*}$, which is assumed to have lognormal fluctuations, with coefficient of variation set to match the variability of initial size.

Reverse variant of the divisor accumulator model.

This model is identical to the previous one, but instead of using promoter expression data to define $r$, it uses the production rate inferred from data on added size and growth rate, assuming the model. Eq. 2, which holds in balanced exponential growth, can be generalized during the shift, under the assumption that the time dependency of the added size emerges as a consequence of the time dependency of the instantaneous growth rate ${\alpha }_{\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{t}}\left(t\right)$ and of the volume-specific expression rate $r\left(t\right)$, while the threshold $N^{*}$ remains constant.

An average cell born at time $t$ with initial volume $V_0\left(t\right)$, at age $a$ will have volume $V\left(a,t\right)=V_0\left(t\right)\exp \left({\int }_t^{t+a}ds\hspace{0.17em}{\alpha }_{\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{t}}\left(s\right)\right)$. The amount of divisor protein of a cell born at time $t$, with age $a$ will be therefore $N\left(a,t\right)={\int }_0^{a}du\hspace{0.17em}r\left(t+u\right)V\left(u,t\right)$. At division, $N\left(a_d,t\right)=N^{*}$, independently of $t$, from which we obtain

$$N^{*}={\int }_0^{a_d}du\hspace{0.17em}r\left(t+u\right)V\left(u,t\right)={\int }_0^{a_d}du\hspace{0.17em}r\left(t+u\right)V_0\left(t\right)\exp \left({\int }_t^{t+u}ds\hspace{0.17em}{\alpha }_{\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{t}}\left(s\right)\right).$$

This expression can be written in terms of the average added size $\mathrm{\Delta }\left(t\right)$ of a cell born at time $t$, by using the fact that

$$\mathrm{\Delta }\left(t\right)=V\left(a,t\right)\exp \left({\int }_{t+a}^{t+a_d}ds\hspace{0.17em}{\alpha }_{\mathrm{i}\mathrm{n}\mathrm{s}\mathrm{t}}\left(s\right)\right).$$

By inverting this expression, we obtain the approximate expression for $r_{\mathrm{r}\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{e}}\left(t\right)$ shown in Eq. 3 and in SI Appendix, Fig. S9. The inferred production rate was compared to the experimental values for the measured promoter ad used in direct simulations of the model.

Data Availability

Experimental datasets and code used in this study have been deposited at Mendeley Data (DOI: 10.17632/5d4yhyjn8j.1). The bugpipe package and its complete documentation is available at GitHub (https://github.com/panlilio/bugpipe).