Circular swimming motility and disordered hyperuniform state in an algae system

Significance

Disordered hyperuniform materials suppress large-scale density fluctuations like crystals and remain locally isotropic as liquids. These materials possess unique properties, such as isotropic photonic gap, and have attracted the attention of scientists from many disciplines. Here we show that circularly swimming marine algae can robustly self-organize into disordered hyperuniform states through long-range hydrodynamic interactions at air–liquid interfaces. Important properties measured from hyperuniform states can be quantitatively reproduced by a numerical model whose main parameters are obtained experimentally. Our work clearly demonstrates the possibility to create disordered hyperuniform states via hydrodynamic interactions and highlights the importance of such interactions in active matter systems.

Abstract

Active matter comprises individually driven units that convert locally stored energy into mechanical motion. Interactions between driven units lead to a variety of nonequilibrium collective phenomena in active matter. One of such phenomena is anomalously large density fluctuations, which have been observed in both experiments and theories. Here we show that, on the contrary, density fluctuations in active matter can also be greatly suppressed. Our experiments are carried out with marine algae ($Effrenium\hspace{0.17em}voratum$), which swim in circles at the air–liquid interfaces with two different eukaryotic flagella. Cell swimming generates fluid flow that leads to effective repulsions between cells in the far field. The long-range nature of such repulsive interactions suppresses density fluctuations and generates disordered hyperuniform states under a wide range of density conditions. Emergence of hyperuniformity and associated scaling exponent are quantitatively reproduced in a numerical model whose main ingredients are effective hydrodynamic interactions and uncorrelated random cell motion. Our results demonstrate the existence of disordered hyperuniform states in active matter and suggest the possibility of using hydrodynamic flow for self-assembly in active matter.

Active matter exists over a wide range of spatial and temporal scales (1–6) from animal groups (7, 8) to robot swarms (9–11), to cell colonies and tissues (12–16), to cytoskeletal extracts (17–20), to man-made microswimmers (21–25). Constituent particles in active matter systems are driven out of thermal equilibrium at the individual level; they interact to develop a wealth of intriguing collective phenomena, including clustering (13, 22, 24), flocking (11, 26), swarming (12, 13), spontaneous flow (14, 20), and giant density fluctuations (10, 11). Many of these observed phenomena have been successfully described by particle-based or continuum models (1–6), which highlight the important roles of both individual motility and interparticle interactions in determining system dynamics.

Current active matter research focuses primarily on linearly swimming particles which have a symmetric body and self-propel along one of the symmetry axes. However, a perfect alignment between the propulsion direction and body axis is rarely found in reality. Deviation from such a perfect alignment leads to a persistent curvature in the microswimmer trajectories; examples of such circle microswimmers include anisotropic artificial micromotors (27, 28), self-propelled nematic droplets (29, 30), magnetotactic bacteria and Janus particles in rotating external fields (31, 32), Janus particle in viscoelastic medium (33), and sperm and bacteria near interfaces (34, 35). Chiral motility of circle microswimmers, as predicted by theoretical and numerical investigations, can lead to a range of interesting collective phenomena in circular microswimmers, including vortex structures (36, 37), localization in traps (38), enhanced flocking (39), and hyperuniform states (40). However, experimental verifications of these predictions are limited (32, 35), a situation mainly due to the scarcity of suitable experimental systems.

Here we address this challenge by investigating marine algae Effrenium voratum (41, 42). At air–liquid interfaces, $E.\hspace{0.17em}voratum$ cells swim in circles via two eukaryotic flagella: a transverse flagellum encircling the cellular anteroposterior axis and a longitudinal one running posteriorly. Over a wide range of densities, circling $E.\hspace{0.17em}voratum$ cells self-organize into disordered hyperuniform states with suppressed density fluctuations at large length scales. Hyperuniformity (43, 44) has been considered as a new form of material order which leads to novel functionalities (45–49); it has been observed in many systems, including avian photoreceptor patterns (50), amorphous ices (51), amorphous silica (52), ultracold atoms (53), soft matter systems (54–61), and stochastic models (62–64). Our work demonstrates the existence of hyperuniformity in active matter and shows that hydrodynamic interactions can be used to construct hyperuniform states.

Results

E. voratum belongs to the family Symbiodiniaceae (41, 42). Dinoflagellates in this family are among the most abundant eukaryotic microbes found in coral reef ecosystems; they convert sunlight and carbon dioxide into organic carbon and oxygen to fuel coral growth and calcification (65). Cell motility of E. voratum has been shown to be important for algal–invertebrate partnerships (66), although quantitative understanding of cell motility is still lacking.

Circular Cell Motion and Associated Flow Field.

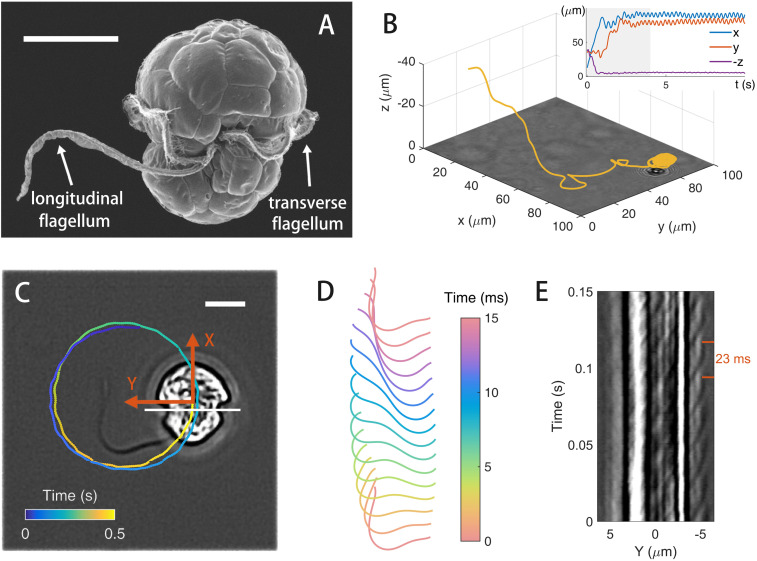
We observe the cells at the air–liquid interface on an upright microscope. As shown in Fig. 1 A and C, E. voratum cells have an approximately elliptic shape and are equipped with both longitudinal and transverse flagella for motility. Away from interfaces, cells swim in helical trajectories which are typical for motile algae; see Fig. 1B and Movie S1. However, when cells get close to an air–liquid interface, they adhere to the interface and start to move in circles; all cells move in a counterclockwise direction when viewed from the air side of the air–liquid interface. In SI Appendix, Fig. S3, we show that cells also adhere to liquid–solid interfaces (67) and estimate the gap between cell and interface to be $0.3\hspace{0.17em}\mathrm{\mu }\mathrm{m}$. A typical counterclockwise circular trajectory at air–liquid interface is plotted on an optical image of a cell in Fig. 1C, where we define the long symmetric axis as the cell body direction, X coordinate. Typical cell circling radius, translation, and angular velocities are $⟨a⟩=11.6\hspace{0.17em}\mathrm{\mu }\mathrm{m}$, $⟨v_{\mathrm{c}}⟩=180\hspace{0.17em}\mathrm{\mu }\mathrm{m}/\mathrm{s}$, and $⟨\omega ⟩=16.2\hspace{0.17em}\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}$, respectively. These motility characteristics depend weakly on cell density, and their variations are quantified in SI Appendix, Fig. S2B.

Fig. 1.

Cell motility and flagellar dynamics. (A) Scanning electron micrograph of E. voratum [reprinted with permission from ref. 41]. (B) A 3D trajectory of a cell approaching an air–liquid interface (at $z=0$) from the bulk. (Inset) Time history of cell coordinates in the laboratory frame ($x$, $y$, and $z$). (C) Circular trajectory plotted on an optical image of a cell at the interface. Undulations in the trajectory reflect beating phases of the longitudinal flagellum. A cell body frame (XY) is defined with X being the direction of body axis. (Scale bars in A and C, $5\hspace{0.17em}\mathrm{\mu }\text{m}$.) (D) Waveform of the longitudinal flagellum over a period. (E) Kymograph to show transverse flagellum dynamics. Intensity profiles of cell image are extracted along the white line (fixed in the cell body frame) in C. See Movies S1 and S2 for cell motion and flagellar dynamics.

As shown in Movie S2, the longitudinal flagellum produces a planar wave in a plane parallel to the air–liquid interface. Waveforms of the longitudinal flagellum in a period ($15\hspace{0.17em}\mathrm{m}\mathrm{s}$) are shown in Fig. 1D. The transverse flagellum sits in a groove (68–71), as shown in Fig. 1A and Movie S2; we cannot separate the flagellum’s image from that of the cell body to extract all information about the flagellum’s waveform. Instead, we extract intensity profiles from optical images along a line (fixed in the cell body frame) cutting through the transverse flagellum (the white line in Fig. 1C) and construct a kymograph from the extracted line profiles. As shown Fig. 1E, the kymograph shows a wave propagation to the negative Y direction with a period of about $23\hspace{0.17em}\mathrm{m}\mathrm{s}$ and a wave speed of $124\hspace{0.17em}\mathrm{\mu }\text{m/s}$.

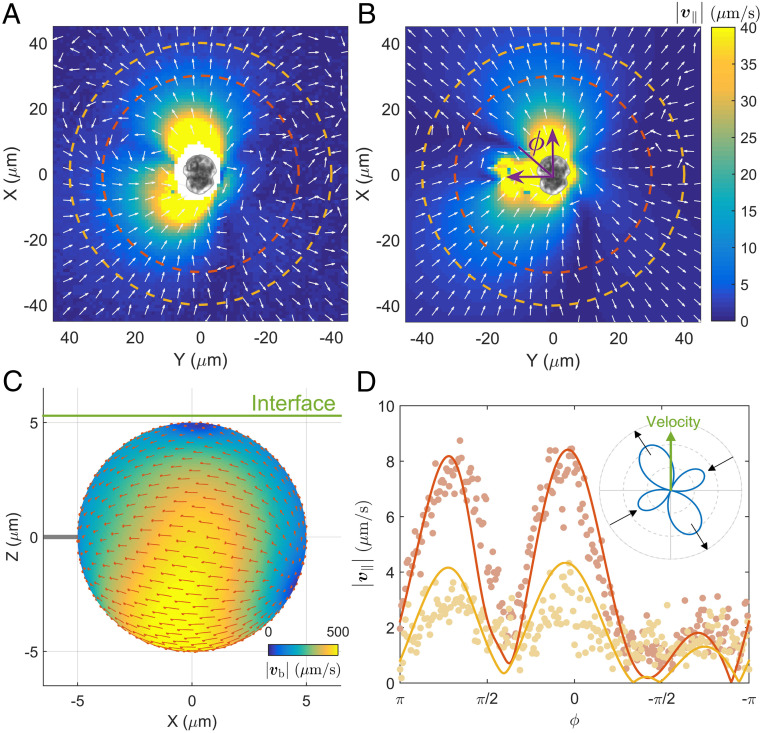
The swimming cell generates fluid flow (denoted by $\mathit{v}$) in space. We measure the two flow components in the plane of cell motion by tracking tracer particles, as shown in Movie S3. The measured fields at different times are then averaged in the cell body (XY) frame. A typical averaged field, ${\mathit{v}}_{\parallel }=v_{\text{X}}\widehat{\text{X}}+v_{\text{Y}}\widehat{\text{Y}}$, is plotted in Fig. 2A. Although bearing some similarities to that of a source dipole, the field does not show any obvious (left–right or fore–after) symmetries, which are frequently found in cases of straight swimmers (72). To reproduce such complex flow, we use a regularized Stokeslet model (73–75). In the model, the cell body is represented by a sphere with a radius of 5 $\mathrm{\mu }$m, which is driven by both longitudinal and transverse flagella. As shown in Fig. 1 C and D, the longitudinal flagellum has a conventional structure; its planar waveform can be readily quantified and is faithfully represented in the model. However, the transverse flagellum is hidden in the groove and difficult to observe; its structure and driving mechanism are still being debated (68–71). We can measure the wave period and speed from Fig. 1E, but the exact waveform of the transverse flagellum is unknown. Due to this lack of information for the transverse flagellum, we represent it in our model by a slip flow pattern on the cell surface, ${\mathit{v}}_{\mathrm{b}}$. For a given slip pattern, we use the regularized Stokeslet method to compute cell (translation and rotation) velocities and a flow field corresponding to the experimental result in Fig. 2A, ${\mathit{v}}_{\parallel }$. We vary the slip flow pattern, ${\mathit{v}}_{\mathrm{b}}$, and search for a pattern that optimizes the match between numerical and experimental results of cell velocities and flow fields. A resultant flow pattern, ${\mathit{v}}_b$, from such a procedure is shown in Fig. 2C, and maximal slip ($500\hspace{0.17em}\mathrm{\mu }$m/s) occurs in the bright yellow region, which approximately corresponds to the location of the transverse flagellum. With this slip pattern, we numerically generate the in-plane flow field around a cell, shown in Fig. 2B; two angular profiles of the in-plane flow speed ($\left|{\mathit{v}}_{\parallel }\right|$) in Fig. 2D show good agreement between experiment and Stokeslet results. See SI Appendix for detailed discussions on the above procedure and results obtained in another cell (SI Appendix, Fig. S6).

Fig. 2.

Mean in-plane flow field, ${\mathit{v}}_{\parallel }$, measured in (A) experiment and (B) regularized Stokeslet model. Flow speed ($\left|{\mathit{v}}_{\parallel }\right|$) is represented by color, and arrows show local flow direction. Cell symmetry axis is oriented along the X axis, and an angle from X direction is defined as $\varphi$ in B. (C) An optimal slip flow pattern obtained from our numerical procedure (see subsection Circular Cell Motion and Associated Flow Field for details). The air–liquid interface is shown by a green line; the gap between cell body and interface is set to be $0.3\hspace{0.17em}\mathrm{\mu }\text{m}$. (D) Angular dependence of the magnitude of the in-plane velocity at two radii, $30\hspace{0.17em}\mathrm{\mu }\text{m}$ and $40\hspace{0.17em}\mathrm{\mu }\text{m}$, dashed lines in A and B, from experiments (symbols) and numerics (lines). (Inset) Angular dependence of far-field flow speed (at the radius of $\mathrm{2,000}\hspace{0.17em}\mathrm{\mu }\text{m}$, computed from regularized Stokeslet calculation). The far-field flow is dominated by a pair of orthogonal pusher–puller dipoles (see SI Appendix for detail). Experimental data are measured from tracer motion around a cell with a swimming speed $v_{\mathrm{c}}=201\hspace{0.17em}\mathrm{\mu }\text{m/s}$ and radius $a=11.5\hspace{0.17em}\mathrm{\mu }\text{m}$; see Movie S3.

Noncircular Cell Motion.

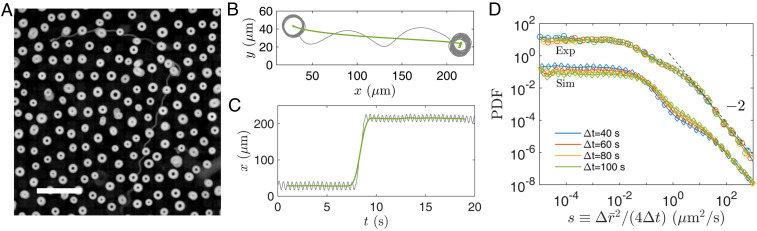
Although circular motion is most frequently observed, cells also exhibit rare noncircular motion. To demonstrate that, we show a streak image of cell motion in Fig. 3A. While majority of cells move in circles and appear as white “donuts,” the image also contains rare long streaks, corresponding to rapid translational motion of cells. The transition to noncircular motion is likely related to changes in the longitudinal flagellar dynamics, as depicted in SI Appendix, Fig. S4 (76, 77). We use a procedure with empirically chosen parameters to identify noncircular motion from instantaneous cell positions (see SI Appendix, Fig. S5 and related discussions in SI Appendix for details). This procedure shows that durations of noncircular motion are usually less than a few seconds and that the occurring rate of noncircular motion is approximately $10^{-3}\hspace{0.17em}{\mathrm{\text{s}}}^{-1}\hspace{0.17em}\text{per cell}$.

Fig. 3.

(A) Streak image of cell motion. Raw images are obtained at cell density $178\hspace{0.17em}{\mathrm{m}\mathrm{m}}^{-\mathrm{2}}$ and averaged over 10 s to produce the streak image. (Scale bar, $200\hspace{0.17em}\mathrm{\mu }\text{m}$.) (B) Instantaneous cell coordinates (gray line, $\mathit{r}\left(t\right)$) are averaged over a sliding window of $2\hspace{0.17em}\mathrm{s}$ to highlight the noncircular motion (green line, $\overline{\mathit{r}}\left(t\right)$). (C) Temporal history of instantaneous (gray) and window-averaged (green) coordinates. (D) Probability distribution functions (PDF) of window-averaged cell displacements (squared and normalized by time separation, $s\equiv △{\overline{r}}^2/4△t$) from experiment (circles) and model (squares) for four time separations. The experiment and model results are in agreement; for presentation clarity, we rescale model results in D by a factor of 100.

To quantify noncircular motion, we first average instantaneous cell coordinates, $\mathit{r}\left(t\right)$, over a sliding window of 2 s ($\sim 5.5$ circling period). As shown in Fig. 3 B and C, circular motion is smoothed out in the window-averaged (green) trajectory, denoted as $\overline{\mathit{r}}\left(t\right)$. From the window-averaged trajectories, we measure probability distributions of cell displacements for different time separations $△t$. After squared displacements $△{\overline{r}}^2\equiv {\left(\overline{\mathit{r}}\left(t+△t\right)-\overline{\mathit{r}}\left(t\right)\right)}^2$ are normalized by the time separation $△t$, all distributions of $s\equiv △{\overline{r}}^2/4△t$ collapse onto a single curve and exhibit a power-law scaling for large $s$, as shown in Fig. 3D. Similar probability distributions have been found under different density conditions; see SI Appendix, Fig. S9.

Experimental Observations of Hyperuniform States.

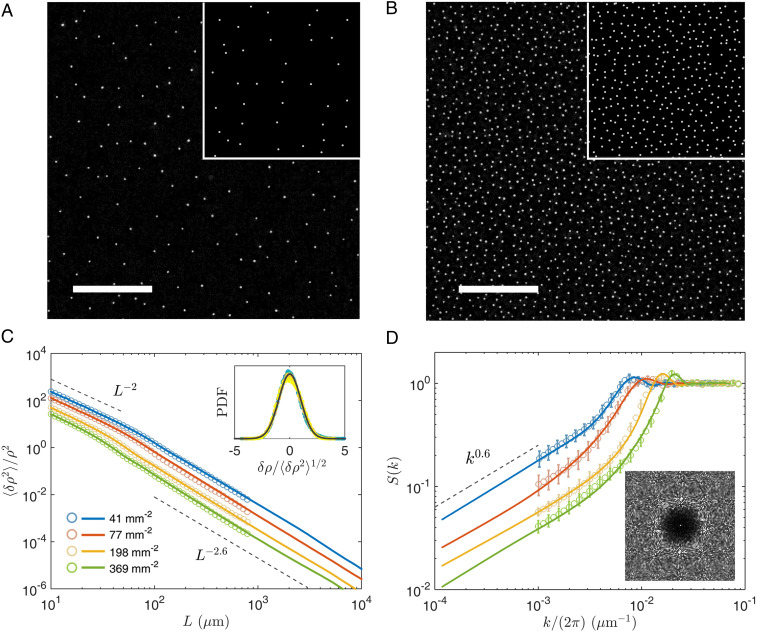
We next investigate collective states of interacting cells at the air–liquid interface. Cells in the bulk suspension swim to adhere at the interface in the first few minutes of experiments, and this leads to a random initial distribution of cells at the interface, with a cell density $\rho$. Then, cells at the interface slowly self-organize into a steady state after a relaxation period of about several thousand seconds, as shown in SI Appendix, Fig. S11. We measure static and dynamic properties of these steady states. Fig. 4 A and B shows typical instantaneous configurations from two experiments; see also Movies S4 and S5. Although no obvious order can be detected in these configurations, spatial distribution of cells appears to be quite uniform at large length scales. Quantitatively, from instantaneous cell positions ${\mathit{r}}^{\left(j\right)}\left(t\right)$, we compute density fluctuations for square interrogation windows of different sizes $L$. For a given window size, we find that density fluctuations follow a Gaussian distribution, as shown in Fig. 4 C, Inset. Variances of density fluctuations are plotted against the window size in Fig. 4C; data follow the scaling determined by the central limit theorem $⟨\delta {\rho }^2⟩\sim L^{-2}$ at small scales and decay faster with the window size at large scales: $⟨\delta {\rho }^2⟩\sim L^{-2.6}$. Similar physics is also reflected by the static structure factors, $S\left(k\right)=⟨1/N{\left|{\sum }_{j=1}^N\exp \left(-i{\mathit{k}\cdot \mathit{r}}^{\left(j\right)}\right)\right|}^2⟩$, where $N$ is the total number of observed cells. In Fig. 4D, $S\left(k\right)$ shows a liquid-like peak in large $k$ region and a scaling $S\left(k\right)\hspace{0.17em}\sim \hspace{0.17em}{k}^{0.6}$ for small $k$. The length scale corresponding to liquid-like peaks matches approximately to the transition length between $⟨\delta {\rho }^2⟩\sim L^{-2}$ and $⟨\delta {\rho }^2⟩\sim L^{-2.6}$ scalings. The same scalings, $⟨\delta {\rho }^2⟩\sim L^{-2.6}$ and $S\left(k\right)\sim k^{0.6}$, are found for different cell densities. Increasing the cell density leads to a decrease of $S\left(k\right)$ for small $k$ and shifts the liquid-like peak to larger $k$, as shown by Fig. 4 C and D. To check the robustness of observed hyperuniformity, we also use window-averaged cell position, $\overline{\mathit{r}}\left(t\right)$ defined in Fig. 3B, to compute density fluctuations and obtain similar results, shown in SI Appendix, Fig. S11.

Fig. 4.

(A and B) Cell configurations at two densities (41 and $369\hspace{0.17em}{\mathrm{m}\mathrm{m}}^{-\mathrm{2}}$). (Insets) Typical output of simulation. (Scale bar, $500\hspace{0.17em}\mathrm{\mu }\text{m}$.) (C) Cell density fluctuations plotted against interrogation window size and (D) static structure factors at four densities. Experimental and numerical results are shown by light symbols and dark lines, respectively. The maximal measurement length scale is $800\hspace{0.17em}\mathrm{\mu }\text{m}$ in experiments and $\mathrm{10,000}\hspace{0.17em}\mathrm{\mu }\text{m}$ in simulations. Inset in C shows distributions of normalized density fluctuations measured at density $198\hspace{0.17em}{\mathrm{m}\mathrm{m}}^{-\mathrm{2}}$; color symbols are experimental data with different window sizes ($L=200$ $\mathrm{\mu }$m to $800\hspace{0.17em}\mathrm{\mu }$m), and the thick line represents a normal distribution. Inset in D shows a 2D static structure factor measured at density $198\hspace{0.17em}{\mathrm{m}\mathrm{m}}^{-\mathrm{2}}$.

Beyond static structures, we also investigate the system’s dynamic properties. To explore the possibility of local synchronization, spatial correlation functions of circling phase and velocity are computed; results in SI Appendix, Fig. S10 C and D show that instantaneous cell motions are not spatially correlated, suggesting a weak interaction between cells. This is confirmed by Fig. 2 which shows that the flow velocity at the nearest cells (at a distance $\sim 30\text{to}100\hspace{0.17em}\mathrm{\mu }\mathrm{m}$) is much smaller than cell swimming speed. Therefore, the cell–cell interaction is not strong enough to significantly affect the instantaneous cell motion. However, as shown below, this weak hydrodynamic interaction can modulate cell positions over a long time, and its long-range nature leads to the formation of hyperuniform states.

Particle-Based Model for Hyperuniformity.

We construct a numerical model to illustrate the origin of observed hyperuniformity. Dynamics in our experiments evolves over a time scale that is much longer than cell circling periods ($\sim 0.4\hspace{0.17em}\mathrm{s}$). This separation of time scales allows us to build a temporally coarse-grained (over a few circling periods) model to capture the emergence of hyperuniformity without fully resolving fast circular cell motion (78). Therefore, particle coordinates in our model represent window-averaged cell positions in experiments ($\overline{\mathit{r}}\left(t\right)$ in Fig. 3B), and particles interact through period-averaged flow field. Beyond flow advection, our model also includes stochastic noncircular particle motion and uses the following equation to determine the displacement of the $i$th particle at time $n\tau$ during a time step $\tau$:

$$\begin{array}{c}\hfill {\overline{\mathit{r}}}^{\left(i\right)}\left(\left(n+1\right)\tau \right)-{\overline{\mathit{r}}}^{\left(i\right)}\left(n\tau \right)\hspace{0.17em}=\hfill \\ \hfill \sum _{j\ne i}\overline{\mathit{V}}\left({\overline{\mathit{r}}}^{\left(i\right)}\left(n\tau \right)-{\overline{\mathit{r}}}^{\left(j\right)}\left(n\tau \right);v_{\mathrm{c}}^{\left(j\right)}\right)\tau \hfill \\ \hfill +\mathit{\eta }\left(D^{\left(i\right)}\right)\delta \left(\text{mod}\left(n,p\right),s^{\left(i\right)}\right)\hfill \end{array}.$$ [1]

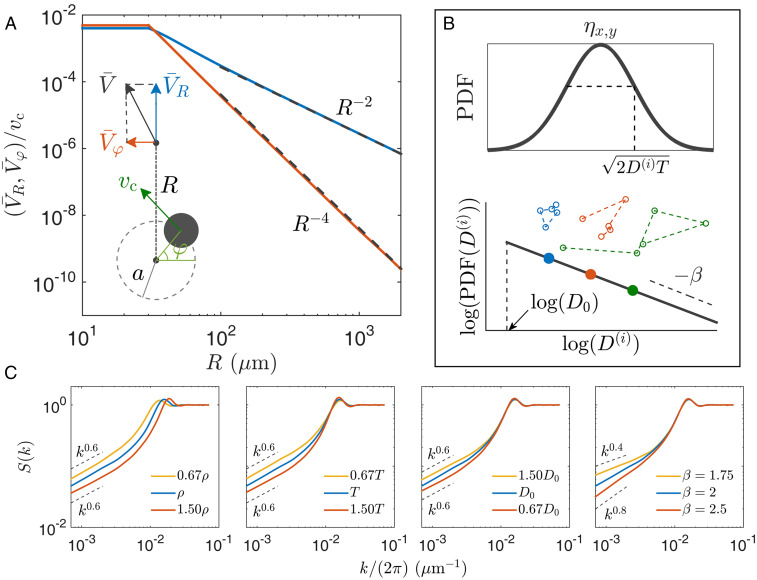
The period-averaged flow field in Eq. 1, $\overline{\mathit{V}}\left(\mathit{R};v_{\mathrm{c}}\right)$, is calculated by the regularized Stokeslet method for a cell circling with a radius $a=10\hspace{0.17em}\mathrm{\mu }$m and velocity $v_{\mathrm{c}}$. As shown in Fig. 5A, $\overline{\mathit{V}}\left(\mathit{R};v_{\mathrm{c}}\right)$ has an outgoing component in the far field; see Materials and Methods for detailed discussions on the period-averaged flow field. In our model, parameter $v_{\mathrm{c}}^{\left(i\right)}$ is sampled from an experimentally determined distribution of cell velocity in SI Appendix, Fig. S2.

Fig. 5.

(A) Radial and tangential components of period-averaged flow field around a swimming cell. (Inset) Flow components, showing a cell circling with a radius $a$ and a velocity $v_{\mathrm{c}}$. Flow strength is capped at $R\hspace{0.17em}=\hspace{0.17em}30\hspace{0.17em}\mathrm{\mu }$m, which approximately corresponds to the minimal distance between circular centers of two cells in experiments. Black dashed lines show the asymptotic behavior in the far field (see Materials and Methods). (B) Normal distribution of jumping displacements $\mathit{\eta }\left(D^{\left(i\right)}\right)$ (Eq. 1) and Pareto distribution of particle diffusivity ($D^{\left(i\right)}$) (Eq. 2). (Inset) Three stochastic trajectories with different diffusivity. (C) Effects of four model parameters on structure factors. A default set of parameters is used unless specified: $\rho =198\hspace{0.17em}{\mathrm{m}\mathrm{m}}^{-\mathrm{2}}$, $T=400\hspace{0.17em}\mathrm{s}$, $D_0=0.95\hspace{0.17em}\mathrm{\mu }{\text{m}}^2/s$, and $\beta =2$.

The second term on the right-hand side of Eq. 1 represents stochastic jumps. The Kronecker delta function δ() dictates that adjacent random jumps for a given particle are temporally separated by $p$ (an integer constant) time steps, defining a waiting time $T=p\tau$. Specifically, the $i$th particle jumps at time $n\tau$ if $\text{mod}\left(n,p\right)=s^{\left(i\right)}$; mod() represents modulo operation, and $s^{\left(i\right)}$ is an integer constant between zero and $p-1$, randomly assigned to all particles. Components of jumping displacements $\mathit{\eta }\left(D^{\left(i\right)}\right)$ are independently drawn from a normal distribution with a standard deviation $\sqrt{2D^{\left(i\right)}T}$, as shown in Fig. 5B. Parameter $D^{\left(i\right)}$ is the diffusivity for the $i$th particle and drawn from a Pareto distribution with a cutoff value $D_0$ and a power index $\beta$,

$$f\left(D;D_0,\beta \right)=\left\{\begin{array}{cc}\left(\beta -1\right)\frac{D_0^{\beta -1}}{D^{\beta }}\hfill & D\ge D_0\hfill \\ 0\hfill & D<D_0\hfill \end{array}\right.,$$ [2]

where $\beta =2$ unless stated otherwise.

In a two-dimensional (2D) periodic domain of size $L_{\mathrm{m}\mathrm{a}\mathrm{x}}=20\hspace{0.17em}\mathrm{m}\mathrm{m}$, we simulate $\rho L_{\mathrm{m}\mathrm{a}\mathrm{x}}^2$ particles following Eq. 1. For a given experimental condition, the cutoff diffusivity $D_0$ and the waiting time $T$ are varied to match simulation results to experiments. The obtained values for $D_0$ ($\sim 1\hspace{0.17em}\mathrm{\mu }{\text{m}}^2/s$) and $T$ ($\sim 500\hspace{0.17em}\mathrm{s}$) are listed for different cell densities in SI Appendix, Table S3.

We measure density fluctuations after randomly initialized particles evolve to a steady state. As shown in Fig. 4 C and D, our simulations can generate hyperuniform states and quantitatively reproduce measured density fluctuation $\delta {\rho }^2$ and structure factor $S\left(k\right)$, highlighting scaling laws $⟨\delta {\rho }^2⟩\sim L^{-2.6}$ and $S\left(k\right)\hspace{0.17em}\sim \hspace{0.17em}{k}^{0.6}$ for hyperuniformity. Distribution functions of cell displacements are also well reproduced in Fig. 3D. The Pareto distribution of $D^{\left(i\right)}$ with a power index $\beta =2$ leads to the observed power-law distribution for large displacements.

We systematically study effects of model parameters; results are shown in Fig. 5C. An increase of particle density $\rho$ shifts the liquid-like peak to higher $k$ and leads to a decrease of density fluctuation for small $k$, which mirrors experimental results in Fig. 4D. Decreasing the waiting time $T$ introduces more fluctuations into the system and leads to an increase in $S\left(k\right)$ for small $k$, as shown by the second panel in Fig. 5C. Smaller cutoff diffusivity $D_0$ allows fewer particles with large $D^{\left(i\right)}$; this leads to fewer stochastic jumps with large displacement, less fluctuations in large scales, and smaller $S\left(k\right)$ values. As shown in the fourth panel in Fig. 5C, the power index of the Pareto distribution, $\beta$ in Eq. 2, can change power-law scaling of $S\left(k\right)$ at small $k$. A larger $\beta$ means fewer particles with large diffusivity; this leads the system to approach the strong hyperuniformity limit (44), and a larger exponent in $S\left(k\right)$ is observed. Fig. 5C also demonstrates that variations in $\rho$, $T$, and $D_0$ have relatively weak effects on the scaling exponent for small $k$ in our observation window (79).

Discussion

In summary, we have studied individual motility and collective dynamics in marine algae E. voratum. Cells swim in circles at the air–liquid interface with a longitudinal flagellum and a transverse one. Combining experimental measurements and the regularized Stokeslet method, we showed that period-averaged flow generated by cells has a long-ranged and out-going radial component that disperses cells uniformly and leads to a disordered hyperuniform state. Stochastic cell motion with a power-law displacement distribution (79) also plays an important role in determining the properties of density fluctuations.

Regularized Stokeslet results in Fig. 2 can be used to clarify the current confusion on the contributions of two flagella to propulsion in E. voratum (68–70). For that, we measure the stalled force and torque with both flagella or only one of them functioning; as shown in SI Appendix, Table S1, the longitudinal flagellum provides about 30% of the total torque and less than 10% of the force. The regularized Stokeslet method is also used to calculate 3D period-averaged flow and show that self-generated flow can lead to directed nutrient/particle transport around cells, as shown in SI Appendix, Fig. S8. These results provide insight into the ecological function and evolutionary traits of two flagella in this ecologically important dinoflagellate (41, 42, 65, 66).

Previous studies have shown that hydrodynamic interactions lead to interesting self-organization (58). For example, bacteria, when oriented perpendicularly to an interface, can generate inward flow that assembles bacterial cells into compact crystals at the interface (80, 81). In contrast, circling E. voratum cells in the current work generate repulsive interactions. This can be understood from the far-field instantaneous flow in the plane of cell motion. As shown in Fig. 2 D, Inset and analysis in SI Appendix, out-going flow in the far field is stronger than its in-coming counterpart. This leads to a period-averaged repulsive interaction between cells in Fig. 5A. The same hydrodynamic mechanism may underlie the formation of sperm vortex in ref. 35. Our work suggests a mechanism of using the average along circular trajectories to generate isotropic hydrodynamic interactions between force-free microswimmers. Such isotropic hydrodynamic interactions in chiral active matter are different from anisotropic dipolar interactions in conventional systems with linearly swimming particles and may produce new collective phenomena.

Fig. 4 shows that hyperuniformity is observed under different cell concentration conditions with a similar scaling exponent. Such a density independence has also been observed in other hyperuniform systems with long-range interactions. In a one-component plasma, particles with the same electrostatic charge interact with repulsive Coulomb potential which imposes an energy penalty on density fluctuations and leads to hyperuniformity under all particle density conditions (44). In a sedimentation system of irregular objects (58), falling objects interact via long-range hydrodynamic (force monopole) flow, and objects’ irregular shapes lead to an anisotropic response to the local flow. A combination of the long-range interaction and anisotropic response in this system produces hyperuniformity with a density-independent exponent.

Hyperuniformity has been observed in many systems exhibiting absorbing-state transition (40, 57, 62–64, 82). For example, a recent numerical work simulated a system of active particles which self-propel in circles (like E. voratum cells here) but interact via short-range repulsive forces; hyperuniformity in this system was only observed in high-density active states (40). In contrast, E. voratum cells self-organize into hyperuniform states under all densities, thanks to the long-range nature of hydrodynamic interactions (44, 48). Phoretic interactions in synthetic active matter systems are also known to be long ranged; both attractive and repulsive phoretic interactions have been realized (24, 83). These long-range interactions may provide a promising avenue to generate novel hyperuniform materials with active matter.

Materials and Methods

Cell Growth and Imaging Procedure.

Species E. voratum cells are cultured in artificial seawater with F/2 medium in a 100-mL flask which is placed in an incubator (INFORS HT Multitron Pro) at $20\hspace{0.17em}°\mathrm{C}$. We use a daily light cycle which consists of 12 h of cool light with an intensity of 2,000 lx and 12 h in dark. The algal cells in the experiments are in an exponential phase after 14-d growth and are observed a few hours after the light period starts, when cells showed excellent motility (see SI Appendix, Fig. S1 and refs. 41 and 42). During experiments, cell culture is placed in a disk-shaped chamber fabricated by cover glass and plastic gasket (8 mm in diameter). Cells gather and form a monolayer at the air–liquid interface. Cell motion in the central region of the sample is recorded by a high-speed camera (Basler acA2040-180 km, 4-m pixel resolution) mounted on an upright microscope (Nikon Ni-U) with a 4× or 40× magnification objective; the acquisition rate varies from 50 frames per s to 850 frames per s. To measure fluid flow, milk (Deluxe Milk, Mengniu) is added to provide passive flow tracers (diameter 1 $\mathrm{\mu }$m to $\sim$2 $\mathrm{\mu }$m). Holographic imaging technique is used to measure 3D cell motion.

Particle-Based Model.

To obtain period-averaged flow field in Fig. 5A, we use the regularized Stokeslet results from Fig. 2 to compute instantaneous flow fields around a cell and average computed fields in the laboratory frame over cell positions in a circling period. The flow field is capped at $R=30\hspace{0.17em}\mathrm{\mu }$m, which approximately corresponds to the minimal distance between the circular center of two cells in experiments. In simulation, we interpolate data in Fig. 5A to find two flow components at any separation; asymptotic expressions for flow components (SI Appendix, Eq. S21) with a cap at $R=30\hspace{0.17em}\mathrm{\mu }$m can also reproduce experimental data; see SI Appendix, Fig. S12 for details. To reduce the computing load, interacting flow is assumed to be zero beyond a cutoff length of $\mathrm{20,000}\hspace{0.17em}\mathrm{\mu }$m, which is twice the maximal length of computed density fluctuations $⟨\delta {\rho }^2⟩$ and structure factor $S\left(k\right)$ in simulations.

In our model, time step $\tau$ is set to be 10 s, during which typical particle displacements ($\sim 1\hspace{0.17em}\mathrm{\mu }$m) are much smaller than typical particle separations ($\sim 50\hspace{0.17em}\mathrm{\mu }\text{m}$). Analysis of experiments shows that durations of random noncircular motion are less than 10 s (SI Appendix, Fig. S5D); such events occur within a single time step in simulation.

Particle positions in simulations represent temporally averaged cell positions ${\overline{\mathit{r}}}^{\left(i\right)}\left(t\right)$; we add a random circling phase (SI Appendix, Fig. S10C) to each particle position to obtain instantaneous cell positions, ${\mathit{r}}^{\left(i\right)}\left(t\right)$, which are used to compute density fluctuations.

Data Availability

All study data are included in the article and SI Appendix.