Auditory Brainstem Models: Adapting Cochlear Nuclei Improve Spatial Encoding by the Medial Superior Olive in Reverberation

Abstract

Listeners typically perceive a sound as originating from the direction of its source, even as direct sound is followed milliseconds later by reflected sound from multiple different directions. Early-arriving sound is emphasised in the ascending auditory pathway, including the medial superior olive (MSO) where binaural neurons encode the interaural-time-difference (ITD) cue for spatial location. Perceptually, weighting of ITD conveyed during rising sound energy is stronger at 600 Hz than at 200 Hz, consistent with the minimum stimulus rate for binaural adaptation, and with the longer reverberation times at 600 Hz, compared with 200 Hz, in many natural outdoor environments. Here, we computationally explore the combined efficacy of adaptation prior to the binaural encoding of ITD cues, and excitatory binaural coincidence detection within MSO neurons, in emphasising ITDs conveyed in early-arriving sound. With excitatory inputs from adapting, nonlinear model spherical bushy cells (SBCs) of the bilateral cochlear nuclei, a nonlinear model MSO neuron with low-threshold potassium channels reproduces the rate-dependent emphasis of rising vs. peak sound energy in ITD encoding; adaptation is equally effective in the model MSO. Maintaining adaptation in model SBCs, and adjusting membrane speed in model MSO neurons, ‘left’ and ‘right’ populations of computationally efficient, linear model SBCs and MSO neurons reproduce this stronger weighting of ITD conveyed during rising sound energy at 600 Hz compared to 200 Hz. This hemispheric population model demonstrates a link between strong weighting of spatial information during rising sound energy, and correct unambiguous lateralisation of a speech source in reverberation.

INTRODUCTION

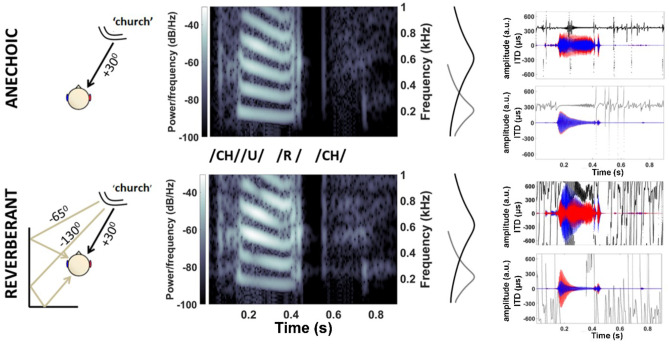
Sound propagating directly from its source to a listener’s ears is typically followed milliseconds later by multiple reverberant copies arriving from different directions (Fig. 1). Despite this mixture of direct and reflected sound generating nonstationary spatial information in the binaural cues—interaural time differences (ITDs) and interaural intensity differences (IIDs)—listeners typically perceive a sound with a distinct onset as punctate, and originating from the direction of its source (Hartmann 1997; Rakerd and Hartmann, 1985, 1986). Accurate perception of the source location can persist even when the intensity of reflected sound exceeds that of direct sound (Haas 1951), facilitating ‘cocktail party listening’: attending to a single talker against a background of many competing voices (Cherry 1953).

Fig. 1.

Reverberation confounds the binaural cues of speech stimuli. Top: anechoic speech (direct sound, without reverberation): ‘church’ spoken at 70 dB SPL by a female talker located +30° to the right and front of a virtual listener; speech spectrogram below 1 kHz at left ear. Right: gammatone filters centred at 200 Hz (light grey) and 600 Hz (dark grey) illustrate cochlear-filtered anechoic vs. reverberant speech waveforms in the left (blue) and right (red) ears; instantaneous ITDs (light/dark grey) (restricted to ±700 μs, human physiological range) were consistently near +363 μs. Bottom: reverberant speech: direct sound plus two simulated reflections from listener’s left, respectively from −65° delayed by 4 ms, and −130° delayed by 8 ms, increasing the energy at the left ear (brighter spectrogram above 400 Hz). Reverberant energy extends into the quiet pause between the vowel and final consonant (0.45–0.55 ms), generating conflicting ILD cues (600-Hz channel) and rapidly varying ITDs

Emphasis of spatial cues in early-arriving sounds, the precedence effect, is described as onset dominance and binaural adaptation (Freyman et al. 1997; Hafter 1997; Houtgast and Plomp 1968; Litovsky et al. 1999; Wallach et al. 1949). In ITD-based and IID-based lateralisation of pulse trains and tones, adaptation prior to binaural integration is proposed to emphasise early-arriving sound, and temporal characteristics of this pre-binaural adaptation are predicted (Brown and Stecker 2010; Diedesch and Stecker 2015; Hafter et al. 1988; Saberi 1996). Adaptation in binaural sensitivity is weak for stimuli with slow pulse rates (200 pulses per second (pps) or less), temporal gaps, or slow ‘second-order’ amplitude modulation (AM) below 256 Hz; ITDs in subsequent pulses or rising AM cycles can be weighted as strongly as in the initial stimulus onset (Freyman and Zurek 2017; Hafter and Buell 1990; Hafter and Dye 1983; Stecker 2018; Stecker and Hafter 2002). For amplitude-modulated 600-Hz sounds, normal-hearing listeners detect ITDs conveyed during rising sound energy more reliably than ITDs at the energy peak; at 200 Hz, listeners are equally sensitive to ITDs during rising and peak energy; for both stimulus rates, listeners are least sensitive to ITDs during falling energy (Hu et al. 2017).

The auditory nerve, brainstem, midbrain, and auditory cortex display neural emphasis of early-arriving sound (Dietz et al. 2014; Fitzpatrick et al. 1999; Liebenthal and Pratt 2002; Litovsky and Yin 1998a, 1998b). In the brainstem, medial-superior-olive (MSO) neurons encode ITD (Goldberg and Brown 1969) using binaural-coincidence detection (Scott et al. 2010; Yin and Chan 1990) sharpened by low-threshold potassium (K_LT) channels (Mathews et al. 2010). MSO neurons respond most strongly to their preferred ITD during rising energy in amplitude-modulated binaural beats (AMBBs), emphasising early-arriving spatial information, consistent with adaptation in their input pathways (Dietz et al. 2014). MSO neurons receive bilateral excitation from spherical bushy cells (SBCs) of the ventral cochlear nuclei (Smith et al. 1993). Each SBC is typically driven by 1–3 auditory nerve fibres (ANFs), each terminating in a calyceal synapse (Lorente De No 1981). Bilateral inhibition of MSO neurons is fast (Couchman et al. 2010; Magnusson et al. 2005), but a slower 25-ms time scale of adaptation occurs in MSO AMBB responses and potential adaptive mechanisms: spike-rate adaptation in ANFs (Moser and Beutner 2000; Zilany and Carney 2010); glycinergic inhibition of SBCs in vivo (Keine et al. 2016; Kuenzel et al. 2015); and short-term plasticity (STP, synaptic depression) in vitro at the inputs to SBCs (Wang and Manis 2008) and MSO neurons (Couchman et al. 2010), similar to STP in the avian nucleus laminaris (Cook et al. 2003; Kuba et al. 2002). STP includes rate dependence in adaptation and in calcium-mediated recovery (Wang and Kaczmarek 1998; Wang and Manis 2008; Xie and Manis 2013). STP in vivo is weak, as GABA inhibits synaptic vesicle release (Brenowitz et al. 1998; Keine et al. 2016; Kuenzel et al. 2011; Lorteije et al. 2009). Modelled K_LT channels support rate-dependent adaptation (Chung et al. 2015; Colburn et al. 2009).

Here, we computationally explore simplified adaptation before and during binaural convergence. In our base models, adapting ANFs (Zilany et al. 2014) project excitatory synapses reflecting STP in vitro, and driving SBCs (Rothman and Manis 2003c) that project nonadapting excitatory synapses to MSO neurons. In MODEL 1 with nonlinear voltage-sensitive ion channels including K_LT channels, an MSO neuron reflects in vivo AMBB responses and the rate-dependent emphasis of ITD during rising vs. peak sound energy; modelled adaptation is similar for inhibition at SBCs, or STP at SBCs or MSO neurons. In MODEL 2 with linear active neuronal membranes and STP at SBCs, populations of fast MSO neurons correctly lateralise a speech source in reverberation, strongly weighting ITD during rising sound energy near 600 Hz, as slow and fast MSO neurons reproduce the weaker weighting near 200 Hz.

METHODS

Two brainstem models are developed: MODEL 1 is more biophysically detailed and accurate, supporting the investigation of K_LT channels, and the rate-dependent emphasis of ITD using a single set of parameter values; MODEL 2 is much more computationally efficient for population modelling with stimulus repetitions.

MODEL 1: Nonlinear Models for ANFs, SBCs, and MSO Neuron

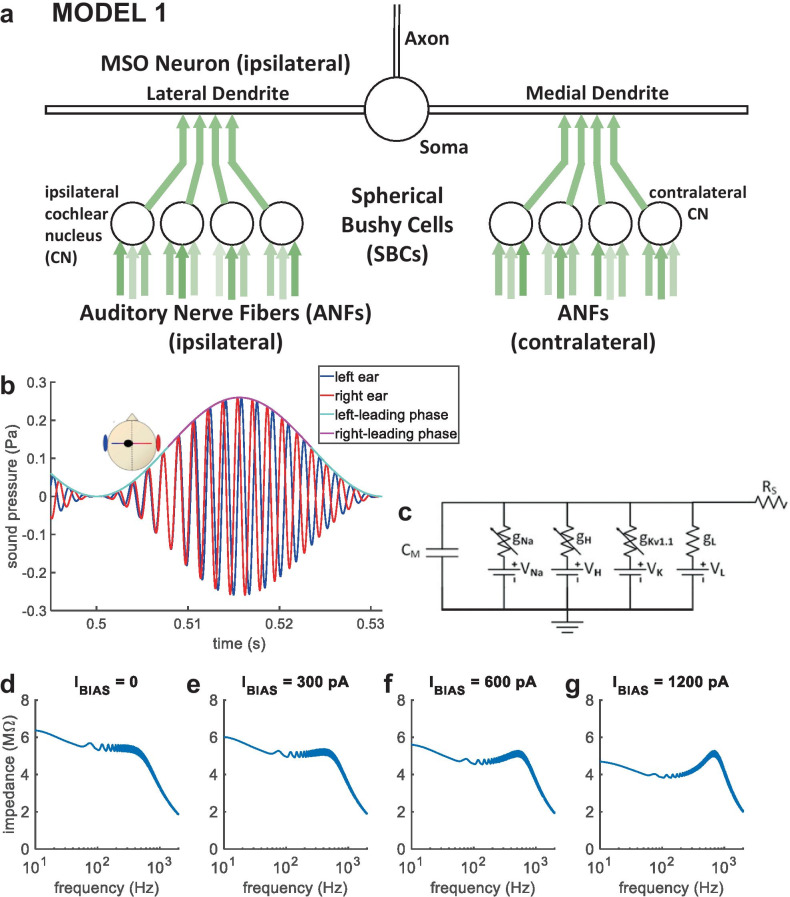
MODEL 1 comprises an MSO neuron and its excitatory input pathways (Fig. 2a), beginning with an auditory-periphery model for humans (Glasberg and Moore 1990; Zilany et al. 2014), with 12 left and 12 right adapting model ANFs of medium spontaneous rate. Three model ANFs drive each model SBC of the ventral cochlear nucleus (VCN) (Rothman and Manis 2003c; Rudnicki and Hemmert 2017), for which adaptation by synaptic depression and synaptic inhibition are explored. Based on anatomical counts (Couchman et al. 2010), four left and four right model SBCs project excitatory synaptic inputs to a multi-compartment model MSO neuron (Brughera et al. 2013), for which synaptic depression is explored. Acoustic stimuli and the auditory periphery model are implemented in Matlab (Natick, Massachusetts, USA) (www.mathworks.com). Model SBCs and MSO neuron are Hodgkin-Huxley (HH) type (Hodgkin and Huxley 1952), implemented in the Python 3.7 Brian2 Neural Simulator (Stimberg et al. 2019).

Fig. 2.

MODEL 1 and AMBB stimulus. (a) MODEL 1: nonlinear model for an MSO neuron and its excitatory inputs. (b) AMBB stimulus: AM rate is set equal to the binaural-beat frequency (the difference in carrier frequency between signals presented to the right and left ears); IPD cycles through 360° at the same rate as AM. The start-IPD (IPD at zero amplitude) is a free parameter. Shown with right-carrier 616 Hz, left-carrier 584 Hz, AM 32 Hz, and start-IPD −90° (right channel trailing by 90°), resulting in zero IPD at the midpoint of rising AM. (c) Sub-compartment within the model MSO neuron, shown as an electrical circuit. (d–g) Model MSO somatic membrane impedance vs. frequency. Injected current was a steady bias current (I_BIAS), plus a frequency-swept sine wave. With increased I_BIAS, a resonance in membrane impedance emerged. The reciprocal of angular resonance frequency indicates membrane time constant

Code is available at Github: https://github.com/AndrewBrughera/Mso_SbcStp_EE1.

Data, analysis scripts, and code are available at figshare: https://doi.org/10.6084/m9.figshare.11955219.v1

AMBB Stimuli

Acoustic stimuli presented to the auditory-periphery model are amplitude-modulated binaural beats (AMBBs) (Fig. 2b) (Dietz et al. 2013): a tone of a slightly different frequency is presented to each ear, and sinusoidally amplitude modulated (SAM) at a rate equal to the difference in frequency between the two ears. Each AM cycle of rising and falling sound energy contains a full cycle of interaural phase disparities. As in Dietz et al. (2013), ‘All stimuli were fully modulated. Each stimulus started and ended in a modulation minimum. Stimulus duration was 750 ms, and all stimuli with modulation frequencies > 8 Hz were gated on with a squared sine ramp of 150-ms duration to minimise the influence of the stimulus onset’. Stimuli were presented to the auditory-periphery model at 78 dB peak SPL at maximum amplitude, by setting the maximum amplitude such that if were sustained, it would produce 75 dB SPL RMS.

IPD and Start-IPD in the AMBB Stimuli

The interaural phase difference (IPD) of the stimulus was defined as the contralateral-ear phase minus the ipsilateral-ear phase. The contralateral ear always received the higher carrier frequency. Thus, the IPD cyclically increased throughout the stimulus.

The point of zero amplitude is considered the start of the AMBB cycle (0° of the 360° AMBB cycle). The IPD at zero amplitude is called the ‘start-IPD’, which is a freely selectable stimulus condition. Start-IPDs of −90°, −180°, and −270° (respectively 270°, 180°, and 90°) were implemented. With a start-IPD of −90°, zero IPD occurred at ¼ period (90°) of the AMBB cycle, at the midpoint of the rising AM. With start-IPD −180°, zero IPD occurred at 1/2 period (180°) of the AMBB cycle, at the peak of AM. With start-IPD −270°, zero IPD occurred at ¾ period (270°) of the AMBB cycle, at the midpoint of the falling AM. The nonlinear model MSO neuron (described below) is tuned to a best ITD of zero (best ITD: the ITD of highest spike rate). Thus, start-IPD −90° produced the model neuron’s best ITD at ¼ period of the AMBB cycle; this condition is labelled ‘best-ITD in rise’ in figures. Similarly, start-IPD −180° is the condition labelled ‘best-ITD at peak’, and start-IPD −270° is the condition labelled ‘best-ITD in fall’.

Start-IPDs were generated by pairing appropriate combinations of stimulus tones of 8 start-phases: 0°, −45°, −90°, −135°, −180°, −225°, −270°, and −315°. The AMBB period histogram for each start-IPD shows pooled spikes from all 8 start-phases. These histograms show the effects of start-IPD, but they cannot show phase-locking to fine structure of the carriers.

Auditory Periphery Model

The acoustic stimuli are processed by an auditory-periphery model for humans (Glasberg and Moore 1990; Zilany et al. 2014). Modelled peripheral processing includes 24 adapting stochastic ANFs of medium spontaneous rate and power-law spike-rate adaptation acting across time scales: 12 ANFs each in the left and right ears, with a 200-Hz or 600-Hz characteristic frequency (CF, the frequency at which a neuron fires above spontaneous rate for the lowest sound pressure level, SPL). CF results from the frequency tuning of the inner ear, and the CFs of ANFs distally driving a neuron.

Model SBCs

SBCs (type II VCN neurons) are modelled as nonlinear, HH-type point neurons (Rothman and Manis 2003c), at human body temperature (37 °C) with three independent excitatory synapses each driven by an ANF (Lorente De No 1981), and optionally with 10 independent inhibitory synapses each driven by an ANF of the same CF (Kuenzel et al. 2015). Physiologically, the inhibition is from interneurons in the ipsilateral VCN and dorsal cochlear nucleus (DCN), driven by the same frequency-specific region of the auditory nerve as for excitation (Campagnola and Manis 2014; Wickesberg and Oertel 1990).

Our modelling of STP in vitro simplifies synaptic depression as vesicle depletion, the dominant mechanism in synaptic depression of SBCs (Yang and Xu-Friedman 2008); recovery is also simplified, as a single exponential function. We omit receptor desensitisation, changes in vesicle release probability, and calcium-mediated recovery. This simplified model of STP was sufficient to generally reflect adaptation in the AMBB responses of MSO neurons in vivo.

Each model excitatory synapse is a variable conductance (g_ESBC) in series with an excitatory reversal potential (V_E) of 0 mV (Table 1). Each input spike increases its synapse’s excitatory conductance by the excitatory synaptic strength Δg_ESBC. The unadapted maximum increment, the unadapted excitatory synaptic strength, is 83 nS; spike threshold was 34 nS for a single input from rest, using the same model membrane and faster synapses at 38 °C (Rothman and Manis 2003c). g_ESBC decays exponentially with a time constant of 0.2 ms (Kuenzel et al. 2011, 2015). In modelled cases with STP at the VCN, the increment Δg_ESBC is variable due to depression at the individual synapses, modelled as in Rudnicki and Hemmert (2017): immediately after an input spike and its associated increment in excitatory conductance, the synaptic strength is multiplied by 1 − u, where u = 0.5, based on measurements in vitro (u = 0.6 in Oleskevich et al. 2000; u = 0.4 in Wang and Manis 2008). This synaptic depression recovers exponentially with a time constant of 25 ms, as measured in vitro in the fast-recovering component comprising 70% of STP at SBCs (the remaining 30% of STP recovers with a slow 2-s time constant) (Wang & Manis 2008). This 25-ms time constant of exponential recovery yields 63% recovery at 25 ms, and 95% recovery at 75 ms. Low synchrony to AM in the model SBCs is consistent with the auditory nerve at high SPL (Joris and Yin 1992), and with lower synchrony in primary-like neurons of the cochlear nuclei (Rhode and Greenberg 1994). Compared with a single input, three inputs per model SBC increased spike rates, reduced synchrony to AM, and supported a small number of excitatory inputs (Couchman et al. 2010) to the model MSO neuron.

Table 1.

Synaptic parameters

Model SBCs
Number of excitatory synapses	3
Excitatory synaptic reversal potential, VE (mV)	0
Unadapted excitatory synaptic strength, ΔgESBC (nS)	83
Excitatory synaptic time constant, τESBC (ms)	0.2
Excitatory synaptic depression, u	0 or 0.5
Excitatory synaptic recovery time constant (ms)	25
Number of inhibitory synapses	0 or 10
Inhibitory synaptic reversal potential, VI (mV)	−75
Inhibitory synaptic strength, ΔgISBC (nS)	1.8
Inhibitory synaptic time constant, τISBC (ms)	23.9
Model MSO neurons
Number of excitatory synapses	8 (4 left; 4 right)
Excitatory reversal potential, VE (mV)	0
Unadapted excitatory synaptic strength, ΔgEMSO (nS)	36 or 25
Excitatory synaptic time constant, τEMSO (ms)	0.4
Excitatory synaptic depression, u	0 or 0.15
Excitatory synaptic recovery time constant (ms)	25

Based on SBCs and an existing model (Kuenzel et al. 2015), each model inhibitory synapse is a variable conductance (g_ISBC) in series with an inhibitory reversal potential (V_I) of −75 mV; each input spike causes an increment in its synapse’s inhibitory conductance by the excitatory synaptic strength, Δg_ISBC = 1.8 nS (based on the 24-nS increment for all 10 synapses simultaneously stimulated (Kuenzel et al. 2015), then reduced slightly to produce an appropriate level of adaptation); g_ISBC decays exponentially with a time constant of 23.9 ms. Inhibition is introduced only in cases without STP, so Δg_ISBC is fixed.

Model MSO Neuron

This nonlinear, HH-type model MSO neuron has separate compartments representing the bilateral dendrites, soma, and axon (Zhou et al. 2005), with anatomically based spatial dimensions (Mathews et al. 2010; Scott et al. 2010). The model axon functions simply as a spike generator, without myelination or nodes of Ranvier. Compared with a previous model (Brughera et al. 2013), the soma is simplified being spherical and iso-potential, and the somatic and dendritic membrane conductances for voltage-sensitive ion-channels are scaled by 0.6. Nonlinear models for fast-acting ion channels, the low-threshold potassium (K_LT) channels (Mathews et al. 2010) and sodium (Na) channels (Scott et al. 2010) are based on the MSO. The nonlinear model for slowly-varying hyperpolarisation-activated cyclic nucleotide (h) channels remains based on the VCN (Rothman and Manis 2003c).

Although models for h channels based on MSO neurons exist (Baumann et al. 2013) with similar reversal potentials, and similar steady-state activation and time-constant functions of membrane voltage, the VCN-based model h channels were maintained for consistency throughout a recent dissertation, which includes model LSO neurons, the nonlinear model MSO neuron presented here, and model MSO neurons (Brughera et al. 2013) originating before MSO h channels were characterised. Supporting resting membrane time constants, and resting potentials that activate K_LT channels, h channels operate with very slow time constants of a few hundred milliseconds (Baumann et al. 2013; Rothman and Manis 2003c). In modelling much faster adaptation with time constants of 25 ms, the effects of h channels can be similarly rendered whether applying MSO-based or VCN-based model h channels. When considering relatively fast time scales, h channels have even been modelled with constant conductance (Mathews et al. 2010).

On the bilateral model dendrites, eight excitatory synapses (Couchman et al. 2010) are located one each at 42.5, 47.5, 52.5, and 57.5% of the dendritic length. Each synapse is modelled as a variable conductance (g_EMSO) in series with an excitatory reversal potential (VE) of 0 mV based on MSO neurons (Scott et al. 2010). These modelled synapses are generally nondepressing. Each synapse is driven by a single model SBC from the same side. An input spike increments its synaptic conductance by the excitatory synaptic strength, Δg_EMSO, and the conductance g_EMSO then decays exponentially with a time constant τ_E = 0.4 ms, within physiological range (Fischl et al. 2012; Franken et al. 2015). The undepressed value of Δg_EMSO is equal to 36 nS, comparable with excitatory fibre conductances of 37 ± 4 nS measured in vitro (Couchman et al. 2010). In a modelled case with STP at the MSO, Δg_EMSO is variable due to depression at the individual synapses, modelled as in Rudnicki and Hemmert (2017): immediately after an input spike and its associated increment in excitatory conductance, the synaptic strength is multiplied by 1 − u, where u = 0.15, based on measurements in vitro (Couchman et al. 2010). Despite only some 30% of STP at the in vitro MSO being fast-recovering (Couchman et al. 2010), the modelled synaptic depression recovers exponentially with a time constant of 25 ms.

Within the nonlinear model MSO neuron, its functional electric-circuit unit, the sub-compartment (Fig. 2c), connects to its neighbouring sub-compartments via series resistivity (R_S) representing the neuron’s internal cytoplasm. In the long, narrow model dendrites and axon, R_S = 150 Ω cm, based on MSO neurons (Mathews et al. 2010). In the relatively short, wide soma, the low series resistance (R_S × length/area) is assumed to be negligible compared with membrane impedance; thus, we have applied the common approach of modelling the soma as iso-potential with R_S zero and a single sub-compartment (Stimberg et al. 2019). Within each sub-compartment, the neural membrane is modelled as a transmembrane capacitance (C_M) in parallel with ion-channel populations: Na, h, K_LT, and leakage (L). C_M = 1 μF/cm², based on MSO neurons (Scott et al. 2010). Each ion-channel population is represented as a physiologically based reversal potential (V_Na, V_h, V_KLT, V_L) in series with a conductance (g_Na, g_h, g_KLT, g_L).

Kirchhoff’s current equation, applied to the model MSO neuron, states that the sum of currents entering any point is zero:

$$0=i_{\mathit{CM}}+i_{\mathit{Na}}+i_{\mathit{KLT}}+i_h+i_L+i_{S1}+i_{S2}$$

Series currents, $i_{S1}$ and $i_{S2}$, are calculated by the Brian2 simulator according to the voltage differences, resistivity, and geometry of the related sub-compartments.

Capacitive membrane current (i_CM) increases with the time derivative of membrane potential V, and is proportional to membrane capacitance:

$$i_{\mathit{CM}}=C_M\frac{\mathit{dV}}{\mathit{dt}}$$

Leakage current: $i_L=g_L(V-V_L)$. Representing effects of voltage-insensitive ion channels, the leakage conductance (g_L = 0.00005 S/cm²) and the reversal potential for leakage (V_L = −65 mV), are based on physiological values and previous modelling of MSO neurons (Scott et al. 2010).

Each voltage-sensitive ionic conductance is equal to a maximum conductance (gmax) multiplied by voltage-sensitive activation and inactivation gating variables with integer exponents (Hodgkin and Huxley 1952). Each activation and inactivation variable has a rate of change governed by a separate first-order differential equation, with a voltage-dependent time constant divided by the $Q_{10}$ temperature factor of 3^{(T − 22)/10}, where T is set equal to human body temperature, 37 °C. The $Q_{10}$ base 3 is consistent, with sodium and potassium currents in a variety of neurons (Belluzzi et al.1985; Connor and Stevens 1971; Frankenhaeuser and Huxley 1964; Hodgkin and Huxley 1952; Sah et al.1988) including $i_{\mathit{Na}}$ in MSO neurons (Scott et al. 2010), and is similar to a measured value of 3.3 for $i_{\mathit{KLT}}$ in MSO neurons (Mathews et al. 2010). The maximum conductance values (Table 2: gmax_KLT, gmax_Na, and gmax_h) are generally consistent with recently characterised MSO neurons (Mathews et al. 2010; Scott et al. 2010), and support physiologically plausible membrane time constants and resting potentials: near −60 mV in the model soma and dendrites, consistent with physiological values in MSO neurons promoting the activation of K_LT channels (Mathews et al. 2010; Scott et al. 2010); and near −64 mV in the model axon (for which a physiological value is not available) which reduces inactivation of model Na channels, sufficient to model large axonal action potentials, without significant back-propagation to the soma (Brughera et al. 2013), consistent with the small somatic action potentials of MSO neurons (Scott et al. 2007). V_AP-THRESHOLD is a computational threshold for counting action potentials: when the membrane voltage at the midpoint of the model axon transitions from −35 mV or less to greater than −20 mV, an action potential (spike) is counted. The numbers of sub-compartments are computational free parameters.

Table 2.

Nonlinear model MSO neuron: compartmental and membrane parameters

Parameter	Dendrites (2)	Soma	Axon
Number of sub-compartments	20	1	51
Diameter (μm)	3.5	30	2
Length (μm)	150	30	400
Resistivity, RS (Ω cm)	150	0	150
CM (μF/cm2)	1	1	1
VKLT (mV)	−106	−106	−106
VNa (mV)	n/a	+62.1	+62.1
Vh (mV)	−43	−43	−43
VL (mV)	−65	−65	−65
gmaxKLT (S/cm2)	0.00132	0.0324	0.0595
gmaxNa (S/cm2)	0 (none)	0.0432	0.25
gmaxh (S/cm2)	0.00066	0.01296	0.0025
gL (S/cm2)	0.00005	0.00005	0.00005
VREST (mV, observed in model)	−60.53	−60.52	−64.35

The model somatic membrane time constant of 0.39 ms is within the 0.3 to 0.6 ms measured in principal MSO neurons near resting potential (Couchman et al. 2010; Scott et al. 2007) and was calculated from the model’s somatic membrane impedance as a function of frequency: determined by simultaneous transmembrane injection of bias current and sinusoidal current containing a linear frequency sweep from 1 to 2000 Hz during 1 s (Hutcheon and Yarom 2000; Puil et al. 1986; Remme et al. 2014). Prior to stimulus, the model membrane settled for 0.1 s to its resting potential, −60.52 mV. Settling was followed by a steady inward bias current (I_BIAS) applied for 0.9 s. I_BIAS was then maintained as the frequency sweep in membrane current (250-pA peak amplitude) was also applied. Membrane impedance was calculated using the fast Fourier transform (FFT). FFTs of the injected transmembrane current, and the resulting membrane voltage, were computed over the duration of the frequency sweep. The FFT of voltage was divided by the FFT of current, yielding the FFT of membrane impedance; plotting its magnitude shows the magnitude of membrane impedance as a function of frequency. With increased I_BIAS, membrane holding potential (V_HOLD) increased, and a resonance in membrane impedance as a function of frequency emerged, and increased in amplitude and resonance frequency (Fig. 2d–g): (D) with I_BIAS = 0, V_HOLD is equal to −60.52 mV, and there is no resonance; (E) with I_BIAS = 300 pA, V_HOLD increased to −59.22 mV, and the resonance frequency (f₀) was 408 Hz; (F) with I_BIAS = 600 pA, V_HOLD increased to −57.88 mV, and f₀ was 513 Hz; (G) with I_BIAS = 1200 pA, V_HOLD increased to −55.24 mV, and f₀ was 692 Hz. Assuming that the resonant membrane is a second-order system, the membrane time constant is equal to the reciprocal of angular resonance frequency (Nilsson and Riedel 2008; Remme et al. 2014). In Fig. 2e, the resonance at 408 Hz indicates a membrane time constant of 1/(2π × 408 Hz) = 0.390 ms.

The Na current (Scott et al. 2010), which is rapidly varying, is based on MSO neurons:

V_Na = +62.1 mV.

$$i_{\mathit{Na}}=g_{\mathit{Na}}(V-V_{\mathit{Na}})$$

$g_{\mathit{Na}}={\mathit{gmax}}_{\mathit{Na}}{m}^4\left(0.993,h,+,0.007\right)$, where m is activation, and h is inactivation.

$$\frac{\mathit{dm}}{\mathit{dt}}=Q_{10}(m_{\infty }-m)/{\tau }_m$$

$$\frac{\mathit{dh}}{\mathit{dt}}=Q_{10}(h_{\infty }-h)/{\tau }_h$$

For model Na channels, steady-state activation ($m_{\infty }$) and inactivation ($h_{\infty })$, and their respective time constants (${\tau }_m$ and ${\tau }_h$) in milliseconds, are functions of membrane potential in millivolts (Scott et al. 2010):

$$m_{\infty }=1./(1+\exp ((V+46.)/(-11.)))$$

$${\tau }_m=((0.141+(-0.0826/(1+\exp ((-20.5-V)/10.8))))/3.)$$

$$h_{\infty }=1./(1+\exp ((V+62.5)/7.77))$$

$${\tau }_h=((4.+(-3.74/(1+\exp ((-40.6-V)/5.05))))/3.)$$

K_LT current (Mathews et al. 2010), which is rapidly varying, is based on MSO neurons:

V_KLT = −106 mV.

$$i_{\mathit{KLT}}=g_{\mathit{KLT}}(V-V_{\mathit{KLT}})$$

$g_{\mathit{KLT}}={\mathit{gmax}}_{\mathit{KLT}}{w}^{4}z$, where w is activation, and z is inactivation.

$$\frac{\mathit{dw}}{\mathit{dt}}=Q_{10}(w_{\infty }-w)/{\tau }_w$$

$$\frac{\mathit{dz}}{\mathit{dt}}=Q_{10}(z_{\infty }-z)/{\tau }_z$$

$$w_{\infty }=1./(1+\exp ((V+57.34)/(-11.7)))$$

$${\tau }_w=((21.5/((6.\ast \exp ((V+60.)/7.))+(24.\ast \exp (-(V+60.)/50.6))))+0.35)$$

$$k=0.27$$

$$z_{\infty }=((1.-k)/(1+\exp ((\mathrm{V}+67.)/6.16)))+k$$

$${\tau }_z=((170./(5.\ast \exp ((V+60.)/10.)+\exp (-(V+70.)/8.)))+10.7)$$

The noninactivating h current (Rothman and Manis 2003c), which is slowly varying, is based on VCN neurons:

V_h = −43 mV.

$$i_h=g_h(V-V_h)$$

$g_h={\mathit{gmax}}_{h}r$ , where r is activation.

$$\frac{\mathit{dr}}{\mathit{dt}}=Q_{10}(r_{\infty }-r)/{\tau }_r$$

$$r_{\infty }=1./(1+\exp ((\mathrm{V}+76.)/7.))$$

$${\tau }_r=((100000./(237.\ast \exp ((\mathrm{V}+60.)/12.)+17.\ast \exp (-(\mathrm{V}+60.)/14.)))+25.)$$

AMBB Period Histograms

For each AMBB period histogram from the nonlinear model, spikes were counted in forty nonoverlapping bins, each covering 1/40 of the AM cycle (unsmoothed). Spike rates were calculated by dividing the spike count by the total time duration for each bin, across the multiple periods of eight different stimulus presentations of 0.75-s duration. Histograms for model SBCs were circularly advanced by approximately 4.7 ms (by fixed numbers of bins: 12 bins at 64-Hz AM; 6 bins at 32-Hz AM; 3 bins at 16-Hz AM; 2 bins at 8-Hz AM; 1 bin at 4-Hz AM), which generally aligned the minimum spike rate with the minimum amplitude of the AM cycle at time zero of the histogram. Histograms for the model MSO neuron were circularly advanced by these amounts, plus an additional 1.56 ms (by fixed numbers of bins, rounded downward: 4 bins at 64-Hz AM; 2 bins at 32-Hz AM; 1 bin at 16-Hz AM; 0 bins at 8-Hz and 4-Hz AM), which compensated for the delay of model MSO spike times relative to model SBCs. These shifts facilitated comparison of the modulated spike rates during AMBBs, with the AM cycle, and with mean spike rates under AM stimuli as functions of static fine-structure IPD, both superimposed on the AMBB histograms.

Chi-Squared Tests for Significant Differences in Model Spike Counts

Within each modulation frequency, a chi-squared test for one and two degrees of freedom (2-way and 3-way comparisons) compared spike counts across the AM cycle from the nonlinear model MSO neuron stimulated with AMBBs with start-IPDs of −90°, −180°, and −270° (respectively, making the best ITD occur during rising vs. peak vs. falling amplitude). Each chi-squared test yielded a probability (P) that the differences in spike count would occur under the null hypothesis that there is no relationship between the start-IPD and spike count.

Synchrony Index and Rayleigh Statistic for Significant Phase-Locking

For each modulation frequency and start-phase combination, the synchrony index (SI, R) of spike times ($t_i$) (Johnson 1980) with respect to their phase ${\theta }_i$ within the AM cycle (with modulation frequency $f_m$ and modulation period $T_m=1/f_m$) was calculated:

$${\theta }_i\triangleq 2\pi f_{m}mod(t_i,T_m)$$

$R=SI=\sqrt{{\left({\sum }_{i=1}^N,\cos ,{\theta }_i\right)}^2+{\left({\sum }_{i=1}^N,\sin ,{\theta }_i\right)}^2}$, where N is the spike count.

The Rayleigh significance statistic (2NR²) was then calculated and converted to a P value, the probability that the AM period histogram of spike times would result given the null hypothesis which is a uniform distribution for spikes across the period (Rhode 1976):

P	0.10	0.05	0.025	0.01	0.001
2NR2	4.605	5.991	7.378	9.210	13.816

MODEL 2: Lateralisation by Linear Membrane Models for SBCs and MSO Neurons, Driven by Nonlinear Model ANFs

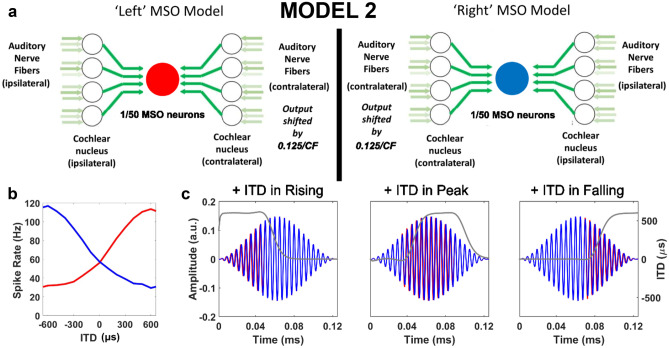
To study how monaural adaptation and neuronal membrane properties can impact lateralisation of acoustic stimuli in anechoic and reverberant conditions, we constructed a population model of lateralisation whose left and right brainstem stages each comprise 400 SBCs and 50 MSO neurons (Fig. 3a) represented by point neurons with computationally efficient, active linear membranes (Remme et al. 2014). Data, analysis scripts, and code are available at figshare: https://doi.org/10.6084/m9.figshare.9899018.v1.

Fig. 3.

MODEL 2 and SAM stimuli. (a) MODEL 2 contains two MSO populations (red: left MSO; blue: right MSO), each comprising fifty linear, single-compartment model neurons, with fast or slow membranes. Each model MSO neuron receives four excitatory inputs ‘bilaterally’ from linear, single-compartment model SBCs. Three independently simulated, medium-spontaneous-rate model ANFs (Zilany et al., 2014) each provide an individually depressing excitatory synapse to a model SBC. (b) ITD tuning functions for the two MSO populations are shown for a 2-s, 600-Hz pure tone. (c) SAM stimuli applied as left (blue) and right (red) inputs, with positive ITD introduced during the rising, peak, or falling portions of the AM cycle (dark grey line shows instantaneous ITD). Speech stimuli (Fig. 1) were presented separately to MODEL 1

Linear differential equations were used to simulate membrane currents in the model neurons, reducing the required computation compared with HH-type models, and helping to match membrane time constants of model MSO neurons more easily to values previously observed for ‘slower’ principal neurons in the superior olivary complex (Bondy and Golding 2018; Remme et al. 2014). For clarity, the results subsection entitled, ‘MODEL 2’, is dedicated to linear model simulations.

Two stimuli were presented to MODEL 2: (1) SAM tones with ITDs briefly manipulated during either the rising, peak or falling phases of their AM cycles (Fig. 3c), as previously applied behaviourally to determine how carrier frequency affects ITD sensitivity over the time course of an AM cycle (Hu et al. 2017); (2) a natural speech stimulus with early reflections, a simple simulation of a reverberant environment where correct lateralisation is possible only if ITD cues in the onset waveform are processed preferentially (Dietz et al. 2014).

SAM Tones with Manipulated ITDs During Brief Periods Aligned to Different AM Cycle Phases

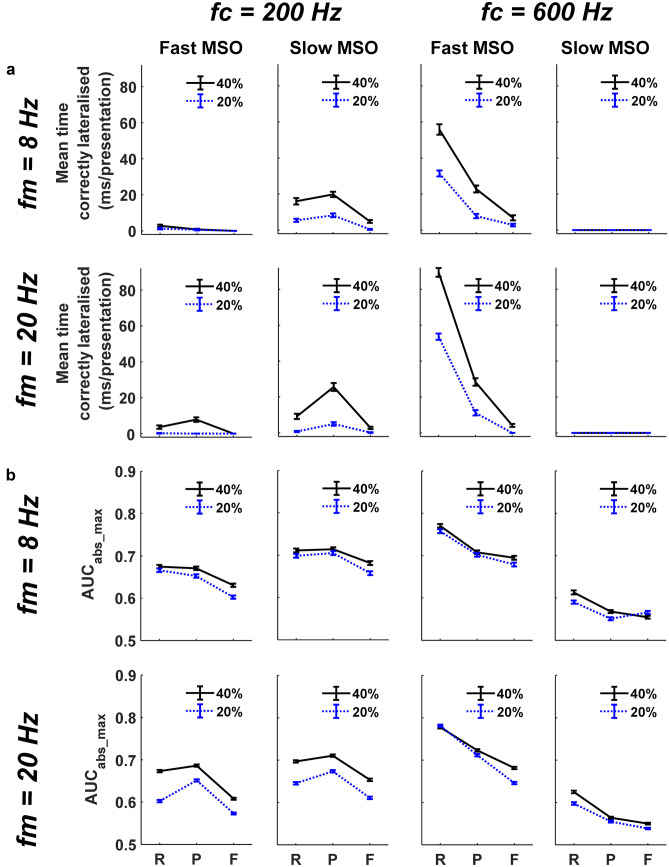
Five hundred millisecond SAM tones were generated according to the Hu et al. (2017) study, and presented at 70dB SPL to the auditory periphery model. These SAM tones were generated from pulse trains that had been bandpass filtered and then amplitude modulated. Nonstationary ITDs were added by temporally shifting individual pulses in one of either the rising, peak, or falling phases of the AM cycle. For the purposes of this study, nonstationary ITDs of + 300 μs and + 150 μs were introduced into SAM tones of either 200-Hz or 600-Hz carrier frequency, respectively. These ITD values were chosen based on individual behavioural thresholds in the Hu et al. (2017) study. At each carrier frequency, four conditions were tested: two different AM cycle frequencies (8 Hz or 20 Hz) and two different proportions of rising, peak or falling AM cycle phases with manipulated ITDs (20% or 40%). For example, for 8-Hz SAM tones, ITDs were manipulated in either 25 ms (20%) or 50 ms (40%) segments associated with either rising, peak, or falling phases of the modulation cycle. These parameters match those tested behaviourally by Hu et al. (2017).

Natural Speech Stimuli with Early Reflections

Six single monosyllabic consonant-vowel nucleus-consonant (CNC) word tokens, ‘church’, ‘shown’, ’fuss’, ‘talk’, ‘mate’, ‘vine’ (spoken by an Australian-English, female voice), were selected as speech stimuli (Figs. 1 and 10). To simulate their arrival from a location one metre away to the right of the midline in an anechoic environment, the words’ waveforms (normalised at 70 dB) were convolved with a large-pinnae, head-related transfer function (HRTF) for +30° azimuthal location (CIPIC database, UC Davis). A reverberant space was simulated by adding to the direct (+30°) pathway two early reflections off virtual walls stood behind and to the right of the subject (Fig. 1). These reflected copies of the words arrived from −65° and −130° angles (again convolved with large-pinnae HRTFs from the CIPIC database) and were delayed by 4 ms and 8 ms, respectively, to reproduce their elongated paths (Dietz et al. 2014).

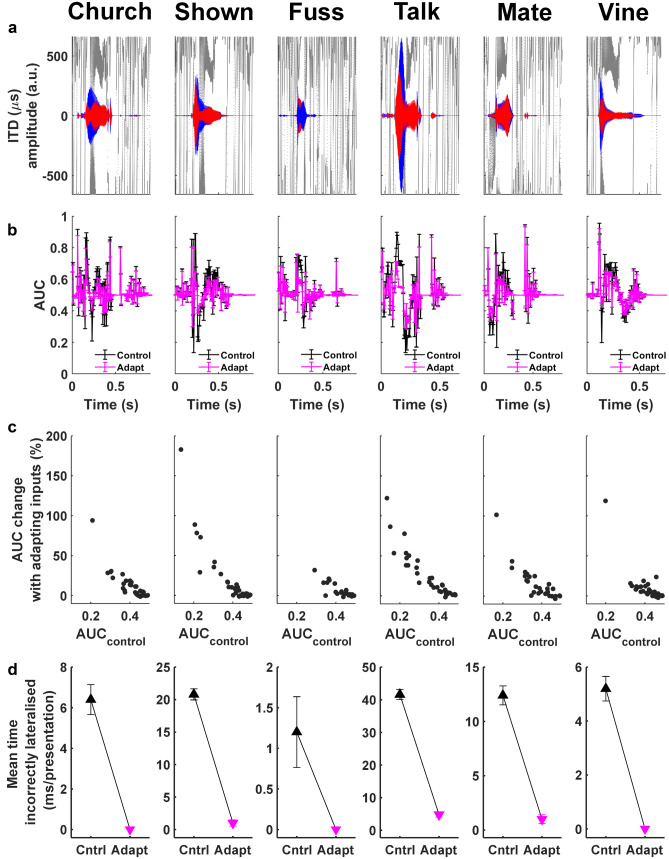
Fig. 10.

MODEL 2 (fast MSOs, 600-Hz channels): for all six reverberant-speech stimuli, adaptation of synaptic CN inputs increased AUC_abs and decreased incorrect lateralisations. (a) Waveforms and ITDs of reverberant speech, gammatone filtered at 600 Hz. (b) AUC_abs (± SEM) for nonadapting (black) and adapting (magenta) inputs. (c) Percentage AUC_abs increase introduced by adapting inputs for time bins in which AUC_abs was significantly below 0.5 for nonadapting inputs (P = 0.001). (d) Mean time incorrectly lateralised per stimulus presentation (number of incorrect lateralisations × bin duration/25 presentations), with nonadapting (CTRL) and adapting (ADAPT) inputs

Auditory Periphery Stage in Linear Model

The linear model is consists of three stages: an initial auditory-periphery stage (the middle/inner ear and stochastic ANFs) and two brainstem stages (cochlear nuclei and MSO). Peripheral processing of the acoustic stimuli in the linear model is performed by a cat middle/inner ear model (Zilany et al. 2014) in Matlab. Outputs from the auditory periphery are restricted to the 200-Hz and 600-Hz channels for the pulse-shifted SAM tones (matching their SAM tone’s carrier frequency), and the 600-Hz channel for lateralisation of speech stimuli. This 600-Hz channel is within the 500–750-Hz frequency range, in which sensitivity to ITD in the temporal fine structure (TFS, ITD_TFS) of sound is considered strongest (Bilsen and Raatgever 1973; Tollin and Henning 1999). When exploring effects, of synaptic depression at the inputs from auditory nerve to VCN, on the lateralisation of a speech stimulus, the same auditory nerve simulations are used for both the depressing and nondepressing inputs.

Brainstem Stages in Linear Model

Following the model concept of Dietz et al. (2009), two parallel, coincidence-detecting circuits were simulated in the linear model to represent the ‘left’ and ‘right’ MSO nuclei and their inputs. The spiking outputs of these parallel circuits are utilised to calculate lateralisation of the natural stimulus. The only difference between ‘left’ and ‘right’ circuits is the contralateral $\frac{1}{8}$ pi shifts in their MSO neurons’ IPD tuning curve peaks which are generated by delaying the outputs from the auditory periphery stage ipsilateral to the MSO nucleus in question. This shift is considered physiological given experimentally observed binaural tuning curves from the auditory brainstem whose optimal characteristics have been corroborated theoretically (McAlpine et al. 2001). ‘Left’ and ‘right’ MSO populations contained 50 neurons each, of either fast or slow membrane properties on both sides and received bilateral inputs from the VCNs, for which ‘contralateral’ inputs were delayed by 0.125 cycles of IPD (equal to ITD × frequency) such that their MSO neurons spiked preferentially for sounds arriving from contralateral spatial locations (Fig. 3b).

Linear-Membrane Model Properties

Single-compartment, linear-membrane models are used to represent both SBC and MSO neurons in the linear model. These linear-membrane models incorporate two dynamic currents (Remme et al. 2014): I_w, a resonant current, and I_n, an amplifying current. The current balance equation for the neural model is as follows:

$$\mathrm{c}\frac{\mathit{dv}}{\mathit{dt}}=-g_{\mathrm{M}}v-g_{\mathrm{w}}{w}_{\mathrm{w}}+g_{\mathrm{n}}{w}_{\mathrm{n}}+I_{\mathit{app}}\left(t\right)$$

Where c is membrane capacitance (25 pF in MODEL-2 neurons), g_M is a passive membrane conductance (nS) and I_app is the current (pA) applied to the neural model. The resonant and amplifying currents, I_w and I_n, are described by their conductances, g_W and g_n (in nS); the dynamics of their gating variables, w_w and w_n (in millivolts) are described by equations with time constants τ_w and τ_n, respectively:

$${\tau }_{\mathrm{w}}\frac{d{w}_{\mathrm{w}}}{\mathit{dt}}=v-w_{\mathrm{w}}$$

$${\tau }_{\mathrm{n}}\frac{d{w}_{\mathrm{n}}}{\mathit{dt}}=v-w_{\mathrm{n}}$$

Two parameter sets are chosen to represent the range of membrane speeds recently observed in MSO neurons (Bondy and Golding 2018; Remme et al. 2014). These example model membranes can be broadly characterised as either fast with a high resonance frequency (g_W = 50 nS, τ_w = 0.8 ms, g_n = 0 nS, g_M = 30 nS) or slow with a low resonance frequency (g_W = 15 nS, τ_w = 2 ms, g_n = 27 nS, τ_n = 0.5 ms, g_M = 30 nS), as previously modelled by Remme et al. (2014). While both fast and slow model membranes are used to represent MSO neurons, only the fast model membrane was chosen to represent all SBCs.

Synaptic Properties and Plasticity

Providing excitatory drive to each linear model SBC, again 3 independently simulated ANFs were applied. Excitatory unitary conductances at this synapse are modelled as alpha functions with an exponential time course of 0.2 ms. Synaptic depression with a single exponential recovery is also implemented at this stage, with similar parameters values (u = 0.55; τ = 25 ms) to the HH-type model SBCs.

Each MSO neuron receives 4 (independently simulated) excitatory cochlear nucleus inputs from ‘either ear’ in the linear model. Alpha functions are again used to model the unitary excitatory conductances at this synapse, with time constants: 0.2 ms paired with fast model membranes, and 0.5 ms paired with slow model membranes. Where comparisons of fast and slow model neurons are made, the same adapting auditory nerve inputs are presented to their respective cochlear nucleus stages.

Spike Thresholds in the Linear-Membrane Model

The linear-membrane model applies idealised spike thresholds (Remme et al. 2014). A slope threshold (dv/dt) is used for all neuronal types. Threshold values for cochlear nucleus cells are selected to produce good average firing rate without undermining the effects of synaptic depression. Threshold values for the MSO neurons are selected to obtain maximum dynamic range of ITD tuning functions for 200/600 Hz pure tone stimuli (where dynamic range is considered the difference between the maximum and minimum ITD-modulated spike rate). A refractory period of 1 ms is implemented as in Remme et al. (2014) for model SBCs and fast model MSO neurons, whereas a longer refractory period of 2 ms is used for slow model MSO neurons, reflecting longer refractory periods in neurons with lower densities of K_LT channels (Rothman and Manis 2003a, 2003b, 2003c).

Calculating Lateralisation Using AUC Values

The population activity of ‘left’ and ‘right’ MSO model neurons is used to calculate values of area under the curve (AUC) as a neurometric of lateralisation. These AUCs are calculated empirically by estimating the Mann-Whitney U statistic (closely related to generating receiver operator curves to calculate AUCs) using a fast version of the DeLong method (Bamber 1975; Delong et al. 1988; Sun and Xu 2014). AUC equal to 1 would indicate that the linear model 100% correctly predicted the stimulus’ arrival from the right in that time bin; AUC of 0.5 would represent an inability to make a left/right discrimination; AUC of zero would indicate a 100% incorrectly predicted lateralisation to the left.

To generally probe lateralisation of SAM and speech stimuli, AUC_trial is calculated for each 5-ms time bin within a stimulus presentation or ‘trial’ (among 25 presentations overall) from the spike rates of 50 MSO neurons in the left and right populations. Threshold values of ≥ 0.75 or ≤ 0.25 are used to categorise a right or left lateralisation, respectively, in a 5-ms time bin; these threshold values are associated with excellent discrimination ability of a classifier (Hosmer et al. 2013). Time correctly/incorrectly lateralised is subsequently calculated by multiplying the number of bins where AUC_trial ≥ 0.75 or ≤ 0.25 by the 5-ms bin duration.

To test if absolute lateralisation performance changed significantly across different conditions of stimuli, neuronal membranes, and adaptation: spike rates resulting from 25 stimulus presentations to 50 neurons per ‘left’/‘right’ MSO population are used to calculate AUC_abs and AUC_{abs_max}, and their variances. While AUC_abs is quantified by comparing activity of the 1250 stimulus reponses per ‘left’/‘right’ MSO population for each 5-ms time bin of a stimulus, AUC_{abs_max} generates a single AUC for each SAM stimulus condition, by using the aggregated MSO activity from those 5-ms time bins where AUC_abs is maximal in each AM cycle (4 time bins for the 8-Hz AM stimuli of 0.5-s duration; 10 time bins for 20-Hz AM stimuli). Given that all ANF inputs to SBCs were independently realised, the same MSO simulations are used to calculate AUC_trial as well as AUC_abs and AUC_{abs_max}. For speech stimuli, we calculate the percentage change in AUC_abs after adapting inputs are introduced in those time bins where AUC_abs were significantly < 0.5 (p < 0.001) in the original nonadapting condition.

Statistical Tests for Significant Differences in Lateralisation

Statistical comparisons of AUC with baseline value of 0.5 are performed by calculating z scores as part of the DeLong Test (covariance parameter was removed as unnecessary given the uncorrelated nature of the comparisons) (DeLong et al. 1988). Two-way or three-way ANOVAs are implemented with either percentage ITD insertion and AM phase as factors (two-way ANOVA) or membrane speed of neurons, percentage ITD insertion and AM phase as factors (three-way ANOVA) to compare the summary AUC_{abs_max} data for either 8- or 20-Hz SAM stimuli. Tukey’s multiple comparison test was applied afterwards. A Wilcoxon signed-rank test is used to compare matched values of AUC_abs with nonadapting and adapting inputs when speech stimuli were presented.

RESULTS

Our investigation first modelled effects of STP at the synaptic inputs from ANFs to SBCs in the VCN: in matching responses of in vivo MSO neurons to AMBBs (MODEL 1 with nonlinear voltage-sensitive membrane ion-channel conductances); and in improving the ability of bilateral MSO populations to correctly lateralise SAM tones with ITD and speech sources in reverberation (MODEL 2 with linear active neuronal membranes). In our further investigation, modelled adaptation in AMBB responses was largely similar for STP in the MSO, STP in the VCN, and inhibition in the VCN; model K_LT channels also contributed to the adaptation (MODEL 1). Given the efficacy of the modelled STP in the VCN, we present all the results from MODEL 1, followed by the results from MODEL 2.

MODEL 1: Nonlinear Models for ANFs, SBCs, and MSO Neuron

We explored the extent to which adaptive brainstem mechanisms can account for the rate-dependent emphasis of ITDs during rising vs. peak energy of modulated sounds.

Adaptive Mechanisms in the VCN and MSO Can Each Support In Vivo AMBB Responses that Reflect Behavioural ITD Detection

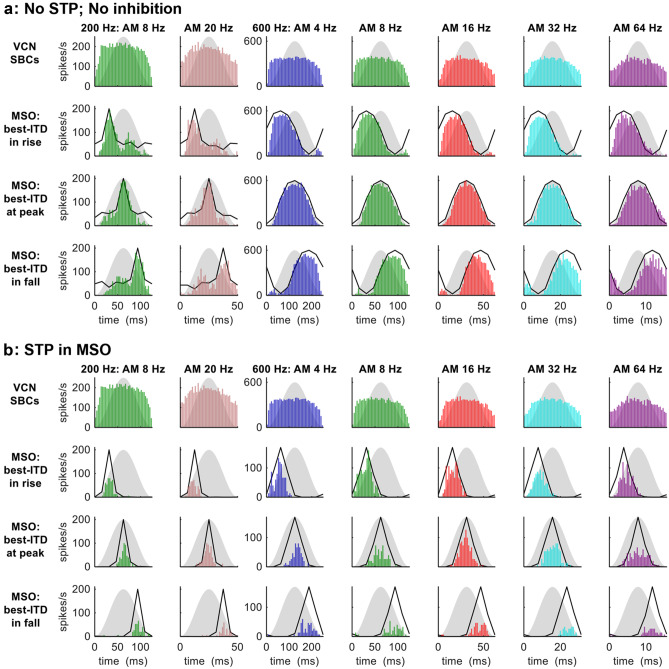
No STP; No Inhibition

We begin with no STP and no inhibition, the control condition of weakest adaptation.

For AMBBs centred at 200-Hz, at the modulation rates of 8 and 20 Hz employed by Hu et al. (2017), the model SBCs displayed very slight adaptation in spike rates across the AM cycle, interrupted by a slight increase in spike rate at near the peak of AM (Fig. 4a, top row, leftmost 2 columns). The model MSO neuron (Fig. 4a, lower three rows, 2 leftmost columns) responded strongly to zero ITD (its predetermined best ITD) across the AM cycle, with no significant differences in spike counts between the responses to AMBBs of different start IPDs for which the best-ITD occurred during rising vs. peak vs. falling sound energy. The synchrony index (SI)—applied as a measure of temporal alignment of spikes over the AM cycle (see ‘METHODS’)—ranged from 0.10 at 8 Hz to 0.13 at 20 Hz for the model SBCs; for the model MSO neuron, SI ranged from 0.33 (20 Hz, when the best ITD occurred during falling energy) to 0.65 (20 Hz, when the best ITD occurred during peak energy) (Rayleigh statistic: P < 0.001 in all cases).

Fig. 4.

MODEL 1: AMBB-cycle spike-rate histograms of SBCs and MSO neuron for AMBBs centred at CFs 200 Hz (leftmost 2 columns) and 600 Hz (rightmost 5 columns): (a) with no inhibition and no STP; (b) with STP in the MSO. Definitions: grey silhouettes: AM envelope; black lines: normalised static-IPD functions for a single amplitude-modulated carrier frequency at CF. The model MSO neuron has a best ITD of zero: ‘best-ITD in rise’ denotes start-IPD = −90° (270°); ‘best-ITD at peak’ denotes start-IPD = −180° (180°); and ‘best-ITD in fall’ denotes start-IPD = −270° (90°)

For AMBBs centred at 600 Hz, at the modulation rates of 4, 8, 16, 32, and 64 Hz employed by Dietz et al. (2014), the model SBCs produced very slight adaptation in the spike rates across the AM cycle, with slight adaptation for 64-Hz modulation (Fig. 4a, top row, rightmost 5 columns). The model MSO neuron (Fig. 4a, lower three rows, rightmost 5 columns) responded strongly to its best ITD across the AM cycle: more strongly at peak sound energy than during rising energy (P < 10⁻⁴, chi-squared tests for 2-way comparison at each modulation frequency) and falling energy (P < 10⁻⁴, chi-squared tests for 2-way comparison at each modulation frequency) (chi-squared tests for 3-way comparison, P < 10⁻⁴ at each modulation frequency). The synchrony index (SI)—applied as a measure of temporal alignment of spikes over the AM cycle (see ‘METHODS’)—ranged from 0.11 at 64 Hz to 0.15 at 16 Hz for the model SBCs; for the model MSO neuron, SI ranged from 0.43 (64 Hz, when the best ITD occurred during peak energy) to 0.59 (8 Hz, when the best ITD occurred during rising energy) (Rayleigh statistic: P < 0.001 in all cases).

STP in the MSO

Here, we applied STP strictly in the MSO. In this condition, the spike responses and statistics of the model SBCs (Fig. 4b, top row) were identical to those in the previous condition, No STP; No Inhibition. With STP at its synaptic inputs, the model MSO neuron responded differently.

For AMBBs centred at 200 Hz, spike counts in the model MSO neuron (Fig. 4b, lower three rows, 2 leftmost columns) matched the patterns of significance in ITD detection by human listeners for AM stimuli at 200 Hz (Hu et al. 2017): spike counts were marginally higher when the best ITD occurred during peak vs. rising energy (ranging from a 1-spike difference at 8-Hz AM, to marginally significance at 20 Hz AM: P = 0.050); spike counts were lower when the best ITD occurred during falling vs. peak energy (P = 0.052 at 8 Hz; P < 10⁻⁵ at 20 Hz). The SI to AM for the model MSO neuron ranged from 0.83 (20 Hz, when the best ITD occurred during falling energy) to 0.93 (8 Hz, when the best ITD occurred during peak energy) (Rayleigh statistic: P < 0.001 in all cases).

For AMBBs centred at 600 Hz, consistent with physiological and behavioural data at 600 Hz (Dietz et al. 2014; Hu et al. 2017), the model MSO neuron responded to its best ITD moderately during rising amplitude, weakly to moderately at peak energy, and only weakly during falling energy (Fig. 4b, lower three rows; in this 3-way comparison of spike counts, P < 10⁻⁸ at each modulation frequency). The model MSO neuron had higher spike counts in response to its best ITD during rising energy vs. peak energy at 4- and 8-Hz modulation (P < 10⁻⁴), and during peak vs. falling energy at 8- to 64-Hz modulation (P < 0.0025). The SI to AM for the model MSO neuron ranged from 0.64 (64 Hz, when the best ITD occurred during peak energy) to 0.87 (4 Hz, when the best ITD occurred during peak energy) (Rayleigh statistic: P < 0.001 in all cases).

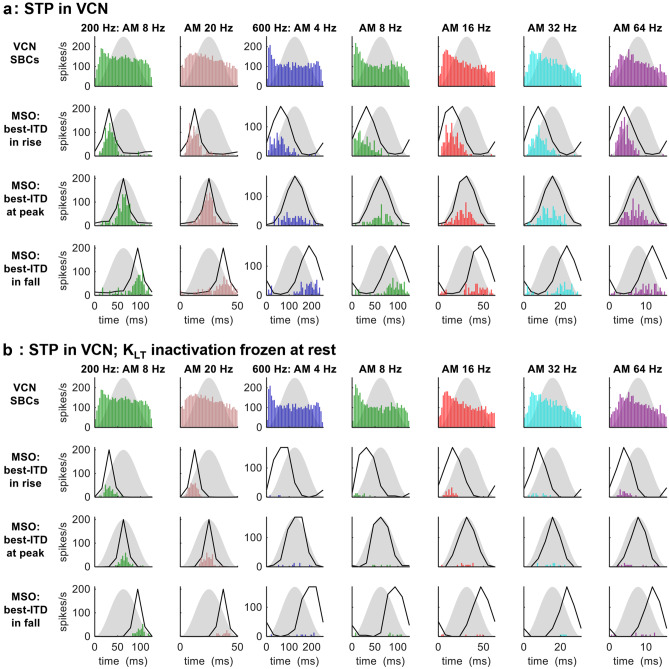
STP in the VCN

Here, we applied STP strictly in the VCN. For AMBBs centred at 200 Hz, the model SBCs showed slight adaptation in spike rate across the AM cycle (Fig. 5a, top row, 2 leftmost columns). Spike counts in the model MSO neuron (Fig. 5a, lower three rows, 2 leftmost columns) matched the patterns of significance in ITD detection by human listeners for AM stimuli at 200 Hz (Hu et al. 2017): spike counts were slightly higher but not significantly when the best ITD occurred during peak vs. rising energy, and spike counts were significantly lower when the best ITD occurred during falling energy vs. peak energy (P = 0.011 for modulation at 8 Hz; P = 0.0019 for modulation at 20 Hz). The SI to AM for model SBCs ranged from 0.076 at 8 Hz to 0.11 at 20 Hz; and for the model MSO neuron, from 0.45 (20 Hz, when the best ITD occurred during falling energy) to 0.81 (8 Hz, when the best ITD occurred during rising energy) (Rayleigh statistic: P < 0.001 in all cases).

Fig. 5.

MODEL 1: AMBB-cycle spike-rate histograms of SBCs and MSO neuron for AMBBs centred at CFs 200 Hz (leftmost 2 columns) and 600 Hz (rightmost 5 columns): (a) with STP in the VCN; (b) with STP in the VCN, and K_LT inactivation frozen at rest in the VCN and MSO. Black lines: normalised static-IPD functions for a single amplitude-modulated carrier frequency at CF. For more definitions, see Fig. 4 caption

For AMBBs centred at 600 Hz, the model SBCs adapted more strongly than at 200 Hz (Fig. 5a, top row, 5 rightmost columns); this adaptation in spike rate followed a similar time course across AM rates, such that at low to moderate AM rates (4 to 16 Hz) most of the adaptation occurred by the peak in the AM cycle, and at moderate to high rates (16 to 64 Hz) gradual adaptation was evident across much of the AM cycle. Consistent with physiological and behavioural data at 600 Hz (Dietz et al. 2014; Hu et al. 2017), the model MSO neuron responded to its best ITD moderately during rising amplitude, weakly to moderately at peak energy, and only weakly during falling energy (Fig. 5a, lower three rows; in this 3-way comparison of spike counts, P < 0.05 at each modulation frequency). Adapting similarly in spike rate to the model SBCs, the model MSO neuron had higher spike counts in response to its best ITD during rising energy vs. peak energy at 4- to 16-Hz modulation (4 Hz: P = 0.057; 8 Hz: P < 0.001; 16 Hz: P < 0.001), and during peak vs. falling energy at 16- to 64-Hz modulation (P < 0.0025). The synchrony index to AM for model SBCs ranged from 0.049 at 4 Hz to 0.17 at 32 Hz; and for the model MSO neuron, from 0.47 (16 Hz, when the best ITD occurred during falling energy) to 0.82 (64 Hz, when the best ITD occurred during rising energy) (Rayleigh statistic: P < 0.01 for model SBCs at 4 Hz; otherwise P < 0.001).

Modelling STP simply as synaptic depletion, the major component of synaptic depression of the inputs to SBCs (Yang and Xu-Friedman 2008), produced a reasonable degree of rate-dependent emphasis of ITD during rising vs. peak energy, compared with behavioural data for AM stimuli at 200 and 600 Hz in Hu et al. (2017) and in vivo MSO responses to AMBBs near 600 Hz in Dietz et al. (2014). A hypothetical addition of specifically rate-dependent STP (Wang and Kaczmarek, 1998; Wang and Manis 2008; Xie and Manis 2013) to our modelled STP would presumably increase the rate-dependent emphasis of ITD during rising vs. peak sound energy. Adjusting the balance between rate-dependent STP and synaptic depletion might maintain the overall rate-dependent emphasis, as rate-dependent STP slightly increases the emphasis of rising energy at high modulation rates for 600-Hz carriers to better match the in vivo responses.

STP in the VCN; K_LT Inactivation Frozen at Rest

Under normal physiological conditions, above resting potential, K_LT channels activate (speeding the repolarisation of excitatory postsynaptic potentials (EPSPs)) and slowly inactivate (eventually opposing activation) (Khurana et al. 2011). In model neurons, freezing K_LT inactivation (z) at its voltage-dependent steady-state value for resting potential, z = z_∞(V_REST), while K_LT activation is allowed to increase with increasing membrane potential, is expected to increase the EPSP suppression by K_LT channels. With K_LT inactivation frozen at rest, in the model SBCs with their very slow time constant of K_LT inactivation (Rothman and Manis 2003c) and supra-threshold excitatory synapses, spike rates decreased very slightly; in the model MSO neuron with its faster time constant of K_LT inactivation (Mathews et al. 2010) and sub-threshold excitatory synapses, spike rates decreased, remaining below 70 spikes per second (spikes/s) for AMBBs at 200 Hz, and below 40 spikes/s at 600 Hz (Fig. 5b).

STP in the VCN and MSO

When the modelled STP at the VCN and MSO were both active, spike rates of the model MSO neurons remained below 70 spikes/s for AMBBs at 200 Hz, and below 40 spikes/s at 600 Hz (not shown). Whilst the modelled MSO spike rates might be increased by increasing the strength of excitatory synaptic inputs to model SBCs to suit in vitro conditions, all the adaptation from STP in vitro may be too much to account for in vivo conditions.

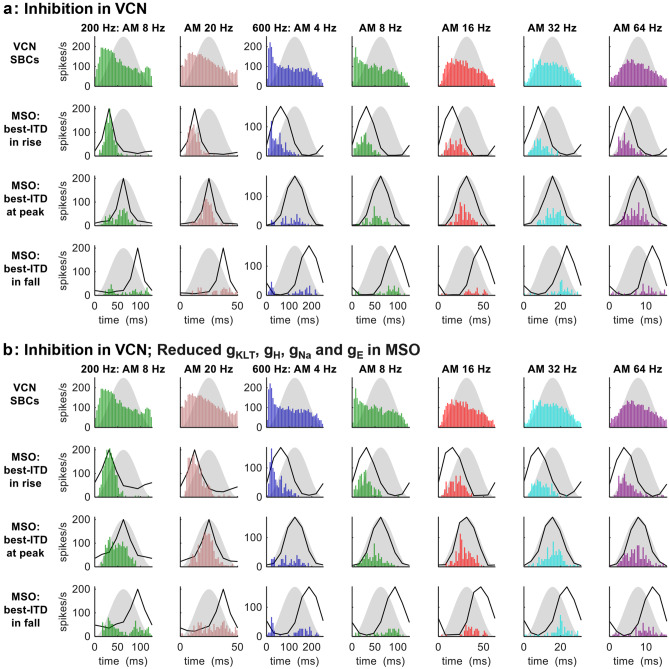
Inhibition in the VCN

We then removed STP, and applied inhibition to each model SBC, driven by ten independent model ANFs, and decaying with a 23.9-ms time constant.

For AMBBs centred at 200 Hz, the model SBCs adapted in spike rate across the moderately low to high portions of the AM cycle (Fig. 6a, top row, 2 leftmost columns). At 8-Hz AM, the adaptation was fairly rapid after a robust onset response in spikes. Spike counts in the model MSO neuron (Fig. 6a, lower three rows, 2 leftmost columns) were higher in response to best ITD during rising energy vs. peak energy at 8-Hz AM (P < 10⁻⁴), but insignificantly higher at 20-Hz AM (P = 0.46); spike counts were significantly lower when the best ITD occurred during falling energy vs. peak energy (8 Hz: P < 0.001; 20 Hz: P < 10⁻⁶). Thus, the patterns of significance in ITD detection by human listeners for AM stimuli at 200 Hz (Hu et al. 2017) were matched fully at 20-Hz AM, and partially at 8-Hz AM. SI to AM for model SBCs ranged from 0.19 at 20 Hz to 0.22 at 8 Hz; SI to AM for the model MSO neuron was insignificant for 8 Hz when the best ITD occurred during rising energy, and ranged from 0.23 (20 Hz, when the best ITD occurred during falling energy) to 0.87 (8 Hz, when the best ITD occurred during rising energy) (Rayleigh statistic: P > 0.1 for the model MSO neuron at 8 Hz with best ITD during rise; P < 0.025 for the model MSO neuron at 20 Hz with best ITD during fall; otherwise P < 0.001).

Fig. 6.

MODEL 1: AMBB-cycle spike-rate histograms of SBCs and MSO neuron for AMBBs centred at CFs 200 Hz (leftmost 2 columns) and 600 Hz (rightmost 5 columns): (a) with inhibition in the VCN; (b) with inhibition in the VCN, and reduced g_KLT, g_H, g_Na, and g_E in the MSO. Black lines: normalised static-IPD functions for a single amplitude-modulated carrier frequency at CF. For more definitions, see Fig. 4 caption

For AMBBs centred at 600 Hz, for the model SBCs (Fig. 6a, top row, 5 rightmost columns), more strongly than at 200 Hz. In the model SBCs, the adaptation in spike rate contained a gradual component across most of the AM cycle for all modulation rates. At low AM rates (4 and 8 Hz), adaptation was also rapid after a robust onset response in spikes, and most of the adaptation occurred by the peak in the AM cycle. At moderate to high AM rates (16 to 64 Hz), gradual adaptation was evident across much of the AM cycle. Consistent with physiological and behavioural data at 600 Hz (Dietz et al. 2014; Hu et al. 2017), the model MSO neuron responded to its best ITD moderately during rising amplitude, weakly to moderately at peak energy, and only weakly during falling energy (Fig. 6a, lower three rows; in this 3-way comparison of spike counts, P < 0.001 at each modulation frequency). Adapting similarly in spike rate to the model SBCs, the model MSO neuron had higher spike counts in response to its best ITD during rising vs. peak energy at 4- to 8-Hz modulation (P < 0.005), and during peak vs. falling energy at 8- to 64-Hz modulation (P < 0.05). The synchrony index to AM for model SBCs ranged from 0.13 at 4 Hz to 0.27 at 16 Hz; and for the model MSO neuron, from 0.23 (4 Hz, when the best ITD occurred during falling energy) to 0.80 (8 Hz, when the best ITD occurred during rising energy) (Rayleigh statistic: P < 0.10 for model SBCs at 4 Hz; otherwise P < 0.001).

Adaptation from the modelled inhibition produced AMBB responses generally similar to those at 600 Hz for MSO neurons in vivo; however, comparing with the adaptation from modelled STP, for the inhibition as each ANF spike adds a fixed increment to the total inhibitory conductance without limit, there is notably more gradual adaptation across the AM cycle, particularly at low modulation rates and the low carrier frequencies centred near 200 Hz (Fig. 6a).

The emphasis of ITD during rising 8-Hz AM at 200 Hz is not entirely surprising. Contrary to the behavioural emphasis, a fast MSO neuron with CF near 250 Hz emphasised ITD during rising AM (Michael Pecka & Mathias Dietz, personal communication).

Inhibition in the VCN; Reduced g_KLT, g_h, g_Na, and g_E in the MSO

Maintaining the same inhibition of SBCs, we reduced the MSO dendritic and somatic voltage-sensitive membrane conductances (g_KLT, g_h, g_Na) to 1/3 of our standard values, remaining within the physiological range of principal MSO neurons (Remme et al. 2014). With all ion-channel conductances identically reduced, a decreased suppression from model K_LT channels was the outcome, both direct and indirect, as the opposition by Na channels remains balanced, and the weaker h current is less effective in membrane depolarisation and its resulting support of K_LT activation. We also reduced the MSO excitatory synaptic strength (g_E) from 36 to 25 nS in order to maintain unsaturated ITD sensitivity. Despite these weaker excitatory synapses, model MSO spike rates increased along with the decrease in g_KLT. As our standard model MSO excitatory synaptic strength of 36 nS is based on well-known in vitro measurements (Couchman et al. 2010), the weaker synapses applied here might actually contribute to the matching of in vivo conditions and responses, even if paired with larger ion-channel conductances, if also combined with larger dendritic radii which can be doubled while remaining within anatomical range.

With the same spike patterns of excitation and inhibition to same model SBCs as in the condition Inhibition in the VCN, the model SBCs produced identical adaptation in spike rate that persisted across the AM cycle (Fig. 6b, top row, 2 leftmost columns).

For AMBBs centred at 200-Hz, with the reduced voltage-sensitive membrane conductances, spike counts in the model MSO neuron (Fig. 6b, lower three rows, 2 leftmost columns) matched the patterns of significance in ITD detection by human listeners for AM stimuli at 200 Hz (Hu et al. 2017): spike counts were slightly higher but not significantly when the best ITD occurred during rising vs. peak energy, and spike counts were significantly lower for best ITD during falling energy (P < 10⁻⁴). The synchrony index to AM for model SBCs ranged from 0.22 at 8 Hz to 0.19 at 20 Hz; and for the model MSO neuron, from 0.15 (8 Hz, when the best ITD occurred during falling energy) to 0.84 (8 Hz, when the best ITD occurred during rising energy) (Rayleigh statistic: P < 0.05 for the model MSO neuron at 8 Hz with best ITD during fall; otherwise P < 0.001).

For AMBBs centred at 600 Hz, consistent with physiological and behavioural data at 600 Hz (Dietz et al. 2014; Hu et al. 2017), the model MSO neuron responded to its best ITD moderately during rising amplitude, weakly to moderately at peak energy, and only weakly during falling energy (Fig. 6b, lower three rows; in this 3-way comparison of spike counts, P < 0.001 at each modulation frequency). Adapting similarly in spike rate to the model SBCs, the model MSO neuron had higher spike counts in response to its best ITD during rising energy vs. peak energy at 4-Hz (P < 10^-8) and 8-Hz modulation (P = 0.074), and during peak vs. falling energy at 8- to 64-Hz modulation (P < 0.001). The synchrony index to AM for model SBCs ranged from 0.13 at 4 Hz to 0.25 at 32 Hz; and for the model MSO neuron, from 0.18 (4 Hz, when the best ITD occurred during falling energy) to 0.76 (8 Hz, when the best ITD occurred during rising energy) (Rayleigh statistic: P < 0.10 for the model MSO neuron at 4 Hz with best ITD during fall; otherwise P < 0.001).

MODEL 1 Summary

This nonlinear model applied adaptation in various forms, in reproducing the emphasis of rising energy in ITD encoding by MSO neurons at 600 Hz. Without this adaptation, the preference for spatial cues during rising sound energy was absent, suggesting a critical role for the largely monaural input pathways to binaural neurons in emphasising spatial information that is likely to be reliable in reverberant listening conditions. MODEL 1 was also largely consistent with the shift from very strong human ITD sensitivity during rising energy at 600 Hz, to strong sensitivity during both peak and rising energy at 200 Hz, and consistent with relatively weak sensitivity during falling energy at both frequencies.

MODEL 2: Lateralisation by Linear Membrane Models for SBCs and MSO Neurons, Driven by Nonlinear Model ANFs

MSO Populations Driven by Adapting SBCs Correctly Lateralise Amplitude-Modulated Stimuli with Temporally Specific ITDs

To test whether monaural adaptation before binaural integration (Dietz et al. 2014; Hafter et al. 1988), combined with heterogeneous populations of MSO neurons (Bondy and Golding 2018; Remme et al. 2014), are consistent with an example of rate-dependent, behavioural emphasis of ITD during rising sound energy (Hu et al. 2017), we employed populations of computationally efficient model neurons with linear membranes to populate VCNs and MSOs bilaterally (Remme et al., 2014), using the resulting MSO outputs to generate neurometrics of lateralisation. As the nonlinear model produced similar rate-dependent adaptation from inhibition or synaptic depression, and the nonlinear model MSO neuron with synaptic depression in the VCN slightly better matched the AMBB responses of MSO neurons in vivo observed in Dietz et al. (2014), our linear model incorporates synaptic depression in the VCN, between ANF and target SBC (u = 0.55) (Rudnicki and Hemmert 2017).

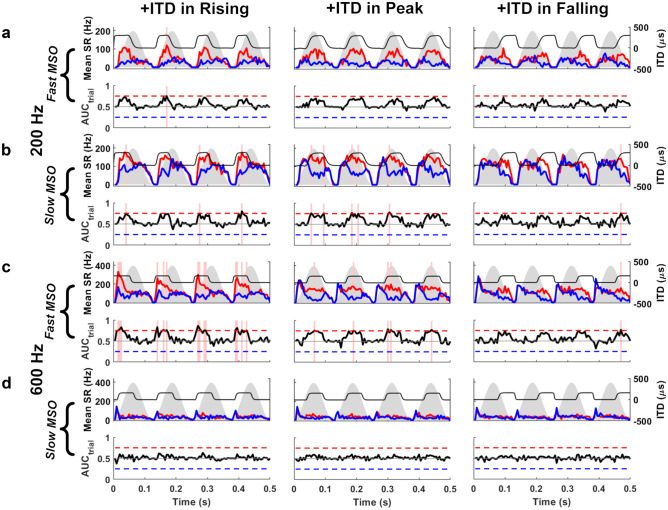
At 600 Hz, populations of model MSO neurons with fast active linear membranes, akin to the nonlinear MSO model, demonstrated strong lateralisation performance for onset ITDs, as indicated by the increased number of instances when the AM stimulus containing a + 150 μs ITD in its rising-energy phase was correctly lateralised (Fig. 7c, left column, pink vertical bands, and Fig. 8a, third column). Correct lateralisation was realised during a stimulus-presentation trial when our running lateralisation neurometric AUC_trial (Fig. 7), based on 50 ‘left’ and ‘right’ model MSO neurons, exceeded its threshold of 0.75 within a 5-ms time bin (AUC: area under the receiver-operator curve, see ‘METHODS’). Lateralisation of these SAM stimuli decreased across the AM cycle, reaching a minimum when the ITD cues were restricted to the falling-energy phase (Fig. 7c, third column and Fig 8a, third column). The trend for onset dominance at 600 Hz was true for both modulation rates (8 Hz and 20 Hz), and when the proportion of the AM cycle containing nonzero ITDs was either 20% or 40% (Fig. 8, third column). Additionally, in all three AM cycle phases, the number of correct lateralisations decreased as the proportion of an AM cycle containing an ITD cue was reduced from 40 to 20% (Fig. 8a, third column, dotted blue line). Analysis of our lateralisation summary statistic AUC_{abs_max} (based on maximal performance of 50 ‘left’ and ‘right’ model MSO neurons within each AM cycle, across 25 stimulus-presentation trials) confirmed the greater importance of the rising AM phase to lateralisation performance at 600 Hz (P = 0.0001, AM phase at 8-Hz AM, 600 Hz; P = 0.0001, AM phase at 20-Hz AM, 600 Hz. 2-way ANOVA), as well as demonstrating better performance in general for 40% conditions at both AM rates (P = 0.0015, Percentage ITD insertion at 8-Hz AM, 600 Hz; P = 0.0001, Percentage ITD insertion at 20-Hz AM, 600 Hz, 2-way ANOVA) (Fig. 8b, third column). In contrast, the linear model containing slow model MSO neurons displayed weak lateralisation performance, as demonstrated by the absence of correct lateralisations in any AM cycle phase (Fig 8a, fourth column). Analysis of summary AUC_{abs_max} data confirmed that lateralisation was significantly poorer across all AM cycle phases when slow models replaced their fast counterparts in the MSO populations (P = 0.0001, interaction of neuron speed vs. AM phase at 8-Hz AM, 600 Hz; P = 0.0001, interaction of neuron speed vs. AM phase at 20-Hz AM, 600 Hz, 3-way ANOVA) (Fig. 8b, fourth column).

Fig. 7.

MODEL 2: lateralisation within stimulus trials of 8-Hz SAM stimuli centred at 200 Hz (a, b) and 600 Hz (c, d). At 200 Hz, b slow MSO neurons, but not (a) fast MSO neurons, correctly lateralised + 300 μs ITDs (top row, black) to the right, based on AUC_trial > 0.75 in any 5-ms bin (pink vertical bands), most often at peak (middle column) of the AM cycle (grey silhouettes) compared to rising (left column) and falling (right column) phases (slow MSO: rising, 3 bins; peak, 5 bins; falling, 1 bin. Fast MSO: rising, 1 bins; peak, 0 bins; falling, 0 bins); AUC_trial (bottom rows, black) and mean spike rate (mean SR) for left (top rows, red) and right (top rows, blue) MSO populations. At 600 Hz, introducing +150 μs ITD (top row, black) to c fast MSO neurons, but not (d) slow MSO neurons, produced strong onset ITD sensitivity during rising phase (left column) that decreased across the AM cycle (fast MSO: rising, 14 bins; peak, 5 bins; falling, 1 bin; slow MSO: rising, 0 bins; peak, 0 bins; falling, 0 bins). The same adapting inputs were used for both MSO neuronal speeds

Fig. 8.

MODEL 2: summarising correct lateralisations of SAM stimuli, comparing between: fast and slow MSOs; carrier frequencies (f_c) of 200 and 600 Hz; modulation rates (f_m) of 8 and 20 Hz; and ITDs inserted into either 20% (blue dotted lines) or 40% (black solid lines) of the AM cycle during rising (R), peak (P), or falling (F) energy. (a) Mean (± SEM) time correctly lateralised per presentation (number of correct lateralisations × bin duration/25 presentations). (b) Peak absolute lateralisation performance, calculated as a AUC_{abs_max} (± SEM)

When an amplitude-modulated 200-Hz tone (with a right-leading ITD of + 300 μs) was presented to the linear model with fast model MSO neurons, the model’s ability to lateralise SAM stimuli was reduced considerably, leading to the absence (or near absence) of correct lateralisations for 40% and 20% 8-Hz AM and 20% 20-Hz AM stimuli (Fig. 7a, left column, pink vertical bands, and Fig 8, first column). In the few instances where correct lateralisations were observed for 40% 20-Hz AM stimuli at 200 Hz, the onset dominance observed for 600 Hz was replaced by an increased weighting of ITD cues towards the peak of the AM cycle (Fig. 8a, first column). This increased ability to lateralise 200-Hz tones using ITD cues conveyed at the peak of 20-Hz AM cycles was significant in the summary AUC_{abs_max} data (P = 0.0001. AM phase at 20-Hz AM, 200 Hz, 2-way ANOVA) (Fig. 8b, first column). Similar analysis for 8-Hz AM, 200-Hz tones, however, demonstrated no such enhanced lateralisation at the AM cycle peak (P = 0.0898, AM phase at 8-Hz AM, 200 Hz, 2-way ANOVA) and even suggested that some onset sensitivity remained (mean AUC_{abs_max_PEAK}/AUC_{abs_max_RISING} for Fast linear model at 8-Hz AM, 200 Hz = 0.9869) (Fig 8b, first column).

Although the linear model with fast model MSO neurons partially reproduced behavioural trends for amplitude-modulated 200-Hz tones (Hu et al. 2017), it led to very few correct lateralisations overall (Fig. 8, first column). We therefore presented the same 200-Hz stimuli to the linear model MSO neurons with slower membrane properties (Fig. 7b). This generated a higher number of correct lateralisations overall, while maintaining, or even augmenting, the maximum weighting of ITD at the peak AM energy in all conditions (Fig. 7b, middle column, pink vertical bands, and Fig. 8a, second column). The summary AUC_{abs_max} data confirmed both the overall improvement in lateralisation performance with slow model MSO neurons (P = 0.0081, Interaction of neuron speed vs. AM phase at 8-Hz AM, 200 Hz; P = 0.0001, Interaction of neuron speed vs. AM phase at 20-Hz AM, 200 Hz, 3-way ANOVA) and the enhanced lateralisation at the peak of 20-Hz AM, 200-Hz tones (P = 0.0001, AM phase at 20-Hz AM, 200 Hz, 2-way ANOVA) (Fig. 8b, second column). Although using MSO neurons with slow membrane properties was conducive to a peak vs. rising AUC_{abs_max} ratio that now slightly favoured the AM peak for 8-Hz AM, 200-Hz tones (mean AUC_{abs_max_PEAK}/AUC_{abs_max_RISING} for slow linear model at 8-Hz AM, 200 Hz = 1.0067), this did not translate into a significant enhancement of lateralisation at peak phase over the rising phase (P = 0.6596, AM phase at 8-Hz AM, 200 Hz, two-way ANOVA) (Fig. 8b, second column). Nevertheless, as observed at 600 Hz with the fast model MSO neurons, both the number of correct lateralisations and the summary AUC_{abs_max} data highlighted an improved general lateralisation performance when 40% (compared with 20%) of AM cycles conveyed an ITD (P = 0.0001, percentage ITD insertion at 8-Hz AM, 200 Hz; P = 0.0001, percentage ITD insertion at 20-Hz AM, 200 Hz, 2-way ANOVA) (Fig. 8a, b, second column).

The relative activity of the ‘left’ and ‘right’ linear MSO neuron populations suggests that a slower, more integrative MSO neuron may assist lateralisation in lower sound-frequency channels, and may even enhance extraction of ITD information at the peak energy in AM cycles, where human ITD detection appears equally good as at onset for 200-Hz tonal carriers (Hu et al., 2017). Additionally, our model qualitatively matched the behavioural data by demonstrating a higher propensity to lateralise stimuli of either frequency when 40% vs. 20% of the AM cycle contained a nonzero ITD.

Adapting Linear SBCs Improve the Ability of an MSO Population Model to Lateralise Speech in Artificial Reverberation

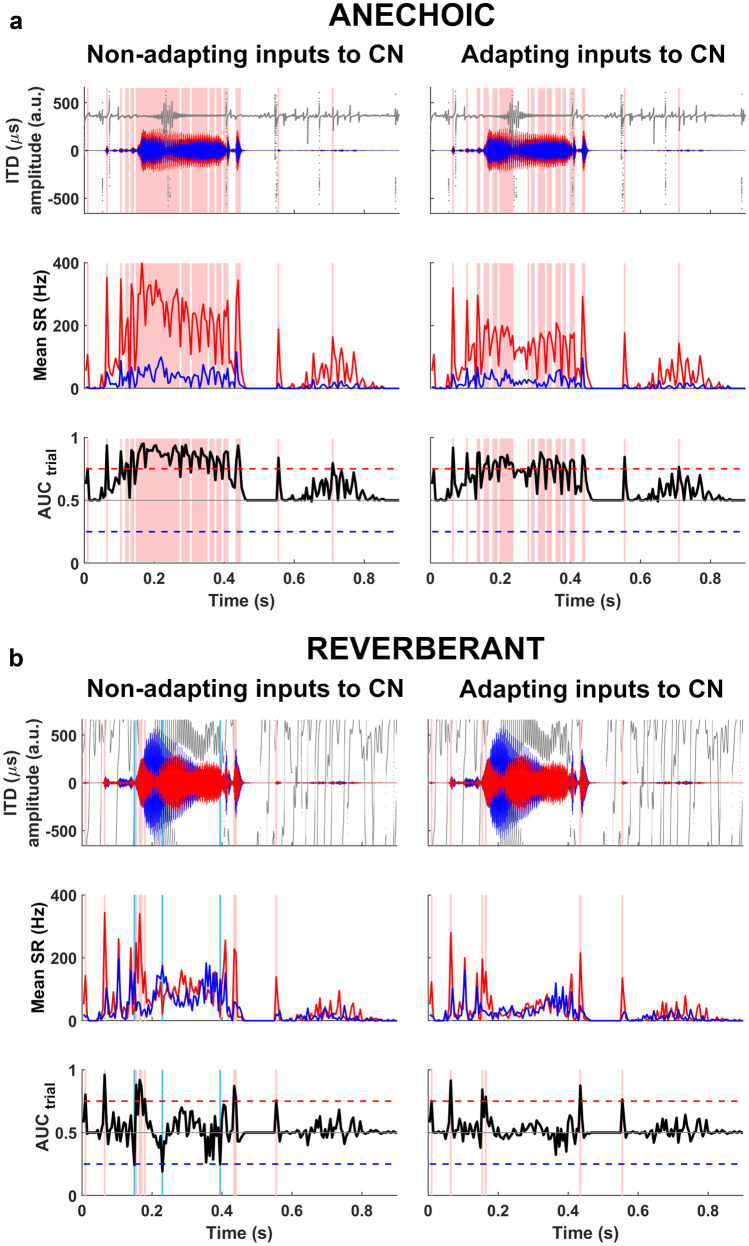
If neural adaptation prior to binaural integration contributes to accurate source localisation, we would expect it to aid lateralisation of speech in a reverberant room, by emphasising ITD cues associated with direct sound over reverberation (Fig. 1, far left) (Dietz et al. 2014). To test this hypothesis, speech signals were presented to the neural model of lateralisation under anechoic (nonreverberant) conditions, and simulated reverberant conditions with direct sound and early reflections off virtual walls (Dietz et al. 2014). In the presence or absence of synaptic depression in SBCs of the cochlear nuclei, we assessed whether the model correctly lateralised the side to which the source was located.

In the anechoic condition (Fig. 9a), a word token (‘church’) was presented, to the fast linear model with nonadapting inputs, from a virtual location 1 m from the target, and 30° to the right of the midline. The speech waveform—gammatone filtered at 600 Hz (Fig. 9a, top row)—was more intense at the right ear (red), and led the left-ear signal (blue) by an average ITD of + 363 μs (Fig. 9a, top row, dark grey). This generated a larger response from model neurons in the ‘left’ MSO (Fig. 9a, middle row) in multiple bins throughout the speech token, indicated by AUC_trial ≥ 0.75 (Fig. 9a, pink vertical bands), demonstrating that the talker was correctly lateralised to the right in the linear model with nonadapting inputs.

Fig. 9.

MODEL 2 (fast MSO neurons, 600-Hz channels): lateralisation of anechoic and reverberant speech ‘church’, with and without adaptation of synaptic inputs from auditory nerve to CN: (a) waveforms and ITDs of anechoic speech, gammatone filtered at 600 Hz (top row); mean firing rates in left MSO (middle row, red) and right MSO (middle row, blue); AUC_trial neurometric (bottom row). Anechoic speech is correctly lateralised to the right (pink vertical bands) with nonadapting (left column) or adapting synapses (right column). (b) Reverberant speech produces highly variable ITDs and confounding ILDs (top row), and requires adapting synapses (right column) for consistently correct lateralisations (pink vertical bands). Nonadapting synapses (left column) produced both correct (pink vertical bands) and incorrect lateralisations (light blue vertical bands). Synaptic adaptation removed all the incorrect lateralisations, leaving correct lateralisations at stimulus onsets

In the reverberant condition, the ‘church’ token was presented to the fast linear model with nonadapting inputs from the same angle and distance, but with two delayed copies generated by early reflections off virtual walls added behind, and to the left of, the listener (Fig. 1, far left). This mixture of sound arriving direct from the source and from early reflective copies led to a more complex waveform, including a more intense signal at the ‘left ear’ (direct-to-reverberant ratio − 4dB; mean ILD − 3 dB) whose running ITDs fluctuated between extremely large positive and negative values, culminating in an average IPD of +155º, a value that might easily lead to incorrect lateralisation for sine tones (Yost 1981). Although the resulting AUC_trial output exceeded 0.75 in nine epochs coinciding with waveform onsets (Fig. 9b, left column, pink vertical bands), it was also briefly lower than 0.25 in the opposite direction during three intermediate epochs (Fig. 9b, left column, blue vertical bands), leading to a potentially ambiguous left/right localisation of the MSO output overall.

We then introduced synaptic depression to the monaurally driven inputs from ANFs to the cochlear nucleus (CN) and presented the same reverberant stimulus to this linear model with fast model MSO neurons (Fig. 9b, right column). Despite the presence of potentially confounding ITD (and ILD) cues (Fig. 9b, right column, top row), the addition of adaptation to the monaural input pathways enhanced the performance of the model MSO neurons in the example presentation, generating only correct lateralisations of the true source to the right: AUC_trial output exceeding 0.75 in six time bins without ever crossing below 0.25 (Fig. 9b, bottom row, right).

When the number of incorrect lateralisations was tallied over twenty-five presentations for six reverberant word tokens (‘church’, ‘shown’, ‘fuss’, ‘talk’, ‘mate’, ‘vine), incorrect lateralisations were always observed less frequently when synaptically depressing auditory nerve inputs were implemented in the linear model (Fig. 10). The mean time for which different words were incorrectly lateralised (number of time bins with AUC_trial ≤ 0.25 × duration of time bin), for the linear model with nonadapting ANF-CN inputs, ranged from 1.2 ms (‘fuss’) to 41.6 ms (‘talk’) (median = 9.4 ms) per presentation. This range decreased to 0 ms (‘church’, ‘fuss’, ‘vine’) to 4.8 ms (‘talk’) (median = 0.5 ms) per presentation when adaptation was introduced.

To confirm that adapting inputs had indeed enhanced the linear model’s ability to lateralise speech tokens with less ambiguity, we used the AUC_abs neurometric: an absolute measure of lateralisation (based on 50 ‘left’ and 50 ‘right’ model MSO neurons across 25 stimulus-presentation trials) calculated in each 5-ms time bin so that lateralisation can be tracked across a speech token’s time course, with and without adaptation. For each word token, the percentage AUC_abs change after adding adaptation was calculated in time bins where the nonadapting linear model originally favoured incorrect lateralisations to the left [i.e. where AUC_abs without adaptation was significantly smaller than 0.5 (P = 0.0001)] (Fig. 10). Average percentage AUC_abs changes were universally positive, indicating that, after the introduction of adaptation, all word tokens were more likely to be lateralised correctly to the right [Mean percentage change (±SE) in ‘incorrectly lateralising’ AUC_abs after adding adaptation: ‘church’ = +11.416 ± 2.85%; ‘shown’ = +17.8811 ± 5.75%; ‘fuss’ = +4.973 ± 1.45%; ‘talk’ = +24.904 ± 4.66%; ‘mate’ = +15.256 ± 3.96%; ‘vine’ = +9.21 ± 3.59%. Significance was at P = 0.0001, Wilcoxon signal rank with matched AUC_abs values (Fig. 10). Furthermore, with adaptation present, minimum values of AUC_abs all laid above 0.25, highlighting the extent to which incorrect lateralisations had been supressed in individual time bins. This neurometric profile is consistent with the psychoacoustic percept previously described for similar word tokens (Seeber and Hafter 2011, Dietz et al. 2013), suggesting that monaural adaptation increases the weighting of spatial information during rising sound energy to improve lateralisation of ethological sounds in reverberant environments.

DISCUSSION

The ability to localise sound sources in reverberant environments improves speech understanding by human listeners (Kidd et al. 2005) and is critical to predator and potential prey alike. Despite reflections from acoustically opaque surfaces degrading spatial cues, source localisation must remain accurate.

Brainstem Models with Adaptation Before and at Binaural Integration Suppress Responses to Late-Arriving Sound While Encoding Spatial Cues

Consistent with the hypothesis of Hafter et al (1988), our computational models demonstrate that adaptation prior to binaural integration can suppress responses to late-arriving reverberant sound, thus emphasising early-arriving sound direct from the source during its rising envelope for the encoding of spatial cues. In our models, accurate lateralisation of a speech source in reverberation is enhanced by adapting SBCs in the VCN, which project bilaterally to the MSO, a site of primary binaural integration. In addition, we show that modelled adaptation at SBCs or MSO neurons produced a rate-dependent emphasis of ITD during rising vs. peak sound energy. Thus adaptation prior to binaural integration, and at binaural integration, can each account for the observed ability of binaural MSO neurons in vivo to respond preferentially to ITDs conveyed during the early, rising-energy portion of low-frequency sounds near 600 Hz (Dietz et al. 2014). Reflecting perception of normal-hearing listeners for amplitude-modulated 500- to 600-Hz tones (Dietz et al. 2013; Hu et al. 2017), our models indicate a process of glimpsing ITD_TFS cues during the rising portion of an AM stimulus, and suppressing spatial information conveyed at later times in the AM cycle, including when stimulus energy is at its highest. Successful glimpsing of ITD cues near the onset of the AM cycle can explain behavioural responses to stimuli with time-varying ITD cues such as AMBBs, SAM tones, and click trains (Stecker and Hafter 2002; Dietz et al. 2013; Diedesch and Stecker 2015; Hu et al. 2017). This glimpsing extends to reliable lateralisation of complex, speech sounds in reverberant environments (Dizon and Colburn 2006; Haas 1951; Seeber and Hafter 2011).

Our results complement previous findings that binaural cues in rising sound envelopes can support robust source localisation in reverberant environments, in modelling studies that applied a variety of techniques: selectively extracting ITD from positive-going temporal envelopes (Wolf 1991); performing binaural detection based on the slope of the interaural envelope difference (Mao and Carney 2014); applying interaural coherence to identify time instants when only the direct sound of a single source has nonnegligible energy in a critical band, when the ITD and ILD will represent the source direction (Faller and Merimaa 2004); modelling receptive fields that respond when their spatial region within the barn owl’s topographic map of auditory space is presented with the loudest, most-response-inducing amplitude-modulated sound (Nelson and Takahashi 2010; Baxter et al. 2013); adaptively inhibiting the IC, which follows after the rising envelope and excitation in the MSO and IC (Xia et al. 2010); comparing signal-processing models that apply adaptation before or after binaural interaction (Dietz et al. 2014).

Adaptive Mechanisms with 25-ms Recovery Time Constants Are Consistent with AMBB Responses of MSO Neurons Recorded In Vivo

In matching AMBB responses of MSO neurons in vivo, our modelled adaptation included the following: the majority 25-ms recovery component of STP at SBCs in vitro (Wang and Manis 2008); or the minority 25-ms recovery component of STP at MSO neurons in vitro (Couchman et al. 2010); or glycinergic inhibition of SBCs in vivo with a decay time constant of 23.9 ms (Keine et al. 2016; Kuenzel et al. 2015). Physiologically, the inhibition is driven by the auditory nerve via the ipsilateral VCN and DCN (Campagnola and Manis 2014; Wickesberg and Oertel 1990). In vivo, STP alone is too weak to account for nonmonotonic rate-level functions in SBCs, and glycinergic inhibition of SBCs is the major underlying mechanism (Keine et al. 2016). These measurements in vivo, combined with our model results, suggest glycinergic inhibition of SBCs as a contributing mechanism in the adaptive emphasis of early-arriving spatial information. In vivo, despite weak STP, as high concentrations of GABA activate GABA-b receptors limiting synaptic vesicle release (Brenowitz et al. 1998; Keine et al. 2016; Kuenzel et al. 2011; Lorteije et al. 2009), rate-dependent calcium-mediated recovery (Wang and Kaczmarek 1998; Wang and Manis 2008; Xie and Manis 2013) may still play a significant role, by quickly countering the weak STP to produce fast-recovering synapses that can function practically as nonadapting. Inhibition may not entirely explain the in vivo adaptation, as some bushy cells (BCs) emphasise onset in vivo with and without pharmacological blocking of glycinergic and GABA-a receptor-mediated inhibition (Gai and Carney 2008).

Cochlear processing (Bianchi et al. 2013; Brown et al. 2015b, a; Hartung and Trahiotis 2001) and spike-rate adaptation of ANFs (Zilany and Carney 2010) can also temporally shape monaural inputs, increasing the onset emphasis from model ANFs to globular BCs (Ashida et al. 2019; Stecker 2020), and increasing precedence effects for transient stimuli (Brown and Stecker 2012; Brown et al. 2015b, a; Tollin and Henning 1998). With our AMBB stimuli, modelled peripheral processing was not sufficient for onset emphasis, nor to disambiguate lateralisation of reverberant speech, suggesting that the number, synaptic strength, and CF span of ANF inputs to BCs influence how ANF adaptation contributes to pre-binaural adaptation overall (Carney 1990, 1992; Brughera et al. 1996; Rudnicki and Hemmert 2017; Ashida et al. 2019).

Model MSO Neurons with a Plausible Range of Membrane Speeds are Effective at Low Sound Frequencies

Although faster than other neuron types in the central nervous system, principal MSO neurons display a range of intrinsic membrane speeds (time constants) and resonance frequencies (Bondy and Golding 2018; Remme et al. 2014). Using a model with linear membrane properties (Remme et al. 2014), we demonstrated that a slow MSO neuron was unsuitable for lateralising modulated 600-Hz tones: its slow input integration and refractory period (2 ms, therefore longer than the 600-Hz carrier’s 1.67-ms cycle) producing poor ITD sensitivity. However, at 200 Hz, these slower MSO neurons boosted the linear model’s ability to lateralise modulated signals, especially at peak energy. They did this while offering cellular energetic advantage by not expressing more ion channels than required, thus encoding ITD more efficiently.

Rate-Dependent Emphasis of Early-Arriving Sound in ITD Encoding

Displaying rate-dependent emphasis of early-arriving sound, our nonlinear model MSO neuron with K_LT channels responds: preferentially to ITD during the rise of 600-Hz AMBBs; equally well to ITD during the rise and peak of 200-Hz AMBBs; and weakly to ITD during the fall of 200-Hz and 600-Hz AMBBs. Similarly, as fast linear-model MSO membranes enhance lateralisation of 600-Hz signals, especially during rising energy, and slower linear-model MSO membranes enhance lateralisation of 200-Hz signals, especially at energetic peaks, slow membranes are not necessary for good lateralisation performance at the peak of 200-Hz signals. Although slow linear model MSO neurons in a 200-Hz channel continue to respond preferentially to ITDs at the peak of 600-Hz SAM tones, fast linear model MSO neurons with 600-Hz CF respond preferentially to ITDs at the peak of 200-Hz SAM tones (Mikiel-Hunter et al. 2019). Our data suggest that a slower build-up of pre-binaural adaptation, from the slower carrier cycles of 200-Hz stimuli, preserves ITD sensitivity beyond the rising AM phase. This rate dependence of ITD weighting across an AM cycle is qualitatively consistent with predictions of pre-binaural adaptation made by Hafter et al. (1988), and quantitatively matches the carrier frequencies and presentation rates at which onset dominance (≥ 400 Hz) and equal ITD weighting (125–250 Hz) occur for SAM tones and click trains with time-varying ITD (Brown and Stecker 2010; Hu et al. 2017). Our current findings also support the long-standing hypothesis that ITD sensitivity can recover from the adaptation if sufficient temporal gaps exist between neighbouring stimulus presentations, i.e. for the long quiet portion of very slow AM cycles, for slow carrier cycles within AM stimuli, and for slow presentation rates of click trains (Dietz et al. 2015; Hafter and Buell 1990; Hu et al. 2017; Klein-Hennig et al. 2011; Stecker and Hafter 2002).

Rate Dependence of Onset Emphasis Suits the Frequency Dependence of Reverberation Time in Natural Outdoor Environments

The rate-dependent emphasis for spatial information in early-arriving sound is compatible with natural outdoor acoustics for low-frequency sound. In many outdoor environments, including forests, fields, and streets, reverberation time (‘T60’: the time for reverberant energy to fall by 60 decibels) decreases as sound frequency decreases below 1500 Hz (Traer and McDermott 2016). Weaker binaural adaptation at lower stimulus rates (weakest below 200 Hz) (Freyman and Zurek 2017; Hafter and Buell 1990; Hafter and Dye 1983; Stecker 2018; Stecker and Hafter 2002) suits the shorter reverberation times at lower sound frequencies in outdoor environments, as there is less need to suppress responses to reverberation for lower sound frequencies within these natural environments.

Early-Arriving Spatial Cues for Users of Bilateral Cochlear Implants

Bilateral-cochlear-implant (BCI) users are most sensitive to ITDs during peaks in sound energy (Hu et al. 2017), but acoustically the most accurate ITD information for source location likely occurs during rising sound energy (Dietz et al. 2013), especially in noisy or reverberant environments. Building upon findings with jittered inter-pulse intervals (Hancock et al. 2012; Laback and Majdak 2008; Van Hoesel 2008), BCI stimulation using high-rate pulses can provide detectable ITD by including bursts of even more rapidly successive pulses that overcome adaptation (Srinivasan et al. 2020, 2018). Therefore, to help BCI users receive spatial information that emphasises sound sources, BCI processors could, during peak energy, provide pulse bursts to convey spatial cues derived milliseconds earlier during rising energy. Nonburst pulse rates up to 1000 or 1200 pulses per second (pps), with amplitude driven by sound, can be applied for both ITD sensitivity and speech intelligibility (Fu and Shannon 2000; Shader et al. 2020; Shannon et al. 2011). Rapidly updating binaural masks (Cantu 2018) can further enhance target sound sources while preserving spatial cues.

CONCLUSIONS

Our models suggest that adaptive brainstem mechanisms contribute to sound-source localisation, emphasising early-arriving sound which is relatively high in direct sound that conveys reliable spatial information during neural encoding, by suppressing responses to late-arriving sound which is relatively high in reverberation. The rate-dependent emphasis of auditory spatial information conveyed in early-arriving sound is consistent with brain mechanisms that transmit reliable information, and suppress unreliable information. As the auditory brainstem encodes ITDs for determining sound-source locations, its suppression of late-arriving spatial information promotes accuracy and appears to counter typical frequency profiles of reverberation times in natural outdoor scenes.

Author Contribution

Andrew Brughera and Jason Mikiel-Hunter contributed equally; conceptualisation: David McAlpine and Mathias Dietz; data curation: Andrew Brughera and Jason Mikiel-Hunter; formal analysis: Jason Mikiel-Hunter and Andrew Brughera; funding acquisition: David McAlpine; investigation: Andrew Brughera and Jason Mikiel-Hunter; methodology: Andrew Brughera (nonlinear modelling) and Jason Mikiel-Hunter (linear modelling); resources: David McAlpine, Andrew Brughera, and Jason Mikiel-Hunter; software: Andrew Brughera and Jason Mikiel-Hunter; supervision: David McAlpine; visualisation: Jason Mikiel-Hunter and Andrew Brughera; validation: Andrew Brughera and Jason Mikiel-Hunter; writing—original draft preparation: Andrew Brughera, Jason Mikiel-Hunter, and David McAlpine; writing—review and editing: Andrew Brughera, David McAlpine, Jason Mikiel-Hunter, and Mathias Dietz.

Funding

This work was supported by an Australian-Research-Council Laureate Fellowship (FL160100108) awarded to David McAlpine.

Data Availability

For the nonlinear model: data, analysis scripts, and code are available at figshare: 10.6084/m9.figshare.11955219.v1. For the linear model: data, analysis scripts, and code are available at figshare: 10.6084/m9.figshare.9899018.v1.

Code Availability

For the nonlinear model: code is available at Github: https://github.com/AndrewBrughera/Mso_SbcStp_EE1. For the linear model: code is available at figshare: 10.6084/m9.figshare.9899018.v1.

DECLARATIONS

Consent for Publication

For this strictly computational study, there are no human subjects from whom consent is required. All authors and responsible authorities approve the publication of this manuscript.

Conflict of Interest

The authors declare that they have no conflict of interest.