Unveiling the polarity of actin filaments by cryo-electron tomography

Summary

The actin cytoskeleton plays a fundamental role in numerous cellular processes, such as cell motility, cytokinesis, and adhesion to the extracellular matrix. Revealing the polarity of individual actin filaments in intact cells would foster an unprecedented understanding of cytoskeletal processes and their associated mechanical forces. Cryo-electron tomography provides the means for high-resolution structural imaging of cells. However, the low signal-to-noise ratio of cryo-tomograms obscures the high frequencies, and therefore the polarity of actin filaments cannot be directly measured. Here, we developed a method that enables us to determine the polarity of actin filaments in cellular cryo-tomograms. We applied it to reveal the actin polarity distribution in focal adhesions, and show a linear relation between actin polarity and distance from the apical boundary of the adhesion site.

Graphical abstract

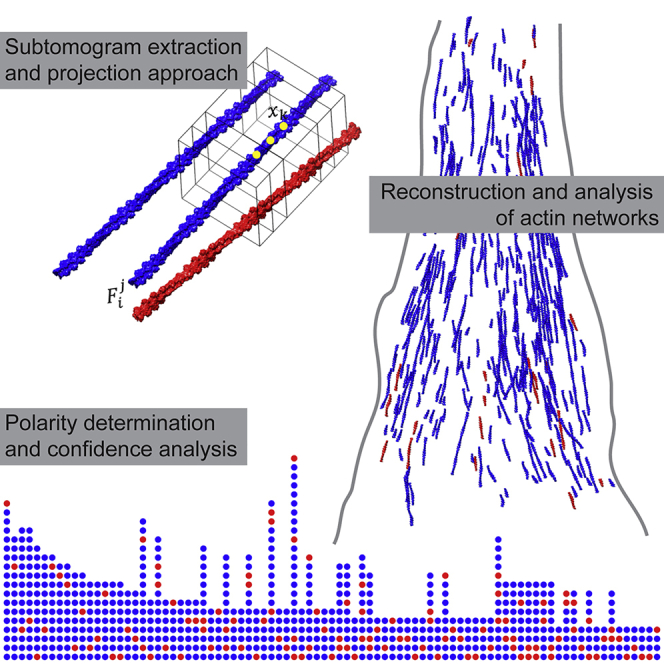
Highlights

• •Determining the polarity of individual actin filaments inside cells
• •Reconstruction of actin networks from cryo-tomograms
• •The polarity of actin changes from mixed to uniform along focal adhesions

Martins et al. developed a method to reconstruct actin networks and measure the polarity of individual actin filaments in vitrified cells, using cryo-electron tomography.

Introduction

Actin polymerization drives cell motility and is a central factor in mediating contractile forces in cells (Holmes et al., 1990; Merino et al., 2018; Pollard and Borisy, 2003). Actin filaments (Egelman et al., 1982; Galkin et al., 2015) assemble into complex networks (Malik-Garbi et al., 2019; Xu et al., 2012), which are essential for their activity in the cell. Reconstructing individual actin filaments at sub-nanometer resolution inside cells would provide an unparalleled view on actin networks, and would allow a more fine-grained modeling of cytoskeletal-based mechanical processes (Hervas-Raluy et al., 2019).

A prominent mechanosensitive mechanism, involving actomyosin contractility, occurs at the integrin-based interaction sites of cells with the extracellular matrix (Burridge and Guilluy, 2016; Geiger et al., 2009). These interactions are mediated by adhesive structures such as focal adhesions (FAs) (Legate et al., 2011; Shemesh et al., 2005; Zaidel-Bar et al., 2007). The organization of proteins and the role of the actin network in FAs has been intensively studied using fluorescent and electron microscopy (Kanchanawong et al., 2010; Patla et al., 2010); however, the 3D architecture of FAs, including the polarity and position of each individual actin filament, has not been shown.

Cryo-electron tomography (cryo-ET) allows reconstruction of 3D density maps of unperturbed cells at a resolution of 2–3 nm (Beck and Baumeister, 2016; Lucic et al., 2005; Weber et al., 2019). Therefore, single actin filaments can readily be detected in tomograms of eukaryotic cells (Jasnin et al., 2019; Medalia et al., 2002). Moreover, using direct electron detectors permits recognition of the characteristic helical shape of F-actin, which is in clear distinction to other cellular filaments. However, cryo-tomograms suffer from a low signal-to-noise ratio (SNR) (Forster et al., 2008; Pei et al., 2016), and from missing information due to the limited tilt range during data acquisition, referred to as the missing wedge (Lucic et al., 2005). Subtomogram averaging can compensate for these issues (Beck and Baumeister, 2016; Forster et al., 2005; Himes and Zhang, 2018; Schur et al., 2016), but it is computationally more demanding and lacks the robustness and level of standardization of the procedures used for data analysis in single-particle cryo-electron microscopy (cryo-EM) (Nogales, 2016; Scheres, 2012).

Here we developed a set of MATLAB scripts that enable, in conjunction with RELION (Scheres, 2012), the 3D reconstruction of actin filaments from cryo-tomograms. It is based on transforming subtomogram averaging into a single-particle task, and the determination of the actin filament's polarity is built on a robust statistical analysis of the individual filaments. Furthermore, this actin polarity toolbox (APT) features tools for spatial and topological analysis of the reconstructed actin filament networks and their visualization.

Using a correlative fluorescence microscopy and cryo-ET approach (Patla et al., 2010; Sartori et al., 2007), we unveil the 3D architecture of the actin cytoskeleton at FAs. We show that the actin polarity distribution correlates with the position along the FA and that regions of mixed polarity are concentrated at the periphery of the characteristic actin bundles.

Results

Determining actin polarity by APT

The first aim of APT is the reconstruction of an actin filament at a resolution that allows the unambiguous determination of the filament's polarity (better than 20 Å). Therefore, APT requires cryo-tomograms and segmentations of the actin cytoskeleton as input data (Figure 1A). Subsequently, the segmented filaments are subdivided into segments with equidistant spacing. We make use of the observation that a projection of a subtomogram along the electron beam axis is approximately invariant of the missing wedge orientation and can be treated as a single-particle image (Figures S1A–S1D). Thus, single-particle image processing packages, such as cryoSPARC (Punjani et al., 2017) or RELION (Scheres, 2012), can be used to reconstruct the actin filament from the segments. Interestingly, this approach is not only restricted to filamentous structures (Figures S1E–S1H).

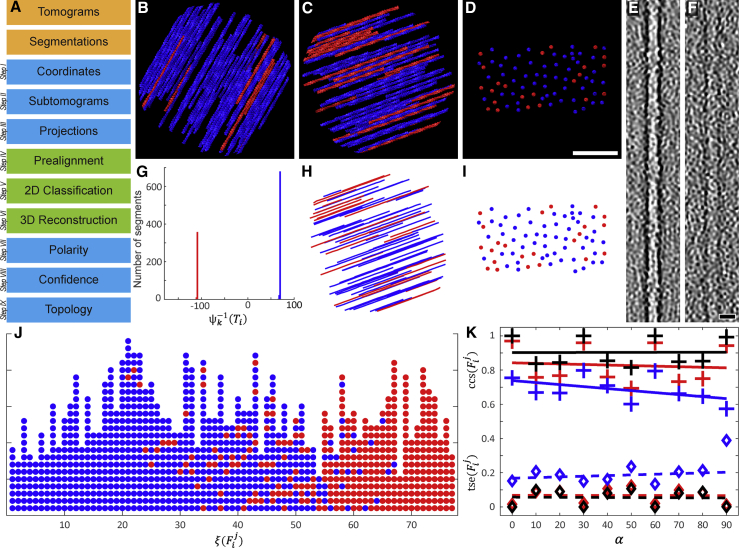
Figure 1.

Polarity determination of modeled actin bundles

(A) The workflow of APT consists of consecutive modules. The orange modules symbolize the required input data. The blue modules were implemented in MATLAB, and the green modules were executed in RELION.

(B) Top view of one of the modeled actin bundles, which were used for the validation of APT. The bundles were rendered without noise for visualization purposes. Here the angle $\alpha$ between bundle and tilt axis is 30°, and the fraction ${\rho }_r$ of actin filaments that are oriented in the opposite direction (red colored filaments) was set to 0.1.

(C) Top view of an additional bundle with $\alpha$ increased to 70°, and ${\rho }_r$ to 0.3.

(D) The same bundle seen from the side with the viewing axis adjusted parallel to the filaments. The distance between the filaments is 10–37 nm. Scale bar, 100 nm.

(E and F) (E) In order to quantify the impact of noise on the precision of APT, the bundles were modeled with defined SNRs. The depicted bandpass filtered slice of a filament was extracted from a bundle with SNR = ${10}^{-3}$. For comparison, the filament shown in (F) originates from a bundle with SNR = ${10}^{-4}$. Scale bar, 10 nm.

(G) The modeled bundles were processed with APT. The plot shows the resulting ${\text{ψ}}_k^{-1}\left(T_i\right)$ histogram of the bundle displayed in (C). Segments in the blue peak mainly originate from blue filaments, and the opposite for the red peak. The filaments point with their plus ends in opposite directions, so the peaks are separated by 180°. Since ${\rho }_r$ was set to 0.3 in this bundle, the number of segments in the red peak is $\approx$30% of the total number of segments.

(H and I) (H) The line plot shows the filament positions and polarities of the bundle, shown in (C), as recovered by APT. It was affected with SNR = ${10}^{-3}$; however, in this case the match between original and recovered bundle (the side view is shown in [I], and can be compared with [D]) is almost error free.

(J) Here the $\xi \left(F_i^j\right)$ vectors of the recovered bundle are depicted. Segments that originate from the same filament are plotted as columns of circles. The color scheme reflects to which peak the segments were assigned in the ${\text{ψ}}_k^{-1}\left(T_i\right)$ histogram, shown in (G), and the $\xi \left(F_i^j\right)$ vectors are sorted according to their fraction of segments linked to the blue peak. In this representation of the filaments, segments with incorrect orientation determination appear as distortions of otherwise uniformly colored columns.

(K) Three modeled datasets with three different SNRs were produced, each comprising 10 bundles with varying orientation $\alpha$ between $0°$ and $90°$. The data were processed with APT and the $ccs\left(F_i^j\right)$ and $tse\left(F_i^j\right)$ values were analyzed. Each cross in the plot marks the average of all $ccs\left(F_i^j\right)$ values in a bundle and diamond symbols indicate averaged $tse\left(F_i^j\right)$ values per bundle. The SNR of the respective dataset can be identified by the color scheme: black, SNR = ${10}^{-2}$; red, SNR = ${10}^{-3}$; and blue, SNR = ${10}^{-4}$, respectively. Linear regression lines are depicted as solid or dashed lines.

See also Figures S1 and S2.

Our main goal is to determine the polarity of all the initially segmented filaments. Therefore, based on the filament average, APT calculates for each segment the position of its plus end in the cryo-tomograms. During the 3D reconstruction step, APT obscures the correlation between segments and filaments, thus for each filament multiple independent polarity observations can be statistically evaluated, which greatly reduces the error of polarity determination, as we show in the validation of the method (see below).

The segmentations can be conducted on contrast-enhanced tomograms in order to facilitate a better detection of actin filaments. We do not assume the segmentations to be free of false-positives, because they will be efficiently sorted out at a later stage. However, we assume that each filament or detected part is represented by a unique set of voxels; therefore, filaments should not touch each other in the segmentations. The fact that a filament may appear divided into parts (for instance, when it runs through low-contrast, dense, or crowded regions, where it cannot be tracked unambiguously) has no detrimental effect on its polarity determination but leads to an underestimation of the actual filament length.

The workflow of APT is shown in Figure 1A. A detailed description of the method can be found in the following subsections.

Step I: coordinates. The input data is a set of $N_T$ cryo-electron tomograms $T_i$ $\left(i=1,\cdots ,N_T\right)$ and for each $T_i$ there is an associated segmentation $S_i$ of the actin filaments. Each $S_i$ defines a set of filaments $F_i^j$ $\left(j=1,\cdots ,N_i\right)$, with $N_i$ being the number of detected filaments in $T_i$. Firstly, APT utilizes $S_i$ to construct for each $F_i^j$ a set of 3D coordinates $\left\{x_1,x_2,\cdots ,x_{N_i^j}\right\}$ that are evenly spaced along $F_i^j$, and will be the sampling points for polarity determination. Here $N_i^j$ indicates the number of sampling points per filament, which we term segments. For example, the second filament segmented in the first tomogram is denoted with $F_1^2$. If this filament was subdivided into 12 segments, $N_1^2=12$.

Step II: subtomograms. Next, APT pools all these $N_C=\sum N_i^j$ segments $x_k$ $\left(k=1,\cdots ,N_C\right)$, stores the index relation $k\leftrightarrow F_i^j$ for polarity determination at a later stage, and extracts $N_C$ subtomograms centered on $x_k$ from a ctf-corrected version of the dataset $T_i$.

Step III: projections. Subsequently, APT masks and then projects the subtomograms in the direction of the electron beam (z axis). The applied cuboid mask diminishes the influence of filaments and other electron densities above and below the projected segment. We term the height of this mask the projection thickness parameter.

Step IV: prealignment. The purpose of this module is to align the (central) filament density in the projected subtomograms parallel to the x axis (see STAR methods). The detected orientations will be used as priors in the next step.

Step V: 2D classification. In this module class averages of the actin segments will be calculated (see STAR methods). It allows us to sort out false-positive and low-quality segments (Bharat and Scheres, 2016). Using the priors from the previous step, the segments are prealigned parallel to the x axis, and therefore a second, rectangular mask can be applied in order to further diminish the influence of neighboring filaments and other electron densities.

Step VI: 3D reconstruction. In order to obtain an actin filament structure from the projected subtomograms we use a helical reconstruction 3D refine job in RELION (He and Scheres, 2017) (see STAR methods). Subsequently, APT combines all transformations, and as a result we have the forward transformation ${\text{Ω}}_k$, which describes how filament $F_i^j$ has to be transformed at sampling point $x_k$ in order to align with the filament average.

Step VII: polarity. To resolve actin polarity, it is crucial that the filament average reaches a resolution better than 20 Å. Once this has been achieved, APT calculates the inverse transformation ${\text{Ω}}_k^{-1}$, which describes how filament $F_i^j$ is oriented at sampling point $x_k$ with respect to the filament average. Particularly filament polarity is encoded in the inverted psi angle ${\text{ψ}}_k^{-1}$, which indicates the position of the plus end of $F_i^j$ relative to the y axis of $T_i$.

Next, APT uses the index relation $k\leftrightarrow F_i^j$ to extract all ${\text{ψ}}_k^{-1}\left(T_i\right)$ that are originating from the same tomogram $T_i$. If $T_i$ contains a filament bundle with mixed polarity, then the histogram of ${\text{ψ}}_k^{-1}\left(T_i\right)$ shows two distinct peaks that are separated by 180°. The height of each peak indicates how many segments were aligned with their plus ends in the respective direction, and allows an estimation of the polarity ratio within the bundle, while the peak width decreases with increasing parallelism of the filaments. Obviously, if a bundle exhibits a uniform polarity distribution, then the histogram of ${\text{ψ}}_k^{-1}\left(T_i\right)$ shows a single peak.

Subsequently, APT assigns to each segment a direction label. Per default, segments included in the right peak are labeled with 0, and segments included in the left peak are labeled with 1. Therefore, each filament can be represented as a vector $\xi \left(F_i^j\right)$ of polarity labeled segments. The centerpiece of APT is that the elements of $\xi \left(F_i^j\right)$ are computed statistically independent. Segments whose directionality was detected incorrectly do not prohibit the correct polarity determination of a filament as a whole, as long as the majority of segments building that filament were determined accurately.

Consequently, the final polarity label $P\left(F_i^j\right)$ of filament $F_i^j$ is defined as follows:

$$P\left(F_i^j\right)=\{\begin{array}{ll}0\hfill & if\text{mean}\left(\xi \left(F_i^j\right)\right)<0.5\hfill \\ 0.5\hfill & if\text{mean}\left(\xi \left(F_i^j\right)\right)=0.5\hfill \\ 1\hfill & if\text{mean}\left(\xi \left(F_i^j\right)\right)>0.5\hfill \end{array}.$$

If $P\left(F_i^j\right)=0.5$, the polarity of that filament is maximally uncertain.

Step VIII: confidence. We suggest that the closer $mean\left(\xi \left(F_i^j\right)\right)$ is to 0 or to 1, respectively, the higher the probability that $P\left(F_i^j\right)$ was determined correctly. We use this relation to define a confidence score for each filament, termed majority confidence score, as follows:

$$\text{mcs}\left(F_i^j\right)=\max \left(\text{mean}\left(\xi \left(F_i^j\right)\right),\text{mean}\left(\sim \xi \left(F_i^j\right)\right)\right),$$

with $\sim \xi \left(F_i^j\right)$ the logical complement of $\xi \left(F_i^j\right)$. The values of $mcs\left(F_i^j\right)$ range between 0.5 (maximum uncertainty) and 1 (minimal uncertainty), and are the fraction of segments per filament that are pointing in the majority direction. The mcs measures the consistency of the segment's directionality determination along a filament.

Additionally, we define a second confidence score, termed sensitivity confidence score. Here the reconstruction of the filament average is repeated, but the direction of the template initially used in the 3D reconstruction step (see STAR methods) is reversed from plus end up to plus end down. Subsequently, APT initializes for each $F_i^j$ a vector $\lambda \left(F_i^j\right)$ that has $N_i^j$ elements. Those segments that reverse their plus-end orientation as well are orientation sensitive, and APT sets the respective elements of $\lambda \left(F_i^j\right)$ to 1. On the other hand, if a segment shows no logical behavior upon change in template direction, the respective element of $\lambda \left(F_i^j\right)$ is set to 0. Then we define the sensitivity confidence score as follows:

$$scs\left(F_i^j\right)=mean\left(\lambda \left(F_i^j\right)\right).$$

The values of $scs\left(F_i^j\right)$ range between 0 (no segment of $F_i^j$ is orientational sensitive) and 1 ($F_i^j$ is built exclusively from orientational sensitive segments). Comparable with the majority confidence score, the sensitivity confidence score is an alternative to measure the self-consistency of the segment's directionality determination.

Finally, we define the combined confidence score of filaments $F_i^j$ as follows:

$$ccs\left(F_i^j\right)=mcs\left(F_i^j\right)\cdot scs\left(F_i^j\right).$$

Moreover, the polarity labels $\xi \left(F_i^j\right)$ can be considered as $N_i^j$ independent observations of the filament's polarity $P\left(F_i^j\right)$, which follow a binominal probability distribution. It can be shown that the maximum likelihood estimation of $P\left(F_i^j\right)$ is the observed proportion of polarity labels $mcs\left(F_i^j\right)$ (Lynch, 2007), and the standard error of $mcs\left(F_i^j\right)$ is:

$$\text{σ}\left(F_i^j\right)=\sqrt{\frac{\text{mcs}\left(F_i^j\right)\left(1-\text{mcs}\left(F_i^j\right)\right)}{N_i^j}.}$$

We use $\sigma \left(F_i^j\right)$ to calculate the lower bound of a 95% confidence interval around $mcs\left(F_i^j\right)$, which allows us to define an additional confidence score for the polarity determination of filaments $F_i^j$ as follows:

$$mc{s}^{†}\left(F_i^j\right)=mcs\left(F_i^j\right)-1.96\cdot \sigma \left(F_i^j\right)\text{,}$$

with $mc{s}^{†}\left(F_i^j\right)$ termed the extended majority confidence score. If $mc{s}^{†}\left(F_i^j\right)<0.5$, the polarity determination of filament $F_i^j$ is uncertain.

The minimal length of a filament that comprises one polarity outlier is six segments, in order to reach $mc{s}^{†}\left(F_i^j\right)\ge 0.5$; for example, $\xi \left(F_1^1\right)=\left(101111\right)$ would yield $mc{s}^{†}\left(F_1^1\right)=0.54$. On the other hand, choosing a threshold of $ccs\left(F_i^j\right)\ge 0.6$ would allow for shorter filaments built from three segments with one polarity outlier, only if all three segments are orientational sensitive. Typically, we use $ccs\left(F_i^j\right)\ge 0.6$ to allow for a denser visualization of actin filament networks, but secure statistical conclusions about the polarity distribution in that networks with the stricter confidence score $mc{s}^{†}\left(F_i^j\right)\ge 0.5$.

Step IX: topology. In this module, APT performs a 3D neighborhood analysis of the actin filaments in order to characterize their polarity distribution in the observed bundles. Therefore, centered around each segment $x_k$, APT constructs a sphere ${\mathcal{K}}_{\epsilon }\left(x_k\right)$ with radius $\epsilon$, defining the neighborhood of $x_k$. Then, APT extracts number, distance, and polarity of all filaments passing through ${\mathcal{K}}_{\epsilon }\left(x_k\right)$. For instance, let the polarity of $F_i^j$ be $P\left(F_i^j\right)=0$, and imagine $F_i^j$ is surrounded at coordinate $x_k$ by four filaments within ${\mathcal{K}}_{\epsilon }\left(x_k\right)$, of which one displays the same polarity and three reversed polarity. Then, the probed segment of the filament is located in a neighborhood that exhibits 75% mixed polarity and 25% uniform polarity, respectively. This calculation is performed by APT for all ${\mathcal{K}}_{\epsilon }\left(x_k\right)$, and subsequently it sums the degrees of uniform polarity $P_{\parallel }$ and mixed polarity $P_{\nparallel }$ of all neighborhoods in a given actin bundle. Finally, the topology score $\tau$ of an actin bundle is defined as follows:

$$\text{τ}=\frac{P_{\parallel }-P_{\nparallel }}{P_{\parallel }+P_{\nparallel }}.$$

The topology score $\tau$ ranges from −1 to +1. The more filaments are organized in a uniform polarity configuration, the closer the value of $\tau$ will be to +1. If the bundle shows a phase separated topology, so that filaments with opposite polarities adjoin mainly at phase boundaries, $\tau$ will be reduced accordingly. However, the more the bundle favors a close proximity between filaments with opposite polarities, the more $\tau$ will approach −1.

Validation of APT

The missing wedge affects the reconstruction of a tomogram in an anisotropic manner (Lucic et al., 2005). As a consequence, filaments parallel to the tilt axis are better resolved than filaments oriented orthogonal to the tilt axis (Figures S1A and S1B). It is fundamental to ensure that our projection approach for subtomogram averaging is not biased by the missing wedge. Additionally, the impact of SNR and polarity distribution on the output precision of APT should be verified, as well as the influence of out-of-plane tilt of filaments.

For validation purposes, we implemented a ground truth data generator (see STAR methods) that creates modeled tomograms of actin bundles (volume 353 × 353 × 353 nm³ with a pixel size of 3.44 Å), utilizing EMD-6179 (Galkin et al., 2015) as filament density, with four adjustable parameters: the angle $\alpha$ of the bundle with the tilt axis, the angle $\beta$ creating an out-of-plane tilt of the bundle, the SNR of the tomogram (Forster et al., 2008; Pei et al., 2016), and the polarity ratio ${\rho }_r$, namely the fraction of filaments in the bundle oriented in opposite direction. Each of the bundles comprises, on average, 73 filaments, with a uniform length distribution of 86–282 nm and a uniform distance distribution of 10–37 nm between neighboring filaments.

In the first model experiment, we created three ground truth datasets with three different SNRs, which are ${10}^{-2}$, ${10}^{-3}$, and ${10}^{-4}$. Each dataset consists of 10 tomograms of different bundles that are oriented in 10° steps from $\alpha =0°$ (filaments $\parallel$ to the tilt axis) to $\alpha =90°$ (filaments $\perp$ to the tilt axis). Additionally, within each set we varied the polarity ratio ${\rho }_r$ in triplets, meaning that the first four tomograms ($\alpha =0°,10°,20°,30°$) were modeled with ${\rho }_r=0.1,0.3,0.5,0.1$, and so forth, except the last tomogram ($\alpha =90°$) was constructed with ${\rho }_r=0.5$. In the first model experiment, we neglected an out-of-plane tilt of the bundles ($\beta =0°$).

A top view on one of the modeled bundles ($\alpha =30°$, ${\rho }_r=0.1$) is shown in Figure 1B (without noise, only for visualization purposes). A second example is depicted in Figure 1C. This bundle is oriented 70° with respect to the tilt axis and the polarity ratio is 0.3. Its side view is displayed in Figure 1D, with the viewing axis oriented parallel to the filaments. A bandpass filtered slice of a filament that was boxed out of one of the modeled tomograms ($\alpha =0°$, SNR = ${10}^{-3}$) is shown and can be compared with a filament parallel to the tilt axis as well, but affected with an SNR of ${10}^{-4}$ (Figures 1E and 1F, respectively).

We applied the APT workflow on each of the three datasets independently. Since segmentation of the filaments is given by the ground truth data, we first established the segment coordinates (step I), with an equidistant spacing of 11 nm, corresponding to ~1,000 segments per modeled bundle. Next, the subtomograms were extracted using a box size of 50 × 50 × 50 nm³ (step II) and subsequently projected using a projection thickness of 11 nm (step III). In the next step, segments were prealigned (step IV), followed by the 2D classification module (step V). In Figures S2A–S2F, the results of prealignment and 2D classification are exemplified for the dataset with SNR = ${10}^{-4}$.

Following this, we executed 3D reconstruction (step VI) of the three actin filament averages from a similar number of particles (~10,000 segments per average), distributed approximately uniform over the modeled bundles. As expected, the resolutions of the filament structures decrease with decreasing SNR (Figure S2G).

Subsequently, we determined the polarity of all bundles (step VII). All ${\text{ψ}}_k^{-1}\left(T_i\right)$ histograms showed two distinct peaks (Figure 1G), separated by 180°, indicating the opposite plus-end orientations of the segments, and the height of the peaks reproduce the respective polarity ratios. All restored bundles from all three SNR conditions coincide with the ground truth bundles (Figures 1H and 1I). Furthermore, we visualized the $\xi \left(F_i^j\right)$ vectors of all the recovered bundles (Figure 1J). The position of incorrect assigned segments is randomly distributed and their number increases with decreasing SNR.

The results of the confidence analysis (step VIII) are plotted in Figure 1K. The $ccs\left(F_i^j\right)$ of filaments with SNR = ${10}^{-3}$ decreased slightly in comparison with SNR = ${10}^{-2}$, but show no trend to lower $ccs\left(F_i^j\right)$ with increasing $\alpha$ angle (slopes of black and red linear regression lines in Figure 1K are $2.72\cdot {10}^{-5}\pm 1.04\cdot {10}^{-3}$ and $-3.25\cdot {10}^{-4}\pm 1.42\cdot {10}^{-3}$, and p values of the slopes are 0.98 and 0.83, respectively). We conclude that the missing wedge-induced anisotropic deterioration does not negatively influence the precision of APT for low SNR values, as found in cellular cryo-tomograms (Forster et al., 2008; Pei et al., 2016). However, for the markedly challenging SNR = ${10}^{-4}$, the $ccs\left(F_i^j\right)$ show a trend to decrease with increasing $\alpha$ angle (the slope of the blue linear regression line in Figure 1K is $-1.17\cdot {10}^{-3}\pm 8.37\cdot {10}^{-4}$ and its p value is 0.20).

Next, we evaluated the total segment error $tse\left(F_i^j\right)$, namely the fraction of segments with an incorrect orientation determination compared with the ground truth. The $tse\left(F_i^j\right)$ values for filaments affected with SNRs of ${10}^{-2}$, ${10}^{-3}$, and ${10}^{-4}$ (Figure 1K, black, red, and blue diamond symbols) are $0.05\pm 0.05$, $0.07\pm 0.04$, and $0.20\pm 0.07$, respectively. These values can be compared with the total filament error $tfe\left(F_i^j\right)$; that is, the fraction of filaments with incorrect polarity determination compared with the ground truth. Here we find for all modeled bundles (independently of both $\alpha$ and ${\rho }_r$) with SNRs of ${10}^{-2}$ and ${10}^{-3}$ that $tfe\left(F_i^j\right)=0$, and for bundles modeled with an SNR of ${10}^{-4}$ the $tfe\left(F_i^j\right)$ is $0.05\pm 0.06$ (here the polarity of 34 out of 712 filaments was determined incorrect). This shows that APT is capable of reliably correcting noise-induced polarity errors on the filament level.

In the second model experiment we again created three ground truth datasets with previously chosen SNRs. However, in order to study the influence of an out-of-plane tilt of the filaments on the precision of APT, we varied the bundle tilt $\beta$ between $0°$ and $38°$ in steps of $2°$, which resulted in 20 modeled bundles per SNR condition. This time we neglected bundle orientation ($\alpha =0°$) and kept the polarity ratio constant (${\rho }_r=0.5$).

Subsequently, we applied the APT workflow on each of the three datasets independently. Here the projection thickness parameter (step III) had to be increased to capture the tilted segments in the projection completely. Consequently, we increased the projection thickness from 11 nm to 44 nm for all segments, assuming no prior knowledge about the tilt of individual segments.

Based on regression line analysis of the resulting $ccs\left(F_i^j\right)$ values (Figure S2H), we conclude that out-of-plane tilt at least up to $38°$ has no detrimental effect on the precision of APT. Similar to what we observed in the first model experiment, the $tse\left(F_i^j\right)$ values increase with decreasing SNR (Figure S2H). The same holds true for the $tfe\left(F_i^j\right)$ values, which are $0.004\pm 0.008$ and $0.01\pm 0.02$ for tilted bundles with SNRs of ${10}^{-2}$ and ${10}^{-3}$, respectively. However, at SNR = ${10}^{-4}$, the $tfe\left(F_i^j\right)$ increases sharply ($0.33\pm 0.06$). Here the polarity of 487 out of 1,462 filaments was determined incorrect.

In order to confirm that this effect can be attributed to the 4-fold increased projection thickness (Figure S2I), we generated an additional tilted ground truth dataset with SNR = ${10}^{-4}$, but this time we assumed that prior knowledge about the tilt of individual segments exists; e.g., by estimating $\beta$ from the segmentations. Based on that prior knowledge we tilted the projection mask individually for each segment, so that the projection thickness parameter can be reverted to 11 nm. As a result, the $tfe\left(F_i^j\right)$ was diminished substantially ($0.01\pm 0.02$). Here the polarity of 22 out of 1,465 filaments was determined incorrect.

In situ actin reconstruction at FAs

Here we applied APT on the actin cytoskeleton inside FAs, using a correlative fluorescence microscopy and cryo-ET approach (Patla et al., 2010; Sartori et al., 2007) (see STAR methods). Mouse embryonic fibroblasts (MEFs), expressing vinculin-venus as a marker for FAs (Grashoff et al., 2010; Ringer et al., 2017), were cultured on electron microscopy grids with silicon oxide support and imaged by fluorescence microscopy (Figure 2A). Conspicuous FAs were identified and found again under the electron beam.

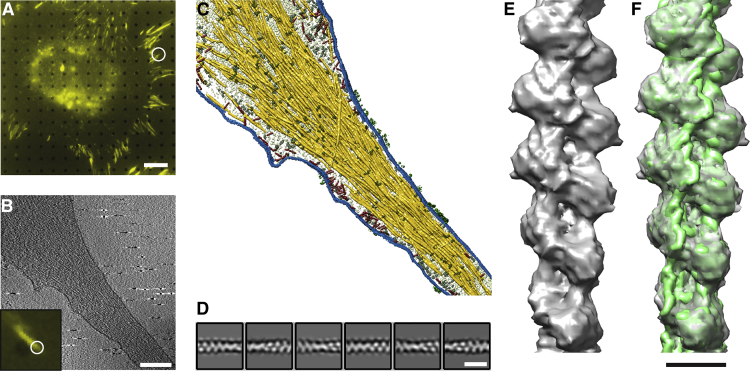
Figure 2.

Cryo-tomography of FAs and actin filament structure from inside cells

(A and B) Correlated microscopy combining fluorescence microscopy (A and B, inset) and cryo-ET (B) was used to identify FA sites. Scale bar in (A), 10 μm. (B) A 1.4-nm thick slice through a cryo-tomogram of an FA (A, B, white circles) shows individual actin filaments and plasma membrane. Scale bar, 200 nm.

(C) Surface rendering view of the FA site. Actin is depicted in yellow, membranes in blue, macromolecules in red and gray, and receptor densities in green. The segmentation of the actin filaments served as input for APT.

(D) Class averages obtained by 2D classification of the extended dataset. Scale bar, 18 nm.

(E) Structure of an actin filament at FAs, shown as gray isosurface.

(F) The in-vitro structure EMD-6179 (Galkin et al., 2015) (green isosurface) was docked into the in situ structure. Scale bar, 5 nm.

See also Figures S3 and S4.

Due to the sheer size of FAs, tomograms cannot cover a complete adhesion site ($⪆$3 μm in length), and, due to electron dose sensitivity of the sample, only a single tomogram can be acquired per FA. Therefore, we recorded cryo-tomograms at a spectrum of positions, namely from proximal regions, where a stress fiber enters the FA, to distal regions, where they are oriented toward the plasma membrane. Seven cryo-tomograms of FAs (Figure 2B), covering positions from proximal to distal, were selected in the first place, and the actin filaments were manually segmented (Figure 2C).

Following this, we applied the APT workflow on this dataset. Firstly, we extracted a total of 43,400 segments with an equidistant spacing of 11 nm (step I). The box size of the subtomograms was set to 50 × 50 × 50 nm³ (step II), and the projection thickness to 11 nm (step III), since the analyzed actin bundles are oriented in a good approximation planar within the tomograms ($\beta \approx 0$). After prealignment and 2D classification (steps IV–V), we finally selected 20,585 segments (Figure S3A) for 3D reconstruction (step VI).

The obtained in situ actin filament structure was resolved to 18 Å, and allows us to unambiguously detect the position of its plus end (Figures S3B–S3D). This shows that the APT workflow is capable of producing sufficient resolution for subsequent mapping of the filament's polarity distribution, although the dataset was relatively limited and the filaments originate from a crowded and dense cellular environment, with multiple possible binding partners and modulations of their helical symmetry.

In order to efficiently increase the size of the dataset, we used the previous seven manual segmentations to train a convolutional neural network with EMAN2 (Chen et al., 2017), capable of detecting actin filaments (see STAR methods). Using this approach, we additionally created 31 segmentations of the actin cytoskeleton at FAs.

We then applied the APT workflow to this extended dataset. Here we extracted a total of 247,940 segments (11 nm spacing) with a box size of 36 × 36 × 36 nm³ and a projection thickness of 11 nm (steps I–III). After prealignment and 2D classification (steps IV–V), we finally selected 72,973 segments (Figures S4A and 2D) for 3D reconstruction (step VI).

Subsequently, we performed a 3D classification with RELION (Figures S4B–S4H). The highest resolved class average with 14 Å is shown in Figure 2E, together with a docking of EMD-6179 (Galkin et al., 2015) in Figure 2F.

Polarity distribution of actin bundles at FAs

Finally, we utilized APT to reconstruct actin networks in situ, including the polarity of the filaments. Therefore, we continued the APT workflow with the polarity determination module (step VII), based on the in situ actin filament reconstruction (Figure S3), previously obtained from seven manual segmentations of actin bundles at FAs. All ${\text{ψ}}_k^{-1}\left(T_i\right)$ histograms showed two distinct peaks, separated by 180°. We extracted the $\xi \left(F_i^j\right)$ vectors of the resulting 2,893 filaments, and used APT to calculate the confidence scores (step VIII), plotted in Figures 3A–3C. The minimum reliable $ccs\left(F_i^j\right)$ was set to 0.6 (Figure 3C), thereby leaving a total number of 2,146 actin filaments with determined polarity (Figure S3E). The total length of the filaments is ~149 μm, with an average length of ~70 nm, and a maximum length of ~350 nm (Figures S5A–S5B).

Figure 3.

Architecture of actin bundles at FAs

(A) Histogram of the $mcs\left(F_i^j\right)$ values from 2,893 reconstructed actin filaments, extracted from seven manually segmented cryo-tomograms acquired at FAs.

(B) Histogram of the respective $scs\left(F_i^j\right)$ values.

(C) Plot of the respective $ccs\left(F_i^j\right)$ values. Each red cross marks the $ccs\left(F_i^j\right)$ of one filament, and the scores are plotted as a function of the bundle orientation $\alpha$. The blue crosses indicate the average of all $ccs\left(F_i^j\right)$ values that are originating from the same actin bundle, and a regression line was fitted to these values (blue line with a slope of $-9.24\cdot {10}^{-4}\pm 7.31\cdot {10}^{-4}$; the p value of the slope is 0.26). Only filaments reaching a $ccs\left(F_i^j\right)\ge 0.6$ (dashed line) were accepted; therefore, 2,146 reconstructed actin filaments were used for subsequent bundle visualization and topology analysis.

(D) Visualization of the resulting $\xi \left(F_i^j\right)$ vectors of a bundle that was recorded at a proximal FA region. Segments that originate from the same filament are plotted as columns of circles. Blue segments are oriented with their plus ends toward the cell tip, and red segments point in the direction of the cell body. In this bundle, 495 filaments with an average length of 7.1 segments were analyzed. Approximately two-thirds of the segments are directed toward the cell tip.

(E–H) Top views on the architecture and polarity distribution of four actin bundles, recorded at proximal (E and F) and distal (G and H) FA regions. Blue actin filaments are oriented with their plus ends toward the cell tip, and red filaments point in the direction of the cell body. Proximal FA bundles are characterized by a tendentially mixed polarity distribution, and distal FA bundles converge to a predominantly uniform polarity distribution.

(I and J) Side views on the bundles shown in (E) and (H), respectively. (I) Filaments, which are directed toward the cell body (red filaments), are found with a higher probability at outer regions of proximal FA actin bundles.

This relation is displayed in (K) as well, showing the long axis of bundle (E). In all visualizations (E–K), actin filaments were rendered from EMD-6179 (Galkin et al., 2015), the dashed rectangles are bounding boxes surrounding the actin bundles. Scale bars, 100 nm. Additionally, positions of plasma membrane are suggested by light gray lines, and support planes by dark gray lines.

See also Figure S5.

In Figure 3D the resulting $\xi \left(F_i^j\right)$ vectors of one of the bundles are displayed. Here we found that 62% of the segments are pointing with their plus ends toward the cell tip (blue segments), and 38% in the opposite direction (red segments). The actin polarity distribution of this actin bundle is visualized in Figure 3E. The blue filaments are pointing with their plus ends toward the cell tip, and the red filaments in the opposite direction.

The two bundles shown in Figures 3E and 3F were acquired at proximal regions of FAs, whereas the two bundles shown in Figures 3G and 3H were acquired at distal regions. We applied APT's topology module (step IX), and sorted the bundles with increasing topology score (Figure S5C) from left ($\tau$=0.25) to right ($\tau$=0.87), which reflects their transition from a tendentially mixed polarity distribution to a predominantly uniform polarity distribution. In Figure 3E, for example, 65% of the filaments are directed toward the cell tip, whereas in Figure 3H this fraction is increased to 96%. Applying $mc{s}^{†}\left(F_i^j\right)\ge 0.5$ for filament selection (step VIII) reveals similar topology values and filament distributions as before; however, the number of actin filaments with determined polarity is reduced to 1,464.

The bundles in Figures 3E and 3H are shown from the side in Figures 3I and 3J. Furthermore, the long axis of the bundle in Figure 3E is shown in Figure 3K. The data suggest that filaments that are directed toward the cell tip, forming the core of the FA actin bundle, and the reversely directed filaments are organized around this core. The positive topology scores of bundles with mixed polarity distributions are a further indication for this architectural principle. If the reversed actin filaments would be diffused into the bundles, the topology score would approach negative values. In addition, we analyzed the polarity distribution in layers parallel to the support, finding that reversed filaments are enriched on top and bottom of the mixed polarity bundles (Figure S5D).

The number of filaments within neighborhood spheres ${\mathcal{K}}_{\epsilon }\left(x_k\right)$, which were evaluated during topology analysis (step IX), using a radius of $\epsilon$ = 40 nm, has its maximum at six neighbors (Figure S5E), and the mean filament distance is ~28 nm (Figure S5F).

Finally, we completed the APT workflow (steps VII–IX) for the extended dataset with previously obtained 31 automatic segmentations (Figures 2D–2F and S4). Seven tomograms were excluded, because they contained ill-defined or multiple bundles with similar orientation, so that the ${\text{ψ}}_k^{-1}\left(T_i\right)$ histograms did not exhibit two clearly defined peaks. Here we applied $mc{s}^{†}\left(F_i^j\right)\ge 0.5$ for filament selection, thereby leaving a total number of 3,460 actin filaments with determined polarity.

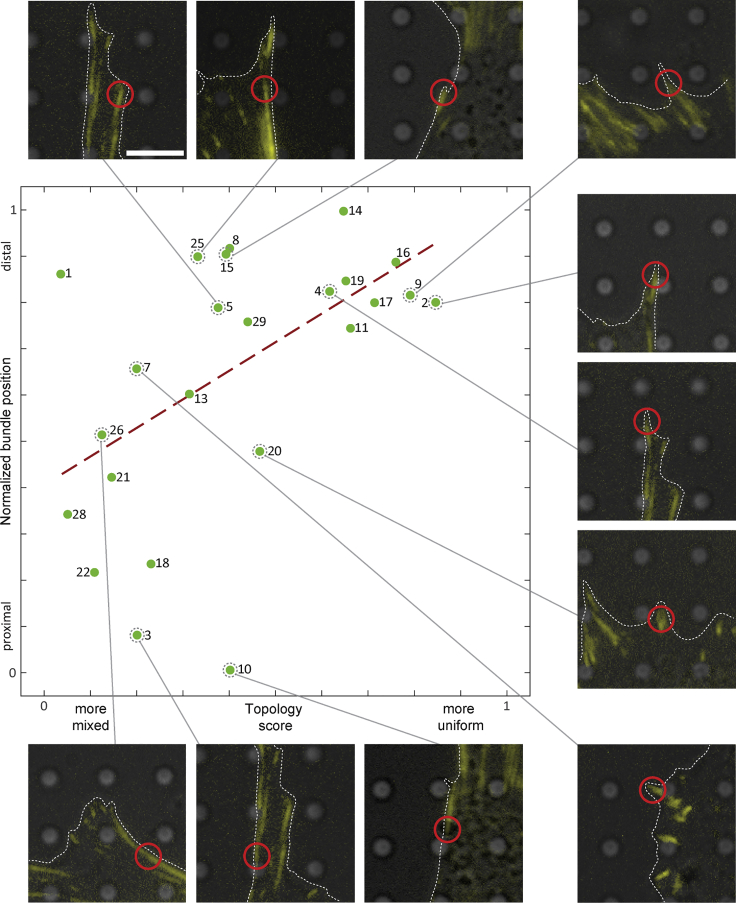
In Figure 4 we plotted the topology score $\tau$ of these 24 bundles versus their normalized position along an FA (see STAR methods). Strikingly, pronounced uniform polarity distribution can be found in distal regions of FAs exclusively. For most of the analyzed bundles (Figure 4, green dots) the plot suggests a linear correlation between topology score and normalized bundle position (the slope of the red dashed linear regression line in Figure 4 is $0.62\pm 0.21$ and its p value is 0.007). In other words, within an FA, from proximal to distal regions, the polarity distribution of the actin filaments transforms smoothly from a mixed to uniform actin polarity organization.

Figure 4.

The distribution of actin polarity at FAs

Plot of topology score versus normalized bundle position along an FA. The green datapoints (fitted by the red dashed regression line) suggest a correlation between these two parameters. The polarity distribution along FAs transitions smoothly from mixed to uniform. Some datapoints in the plot are accompanied by their fluorescence microscopy signal. The plasma membrane is outlined by white dashed lines, and the tomogram position is indicated by a red circle. Scale bar, 5 μm.

Discussion

In order to reconstruct structure and polarity of actin filaments in cells, we developed an alternative procedure for subtomogram averaging. The key operation is to project subtomograms in the direction of the electron beam, and then perform 3D reconstruction from the projected subtomograms. Compared with classic subtomogram averaging, where 3D volumes have to be aligned and averaged, here the 3D reconstruction is computed from 2D images, like in single-particle analysis. Obviously, this reduces the amount of processed data by a factor $1/z$, with $z$ being the number of voxels of the processed subtomograms in z direction. This results in a substantial speedup, which allows an efficient processing of large datasets, finer angular samplings, deeper classifications, and comprehensive hyperparameter tuning. Conceptually, this approach transforms a subtomogram averaging task into a single-particle cryo-EM task, and keeps the unique benefit of cryo-ET, that the molecular structure under investigation can be computationally purified from its natural environment.

Within APT, an actin filament is dissected into multiple segments, and subsequently their polarity is measured. Thereby a set of statistically independent estimations of the filament's polarity is generated. This allows evaluation of the confidence of the polarity assignment with statistical methods. Based on that, filaments with low confidence can be sorted out and conclusions about the polarity distribution in actin networks can be drawn using a solid statistical basis.

A previous approach to decipher actin polarity from tomographic data necessitated chemical extraction and negative staining of the cytoskeleton (Narita et al., 2012), in order to increase the SNR of the tomograms. However, the challenge of resolving actin filament structure and polarity in situ requires a tomographic dataset from intact cells (Beck and Baumeister, 2016; Lucic et al., 2005), which involves vitrification of the sample, and therefore the method needs to successfully handle low SNR (Forster et al., 2008; Pei et al., 2016). We used model calculations in order to investigate how the error rate of APT depends on the SNR. Even for a very low and challenging SNR of ${10}^{-4}$, the polarity of only 5% of the modeled filaments was assigned incorrect.

We applied APT on actin bundles found at FAs (Kanchanawong et al., 2010; Patla et al., 2010). Here, we find that the majority of the filaments are directed toward the cell tip (Figures 3E–3H), and form the core of the bundles, whereas filaments with reversed polarity organize around this core (Figures 3I–3K and S5D). Ultimately, the polarity distribution depends on the position of the bundle along the FA (Figure 4). The more distal the position, the more uniform the polarity distribution, while mixed polarity can be observed mainly in the proximal regions.

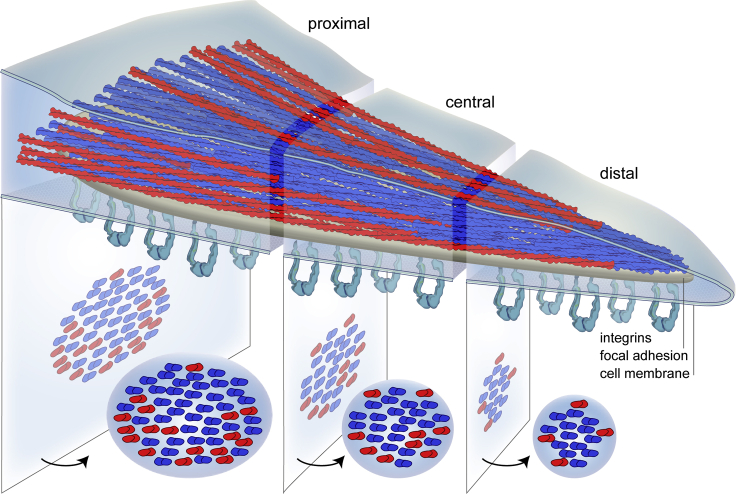
Stress fibers are contractile actin assemblies (Malik-Garbi et al., 2019), enriched with actomyosin interactions, which favor a mixed polarity distribution of actin filaments. Proximal regions of FAs anchor to stress fibers (Burridge and Guilluy, 2016), therefore exhibiting a mixed polarity actin bundle. However, at distal regions of FAs, more vectoral or even protruding forces may play a role that resembles a more uniform polarity distribution (Figure 5).

Figure 5.

A model for actin polarity at FAs

Actin bundles within FAs are characterized by a mixed polarity distribution at proximal regions. However, there is a smooth transition toward a uniform polarity distribution at distal regions. Actin filaments, which are directed with their plus ends toward the cell body (red), are arranged around a central core of filaments pointing toward the cell periphery (blue).

Since the polarity of an individual actin filament is determined from its segments exclusively, the polarity of surrounding filaments does not bias the polarity measurement. As shown in the model calculations, the confidence scores reflect the SNR of the data. In turn, the confidence scores can be used to estimate the effective SNR within different filament bundles.

In Figure 3C, the averaged $ccs\left(F_i^j\right)$ values of different actin bundles are plotted (blue crosses). Since these values are relatively similar between different bundles (mean $\pm$ SD is $0.75\pm 0.04$), we conclude that the effective SNRs of the bundles are comparable. Based on this argument, we are confident that the measured differences between the bundles are not biased by data quality differences between the tomograms.

Technical developments in sample preparation allowed cryo-ET to provide fundamental insights into cellular assemblies and processes in situ (Mahamid et al., 2016; Marko et al., 2007; Schaffer et al., 2019). Equally important, it requires the development of powerful tools to analyze the data (Chen et al., 2017; Himes and Zhang, 2018; Martinez-Sanchez et al., 2020; Song et al., 2019). APT extends this toolbox and allows actin filaments to be analyzed in physiological relevant processes. We hope that it will help to provide a better understanding of actin networks, such as the actin cortex (Chugh et al., 2017), stereocilia organization (Metlagel et al., 2019), or remodeling of actin during phagocytosis (Gerisch, 2011).

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited data
Manually segmented dataset (7 cryo-tomograms of FAs from MEFs) and APT workflow	This paper	EMPIAR-10570
In-situ structure of an actin filament from FAs of MEFs	This paper	EMD-11976
Near-atomic resolution for one state of F-actin	(Galkin et al., 2015)	EMD-6179
Talin-activated vinculin interacts with branched actin networks to initiate bundles	(Boujemaa-Paterski et al., 2020)	EMD-10737
Crystal-structure of the 20s proteasome from the archaeon T-acidophilum at 3.4-angstrom resolution	(Lowe et al., 1995)	PDB-1PMA
Crystal structure of the thermosome, the archaeal chaperonin and homolog of CCT	(Ditzel et al., 1998)	PDB-1A6D
Experimental models: cell lines
MEFs stably expressing vinculin-venus	(Ringer et al., 2017)	N/A
Software and algorithms
Actin polarity toolbox (APT)	This paper	github.com/meibauer/ActinPolarityToolbox
RELION	(Scheres, 2012)	https://www3.mrc-lmb.cam.ac.uk/relion/index.php/Main_Page
MATLAB	MathWorks, Natick, USA	N/A
SerialEM	(Mastronarde, 2005)	https://bio3d.colorado.edu/SerialEM/
MotionCorr	(Li et al., 2013)	https://cryoem.ucsf.edu/software
TOM toolbox	(Nickell et al., 2005)	https://www.biochem.mpg.de/6348566/tom_e
AMIRA	Thermo Fisher Scientific, Waltham, USA	N/A
EMAN2	(Chen et al., 2017)	https://blake.bcm.edu/emanwiki/EMAN2
UCSF chimera	(Pettersen et al., 2004)	https://www.cgl.ucsf.edu/chimera/

Resource availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Ohad Medalia, omedalia@bioc.uzh.ch.

Materials availability

This study did not generate new unique reagents.

Data and code availability

The APT code is available at github.com/meibauer/ActinPolarityToolbox. The manual segmented dataset (7 cryo-tomograms of FAs) together with the APT workflow is deposited at the Electron Microscopy Public Image Archive under accession code EMPIAR-10570. The in-situ structure of an actin filament from FAs of MEFs is deposited in the Electron Microscopy Data Bank under accession code EMD-11976.

Experimental model and subject details

Cell culture

MEFs stably expressing vinculin-venus (Grashoff et al., 2010; Ringer et al., 2017) were cultured in Dulbecco's Modified Eagle's Medium (Sigma-Aldrich, D5671), supplemented with 10% (v/v) fetal bovine serum (Sigma-Aldrich, G7524), 2 mM L-glutamine (Sigma-Aldrich, G7513) and 100 μg/ml penicillin-streptomycin (Sigma-Aldrich, P0781), at 37˚C and 5% CO₂.

Method details

Step IV: prealignment

This is the first of three steps that were performed in RELION. First, a starfile was created only passing the name of each projected subtomogram (rlnImageName) and its originating tomogram (rlnMicrographName) to RELION. Next, the projected subtomograms were normalized with relion_preprocess. Please note that the index relation $k\leftrightarrow F_i^j$ was kept invisible for RELION (for example no metadata label rlnHelicalTubeID was provided (He and Scheres, 2017)). Furthermore, CTF correction in RELION jobs was switched off, because the tomograms were CTF corrected by phase-flipping prior to subtomogram extraction.

For prealignment of the segments a 2D classification with the prepared starfile as input was performed. The purpose of this step is to align the (central) actin filament density parallel with the x-axis, which is the RELION convention for helical reconstruction (He and Scheres, 2017). Therefore, we created a set of projection images (the template library) from an actin filament structure, which was oriented along the x-axis, rotated in 3° increments and subsequently projected. The template library was used as initial references for prealignment (Figure S2A).

Since the resolution of the actin filament averages was determined by Fourier shell correlation between the averages and EMD-6179 (Galkin et al., 2015) as an external reference (Figures S2G, S3D, S3E, and S4H), we were reluctant to use the same structure for the construction of the template library. For that purpose, we used the actin filament structure EMD-10737 (Boujemaa-Paterski et al., 2020).

Step V: 2D classification

Subsequently a second 2D classification was performed, passing previously found psi angles and translations as priors (rlnAnglePsiPrior, rlnOriginXPrior, rlnOriginYPrior). In contrast to the prealignment step, it is crucial that this 2D classification is unsupervised, in order to extract the structural heterogeneity in the data unbiasedly (Figures S2C–S2F).

The psi search was conducted local around the psi prior. Therefore, it is possible to apply a second mask (the first mask is applied during the projection step), which allows to focus the alignment on the (central) actin filament density.

This second 2D classification is capable of producing high quality class averages of filamentous actin from inside intact cells (Figure S3A and S4A), and allows to sort out false positive actin detections and segments of lower quality (Bharat and Scheres, 2016). Based on this classification we selected the segments for subsequent 3D reconstruction.

Step VI: 3D reconstruction

For actin filament alignment and averaging a 3D refine job in RELION was performed with helical reconstruction (He and Scheres, 2017). As helical rise 27.6 Å and as helical twist -166.7° was used (Galkin et al., 2015). In the input starfile, the refined psi angles and translations found in the previous step were passed as priors plus for each segment a random rot angle as prior was added (rlnAngleRotPrior) and the tilt prior (rlnAngleTiltPrior) was set to 90° (He and Scheres, 2017). As initial template the same structure as for construction of the template library was used, low-pass filtered to 30 Å (Figure S3D).

Ground truth data generator

In the first step of modelling a cryo-tomogram of an actin bundle, filament x-z-coordinates were calculated based on random close packing (Desmond and Weeks, 2009), with a uniform distance distribution in the range between 10-37 nm. As a consequence of the modelled x-z-dimension of the bundles of 282 x 150 nm, on average 73 filaments could be packed in each bundle. Next, position and length of each filament in y-direction was randomly chosen from a uniform distribution between 86-282 nm. According to these coordinates, actin filaments based on EMD-6179 (Galkin et al., 2015), were pasted in an empty volume of 353 x 353 x 353 nm³, however, a fraction of ${\rho }_r$ randomly selected filaments were pasted in the volume after 180° rotation around the x-axis (Figures 1B–1D, red filaments).

After that the modelled bundle was rotated around $\alpha °$, to adjust the bundle orientation, and $\beta °$, to adjust the bundle tilt, then Gaussian noise was added to set the targeted SNR, and finally the missing wedge of a tilt-series with tilt-range from -60° to +60° was applied in Fourier space.

Fluorescence microscopy

The MEFs were applied onto glow-discharged EM grids with a silicon-oxide support film (R1/4, Au mesh; Quantifoil, Jena, Germany). After incubation, the cells were fixed in a 4% paraformaldehyde solution (Sigma-Aldrich, 16005), and washed 3 times with 1x PBS (Fisher Scientific, BP399-1). The EM grids were transferred to a 35x14 mm glass-bottom cell culture dish (MatTek, P35G-0-14-C) for fluorescence microscopy analysis of the FAs. Adherent MEFs were imaged using an automated inverted microscope (DMI4000 B, Leica Microsystems, Wetzlar, Germany) equipped with a fluorescence lamp and a monochromatic digital camera (DFC365 FX, Leica Microsystems). Overview images of the EM grids were acquired using a 10x dry objective (HCX PL Fluotar 10x/0.30, Leica Microsystems). All images of individual cells (Figure 2A) were acquired in phase contrast and fluorescence mode using a 63x oil objective (HCX PL APO 63x/1.40-0.6, Leica Microsystems).

Cryo-electron tomography

A drop of 4 μl BSA-coated 10 nm fiducial gold markers (Aurion, Wageningen, Netherlands) was applied on the EM grids before plunging them into liquid nitrogen cooled ethane.

A Titan Krios transmission electron microscope (Thermo Fisher Scientific, Waltham, USA) equipped with a Quantum energy filter and a K2-Summit direct electron detector (Gatan, Pleasanton, USA) was used for cryo-EM data acquisition. The microscope was operated at 300 keV in zero-loss mode with the energy filter slit width set to 20 eV.

The position of the cells and FAs were identified by overlaying the fluorescence signal to low magnification EM images of the grids. At tomography positions image stacks were recorded at each tilt angle in super-resolution mode with an electron flux of ~8 electrons per pixel per second using SerialEM (Mastronarde, 2005). All tomograms were acquired at a magnification of 42’000x, and a dose-fractionated frame rate of 6 frames per 1.2 s. The tilt-series covered an angular range of -60° to +60°, and were recorded with tilt increments of 2° and a defocus of -4 μm. The accumulated electron dose did not exceed ~75 e^-/Ų.

All image stacks were down-sampled and motion corrected using MotionCorr (Li et al., 2013), resulting in a final pixel size of 3.44 Å. Next, CTF correction of the tilt-series was applied (Eibauer et al., 2012). Overview tomograms (Figure 2B) for actin filament segmentation (Figure 2C) and subtomograms of actin segments were reconstructed by weighed back-projection using the TOM Toolbox (Nickell et al., 2005).

Normalized bundle position of FA

The tomographic position within a FA was determined by overlaying the light microscopy images of the individual cells with cryo-EM images.

First, phase contrast and fluorescence images were overlaid, hereby enabling the identification of the cell membrane and enclosing grid holes. Second, low magnification EM images (4’800x) of the FA tomography position were overlaid such, that the cell membrane and grid holes coincided with the light microscopy images. Third, the zero-degree tilt-series image (42’000x) was aligned with the low magnification EM image such, that the cell membrane shape matched. By increasing the opacity of the EM images, we displayed the FA fluorescence signal on the tomography position.

We defined the center of the tomogram as the tomography position FA_T. In order to determine the relative position of FA_T within the entire FA, we defined the proximal end (closest to the cell body) and distal end (closest to the cell periphery) fluorescence microscopy signal pixels as FA_P and FA_D, respectively. The distance $d$ between FA_T and FA_D and the length $l$ of the FA (distance between FA_P and FA_D) was measured (the pixel size of the fluorescence microscopy images was 91 nm). Finally, the normalized bundle position of the FA (plotted on the y-axis in Figure 4) was calculated as $1-d/l$.

Automatic segmentation

We developed a script in MATLAB to automatize the convolutional neural network (CNN) segmentation with EMAN2 (Chen et al., 2017, 2019).

The method requires three image stacks with fixed x-y-dimension of 64 x 64 pixels as input files. Firstly, the positive training stack contains 2D images of densities targeted for segmentation. These images are slices, boxed out of cryo-tomograms. In our case they contain actin filament densities. Secondly, an image stack that provides for each image in the positive training stack an associated segmentation mask. Thirdly, the negative training stack, which contains 2D images of densities not targeted for segmentation, for example gold particles used as fiducial markers, backprojection rays, tomogram edges, plasma membrane, and regions without actin filaments in general.

As a starting point we created seven manual segmentations of actin filaments in cryo-tomograms of FA actin bundles (Figure 2C) with AMIRA (Thermo Fisher Scientific, Waltham, USA). The segmentations were skeletonized, then the filaments were dissected in segments, and around each 3D coordinate of a segment one positive training image was extracted from the tomogram at respective z-position. For each manual segmentation one positive training stack was created, limited to 3’000 images.

In order to create the associated segmentation masks, we extended the skeletonized filaments to the diameter of an actin filament. Subsequently, the segmentation masks were extracted from the extended segmentation at the same coordinates as the positive training images. For each manual segmentation one stack with segmentation masks was created, with the same dimension as the associated positive training stack.

Negative training images were extracted at random positions from the tomograms, but the volume of the actin bundle was excluded. For each manual segmentation one negative training stack was created, limited to 3’000 images as well.

Based on these image stacks, we trained one CNN for each manually segmented tomogram, using default EMAN2 data augmentation, network and training parameters. In the next step, the resulting seven CNNs were applied to each of the 31 tomograms in the extended dataset, thereby creating a total amount of 217 segmentations. Finally, the segmentations belonging to the same tomogram were averaged and post-processed in UCSF Chimera (Pettersen et al., 2004) with the hide dust command.

Visualization

All isosurface visualizations of actin filament structures and actin bundles were rendered with UCSF Chimera or AMIRA. For the visualizations of actin bundles in Figures 3E–3K we used EMD-6179 (Galkin et al., 2015) to represent the filaments. Therefore, we used a b-spline registration algorithm to bend the filaments in order to match their 3D shape defined by the segment coordinates (Rueckert et al., 1999).

Quantification and statistical analysis

Slopes of linear regression lines are given in the form $slope\pm standarderroroftheslope$. Linear regression lines were computed with the robustfit function in MATLAB. The total segment errors $tse\left(F_i^j\right)$ and total filament errors $tfe\left(F_i^j\right)$ are given in the form $mean\pm standarddeviationofthemean$. Furthermore, the developed method determines the polarity of individual actin filaments based on a statistical analysis, which is described in detail in the results section.

Published: January 20, 2021

Supporting Citations

The following references appear in the supplemental information: Rosenthal and Henderson (2003).