Microswimmers learning chemotaxis with genetic algorithms

Significance

Swimming microorganisms and migrating cells have developed various strategies in order to move in nutrient-rich or other chemical environments. We apply a genetic algorithm to the internal decision-making machinery of a model microswimmer and show how it learns to approach nutrients in static and dynamic environments. Strikingly, the emerging dynamics resembles the well-known run-and-tumble motion of swimming cells. We demonstrate that complex locomotion and navigation strategies in chemical environments can be achieved by developing a surprisingly simple internal machinery, which in our case, is represented by a small artificial neural network. Our findings shed light on how small organisms have developed the capability to conduct environment-dependent tasks.

Abstract

Various microorganisms and some mammalian cells are able to swim in viscous fluids by performing nonreciprocal body deformations, such as rotating attached flagella or by distorting their entire body. In order to perform chemotaxis (i.e., to move toward and to stay at high concentrations of nutrients), they adapt their swimming gaits in a nontrivial manner. Here, we propose a computational model, which features autonomous shape adaptation of microswimmers moving in one dimension toward high field concentrations. As an internal decision-making machinery, we use artificial neural networks, which control the motion of the microswimmer. We present two methods to measure chemical gradients, spatial and temporal sensing, as known for swimming mammalian cells and bacteria, respectively. Using the genetic algorithm NeuroEvolution of Augmenting Topologies, surprisingly simple neural networks evolve. These networks control the shape deformations of the microswimmers and allow them to navigate in static and complex time-dependent chemical environments. By introducing noisy signal transmission in the neural network, the well-known biased run-and-tumble motion emerges. Our work demonstrates that the evolution of a simple and interpretable internal decision-making machinery coupled to the environment allows navigation in diverse chemical landscapes. These findings are of relevance for intracellular biochemical sensing mechanisms of single cells or for the simple nervous system of small multicellular organisms such as Caenorhabditis elegans.

Microorganisms possess a huge variety of different self-propulsion strategies in order to actively swim through viscous fluids such as water, which is realized by performing periodic nonreciprocal deformations of their body shape (1–4). In order to search for nutrients, oxygen, or light, they have developed mechanisms to change their shape and, hence, their swimming direction abruptly. An important example is the run-and-tumble motion of various bacteria such as Escherichia coli (5, 6) or of the algae Chlamydomonas (7). Bacteria use temporal information of chemical field concentrations to perform chemotaxis. This process is mediated by a time-dependent response function which suppresses tumbling when swimming upward chemical gradients (CGs) (5, 8–10). Some bacteria follow more diverse chemotactic strategies, which can be related to their specific propulsion mechanisms (11). In contrast to bacteria, many eukaryotic cells such as Dictyostelium (12, 13), leukocytes (14), or cancer cells (15) are able to perform chemotaxis by adapting their migration direction in accordance with the CG by spatial sensing with membrane receptors. From an evolutionary point of view, it remains elusive how motility and chemotactic patterns evolved together, bearing in mind that both different prokaryotic and eukaryotic cells with diverse self-propulsion mechanisms developed surprisingly similar chemotactic machinery (14, 16, 17).

In our work, we use machine learning (ML) techniques in order to investigate how chemotaxis-based decision making can be learned and performed in a viscous environment. During past years, various ML approaches have become increasingly appealing in different fields of physics: for example, in materials science, soft matter, and fluid mechanics (18–20). Unsupervised reinforcement learning (RL) has been used in various biologically motivated active matter systems (21) to investigate optimum strategies, used by smart, self-propelled agents; examples are to navigate in fluid flow (22–25) and airflow (26), in complex environments, external fields (27), and potentials (28). Notably, two contributions have taken the viscous environment into account, namely one applying Q-learning to a three-bead-swimmer (29) and one using deep learning to find energetically efficient collective swimming of fish (30). Experimental realizations of ML applied to self-propelled objects are navigation of microswimmers on a grid (31) or macroscopic gliders learning to soar in the atmosphere (32).

Here, we address the problem of how a microswimmer is able to make decisions by adapting its shape in order to perform chemotaxis. To use adaptive swimming behavior, microswimmers need to be—to a certain extent—aware of both their environment and their internal physiological state. Substituting the complex biochemical sensing machinery of unicellular organisms, or real sensory and motor neurons of small multicellular organisms such as Caenorhabditis elegans, we therefore use the evolution of a simple artificial neural network (ANN), which is able to sense the environment and proposes actions to deform the body shape accordingly. We introduce both spatial and temporal CG sensing leading to different decision-making strategies and dynamics in chemical environments.

Results

Microswimmer Model.

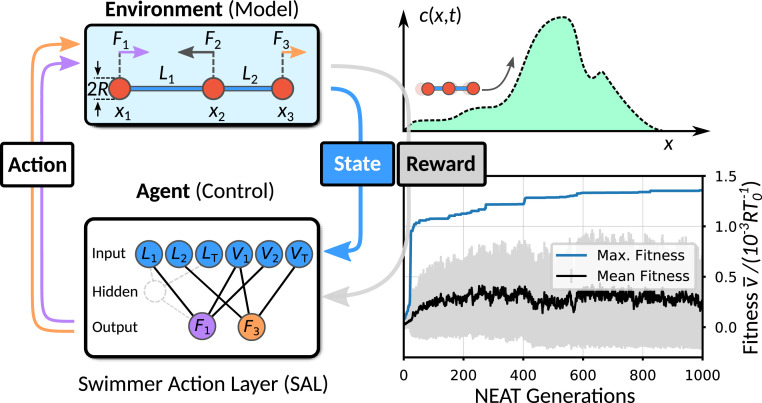
As a simple model, we use the so-called three-bead swimmer introduced originally by Najafi and Golestanian (33). It swims in a viscous fluid of viscosity $\eta$ via periodic, nonreciprocal deformations of two arms, connecting three aligned beads of radius $R$, located at positions $x_i$, $i=\mathrm{1,2,3}$ (Fig. 1, Upper Left). The central bead is connected to the outer beads by two arms; their variable lengths $L_1$ and $L_2$ are extended and stretched by time-dependent forces $F_i\left(t\right)$ acting on the hydrodynamically interacting beads, which determine the bead velocities $v_i\left(t\right)$ (34) (SI Appendix). In this manner, a force-free microswimmer (i.e., ${\sum }_i{F}_i=0$) is able to perform locomotion via nonreciprocal motions of the beads, resulting in a directed displacement of the center of mass (COM) position $x_{\mathrm{c}}=\left(x_1+x_2+x_3\right)/3$ (33). We choose as basic units the bead radius $R$, the viscosity $\eta$, and the maximum force on a bead $F_0$ such that $\left|F_i\right|<F_0$. Hence, the unit of time is $T_0=\eta R^2/F_0$. In previous studies of this model, either the forces or the linearly connected bead velocities $v_i\left(t\right)$ have been prescribed via a periodic, nonreciprocal motion pattern (33–35). Alternatively, a Q-learning procedure (29) has been applied (Discussion). In our ML approach, the swimmer does not follow a prescribed motion but is able to move forward after sufficiently long training and to respond to chemical fields autonomously by a continuous change of the arm lengths.

Fig. 1.

Schematic representation of the RL cycle for a three-bead swimmer moving in a viscous environment (Upper Left) controlled by an ANN-based agent (Lower Left). Reward is maximized during training and is granted either for unidirectional locomotion—phase 1—or for chemotaxis (Upper Right)—phase 2. (Lower Right) Typical NEAT training curves showing the maximum (blue), the mean (black), and the SD (gray) of the fitness (i.e., of the cumulative reward) of successive NEAT generations each covering 200 neural networks when learning unidirectional locomotion.

Phase 1: Learning Unidirectional Locomotion.

We start by demonstrating that a microswimmer is able to learn swimming in the absence of a chemical field with the help of a simple genetic algorithm. This is achieved by applying RL (36) using a reward scheme, which optimizes the microswimmer’s strategy of locomotion along a prescribed direction within a viscous fluid environment.

RL algorithms are designed to optimize the policy of a so-called agent during training: In general, the policy is a highly complex and task-specific function that maps the state of an environment (i.e., everything the agent can perceive [input]) onto actions, which the agent can actively propose (output) in order to maximize an objective (or reward) function (Fig. 1). Such rewards might be related to maximize the score of a computer game (37), to minimize the (free) energy when folding proteins (38), or—as in our case—to maximize the distance that a microswimmer actively moves along a certain direction.

In our approach, the agent represents the internal decision-making machinery responsible for the deformations of the microswimmer. The agent takes as input (i.e., as information it needs to decide about future actions) the state of the environment given by the instantaneous arm lengths $L_1\left(t\right)$ and $L_2\left(t\right)$ and arm velocities $V_i\left(t\right)=d{L}_i\left(t\right)/dt$, $i=\mathrm{1,2}$. In addition, we use the total length $L_{\mathrm{T}}\left(t\right)=L_1\left(t\right)+L_2\left(t\right)$ and the velocity $V_{\mathrm{T}}\left(t\right)=V_1\left(t\right)+V_2\left(t\right)$ as input. The arm lengths are normalized by the default length $L_0=10R$ and subjected to restoring forces acting when $L_1,L_2$ are $>1.3L_0$ or $<0.7L_0$ in order to limit the extent of $L_1$ and $L_2$ (SI Appendix). With this information, the agent proposes actions, which in our case, are the forces $F_1\left(t\right)$ and $F_3\left(t\right)$ that determine the dynamics of the swimmer. The full hydrodynamic environment, including the three-bead model of the microswimmer, represents the (interactive) environment, whose state is updated after the agent has actively proposed its actions (Fig. 1, Left). In an effort to train unidirectional motion, we choose the COM position $x_{\mathrm{c}}$ of a microswimmer to be maximized after a fixed integration time $T_{\mathrm{I}}$; $x_{\mathrm{c}}$ thus represents the cumulative reward of this training process. In this manner, we achieve positive reinforcement when the swimmer moves to the right (positive $x$ direction) and negative reinforcement when it swims to the left (negative $x$ direction).

In order to approximate the analytically unknown optimum policy of the microswimmer, we use ANNs where the output neurons are connected to the input vector, either directly or through emergent hidden neurons, using nonlinear activation functions whose arguments depend on the weights of the connections (Fig. 1, Lower Left and Materials and Methods). In our case, the internal structure of the ANN (weights and topology) is successively optimized using the NeuroEvolution of Augmenting Topologies (NEAT) genetic algorithm to maximize the reward (details are in Materials and Methods and SI Appendix).

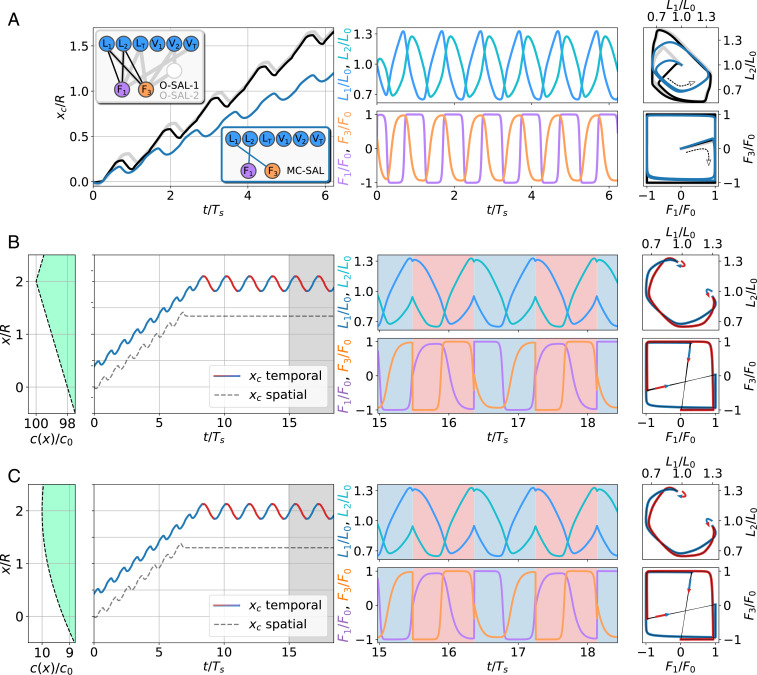
The training of the swimmer agent is performed over multiple RL steps, which correspond to successive NEAT generations. At each step, an ensemble of $N=200$ ANNs (representing one generation) controls the swimming gaits of an ensemble of $N$ independent microswimmers. The cumulative reward $x_{\mathrm{c}}\left(T_{\mathrm{I}}\right)$ is evaluated separately for each microswimmer trajectory defining the fitness $\overline{v}=x_{\mathrm{c}}\left(T_{\mathrm{I}}\right)/T_{\mathrm{I}}$ of the related ANN-based agent, which is simply the mean swimming velocity (i.e., reward per unit time). To start the training, we initialize $N$ ANNs where input neurons are only sparsely connected to output neurons by using random weights. The NEAT algorithm then dynamically produces ANN solutions, which differ in number of connections and values of the weights and may contain hidden neurons. We use the hyperbolic tangent—tanh(x)—as output activation functions. ANN solutions with large fitness values are retained and are preferentially selected for reproduction to form the next generation of ANNs. Thus, good traits of the controlling networks will prevail over time, directing thereby the entire ensemble of ANNs to the desired solution. In order to capture the possible diversity of genetic pathways, we have performed 10 independent training runs. A typical evolution of the fitness values of the ANN ensemble is shown in Fig. 1, Lower Right, highlighting the maximum fitness per generation (blue curve), which converges to $\overline{v}\to 1.36\cdot 10^{-3}R/T_0$. Similar maximum fitness curves are obtained from the other training runs (SI Appendix, Fig. S1). Interestingly, our NEAT training procedure reveals a broad spectrum of network topology solutions (typical time evolution is shown in Movie S1 and SI Appendix, Fig. S2), differing in number of connections and hidden neurons. Various solutions have high fitness ${\overline{v}}_{\mathrm{O}}\approx 1.33-1.36\cdot 10^{-3}R/T_0$, which we refer to as optimal swimmer action layer (O-SAL) solutions, and two of them illustrated in Fig. 2 A, Upper Inset: The simplest O-SAL solution does not use any hidden neurons and consists of a sparse architecture containing only four connections (O-SAL-1; thin black connections). Increasing the number of connections or including hidden neurons only slightly helps to improve the fitness (by $\sim 2\%$) (SI Appendix, Fig. S3). The fittest solution we have found (O-SAL-2; thick gray connections) uses one hidden neuron and eight connections. We note that more O-SAL solutions exist, again of different topology but of very similar fitness, demonstrating the various possible ANN topologies to obtain maximum fitness (SI Appendix, Fig. S4). The resulting back-and-forth motion of the corresponding swimmer’s COM positions $x_{\mathrm{c}}\left(t\right)$ obtained after training is shown in Fig. 2 A, Left. The learned optimum policy describes a square-like shape in $\left(F_1,F_3\right)$ action space, while the shape of the $\left(L_1,L_2\right)$ curve is nontrivial (Fig. 2 A, Right). Again, all O-SAL solutions feature similar trajectories $x_{\mathrm{c}}\left(t\right)$ and a robust swimming gait (Fig. 2A and SI Appendix, Fig. S4).

Fig. 2.

Trajectories of the three-bead swimmer after training. (A) Swimming in the absence of a chemical field. (Left) Time evolution of the COM $x_{\mathrm{c}}$ for optimum (O-SAL-1 [black] and O-SAL-2 [gray]) and minimal complexity (MC-SAL; blue) ANN solutions. Insets show the corresponding topologies. Time $t$ is shown in units of the MC-SAL stroke period $T_S=217T_0$. (Center) Corresponding arm length solutions, $L_1\left(t\right)$ and $L_2\left(t\right)$, and arm forces, $F_1\left(t\right)$ and $F_3\left(t\right)$, shown for MC-SAL. (Right) Phase-space curves ($L_1,L_2$) and ($F_1,F_3$) for O-SAL-1 (black), O-SAL-2 (gray), and MC-SAL (blue). (B) Similar to A but for an MC-SAL swimmer in a linear chemical field (first panel on the left), $c\left(x\right)=max\left(0,a-k|x-x_0|\right)$ for an amplitude $a=100c_0$, slope $k=c_0/R$, and peak position $x_0=2R$, with temporal (red and blue trajectories of $x_{\mathrm{c}}$) and spatial (black dashed trajectory of $x_{\mathrm{c}}$) CG sensing (Fig. 3 shows ANN solutions). Temporal sensing trajectories and phase-space plots are color coded by the currently estimated gradient direction (blue: rightward, red: leftward). The lengths $L_i\left(t\right)$ and forces $F_i\left(t\right)$ are shown for the time domain highlighted by a gray area in the left trajectory plot. Blue and red background colors correspond to gradient direction estimation (rightward and leftward, respectively). Arrows in phase space indicate locomotive strategy change (gait adaptation) due to gradient estimation (change from rightward to leftward locomotion: blue to red and vice versa). (C) Same as in B but for a swimmer in a Gaussian chemical field (the first panel on the left) $c\left(x\right)=a\exp \left(-|x-x_0{|}^2/2{\sigma }^2\right)$ for $a=10c_0$, $\sigma =5R$, and $x_0=2R$.

Strikingly, the algorithm identified intermediate, nonoptimum but extremely simple solutions, which can be easily interpreted and consist of as few as two connections (SI Appendix, Figs. S3 and S4). The best of those solutions identified during the NEAT training (Fig. 2 A, Lower Inset) still has good fitness, ${\overline{v}}_{MC}=0.95\cdot 10^{-3}R/T_0$, and we refer to this solution as the minimal complexity swimmer action layer (MC-SAL): $F_1=F_0\tanh \left(w_1{L}_2+b_1\right)$ and $F_3=F_0\tanh \left(w_2{L}_1+b_2\right)$, with weights $w_1=20.2/L_0$, $w_2=5.7/L_0$, $b_1=-18.6$, and $b_2=-5.4$. Here, the simple topology, together with the sign and strengths of the weights, allows us to interpret the occurrence of the phase-shifted periodic output of the arm lengths and the forces (Fig. 2A, Movie S2, and SI Appendix, Supporting Information Text). Finally, alternative yet less efficient minimal complexity strategies are also possible (SI Appendix, Fig. S4).

Phase 2: Learning Chemotaxis in a Constant Gradient—Spatial Vs. Temporal Gradient Detection.

Now, we proceed to the challenging problem of finding a policy that allows the microswimmer to navigate on its own within a complex environment such as a chemical field, $c\left(x\right)$ (cf. Fig. 1, Upper Right), and perform positive chemotaxis [i.e., motion toward local maxima of $c\left(x\right)$].

We first extend the agent’s perception of the environment such that it is able to sense the field $c\left(x\right)$ (which we normalize by an arbitrary concentration strength $c_0$) and which we use as an additional input for a more advanced chemotaxis agent. We expect that such an agent is able to evaluate the CG $\nabla c\left(x\right)$ in order to conditionally control the lengths of its arms in a way to steer its motion toward maxima of $c\left(x\right)$. Compared with phase 1, we propose a slightly more complex cumulative reward scheme for the training phase: We use $r_{\mathrm{c}}={\sum }_{i=1}^{N_{\mathrm{I}}}\left[x_{\mathrm{c}}\left(t_i\right)-x_{\mathrm{c}}\left(t_{i-1}\right)\right]D\left(t_i\right)$ where $D\left(t_i\right)=\text{sign}\left[\nabla c\left(x_{\mathrm{c}}\left(t_i\right)\right)\right]=\pm 1$ represents the sign of the gradient at instant $t_i={iT}_0$; thus, $r_{\mathrm{c}}$ measures the total distance that the swimmer moves along an ascending gradient during the total integration time $T_{\mathrm{I}}=N_{\mathrm{I}}{T}_0$.

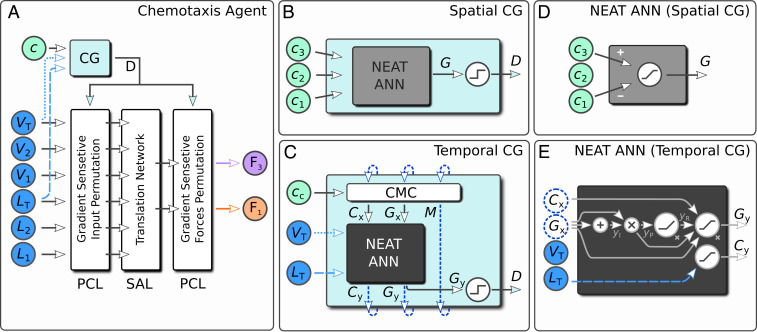
Prior to applying any RL scheme, we decompose the problem of chemotaxis into two tasks. First, we require a mechanism that allows the agent to discern the direction $D$ of the gradient (i.e., $D=1$ for ascending or $D=-1$ for descending); we introduce this tool as a CG block in the ANN of the chemotaxis agent (Fig. 3A) as described below. Second, we identify a pure locomotive part of the agent that can be rooted on already acquired skills—i.e., the unidirectional motion learned in phase 1 (and covered by the above-mentioned swimmer action layer [SAL] solutions)—and on the inherent symmetries of the swimmer model: Swimming to the left and swimming to the right are symmetric operations. Based on the actual value of $D$, conditional directional motion (i.e., either to the left or to the right) can be induced by introducing two permutation control layers (PCLs) to the ANN (Fig. 3A and SI Appendix have details).

Fig. 3.

(A) Schematic view of full ANN-based chemotaxis agent. A chemical field $c\left(x\right)$, swimmer arm lengths ($L_1$, $L_2$, $L_{\mathrm{T}}=L_1+L_2$), and respective arm velocities ($V_1$, $V_2$, $V_{\mathrm{T}}$) are used as input. By measuring the CG through the CG block, the swimmer controls the forces $F_1$ and $F_3$ in order to perform directed locomotion toward an ascending gradient of $c\left(x\right)$. Directed locomotion is split into two PCLs, which permute input and output of the SAL (Fig. 2 A, Insets) according to a predicted sign $D$ of the CG. The prediction of $D$ by the CG block (cyan) can be performed either by directly measuring $D=\text{sign}\left(\nabla c\left(x_{\mathrm{c}}\right)\right)$, by (B) spatial resolution of the chemical field, or by (C) temporal sensing at the COM position $x_{\mathrm{c}}$. The respective solutions for the ANNs (gray and dark gray) found by NEAT are shown in D and E; details are in SI Appendix.

In order to obtain chemotaxis strategies using NEAT, the remaining task is to identify an (potentially recurrent) ANN structure for the CG block (Fig. 3A) (i.e., an ANN that is able to predict the sign $D$ of the CG). For this purpose, we have considered three different methods that allow the microswimmer to sense $\nabla c\left(x\right)$. First, we assume that the chemotaxis agent can directly measure the sign of the gradient at its COM position $x_{\mathrm{c}}\left(t\right)$; here, $D$ is automatically known. Second, we allow the swimmer to simultaneously evaluate the chemical fields $c_i\left(t\right)$ at the bead positions $x_i\left(t\right)$ to predict the sign of the gradient via $D=\text{sign}\left(G\right)$ from the output $G$ of the ANN (Fig. 3B), determined by NEAT during training (see below). Third, in an effort to model temporal sensing of CGs, which is relevant for bacterial chemotaxis, we consider recurrent ANNs (Fig. 3C). In this case, we explicitly provide the CG agent with inputs that describe the internal, physiological state (total arm length $L_{\mathrm{T}}$ and velocity $V_{\mathrm{T}}$), as well as with the chemical field at the COM position $c_c=c\left(x_c\right)$ at each instance of time $t_i$. To train the CG agent, we subdivide its task into a block, which estimates the gradient, and into another block that controls an internal memory of the chemical field (i.e., the chemical memory control [CMC] cell). The latter is inspired by the well-known long short-term memory cell (39, 40).

The first block is trained using the NEAT algorithm: It takes as input $L_{\mathrm{T}}\left(t_i\right)$ and $V_{\mathrm{T}}\left(t_i\right)$ as well as two recurrent variables $C_x\left(t_i\right)$ and $G_x\left(t_i\right)$ and maps this information onto a control output $C_y\left(t_i\right)$ and an estimated value of the instantaneous CG $G_y\left(t_i\right)$, both to be processed by the CMC cell in the next time step. The CMC cell temporally feeds back $G_y$ as input to the NEAT ANN as $G_x\left(t_i\right)=G_y\left(t_{i-1}\right)$. Furthermore, the CMC cell controls via the binary variable $\beta =\mathrm{\Theta }\left(C_y\left(t_{i-1}\right)\right)=\left\{\mathrm{0,1}\right\}$ [with $\mathrm{\Theta }\left(\cdot \right)$ the Heaviside function], the state of an internal memory $M\left(t_i\right)=\left(1-\beta \right)\hspace{0.17em}M\left(t_{i-1}\right)+\beta \hspace{0.17em}{c}_c\left(t_i\right)/c_0$, and the state of the NEAT ANN input $C_x\left(t_i\right)=\left(1-\beta \right)\hspace{0.17em}{C}_y\left(t_{i-1}\right)+\beta \hspace{0.17em}\left(c_c\left(t_i\right)/c_0-M\left(t_{i-1}\right)\right)$. In that way, the CG agent can actively control the time interval between successive measurements: An update of $M\left(t_i\right)$ is performed whenever $C_y\left(t_{i-1}\right)>0$; otherwise, $M\left(t_{i-1}\right)$ is maintained over time. Notably, the chemical field input of the CG agent is directly forwarded to the CMC cell, and the trained NEAT ANN operates on time-delayed gradients rather than directly on the values of the chemical field $c_c$. Whenever $C_y\left(t_{i-1}\right)>0$, the CMC cell explicitly provides temporal gradient information $\left(c_c\left(t_i\right)/c_0-M\left(t_{i-1}\right)\right)$ to the NEAT ANN via $C_x\left(t_i\right)$ and otherwise, feeds back $C_y\left(t_{i-1}\right)$. Eventually, the output of the temporal CG agent is $D=\text{sign}\left(G_y\right)$.

For spatial and temporal gradient sensing (Fig. 3 B and C), training is necessary. For simplicity, we train the swimmer on a piecewise linear field, $c\left(x\right)=max\left(0,a-k|x-x_0|\right)$, with amplitude $a$ and slope $k$ using the MC-SAL solution obtained in phase 1 (Movies S3 and S4 and SI Appendix, Supporting Information Text and Figs. S9 and S12 have details).

Both for spatial and temporal sensing methods, the resulting ANNs are strikingly simple, and their topology can be well interpreted: The NEAT ANN solution for spatial sensing, shown in Fig. 3D, only requires a single neuron, which predicts $D\left(t\right)\approx \text{sign}\left(c_3\left(t\right)-c_1\left(t\right)\right)$ (SI Appendix has details). During training of the temporal gradient sensing ANN, we determine the precise way that the output signals of the ANN $C_y\left(t_i\right)$ and $G_y\left(t_i\right)$ are used as recurrent input signals in the next time step and how $C_y\left(t_i\right)$ controls the way the chemical memory is updated. The solution for temporal sensing is shown in Fig. 3E. The NEAT-evolved ANN converts the recurrent inputs $G_x\left(t_i\right)$ and $C_x\left(t_i\right)$ through a series of operations processed by four hidden neurons (with intermediate outputs $y_I$, $y_P$, $y_R$) (SI Appendix) into a prediction of the spatial CG $G_y\left(t_i\right)$. Thus, the ANN output $G_y\left(t_i\right)$ is a highly nonlinear function of the input. In contrast, the trained ANN has learned to directly utilize the periodically changing total arm length $L_{\mathrm{T}}\left(t_i\right)$ as a pacemaker to trigger measurements of the chemical field: $C_y\left(t_{i-1}\right)>0$ whenever $L_{\mathrm{T}}\left(t_{i-1}\right)\gtrsim 2.23L_0$, inducing a chemical memory update in the CMC cell in the next time step. In this case, time-delayed CG information $C_x\left(t_i\right)=c_c\left(t_i\right)/c_0-M\left(t_{i-1}\right)$ is provided to the ANN; notably, these measurement requests are triggered only occasionally. Furthermore, the ANN has learned to exploit information of the total arm length through $C_x\left(t_i\right)=C_y\left(t_{i-1}\right)$ when no time-delayed gradient information is being used [$C_y\left(t_{i-1}\right)<0$]. In this way, the temporal gradient sensing ANN enables the CG agent to correlate its direction of propagation with the gradient of a chemical field. Numerical details on the weights and biases and further interpretation of the ANN solution depicted in Fig. 3E are provided in SI Appendix.

In Fig. 2 B and C, we present typical trajectories after successful training obtained for chemical fields of piecewise linear shape and of Gaussian shape, respectively. In both cases, the swimmer—controlled by spatial sensing—suddenly stops as soon as its COM position $x_{\mathrm{c}}$ is reasonably close to the maximum $x_0$ of the chemical field (Movie S7). In contrast, the swimmer controlled by temporal sensing performs oscillations around $x_0$ due to its time-delayed measurements of the chemical field and its internal, recurrent processes (Fig. 3C and Movies S5 and S6).

We observe that the ANNs of both spatial and temporal sensing methods are able to generalize their capability to predict the CG over a much wider range of parameters (i.e., amplitude $a$ and slope $k$ of a chemical field) than they were originally trained on (Fig. 2 and SI Appendix, Supporting Information Text and Figs. S9 and S14).

Emergent Run-Reverse Motion from Noisy Memory Readings.

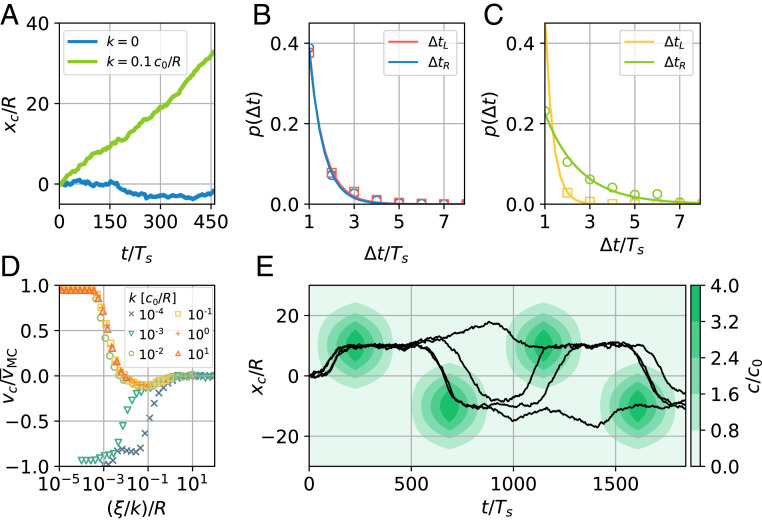
Realistic chemotactic pathways are always influenced by thermal noise. In our implementation, we apply stochastic memory readings of the CMC cell for the temporally sensing swimmer, mimicking the fact that the chemotactic signal cannot be detected perfectly. In this spirit, the swimmer measures a field, $M\left(t\right)=\left(c_c\left(t\right)+\delta c\right)/c_0$, $\delta c$ being a normal distributed random number with zero mean and SD $\xi$, which sets the strength of the noise. We apply this feature to an ensemble of 100 noninteracting microswimmers moving in a constant CG $c\left(x\right)=kx$ but that have learned chemotaxis in the absence of noise in phase 2. Strikingly, a one-dimensional run-and-tumble (run-and-reverse) motion emerges naturally, even in the absence of a chemical field ($k=0$). In Fig. 4A, we present typical trajectories both in the absence and in the presence ($k=0.1c_0/R$) of a chemical field (Movie S8). These trajectories consist of segments of rightward motion (over run times $\mathrm{\Delta }{t}_{\mathrm{R}}$), alternating with segments of leftward motion ($\mathrm{\Delta }{t}_{\mathrm{L}}$). The stochastic nature of the underlying process leads to approximately exponentially distributed run times, $\sim e^{-\mathrm{\Delta }{t}_R/{\tau }_R}$ and $\sim e^{-\mathrm{\Delta }{t}_L/{\tau }_L}$, following thus a similar behavior as the one measured for microorganisms (5, 7, 41). As expected, in the absence of a field, ${\tau }_R\approx {\tau }_L$ (Fig. 4B). In the presence of a field, the swimmer exhibits a tendency for longer run times, moving the gradient upward (${\tau }_R>{\tau }_L$) (Fig. 4C).

Fig. 4.

Stochastic microswimmer dynamics from noisy memory readings for noise level $\xi =2\cdot 10^{-4}{c}_0$. (A) Sample trajectories in the absence (blue) and in the presence (green) of a linear chemical field. (B and C) Run time distributions for moving the field upward ($\mathrm{\Delta }{t}_R$) and downward ($\mathrm{\Delta }{t}_L$) in the absence (B) and in the presence (C) of a field. Note that the run time axis starts at the minimal possible run time $\mathrm{\Delta }t/T_0=1$ because of the used discretization. (D) Chemotactic drift velocity $v_c$ as a function of noise-to-signal ratio $\xi /\left(kR\right)$ for different values of gradient steepness $k$. Each data point corresponds to a simulation time of $10^6{T}_0$. (E) Sample trajectories in time-dependent Gaussian profiles $c\left(x,t\right)$ (see color bar) centered at $x_{0\pm }=\pm 10R$ of width $\sigma =8R$ and height $a=4c_0$ and modulated with period $T=461T_{\mathrm{S}}$.

In general, the chemotactic performance, quantified by the mean net chemotactic drift velocity $v_{\mathrm{c}}$ (i.e., mean swimmer velocity), depends on the gradient steepness $k$ and is strongly influenced by the noise level $\xi$ as shown in Fig. 4D: As expected, for very small noise the motion is almost ballistic, $v_{\mathrm{c}}\to {\overline{v}}_{MC}$, while biased run-and-reverse motion ($0<v_{\mathrm{c}}<{\overline{v}}_{MC}$) emerges for larger noise. Interestingly, for different values of $k$, this can be quantified by the noise-to-signal ratio $\xi /\left(kR\right)$, leading to a universal chemotactic behavior for a large range of $k$ values (SI Appendix, Fig. S21). Note that there exists a noise-to-signal regime where the chemotactic velocity becomes negative due to the small bias of the microswimmer obtained during training (SI Appendix).

Run-and-reverse behavior depends on the values of the chemical field $c_c\left(t_j\right)$ and of the internal memory $M\left(t_i\right)$ at two distinct points in time $t_i<t_j$ the microswimmer chooses to perform successive measurements. If the noise $\delta c$ dominates in the swimmer’s input $C_x\left(t_j\right)=\left(c_c\left(t_j\right)-c_c\left(t_i\right)+\delta c\right)/c_0$, the swimmer is unable to correctly determine the time-delayed CG and moves erratically. This happens either if measurements are performed too frequently or if the noise-to-signal ratio is above a critical value of $\xi /\left(kR\right)\gtrsim 10^{-2}$ (Fig. 4D). A detailed account of how and when our solution performs a measurement of the chemical field is in SI Appendix, Figs. S18 and S19.

Chemotaxis in Time-Dependent Chemical Fields.

Eventually, we study the dynamics of temporal gradient sensing microswimmers, which perform noisy memory readings in a more complicated, time-dependent chemical environment. Notably, the microswimmers have solely been trained in a constant CG as described in phase 2. We now use time-dependent chemical fields of the form $c\left(x,t\right)=h_{+}\left(t\right)c_{+}\left(x\right)+h_{-}\left(t\right)c_{-}\left(x\right)$ where $c_{\pm }\left(x\right)$ are of Gaussian shape with maximum height $a$ and centered at peak positions $x_{0\pm }$. The peak amplitudes are modulated via $h_{\pm }\left(t\right)={\sum }_{i=0}\mathrm{m}\mathrm{a}\mathrm{x}\left[\left(1-|4\left(i-t/T\right)\pm 1|\right),0\right]$ with period $T$; in the contour plot in Fig. 4E, we also show typical microswimmer trajectories. Swimmers may explore consecutive peaks by hopping between chemical sources of $c_{+}$ and $c_{-}$ or may miss peaks by residing in the vicinity of the previously visited chemical source. Thus, the actual swimming paths strongly depend on prior decisions of the chemotaxis agent. In field-free regions, microswimmers perform approximately unbiased run-and-reverse strategies, and they use positive chemotaxis in regions featuring CGs. Hence, the combination of chemotactic response and noise enables useful foraging strategies in time-dependent fields.

Discussion

We modeled the response of a simple microswimmer to a viscous and chemical environment using the NEAT genetic algorithm to construct ANNs that describe the internal decision-making machinery coupled to the motion of two arms. First, our model microswimmer learned to swim in the absence of a chemical field in a “1 step back, 2 steps forward” motion as it appears, for example, for the swimming pattern of the algae Chlamydomonas.

In contrast to a recently used Q-learning approach, which uses a very limited action space (29), we allow continuous changes of the microswimmer’s shape and thus, permit high flexibility in exploring many different swimming gaits during training. This feature allowed us to find optimum swimming policies where the forces on the beads are limited, in contrast to fixing arm velocities (SI Appendix). Furthermore, the NEAT algorithm has created surprisingly simple ANNs, which we were able to fully understand and interpret, in contrast to often used complex deep neural networks (42–45) or the lookup–table-like Q-learning algorithm (45).

We used biologically relevant chemotactic sensing strategies, namely spatial gradient sensing usually performed by slow-moving eukaryotic cells and temporal gradient sensing performed by fast swimming bacteria. We used the latter to explore the influence of a single noisy channel, namely for the reading of the value of the chemical concentration, on the chemotactic response. Interestingly, we identified for different values of gradient steepness a broad range of noise levels that give rise to biased run-and-reverse dynamics with exponentially distributed run times. The run times can be scaled onto a master curve using the noise-to-signal ratio of the chemical field measurement. However, this behavior depends on the specific network solution obtained during training in phase 2 (SI Appendix, Fig. S21). Indeed, for real existing signal sensing mechanisms in microorganisms, the role of the noise and the precision of signal detection are an active field of research (e.g., refs. 46 and 47).

The run-and-reverse behavior in our system is an emergent feature, which sustains in the absence of a chemical field (as observed, for example, for swimming bacteria) without explicitly challenging the microswimmer to exploit search strategies in the absence of a field during training. From an evolutionary point of view, it makes sense that bacteria have learned this behavior in complex chemical environments. We also find that individual microswimmers performing run-and-reverse motion may show a small bias to the left or to the right even in the absence of a field due to the stochastic nature of the genetic optimization (SI Appendix, Figs. S14 and S21).

The question of how single cells make decisions that affect their motion in their environment is an active field of research (48–51). For example, bacteria, protists, plants, and fungi make decisions without using neurons but rather, use a complex chemotactic signaling network (52). On the other hand, small multicellular organisms such as the worm C. elegans use only a small number of neurons in order to move and perform chemotaxis (53, 54). Our approach therefore offers tools in order to investigate possible architectures, functionalities, and the necessary level of complexity of sensing and motor neurons coupled to muscle movement in silico by evolutionary developed ANNs. In the future, our work can be extended to more specific microswimmers moving in two or three dimensions, in order to extract the necessary complexity of the decision-making machinery used for chemotaxis, mechanosensing, or even more complex behavioral responses such as reproduction.

Materials and Methods

ANNs.

An ANN is a set of interconnected artificial neurons that collect weighted signals (either from external sources or from other neurons) and create and redistribute output signals generated by a nonlinear activation function (55) (SI Appendix has details). In that way, an ANN can process information in an efficient and flexible way: By adjusting the weights and biases of connections between different neurons or by adjusting the network topology, ANNs can be trained to map network input to output signals, thereby realizing task-specific operations, which are often too complicated to be implemented manually (56).

NEAT Algorithm.

NEAT (57) is a genetic algorithm designed for constructing neural networks. In contrast to most learning algorithms, it not only optimizes the weights of an ANN (in an effort to optimize a so-called target function) but moreover, generates the weights and the topology of the ANN simultaneously (SI Appendix has details). This process is guided by the principle of complexification (57): Starting from a minimal design of the ANN, the algorithm will gradually add or remove nodes and connecting neurons with certain probabilities according the evolutionary process (schematically depicted by the gray dashed lines in Fig. 1 Lower Left) in order to keep the resulting network as simple and sparse as possible. The resulting ANN solutions can then be used to perform their target task, even for situations that the ANNs never explicitly experienced during training.

Data Availability

Computational protocols and numerical data that support the findings of this study are shown in this article and supporting information.