Abstract
Motivation
Biological and cellular systems are often modeled as graphs in which vertices represent objects of interest (genes, proteins and drugs) and edges represent relational ties between these objects (binds-to, interacts-with and regulates). This approach has been highly successful owing to the theory, methodology and software that support analysis and learning on graphs. Graphs, however, suffer from information loss when modeling physical systems due to their inability to accurately represent multiobject relationships. Hypergraphs, a generalization of graphs, provide a framework to mitigate information loss and unify disparate graph-based methodologies.
Results
We present a hypergraph-based approach for modeling biological systems and formulate vertex classification, edge classification and link prediction problems on (hyper)graphs as instances of vertex classification on (extended, dual) hypergraphs. We then introduce a novel kernel method on vertex- and edge-labeled (colored) hypergraphs for analysis and learning. The method is based on exact and inexact (via hypergraph edit distances) enumeration of hypergraphlets; i.e. small hypergraphs rooted at a vertex of interest. We empirically evaluate this method on fifteen biological networks and show its potential use in a positive-unlabeled setting to estimate the interactome sizes in various species.
Availability and implementation
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
Graphs provide a mathematical structure for describing relationships between objects in a system. Due to their intuitive representation, well-understood theoretical properties, the wealth of methodology and available code base, graphs have also become a major framework for modeling biological systems. Protein–protein interaction networks, protein 3D structure graphs, drug–target interaction networks, metabolic networks and gene regulatory networks are some of the major representations of biological systems. Unfortunately, molecular and cellular systems are only partially observable and may contain significant amount of noise due to their inherent stochastic nature as well as the limitations of experimental techniques. This highlights the need for the development and application of computational approaches for predictive modeling (e.g. inferring novel interactions) and identifying interesting patterns in such data.
Learning on graphs can be generally seen as supervised or unsupervised. Under a supervised setting, typical tasks involve graph classification; i.e. the assignment of class labels to entire graphs, vertex or edge classification; i.e. the assignment of class labels to vertices or edges, or link prediction; i.e. the prediction of the existence of edges in graphs. Alternatively, frequent subgraph mining, motif finding and clustering are traditional unsupervised approaches. Regardless of the category, the development of techniques that capture network structure, measure graph similarity and incorporate domain-specific knowledge in a principled manner lie at the core of all these problems.
The focus of this study is on classification problems across various biological networks. A straightforward approach to this problem is the use of topological and other descriptors (e.g. vertex degree, clustering coefficient and betweenness centrality) that summarize graphs and graph neighborhoods. These descriptors, much like embedding techniques (Grover and Leskovec, 2016; Goyal and Ferrara, 2018), readily form vector-space representations, after which standard machine learning algorithms can be applied to learn target functions (Xu and Li, 2006). Another strategy involves the use of kernel functions on graphs (Vishwanathan et al., 2010). Kernels are symmetric positive semidefinite mappings of pairs of objects from an input space to , that lead to efficient learning. Finally, classification on graphs can be seen as inference over Markov networks (Deng et al., 2003) and can be approached using related label-propagation (Zhu and Ghahramani, 2002) or flow-based (Nabieva et al., 2005) methods. These inference strategies are often well adjusted to learning smooth functions over neighboring nodes.
Despite the success and wide adoption of these methods in computational biology, it is well-understood that graph representations suffer from information loss since every edge can only encode pairwise relationships (Klamt et al., 2009). A protein complex, for instance, cannot be distinguished from a set of proteins that interact only pairwise. Such disambiguation, however, is important to understand the biological activity of these molecules (Gaudelet et al., 2018). Hypergraphs, a generalization of graphs, naturally capture these higher-order relationships (Berge, 1973). As we show later, they also provide a representation that can be used to unify several conventional classification problems on (hyper)graphs as an instance of vertex classification on hypergraphs.
In this article, we present and evaluate a kernel-based framework for the problems of vertex classification, edge classification and link prediction in graphs and hypergraphs. We first use the concepts of hypergraph duality to demonstrate that all such classification problems can be unified through the use of hypergraphs. We then describe the development of edit-distance hypergraphlet kernels; i.e. similarity functions between local vertex neighborhoods based on flexibly enumerating small labeled hypergraphs rooted at vertices of interest. These similarity functions were subsequently incorporated into a semisupervised methodology for predicting class labels on vertices. Finally, we use 15 biological networks to provide evidence that the proposed approaches present an attractive option in this setting.
2 Background
2.1 Graphs and hypergraphs
Graphs. A graph G is a pair (V, E), where V is a set of vertices (nodes) and is a set of edges. In a vertex-labeled graph, a labeling function f is defined as , where Σ is a finite alphabet. Similarly, in an edge-labeled graph, another labeling function g is given as , where Ξ is also a finite set. We will focus on undirected graphs (E is symmetric), without self-loops and weights associated with edges. Generalization of our approach to directed and weighted graphs is relatively straightforward.
A rooted graph G is a graph together with one distinguished vertex called the root. We denote such graphs as , where is the root. A walk w of length k in a graph G is a sequence of nodes such that , for . A connected graph is a graph where there exists a walk between any two nodes.
Hypergraphs. A hypergraph G is a pair (V, E), where V again is the vertex set and E is a family of non-empty subsets of V, referred to as hyperedges. A hyperedge e is said to be incident with a vertex v if . Two vertices are called adjacent if there is an edge that contains both vertices and two hyperedges are said to be adjacent if their intersection is non-empty. The neighbors of a vertex v in a hypergraph are the vertices adjacent to v. Finally, the degree d(v) of a vertex v in a hypergraph is given by , whereas the degree of a hyperedge e is defined as .
As before, one can define a vertex-labeled, edge-labeled and rooted hypergraphs. When the multiplicity of each hyperedge is one, the hypergraph is said to be simple. A walk w of length k in a hypergraph is a sequence of vertices and hyperedges such that for each and . A connected hypergraph is a hypergraph where there exists a walk between any two nodes.
Since we are interested in counting small predefined hypergraphs in large hypergraphs, we define two distinct ways in which these substructures can be counted, as section hypergraphs or subhypergraphs. Given a hypergraph , a section hypergraph of G is a hypergraph where and . A subhypergraph of G is a hypergraph where and . In other words, when nodes are removed from V, section hypergraphs retain only those edges that were subsets of the remaining nodes . In subhypergraphs, on the other hand, the edges that originally contained nodes from both removed () and unremoved () nodes are retained as subsets of the original edges that now include nodes only from . Edges from the original graph that only included nodes from can now have increased multiplicity.
Isomorphism. Consider two graphs, and . We say that G and H are isomorphic, denoted as , if there exists a bijection such that if and only if for all . If G and H are hypergraphs, an isomorphism is defined as inter-related bijections and such that if and only if for all hyperedges . Isomorphic (hyper)graphs are structurally identical. An automorphism is an isomorphism of a (hyper)graph to itself.
Edit distance. Let G and H be two vertex- and hyperedge-labeled hypergraphs. The edit distance between these hypergraphs corresponds to the minimum number of edit operations necessary to transform G into H, where edit operations are often defined as insertion/deletion of vertices/hyperedges and substitutions of vertex and hyperedge labels. Any sequence of edit operations that transforms G into H is called an edit path; hence, the hypergraph edit distance between G and H is the length of the shortest edit path between them. This concept can be generalized to the case where each edit operation is assigned a cost. Hypergraph edit distance then corresponds to the edit path of minimum cost.
2.2 Hypergraph duality
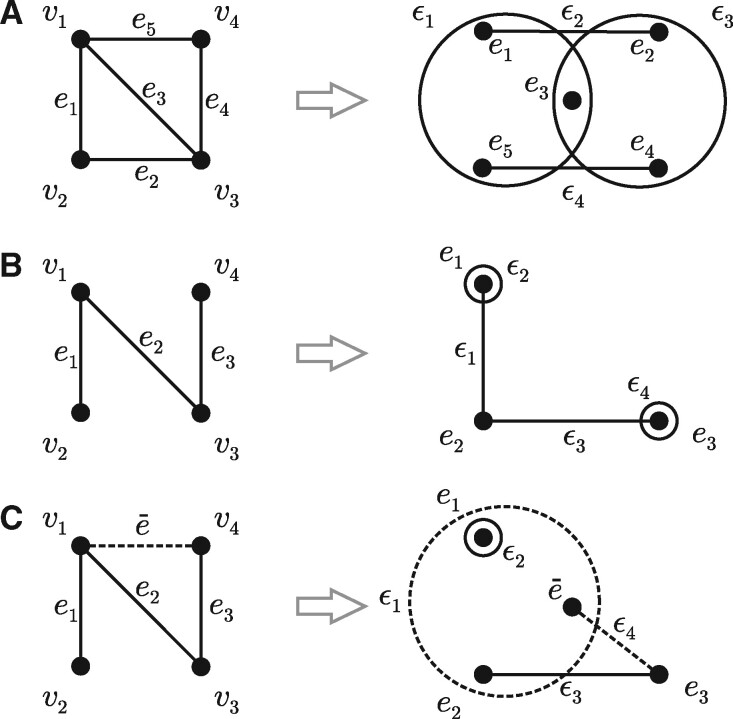
Let be a hypergraph, where and . The dual hypergraph of G, denoted as , is obtained by constructing the set of vertices as and the set of hyperedges as such that . Thus, the vertices of the dual hypergraph are hyperedges of the original hypergraph G, whereas the hyperedges of are constructed using the hyperedges of G that are incident with the respective vertices. Figure 1A, B shows two examples of a hypergraph G and its dual hypergraph .
Fig. 1.
Examples of hypergraph duality. (A) A hypergraph , where and with its dual hypergraph , where and such that and . (B) An example of graph G with two degree-one vertices that lead to the dual hypergraph with self-loops; ϵ2 and ϵ4. (C) An extended dual hypergraph that is proposed to formulate link prediction as an instance of vertex classification in hypergraphs. To make a prediction regarding the existence of edge , shown as a dashed line on the left side, an extended dual hypergraph is created in which is added to the set of vertices . Updates are made to hyperedges ϵ1 and ϵ4 (dashed) that correspond to those vertices in G that are incident with the edge
2.3 Classification on hypergraphs
We are interested in binary classification on (possibly disconnected) hypergraphs. The following paragraphs briefly introduce three classification problems on hypergraphs, formulated here so as to naturally lead to the methodology proposed in the next section.
Vertex classification. Given a hypergraph and a training set , where is the class label of vertex vi and , the goal is to predict class labels of unlabeled vertices. A number of classical problems in computational biology map straightforwardly to vertex classification; e.g. network-based protein function prediction, disease gene prioritization, etc.
Hyperedge classification. Given a hypergraph and a training set , where is the class label of hyperedge ei and , the goal is to predict class labels of unlabeled hyperedges. An example of hyperedge classification is the prediction of functional annotations for protein complexes.
Link prediction. Let be a hypergraph with some missing hyperedges and let be all non-existent hyperedges in G; i.e. , where represents all possible hyperedges over V. The goal is to learn a target function and infer the existence of all missing hyperedges. Examples of link prediction include predicting protein–protein interactions, predicting drug–target interactions and so on.
2.4 Positive-unlabeled learning
A number of prediction problems in computational biology can be considered within a semisupervised framework, where a set of labeled and a set of unlabeled examples are used to construct classifiers that discriminate between positive and negative examples. A special category of semisupervised learning occurs when labeled data contain only positive examples; i.e. where the negative examples are either unavailable or ignored; say, if the set of available negatives is small or biased. Such problems are generally referred to as learning from positive and unlabeled data or positive-unlabeled learning (Denis et al., 2005). Many problems in molecular biology that are often referred to as the open world problems lend themselves naturally to the positive-unlabeled setting.
Research in machine learning has recently established tight connections between traditional supervised learning and (non-traditional) positive-unlabeled learning. Under mild conditions, a classifier that optimizes the ranking performance; e.g. area under the ROC curve (Fawcett, 2006), in the non-traditional setting has been shown to also optimize the performance in the traditional setting (Reid and Williamson, 2010). Similar relationships have been established in approximating posterior distributions (Jain et al., 2016a,b) as well as in recovering the true performance accuracy in the traditional setting for a classifier evaluated in a non-traditional setting (Jain et al., 2017; Menon et al., 2015; Ramola et al., 2019).
3 Materials and methods
3.1 Problem formulation
We consider binary classification problems on graphs and hypergraphs and propose to unify all such learning problems through semisupervised vertex classification on hypergraphs. First, vertex classification falls trivially into this framework. Second, the problems of edge classification in graphs and hyperedge classification in hypergraphs are equivalent to the problem of vertex classification on dual hypergraphs. As discussed in Section 2.2, both graphs and hypergraphs give rise to dual hypergraph representations and, thus, (hyper)edge classification on a graph G straightforwardly translates into vertex classification on its dual hypergraph . We note here that vertices with the degree of one in G give rise to self-loops in the dual hypergraph . To account for them, we add one dummy node per self-loop with the same vertex label as the original vertex and connect them with an appropriately labeled edge. Third, one can similarly see link prediction as vertex classification on dual hypergraphs, where the set of existing links is treated as positive data, the set of known non-existing links is treated as negative data and the remaining set of missing links is treated as unlabeled data. This formulation further requires an extension of dual hypergraph representations as follows. Consider a particular negative or missing link in the original graph G with its dual hypergraph (Fig. 1C). To make a prediction on this edge , we must first introduce a new vertex in the dual hypergraph as well as modify those hyperedges in that correspond to the vertices in G (Fig. 1C). We denote this extended hypergraph as . It now easily follows that the sets of negative and unlabeled examples can be created by considering a collection of extended graphs , one at a time, for select vertices .
Since most biological networks lack large sets of representative negative examples, we approach vertex classification, (hyper)edge classification and link prediction as instances of vertex classification on (extended, dual) hypergraphs in a positive-unlabeled setting. We believe this is a novel and useful attempt at generalizing three distinct graph classification problems in a common semisupervised setting. The following sections introduce hypergraphlet kernels that are the next step of our classification approach.
3.2 Hypergraphlets
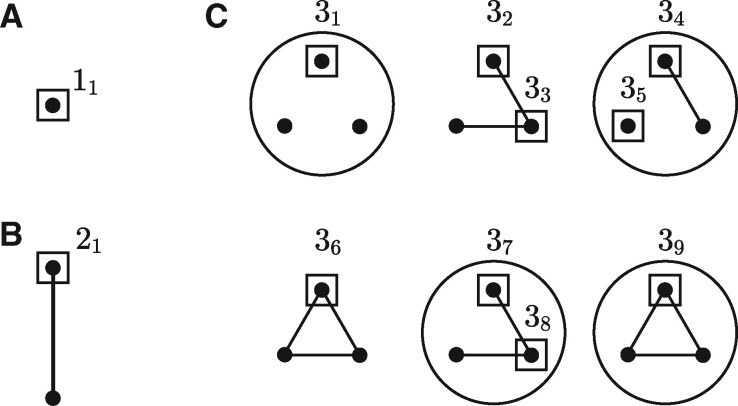
Inspired by graphlets (Przulj et al., 2004; Przulj, 2007), we define a hypergraphlet as a small, simple, connected, rooted hypergraph, without self-loops, where the root of the hypergraph is its automorphism orbit (Gaudelet et al., 2018). A hypergraphlet with n vertices is called an n-hypergraphlet; and the ith hypergraphlet of order n is denoted as ni. We consider hypergraphlets up to isomorphism and will refer to these isomorphisms as root- and label-preserving isomorphisms when hypergraphs are rooted and labeled. Figure 2 displays all non-isomorphic unlabeled n-hypergraphlets with up to three vertices. There is only one hypergraphlet of order 1 (11; Fig. 2A), one hypergraphlet of order 2 (21; Fig. 2B), nine hypergraphlets of order 3 (; Fig. 2C) and 461 hypergraphlets of order 4 (Supplementary Materials). We refer to all these hypergraphlets as base hypergraphlets since they correspond to the case when .
Fig. 2.
Undirected base hypergraphlets with 1, 2 and 3 vertices. The root node of each hypergraphlet is inscribed in a square. Hypergraphlets are presented in a compressed notation; e.g. structures 32 and 33 are shown in one drawing
Consider now a vertex- and hyperedge-labeled (or fully labeled for short) hypergraphlet with n vertices and m hyperedges, where Σ and Ξ denote the vertex-label and hyperedge-label alphabets, respectively. If and/or , automorphic structures corresponding to the same base hypergraphlet may exist; hence, the number of fully labeled hypergraphlets per base structure is generally smaller than . For example, if one only considers vertex-labeled 3-hypergraphlets, then there are vertex-labeled hypergraphlets corresponding to the asymmetric base hypergraphlets 32, 34 and 37 but only corresponding to the base hypergraphlets 31, 33, 35, 36, 38 and 39. This is a result of symmetries in the base hypergraphlets that give rise to automorphisms among vertex-labeled structures. Similarly, if , new symmetries may form with respect to the base hypergraphlets that give rise to different automorphisms among hyperedge-labeled structures.
These symmetries are important for counting vertex- and hyperedge-labeled hypergraphlets within larger graphs. The enumeration steps described above also determine the dimensionality of the Hilbert space in which the prediction is carried out. Detailed results on hypergraph enumeration are given in Supplementary Materials.
3.3 Hypergraphlet kernels
Motivated by the case for graphs (Lugo-Martinez and Radivojac, 2014; Shervashidze et al., 2009; Vacic et al., 2010), we introduce hypergraphlet kernels. Let be a fully labeled hypergraph where f is a vertex-labeling function , g is a hyperedge-labeling function and . The vertex- and hyperedge-labeled n-hypergraphlet count vector for any is defined as
| (1) |
where is the count of the ith fully labeled n-hypergraphlet rooted at v and is the total number of vertex- and hyperedge-labeled n-hypergraphlets. Observe that, must be defined over a section hypergraph or subhypergraph of G which will lead to distinct vectors of counts . A kernel between the n-hypergraphlet counts for vertices u and v is defined as an inner product between and ; i.e.
| (2) |
The hypergraphlet kernel function incorporating all hypergraphlets up to the size N is given by
| (3) |
where N is a small integer. In this work, we use N = 4 due to the exponential growth of the number of base hypergraphlets.
3.4 Edit-distance hypergraphlet kernels
Consider a fully labeled hypergraph . Given a vertex , we define the vector of counts for a τ-generalized edit-distance hypergraphlet representation as
| (4) |
where
| (5) |
Here, is the set of all n-hypergraphlets such that for each there exists an edit path of total cost at most τ that transforms ni into nj and is a user-defined parameter. In other words, the counts for each hypergraphlet ni are updated by also counting all other hypergraphlets nj that are in the τ vicinity of ni. The parameter c can be used to adjust the weights of these pseudocounts or learned from data to add sophistication. We set for all i and j and the cost of all edit operations was also set to 1. This restricts τ to non-negative integers.
The length-τ edit-distance n-hypergraphlet kernel between vertices u and v can be computed as an inner product between the respective count vectors and ; i.e.
| (6) |
The length-τ edit-distance hypergraphlet kernel function is given as
| (7) |
The edit operations considered here incorporate substitutions of vertex labels, substitutions of hyperedge labels and insertions/deletions (indels) of hyperedges (see example in Supplementary Fig. S1). Given these edit operations, we also define three subclasses of edit-distance hypergraphlet kernels referred to as vertex label-substitution , hyperedge label-substitution and hyperedge-indel kernels . Although the functions from Equations (2) and (6) are defined as inner products, other formulations such as radial basis functions can be similarly considered (Shawe-Taylor and Cristianini, 2001). We also note that the combined kernels from Equations (3) and (7) can be generalized beyond linear combinations. For the simplicity of this work, however, we only explore equal-weight linear combinations and normalize the functions from Equations (3) and (7) using the cosine transformation. Computational complexity and implementation details are described in Supplementary Materials.
4 Experiment design
4.1 Datasets
Protein–protein interaction data. The protein–protein interaction (PPI) data were used for both edge classification and link prediction. In the context of edge classification, we are given a PPI network where each interaction is annotated as either direct physical interaction or a comembership in a complex. The objective is to predict the type of each interacting protein pair as physical versus complex (PC). For this task, we used the budding yeast Saccharomyces cerevisiae PPI network assembled by Ben-Hur and Noble (2005).
Another important task in PPI networks is discovering whether two proteins interact. Despite the existence of high-throughput experimental methods for determining interactions between proteins, the PPI network data of all organisms is incomplete (Lewis et al., 2012). Furthermore, high-throughput PPI data contains a potentially large fraction of false-positive interactions (von Mering et al., 2002). Therefore, there is a continued need for computational methods to help guide experiments for identifying novel interactions. Under this scenario, there are two classes of link prediction algorithms: (i) prediction of direct physical interactions (Ben-Hur and Noble, 2005; Gomez et al., 2003) and (ii) prediction of comembership in a protein complex (Ma et al., 2017; Zhang et al., 2004). We focused on the former task and assembled six species-specific datasets comprised solely of direct protein–protein interaction data derived from public databases (BIND, BioGRID, DIP, HPRD and IntAct) as of January 2017. We considered only one protein isoform per gene and used experimental evidence types described by Lewis et al. (2012). Specifically, we constructed link prediction tasks for: (i) Escherichia coli (EC), (ii) Schizosaccharomyces pombe (SP), (iii) Rattus norvegicus (RN), (iv) Mus musculus (MM), (v) Caenorhabditis elegans (CE) and (vi) Arabidopsis thaliana (AT).
Drug–target interaction data. Identification of interactions between drugs and target proteins is an area of growing interest in drug design and therapy (Wang and Zeng, 2013; Yamanishi et al., 2008). In a drug–target interaction (DTI) network, nodes correspond to either drugs or proteins and edges indicate that a protein is a known target of the drug. Here, we used DTI data for both edge classification and link prediction. In the context of edge labeling, we are given a DTI network where each interaction is annotated as direct (binding) or indirect, as well as assigned modes of action as activating or inhibiting. The objective is to predict the type of each interaction between proteins and drug compounds. For this task, we derived two datasets: (i) indirect versus direct (ID) binding derived from MATADOR and (ii) activation versus inhibition (AI) assembled from STITCH. Under link prediction setting, the learning task is to predict drug–target protein interactions. We focused on four drug–target classes: (i) enzymes (EZ), (ii) ion channels (IC), (iii) G protein-coupled receptors (GR) and (iv) nuclear receptors (NR); originally assembled by Yamanishi et al. (2008).
Hyperedge classification data. Hypergraphs provide a natural way to encode protein complexes. Here, we used Corum 3.0 (Giurgiu et al., 2019) which provides manually annotated protein complexes from mammalian organisms. Under this setting, the learning objective is to predict the functional annotation of each protein complex. For this task, we defined two datasets: (i) protein binding versus cell cycle (BC) and (ii) protein modification versus DNA processing (MP). Table 1 summarizes all datasets used in this work.
Table 1.
Summary of binary classification tasks and datasets
| Type | Dataset | ||||
|---|---|---|---|---|---|
| Edge classification | |||||
| PPI | PC | 4761 | 22 988 | 10 517 | 12 471 |
| DTI | ID | 544 drugs | 10 436 | 4284 | 6152 |
| 2261 targets | |||||
| AI | 378 drugs | 1039 | 249 | 790 | |
| 267 targets | |||||
| Hyperedge classification | |||||
| PPI | BC | 3436 | 2357 | 145 | 161 |
| MP | 3436 | 2357 | 175 | 200 | |
| Link prediction | |||||
| |Elcc|a | |||||
| PPI | EC | 393 | 391 | 100 | 153 |
| CE | 3026 | 5163 | 2779 | 5014 | |
| AT | 5391 | 12 825 | 5063 | 12 631 | |
| SP | 853 | 1197 | 685 | 1092 | |
| RN | 526 | 532 | 301 | 388 | |
| MM | 2065 | 2833 | 1590 | 2522 | |
| DTI | EZ | 445 drugs | 2926 | 809 | 2556 |
| 664 targets | |||||
| IC | 210 drugs | 1476 | 409 | 1473 | |
| 204 targets | |||||
| GR | 223 drugs | 635 | 240 | 570 | |
| 95 targets | |||||
| NR | 54 drugs | 90 | 42 | 50 | |
| 26 targets | |||||
Note: For each learning problem, we show the number of vertices (V) and edges (E) in the full hypergraph, as well as the largest connected component (). We also show the number of positive (), negative () or unlabeled (nu) data points.
The size of and nu is given by .
4.2 Integrating domain knowledge via a vertex alphabet
To incorporate domain knowledge into the PPI networks, we exploited the fact that each vertex (protein) in the graph is associated with its amino acid sequence. In particular, we used protein sequences to predict their Gene Ontology (GO) terms using the FANN-GO algorithm (Clark and Radivojac, 2011). Hierarchical clustering was subsequently used on the predicted term scores to group proteins into broad functional categories. In the case of DTI data, target proteins were annotated in a similar manner. For labeling drug compounds, we used the chemical structure similarity matrix computed from SIMCOMP (Hattori et al., 2003), transformed it into a dissimilarity matrix and then applied hierarchical clustering to group compounds into structural categories.
4.3 Evaluation methodology
We evaluated all hypergraphlet kernels by comparing them to two in-house implementations of random-walk-with-restarts kernels. Given a hypergraph G and two vertices u and v, simultaneous random walks wu and wv were generated from u and v for a fixed number of times (). In each step during a walk, one must pick hyperedges and incident with current vertices and , respectively, and then pick next vertices and . After a transition is made to the next pair of nodes and , the walk is terminated with some probability , or continued. In the conventional random walk implementation, a walk is scored as 1 if the sequences of all vertex and hyperedge labels between wu and wv are identical; otherwise, a walk is scored as 0. After = 10 000 walks are completed, the scores over all walks are summed to produce a kernel value between the starting vertices u and v. To construct a random walk similar to the hypergraphlet edit-distance approach, a cumulative random walk kernel was also implemented. Here, any match between the labels of vertices and , or hyperedges and of each walk is scored as 1, while a mismatch is scored as 0. Thus, a walk of length can contribute between 0 and to the total count. In each of the random walks, the probability of restart P was selected from a set . On the link prediction datasets, we also evaluated the performance of the preferential attachment method (Barabási et al., 2002) and the L3 framework (Kovács et al., 2019). Furthermore, we evaluated pairwise spectrum kernels (Ben-Hur and Noble, 2005) on the PPI datasets (excluding the protein complex data). The k-mer size for pairwise spectrum kernels was varied from . Finally, in the case of the edit-distance kernels, we computed the set of normalized hypergraphlet kernel matrices using and for all pairs (xi, xj) obtained from a grid search over and .
The performance of each method was evaluated through a 10-fold cross-validation. In each iteration, 10% of nodes in the dual network were selected for the test set, whereas the remaining 90% were used for training. When evaluating link prediction methods, the negative examples were sampled with probabilities proportional to the product of degrees of the two nodes. Support vector machine (SVM) classifiers were used to construct all predictors and perform comparative evaluation. We used SVMlight with the default value for the capacity parameter (Joachims, 2002). Once each predictor was trained, we used Platt’s correction to adjust the outputs of the predictor to the 0–1 range (Platt, 2000). Finally, we estimated the area under the ROC curve (AUC), which plots the true positive rate (sensitivity, sn) as a function of false-positive rate (1—specificity, ). Area under the ROC curve is an easily interpretable quantity that has advantages over precision-recall curves in the positive-unlabeled setting because the class priors are difficult to estimate (Jain et al., 2017; Ramola et al., 2019).
5 Results
5.1 Performance on edge and hyperedge classification
We first evaluated the performance of hypergraphlet kernels in the task of predicting the types of interactions between pairs of proteins in a PPI network, as well as interaction types and modes of action between proteins and chemicals in DTI data. As described in Section 3.1, we first converted each input hypergraph to its dual hypergraph and then used the dual hypergraph for vertex classification. Table 2 lists AUC estimates for each method and each dataset. Figure 3 shows ROC curves for one representative dataset from each classification task and network type. Observe that hypergraphlet kernels achieved the highest AUCs on the three datasets, thus, outperforming all other methods. Therefore, these results provide evidence of the feasibility of this alternative approach to edge classification via exploiting hypergraph duality. Next, we evaluated the performance of the hypergraphlet kernels for predicting functional annotation of protein complexes in Corum. As shown in Table 2, traditional hypergraphlet kernel (τ = 0) also performed favorably over the edit-distance kernels. In general, hypergraphlet kernels achieved the highest AUCs on both hyperedge classificatiton datasets over random walk kernels.
Table 2.
Area under the ROC curve estimates for PPI/DTI datasets using 10-fold cross-validation
| Method/dataset | (Hyper)edge classification |
Link prediction |
|||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PC | ID | AI | BC | MP | EC | SP | RN | MM | CE | AT | EZ | IC | GR | NR | |
| Without domain information, | |||||||||||||||
| Section hypergraphlet kernel (τ = 0) | 0.647 | 0.555 | 0.529 | 0.546 | 0.585 | 0.724 | 0.639 | 0.671 | 0.628 | 0.762 | 0.578 | 0.537 | 0.542 | 0.552 | 0.783 |
| Subhypergraphlet kernel (τ = 0) | 0.838 | 0.633 | 0.675 | 0.830 | 0.787 | 0.692 | 0.691 | 0.651 | 0.612 | 0.873 | 0.681 | 0.788 | 0.711 | 0.579 | 0.732 |
| Section hypergraphlet kernel (τ = 1) | 0.649 | 0.551 | 0.521 | 0.570 | 0.599 | 0.708 | 0.641 | 0.678 | 0.628 | 0.772 | 0.581 | 0.535 | 0.550 | 0.542 | 0.791 |
| Subhypergraphlet kernel (τ = 1) | 0.834 | 0.632 | 0.672 | 0.827 | 0.767 | 0.681 | 0.686 | 0.649 | 0.611 | 0.871 | 0.683 | 0.784 | 0.702 | 0.580 | 0.736 |
| L3 framework | – | – | – | – | – | 0.717 | 0.577 | 0.634 | 0.573 | 0.511 | 0.501 | 0.629 | 0.642 | 0.596 | 0.505 |
| Preferential attachment | – | – | – | – | – | 0.814 | 0.492 | 0.552 | 0.498 | 0.660 | 0.449 | 0.534 | 0.561 | 0.545 | 0.497 |
| With domain information, | |||||||||||||||
| Random hyperwalk | 0.741 | 0.626 | 0.807 | 0.792 | 0.936 | 0.815 | 0.610 | 0.599 | 0.588 | 0.597 | 0.608 | 0.523 | 0.543 | 0.534 | 0.548 |
| Cumulative random hyperwalk | 0.711 | 0.837 | 0.822 | 0.800 | 0.937 | 0.848 | 0.681 | 0.647 | 0.670 | 0.569 | 0.637 | 0.844 | 0.617 | 0.550 | 0.518 |
| Pairwise spectrum kernel () | 0.780 | – | – | – | – | 0.816 | 0.584 | 0.716 | 0.689 | 0.754 | 0.629 | – | – | – | – |
| Section hypergraphlet kernel (τ = 0) | 0.651 | 0.634 | 0.681 | 0.663 | 0.784 | 0.861 | 0.677 | 0.698 | 0.655 | 0.804 | 0.559 | 0.633 | 0.583 | 0.625 | 0.775 |
| Subhypergraphlet kernel (τ = 0) | 0.940 | 0.936 | 0.918 | 0.935 | 0.952 | 0.796 | 0.740 | 0.676 | 0.708 | 0.846 | 0.678 | 0.936 | 0.879 | 0.724 | 0.757 |
| Section hypergraphlet kernel (τ = 1) | 0.650 | 0.635 | 0.693 | 0.674 | 0.795 | 0.875 | 0.697 | 0.706 | 0.667 | 0.786 | 0.574 | 0.637 | 0.585 | 0.619 | 0.777 |
| Subhypergraphlet kernel (τ = 1) | 0.940 | 0.939 | 0.922 | 0.930 | 0.952 | 0.812 | 0.750 | 0.719 | 0.736 | 0.860 | 0.728 | 0.944 | 0.884 | 0.747 | 0.764 |
Note: The highest performance for each dataset is shown in boldface.
Fig. 3.
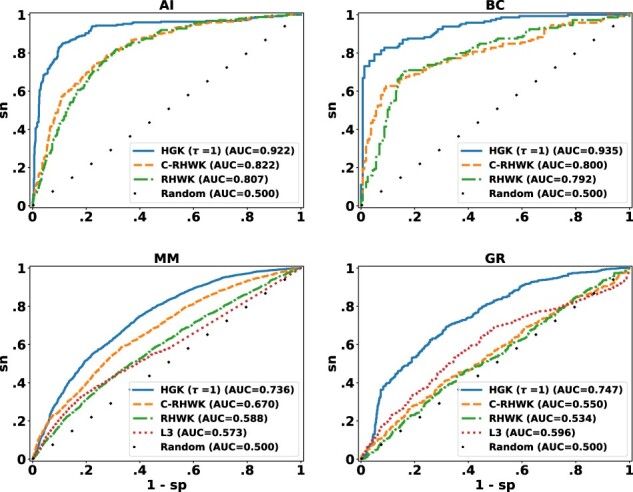
ROC curves for different kernel methods for four representative datasets: AI, BC, MM and GR, as described in Table 1. Methods: RHWK, random hyperwalk kernel; C-RHWK, cumulative RHWK; HGK, hypergraphlet kernel; L3, L3 framework
5.2 Performance on link prediction
The performance of hypergraphlet kernels was further evaluated on the problem of link prediction on multiple PPI and DTI network datasets. Table 2 and Supplementary Table S2 show the performance accuracies for each hypergraph-based method across all link prediction datasets. These results demonstrate good performance of our methods, with edit-distance kernels generally having the best performance. Interestingly, the bona fide hypergraphlet approaches displayed the highest accuracy on most PPI datasets (excluding CE), with a minor variation regarding the best method between section hypergraphlet and subhypergraphlet approaches. Both approaches have outperformed the state-of-the-art L3 link prediction framework as well as preferential attachment method and pairwise spectrum kernels. On the other hand, dual graphlet kernels (Supplementary Materials) showed the best performance on drug–target datasets suggesting that at this time, the increased resolution of modeling does not lead to increased performance on these networks (Supplementary Table S3). Note that pairwise spectrum kernels could not be applied to DTI datasets because they expect two pairs of objects of the same type as input, which further strengthens the appeal of our approach. Further breakdown of results based on the categories of difficulty identified by Park and Marcotte (2012) is shown in Supplementary Tables S2 and S3.
5.3 Estimating interactome sizes
A positive-unlabeled formulation for link prediction presents an opportunity to estimate interactome sizes in biological networks. As a proof of concept, here we used the AlphaMax algorithm (Jain et al., 2016a) for estimating class priors in positive-unlabeled learning to estimate both the number of missing links and false-positive interactions in different PPI networks. To do this, we used BIND, BioGRID, DIP, HPRD and IntAct to construct Homo sapiens and S.cerevisiae PPI networks. The human network contained 10 841 nodes and 45 386 edges (10 729 and 45 327 in the largest connected component), whereas the yeast network contained 4690 nodes and 26 165 edges (4674 and 26 156 in the largest connected component). The negative examples were sampled uniformly randomly from the set of all possible edges, which was necessary to correctly estimate class priors and posteriors (Jain et al., 2016a).
Assuming a tissue and cellular component agnostic model (i.e. any two proteins can interact), we obtained that the number of missing interactions on the largest component of the human PPI network is about 5% (i.e. ≈2.5 million interactions), while the number of misannotated interactions is close to 11% which translates to about 4985 false interactions. In the case of yeast, we computed that less than 1% of the potential protein interactions are missing which is close to 95 000. At the same time, the number of misannotated interactions is close to 13%, which is about 3400 misannotated protein pairs. Some of these numbers fall within previous studies that suggest that the size of the yeast interactome is between 13 500 (Stumpf et al., 2008) and 137 000 (Huang et al., 2007); however, the size of the human interactome is estimated to be within 130 000 (Venkatesan et al., 2009) and 650 000 (Stumpf et al., 2008) interactions. A more recent paper by Lewis et al. (2012) presents a scenario where yeast and human interactome size could reach 400 000 and over two million interactions, respectively. Although these results serve as a validation of our problem formulation and approach, additional tests and experiments, potentially involving exhaustive classifier and parameter optimization, will be necessary for more accurate and reliable estimates, especially for understanding the influence of potential biases within the PPI network data.
6 Related work
The literature on the similarity-based measures for learning on hypergraphs is relatively scarce. Most studies revolve around the use of random walks for clustering that were first used in the field of circuit design (Cong et al., 1991). Historically, typical hypergraph-based learning approaches can be divided into (i) tensor-based approaches, which extend traditional matrix (spectral) methods on graphs to higher-order relations for hypergraph clustering (Cong et al., 1991; Leordeanu and Sminchisescu, 2012), and (ii) approximation-based approaches that convert hypergraphs into standard weighted graphs and then exploit conventional graph clustering and semisupervised learning (Agarwal et al., 2005; Zhou et al., 2006). The methods from the first category provide a direct and mathematically rigorous treatment of hypergraph learning, although most tensor problems are NP-hard. As a consequence, this line of research remains largely unexplored despite a renewed interest in tensor decomposition approaches (Hein et al., 2013; Purkait et al., 2014). Regarding the second category, there are two commonly used transformations for graph-based hypergraph approximation, reviewed and compared in the study by Agarwal et al. (2006).
Under a supervised learning framework, Wachman and Khardon (2007) proposed walk-based hypergraph kernels on ordered hypergraphs, while Sun et al. (2008) presented a hypergraph spectral learning formulation for multilabel classification. More recently, Bai et al. (2014) introduced a hypergraph kernel that transforms a hypergraph into a directed line graph and computes a Weisfeiler–Lehman isomorphism test between directed graphs. A major drawback of most such approaches is that no graph representation fully captures the hypergraph structure.
7 Conclusions
This article presents a learning framework for the problems of vertex classification, (hyper)edge classification and link prediction in graphs and hypergraphs. The key ideas in our approach were (i) the use of hypergraph duality to cast each classification problem as an instance of vertex classification, and (ii) the use of a new family of kernels defined directly on labeled hypergraphs. Using the terminology of Bleakley et al. (2007), our method belongs to the category of ‘local’ learners. That is, it captures the structure of local neighborhoods, rooted at the vertex of interest, and should be distinguished from ‘global’ models such as Markov Random Fields or diffusion kernels (Kondor and Lafferty, 2002). The body of literature on graph learning is vast; see Supplementary Materials for more details. We therefore selected to perform extensive comparisons against a limited set of methods that are most relevant to ours.
The development of hypergraphlet kernels derives from the graph reconstruction conjecture, an idea of using small graphs to probe large graphs (Bondy and Hemminger, 1977; Borgs et al., 2006). Hypergraphlet kernels prioritize accuracy over run time and are not an optimal choice for huge dense graphs where real-time performance is critical. However, biological networks (for now) are sparse and moderate in size, making accurate prediction to prioritize biological experiments an appealing choice. We additionally believe that unification of disparate prediction tasks on biological networks via hypergraph duality reduces the need for custom method development. Overall, our work provides evidence that hypergraph-based inference and hypergraphlet kernels are competitive with other approaches and readily deployable in practice.
Supplementary Material
Acknowledgements
The authors thank two anonymous reviewers for their suggestions that have improved the quality of this article.
Funding
This work was partially supported by the National Science Foundation (NSF) [DBI-1458477], National Institutes of Health (NIH) [R01 MH105524], the Indiana University Precision Health Initiative, the European Research Council (ERC) [Consolidator Grant 770827], UCL Computer Science, the Slovenian Research Agency project [J1-8155], the Serbian Ministry of Education and Science Project [III44006] and the Prostate Project.
Conflict of Interest: none declared.
Contributor Information
Jose Lugo-Martinez, Computational Biology Department, Carnegie Mellon University, Pittsburgh, PA 15213, USA.
Daniel Zeiberg, Khoury College of Computer Sciences, Northeastern University, Boston, MA 02115, USA.
Thomas Gaudelet, Department of Computer Science, University College London, London WC1E 6BT, UK.
Noël Malod-Dognin, Barcelona Supercomputing Center (BSC), Barcelona 08034, Spain.
Natasa Przulj, Barcelona Supercomputing Center (BSC), Barcelona 08034, Spain; ICREA, Pg. Lluis Companys 23, Barcelona 08010, Spain.
Predrag Radivojac, Khoury College of Computer Sciences, Northeastern University, Boston, MA 02115, USA.
References
- Agarwal S. et al. (2005) Beyond pairwise clustering. In Proceedings of the 18th Conference on Computer Vision and Pattern Recognition, CVPR ’05, pp. 838–845, Piscataway, NJ, USA. IEEE.
- Agarwal S. et al. (2006) Higher order learning with graphs. In Proceedings of the 23rd International Conference on Machine Learning, ICML ’06, pp. 17–24, New York, NY, USA. ACM.
- Bai L. et al. (2014) A hypergraph kernel from isomorphism tests. In Proceedings of the 22nd International Conference on Pattern Recognition, ICPR ’14, pp. 3880–3885, Piscataway, NJ, USA. IEEE.
- Barabási A.L. et al. (2002) Evolution of the social network of scientific collaborations. Physica A, 311, 590–614. [Google Scholar]
- Ben-Hur A., Noble W.S. (2005) Kernel methods for predicting protein-protein interactions. Bioinformatics, 21, i38–i46. [DOI] [PubMed] [Google Scholar]
- Berge C. (1973) Graphs and Hypergraphs. In North-Holland Mathematical Library, Vol 6. Elsevier, Amsterdam, Netherlands. [Google Scholar]
- Bleakley K. et al. (2007) Supervised reconstruction of biological networks with local models. Bioinformatics, 23, i57–i65. [DOI] [PubMed] [Google Scholar]
- Bondy J.A., Hemminger R.L. (1977) Graph reconstruction—a survey. J. Theory, 1, 227–268. [Google Scholar]
- Borgs C. et al. (2006) Counting graph homomorphisms. In: Topics Discrete Math, Algorithms and Combinatorics. Springer, Berlin, Heidelberg, pp. 315–371. [Google Scholar]
- Clark W.T., Radivojac P. (2011) Analysis of protein function and its prediction from amino acid sequence. Proteins, 79, 2086–2096. [DOI] [PubMed] [Google Scholar]
- Cong J. et al. (1991) Random walks for circuit clustering. In Proceedings of the 4th International ASIC Conference, ASIC ’91, pp. P14–2.1–P14–2.4, Piscataway, NJ, USA. IEEE.
- Deng M. et al. (2003) Prediction of protein function using protein-protein interaction data. J. Comput. Biol., 10, 947–960. [DOI] [PubMed] [Google Scholar]
- Denis F. et al. (2005) Learning from positive and unlabeled examples. Theor. Comput. Sci., 348, 70–83. [Google Scholar]
- Fawcett T. (2006) An introduction to ROC analysis. Pattern Recogn. Lett., 27, 861–874. [Google Scholar]
- Gaudelet T. et al. (2018) Higher-order molecular organization as a source of biological function. Bioinformatics, 34, i944–i953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giurgiu M. et al. (2019) CORUM: the comprehensive resource of mammalian protein complexes. Nucleic Acids Res., 47, D559–D563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gomez S.M. et al. (2003) Learning to predict protein-protein interactions from protein sequences. Bioinformatics, 19, 1875–1881. [DOI] [PubMed] [Google Scholar]
- Goyal P., Ferrara E. (2018) Graph embedding techniques, applications, and performance: a survey. Knowl. Based Syst., 151, 78–94. [Google Scholar]
- Grover A., Leskovec J. (2016) node2vec: Scalable feature learning for networks. In: Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD ’16, pp. 855–864, New York, NY, USA. ACM. [DOI] [PMC free article] [PubMed]
- Hattori M. et al. (2003) Development of a chemical structure comparison method for integrated analysis of chemical and genomic information in the metabolic pathways. JACS, 125, 11853–11865. [DOI] [PubMed] [Google Scholar]
- Hein M. et al. (2013) The total variation on hypergraphs - learning on hypergraphs revisited. In Proceedings of the 26th Advances in Neural Information Processing Systems, NIPS ’13, pp. 2427–2435, Red Hook, NY, USA. Curran Associates Inc.
- Huang H. et al. (2007) Where have all the interactions gone? Estimating the coverage of two-hybrid protein interaction maps. PLoS Comput. Biol., 3, e214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jain S. et al. (2016. a) Estimating the class prior and posterior from noisy positives and unlabeled data. In Proceedings of the 30th Advances in Neural Information Processing Systems, NIPS ’16, pp. 2693–2701, RedHook, NY, USA. Curran Associates Inc.
- Jain S. et al. (2016. b) Nonparametric semi-supervised learning of class proportions. arXiv preprint arXiv : 1601.01944.
- Jain S. et al. (2017) Recovering true classifier performance in positive-unlabeled learning. In Proceeding of the 31st AAAI Conference on Artificial Intelligence, AAAI ’17, pp. 2066–2072, Cambridge, MA, USA. AAAI Press.
- Joachims T. (2002) Learning to Classify Text Using Support Vector Machines: Methods, Theory, and Algorithms. Kluwer Academic Publishers, Norwell, MA, USA. [Google Scholar]
- Klamt S. et al. (2009) Hypergraphs and cellular networks. PLoS Comput. Biol., 5, e1000385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kondor R.I., Lafferty J.D. (2002) Diffusion kernels on graphs and other discrete structures. In Proceedings of the 19th International Conference on Machine Learning, ICML ’02, pp. 315–322, Burlington, MA, USA. Morgan Kaufmann Publishers.
- Kovács I.A. et al. (2019) Network-based prediction of protein interactions. Nat. Commun., 10, 1240–1247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leordeanu M., Sminchisescu C. (2012) Efficient hypergraph clustering. In Proceedings of the 15th International Conference on Artificial Intelligence and Statistics, volume 22 of AISTATS ’12, pp. 676–684, La Palma, Canary Islands. PMLR.
- Lewis A.C.F. et al. (2012) What evidence is there for the homology of protein-protein interactions? PLoS Comput. Biol., 8, e1002645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lugo-Martinez J., Radivojac P. (2014) Generalized graphlet kernels for probabilistic inference in sparse graphs. Network Sci., 2, 254–276. [Google Scholar]
- Ma C.-Y. et al. (2017) Identification of protein complexes by integrating multiple alignment of protein interaction networks. Bioinformatics, 33, 1681–1688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Menon A.K. et al. (2015) Learning from corrupted binary labels via class-probability estimation. In Proceedings of the 32nd International Conference on Machine Learning, ICML ’15, pp. 125–134, Lille, France. PMLR.
- Nabieva E. et al. (2005) Whole-proteome prediction of protein function via graph-theoretic analysis of interaction maps. Bioinformatics, 21, i302–i310. [DOI] [PubMed] [Google Scholar]
- Park Y., Marcotte E.M. (2012) Flaws in evaluation schemes for pair-input computational predictions. Nat. Methods, 9, 1134–1136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Platt J. (2000) Probabilistic outputs for support vector machines and comparisons to regularized likelihood methods. In Smola,A. (eds), Advances in Large Margin Classifiers, pp. 61–74, Cambridge, MA, USA. MIT Press. [Google Scholar]
- Przulj N. (2007) Biological network comparison using graphlet degree distribution. Bioinformatics, 23, e177–e183. [DOI] [PubMed] [Google Scholar]
- Przulj N. et al. (2004) Modeling interactome: scale-free or geometric? Bioinformatics, 20, 3508–3515. [DOI] [PubMed] [Google Scholar]
- Purkait P. et al. (2014) Clustering with hypergraphs: the case for large hyperedges. In Proceedings of the 13th European Conference on Computer Vision, ECCV ’14, pp. 672–687, Piscataway, NJ, USA. IEEE.
- Ramola R. et al. (2019) Estimating classification accuracy in positive-unlabeled learning: characterization and correction strategies. Pac. Symp. Biocomput., 24, 124–135. [PMC free article] [PubMed] [Google Scholar]
- Reid M.D., Williamson R.C. (2010) Composite binary losses. J. Mach. Learn. Res., 11, 2387–2422. [Google Scholar]
- Shawe-Taylor J., Cristianini N. (2001) Kernel Methods for Pattern Analysis. Cambridge University Press, Cambridge, MA, USA. [Google Scholar]
- Shervashidze N. et al. (2009) Efficient graphlet kernels for large graph comparison. In Proceedings of the 12th International Conference on Artificial Intelligence and Statistics, AISTATS ’09, pp. 488–495, Clearwater Beach, FL USA, PMLR.
- Stumpf M.P.H. et al. (2008) Estimating the size of the human interactome. Proc. Natl. Acad. Sci. USA, 105, 6959–6964. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun L. et al. (2008) Hypergraph spectral learning for multi-label classification. In Proceedings of the 14th International Conference on Knowledge Discovery and Data Mining, KDD ’08, pp. 668–676, New York, NY, USA, ACM.
- Vacic V. et al. (2010) Graphlet kernels for prediction of functional residues in protein structures. J. Comput. Biol., 17, 55–72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Venkatesan K. et al. (2009) An empirical framework for binary interactome mapping. Nat. Methods, 6, 83–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vishwanathan S.V.N. et al. (2010) Graph kernels. J. Mach. Learn. Res., 11, 1201–1242. [Google Scholar]
- von Mering C. et al. (2002) Comparative assessment of large-scale data sets of protein-protein interactions. Nature, 417, 399–403. [DOI] [PubMed] [Google Scholar]
- Wachman G., Khardon R. (2007) Learning from interpretations: a rooted kernel for ordered hypergraphs. In Proceedings of the 24th International Conference on Machine Learning, ICML ’07, pp. 943–950, New York, NY, USA, ACM.
- Wang Y., Zeng J. (2013) Predicting drug–target interactions using restricted Boltzmann machines. Bioinformatics, 29, i126–i134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu J., Li Y. (2006) Discovering disease-genes by topological features in human protein–protein interaction network. Bioinformatics, 22, 2800–2805. [DOI] [PubMed] [Google Scholar]
- Yamanishi Y. et al. (2008) Prediction of drug–target interaction networks from the integration of chemical and genomic spaces. Bioinformatics, 24, i232–i240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang L.V. et al. (2004) Predicting co-complexed protein pairs using genomic and proteomic data integration. BMC Bioinformatics, 5, 38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou D. et al. (2006) Learning with hypergraphs: clustering, classification, and embedding. In Proceedings of the 19th Advances in Neural Information Processing Systems, NIPS ’06, pp. 1601–1608, Cambridge, MA, USA, MIT Press.
- Zhu X., Ghahramani Z. (2002) Learning from labeled and unlabeled data with label propagation. Technical report CMU-CALD-02-107. Carnegie Mellon University.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.