Abstract
Developmental epidemiological work shows that rates of depression as assessed by diagnostic interviews increase from childhood through early adulthood. It could be assumed that the trajectory of depression as assessed by self-report questionnaire measures would be characterized by a similar pattern. We aimed to evaluate this assumption and more clearly establish the longitudinal trajectory of depression in youth, when repeatedly assessed over time with a self-report questionnaire and with a diagnostic interview. Participants were 679 youth ages 7–16 years at baseline (Mage=11.8, SD=2.4, 56% girls). They completed the Children’s Depression Inventory (CDI) every 3 months for 3 years (13 time points) and were interviewed every 6 months using the Kiddie Schedule for Affective Disorders and Schizophrenia (K-SADS) to ascertain onset of depression diagnosis. A series of growth curve models was fit to the CDI and K-SADS data. A piecewise model characterized growth in depression as assessed by the CDI, with an initial negative linear slope (b =−0.64) spanning the first 3 assessments, and a positive quadratic second slope (b=0.015; linear component: b=−0.22) spanning the remaining 10 assessments. Depression, as assessed by the K-SADS, grew continuously over time via a positive linear slope (b=0.22). Findings illustrate differences between longitudinal trajectories of depression when assessed repeatedly by self-report questionnaire and diagnostic interview. Implications for research designed to study longitudinal depression trajectories are discussed.
Keywords: depression, trajectories, growth curve modeling, self-report, diagnostic interview
Epidemiological research has established that many common psychopathologies are developmental phenomena, and they exhibit predictable growth trajectories across the lifespan. It is well-known, for example, that DSM-based diagnoses of depression markedly increase from childhood into adolescence (e.g., Hankin et al., 2015; Merikangas et al., 2010). As a result, many researchers have turned to prospective longitudinal studies with repeated-measures designs to better capture and predict the developmental trajectory of depression and other psychopathological outcomes. Increasingly, investigators are using multi-wave longitudinal designs with repeated administrations of self-report questionnaire measures and analyzing the resulting data with advanced longitudinal data analytic techniques (e.g. Curran & Willoughby, 2003; Singer & Willett, 2003) to more precisely capture change and predict trajectories of psychopathology over time.
This shift towards the use of repeated administrations of self-report questionnaire measures of depression to characterize its trajectory raises a significant question. Do multiple waves of self-report questionnaires of depression reflect a similar pattern to that which has been established in the developmental epidemiological literature based on DSM-defined, diagnostic interviews? At present, there exists an underexamined assumption that the same developmental trends in depression that are observed from childhood through adolescence and adulthood based on diagnostic interviews (i.e., marked increases in rates of depression; e.g., Hankin et al., 2015; Merikangas et al., 2010) will also be found when self-report questionnaire measures of depression are used. This presumption of equivalent trajectories over time may be based on evidence that depression is dimensionally distributed at the latent level (Hankin, Fraley, Lahey, & Waldman, 2005; Liu, 2016). So, clinical scientists could assume that the developmental trajectory of depression would be characterized by reasonably similar patterns, regardless of whether interview or self-report assessment methods are used, as the construct being assessed is purportedly the same.
However, this assumption remains largely untested, especially using a design in which both self-report and diagnostic interview assessments of depression are conducted repeatedly over time and in the same sample. Some evidence indicates that different patterns of depression development may emerge depending on which method (i.e., self-report questionnaires or diagnostic interviews) is used (e.g., Twenge & Nolen-Hoeksema, 2002). A pattern that has emerged from research that uses longitudinal administrations of self-report questionnaire measures of depression, but not diagnostic interviews, suggests an attenuation, repeated measures, or repeated administration effect – that is, a decrease in reported levels of depression across successive assessments (Angold et al., 1996; Ge, Conger, & Elder, 2001; Ge, Lorenz, Conger, Elder, & Simons, 1994; Johnson, Whisman, Corley, Hewitt, & Rhee, 2012; Klein, Dougherty, & Olino, 2005; Sharpe & Gilbert, 1998; Slavin & Rainer, 1990). However, the shape and duration of this decline in self-reported depression over time are unclear. Some work suggests that the decrease occurs steadily (Johnson et al., 2012; Twenge & Nolen-Hoeksema, 2002), whereas other work indicates the decline may be limited to the first few time points before levels of depression stabilize or begin to increase (Angold et al., 1996; Ge et al., 1994; Ge et al., 2001; Sharpe & Gilbert, 1998; Slavin & Rainer, 1990).
The current study therefore sought to establish more clearly the trajectory of mean levels of depression over time. Information about the longitudinal patterning of depression with repeated measures across time is essential to inform reliable, valid, and accurate assessment, prediction, and understanding of depression trajectories. We investigated longitudinal patterns of depression when assessed with self-report questionnaires and when ascertained via diagnostic interviews.
Evidence of a repeated-measures effect
Twenge and Nolen-Hoeksema (2002) observed in a meta-analysis of Children’s Depression Inventory (CDI) data collected from 30 samples of children and adolescents that levels of depression steadily decreased across successive administrations in longitudinal studies with up to 6 time points. This decline in levels of depression in longitudinal studies has also been observed with several other self-report depression scales. Sharpe and Gilbert (1998) empirically tested the repeated-measures effect across three time points, each one week apart, in a sample of adults using self-report measures of depression, including the Beck Depression Inventory and the Depression Adjective Check List. Scores decreased over 20% on average from Time 1 to Time 2, and then stabilized from Time 2 to Time 3. They did not find similar decreases over time in measures of positive affect or state anxiety; both were stable across time points. Other studies have also observed similar declines across the first two administrations of self-report measures of depression, including the Symptom-Checklist-90 – Revised (Ge et al., 1994; Ge et al., 2001) and the CDI (Slavin & Rainer, 1990). Angold and colleagues observed sharp initial decreases in boys’ self-reported symptoms of depression in a study with four annual assessments using the Short Mood and Feelings Questionnaire (SMFQ). They found that symptoms of depression declined between ages 8–11; depression stabilized between ages 12–15 (i.e., decline across the first four assessments and increase across the last three; Angold et al., 1996). Other research has observed more extensive declines in depression when assessed annually using the SMFQ: self-reported symptoms decreased from ages 7 to 12, and increased from ages 13 to 15 (i.e., decline across the first five and increase across the last two; Cohen, Andrews, Davis, & Rudolph, 2018). This decline across repeated administrations of self-report questionnaire measures appears to be relatively specific to depression and has not been found to characterize other forms of psychopathology or mood measures. In sum, available evidence suggests a repeated administration decline in self-report questionnaire measures of depression, although the duration and form of this decline remains unclear.
Importantly, this decline in levels of depression is not consistently found across assessment methodologies. Rather, this effect appears to be unique to repeated administrations of self-report questionnaires assessing depression. The shape and pattern of depression trajectories may differ when self-report questionnaire measures are used as opposed to diagnostic interviews to ascertain levels of depression. Using different assessment approaches may yield different conclusions about the developmental trajectory of depression over time. Prospective longitudinal research using DSM-based diagnostic interviews consistently finds that rates of depression increase substantially from childhood through adolescence, and reach adult rates by age 18 (e.g., Cohen et al., 1993; Costello et al., 2003; Hankin et al., 1998; Hankin et al., 2015; Kessler et al., 2003; Merikangas et al., 2010; Weissman et al., 1999).
Current Study and Hypotheses
Prior research has not explored the “repeated measures effect” when both questionnaire and diagnostic interview data were collected in the same sample of individuals. Both assessment approaches seek to measure depression in youth, and as such, we suspect that many investigators who wish to assess depression repeatedly over time presume that the longitudinal patterning from one assessment approach (e.g., self-report) applies to another depression assessment method (e.g., diagnostic interview). The present study aimed to directly examine this assumption and key assessment question empirically. Therefore, the goal of this study is to use longitudinal growth curve data analyses to accurately characterize the descriptive trajectories of depression from self-report questionnaires and diagnostic interviews among children and adolescents.
Existing literature indicates that depression consistently declines across initial assessments when assessed via repeated self-report questionnaire measures (Ge et al., 2001; Sharpe & Gilbert, 1998; Twenge & Nolen-Hoeksema, 2002); however, the literature is equivocal regarding the later shape of growth of depression using these measures. Some prior work has found levels of depression to steadily decrease (Twenge & Nolen-Hoeksema, 2002), whereas other work has found that levels of depression subsequently stabilize after the initial decline (Sharpe & Gilbert, 1998) or increase (Cohen et al., 2018; Ge et al., 1998; Ge et al., 2001). Taken together, existing evidence suggests that trajectories of self-reported depression may be best conceptualized in two parts. However, a minimum of four time points is necessary to test the possibility that the trajectory of depression may best be captured by two slopes; the majority of the extant literature has been unable to rigorously test this hypothesis (Curran & Willoughby, 2003). We hypothesized that a piecewise, or discontinuous growth curve model, with a first slope to account for the initial decrease in levels of self-reported depression and a second increasing slope to represent change in later scores, may best characterize change in depression as assessed by the CDI over time. Prior literature indicates that the “knot,” or the change in slopes, occurs between the second and sixth measurement occasions. We thus examined those potential locations of the knot, but did not make more specific hypotheses about the exact location of the change in slopes. Finally, given that prior work has found gender differences in the trajectory of depression across development (e.g., Hankin et al. 1998; Salk et al., 2017), we examined whether gender predicted the growth parameters of depression, both as assessed by the CDI and by the K-SADS. We used growth curve modeling to examine these questions in a community sample (N=679) of youth in which repeated assessments of depression were collected over a three-year follow-up, including every 3 months for self-reported questionnaires (13 time points) and every 6 months for diagnostic interviews (7 time points).
Methods
Participants
Data were collected as part of a larger study, the Gene Environment and Mood Study (Hankin et al., 2015). Participants (youth and a caretaker) were recruited from the Denver and central New Jersey areas. Inclusion criteria included English fluency, as well as absence of an autism spectrum disorder, psychotic disorder, or intellectual disability. The current sample comprised 679 youth from the general community from ages 7–16 years at baseline (mean age=11.8, SD=2.4; 56% girls). The sample was representative of the community from which it was recruited; 62.2% of participants identified their race and ethnicity as white, 11.3% as African American, 7.5% as Latino/a, 9.6% as Asian or Pacific Islander, and 9.3% as another race or ethnicity. Additional sample characteristics can be found in Hankin et al., 2015.
Procedure
Participants visited the laboratory for the baseline assessment. Youth provided informed written assent, and a parent or guardian provided informed written consent. Follow-up assessments evaluating child-reported symptoms of depression using the CDI occurred every 3 months after baseline for 3 years, providing a total of 13 time points. Follow-up assessments evaluating depression diagnoses using the K-SADS occurred every 6 months after baseline for 3 years, providing a total of 7 time points. Participants were compensated monetarily for their participation. The Institutional Review Boards at the University of Denver and Rutgers University approved all procedures.
Measures
Depressive symptoms.
Depressive symptoms were measured via child self-report with the Children’s Depression Inventory (CDI; Kovacs, 1992). The CDI is a widely-used measure of depression in children and adolescents that was administered to participants at baseline and at each subsequent 3-month assessment (see Figure 1). Youth are instructed to report on their symptoms of depression over the prior two weeks. A total score, ranging from 0 to 54, is generated by summing all 27 items. Higher scores indicate higher levels of depressive symptoms. The CDI has sound psychometric properties, including good internal consistency and construct validity (Klein et al., 2005). In the present study, internal consistency (α) was between 0.79 and 0.90 across all time points.
Figure 1.
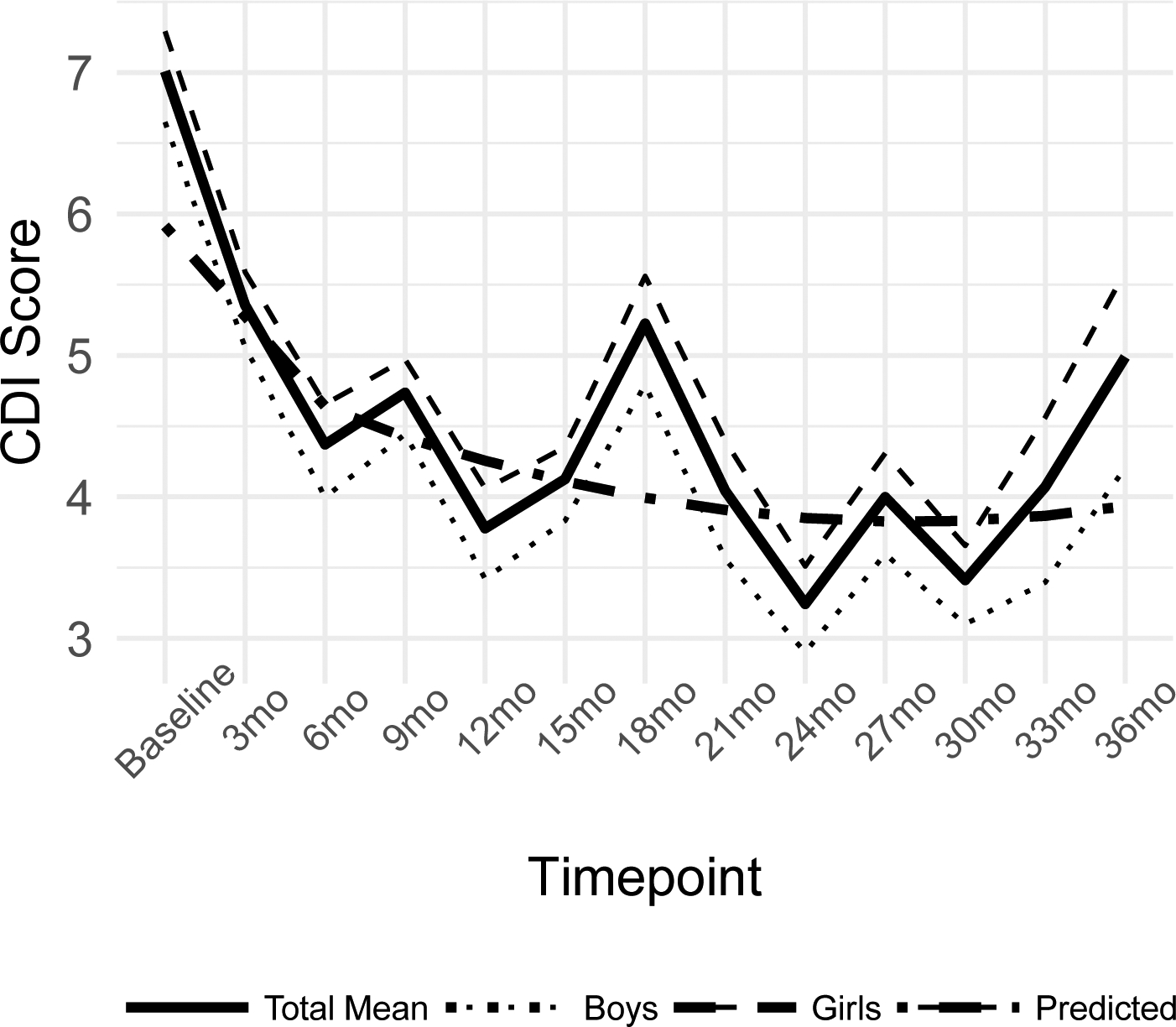
CDI scores over time.
Note: Total Mean, Boys, and Girls lines depict the average trajectory of CDI scores for each respective group from baseline to the 36-month follow-up assessment. The Predicted line depicts the best-fitting piecewise growth curve. CDI = Children’s Depressive Inventory.
Depression diagnoses.
Diagnoses of depression according to DSM-IV criteria (American Psychiatric Association, 1994) were assessed via the Kiddie Schedule for Affective Disorders and Schizophrenia (K-SADS; Kaufman et al., 1997; see Hankin et al., 2015, for additional description of methods). The K-SADS was administered at the study baseline and then regularly every 6 months for the 3 years of the prospective study (see Figure 2). Interviewers used both youth report and parent report on the K-SADS to determine youths’ diagnostic status using best estimate diagnostic procedures (Klein et al., 2005). For purposes of the present analyses, youth were determined to have a diagnosis of a depressive episode if they met DSM-IV criteria for a major depressive disorder (MDD); MDD-probable (defined as four threshold depressive symptoms); or minor depressive disorder (mDD; defined as two or three threshold depressive symptoms) for at least two weeks. This decision was based on extant literature demonstrating that depression is dimensionally distributed at the latent level (Hankin et al., 2005), and that MDD, MDD-probable, and mDD are all associated with clinically significant distress and impairment (Avenevoli, Swendsen, He, Burstein, & Merikangas, 2015; Gotlib, Lewinsohn, & Seeley, 1995). At the prospective follow-ups after the baseline assessment, participants were interviewed about the 6 months that had elapsed since the previous diagnostic interview to ascertain whether participants met criteria for a depression diagnosis in that six-month time frame. Interviewers were graduate students trained and subsequently supervised by PhD-level, licensed clinical psychologists. Twenty percent of the interviews were reviewed for reliability, and interrater reliability was good (κ = .91).
Figure 2.
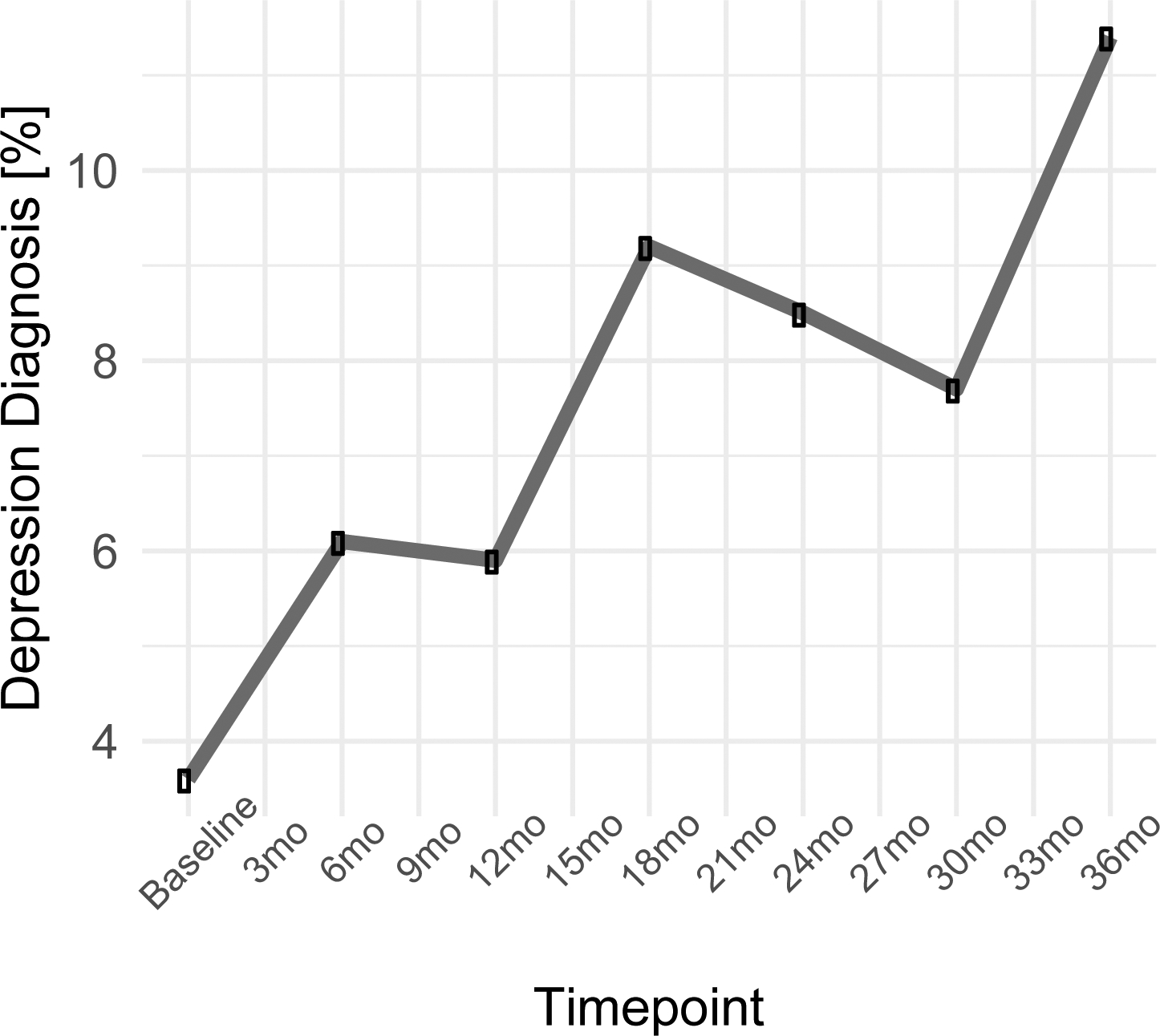
Percentage of sample meeting depression diagnostic criteria over time.
Note: Figure 2 depicts the average trajectory of depression diagnoses in percentages using the K-SADS from baseline to the 36-month follow-up assessment
Data Analytic Plan
The data analytic plan of the present study was preregistered on the Open Science Framework (masked project link: https://osf.io/2y6bt/?view_only=1b744402c9e94cf7ad749726dd30840b). Analyses were conducted using the lavaan package for Structural Equation Modeling in R (Rosseel, 2012; R Core Team, 2017). All data were missing completely at random (MCAR) or assumed to be missing at random (MAR) across the 13 time points. Missingness was not consistently correlated with scores on the CDI across the 13 time points. Full information maximum likelihood (FIML) estimation was used to address missing data. As it is not possible to test whether data are truly MAR, researchers make an assumption that data are MAR when using FIML (Schafer & Graham, 2002).
To accomplish our goal of more clearly establishing the longitudinal trajectory of the development of depression as assessed with dimensional self-report questionnaires, we fit a series of models to the CDI data in several steps.
Continuous growth models.
We began by fitting a series of continuous growth models to the repeated measures CDI data over the 13 time points. We first fit an unconditional means (no-growth) model to the data, then included a linear slope, followed by a quadratic slope. To identify the best-fitting continuous growth model, we examined convergence across multiple fit indices, including Root Mean Square Error of Approximation (RMSEA), Standardized Root Mean Square Residual (SRMR), and Comparative Fit Index (CFI), following the recommendations proposed by Hu and Bentler (1999). Specifically, good fit was indicated by RMSEA≤.06, SRMR≤.08, and CFI≥.95. Acceptable fit was indicated by RMSEA≤.08, SRMR≤.10, and CFI≥.90 (Hu & Bentler, 1999). When evaluating goodness of fit, we prioritized convergence across indices over reliance on any one particular measure of fit (Barrett, 2007; Kenny, 2015). The introduction of additional slope terms results in models that are no longer nested and cannot be compared via chi-squared tests of difference. Therefore, to compare models with similar fit statistics, we examined Akaike Information Criteria (AIC) and Bayesian Information Criteria (BIC) values (lower values indicating better fit). We interpreted a change in AIC/BIC of ≥10 as indicating an improvement in model fit (Burnham & Anderson, 2004).
Piecewise growth models.
After identifying the best-fitting continuous growth model, we fit a piecewise growth curve model to the data to test whether a discontinuous trajectory better captured dimensional self-reported depression symptoms, given the initial symptom decline observed in prior work (Ge et al., 1994; Ge et al., 2001; Johnson et al., 2012; Klein et al., 2005; Sharpe & Gilbert, 1998; Slavin & Rainer, 1990). We tested model fit with the “knot,” or the change in slopes, placed at several different timepoints, informed by prior theory and research indicating that the knot occurs between the second and sixth measurement occasion. A visual examination of the CDI data indicated that the observed symptom trajectory appeared to change between Time 3 (i.e., 6-month follow-up) and Time 5 (i.e., 12-month follow-up; see Figure 1). We used a profile likelihood approach (McArdle & Wang, 2008), in which a series of piecewise growth models were fit to the data with knots at Time 3, Time 4, and Time 5 to identify the knot point resulting in the best-fitting model. The first slope reflected the anticipated initial decrease, and the slope after the knot point reflected change processes over the subsequent time points. In all models, we constrained the first slope to be linear, based on existing empirical evidence (Cohen et al., 2018; Twenge & Nolen-Hoeksema, 2002). We tested whether symptom change in the second slope was best characterized by a linear or a quadratic function, as existing work indicates that the longitudinal trajectory of depression symptoms across development may be linear (Cole et al., 2002; Dekker et al., 2007) or quadratic (Ge et al., 2001). Models were compared using standard fit indices described above to determine whether a linear or quadratic second slope best fit the data.
We then compared fit statistics of the best-fitting piecewise model of the CDI data to the best-fitting continuous model of the CDI to determine whether a continuous or discontinuous function best described the developmental trajectory of depressive symptoms. The final model was selected based on convergence across multiple fit indices.
Method factor.
A visual examination of the plot of mean CDI scores at each timepoint suggested that the scores from Time 1, Time 7, and Time 13 (i.e., baseline, 18-month follow-up, 36-month follow-up) were elevated relative to the rest of the data (see Figure 1). These three timepoints corresponded to visits in which participants visited the laboratory to complete a larger in-person study visit. A dummy-coded variable was created to indicate whether each timepoint took place in-person or off-site, and a t-test comparing scores from the in-person timepoints to the off-site timepoints indicated that the in-person visits were significantly different from the off-site timepoints (t(298)=8.86, p<.001). Therefore, we created a method factor to account for the variance attributable to the in-person visit to more accurately characterize the trajectory of CDI growth over time. The method factor was created by loading CDI scores at Time 1, Time 7 and Time 13 onto a single latent variable. The loadings were constrained to 1, and the factor was made orthogonal to all other variables in the model.
Depression Diagnoses Growth Model
To address our goal of comparing the trajectory of depression as assessed by self-report questionnaires to the trajectory of depression as assessed by diagnostic interviews within the same sample of youth, a linear growth model using recommended practices for categorical outcomes (estimator=WLSMV, link=probit) (Grimm & Liu, 2016; Grimm, Ram, & Estabrook, 2016; Muthén & Muthén, 2009) was fit to the diagnostic interview data using Mplus version 7.4 (Muthén & Muthén, 2012). As it is not statistically possible to directly compare a categorical outcome (i.e., K-SADS data) to a continuous outcome (i.e., CDI data), we did not examine the diagnostic interview data and the questionnaire data in the same model.
Gender Differences
To examine whether gender is associated with trajectories of self-report measures of depression, as well as starting levels of depression, we regressed the intercept and slope(s) of the final CDI model onto youths’ gender. Likewise, we regressed the intercept and linear slope from the final model of depression diagnoses onto youths’ gender.
Results
Descriptive Statistics
Means and standard deviations of the CDI data are reported in Table 1. Mean levels of depression fell within ranges typically reported for a community sample of youth of this age range.
Table 1 –
Descriptive Statistics and Gender Differences in Self-Reported Depressive Symptoms
| Timepoint | Mean | SD | Female | Male | t-score(df) |
|---|---|---|---|---|---|
| Baseline | 7.01 | 5.83 | 7.29 | 6.65 | 1.43 (644) |
| 3mo | 5.35 | 5.31 | 5.59 | 5.06 | 1.24 (602) |
| 6mo | 4.37 | 4.56 | 4.65 | 4.00 | 1.8 (594) |
| 9mo | 4.74 | 4.96 | 4.97 | 4.44 | 1.31 (583) |
| 12mo | 3.78 | 4.33 | 4.06 | 3.42 | 1.82 (588) |
| 15mo | 4.13 | 4.60 | 4.35 | 3.83 | 1.39 (588) |
| 18mo | 5.23 | 5.81 | 5.56 | 4.79 | 1.59 (548) |
| 21mo | 4.04 | 4.53 | 4.39 | 3.56 | 2.13 (503)* |
| 24mo | 3.24 | 3.98 | 3.51 | 2.90 | 1.81 (519) |
| 27mo | 4.00 | 4.86 | 4.31 | 3.60 | 1.73 (532) |
| 30mo | 3.41 | 4.07 | 3.66 | 3.10 | 1.58 (518) |
| 33mo | 4.07 | 5.11 | 4.56 | 3.40 | 2.66 (468)* |
| 36mo | 4.99 | 5.51 | 5.59 | 4.21 | 3.01 (525)* |
p<.05
Continuous Growth Model
Fit statistics are reported in Table 2. An unconditional means model was initially fit to the data, with only a latent intercept and the method factor (i.e., Time 1, Time 7, and Time 13). This model fit the data poorly (CFI=0.80, SRMR=0.11, RMSEA=0.12). Introducing a linear slope improved the fit of the model (CFI=.91, SRMR=.08, RMSEA=.08), resulting in overall acceptable fit. Adding a quadratic slope further improved model fit (CFI=.94, SRMR=.08, RMSEA=.07, ΔAIC=25.78; ΔBIC=25.77). The model with both a linear and quadratic slope fit the data best with a significant intercept (b=5.64, p<.001, 95% CI [5.22, 6.05]), linear slope (b= −0.43, p<.001, 95% CI [−0.54, −0.32]), quadratic slope (b=0.025, p<.001, 95% CI [0.02, 0.03]), and variance for intercept, linear and quadratic slope (Table 3).
Table 2 -.
Growth Model Fit Statistics
| Continuous Growth | Piecewise Growth | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Linear-Linear Growth | Linear-Quadratic Growth | ||||||||
| No Growth | Linear Growth | Quadratic Growth | Knot T3 | Knot T4 | Knot T5 | Knot T3 | Knot T4 | Knot T5 | |
| 40416.71 | 39909.58 | 39790.36 | 39874.56 | 39853.69 | 39827.91 | 39730.70 | 39737.69 | 39735.37 | |
| BIC | 40493.56 | 40000.00 | 39898.86 | 39983.06 | 39962.19 | 39936.41 | 39861.80 | 39868.79 | 39866.47 |
| CFI | 0.80 | 0.91 | 0.94 | 0.92 | 0.92 | 0.93 | 0.95 | 0.95 | 0.95 |
| Chi-sq. | 1000.33 | 487.20 | 359.98 | 444.18 | 423.30 | 397.53 | 290.32 | 297.31 | 294.98 |
| df | 87.00 | 84.00 | 80.00 | 80.00 | 80.00 | 80.00 | 75.00 | 75.00 | 75.00 |
| RMSEA | 0.12 | 0.08 | 0.07 | 0.08 | 0.08 | 0.08 | 0.07 | 0.07 | 0.07 |
| SRMR | 0.11 | 0.08 | 0.08 | 0.08 | 0.08 | 0.08 | 0.07 | 0.07 | 0.07 |
Table 3 -.
Best Fitting Model Parameter Estimates
| Continuous Growth - Quadratic | Piecewise Growth - Linear-Quadratic Knot T3 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Estimate (SE) | 95% CI | Standardized | p-value | Variance | 95% CI | p-value | Estimate (SE) | 95% CI | Standardized | p-value | Variance | 95% CI | p-value | |
| 5.638 (0.21) | [5.22, 6.05] | 1.23 | <.001 | 21.16 | [18.12, 24.21] | <.001 | 4.64 (0.18) | [4.29, 4.99] | 1.17 | <.001 | 15.79 | [13.51, 18.07] | <.001 | |
| Linear Slope | −0.432 (0.06) | [−0.54, −0.32] | −0.48 | <.001 | 0.82 | [0.62, 1.02] | <.001 | −0.637 (0.10) | [−0.83, −0.45] | −0.75 | <.001 | 0.73 | [−0.08, 1.54] | 0.078 |
| Linear Second Slope | - | - | - | - | - | - | - | −0.222 (−0.21) | [−0.34, −0.11] | −0.21 | <.001 | 1.15 | [0.89, 1.4] | <.001 |
| Quadratic Slope | 0.025 (0.004) | [0.02, 0.03] | 0.39 | <.001 | 0.004 | [0.003, 0.005] | <.001 | 0.015 (0.15) | [0.004, 0.03] | 0.15 | 0.01 | 0.01 | [0.008, 0.01] | <.001 |
Piecewise Growth Model
To evaluate whether the trajectory of depression as assessed by self-report questionnaire was better characterized by a pattern of piecewise growth, a series of discontinuous growth models were fit to the CDI data. First, three models with two slopes were fit to the data with the knot placed sequentially at Time 3, Time 4, and Time 5. In all three models, both the first and second slopes were linear; we therefore refer to these as “linear-linear models.” Fit statistics for each of the piecewise growth models are reported in Table 2. Placing the knot at Time 3 resulted in acceptable model fit; the models with the knot at Time 4 and Time 5 both fit better relative to the model with the knot at Time 3. The linear-linear model with the knot at Time 5 had lower AIC and BIC values than the knot at Time 4 (ΔAIC=25.78; ΔBIC=25.77; see Table 2).
Next, we fit three models with a linear first slope and a quadratic slope added to the second linear slope (linear-quadratic models), with the knot placed at Time 3, Time 4, and Time 5. All linear-quadratic models demonstrated good fit across most fit indices (for all three linear-quadratic models: CFI=0.95, SRMR=.07, RMSEA=.07). The model with the knot at Time 3 had lower AIC/BIC values than the models with the knot at Time 4 or Time 5, which indicates a better fitting model (Burnham, Anderson, & Huyvaert, 2011). Additionally, a visual inspection of the data (Fig. 1) highlighted Time 3 as the likely transition point. It was therefore selected as the knot point.
The best-fitting linear-linear piecewise model was compared to the best-fitting linear-quadratic piecewise model on AIC and BIC to determine the best-fitting piecewise model. The linear-quadratic model with the knot placed at Time 3 had lower AIC/BIC values (ΔAIC=97.2; ΔBIC=74.61) and was therefore selected as the best-fitting piecewise model.
Final Model
The best fitting model from each set of analyses (i.e., continuous and piecewise functions) were compared on fit indices to identify the overall best-fitting model. Both the continuous quadratic model and piecewise linear-quadratic model growth functions fit the data well across multiple fit indices. The piecewise growth function had lower AIC/BIC values (ΔAIC=59.66; ΔBIC=37.06), so the linear-quadratic piecewise model was retained as the final model (see Figure 1). This model had a significant intercept (b=4.64, p<.001, 95% CI [4.29, 4.99]), linear first slope (b= −0.64, p<.001, 95% CI [−0.83, −0.45]), linear second slope (b= −0.22, p<.001, 95% CI [−0.34, −0.11]), quadratic second slope (b=0.015, p=.009, 95% CI [0.004, 0.03]), and the variances for each of these components were also significant (Table 3).
Gender differences.
We then examined whether gender predicted the intercept and slopes in the final piecewise model by regressing all of the latent variables (i.e., the intercept, the first linear slope, the second linear slope, and the quadratic slope) on gender. Gender did not significantly predict any of the growth factors: intercept (b=0.63, 95% CI [−0.06, 1.33]), first linear slope (b=0.029, 95% CI [−0.32, 0.38]), second linear slope (b= − 0.06, 95% CI [−0.29, 0.17]), and second quadratic slope (b=0.013, 95% CI [−0.01, 0.04]).
Depression Diagnoses Growth Model
We next fit a linear growth model to the diagnostic interview data to examine the trajectory of depression diagnoses over time. The model demonstrated adequate fit to the data (CFI=.85, RMSEA=.05). Model fit was improved by the addition of gender as a covariate (CFI=0.91, RMSEA=0.04) with a significant linear slope (b=0.22, p<.001, 95% CI [.12, .32]); on average, the propensity for experiencing a depressive episode increased .22 units every 6 months. The variance of the intercept was significant (b=0.67, p<.001, 95% CI [.40, .94]), indicating that individuals varied in their propensity to be depressed at baseline. The variance of the slope was significant (b=0.02, p<.001, 95% CI [.01, .03]), indicating that individuals varied in how quickly their propensity to be depressed changed over time.
Gender differences.
Gender predicted the intercept (b=−0.24, p=.04, 95% CI [−.47, −.01]) but not the slope (b=0.02, p=.47, 95% CI [−.04, .08]) of the linear model of diagnostic interview data. Girls had a higher propensity to be depressed at baseline.
Discussion
It has been well-established that DSM-defined diagnoses of depression increase from childhood into adolescence, and reach adult rates by age 18 (e.g., Cohen et al., 1993; Costello et al., 2003; Hankin et al., 1998; Hankin et al., 2015; Kessler et al., 2003; Weissman et al., 1999). However, both meta-analytic and empirical work have identified a pattern that has emerged from studies implementing longitudinal administrations of questionnaire measures of depression suggesting a decrease in reported levels of depression across initial assessments (Cohen et al., 2018; Angold et al., 1996; Ge et al., 2001; Sharpe & Gilbert, 1998; Twenge & Nolen-Hoeksema, 2002). The present study used 13 repeated administrations of a self-report questionnaire measure of depression to examine the trajectory of depression from childhood into adolescence and compared it to the trajectory of depression diagnoses, as assessed by diagnostic interviews, in the same sample. We found that symptom change in self-reported depression was discontinuous. That is, a piecewise model, with an initial negative linear slope capturing the first three assessments, and a second positive quadratic slope capturing the remaining 10 assessments, best described the growth of depression as assessed by self-report questionnaire over the three-year assessment period. This model suggested that on average, children exhibited a linear decline in depression across initial time points, after which youths’ levels of depression slowly increased quadratically across the remaining 10 time points. In contrast, over the same time period, the trajectory of youths’ depression diagnoses, assessed via diagnostic interviews, increased linearly. Taken together, these findings suggest that the longitudinal patterning over repeated assessments of the construct of depression in youth depends on the assessment used. Researchers cannot assume that the increasing trajectory of depression, as established in developmental epidemiological investigations using diagnostic interviews, will apply equivalently to the longitudinal patterns of depression when measured repeatedly across time via self-report questionnaires.
Results of the current study are consistent with past empirical work that has observed initial declines in longitudinal administrations of self-report questionnaire measures of depression (Ge et al., 2001; Sharpe & Gilbert, 1998; Twenge & Nolen-Hoeksema, 2002). Existing work, however, had yet to clarify the duration and shape of this decline. Prior empirical studies that have reported an attenuation effect have used two (Slavin & Rainer, 1990), three (Sharpe & Gilbert, 1998), or four (Angold et al., 1996; Finch, Saylor, Edwards, & McIntosh, 1987; Ge et al., 1994; Ge et al., 2001) assessments of repeated-measures self-report depression questionnaires; a limited number of studies have used sufficient time points to capture discontinuous growth. The present study built on the important contributions of this prior work. We examined the trajectory of depression as assessed longitudinally by the CDI over 13 time points spanning three years, providing a rigorous test of the “attenuation effect.” Results suggest that scores decline over the first three assessments, then increase quadratically across the remaining assessments.
These results have important implications for both study design and intervention work. First, researchers and clinicians should anticipate initial declines in self-reported levels of depression based on questionnaire measures like the CDI. Clinical and developmental scientists might have expected depression levels to rise across repeated assessments spanning the transition from childhood into adolescence. However, investigators should be aware that the pattern of results may depend on the measure of depression used (i.e., self-report questionnaires vs. diagnostic interviews). Importantly, the repeated-measures effect has been observed across multiple self-report questionnaire measures of depression, including the Beck Depression Inventory, the Depression Adjective Check List, the Symptoms-Checklist-90 – Revised, and the SMFQ, and does not appear to be specific to the CDI (Angold et al., 1996; Cohen et al., 2018; Ge et al., 1994; Ge et al., 2001; Sharpe & Gilbert, 1998).
Second, researchers should consider this initial symptom decline in study design, especially when deciding how many time points to include in their studies. Results of the present study indicate that youth self-reported depression does not demonstrate the anticipated increase until after the third assessment point. With three time points or fewer, it would appear as though levels of depression linearly decrease during childhood and adolescence. Researchers who use self-report questionnaire measures of depression should be aware of the repeated-measures effect when determining the most appropriate data analytic approach and should consider using piecewise growth models to examine trajectories of longitudinal depression data. Continuous growth functions, such as a single linear or quadratic estimate across the entire longitudinal follow-up covering multiple repeated measures, likely do not accurately capture the pattern and shape of growth as accurately as a piecewise growth model, which can effectively parse the initial slope of depression from the second slope. Separating these two growth processes can meaningfully impact interpretation of study findings. Such considerations are also important for prevention and treatment researchers as they interpret the effectiveness of their intervention. Clinicians should use caution when interpreting initial declines in patient-reported depression.
Researchers have postulated several potential theories as to why the repeated-measures effect occurs in self-report questionnaire measures of depression (Sharpe & Gilbert, 1998; Twenge & Nolen-Hoeksema, 2002). While the present study did not directly examine this question, our results can inform hypotheses for future research. First, it has been suggested that social desirability may be responsible for the decrease in self-reported depression over time; that is, as participants discover that the measure assesses depression, they become motivated by social pressure to present themselves more favorably over time (Choquette & Hesselbrock, 1987). However, this explanation may be inconsistent with the observed increase in levels of depression diagnoses as assessed by semi-structured interviews like the K-SADS. Further, prior empirical work has not found evidence of a repeated-measures effect in self-report questionnaire measures of anxiety, which in theory would be subject to similar pressures of socially desirable responding (Sharpe & Gilbert, 1998). Therefore, it seems unlikely that socially desirable responding can entirely account for the repeated-measures effect.
Second, researchers have hypothesized that decreases in test anxiety over subsequent administrations may explain the repeated-measures effect (Sharpe & Gilbert, 1998; Twenge & Nolen-Hoeksema, 2002). However, if this were the case, researchers should again observe the repeated-measures effect across domains of psychopathology, and not just in self-report questionnaire measures of depression. As reviewed above, empirical work has not found evidence of a repeated-measures effect in questionnaires assessing anxiety or positive affect (Sharpe & Gilbert, 1998), suggesting that test anxiety does not explain the observed decrease in depressive symptoms.
Third, Sharpe & Gilbert (1998) proposed that the activation of coping mechanisms may account for the repeated-measures effect. That is, the act of repeatedly reporting on their levels of depression may have helped participants to recognize their feelings of distress and implement coping strategies. Relatedly, the “Hawthorne effect,” or the idea that participants in clinical research may gain some nonspecific benefit via their participation, has been proposed as a potential explanation for observed declines in scores over time (McCarney et al., 2007; Wickström & Bendix, 2000). According to the Hawthorne effect, however, symptom levels should continue to decline across successive assessments. Further, the increase in depression diagnoses observed in the present sample may be inconsistent with the Hawthorne effect. Therefore, neither the Hawthorne effect nor the implementation of coping strategies would seem to fully capture the pattern of the results of the present study.
Finally, diagnostic interviews, such as the K-SADS, assess for the presence of depression using a symptom count, a required minimum duration of symptoms (i.e., 2 weeks), and the presence of distress and/or impairment. It may be that, for a subset of youth, the necessary number of symptoms along with depression-related distress and/or impairment increases across development, while the average youth experiences initial decreases in normative self-reported symptoms of depression, only to show a later gradual increase in self-reported symptom levels. Both of these groups (i.e., the more severe subset, as well as average youth) are represented in trajectories of depression as assessed by self-report questionnaire. However, only youth with substantial symptoms of depression are represented in trajectories of depression as assessed by diagnostic interview, in part due to skip out criteria whereby the interview is discontinued with youth who do not endorse a primary symptom of depression (i.e., depressed mood, irritability, anhedonia or apathy). This possibility highlights further potential issues with assuming equivalence between diagnostic interview and self-report questionnaire measures of depression, as the KSADS factors in information (i.e., number of symptoms, presence/absence of criterial symptoms, duration, distress, and impairment) that self-report questionnaires do not assess (Angold & Costello, 2009).
The present study represents the first investigation of the “attenuation effect” or initial decline in self-reported questionnaire measures of depression, to our knowledge, in which both questionnaire (i.e., CDI) and interview (i.e., K-SADS) data were collected and modeled in the same sample of children and adolescents. As previously described, change in depression as assessed by self-report questionnaire was best captured by a discontinuous trajectory with an initial negative linear slope, and a second positive quadratic slope. However, in this same sample, depression as assessed by diagnostic interview increased linearly from childhood through adolescence, following the anticipated pattern often described in the literature (Cohen et al., 1993; Costello et al., 2003; Hankin et al., 1998; Hankin et al., 2015; Kessler et al., 2003; Merikangas et al., 2010; Weissman et al., 1999). Prior studies of the “attenuation effect” have not compared longitudinal pattering over time of scores on self-report questionnaire measures of depression and with diagnostic-level depression data collected, so any potential differences in longitudinal trajectories in depression measurement between self-report and diagnostic interview had to be inferred. By modeling trajectories of questionnaire and interview data on depression within the same group of youth, we could ensure that repeated-measures phenomenon seen in questionnaire data is specific to the method (i.e., self-report questionnaire). That is, we observed the repeated-measures phenomenon in a sample in which depression diagnoses are linearly increasing over the same time period that self-reported levels of depression, as assessed by CDI, decrease initially and then later grow.
The current investigation benefits from a number of methodological strengths that help to advance knowledge regarding the longitudinal trajectory of depression in youth. First, the use of 13 assessments administered every three months for three years permitted a nuanced, detailed examination of the trajectory of self-reported depression across a key window of development. Further, the use of sophisticated growth curve modeling techniques allowed for a rigorous test of symptom development over time. Additionally, the collection of both CDI data and KSADS data in the same sample of youth strengthened our confidence that findings regarding initial declines in CDI scores are not attributable to idiosyncratic sample characteristics (e.g., a sample in which depression diagnoses are also declining over the same time period).
The strengths of this study should be considered in the light of limitations which represent potential avenues for future research. First, while the CDI was administered to participants every 3 months during the study period, the K-SADS was administered every 6 months. It is possible that the difference in number of assessments across these measures could impact study findings. However, although the K-SADS was administered less frequently, with 7 time points of data our study was still well-positioned to examine its trajectory of growth over time. Second, as it is not statistically possible to directly compare a categorical outcome (i.e., K-SADS data) to a continuous outcome (i.e., CDI data), we did not examine the diagnostic interview data and the questionnaire data in the same model. Further, it remains to be determined what variables may predict initial declines in CDI scores at an individual level. Future research should examine the degree to which individuals differ in their initial slope of depression, and potential predictors of between-person differences in initial slopes.
Taken together, the results of the present study contribute to a more accurate descriptive trajectory of depression in youth, and demonstrate how the longitudinal trajectory of depression that is found may differ based on the assessment method used. We found that levels of depression, as assessed longitudinally by a frequently-used self-report questionnaire measure, decreased linearly over the initial three administrations of the measure, and then increased quadratically. Importantly, this longitudinal patterning of symptom data differed from that of diagnostic interview data collected in the same sample, which indicated consistent increases in depression in youth over time. These findings have important implications for researchers and clinicians alike. The current study helps to more clearly establish the trajectory of mean levels of depression assessed longitudinally with self-report questionnaires across childhood and adolescence and illustrates significant and meaningful differences between the pattern of self-report questionnaire measures of depression, and the pattern established by diagnostic interviews.
Public Significance Statement.
This study suggests that the developmental trajectory of depression may differ when it is assessed via self-report questionnaires versus diagnostic interviews. Depression as assessed by questionnaires initially decreases, and then increases; depression as assessed by interviews steadily increases across development. Findings have implications for research design and clinical work.
Funding Source:
The research reported in this article was supported by grants from the National Institute of Mental Health to Benjamin L. Hankin, R01MH077195, R01MH105501, R01MH109662, and to Jami F. Young, R01MH077178.
Footnotes
Conflict of Interest: The authors declare that they have no conflict of interest.
References
- American Psychiatric Association (1994). Diagnostic and statistical manual of mental disorders (4th ed.). Washington, DC: Author. [Google Scholar]
- Angold A, & Jane Costello E (2009). Nosology and measurement in child and adolescent psychiatry. Journal of Child Psychology and Psychiatry, 50(1‐2), 9–15. [DOI] [PubMed] [Google Scholar]
- Angold A, Erkanli A, Loeber R, Costello EJ, Van Kammen WB, & Stouthamer-Loeber M (1996). Disappearing depression in a population sample of boys. Journal of Emotional and Behavioral Disorders, 4(2), 95–104. [Google Scholar]
- Avenevoli S, Swendsen J, He JP, Burstein M, & Merikangas KR (2015). Major depression in the National Comorbidity Survey—Adolescent Supplement: Prevalence, correlates, and treatment. Journal of the American Academy of Child & Adolescent Psychiatry, 54, 37–44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barrett P (2007). Structural equation modelling: Adjudging model fit. Personality and Individual Differences, 42(5), 815–824. [Google Scholar]
- Burnham KP, & Anderson DR (2004). Multimodel inference: Understanding AIC and BIC in model selection. Sociological Methods & Research, 33(2), 261–304. [Google Scholar]
- Burnham KP, Anderson DR, & Huyvaert KP (2011). AIC model selection and multimodel inference in behavioral ecology: Some background, observations, and comparisons. Behavioral Ecology and Sociobiology, 65(1), 23–35. [Google Scholar]
- Choquette KA, & Hesselbrock MN (1987). Effects of retesting with the Beck and Zung depression scales in alcoholics. Alcohol and Alcoholism, 22(3), 277–283. [PubMed] [Google Scholar]
- Cohen JR, Andrews AR, Davis MM, & Rudolph KD (2018). Anxiety and depression during childhood and adolescence: Testing theoretical models of continuity and discontinuity. Journal of Abnormal Child Psychology, 46(6), 1295–1308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen P, Cohen J, Kasen S, Velez CN, Hartmark C, Johnson J, … & Streuning EL (1993). An epidemiological study of disorders in late childhood and adolescence—I. Age‐and Gender‐Specific Prevalence. Journal of Child Psychology and Psychiatry, 34(6), 851–867. [DOI] [PubMed] [Google Scholar]
- Cole DA, Tram JM, Martin JM, Hoffman KB, Ruiz MD, Jacquez FM, & Maschman TL (2002). Individual differences in the emergence of depressive symptoms in children and adolescents: A longitudinal investigation of parent and child reports. Journal of Abnormal Psychology, 111(1), 156. [PubMed] [Google Scholar]
- Costello EJ, Mustillo S, Erkanli A, Keeler G, & Angold A (2003). Prevalence and development of psychiatric disorders in childhood and adolescence. Archives of General Psychiatry, 60(8), 837–844. [DOI] [PubMed] [Google Scholar]
- Curran PJ, & Willoughby MT (2003). Implications of latent trajectory models for the study of developmental psychopathology. Development and Psychopathology, 15(3), 581–612. [DOI] [PubMed] [Google Scholar]
- Dekker MC, Ferdinand RF, Van Lang ND, Bongers IL, Van Der Ende J, & Verhulst FC (2007). Developmental trajectories of depressive symptoms from early childhood to late adolescence: Gender differences and adult outcome. Journal of Child Psychology and Psychiatry, 48(7), 657–666. [DOI] [PubMed] [Google Scholar]
- Finch AJ Jr, Saylor CF, Edwards GL, & McIntosh JA (1987). Children’s Depression Inventory: Reliability over repeated administrations. Journal of Clinical Child Psychology, 16(4), 339–341. [Google Scholar]
- Ge X, Conger RD, & Elder GH Jr (2001). Pubertal transition, stressful life events, and the emergence of gender differences in adolescent depressive symptoms. Developmental Psychology, 37(3), 404. [DOI] [PubMed] [Google Scholar]
- Ge X, Lorenz FO, Conger RD, Elder GH, & Simons RL (1994). Trajectories of stressful life events and depressive symptoms during adolescence. Developmental Psychology, 30(4), 467. [Google Scholar]
- Gotlib IH, Lewinsohn PM, & Seeley JR (1995). Symptoms versus a diagnosis of depression: Differences in psychosocial functioning. Journal of Consulting and Clinical Psychology, 63, 90–100. [DOI] [PubMed] [Google Scholar]
- Grimm KJ, & Liu Y (2016). Residual structures in growth models with ordinal outcomes. Structural Equation Modeling: A Multidisciplinary Journal, 23(3), 466–475. [Google Scholar]
- Grimm KJ, Ram N, & Estabrook R (2016). Growth modeling: Structural equation and multilevel modeling approaches. Guilford Publications. [Google Scholar]
- Hankin BL, Abramson LY, Moffitt TE, Silva PA, McGee R, & Angell KE (1998). Development of depression from preadolescence to young adulthood: Emerging gender differences in a 10-year longitudinal study. Journal of Abnormal Psychology, 107(1), 128–140. [DOI] [PubMed] [Google Scholar]
- Hankin BL, Fraley RC, Lahey BB, & Waldman ID (2005). Is depression best viewed as a continuum or discrete category? A taxometric analysis of childhood and adolescent depression in a population-based sample. Journal of Abnormal Psychology, 114(1), 96–110. [DOI] [PubMed] [Google Scholar]
- Hankin BL, Young JF, Abela JRZ, Smolen A, Jenness JL, … & Oppenheimer CW (2015). Depression from childhood into late adolescence: Influence of gender, development, genetic susceptibility, and peer stress. Journal of Abnormal Psychology, 124(4), 803–816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu LT, & Bentler PM (1999). Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Structural Equation Modeling, 6, 1–55. [Google Scholar]
- Johnson DP, Whisman MA, Corley RP, Hewitt JK, & Rhee SH (2012). Association between depressive symptoms and negative dependent life events from late childhood to adolescence. Journal of Abnormal Child Psychology, 40(8), 1385–1400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaufman J, Birmaher B, Brent D, Rao UMA, Flynn C, Moreci P, … & Ryan N (1997). Schedule for affective disorders and schizophrenia for school-age children-present and lifetime version (K-SADS-PL): Initial reliability and validity data. Journal of the American Academy of Child & Adolescent Psychiatry, 36(7), 980–988. [DOI] [PubMed] [Google Scholar]
- Kenny DA (2015, November 24). Measuring model fit. Retrieved from davidakenny.net/cm/fit.htm.
- Kessler R, Berglund P, Demler O, Jin R, Koretz D, Merikangas K, …& Wang P (2003). The epidemiology of major depressive disorder: Results from the National Comorbidity Survey Replication. Journal of the American Medical Association, 289(23), 3095–3105. [DOI] [PubMed] [Google Scholar]
- Klein DN, Doughtery LR, & Olino TM (2005). Toward guidelines for evidence-based assessment of depression in children and adolescents. Journal of Clinical Child and Adolescent Psychology, 34(5), 412–432. [DOI] [PubMed] [Google Scholar]
- Kovacs M (1992). Children’s Depression Inventory (CDI) Manual. Toronto. Multi Health Systems. [Google Scholar]
- Liu RT (2016). Taxometric evidence of a dimensional latent structure for depression in an epidemiological sample of children and adolescents. Psychological Medicine, 46(6), 1265–1275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McArdle JJ, Wang L, & Cohen P (2008). Modeling age-based turning points in longitudinal life-span growth curves of cognition. In Cohen P (Ed.), Applied data analytic techniques for turning points research (105–128). Routledge. [Google Scholar]
- McCarney R, Warner J, Iliffe S, Van Haselen R, Griffin M, & Fisher P (2007). The Hawthorne Effect: A randomised, controlled trial. BMC Medical Research Methodology, 7(1), 30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Merikangas KR, He JP, Burstein M, Swanson SA, Avenevoli S, Cui L, … & Swendsen J (2010). Lifetime prevalence of mental disorders in US adolescents: Results from the National Comorbidity Survey Replication–Adolescent Supplement (NCS-A). Journal of the American Academy of Child & Adolescent Psychiatry, 49(10), 980–989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muthén B, & Muthén BO (2009). Statistical analysis with latent variables. New York: Wiley. [Google Scholar]
- Muthén LK, & Muthén BO (2012). Mplus User’s Guide (7 ed.). Los Angeles, CA: Muthén & Muthén. [Google Scholar]
- Rosseel Y (2012). Lavaan: An R package for structural equation modeling and more. Version 0.5–12 (BETA). Journal of Statistical Software, 48(2), 1–36. [Google Scholar]
- Salk RH, Hyde JS, & Abramson LY (2017). Gender differences in depression in representative national samples: Meta-analyses of diagnoses and symptoms. Psychological Bulletin, 143(8), 783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schafer JL, & Graham JW (2002). Missing data: Our view of the state of the art. Psychological Methods, 7(2), 147. [PubMed] [Google Scholar]
- Sharpe JP, & Gilbert DG (1998). Effects of repeated administration of the Beck Depression Inventory and other measures of negative mood states. Personality and Individual Differences, 24(4), 457–463. [Google Scholar]
- Singer JD, & Willett JB (2003). Applied longitudinal data analysis: Modeling change and event occurrence. Oxford University Press, New York, NY. [Google Scholar]
- Slavin LA, & Rainer KL (1990). Gender differences in emotional support and depressive symptoms among adolescents: A prospective analysis. American Journal of Community Psychology, 18(3), 407–421. [DOI] [PubMed] [Google Scholar]
- Twenge JM, & Nolen-Hoeksema S (2002). Age, gender, race, socioeconomic status, and birth cohort difference on the Children’s Depression Inventory: A meta-analysis. Journal of Abnormal Psychology, 111(4), 578–588. [DOI] [PubMed] [Google Scholar]
- Weissman MM, Wolk S, Goldstein RB, Moreau D, Adams P, Greenwald S, … & Wickramaratne P (1999). Depressed adolescents grown up. Journal of the American Medical Association, 281(18), 1707–1713. [DOI] [PubMed] [Google Scholar]
- Wickström G, & Bendix T (2000). The Hawthorne effect: What did the original Hawthorne studies actually show? Scandinavian Journal of Work, Environment & Health, 26(4), 363–367. [PubMed] [Google Scholar]


