Improved doubly robust estimation in learning optimal individualized treatment rules

Abstract

Individualized treatment rules (ITRs) recommend treatment according to patient characteristics. There is a growing interest in developing novel and efficient statistical methods in constructing ITRs. We propose an improved doubly robust estimator of the optimal ITRs. The proposed estimator is based on a direct optimization of an augmented inverse-probability weighted estimator (AIPWE) of the expected clinical outcome over a class of ITRs. The method enjoys two key properties. First, it is doubly robust, meaning that the proposed estimator is consistent when either the propensity score or the outcome model is correct. Second, it achieves the smallest variance among the class of doubly robust estimators when the propensity score model is correctly specified, regardless of the specification of the outcome model. Simulation studies show that the estimated ITRs obtained from our method yield better results than those obtained from current popular methods. Data from the Sequenced Treatment Alternatives to Relieve Depression (STAR*D) study is analyzed as an illustrative example.

1. Introduction

In recent years, personalized medicine, or precision medicine, has received tremendous attention in clinical practice and medical research (Hamburg and Collins, 2010; Chan and Ginsburg, 2011; Collins and Varmus, 2015). Its development originates from the fact that patients often exhibit heterogenous responses to treatments. A drug that works for the majority of individuals may not work for a subgroup of patients with certain characteristics. For example, trastuzumab is shown to be effective for treating HER2-overexpressing metastatic breast cancer as it is specifically designed to target HER2 amplification (Vogel et al., 2002). Individualized treatment rules (ITRs) formalize personalized treatment decisions, which recommend treatments using patients’ own information, with the optimal ITR maximizing the mean of a pre-specified clinical outcome if followed by the patient population.

Using data collected from clinical trials or observational studies, numerous methods have been developed on estimation of optimal ITRs. One approach is to fully or partly specify a model of the clinical outcome given treatment and covariates, and then use the fitted model to infer the optimal ITR. This includes Q-learning (Qian and Murphy, 2011) and A-learning (Murphy, 2003; Robins, 2004; Blatt et al., 2004). Q-learning models the conditional mean of the outcome given treatment and covariates while A-learning directly models the differential treatment effects between treatments. However, one drawback of Q- and A-learning is that the optimal treatment rule is indirectly estimated through posited regression models, and thus sensitive to model misspecification. Value-search or direct-maximization methods offer an alternative to regression-based methods by directly maximizing an estimator of the marginal mean outcome over a pre-specified class of ITRs (Zhao et al., 2012; Zhang et al., 2012; Zhou et al., 2017; Zhao et al., 2019), thereby separating the class of decision rules from the posited regression models.

In particular, Zhang et al. (2012) estimated the optimal ITR by maximizing an augmented inverse-probability weighted estimator (AIPWE) for the population mean outcome over a class of ITRs. The aforementioned estimator is doubly robust (DR) in the sense that it consistently estimates the optimal ITR if either the propensity score or the outcome regression model is correctly specified. Doubly robust estimation has enjoyed great popularity in missing data and causal inference models (Scharfstein et al., 1999; Robins and Rotnitzky, 2001; Van der Laan and Robins, 2003; Bang and Robins, 2005). The DR estimators require specification of two nuisance working models, one for the missingness or treatment assignment mechanism, and another one for the distribution of complete data or potential outcomes. Historically, estimation of the nuisance parameters indexing the working models in DR estimators had received little attention, partly because the asymptotic properties of the DR estimators do not depend on the choice of nuisance parameter estimates when both working models are correctly specified (Tsiatis, 2007). As a result, standard maximum likelihood estimators are used, i.e., logistic regression for the propensity score model, and linear regression for the outcome model. This standard practice starts to change after Kang and Schafer (2007) cautioned against the use of DR estimators when both working models are misspecified. Several discussion articles (Robins et al., 2007; Tsiatis and Davidian, 2007; Tan, 2007) further pointed out that the choice of nuisance parameter estimates can have a dramatic impact on the properties of the DR estimators when at least one working model is misspecified. Indeed, in the context of estimating optimal ITRs using DR methods, there is still room for improved performance. For example, as illustrated in simulation studies of Zhao et al. (2019), the usual DR estimator (Zhang et al., 2012) can be inefficient, i.e, exhibits a large variation when the outcome regression model is misspecified. The poor performance may be partly a consequence of the default use of maximum likelihood estimators for the coefficients in the misspecified outcome regression model (Cao et al., 2009). This motivates us to develop improved DR approaches for learning optimal ITRs.

Several improved DR estimators have been proposed in missing data and causal inference models for the purpose of variance reduction. The nuisance parameters indexing the outcome model are estimated so as to minimize the variance of the DR estimator under a correctly specified propensity score model (Rubin and van der Laan, 2008; Cao et al., 2009; Tan, 2010; Tsiatis et al., 2011). In this article, we propose to estimate the optimal ITR by maximizing an improved DR estimator of the population mean outcome among a set of ITRs. Our proposed estimator is doubly robust. In addition, it achieves the smallest variance among its class of DR estimators when the propensity score models are correctly specified, regardless of the specification of the outcome models. As we demonstrate, this approach leads to estimated optimal regimes achieving comparable or better performance than those from Zhang et al. (2012).

The heterogeneity in response to treatments exists not only between patients but also within each patient. A patient’s response to treatment can change over time because individual characteristics, and the nature of disease itself, evolve. This motivates the development of dynamic treatment regimes (DTRs) (Murphy, 2003), which are sequential decision rules that adapt over time to the clinical status of each patient. At each decision point, the available patient history data are used as input for the decision rule, and an individualized treatment is recommended for the next stage. Construction of optimal DTRs has been of great interest, where several methods are developed to handle multi-stage problems (Zhang et al., 2013; Laber et al., 2014; Schulte et al., 2014; Zhao et al., 2015; Wallace and Moodie, 2015; Liu et al., 2018). In this paper, we also discuss extending the proposed method to estimate optimal DTRs with added efficiency and robustness.

This article proposes 2 major contributions to the literature. (1) We propose improved DR approaches for estimating optimal ITRs, which has not been investigated in the field of personalized medicine. (2) Current literature such as Cao et al. (2009) and Tsiatis et al. (2011) employed inverse-probability weighted estimating equations to estimate the nuisance parameters. Instead, we propose augmented inverse-probability weighted estimating equations for this purpose, which brings further stability.

The remainder of the article is organized as follows. In Section 2, we introduce background information and review existing doubly robust estimators in learning optimal ITRs. We then formally describe the proposed improved doubly robust estimator in single-stage optimal treatment problems. Theoretical results are presented in Section 3. In Section 4, we present simulation studies to evaluate finite sample performance of the proposed method. The method is then illustrated using data from the Sequenced Treatment Alternatives to Relieve Depression (STAR*D) Study in Section 5. Some concluding remarks are given in Section 6. Technical results are relegated to the supplementary material.

2. Method

2.1. Background and preliminaries

We consider the estimation of the optimal ITR in the single-stage setting. We observe ${\{({\mathit{X}}_i,A_i,Y_i)\}}_{i=1}^n$, comprising n independent and identically distributed triplets of $(\mathit{X},A,Y)$, where $\mathit{X}\in \mathcal{X}$ denotes the patient’s baseline variables; $A\in \mathcal{A}=\{-1,1\}$ denotes the assigned treatment; Y denotes the clinical outcome of interest, coded so that the larger the better. The data comes from either randomized trials or observational studies. An ITR is a map $d:\mathcal{X}\mapsto \mathcal{A}$ such that a patient presenting with $\mathit{X}=\mathit{x}$ will receive treatment $d(\mathit{x})$.

Let $\mathcal{D}$ denote a class of ITRs of interest. To formally define the optimal ITR, $d^{\text{opt}}$, we adopt the potential outcome framework (Rubin, 1974). Let Y(a) denote the potential outcome under treatment $a\in \{-1,1\}$. The potential outcome under any ITR, d, can be defined as $Y(d)=Y(1)I\{d(\mathit{X})=1\}+Y(-1)I\{d(\mathit{X})=-1\}$, where $I\{\cdot \}$ is the indicator function. Here we suppress the dependence of Y(d) on X. The performance of d is measured by the marginal mean outcome $V(d)\triangleq E\{Y(d)\}$, the so-called value function associated with the rule d. In other words, the value function V(d) represents the overall population mean if treatment were to be assigned according to d. The optimal ITR, $d^{\text{opt}}$, is a rule that maximizes V(d) among $\mathcal{D}$, i.e., $V(d^{\text{opt}})\ge V(d)$ for all $d\in \mathcal{D}$.

In order to connect the potential outcomes with the observed data, we make the following assumptions: (i) consistency, $Y=Y(1)I(A=1)+Y(-1)I(A=-1)$; (ii) positivity, $P(A=a|\mathit{X})>0$ for $a=\pm 1$ and for all X; (iii) no unmeasured confounding, $A\perp \{Y(-1),Y(1)\}|\mathit{X}$. These are standard and well-studied assumptions in causal inference (Imbens and Rubin, 2015). Assumption (iii) is trivial in a randomized trial but unverifiable in an observation study (Robins et al., 2000).

Define $Q_0(\mathit{x},a)\triangleq E(Y|\mathit{X}=\mathit{x},A=a)$, then under the aforementioned assumptions, it can be shown that

$$V(d)=E_{\mathit{X}}\left[Q_0(\mathit{X},1)I\{d(\mathit{X})=1\}+Q_0(\mathit{X},-1)I\{d(\mathit{X})=-1\}\right],$$

where the outer expectation $E_{\mathit{X}}[\cdot ]$ is taken with respect to the marginal distribution of X. The above formulation implies that $d^{\text{opt}}(\mathit{x})=\arg {\max }_{a\in \{-1,1\}}{Q}_0(\mathit{x},a)$. One approach is to posit a regression model $Q(\mathit{X},A;\mathit{\beta })$ for $Q_0(\mathit{X},A)$, and estimate the nuisance parameter β by some β; e.g. least squares. Subsequently the optimal ITR is estimated by $\widehat{d}(\mathit{x})=\arg {\max }_{a\in \{-1,1\}}Q(\mathit{x},a;\mathit{\beta })$ (Qian and Murphy, 2011). This is usually referred to as an indirect approach, which could lead to inconsistent estimators of $d^{\text{opt}}$ when the posited model Q(X, A; β) is incorrect.

To alleviate the above issue, value-search or direct-maximization methods attempt to estimate $d^{\text{opt}}$ by directly maximizing an estimator of the value function over the class $\mathcal{D}$. The key step is to construct a consistent and robust estimator of the value function, say $\widehat{V}(\cdot )$. Then $d^{\text{opt}}$ is estimated by $\widehat{d}=\arg {\max }_{d\in D}\widehat{V}(d)$. Let ${\pi }_0(a,\mathit{x})\triangleq P(A=a|\mathit{X}=\mathit{x})$ denote the true propensity score, so the value function can be rewritten as (Qian and Murphy, 2011; Zhao et al., 2012)

$$V(d)=E\left[\frac{Y}{{\pi }_0(A,\mathit{X})}I\{A=d(\mathit{X})\}\right].$$

In an observation study, ${\pi }_0(A,\mathit{X})$ is unknown. A parametric model $\pi (A,\mathit{X};\mathit{\gamma })$ may be posited; for example, a logistic regression model $\pi (1,\mathit{X};\mathit{\gamma })={\{1+\exp (-{\mathit{X}}^{\top }\mathit{\gamma })\}}^{-1}$, $\mathit{X}={(1,{\mathit{X}}^{\top })}^{\top }$. Let $\widehat{\mathit{\gamma }}$ denote the maximum likelihood estimator for $\mathit{\gamma }$ based on ${\{(A_i,{\mathit{X}}_i)\}}_{i=1}^n$, an inverse-probability weighted estimator (IPWE) for V(d) is

$${\widehat{V}}^{\text{IPWE}}(d;\widehat{\mathit{\gamma }})\triangleq {\mathbb{P}}_n\left[\frac{Y}{\pi (A,\mathit{X};\widehat{\mathit{\gamma }})}I\{A=d(\mathit{X})\}\right],$$

where ${\mathbb{P}}_n$ is the empirical measure. It is straightforward to show that the IPWE is consistent for V(d) if $\pi (A,\mathit{X};\mathit{\gamma })$ is correctly specified, that is, ${\pi }_0(A,\mathit{X})=\pi \left(A,\mathit{X};{\mathit{\gamma }}_0\right)$ for some γ₀, but may not be otherwise.

Following ideas from Robins et al. (1994), an AIPWE can be constructed:

$${\widehat{V}}^{\text{AIPWE}}(d;\widehat{\mathit{\gamma }},\mathit{\beta })\triangleq {\mathbb{P}}_n\left[\frac{YI\{A=d(\mathit{X})\}}{\pi \{d(\mathit{X}),\mathit{X};\widehat{\mathit{\gamma }}\}}-\frac{I\{A=d(\mathit{X})\}-\pi \{d(\mathit{X}),\mathit{X};\widehat{\mathit{\gamma }}\}}{\pi \{d(\mathit{X}),\mathit{X};\widehat{\mathit{\gamma }}\}}Q\{\mathit{X},d(\mathit{X});\mathit{\beta }\}\right].$$ (1)

By adding an augmentation term that involves both estimated propensity scores and regression models, the AIPWE improves efficiency and provides additional protection against model misspecification. The AIPWE is doubly robust in that it consistently estimates V(d) as long as one of the nuisance working models is correctly specified, i.e., $\pi (A,\mathit{X};\widehat{\mathit{\gamma }})\stackrel{p}{\to }{\pi }_0(A,\mathit{X})\text{or}Q(\mathit{X},A;\mathit{\beta })\stackrel{p}{\to }{Q}_0(\mathit{X},A)$.

Throughout the paper, we focus on the AIPWE, and suppress the superscript ‘AIPWE’ in $\widehat{V}(d;\widehat{\mathit{\gamma }},\mathit{\beta })$. We refer to the estimator (1), with γ estimated by maximum likelihood and β estimated by least squares, as the usual doubly robust estimator from Zhang et al. (2012). However, when the propensity score model is correctly specified, but the outcome model is not, it is inefficient to adopt the least squares estimates of β in (1), where $\widehat{V}(d;\widehat{\mathit{\gamma }},\mathit{\beta })$ could have a large variation. This motivates us to develop improved DR estimators with desirable efficiency properties.

2.2. Improved doubly robust estimators when the propensity score is fully specified

We first consider a fully specified propensity score model $\pi (A,\mathit{X})$, say, involving no nuisance parameters. We will relax this shortly. Here, the specified propensity score model $\pi (A,\mathit{X})$ may or may not be the same as the true propensity ${\pi }_0(A,\mathit{X})$. For a fixed treatment regime d, the class of AIPW estimators for V(d) is

$$\widehat{V}(d;\mathit{\beta })\triangleq {\mathbb{P}}_n\left[\frac{YI\{A=d(\mathit{X})\}}{\pi \{d(\mathit{X}),\mathit{X}\}}-\frac{I\{A=d(\mathit{X})\}-\pi \{d(\mathit{X}),\mathit{X}\}}{\pi \{d(\mathit{X}),\mathit{X}\}}Q\{\mathit{X},d(\mathit{X});\mathit{\beta }\}\right].$$ (2)

We use $\widehat{V}(d;\mathit{\beta })$ to emphasize that the estimator does not involve the nuisance parameters related to propensity score, and varying the choice of β leads to different DR estimators with potentially very different behaviors. In the following, we will derive an estimator for β, denoted by ${\mathit{\beta }}^{\text{opt}}$, such that the resulting value function estimator $\widehat{V}(d;{\mathit{\beta }}^{\text{opt}})$ satisfies two properties:

• (i)Doubly robust. $\widehat{V}(d;{\mathit{\beta }}^{\text{opt}})$ consistently estimates V(d) when either the propensity score or the outcome model is correctly specified.
• (ii)If the propensity score is correctly specified, it achieves the smallest asymptotic variance among all estimators of form (2), regardless of the specification of the outcome model.

Hence, when the outcome model is correctly specified, but the propensity score may not be, the desired ${\mathit{\beta }}^{\text{opt}}$ must converge in probability to β₀, where $Q\left(\mathit{X},A;{\mathit{\beta }}_0\right)=Q_0(\mathit{X},A)$. On the other hand, when the propensity score is correctly specified, $\mathrm{Var}\{\widehat{V}(d;{\mathit{\beta }}^{\text{opt}})\}\le \mathrm{Var}\{\widehat{V}(d;\mathit{\beta })\}$ for any $\mathit{\beta }$.

Lemma 1.

Let β be any root-n consistent estimator converging in probability to some ${\mathit{\beta }}^{*}$, i.e., $\mathit{\beta }-{\mathit{\beta }}^{*}=O_p(n^{-1/2})$. When the propensity score is correct, $\pi (A,\mathit{X})={\pi }_0(A,\mathit{X})$, but $Q(\mathit{X},A;\mathit{\beta })$ may or may not be, the influence function for $\widehat{V}(d;\mathit{\beta })$ is

$$\frac{YI\{A=d(\mathit{X})\}}{{\pi }_0\{d(\mathit{X}),\mathit{X}\}}-\frac{I\{A=d(\mathit{X})\}-{\pi }_0\{d(\mathit{X}),\mathit{X}\}}{{\pi }_0\{d(\mathit{X}),\mathit{X}\}}Q\{\mathit{X},d(\mathit{X});{\beta }^{*}\}-V(d).$$ (3)

A proof is given in Appendix A. The preceding result shows that when the propensity score is correct, the asymptotic variance of $\widehat{V}(d;\mathit{\beta })$ does not depend on the sampling variation of β but only on its limit in probability β*. Based on Lemma 1 and the law of total variance, its asymptotic variance is proportional to

$$\begin{gathered} E\left(\mathrm{Var}\left[\frac{YI\{A=d(\mathit{X})\}}{{\pi }_0\{d(\mathit{X}),\mathit{X}\}}-\frac{I\{A=d(\mathit{X})\}-{\pi }_0\{d(\mathit{X}),\mathit{X}\}}{{\pi }_0\{d(\mathit{X}),\mathit{X}\}}Q\left\{\mathit{X},d(\mathit{X});{\beta }^{*}\right\}|\mathit{X}\right]\right) \\ +\mathrm{Var}\left(E\left[\frac{YI\{A=d(\mathit{X})\}}{{\pi }_0\{d(\mathit{X}),\mathit{X}\}}-\frac{I\{A=d(\mathit{X})\}-{\pi }_0\{d(\mathit{X}),\mathit{X}\}}{{\pi }_0\{d(\mathit{X}),\mathit{X}\}}Q\left\{\mathit{X},d(\mathit{X});{\beta }^{*}\right\}|\mathit{X}\right]\right) \\ =(I)+(II). \end{gathered}$$ (4)

Notice that (II) in (4) equals $\mathrm{Var}\left[Q_0\{\mathit{X},d(\mathit{X})\}\right]$, which does not depend on β*. Furthermore, it can be shown that (see Appendix A for details)

$$\begin{gathered} (I)=E\left[\frac{1-{\pi }_0\{d(\mathit{X}),\mathit{X}\}}{{\pi }_0\{d(\mathit{X}),\mathit{X}\}}{Q}^2\{\mathit{X},d(\mathit{X});{\mathit{\beta }}^{*}\}\right]+E{\left[\frac{YI\{A=d(\mathit{X})\}}{{\pi }_0\{d(\mathit{X}),\mathit{X}\}}-Q_0\{\mathit{X},d(\mathit{X})\}\right]}^2 \\ -2E\left[\frac{1-{\pi }_0\{d(\mathit{X}),\mathit{X}\}}{{\pi }_0\{d(\mathit{X}),\mathit{X}\}}{Q}_0\{\mathit{X},d(\mathit{X})\}\cdot Q\{\mathit{X},d(\mathit{X});{\mathit{\beta }}^{*}\}\right] \end{gathered}$$

Denote the minimizer of (4) as β^opt. By taking the derivative of (4) with respect to β* and setting it equal to zero, β^opt is the solution to

$$E\left(\frac{1-{\pi }_0\{d(\mathit{X}),\mathit{X}\}}{{\pi }_0\{d(\mathit{X}),\mathit{X}\}}\left[Q_0\{\mathit{X},d(\mathit{X})\}-Q\{\mathit{X},d(\mathit{X});\mathit{\beta }\}\right]Q_{\mathit{\beta }}\{\mathit{X},d(\mathit{X});\mathit{\beta }\}\right)=0,$$ (5)

where $Q_{\mathit{\beta }}(\mathit{X},A;\mathit{\beta })\triangleq \partial Q(\mathit{X},A;\mathit{\beta })/\partial \mathit{\beta }$.

Hence, if the outcome model $Q(\mathit{X},A;\mathit{\beta })$ is correct; that is, $Q(\mathit{X},A;{\mathit{\beta }}_0)=Q_0(\mathit{X},A)$ for some β₀, then in fact ${\mathit{\beta }}^{\text{opt}}={\mathit{\beta }}_0$. If the outcome model is incorrect, such ${\mathit{\beta }}^{\text{opt}}$ still exists and minimizes (4). However, the usual least squares estimates ${\mathit{\beta }}^{\text{LS}}$ solving ${\mathbb{P}}_n\left[\{Y-Q(\mathit{X},A;\mathit{\beta })\}{Q}_{\mathit{\beta }}(\mathit{X},A;\mathit{\beta })\right]=0$ does not converge to this ${\mathit{\beta }}^{\text{opt}}$. This explains why the usual DR estimator $\widehat{V}(d;{\mathit{\beta }}^{\text{LS}})$ is sub-optimal when the outcome regression model is misspecified.

In the following, we will propose two different forms of estimators ${\mathit{\beta }}^{\text{opt}}$, which converge in probability to ${\mathit{\beta }}^{\text{opt}}$ and satisfy (i) and (ii) simultaneously. We first consider ${\mathit{\beta }}^{\text{opt1}}$ as the solution to the following inverse-probability weighted estimating equation

$${\mathbb{P}}_n\left(\frac{I\{A=d(\mathit{X})\}}{\pi \{d(\mathit{X}),\mathit{X}\}}\frac{1-\pi \{d(\mathit{X}),\mathit{X}\}}{\pi \{d(\mathit{X}),\mathit{X}\}}[Y-Q\{\mathit{X},d(\mathit{X});\mathit{\beta }\}]Q_{\mathit{\beta }}\{\mathit{X},d(\mathit{X});\mathit{\beta }\}\right)=0.$$ (6)

This can be viewed as a weighted least squares based on subjects whose treatment assignments coincide with those recommended by d, with weights $[1-\pi \{d(\mathit{X}),\mathit{X}\}]/{\pi }^2\{d(\mathit{X}),\mathit{X}\}$. When the propensity score is correct, but the outcome regression may not be, the left-hand side of (6) converges in probability to the left-hand side of (5), hence ${\mathit{\beta }}^{\text{opt}1}\stackrel{p}{\to }{\mathit{\beta }}^{\text{opt}}$. On the other hand, when the outcome regression is correct but the propensity score may not be, the left-hand side of (6) converges in probability to

$$E\left(\frac{{\pi }_0\{d(\mathit{X}),\mathit{X}\}[1-\pi \{d(\mathit{X}),\mathit{X}\}]}{{\pi }^2\{d(\mathit{X}),\mathit{X}\}}\left[Q_0\{\mathit{X},d(\mathit{X})\}-Q\{\mathit{X},d(\mathit{X});\mathit{\beta }\}\right]Q_{\mathit{\beta }}\{\mathit{X},d(\mathit{X});\mathit{\beta }\}\right),$$

which equals 0 when $\mathit{\beta }={\mathit{\beta }}_0$, thus ${\mathit{\beta }}^{\text{opt}1}\stackrel{p}{\to }{\mathit{\beta }}_0$. The following lemma formally establishes the improved doubly robust property of the proposed estimator $\widehat{V}(d;{\mathit{\beta }}^{\text{opt}1})$. See Appendix A for the proof.

Lemma 2.

$\widehat{V}(d;{\mathit{\beta }}^{\text{opt}1})\stackrel{p}{\to }V(d)$ when either the propensity score or the outcome regression model is correctly specified. In addition, when the propensity score model is correct, $\widehat{V}(d;{\mathit{\beta }}^{\text{opt}1})$ achieves the smallest asymptotic variance among all estimators of form (2).

The estimating equation (6) only utilizes the subjects whose treatment assignments coincide with those recommended by d. Since we need to search for the best treatment rule in a large class of ITRs, $\mathcal{D}$, it is possible that for some d, there are very few subjects satisfying $A=d(\mathit{X})$. This leads to highly unstable ${\mathit{\beta }}^{\text{opt}1}$ and could be problematic, in particular when the sample size n is very small. To address this issue, we propose an augmented inverse-probability weighted estimating equation, denoted by ${\mathit{\beta }}^{\text{opt}2}$, which is the solution to

$$\begin{gathered} (*)-{\mathbb{P}}_n(\frac{I\{A=d(\mathit{X})\}-\pi \{d(\mathit{X}),\mathit{X}\}}{\pi \{d(\mathit{X}),\mathit{X}\}}. \\ \frac{1-\pi \{d(\mathit{X}),\mathit{X}\}}{\pi \{d(\mathit{X}),\mathit{X}\}}\left[{\widehat{Q}}_0\{\mathit{X},d(\mathit{X})\}-Q\{\mathit{X},d(\mathit{X});\mathit{\beta }\}\right]Q_{\mathit{\beta }}\{\mathit{X},d(\mathit{X});\mathit{\beta }\})=0. \end{gathered}$$

Here, (*) is the left hand side of (6), and ${\widehat{Q}}_0\{\mathit{X},d(\mathit{X})\}={\widehat{Q}}_0(\mathit{X},1)I\{d(\mathit{X})=1\}+{\widehat{Q}}_0(\mathit{X},-1)I\{d(\mathit{X})=-1\}.{\widehat{Q}}_0(\mathit{X},a)$ is the estimator for $E(Y|\mathit{X},A=a)$. We propose to use nonparametric techniques for obtaining ${\widehat{Q}}_0(\mathit{X},a)$, which provides flexibility in model specification. For continuous X, we apply the kernel regression method, i.e.,

$${\widehat{Q}}_0(\mathit{X},a)=\frac{\sum _{i=1}^n{K}_H({\mathit{X}}_i-\mathit{X})I(A_i=a)Y_i}{\sum _{i=1}^n{K}_H({\mathit{X}}_i-\mathit{X})I(A_i=a)},$$

where $K_{\mathit{H}}(\cdot )=|\mathit{H}{|}^{-1/2}K({\mathit{H}}^{-1/2}\cdot )$ is a multivariate kernel with a bandwidth matrix H. When X contains both continuous and categorical variables, the ‘generalized product kernels’ from Racine and Li (2004) is used. Under some regularity conditions, ${\widehat{Q}}_0\{\mathit{X},d(\mathit{X})\}$ is a consistent estimator for $Q_0\{\mathit{X},d(\mathit{X})\}$. As a consequence, ${\mathit{\beta }}^{\text{opt}2}\stackrel{p}{\to }{\mathit{\beta }}^{\text{opt}}$ when the propensity score is correct; and ${\mathit{\beta }}^{\text{opt}2}\stackrel{p}{\to }{\mathit{\beta }}_0$ when the outcome regression is correct. The following lemma formally establishes the improved doubly robust property of the estimator $\widehat{V}(d;{\mathit{\beta }}^{\text{opt}2})$. The technical conditions and the proofs are provided in Appendix A.

Lemma 3.

$\widehat{V}(d;{\mathit{\beta }}^{\text{opt}2})\to V(d)$ when either the propensity score or the outcome regression model is correctly specified. In addition, when the propensity score is correct, $\widehat{V}(d;{\mathit{\beta }}^{\text{opt}2})$ achieves the smallest asymptotic variance among all estimators of form (2).

2.3. Scenario where there is a nuisance parameter in the propensity score model

In practice, if the propensity scores are unknown, we can posit a parametric propensity score model $\pi (A,\mathit{X};\mathit{\gamma })$ involving some nuisance parameters. To construct an improved DR estimator for the value function, we must take into account the effect of estimating γ. Consider the class of AIPW estimators presented in (1). Let $\widehat{\mathit{\gamma }}$ be the maximum likelihood estimator of γ based on ${\{(A_i,{\mathit{X}}_i)\}}_{i=1}^n$. We aim to find ${\mathit{\beta }}^{\text{opt}}$ such that $\widehat{V}(d;\widehat{\mathit{\gamma }},{\mathit{\beta }}^{\text{opt}})$ is doubly robust, and has the smallest asymptotic variance among the class of estimators (1) when the propensity score is correctly specified.

Since $\widehat{\mathit{\gamma }}$ is the maximizer of the binomial likelihood

$$\prod _{i=1}^n\pi {(1,{\mathit{X}}_i;\mathit{\gamma })}^{I(A_i=1)}{\{1-\pi (1,{\mathit{X}}_i;\mathit{\gamma })\}}^{I(A_i=-1)},$$

the score vector for γ is

$$S_{\mathit{\gamma }}(A,\mathit{X},\mathit{\gamma })=I(A=1)\frac{{\pi }_{\mathit{\gamma }}(1,\mathit{X};\mathit{\gamma })}{\pi (1,\mathit{X};\mathit{\gamma })}-I(A=-1)\frac{{\pi }_{\mathit{\gamma }}(1,\mathit{X};\mathit{\gamma })}{1-\pi (1,\mathit{X};\mathit{\gamma })},$$

where ${\pi }_{\mathit{\gamma }}(1,\mathit{X};\mathit{\gamma })=\partial \pi (1,\mathit{X};\mathit{\gamma })/\partial \mathit{\gamma }$. When $\pi (A,\mathit{X};\mathit{\gamma })$ is correctly specified, i.e. $\pi \left(A,\mathit{X};{\mathit{\gamma }}_0\right)={\pi }_0(A,\mathit{X})$ for some γ₀, and β converging in probability to β*, the influence functions corresponding to estimators of the form (1) have the following expression

$$\tilde{\phi }(Y,A,\mathit{X},{\mathit{\gamma }}_0,{\mathit{\beta }}^{*})-{\mathrm{\Gamma }}_0({\mathit{\beta }}^{*}){\mathrm{\Sigma }}_{\mathit{\gamma }\mathit{\gamma },0}^{-1}{S}_{\mathit{\gamma }}\left(A,\mathit{X},{\mathit{\gamma }}_0\right),$$ (7)

where ${\mathrm{\Sigma }}_{\mathit{\gamma }\mathit{\gamma },0}=E\{S_{\mathit{\gamma }}(A,\mathit{X},{\mathit{\gamma }}_0)S_{\mathit{\gamma }}^{\top }(A,\mathit{X},{\mathit{\gamma }}_0)\},{\mathrm{\Gamma }}_0(\mathit{\beta })=-E\{\partial \tilde{\phi }(Y,A,\mathit{X},{\mathit{\gamma }}_0,\mathit{\beta })/\partial {\mathit{\gamma }}^{\top }\}$, and $\tilde{\phi }(Y,A,\mathit{X},\mathit{\gamma },\mathit{\beta })=\frac{YI\{A=d(\mathit{X})\}}{\pi \{d(\mathit{X}),\mathit{X};\mathit{\gamma }\}}-\frac{I\{A=d(\mathit{X})\}-\pi \{d(\mathit{X}),\mathit{X};\mathit{\gamma }\}}{\pi \{d(\mathit{X}),\mathit{X};\mathit{\gamma }\}}Q\{\mathit{X},d(\mathit{X});\mathit{\beta }\}-V(d).$

Compared with (3), the influence functions (7) involve an additional term due to estimation of γ. However, this additional term disappears when both models are correct. Define ${\mathrm{\Phi }}_0(\mathit{\beta })\triangleq -E\{{\partial }^2\tilde{\phi }\left(Y,A,\mathit{X},{\mathit{\gamma }}_0,\mathit{\beta }\right)/\partial {\mathit{\gamma }}^{\top }\partial \mathit{\beta }\}$. In a slight abuse of notation, denote the minimizer of the variance of (7) as ${\mathit{\beta }}^{\text{opt}}$. It is the solution to

$$\begin{gathered} E(\frac{1-{\pi }_0\{d(\mathit{X}),\mathit{X}\}}{{\pi }_0\{d(\mathit{X}),\mathit{X}\}}\left[Q_{\mathit{\beta }}\{\mathit{X},d(\mathit{X});\mathit{\beta }\}+{\mathrm{\Phi }}_0(\mathit{\beta }){\mathrm{\Sigma }}_{\mathit{\gamma }\mathit{\gamma },0}^{-1}\frac{{\pi }_{\mathit{\gamma }}\left\{d(\mathit{X}),\mathit{X};{\mathit{\gamma }}_0\right\}}{1-{\pi }_0\{d(\mathit{X}),\mathit{X}\}}\right] \\ .\left[Q_0\{\mathit{X},d(\mathit{X})\}-Q\{\mathit{X},d(\mathit{X});\mathit{\beta }\}-{\mathrm{\Gamma }}_0(\mathit{\beta }){\mathrm{\Sigma }}_{\mathit{\gamma }\mathit{\gamma },0}^{-1}·\frac{{\pi }_{\mathit{\gamma }}\left\{d(\mathit{X}),\mathit{X};{\mathit{\gamma }}_0\right\}}{1-{\pi }_0\{d(\mathit{X}),\mathit{X}\}}\right])=0. \end{gathered}$$ (8)

Detailed derivations of the influence function and its variance are deferred to Appendix A.

To compress notations, we write to $R\triangleq I\{A=d(\mathit{X})\}$. Consider ${\mathit{\beta }}^{\text{opt}3}$ as the solution to

$$\begin{gathered} {\mathbb{P}}_n\left(\frac{R[1-\pi \{d(\mathit{X}),\mathit{X};\widehat{\mathit{\gamma }}\}}{{\pi }^2\{d(\mathit{X}),\mathit{X};\widehat{\mathit{\gamma }}\}}\right[Q_{\mathit{\beta }}\{\mathit{X},d(\mathit{X});\mathit{\beta }\}+\widehat{\mathrm{\Phi }}(\mathit{\beta }){\widehat{\mathrm{\Sigma }}}_{\mathit{\gamma }\mathit{\gamma }}^{-1}·\frac{{\pi }_{\mathit{\gamma }}\{d(\mathit{X}),\mathit{X};\widehat{\mathit{\gamma }}\}}{1-\pi \{d(\mathit{X}),\mathit{X};\widehat{\mathit{\gamma }}\}}] \\ \left[Y-Q\{\mathit{X},d(\mathit{X});\mathit{\beta }\}-\widehat{\mathrm{\Gamma }}(\mathit{\beta }){\widehat{\mathrm{\Sigma }}}_{\mathit{\gamma }\mathit{\gamma }}^{-1}\frac{{\pi }_{\mathit{\gamma }}\{d(\mathit{X}),\mathit{X};\widehat{\mathit{\gamma }}\}}{1-\pi \{d(\mathit{X}),\mathit{X};\widehat{\mathit{\gamma }}\}}\right])=0, \end{gathered}$$ (9)

where ${\widehat{\mathrm{\Sigma }}}_{\mathit{\gamma }\mathit{\gamma }}={\mathbb{P}}_{\mathit{\gamma }\mathit{\gamma }}\left\{S_{\mathit{\gamma }}(A,\mathit{X},\widehat{\mathit{\gamma }})S_{\mathit{\gamma }}^{\top }(A,\mathit{X},\widehat{\mathit{\gamma }})\right\},\widehat{\mathrm{\Gamma }}(\mathit{\beta })=-{\mathbb{P}}_n\left\{\partial \tilde{\phi }(Y,A,\mathit{X},\widehat{\mathit{\gamma }},\mathit{\beta })/\partial {\mathit{\gamma }}^{\top }\right\}$, and $\widehat{\mathrm{\Phi }}(\mathit{\beta })=-{\mathbb{P}}_n\left\{{\partial }^2\tilde{\phi }(Y,A,\mathit{X},\widehat{\mathit{\gamma }},\mathit{\beta })/\partial {\mathit{\gamma }}^{\top }\partial \mathit{\beta }\right\}$. In Appendix A, we show that $\widehat{V}(d;\widehat{\mathit{\gamma }},{\mathit{\beta }}^{\text{opt}3})$ is doubly robust, and achieves the smallest asymptotic variance with ${\mathit{\beta }}^{\text{opt}3}\stackrel{p}{\to }{\mathit{\beta }}^{\text{opt}}$ when the propensity score is correct.

Correspondingly, we can construct an augmented inverse-probability weighted estimating equation and consider ${\mathit{\beta }}^{\text{opt4}}$ as the solution to

$$\begin{gathered} (**)-{\mathbb{P}}_n(\frac{[R-\pi \{d(\mathit{X}),\mathit{X};\widehat{\mathit{\gamma }}\}][1-\pi \{d(\mathit{X}),\mathit{X};\widehat{\mathit{\gamma }}\}]}{{\pi }^2\{d(\mathit{X}),\mathit{X};\widehat{\mathit{\gamma }}\}} \\ ·\left[Q_{\mathit{\beta }}\{\mathit{X},d(\mathit{X});\mathit{\beta }\}+\widehat{\mathrm{\Phi }}(\mathit{\beta }){\widehat{\mathrm{\Sigma }}}_{\mathit{\gamma }\mathit{\gamma }}^{-1}\cdot \frac{{\pi }_{\mathit{\gamma }}\{d(\mathit{X}),\mathit{X};\widehat{\mathit{\gamma }}\}}{1-\pi \{d(\mathit{X}),\mathit{X};\widehat{\mathit{\gamma }}\}}\right] \\ ·\left[{\widehat{Q}}_0\{\mathit{X},d(\mathit{X})\}-Q\{\mathit{X},d(\mathit{X});\mathit{\beta }\}-\widehat{\mathrm{\Gamma }}(\mathit{\beta }){\widehat{\mathrm{\Sigma }}}_{\mathit{\gamma }\mathit{\gamma }}^{-1}\frac{{\pi }_{\mathit{\gamma }}\{d(\mathit{X}),\mathit{X};\widehat{\mathit{\gamma }}\}}{1-\pi \{d(\mathit{X}),\mathit{X};\widehat{\mathit{\gamma }}\}}\right])=0, \end{gathered}$$ (10)

where (**) is the left hand side of (9). Using a similar argument, $\widehat{V}(d;\widehat{\mathit{\gamma }},{\mathit{\beta }}^{\text{opt}4})$ satisfies (i) and (ii), and is improved doubly robust.

In the above discussion, we proposed improved DR estimators of V(d) for a fixed treatment regime d. Notice that by (8), the optimal value ${\mathit{\beta }}^{\text{opt}}$ is d-dependent, i.e., different d’s correspond to different ${\mathit{\beta }}^{\text{opt}}$. Rigorously speaking, we should write ${\mathit{\beta }}^{\text{opt}}$(d), and ${\mathit{\beta }}^{\text{opt}}$(d) for the nuisance parameter estimates. To estimate $d^{\text{opt}}$, we first identify the corresponding ${\mathit{\beta }}^{\text{opt}}(d)$ and the $\widehat{V}\{d;\widehat{\mathit{\gamma }},{\mathit{\beta }}^{\text{opt}}(d)\}$, for each $d\in \mathcal{D}$. We then find the optimal d among the class $\mathcal{D}$ that leads to the largest $\widehat{V}\{d;\widehat{\mathit{\gamma }},{\mathit{\beta }}^{\text{opt}}(d)\}$, i.e., $\widehat{d}=\arg {\max }_{d\in \mathcal{D}}\widehat{V}\{d;\widehat{\mathit{\gamma }},{\mathit{\beta }}^{\text{opt}}(d)\}$. In practice, the ITR is often indexed by a set of parameters, for instance, $d(\mathit{x})=\mathrm{sign}\{{\mathit{x}}^{\top }\mathit{\eta }\}$, where $\mathit{x}={(1,{\mathit{x}}^{\top })}^{\top }$. Since $\widehat{V}\{d;\widehat{\mathit{\gamma }},{\mathit{\beta }}^{\text{opt}}(d)\}$ is a nonsmooth function of η, standard optimization methods can be problematic. We used a genetic algorithm discussed by Goldberg (1989), which is available in the R package rgenoud (Mebane Jr and Sekhon, 2011). In the rest of the paper, we suppress the letter d in ${\mathit{\beta }}^{\text{opt}}(d)$ and ${\mathit{\beta }}^{\text{opt}}(d)$ when there is no confusion.

3. Theoretical results

In this section, we establish asymptotic normality of the proposed estimators and the usual doubly robust estimator of V(d). We do not discuss the situation when both propensity score and outcome models are misspecified, given that the resulting estimator is not consistent for V(d). We first consider the case where propensity score is fully specified. We have the following result.

Theorem 1.

(Asymptotic normality when propensity score model is full specified). When either the propensity score or the outcome model is correct,

$$\sqrt{n}\left\{\widehat{V}(d;{\mathit{\beta }}^{\text{LS}})-V(d)\right\}\stackrel{D}{\to }N(0,U_1({\mathit{\theta }}_0^{\text{LS}})),$$

$$\sqrt{n}\left\{\widehat{V}(d;{\mathit{\beta }}^{\text{opt1}})-V(d)\right\}\stackrel{D}{\to }N(0,U_2({\mathit{\theta }}_0^{\text{opt1}})),$$

$$\sqrt{n}\left\{\widehat{V}(d;{\mathit{\beta }}^{\text{opt2}})-V(d)\right\}\stackrel{D}{\to }N(0,U_3({\mathit{\theta }}_0^{\text{opt2}})).$$

See Appendix C for detailed expressions of $U_1(\mathit{\theta }),U_2(\mathit{\theta }),U_3(\mathit{\theta })$. The true parameters are ${\mathit{\theta }}_0^{\text{LS}}={({\mathit{\beta }}_{\text{LS}}^{*\top },V(d))}^{\top }$ where ${\mathit{\beta }}_{\text{LS}}^{*}$ satisfies $E\left[Q_{\mathit{\beta }}(\mathit{X},A;{\mathit{\beta }}_{\text{LS}}^{*})\left\{Y-Q(\mathit{X},A;{\mathit{\beta }}_{\text{LS}}^{*})\right\}\right]=\mathit{0}$. ${\mathit{\theta }}_0^{\text{opt}1}={({{\mathit{\beta }}_{\text{opt}1}^{*}}^{\top },V(d))}^{\top }$ where ${\mathit{\beta }}_{\text{opt}1}^{*}$ satisfies $E\left(\frac{I\{A=d(\mathit{X})\}}{\pi \{d(\mathit{X}),\mathit{X}\}}·\frac{1-\pi \{d(\mathit{X}),\mathit{X}\}}{\pi \{d(\mathit{X}),\mathit{X}\}}\left[Y-Q\left\{\mathit{X},d(\mathit{X});{\mathit{\beta }}_{\text{opt2}}^{*}\right\}\right]Q_{\mathit{\beta }}\left\{\mathit{X},d(\mathit{X});{\mathit{\beta }}_{\text{opt1}}^{*}\right\}\right)=\mathit{0}$. ${\mathit{\theta }}_0^{\text{opt}2}={({{\mathit{\beta }}_{\text{opt}2}^{*}}^{\top },V(d))}^{\top }$ where ${\mathit{\beta }}_{\text{opt}2}^{*}$ satisfies

$$\begin{gathered} E\left(\frac{I\{A=d(\mathit{X})\}}{\pi \{d(\mathit{X}),\mathit{X}\}}·\frac{1-\pi \{d(\mathit{X}),\mathit{X}\}}{\pi \{d(\mathit{X}),\mathit{X}\}}\left[Y-Q\left\{\mathit{X},d(\mathit{X});{\mathit{\beta }}_{\text{opt2}}^{*}\right\}\right]Q_{\mathit{\beta }}\left\{\mathit{X},d(\mathit{X});{\mathit{\beta }}_{\text{opt}2}^{*}\right\}\right) \\ -E(\frac{I\{A=d(\mathit{X})\}-\pi \{d(\mathit{X}),\mathit{X}\}}{\pi \{d(\mathit{X}),\mathit{X}\}}\cdot \frac{1-\pi \{d(\mathit{X}),\mathit{X}\}}{\pi \{d(\mathit{X}),\mathit{X}\}}. \\ \left[Q_0\{\mathit{X},d(\mathit{X})\}-Q\left\{\mathit{X},d(\mathit{X});{\mathit{\beta }}_{\text{opt2}}^{*}\right\}\right]Q_{\mathit{\beta }}\left\{\mathit{X},d(\mathit{X});{\mathit{\beta }}_{\text{opt}2}^{*}\right\})=\mathit{0}. \end{gathered}$$

The estimators $\widehat{V}(d;{\mathit{\beta }}^{\text{LS}})$ and $\widehat{V}(d;{\mathit{\beta }}^{\text{opt1}})$ involve solving jointly a set of M-estimating equations (Stefanski and Boos, 2002). Thus, the asymptotic variance of $\widehat{V}(d;{\mathit{\beta }}^{\text{LS}})$ and $\widehat{V}(d;{\mathit{\beta }}^{\text{opt1}})$ can be calculated based on standard M-estimation theory. The estimator $\widehat{V}(d;{\mathit{\beta }}^{\text{opt2}})$ is obtained by solving a set of estimating equations where some infinite dimensional parameters, in this case, $Q_0(\mathit{X},a),a=\pm 1$, are estimated nonparametrically in the first stage, which is referred to as semiparametric M-estimators (Andrews, 1994; Newey, 1994; Chen et al., 2003; Ichimura and Lee, 2010). In Appendix B, we establish asymptotic normality of such semiparametric M-estimators by extending Theorem 2 in Chen et al. (2003). The detailed proof of Theorem 1 can be found in Appendix C.

Remark 1.

When propensity score is correct, it can be shown that $U_1(\mathit{\theta })=U_2(\mathit{\theta })=U_3(\mathit{\theta })$ which equals to (4), the asymptotic variance of the influence function for $\widehat{V}(d;\mathit{\beta })$. In addition, when propensity score is correct but outcome model incorrect, ${\mathit{\beta }}_{\text{opt1}}^{*}={\mathit{\beta }}_{\text{opt2}}^{*}={\mathit{\beta }}^{\text{opt}}$. Recall that ${\mathit{\beta }}^{\text{opt}}$ is defined in (5), which minimizes the asymptotic variance (4). However, ${\mathit{\beta }}_{\text{LS}}^{*}$, the limit of least squares estimates, is different from ${\mathit{\beta }}^{\text{opt}}$. Consequently, $\widehat{V}(d;{\mathit{\beta }}^{\text{opt1}})$ and $\widehat{V}(d;{\mathit{\beta }}^{\text{opt2}})$ have the same asymptotic variance, which is smaller than that of $\widehat{V}(d;{\mathit{\beta }}^{\text{LS}})$. Though, in small sample size scenarios, $\widehat{V}(d;{\mathit{\beta }}^{\text{opt2}})$ is preferred since it utilizes the complete data, and could lead to a more stable estimate. When both models are correct, ${\mathit{\beta }}^{\text{opt}}={\mathit{\beta }}_{\text{LS}}^{*}={\mathit{\beta }}_0$, where ${\mathit{\beta }}_0$ satisfies $Q\left(\mathit{X},A;{\mathit{\beta }}_0\right)=Q_0(\mathit{X},A)$. As a result, all three estimators have the same asymptotic variance. When the outcome model is correct but propensity score incorrect, it is not possible to directly compare the asymptotic variances of these estimators.

The following theorem presents asymptotic properties of $\widehat{V}(d;\widehat{\mathit{\gamma }},{\mathit{\beta }}^{\text{opt}3})$ and $\widehat{V}(d;\widehat{\mathit{\gamma }},{\mathit{\beta }}^{\text{opt}4})$, the estimators for the value function of d where there is a nuisance parameter in the propensity score model.

Theorem 2.

(Asymptotic normality when there is a nuisance parameter in the propensity score model). When either the propensity score or the outcome model is correct,

$$\sqrt{n}\left\{\widehat{V}(d;\widehat{\mathit{\gamma }},{\mathit{\beta }}^{\text{LS}})-V(d)\right\}\stackrel{D}{\to }N(0,U_4({\mathit{\theta }}_0^{\text{LS}2})).$$

The true values arewhere ${\mathit{\theta }}_0^{\text{LS}2}={({\mathit{\gamma }}^{*\top },{{\mathit{\beta }}_{\text{LS}}^{*}}^{\top },V(d))}^{\top }$ where ${\mathit{\gamma }}^{*}$ satisfies $E\left\{S_{\mathit{\gamma }}(A,\mathit{X};{\mathit{\gamma }}^{*})\right\}=\mathit{0}$.

When either the propensity score or the outcome model is correct,

$$\sqrt{n}\left\{\widehat{V}(d;\widehat{\mathit{\gamma }},{\mathit{\beta }}^{\text{opt}3})-V(d)\right\}\stackrel{D}{\to }N(0,U_5({\mathit{\theta }}_0^{\text{opt}3})),$$

$$\sqrt{n}\left\{\widehat{V}(d;\widehat{\mathit{\gamma }},{\mathit{\beta }}^{\text{opt4}})-V(d)\right\}\stackrel{D}{\to }N(0,U_6({\mathit{\theta }}_0^{\text{opt4}})).$$

The true parameters are ${\mathit{\theta }}_0^{\text{opt}3}={({\mathit{\gamma }}^{*\top },{{\mathit{\zeta }}_{\text{opt3}}^{*}}^{\top },{{\mathit{\beta }}_{\text{opt}3}^{*}}^{\top },V(d))}^{\top }$ where $({\mathit{\zeta }}_{\text{opt}3}^{*},{\mathit{\beta }}_{\text{opt3}}^{*})$ is the solution to the following set of equations:

$$\begin{gathered} \mathit{\alpha }+E\left\{\partial \tilde{\phi }(Y,A,\mathit{X},{\mathit{\gamma }}^{*},\mathit{\beta })/\partial \mathit{\gamma }\right\}=\mathit{0}, \\ [{\mathit{\psi }}_1,\dots ,{\mathit{\psi }}_q]-E\left\{S_{\mathit{\gamma }}(A,\mathit{X},{\mathit{\gamma }}^{*})S_{\mathit{\gamma }}^{\top }(A,\mathit{X},{\mathit{\gamma }}^{*})\right\}=\mathit{0}, \\ [{\varphi }_1,\dots ,{\varphi }_q]+E\left\{{\partial }^2\tilde{\phi }(Y,A,\mathit{X},{\mathit{\gamma }}^{*},\mathit{\beta })/\partial {\mathit{\gamma }}^{\top }\partial \mathit{\beta }\right\}=\mathit{0}, \end{gathered}$$ (11)

and

$$\begin{gathered} E(\frac{R\left[1-\pi \left\{d(\mathit{X}),\mathit{X};{\mathit{\gamma }}^{*}\right\}\right]}{{\pi }^2\left\{d(\mathit{X}),\mathit{X};{\mathit{\gamma }}^{*}\right\}}\left[Q_{\mathit{\beta }}\{\mathit{X},d(\mathit{X});\mathit{\beta }\}+\left[{\varphi }_1,\dots ,{\varphi }_q\right]{\left[{\mathit{\psi }}_1,\dots ,{\mathit{\psi }}_q\right]}^{-1}\frac{{\pi }_{\mathit{\gamma }}\left\{d(\mathit{X}),\mathit{X};{\mathit{\gamma }}^{*}\right\}}{1-\pi \left\{d(\mathit{X}),\mathit{X};{\mathit{\gamma }}^{*}\right\}}\right] \\ ·\left[Y-Q\{\mathit{X},d(\mathit{X});\mathit{\beta }\}-{\mathit{\alpha }}^{\top }{\left[{\mathit{\psi }}_1,\dots ,{\mathit{\psi }}_q\right]}^{-1}\frac{{\pi }_{\mathit{\gamma }}\left\{d(\mathit{X}),\mathit{X};{\mathit{\gamma }}^{*}\right\}}{1-\pi \left\{d(\mathit{X}),\mathit{X};{\mathit{\gamma }}^{*}\right\}}\right])=\mathit{0}. \end{gathered}$$ (12)

The true parameters are ${\mathit{\theta }}_0^{\text{opt}4}={({\mathit{\gamma }}^{*\top },{{\mathit{\zeta }}_{\text{opt}4}^{*}}^{\top },{{\mathit{\beta }}_{\text{opt}4}^{*}}^{\top },V(d))}^{\top }$ where $({\mathit{\zeta }}_{\text{opt}4}^{*},{\mathit{\beta }}_{\text{opt}4}^{*})$ is the solution to (11) and

$$\begin{gathered} (***)-E(\frac{\left[R-\pi \{d(\mathit{X}),\mathit{X};{\mathit{\gamma }}^{*}\}\right]\left[1-\pi \{d(\mathit{X}),\mathit{X};{\mathit{\gamma }}^{*}\}\right]}{{\pi }^2\left\{d(\mathit{X}),\mathit{X};{\mathit{\gamma }}^{*}\right\}} \\ ·\left[Q_{\mathit{\beta }}\{\mathit{X},d(\mathit{X});\mathit{\beta }\}+\left[{\varphi }_1,\dots ,{\varphi }_q\right]{\left[{\mathit{\psi }}_1,\dots ,{\mathit{\psi }}_q\right]}^{-1}\frac{{\pi }_{\mathit{\gamma }}\left\{d(\mathit{X}),\mathit{X};{\mathit{\gamma }}^{*}\right\}}{1-\pi \left\{d(\mathit{X}),\mathit{X};{\mathit{\gamma }}^{*}\right\}}\right] \\ ·\left[Q_0\{\mathit{X},d(\mathit{X})\}-Q\{\mathit{X},d(\mathit{X});\mathit{\beta }\}-{\mathit{\alpha }}^{\top }{\left[{\mathit{\psi }}_1,\dots ,{\mathit{\psi }}_q\right]}^{-1}\frac{{\pi }_{\mathit{\gamma }}\left\{d(\mathit{X}),\mathit{X};{\mathit{\gamma }}^{*}\right\}}{1-\pi \left\{d(\mathit{X}),\mathit{X};{\mathit{\gamma }}^{*}\right\}}\right])=\mathit{0}, \end{gathered}$$

where (***) is the left hand side of (12). See Appendix D for detailed expressions of $U_4(\mathit{\theta }),U_5(\mathit{\theta }),U_6(\mathit{\theta })$ and the definitions of $\mathit{\zeta }={({\mathit{\alpha }}^{\top },{\mathit{\psi }}^{\top },{\varphi }^{\top })}^{\top }$, $\mathit{\psi }={({\mathit{\psi }}_1^{\top },\dots ,{\mathit{\psi }}_q^{\top })}^{\top }$, $\varphi ={({\varphi }_1^{\top },\dots ,{\varphi }_q^{\top })}^{\top }$. Note that here we use $[{\varphi }_1,\dots ,{\varphi }_q]$ to represent a matrix with j-th column being ${\varphi }_j$, similarly for $[{\mathit{\psi }}_1,\dots ,{\mathit{\psi }}_q]$.

Remark 2.

When the propensity score model is correct, observe that ${\mathit{\theta }}_0^{\text{opt}3}={\mathit{\theta }}_0^{\text{opt}4}$ where ${\mathit{\beta }}_{\text{opt}3}^{*}={\mathit{\beta }}_{\text{opt}4}^{*}={\mathit{\beta }}^{\text{opt}}$, where ${\mathit{\beta }}^{\text{opt}}$ is the the minimizer of the variance of (7) in this case. Furthermore, it can be shown that $U_4({\mathit{\theta }}_0^{\text{LS}2})$, $U_5({\mathit{\theta }}_0^{\text{opt}3})$, $U_6({\mathit{\theta }}_0^{\text{opt}4})$ equal to the variance of (7) evaluated at $\mathit{\beta }={\mathit{\beta }}_{\text{LS}}^{*}$ and ${\mathit{\beta }}^{*}={\mathit{\beta }}^{\text{opt}}$, respectively. Therefore, when the propensity score is correct but outcome incorrect, $\widehat{V}(d;\widehat{\mathit{\gamma }},{\mathit{\beta }}^{\text{opt}3})$ and $\widehat{V}(d;\widehat{\mathit{\gamma }},{\mathit{\beta }}^{\text{opt4}})$ are asymptotically equivalent and more efficient than $\widehat{V}(d;\widehat{\mathit{\gamma }},{\mathit{\beta }}^{\text{LS}})$. When both models are correct, all three estimators are asymptotically equivalent.

Remark 3.

An estimator for $V(d^{\text{opt}})$, the overall population mean under the optimal regime, may be found as $\widehat{V}\{\widehat{d};\widehat{\mathit{\gamma }},{\mathit{\beta }}^{\text{opt}}(\widehat{d})\}$. Following Zhang et al. (2012), $n^{1/2}\left[\widehat{V}\{\widehat{d};\widehat{\mathit{\gamma }},{\mathit{\beta }}^{\text{opt}}(\widehat{d})\}-V(d^{\text{opt}})\right]=n^{1/2}\left[\widehat{V}\{d^{\text{opt}};\widehat{\mathit{\gamma }},{\mathit{\beta }}^{\text{opt}}(d^{\text{opt}})\}-V(d^{\text{opt}})\right]+o_p(1)$.

Thus, the asymptotic variance of $\widehat{V}\{\widehat{d};\widehat{\mathit{\gamma }},{\mathit{\beta }}^{\text{opt}}(\widehat{d})\}$ can be approximated by that of $\widehat{V}\{d^{\text{opt}};\widehat{\mathit{\gamma }},{\mathit{\beta }}^{\text{opt}}(d^{\text{opt}})\}$, which by Theorem 2 can be estimated using the usual sandwich technique.

4. Simulation Studies

We conducted several simulation studies to evaluate the finite sample performance of our proposed method. The following six methods were compared: Q-learning based on linear regression (QL-LR, Qian and Murphy (2011)); Q-learning based on kernel regression (QL-KR); maximizing ${\widehat{V}}^{\text{IPWE}}(d;\widehat{\mathit{\gamma }})$ within a pre-specified class of ITRs (IPWE); maximizing $\widehat{V}(d;\widehat{\mathit{\gamma }},\mathit{\beta })$ where standard maximum likelihood estimators are used for the nuisance parameters (Usual-DR, Zhang et al. (2012)); maximizing $\widehat{V}(d;\widehat{\mathit{\gamma }},{\mathit{\beta }}^{\text{opt3}})$ where ${\mathit{\beta }}^{\text{opt3}}$ solves the IPW estimating equation (9) (Improved-DR); maximizing $\widehat{V}(d;\widehat{\mathit{\gamma }},{\mathit{\beta }}^{\text{opt}4})$ where DR). ${\mathit{\beta }}^{\text{opt}4}$ solves the augmented IPW estimating equation (10) (Aug-Improved-DR).

The simulation set up is similar to Kang and Schafer (2007) with some modifications. $\mathit{Z}=\left(Z_1,Z_2,Z_3,Z_4\right)$ was generated as standard multivariate normal, and $\mathit{X}=\left(X_1,X_2,X_3,X_4\right)$ was defined as $X_1=\exp \left(Z_1/2\right),X_2=Z_2/\left\{1+\exp \left(Z_1\right)\right\}+10,X_3={\left(Z_1{Z}_3/25+0.6\right)}^3,X_4={\left(Z_2+Z_4+20\right)}^2$, so that Z can be expressed in terms of X. The treatment A was generated from $\{-1,1\}$ according to the model $P(A=1|\mathit{X})=\exp \{l(\mathit{X})\}/[1+\exp \{l(\mathit{X})\}]$, where l(x) = − z₁ + 0.5z₂ − 0.25z₃ − 0.1z₄ in Scenario 1, and $l(\mathit{x})=0.5z_1-0.5$ in Scenario 2. The response variable was normally distributed with $Y=10+27.4Z_1+13.7Z_2+13.7Z_3+13.7Z_4+A\left(-1-10Z_1+10Z_2\right)+ϵ$, where $ϵ~N(0,1)$. It is straightforward to deduce that $d^{\text{opt}}(\mathit{x})=\mathrm{sign}\left(-1-10z_1+10z_2\right)$. Via Monte Carlo simulation with 10⁶ replicates, we obtained $E\{Y(d^{\text{opt}})\}=21.32$. The following modeling choices are considered for the propensity and outcome regression models.

CCA correctly specified logistic regression model for ${\pi }_0(A;\mathit{X})$ with Z as predictors in both scenarios, and a correctly specified model for $Q_0(\mathit{X},A)$ with Z, A, ZA as predictors in both scenarios.

CI A correctly specified logistic regression model for ${\pi }_0(A;\mathit{X})$ with Z as predictors in both scenarios, and an incorrectly specified model for $Q_0(\mathit{X},A)$ with $\mathit{X},A,\mathit{Z}A$ as predictors in both scenarios.

IC An incorrectly specified logistic regression model for ${\pi }_0(A;\mathit{X})$ with X as predictors in Scenario 1, and without any predictors in Scenario 2, and a correctly specified model for $Q_0(\mathit{X},A)$ with Z, A, ZA as predictors in both scenarios.

II An incorrectly specified logistic regression model for ${\pi }_0(A;\mathit{X})$ with X as predictors in Scenario 1, and without any predictors in Scenario 2, and an incorrectly specified model for $Q_0(\mathit{X},A)$ with $\mathit{X},A,\mathit{Z}A$ as predictors in both scenarios.

For IPWE, we use C. and I. to denote correct and incorrect propensity models, respectively. For QL-LR, we use.C and.I to denote correct and incorrect linear regression models. For QL-KR, we use .C and .I to denote kernel regression based on (Z, A) and based on (X, A), respectively. In all direct-maximization methods (IPWE, Usual-DR, Improved-DR, Aug-Improved-DR), we choose $\mathcal{D}=\{\mathrm{sign}({\eta }_0+{\eta }_1{z}_1+{\eta }_2{z}_2+{\eta }_3{z}_3+{\eta }_4{z}_4)\}$ so that $d^{\text{opt}}\in \mathcal{D}$. By imposing $\Vert \mathit{\eta }\Vert =1$, $d^{\text{opt}}$ corresponds to $\left({\eta }_0,{\eta }_1,{\eta }_2,{\eta }_3,{\eta }_4\right)=(-0.07,-0.71,0.71,0,0)$.

For each scenario, we considered four sample sizes for training datasets: n = 100, 250, 500 or 1000, and repeated the simulation 500 times. The ITRs are constructed based on the training set and then evaluated on a large and independent test set (size 10000) based on two criteria: value function, i.e., the overall population mean when we apply the estimated optimal ITR to the test dataset; the misclassification error rate of the estimated optimal ITR from the true optimal ITR, i.e., ${\mathbb{P}}_n^{*}\left[I\{\widehat{d}(\mathit{X})\ne d^{\text{opt}}(\mathit{X})\}\right]$. Here ${\mathbb{P}}_n^{*}$ denotes the empirical measure using the test data.

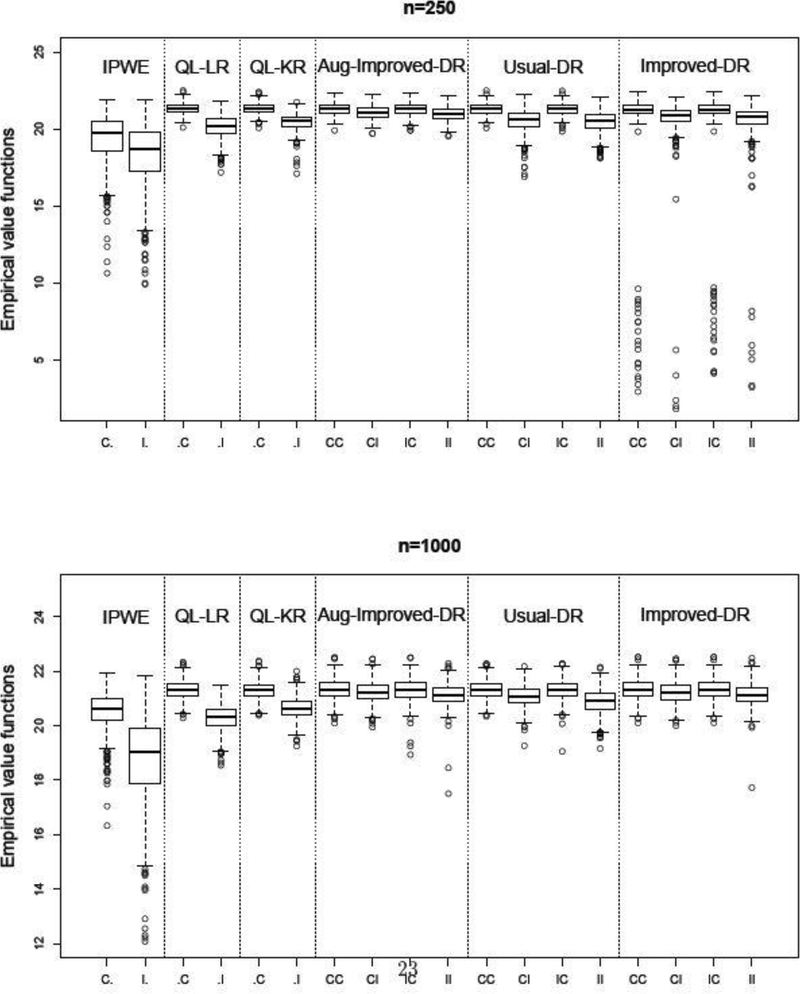
Results for Scenario 1 are presented in Figure 1, where we draw boxplots of the value functions over 500 replications. Here we only report the results for n = 250 or 1000 (see Appendix E for further results, e.g., n = 100 or 500). As expected, Q-learning works the best if the outcome model is correctly specified but has relatively poor performance if this model is incorrect. When the outcome model is correct (CC, IC), Aug-Improved-DR and Usual-DR have similar performance. This is not surprising. Recall that when the outcome model is correct, the proposed nuisance parameter estimate ${\mathit{\beta }}^{\text{opt4}}$ converges in probability to ${\mathit{\beta }}_0$, the same limit of the least squares estimates. When the propensity model is correct but the outcome regression model is misspecified (CI), Aug-Improved-DR dominates Usual-DR, evidenced by larger value functions and smaller variance in value functions, e.g., the mean (sd) of value functions for Aug-Improved-DR are 21.07 (0.43) and 21.23 (0.39) when the sample size is 250 and 1000, respectively. Comparatively, for Usual-DR, the mean (sd) of value functions are 20.52 (0.76) and 21.07 (0.40). In addition, note that Improved-DR and Aug-Improved-DR have almost identical performance when the sample size is large (n = 1000). However, Improved-DR is unstable under small sample size (n = 250). This justifies the need to construct augmented IPW estimating equations to estimate the nuisance parameters, as we discussed in the method section.

Fig. 1.

Simulation results for Scenario 1. Value functions over 500 replications. The optimal value is E{Y(d^opt)} = 21.32.

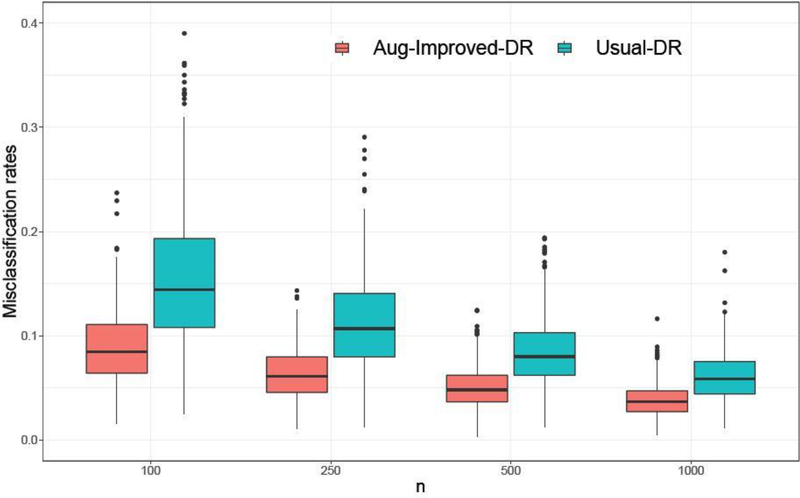
To better demonstrate the superior performance of our proposed method under the CI setting, we focus on the comparison between Aug-Improved-DR and Usual-DR in terms of the misclassification rates. Results for Scenario 1 are shown in Figure 2 with sample sizes ranging from 100 to 1000. Notice that Aug-Improved-DR produced much smaller misclassification rates as well as smaller variations. In particular, it outperforms the usual DR estimator by a large margin when the sample size is small.

Fig. 2.

Simulation results for Scenario 1 under CI: propensity score correct, outcome model incorrect. Misclassification rates over 500 replications.

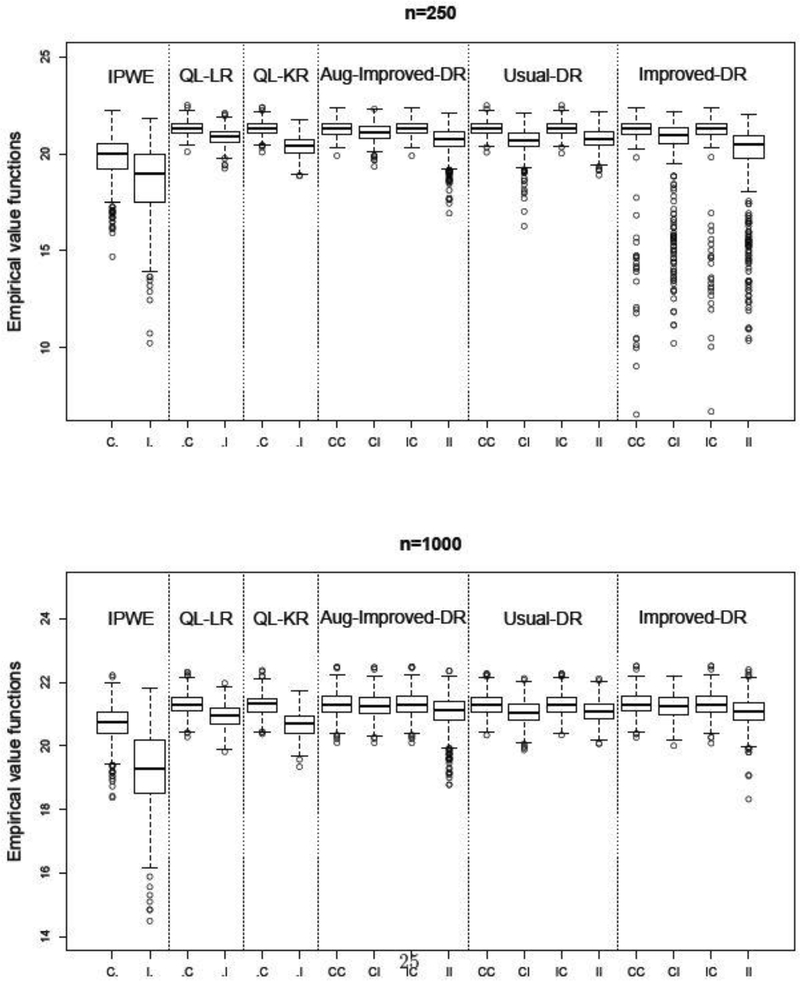
Simulation results for Scenario 2 are provided in Figure 3 and Appendix E. Again, the proposed method outperforms other competing methods in both value functions and misclassification rates. In Appendix E, we also report the mean squared errors (MSE) of different methods in terms of estimating η. Aug-Improved-DR has smaller MSE than its competitors.

Fig. 3.

Simulation results for Scenario 2. Value functions over 500 replications. The optimal value is E{Y(d^opt)} = 21.32.

5. Application to the STAR*D Study

We apply the proposed method to analyze data from the STAR*D Study (Rush et al., 2004). Funded by the National Institute of Mental Health, the study was conducted to compare various treatment options for major depressive disorder when patients fail to respond to the initial treatment of citalopram (CIT). From 2001 to 2006, a total of 4041 outpatients with nonpsychotic depression, aged 18–75, were enrolled from 41 clinical sites in the U.S. The score on the 16-item Quick Inventory of Depressive Symptomatology (QIDS) was the primary outcome. The QIDS score ranges from 0 to 27, where higher scores indicate more severe depression.

The trial had four levels (see Fig. 1 in Rush et al. (2004)). Here, we focused on the first two levels. At level-1, patients received CIT for 12 to 14 weeks. Those who achieved clinically meaningful response (total QIDS score under 5) were remitted from future treatments. At level-2, participants without a satisfactory response to CIT had the option to either switch to a different medication, or to augment their existing citalopram. Those in the “switch” group were randomly assigned to bupropion (BUP), cognitive therapy (CT), sertraline (SER), or venlafaxine (VEN). Those in the “augment” group were randomly assigned to CIT+BUP, CIT+buspirone (BUS), or CIT+CT. If a patient had no preference, he/she was assigned to any of the above treatments.

We use the QIDS score at the end of level-2 as the clinical outcome Y and compared two categories of treatments: (i) treatment with selective serotonin reputake inhibitors (SSRI): CIT+BUP, CIT+BUS, CIT+CT, and SER; (ii) non-SSRI: BUP, CT, and VEN. Denote A = 1 for SSRI and A = − 1 for non-SSRI. Since patients in the “augment” group were all treated with SSRIs (violating the positivity assumption), we exclude these subjects from our analysis, which leaves a total of 817 subjects. Among them, 656 and 161 patients were in the “switch” and “no preference” group, respectively. 296 patients received SSRI treatments, while 521 patients received non-SSRI treatments. Comparisons using t-test show that there is no significant difference between the SSRI and the non-SSRI category with respect to QIDS scores.

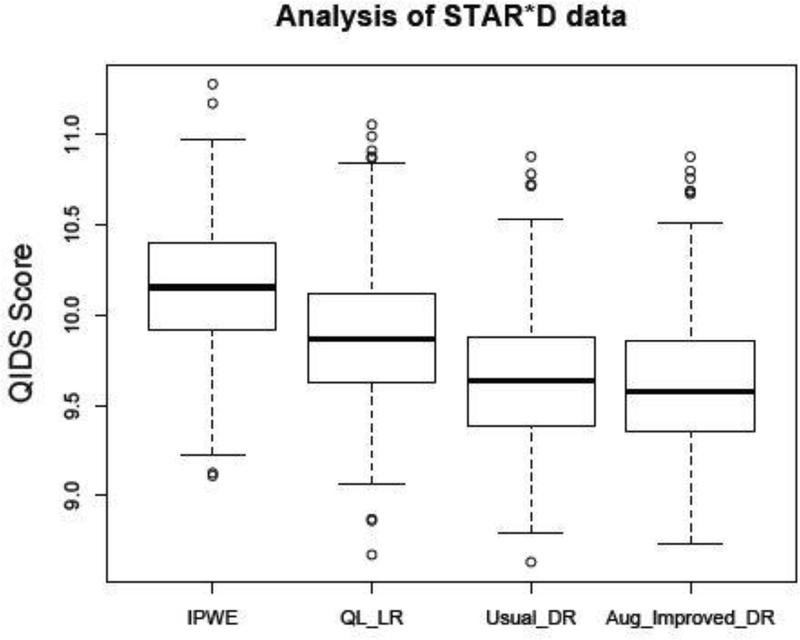
We applied four methods to estimate the optimal ITR for those patients who had entered level-2. Prognostic variables X include QIDS score at the start of level-2, change of QIDS score during the level-1 period, preference regarding level-2 treatment, and other demographic variables such as gender, race, age, education level and employment status. The propensity scores ${\pi }_0(A,\mathit{X})$ estimated by empirical proportions based on preferring to switch or no are preference. We used a linear regression of Y given $(\mathit{X},A,\mathit{X}A)$ for the outcome model. For all methods, we randomly split the data into training and test set with 1:1 ratio. The estimated ITR was obtained using the training set, and then evaluated on the test set by ${\mathbb{P}}_n^{*}\left[YI\{A=\widehat{d}(\mathit{X})\}/{\widehat{\pi }}_0(A,\mathit{X})\right]/{\mathbb{P}}_n^{*}\left[I\{A=\widehat{d}(\mathit{X})\}/{\widehat{\pi }}_0(A,\mathit{X})\right]$. This procedure is repeated 500 times. Results for IPWE, QL-LR, Usual-DR and Aug-Improved-DR are displayed in Figure 4, where lower scores are desirable. The estimated QIDS score by using Aug-Improved-DR is 9.62 (sd = 0.37), which is smaller than IPWE (10.15, sd = 0.36), QL-LR (9.87, sd = 0.38), and Usual-DR (9.65, sd = 0.40). In addition, Aug-Improved-DR outperformed the one-size-fits-all approaches (QIDS score of 9.98 for SSRI and 10.12 for non-SSRI).

Fig. 4.

QIDS score based on 500 replications. Lower scores are more preferable.

6. Discussion

In this article, we proposed an improved DR estimator for the optimal ITRs by directly maximizing an AIPWE of the marginal mean outcome over a class of ITRs. Our estimator is doubly robust, and designed to be more efficient than other DR estimators when the propensity score model is correctly specified, regardless of the specification of the outcome model. As shown in the numerical studies, the proposed method achieves better performance compared to other existing methods. The proposed method is appealing, given that in many practical applications, correct specification of the outcome model can be challenging, while the propensity score is either known by design or more likely to be correctly specified.

There are several important ways this work may be extended. The first is to extend it to the multi-stage decision setting. Zhang et al. (2013) proposed a doubly robust estimator for the optimal DTR where the nuisance parameters indexing the outcome models are estimated iteratively by a sequence of least squares regressions. More efficient DR estimators could be obtained if we use IPW or augmented IPW estimating equations to estimate these nuisance parameters. This is the direction we are currently pursuing.

Another future direction is to consider biased-reduced doubly robust estimation, i.e., estimate the nuisance parameters so as to minimize the bias of the DR estimator under misspecification of both working models. Vermeulen and Vansteelandt (2015) proposed biased-reduced DR estimators for several missing data and causal inference models. It would be interesting to investigate whether this principle can be adapted to the context of estimating optimal treatment regimes.