Do Critical and Functional Threshold Powers Equate in Highly-Trained Athletes?

Abstract

The purpose of this investigation was to determine whether Critical Power (CP) and Functional Threshold Power (FTP) can be used interchangeably for a highly-trained group of cyclists and triathletes. CP was ascertained using multiple fixed load trials and FTP determined from a single cycling trial. Three different models for the determination of CP were initially addressed, one hyperbolic (H_model) and two linear (J_model and I_model). The J_model was identified as most appropriate for a comparison with FTP. The J_model and FTP were not found to be interchangeable as ANOVA detected significant differences (282 ± 53 vs. 266 ± 55 W, p < 0.001) between these indices and the associated Bland-Altman 95% limits of agreement exceeded those set a priori. As the J_model was found to be consistently higher than FTP, a correction factor was posited to anticipate CP from FTP in this homogenous group of athletes using the mean bias (16 W). An alternate method for assessing CP trial intensities using Dmax as a proxy for ventilatory threshold is also proposed. The concept of both CP and FTP representing a maximal metabolic steady-state requires further investigation as the mechanical power at CP was significantly greater than at FTP.

INTRODUCTION

Critical power (CP) is the uppermost exercise intensity that a cyclist can maintain without the necessity for maximum oxygen uptake (VO₂max) and can be maintained in steady-state for up to approximately 30-min (19). Although CP is associated with a physiological demarcation (the upper limit intensity that does not cause a VO₂max response), it is frequently calculated using a choice of mathematical models (9, 12, 22) (Figures 1a, b and c). Functional Threshold Power (FTP) is the “uppermost power a cyclist can maintain in a quasi steady-state for 60-min” (1, 14). Similarly to CP, FTP is not determined using a physiological test rather using a percentage of mean mechanical power output maintained over a 20-min time-trial (1).

Figure 1.

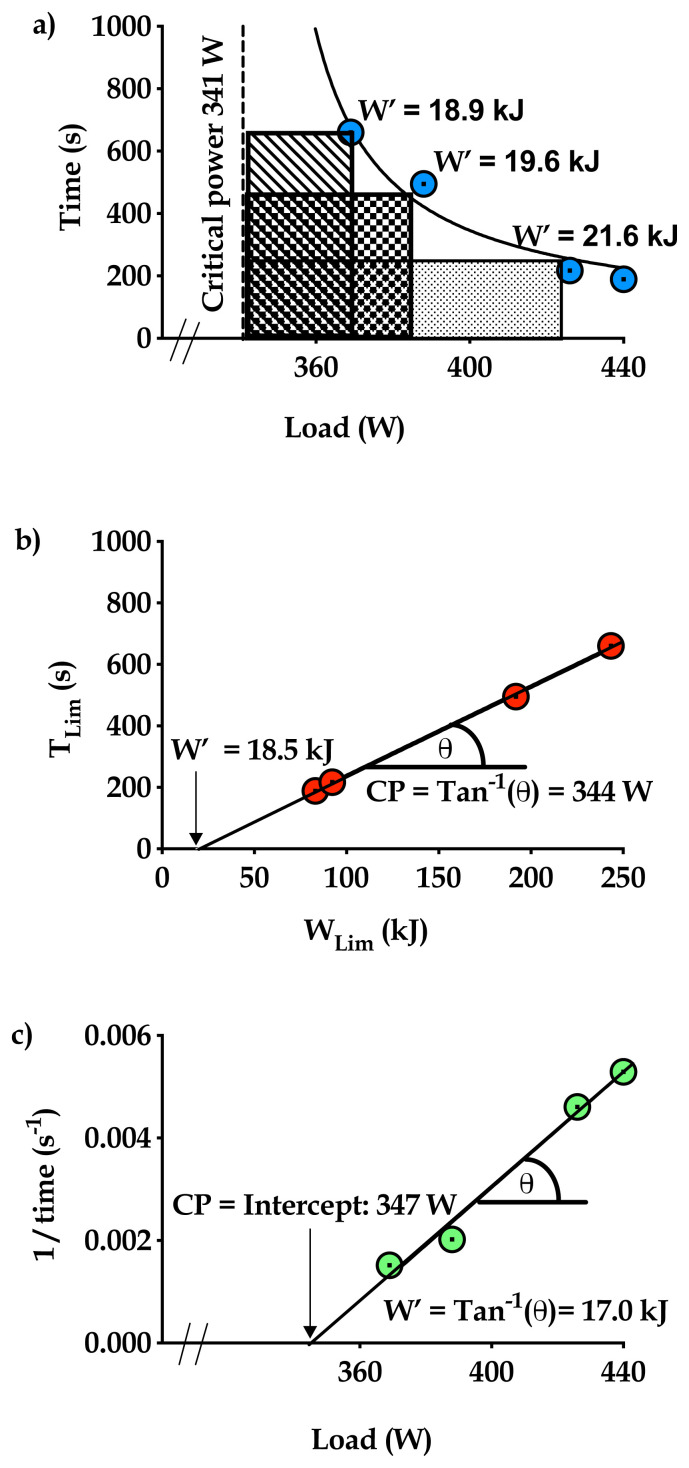
Plots of models used to compute CP and W′ for athlete “A” identifying CP and W’, a) H_model; CP of 341 W, and three measures of W′ derived from three alternate coordinates (19.0, 19.6 and 21.6 kJ), b) J_model; CP of 344 W (inverse of slope of line of best fit; solid black line) and W′ of 18.5 kJ by point of intersection with the X-axis and c) I_model; CP of 347 W by point of intercept with the X-axis and a W′ of 17.0 kJ (inverse of slope of the line of best fit; solid black line).

The gold standard protocol for determining CP involves multiple cycling trials (22). Fixed power trial intensities are orchestrated with the goal of attaining volitional exhaustion, or an inability to sustain a predetermined cadence, after a minimum of 2-min and a maximum of 15-min (21). The fixed power trial exercise intensities may be calculated by adding power at ventilatory threshold (T_vent) to percentages of the difference data between power at T_vent and maximum power (Pmax) attained during a VO₂max test (4, 23). There are multiple equations that can then be applied to this data to estimate CP, with varying results (9). In this investigation, three equations were initially applied to data to determine if there was an optimal model for comparison with FTP.

The first model applied to compute CP plots power (W) against time (s) on a scatter plot, creating a hyperbolic curve (H_model) (9). There is a theoretical upper-limit power output on this hyperbolic curve that a cyclist can sustain indefinitely (Figure 1a). In mathematical modelling this point on the hyperbolic curve is termed an asymptote, and in the context of energetics reflects CP (Figure 1a). The second model that was applied (J_model) converts the hyperbolic curve to a straight-line format by plotting the product of the fixed power output assessed and duration (W_Lim in kJ) against time (T_Lim in s) (15) (Figure 1b). Graphically, the identification of the independent and dependent variable of these variables is difficult to discern as the W_Lim in this instance includes both an independent fraction (power) and a dependent fraction (time). Nevertheless, the alternate axis is the open-ended time that a cyclist can sustain a fixed load (T_Lim). Consequently, W_Lim is placed on the abscissa and time is placed on the ordinate axis. In this linear J_model format, CP is equal to the inverse of the slope of the line fitted to minimize the squared errors (3). The third and final model (I_model) applied to compute CP data also converts the hyperbolic power-time relationship into a linear arrangement (Figure 1c). This linear transformation is achieved by plotting power (W) against the inverse of time (s⁻¹). The I_model also uses linear regression to fit the data and the point of intercept with the abscissa determines CP.

The J_model was first introduced as a model for dynamic exercise, and plotted T_Lim (X-axis) against W_Lim (Y-axis) (15) to identify CP. This seminal paper also highlighted an “energetic reserve”, a source of energy distinct from CP, as the point of the Y-intercept (W_Lim). This energetic reserve was later renamed W′, pronounced W-prime (19). Researchers are currently unable to measure W′ directly, or indeed to define the index physiologically. Broadly, W′ purports to reflect a “finite energy store comprising O₂ stores, a phosphagen pool, aerobic and a source of anaerobic glycogenolysis” (3). The variable W′ is reportedly a fixed constant and will only replenish if power output is reduced to a level below CP (7). Practically, each Joule contained in W′ equates to one Watt for one second. The quantum of energy (J) available is limited by the magnitude of W′. The rate at which W′ is used is dependent on the amount of power produced above CP. In the current investigation, W′ data from the H_model equates to the integrated area between an X-intercept above CP and the associated Y-intercept on the fitted hyperbola (Figure 1a). Using the J_model, W′ is the point of intersection of the line of best fit through the abscissa (Figure 1b). In respect to the I_model, W′ is computed from the inverse slope of the line of best fit where power is the independent variable and the inverse of time the dependent variable (Figure 1c).

Although a stand-alone index, CP is purportedly used principally in conjunction with W′ to predict the time duration a specific power output can be sustained in competition using Equation 1:

$${\text{T}}_{\text{Lim}}={\text{W}}^{\prime }/(\text{P}-\text{CP})$$ Equation 1

Where T_Lim is the limits of tolerance, P = power above CP, and CP is critical power.

Alternatively, rearranging Equation 1; the upper limit power that can be sustained for a given time can be calculated using Equation 2.

$$\text{P}=({\text{W}}^{\prime }/{\text{T}}_{\text{Lim}})+\text{CP}$$ Equation 2

The foundation of these equations is that there is a power output that can be sustained indefinitely; namely, CP, and that any power output above CP is limited by the magnitude of W′. The kernel here is that if W′ lacks foundation or is variable, the predictive capacity of CP in competition is defunct. That stated our limited understanding of the underpinnings of W′ should not impact upon resolution of the relationship, if any, between CP and FTP.

The mean power during a self-paced 20-min time-trial is reduced by 5 % to identify FTP (Table 1). In a trained cohort, FTP has been shown to be sustainable for 60-min with VO₂ and BLa data remaining in a metabolic steady-state (14). Borszcz et al. (5) investigated whether FTP and a 60-min time-trial could be used interchangeably. Their study concluded that these indices should not be used interchangeably as they reported wide T_Lim data (50.9 ± 15.7 min). The cyclists in the Borszcz et al. (5) study adopted an open-paced strategy for their 60-min time-trial; however, a variable paced strategy is likely to produce a smaller mean power than a uniform power output (8). Indeed, the creators of the FTP test furnished an incipient un-validated algorithm, “Normalized Power”, that claimed to convert the additional stress of a variable power output into a constant power output equivalent (1). The cyclists assessed by McGrath et al. (14) were tasked with sustaining FTP uniformly for 60-min. These participants appeared to have had more success, as of the nineteen athletes assessed seventeen completed the 60-min at FTP, while two were unable to maintain FTP beyond 35-min and 52-min, respectively. Borszcz et al. (5) questioned whether the first 46-min of the FTP protocol (Table 1) negated the FTP index. These authors (5) pointed to the FTP warm-up being too long and reported that blood lactate data were too high between the end of the 5-min maximal effort trial and the commencement of the 20-min time-trial. One might argue that the impact of the warm-up, whether positive or negative, is part of the FTP test protocol. Consequently, the adequacy of the recommended warm-up should perhaps be assessed by the outcome of the FTP test as a whole, that is, the ability to predict an upper-limit 60-min steady-state power. The nutrition strategies in these investigations may also have partly impacted on T_Lim data (5, 14), as participants drank CHO beverages between minutes 10 and 50 (14) versus water alone (5).

Table 1.

Protocol for performing the FTP test, replicated from Allen and Coggan (1).

	Time	Description	% FTP
Warm-up	20 min	Endurance pace	65
	3 by 1 min, rest 1-min	Fast pedaling, 100 rev·min−1	Not applicable
	5 min	Easy riding	65
	5 min	Time-trial	Maximum effort
	10 min	Easy riding	65
FTP test	20 min	Time-trial	Maximum effort
Cool down	10 to 15 min.	Easy riding	65

Note. FTP = Functional threshold power; min = minute; rev·min⁻¹ = revolution per minute

The null hypothesis of the current study was that, at the very least CP and FTP would correlate, as both indices (CP and FTP) propose to demark a change from steady to non-steady-state metabolism. Sequentially, we proposed that anticipated narrow limits of agreement (LoA) between CP and FTP would support the respective tests being used interchangeably.

METHODS

Participants

The current study obtained ethical approval from the Faculty of Health Sciences Research Ethics Committee in Trinity College Dublin and was performed in accordance with the ethics standards of the International Journal of Exercise Science (17). Participants completed a consent form prior to beginning any trials. Fifteen (8 female, 7 male) highly-trained cyclists and triathletes, mean age 28 ± 6 y participated. Mean VO₂max data (mL·kg⁻¹·min⁻¹) was 58.8 ± 4.5 and 65.4 ± 7.9 for the female and male cohorts, respectively. Mean anthropometric and related training data are presented in Table 2.

Table 2.

Mean ± standard deviation anthropometric, weekly training duration, and training experience for male (n = 7) and female (n = 8) participants.

Gender	Mass (kg)	Height (m)	BMI (kg·m−2)	Weekly volume (h)	Training (y)
Male	74.6 ± 6.2	1.80 ± 0.05	23.1 ± 2.5	18.3 ± 2.8	5.7 ± 1.9
Female	57.5 ± 6.5	1.69 ± 0.07	20.1 ± 1.0	19.1 ± 3.1	5.9 ± 1.5

Note. kg = kilogram; m = metre; kg·m⁻² = kilogram per metre squared; h = hour; y = year

Protocol

Participants attended the laboratory on seven to eight occasions, in a rested, carbohydrate loaded and euhydrated state, having abstained from alcohol and caffeine in the 24-h prior to testing. A 24-h food diary completed prior to the first trial identified that enlisted participants were consuming a training load adjusted isocaloric diet (macronutrient breakdown; ≥ 60% carbohydrate, ≤ 20% fat and ≤ 20% protein). Each food diary was duplicated and a single copy retained by both the researcher and participant. Each participant was requested to replicate their food intake prior to all subsequent tests, or if different, to consume comparable carbohydrate quantities. When necessary, participants were helped to plan their pre-test meals. A full blood count was performed to screen for sub-clinical anemia and infection. Trials were separated by a minimum of 2 and maximum of 7-day. Training loads were agreed with both athletes and coaches prior to commencing the study, with weekly training load and other stimuli remaining as constant as possible during the testing period. Exercise was limited to aerobic work for 24-h prior to each test. Prior to testing, participants endeavored to duplicate their own bicycle geometry on an electromagnetically braked cycle ergometer (Lode Excalibur Sport; Groningen, The Netherlands), adjusting saddle height and fore-aft position, handlebar height and reach. Individual participant ergometer geometry was recorded and replicated during all subsequent ergometer tests. The same Lode cycle ergometer was used for all test sessions with the exception of the FTP test (athlete’s own bicycle).

The first two tests performed were a 3-min graded incremental test (GxT) and a VO₂max test. Thereafter, two CP tests, a FTP test and two more CP tests were completed. The order of the respective CP tests was agreed with the athlete, and/or coach, so as to balance the athlete’s training programme. Earlobe blood samples for lactate analysis were collected during all tests and analyzed using an Arkray Lactate Pro 2 (Arkray, Shiga, Japan), which required 0.4 μL whole blood samples and had an operating range of 0.5 to 25 mmol·L⁻¹. During all tests, breath-by-breath ventilatory (VE, VO₂ and VCO₂) and heart rate (HR) data were recorded using a calibrated cardio-metabolic cart (CPET; Cosmed, Rome, Italy).

The GxT test commenced with a 10-min warm-up at 100 and 120 W for female and male participants, respectively. The increments for the female and male cohorts were 20 and 25 W, respectively, cadence was controlled between 75 and 110 rev·min⁻¹ and increment duration was 3-min. Blood samples for lactate analysis were collected at 2.5-min into each 3-min increment. Breath-by-breath ventilatory (VE, VO₂ and VCO₂) and HR data were averaged across the final minute of each increment.

The VO₂max test commenced with a 4-min load of 20 W. The female participant protocol stepped the load up to 100W in 1-s and ramped up at a rate of 25 W·min⁻¹ thereafter. The male participant protocol stepped the load to 170 W in 1-s and ramped up at a rate of 30 rev·min⁻¹ thereafter. Tests were continued to volitional exhaustion or until cadence dropped below 70 rev·min⁻¹. VO₂max was classified as the highest mean VO₂ response across ten consecutive breaths.

Data recorded during the VO₂max test data were also used to identify ventilatory threshold (T_vent) using the volume of the slopes of O₂ and CO₂ (V-slope method) (2). The mechanistic basis of this determination is that “excess CO₂ is generated when lactate concentration is increased during exercise because extracellular [H+] is buffered primarily by HCO_3⁻ (22 mL for each mEq of lactate)” (2). Prior to analysis, metabolic data were filtered into 10-s windows to compensate for breathing irregularities (2). A double linear regression model was used to identify this metabolic transition from aerobic to anaerobic exercise. However, prior to applying these two lines of best fit, it was necessary to remove data at the start and end of the test to ensure the two lines of best fit were not affected by irrelevant datum points. Recorded data during the 20 W load period and the first minute of the exercise ramp were therefore excluded, facilitating an initial adjustment in CO₂ stores (2). Later, if the participant commenced hyperventilation, demarked as the point of respiratory compensation (RC), the data above this point were excluded as these data did not reflect metabolic and buffering events in the tissues (2). Hyperventilation was identified using a scatter plot of VCO₂ and VE, with a double linear regression applied with a constraint of > 15 % change in the slope prior to the second line being fitted (2). The remaining VO₂ and VCO₂ data were assessed for a change in the expected slope of > 10 % to demark a transition in metabolism. This constraint, namely, an increase of > 10 % above that expected was built into the modeled regression lines to obscure misleading respiratory data (2). The load for the CP trials was calculated by adding the load at T_vent minus two-thirds of the ramp rate (25 or 30 W·min⁻¹) to 65, 75, 85 and 90% of the delta power between T_vent and the maximum power achieved in the VO₂max test (10). In circumstances where the participant could not complete a minimum of 2-min or exceeded 15-min, a fifth CP trial was completed to fill the pertinent void. The fifth trial was set at a load that was informed by the four pervious trials, using Equation 1, and the experience of the researchers (9). Each CP trial was preceded by a 10-min warm-up at 100 W and a 5-min seated rest. Trials commenced with a low-intensity phase (4-min at 20 W; cadence 90 rev·min⁻¹), the applied load then increased to the desired CP trial intensity over 1-s and thereafter remained constant for the test duration. CP trials continued to volitional exhaustion or until cadence dropped below 70 rev.min⁻¹. The VO₂ on cessation had to have reached 95% of that attained in the VO₂max test to be considered maximal (12).

The FTP test was performed on the athlete’s own bicycle using Garmin pedals (Garmin, KA, USA) to measure power, with the bicycle mounted on an indoor trainer (LeMond Revolution, WA, USA). All pedals used were calibrated prior to each trial as per the manufacturer’s instructions to zero offset. Having completed the FTP test, the Garmin pedals were subsequently placed on the Lode cycle ergometer and calibrated at their ascertained FTP to mitigate any differences in the respective devices. The corrected FTP (that measured on the Lode ergometer) was subsequently used for all proceeding analyses throughout the current investigation.

Endeavoring to adhere as closely as possible to the construct of the FTP warm-up, the warm-up intensity was set at 65% of Dmax as a proxy for 65% FTP (14) (Table 1). The line of best fit for the Dmax computation was determined using third order curvilinear regression using VO₂ and BLa data at each workload during the GxT test. Thereafter, the maximum perpendicular distance to the straight line between the lowest and highest exercise BLa data identified load at Dmax (6). FTP was determined by reducing the mean power across the 20-min time-trial by 5% (1). In addition, all participants were fully familiarized with the FTP protocol having previously completed a FTP test prior to participation in the current study.

Statistical Analysis

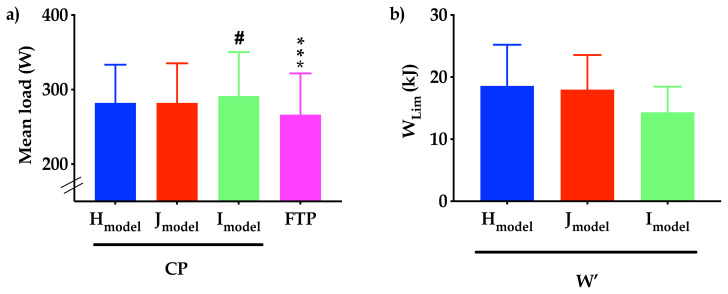
All CP and FTP data were analyzed using Prism 7 (Graph Pad, CA, USA). Each participant’s FTP datum was corrected to the calibrated Lode ergometer equivalent _prior to any data reduction and subsequent statistical analyses. Data normality was confirmed using D'Agostino and Pearson’s omnibus normality test. Group data are presented as mean and standard deviation (SD). Group comparisons were performed using one-way repeated measures ANOVA with detected differences quantified using post-hoc Tukey HSD testing and statistical significance was set at p < 0.05. ANOVA was applied to CP derived data from the H_model, J_model, I_model and FTP to identify potential differences between derived CP and FTP. Derived W’ data from the H_model, J_model and I_model were compared (ANOVA) to assess differences, if any, between models. The results of both ANOVA calculations are presented graphically in Figure 2. The coefficient of determination (r²) was calculated for the identification of CP using the H_model, J_model, I_model for each individual athlete. The average r² for all athletes within each of the three models is reported. The standard deviation of the residuals (Sy.x) between the three CP models and FTP is stated.

Figure 2.

Bar graphs of mean and standard deviation data for a) CP using H_model, J_model, and I_model versus FTP and b) W’ using H_model, J_model, and I_model. Asterisk (*) symbol infers significantly lower than CP using H_model, J_model, and I_model, *** infer p < 0.001, hash-tag (#) symbol infers CP significantly higher than H_model, # infer p < 0.05.

W′ from the H_model is the integrated area between an X-intercept above CP and the associated Y-intercept on the fitted hyperbola (7). The size of the integrated area changed depending on which sets of coordinates were used. Consequently, 1000 X- and Y-intercepts were interpolated permitting 1000 measures of area between 2-min and 12-min; the mean of these 1000 iterations was subsequently used as each participant’s W′ datum for the H_model. Participant W′ data were determined as the X-intercept of the line of best fit and as the inverse slope of the line of best fit for the J_model and I_model, respectively (Figures 1b and 1c).

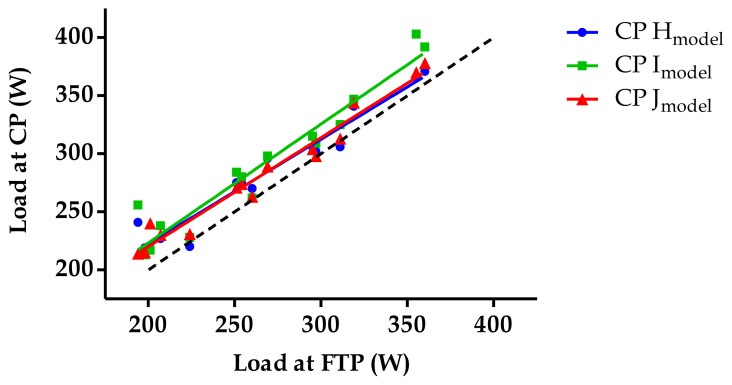
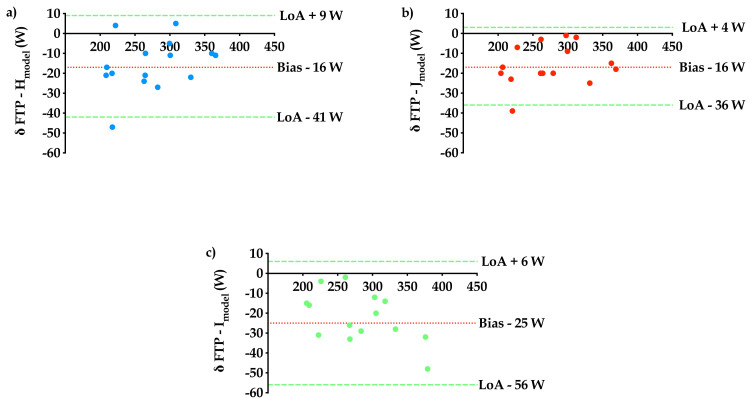
Regression analysis to identify line of identity (Figure 3); and Bland Altman analysis with computation of 95% limits of agreement (95% LoA) were used to assess agreement between the H_model, J_model and I_model with FTP. The 95% LoA were set a priori at + 20 and − 20 W to satisfy agreement between CP and FTP as these limits previously conferred FTP reproducibility (14). Bland Altman 95% LoA was also used to assess agreement between models (H_model, J_model, I_model) in their determination of W′. The load at Dmax was determined using the Lactate E software (17). No further data analysis derived from blood lactate sampling is presented currently, as these data form part of an on-going cardio-metabolic study.

Figure 3.

Scatter plots of CP data using H_model, J_model and I_model versus FTP. Dashed black line represents line of equality.

RESULTS

Mean power (W·kg⁻¹) at exhaustion during VO₂max testing for female and male cohorts were 6.0 ± 0.6 and 6.1 ± 0.7, respectively. The mean powers at Dmax (W·kg⁻¹) for female and male cohorts were 3.7 ± 0.5 and 4.0 ± 0.5, respectively. Mean powers (W·kg⁻¹) during the final incremental step of the GxT for female and male cohorts were 4.9 ± 0.6 and 5.2 ± 0.6, respectively. Detected differences between Garmin pedal and Lode ergometer power assessments were on average 1.0 ± 3.3 W. The mean FTP normalized to body mass (W·kg⁻¹) for female and male cohorts were 3.9 ± 0.4 and 4.3 ± 0.6, respectively.

Mean power at CP derived from the J_model was significantly higher than at FTP (282 ± 53 vs. 266 ± 55 W, p < 0.001). The final comparisons between CP and FTP were refined to the J_model on the basis of the following data analyses. A one-way repeated measures ANOVA comparing CP from the H_model, J_model, and I_model detected significant differences (p < 0.05) between the H_model versus the I_model, no significant differences (p > 0.05) were detected comparing H_model and J_model or J_model and I_model (Figure 2a). The 95 % LoA between the H_model and J_model were more favorable (+ 21 to −21 W) than between the H_model and the I_model (+13 and −31 W) and between the J_model and I_model (+21 and −38 W) (Table 2). The calculated r² associated with the estimation of CP were very high, for J_model 99.7% (CI = 99.5 to 99.8), for H_model 94.3% (CI = 90.7 to 97.8) and for I_model 92.9 % (CI = 89.4 to 96.3). The r² and Sy.x between FTP and the H_model was 0.95 and 13 W, between FTP and J_model was 0.97 and 10 W and between FTP and I_model was 0.93 and 15 W. The 95% LoA comparing CP derived from H_model, J_model and I_model versus FTP are presented in Figure 4. The tightest LoA were observed between the J_model and FTP (+ 4 W to −36 W) (Figure 4b). The differences between all CP models and FTP were homoscedastically distributed. The 95% LoA for W′ were tightest between the J_model and the H_model (+5.83 and −4.61 kJ), as compared with the H_model and I_model (+19.51 and −11.02 kJ) or the J_model and I_model (+15.54 and −9.27 kJ) (Table 3).

Figure 4.

Bland-Altman plots for a) H_model vs. FTP, b) J_model vs. FTP and c) H_model vs. FTP identifying mean bias (dashed red line) and upper and lower 95% LoA (dashed green lines).

Table 3.

Bland-Altman computed 95% LoA and mean bias for CP and W’ using three CP models (H_model, J_model and I_model).

	CP 95% LoA (W)	CP mean bias (W)	W′ 95% LoA (kJ)	W′ mean bias (kJ)
Hmodel vs. Jmodel	+21 to −21	0	+5.8 to −4.6	+0.6
Hmodel vs. Imodel	+13 to −31	−9	+19.5 to −11.0	+4.3
Jmodel vs. Imodel	+ 21 to −38	−9	+15.5 to −9.3	+3.6

Note. CP = Critical power; W’ = W-prime; LoA = Limit of agreement; W = Watt; kJ = kiloJoule

The line of equality, depicted by the dashed black line in Figure 3, provides a visual representation of the theoretical instance whereby CP and FTP data equate. The blue, green and red identity lines (Figure 3) represent the actual relationships between loads at CP for H_model, I_model and J_model, respectively, and FTP. For the majority of assessed data pairs CP exceeded FTP data.

DISCUSSION

Given the histrionics associated with disparities between fitness test indices (6), three CP models were thoroughly assessed to elucidate any rationale to support the incorporation of one CP model over another, for a comparison with FTP. The correlation coefficient for the determination of CP using all three models was high and therefore we proceeded to analyze agreement between CP models and FTP. Having considered the results as a whole, the J_model was identified as the model of choice for the purpose of comparing CP and FTP. Chronologically, the basis of this decision was firstly that the r² for the J_model in determining CP was itself almost “perfect”. Inter-CP model comparisons of r² is inappropriate (9), however, the J_model r² of almost 1 is reassuring. Next, the computed r² between FTP and the J_model was highest and yielded the lowest Sy.x data (10 W) compared to 13 and 15 W for the H and I_model, respectively. Previous research (3, 9) concluded that the selection of a linear model (J_model) over the hyperbolic model (H_model) to determine CP might result in an overestimation of CP. The explanation for this possibility was that a fitted straight line may be projected above the longest CP trial, whereas the final datum point on the hyperbolic H_model is forced through the centre of the longest trial (3, 9), thereby, precluding an overestimation of the longest trial. However, this scenario was not apparent in the current investigation when comparing the linear J_model versus the hyperbolic H_model.

CP data derived from all three models were found to be significantly higher than FTP and consequently we can reject the null hypothesis that the two tests can be used interchangeably in a highly-trained athletic cohort. However, the range of the 95%LoA set a priori between computed CP using the J_model and FTP were deemed somewhat satisfactory (a range of 40 W between upper and lower 95% LoA). Consequently, if a simple correction factor was applied then either test could potentially be estimated using the alternate test. In the current study, as the individual error data between computed CP using the J_model and FTP was homoscedastically distributed (Figure 4b), we consequently and tenuously suggest that any correction factor should be an integer rather than a percentage. In the current cohort of highly-trained athletes the mean bias of 16 W would approximately equate to a suitable correction factor. However, given the small homogenous sample (n = 15) assessed in the current study we suggest that further investigation is warranted evaluating other athletic cohorts of varying fitness.

The principal focus of the current study was to determine the inter-changeability of CP and FTP, which we currently report to be inappropriate. The relevance of W′ here pertains to the natural discourse as to whether the CP or FTP is a “better test”. If the principle use of CP is pacing or the ability to extract the minutia from exercise tests, the LoA associated with W′ in the current study may not always support this role. Ideally, 95% LoA should be rationalized a priori, this was not undertaken prior to commencing data collection for the current study. On reflection, we would venture to suggest that 95% LoA would need to be addressed relative to specific time epochs. The narrowest LoA, derived from the H_model and J_model were equivalent to +5.83 and −4.61 kJ. In the context of a 2-min maximal effort this equates to +48 and −38 W, whereas over a 12-min window this equates to +8 and −6 W. Applying the same concept to the wider 95% LoA reported between the H_model and I_model equates to +162 and −92 W over 2-min, and +27 and −15 W over 12-min. Therein, it is apparent that the application of CP to competition from a priori 95% LoA must consider individual competition duration.

The J_model and FTP both purport to represent a breakpoint between steady and non-steady-state exercise, but the J_model can only be sustained for up to 30-min (12) whereas FTP has been demonstrated to be sustained for 60-min (14). Prior to the current investigation, we reasoned that training status might account for this disconnect as participants in many CP trials are recreational or untrained (Table 4), whereas recently FTP was sustained for 60-min in highly-trained athletes (14). However, the current investigation using a cross-over design infers that training status does not account for diverging T_Lim, rather, CP is “simply” higher than FTP (Figure 3). The confusing common description of both CP and FTP demarking a transition from steady-state VO₂ however remains. One might posit this may be a consequence of VO₂ measures being insufficiently sensitive to quantify the small, yet important, power difference apparent between CP and FTP. Although there is a 30-min difference (< 30-min vs. 60-min), the respective epochs lie at the nadir of the asymptote of the hyperbolic curve, resulting in a minimum change in load. This concept is of course speculative and requires further scientific investigation.

Table 4.

Summary table of study population sizes and backgrounds in highlighted CP studies.

Author	Population Size	Study Participants
McGrath (current)	15	Highly-trained cyclists and triathletes
Bishop (3)	10	PE students
Black (4)	10	Physically active
Chidnoc (7)	8	Recreationally active
Gaesser (9)	16	Non-sports
Jones (13)	6	Recreationally active
Moritani (16)	8	Students
Vanhataloe (23)	10	6 cyclists, 2 runners, 2 generally fit
Moritani (16)	8	Students

CP is a variable not used routinely in performance sport, possibly as a consequence of the cumbersome multiple trials required (12). The function of T_vent in the current study was to determine the appropriate load for the four subsequent CP trials. The CP trial loads derived from T_vent resulted in four of the fifteen participants being required to complete an additional trial as their T_Lim were outside of the 2- to 15-min boundary. Similarly, other investigations have reported the necessity to wait until the penultimate trial is completed to decide on the appropriate intensity of their final trial (13, 23). The cause of erroneous predictions can only be posited, but may include potential errors associated with determination of T_vent. The landmark paper (2) that originally introduced the V-slope method for determining T_vent used an indwelling brachial catheter to derive blood samples from 10 healthy male participants to identify lactate threshold. Concurrently, ventilatory data were collected to identify T_vent comparing two methodologies, a visual inspection of data versus the objective V-slope calculation. Visual inspection of metabolic data by six experts resulted in T_vent being identified in just five of the ten participants, nevertheless the visual method is commonly used in CP testing (10, 13). In addition, the application of T_vent to well-trained athletes has been documented as questionable if the objective is to reflect blood lactate changes as a consequence of athletic training (9, 11). Given that the preliminary VO₂max test was performed to predict

CP trial intensities, we propose that the option of a GxT based determination of CP trial loads would potentially furnish the athlete with an alternative test format deriving additional physiological and pertinent collateral performance information; namely, a lactate profile. Consequently, we trialed this concept using retrospective data gleaned from our current study data. In keeping with the calculation for CP trial intensities, whereby a fraction of a metabolic turning point in conjunction with peak power are used to project T_Lim, the variable T_vent was substituted by Dmax (a marker commonly used in athletic populations). The peak power at VO₂max was replaced by the power sustained during the final increment of the GxT. The original T_vent method of anticipating CP trial-loads subtracts 66% of the ramp rate power from T_vent prior to determining a delta calculation. This amendment reportedly accounts for the time delay in VO₂ data as a response to changes in external work (24). This methodology was not applied to the fraction of Dmax based calculation as a 3-min step rate is sufficient for VO₂ to meet the external work-load (24). Load at Dmax was added to 55, 80, 105 and 130% of the power difference between Dmax and the last completed increment of the GxT. When applied retrospectively to the GxT data this proposed methodology correctly predicted all four exercise intensities that participants actually completed in the current investigation. Finally, these GxT derived calculations of appropriate exercise intensities also concurred with the predicted epochs within the 2- and 15-min limitations using Equation 1.

The exercise physiology literature is currently littered with numerous examples of individual physiological markers of a metabolic transition that cannot be reconciled with one another (6). The shared description, in the literature, of a metabolic transition between CP and FTP might be observed similarly. However, the apparent sensitivity of both the CP and FTP tests to small changes in position on the power-time curve is nevertheless exciting.

The current study is not without limitations. Although the number of participants in the current investigation is comparable to other CP studies (Table 4), it could still be deemed potentially under-powered. However, the current homogenous athletic cohort while mitigating for this, unfortunately limits extrapolation to dissimilar individuals or groups. The adoption of two power-measuring devices is also not ideal; however, we would argue that the robust compromise used eliminated potential discrepancies. The Lode cycle ergometer is considered a gold standard in cycling research studies and was ideal for the fixed pace trials, GxT and VO₂max tests. Although it is possible to complete the FTP test on the Lode cycle ergometer using the linear mode, the cyclist’s FTP would have to be anticipated prior to the test. Thereafter, any divergence from this pre-ordained FTP could only be achieved if the cyclist changed their self-selected “preferred cadence”. Although this methodology has been used previously (23) such a study design might be considered to bias the results. In addition, Garmin pedals can be calibrated independently and assessed on the Lode cycle ergometer to eliminate any potential power errors.

The current investigation clarifies that CP is a higher cycling intensity than FTP. Previous findings that the linear J_model resulted in an overestimation of CP were not borne out in our findings. The current investigation does not support the posited notion that differences between FTP and CP are based on trained status, as differences remained within this crossover design study. Although CP and FTP share the common description of being the upper-limit in steady-state oxygen consumption, were the indices used interchangeably, the precision of tracking changes in fitness, particularly in a highly-trained cohort where the anticipated changes are smaller, is likely inadequate. Moreover, the assimilation of test data into the ensuing program would be confounding. Current results do indicate that it is possible to anticipate CP from FTP (or FTP from CP) in a homogenous group of elite-athletes. Plainly, this does not reconcile CP and FTP; it simply facilitates acquisition of a second physiological demarcation without additional testing.