The stability flexibility tradeoff and the dark side of detail

Abstract

Learning in dynamic environments requires integrating over stable fluctuations to minimize the impact of noise (stability) but rapidly responding in the face of fundamental changes (flexibility). Achieving one of these goals often requires sacrificing the other to some degree, producing a stability-flexibility tradeoff. Individuals navigate this tradeoff in different ways, with some people learning rapidly (emphasizing flexibility) and others relying more heavily on historical information (emphasizing stability). Despite the prominence of such individual differences in learning tasks, the degree to which they relate to broader characteristics of real-world behavior or pathologies has not been well explored. Here we relate individual differences in learning behavior to self-report measures thought to collectively capture characteristics of the Autism spectrum. We show that young adults who learn most slowly tend to integrate more effective samples into their beliefs about the world making them more robust to noise (more stability), but are more likely to integrate information from previous contexts (less flexibility). We show that individuals who report paying more attention to detail tend to use high flexibility and low stability information processing strategies. We demonstrate the robustness of this inverse relationship between attention to detail and formation of stable beliefs in a heterogeneous population of children that includes a high proportion of Autism diagnoses. Together, our results highlight that attention to detail reflects an information processing policy that comes with a substantial downside, namely the ability to integrate data to overcome environmental noise.

Introduction

Successful decision making requires inferring important quantities such as the values and probabilities associated with potential decision outcomes through sequential observations over time. This inference process is difficult in changing environments, where optimal inference requires tracking the environmental statistics necessary to determine the most appropriate rate of learning (Behrens, Woolrich, Walton, & Rushworth, 2007; Browning, Behrens, Jocham, O’Reilly, & Bishop, 2015; McGuire, Nassar, Gold, & Kable, 2014; Nassar, McGuire, Ritz, & Kable, 2019b; Nassar et al., 2012; Prescott Adams & MacKay, 2007; Wilson, Nassar, & Gold, 2010; Yu & Dayan, 2005). In general, learning should be slow during periods of environmental stability in order to average over as many relevant observations as possible, but fast during periods of environmental change that render prior observations irrelevant to the problem of predicting future ones (Behrens et al., 2007; Browning et al., 2015; Nassar et al., 2016; Nassar, Wilson, Heasly, & Gold, 2010; Vaghi et al., 2017; Wilson, Nassar, & Gold, 2013). Human behavior, fMRI BOLD responses, and measures of physiological arousal display qualitative hallmarks of this sort of learning rate adjustment, suggesting that the brain implements meta-control over its own rate of learning in order to optimize behaviorally relevant inferences (Behrens et al., 2007; Browning et al., 2015; McGuire et al., 2014; Nassar et al., 2012; Nassar, McGuire, Ritz, & Kable, 2019b; Prescott Adams & MacKay, 2007; Wilson et al., 2010; Yu & Dayan, 2005).

However, learning rate, and adjustments thereof, differ dramatically across individuals, age groups, and clinical populations (Behrens et al., 2007; Browning et al., 2015; Nassar et al., 2010; 2016; Vaghi et al., 2017; Wilson et al., 2013). Some individuals tend to adjust beliefs rapidly irrespective of environmental statistics, leading to flexible but unstable beliefs, whereas others tend to adjust more slowly giving rise to inflexible but stable beliefs (Nassar et al., 2010). In principle, such differences might arise through learning about environmental statistics over a much longer time course, such as over development (Nassar et al., 2016) or even evolution (Krugel, Biele, Mohr, Li, & Heekeren, 2009; Stein, Newman, Savitz, & Ramesar, 2006). This longer timescale meta-learning might in some cases appropriately bias an individual towards one end of the stability/flexibility spectrum; however in other cases it could potentially go awry and give rise to pathological belief updating. For example, recent work has suggested individuals with obsessive compulsive disorder tend to over-learn from new information (Vaghi et al., 2017), limiting stability of beliefs. Consistent with a prominent theory of autism (Sinha et al., 2014), similar conclusions have been made about autistic individuals under some conditions (Lawson, Mathys, & Rees, 2017), although other studies have failed to identify differences between autistic individuals and controls (Manning, Kilner, Neil, Karaminis, & Pellicano, 2016).

These mixed results may result in part from heterogeneity within the autism spectrum. Autism is a broad diagnostic category characterized by deficits in social communication as well as restricted and repetitive patterns of behavior (RRBs). RRBs include inflexible adherence to routines, inflexibility to changing contexts, rigid thinking patterns, and increased attention to detail. Although the neural origins of an increased focus on details remains unknown, it has been described colloquially as “missing the forest for the trees” and theoretically as “weak central coherence” (Frith, 1989; Happé & Frith, 2006), “enhanced discrimination and reduced generalization” (Plaisted, 2001), “enhanced perceptual functioning” (Mottron, Dawson, Soulières, Hubert, & Burack, 2006), as well as other theoretical explanations (Belmonte et al., 2004; Just, Keller, Malave, Kana, & Varma, 2012; Kana, Libero, & Moore, 2011; Lawson, Rees, & Friston, 2014; Williams, Goldstein, & Minshew, 2006).

Although these psychological models differ in terms of the origin of these deficits, they all generally describe an imbalance of global and local information processing, with RRBs emerging from overstimulation stemming from increased local/primary sensory information processing. Here we extend this notion of locality to the temporal domain. For the purposes of learning in dynamic environments, we refer to ‘flexibility’ as the ability to prevent integration of information across a change point. We propose that such flexibility might be enhanced through a focus on local details, such as the most recent observation, rather than more global information, such as a long term average over observations. From this perspective, the greater reliance on local information characteristic of heightened attention to detail in individuals with autism might result in a particular learning profile favoring flexibility as opposed to stability.

One factor limiting much of the previous research on attention to detail is the focus on dichotomous groups of individuals with or without an ASD diagnosis, a study design that does not take into account that behavioral manifestations of ASD. Importantly, local/global perception has also been shown to vary in the general population (Dale & Arnell, 2013; McKone et al., 2010; Scherf, Behrmann, Kimchi, & Luna, 2009). Thus, quantitative measurement of attention to detail along with measurement of learning behavior that differs based on information processing policies in those with and without ASD would be particularly powerful. Recent work that has used the approach has shown that quantitative traits of autism measured both in the general population and within clinically-diagnosed cohorts are associated with the ability to disembed a smaller figure from a larger shape (Sabatino DiCriscio & Troiani, 2017; 2018). Further, it has been shown that the ability to disembed a local part from a global whole are not present in every individual with ASD, indicating that measuring trait dimensions is important in heterogeneous disorders like autism (DiCriscio, Hu, & Troiani, 2019). Additional studies have used the AQ to screen participants and split them into “High AQ” and “Low AQ” groups or to link quantitative measures of autism traits to a given behavior. These studies also show that there is a documented relationship between visual perceptual skills and autism traits in neurotypical individuals as measured by the AQ (Burghoorn, Dingemanse, van Lier, & van Leeuwen, 2020).

Here we use a trait dimension approach to examine the relationship between attention to detail, a prominent feature of autism, and the degree to which individuals implement learning policies favoring either stability or flexibility. We relate individual differences in learning behavior (stability/flexibility tradeoff) to a quantitative measure of autism traits (Autism Spectrum Quotient; AQ), designed to capture characteristics of autism that extend outside of traditional diagnostic boundaries. We examine this in two separate populations: healthy young adults and children with a range of developmental abilities, including autism. We show that the young adults who update beliefs the least in the face of conflicting information integrate more effective samples into their beliefs about the world, making them more robust to noise (more stability), but also are more likely to integrate information from previous contexts (less flexibility). The individuals who show the opposite pattern of results (high flexibility/low stability), tended to score higher on the attention to detail subscale of the AQ. We confirm this inverse relationship between attention to detail and formation of stable beliefs in a population of children that includes a high proportion of clinical autism diagnoses. Together, our results highlight that attention to detail reflects an information processing policy that comes with a substantial downside, namely the inability to integrate data to overcome environmental noise.

Methods

Subject populations:

Experiment 1: 43 young adults (20 female, mean[std] age = 2.4[3.4] years, Mean[std] WASI FSIQ = 112[10.4]) were recruited from a local community population to participate in our first behavioral study.

Experiment 2: 37 children (17 female, mean[std] age = 9.5 [2.5]) were recruited to participate in our second behavioral study. In order to obtain a range of autism traits in the sample, we identified participants using a broad recruitment strategy. This included identifying participants based on patient referral to a neurodevelopmental clinic in Lewisburg, Pennsylvania, as well as from health system wide advertisement and the surrounding community. On the day of research testing, all participants completed a cognitive assessment to document IQ (WASI-II: Wechsler abbreviated scale of intelligence, 2nd edition; Wechsler, 2011). If an IQ test was ascertained as part of their clinic appointment that day, we used the clinically ascertained IQ score. All participants assented to protocols approved by the institutional review board (IRB) at the authors’ home institution. Twelve of our participants had a clinical diagnosis of autism or ASD based on assessment by our neurodevelopmental pediatricians and support staff.

Study Session:

Each experimental session involved performing a computerized predictive inference task (Nassar et al., 2016; Nassar, Bruckner, & Frank, 2019a), completing the Autism Quotient questionnaire, and a cognitive assessment (WASI FSIQ). Thirteen of the 43 young adult participants did not complete the WASI FSIQ due to time constraints.

Predictive inference task:

Each participant completed a computerized predictive inference task that required them to infer the location of an unobservable helicopter based on the locations of bags that had previously fallen from it (McGuire et al., 2014). The task included two conditions that favor different adaptive learning strategies (d’Acremont & Bossaerts, 2016; Nassar, Bruckner, & Frank, 2019a). In one condition the helicopter was generally stationary but occasionally underwent “changepoints” (hazard rate = 0.125) at which its position was reset to a random horizontal position on the visible screen (arbitrarily defined using screen positions on a scale from 0 to 300), and in the other condition the helicopter “drifted” slightly from trial-to-trial (implemented as a normal random walk with standard deviation = 10 screen units). On each trial a bag would fall from the top of the screen, horizontally displaced slightly from the true horizontal position of the helicopter (noise standard deviation = 20 screen units), providing the participant with some information about the helicopter location. In the changepoint condition this information was always relevant – as bag locations were normally distributed around the helicopter position. However, in the condition with the drifting helicopter, bags were occasionally (hazard rate = 0.125) sampled from a uniform distribution extending across the entire screen, giving rise to “oddball” events that were unrelated to the true helicopter location. On half of trials, the contents of bags were worth points that accumulated in the bucket across trials and were translated into incentive payments at the end of the session. On the other half of trials contents were worthless, but nonetheless bag positions provided important information about the position of the helicopter, and thus upcoming bag locations. The value of bag contents was designated by color (counterbalanced across participants) and could not be predicted such that the best strategy on each trial was to move the bucket to the inferred location of the helicopter in order to maximize the chances of “catching” valuable tokens.

Subjects were trained separately and explicitly on each of the two conditions. Training on each task condition consisted of 1) a set of instructions slides that explicitly described the generative environment (eg. changepoint or oddball condition; see appendix 1 for complete instructions) and 2) a visible helicopter training version of the task in which participants could observe the bags fall from the helicopter directly. After performing 50 trials of the visible helicopter training task for a given condition, participants were told that the helicopter would be obscured by clouds and that they would need to infer its position based on previous bag locations. Thus, participants were made explicitly aware of the condition that they were in (changepoint/oddball) prior to beginning each condition of the predictive inference task. Performance of both cohorts on the visible helicopter task indicated a general understanding of the task (Fig S1).

Autism Spectrum Quotient (AQ):

The AQ is a self-report measure aimed to assess ASD-like traits across the general population (Baron-Cohen, Wheelwright, Skinner, Martin, & Clubley, 2001). This measure assesses five trait domains, including communication, social skills, attention switching, imagination, and attention to detail. Using a 4-point Likert scale, a participant responds with how strongly they agree or disagree with a given statement. Each item is scored based on whether a given trait is endorsed, with half of the items requiring an agree and half requiring a disagree response to endorse an ASD-like trait. Item scores are summed to generate both a total score as well as subscale scores. In Experiment 1, young adults completed a self-report version of the AQ, while in Experiment 2, parents completed a parental-report version of the AQ on their child’s behavior.

Subject Exclusion

For both studies, subjects were excluded if they did not meet a basic performance standard designed to determine whether they were actually attempting to complete the task (mean distance between bucket and helicopter position of less than 45 units). This performance standard was met by all participants in the young adult population but did lead to exclusion of one participant in the developmental cohort (see fig S7). In addition, 8 participants in the developmental cohort did not complete the AQ due to time constraints, and thus were not included in the correlations between AQ measures and task performance. After participant exclusion, our developmental cohort included 29 participants who had completed the AQ, 9 of whom had an autism diagnosis.

Normative learning model:

Normative learning was assessed using a reduced Bayesian model that has been described previously for the changepoint (Nassar et al., 2010) and oddball (Nassar, Bruckner, & Frank, 2019a) conditions. In both conditions, model updates correspond to an error driven learning rule where the learning rate depends on trial-by-trial estimates of the probability of an extreme event (referred to as changepoint or oddball probability, depending on the block type), which is computed according to Bayes rule:

$$p(\mathit{\text{extreme event on trial }}t)={\Omega }_t=\frac{\frac{H}{300}}{N\left(PE;0,{\sigma }^2\right)(1-H)+\frac{H}{300}}$$ Eq 1

Where H is an a priori expectation about the rate of extreme events (hazard rate), PE refers to the difference between the actual and expected outcomes (prediction error), and σ² is the variance on the models estimate of the current helicopter location. This variance is derived from two sources, the irreducible variability attributable to the width of the bag distribution $\left({\sigma }_N^2\right)$ and the uncertainty attributable to imprecise estimates of the helicopter location $\left({\sigma }_{\mu }^2\right)$. For normative model simulations, ${\sigma }_N^2$ was set to its true value in the task (20 screen units) and ${\sigma }_{\mu }^2$ was inferred on each trial as has been described previously for the changepoint (McGuire et al., 2014) and oddball conditions (Nassar, Bruckner, & Frank, 2019a).

The fraction of total uncertainty (σ²) that is due to an imprecise estimate of the helicopter location $\left({\sigma }_{\mu }^2\right)$ is termed relative uncertainty:

$${\tau }_{t+1}=\frac{{\sigma }_{\mu }^2}{{\sigma }_N^2+{\sigma }_{\mu }^2}$$ Eq 2

In the changepoint condition, learning rates in the model are driven up by both the probability of an extreme event and the relative uncertainty about the helicopter position:

$${\alpha }_t(\mathit{\text{changepoint condition}})={\Omega }_t+{\tau }_t-{\Omega }_t{\tau }_t$$ Eq 3

This is not the case for the oddball condition, where probable oddballs should be ignored:

$${\alpha }_t(\text{oddball condition})={\tau }_t-{\Omega }_t{\tau }_t$$ Eq 4

Single trial learning rates:

Participant bucket positions and computer generated bag locations were used to compute trial-by-trial prediction errors (the difference between bag location and the center of the bucket on a given trial) and prediction updates (the bucket location on a subsequent trial minus the bucket location on the current trial). In order to estimate the degree of influence of each bag on the subsequent behavior of the participant, we computed a single trial learning rate by dividing the update made on each trial by the prediction error observed on that trial (Nassar et al., 2010). Learning rates computed in this way that were greater than 1 or less than 0 were set to 1 or 0, respectively. Single trial learning rates were also categorized into three groups: 1) total updates [> 0.8], 2) moderate updates [0.2 to 0.8], and 3) non-updates (<0.2).

Characterizing the content of participant beliefs

To better understand how the exact sequence of learning rates employed by each participants affected the precision and flexibility of their beliefs, we re-represented participant beliefs (bucket position) on each trial as a weighted mixture of previous outcomes (bag locations). This is made possible through the following equivalency for error driven learning systems (Sutton & Barto, 1998):

$$B_t={\left(1-\alpha \right)}^t{B}_0+\sum _{i=1}^{t-1}{\alpha }_i\left(1-{\alpha }_{i+1}\right)\left(1-{\alpha }_{i+2}\right)\dots \left(1-{\alpha }_t\right)X_i$$

Where B_t is the belief on timestep t, X_i is the position of the bag on the ith trial, and α_i is the empirical learning rate describing how the participant updated his or her bucket position in response to that observed bag position. Thus, the contribution of the ith outcome to the belief on trial t is greatest when a participant used a high learning rate in response to that outcome (α_i) and extremely small learning rates in response to all subsequent outcomes ((1 − α_{i +1}) …).

We implemented this procedure by stepping through the sequence of single trial learning rates and for each trial to 1) assign weight to the newest outcome in proportion to the learning rate on that trial α_i, and 2) updated the weight assigned to all previous outcomes by multiplying their weight (computed on the previous trial) by one minus the current trials learning rate (1 − α_{i +1}). This procedure produced a vector of weights that, when multiplied by the corresponding vector of bag positions, resulted in the exact belief of the participant. We note that this procedure does not involve any model fitting and only relies on the Markov assumption that the influence of each bag impacts immediate beliefs immediately, without having any delayed effects.

In order to understand how stability and flexibility of beliefs might be assessed through the weight attributed to previous outcomes, it is useful to consider what optimal inference might look like, when recast as a set of weights to previous outcomes. If a changepoint is correctly identified, then optimal inference would correspond to a flat weight profile across all outcomes subsequent to the most recent changepoint, and zero weight attributed to all outcomes prior to the most recent changepoint. A belief updating strategy that attributes weight to outcomes preceding the most recent changepoint could be considered inflexible, in that it failed to replace information from an irrelevant context. A belief updating strategy that unevenly attributes weight to the relevant outcomes, in the extreme giving all weight to a single outcome, could be considered unstable and imprecise, in that it limits the degree to which noise in individual observations can be averaged out, and thus would provide a less precise estimate of the underlying mean.

With these considerations in mind, to assess the flexibility of beliefs, we quantified the proportion of the weight profile that was attributed to relevant outcomes (proportion relevant). In the changepoint condition, relevant outcomes were defined as those having occurred since the most recent changepoint (eg. bags that fell from the current helicopter location). In the oddball condition, all non-oddball outcomes were considered to be relevant (eg. bags normally distributed around helicopter).

In order to assess precision and stability of beliefs, we quantified the effective number of outcomes from which they were composed. Specifically, we computed effective samples as follows:

$$p=\frac{1}{{\sigma }_{tot}^2}=\frac{1}{{\left(w_1{\sigma }_{\mathit{\text{samp}}}\right)}^2+{\left(w_2{\sigma }_{\mathit{\text{samp}}}\right)}^2\dots +{\left(w_{t-1}{\sigma }_{\mathit{\text{samp}}}\right)}^2}$$ Eq 5

$$\mathit{\text{Effective samples}}=\frac{p}{{\sigma }_{\mathit{\text{samp}}}^2}$$ Eq 6

where p reflects the precision (inverse variance) of beliefs, ${\sigma }_{tot}^2$ is the variance on the weighted mean of samples, ${\sigma }_{\mathit{\text{sample}}}^2$ is the variance on each sample, and w reflects the weight given to that sample during updating. Our effective samples measure simply normalized the belief precision in terms of the precision of a belief based on a single observation allowing absolute values to be more interpretable. The resulting measure of effective samples reflects the effective number of samples comprising the current prediction.

Statistical analysis:

Rank order correlations between task measures and AQ sub-scale measures were computed using Spearman’s Rho. Linear regression was used for followup analyses designed to statistically control for other factors including IQ, age, and gender. When additional factors were used as covariates, missing data was replaced with group mean values. All analyses and models were implemented in Matlab (The MathWorks, Natick, MA) and all code and anonymized data will be made available upon publication on the corresponding author’s website (https://sites.brown.edu/mattlab/resources/).

Results

Experiment 1

Young adults made predictive inferences in both changepoint and oddball contexts. Participants specified predictions about the location of an unobservable helicopter (Fig 1A, prediction panel) in order to catch bags (Fig 1A, outcome panel). Predictions were updated on each trial (Fig 1A, update panel) according to the most recently observed bag location, and knowledge of the underlying generative structure (changepoint/oddball). In the changepoint condition, normative learning (Fig 1B, pink line) prescribed rapid updating in response to unexpected bag locations, as these outcomes were likely associated with a change in the helicopter location. In contrast, in the oddball condition normative learning (Fig1B, pink) required ignoring unexpected bag locations, which were likely to be oddballs unrelated to the actual helicopter position. Predictions made by an example participant (Fig1B&C, blue) conform well to normative model predictions. The normative learning model adjusts learning rate from trial to trial according to the probability that the observed outcome reflects a changepoint (Fig 1D, orange) or oddball (Fig 1E, orange), depending on the current task condition, as well as an estimate of uncertainty about the current helicopter location (Fig 1D&E, yellow; (Nassar et al., 2012)).

Figure 1:

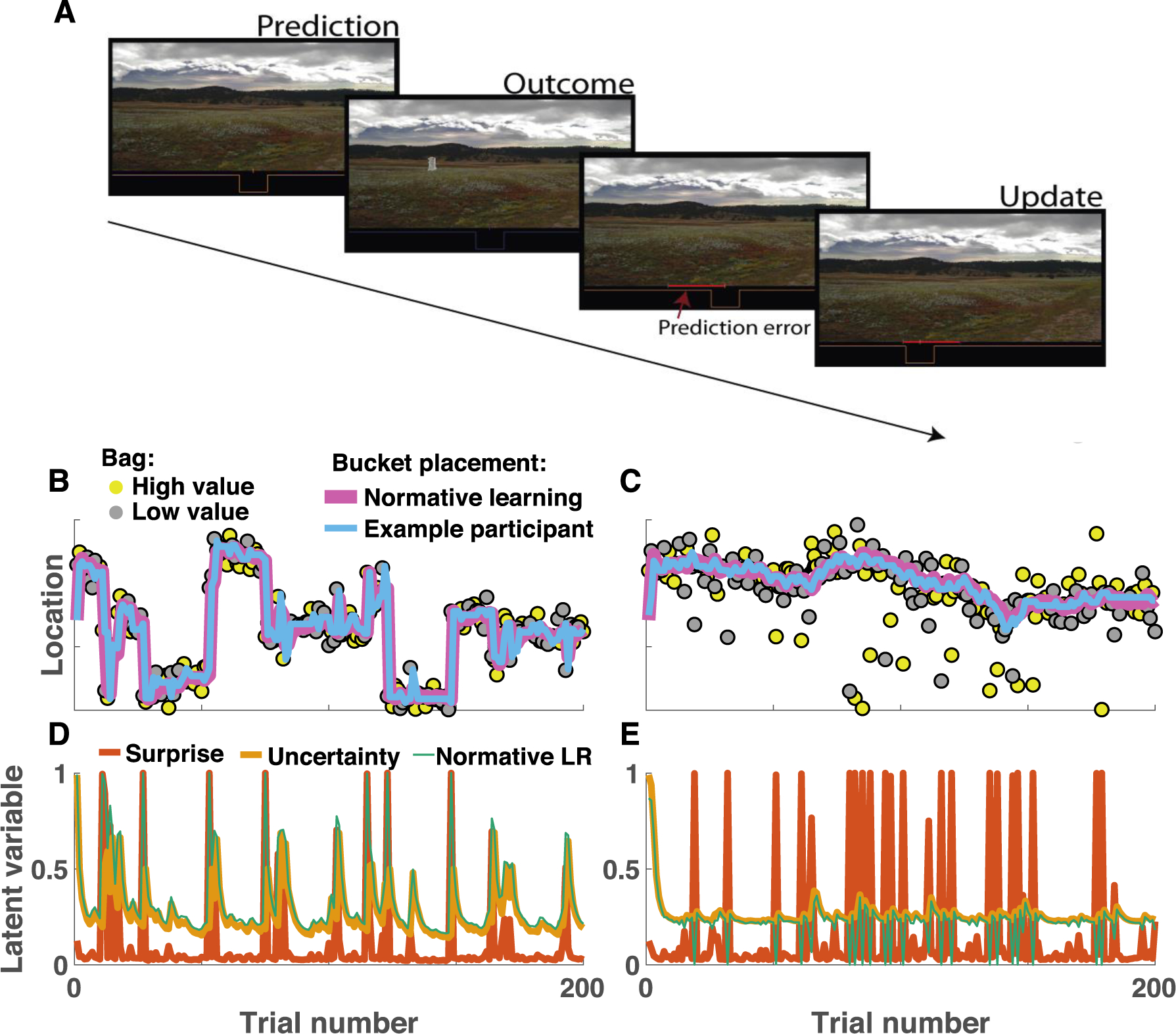
Predictive inference task measures learning in different statistical contexts. A) On each trial, participants were required to adjust the position of a bucket to catch bags of coins that would be dropped from an unobservable helicopter. Subjects were not able to observe the helicopter, and thus forced to use the history of bag locations and knowledge about the environmental statistics to inform bucket placement. B-C) Example data from a single subject performing the predictive inference task in changepoint (B) and oddball (C) conditions. B) In the changepoint condition, the helicopter (not shown) remained in a single screen position (ordinate) for a number of trials (abscissa), before occasionally relocating to a new screen position (changepoint). Bag locations (yellow and gray points) were drawn from a normal distribution centered on the helicopter location. Inferences about the helicopter location made by a normative learning model (pink line) and bucket placements made by an example subject (blue line) are both rapid to adjust after changepoints in the helicopter location. C) In the oddball condition, the helicopter position drifted slowly from one trial to the next, and bag positions were either drawn from a normal distribution centered on the helicopter location (90% of trials) or a uniform distribution across the entire task space (10% of trials). D&E) The normative learning model adjusted learning rate (green line) on each trial according to uncertainty (yellow) and surprise (orange). In the changepoint condition (D) surprise was indicative of changepoints and increased learning rates, whereas in the oddball condition (E) surprise was indicative of an uninformative oddball and thus promoted lower learning rates.

In order to better understand how participants adjusted learning across trials and conditions, we computed single trial learning rates based on the prediction errors that participants experienced on each trial and the bucket updates that they produced (Fig S2). The distribution of single trial learning rates used by participants differed across the two conditions, qualitatively in accordance with the normative predictions. On changepoint trials, participants tended to use high learning rates (Fig 2A), whereas on oddball trials where bag locations were equally surprising but unrelated to the true helicopter location, participants tended to use learning rates near zero (Fig 2B). Distribution of learning rates across unsurprising trials tended to be more similar across the conditions, with a fair number of small and moderate learning rates employed (Fig 2C&D). These relative patterns of learning were consistent across subjects, with total-updates (learning rate > 0.8) decreasing with increasing trials after a changepoint (Fig 2E; linear effect of trials after changepoint on total updating: t = −8.0, df = 42, p=5×10⁻¹⁰) and non-updates (learning rate < 0.2) elevated on oddball trials (Fig 2F; contrast non-updating on oddball versus other trials: t = 2.9, df = 42, p=0.007). On average, young adult participants demonstrated context-sensitive adjustments in learning that qualitatively matched model prescriptions for how learning should be adjusted according to surprise (Fig S3).

Figure 2:

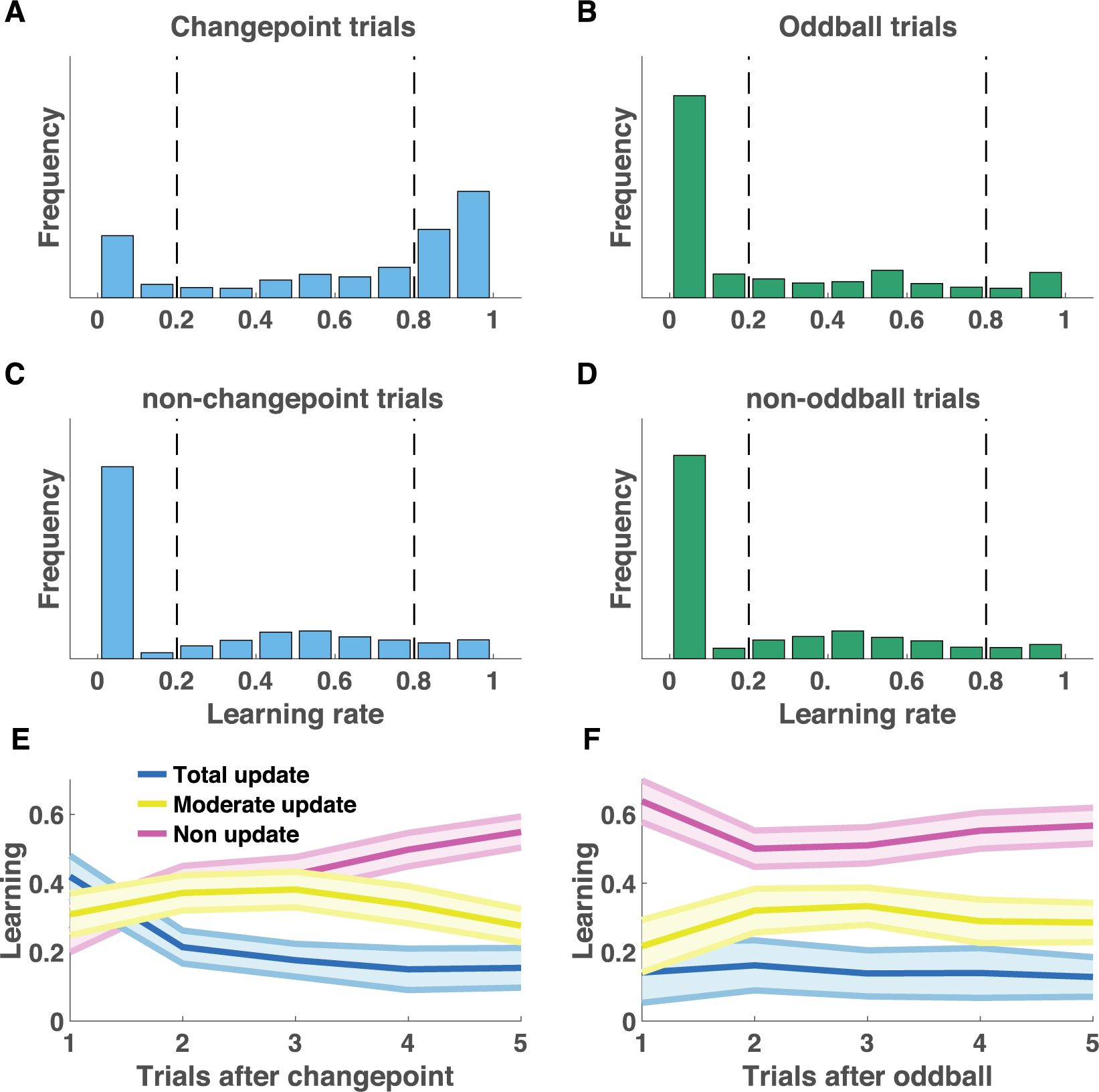
Participant learning rates were sensitive to task condition and surprising outcomes. A-D) Single trial learning rate frequency histograms for changepoint (A) and oddball (B) trials, as well as for non-changepoint (C) and non-oddball (D) trials. Single trial learning rates are categorized into three types: non updates, moderate updates, and total updates, depending on their value with respect to criterion values (dotted vertical lines). E-F) Mean/SEM proportion of each category of learning rates used as a function of time since the previous surprising event [changepoint (E) or oddball (F)].

Despite the preservation of context sensitive adjustments of learning across participants, individuals differed markedly in their overall learning rate distributions, with some participants almost never making a total update and others using total updates on approximately six out of ten trials. In principle, these differences could reflect different policies toward optimizing either the stability or flexibility of beliefs. In order to test whether such a stability/flexibility tradeoff exists, we examined how individual differences in total update frequency related to performance in each of the task conditions. In the changepoint condition, higher total update frequency tended to be associated with smaller errors on changepoint trials (Figure 3A; Spearman’s rho = −0.34, p = 0.02) but larger errors during periods of stability (Figure 3C; Spearman’s rho = 0.66, p = 1.5 × 10⁻⁶), supporting the idea that individuals may differ in their relative concern for stability versus flexibility of beliefs. Performance in the oddball condition, in contrast, tended to favor more stable belief updating strategies, with more frequent total updates leading to worse performance on oddball trials (Fig 3B&D; Spearman’s rho = 0.66, p = 1.5 × 10⁻⁶). Thus, individual differences in learning, specifically the frequency of total updating, predicted individual differences in performance in a manner that suggests different policies regarding toward optimizing stability or flexibility.

Figure 3:

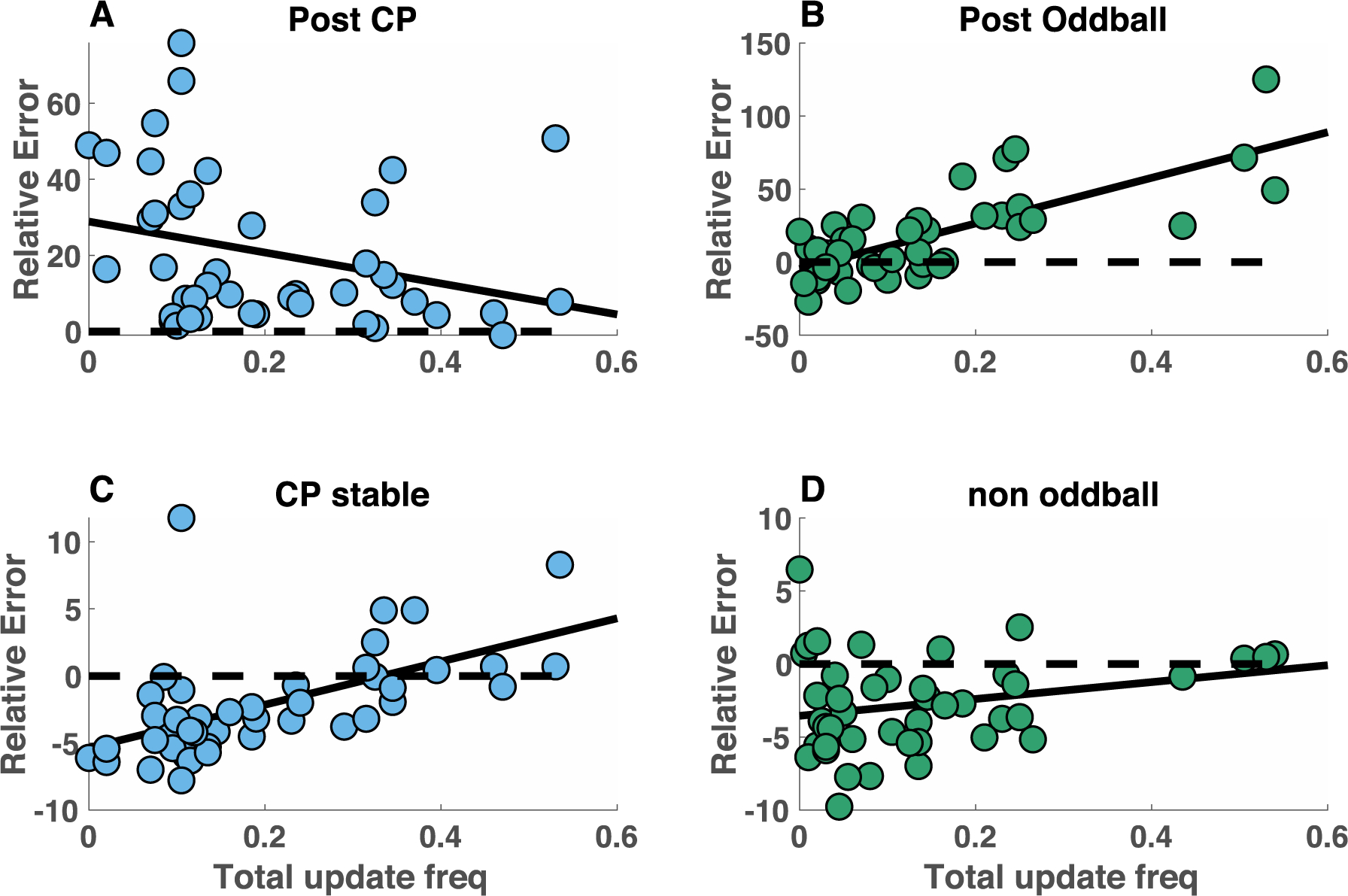
Individual differences in performance were driven by individual differences in the frequency of total updates. A-D) Relative error magnitude (ordinate) is plotted against frequency of total updating (abscissa) for each individual subject (points) in the two task conditions (changepoint = blue, oddball = green). Top panels reflect performance on the trial subsequent to a surprising outcome (A = post-changepoint, B = post-oddball) whereas bottom panels reflect performance during periods of stability (>5 trials after most recent changepoint (C) or oddball (D)). Relative error would be zero if participants were using only the most recent relevant outcome in order to make their prediction (dotted line) and thus achieving negative relative errors requires using bucket placements that integrate information from more than one previous outcome.

In order to more explicitly test for individual differences in the stability and flexibility of beliefs, we used the sequence of learning rates preceding each prediction to determine the weighted contribution of each previous outcome to that prediction (see methods; Fig. 4a). In order to demonstrate how the method works, we first applied it to behavior of model agents. When applied to simple fixed learning rate models, the method revealed the expected exponential decay of weight across previous outcomes, with higher learning rates corresponding to higher rates of decay (Fig. 4b, blue&yellow). Applying the method to our normative learning model identifies weights with more complex dynamics, which are approximately uniform across trials since the most recent changepoint, but zero on trials prior to the most recent changepoint (Fig. 4b, green).

Figure 4:

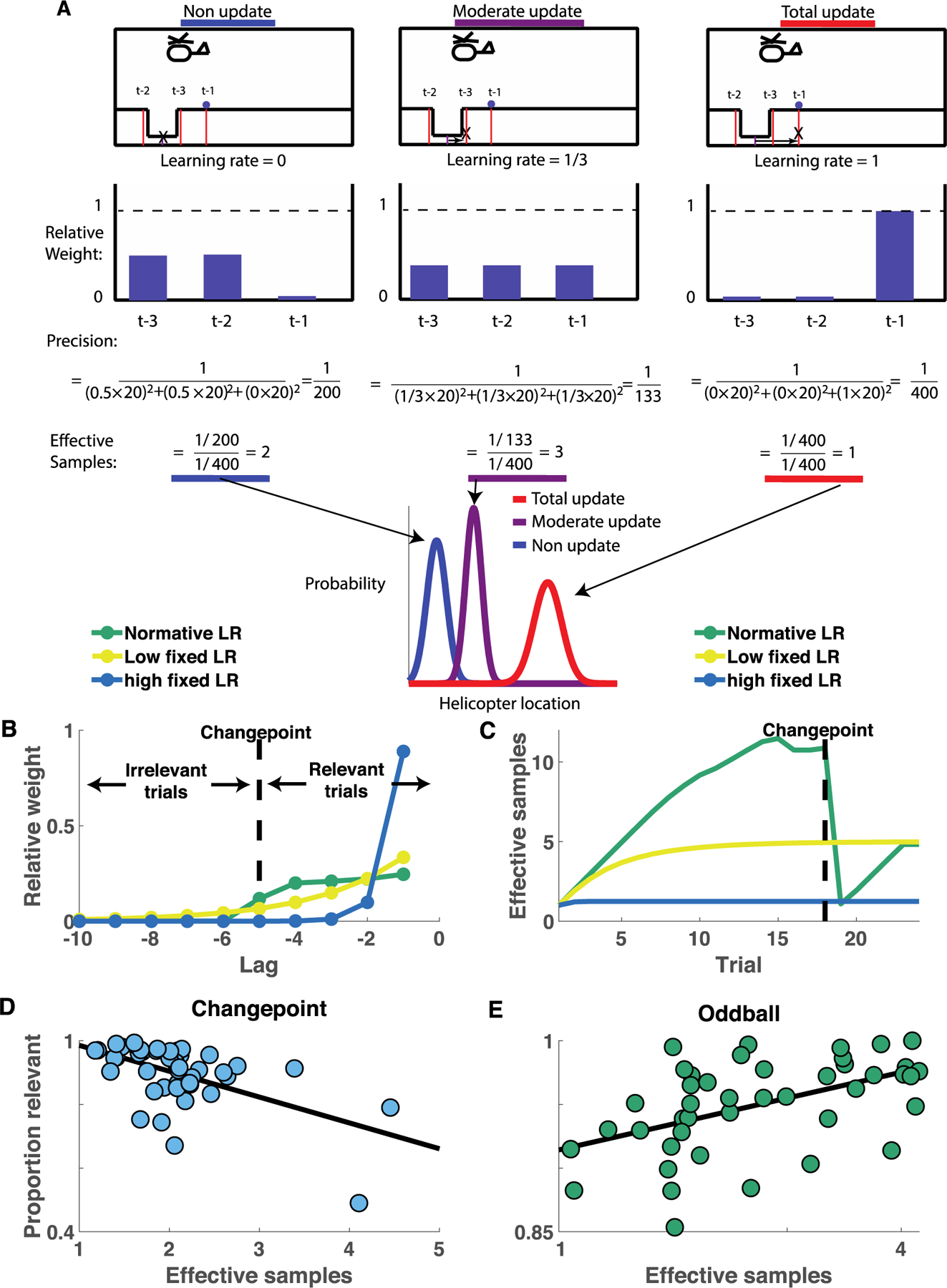
Individual differences in performance are attributable to a fundamental tradeoff in the quantity and relevance of samples from which a belief is composed. A) Learning rates can be used to infer the weight attributed to previous outcomes, providing insight into the stability and flexibility of participant beliefs. Schematic (top) depicts an example where the bucket is placed halfway between two previous bag locations (t-2, t-3) and a new outcome is observed (t-1). Three different update strategies are depicted: non-update (left), moderate update (middle), and total update (right). After the bucket position is updated (arrow and X in schematics), the relative weight attributed to each previous outcome is assessed to reveal the contents of updated beliefs for each case (second row), the precision of those beliefs, and our normalized measure of belief precision, “effective samples”, which quantifies the effective number of previous outcomes incorporated into beliefs. Note that the total update pushes all weight onto the most recent outcome, leading to single effective sample, whereas the moderate update (learning rate = 1/3) gives rise to a flat weight profile over the three observations, resulting in the highest possible effective sample size (3). B) In general, higher learning rates correspond to a greater proportion of weight attributed to recent observations (compare blue and yellow lines) and normative learning approximates a flat weighting of all observations since the previous changepoint (green). Observations occurring prior to the most recent changepoint are irrelevant to the inference process, and thus the proportion of weights attributed to observations occurring since the last changepoint quantifies the relevance of samples from which the belief is composed. C) For a bucket placement on a given trial, the distribution of weights over previous observations can be used to infer the effective number of samples incorporated into that belief (which scales with the precision – or inverse variance – of that belief). High learning rate models, which rely predominantly on the most recent observations, rely on beliefs with the fewest effective samples (blue). Normative learning approximates linear growth of effective samples during periods of stability, but rapid collapse of effective samples after observing a changepoint (green). D-E) Participants who incorporated the most samples into their beliefs (abscissa) tended to rely on less relevant information (ordinate) in the change-point condition (D), whereas this relationship reversed in the oddball condition (E).

The weight profile characterizing the influence of outcomes on the normative learning model reveals hallmarks of both flexibility and stability. The lack of weight attributed to outcomes prior to the previous changepoint affords the normative model flexibility (Fig. 4b, green), which is to say an ability to disengage from irrelevant information after a change in context. With this in mind, we could quantify the flexibility of any agent, or indeed our subjects, by calculating the fraction of the weight profile that is attributed to “relevant” trials, which, in the case of the changepoint environment, occurred subsequent to the most recent changepoint (proportion relevant). The stability of beliefs held by the normative model is evident in the roughly uniform weighting of outcomes since the previous changepoint (Fig 4b, green, relevant trials). This near-equal weighting of relevant outcomes “averages out” the independent noise associated with each individual outcome, providing more stable beliefs, which more precisely estimate of the mean (helicopter location) that gave rise to them (Fig 4a, bottom). This benefit in stability/precision can be quantified through the number of effective samples comprising the current prediction, which grows nearly linearly for the normative model during periods of stability but rapidly decays to one after a changepoint (Fig 4c, green; effective samples). Note that a simple high fixed learning rate model, which is flexible in that it rapidly discards old and potentially irrelevant information (Fig 4b, blue), never accumulates even two effective samples (Fig 4c, blue), and is therefore highly sensitive to the noise inherent in individual outcomes. This illustrates the stability flexibility tradeoff – rapid learning can promote flexibility (high proportion relevant) at the expense of precision during periods of stability (low effective samples). Our analysis methods allow us to characterize this tradeoff, even in the presence of response variability (Fig S4), in order carefully examine how individuals might differentially navigate it.

The stability flexibility tradeoff was also evident from individual differences in the changepoint condition of our task. Individuals who were most flexible (eg. had a high proportion of weight associated to relevant outcomes) tended to base predictions on fewer samples (Fig 4d; Spearman’s rho = −0.49, p = 9.1 × 10⁻⁴) in the changepoint condition. Conversely, individuals who incorporated more outcomes into their predictions, tended to include a higher proportion of irrelevant outcomes, making their predictions less flexible in the face of changepoints. In the oddball condition, where task-relevance was unrelated to recency, this relationship reversed such that participants who incorporated the most samples, also tended to have the highest proportion of relevant ones (Fig4e; Spearman’s rho = 0.53, p = 3.1 × 10⁻⁴). Taken together, these results suggest that individuals differ in their relative emphasis on the precision of beliefs, or their flexibility in the face of changing contexts.

An important motivating question of this work was to examine the degree to which such differences in stability/flexibility policy might relate to broader patterns of real-world behavior, with respect to traits that are elevated in ASD. In line with this idea, healthy young adults who scored highest on the attention to detail subdomain of the AQ incorporated fewer effective samples into beliefs in the changepoint condition (Fig 5A; Spearman’s rho = −0.43, p = 0.005), but those samples tended to be more relevant (Fig 5C; Spearman’s rho = 0.33, p = 0.03). Consistent with attention to detail reflecting an emphasis on flexibility, as opposed to stability, it was associated with more frequent use of high learning rates, and less frequent use of low ones (Fig S5). Both relationships between attention to detail and key metrics of changepoint task behavior (effective samples & proportion relevant) persisted in a regression model that included IQ and age as covariates: (effective samples: t=−2.7, dof = 37, p = 0.01; proportion relevant: t = 2.8, dof = 37, p = 0.007). The relationship of attention to detail to belief precision, as quantified by effective samples, was robust to exclusion of individual subjects and remained statistically significant after controlling for multiple comparisons to account for other AQ subdomains (Bonferroni corrected p = 0.02). The relationship between attention to detail and belief flexibility, as quantified by proportion relevant samples in the changepoint condition, was less robust, and not statistically significant after removing the lowest attention to detail participant (rho = 0.29, p = 0.07) or after controlling for all five possible comparisons (Bonferroni corrected p = 0.15). As might be expected, the lower precision beliefs in high attention to detail individuals conferred a small performance disadvantage during periods of stability in the changepoint task (correlation between mean relative error > 5 trials after a changepoint and attention to detail: rho = 0.35, p = 0.02), whereas the trend toward higher flexibility did not produce a significant performance advantage immediately after changepoints (correlation between mean relative error on trial after changepoint and attention to detail: rho = −0.16, p = 0.33). Thus, attention to detail conferred a clear disadvantage in terms of belief precision, and our data hints that this disadvantage comes with a benefit of increased flexibility, although the data are less clear on that issue.

Figure 5:

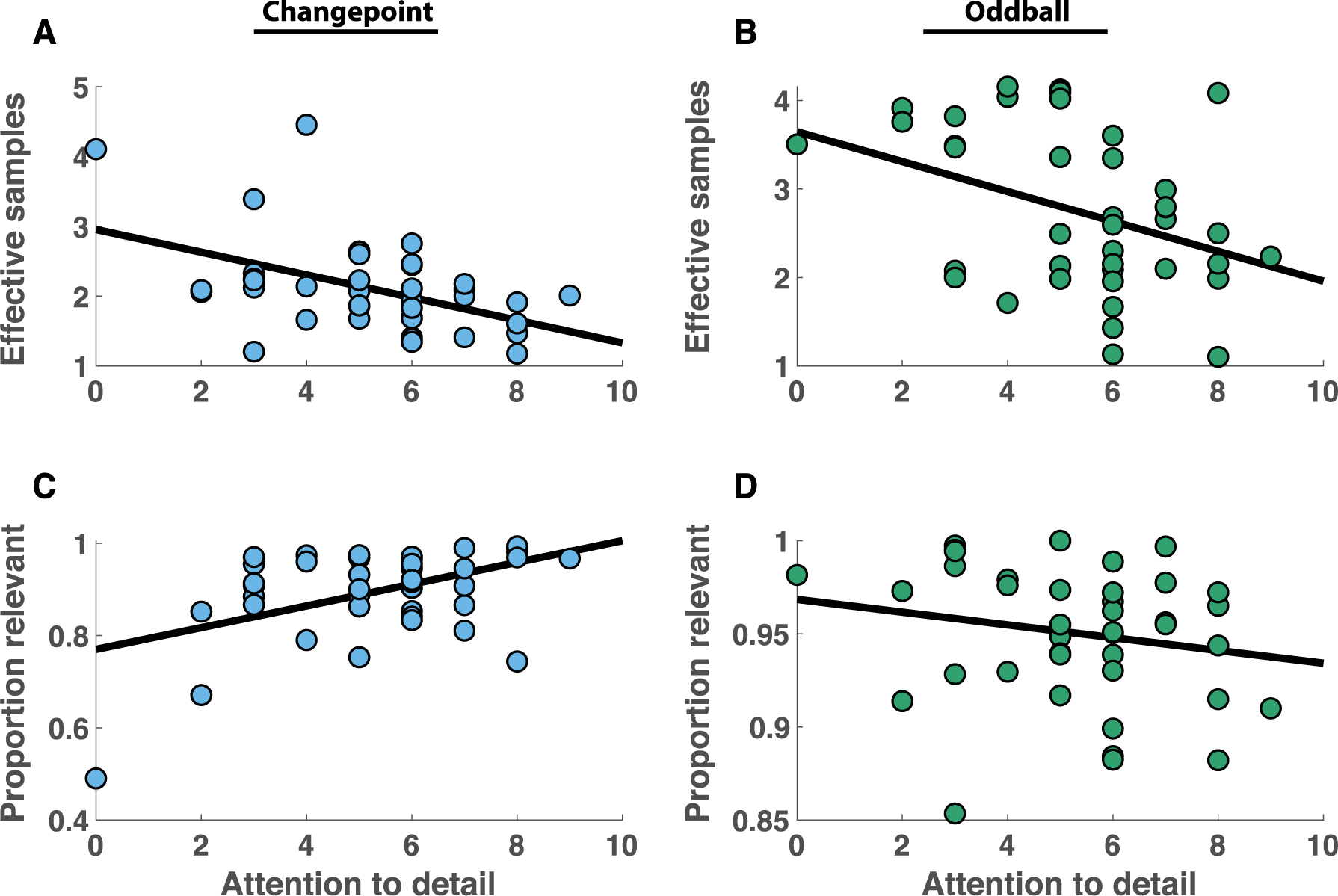
Attention to detail predicts individual differences in stability/flexibility policy. A-B) Individual differences in the effective sample size of beliefs (ordinate) were negatively related to self reported scores on the attention to detail subscale of the Autism Spectrum Questionnaire (abscissa) in both changepoint (A) and oddball (B) conditions. C-D) Individual differences in the proportion of samples attributed to relevant observations (ordinate) were positively related to self reported scores on the attention to detail subscale of the Autism Spectrum Questionnaire (abscissa) in the changepoint (A) but not the oddball (B) conditions.

No relationships between these measures of stability and flexibility were observed in relation to other sub-domains of the AQ (see Fig S6 for all pairwise correlations and relevant statistics) or in relation to IQ (p = 0.16, 0.28). There was a trend toward the same negative relationship between precision and attention to detail in the oddball condition (Spearman’s rho = −0.30, p = 0.06), however the advantage of high attention to detail individuals in terms of sample relevance was not apparent in this condition (Spearman’s rho = −0.22, p = 0.17). Taken together, these results suggest “attention to detail”, one specific aspect of behavioral variability that has been associated with ASD, directly relates to stability/flexibility policy, with individuals higher on “attention to detail” favoring flexibility at the expense of stability.

Experiment 2

In order to test the generality of the relationship between attention to detail and stability/flexibility and to examine it across a wider range of behavioral phenotypes that includes individuals with ASD, we conducted a second behavioral study in a heterogenous population of children (N = 37, mean[STD] age = 9[2.5], 17 female). The group included 12 participants diagnosed with ASD, as well as 25 children recruited from the local community. Overall performance of the developmental cohort was considerably worse on the task than that of our young adult cohort, owing in part to a lack of context dependent learning rate adjustments in the developmental group (Fig S2).

More generally, behavior of the children included far fewer updates than that of the young adult population. Non-updates were the most common updating category, even on changepoint trials that should require total updates (Figure 6). In principle, non-updates could limit flexibility by reducing responsiveness to new information after a changepoint, but could also limit precision of beliefs during periods of stability by preventing incorporation of new information into existing beliefs (Fig 4a, non-update). Consistent with this idea, there was no evidence for a stability flexibility tradeoff in either condition for the developmental cohort (Figure 7A; Spearman’s Rho 0.21, p = 0.2 for the changepoint condition and Rho −0.03, p = 0.87 for the oddball condition).

Figure 6:

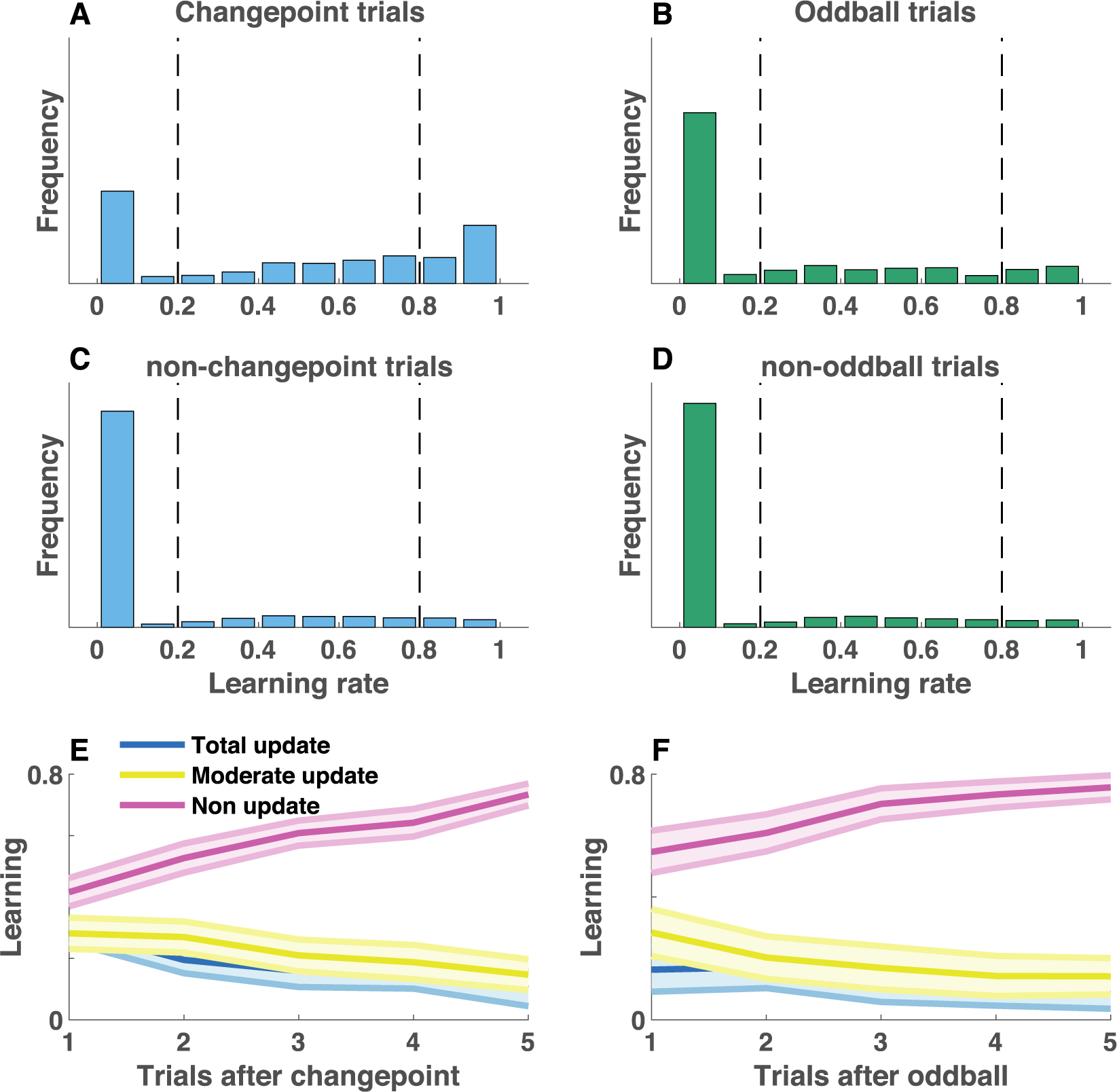
Non-updates are increased and condition-differences are less pronounced in a heterogeneous population of children. A-D) Single trial learning rate frequency histograms for changepoint (A) and oddball (B) trials, as well as for non-changepoint (C) and non-oddball (D) trials. Single trial learning rates are categorized into three types: non updates, moderate updates, and total updates, depending on their value with respect to criterion values (dotted vertical lines). E-F) Mean/SEM proportion of each category of learning rates used as a function of time since the previous surprising event [changepoint (E) or oddball (F)].

Figure 7:

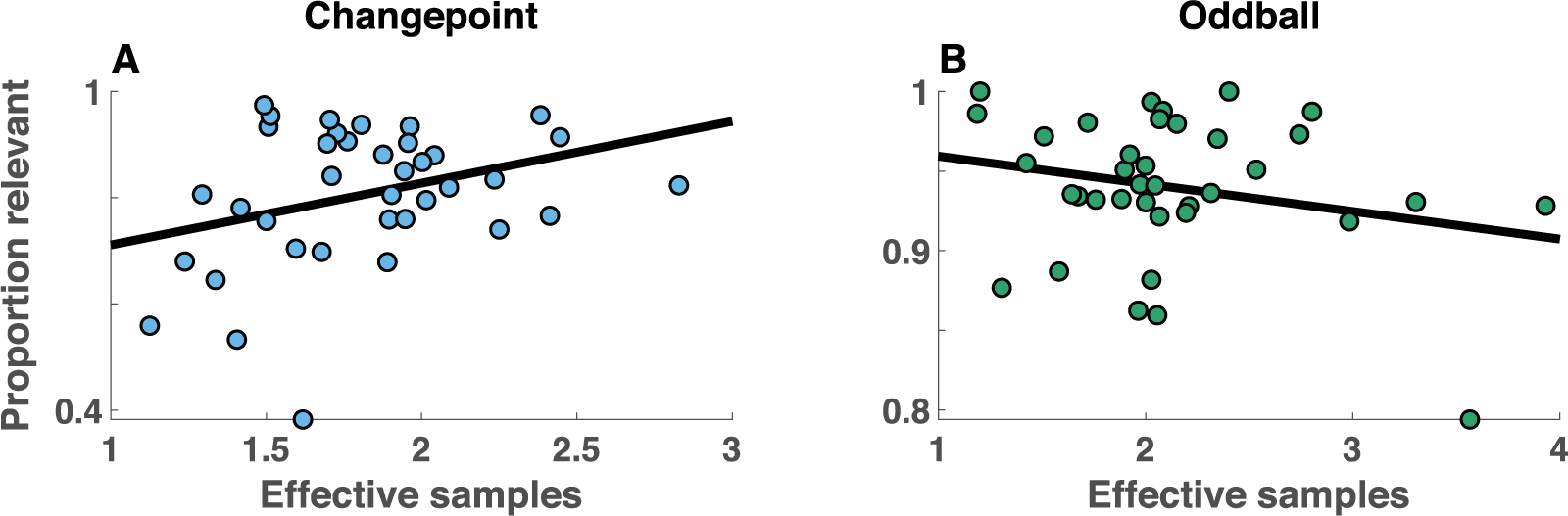
Stability/flexibility tradeoff does not explain individual differences in updating among a heterogeneous population of children. A-B) For each participant (points), the mean proportion of samples composing the belief that are relevant to the current statistical context (abscissa) is plotted against the total number of effective samples composing the belief (ordinate) separately for changepoint (A) and oddball (B) conditions. Trend lines indicate least squares fit to data.

Despite the lack of evidence for a stability flexibility tradeoff in this heterogenous population of children, attention to detail was still related across participants to lower precision beliefs, as quantified by effective samples. The average number of effective samples in participant beliefs aggregated across conditions was greatest for individuals with the lowest attention to detail scores (Spearman’s Rho = −0.50, p = 0.006). This relationship was similar in the two conditions (Fig 8A&B), but only reached statistical significance in the oddball condition (Spearman’s Rho for CP and ODD conditions: −0.25, −0.56; p values: 0.19, 0.001). Unlike in the young adult population, attention to detail did not confer any advantage in terms of flexibility to children (Fig 8C&D; p-value for correlations in both conditions > 0.5), likely due to additional variance in flexibility measures attributable to non-updating at changepoints (Fig 6E, pink). The relationship between attention to detail and belief precision was robust to inclusion of IQ, age, and gender into the explanatory model (Mean[95% conf int] beta for extended regression model = −0.20[−0.33, −0.06], t = −3.0, dof = 24, p = 0.006). The relationship was selective for attention to detail and categorical autism diagnosis did not relate to any of our task measures (Fig S8). Taken together, these results suggest that attention to detail comes at a significant cost to the precision of beliefs, whereas the potential benefits of attention to detail in terms of belief flexibility are population dependent.

Figure 8:

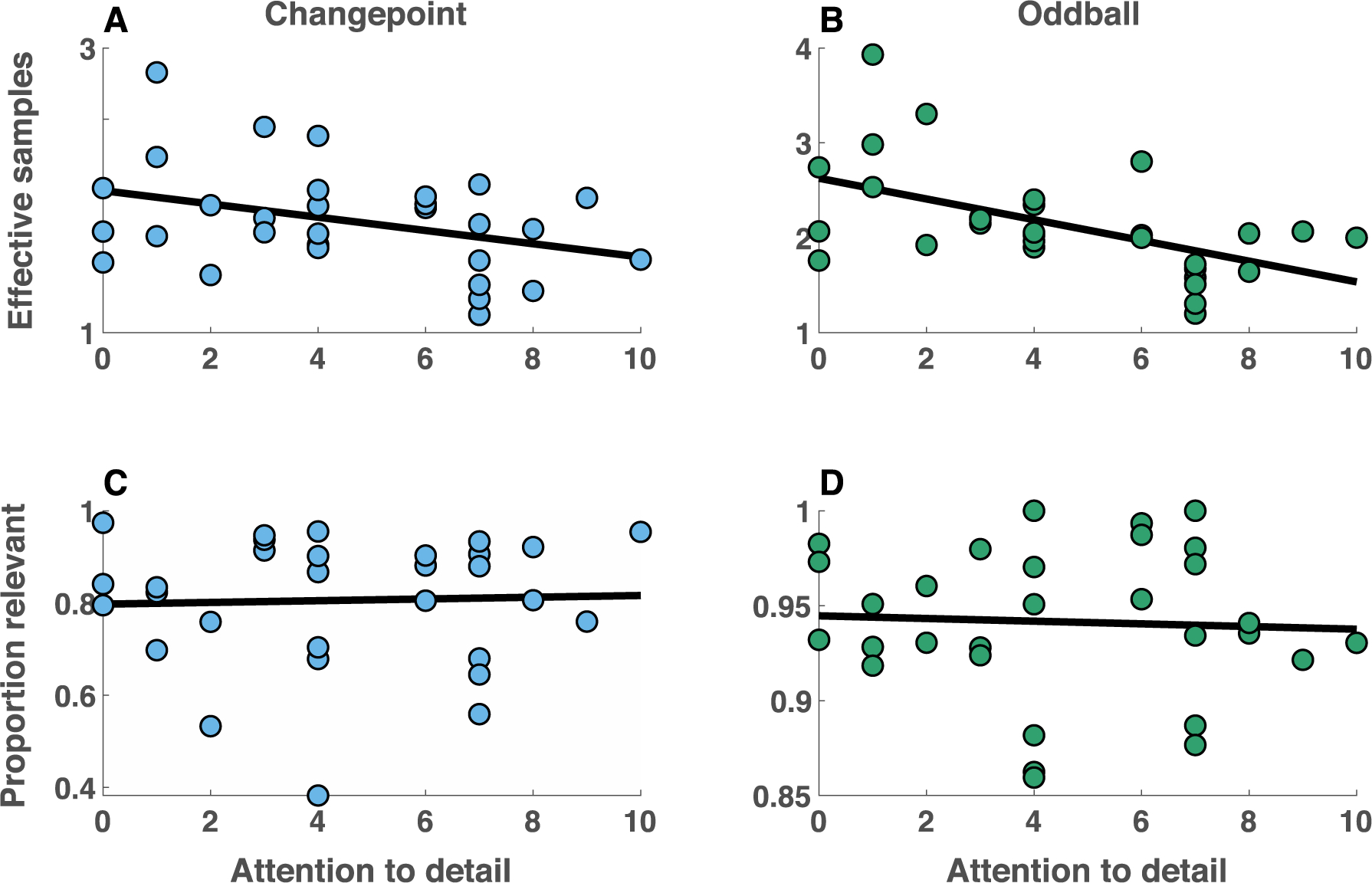
Attention to detail is inversely related to the number of effective samples composing beliefs in a heterogeneous population of children. A-B) For each participant (points), the total number of effective samples composing the belief (abscissa) is plotted against self reported scores on the attention to detail subscale of the AQ (ordinate) revealing a negative relationship in both changepoint (A) and oddball (B) conditions. C-D) In contrast, the proportion of relevant samples (abscissa) was unrelated to attention to detail scores (ordinate) for both changepoint (A) and oddball (B) conditions.

Discussion

Autism is a multi-dimensional construct with a broad behavioral profile. One autism-linked dimension, attention to detail, has been related to a focus on local, as opposed to global, stimulus information. Here we explored whether this local bias might exist in time as well as in space, and whether such a bias would manifest in highly flexible but unstable beliefs. We confirmed high attention to detail young adults were more prone to completely updating beliefs in the face of contradictory information, and that this led them to form beliefs that were more flexible but which incorporated fewer observations, and thereby less robust to noise during periods of stability. We replicated the negative relationship between attention to detail and belief precision in a developmental cohort that included both typically developing and children with autism, but did not identify any advantages of higher attention to detail individuals in this population with respect to flexibility. Taken together, our results highlight that high attention to detail, a prominent feature of autism, has profound implications for the way that information is used over time – promoting the use of recent, rather than historical information, and limiting the degree to which beliefs integrate over multiple observations.

To a first approximation, our results are consistent with basic tenants of “Weak Central Coherence Theory” (Frith, 1989; Happé & Frith, 2006). Specifically, the “global” aspect of our task might be considered to be the entire sequence of bag locations falling from the current helicopter location, whereas the “local” aspect might be considered to be the most recent bag location. We found that individuals who are high on attention to detail, a trait sometimes associated with autism, tend to focus on temporally local information, and form beliefs that incorporate fewer samples from the “global” category. This work nicely parallels work in the perceptual domain that has defined local and global in terms of space (O’Riordan & Plaisted, 2001; Plaisted, Dobler, Bell, & Davis, 2006; Sabatino DiCriscio & Troiani, 2017; Suzanne Scherf, Luna, Kimchi, Minshew, & Behrmann, 2008).

Although perceptual differences in ASD have been conceptualized as a manifestation of RRBs, the relationship between the presence of motor stereotypies, circumscribed interests, and perceptual differences in a given individual remains unclear. For this reason, we do not intend to suggest that greater flexibility in our task would be necessarily linked to manifestations of all RRBs observed in those with ASD. Our work did not focus on the binary autism distinction, but rather directly linked to measures of attention to detail. Thus, this is only one of many traits that is prevalent in ASD and indeed, in our populations was only very minimally related to other autism-linked traits (See supplementary figures 6&8). Some RRBs, particularly those in the visual perceptual domain, likely extend into the general population, whereas others (motor stereotypies) do not. Thus, our focus on traits might have heightened our ability to see such an effect, where other recent work that has compared autism to controls has had mixed results (Lawson et al., 2017; Manning et al., 2016). Given the heterogeneity of autism phenotype and manifestations of RRBs, it would be good for future work to delineate the relationship of various RRBs to each other and the presence of each RRB in the general population.

We find significant relationships with only the AQ Attention to Detail subscale. Given that performance on our task requires shifting responses in the face of altered contexts, one might expect a relationship between aspects of performance and the Attention Switching subscale. It may be that this subscale better captures aspects of visual pattern detection and detail-focused attention that scale with the particular type of performance pattern in this task. Others have also found distinct associations with the Attention to Detail subscale, including one study that demonstrated the Attention to Detail subscale was associated with better visual working memory (Richmond, Thorpe, Berryhill, Klugman, & Olson, 2013) as well as a study that found the Attention to Detail subscale was associated with improved performance on the Embedded Figures Task, a classic paradigm to measure one’s ability to extract a small object from a larger context (Burghoorn et al., 2020). Thus, this work adds to a growing body of evidence linking the Attention to Detail trait dimension that favor local information processing. One interesting and open question is whether the individual differences in temporal information processing that emphasize flexibility, as the cost of stability, which we highlight here, might directly relate to the perceptual enhancements that have previously been reported in high attention to detail individuals.

Our results also speak to the more general tradeoff that the brain faces with respect to controlling the use of recent versus historical information. In stable regimes, optimizing this tradeoff requires integrating over all relevant historical observations, but changes in the environment require rapidly refocusing on recent observations to afford flexibility. We found, as had been reported previously, dynamic adjustments in the use of information according to environmental statistics, but we also noted an extremely wide range of overall learning behaviors (Figure 3). Note that this need not be the case from a computational perspective; participants were trained explicitly on the generative structure of the task, and had more than enough experience to estimate the rate of changepoints and oddballs, were they inferring these meta-parameters from the task observations (Nassar, Bruckner, & Frank, 2019a; Wilson et al., 2010). Thus, if participants came into the task without strong predispositions towards favoring either stability or flexibility, then they should have all arrived at similar policies by the end of the training session. However, this is not what we observed. One might argue that the heterogeneity across the individual participants reflects completely different task strategies, however the link between attention to detail and learning policy observed in our two experiments (Figures 5&8) suggests that participants come to the task with a systematic predisposition toward a specific learning strategy, either favoring the use of recent information for flexibility (high attention to detail) or favoring the integration of data over time for stability (low attention to detail).

One interesting question stemming from this work relates to the developmental timescale and origin of these predispositions from a neural perspective. For example, many aspects of RRBs present in ASD are considered age appropriate for most neurotypical toddlers (i.e. insistence on sameness, circumscribed/hyperfocused interests, inflexibility). One reason these behaviors are considered atypical in ASD is that they persist in older children and adults with the diagnosis, significantly contributing to impairment in real-world situations. From the neural perspective, the heterogenous behavioral traits of ASD are not thought to stem from specific regions of the brain, but rather from atypical connectivity between brain regions. Atypical connectivity has been identified in numerous studies across multiple brain networks in ASD using various neuroimaging methods, including structural and functional MRI, EEG and MEG, and fNIRS (Hull et al., 2017; O’Reilly, Lewis, & Elsabbagh, 2017; Rane et al., 2015; Zhang & Roeyers, 2019). Although the findings of altered connectivity in ASD are vast, one finding that is particularly relevant to the current design is that Inflexibility of neural circuitry has been linked to behavioral inflexibility in ASD. For example, it is more difficult to discriminate functional connectivity of specific brain networks (namely, the salience network (SN), default mode network (DMN), and central executive network (CEN)) from each other in ASD relative to typical controls (Uddin et al., 2014). The SN and CEN networks are associated with salient information processing and cognitive control, respectively and nodes include the insula (SN), anterior cingulate (SN), dorsolateral prefrontal cortex (CEN) and posterior parietal cortex (CEN), which have been found to be relevant in performing the current task (see below).

The neural mechanisms of trial-to-trial adjustments and individual differences in learning rate have also been the focus of much recent work. Dynamic fluctuations in learning rate relate to overall arousal levels as measured by pupil diameter (Nassar et al., 2012), as well as activation in a network that includes insula, dorsomedial prefrontal cortex, and parietal cortex, and parts of dorsolateral prefrontal cortex (Behrens et al., 2007; McGuire et al., 2014; Payzan-LeNestour, Dunne, Bossaerts, & O’Doherty, 2013). Functional connectivity over a subgraph that includes many of these regions, and is closely related to both the salience and central executive networks described above, predicts individual differences in learning behavior (Kao et al., 2019). Given the well established connectivity differences in ASD, it is possible both attention to detail and adaptive learning in our task are jointly driven by individual differences in functional connectivity, and we hope that our work motivates future explorations of these brain-behavior relationships.

One important question is whether the brain networks that reflect learning rate are actually implementing a learning signal, or doing something more general such as assigning salience to unexpected observations. Two recent studies that clearly dissociate salience from learning using a generative structure like our oddball condition have suggested that the latter may be the case (d’Acremont & Bossaerts, 2016; Nassar, Bruckner, & Frank, 2019a). One recent idea that attempts to rectify differences between the relationship between brain activity and learning rate observed across different statistical environments is that learning rate adjustments are implemented through changes in the active latent state (Nassar, Bruckner, & Frank, 2019a; Nassar, McGuire, Ritz, & Kable, 2019b; Wilson, Takahashi, Schoenbaum, & Niv, 2014). When changes to this latent state are carried forward in time (eg. changepoints) then they could drive increases in learning rate, whereas when they are rapidly replaced (eg. oddballs) then they could drive reductions in learning rate (Razmi & Nassar, 2020). Within this framework, the fronto-parietal control network could be thought of as providing a signal to load a new state representation (Nassar, Bruckner, & Frank, 2019a), whereas regions including the orbitofrontal cortex seem to reflect the newly loaded state itself (Nassar, McGuire, Ritz, & Kable, 2019b). An important question raised by our work is where individual differences would fall in such a mechanistic process. If the primary determinant of individual differences were in the salience assignments then one might expect divergent individual difference relationships across the changepoint and oddball conditions. However, we observe similar individual difference relationships across the changepoint and oddball conditions, suggesting that attention to detail is less related to salience assignments than to the learning itself. This raises important questions about how such individual differences could emerge in the mechanistic model above, and should motivate future neuroimaging studies using individual differences in both task conditions to dissect the neural mechanisms through which attention to detail promotes flexible, but unstable, beliefs.

While our results provide some evidence for normative learning rate adjustment, they also highlight the impressive heterogeneity of learning strategies across individuals, and the degree to which all individuals fail to fully embody normative inference. The best participants in the young adult condition reported beliefs that, by our measures, only averaged across 2–4 observations, thereby leaving them susceptible to noise inherent in single observations. The deviations from normative learning were even more extreme in the developmental cohort, which did not show context dependent adjustments of learning (Fig S3). It is tempting to speculate that such context dependent adjustments might require cognitive architecture that is refined late in development, however another possibility is that children simply lacked the ability to translate our explicit instructions into a useful belief updating policy. Thus our results highlight the need for future developmental work on context-dependent learning rate adjustment, particularly using tasks where generative structures are learned implicitly (Bakst & McGuire, 2019) removing instructional confounds. Our developmental group also deviated from normative inference in the frequent use of non-updates. This finding is in line with other recent work that has suggested that increased perseveration and increased response variability in children might both stem from a liberal satisficing policy that leaves children highly influenced by default beliefs (Bruckner, Nassar, Li, & Eppinger, 2020). Taken together, these findings suggest that despite showing qualitative hallmarks of adaptive learning, people deviate substantially from optimality in a manner that depends on factors including their age and attention to detail.

Conclusions

Our results identify a link between attention to detail, a trait elevated in autism, and learning policies that favor flexibility over stability. Individuals high on attention to detail pay a price in terms of stability, with beliefs that tend to incorporate fewer observations than they would otherwise. These results were specific to attention to detail and unrelated to IQ or other autism linked traits. Overall, our findings demonstrate a core negative consequence of attention to detail, namely that by focusing attention on the newest observation, it limits the ability to integrate relevant information across a broader temporal context.

Appendix 1: Task instructions

Instructions for one counterbalance condition of the predictive inference task are reproduced below. Instructions also included screenshots of the task, which are not reproduced here. All instructions were read aloud to participants in the developmental cohort.

General instructions:

“Instructions. Press any key to move onto the next screen.”

“Bags of stones fall out of the helicopter. You’ll want to catch as many as you can”.

“Use the F,G,H, and J keys to move your bucket”

“When you are satisfied with the position of your bucket, press the space bar”.

Oddball context instructions:

“The helicopter will not stay in one location, it will make small but unpredictable movements. Most of the time, bags will fall near the helicopter. But on some trials, bags will be dropped from a plane way up above. On these trials the bag is equally likely to fall in any location.”

Screen display then indicates which color stones the participant will receive points for collecting (depends on counterbalance condition). They will not know which color stone the bag contains until it lands. Example text:

“Red stones are worth money

You will get paid an extra $5 for every 10 buckets you fill with red stones.

Green stones are not worth anything.

There is no way to tell what kind of stones are in the bag until it lands.”

[Run visible oddball block]

“Now the helicopter will be hidden by clouds. Everything else will be exactly the same as the previous blocks. You should continue to keep your bucket directly under the helicopter, even though you can no longer see it.”

[Run cloudy oddball block]

“Bags will fall near the helicopter but their exact position is random. Your best strategy is to keep the bucket directly underneath the helicopter.

The helicopter usually stays in one place, but occasionally it moves to a new location.”

[Run visible changepoint block].

“Now the helicopter will be hidden by clouds. Everything else will be exactly the same as the previous blocks. You should continue to keep your bucket directly under the helicopter, even though you can no longer see it.”

[Run cloudy changepoint block].