Abstract
Beyond the absence of long-range magnetic orders, the most prominent feature of the elusive quantum spin liquid (QSL) state is the existence of fractionalized spin excitations, i.e., spinons. When the system orders, the spin-wave excitation appears as the bound state of the spinon-antispinon pair. Although scarcely reported, a direct comparison between similar compounds illustrates the evolution from spinon to magnon. Here, we perform the Raman scattering on single crystals of two quantum kagome antiferromagnets, of which one is the kagome QSL candidate Cu3Zn(OH)6FBr, and another is an antiferromagnetically ordered compound EuCu3(OH)6Cl3. In Cu3Zn(OH)6FBr, we identify a unique one spinon-antispinon pair component in the E2g magnetic Raman continuum, providing strong evidence for deconfined spinon excitations. In contrast, a sharp magnon peak emerges from the one-pair spinon continuum in the Eg magnetic Raman response once EuCu3(OH)6Cl3 undergoes the antiferromagnetic order transition. From the comparative Raman studies, we can regard the magnon mode as the spinon-antispinon bound state, and the spinon confinement drives the magnetic ordering.
Subject terms: Electronic properties and materials, Magnetic properties and materials, Phase transitions and critical phenomena
Spinon excitations of a Kagome quantum spin liquid are expected to give rise to a magnetic continuum in Raman spectroscopy. Here, the authors report a magnetic Raman continuum in the Kagome spin liquid candidate Cu3Zn(OH)6FBr, in contrast to a sharp magnon Raman peak in the Kagome antiferromagnet EuCu3(OH)6Cl3.
Introduction
Quantum spin liquid (QSL) represents a new class of condensed matter states characterized by the long-range many-body entanglement of topological orders1–9. The lattice of the spin-1/2 kagome network is a long-sought platform for antiferromagnetically interacting spins to host a QSL ground state10–16. However, a structurally ideal realization of the kagome lattice in experiments is rare. Herbersmithite [ZnCu3(OH)6Cl2] is the first promising kagome QSL candidate3,16–23, in which no long-range magnetic order was detected down to low temperature17,18, and inelastic neutron scattering revealed a magnetic continuum, as a hallmark of fractionalized spin excitations20,22. Up to date, most, if not all, experimental information on the nature of kagome QSL relies on a single compound of Herbertsmithite. Considering the fact that a lattice distortion has recently been confirmed in Herbersmithite24,25, which stimulates investigations on the subtle magneto-elastic effect in the kagome materials26,27, an alternative realization of the QSL compound with the ideal kagome lattice is still in urgent need. Zn-Barlowite [Cu3Zn(OH)6FBr] is another candidate for a kagome QSL ground state28–38 with no lattice distortion being reported yet. Measurements on the powder samples didn’t detect the long-range magnetic order down to temperatures of 0.02 K, four orders of magnitude lower than the Curie–Weiss temperature30,32. Besides the lack of magnetic order, the fractionalized spin excitations, i.e., spinons, is essential evidence for the long-range entanglement pattern in QSL. However, spectroscopic evidence for the deconfined spinon excitations in Zn-Barlowite is still lacking, in part due to unavailable single-crystal samples.
Raman scattering is sensitive to the local symmetries depending on the light polarization39,40, and also capable of detecting magnetic excitations ranging from the spin-wave magnon excitation to deconfined spionons41–50. Raman scattering has previously been reported for Herbertsmithite and revealed the multiple spinon scattering process19. In recent years, the atacamite family ReCu3(OH)6Cl3 (Re=Y, Eu, Sm, and Nd) with the perfect kagome lattice has been synthesized and a chiral 120∘ antiferromagnetic (AFM) order with the wave vector q = 0 is identified in the ground state51–55. The kagome spin systems can be described by the kagome Heisenberg model with the Dzyaloshinski–Moriya (DM) interaction
| 1 |
where summation runs over nearest-neighbor bonds 〈ij〉, and J and D are the nearest-neighbor exchange and the DM interaction constants, respectively, for the spins Si,j on the i- and j-th sites. We ignore the in-plane DM interactions regarding to the previous electron paramagnetic resonance measurements in the related kagome systems55,56. A DM interaction larger than the critical value of (D/J)c ~ 0.08 induces a chiral 120° AFM order from the QSL state57–59. By the first-principle calculations (Supplementary Note 1), Zn-Barlowite and EuCu3(OH)6Cl3 have D/J values of 0.05 and 0.3, resulting in QSL and AFM ground states, respectively, consistent with the experimental identification of the ground states30,54. While the elementary spin excitation of the kagome QSL is the deconfined spinon, the low energy excitation in the kagome AFM ordered states is the magnon. A direct comparison by the magnetic Raman scattering can reveal the evolution from deconfined spinons in Zn-Barlowite to magnons in EuCu3(OH)6Cl3, but has not been performed yet.
In this work, we exclude the kagome lattice distortion by angle-resolved polarized Raman (ARPR) scattering and second-harmonic-generation (SHG), and reveal the spin dynamics of spinon excitations on the single-crystalline Cu3.18Zn0.82(OH)6FBr. We observe a remarkable E2g magnetic Raman continuum, which can be decomposed into one spinon–antispinon pair (one-pair (1P)) and two spinon–antispinon pair (two-pair (2P)) components of spinon excitations, in line with theoretical studies of the kagome QSL60. The one-pair continuum is unique, serving as the fingerprint of spinons. In a control experiment, beside the two-magnon (2M) magnetic Raman continuum, we probe a sharp one-magnon (1M) Raman peak in EuCu3(OH)6Cl3 below the AFM transition temperature. The magnon peak emerges from the 1P continuum in the magnetic Raman scattering, can be regarded as the bound state of the spinon–antispinon excitations. As schematically summarized in Fig. 1, our comparative Raman study demonstrates the spinon deconfinement and confinement in the kagome QSL compound and ordered antiferromagnet, respectively. The AFM order transition can be thought to be driven by the spinon confinement.
Fig. 1. Schematical comparative Raman responses for the AFM and QSL states.
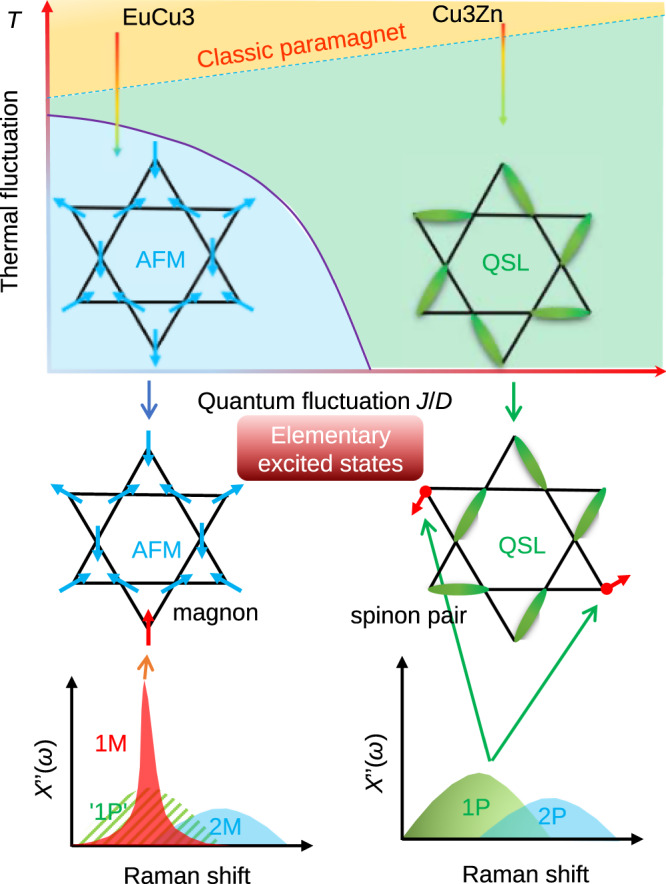
With a large DM interaction D, the kagome antiferromagnet develops a chiral 120° AFM ground state. Increasing J/D, the fluctuation of the kagome system increases, driving the system into the QSL state. By increasing the temperature, the thermal fluctuation melts the magnetic order and turns the system into the classic paramagnetic state at high temperatures. Cu3Zn and EuCu3 have the QSL and AFM ground states, and allow spinon and magnon excitations, respectively. Magnetic Raman scattering measures different elementary excited states in the two different ground states. Here 1P and 2P denote the one-pair and two-pair spinon excitations, respectively. 1M and 2M in AFM ordered state denote the one- and two-magnon excitations, respectively. The 1M Raman peak in AFM measures the magnon while the 1P Raman continuum in QSL probes the spinon excitations. The shadow background of the 1M peak, marked as `1P', denotes the continuum above TN in EuCu3, mimicking the 1P continuum in the QSL state.
Results
We grown single crystals of Barlowite Cu4(OH)6FBr, Zn-Barlowite Cu3.18Zn0.82(OH)6FBr, and EuCu3(OH)6Cl3 (we use the short-hand notation Cu4, Cu3Zn, and EuCu3, respectively) with high quality (“Methods” and Supplementary Note 2). The interlayer Cu2+ concentration (18%) is comparable to that (15%) in Herbertsmithite61. We estimate the superexchange strength for the kagome spins in Cu3Zn as J ≃ 13 meV by the Curie–Weiss temperature ΘCW = −220 K (Supplementary Note 2)62. The superexchange interaction for EuCu3 is about J ≃ 7 meV53–55. Note the electronic ground state of Eu3+ in EuCu3 is the non-magnetic 7F0 configuration.
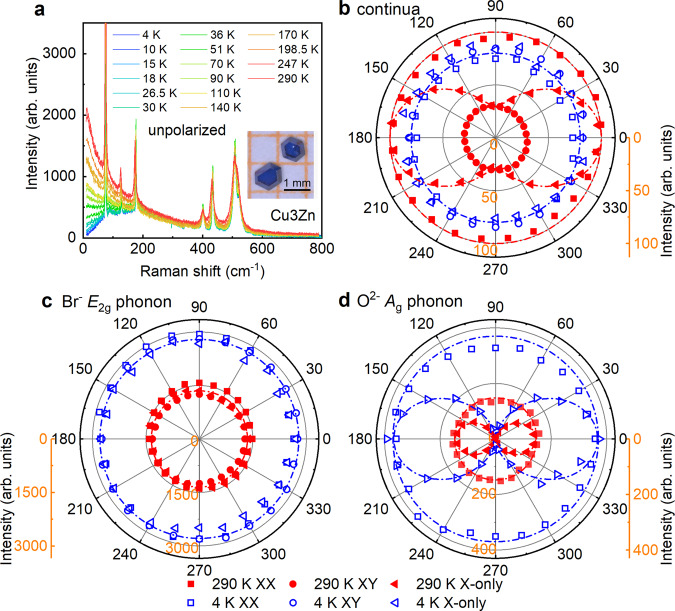
Figure 2a presents the temperature evolution of Raman spectra in Cu3Zn with sharp phonon modes superimposing on the magnetic continuum background. With the help of first-principles calculations, we assign the symmetry representations for phonon modes in Supplementary Note 3. No structural phase transition is observed in Cu3Zn down to 4 K. We tracked the Raman spectral evolution of the crystal structures from Cu4 to Cu3Zn (Supplementary Note 4). Cu3Zn has no Raman-active mode related to the kagome Cu2+ vibrations, indicating the kagome layer remains intact. Cu4 has distorted kagome layers at 200 K, signaled by an extra phonon mode at 62 cm−1 corresponding to the kagome Cu2+ vibration. The previous SHG study revealed the parity symmetry in Barlowite 2 [Cu4(OH)6FBr] and Zn-Barlowite [Cu3.66Zn0.33(OH)6FBr]25. We confirmed the inversion symmetry by SHG in our single crystals of Cu3Zn (Supplementary Note 6).
Fig. 2. Temperature dependent and ARPR spectra in Cu3Zn.
a Temperature evolution of unpolarized Raman spectra in Cu3Zn. The inset is the photo of single crystals. ARPR intensity for low-energy continua (b), the Br−E2g phonon (75 cm−1) (c), and the O2−A1g phonon (429 cm−1) (d). The dash-dotted lines are the corresponding theoretical curves based on the C3 rotation symmetry.
Figures 2b–d are the ARPR responses of Cu3Zn in three different polarization configurations (“Methods” and Supplementary Note 5). In the XX (XY) configuration, the incoming and outgoing light polarizations are parallel (perpendicular) and rotated simultaneously. In the X-only configuration, the outgoing polarization is fixed and only incoming light is rotated. Theoretically, the Raman cross section of a Kagome QSL ground state does not depend on the polarization of the incoming or outgoing light39 and keeps invariant against rotating light polarization in the XX, XY, and X-only configurations. Figure 2b is the ARPR response for the magnetic continua at low frequency with the integrated Raman susceptibility , where the susceptibility is related to the Raman intensity I(ω) = (1 + n(ω))χ″(ω) with the bosonic temperature factor n(ω). Figure 2c and d are the corresponding results of the Br−E2g phonon, and O2−A1g phonon modes, respectively. For threefold rotation symmetry, the A1g mode response follows the function of the rotation angle θ in X-only configuration, keeps constant in XX polarization, and vanishes in XY configuration; the E2g mode is isotropic in all the three configurations. The magnetic continuum contains both A1g and E2g channels at high temperature (290 K), and only the E2g channel at low temperature (4 K). The experimental ARPR responses agree well with the theoretical dash-dotted curves, confirming the threefold rotational symmetry in the magnetic excitations (Fig. 2b) and lattice vibrations (Figs. 2c, d). We notice that in Herbertsmithite, although it was not discussed, the lattice distortion was evident by the anisotropic ARPR responses19 and may account for the difference from our results.
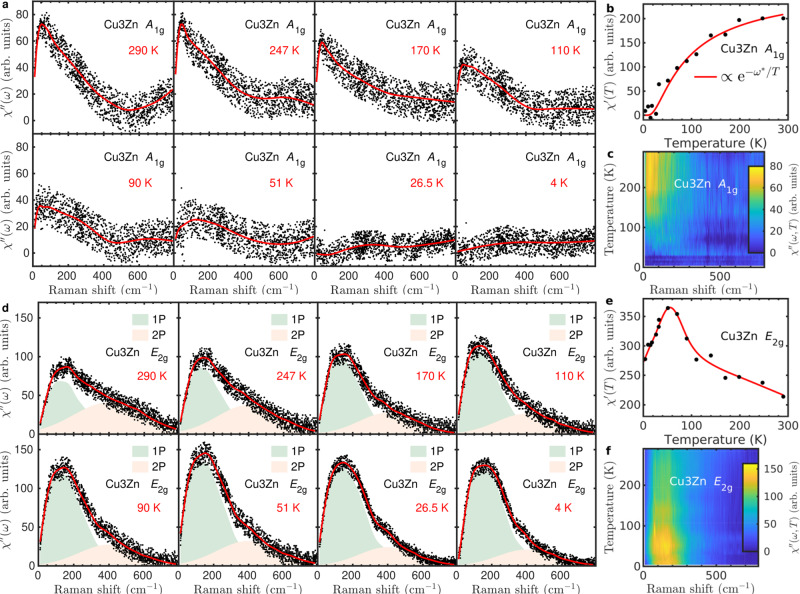
Having established the structurally ideal realization of the kagome lattice by SHG and ARPR scattering, and the absence of the thermodynamic anomaly, we now present our spectroscopic results of spin dynamics in Cu3Zn with subtracting phonon contributions. Figure 3a–c are the magnetic continuum of Cu3Zn in the A1g channel, which is activated only at high temperatures, and disappears at low temperatures. The integrated Raman susceptibility in Fig. 3b fits the thermally activated function, with ω* = 53 cm−1. The result suggests the A1g continuum measures the thermal fluctuation of the interacting kagome spins41,63,64. Different from the A1g channel, the pronounced E2g magnetic Raman continuum persists down to 4 K (Fig. 3d–f), indicating the intrinsic quantum fluctuation of the kagome spins. The substantial low energy component has a non-monotonic temperature dependence. It increases with the temperature decreasing from 290 K to 50 K, but decreases with further temperature reducing as shown in Fig. 3d–f. The E2g magnetic Raman susceptibility χ″(ω, T) distributes the main spectral weight among the frequency region less than 400 cm−1, and reaches the maximum at around 150 cm−1 and 50 K, as shown in Fig. 3f.
Fig. 3. Temperature dependent magnetic Raman continua in Cu3Zn.
a The A1g Raman susceptibility . The solid lines are guides to the eye. b Temperature dependence of the A1g static Raman susceptibility . The solid line is a thermally activated function. c Color map of . d The E2g Raman response function . The solid lines are guides to the eye. The light green and pink shadow marked as “1P” and “2P” represent the one-pair and two-pair components of Raman continuum. e Temperature dependence of the E2g static Raman susceptibility . The solid line is a guide to the eye. f Color map of .
The low-energy E2g Raman continuum is crucial as it has an origin of the spinon excitation in the kagome QSL from the theoretical perspective60. In the XY configuration for the E2g channel, the Raman tensor on the kagome lattice is written in terms of spin-pair operators39,60,65,66
| 2 |
where SR1,2,3 are spin operators on three sites of the R-th kagome unit cell and a1,2 are the lattice vectors. The spin operator has the spinon fiσ representation where τα is the α-th Pauli matrix. The spin-pair is with . In the mean field theory, the spinon hopping amplitude is non-zero. So we have 1P and 2P components in the Raman tensor60
| 3 |
| 4 |
where ⋯ denotes omitted terms in Eq. (2) for the notation simplicity. While the 2P component is analogous to the 2M scattering, the 1P contribution is a unique prediction for spinon excitations in the kagome QSL. In Fig. 3d, we schematically decompose the E2g Raman continuum into 1P and 2P components of spinon–antispinon excitations. The 1P component has the maximum at 150 cm−1 (1.4J), and extends up to 400 cm−1 (3.8J) at low temperatures. The 2P component has the maximum at 400 cm−1 (3.8J) and the cut-off around 750 cm−1 (6.7J). The mentioned features (maxima and cut-offs) of 1P and 2P excitations in the E2g Raman response agree well with the theoretical prediction for the kagome QSL state60.
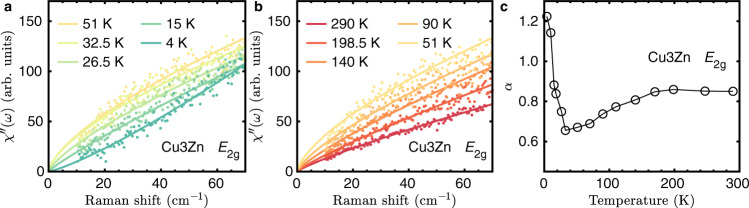
In more detail, the 1P component dominates the E2g magnetic Raman continuum at low frequency. It displays the power-law behavior up to 70 cm−1, with a significantly nonmonotonic temperature dependence, as shown in Fig. 4. The low-energy continuum evolves from a sublinear behavior Tα with α < 1 to a superlinear one Tα with α > 1 as reducing the temperature. A central question for the kagome QSL is whether a spin gap exists. Previous results on the powder samples of Cu3Zn suggest a small spin gap30,32. If such a gap exists, the power-law behavior of the E2g magnetic Raman continua sets an upper bound for the spin gap of 2 meV.
Fig. 4. Power-law behavior for E2g magnetic Raman continua at low frequency in Cu3Zn.
a, b are power-law fitting of at low and high temperatures, respectively. c Temperature-dependent exponent α for the power-law fitting.
The theoretical calculation for kagome Dirac spin liquid (DSL) predicts the power-law behavior for the Raman susceptibility in the E2g channel at low frequency60. The 1P spinon excitation in DSL gives the linear density of state (DOS) . The matrix element turns out to be exactly zero for all 1P excitations with ω = 0 in the mean field Dirac Hamiltonian. As a result a Raman spectrum that scales as ω3 was predicted. However, the vanishing of the matrix element is somewhat accidental and depends on the assumption of a DSL in an ideal kagome Heisenberg model. Any deviation from the ideal DSL state, e.g., a small gap in the ground state30,32, DM interactions, or other effects of perturbations26,67, changes the wave functions and may result in a constant matrix element. In that case, the Raman spectrum will be simply proportional to the DOS of the 1P component which is linear in ω. From our fitting for Cu3Zn in Fig. 4, we find that α = 1.3 when approaching zero temperature. The existence of a small gap in the spinon spectrum may explain the discrepancy.
Considering the interlayer Cu2+ concentration (18%) in Cu3Zn, we make a remark here about the disorder effect in the magnetic Raman scattering. The temperature-dependent E2g static magnetic susceptibility of Cu3Zn in Fig. 3 exhibit the maximal spin fluctuations at 50 K. The non-monotonic T-dependence deviating from the Curie–Weiss behavior is associated with the enhancement of nearest-neighbor spin correlations at low temperatures67. However, such significant deviation from Curie–Weiss behavior is masked by the interlayer Cu2+ moments in the bulk thermodynamic measurements, e.g., heat capacity and bulk magnetization30. In contrast to a significant energy dependent magnetic Raman susceptibility at 4 K in Cu3Zn, the scattered neutron signal in Herbertsmithite is overall insensitive to energy transfer, rather flat above 1.5 meV, but increases significantly with reducing energy below 1.5 meV due to the interlayer Cu2+ ions20,22. So Raman scattering singles out the kagome magnetic excitations and remains unmasked in the presence of the interlayer Cu2+ due to the matrix element effect as explained below. The Raman scattering measures the nearest-neighbor spin-pair τR ∝ Si ⋅ Sj dynamics, but the spin pairs associated with the interlayer Cu2+ ions are weaker than the singlet pairs for the kagome spins. As the light polarization in our Raman measurements is in the kagome ab plane, and the projected factor of the spin-pairs associated with the interlayer Cu2+ ions, , is small, as the related pair bond vector rij has the angle around 52° with respect to the kagome plane. As a result, the interlayer Cu2+ ions contribute a negligible Raman matrix element and we ignore their effect in the discussions about the Raman experiments. Moreover, the inelastic neutron scattering in Herbertsmithite measures the magnetic continuum up to 3J20, the same energy range as the 1P Raman component in Cu3Zn. These results suggest that the magnetic Raman continuum originates from the kagome spins, and the 1P component has an origin of spinon excitations.
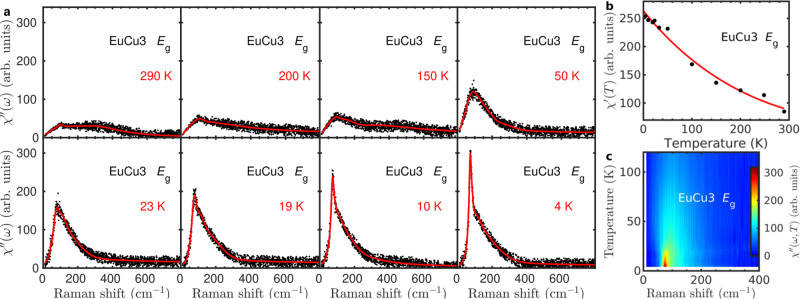
Figure 5 presents a control Raman study on the magnetic ordered kagome antiferromagnet EuCu3, which has the antiferromagnetic superexchange strength J ≃ 7 meV. In Supplementary Note 7, the ARPR scattering on EuCu3 confirms the threefold rotational symmetry. Above the ordering temperature TN = 17 K, the magnetic Raman continuum in the Eg channel displays the extended continuum, similar to the E2g magnetic continuum at 4 K in Cu3Zn. Below TN, a sharp peak, i.e., 1M peak as discussed below, is observed on top of the magnetic continuum. The integrated Raman susceptibility monotonically increases as lowering the temperature as shown in Fig. 5b, different from non-monotonic behavior in of Cu3Zn in Fig. 3e. The magnetic Raman susceptibility χ″(ω, T) in EuCu3 distributes the main spectral weight among the frequency region less than 400 cm−1, and the magnon peak locates at 72 cm−1 below 17 K, as shown in Fig. 5c.
Fig. 5. Temperature dependent Eg magnetic Raman continua in EuCu3.
a The Eg Raman susceptibility . The solid lines are guides to the eye. A sharp magnon peak appears in the Eg magnetic Raman continuum below the magnetic transition temperature TN = 17 K. b Temperature dependence of the static Raman susceptibility in the Eg channel . The solid line is a guide to the eye. c Color map of .
To directly compare the 1P spinon continuum in Cu3Zn and the 1M peak in EuCu3, we plot the Eg Raman response in EuCu3 at selected temperatures in Fig. 6. The E2g Raman continuum in Cu3Zn at 4 K is also plotted with the proper scale for the Raman frequency. Above TN = 17 K, EuCu3 has the substantial magnetic continuum with the profile similar to that in Cu3Zn at 4 K. There are less pronounced low-energy continuum excitations in EuCu3 than those in Cu3Zn, probably due to the large DM interaction which suppresses the low-energy quantum fluctuations. Below TN, a sharp magnon peak at 72 cm−1 appears in EuCu3 with the corresponding energy scale of the 1P continuum maximum in Cu3Zn. We stress that the magnon Raman peak is direct spectroscopic evidence for the q = 0 120° non-collinear AFM spin configurations, and invisible in the structure of the 120∘ AFM (“Methods”).
Fig. 6. Comparative Raman studies of EuCu3 and Cu3Zn.
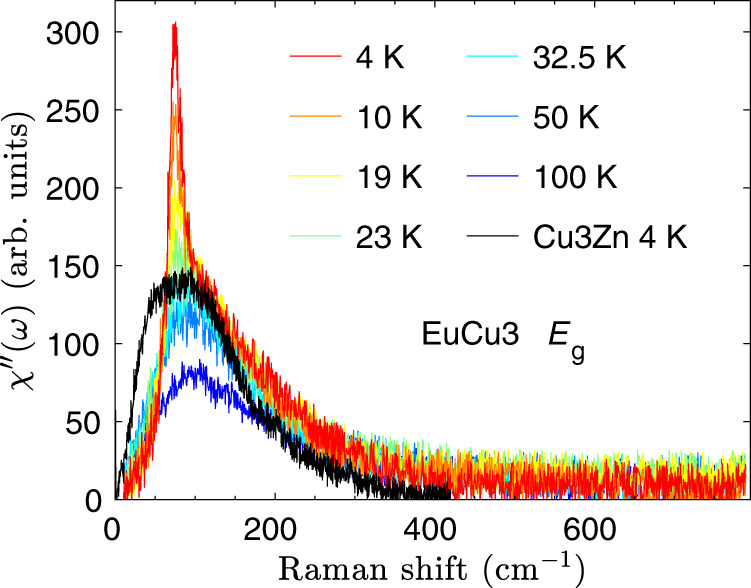
We select the Eg magnetic Raman continua in EuCu3 at several temperatures. For a comparison, we also plot the E2g magnetic Raman continuum in Cu3Zn at 4 K with the Raman shift scaled by the superexchange energy ratio of 1.9.
For the AFM order state, the low-energy excitation is the spin-wave magnon which can be described in the spin-wave theory68. In the local spin basis of the AFM order, we have the Raman tensors in the XY configuration of the Eg channel for 1M and 2M components as following
| 5 |
| 6 |
with the 2M spin-pair operator . For the details, please refer to the “Methods” section. Therefore, the Eg Raman scattering in the AFM order state measures 1M and 2M excitations as demonstrated in Fig. 1. Thus, the magnon excitation emerges from the 1P continuum and can be regarded as the bound state of the spinon–antispinon excitations.
Discussion
Deconfined spinons yield to the magnetic continuum, however, the Raman continuum does not necessarily imply the spin fractionalization. Only 2M excitation itself gives rise to a Raman continuum in the ordered antiferromagnet42. In this work, the comparative Raman study in Cu3Zn and EuCu3 resolves this uncertainty. Guided by the theoretical prediction60, the E2g Raman continuum can be decomposed into 1P and 2P components of the spinon–antispinon excitations. While the 2P component has the maximum at 3.8J, resembling the 2M broad peak42, the 1P continuum in Raman is unique for QSL. Its maximum and extended range have the same energy scale as the spin-wave magnon peak in EuCu3 and the inelastic neutron continuum cutoff (up to 3J) in the Herbertsmithite, respectively.
The 1P component of Raman continuum reveals fractionalized spin excitations, providing strong evidence for the kagome QSL ground state in Cu3Zn. Our comparative Raman studies explicitly show the evolution from the deconfined spinon excitation in the kagome quantum spin liquid compound Cu3Zn to the conventional magnon in the kagome ordered antiferromagnet EuCu3. On the material side, Zn-Barlowite is an ideal structural realization of the kagome lattice. Along with Herbertsmithite, the single-crystalline Zn-Barlowite stands able to single out the intrinsic properties of the kagome QSL.
Methods
Sample preparation and characterization
High qualified single crystals of Zn-Barlowite was grown by a hydrothermal method similar to crystal growth of herbertsmithite69,70. CuO (0.6 g), ZnBr2 (3 g), and NH4F (0.5 g) and 18 ml deionized water were sealed in a quartz tube and heated between 200 °C and 140 °C by a two-zone furnace. After 3 months, we obtained millimeter-sized single crystal samples. The value of x in Cu4−xZnx(OH)6FBr has been determined as 0.82 by Inductively Coupled Plasma-Atomic Emission Spectroscopy (ICP-AES). The single-crystal X-ray diffraction has been carried out at room temperature by using Cu source radiation (λ = 1.54178 Å) and solved by the Olex2.PC suite programs71. The structure and cell parameters of Cu4−xZnx(OH)6FBr are in coincidence with the previous report on polycrystalline samples30,32. For Barlowite(Cu4(OH)6FBr), the mixture of CuO (0.6 g), MgBr2 (1.2 g), and NH4F (0.5 g) was transferred into Teflon-lined autoclave with 10 ml water. The autoclave was heated up to 260 °C and cooled to 140 °C after 2 weeks. A similar growth condition to Barlowite was applied for the growth of EuCu3(OH)6Cl3 with staring materials of EuCl3 ⋅ 6H2O (2 g) and CuO (0.6 g).
Measurement methods
Our thermodynamical measurements were carried out on the Physical Properties Measurement System (PPMS, Quantum Design) and the Magnetic Property Measurement System (MPMS3, Quantum Design).
The temperature-dependent Raman spectra are measured in a backscattering geometry using a home-modified Jobin-Yvon HR800 Raman system equipped with an electron-multiplying charged-coupled detector (CCD) and a ×50 objective with long working distance and numerical aperture of 0.45. The laser excitation wavelength is 514 nm from an Ar+ laser. The laser-plasma lines are removed using a BragGrate bandpass filter (OptiGrate Corp.), while the Rayleigh line is suppressed using three BragGrate notch filters (BNFs) with an optical density 4 and a spectral bandwidth ~ 5–10 cm−1 72. Thus, Raman signal down to 5 cm−1 can be measured73. The 1800 lines/mm grating enables each CCD pixel to cover 0.6 cm−1. The samples are cooled down to 30 K using a Montana cryostat system under a vacuum of 0.4 mTorr and down to 4 K using an attoDRY 1000 cryogenic system. All the measurements are performed with a laser power below 1 mW to avoid sample heating. The temperature is calibrated by the Stokes-anti-Stokes relation for the magnetic Raman continuum and phonon peaks. The intensities in two cryostat systems are matched by the Raman susceptibility. The ARPR measurements40 with light polarized in the ab kagome plane of samples were performed in parallel (XX), perpendicular (XY), and X-only polarization configurations (Supplementary Note 5).
SHG measurements were performed using a homemade confocal microscope in a backscattering geometry. A fundamental wave centered at 800 nm was used as excitation source, which was generated from a Ti-sapphire oscillator (Chameleon Ultra II) with an 80 MHz repetition frequency and a 150 fs pulse width. After passing through a ×50 objective, the pump beam was focused on the sample with a diameter of 2 μm. The scattering SHG signals at 400 nm were collected by the same objective and led to the entrance slit of a spectrometer equipped with a thermoelectrically cooled CCD. Two shortpass filters were employed to cut the fundamental wave.
Magnon Raman peak in kagome AFM ordered state
With a large DM interaction D, the kagome antiferromagnet in Eq. (1) devoleps a q = 0 type 120° AFM order at low temperature in EuCu353–55,57–59. In terms of the local basis for the AFM order, we rewrite the Hamiltonian as
| 7 |
with
| 8 |
| 9 |
where θij is an angle between two neighboring spins and below denotes the local basis of the AFM order. The effective linear spin wave Hamiltonian is given as
| 10 |
for which the Holstein-Primakoff representation for spin operators in the local basis was applied and the energy dispersion was obtained in ref. 68.
In the local spin basis, we have the Raman tensor in the XY configuration is given as
| 11 |
In the spin-pair operator in Eq. (8), there are two-magnon contribution in terms of , and one- and three-magnon contributions in terms of . For the q = 0 spin configuration, we find that in Eq. (11) has the non-vanished one magnon contributions. For the AFM state, has no one-magnon contribution. Therefore, the observed one-magnon peak in the Eg channel in EuCu3 provides evidence for the q = 0 spin ordering at low temperatures. In the linear spin-wave theory, we take Sz in the local basis as a constant, , and the Raman tensor in XY configuration is given as
| 12 |
in terms of the local basis, directly measuring the one magnon excitation.
For EuCu3, the exchange interaction parameters are estimated as J = 7 meV, D/J = 0.3, leading to the magnon peak position of Δsw = 1.1J = 77 cm−1, very close to the measured value 72 cm−1 in our Raman measurement of the one-magnon peak.
Supplementary information
Acknowledgements
This work was supported by the National Key Research and Development Program of China (2016YFA0301204), the program for Guangdong Introducing Innovative and Entrepreneurial Teams (No. 2017ZT07C062), by Shenzhen Key Laboratory of Advanced Quantum Functional Materials and Devices (No. ZDSYS20190902092905285), Guangdong Natural Science Foundation (No. 2020B1515120100) and by National Natural Science Foundation of China (Grant Nos. 11774143, 12004377 and 11874350), the CAS Key Research Program of Frontier Sciences (ZDBS-LY-SLH004) and China Postdoctoral Science Foundation (2019TQ0317 and 2020M682780). P.A. Lee acknowledges support by the US Department of Energy under grant number DE-FG02-03ER46076.
Author contributions
J.W.M. conceived the project. P.H.T. conceived the experimental work of Raman spectroscopy. Y.F., L.W., L.H., W.J., and Z.H. synthesized single crystals of samples. M.L. and P.H.T. designed the Raman experiments. M.L., J.Z., and P.H.T. performed Raman measurements. Q.L. and J.D. performed the SHG measurements. Y.F., L.W., L.H., and C.L. performed and analyzed magnetic susceptibility and heat capacity measurements. H.Z., X.S., and J.W.M. performed first-principles calculations. J.W.M., Y.F., M.L., and P.H.T. analyzed the Raman data. P.A.L., J.W.M., and F.Y. worked on the theory. P.A.L., J.W.M., F.Y., P.H.T., and M.L.L. wrote the manuscript with contributions and comments from all authors.
Data availability
All data supporting the findings of this study are available from the corresponding authors upon reasonable request.
Competing interests
The authors declare no competing interests.
Footnotes
Peer review information Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
These authors contributed equally: Ying Fu, Miao-Ling Lin.
Contributor Information
Ping-Heng Tan, Email: phtan@semi.ac.cn.
Jia-Wei Mei, Email: meijw@sustech.edu.cn.
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-021-23381-9.
References
- 1.Anderson PW. Resonating valence bonds: a new kind of insulator? Mater. Res. Bull. 1973;8:153. doi: 10.1016/0025-5408(73)90167-0. [DOI] [Google Scholar]
- 2.Anderson PW. The resonating valence bond state in La2CuO4 and superconductivity. Science. 1987;235:1196. doi: 10.1126/science.235.4793.1196. [DOI] [PubMed] [Google Scholar]
- 3.Lee PA. An end to the drought of quantum spin liquids. Science. 2008;321:1306. doi: 10.1126/science.1163196. [DOI] [PubMed] [Google Scholar]
- 4.Balents L. Spin liquids in frustrated magnets. Nature. 2010;464:199. doi: 10.1038/nature08917. [DOI] [PubMed] [Google Scholar]
- 5.Zhou Y, Kanoda K, Ng T-K. Quantum spin liquid states. Rev. Mod. Phys. 2017;89:025003. doi: 10.1103/RevModPhys.89.025003. [DOI] [Google Scholar]
- 6.Broholm C, et al. Quantum spin liquids. Science. 2020;367:eaay0668. doi: 10.1126/science.aay0668. [DOI] [PubMed] [Google Scholar]
- 7.Kitaev A. Anyons in an exactly solved model and beyond. Ann. Phys. 2006;321:2. doi: 10.1016/j.aop.2005.10.005. [DOI] [Google Scholar]
- 8.Levin M, Wen X-G. Detecting topological order in a ground state wave function. Phys. Rev. Lett. 2006;96:110405. doi: 10.1103/PhysRevLett.96.110405. [DOI] [PubMed] [Google Scholar]
- 9.Wen X-G. Choreographed entanglement dances: topological states of quantum matter. Science. 2019;363:eaal3099. doi: 10.1126/science.aal3099. [DOI] [PubMed] [Google Scholar]
- 10.Ran Y, Hermele M, Lee PA, Wen X-G. Projected-wave-function study of the spin-1/2 heisenberg model on the kagomé lattice. Phys. Rev. Lett. 2007;98:117205. doi: 10.1103/PhysRevLett.98.117205. [DOI] [PubMed] [Google Scholar]
- 11.Hermele M, Ran Y, Lee PA, Wen X-G. Properties of an algebraic spin liquid on the kagome lattice. Phys. Rev. B. 2008;77:224413. doi: 10.1103/PhysRevB.77.224413. [DOI] [Google Scholar]
- 12.Yan S, Huse DA, White SR. Spin-liquid ground state of the S = 1/2 Kagome Heisenberg antiferromagnet. Science. 2011;332:1173. doi: 10.1126/science.1201080. [DOI] [PubMed] [Google Scholar]
- 13.Jiang H-C, Wang Z, Balents L. Identifying topological order by entanglement entropy. Nat. Phys. 2012;8:902. doi: 10.1038/nphys2465. [DOI] [Google Scholar]
- 14.Zaletel MP, Vishwanath A. Constraints on topological order in mott insulators. Phys. Rev. Lett. 2015;114:077201. doi: 10.1103/PhysRevLett.114.077201. [DOI] [PubMed] [Google Scholar]
- 15.Mei J-W, Chen J-Y, He H, Wen X-G. Gapped spin liquid with topological order for the kagome Heisenberg model. Phys. Rev. B. 2017;95:235107. doi: 10.1103/PhysRevB.95.235107. [DOI] [Google Scholar]
- 16.Norman MR. Colloquium: Herbertsmithite and the search for the quantum spin liquid. Rev. Mod. Phys. 2016;88:041002. doi: 10.1103/RevModPhys.88.041002. [DOI] [Google Scholar]
- 17.Shores MP, Nytko EA, Bartlett BM, Nocera DG. A structurally perfect S = 1/2 kagome antiferromagnet. J. Am. Chem. Soc. 2005;127:13462. doi: 10.1021/ja053891p. [DOI] [PubMed] [Google Scholar]
- 18.Mendels P, et al. Quantum magnetism in the paratacamite family: towards an ideal kagomé lattice. Phys. Rev. Lett. 2007;98:077204. doi: 10.1103/PhysRevLett.98.077204. [DOI] [PubMed] [Google Scholar]
- 19.Wulferding D, et al. Interplay of thermal and quantum spin fluctuations in the kagome lattice compound herbertsmithite. Phys. Rev. B. 2010;82:144412. doi: 10.1103/PhysRevB.82.144412. [DOI] [Google Scholar]
- 20.Han T-H, et al. Fractionalized excitations in the spin-liquid state of a kagome-lattice antiferromagnet. Nature. 2012;492:406. doi: 10.1038/nature11659. [DOI] [PubMed] [Google Scholar]
- 21.Fu M, Imai T, Han T-H, Lee YS. Evidence for a gapped spin-liquid ground state in a kagome heisenberg antiferromagnet. Science. 2015;350:655. doi: 10.1126/science.aab2120. [DOI] [PubMed] [Google Scholar]
- 22.Han T-H, et al. Correlated impurities and intrinsic spin-liquid physics in the kagome material herbertsmithite. Phys. Rev. B. 2016;94:060409. doi: 10.1103/PhysRevB.94.060409. [DOI] [Google Scholar]
- 23.Khuntia P, et al. Gapless ground state in the archetypal quantum kagome antiferromagnet ZnCu3(OH)6Cl2. Nat. Phys. 2020;16:469. doi: 10.1038/s41567-020-0792-1. [DOI] [Google Scholar]
- 24.Zorko A, et al. Symmetry reduction in the quantum kagome antiferromagnet herbertsmithite. Phys. Rev. Lett. 2017;118:017202. doi: 10.1103/PhysRevLett.118.017202. [DOI] [PubMed] [Google Scholar]
- 25.Laurita, N. J. et al. Evidence for a parity broken monoclinic ground state in the S = 1/2 kagomé antiferromagnet herbertsmithite. Preprint at https://arxiv.org/abs/1910.13606 (2019).
- 26.Norman MR, Laurita NJ, Hsieh D. Valence bond phases of herbertsmithite and related copper kagome materials. Phys. Rev. Res. 2020;2:013055. doi: 10.1103/PhysRevResearch.2.013055. [DOI] [Google Scholar]
- 27.Li Y, et al. Lattice dynamics in the spin- frustrated kagome compound herbertsmithite. Phys. Rev. B. 2020;101:161115. doi: 10.1103/PhysRevB.101.161115. [DOI] [Google Scholar]
- 28.Han T-H, Singleton J, Schlueter JA. Barlowite: a spin-1/2 antiferromagnet with a geometrically perfect kagome motif. Phys. Rev. Lett. 2014;113:227203. doi: 10.1103/PhysRevLett.113.227203. [DOI] [PubMed] [Google Scholar]
- 29.Liu Z, Zou X, Mei J-W, Liu F. Selectively doping barlowite for quantum spin liquid: a first-principles study. Phys. Rev. B. 2015;92:220102. doi: 10.1103/PhysRevB.92.220102. [DOI] [Google Scholar]
- 30.Feng Z, et al. Gapped spin-1/2 spinon excitations in a new kagome quantum spin liquid compound Cu3Zn(OH)6 FBr. Chinese Phys. Lett. 2017;34:077502. doi: 10.1088/0256-307X/34/7/077502. [DOI] [Google Scholar]
- 31.Feng Z, et al. Effect of Zn doping on the antiferromagnetism in kagome Cu4−x Znx(OH)6FBr. Phys. Rev. B. 2018;98:155127. doi: 10.1103/PhysRevB.98.155127. [DOI] [Google Scholar]
- 32.Wei, Y. et al. Evidence for a Z2 topological ordered quantum spin liquid in a kagome-lattice antiferromagnet. Preprint at https://arxiv.org/abs/1710.02991 (2017).
- 33.Henderson A, et al. Order-disorder transition in the S = kagome antiferromagnets claringbullite and barlowite. Chem. Commun. 2019;55:11587. doi: 10.1039/C9CC04930D. [DOI] [PubMed] [Google Scholar]
- 34.Pasco C, et al. Single-crystal growth of Cu4 (OH)6 BrF and universal behavior in quantum spin liquid candidates synthetic barlowite and herbertsmithite. Phys. Rev. Mater. 2018;2:044406. doi: 10.1103/PhysRevMaterials.2.044406. [DOI] [Google Scholar]
- 35.Smaha RW, He W, Sheckelton JP, Wen J, Lee YS. Synthesis-dependent properties of barlowite and Zn-substituted barlowite. J. Solid State Chem. 2018;268:123. doi: 10.1016/j.jssc.2018.08.016. [DOI] [Google Scholar]
- 36.Smaha RW, et al. Materializing rival ground states in the barlowite family of kagome magnets: quantum spin liquid, spin ordered, and valence bond crystal states. npj Quantum Mater. 2020;5:1. doi: 10.1038/s41535-019-0206-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Tustain, K. et al. From magnetic order to quantum disorder in the Zn-barlowite series of kagomé antiferromagnets. npj Quantum Mater.5, 74 (2020).
- 38.Wei, Y. et al. Magnetic phase diagram of Cu4−xZnx(OH)6FBr studied by neutron-diffraction and μSR techniques. Chinese Phys. Lett.37, 107503 (2020).
- 39.Cépas O, Haerter JO, Lhuillier C. Detection of weak emergent broken-symmetries of the kagome antiferromagnet by Raman spectroscopy. Phys. Rev. B. 2008;77:172406. doi: 10.1103/PhysRevB.77.172406. [DOI] [Google Scholar]
- 40.Liu X-L, Zhang X, Lin M-L, Tan P-H. Different angle-resolved polarization configurations of raman spectroscopy: A case on the basal and edge plane of two-dimensional materials. Chin. Phys. B. 2017;26:067802. doi: 10.1088/1674-1056/26/6/067802. [DOI] [Google Scholar]
- 41.Lemmens P, Güntherodt G, Gros C. Magnetic light scattering in low-dimensional quantum spin systems. Physics Reports. 2003;375:1. doi: 10.1016/S0370-1573(02)00321-6. [DOI] [Google Scholar]
- 42.Devereaux TP, Hackl R. Inelastic light scattering from correlated electrons. Rev. Mod. Phys. 2007;79:175. doi: 10.1103/RevModPhys.79.175. [DOI] [Google Scholar]
- 43.Wulferding D, Choi Y, Lee W, Choi K-Y. Raman spectroscopic diagnostic of quantum spin liquids. J. Phys. Condens. Mat. 2019;32:043001. doi: 10.1088/1361-648X/ab45c4. [DOI] [PubMed] [Google Scholar]
- 44.Sandilands LJ, Tian Y, Plumb KW, Kim Y-J, Burch KS. Scattering continuum and possible fractionalized excitations in α -RuCl3. Phys. Rev. Lett. 2015;114:147201. doi: 10.1103/PhysRevLett.114.147201. [DOI] [PubMed] [Google Scholar]
- 45.Glamazda A, Lemmens P, Do SH, Choi YS, Choi KY. Raman spectroscopic signature of fractionalized excitations in the harmonic-honeycomb iridates β - and γ -Li2 IrO3. Nat. Commun. 2016;7:12286. doi: 10.1038/ncomms12286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Glamazda A, Lemmens P, Do SH, Kwon YS, Choi KY. Relation between Kitaev magnetism and structure in α -RuCl3. Phys. Rev. B. 2017;95:174429. doi: 10.1103/PhysRevB.95.174429. [DOI] [Google Scholar]
- 47.Li G, et al. Raman spectroscopy evidence for dimerization and Mott collapse in α -RuCl3 under pressures. Phys. Rev. Mater. 2019;3:023601. doi: 10.1103/PhysRevMaterials.3.023601. [DOI] [Google Scholar]
- 48.Pei S, et al. Magnetic Raman continuum in single-crystalline H3 LiIr2 O6. Phys. Rev. B. 2020;101:201101. doi: 10.1103/PhysRevB.101.201101. [DOI] [Google Scholar]
- 49.Wulferding D, et al. Magnon bound states versus anyonic Majorana excitations in the Kitaev honeycomb magnet α -RuCl3. Nat. Commun. 2020;11:1603. doi: 10.1038/s41467-020-15370-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Wang Y, et al. The range of non-Kitaev terms and fractional particles in α -RuCl3. npj Quantum Mater. 2020;5:14. doi: 10.1038/s41535-020-0216-6. [DOI] [Google Scholar]
- 51.Sun W, Huang Y-X, Nokhrin S, Pan Y, Mi J-X. Perfect Kagomé lattices in YCu3(OH)6 Cl3 : a new candidate for the quantum spin liquid state. J. Mater. Chem. 2016;4:8772. [Google Scholar]
- 52.Sun W, Huang YX, Pan Y, Mi JX. Strong spin frustration and negative magnetization in LnCu3(OH)6 Cl3 (Ln=Nd and Sm) with triangular lattices: the effects of lanthanides. Dalton Trans. 2017;46:9535. doi: 10.1039/C7DT01798G. [DOI] [PubMed] [Google Scholar]
- 53.Puphal P, Zoch KM, Désor J, Bolte M, Krellner C. Kagome quantum spin systems in the atacamite family. Phys. Rev. Mater. 2018;2:063402. doi: 10.1103/PhysRevMaterials.2.063402. [DOI] [Google Scholar]
- 54.Zorko A, et al. Negative-vector-chirality 120° spin structure in the defect- and distortion-free quantum kagome antiferromagnet YCu3(OH)6Cl3. Phys. Rev. B. 2019;100:144420. doi: 10.1103/PhysRevB.100.144420. [DOI] [Google Scholar]
- 55.Arh T, et al. Origin of magnetic ordering in a structurally perfect quantum kagome antiferromagnet. Phys. Rev. Lett. 2020;125:027203. doi: 10.1103/PhysRevLett.125.027203. [DOI] [PubMed] [Google Scholar]
- 56.Zorko A, et al. Dzyaloshinsky-Moriya anisotropy in the spin-1/2 kagome compound ZnCu3(OH)6 Cl2. Phys. Rev. Lett. 2008;101:026405. doi: 10.1103/PhysRevLett.101.026405. [DOI] [PubMed] [Google Scholar]
- 57.Cépas O, Fong CM, Leung PW, Lhuillier C. Quantum phase transition induced by Dzyaloshinskii-Moriya interactions in the kagome antiferromagnet. Phys. Rev. B. 2008;78:140405. doi: 10.1103/PhysRevB.78.140405. [DOI] [Google Scholar]
- 58.Rousochatzakis I, Manmana SR, Läuchli AM, Normand B, Mila F. Dzyaloshinskii-Moriya anisotropy and nonmagnetic impurities in the kagome system ZnCu3(OH)6Cl2. Phys. Rev. B. 2009;79:214415. doi: 10.1103/PhysRevB.79.214415. [DOI] [Google Scholar]
- 59.Zhu W, Gong S-S, Sheng DN. Identifying spinon excitations from dynamic structure factor of spin-1/2 Heisenberg antiferromagnet on the Kagome lattice. Proc. Natl. Acad. Sci. U.S. 2019;116:5437. doi: 10.1073/pnas.1807840116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Ko W-H, Liu Z-X, Ng T-K, Lee PA. Raman signature of the U(1) Dirac spin-liquid state in the spin- kagome system. Phys. Rev. B. 2010;81:024414. doi: 10.1103/PhysRevB.81.024414. [DOI] [Google Scholar]
- 61.Freedman DE, et al. Site specific X-ray anomalous dispersion of the geometrically frustrated KAGomé magnet, herbertsmithite, ZnCu3(OH)6 Cl2. J. Am. Chem. Soc. 2010;132:16185. doi: 10.1021/ja1070398. [DOI] [PubMed] [Google Scholar]
- 62.Helton JS, et al. Spin dynamics of the spin-1/2 kagome lattice antiferromagnet ZnCu3(OH)6Cl2. Phys. Rev. Lett. 2007;98:107204. doi: 10.1103/PhysRevLett.98.107204. [DOI] [PubMed] [Google Scholar]
- 63.Halley JW. Light scattering as a probe of dynamical critical properties of antiferromagnets. Phys. Rev. Lett. 1978;41:1605. doi: 10.1103/PhysRevLett.41.1605. [DOI] [Google Scholar]
- 64.Reiter GF. Light scattering from energy fluctuations in magnetic insulators. Phys. Rev. B. 1976;13:169. doi: 10.1103/PhysRevB.13.169. [DOI] [Google Scholar]
- 65.Fleury PA, Loudon R. Scattering of light by one- and two-Magnon excitations. Phys. Rev. 1968;166:514. doi: 10.1103/PhysRev.166.514. [DOI] [Google Scholar]
- 66.Shastry BS, Shraiman BI. Theory of Raman scattering in Mott-Hubbard systems. Phys. Rev. Lett. 1990;65:1068. doi: 10.1103/PhysRevLett.65.1068. [DOI] [PubMed] [Google Scholar]
- 67.Bernu B, Pierre L, Essafi K, Messio L. Effect of perturbations on the kagome antiferromagnet at all temperatures. Phys. Rev. B. 2020;101:140403. doi: 10.1103/PhysRevB.101.140403. [DOI] [Google Scholar]
- 68.Chernyshev AL, Zhitomirsky ME. Quantum selection of order in an XXZ antiferromagnet on a kagome lattice. Phys. Rev. Lett. 2014;113:237202. doi: 10.1103/PhysRevLett.113.237202. [DOI] [PubMed] [Google Scholar]
- 69.Chu S, Müller P, Nocera DG, Lee YS. Hydrothermal growth of single crystals of the quantum magnets: Clinoatacamite, paratacamite, and herbertsmithite. Appl. Phys. Lett. 2011;98:092508. doi: 10.1063/1.3562010. [DOI] [Google Scholar]
- 70.Velázquez M, et al. Aqueous solution growth at 200 °C and characterizations of pure, 17O-or D-based herbertsmithite ZnxCu4−x (OH)6 Cl2 single crystals. J. Cryst. Growth. 2020;531:125372. doi: 10.1016/j.jcrysgro.2019.125372. [DOI] [Google Scholar]
- 71.Dolomanov OV, Bourhis LJ, Gildea RJ, Howard JA, Puschmann H. Olex2: a complete structure solution, refinement and analysis program. J. Appl. Crystallogr. 2009;42:339. doi: 10.1107/S0021889808042726. [DOI] [Google Scholar]
- 72.Tan PH, et al. The shear mode of multilayer graphene. Nat. Mater. 2012;11:294. doi: 10.1038/nmat3245. [DOI] [PubMed] [Google Scholar]
- 73.Lin M-L, et al. Cross-dimensional electron-phonon coupling in van der Waals heterostructures. Nat. Commun. 2019;10:2419. doi: 10.1038/s41467-019-10400-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All data supporting the findings of this study are available from the corresponding authors upon reasonable request.