Rapid frequency modulation in a resonant system: aerial perturbation recovery in hawkmoths

Abstract

Centimetre-scale fliers must contend with the high power requirements of flapping flight. Insects have elastic elements in their thoraxes which may reduce the inertial costs of their flapping wings. Matching wingbeat frequency to a mechanical resonance can be energetically favourable, but also poses control challenges. Many insects use frequency modulation on long timescales, but wingstroke-to-wingstroke modulation of wingbeat frequencies in a resonant spring-wing system is potentially costly because muscles must work against the elastic flight system. Nonetheless, rapid frequency and amplitude modulation may be a useful control modality. The hawkmoth Manduca sexta has an elastic thorax capable of storing and returning significant energy. However, its nervous system also has the potential to modulate the driving frequency of flapping because its flight muscles are synchronous. We tested whether hovering hawkmoths rapidly alter frequency during perturbations with vortex rings. We observed both frequency modulation (32% around mean) and amplitude modulation (37%) occurring over several wingstrokes. Instantaneous phase analysis of wing kinematics revealed that more than 85% of perturbation responses required active changes in neurogenic driving frequency. Unlike their robotic counterparts that abdicate frequency modulation for energy efficiency, synchronous insects use wingstroke-to-wingstroke frequency modulation despite the power demands required for deviating from resonance.

1. Introduction

From undulatory swimming to legged locomotion, animals must contend with the dual challenges of control and energetics while constrained by the physics of their mechanical bodies [1]. These challenges are particularly acute for flying animals, which must simultaneously generate sufficient lift and counteract inherent instabilities to remain airborne. Like resonant oscillators, insects may store excess kinetic energy during a wing stroke in spring-like structures and return this energy to reaccelerate the wings. This strategy would effectively reduce the inertial power requirements necessary for flight [2–7]. Recent work directly measuring resonance properties in bees suggests that wingbeat frequencies are directly tuned to match resonance frequencies [8]. It remains an open question to what degree this resonance tuning is used among other insects and the potential implications for control, especially changing frequency. When typical wingbeat frequencies are near the resonant frequency of the mechanical system, resonance may constrain wingbeats to a narrow range of energetically optimal frequencies [9–11]. With a resonance peak, small changes in wingbeat frequency may attenuate wingstroke amplitude and cause muscle work to operate against the mechanical energy of the wings. As a result, it has been proposed that insects are unlikely to modulate wingbeat frequency nor wingbeat amplitude on short timescales [12–14]. On the other hand, if insects operate far from the resonance peak or if they require frequency control despite the potential power costs, then insects might freely modulate frequency from wingstroke-to-wingstroke, but would forego the energetic benefits of resonance. Because wingbeat frequency is an effective variable for adjusting flight forces, short time-scale frequency modulation may play an underappreciated role in insect flight control, regardless of where insects operate with respect to their steady-state resonance frequency.

Insects have the capacity to change frequency, but face potential constraints from resonance regardless of whether they possess synchronous (neurogenic) or asynchronous (myogenic) flight strategies. In species with synchronous flight muscles such as Manduca sexta, a downstroke is typically triggered by a single action potential with sub-millisecond precision to the dorsolongitudinal muscles (DLMs) [15]. Although the nervous system can shift the timing of muscle activation [15], synchronous hawkmoths are often observed [4] and modelled [15] as maintaining a constant wingbeat frequency. By contrast, asynchronous muscles are activated by mechanical strain and pairs of asynchronous muscles antagonistically stretch each other to generate rhythmic wing motion [16]. In this system, the wingbeat frequency entrains to the resonance frequency of the muscle-wing-thorax system [17,18]. To change wingbeat frequency, small accessory muscles can shift the resonance frequency of the thoracic structure [18], but this is a slow process because the accessory muscles only activate once per many wingstrokes [19]. For both synchronous and asynchronous insects, a dependence on resonance to reduce power requirements could limit the capacity for wingstroke-to-wingstroke changes in wingbeat frequency.

Despite the wingbeat frequency constraints imposed by resonance, modest changes in wingbeat frequency over long timescales are frequently observed in both asynchronous and synchronous insects. For asynchronous species, tethered Drosophila melanogaster, Drosophila virilis and Drosophila mimica all exhibited a 10% change in wingbeat frequency in response to a slowly oscillating visual stimulus [9]. Under load-lifting conditions, bumblebees (asynchronous) increase wingbeat frequency by approximately 5% between light and heavy load conditions, although an extreme individual changed frequency by 10% [20]. In synchronous species, studies investigating wing damage [21], flight in turbulent flows [22] and varying forward velocities [23] in free flying Manduca sexta reported 5–10% changes in wingbeat frequency. These results are consistent with 10% increases in wingbeat frequency when tethered locusts (synchronous) were flown in a wind tunnel at different wind speeds [24]. These studies suggest that modest changes in frequency may be a common method to adjust flight forces over the duration of many wingbeats. However, long-time-scale frequency modulation can still be consistent with flight at resonance because the animal could slowly modulate frequency or even change the resonant peak frequency which depends on wing mass, material properties and indirect muscle activity.

In contrast to prior studies which probe changes in wing kinematics over long timescales, it remains unclear how insects balance the needs for economical and controllable flight on the wingstroke-to-wingstroke timescale. Insects could (i) forego wingbeat frequency modulation that might require increased power to act against spring-wing resonance, (ii) trade off energy economy for increased control capacity in response to sudden perturbations. Ellington hypothesized that the sharp resonant mechanics of Manduca wings would preclude rapid wingbeat modulation. However, recent observations of pitching during free flight by Cheng et al. [25] suggest that wingbeat frequency can change by at least 10% in as little as a wingstroke. However, the occurrence, duration and magnitude of frequency variation and the neural versus physical origins of this modulation were not quantitatively assessed and thus it remains a question whether frequency modulation is a consistent control response in perturbed hawkmoths and whether these changes are neurogenic or mechanical. Nonetheless, given the control implications and this prior observation, we hypothesize that Manduca sexta may be able to overcome its resonant mechanics to still achieve neurogenic changes in wingbeat frequency.

One of the major challenges in measuring wingbeat frequency modulation is in designing experiments to elicit behaviours that deviate from steady state [26]. In particular, prior work has shown that vortex rings can perturb moths while they hover feed from flowers [27]. We adopted a similar experimental paradigm and tuned the strength of the vortex perturbation to be just weak enough for the moth to remain airborne. This set-up enabled us to measure the steady-state behaviour (hover-feeding) in comparison to the recovery manoeuver, visualize the perturbations and allow the animals to freely maneuver.

Observing changes in wingbeat frequency does not necessarily alone reflect a change in the underlying oscillation frequency set by the nervous system of synchronous insects. Mechanical perturbations could physically move the wings to produce kinematic wingbeat frequency modulation without changing the underlying time-periodic forcing frequency. We hypothesized that any observed modulation in wingbeat kinematic frequency would be owing to changes in the underlying neural driving frequency. Modulation of the neurogenic driving frequency can be inferred by comparing the kinematic phases of the wings pre- and post-perturbation [28]. If the wingstroke’s kinematic frequency is disturbed during the perturbation but returns to the same original phase it had before perturbation, then underlying neurogenic frequency modulation did not necessarily occur. If the wingstrokes adopt a new, persistent kinematic phase relative to wingstrokes prior to perturbation, then the neurogenic frequency must have been modulated during the perturbation recovery. In other words, a persistent phase offset indicates that there was a transient frequency change. A third alternative is that the moth may adopt an entirely new, persistent wingbeat frequency after the perturbation.

2. Methods

(a) . Free flight experiments

(i) . Animal care

Manduca sexta pupae raised on a diet containing retinoic acid were acquired from the University of Washington and Case Western Reserve University colonies. Adults were housed in an incubator with a 12L : 12D cycle. Each moth (n = 8) was used for one set of experiments ranging from 1 to 22 perturbations, depending on the willingness of the moth to return to feed from an artificial flower. Moths had no prior exposure to the artificial flower and were dark adapted for at least 30 min before experiments.

(ii) . Vortex ring perturbations

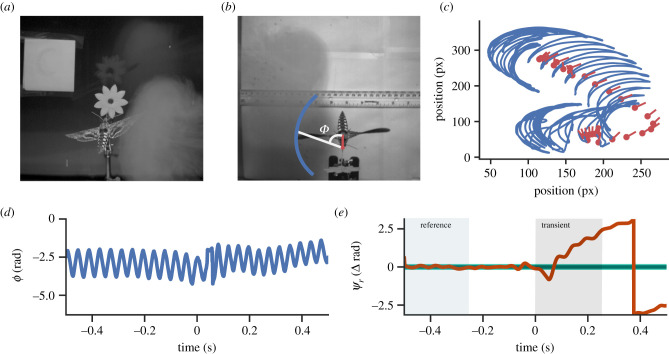
Perturbations (n = 58) were performed on adult Manduca sexta in a 1 cubic metre free flight chamber. The flower face was illuminated at 0.3 lux with a white LED ‘moon’ light (CW-126, Neewer, Shenzhen, China). Once the moth began feeding from the artificial flower, a lateral perturbation was generated via a vortex ring generator (MIGHTY Blaster Fog Ring Launcher, Incredible Science, USA) (figure 1a). The generator simultaneously produced artificial smoke composed of propylene glycol, glycerin and distilled water (Super Zero Fog Fluid, Zero Toys, Concord, MA 01742) for vortex ring visualization. We saw no noticeable response in the moths to the approaching vortex ring. We were able to generate consistent vortex rings with an average diameter of (19.9 ± 0.6 cm; n = 10) with a velocity of (440 ± 30 cm s⁻¹; n = 10). We positioned the vortex generator such that the impact was sufficient to knock most moths completely away from hover-feeding but not so great as to cause collision with the chamber walls. Moths were perturbed from the right posterior direction at constant elevation (figure 1a) (electronic supplementary material, Movie S1). Given the speed and size of the vortex ring, moths encountered the main vortex structure for approximately one wingstroke. However, given the animal’s translation and residual unsteady airflow, the mechanical effects of the perturbation probably persisted over several wingstrokes and would depend on the particular trial.

Figure 1.

Vortex ring perturbations drive active recovery manoeuvers in Manduca sexta. (a) Rear view of a hawkmoth hovering in front of an artificial flower with an approaching vortex ring. (b) Top-down view of a perturbation. Blue trace denotes approximate wingtip trajectory. Red dot marks proboscis base and the red line points towards the thorax. ϕ is the instantaneous angle between wing position and body axis. (c) Raw kinematic traces. Blue trace marks wing position, red dot is the base of the proboscis and the red line points towards the centre of the thorax. (d) Wing angle, ϕ, from the experiment in (c). Perturbation occurs at t = 0 s. (e) Phase difference between actual phase and reference phase. The green rectangle highlights the region during which we build a reference phase and the grey rectangle marks the transient region from which we classify the perturbation. The light green region is the 95% confidence band of the reference phase while dark green is the mean projected phase. Orange line is the measured phase. Perturbation occurs at 0 s. (Online version in colour.)

(iii) . Kinematic extraction from high-speed video recordings

All perturbation trials were filmed from above (dorsal view) at 2000 fps using a high speed camera (IL3, Fastec Imaging, San Diego, CA 92127). Infrared lights (LEDLB-16-IR-F-850nm-BLK, Larson Electronics, Kemp, TX 75143), which emits infrared light not visible to Manduca sexta, provided illumination for high-speed videography. We only analysed videos where the tracked wing, head and thorax remained in frame for 10 wingstrokes post-perturbation.

To improve kinematic tracking fidelity, we background subtracted all video frames. We used DeepLabCut (v. 2.1.1) to extract x-y position for the wingtips, thorax and base of the proboscis (figure 1b) [29] (electronic supplementary material, Movie S2). To train, we used 7111 frames split over nine perturbations that were semimanually digitized via DLTDdv7 [30] for 135 000 training iterations. Some perturbations had poor tracking performance because the moth flew over the flower or passed over the ruler. To refine the tracking, we manually digitized an additional 474 frames.

To quantitatively reject perturbations with poor tracking quality, we did not analyse any perturbation with over 1% of data points outside of the 95% confidence interval (CI) of dϕ/dt (13 of 71 perturbations). Qualitatively, this typically happens when a moth moves out of frame and the tracked points jump from one wing to the other.

(b) . Estimating wingbeat frequency from wing kinematics via instantaneous phase

We adopted an instantaneous phase approach inspired by prior work on cockroach perturbation recovery (see the electronic supplementary material, Movie S3 for animated description) [28]. To convert kinematic measurements to a continuous phase variable, we first defined a vector from the proboscis base to the thorax (figure 1a). We defined a second vector from the thorax to the wingtip. We then calculated the angle (ϕ) between these two vectors (figure 1c). We then applied a Hilbert transform (equation (2.1)), which converts a real signal into the complex domain by convolving the signal with $\frac{1}{\pi t}$:

$$H(\varphi )(t)=\frac{1}{\pi }{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\frac{\varphi (\tau )}{t-\tau }\hspace{0.17em}\mathrm{d}\tau .$$ 2.1

From here, we calculated the instantaneous phase ψ(t) as the complex angle of H(ϕ)(t) as in prior studies [31–33].

Although calculating dψ/dt provides an estimate of instantaneous frequency, we still needed to estimate wingbeat frequency from ψ(t). Therefore, we defined an arbitrary phase threshold and defined wingbeat frequency as the inverse of the time between threshold crossings. The period of any individual wingstroke may depend on our set threshold, but we find that the overall magnitude of frequency modulation is robust to changes in phase threshold (electronic supplementary material, figure S1).

(c) . Measuring wingbeat frequency modulation

To assess the magnitude of wingbeat frequency modulation, we calculated the width of the 95% quantile (97.5th percentile–2.5th percentile) for each perturbation. The first nine wingstrokes post-perturbation were statistically significantly different from the pre-perturbation mean, so we divided each trial into three intervals: wingstrokes −4 to −1, wingstrokes 1 to 4, and wingstrokes 5 to 8, where the perturbation occurs at wingstroke 0. Within each interval, we calculated the 95% quantile width for each perturbation. We aligned each perturbation to wingstroke 0 by visually examining high-speed videos to determine the frames at which moths were initially perturbed.

To assess whether there was significant individual-to-individual variation, we used a two-way ANOVA with individuals and intervals (pre-perturbation, post-perturbation wingstrokes 1–4 and post-perturbation wingstrokes 5–8) as factors. Normalized wingbeat frequency modulation (95% quantile width/mean wbf) was the dependent variable. Raw data for each individual are shown in the electronic supplementary material, figure S2.

(d) . Measuring wingbeat amplitude modulation

We used the previously identified phase threshold crossings used to calculate wingbeat frequency to estimate wingbeat amplitude per wingstroke. These threshold crossings denote the start and end of an individual wingstroke. We then calculated the difference between the maximum and minimum ϕ within a single period, which represents the wingbeat amplitude projected onto the two-dimensional camera plane. We projected this value into the stroke plane by assuming a pre-perturbation stroke plane angle of 18 ± 4° based on previously published Manduca sexta kinematics during hover [4].

To correct for changes in body pitch post-perturbation, we assumed that the pre-perturbation body pitch matched previously reported values of 36 ± 3° [4]. We then used changes in head-thorax distance to estimate wingstroke-averaged changes in body pitch and projected ϕ_max − ϕ_min into the perturbed stroke plane. These approaches follow previous work estimating wingbeat amplitude from a single dorsal camera angle, but include changes to body pitch [34]. Changes in stroke plane could influence stroke amplitude.

We used the same technique described for calculating wingbeat frequency modulation to determine wingbeat amplitude modulation. However, unlike calculations for wingbeat frequency, there is no clear way to disambiguate whether observed changes in wingbeat amplitude are owing to changes in motor input or a mechanical response to the perturbation.

(e) . Instantaneous phase analysis to assess changes in driving frequency

Following the methods of Revzen et al. [28,35], we first estimated a reference clock frequency and projected this oscillator forward in time by fitting a regression line to ψ from −0.5 s to −0.25 s. From here, we subtracted the measured phase from the reference phase to calculate the phase residual (ψ_r) (figures 1c and 2; electronic supplementary material, Movie S3). Instantaneous phase has better noise properties than using extremal events (wingstroke reversals), which could overestimate variation [36]. Residual phase shows how much the perturbation has caused the animal to deviate from the phase it would have had if there was no perturbation. Following a perturbation, there are three classes of possible ψ_r outcomes: (1) no difference (figure 2a), (2) constant phase offset (figure 2b), and (3) continuous phase divergence (figure 2c).

Figure 2.

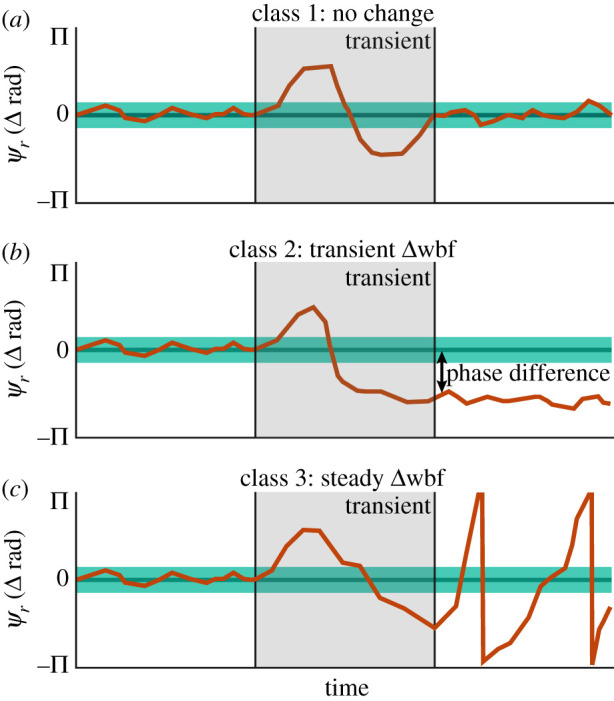
Schematic of instantaneous phase analysis and possible responses. Comparing post-perturbation to a pre-perturbation reference phase enables inference of neurogenic frequency modulation. For all panels, the dark green line denotes the projected reference phase, while light green bands are the 95% CI of the projection. Orange lines are hypothetical traces for each response classes. (a) Class 1 responses, where ψ_r(t) returns to the pre-perturbation phase, do not require a change in driving frequency. (b) Class 2 responses, where ψ_r(t) = c, require there to have been a change in driving frequency during the transient period. (c) Class 3 responses, where ψ_r(t) continuously diverges, require a lasting change in motor input. See the electronic supplementary material, Movie S3 for an animated description. (Online version in colour.)

Class 1 responses exhibit no lasting change in ψ_r(t). This indicates that the underlying frequency modulation was not necessary and is consistent with the insects responding purely mechanically and pacing the flight muscles at a constant frequency (figure 4a). Class 1 responses would support the null hypothesis where the kinematic phase of the wing may change transiently because of external forces, but the driving frequency does not. In these cases, the kinematic frequency must eventually come back into sync. Class 2 responses are characterized by a constant ψ_r(t) offset after the initial transient (figure 4b). To achieve a lasting phase difference in an oscillatory system, there must be at least a temporary increase or decrease in phase velocity (i.e. frequency). Therefore, a class 2 response requires a transient wingbeat frequency modulation. Finally, class 3 responses have a continuously diverging ψ_r(t). Diverging phase requires that the moth adopt a new pacing frequency in response to the perturbation (figure 4c). For our hypothesis, both class 2 and class 3 responses require active neurogenic changes in wingbeat frequency.

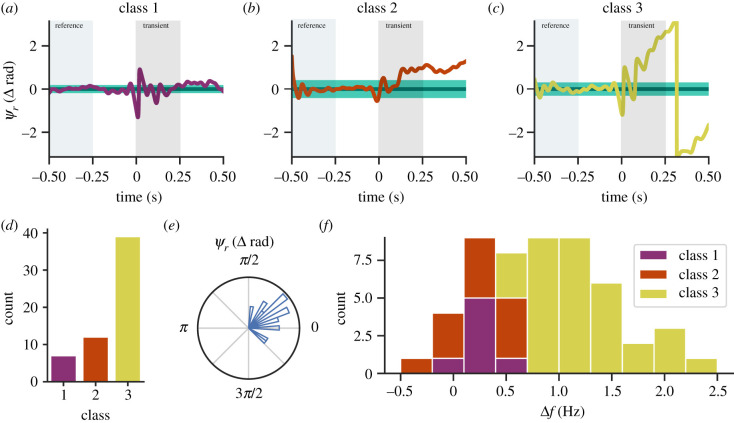
Figure 4.

Over 85% of perturbations require a change in neural input frequency. Representative ψ_r(t) for (a) class 1, (b) class 2 and (c) class 3 responses, where the perturbation began at 0 s. The green horizontal bar denotes the mean and 95% CI of the projected phase. Purple, orange and yellow traces are measured ψ_r(t). Light green and grey rectangles mark the regions where we build the reference phase and the transient perturbation response. (d) Counts of class responses. (e) Circular histogram of ψ_r(t) for class 1 and class 2 responses. Density is denoted by area instead of radii. (f) Histogram of mean frequency change for all three classes calculated as the slope in ψ_r(t) slope from 0 to 0.5 s. This Δf represents mean changes in wingbeat frequency over 0.5 s and not wingbeat-to-wingbeat frequency modulation. (Online version in colour.)

To distinguish between classes, we first fit a line to ψ_r(t) from 0 to 0.5 s following the perturbation (accounting for the wrapping of phase at π and −π). Prior literature has found roughly 5% changes in wingbeat frequency in Manduca sexta over longer timescales [21–23]. Therefore, we set a frequency change threshold of ±2.5% (±0.625 Hz). To distinguish between class 1 and class 2 from class 3 responses, we tested if there was a significant slope to the residual phase line after the perturbation. To distinguish class 1 and class 2 responses, we determined if there was a significant change in the residual phase. To do so, we looked at the average value of the line (i.e. at 0.25 s). If this value was outside of the 95% CI of our projected phase, we conclude that a phase shift must have occurred (class 2 response). Otherwise, if there is no significant slope and no significant phase residual, we classify the response as class 1. We used the following criteria to distinguish between classes:

• 1. class 1: |m| < 0.625 Hz, 5% CI < b < 95% CI;
• 2. class 2: |m| < 0.625 Hz; and
• 3. class 3: |m| > 0.625 Hz.

3. Results

(a) . Manduca sexta rapidly modulates frequency during perturbation recovery

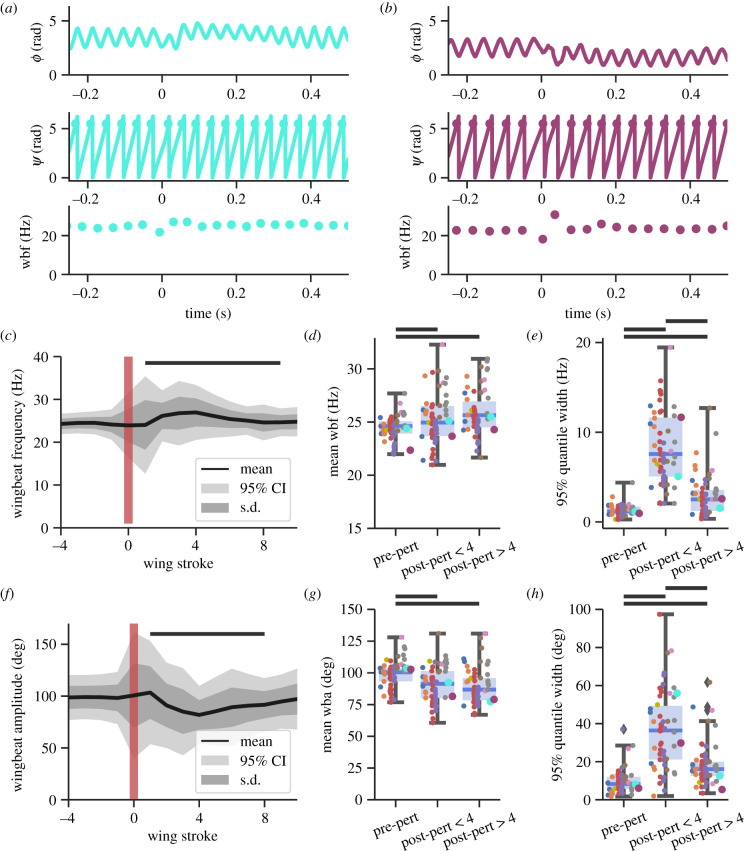
To test for the consequences of resonant mechanics on frequency and amplitude variation at the wingstroke-to-wingstroke timescale, we quantified wingbeat frequency modulation as the mean of the 95% quantile width of wingbeat frequency. Intuitively, this measurement quantifies the variation in wingbeat frequency within each perturbation. Consistent with prior literature, we found a tightly bounded frequency (only a 1.28 ± 0.68 Hz 95% quantile width) for the four wingstrokes immediately prior to perturbations [22]. Therefore, we would typically only observe a 1 Hz change above or below the mean flapping frequency during steady-state flight (24.4 Hz).

By contrast, in the recovery immediately after perturbations, moths must adjust aerodynamic force production to remain airborne. Because hawkmoths may be operating on resonance, we hypothesized that any changes in aerodynamic force production are accomplished by methods other than wingbeat frequency or amplitude modulation (e.g., wing pitching). Our data reject this hypothesis. The 95% quantile width increased over 600% during the first four wingstrokes post-perturbation to 8.25 ± 3.96 Hz modulation (p < 1 × 10⁻¹⁸) (figure 3c). This corresponds to a modulation range of 32%. When we analysed wingbeats 5–8 following the perturbation, we observed a decrease in the 95% quantile width to 2.88 ± 2.3 Hz (p = 0.03).

Figure 3.

Manduca sexta exhibits rapid wingbeat frequency modulation immediately post-perturbation. (a) Representative analysis for a low frequency modulation perturbation. (b) Representative analysis for a high-frequency modulation perturbation. Fluctuations in ϕ propagate to ψ and wbf. (c) Mean, s.d. and 95% CI of wingbeat frequency for 58 perturbations. The red vertical line marks perturbation onset (wingstroke 0). The black horizontal bar denotes wing strokes statistically significant from pre-perturbation wingbeat frequencies. (d) Boxplots of mean wingbeat frequency for pre-perturbation (wing strokes −4 to −1), recovery response (wing strokes 1 to 4) and equilibrium response (wing strokes 5 to 8). Each colour denotes a unique individual. (e) This shows the 95% quantile width of wingbeat frequency (wbf) for the same intervals as (d). (f–h) Same as (c–d) but for wingbeat amplitude (wba) instead of wingbeat frequency. For (d,e,g,h), black horizontal bars denote statistical significance p < 0.05. The cyan and purple dots correspond to the traces in (a) and (b). (Online version in colour.)

There was a large degree of variation across individual perturbation responses. Qualitatively, we observed the largest modulation when the animals had the largest changes in their flight trajectory following a perturbation. In a few perturbation responses, the degree of modulation did not exceed the steady-state variations (2 Hz at 5th percentile of perturbation responses). However, in the most extreme case, moths could change their wingbeat frequency by as much as 14.5 Hz (95th percentile of perturbation responses), indicating an even larger capacity for modulation.

We also observed statistically significant increases in mean wingbeat frequency following the perturbation, although the differences were small compared to the overall modulation range. Before the perturbation, the mean wingbeat frequency was 24.4 ± 1.3 Hz. The first four wingstrokes post-perturbation increased to 25.2 ± 2.3 Hz (p = 0.01) and the subsequent four wingstrokes were also elevated at 25.9 ± 2.1 Hz (p < 1 × 10⁻⁷). Normalizing wingbeat frequency modulation by these mean values results in normalized modulations of ±2.5%, ±16% and ±5%, respectively.

In our two-factor ANOVA, we did find that individual moths had a weak effect (p < 0.01, η² = 0.12) and individuals had different patterns of frequency modulation (interaction term; p < 0.01, η² = 0.18). However, independent of individual considerations, perturbations interval was still the largest determining factor for the frequency modulation (p < 1 × 10⁻³², η² = 0.63). By overlaying the raw data points for every perturbation and colour coding individuals, our conclusion that Manduca sexta uses wingstroke-to-wingstroke wingbeat frequency modulation is supported by the data (figure 3e).

(b) . Wingbeat amplitude also modulates during perturbation recovery

We similarly analysed changes in wingbeat amplitude and wingbeat amplitude modulation. We found that the wingbeat amplitudes for the first eight wingstrokes were statistically different than pre-perturbation amplitudes (p < 0.05) (figure 3f). As with wingbeat frequency, there was a small but significant change in mean amplitude from 98.7 ± 10.5° before the perturbation to 90.4 ± 14.3° (p < 1 × 10⁻⁵) in the four subsequent wingstrokes (figure 3g). Wingbeat amplitude then remained constant for the next four wingstrokes at 89.3 ± 13.9° (p = 0.52). Like wingbeat frequency, we quantified wingbeat amplitude modulation as the 95th quantile width (figure 3h). Pre-perturbation, the width was 9.6 ± 6.3°, which increased during the next four wingstrokes to 36.5 ± 19.9° (p < 1 × 10⁻¹³) and then decreased to 18.2 ± 10.9° (p < 1 × 10⁻⁷). Normalizing wingbeat amplitude modulation by the mean results in modulation of ±5%, ±20% and ±10%, respectively.

(c) . Changes in wingbeat frequency reflect changes in motor activation frequency

One advantage of measuring instantaneous phase in a perturbation-based experimental paradigm is the ability to assess changes in neural drive frequency [28,35]. If there is a persistent phase offset following the perturbation (class 2), then the underlying neural driving frequency must have transiently changed during recovery. If there is a steadily changing phase offset, then the moth has adopted a new steady wingbeat frequency (class 3). Of the 58 perturbations, we recorded, over 85% exhibited a class 2 or 3 response (figure 4d), which all require a change in the frequency of the underlying neural commands. Regardless of where changes in motor commands arise in the nervous system, we infer that changes in the observed wingbeat frequency are driven by an active modulation of motor input.

(d) . Moths do not demonstrate random phase resetting

For class 1 and class 2 responses, it is possible that Manduca sexta randomly adopts a new phase. Because we could not control for the timing of when the perturbation impacts the wing, we predicted a uniform distribution of post-perturbation phases. To test this hypothesis, we analysed the post-perturbation phase for the aggregate of class 1 and class 2 responses. We were also able to test whether class 1 responses are a subset of class 2 responses that adopted the same initial phase. Using a Rayleigh test [37], we found that post-perturbation phases were not uniformly distributed (p < 1 × 10⁻⁶; figure 4d). Instead, we report a vector strength of 0.87 with a mean phase of 0.49 rad, where a vector strength of 1.0 is perfect phase synchrony (figure 4e). Therefore, the perturbations do not have random effects on phase.

4. Discussion

(a) . Manduca sexta uses substantial wingbeat frequency modulation during maneuvers

Our results support the hypothesis that Manduca sexta can adjust wingbeat frequency by an average of 32% at the wingstroke timescale. The capacity of some moths was even greater. One alternative measure of frequency modulation capacity is to take the most extreme example of each individual, which corresponds to a 12.7 Hz bandwidth or 50% modulation range. In this case, Manduca sexta had the capacity to range from approximately 19 to 31 Hz within four wingstrokes. Despite the difficulty of producing rapid frequency and amplitude changes in a resonant system, moths nonetheless use these control strategies to achieve recovery from aerial perturbations. Given the potential for energy savings through spring-wing resonance [13] and observations of nearly constant wingbeat frequency in Manduca flight [4], most prior studies predicted that hawkmoths would not use wingstroke-to-wingstroke frequency modulation during perturbation recovery. However, frequency is an effective mode of control over longer time scales and Cheng et al. [25] did indicate that frequency changes to an unspecified degree during pitching manoeuvers. They modelled this response as a 10% frequency change and showed this can contribute to the angular acceleration during pitching, although the necessity of frequency modulation was not clear in those experiments. Our results build on these prior observations to show that frequency modulation occurs in most perturbation responses even on short timescales and goes beyond what would be expected for a resonant system.

Given the oscillatory nature of flapping wing flight, changes in wingbeat frequency and amplitude have significant implications for power requirements. Inertial and aerodynamic power requirements both scale with frequency cubed [2], which suggests that modulation in both frequency and amplitude can rapidly change the power requirements of flight. Spring-like structures in the insect flight system have a finite capacity for elastic energy exchange [6] and can return energy only at specific phases. Therefore, the musculature would probably have to supply any increased power demand. Under tethered in vivo conditions, Manduca sexta power muscles produce only 50% of peak power and this power can be modulated with precise timing [15,38]. These experiments suggest that the muscles may have excess capacity to drive rapid changes in wingbeat frequencies and enable this control strategy despite energetic costs of resonance.

The instantaneous phase analysis (figures 2 and 4) allowed us to test our second hypothesis that kinematic frequency modulation reflects changes in the underlying driving frequency (the firing of the synchronous, indirect flight muscles). In support of our hypothesis, we found that over 85% of perturbations required active changes in motor input frequency. The force of the vortex ring may well have contributed to the disruption of the kinematic phase during the transient period, but the persistent shift in phase in many trials indicates there was an active modulation of frequency as well. Instantaneous phase analysis was used previously to show that cockroaches also have active changes in stride frequency, although in that case, it was only after an approximately 100 ms initial response that was consistent with passive mechanical stabilization. In our study, the analysis was sufficient to infer active modulation, but also showed that, following perturbations, the moth resets to a non-random phase (figure 3e). This suggests two non-mutually exclusive possibilities. The simplest explanation is that the persistent phase lead comes from a transient increase in wingbeat frequency—the moths take a few faster wingstrokes during perturbation recovery. This would be consistent with the need to generate more aerodynamic force during perturbation recovery than steady hovering and we did observe a small increase in mean frequency during the recovery (figure 3c,d). Non-random phases could also arise from the indirect flight and direct steering muscles acting at specific phases in the wingstroke, as was shown by comprehensive muscle recordings of the flight motor programme [33].

(b) . Wingstroke-to-wingstroke frequency and amplitude modulation complements a broad suite of control strategies in Manduca sexta

Wingbeat frequency modulation over long timescales is a common strategy to respond to changing aerodynamic requirements. Insects can respond to perturbations at the wingstroke timescale [25,32,39,40], but previous evidence for frequency changes was typically over many wingstrokes (figure 5a) [3,9,20–23,26,41–45]. Manduca sexta increases wingbeat frequency in response to wing damage [47], while the hummingbird hawkmoth, Macroglossum stellatarum, increases both frequency and amplitude [34]. In air disturbed with vortex streets, hawkmoths also slightly increase steady-state wingbeat frequency, probably to compensate for a reduction in force production associated with flying in disturbed air [22].

Figure 5.

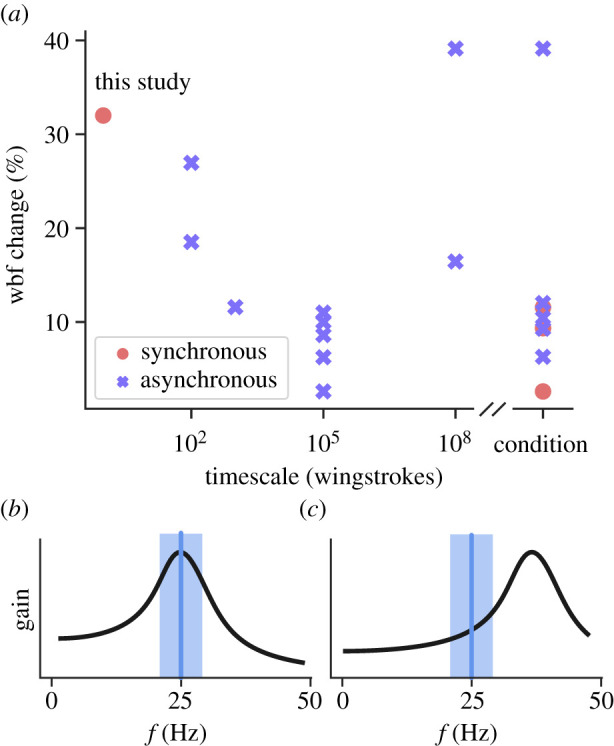
(a) Brief survey of literature comparing wingbeat frequency (wbf) modulation and the timescales of these changes. ‘Condition’ refers to studies where wingbeat frequency change is observed over discrete conditions an indeterminate experimental intervals. The synchronous leftmost point is from data collected from Manduca sexta in this manuscript. Other data were aggregated from [3,9,20–23,26,41–46]. Cheng et al. [25] reported wingstroke scale frequency modulation during pitch manoeuvers of an unspecified degree in Manduca sexta. (b,c) Possible resonance curves with mean wingbeat frequency (blue vertical line) and modulation (blue rectangle). (b) Resonance matches typical wingbeat frequencies. (c) Resonance frequency is 50% greater than typical wingbeat frequencies. (Online version in colour.)

In contrast to the rapid, wingstroke time-scale changes in frequency and amplitude seen here, these longer-term shifts can still be consistent with operating at a resonant peak because the insect could slowly adopt new steady-state frequencies or shift the resonant peak itself. Reduction in wing mass predicts a corresponding increase in the natural frequency and hence resonance of the flight system as was shown for asynchronous wings [48]. The relatively slow wingbeat frequency changes in asynchronous insects may be because wingbeat frequencies entrain to the resonant frequency of the wing-thorax system. Active changes in resonance frequency are probably driven by the pleurosternal muscles [18], which stiffen the thorax, but only activate once per many wingstrokes [19].

Unlike these changes that play out over many wingstrokes or between distinct conditions, controlling wingbeat frequency and amplitude on the timescale of a single wingstroke is a different control challenge. The 32% modulation during a typical perturbation recovery in Manduca sexta is not only more rapid, but also larger than what has previously been reported even for long-term changes [21–23], and is comparable to what other insects achieve over long timescales (figure 5a).

Rapid frequency and amplitude modulation probably works in tandem with other mechanisms for overcoming perturbations. By virtue of having flapping wings, Manduca sexta can dampen rotational perturbations with no active change in kinematics via passive flapping wing counter torque [49]. In addition to passive control mechanisms, wing kinematics are controlled by a set of 10 flight and steering muscles tightly coordinated in their activation timing [33]. So any changes in wingbeat frequency probably affects the coordination of these muscles. Precise changes in the activation phase of the DLMs can account for 50% of yaw torque production [15]. Because of the strong phase dependence of wing muscles, the nervous system may need to maintain precise control over the muscle activation phase while the frequency of muscle strain changes from wingstroke-to-wingstroke.

(c) . Resonant systems must face trade-offs between energy and control

Many authors have stated that insects are tuned to resonance [8,12–14,16,18] (figure 5b) owing to observations of constant wingbeat frequencies and estimates [13] and direct measurements [8] of a dominant resonance peak. Elastic energy exchange can substantially reduce the power requirements of insect flight [2–6]. As the wing decelerates, elastic elements store excess kinetic energy and subsequently return this energy to re-accelerate the wing. Critically, this elastic energy exchange process has an intrinsic timescale (resonant frequency). Therefore, efficient energy exchange requires an insect’s wingbeat frequency to match the resonance frequency of the wing-thorax system. Even in the case where wingbeat frequencies are off resonance, large amplitude changes in wingbeat frequency can have significant consequences in a resonant system.

A singifcant peak around the resonant frequency introduces frequency-dependent mechanics. Because the exact resonant mechanics in hawkmoths are unknown [13], we generated two hypothetical resonance curves to illustrate the effects of frequency modulation in resonant systems. In the first case, steady-state wingbeat frequencies match resonance (figure 5b). In the second, they are off resonance (figure 5c). If steady-state wingbeat frequencies are tuned to resonance [8,12–14,16,18], the elastic recoil of the wing-thorax system would increase the ratio (i.e. gain) between output wing amplitude to input force (figure 5b). Critically, this gain is itself frequency-dependent, so small deviations in wingbeat frequency could cause large changes in wingbeat amplitude [13]. Both increases and decreases in wingbeat frequency would lead to reduced wingbeat amplitude unless the muscles generated additional power. Consistent with this perspective, metabolic rate increases with increased wingbeat frequency in bumblebees [20]. On the other hand, operating away from resonance could lead to a monotonic relationship between frequency and gain (figure 5c). This could enable frequency modulation as a knob to control wingbeat amplitude (figure 5c).

We observed a 32% range in wingbeat frequency in Manduca sexta, which suggests that resonance either (i) adds potential energetic costs when wingbeat frequencies deviate during perturbation recovery (figure 5b), or (ii) amplifies the control potential of wingbeat frequency modulation (figure 5c), but requires the moth to be operating away from the resonant peak. Our finding that wingbeat amplitude decreases on average with increasing wingbeat frequency (figure 3c,f) is consistent with the idea that hawkmoths are on resonance. However, we cannot reject the off-resonance case because it is unclear how the animal may compensate for shifts along the resonance curve. These hypothesized resonance curves provide a qualitative view of the potential trade-offs between energy and control faced by hawkmoths trying to use resonant, flapping wing flight.

The qualitative resonance implications in insects have been quantified in their robotic counterparts. In insect-scale flapping wing vehicles, tuning wingbeat frequencies to resonance improved energy efficiency by 50% [7]. However, the energetic benefits of resonance also restricted the range of attainable wingbeat frequencies to just ±5% around resonance [11]. Owing to these constraints, controlled flight was achieved by modulating stroke amplitude but explicitly holding wingbeat frequency constant [50]. In addition, resonance can filter out subtle wing kinematics that are important in producing aerodynamic forces [3,9,11,51]. By moving off resonance, yaw rate improved 10-fold, but required a 40% increase in voltage [11].

Beyond flapping wing flight, combining actuation and elasticity poses significant dual challenges for control and energetics in other forms of locomotion. For example, elastic elements in swimming cetaceans [52] and running humans [53] introduce frequency-dependent energetic costs. Although energetically beneficial, changes in frequency require changes to elasticity [53] or centre of mass [54]. Extending to impulsive movements, springs are necessary to overcome constraints of power-limited muscles [55]. However, control over these power amplified movements is limited to latch mechanisms with precise morphologies because once the energy is released from storage, active control would require a great deal of rapid power production. A unifying challenge for impulsive and oscillatory systems is that elastically stored energy can be beneficial for certain performance measures, but control becomes challenging when total mechanical energy in the system exceeds the work capacity of the musculature.

Data accessibility

Data is available on Dryad Digital Repository: https://doi.org/10.5061/dryad.95X69p8hX [56].

Authors' contributions

J.G., J.L., N.G. and S.S. designed research. J.G., R.G. and F.M. subteam conducted experiments and collected data, J.G. and R.G. analysed data, F.M. subteam, J.G. and R.G. ran DeepLabCut analysis, J.G., R.G., J.L., N.G. and S.S. interpreted data, and J.G., J.L., N.G. and S.S. wrote the paper. The frequency modulation subteam of the Living Dynamical Systems Vertically Integrated Project (LDS-VIP) is a team-based undergraduate research programme affiliated with the Sponberg Laboratory at Georgia Tech. Team members contributed collectively. All authors gave final approval for publication and agreed to be held accountable for the work performed therein.

Competing interests

We declare we have no competing interests.

Funding

This work was supported by US National Science Foundation CAREER grant no. 1554790 (MPS-PoLS) and a Dunn Family Professorsip to S.S. as well as the US National Science Foundation Physics of Living Systems SAVI student research network (GT node grant no. 1205878).