Abstract
Volumetric placental measurement using 3D ultrasound has proven clinical utility in predicting adverse pregnancy outcomes. However, this metric can not currently be employed as part of a screening test due to a lack of robust and real-time segmentation tools. We present a multi-class convolutional neural network (CNN) developed to segment the placenta, amniotic fluid and fetus. The ground truth dataset consisted of 2,093 labelled placental volumes augmented by 300 volumes with placenta, amniotic fluid and fetus annotated. A two pathway, hybrid model using transfer learning, a modified loss function and exponential average weighting was developed and demonstrated the best performance for placental segmentation, achieving a Dice similarity coefficient (DSC) of 0.84 and 0.38 mm average Hausdorff distance (HDAV). Use of a dual-pathway architecture, improved placental segmentation by 0.03 DSC and reduced HDAV by 0.27mm when compared with a naïve multi-class model. Incorporation of exponential weighting produced a further small improvement in DSC by 0.01 and a reduction of HDAV by 0.44mm. Per volume inference using the FCNN took 7–8 seconds. This method should enable clinically relevant morphometric measurements (such as volume and total surface area) to be automatically generated for the placenta, amniotic fluid and fetus. Ready availability of such metrics makes a population-based screening test for adverse pregnancy outcomes possible.
Index Terms—: Medical Diagnostic Imaging, Ultrasonic Imaging, Image Segmentation, Pregnancy, Sonogram, Convolutional Neural Networks, Deep Learning, Transfer Learning
I. Introduction
Placental insufficiency is the most common cause of stillbirth [1] as well as other adverse pregnancy outcomes such as fetal growth restriction [2] and pre-eclampsia [3]. The consequences of a poorly functioning placenta last well beyond pregnancy for the fetus, conferring them with an increased risk of developing obesity, diabetes and high blood pressure in adulthood [4]. A robust early screening test which can reliably predict those pregnancies destined to develop placental insufficiency would allow increased monitoring of fetal growth with early delivery if the baby becomes compromised thereby prevent a stillbirth occurring. It could also facilitate targeted treatment strategies such as low-dose aspirin which, if started in the first trimester, has been shown to reduce the incidence of preeclampsia and improved triage of perinatal care. This could have far reaching, long-term health benefits globally [4].
A. Clinical Motivation
Placentas destined to fail later in pregnancy already show signs of sub-optimal performance in the first trimester, (11–14 weeks) such as reduced volume and vascularity [5]. A systematic literature review concluded that placental volume, measured by 3D ultrasound (3D-US), could have value when integrated into a multivariable screening method for fetal growth restriction in the first trimester [6]. However, volume estimation currently requires off-line manual annotation by a trained sonographer which is time-consuming and cannot be performed within the 15 minutes in which a standard scan takes place [6]. Furthermore, manual labelling is highly operator dependent, inter-observer reproducability studies have demonstrated very different intra-class correlation coefficients (ICC; 95% CI)) of 0.59 (0.33–0.80) [7] and 0.81 (0.68–0.91) [8].
There is a clinical need for a precise, fully automated, method for real-time 3D-US image segmentation which can be used to provide an estimation of placental volume and demarcate its boundaries (enable identification of the interface between placenta and uterus, thereby providing the basis for automated perfusion assessment [9], [10]). These imaging biomarkers could then be incorporated into a multi-factorial population-based screening test to improve early prediction of adverse pregnancy outcomes.
B. Related Works
Real-time volume estimation has been achieved using fully convolutional neural networks (FCNNs) [11] to produce state-of-the-art performance in a range of medical imaging modalities [12]. FCNNs are particularly suited to segmentation since the parameters are shared and independent of image size. Segmentation accuracy of FCNNs can be further improved with technical enhancements such as loss function modification, which has demonstrated improved performance in segmenting the prostate in MRI images [13]. Use of multiple pathways, to increase the context of an FCNN, has improved accuracy [14] and has been successfully applied to placental segmentation in both MRI [15] and 3D-US [16].
Image analysis in feto-placental ultrasound imaging is relatively understudied compared to other areas of medical image analysis. A recent review [17] describes the unique challenges of placental segmentation. The placenta has a heterogeneous appearance and can implant on any of the uterine walls. Placentas that implant on the posterior uterine wall present a significant segmentation challenge as the overlying fetus can attenuate and scatter the US signal causing shadows and image artefact.
Attempts at placental MRI segmentation have shown promise. A semi-automated technique combining multiple volumes and a single annotated slice, with learned random forest and random field features combined with a 4D graph cut, demonstrated a mean Dice similarity coefficient (DSC) in 16 cases of 0.89 ± 0.02 (std. dev) [18]. An FCNN method applied to placental MRI data using a V-Net architecture in 12 patients provided a mean DSC of 0.75 ± 0.11 [19]. Using 3D-US, automated methods of segmenting first trimester placentas (n = 13) in an anterior position using a joint label fusion and majority vote technique achieved a mean DSC of 0.83 ± 0.05 [20], [21]. Yang et al in [22] used a U-Net style encoder/decoder FCNN to perform automatic multi-class segmentation of the placenta, amniotic fluid and fetus: 104 cases were used to develop the FCNN incorporating a recurrent neural network, of which 50 volumes were used to train, 10 to validate and 44 were tested. This achieved a mean DSC of 0.64 for the placenta, 0.89 for the amniotic fluid, and 0.88 for the fetus, while variability was not reported.
C. Contributions
Previously using 2,393 cases, an FCNN segmented placental volumes to predict small for gestational age (SGA) babies [23] which obtained a mean DSC of 0.82 ± 0.10 (std. dev) for placental segmentation. The size of the dataset, being ~20 times of that used by Yang et al. [22], indicates the obvious benefits of dataset size in improving segmentation accuracy when our previous work is compared to a multi-class FCNN trained on a smaller set of data.
This work aims to exploit the strong performance of this large-scale FCNN network and incorporate it into a framework that can solve the problem of multi-class labelling. We present a number of technical enhancements to solve this problem and present a full evaluation of the performance of the new FCNN, which are summarized as follows:
The use of multiple pathway FCNNs trained on single and multi-class datasets, which by addition of a modified loss function, exponential averaging (EA) and transfer learning improved average DSC to segment the placenta, amniotic fluid and fetus.
By combining pathways from different models and using these features, our previous state of the art segmentation performance on the placenta was combined with segmentation of the amniotic fluid and fetus that was comparable to the state of the art as measured by DSC and Hausdorff distance (HD) and compared to other works and to more classical U-Net based FCNNs the features of which are listed in Table I.
An evaluation technique to test real-world performance using a comparative Turing test indicated that automated segmentation was highly comparable to human performance (<50% positive prediction rate; i.e. the automated segmentation was selected blindly as better quality more often than the human.). Repeatability measured by intra-class correlation coefficients (ICC), showed good to excellent repeatability (measured by ICC) for respective organs.
TABLE I.
Summary of the features of each fully convolutional neural network (FCNN) describing class (S - Single; M - Multiple), use of exponential averaging (EA), application of transfer learning (TL) from other models and number of pathways used.
| Acronym | Model | Class | EA | TL | Pathways |
|---|---|---|---|---|---|
| PS | Placenta Segmentation | S | N | N | 1 |
| PSEA | Placenta Segmentation with EA | S | Y | N | 1 |
| MC | Multi-class Segmentation | M | N | N | 1 |
| MCTL | Multi-class Segmentation with TL | M | N | PS | 1 |
| HB | Hybrid | M | N | PS | 2 |
| HBEA | Hybrid with EA | M | Y | PSEA | 2 |
II. Method
The data used was from a research study conducted at a large UK tertiary referral hospital with local ethical approval (NHSREC ID: 02-03-033). Following signed, informed consent, a 3D ultrasound scan containing the placenta was recorded for singleton pregnancies in women at 11+0 to 13+6 weeks of gestation. The 3D-US volume was acquired by transabdominal sonography using a GE Voluson™ 730 Expert system (GE Healthcare, Milwaukee, WI, USA) using a 3D RAB4/8L transducer [24]. All 2,392 participants went on to deliver a chromosomally normal baby. Data were exported for off-line analysis to hard drive by USB and converted from scan-line representation into a 3D Cartesian volume [25] with an 0.6 mm isotropic voxel spacing. A complete digest of ultrasound settings used can be found in the original clinical paper [26].
Segmentation of the placenta used as label map was performed using the semi-automated Random Walker algorithm, as described in our previous study [9]. Initialisation or ‘seeding’ of the placental segmentation was performed by a clinical expert (SN). These “seedings” then underwent quality control with each one being examined by a second, independent, clinical expert (MM) and “re-seeded” where mistakes were evident. A third clinical expert (SC) examined cases where there was uncertainty or dispute regarding the boundaries of the placenta. From the available 2,393 3D-US volumes with an existing placental segmentation, 300 volumes were randomly selected for multi-class segmentation. The amniotic fluid and the fetus were “seeded” (PL and YY) and combined with the placental “seeding” performed from the previous study. Initialisation of the amniotic fluid and fetus is much easier than the placenta because the edges of the structures are easier to discriminate but any cases where there was ambiguity were examined by a clinical expert (SC). These three different classes were then segmented as a multi-class label map using the Random Walker algorithm [9], [27]. Mean time (± std. dev) to “seed” the two new features in a single volume was 30 ± 10 min.
A. Placenta segmentation (PS) model
The remaining 2,093 cases were partitioned into 1,893 training cases, 150 validation cases and 50 test cases. These were used to train an FCNN, similar in architecture to the U-Net [28], extended to 3D and shown in Figure 1a. Image volumes varied in size but were typically had dimensions of 200 × 300 × 300 voxels. The volume was decomposed into patches that overlapped such that the output of the convolutional neural network that used convolutions without padding was non-overlapping to avoid edge effects. Input patches with isotropic dimensions of 863 voxels were passed through three down-sampling blocks, three up-sampling blocks, two convolutional layers and a final classification layer. A down-sampling block used convolution followed by convolution with a stride of 2 voxels wide and a 2×2×2 kernel. An up-sampling block used convolution followed by transpose convolution of stride 2 and a 2×2×2 kernel. All other kernels had size 3×3×3. Features from layers with the same resolution were forwarded from earlier layers to later layers.
Fig. 1.
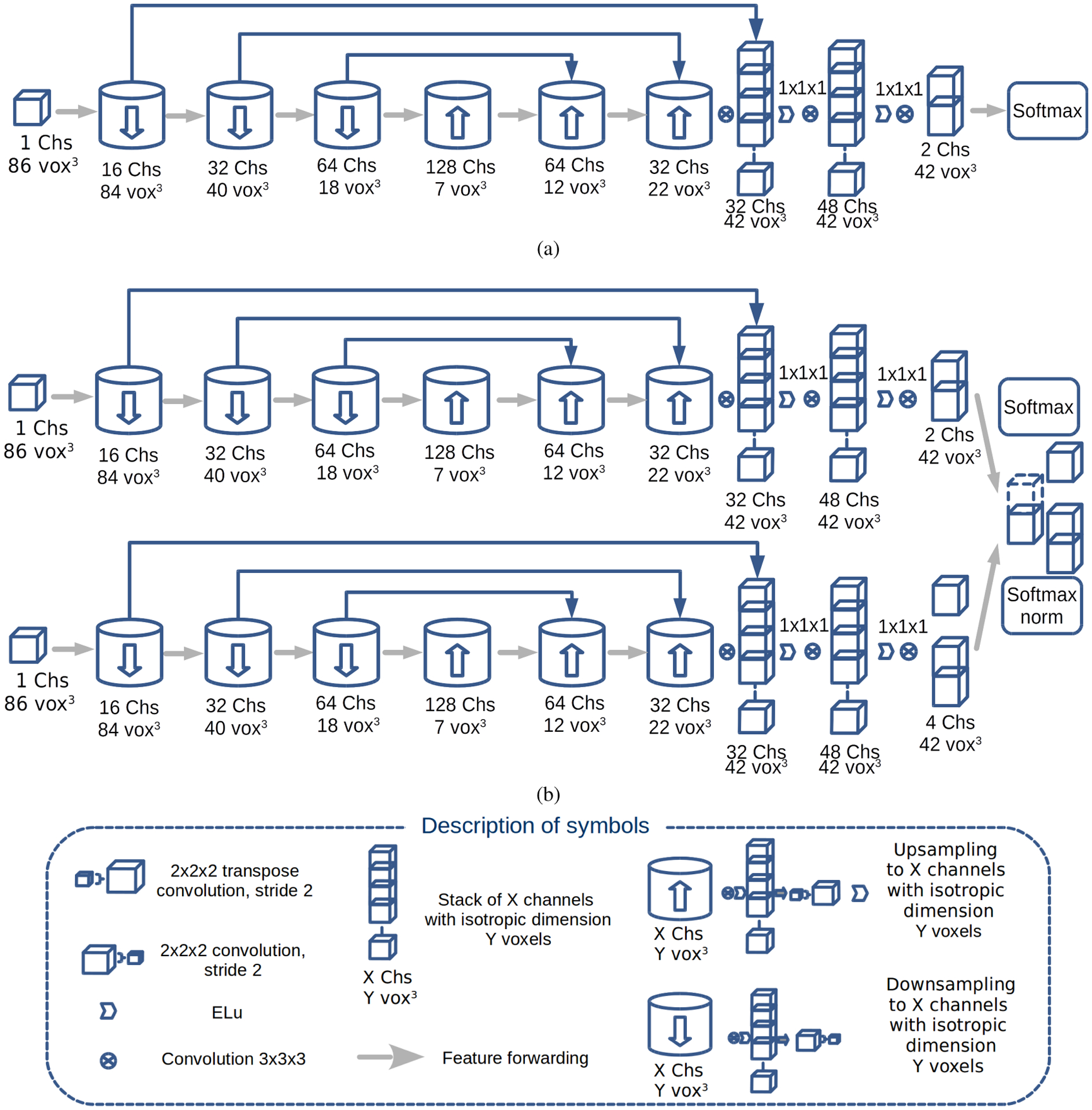
Convolutional neural network architecture of the models: (a) placental segmentation (PS) model; (b) the dual pathway (T - top; B - bottom pathway) hybrid (HB) model, where T encodes the PS model. The architectures of the multi-class (MC) and multi-class transfer learning (MCTL) models are not shown as they are identical to Fig 1a except for having four channels instead of two in the layer before softmax.
The FCNN was trained for 30 epochs (373 steps per epoch), where a single epoch was defined as all the patches for the whole dataset. The placenta segmentation (PS) model was chosen by selecting the highest mean DSC on the validation set that was not improved upon by ten percent within the next five epochs. The parameters: Adam optimizer learning rate, β1, β2 and ϵ were set as 0.001, 0.9, 0.999 and 1 × 10−8, respectively. The learning rate decayed at a rate of 0.92 every 1000 steps. Variance scaling was used to initialise the parameters of the model. L2 regularisation was used with a coefficient of 0.0001. A batch size of 40 was used while training the model. Full validation was performed every 1000 steps. An averaged version of the PS model (PSEA) was created using an exponential moving average during training. Exponential moving averaging reduces noise by averaging the weights of the model over the training process and favouring more recent values of the weights as well as providing computational efficiency, since it does not require the storage of all the weights [29].
B. Multi-class (MC) models
The 300 multi-class (MC) cases were sub-divided into 200 training cases, 40 validation cases and 60 test cases. Four multi-class models were each trained for 40 epochs with a batch size of 30. Firstly, a MC model was trained using a network identical to the architecture in Fig. 1a but with four output classes in the layer before the softmax function with parameters initialised using variance scaling. Then, a multi-class transfer learning (MCTL) model, using the same architecture as the MC model, with the weights and biases for all layers except the last taken from the PS model, was trained. By initialising the weights and biases of the MCTL model using the PS model, the MCTL had effectively a larger training dataset of 1,893 cases in addition to the 200 cases of the MC model. Since the PS model was trained to detect placenta, we hypothesised that the MCTL model may better segment the placenta at the expense of fetal and amniotic fluid segmentation performance compared to the MC model, this will be discussed in later sections.
C. Hybrid (HB) models
To overcome the shortcomings of MC/MCTL models, two hybrid models were used. The hybrid model (HB) and hybrid model with exponential averaging (HBEA) both consisted of a dual pathway model which were implemented as shown in Fig. 1b. In the top pathway, which encoded the placental segmentation, parameters for HB model were initialised using the values from the large-scale PS model and the HBEA model were initialised using the PSEA model. In the bottom pathway, which encoded the remaining classes, parameters were initialised using variance scaling and then trained on the MC data. For both HB and HBEA models, parameters in the bottom pathway were allowed to change but for the top pathway were fixed, in order to encorporate the results for placental segmentation from the PS/PSEA models. The Adam optimizer parameters were identical to those used in the PS training. Batch size and number of epochs were altered to accommodate the differences in number of parameters and data used for each model evaluated.
The features of the two pathways were combined as follows: let PBackground, PPlacenta, PAmniotic, and PFetus be the confidences that a voxel belongs to the background, placenta, amniotic fluid and fetus, respectively. For a given voxel i, the softmax output of the top pathway (T) was given as only two values and that summed to 1. In this case, the fetus and amniotic fluid were included in the background. In the bottom pathway (B), the softmax of the final layer produced a confidence for membership of a given voxel with scalar values of , , and that summed to 1. The indicated the confidence that a voxel is neither placenta, fetus or amniotic fluid.
By design, the regions of the output layer that are characterised as placenta cannot change through training. Placental regions will still contribute to the loss but the neural network will be unable to modify the parameters to reduce the loss from these regions of the image. This motivates the use of a modified loss function to ignore the contribution from placental regions to the loss. The loss function L was defined combining the outputs of two pathways as
| (1) |
where M was a binary mask whose value mi was 0 for a voxel i within the placental segmentation and 1 otherwise, oi was the output of the bottom pathway B, sl was the softmax cross entropy function and ni was the normalisation factor defined as 1 minus , the confidence of voxel i is placenta from the output from softmax layer of the top pathway T.
Since the loss function was masked over the placental region/segmentation, the placenta did not contribute to the training of the model. The final confidence vector in the HB model had scalar components given as:
| (2) |
| (3) |
| (4) |
| (5) |
where the final segmentation of a voxel was the maximum of the four values defined in Eq. 2–5. The sum of the terms in Eq. 2,4 & 5 are equal to . From Equation 3, the placental segmentation of the HB model was set to the PS model for all voxels where .
For voxels where , a voxel was classified as placenta by the HB model but classified as background by the PS model if the remaining classes, , and , each had values .
D. Post-Processing, Implementation & Analysis
The predictions for test data were post processed using morphological filters using the same process as described in [23] but performed on each of the three classes. Region fragments of the placenta < 40% of the size of the largest region were omitted. Only the largest continuous region of amniotic fluid and fetus were retained as part of the final segmentation. The segmentation was then grayscale closed using a 3D kernel (3 voxel radii) and a hole filling filter was applied. This removed small regions separated from the largest, contiguous placental segmented regions, smoothed the boundary of the placenta, amniotic fluid and fetus and filled any holes. Ultrasound volumes were processed and visualised using SimpleITK (version 1.2.4) [30], ITK [30] and VTK (version 8.2) [31]. R (version 3.3.2) [32] was used for data analysis and hypothesis testing and ggplot2 (version 2.2) [33] for plotting. The models were implemented in Python (version 3.6) using the open-source OxNNet [34] library developed for 3D-US segmentation and Tensorflow (version 1.12) [35]. Training and inference was performed on a Linux PC (Intel i7 5820) using a Titan X GPU (NVidia Corporation, Santa Clara, CA) with 12Gb VRAM. The CNN models are fully available online [36].
E. Evaluation
Comparison between model generated volumetric binary volumes was assessed by similarity metrics: Dice similarity coefficient (DSC), Hausdorff Distance (HD) and the average Hausdorff distance (HDAV) defined for two segmentations X and Y and a Euclidean distance metric d reported in millimetres [23]. The significance threshold was set at P < .05. Pairwise comparison between DSC measurements between models were assessed using Student’s paired t-test.
Reproducibility of the final placenta, fetus and amniotic fluid volume in millilitres was assessed using the ICC (2,1) [37], [38] for inter-observer repeatability between the semi-automated Random Walker results, regarded as the ground-truth used for performance evaluation, and the newly generated FCNN outputs. Finally, a blinded comparison was performed to assess an experienced operator’s (GS) ability to discriminate between the manual and automated outputs using a side-by-side comparison, akin to a comparative Turing test [39] for the 60 multi-class test cases. The user was presented with two B-Mode volumes sliced in 2D and scrolling between both volumes linked using a mouse, the contours of each segmentation class were displayed with the Random Walker result presented in one randomly assigned viewport and the FCNN contours in the other. The operator used the arrow keys to denote which contours deemed ‘best’ once viewed each image within the volume through scrolling through. This viewer and test is available online [40]. The positive recognition rate (%) or percentage that the operator selected a Random Walker based contour set for each model was reported.
III. Results
A. Placental segmentation (PS) model
The PS model obtained the best mean DSC (std. dev) on the validation set of 0.85 (0.09) after 17,000 training steps. The performance of the model is shown in Fig. 3. On the 50 test cases, the PS model had a mean DSC (std. dev) of 0.85 (0.05) and the PSEA model had a mean DSC of 0.85 (0.05)).
Fig. 3.
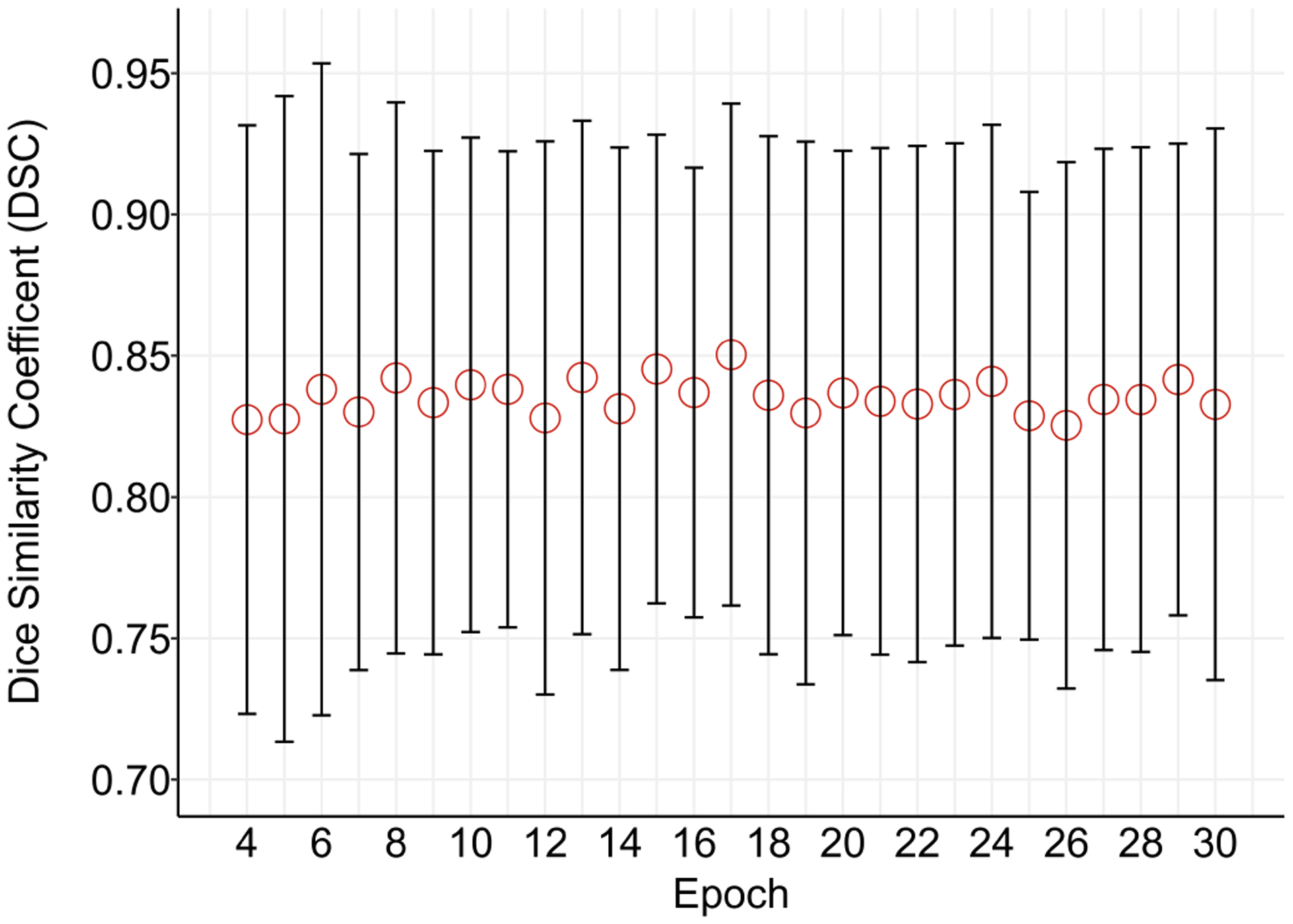
Error plot of median (interquartile range) Dice similarity coefficient (DSC) on the 150 PS validation cases during training for the PS model to segment the placenta.
The data publicly available and published by [21] was also used to evaluate the performance of the PS model. The available images were resampled to the same isotropic spacing and the same pre-processing, PS model application and post-processing was applied as described in Section II. The mean DSC (std. dev) on this data set was 0.67 (0.24), mean HD was 21.28 (14.18) mm and mean HDAV was 1.59 (2.27) mm.
B. Multi-class (MC) and Hybrid Models
To compare performance to a reduced dataset size, as per Yang et al, using 50 training data the model was trained over 40 epochs. Placental DSC was 0.73 (0.1), amniotic fluid DSC was 0.90 (0.06) and fetus DSC was 0.83 (0.08) for the HBEA model. For HD (mm), the placenta was 22.48 (8.78), amniotic fluid was 14.20 (9.25) and fetus was 21.74 (11.79). For HDAV (mm), the placenta was 1.23 (1.16), amniotic fluid was 0.36 (0.84) and fetus was 21.74 (11.79).
Comparing the same HB model using the modified loss function defined in Eq. 1 to standard cross entropy loss, similarity metrics improved. DSC for placenta increased by 0.01 and remained the same for the fetus and amniotic fluid. For surface similarity metrics, small increases in HD (mm) (placenta +0.44; amniotic fluid −0.01; fetus 1.4) and decreases in HDAV (placenta −0.04mm; amniotic fluid −0.01; fetus 0.0mm) were observed.
For the multi-class models, when trained on the fullest set of data, compared to the dataset of 50, results improved for all metrics. The mean DSC of the segmentation of the placenta, amniotic fluid and fetus on the validation set during training are shown in Fig. 4. After 40 epochs, the MC model obtained the lowest placenta DSC of 0.78 (0.09). The MCTL model was better at 0.80 (0.09). Both hybrid models were at 0.81 (0.09) for the HB and the HBEA model was 0.82 (0.08). Similiar values for amniotic fluid DSC were obtained for the MC model at 0.93 (0.04), 0.92 (0.04) for the MCTL model, 0.92 (0.04) for HB and 0.93 (0.04) for the HBEA model. The DSC of the fetus was 0.88 (0.05) for the MC model, 0.87 (0.05) for the MCTL model, 0.87 (0.05) for the HB model and 0.88 (0.04) for the HBEA model. Fig. 4 shows the expected behaviour for the hybrid models incorporating the PS model, where in the DSC did not alter for the placenta over the epochs, as compared to the other classes segmented.
Fig. 4.
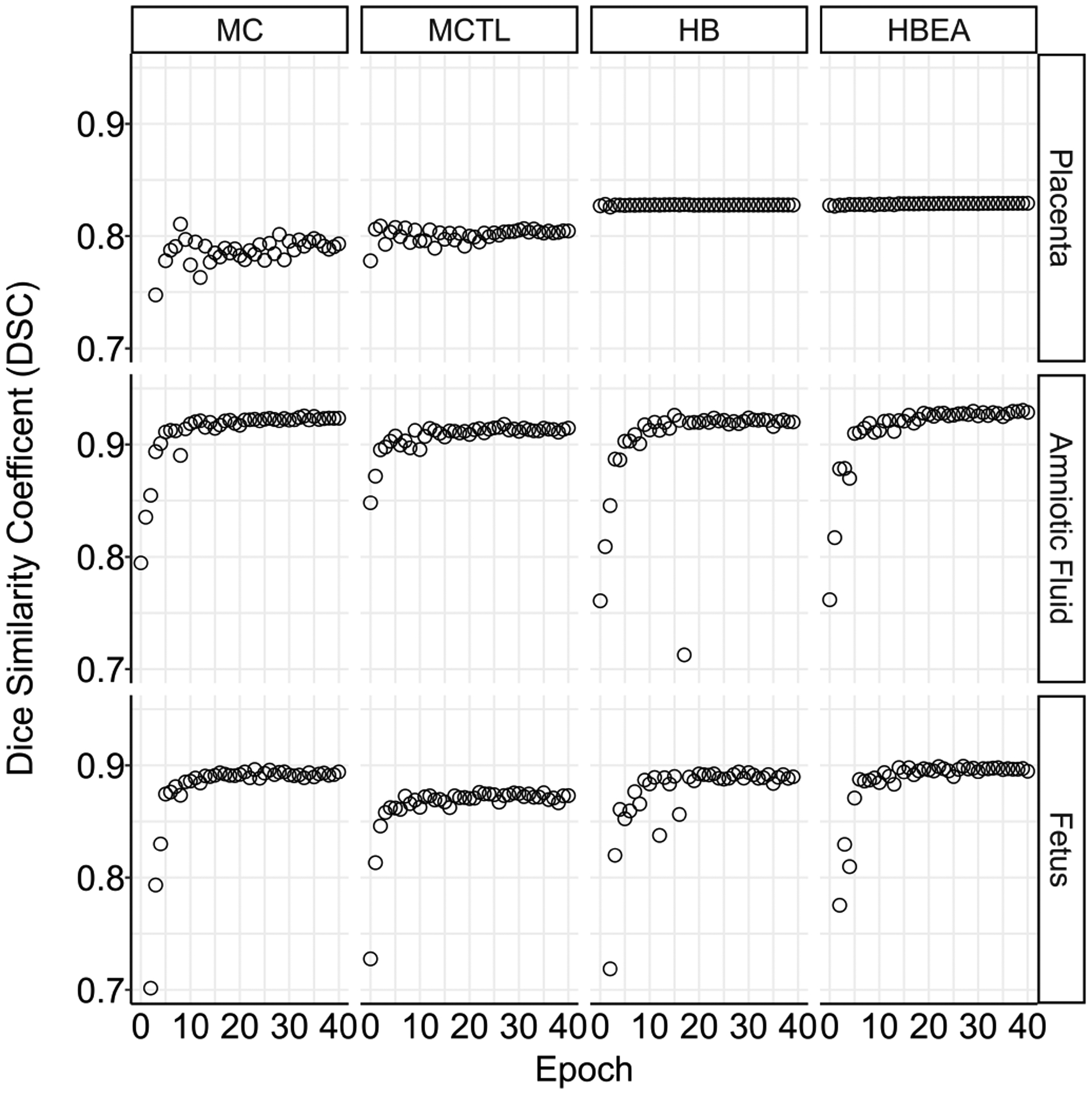
Median Dice similarity coefficient (DSC) on the 40 MC validation cases during training for the placenta, amniotic fluid and fetus, showing the performance difference between the multi-class models defined in Table I.
The comparison of the performance of the models on the test set after post processing is shown in Table II and Fig. 5. The mean (std. dev) of the placenta DSC for the MC, MCTL HB and HBEA models were 0.78 (0.09), 0.80 (0.09), 0.81 (0.09) and 0.82 (0.08) respectively. The HDAV of the placenta segmentation was lowest for the HBEA model at 0.58 (0.70) mm. The mean of the amniotic fluid DSC for the MC, MCTL, HB and HBEA models were 0.93 (0.04), 0.92 (0.04), 0.92 (0.04) and 0.93 (0.04) respectively. The mean of the fetus DSC for the MC, HB and HBEA models were all 0.88 (0.04) but was 0.87 (0.04) for the MCTL model. Examples showing segmentations using the Random Walker and HBEA model are shown in Fig. 2. DSC was 0.85, 0.85 and 0.71 for the placenta; 0.96, 0.96 and 0.95 for the amnion and 0.94, 0.92 and 0.90 for the fetus, in the three subjects shown. Timings for the inference of each model indicate an average inference of 7–8 seconds per image. Statistical comparison of the DSC for all models using a paired t-test showed significant differences for the placenta (P < 0.001) and fetus (P < 0.005). There was no significant difference for amniotic fluid (P > 0.3).
TABLE II.
Mean (std. dev) of the Dice similarity coefficient (DSC), Hausdorff distance (HD) and average HD (HDAV) and time to infer segmentation performance for the multi-class (MC) model, multi-class model with transfer learning (MCTL), the hybrid model (HB) and the exponential moving averaged hybrid model (HBEA) on the MC test set after post processing.
| Placenta | Amniotic Fluid | Fetus | Time | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Model | DSC | HD | HDAV | DSC | HD | HDAV | DSC | HD | HDAV | (s) |
| MC | 0.78 (0.09) | 19.43 (8.22) | 0.86 (0.93) | 0.93 (0.04) | 11.80 (6.85) | 0.15 (0.22) | 0.88 (0.05) | 16.88 (10.48) | 0.25 (0.36) | 8.13 (1.86) |
| MCTL | 0.80 (0.09) | 17.71 (8.12) | 0.70 (0.92) | 0.92 (0.04) | 11.68 (5.27) | 0.12 (0.14) | 0.87 (0.05) | 17.83 (10.77) | 0.29 (0.47) | 7.75 (1.94) |
| HB | 0.81 (0.09) | 15.38 (7.75) | 0.59 (0.74) | 0.92 (0.04) | 11.00 (5.58) | 0.13 (0.17) | 0.87 (0.05) | 15.59 (9.32) | 0.21 (0.24) | 8.46 (2.54) |
| HBEA | 0.82 (0.08) | 16.22 (8.11) | 0.58 (0.70) | 0.93 (0.04) | 10.86 (5.28) | 0.13 (0.17) | 0.88 (0.04) | 16.57 (10.22) | 0.22 (0.25) | 8.46 (2.54) |
Fig. 5.
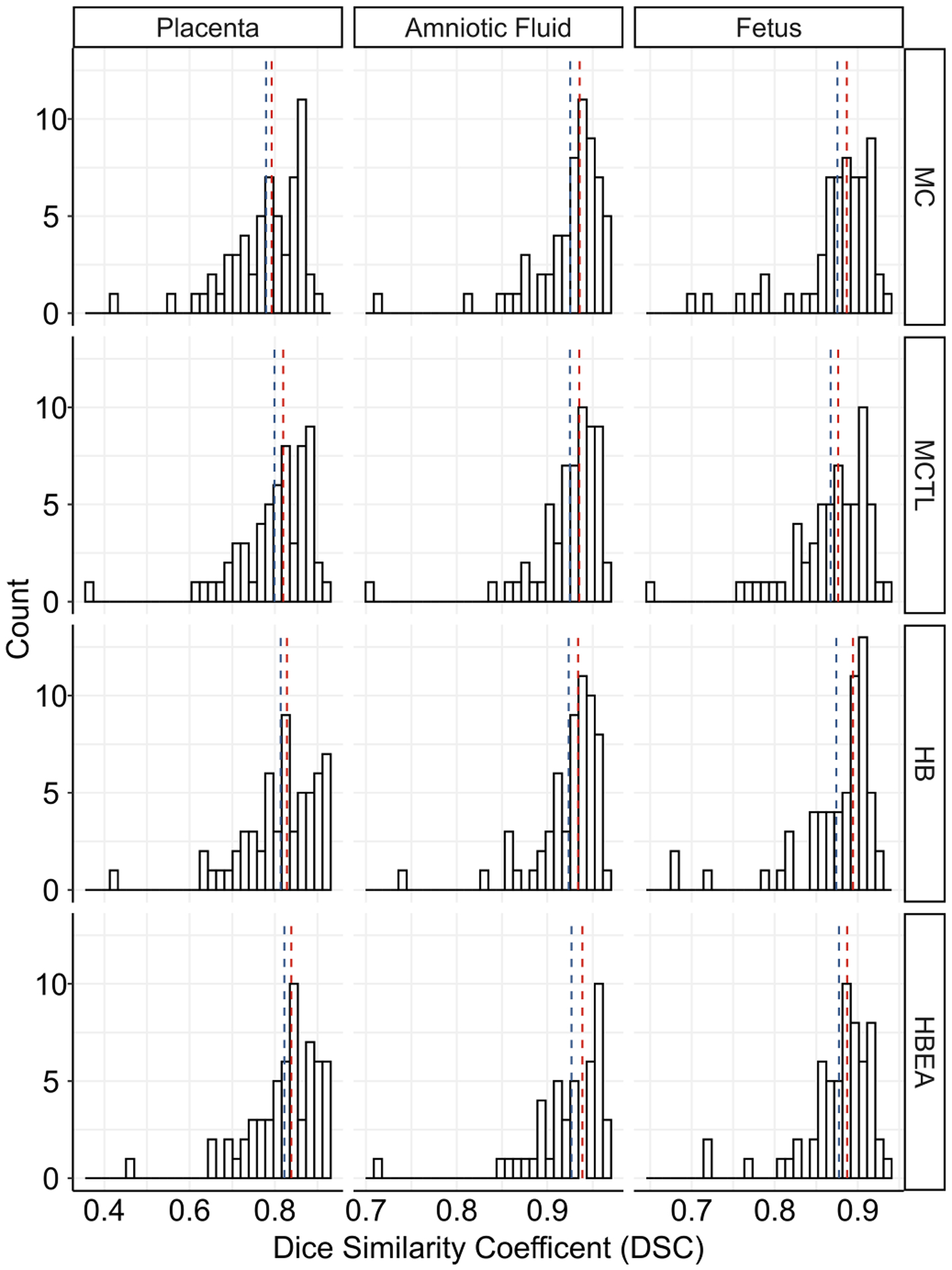
Histograms of the Dice similarity coefficient (DSC) for the placenta, amniotic fluid and fetus for all four FCNN models on 60 MC test cases. The median and mean values are shown as red and blue vertical lines, respectively.
Fig. 2.
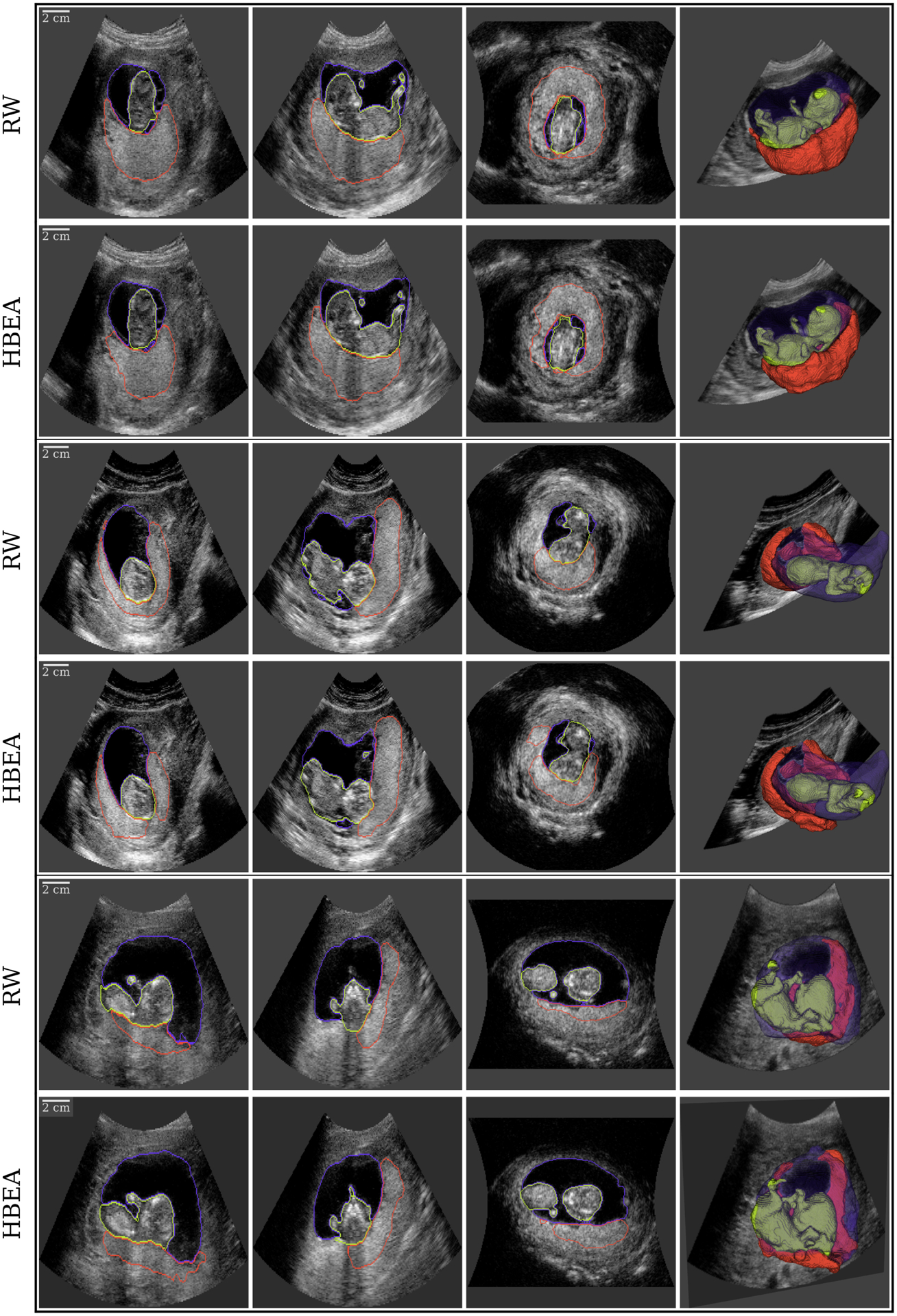
Visualization of multi-class 3D ultrasound (3D-US) segmentation of the placenta ■, amniotic fluid ■ and fetus ■ in three subjects (each outlined in black) performed using the Random Walker (RW; top) and Hybrid Averaged model (HBEA; bottom) shown as three orthogonal views and a semi-opaque 3D rendering (left to right).
C. Repeatability
Repeatability as assessed by ICC (95 CI%) for each segmentation across the four models is provided in Table III. ICC values for the placenta were lower than for those for the fetus and amniotic fluid which reported excellent reproducability. For the placenta, ICC was increased for the HB models over the MC models. Using the lower end of the CI reported, it was shown the HBEA model was significantly better than the MC model in terms of repeatability as reported by ICC. For the other classes, no significant differences were observed although. There were small increases in ICC when the HBEA model was compared to the others. The positive recognition rates for the Random Walker based ground-truth data when compared to the four different models were: MC 52.5%, MCTL 44.0%, HB 56.0% and HBEA 45.8%.
TABLE III.
Intra-class correlation coefficients (95% CI) for each organ volume from a given multi-class FCNN defined in Table I to the random walker estimate.
| Model | Placenta | Amniotic Fluid | Fetus |
|---|---|---|---|
| MC | 0.52 (0.31 – 0.69) | 0.98 (0.96 – 0.99) | 0.850 (0.76 – 0.91) |
| MCTL | 0.56 (0.36 – 0.71) | 0.98 (0.96 – 0.99) | 0.839 (0.75 – 0.90) |
| HB | 0.64 (0.45 – 0.77) | 0.98 (0.96 – 0.99) | 0.831 (0.73 – 0.90) |
| HBEA | 0.69 (0.53 – 0.80) | 0.98 (0.96 – 0.99) | 0.863 (0.78 – 0.91) |
IV. Discussion
In this work, we demonstrated improved performance of a FCNN for segmentation of anatomical structures in early pregnancy using 3D ultrasound. By using a combined dataset of images, with both single and multi-class label maps generated by Random Walker as ground truth, a state-of-the-art performance was achieved for segmentation of the placenta.
Our results show that there are differences in the performance of each multi-class FCNN model. The MC and MCTL models have identical architectures but the performance of the MC model in segmenting the placenta is reduced in comparison to the MCTL model although the amniotic fluid and fetus segmentation is improved. As the MCTL model parameters were initialised using the PS model it is unsurprising that it appears to be biased towards segmenting the placenta. Additionally, the MC model was trained using only 200 MC training cases which confirms previous findings that performance is related to the size of the training dataset [23]. By adding the PS model as an extra pathway, the performance gained from training on 2,093 placentas is added, giving the hybrid model improved placental segmentation when compared to a single pathway model which is only trained on 300 cases. The HB and HBEA models have an almost constant performance in the placenta segmentation, as shown in Fig. 4, reflecting the fixed nature of the parameters of the top pathway which we used to exploit the more accurate PS model that has been trained on the largest set of cases. Small differences between the PS and HB models can occur, when some background voxels can be classified as placenta if their background probability was distributed among the other classes such that the placental probability was maximum. We also showed that the modified loss function allows for the bottom pathway to focus on segmenting the fetus and amniotic fluid. The exponential moving averaged reduced volatility in the weights which we propose improved model inference. This is reflected in the HBEA model yielding the best performance of the four models.
The performance of the PS model on the publicly available data set in [21] were reduced compared to data used for this study. The data used to train our model was translated from a toroidal coordinate system [25] while the publicly available data was already in a Cartesian geometry and was resampled to have isotropic spacing of 0.6 mm and did not contain the full scan region. We speculate that the reduced performance maybe due to error introduced from the resampling or the effect on the normalisation due to the cropping of the volume. With the availability of multi-class prediction results of placenta, amniotic fluid and fetus on this public data set online and the models we would expect that improvements can be made by interested researchers [41]. The only other multi-class segmentation work in this field by Yang et al. [22] obtained DSC values of 0.64, 0.89 and 0.88 to segment the placenta, amniotic fluid and fetus, respectively, using 104 3D-US scans. They also used a 3D extension of U-Net [28] and combined the output with a recurrent neural network. This strategy uses four times the number of features compared to the FCNN models used in our work. Other differences in the implementation included patch size, batch normalisation and image spacing. These differences as well as the greater number of training cases used may account for the increased performance in this study, particularly in segmenting the placenta (DSC of 0.82 compared with 0.64). The ground truths in [22] were obtained using manual segmentation. Whilst it has been demonstrated that the much faster Random-Walker technique has equivalent performance to manual segmentation in terms of both inter and intra-operator variability [9], the same has not been demonstrated for segmentation of the fetus or amniotic fluid.
Having shown that performance based on similarity metrics leads to good estimation of the organs, we applied clinically used statistics for reproducability assessment. These provide a measure of performance from medical studies where human operators have compared their performance where commercial software would not allow voxel-wise comparison. As shown in Table III, the ICC for amniotic and fetal estimation were excellent based on standard interpretations for ICC > 0.75. For the placenta, ICC values increased with the HBEA model providing best performance at a moderate level of reported ICC. We went further in this assessment, given that the nature of placental segmentation combined with ultrasound imaging is a hard task. The standard for evaluation of the performance of the automated detection is an operator defined ground truth and the ‘human eye’ is not necessarily always accurate. In this problem, the border between the placenta and the surrounding tissue often appears very diffuse making it difficult for even highly experienced sonographers to distinguish the boundary between placenta and the uterine myometrium. However, where there is a low DSC, trying to ascertain whether the ground truth or the predicted segmentation more closely represents the ‘true’ anatomy is extremely difficult. As such, using a comparative Turing test we showed < 50% positive prediction rate for the original Random Walker labelled result versus the MCTL and HBEA models. This indicates that for a blinded observer, the automated labelling would seem be considered more “human” over 60 cases. This result is encouraging and with additional analysis using multiple observers and an increased size of dataset will bolster these findings.
As discussed, this work does have limitations. The 3D-US data were collected a number of years ago using an US machine that has been superseded by two newer generations of hardware. It is hoped that the image quality will be increased in future studies facilitating easier segmentation since signal-to-noise ratio and spatial resolution have significantly improved. The use of methods of ultrasound reconstruction such as spatial averaging [42] may change the texture of the image and impact the performance of our FCNN which would need to be considered. However, in future studies useful features learned by our models could still be used with transfer learning on newer modalities. The effect of the many parameters within the model have not been investigated with full ablation studies nor full evaluation of other post-processing strategies. However, suitable choices of the parameters have been suggested and the effect of patch size has previously been studied by other authors [14], [43] and we would foresee these only provide minor increases in performance compared to increasing the dataset trained on which we have previously shown [23].
The HBEA model had a median segmentation time of 8.46 seconds compared to the 30 minutes required for semi-automated segmenation. Hence, the model realised in this work will allow rapid calculation of not only placental volume but other important morphometrics such as shape and surface area of the utero-placental interface since these can now also be calculated using the MC segmentation. When combined with power Doppler ultrasound this will allow for automated measurement of perfusion of the utero-placental interface [10], [44]. These measurements when combined with blood serum and maternal characteristics, [45] should improve population-based screening algorithms for the prediction of adverse pregnancy outcomes in early pregnancy.
V. Conclusion
We present an automated method based on deep learning that achieves state-of-the-art performance, measured using DSC, HD, and HDAV in segmenting the placenta while obtaining similar values to the state-of-the-art performance for the amniotic fluid and fetus. This was possible by combining a multi-class dataset labelled by a semi-automatic technique with a multiple pathway FCNN using a modified loss function. This image analysis technique demonstrates a FCNN can now provide estimates of placental volume, surface area of the utero-placental interface and other morphometric measurements in real-time to facilitate population-based ultrasound screening. These measures, combined with maternal characteristics and serum biomarkers, can now be used to develop a first trimester screening tool aimed at improving identification of pregnancies at-risk of later complications.
Acknowledgments
Research reported in this publication was supported by the Eunice Kennedy Shriver National Institute of Child Health and Human Development (NICHD) Human Placenta Project of the National Institutes of Health under award number UO1-HD087209. We gratefully acknowledge the support of NVIDIA Corporation who donated the Tesla GTX Titan X GPU used for the image analysis. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Contributor Information
Sally L. Collins, Nuffield Department of Women’s and Reproductive Health, University of Oxford, UK Fetal Medicine Unit, The Women’s Centre, John Radcliffe Hospital, Oxford, UK.
Kypros H. Nicolaides, Harris Birthright Research Centre of Fetal Medicine, King’s College Hospital, UK
Walter Plasencia, Fetal Medicine Unit, Hospiten Group, Tenerife, Spain.
Malid Molloholli, Department of Obstetrics and Gynaecology, Wexham Park Hospital, Slough, UK.
Stavros Natsis, Nuffield Department of Women’s and Reproductive Health, University of Oxford, UK; Fetal Medicine Unit, The Women’s Centre, John Radcliffe Hospital, Oxford, UK.
Gordon N. Stevenson, School of Women’s and Children’s Health, University of New South Wales, Sydney, NSW, AU.
References
- [1].Seaton SE, Field DJ, Draper ES, Manktelow BN, Smith GC, Springett A et al. , “Socioeconomic inequalities in the rate of stillbirths by cause: a population-based study,” BMJ open, vol. 2, no. 3, p. e001100, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Sankaran S and Kyle PM, “Aetiology and pathogenesis of IUGR,” Best Practice & Research Clinical Obstetrics & Gynaecology, vol. 23, no. 6, pp. 765–777, 2009. [DOI] [PubMed] [Google Scholar]
- [3].Redman CW and Sargent IL, “Latest advances in understanding preeclampsia,” Science, vol. 308, no. 5728, pp. 1592–1594, 2005. [DOI] [PubMed] [Google Scholar]
- [4].Burton GJ, Fowden AL, and Thornburg KL, “Placental origins of chronic disease,” Physiological reviews, vol. 96, no. 4, pp. 1509–1565, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Collins SL, Welsh AW, Impey L, Noble JA, and Stevenson GN, “3D fractional moving blood volume (3D-FMBV) demonstrates decreased first trimester placental vascularity in pre-eclampsia but not the term, small for gestation age baby,” PloS one, vol. 12, no. 6, p. e0178675, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Farina A, “Systematic review on first trimester three-dimensional placental volumetry predicting small for gestational age infants,” Prenatal diagnosis, vol. 36, no. 2, pp. 135–141, 2016. [DOI] [PubMed] [Google Scholar]
- [7].Jones NW, Raine-Fenning NJ, Mousa HA, Bradley E, and Bugg GJ, “Evaluating the intra- and interobserver reliability of three-dimensional ultrasound and power Doppler angiography (3D-PDA) for assessment of placental volume and vascularity in the second trimester of pregnancy,” UMB, vol. 37, no. 3, 2011. [DOI] [PubMed] [Google Scholar]
- [8].Larsen M, Naver K, Kjaer M, Jorgensen F, and Nilas L, “Reproducibility of 3-dimensional ultrasound measurements of placental volume at gestational ages 11–14 weeks,” Facts, Views & Vision in ObGyn, vol. 7, no. 4, p. 203, 2015. [PMC free article] [PubMed] [Google Scholar]
- [9].Stevenson GN, Collins SL, Ding J, Impey L, and Noble JA, “3D ultrasound segmentation of the placenta using the Random Walker algorithm: reliability and agreement,” Ultrasound in Medicine & Biology, vol. 41, no. 12, pp. 3182–3193, 2015. [DOI] [PubMed] [Google Scholar]
- [10].Welsh AW, Fowlkes JB, Pinter SZ, Ives KA, Owens GE, Rubin JM et al. , “Three-dimensional US Fractional Moving Blood Volume: Validation of Renal Perfusion Quantification,” Radiology, p. 190248, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Krizhevsky A, Sutskever I, and Hinton GE, “Imagenet classification with deep convolutional neural networks,” in Advances in neural information processing systems, 2012, pp. 1097–1105. [Google Scholar]
- [12].Litjens G, Kooi T, Bejnordi BE, Setio AAA, Ciompi F, Ghafoorian M et al. , “A survey on deep learning in medical image analysis,” Medical image analysis, vol. 42, pp. 60–88, 2017. [DOI] [PubMed] [Google Scholar]
- [13].Milletari F, Navab N, and Ahmadi S-A, “V-net: Fully convolutional neural networks for volumetric medical image segmentation,” in 3D Vision (3DV), 2016 Fourth International Conference on. IEEE, 2016, pp. 565–571. [Google Scholar]
- [14].Kamnitsas K, Ledig C, Newcombe VF, Simpson JP, Kane AD, Menon DK et al. , “Efficient multi-scale 3D (CNN) with fully connected (CRF) for accurate brain lesion segmentation,” Medical Image Analysis, vol. 36, pp. 61 – 78, 2017. [DOI] [PubMed] [Google Scholar]
- [15].Alansary A, Kamnitsas K, Davidson A, Khlebnikov R, Rajchl M, Malamateniou C et al. , “Fast fully automatic segmentation of the human placenta from motion corrupted MRI,” in International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer, 2016, pp. 589–597. [Google Scholar]
- [16].Looney P, Stevenson GN, Nicolaides KH, Plasencia W, Molloholli M, Natsis S et al. , “Automatic 3D ultrasound segmentation of the first trimester placenta using deep learning,” in Biomedical Imaging, IEEE 14th International Symposium on. IEEE, 2017, pp. 279–282. [Google Scholar]
- [17].Torrents-Barrena J et al. , “Segmentation and classification in MRI and US fetal imaging: Recent trends and future prospects,” Medical Image Analysis, vol. 51, pp. 61–88, 2019. [DOI] [PubMed] [Google Scholar]
- [18].Wang G, Zuluaga MA, Pratt R, Aertsen M, Doel T, Klusmann M et al. , “Slic-seg: A minimally interactive segmentation of the placenta from sparse and motion-corrupted fetal mri in multiple views,” Medical image analysis, vol. 34, pp. 137–147, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Torrents-Barrena J et al. , “Lstm fully convolutional neural networks for umbilical cord segmentation in ttts foetal surgery planning,” in Proc. 32nd International Conference on Computer Assisted Radiology and Surgery, 2018. [Google Scholar]
- [20].Oguz I, Pouch AM, Yushkevich N, Wang H, Gee JC, Schwartz N et al. , “Automated placenta segmentation from 3D ultrasound images,” in MICCAI workshop on perinatal, preterm and paediatric image analysis (PIPPI), 2016. [Google Scholar]
- [21].Yushkevich PA, Pashchinskiy A, Oguz I, Mohan S, Schmitt JE, Stein JM et al. , “User-guided segmentation of multi-modality medical imaging datasets with ITK-SNAP,” Neuroinformatics, vol. 17, no. 1, pp. 83–102, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Yang X, Yu L, Li S, Wen H, Luo D, Bian C et al. , “Towards automated semantic segmentation in prenatal volumetric ultrasound,” IEEE Transactions on Medical Imaging, 2018. [DOI] [PubMed] [Google Scholar]
- [23].Looney P, Stevenson GN, Nicolaides KH, Plasencia W, Molloholli M, Natsis S et al. , “Fully automated, real-time 3D ultrasound segmentation to estimate first trimester placental volume using deep learning,” JCI insight, vol. 3, no. 11, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Wegrzyn P, Faro C, Falcon O, Peralta C, and Nicolaides K, “Placental volume measured by three-dimensional ultrasound at 11 to 13+ 6 weeks of gestation: relation to chromosomal defects,” Ultrasound in Obstetrics & Gynecology, vol. 26, no. 1, pp. 28–32, 2005. [DOI] [PubMed] [Google Scholar]
- [25].Looney P, Stevenson GN, and Collins SL, “plooney/kretz v1.1,” January 2019. [Online]. Available: 10.5281/zenodo.2537876 [DOI] [Google Scholar]
- [26].Plasencia W, Akolekar R, Dagklis T, Veduta A, and Nicolaides KH, “Placental volume at 11–13 weeks’ gestation in the prediction of birth weight percentile,” Fetal Diagnosis and Therapy, vol. 30, no. 1, pp. 23–28, 2011. [DOI] [PubMed] [Google Scholar]
- [27].Grady L, “Random walks for image segmentation,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 28, no. 11, pp. 1768–1783, 2006. [DOI] [PubMed] [Google Scholar]
- [28].Ronneberger O, Fischer P, and Brox T, “U-net: Convolutional networks for biomedical image segmentation,” in International Conference on Medical image computing and computer-assisted intervention. Springer, 2015, pp. 234–241. [Google Scholar]
- [29].Holt CC, “Forecasting seasonals and trends by exponentially weighted moving averages,” International journal of forecasting, vol. 20, no. 1, pp. 5–10, 2004. [Google Scholar]
- [30].Johnson HJ, McCormick M, Ibáñez L, and Consortium TIS, The ITK Software Guide, 3rd ed., Kitware, Inc., 2013. [Google Scholar]
- [31].Schroeder W, Martin K, and Lorensen B, The Visualization Toolkit–An Object-Oriented Approach To 3D Graphics, 4th ed. Kitware, Inc., 2006. [Google Scholar]
- [32].R Core Team, R: A Language and Environment for Statistical Computing, R Foundation for Statistical Computing, Vienna, Austria, 2013. [Google Scholar]
- [33].Wickham H, ggplot2: Elegant Graphics for Data Analysis. Springer-Verlag New York, 2016. [Google Scholar]
- [34].Looney P, “OxNNet,” https://github.com/plooney/oxnnet, 2017, online; accessed January 13, 2021.
- [35].Abadi M, Agarwal A, Barham P, Brevdo E, Chen Z, Citro C et al. , “Tensorflow: large-scale machine learning on heterogeneous distributed systems. arxiv preprint (2016),” arXiv preprint arXiv:1603.04467, 2016. [Google Scholar]
- [36].Looney Pádraig. IEEE models. [Online]. Available: https://github.com/plooney/IEEE_models/
- [37].Shrout PE and Fleiss JL, “Intraclass correlations: uses in assessing rater reliability.” Psychological bulletin, vol. 86, no. 2, p. 420, 1979. [DOI] [PubMed] [Google Scholar]
- [38].Koo TK and Li MY, “A guideline of selecting and reporting intraclass correlation coefficients for reliability research,” Journal of Chiropractic Medicine, vol. 15, no. 2, pp. 155–163, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Gooding MJ et al. , “Comparative evaluation of autocontouring in clinical practice: A practical method using the turing test,” Medical Physics, vol. 45, no. 11, pp. 5105–5115, 2018. [DOI] [PubMed] [Google Scholar]
- [40].Stevenson G, “imageturingtest,” https://github.com/gordon-n-stevenson/imageturingtest, 2020, online; accessed January 13, 2021.
- [41].Looney P, “OxNNet,” https://github.com/plooney/oxnnet, 2017, online; accessed January 13, 2021.
- [42].O’Brien RT and Holmes SP, “Recent advances in ultrasound technology,” Clinical techniques in small animal practice, vol. 22, no. 3, pp. 93–103, 2007. [DOI] [PubMed] [Google Scholar]
- [43].Bengio Y, “Practical recommendations for gradient-based training of deep architectures,” in Neural networks: Tricks of the trade. Springer, 2012, pp. 437–478. [Google Scholar]
- [44].Stevenson GN, Collins SL, Welsh AW, Impey LW, and Noble JA, “A technique for the estimation of fractional moving blood volume by using three-dimensional power Doppler US,” Radiology, vol. 274, no. 1, pp. 230–237, 2014. [DOI] [PubMed] [Google Scholar]
- [45].Salavati N, Smies M, Ganzevoort W, Charles AK, Erwich JJ, Plösch T et al. , “The possible role of placental morphometry in the detection of fetal growth restriction,” Front Physiol, vol. 9, p. 1884, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]


