Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2021 Apr 16;21(8):3386–3392. doi: 10.1021/acs.nanolett.0c04816

Observation of Electric-Field-Induced Structural Dislocations in a Ferroelectric Oxide

Donald M Evans †,*, Didrik René Småbråten †, Theodor S Holstad †, Per Erik Vullum ‡, Aleksander B Mosberg §, Zewu Yan ∥,⊥, Edith Bourret ⊥, Antonius T J van Helvoort §, Sverre M Selbach †, Dennis Meier †,*
PMCID: PMC8155316  PMID: 33861614

Abstract

graphic file with name nl0c04816_0005.jpg

Dislocations are 1D topological defects with emergent electronic properties. Their low dimensionality and unique properties make them excellent candidates for innovative device concepts, ranging from dislocation-based neuromorphic memory to light emission from diodes. To date, dislocations are created in materials during synthesis via strain fields or flash sintering or retrospectively via deformation, for example, (nano)-indentation, limiting the technological possibilities. In this work, we demonstrate the creation of dislocations in the ferroelectric semiconductor Er(Mn,Ti)O3 with nanoscale spatial precision using electric fields. By combining high-resolution imaging techniques and density functional theory calculations, direct images of the dislocations are collected, and their impact on the local electric transport behavior is studied. Our approach enables local property control via dislocations without the need for external macroscopic strain fields, expanding the application opportunities into the realm of electric-field-driven phenomena.

Keywords: Nanotechnology, ferroelectric, semiconductors, functional oxide, dislocations, hexagonal manganites

Introduction

The presence of dislocations transcends condensed matter research and gives rise to a diverse range of emergent phenomena,1−6 ranging from geological effects7 to light emission from diodes.8 Classically, dislocations have often been regarded as imperfections in otherwise perfectly ordered crystals that are detrimental to electronic functionality.9,10 However, very recently, there has been growing interest in the properties of individual dislocations because they have different symmetries, and therefore different properties, from those of the surrounding material.11 Examples of emergent functional physical properties include locally enhanced conductivity,12 ferromagnetic order in antiferromagnets,13 redox-based resistive switching behavior,4 and trapping of light.14 Because of the low dimensionality of dislocations, which makes them highly stackable, and their unique properties, dislocations are now perceived as promising atomic-scale entities for next-generation device applications.10,11 Despite their exciting application potential, there are key limitations to the technological development of dislocations: The most critical is the control of their formation. Currently, dislocations are created by strain engineering, predominantly in one of two ways: either strain fields during growth, so that dislocations form to release the strain,15−17 or postgrowth via applied stress,18 for example, by nanoindentation.19−22 Although strain engineering is a highly efficient tool for creating dislocations, it is challenging to alter the properties of a material exactly via strain fields on the local scale. This is particularly problematic after a material has been implemented into a device architecture. Aside from strain, flash sintering has been applied to produce defects, including structural dislocations. This approach is particularly promising regarding the production of defect-rich samples, but it lacks the nanoscale control required for technological applications.23

Here we use electric fields to create partial dislocations in a ferroelectric material with nanoscale spatial precision, altering the structure and the electronic transport behavior where the field was applied. The hexagonal manganite Er(Mn,Ti)O3 is chosen as the model system (see the Materials and Methods for details),24,25 but similar behavior is expected in structurally equivalent systems such as hexagonal gallates, indates, and ferrites.

Results

Electric-Field Creation of Structural Defects

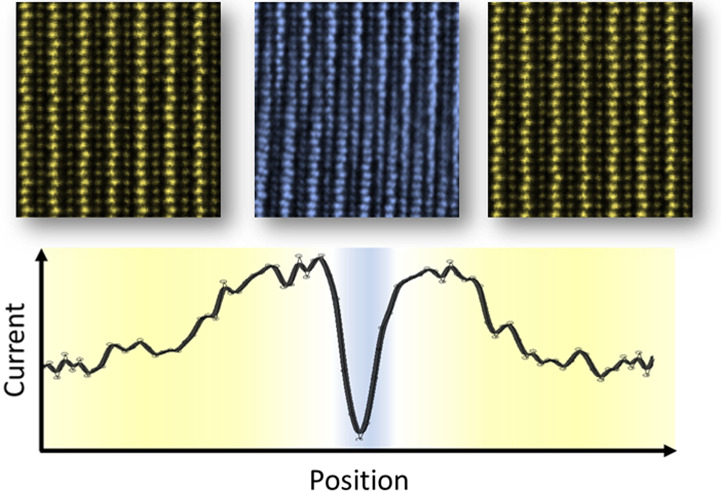
The ferroelectric domain structure of (110)-oriented Er(Mn,Ti)O3 is shown in the piezoresponse force microscopy (PFM) image in Figure 1a. The PFM data demonstrate that the two possible 180° polarization domains, +P and −P, form six-fold meeting points that are characteristic of hexagonal manganites.26,27 After mapping the domain structure of Er(Mn,Ti)O3, we apply −60 V (for 5 s) to the back electrode while keeping the probe tip static. Using a simple point-charge approximation (E = V/rtip), the biased static tip generates an electric field of ∼6 MV/cm.28,29 Subsequent conductive atomic force microscopy (cAFM) images (taken with +45 V) reveal a local modification of the transport behavior, manifesting as an ellipsoidal area of enhanced conductance (gold, in Figure 1b) with an insulating core: The core of reduced conductance occurs directly below the position of the AFM tip, that is, the position of the maximum electric field. A scanning electron microscopy (SEM) image of the same region as in Figure 1b is presented in Figure 1c, which demonstrates that the area of enhanced conductance in the cAFM scan correlates with bright contrast in SEM, associated with an increased yield of secondary electrons. A direct comparison of the SEM and cAFM images is given by the cross-sectional profiles in Figure 1d, showing a clear correlation. Figure 1 thus reveals that the electrically modified region displays two regimes: (i) a broader area with enhanced conductance due to anti-Frenkel defects, as reported in ref (30), and (ii) a highly localized area with reduced conductance. In contrast with the enhanced conductance in regime (i), the suppressed conductance in regime (ii) cannot be explained by the same defect formation process,30 indicating a different microscopic origin.

Figure 1.

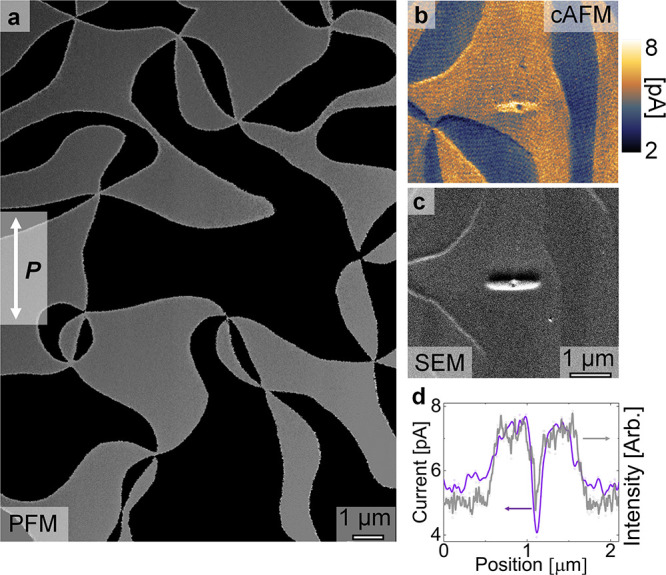
Figure 1

Open in a new tab

Electric-field control of local conductance in Er(Mn,Ti)O3. (a) Lateral dual AC resonance tracking (DART) mode PFM phase image of an in-plane ferroelectric domain pattern, taken with an amplitude of 5V and a frequency range of 784.5–794.5 kHz. Bright and dark contrasts represent ferroelectric 180° domains, revealing the characteristic domain pattern of hexagonal manganites. (b) cAFM scan recorded with +45 V on the same sample after the application of −60 V for 5 s to the back electrode with a stationary AFM tip; the position where the tip was placed coincides with the blue center of the gold elliptical feature seen in the cAFM map. Bright (gold) colors correspond to areas of higher conductance, and dark (blue) colors correspond to areas of lower conductance. (c) SEM image of the feature in panel b demonstrating conductivity-sensitive SEM contrast. (d) Cross-sectional graph, correlating SEM contrast (grey) with cAFM contrast (purple). The images in panels b and c represent a larger view of the same area discussed in ref (30).

Atomic-Scale Imaging of Defects

To investigate the underlying microscopic effect, we study the atomic structure in the electrically modified region using transmission electron microscopy (TEM) techniques on a focused ion beam (FIB) prepared lamella. (See the Materials and Methods.) A bright-field overview image of a lamella, prepared to cross-section the electrically modified region in Figure 1, is given in Figure 2a. The data show that the crystal structure has changed in a limited region around the position where the cAFM tip was placed (indicated schematically). This modified region has a lateral extension of ∼160 nm and protrudes ∼35 nm into the depth of the sample, whereas the rest of the crystal structure has remained in the as-grown state. To discern the differences between the modified region and the as-grown state,26,30,31 high-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM) images of the two regions are presented in Figure 2b,c, respectively. In Figure 2b,c, the bright dots correspond to Er and Mn atomic columns; the heavier Er atoms give brighter dots than the lighter Mn atoms. The HAADF-STEM of Figure 2c shows that the Er layers are disrupted in several places and appear to be displaced, seemingly merging with the Mn layers in the projected image. This disruption of the lattice only occurs directly underneath the cAFM tip, and no such alterations of the lattice are seen in the wider crystal (Figure 2a). To visualize associated local changes in the lattice periodicity, Fourier filtering is applied, as presented in Figure 2d. This treatment reveals discontinuities in the lattice periodicity and the presence of edge dislocations, marked by the green and red circles in Figure 2d. An enlarged section with a higher resolution of the feature in the red box in Figure 2c is shown in Figure 2e. On the left side of the dislocation in Figure 2e, the HAADF-STEM image shows the normal sequence of alternating Er and Mn layers, whereas the right side of the image shows Er columns that continuously merge into Mn columns and vice versa. We note that there is no clear interface where Er columns swap with Mn columns, as the interface is inclined to the [001] viewing direction. The general possibility to stabilize such stacking faults is not surprising,32 as their growth-induced formation has been reported in hexagonal manganites and ferrites.33−35 In contrast with previous work, however, the stacking faults in our system are generated postgrowth and with nanoscale spatial precision by the application of an electric field. We note that the sample used in this work has been cut from the same single crystal studied in, for example, refs (24 and 30) and discussed in, for example, refs (36 and 37). During the previous extensive high-resolution TEM investigations, no partial dislocations were observed in the ErMnO3 crystal lattice, corroborating that such defects are not intrinsic to the lattice or generated by the applied preparation methods.

Figure 2.

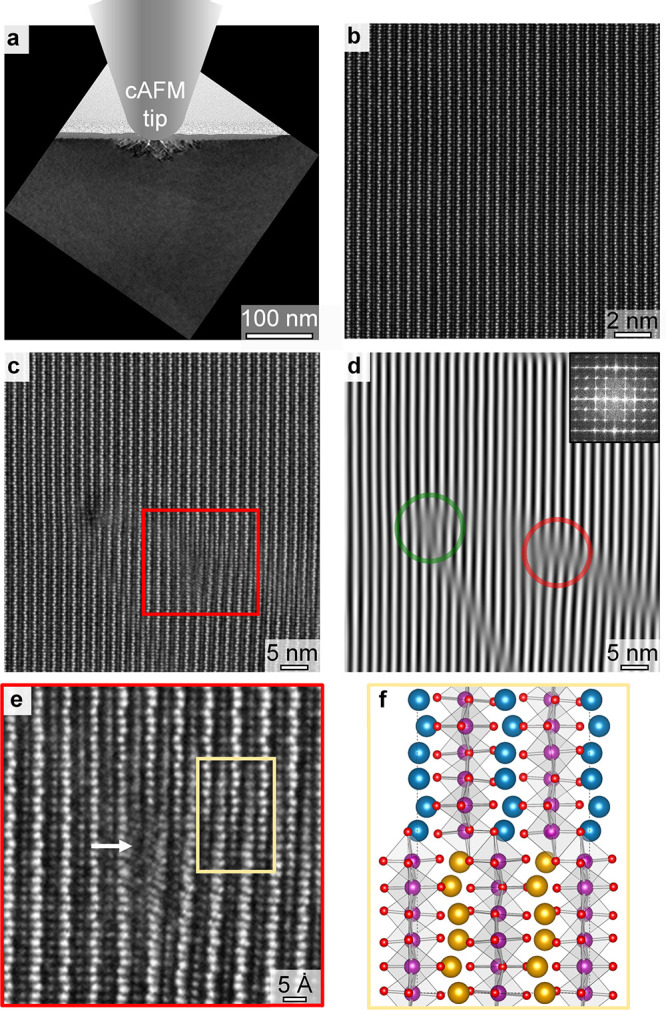
Figure 2

Open in a new tab

Atomic-scale structure of electrically induced dislocations and stacking faults. (a) Bright-field TEM image and schematic of the cAFM tip, illustrating that the perturbed crystal structure is restricted to the area beneath the cAFM tip. (b) HAADF-STEM image viewed down the [1̅00] direction, showing the as-grown state. (c) HAADF-STEM image viewed down the [1̅00] direction, showing the region beneath the position of the AFM tip after the application of the electric field. The periodic crystal structure is interrupted by line features extending in directions close to the ⟨011⟩ directions. The bright and gray dots are Er and Mn atomic columns, respectively. (d) Inverse fast Fourier transformation (FFT) obtained by selecting only the (002) maxima of an FFT of panel b; see the insert. The image shows areas with the same periodicity of the Er lattice, allowing easier identification of lattice defects. Two edge dislocations are highlighted by red and green circles. (e) Representative HAADF-STEM image taken across the crystallographic features, corresponding to the area marked by the red box in panel c. (f) Fully relaxed DFT supercell, modeling the dislocated structure by unit cells dislocated by c/4 and a/3 with respect to each other. Large gold and blue spheres represent Er atoms on either side of the stacking fault; Mn and O atoms are sketched in purple and red, respectively.

To evaluate the stability of the defect structure resolved in Figure 2e, we model the dislocated lattice using density functional theory (DFT), as illustrated in Figure 2f. To look for stable states, we consider the isostructural system YMnO3 (refs (31 and 38)), where multiple 240-atom 1 × 8 × 1 supercells were initialized in the high-symmetry P63/mmc phase with different dislocation configurations and relaxed into the polar state P63cm until the forces on all of the atoms were <0.01 eV Å–1. The analysis of YMnO3 instead of ErMnO3 is standard practice, as their structural and chemical properties are very similar (see Table S1 and Figure S1), but the absence of f electrons significantly reduces the computational cost.31,38,39 The DFT calculations show that a stable dislocated structure exists when the lattice is displaced by c/4 and a/3 (or one of the six symmetry equivalent directions, perpendicular to the unique axis), as shown in Figure 2f. The calculated dislocation configuration is in excellent agreement with our HAADF-STEM data (Figure S2 shows the dislocated structure viewed down the [110] direction, which is symmetry equivalent to [1̅00]), leading us to the conclusion that the merging features in Figure 2e correspond to a stacking fault between two partial dislocations.

On the basis of the DFT calculations, we can predict the expected atomic pattern when we image along other crystallographic directions, allowing us to conduct an independent test experiment. The calculated crystal structure viewed along different directions, with and without the dislocated structure, is presented in Figure S3, including the superposition of the dislocated structure and the unperturbed Er(Mn,Ti)O3 structure with space group symmetry P63cm.40 This superposition accounts for the depth convolution present within TEM lamellas with finite thickness. A representative HAADF-STEM image recorded along the [001] direction of an Er(Mn,Ti)O3 lamella with electrically modified regions (analogous to Figure 1) is presented in Figure 3a. As in Figure 2, the modification of the lattice only occurs in the area exposed to the high electric field. The HAADF-STEM image shows the Er atoms as bright dots, reflecting the characteristic pattern associated with the P63cm space group symmetry of the crystal sketched in Figure S3. The latter is confirmed by the high-resolution HAADF-STEM image in Figure 3b, taken from the area represented in red in Figure 3a. On closer inspection, however, local deviations from the ideal structure are observed, as shown by the HAADF-STEM image in Figure 3c (obtained in the area represented in green in Figure 3a). Here the Er atoms are found to form a close-packed honeycomb-like structure, as illustrated by the schematic overlay, in accordance with the DFT-predicted structure. (See Figure S3; blue and gold dots in the overlay represent Er atoms from volumes on either side of the stacking fault.)

Figure 3.

Figure 3

Open in a new tab

Atomic defect structure viewed along the [001] axis. (a) HAADF-STEM image of a region with electric-field induced defects, written with the same parameters as used in Figures 1 and 2. Bright dots correspond to Er atom columns. (b) HAADF-STEM image of the area represented by the red box of panel a, showing the expected Er cation lattice for a hexagonal crystal when viewed along the [001] direction. The gold dots correspond to a DFT simulation of the structure, looking down the [001] axis. Mn columns can be seen as weak dots in between the more pronounced dots from the Er columns. (c) HAADF-STEM image corresponding to the area represented by the green box in panel a, showing the Er pattern that deviates from the unperturbed crystallographic structure seen in panel b. Gold and blue dots represent the bulk and shifted Er atom columns when the stable dislocation of Figure 2 is viewed down the [001] axis. The overlay shows that the dislocated structure reproduces the pattern resolved by HAADF-STEM.

Calculated Defect Properties

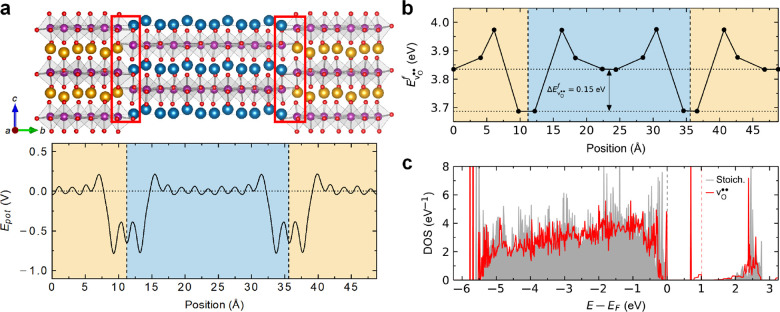
After establishing the presence of the structural defects in the region of reduced conductance, we calculate the associated formation energy. Note that because of the thermal stability of the structural ground state and the ferroelectric polarization,41−43 finite temperature effects would be subtle at room temperature and would not change the results qualitatively, and hence they are not considered. For the partially dislocated structure in Figure 2f, we find a formation energy of ∼755 mJ m–2, which is only about seven times higher than for the charged domain walls, which naturally occur in the hexagonal manganites.44 The DFT calculations further show that the dislocated structure significantly alters the electrostatic potential. To quantify this, we calculate the planar average across the supercell in Figure 4a, which shows a decrease in the potential energy of ∼0.75 eV (∼1/2Eg) compared with the bulk, corresponding to bound negative charges associated with the stacking fault. However, in contrast with the negatively charged tail-to-tail domain walls in hexagonal manganites,44 neither calculated Bader charges nor Mn magnetic moments reveal any inherent electronic charge transfer between the dislocated structure and the bulk. This is because the magnitude of the band bending (visualized in Figure S4) does not fulfill the Zener-like breakdown criterion,44 meaning that our defects are not compensated by electronic charge carriers.

Figure 4.

Figure 4

Open in a new tab

Calculation of the electronic defect structure. (a) Dislocated structure (upper part) and electrostatic potential (lower part) calculated by density functional theory (DFT). The calculated electrostatic potential is scaled relative to the potential away from the dislocated interfaces, which are indicated by the red boxes. The significant reduction in the potential (ca. 1/2Eg at the interface) corresponds to bound negative charges, which are likely to attract positively charged vO••. (b) vO formation energy with increasing distance from the interface(s), showing a significant energy preference, 0.15 eV, for forming vO•• at the interface(s) compared with the bulk. (c) Calculated local DOS at the partial dislocations in a stoichiometric supercell (gray) and with an accumulation of oxygen vacancies (red). The corresponding Fermi levels for the pristine cell and the vO defect cell are marked by dashed gray and red lines in panel c, respectively. The DOSs are aligned to core states.

However, the bound negative charges associated with the dislocated structure in Figure 4a can attract mobile ionic defects with a relative positive charge, such as oxygen vacancies (vO••). In fact, we find that the vO formation energy is reduced by ∼0.15 eV compared with the bulk (Figure 4b), demonstrating a significant defect segregation enthalpy. To contextualize the strength of this driving force, it is five times higher than the attraction of oxygen interstitials (Oi″) to neutral domain walls in the hexagonal manganites (∼0.03 eV), which are experimentally well documented to have enhanced conductance.45 As such, the five times higher driving force is expected to pin vO to the stacking faults and vice versa. To illustrate the corresponding changes in the electronic state, we calculate the density of states (DOS) in YMnO3 with and without vO•• at the dislocated structure (Figure 4c). The DOSs are qualitatively similar, but the vO DOS has a strongly localized state within the band gap and a higher Fermi energy. This increase in Fermi energy at the interface gives a variation in electronic charge carrier concentration and—in a p-type system with holes as the majority carriers—38 is expected to cause a diffusion current, leading to a local reduction in the number of available electronic charge carriers. As a consequence, the dislocation-induced structural changes enhance the resistivity relative to the bulk, which is consistent with the lower conductance observed in the cAFM data in Figure 1b.

Discussion

Our experimental observations and DFT results reveal two important criteria for the formation of dislocations in ferroelectric oxides under locally applied voltage, promoting their injection postgrowth and with nanoscale spatial precision: (i) The cation has access to a new (meta-)stable cation configuration and (ii) the applied electric field generates enough energy to overcome the barrier toward the new (meta-)stable state without leading to amorphization from leakage currents. A possible driving force for the spontaneous dislocation of the lattice observed in Er(Mn,Ti)O3 is electric-field gradients that act on the uniaxial polarization (F = P·∇E). At present, however, no microscopic model exists that can capture the emergence of dislocations in electric fields, and theoretical in-depth studies are highly desirable.

Conclusions

Our work demonstrates that electric fields can be used to create partial dislocations in a complex oxide to engineer the local structure and electronic response, bypassing the necessity of applied strain fields. The ability to induce such changes postgrowth, on demand, and with nanometer spatial precision provides a conceptually different approach to local property engineering, as exemplified by the enhanced resistance in hexagonal manganites. Our approach is expected to be generally applicable to dielectric materials close to a structural instability, where a sufficiently large electric field can build up. Because the electric-field-driven dislocation injection is applicable after a material has been synthesized or integrated into a device, it presents an opportunity for engineering functional materials via low-dimensional structural defects.

Materials and Methods

Samples

Single crystals of Er(Mn1–x,Tix)O3+δ with x = 0.002 were grown using the pressurized floating zone method (ref (25)). From this, we prepared samples with the ferroelectric polarization parallel to the sample surface (in-plane P). The crystals were orientated by Laue diffraction, cut to have thicknesses of ∼0.5 mm, and electromechanically polished to give a root-mean-square (RMS) surface roughness of ∼1 nm.

Focused Ion Beam

TEM specimen preparation was carried out using a Thermo Fisher Scientific Helios G4 UX DualBeam FIB. Lamellas were prepared “flipped” with in situ lift-out and backside milling. Final polishing was carried out at 2 kV. High-resolution Pt markers were used in conjunction with C protection layers to ensure that the final lamellas were centered on the region with suppressed conductance.

Transmission Electron Microscopy

TEM analysis was performed using a double-Cs aberration-corrected cold field emission gun JEOL ARM 200FC apparatus operated at 200 kV. STEM imaging was performed with a 27 mrad semiconvergence angle.

Atomic Force Microscopy

The lateral DART–PFM was performed on a Cypher ES Environmental AFM using an Oxford Instruments Asylec-01-R2 Pt/Ir tip. The remaining scanning probe microscopy (SPM) measurements were performed on an NT-MDT NTEGRA SPM using a TipsNano DCP20 tip. The voltage was applied to the sample back-electrode with the tip connected to ground.

Density Functional Theory

Calculations on isostructural YMnO3 (isostructural and electronically similar to ErMnO3 but without complicating f electrons) were carried out using the projector augmented wave (PAW) method, as implemented in the Vienna Ab initio Simulation Package (VASP),46−48 using the Y_sv Mn_sv and standard O pseudopotentials supplied with VASP. PBEsol+U49,50 with U = 5 eV on Mn 3d states, combined with a collinear frustrated antiferromagnetic order on the Mn sublattice, was used to reproduce the experimental lattice parameters43 and the electronic band gap.51 The energy cutoff of the plane-waves was set to 550 eV. The Brillouin zone was sampled with a Γ-centered 4 × 1 × 2 k-point grid for geometry optimization and a 6 × 1 × 3 grid for DOS and electrostatic potential calculations. 240-atom 1 × 8 × 1 supercells were initialized in the high-symmetry P63/mmc phase with different dislocation configurations and relaxed until the forces on all atoms were <0.01 eV Å–1. Ferroelectric polarizations were calculated from a simple point-charge model using formal charges.52 The dislocation formation energy was calculated as

graphic file with name nl0c04816_m001.jpg

where Edisf and Eref are the energies of a dislocation supercell and a monodomain supercell, respectively, and A is the cross-sectional area.

Acknowledgments

We thank Knut Marthinsen and Jan Schultheiß for helpful and insightful discussions about dislocations.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.nanolett.0c04816.

  • Comparison of the calculated electronic properties of YMnO3 and ErMnO3, DFT simulations of how the dislocations would look in different viewing directions and the depth effects, and calculations of the changes in electronic orbitals at the dislocations. (PDF)

Author Present Address

# D.M.E.: Center for Electronic Correlations and Magnetism and Institute of Materials Resource Management, University of Augsburg, D-86159 Augsburg, Germany.

Author Present Address

▽ D.R.S.: Department of Chemistry, Biochemistry and Pharmaceutical Sciences, University of Bern, Bern 3012, Switzerland.

Author Contributions

D.M.E. coordinated the project and lead the scanning probe microscopy work together with T.S.H., both supervised by D.M. A.B.M. was supervised by A.T.J.v.H. and conducted the FIB and SEM work. P.E.V. and A.B.M. conducted the TEM work. D.R.S. performed the DFT calculations, supervised by S.M.S. Z.Y. and E.B. provided the materials. D.M.E. and D.R.S. analyzed and interpreted the data, under the supervision of D.M. and S.M.S., respectively. D.M.E. and D.M. wrote the manuscript. All authors discussed the results and contributed to the final version of the manuscript.

D.R.S. and S.M.S. were supported by the Research Council of Norway (FRINATEK project number 231430/F20 and 275139/F20) and acknowledge UNINETT Sigma2 (project no. NN9264K) for providing the computational resources. A.B.M. was supported by NTNU’s Enabling technologies: Nanotechnology. The Research Council of Norway is acknowledged for the support to the Norwegian Micro- and Nano-Fabrication Facility, NorFab, project number 245963/F50 and the Norwegian Centre for Transmission Electron Microscopy, NORTEM, grant no. 197405. Z.Y. and E.B. were supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division under contract no. DE-AC02–05-CH11231 within the Quantum Materials program-KC2202. D.M. thanks NTNU for support through the Onsager Fellowship Programme and NTNU Stjerneprogrammet.

The authors declare no competing financial interest.

Supplementary Material

nl0c04816_si_001.pdf (920.5KB, pdf)

References

  1. Singer A.; Zhang M.; Hy S.; Cela D.; Fang C.; Wynn T. A.; Qiu B.; Xia Y.; Liu Z.; Ulvestad A.; Hua N.; Wingert J.; Liu H.; Sprung M.; Zozulya A. V.; Maxey E.; Harder R.; Meng Y. S.; Shpyrko O. G. Nucleation of Dislocations and Their Dynamics in Layered Oxide Cathode Materials during Battery Charging. Nat. Energy 2018, 3 (8), 641–647. 10.1038/s41560-018-0184-2. [DOI] [Google Scholar]
  2. Choi S.; Tan S. H.; Li Z.; Kim Y.; Choi C.; Chen P. Y.; Yeon H.; Yu S.; Kim J. SiGe Epitaxial Memory for Neuromorphic Computing with Reproducible High Performance Based on Engineered Dislocations. Nat. Mater. 2018, 17 (4), 335–340. 10.1038/s41563-017-0001-5. [DOI] [PubMed] [Google Scholar]
  3. Sun B.; Haunschild G.; Polanco C.; Ju J.; Lindsay L.; Koblmüller G.; Koh Y. K. Dislocation-Induced Thermal Transport Anisotropy in Single-Crystal Group-III Nitride Films. Nat. Mater. 2019, 18 (2), 136–140. 10.1038/s41563-018-0250-y. [DOI] [PubMed] [Google Scholar]
  4. Szot K.; Speier W.; Bihlmayer G.; Waser R. Switching the Electrical Resistance of Individual Dislocations in Single-Crystalline SrTiO3. Nat. Mater. 2006, 5 (4), 312–320. 10.1038/nmat1614. [DOI] [PubMed] [Google Scholar]
  5. Kuzmina M.; Herbig M.; Ponge D.; Sandlöbes S.; Raabe D. Linear Complexions: Confined Chemical and Structural States at Dislocations. Science 2015, 349 (6252), 1080–1083. 10.1126/science.aab2633. [DOI] [PubMed] [Google Scholar]
  6. Chen C. C.; Zhu C.; White E. R.; Chiu C. Y.; Scott M. C.; Regan B. C.; Marks L. D.; Huang Y.; Miao J. Three-Dimensional Imaging of Dislocations in a Nanoparticle at Atomic Resolution. Nature 2013, 496 (7443), 74–77. 10.1038/nature12009. [DOI] [PubMed] [Google Scholar]
  7. Kohlstedt D. L.; Goetze C.; Durham W. B.; Sande J. V. New Technique for Decorating Dislocations in Olivine. Science 1976, 191 (4231), 1045–1046. 10.1126/science.191.4231.1045. [DOI] [PubMed] [Google Scholar]
  8. Nakamura S. The Roles of Structural Imperfections in InGaN-Based Blue Light- Emitting Diodes and Laser Diodes. Science 1998, 281 (5379), 956–961. 10.1126/science.281.5379.956. [DOI] [PubMed] [Google Scholar]
  9. Dawber M.; Rabe K. M.; Scott J. F. Physics of Thin-Film Ferroelectric Oxides. Rev. Mod. Phys. 2005, 77 (4), 1083–1130. 10.1103/RevModPhys.77.1083. [DOI] [Google Scholar]
  10. Ramesh R. Defect Engineering Using Crystal Symmetry. Proc. Natl. Acad. Sci. U. S. A. 2018, 115 (38), 9344–9346. 10.1073/pnas.1812554115. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Sandiumenge F. A Multiscale Perspective on Misfit Dislocations in Oxide Films. Front. Mater. 2019, 6, 13. 10.3389/fmats.2019.00013. [DOI] [Google Scholar]
  12. Nakamura A.; Matsunaga K.; Tohma J.; Yamamoto T.; Ikuhara Y. Conducting Nanowires in Insulating Ceramics. Nat. Mater. 2003, 2 (7), 453–456. 10.1038/nmat920. [DOI] [PubMed] [Google Scholar]
  13. Sugiyama I.; Shibata N.; Wang Z.; Kobayashi S.; Yamamoto T.; Ikuhara Y. Ferromagnetic Dislocations in Antiferromagnetic NiO. Nat. Nanotechnol. 2013, 8 (4), 266–270. 10.1038/nnano.2013.45. [DOI] [PubMed] [Google Scholar]
  14. Li F. F.; Wang H. X.; Xiong Z.; Lou Q.; Chen P.; Wu R. X.; Poo Y.; Jiang J. H.; John S. Topological Light-Trapping on a Dislocation. Nat. Commun. 2018, 9 (1), 2462. 10.1038/s41467-018-04861-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Tagantsev A. K.; Cross L. E.; Fousek J.. Domains in Ferroic Crystals and Thin Films; Springer-Verlag: New York, 2010. [Google Scholar]
  16. Zou L.; Yang C.; Lei Y.; Zakharov D.; Wiezorek J. M. K.; Su D.; Yin Q.; Li J.; Liu Z.; Stach E. A.; Yang J. C.; Qi L.; Wang G.; Zhou G. Dislocation Nucleation Facilitated by Atomic Segregation. Nat. Mater. 2018, 17 (1), 56–62. 10.1038/nmat5034. [DOI] [PubMed] [Google Scholar]
  17. Putnis A.An Introduction to Mineral Sciences; Cambridge University Press: Cambridge, U.K., 1992. [Google Scholar]
  18. Zhou X.; Feng Z.; Zhu L.; Xu J.; Miyagi L.; Dong H.; Sheng H.; Wang Y.; Li Q.; Ma Y.; Zhang H.; Yan J.; Tamura N.; Kunz M.; Lutker K.; Huang T.; Hughes D. A.; Huang X.; Chen B. High-Pressure Strengthening in Ultrafine-Grained Metals. Nature 2020, 579 (7797), 67–72. 10.1038/s41586-020-2036-z. [DOI] [PubMed] [Google Scholar]
  19. Rösler J.; Harders H.; Bäker M.. Mechanical Behaviour of Engineering Materials: Metals, Ceramics, Polymers, and Composites; Springer Berlin Heidelberg, 2007. [Google Scholar]
  20. Schuh C. A.; Mason J. K.; Lund A. C. Quantitative Insight into Dislocation Nucleation from High-Temperature Nanoindentation Experiments. Nat. Mater. 2005, 4 (8), 617–621. 10.1038/nmat1429. [DOI] [PubMed] [Google Scholar]
  21. Miller R. E.; Rodney D. On the Nonlocal Nature of Dislocation Nucleation during Nanoindentation. J. Mech. Phys. Solids 2008, 56 (4), 1203–1223. 10.1016/j.jmps.2007.10.005. [DOI] [Google Scholar]
  22. Dehm G.; Jaya B. N.; Raghavan R.; Kirchlechner C. Overview on Micro- and Nanomechanical Testing: New Insights in Interface Plasticity and Fracture at Small Length Scales. Acta Mater. 2018, 142, 248–282. 10.1016/j.actamat.2017.06.019. [DOI] [Google Scholar]
  23. Yu M.; Grasso S.; Mckinnon R.; Saunders T.; Reece M. J. Review of Flash Sintering: Materials, Mechanisms and Modelling. Adv. Appl. Ceram. 2017, 116 (1), 24–60. 10.1080/17436753.2016.1251051. [DOI] [Google Scholar]
  24. Holstad T. S.; Evans D. M.; Ruff A.; Småbråten D. R.; Schaab J.; Tzschaschel C.; Yan Z.; Bourret E.; Selbach S. M.; Krohns S.; Meier D. Electronic Bulk and Domain Wall Properties in B-Site Doped Hexagonal ErMnO3. Phys. Rev. B 2018, 97 (8), 85143. 10.1103/PhysRevB.97.085143. [DOI] [Google Scholar]
  25. Yan Z.; Meier D.; Schaab J.; Ramesh R.; Samulon E.; Bourret E. Growth of High-Quality Hexagonal ErMnO3 Single Crystals by the Pressurized Floating-Zone Method. J. Cryst. Growth 2015, 409, 75–79. 10.1016/j.jcrysgro.2014.10.006. [DOI] [Google Scholar]
  26. Holtz M. E.; Shapovalov K.; Mundy J. A.; Chang C. S.; Yan Z.; Bourret E.; Muller D. A.; Meier D.; Cano A. Topological Defects in Hexagonal Manganites: Inner Structure and Emergent Electrostatics. Nano Lett. 2017, 17 (10), 5883–5890. 10.1021/acs.nanolett.7b01288. [DOI] [PubMed] [Google Scholar]
  27. Griffin S. M.; Lilienblum M.; Delaney K. T.; Kumagai Y.; Fiebig M.; Spaldin N. A. Scaling Behavior and beyond Equilibrium in the Hexagonal Manganites. Phys. Rev. X 2012, 2 (4), 041022. 10.1103/PhysRevX.2.041022. [DOI] [Google Scholar]
  28. Mele E. J. Screening of a Point Charge by an Anisotropic Medium: Anamorphoses in the Method of Images. Am. J. Phys. 2001, 69 (5), 557–562. 10.1119/1.1341252. [DOI] [Google Scholar]
  29. Wang B.; Woo C. H. Atomic Force Microscopy-Induced Electric Field in Ferroelectric Thin Films. J. Appl. Phys. 2003, 94 (6), 4053–4059. 10.1063/1.1603345. [DOI] [Google Scholar]
  30. Evans D. M.; Holstad T. S.; Mosberg A. B.; Småbråten D.; Vullum P. E.; Dadlani A. L.; Shapovalov K.; Yan Z.; Bourret E.; Gao D.; Akola J.; Torgersen J.; van Helvoort A. T. J.; Selbach S. M.; Meier D. Conductivity Control via Minimally Invasive Anti-Frenkel Defects in a Functional Oxide. Nat. Mater. 2020, 19, 1195–2000. 10.1038/s41563-020-0765-x. [DOI] [PubMed] [Google Scholar]
  31. Mundy J. A.; Schaab J.; Kumagai Y.; Cano A.; Stengel M.; Krug I. P.; Gottlob D. M.; Doǧanay H.; Holtz M. E.; Held R.; Yan Z.; Bourret E.; Schneider C. M.; Schlom D. G.; Muller D. A.; Ramesh R.; Spaldin N. A.; Meier D. Functional Electronic Inversion Layers at Ferroelectric Domain Walls. Nat. Mater. 2017, 16 (6), 622–627. 10.1038/nmat4878. [DOI] [PubMed] [Google Scholar]
  32. Hull D.; Bacon D. J. In Introduction to Dislocations, 5th ed.; Butterworth-Heinemann: Oxford, U.K., 2011; pp 137–155. [Google Scholar]
  33. Baghizadeh A.; Vieira J. M.; Stroppa D. G.; Willinger M. G.; Amaral V. S. Nanoscale Analysis of Dispersive Ferroelectric Domains in Bulk of Hexagonal Multiferroic Ceramics. Mater. Charact. 2018, 145, 347–352. 10.1016/j.matchar.2018.08.042. [DOI] [Google Scholar]
  34. Barrozo P.; Småbråten D. R.; Tang Y.; Prasad B.; Saremi S.; Ozgur R.; Thakare V.; Steinhardt R. A.; Holtz M. E.; Stoica V. A.; Martin L. W.; Schlom D. G.; Selbach S. M.; Ramesh R. Defect-Enhanced Polarization Switching in the Improper Ferroelectric LuFeO3. Adv. Mater. 2020, 32, 2000508. 10.1002/adma.202000508. [DOI] [PubMed] [Google Scholar]
  35. Graboy I. E.; Bosak A. A.; Gorbenko O. Y.; Kaul A. R.; Dubourdieu C.; Sénateur J. P.; Svetchnikov V. L.; Zandbergen H. W. HREM Study of Epitaxially Stabilized Hexagonal Rare Earth Manganites. Chem. Mater. 2003, 15 (13), 2632–2637. 10.1021/cm021315b. [DOI] [Google Scholar]
  36. Evans D. M.; Garcia V.; Meier D.; Bibes M. Domains and Domain Walls in Multiferroics. Phys. Sci. Rev. 2020, 5, 20190067. 10.1515/psr-2019-0067. [DOI] [Google Scholar]
  37. Meier D. Functional Domain Walls in Multiferroics. J. Phys.: Condens. Matter 2015, 27 (46), 463003. 10.1088/0953-8984/27/46/463003. [DOI] [PubMed] [Google Scholar]
  38. Skjærvø S. H.; Wefring E. T.; Nesdal S. K.; Gaukås N. H.; Olsen G. H.; Glaum J.; Tybell T.; Selbach S. M. Interstitial Oxygen as a Source of P-Type Conductivity in Hexagonal Manganites. Nat. Commun. 2016, 7, 13745. 10.1038/ncomms13745. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Småbråten D. R.; Holstad T. S.; Evans D. M.; Yan Z.; Bourret E.; Meier D.; Selbach S. M. Domain Wall Mobility and Roughening in Doped Ferroelectric Hexagonal Manganites. Phys. Rev. Res. 2020, 2 (3), 33159. 10.1103/PhysRevResearch.2.033159. [DOI] [Google Scholar]
  40. Yakel H. L. Jr.; Koehler W. C.; Bertaut E. F.; Forrat E. F. On the Crystal Structure of the Manganese(III) Trioxides of the Heavy Lanthanides and Yttrium. Acta Crystallogr. 1963, 16 (10), 957–962. 10.1107/S0365110X63002589. [DOI] [Google Scholar]
  41. Gibbs A. S.; Knight K. S.; Lightfoot P. High-Temperature Phase Transitions of Hexagonal YMnO3. Phys. Rev. B 2011, 83 (9), 94111. 10.1103/PhysRevB.83.094111. [DOI] [Google Scholar]
  42. Lilienblum M.; Lottermoser T.; Manz S.; Selbach S. M.; Cano A.; Fiebig M. Ferroelectricity in the Multiferroic Hexagonal Manganites. Nat. Phys. 2015, 11 (12), 1070–1073. 10.1038/nphys3468. [DOI] [Google Scholar]
  43. Skjærvø S. H.; Meier Q. N.; Feygenson M.; Spaldin N. A.; Billinge S. J. L.; Bozin E. S.; Selbach S. M. Unconventional Continuous Structural Disorder at the Order-Disorder Phase Transition in the Hexagonal Manganites. Phys. Rev. X 2019, 9 (3), 31001. 10.1103/PhysRevX.9.031001. [DOI] [Google Scholar]
  44. Småbråten D. R.; Meier Q. N.; Skjærvø S. H.; Inzani K.; Meier D.; Selbach S. M. Charged Domain Walls in Improper Ferroelectric Hexagonal Manganites and Gallates. Phys. Rev. Mater. 2018, 2 (11), 114405. 10.1103/PhysRevMaterials.2.114405. [DOI] [Google Scholar]
  45. Schaab J.; Skjærvø S. H.; Krohns S.; Dai X.; Holtz M. E.; Cano A.; Lilienblum M.; Yan Z.; Bourret E.; Muller D. A.; Fiebig M.; Selbach S. M.; Meier D. Electrical Half-Wave Rectification at Ferroelectric Domain Walls. Nat. Nanotechnol. 2018, 13 (11), 1028–1034. 10.1038/s41565-018-0253-5. [DOI] [PubMed] [Google Scholar]
  46. Blöchl P. E. Projector Augmented-Wave Method. Phys. Rev. B 1994, 50 (24), 17953–17979. 10.1103/PhysRevB.50.17953. [DOI] [PubMed] [Google Scholar]
  47. Kresse G.; Furthmüller J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 1996, 54 (16), 11169–11186. 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
  48. Kresse G.; Joubert D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 1999, 59 (3), 1758–1775. 10.1103/PhysRevB.59.1758. [DOI] [Google Scholar]
  49. Perdew J. P.; Ruzsinszky A.; Csonka G. I.; Vydrov O. A.; Scuseria G. E.; Constantin L. A.; Zhou X.; Burke K. Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys. Rev. Lett. 2008, 100 (13), 136406. 10.1103/PhysRevLett.100.136406. [DOI] [PubMed] [Google Scholar]
  50. Dudarev S. L.; Botton G. A.; Savrasov S. Y.; Humphreys C. J.; Sutton A. P. Electron-Energy-Loss Spectra and the Structural Stability of Nickel Oxide: An LSDA+U Study. Phys. Rev. B 1998, 57 (3), 1505–1509. 10.1103/PhysRevB.57.1505. [DOI] [Google Scholar]
  51. Degenhardt C.; Fiebig M.; Fröhlich D.; Lottermoser T.; Pisarev R. V. V. Nonlinear Optical Spectroscopy of Electronic Transitions in Hexagonal Manganites. Appl. Phys. B: Lasers Opt. 2001, 73 (2), 139–144. 10.1007/s003400100617. [DOI] [Google Scholar]
  52. Kumagai Y.; Spaldin N. A. Structural Domain Walls in Polar Hexagonal Manganites. Nat. Commun. 2013, 4, 1540. 10.1038/ncomms2545. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nl0c04816_si_001.pdf (920.5KB, pdf)

Articles from Nano Letters are provided here courtesy of American Chemical Society

RESOURCES