Skip to main content
PMC home page
Chemical Science logoLink to Chemical Science
. 2020 Jan 28;11(9):2335–2341. doi: 10.1039/c9sc05116c

Free energy of proton transfer at the water–TiO2 interface from ab initio deep potential molecular dynamics†

Marcos F Calegari Andrade 1, Hsin-Yu Ko 1, Linfeng Zhang 2, Roberto Car 1, Annabella Selloni 1,✉
PMCID: PMC8157430  PMID: 34084393

Abstract

TiO2 is a widely used photocatalyst in science and technology and its interface with water is important in fields ranging from geochemistry to biomedicine. Yet, it is still unclear whether water adsorbs in molecular or dissociated form on TiO2 even for the case of well-defined crystalline surfaces. To address this issue, we simulated the TiO2–water interface using molecular dynamics with an ab initio-based deep neural network potential. Our simulations show a dynamical equilibrium of molecular and dissociative adsorption of water on TiO2. Water dissociates through a solvent-assisted concerted proton transfer to form a pair of short-lived hydroxyl groups on the TiO2 surface. Molecular adsorption of water is ΔF = 8.0 ± 0.9 kJ mol−1 lower in free energy than the dissociative adsorption, giving rise to a 5.6 ± 0.5% equilibrium water dissociation fraction at room temperature. Due to the relevance of surface hydroxyl groups to the surface chemistry of TiO2, our model might be key to understanding phenomena ranging from surface functionalization to photocatalytic mechanisms.

TiO2 is a widely used photocatalyst in science and technology and its interface with water is important in fields ranging from geochemistry to biomedicine.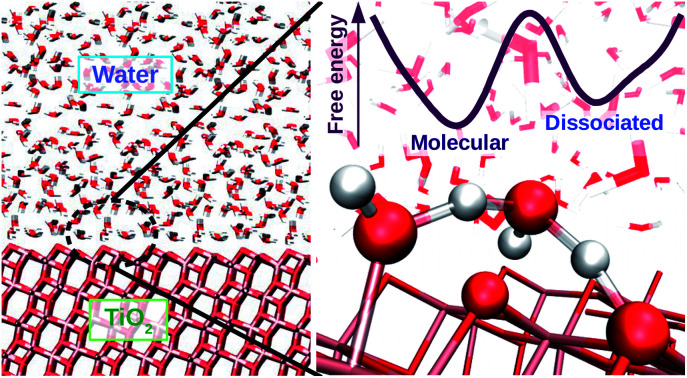graphic file with name c9sc05116c-ga.jpg

1. Introduction

The photocatalytic activity of TiO2 has attracted the attention of researchers for decades. Due to its natural abundance, chemical stability, and environmental compatibility, TiO2 is one of the most widely used photocatalysts for scientific and technological applications to date.1–3 Of particular relevance is the anatase phase of TiO2, which predominates at the nanoscale. Since TiO2 photocatalysis usually takes place in humid or aqueous environment, the interface of anatase TiO2 with water is of fundamental importance, e.g. for elucidating the not yet fully understood mechanisms of photochemical water splitting,4–6 UV-induced hydrophilicity,7–9 and for improving the performance of TiO2 nanomaterials in biomedical applications.10,11 As a specific example, we focus here on the aqueous interface with the majority (101) surface of anatase. Our main goal is to solve an apparently simple but longstanding question: does water spontaneously dissociate on the defect-free anatase (101) surface? Hydroxyl groups are known to trap charges on TiO2 surfaces,12–14 hence the relevance of this particular question extends over the broad field of TiO2 photocatalysis in aqueous environments.

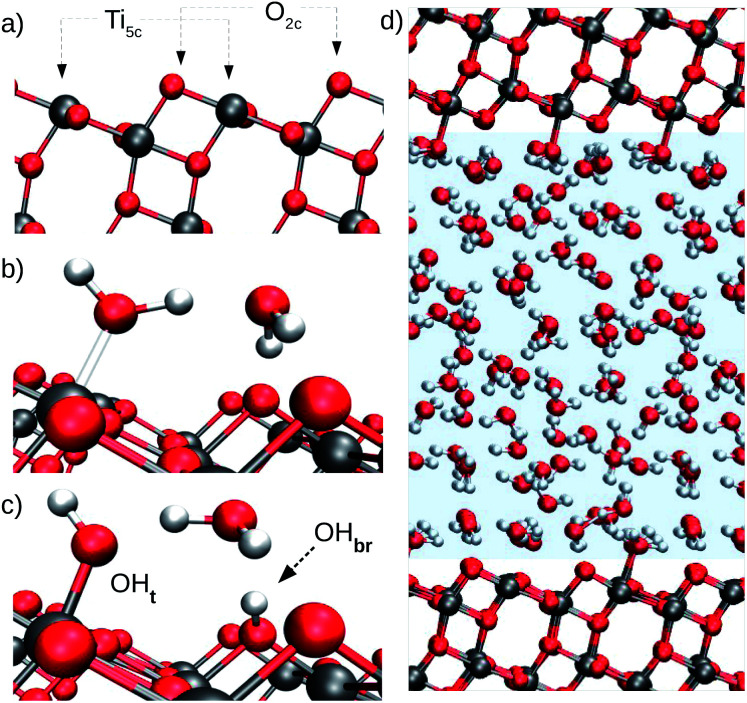
Water adsorption on anatase (101) takes place at the under-coordinated five-fold Ti (Ti5c) and two-fold oxygen (O2c) surface sites (Fig. 1a).15,16 Water oxygen atoms can form dative bonds with Ti5c atoms (Fig. 1b), while surface O2c's can either accept hydrogen bonds (Fig. 1b) or protons from water (Fig. 1c). Both Ti5c and O2c sites participate in water dissociation on the anatase (101) surface. As shown in Fig. 1c, water dissociation involves the transfer of a proton from a molecule adsorbed at a Ti5c site to an O2c. This results in the formation of two surface hydroxyl groups: a terminal hydroxyl on Ti5c (OHt, Fig. 1c, left) and a bridging hydroxyl, corresponding to a protonated O2c atom (OHbr, Fig. 1c, right).

Fig. 1. (a) Surface undercoordinated Ti5c and O2c sites, the most relevant TiO2 atoms for water adsorption on the anatase (101) surface. (b) Molecular adsorption of water on anatase TiO2. (c) Dissociative water adsorption on anatase TiO2. Terminal and bridging hydroxyls are indicated by OHt and OHbr, respectively. (d) Model of the anatase (101)–water interface used to train the DNN potential. The water region is highlighted by the pale blue shading.

Fig. 1

Open in a new tab

The presence/absence of dissociated water plays a major role in the surface chemistry of anatase TiO2. Although both experiments and computer simulations agree on the nature of water adsorption on anatase (101) under vacuum conditions, the picture remains controversial at the interface of anatase (101) with liquid water. In vacuum, Temperature Programmed Desorption (TPD),17 Scanning Tunneling Microscopy16 (STM) and Density Functional Theory (DFT)15,18 all agree that water dissociation can only take place at defect sites on the anatase (101) surface. At the aqueous interface, however, only few experiments can selectively probe water right at the TiO2 surface, and the experimental data currently available for the anatase (101)–water interface were either obtained using reduced anatase,19 or could not unambiguously define the adsorption state of water.20,21

Computational studies based on DFT have provided valuable insights into water adsorption on the surface of metals,22,23 semi-conductors24–26 and insulators.27,28 When coupled with molecular dynamics (MD), DFT has also provided atomic-level interpretation of experimental surface sensitive vibrational spectrocopies.29–31 DFT-based ab initio molecular dynamics (AIMD) employs forces derived from the quantum mechanical ground state of the electrons and could in principle be used to access the stability difference between molecular and dissociative adsorption of water on the anatase (101) surface. However, water dissociation on anatase TiO2 is kinetically hindered and cannot be observed in the short-time dynamics currently accessible to AIMD. Neither the dissociation of water nor the recombination of hydroxyls were indeed observed in AIMD simulations of the anatase (101)–water interface of approximately 40 ps duration.21

In this work we extend both the time and length scales sampled by AIMD using a deep neural network (DNN) to represent the potential energy surface (PES), gaining a substantial speed-up of MD simulations. Several authors have demonstrated the DNNs' ability to reproduce the complex PES of ab initio potentials,32–34 thus allowing accurate long-time simulations of several condensed phase systems35–37 including metal oxide–water interfaces.38,39 In the present study, the ab initio-based DNN potential reproduces energy and atomic forces obtained from DFT at a five orders of magnitude lower computational cost. This allows us to carry out MD simulations at the nanosecond timescale on systems of thousands of atoms and to use enhanced sampling techniques to obtain converged free energy surfaces of proton transfer at the aqueous anatase (101) interface as a function of suitable reaction coordinates. All our simulations are carried out assuming no net electric charge on the surface, a condition that can be experimentally realized at the point of zero charge and flat band potential of TiO2 in contact with water. Altogether, the present results enable us to elucidate both the relative stability of molecular versus dissociated water and the mechanism of proton transport at the aqueous anatase (101) interface, which are two fundamental features for understanding the reactivity of this interface.

2. Methods

2.1. DNN training

Our DNN potential was constructed following the method recently proposed by Zhang et al.34,40 In this scheme, the potential energy E of each atomic configuration is a sum of “atomic energies” 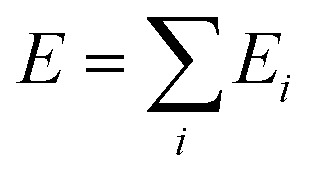Inline graphic, where Ei is determined by the local environment of atom i within a smooth cutoff radius Rc. Ei is constructed in two steps. First, for each atom a set of symmetry-preserving descriptors is constructed. Next, this information is given as input for a DNN, which returns Ei as the output. The additive form of E naturally preserves the extensive character of the potential energy. We refer the reader to ref. 34 and 40 for further details. With this method, the DNN potential has been shown to accurately reproduce interatomic forces and energies predicted by DFT.41

We trained our DNN potential using an active learning approach.41 In this scheme, training data is collected in an iterative scheme consisting of a computationally efficient exploration of the configurational space and evaluation of ab initio energies and atomic forces of a small set of selected atomic configurations. We performed such iterative procedure using three different systems: bulk anatase TiO2 (108 atoms), bulk liquid water (192 atoms), and the anatase (101)–water interface (426 atoms), for which we included configurations with one or few interfacial water molecules either dissociated or near the transition state. The latter were generated with enhanced sampling techniques during the iterative refinement of the DNN and their inclusion has been essential to predict dissociation barriers close to those of DFT.

In more detail, our model of the anatase–water interface consists of 82 water molecules in contact with an anatase (101) slab (five TiO2 layers exposing a (1 × 3) surface supercell) within a periodically repeated unit cell of size 10.4 Å × 11.4 Å × 36.8 Å along the three orthogonal directions [1̄01], [010] and [101] of the anatase TiO2 crystal lattice (Fig. 1d). Forces and energies were computed with the SCAN functional,42 as implemented in the PWscf code of Quantum ESPRESSO.43,44 The SCAN functional has been shown to accurately predict both the structure of water45 and TiO2.21 We performed all DNN potential-based MD simulations using the Lammps code46 interfaced with the DeePMD-kit.47 Enhanced sampling techniques were provided by PLUMED.48 The DeePMD-kit code47 was used to train the DNN potential. Additional details on the DNN training method and DFT calculations can be found in the ESI.† MD performed with the DNN potential is called DPMD in the following.

2.2. DPMD simulations

DPMD simulations of the anatase (101)–water interface sampled the canonical ensemble (constant volume and temperature), while the isobaric–isothermal ensemble (constant pressure and temperature) was sampled for liquid water simulations. Liquid water simulations were performed with a periodically repeated cell containing 64 water molecules. For the anatase (101)–water system, comparison between DPMD and AIMD involved simulations of a 1 × 3 anatase (101) surface supercell exposing 6Ti5c and 6O2c sites. This supercell was used also for umbrella sampling simulations used to evaluate the free energy barrier to transfer a proton from water to a surface O2c atom. All other DPMD simulations of the anatase (101)–water interface were carried out with a larger 4 × 12 anatase (101) surface supercell exposing 96Ti5c and 96O2c sites. In all cases, the system was composed by a slab of 5TiO2 layers in contact with a 20 Å water slab at the experimental density; essentially identical interfacial water properties were obtained in a simulation using a water thickness of 40 Å (see ESI†). Temperature and pressure were controlled by a Nosé–Hoover thermostat49,50 at 330 K and Parrinello–Rahman barostat51 under 1 bar, respectively. A temperature 30 K higher than room temperature was used to roughly mimic nuclear quantum effects on the oxygen distribution in water.52 The classical equations of motion were numerically integrated using Verlet's method53 with a time step of 0.5 fs for D2O (0.25 fs for H2O). Equilibrium properties were computed from simulations with D2O, since it allows a larger time step in the numerical integration of the equations of motion without affecting the equilibrium statistical properties of the investigated systems. All error bars were evaluated from simulations ran with independently trained DNN potentials.

3. Results and discussion

3.1. Validation

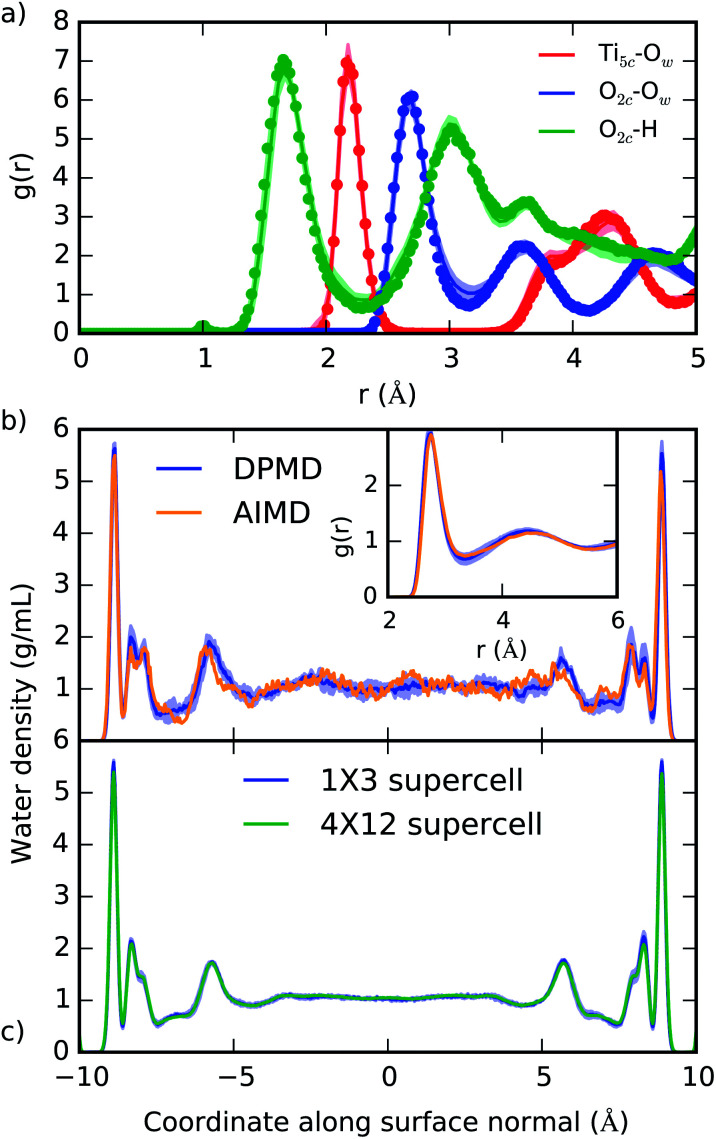
The ability of DPMD to reproduce the DFT-predicted structures of pure water, pure anatase TiO2, and anatase (101)–water interface is confirmed by the following results. (i) The anatase TiO2 lattice constants given by DPMD agree well with the values predicted by SCAN21 (DPMD: a = 3.80 Å, c = 9.52 Å; SCAN: a = 3.77 Å, c = 9.52 Å). (ii) The radial distribution functions and average water density profile obtained from 4 independent 40 ps DPMD simulations of the anatase (101)–water interface agree, within their standard deviation, with analogous quantities obtained from a 40 ps AIMD trajectory of this interface (Fig. 2a and b, respectively). (iii) Our DNN potential reproduces the oxygen radial distribution function and density of bulk liquid water obtained from SCAN AIMD simulations, which are in good agreement with experiment45 (see Fig. 2b, inset). DPMD also yields a water diffusion coefficient that compares well with that given by AIMD (DPMD: 0.17 ± 0.01 Å2 ps−1, AIMD:45 0.19 ± 0.03 Å2 ps−1). (iv) The water density profile along the direction perpendicular to the TiO2 surface derived from DPMD simulations of our large (4 × 12) anatase (101) surface model (surface area of 18.5 nm2) essentially coincides with that obtained from analogous simulations of the smaller (1 × 3) anatase (101) model (surface area of 1.16 nm2) used in our training data (Fig. 2c).

Fig. 2. (a) Radial distribution function of selected atomic type pairs at the anatase (101)–water interface given from DPMD (lines) and AIMD (points). The definition of Ti5c and O2c is given in Fig. 1a, and Ow represents water oxygen atoms. (b) Density profile of water confined between two TiO2 surfaces as predicted by DPMD and AIMD.21 In the inset of (b) we compare the oxygen radial distribution function in water, g(r), as obtained from AIMD45 and DPMD. (c) Comparison of the water density profiles obtained from DPMD simulations of water in contact with 1 × 3 (1.16 nm2) and 4 × 12 (18.5 nm2) anatase (101) surface supercells. Distributions in (a) and (b) were obtained from 40 ps trajectories, while 2.5 ns of dynamics was sampled in (c). Shaded areas indicate the standard deviation obtained from four independent DPMD simulations.

Fig. 2

Open in a new tab

Additional validation tests are reported in the ESI,† where we compare results from DPMD and AIMD for the vibrational densities of states of water and TiO2 at the anatase–water interface and water dissociation at both the dry anatase surface and the aqueous interface. In particular, from Fig. S4 of the ESI,† one can see that the DFT result for the work to move a H+ from a surface O2c to a nearby OHt is reproduced very well by DPMD.

3.2. Equilibrium sampling of aqueous anatase (101) via DPMD

The equilibrium structure of the aqueous anatase (101) interface was determined by averaging the results of 4 independent DPMD trajectories of 25 ns duration each, from which error bars of computed quantities were also estimated. All simulations started from configurations with purely molecular water at the interface and a surface model exposing 96Ti5c and 96O2c sites was used, which allows a minimum non-zero hydroxyl surface coverage of 1.04%. The water density profile predicted by such DPMD simulations is perfectly symmetric with respect to its center (Fig. 2c), consistent with the symmetry of the anatase (101) slab used for the simulations. Since the water density profile does not depend on the surface supercell size (Fig. 2c), the lack of symmetry of the profile in Fig. 2b can be attributed to the short duration of that trajectory. In fact, AIMD simulations have shown a substantial slowdown of the rotational and translational dynamics of water close to the anatase (101) surface relative to bulk liquid water.21 Hence, a longer simulation time is needed to obtain the equilibrium density distribution of interfacial water on the anatase (101) surface relative to bulk liquid water.

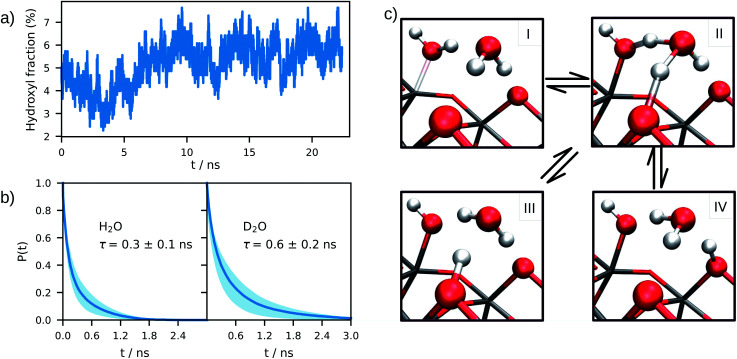
Analysis of the DPMD trajectories shows that the equilibrium adsorption configuration of water at the aqueous anatase (101) interface consists mostly of intact molecules at Ti5c sites, but also includes an average 5.6 ± 0.5% of water dissociated into OHt and OHbr hydroxyl groups (see Fig. 3a; note that the average surface hydroxyl coverage is calculated excluding the first 10 ns of this curve). Hydroxyls have a finite lifetime before they recombine to form molecular water adsorbed at Ti5c sites. This can be important in photo-oxidation processes, e.g. photocatalytic water splitting, where photoexcited holes are transferred from TiO2 to adsorbed hydroxyls to form OH radicals.54–56 The hydroxyl lifetime can be estimated from its survival probability distribution P(t), which is the probability to continuously observe water dissociated during a time interval t. We computed P(t) for OHt and ODt separately (Fig. 3b), and defined the average lifetime (τ) as 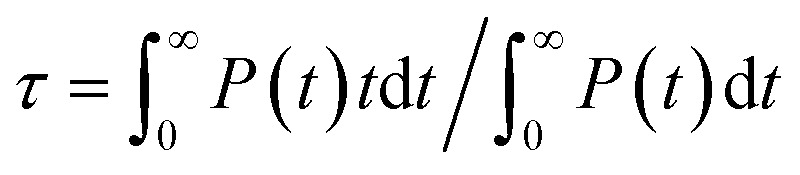Inline graphic. We found the average lifetime of ODt (τ = 0.6 ± 0.2 ns) to be twice as long as the one of OHt (τ = 0.3 ± 0.1 ns). For comparison, the hydroxyl lifetimes observed in our simulation are shorter than the lifetimes of several ns for electron–hole recombination in anatase,57,58 and on the same timescale as the characteristic times of hole transfer to organic adsorbates on TiO2 surfaces.3

Fig. 3. (a) Time evolution of the surface hydroxyl coverage on the anatase (101)–water interface, as obtained from an average of 4 DPMD simulations. (b) Un-normalized survival probability of hydroxyl groups on the anatase (101)–water (H2O and D2O) interface as a function of time. In both plots τ denotes the average lifetime of terminal hydroxyl groups. (c) Mechanisms of proton transfer reaction at the anatase (101)–water interface. I: molecular adsorption; II: transition state; III and IV: equivalent configurations of the dissociated water. Water dissociation mechanism follows the path: I → II → III (or IV), while proton transport follows: III → II → IV or IV → II → III.

Fig. 3

Open in a new tab

The mechanism of hydroxyl formation that emerges from our simulations involves a concerted proton transfer from molecular water to surface O2c sites. As shown in Fig. 3c (path I → II → III or I → II → IV), the initial state is a stable hydrogen-bond complex, in which the path from the water coordinated to a Ti5c site to two adjacent O2c sites is fully connected with hydrogen bonds. The proton transfer proceeds through a Grotthuss-like mechanism,59 with a transient hydronium ion formed along the reaction path. The dissociation reaction produces a terminal (bonded to Ti5c) and a bridging hydroxyl (protonated O2c) connected through an intermediate water molecule that is H-bonded to both of them. The TiO2 surface remains charge neutral along the proton transfer reaction, and no proton transfer to liquid water is observed.

A similar mechanism, involving an intermediate water molecule, is observed also for the proton transport along O2c sites (path III → II → IV in Fig. 3c). A proton at a bridging O2c site can either recombine with a terminal hydroxyl to form molecular water or transfer to a neighboring non-protonated O2c site. The latter proton transport process requires a fully connected hydrogen-bond path between initial and final states similar to that of water dissociation/recombination, and has also the same transition state. For this reason, the recombination of bridging and terminal hydroxyls to form molecular water competes with the proton transfer from one bridging hydroxyl to a non-protonated O2c site.

3.3. Enhanced sampling

We estimated the free energy difference between molecular and dissociated water on aqueous TiO2 from enhanced sampling techniques. Due to the complex nature of proton transfer reactions in water,60–62 we devised a two-step procedure to reconstruct the free energy surface of water dissociation on titania. First, we estimated the free energy barrier to transfer a proton from water to a surface O2c atom using umbrella sampling.63 With this method, the free energy F(So) of the system was obtained as a function of the minimum distance So between a particular surface O2c (index o) and any hydrogen atom. A continuous version of the minimum distance was used, 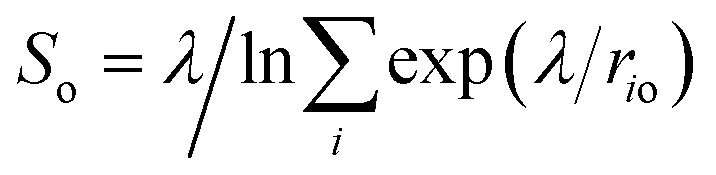Inline graphic (λ = 500 Å), and quadratic (or umbrella) potentials were applied at different values of So, allowing the sampling of configurational space regions that would be rarely visited from unbiased simulations. The free energy surfaces obtained from umbrella sampling are given in the ESI.†

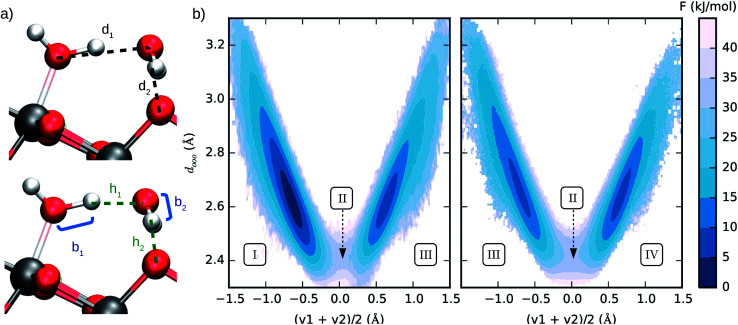
The second step in our procedure involved a new set of enhanced sampling simulations with a bias potential V = Σo − F(So) applied to the O2c sites in the system, in which F(So) is the free energy previously obtained from umbrella sampling. This set of bias potentials enhances the probability of proton transfer to every O2c on the anatase (101) surface. A probability distribution of the two collective variables given in Fig. 4a was then constructed in the biased ensemble and re-weighted by the Boltzmann factor eβV, where β is the inverse temperature. The probability distribution was obtained from the average of 12 independent 3 ns long simulations (viz. 3 simulations with each of the four independent DNN potentials) and the average over all water adsorption sites in the system. The choice of the two collective variables in Fig. 4a was inspired by earlier computer simulations of proton diffusion in basic and acidic aqueous solutions.64

Fig. 4. (a) Interatomic distances used to define the two collective variables (CVs) describing proton transfer reactions. The first CV, dooo = (d1 + d2)/2, represents the average distance between hydrogen-bonded oxygen atoms connecting proton-donor and proton-acceptor sites. The second CV, (v1 + v2)/2 (vi = bi − hi), describes the progress of the proton transfer reaction, with positive and negative values corresponding to the dissociated and the molecular states, respectively. (b) Free energy surface of water dissociation (left) and proton transport (right) at the anatase (101)–water interface. Roman numerals indicate the adsorption state of water at specific regions in the free energy plot, as shown in Fig. 3c. Molecular water is more stable than the dissociated state by 8.0 ± 0.9 kJ mol−1, with a free energy barrier of 32 ± 4 kJ mol−1 separating these states.

Fig. 4

Open in a new tab

From the computed free energy surface in Fig. 4b (left), two main features emerge: (i) water adsorbed in molecular form is thermodynamically more stable than dissociatively adsorbed water on the anatase (101) surface by ΔF = 8.0 ± 0.9 kJ mol−1; (ii) the free energy barrier for water dissociation, ΔF‡d = 32 ± 4 kJ mol−1, is around 13 times larger than the thermal energy at room temperature and would unlikely be crossed during the typical timescale (tens of ps) of AIMD simulations. Analysis of the computed trajectories in the presence of the bias potential confirms the mechanism of water dissociation observed in the unbiased simulations: water dissociation always involves a water molecule mediating the proton transfer between water adsorbed on a Ti5c site and a neighboring O2c atom (Fig. 3c). The enhanced sampling simulations also captured the mechanism of proton transport at the aqueous anatase (101) interface observed in the unbiased simulations. As shown in Fig. 4b (right), proton transport produces an approximately symmetric free energy surface with a free energy barrier of 25 ± 4 kJ mol−1 separating the two equivalent states.

To verify the consistency of the free energy surfaces in Fig. 4b with the results of our unbiased DPMD simulations (Fig. 3), we can estimate the equilibrium fraction of dissociated water on the anatase (101)–water interface from the Boltzmann factor e−βΔF, where β is the inverse temperature and ΔF is the free energy difference between molecular and dissociated water. Using the computed value ΔF = 8.0 kJ mol−1, we obtain a dissociation fraction of 5.0% at our simulation temperature of 330 K, in very good agreement with the DPMD simulations. This result is also confirmed by Monte Carlo sampling of a 2-D lattice gas model that includes the constraint present in the real system: adsorbed water can only dissociate if at least one neighboring O2c site is non-protonated (see ESI†). Using the lattice gas model, we can further estimate the free energy of the anatase (101)–water interface as a function of the surface hydroxyl coverage, which allows us to rule out the existence of additional metastable states at other surface hydroxyl fractions.

Another relevant comparison is that between the hydroxyl lifetime determined from our equilibrium simulations and that estimated from the computed free energy barrier. Using transition-state theory, the recombination rate constant can be written as 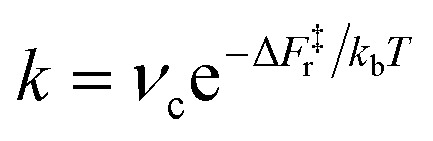Inline graphic, where νc is the attempt frequency and ΔF‡r = ΔF‡d − ΔF is the barrier for a terminal and bridging hydroxyl to recombine into a water molecule. Approximating νc with the H-bonded OD or OH stretching frequency of heavy (νc ≈ 71 THz) and light (νc ≈ 101 THz) water, and taking the recombination barrier ΔF‡r = 25 kJ mol−1, we obtain a lifetime τ = 1/k of the terminal hydroxyl group equal to 0.09 ns and 0.13 ns for OH and OD, respectively. Thus, this simplified approach predicts lifetimes on the same order of magnitude as the ones evaluated from our DPMD simulations, although with slightly underestimated values. However, the fact that the simulations give τOD ∼ 2τOH, rather than τOD ∼ 1.4τOH as in the simplified approach, indicates a process more complex than a simple exponential relaxation dynamics. This is apparent from the curves in Fig. 3b, that cannot be fitted by a single exponential.

4. Conclusions

In summary, the ability of neural networks to reproduce the ab initio potential energy surface of the anatase (101)–water interface together with their scalability has allowed us to substantially extend the size and time scales of our first principles simulations for this system. By combining the computationally efficient neural network potential with enhanced sampling techniques, we have also been able to reconstruct the free energy surface of water dissociation and proton transport at the anatase interface with liquid water. The present simulations support a picture of predominantly molecular adsorption on the defect-free anatase (101) in contact with liquid water at ambient conditions, with an entropically driven 5.6% fraction of water dissociation at the interface. They also provide detailed mechanisms of proton transfer at the interface, free energy barriers and lifetimes that are all features to be taken into account when investigating the reactivity of the TiO2–water interface, either chemical or photo-induced, which is key to many practical applications.

Conflicts of interest

There are no conflicts to declare.

Supplementary Material

SC-011-C9SC05116C-s001

Acknowledgments

This work was conducted within the Computational Chemical Center: Chemistry in Solution and at Interfaces funded by the DoE under Award DE-SC0019394. A. S. acknowledge the support of DoE-BES, Division of Chemical Sciences, Geosciences and Biosciences under Award DE-SC0007347. M. C. A. acknowledges partial financial support from the CNPq-Brazil. We used resources of the National Energy Research Scientific Computing Center (DoE Contract No. DE-AC02-05cH11231). We also acknowledge use of the TIGRESS High Performance Computer Center at Princeton University.

†

Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sc05116c

Notes and references

  1. Fujishima A. Zhang X. Tryk D. A. Surf. Sci. Rep. 2008;63:515–582. doi: 10.1016/j.surfrep.2008.10.001. [DOI] [Google Scholar]
  2. Linsebigler A. L. Lu G. Yates J. T. Chem. Rev. 1995;95:735–758. doi: 10.1021/cr00035a013. [DOI] [Google Scholar]
  3. Schneider J. Matsuoka M. Takeuchi M. Zhang J. Horiuchi Y. Anpo M. Bahnemann D. W. Chem. Rev. 2014;114:9919–9986. doi: 10.1021/cr5001892. [DOI] [PubMed] [Google Scholar]
  4. Fujishima A. Honda K. Nature. 1972;238:37–38. doi: 10.1038/238037a0. [DOI] [PubMed] [Google Scholar]
  5. Khan S. U. M. Al-Shahry M. Ingler Jr W. B. Science. 2002;297:2243–2245. doi: 10.1126/science.1075035. [DOI] [PubMed] [Google Scholar]
  6. Gratzel M. Acc. Chem. Res. 1981;14:376–384. doi: 10.1021/ar00072a003. [DOI] [Google Scholar]
  7. Wang R. Hashimoto K. Fujishima A. Chikuni M. Kojima E. Kitamura A. Shimohigoshi M. Watanabe T. Nature. 1997;388:431–432. doi: 10.1038/41233. [DOI] [Google Scholar]
  8. Zhang L. Dillert R. Bahnemann D. Vormoor M. Energy Environ. Sci. 2012;5:7491. doi: 10.1039/C2EE03390A. [DOI] [Google Scholar]
  9. Zubkoy T. Stahl D. Thompson T. L. Panayotov D. Diwald O. Yates J. T. J. Phys. Chem. B. 2005;109:15454–15462. doi: 10.1021/jp058101c. [DOI] [PubMed] [Google Scholar]
  10. Fujishima A. Rao T. N. Tryk D. A. J. Photochem. Photobiol., C. 2000;1:1–21. doi: 10.1016/S1389-5567(00)00002-2. [DOI] [Google Scholar]
  11. Cai R. Hashimoto K. Itoh K. Kubota Y. Fujishima A. Bull. Chem. Soc. Jpn. 1991;64:1268–1273. doi: 10.1246/bcsj.64.1268. [DOI] [Google Scholar]
  12. Anpo M. Shima T. Kubokawa Y. Chem. Lett. 1985;14:1799–1802. doi: 10.1246/cl.1985.1799. [DOI] [Google Scholar]
  13. Micic O. I. Zhang Y. Cromack K. R. Trifunac A. D. Thurnauer M. C. J. Phys. Chem. 1993;97:7277–7283. doi: 10.1021/j100130a026. [DOI] [Google Scholar]
  14. Szczepankiewicz S. H. Colussi A. J. Hoffmann M. R. J. Phys. Chem. B. 2000;104:9842–9850. doi: 10.1021/jp0007890. [DOI] [Google Scholar]
  15. Vittadini A. Selloni A. Rotzinger F. P. Grätzel M. Phys. Rev. Lett. 1998;81:2954–2957. doi: 10.1103/PhysRevLett.81.2954. [DOI] [Google Scholar]
  16. He Y. Tilocca A. Dulub O. Selloni A. Diebold U. Nat. Mater. 2009;8:585–589. doi: 10.1038/nmat2466. [DOI] [PubMed] [Google Scholar]
  17. Herman G. S. Dohnálek Z. Ruzycki N. Diebold U. J. Phys. Chem. B. 2003;107:2788–2795. doi: 10.1021/jp0275544. [DOI] [Google Scholar]
  18. Tilocca A. Selloni A. Langmuir. 2004;20:8379–8384. doi: 10.1021/la048937r. [DOI] [PubMed] [Google Scholar]
  19. Nadeem I. M. Treacy J. P. W. Selcuk S. Torrelles X. Hussain H. Wilson A. Grinter D. C. Cabailh G. Bikondoa O. Nicklin C. Selloni A. Zegenhagen J. Lindsay R. Thornton G. J. Phys. Chem. Lett. 2018;9:3131–3136. doi: 10.1021/acs.jpclett.8b01182. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Hosseinpour S. Tang F. Wang F. Livingstone R. A. Schlegel S. J. Ohto T. Bonn M. Nagata Y. Backus E. H. J. Phys. Chem. Lett. 2017;8:2195–2199. doi: 10.1021/acs.jpclett.7b00564. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Calegari Andrade M. F. Ko H.-Y. Car R. Selloni A. J. Phys. Chem. Lett. 2018;9:6716–6721. doi: 10.1021/acs.jpclett.8b03103. [DOI] [PubMed] [Google Scholar]
  22. Cerdá J. Michaelides A. Bocquet M. L. Feibelman P. J. Mitsui T. Rose M. Fomin E. Salmeron M. Phys. Rev. Lett. 2004;93:116101. doi: 10.1103/PhysRevLett.93.116101. [DOI] [PubMed] [Google Scholar]
  23. Carrasco J. Santra B. Klimeš J. Michaelides A. Phys. Rev. Lett. 2011;106:026101. doi: 10.1103/PhysRevLett.106.026101. [DOI] [PubMed] [Google Scholar]
  24. Wood B. C. Schwegler E. Choi W. I. Ogitsu T. J. Am. Chem. Soc. 2013;135:15774–15783. doi: 10.1021/ja403850s. [DOI] [PubMed] [Google Scholar]
  25. Pham T. A. Ping Y. Galli G. Nat. Mater. 2017;16:401–408. doi: 10.1038/nmat4803. [DOI] [PubMed] [Google Scholar]
  26. Liao P. Keith J. a. Carter E. a. J. Am. Chem. Soc. 2012;134:13296–13309. doi: 10.1021/ja301567f. [DOI] [PubMed] [Google Scholar]
  27. Ceresoli D. Bernasconi M. Iarlori S. Parrinello M. Tosatti E. Phys. Rev. Lett. 2000;84:3887–3890. doi: 10.1103/PhysRevLett.84.3887. [DOI] [PubMed] [Google Scholar]
  28. Melani G. Nagata Y. Wirth J. Saalfrank P. J. Chem. Phys. 2018;149:014707. doi: 10.1063/1.5023347. [DOI] [PubMed] [Google Scholar]
  29. Sulpizi M. Salanne M. Sprik M. Gaigeot M.-P. J. Phys. Chem. Lett. 2013;4:83–87. doi: 10.1021/jz301858g. [DOI] [PubMed] [Google Scholar]
  30. Khatib R., Backus E. H. G., Bonn M., Perez-Haro M.-J., Gaigeot M.-P. and Sulpizi M., Water orientation and hydrogen-bond structure at the water–fluorite interface, Nature Publishing Group, 2016, vol. 6, p. 24287 [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Dellostritto M. Piontek S. M. Klein M. L. Borguet E. J. Phys. Chem. C. 2018;122:21284–21294. doi: 10.1021/acs.jpcc.8b02809. [DOI] [Google Scholar]
  32. Behler J. Parrinello M. Phys. Rev. Lett. 2007;98:146401. doi: 10.1103/PhysRevLett.98.146401. [DOI] [PubMed] [Google Scholar]
  33. Chmiela S. Tkatchenko A. Sauceda H. E. Poltavsky I. Schütt K. T. Müller K.-R. Sci. Adv. 2017;3:e1603015. doi: 10.1126/sciadv.1603015. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Zhang L. Han J. Wang H. Car R. E W. Phys. Rev. Lett. 2018;120:143001. doi: 10.1103/PhysRevLett.120.143001. [DOI] [PubMed] [Google Scholar]
  35. Cheng B. Engel E. A. Behler J. Dellago C. Ceriotti M. Proc. Natl. Acad. Sci. U. S. A. 2019;116:1110–1115. doi: 10.1073/pnas.1815117116. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Bonati L. Parrinello M. Phys. Rev. Lett. 2018;121:265701. doi: 10.1103/PhysRevLett.121.265701. [DOI] [PubMed] [Google Scholar]
  37. Ko H.-Y. Zhang L. Santra B. Wang H. E W. DiStasio R. A. Car R. Mol. Phys. 2019;117:3269–3281. doi: 10.1080/00268976.2019.1652366. [DOI] [Google Scholar]
  38. Quaranta V. Hellström M. Behler J. J. Phys. Chem. Lett. 2017;8:1476–1483. doi: 10.1021/acs.jpclett.7b00358. [DOI] [PubMed] [Google Scholar]
  39. Hellström M. Quaranta V. Behler J. Chem. Sci. 2019;10:1232–1243. doi: 10.1039/C8SC03033B. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Zhang L. Han J. Wang H. Saidi W. A. Car R. E W. Adv. Neural Inf. Process. Syst. 2018;31:4436–4446. [Google Scholar]
  41. Zhang L. Lin D.-Y. Wang H. Car R. E W. Phys. Rev. Mater. 2019;3:023804. doi: 10.1103/PhysRevMaterials.3.023804. [DOI] [Google Scholar]
  42. Sun J. Ruzsinszky A. Perdew J. P. Phys. Rev. Lett. 2015;115:036402. doi: 10.1103/PhysRevLett.115.036402. [DOI] [PubMed] [Google Scholar]
  43. Giannozzi P. Baroni S. Bonini N. Calandra M. Car R. Cavazzoni C. Ceresoli D. Chiarotti G. L. Cococcioni M. Dabo I. Dal Corso A. de Gironcoli S. Fabris S. Fratesi G. Gebauer R. Gerstmann U. Gougoussis C. Kokalj A. Lazzeri M. Martin-Samos L. Marzari N. Mauri F. Mazzarello R. Paolini S. Pasquarello A. Paulatto L. Sbraccia C. Scandolo S. Sclauzero G. Seitsonen A. P. Smogunov A. Umari P. Wentzcovitch R. M. J. Phys.: Condens. Matter. 2009;21:395502. doi: 10.1088/0953-8984/21/39/395502. [DOI] [PubMed] [Google Scholar]
  44. Giannozzi P. Andreussi O. Brumme T. Bunau O. Buongiorno Nardelli M. Calandra M. Car R. Cavazzoni C. Ceresoli D. Cococcioni M. Colonna N. Carnimeo I. Dal Corso A. De Gironcoli S. Delugas P. Distasio R. A. Ferretti A. Floris A. Fratesi G. Fugallo G. Gebauer R. Gerstmann U. Giustino F. Gorni T. Jia J. Kawamura M. Ko H. Y. Kokalj A. Kücükbenli E. Lazzeri M. Marsili M. Marzari N. Mauri F. Nguyen N. L. Nguyen H. V. Otero-De-La-Roza A. Paulatto L. Poncé S. Rocca D. Sabatini R. Santra B. Schlipf M. Seitsonen A. P. Smogunov A. Timrov I. Thonhauser T. Umari P. Vast N. Wu X. Baroni S. J. Phys.: Condens. Matter. 2017;29:465901. doi: 10.1088/1361-648X/aa8f79. [DOI] [PubMed] [Google Scholar]
  45. Chen M. Ko H.-Y. Remsing R. Calegari Andrade M. F. Santra B. Sun Z. Selloni A. Car R. Klein M. Perdew J. Wu X. Proc. Natl. Acad. Sci. U. S. A. 2017;114:10846–10851. doi: 10.1073/pnas.1712499114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Plimpton S. J. Comput. Phys. 1995;117:1–19. doi: 10.1006/jcph.1995.1039. [DOI] [Google Scholar]
  47. Wang H. Zhang L. Han J. E W. Comput. Phys. Commun. 2018;228:178–184. doi: 10.1016/j.cpc.2018.03.016. [DOI] [Google Scholar]
  48. Tribello G. A. Bonomi M. Branduardi D. Camilloni C. Bussi G. Comput. Phys. Commun. 2014;185:604–613. doi: 10.1016/j.cpc.2013.09.018. [DOI] [Google Scholar]
  49. Nosé S. Mol. Phys. 1984;52:255–268. doi: 10.1080/00268978400101201. [DOI] [Google Scholar]
  50. Hoover W. G. Phys. Rev. A: At., Mol., Opt. Phys. 1985;31:1695–1697. doi: 10.1103/PhysRevA.31.1695. [DOI] [PubMed] [Google Scholar]
  51. Parrinello M. J. Appl. Phys. 1981;52:7182–7190. doi: 10.1063/1.328693. [DOI] [Google Scholar]
  52. Morrone J. A. Car R. Phys. Rev. Lett. 2008;101:1–4. doi: 10.1103/PhysRevLett.101.017801. [DOI] [PubMed] [Google Scholar]
  53. Verlet L. Phys. Rev. 1967;159:98–103. doi: 10.1103/PhysRev.159.98. [DOI] [Google Scholar]
  54. Cheng J. Sulpizi M. Vandevondele J. Sprik M. ChemCatChem. 2012;4:636–640. doi: 10.1002/cctc.201100498. [DOI] [Google Scholar]
  55. Chen J. Li Y.-F. Sit P. Selloni A. J. Am. Chem. Soc. 2013;135:18774–18777. doi: 10.1021/ja410685m. [DOI] [PubMed] [Google Scholar]
  56. Cheng J. Vandevondele J. Sprik M. J. Phys. Chem. C. 2014;118:5437–5444. doi: 10.1021/jp500769q. [DOI] [Google Scholar]
  57. Tang J. Durrant J. R. Klug D. R. J. Am. Chem. Soc. 2008;130:13885–13891. doi: 10.1021/ja8034637. [DOI] [PubMed] [Google Scholar]
  58. Xu M. Gao Y. Moreno E. M. Kunst M. Muhler M. Wang Y. Idriss H. Wöll C. Phys. Rev. Lett. 2011;106:1–4. doi: 10.1103/PhysRevLett.106.138302. [DOI] [PubMed] [Google Scholar]
  59. Marx D. ChemPhysChem. 2006;7:1848–1870. doi: 10.1002/cphc.200600128. [DOI] [PubMed] [Google Scholar]
  60. Geissler P. L. Dellago C. Chandler D. Hutter J. Parrinello M. Science. 2001;291:2121–2124. doi: 10.1126/science.1056991. [DOI] [PubMed] [Google Scholar]
  61. Hassanali A. Prakash M. K. Eshet H. Parrinello M. Proc. Natl. Acad. Sci. U. S. A. 2011;108:20410–20415. doi: 10.1073/pnas.1112486108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Chen M. Zheng L. Santra B. Ko H. Y. Distasio R. A. Klein M. L. Car R. Wu X. Nat. Chem. 2018;10:413–419. doi: 10.1038/s41557-018-0010-2. [DOI] [PubMed] [Google Scholar]
  63. Torrie G. Valleau J. J. Comput. Phys. 1977;23:187–199. doi: 10.1016/0021-9991(77)90121-8. [DOI] [Google Scholar]
  64. Hassanali A. Giberti F. Cuny J. Kühne T. D. Parrinello M. Proc. Natl. Acad. Sci. U. S. A. 2013;110:13723–13728. doi: 10.1073/pnas.1306642110. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

SC-011-C9SC05116C-s001
SC-011-C9SC05116C-s001.pdf (704.1KB, pdf)

Articles from Chemical Science are provided here courtesy of Royal Society of Chemistry

RESOURCES