Abstract
Multiband acquisition, also called simultaneous multislice, has become a popular technique in resting-state functional connectivity studies. Multiband (MB) acceleration leads to a higher temporal resolution but also leads to spatially heterogeneous noise amplification, suggesting the costs may be greater in areas such as the subcortex. We evaluate MB factors of 2, 3, 4, 6, 8, 9, and 12 with 2 mm isotropic voxels, and additionally 2 mm and 3.3 mm single-band acquisitions, on a 32-channel head coil. Noise amplification was greater in deeper brain regions, including subcortical regions. Correlations were attenuated by noise amplification, which resulted in spatially varying biases that were more severe at higher MB factors. Temporal filtering decreased spatial biases in correlations due to noise amplification, but also tended to decrease effect sizes. In seed-based correlation maps, left-right putamen connectivity and thalamo-motor connectivity were highest in the single-band 3.3 mm protocol. In correlation matrices, MB 4, 6, and 8 had a greater number of significant correlations than the other acquisitions (both with and without temporal filtering). We recommend single-band 3.3 mm for seed-based subcortical analyses, and MB 4 provides a reasonable balance for studies analyzing both seed-based correlation maps and connectivity matrices. In multiband studies including secondary analyses of large-scale datasets, we recommend reporting effect sizes or test statistics instead of correlations. If correlations are reported, temporal filtering (or another method for thermal noise removal) should be used. The Emory Multiband Dataset is available on OpenNeuro.
Keywords: acceleration, functional connectivity, noise amplification, putamen, thalamus, simultaneous multislice, subcortical, temporal resolution
1. Introduction
Correlations in spontaneous blood-oxygen-level-dependent (BOLD) signal fluctuations measured using resting state functional magnetic resonance imaging (rs-fMRI) are referred to as functional connectivity, and collectively, are used to reveal the functional connectome (Biswal et al., 2010). Patterns in functional connectivity can provide insight into the pathophysiology of diseases, and rs-fMRI has the potential to be a biomarker of neurological and psychiatric disorders (Greicius, 2008). In particular, functional connectivity in subcortical regions, such as the thalamus and striatum, appears to be altered in many neurological and psychiatric conditions (Greicius et al., 2007; Woodward and Heckers, 2016; Di Martino et al., 2011). Recently, multiband (MB) acquisition, also called simultaneous multislice, has been broadly adopted by large-scale efforts to map the functional connectome across all stages of human development (Glasser et al., 2013; Miller et al., 2016b; Howell et al., 2019; Weiner et al., 2017a; Hagler et al., 2019) in part due to evidence suggesting up-to 60% increases in fMRI signal fluctuation detection sensitivity (Feinberg et al., 2010). Evidence from task-based fMRI data suggest the benefits of multiband acquisition may be non-uniform across the brain and in some instances decline with high MB factors (Todd et al., 2017). Relatively high MB factors (MB 8) are used by most of the large-scale efforts; yet, to date, the impact of MB factor on correlation-based functional connectivity estimation has received little attention.
MB acquisition improves temporal resolution in fMRI by using a multiband radiofrequency pulse to simultaneously excite and receive signals from multiple slices, which can also be leveraged to improve spatial resolution (Moeller et al., 2010; Feinberg and Setsompop, 2013). For a given period of acquisition time and voxel size, the number of volumes collected increases by the MB factor, e.g., an MB factor of eight increases the number of volumes eight-fold. This increase in the number of time points in itself can improve statistical power (Todd et al., 2016). It can also improve the ability to unalias physiological sources of noise during temporal filtering (Todd et al., 2017) and improve artifact removal using independent component analysis (Smith et al., 2013; Griffanti et al., 2017). However, this increase in sampling frequency is accompanied by reduced signal-to-noise ratio from two potential sources. First, noise amplification occurs during image reconstruction when individual slices are recovered from the simultaneously excited overlapping slices. Coil geometry factors (g-factors) are used to quantify this noise amplification and have been shown to vary across the field of view. In general, g-factors tend to be highest in subcortical regions and, in some studies, prefrontal areas where coil elements have lower and less variable sensitivity (Risk et al., 2018; Todd et al., 2017). Second, the signal is attenuated by the shortened repetition time (TR), which reduces equilibrium longitudinal magnetization even when the Ernst angle is used for the excitation radiofrequency pulse.
For some cortical regions, such as the visual and motor cortex, the benefits of MB acceleration up to eight-fold appear to outweigh the costs, with improved detection of task-evoked activity (Chen et al., 2015; Todd et al., 2017; Risk et al., 2018). Some benefits have also been observed in resting-state networks in studies evaluating up to 4-fold acceleration (Demetriou et al., 2018; Boyaciouglu et al., 2015; Preibisch et al., 2015; Chen et al., 2020) and 6-fold acceleration (Feinberg et al., 2010; Chen et al., 2015; Jahanian et al., 2019). However, previous studies have not systematically evaluated how functional connectivity is related to g-factors, nor the implications of this on subcortical regions in which g-factors are higher. Moreover, the majority of the extant literature has only considered selected lower MB factors (summarized in Bhandari et al. 2019) or considered a small number of subjects. A systematic evaluation that includes the higher MB factors that are now common in large-scale rs-fMRI studies is currently lacking.
The aim of this study is to characterize the impact of MB factor on correlation-based functional connectivity in order to provide guidance for the design of rs-fMRI studies. Our assessment uses standard preprocessing pipelines with nuisance regression (Fox et al., 2009) with and without bandpass filtering. We evaluate MB factors ranging from 2 to 12 (2-mm isotropic) and single-band (SB) acquisitions with two voxel sizes (2- and 3.3-mm isotropic) in six-minute runs. We conduct our analyses at two levels: 1) an analysis of seed-based correlation maps for a seed in the right putamen and a seed in the hand region of left primary motor cortex (LM1); and 2) an examination of network connectivity using the 264-node atlas from Power et al. (2011), which includes thirteen subcortical nodes. We examine the putamen as it is in a high g-factor area, forms circuits with cortical regions critical for coordinating various aspects of behavior including movement (Kravitz et al., 2010b), memory (Poldrack et al., 2001), and motivation (Pessiglione et al., 2006), and has been implicated in both movement and cognitive disorders (Kravitz et al., 2010a; Konova et al., 2013; Cerliani et al., 2015). We examine LM1 because it is in a low g-factor area that allows an examination of spatial biases introduced by g-factor. It receives feedforward excitatory input critical for refining movements from the contralateral cerebellar denate nucleus (also a low g-factor area), via the left ventrolateral thalamus (Bastian and Thach, 1995; Dum and Strick, 2003), which is in a high g-factor area.
2. Theoretical Background
2.1. Noise amplification and functional connectivity
Here we present a simplified model of the BOLD signal in which noise amplification reduces correlation. Let xivt represent the BOLD time series for the ith subject, vth location, and tth time point. For the moment, we assume that there is no multiband noise amplification. Let xiv′t denote the time series for another location v′. Then
| (1) |
Here, μv is the mean for the vth location and its variance. The covariance between locations v and v′ is ψvv′. The symbol ~ denotes “distributed as.” In the time series literature, a constant mean and covariance matrix is referred to as “weakly stationary,” which we specify without additional distributional or independence assumptions (Tsay, 2010). In particular, the following model applies to any autocorrelation structure. The contemporaneous correlation between two locations v and v′ is defined as
In SB functional connectivity studies that treat functional connectivity as constant across time, the contemporaneous correlation ρvv′ is the parameter of interest (e.g., Biswal et al. 1995). We do not partition the sources of variance into neuronal, physiological, and thermal noise, as our purpose here is to present a model that conceptualizes the impact of multiband acceleration. Now let yiavt denote the time series with MB factor equal to a. Then we define
| (2) |
where ϵiavt is the noise due to multiband acceleration and is mean zero with variance . Then is the variance due to noise amplification for the ath MB factor and vth location. Additionally, we assume ϵiavt is independent of xivt. In the SB acquisition (a = 1), ϵi1vt = 0 by definition. This model assumes that the covariance is constant across different acceleration factors. In practice, this assumption is likely violated due to signal attenuation in higher MB-factor experiments from shortened TR and therefore reduced equilibrium longitudinal magnetization. However, such reduction in longitudinal magnetization can be reformulated as a proportional increase in noise. Then,
| (3) |
which results in lower correlations.
In this paper, we focus on two possible issues resulting from noise amplification: 1) spatial biases in functional connectivity estimates and 2) statistical power reduction. It is well-known that g-factors vary spatially. Consequently, differs across v. In the model above, this results in spatially heterogeneous noise impacts on the BOLD time series, which lead to differences in functional connectivity between brain regions due to MB factor rather than neural activity.
With regard to statistical power, the trade-off between the costs and benefits of MB acquisition will be impacted by the extent to which the standard errors of the correlations are reduced by the increased number of time points in MB acquisitions. (We assume that the scan time is the same for different MB factors.)
Let zavv′ = arctanh{Corr(yiavt, yiav′t)} be the Fisher z-transformed population correlation. To simplify the discussion, we examine a one-sided one-sample z-test for a true parameter zavv′ with null hypothesis H0 : zavv′ ≤ 0 and alternative hypothesis Ha : zavv′ > 0. (The power function presented here is approximately equal to the power of a t-test for a large number of subjects.) We assume subject Fisher z-correlations have the same mean and variance: for all i = 1, …, N, where the “independently and identically distributed,” is the normal distribution with mean zavv′ and variance , and N is the number of subjects. The BOLD time series generating the correlations are known to contain autocorrelation (i.e., Corr(yiavt, yiav(t−l) ≠ 0 for some lag l), but this does not affect the validity of the assumption that subjects are independent, as discussed in Section 2.2 Autocorrelation and other considerations for multiband data. Let c1−α = Φ−1(1 − α) be the critical value for a level-α test, where Φ(·) is the standard normal cumulative distribution function (CDF) and Φ(·)−1 the inverse CDF. Then the power is
| (4) |
Note that in this model, an increase in the MB factor may simultaneously decrease zavv′, since the noise amplification decreases the correlation via (3), and decrease νavv′, since the higher number of volumes may decrease the standard deviation of the sample correlation (discussed in Section 2.2 Autocorrelation and other considerations for multiband data). Thus, the benefit of MB on functional connectivity estimation depends on the balance between the cost of noise amplification at the locations of interest and the increase in the number of volumes acquired.
Although we have presented (4) for a one-sample test, a similar argument applies to the more common scenario in which correlations are being compared between groups, e.g., healthy and diseased, as described in Appendix A Power when comparing two groups.
2.2. Autocorrelation and other considerations for multiband data
The autocorrelation in multiband data does not affect the validity of the group test statistics in the sense that when the null hypothesis is true, the type-1 error rate is approximately equal to the specified α-level. However, the power is impacted by autocorrelation via the impact on the variance of , denoted . In the absence of autocorrelation (i.e., white noise), , where Ta is the number of time points in acquisition a. For N independent subjects, . In general, in the presence of positive autocorrelation. Intuitively, for a fixed scan time with increasing MB factor a, the benefits of a larger Ta decline as the autocorrelation increases due to a decrease in the effective degrees of freedom. We present an additional discussion of the implications of autocorrelation in Appendix B Implications of autocorrelation on power.
Another complication of MB acquisitions is that correlations may exist between aliased voxels. Voxels collected in the same multiband group are aliased according to the blipped-CAIPI (Controlled Aliasing In Parallel Imaging) field-of-view (FOV) shifts, as illustrated in Todd et al. (2016). In simulations with slice-GRAPPA reconstruction (no leak block), Setsompop et al. (2013) found that MB acquisitions can result in artifactual thermal noise correlations if v and v′ are aliased. Using the model in (2), this implies Cov(ϵiavt, ϵiav′t) ≠ 0 if v and v′ are aliased. Previous studies with task fMRI indicate that the split slice-GRAPPA algorithm, as now used in Siemens reconstruction (leak block), dramatically reduces aliasing artifacts (Cauley et al., 2014; Todd et al., 2016; Risk et al., 2018). In the simplified model in Section 2.1 Noise amplification and functional connectivity, we assume the possible increase in correlations between aliased voxels is negligible. This is discussed more in Section 5.4 Preprocessing pipelines and strategies for artifact and noise removal.
3. Methods
3.1. Participants and imaging protocol
Thirty-two (16 female, ages 19–29) healthy, unmedicated, right-handed young adults participated in this study, who were recruited from Emory University and the surrounding community. Nine six-minute resting-state fMRI runs were acquired from each participant on a 3T MR scanner using a 32-channel head coil padded with foam wedges to decrease head motion. Each participant’s data is from a single session in the same scanner, and two scanners with identical hardware specifications and software version were used throughout the study (MAGNETOM PrismaFit, software version E11C, Siemens Healthcare, Erlangen, Germany). Multiband scans were collected using 2D multiband echo-planar imaging (EPI) sequences with blipped-CAIPI, Development Release R016a, from the Center for Magnetic Resonance Research (CMRR), University of Minnesota (Moeller et al., 2010; Setsompop et al., 2012; Xu et al., 2013). Details on the nine resting-state fMRI acquisitions are in Table 1, with flip angles set to achieve the Ernst angle. Echo time (TE)=32 ms in all acquisitions except MB 12, where TE=32.4. Parameters common to multiband scans include 2 × 2 × 2 mm3 voxels, 208 × 208 mm2 in-plane field of view, 72 slices, 0 mm slice gap, integrated parallel imaging technique (iPat)=none, phase partial Fourier=7/8, anterior-to-posterior (AP) phase encoding direction, interleaved slices, pre-scan normalize, and scanner reconstruction using the LeakBlock option, i.e., split slice-GRAPPA (GeneRalized Autocalibrating Partial Parallel Acquisition) (Cauley et al., 2014), and sum-of-squares coil combination. The MB factors correspond to all possible factors with 72 slices available in the CMRR sequences, which corresponds to all integers a less than or equal to 12 such that 72/a is a whole number. An SB reference acquisition with AP encoding (SBRef AP) was acquired prior to each MB acquisition, which is required for multiband image reconstruction. An additional SB reference acquisition with posterior-to-anterior encoding (SBRef PA) was acquired prior to the MB 3 acquisition for use in distortion correction, as described in Section 3.2 FMRI data processing. The order of the MB factors was randomized for each subject. Participants were asked to lay motionless and look at a cross-hair during resting-state scans. A T1-weighted magnetization-prepared rapid gradient-echo (MPRAGE) sequence (TR/Inversion Time (TI)/TE = 2300/900/3.02 ms, flip angle = 8 degrees, field of view = 256 × 256 mm2, 1 × 1 × 1 mm3 voxels, 176 slices) was collected after the first five resting-state acquisitions. A landscapes movie was played during the MPRAGE acquisition. This study was approved by the Institutional Review Board of Emory University and participants provided written informed consent.
Table 1:
Resting-state fMRI acquisitions. Voxels are isotropic. All runs were approximately six minutes. Volumes corresponding to the first 10 seconds were removed. Degrees of freedom (DF) after 9p+bandpass is equal to the number of volumes minus 3 (constant, linear, quadratic) minus 9 (6 parameters from rigid-body, global signal, white matter, and cerebrospinal fluid) minus the number of frequencies used in the discrete cosine basis in the time-domain bandpass filtering via AFNI’s 3dTproject.
| MB | 1 | 1 | 2 | 3 | 4 | 6 | 8 | 9 | 12 |
|---|---|---|---|---|---|---|---|---|---|
| TR (ms) | 3000 | 5670 | 2850 | 1910 | 1440 | 962 | 736 | 675 | 512 |
| Voxel Size | 3.3 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| Flip Angle | 81 | 88 | 80 | 72 | 65 | 57 | 51 | 48 | 43 |
| Number of volumes | 114 | 62 | 121 | 182 | 241 | 353 | 464 | 505 | 668 |
| DF lost in bandpass | 65 | 13 | 72 | 133 | 192 | 306 | 415 | 458 | 619 |
| DF after 9p+bandpass | 37 | 37 | 37 | 37 | 37 | 35 | 37 | 35 | 37 |
3.2. FMRI data processing
Motion correction.
Volumes corresponding to the first 10 seconds of the run were removed for each acquisition. Then the seven MB acquisitions (MB 2, MB 3, MB 4, MB 6, MB 8, MB 9, MB 12) were motion-corrected to their corresponding SB reference AP images using rigid body alignment (6 DOF) in MCFLIRT (Jenkinson et al., 2002) in FSL 6.0.3. SB 2 mm and SB 3.3 mm were registered to the eighth volume of their scans.
Susceptibility distortion correction.
The SBRef PA acquisition was rigid body aligned to the SBRef AP MB 3. Then FSL’s topup was applied (Andersson et al., 2003; Smith et al., 2004). The 2 mm resting-state acquisitions were then aligned to the SBRef AP MB 3 using a rigid body transformation, topup applied, followed by slice-timing correction. The 3.3 mm acquisition was slice-timing corrected, spline-interpolated to 2 × 2 × 2 mm3 resolution, followed by topup.
Co-registration and normalization to MNI.
Distortion and motion-corrected resting-state acquisitions were then rigid-body aligned to the anatomical image. The anatomical image was non-linearly registered to the Montreal Neurological Institute 152 template in FSL (MNI152_T1_2mm) using FNIRT, and the warping function was then applied to the resting-state acquisitions. Acquisitions were then skull stripped and intensity normalized to result in the global (4d) mean equal to 10,000 (Glasser et al., 2013).
Nuissance regression, temporal filtering, and spatial smoothing.
We further processed the data to minimize BOLD variance unlikely to represent neural activity in preparation for functional connectivity analyses using the “9p” nuisance regression model in Ciric et al. (2017). The nine nuisance regressors in this model are the six rigid body realignment parameters, global signal, average cerebrospinal fluid (CSF) signal, and average white matter (WM) signal. We chose this model because global signal regression (GSR) is particularly effective at removing head motion and respiratory-related artifacts from functional connectivity estimates (Power et al., 2017, 2019, 2020), and the 9p pipeline maximized a measure of network quality in Ciric et al. (2017), suggesting a balance between reducing artifacts and preserving signal. We chose a pipeline commonly found in the literature, rather than a more specialized pipeline, to improve the generalizability of our results. In addition, we implemented three variations of the 9p pipeline to investigate the impacts of temporal filtering and spatial smoothing: 1) 9p with bandpass filtering applied during nuisance regression, hereafter denoted as 9p+bandpass; 2) 9p with 6-mm full width at half maximum (FWHM) spatial smoothing, hereafter 9p+spatial smoothing; and 3) 9p+bandpass+spatial smoothing. We used the FSL tissue priors for WM and CSF, where a binary mask was created by setting voxels equal to one if their probability was greater than > 0.5 and zero otherwise. Nuisance regression, bandpass filtering, and spatial smoothing were implemented using AFNI 19.3.16 (Cox, 1996). We used AFNI’s 3dTproject to bandpass from 0.009 to 0.08 Hz, in which a single design matrix is created from the nuisance regressors and cosine and sine functions (at the frequencies 0 to 0.009 and 0.08 and higher). This simultaneously performs bandpass filtering and nuisance removal, as recommended in Hallquist et al. (2013), Lindquist et al. (2019), and Bright et al. (2017), and the residuals from least squares are retained for subsequent correlation analyses. In Table 1, we indicate the number of regressors included in the nuisance regression, where “DF lost in bandpass” indicates the number of covariates included in the design matrix to achieve bandpass filtering.
In line with recent recommendations (Ciric et al., 2017), we excluded scans with excessive gross motion defined as scans with mean relative root mean squared displacement exceeding 0.2 mm or 1/6th of scans exceeding 0.25 mm relative root mean squared displacement, resulting in the exclusion of nine scans. Additionally, MB 9 scans were not collected in the first two subjects. Thus, there were 277 scans used in subsequent analyses (31 SB 3.3 mm, 31 SB 2 mm, 30 MB 2, 29 MB 3, 31 MB 4, 32 MB 6, 32 MB 8, 29 MB 9, 32 MB 12).
3.3. Noise amplification
For each scan and processing pipeline, we calculated the standard deviation of the time series on a voxel-wise basis, creating a standard deviation map for each scan. Let denote the sample standard deviation for the vth voxel and ath acceleration factor in the ith subject, calculated across the Ta time points. Recall the definitions of and from equations (1) and (2) in Section 2.1 Noise amplification and functional connectivity. Then , where E denotes the expectation. For each pipeline, we calculated , resulting in the average standard deviation maps. We visually assessed how bandpass filtering impacted the variance due to noise amplification, and also the variance due to physiological sources (CSF and cardiac) that still remained after nuisance regression.
The g-factors provide insight into which brain regions may be adversely impacted by noise amplification resulting from multiband acquisition and reconstruction. In the absence of acceleration, thermal noise is white noise that is spatially and temporally homogeneous and independent of the signal (Chen et al., 2019). With no in-plane acceleration, the noise amplification of the thermal noise component can be described by defining the g-factor as g = SNRfull/SNRacc, where SNRfull is the signal-to-noise ratio in the single-band data and SNRacc is the SNR in the accelerated multiband data (Breuer et al., 2009). In this study, we do not use in-plane acceleration in rs-fMRI acquisitions.
Since we obtained SB and MB images from every subject, we generated apparent g-factor maps in the processed data as the ratio of the standard deviation across time in the accelerated acquisitions to the standard deviation in the SB 2 mm acquisition for each subject. Let denote the standard deviation for the ith subject in the SB 2-mm acquisition at the vth location. The apparent g-factor is defined
| (5) |
This definition is similar to that used in Preibisch et al. (2015), except that we use the ratio of standard deviations in preprocessed data rather than SNR from minimally preprocessed data. Recall the mean of the data are scaled to equal 10,000 prior to nuisance regression, which ensures the standard deviations are on comparable scales. Also note the nuisance regression removes the mean, so a ratio of SNRs is not possible. The nuisance regression decreases the standard deviation by reducing physiological and motion effects. If the shorter TR in multiband facilitates the removal of nuisance variance, then this measure accounts for this benefit. It is noteworthy that this ratio combines the effects of reconstruction noise, physiological noise, and reduced signal due to reduced longitudinal magnetization resulting from the shortened TR.
In addition, we partitioned the brain into 247 cortical, 13 subcortical, and four cerebellar regions of interest (ROIs) defined using 5-mm radius spheres centered at the MNI coordinates in Power et al. (2011), and calculated the apparent g-factors for each of the 264 nodes. These g-factors were then visualized using the BrainNet viewer 1.7 (Xia et al., 2013).
3.4. Impacts on seed map correlations
We examined the impact of acquisition on connectivity for two seed regions: 1) a 4-mm radius sphere in the dorsal rostral putamen centered at MNI (25, 8, 6), which is in a high g-factor area and was found to have hyperconnectivity in children with ASD (Di Martino et al., 2011), and 2) a 5-mm radius sphere centered at MNI (−41, −20, 62), which is in a low g-factor area, was identified as the peak task-related activation localized to the precentral gyrus during a right-hand finger sequencing task in Buckner et al. (2011), and is connected to other motor regions in both low and high g-factor areas.
For each seed, scan, and processing pipeline, time series for voxels within the seed region were averaged, and a seed correlation map generated by calculating the correlation between the seed time course and every other voxel in the brain. We visualized maps for each seed by averaging these correlations across subjects for each acquisition and pipeline. We also compared connectivity effect sizes for each seed by Fisher z-transforming the correlations and then calculating Cohen’s d. For a given correlation, the Cohen’s d statistic characterizes the effect size against the null hypothesis that the group correlation is equal to zero. Our primary analysis used the 9p and 9p+bandpass pipelines, allowing the possibility of higher resolution seed maps for the 2 mm acquisitions. Results with smoothing are presented in the Web Supplement.
3.5. Impacts on pairwise correlations in a functional atlas
3.5.1. Impacts on the magnitude of correlations
To calculate functional connectivity between pairs of brain regions, we again used the set of 264 5-mm radius spheres centered at the MNI coordinates in Power et al. (2011). This commonly used atlas is based on functional areas and classifies ROIs (nodes) into thirteen functional communities, with some nodes labeled in a fourteenth category as “uncertain.” An advantage of this parcellation is that all nodes are the same size; parcellations with regions of different size result in an additional source of heteroscedasticity unrelated to noise amplification, where larger regions tend to have reduced variance. Using Matlab R2020a, time series for voxels within each 5-mm sphere were averaged; correlations between average ROI time series were calculated and Fisher z-transformed.
To understand the impact of MB factor on pairwise correlations, we propose a measure that combines the effects of the standard deviations at each node (ROI) in an edge:
| (6) |
where giav is defined in (5). We define two different sets of g*-factors to correspond to the standard deviations from the 9p and 9p+bandpass pipelines. To visualize the impact of g*-factors on edge correlations, we averaged Fisher z-transformed correlations across subjects for each edge, i.e., , and then plotted the MB correlations versus the SB 2 mm correlations for each edge colored by .
Next, we visualized plots of correlation matrices for the 9p and 9p+bandpass pipelines to see where the impacts occurred. We excluded the “uncertain” category from visual summaries of the correlation matrices. Plots from 9p+spatial smoothing and 9p+bandpass+spatial smoothing were similar and are not displayed.
To statistically examine the impacts on power, we subset to select intra-community edges where we expect positive correlations (i.e., edges between nodes within the same functional community) and which represented a range of g*-factors. Specifically, we used an edge between the left and right thalamus (ROIs 224 and 225), left and right putamen (227 and 230), left and right cerebellum (244 and 245), six edges from nodes in executive control (192, 195, 196, 201), salience (212, 217, 218, 220), and default mode (88, 92, 109, 110). The cortical nodes were selected based on their proximity to the regions in Chand et al. (2017).
Using this subset, we created a generalized additive mixed model (GAMM) (Gaussian family) with the Fisher z-transformed correlations as the response variable, a smoother for g*-factor (g*iavv′) with smoothing selected using restricted maximum likelihood (REML), fixed effects of edge, gender, and scanner, a random effect for participant, and a random effect for the interaction between participant and edge using the package mgcv 1.8–33 (Wood, 2017) in R 3.6.0. The use of the GAMM allows for a possible non-linear relationship between the Fisher z-transformed correlations and g*-factor. Note this analysis pools across the MB factors, where the MB factor drives the variation in g*-factors, with repeated measurements accounted for via the random effects. Also note that we did not conduct a parallel analysis with 9p+bandpass because the bandpass filtering results in g*-factors close to one, as will be seen in Section 4.3 Impacts on pairwise correlations in a functional atlas.
We used generalized estimating equations with robust standard errors (Gaussian family) implemented in the R package geepack 1.3–1 (Halekoh et al., 2006) to examine the impact of MB factor on correlations for the subset of intra-community edges described above. We conducted this analysis for the 9p, 9p+bandpass, 9p+spatial smoothing, and 9p+bandpass+spatial smoothing. We created separate models for the thalamus, putamen, cerebellum, executive control, salience, and default mode. The Fisher z-transformed correlation was the response variable with MB factor, gender, and scanner as categorical variables and participant id as the clustering variable. The SB 2 mm acquisition was used as the reference level for MB factor.
3.5.2. Impacts on edge density
We examined edge density for each of the thirteen communities. For each pipeline, we conducted one-sample t-tests for each edge to test that the population correlation was equal to zero using the sample z-transformed correlations from each subject. There were a few spheres in the “uncertain” category (ROIs 4, 5, 9, 10, and 250) and one in default mode (ROI 83) that contained no data in some subjects in the SB 3.3 mm distortion-corrected image. We excluded these six nodes. We calculated the proportion of significant edges for each of the communities in Power et al. (2011) using the Bonferroni-level α = 0.05/(258 * 257/2), which suffices here since the effect sizes are large. The proportions were calculated using all possible edges (i.e., inter- and intra-community). Since the number of subjects for each MB factor varied from 29 to 32, we standardized the power across MB factor by calculating the t-statistics as the Cohen’s d multiplied by (the most common number of subjects) and used a t-distribution with df = 31 for all MB. Thus differences in the proportion of activated voxels are primarily attributable to MB factor rather than sample size.
We assessed whether the differences between the proportion of significant correlations were meaningful by conducting permutation tests using MB 8 as a reference as follows: 1) we subset to subjects that passed the quality control criteria in both the given acquisition and MB 8; 2) permuted the MB factor to create pseudo acquisition groups; 3) for each pseudo group and for each edge, calculated one-sample t-tests; 4) for each pseudo group and each community, calculated the proportion of edges with significant correlations at α = 0.05/(258*257/2) (including all edges in which at least one node belonged to the community); and 5) for each community, calculated the absolute value of the difference between the proportion significant in pseudo group 1 and the proportion significant in pseudo group 2. These steps were repeated 10,000 times, and we then calculated the fraction of absolute differences from the pseudo groups that were greater than the absolute difference when using the true MB factor labels, thereby generating two-sided (uncorrected) p-values. Our primary analysis focused on the 9p and 9p+bandpass pipelines, with additional results for 9p+spatial smoothing in the Web Supplement. We also conducted permutation tests using the same steps to compare the proportion of significant correlations in 9p versus 9p+bandpass for each multiband factor. These tests were implemented using our own scripts in R 3.6.0.
3.6. Impacts in independent datasets
3.6.1. Evaluation of a third scanner using a 64-channel head coil
We examined whether our findings were similar in a dataset with three additional subjects (all 27 years old, 1 female) collected using a 64-channel head and neck coil at the Center for Advanced Brain Imaging and Neurophysiology, University of Rochester, NY, USA. The same acquisition and preprocessing was applied to these subjects. In this cohort, the mean relative root mean squared displacement was < 0.2 mm in all acquisitions. There were four acquisitions in which > 1/6 of volumes had > 0.25 mm framewise displacement (subject 1: SB 2 mm and MB 2; subject 3: MB 4 and MB 6). Unlike the primary cohort, all acquisitions were used in subsequent analyses because we only had three subjects.
We created standard deviation maps averaged across the three subjects, as in 3.3 Noise amplification, for 9p and 9p+bandpass.
We created seed maps for the dorsal rostral putamen described in Section 3.4 Impacts on seed map correlations for the four pipelines (9p, 9p+bandpass, 9p+spatial smoothing, 9p+bandpass+spatial smoothing).
We calculated Fisher z-transformed correlations as described in Section 3.5.1 Impacts on the magnitude of correlations and compared the correlation matrices across multiband factors.
3.6.2. Evaluation of pairwise correlations in the preprocessed Young Adult Human Connectome Project data
To gain insight into the generalizability of spatial differences in correlations and effect sizes to other pipelines and datasets, we estimated correlation matrices from the ICA-FIX preprocessed rs-fMRI data in the Young Adult Human Connectome Project, which used MB 8 (Smith et al., 2013). This analysis in presented in Web Supplement S.4.2 Evaluation of pairwise correlations in the preprocessed Young Adult Human Connectome Project data.
4. Results
4.1. Noise amplification
The impact of multiband acceleration on noise amplification is clearly visible from the voxel-wise standard deviations of the resting-state time series (Figure 1). There is a shift from a physiologically dominated noise regime in SB acquisitions, in which there are large contributions to the BOLD signal from CSF pulsation in the third ventricle, cerebral aqueduct, fourth ventricle, and central canal, and the sagittal sinus is also apparent (prominent in MB 3 in first column), to a reconstruction-noise dominated regime (standard deviations greater than 300 across interior regions in MB 8 and higher, column A of Figure 1). Although CSF nuisance regression reduced physiological noise variance, CSF pulsation still appears to be prominent in some regions. There may also be variance due to intracranial brain motion during the cardiac cycle. Examining column B, it is clear that the bandpass filtering reduces physiological sources of variance in the acquisitions with higher sampling rates, as the CSF contributions in MB 4 to MB 12 are much less prominent relative to SB 3.3 mm, SB 2 mm, MB 2, and MB 3. Adjusting the color gradient to increase the contrast in the 9p+bandpass maps, in column D we see that there are still sources of physiological variance at the high sampling rates, but it is reduced relative to slower acquisitions. Overall, the variance of MB 4 and greater is reduced relative to SB, MB 2, and MB 3. In the SD maps for the 9p+spatial smoothing and 9p+bandpass+spatial smoothing, the standard deviation is greatly reduced relative to unsmoothed data, as expected. The noise amplification increases with MB factor in the 9p+smooth pipeline, and physiological noise variance is reduced with bandpass filtering at higher MB factors, similar to the unsmoothed data (Web Supplement Figure S.3).
Figure 1:
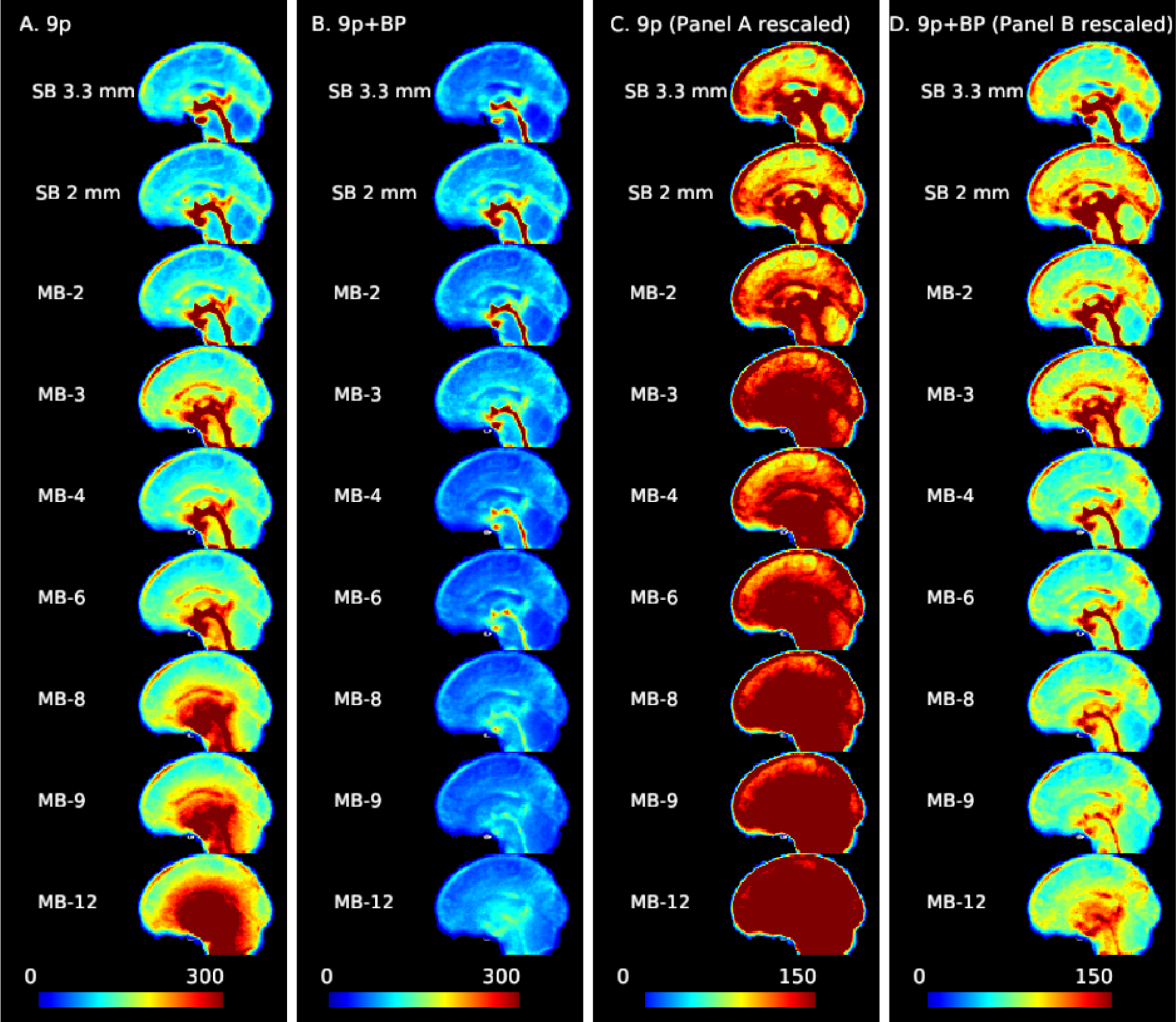
Noise amplification due to multiband acceleration and impacts of bandpass filtering. The standard deviation of the time series for each voxel (averaged across subjects) with 9p preprocessing (columns A and C) and 9p+bandpass (columns B and D). Sagittal slice with cursor at MNI=0. At higher MB factors, variance from noise amplification becomes more prominent. Columns A and B use a scale from 0 to 300, and columns C and D are the same data but using a scale from 0 to 150. As the MB factor increases, there is a shift from the physiologically dominated noise regime (in which the CSF pulsation is visible in the central canal, third ventricle, cerebral aqueduct, and fourth ventricle, with possible contributions from the superior and inferior sagittal sinus) to physiological plus noise amplification. The bandpass filtering reduces the overall variance and physiological contributions of CSF, veins, and arteries. In the rescaled version (column D), some ventricles, veins, and arteries are still visible at higher MB factors but less prominent.
Examining g-factor by node revealed patterns largely consistent with those observed in the standard deviation maps. For the 9p processed data, g-factors are smallest for MB 2 (close to one) with increases in subcortical areas, as well as some nodes in the insula and medial areas (Web Supplement Figures S.1 and S.2). In subcortical nodes, g-factors were near 1.5 in MB 4, 2.25 in MB 8, and 3 in MB 12 (see Web Supplement File 1 containing g-factors for each node), moderate noise amplification in the cerebellum (approximately 1.3 in MB 4, 1.6 in MB 8, and 2.4 in MB 12), low noise amplification in somatomotor regions (approximately 1.2, 1.3, and 1.6 for MB 4, 8, and 12), and low in visual regions (approximately 1.3, 1.4, and 1.6 for MB 4, 8, and 12). For 9p+bandpass data, g-factors are close to one even in subcortical regions (approximately 1.0 in MB 4, 1.1 in MB 8, and 1.2 in MB 12), and tend to be less than 1 in cortical regions, indicating decreased variation relative to the SB 2 mm (e.g., MB 8 in the right column in Web Supplement Figure S.2 is in general more blue than MB 2 in the right column in Web Supplement Figure S.1). This is consistent with Figure 1, in which the higher MB factors have smaller standard deviations.
4.2. Impacts on seed map correlations
Figure 2 illustrates correlation and effect size maps for the dorsal rostral putamen seed. For the 9p pipeline (column A), robust functional connectivity is observed with the left putamen as well as with the insula (fuchsia arrow) and bilateral thalamus (green arrow) in the SB 3.3 mm data. Weak correlations with the cingulate cortex (anterior and medial to the putamen, red arrow) are also visible. For SB 2 mm, MB 2, and MB 4, correlations with the left putamen and bilateral insula are visible but weaker than SB 3.3 mm, whereas these correlations are very small in MB 8 and higher. For the 9p+bandpass pipeline (column B), the correlations are generally higher, resulting in clear delineation of the left putamen in MB 2 to MB 8, although correlations with the cingulate are still not visible. Correlations in the insula and thalamus are stronger in SB 3.3 mm, MB 2, and MB 4 than in other acquisitions. In the left insula, there is a suggestion of better spatial specificity in MB 2 and MB 4 versus SB 3.3 mm, where the higher resolution may result in an improvement in the boundary between the left putamen and insula.
Figure 2:
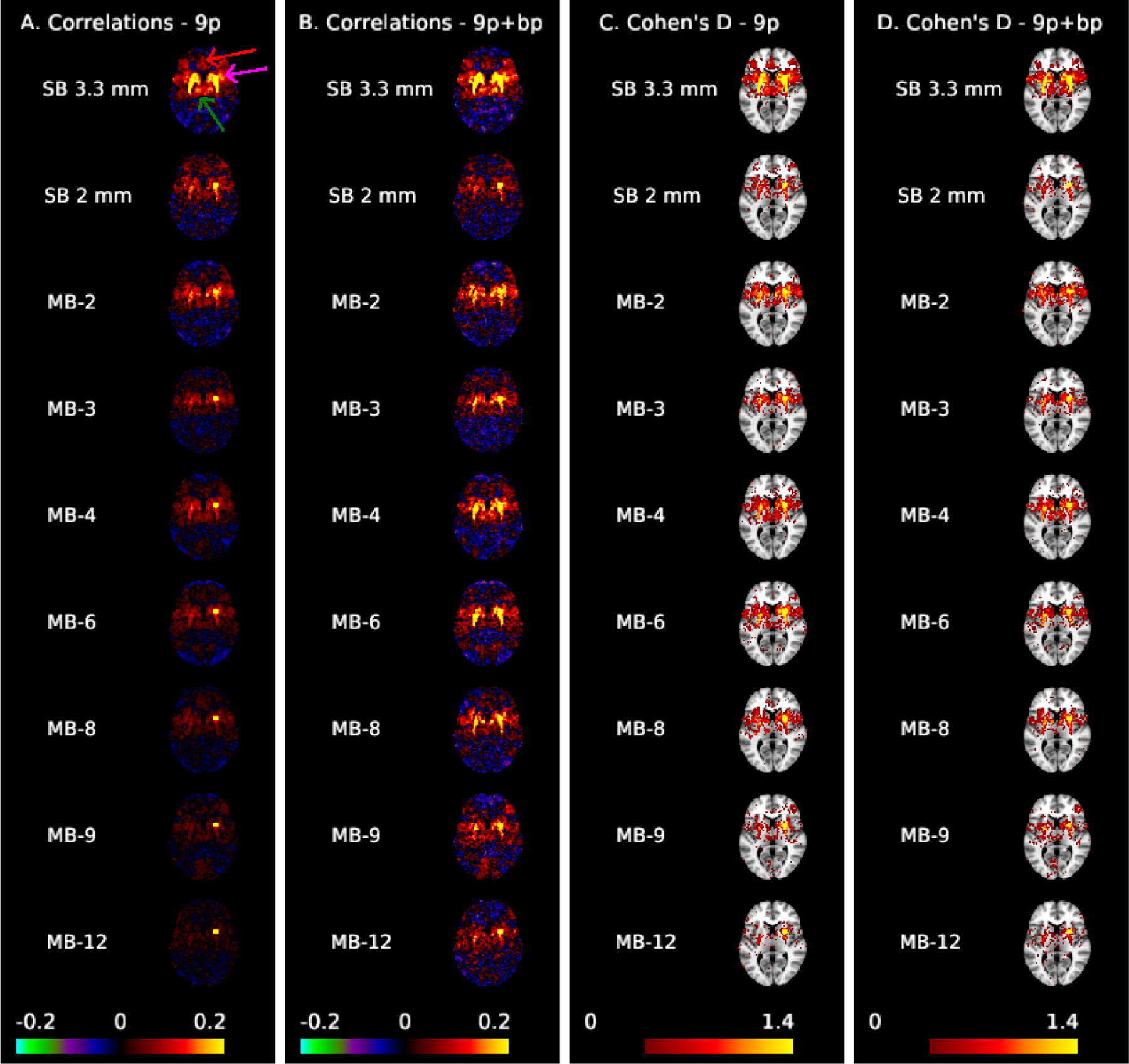
Correlation (A,B) and Cohen’s d maps thresholded to display values >0.4 (C,D) for the dorsal rostral putamen seed (MNI: 25, 8, 6) shown at MNI axial slice 6. The arrows in column A highlight the cingulate cortex (red), insula (fuchsia), and thalamus (green). Spatial biases in the correlations increase as MB factor increases; ipsilateral correlations with the thalamus and insula, as well as contralateral correlations are not apparent for MB 8 and higher in preprocessing without temporal filtering (A). These biases are reduced with bandpass filtering (B), which results in clear left-right putamen functional connectivity in MB 2 to MB 8. Effect sizes are larger in single-band 3.3 mm.
Comparing the rows in column C of Figure 2, the effect sizes within the putamen are notably higher in SB 3.3 mm compared to the other acquisitions. Among the 2 mm acquisitions, contralateral effects are more apparent in MB 4, MB 2, and MB 6 than others. Contralateral effects decline at MB 8 and higher, and are also relatively poor in SB 2 mm. Putamen-cortical and putamen-thalamic connectivity also appear higher in SB 3.3 mm compared to the 2 mm acquisitions. Areas of the cingulate cortex are visible in SB 3.3 mm in 9p (see red arrow in column A) but are reduced in 9p+bandpass (column D); this area has Cohen’s d < 0.4 in the MB and SB 2 mm acquisitions (columns C and D). In spatially smoothed data, the effect sizes were also largest in SB 3.3 mm (Web Supplement Figures S.4 and S.5). Effect sizes were overall much higher in spatially smoothed data, but at the cost of a decrease in spatial specificity, and large effect sizes extended across anatomical boundaries. In particular, the putamen and thalamus appear as a single structure (Web Supplement Figure S.4). The differences in effect sizes between SB 3.3 mm and the MB acquisitions are clearly illustrated in Web Supplement Figure S.5. In summary, SB 3.3 mm most clearly reveals both cortical and subcortical functional connectivity with the putamen.
Figure 3 illustrates correlation and effect size maps for the LM1 seed. The correlations between the motor cortex and the thalamus (green arrow) are clearly visible in the SB 3.3 mm acquisition for both 9p and 9p+bandpass (columns A and B, respectively), but less apparent in the MB acquisitions. The left motor cortex is an area with low g-factor (approximately 1.15, 1.25, and 1.7 for MB 4, MB 8, and MB 12, respectively), while the thalamus is an area with high g-factor (approximately 1.25, 3.25, and 4.75 for MB 4, MB 8, and MB 12). Thalamocortical correlations are very small in the MB acquisitions with 9p, and are still weak in most MB acquisitions in 9p+bandpass, with MB 2 and MB 4 showing stronger correlations than higher MB factors. In the thresholded Cohen’s d maps, the 9p and 9p+bandpass (columns C and D, respectively) show similar results overall. Again, thalamocortical connectivity is clearly apparent in the SB 3.3 mm acquisition, with smaller but notable effect sizes in the MB 2 to MB 6 acquisitions. In contrast, connectivity with right M1, which is in a low g-factor area, is strong across all acquisitions. In addition, seed and Cohen’s D maps in Figure 3 nicely trace portions of the insular cortex, with larger effect sizes in SB 3.3 mm.
Figure 3:
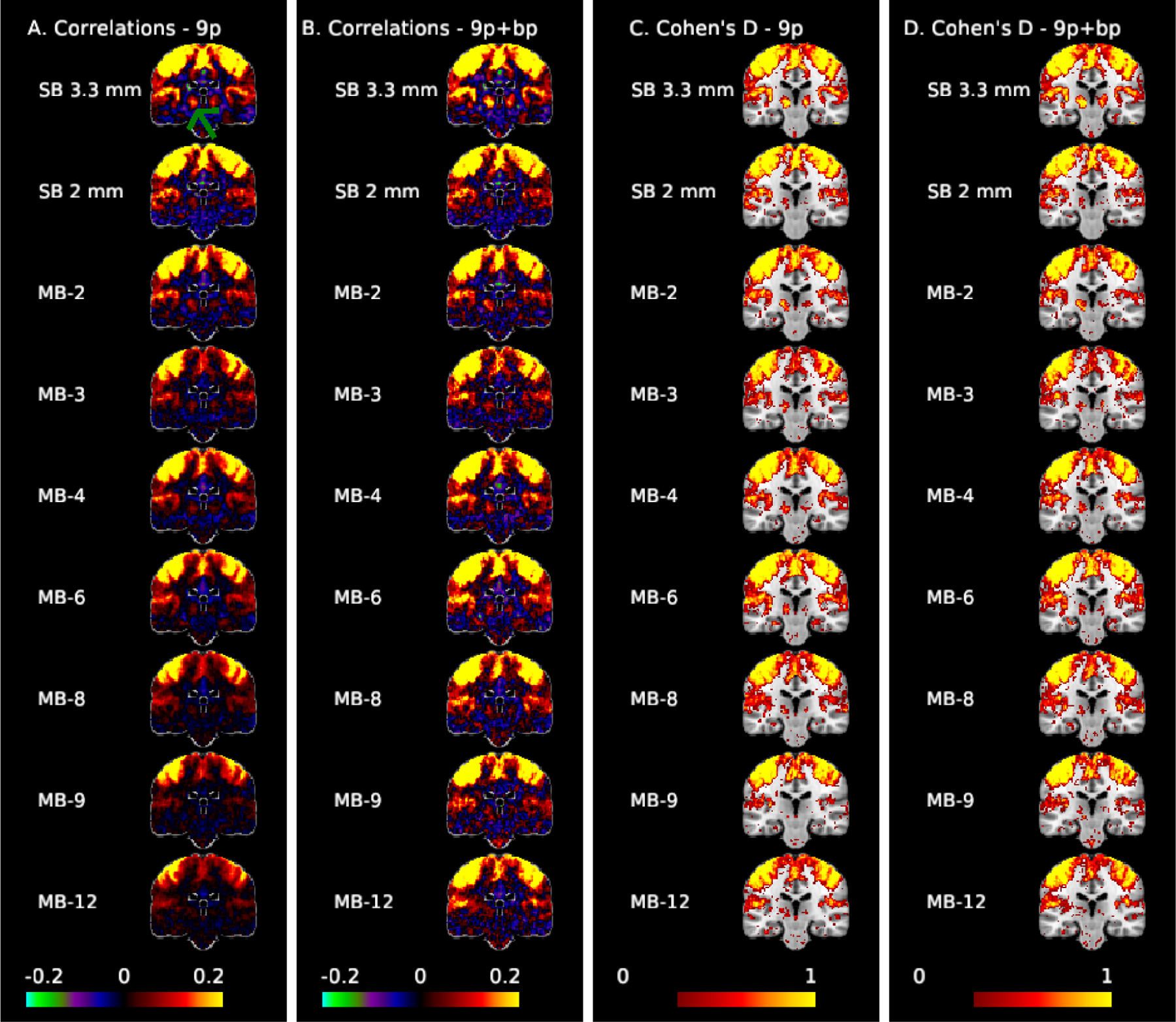
Correlation (A,B) and Cohen’s d maps thresholded to display values >0.3 (C,D) for the motor seed (MNI: −41, −20, 62) at coronal slice −24 to examine motor-thalamic pathways. The green arrow points to the thalamus. Thalamocortical connectivity is clearly apparent in the SB 3.3 mm acquisition, with smaller but notable effect sizes in the MB 2 to MB 6 acquisitions.
We also examined the correlations between the left motor cortex and a region in right lobule V of the cerebellum with low-to-moderate g factor (approximately 1.5, 2.2, and 3.7 for MB 4, MB 8, and MB 12). The cerebellum is structurally connected to the motor cortex via both efferent and afferent pathways through the ventrolateral thalamus and the pontine nucleus, respectively; consequently, some degree of functional connectivity is expected. For example, Buckner et al. (2011) observed correlations of roughly 0.08 between the left motor cortex and the right lobule V using SB data collected from 1000 participants, and these correlations were notably higher than in neighboring locations within the cerebellum. In Web Supplement Figure S.6, this area is only faintly apparent in most acquisitions in 9p, with largest correlations at MB 2 (around 0.10), most acquisitions around 0.05, and small or negligible correlations in SB 2 mm and MB 12. The region is more apparent in 9p+bandpass, with correlations greater than 0.10 for SB 3.3, MB 2, 3, 4, 6, 8, and 9, but are poorly captured at SB 2 mm and MB 12. In the Cohen’s d maps (Web Supplement Figure S.7), these areas are best represented by MB 2 in both 9p and 9p+bandpass, with comparable spatial extents from MB 2 to MB 8. The effect sizes in this region of the cerebellum for SB 3.3 mm are smaller than MB 2 to MB 8. This implies that there is not a single optimal MB factor for seed maps, but the general pattern is that SB 3.3 mm performs better in areas with high g-factor and MB 2 to 6 in areas with moderate and low g-factor.
4.3. Impacts on pairwise correlations in a functional atlas
4.3.1. Impacts on the magnitude of correlations
Higher standard deviations in multiband acquisitions led to smaller correlations in the 9p pipeline, and bandpass filtering reduced g*-factors to result in greater similarity across acquisitions. Figure 4 depicts scatterplots of the correlations for each edge at a given MB factor versus the correlation for the SB 2 mm acquisition. Each data point corresponds to the average of the Fisher z-transformed correlations for an edge in the 264-node atlas. The points are colored according to their g*-factor, where the color scale varies from a g*-factor of one in blue, which represents no noise amplification relative to SB 2 mm, to four in red, in which the denominator in the correlation is approximately four times larger in the MB acquisition than SB 2 mm. In the absence of multiband impacts, we expect the points to lie approximately along the line y = x. In the positive quadrant x > 0, y > 0, points below the line y = x indicate correlations that are smaller in the MB acquisition along the y-axis than in the SB 2 mm; similarly, points above the line y = x in the quadrant x < 0, y < 0 represent smaller correlations relative to SB 2 mm.
Figure 4:
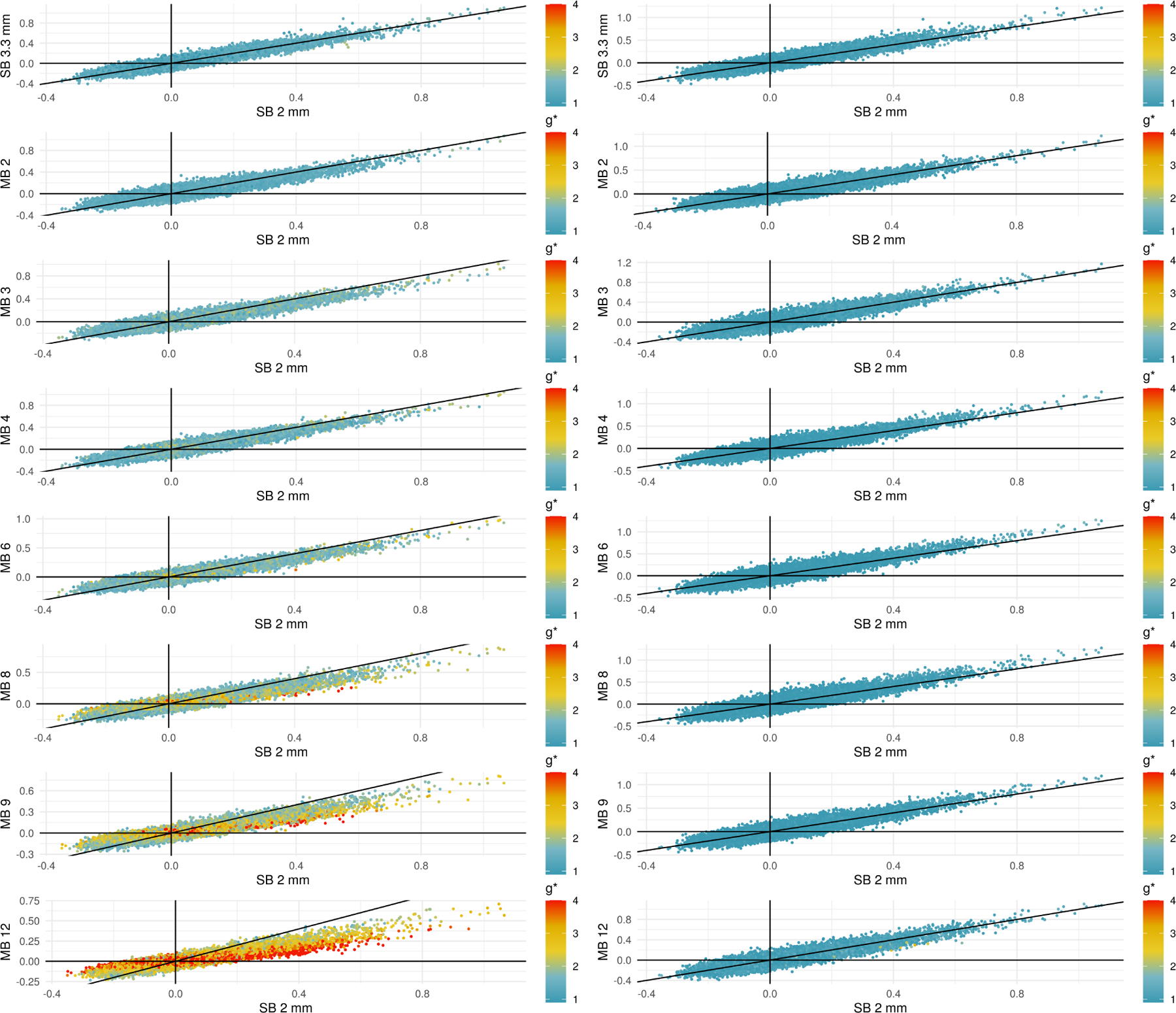
Scatterplots comparing correlations in SB to different MB acquisitions using 9p processing (left) and 9p+bandpass (right). The black line occurs at y = x, and points below the line in the quadrant x > 0, y > 0 represent positive correlations that are attenuated in the MB acquisition. Points above the line in x < 0, y < 0 represent negative correlations that are attenuated at the higher MB factors. Points are colored by their g*-factors, which are defined for each pipeline; see (6). In the 9p pipeline, the g*-factors are larger at higher MB factors, and points with high g-factors tend to lie closer to the line y = 0. In the 9p+bandpass, the g*-factors are closer to one, even at higher MB factors, and the points tend to fall closer to the line y = x.
In the 9p pipeline (left column), we see that at higher MB factors, the g*-factors are larger, and points with high g-factors tend to lie closer to the line y = 0. This provides evidence that noise amplification can lead to smaller correlations.
In the 9p+bandpass (right column), we see that overall the g*-factors are closer to one, even at higher MB factors, and the points tend to fall closer to the line y = x. This indicates that the correlations are now more comparable across MB factors.
Using generalized additive mixed models to statistically test these patterns, we observed that increased g*-factors did, in fact, significantly decrease correlations for the subset of edges described in Section 3.5.1 Impacts on the magnitude of correlations (p < 0.001). For example, a Fisher z-correlation equal to 0.35 decreased to approximately 0.05 for g*-factor=1 versus g*-factor=8 when controlling for edge, gender, and scanner (Figure 5). Note gender and scanner were not significant (p > 0.05).
Figure 5:
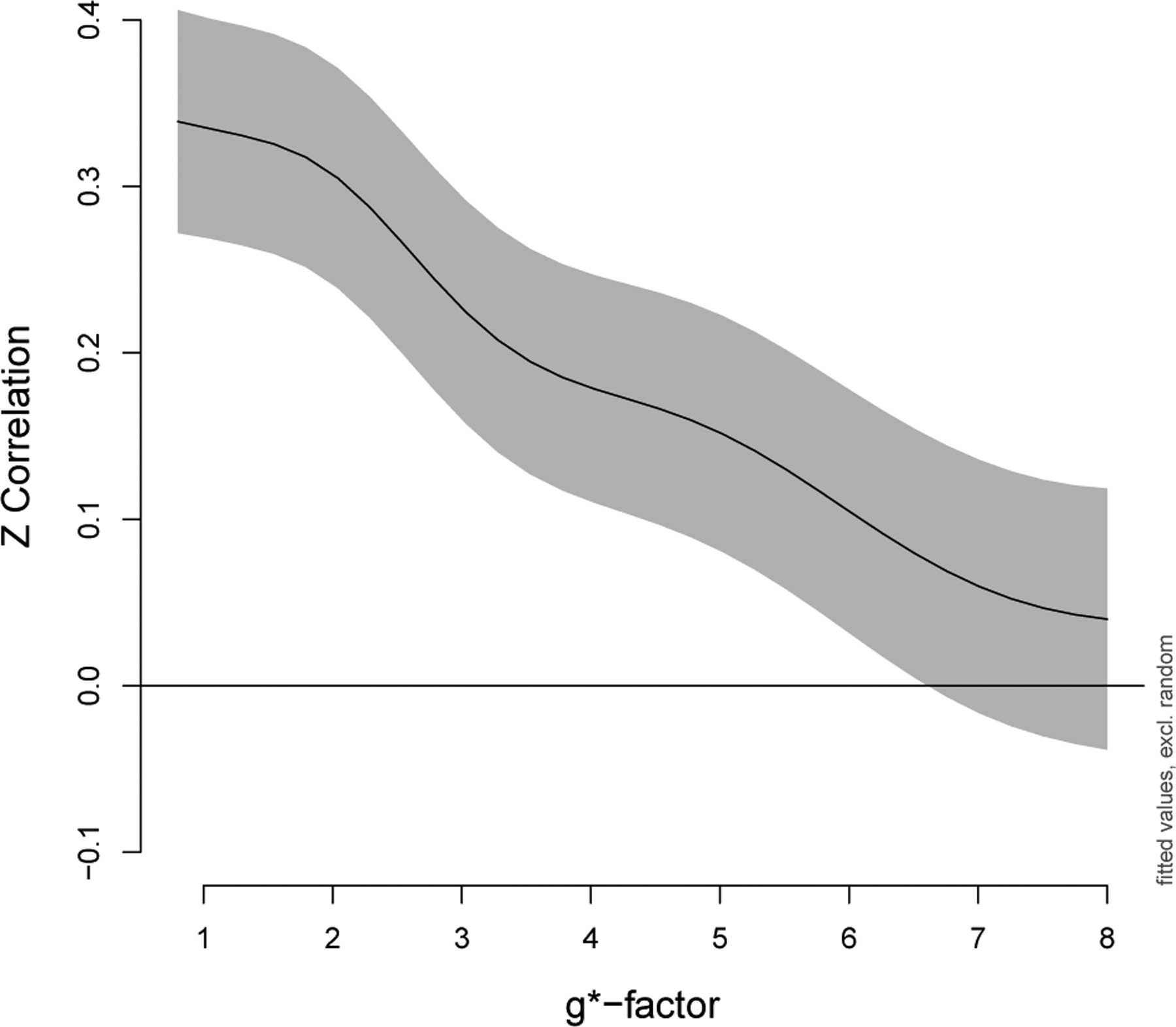
Correlations decrease as noise amplification increases. Fisher z-transformed correlations in a subset of edges that were a priori expected to have positive correlations, as described in Section 3.5.1 Impacts on the magnitude of correlations, were analyzed using a generalized additive mixed model. The overall effect of g*-factor was highly significant (p < 0.001). The GAMM includes a smoother for g*-factor with penalty selected using REML, fixed effects for edge, gender, and scanner, and random effects for participant and participant × edge. The y-intercept in this figure corresponds to the edge with median correlation (nodes 92 and 109, default mode). Gray indicates point-wise 95% confidence intervals.
Examining plots of the correlation matrices sorted by community allows us to explore where these impacts occur (Figure 6). For 9p processed data (upper diagonals in Figure 6), we see that the effects of acceleration differ across space. A close inspection reveals that when comparing the upper diagonal in MB 4 to the upper diagonal in MB 8, intra- and inter-community correlations involving salience, auditory, cingulo-opercular task control, somatomotor, and subcortical regions tend to be smaller in MB 8 than MB 4. In contrast, correlations are more comparable within the visual system across most acquisitions. A focused view on subcortical and cerebellar ROIs reveals large decreases in correlations when no temporal filtering is applied (upper diagonal of Web Supplement Figure S.8). Many correlations exceed 0.3 in SB and MB 2 to 4, but these correlations are decreased in MB 8 to MB 12.
Figure 6:
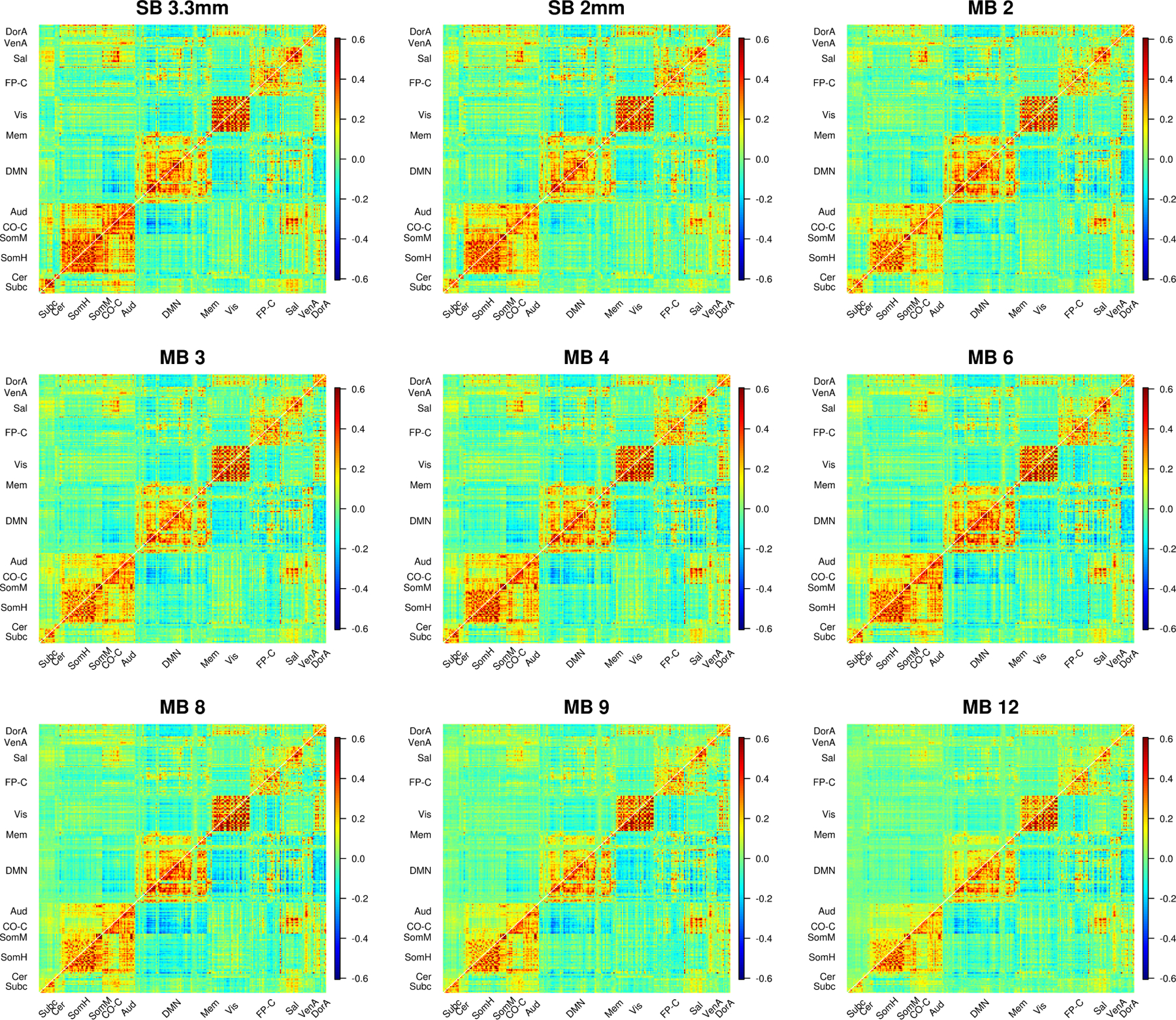
Average correlations (Fisher z-transformed) for SB and MB acquisitions. 9p processing is above the diagonal and 9p+bandpass below. In 9p, the effects of acceleration differ across space, e.g., we see smaller correlations involving salience, auditory, cingulo-opercular task control, and subcortical regions in MB 12 than MB 4; a close inspection reveals MB 8 also tends to be lower than MB 4 in these edges. In contrast, correlations are more comparable within the visual system across most acquisitions. In 9p+bandpass, the correlations across MB factor are more similar (below diagonal). Web Supplement Figure S.8 depicts a zoomed in version of subcortical and cerebellar edges that more clearly illustrates lower correlations at higher MB factors for these regions. Web Supplement S.9 and S.10 illustrate impacts on edges that are expected to have positive correlations.
In contrast, correlations in the 9p+bandpass processed data (lower diagonals in Figure 6) appear similar across MB acquisition. A close inspection indicates that SB 3.3 mm has the highest correlations within subcortical and within cerebellum, and correlations are somewhat reduced in MB 8 to MB 12 (Web Supplement Figure S.8). In general, temporal filtering tends to increase correlations in MB accelerations, with relatively minor effects for SB and MB 2.
Next, we narrowed our focus to edges expected to have positive correlations (as described in Section 3.5.1 Impacts on the magnitude of correlations). In the 9p processed data, we observed large differences between the SB 2 mm acquisition and other acquisitions, with Fisher z-transformed correlations tending to decrease as MB factor increases for all communities (Table 2 and Web Supplement Figure S.9). Correlations were lower in MB 8, MB 9, and MB 12 compared to SB 2 mm for all communities (p ≤ 0.001). These decreases were most prominent in the thalamus and putamen, and in particular the impacts were more severe when the g*-factors were higher (Web Supplement Figure S.9). In the thalamus, MB 2 to 6 correlations were comparable to SB 2 mm correlations (p > 0.05). The putamen appears more sensitive to MB acquisitions than the thalamus, as MB 3 to MB 6 correlations were lower than SB 2 mm (p < 0.01) in addition to MB 8 to MB 12. Correlations involving the thalamus and putamen were higher in SB 3.3 mm data compared to SB 2 mm data (p < 0.001).
Table 2:
Impact of MB factor on Fisher z-transformed correlations for selected edges (see Section 3.5 Impacts on pairwise correlations in a functional atlas). Estimates, standard errors, and p-values (uncorrected) from generalized estimating equations with robust standard errors. The intercept is the average Fisher z-transformed correlation for edges in the indicated community for SB 2 mm controlling for gender and scanner. P-values represent whether the correlation of the acquisition differs significantly from SB 2 mm. Differences with p ≤ 0.001 are in bold and colored red for acquisitions significantly lower than SB 2 mm and blue for acquisitions significantly higher. Top: 9p. Bottom: 9p+bandpass.
| Thalamus - 9p | Putamen - 9p | Cerebellum - 9p | Executive - 9p | Salience - 9p | DMN - 9p | |
|---|---|---|---|---|---|---|
| Int. | 0.54(0.05) | 0.59(0.05) | 0.29(0.04) | 0.39(0.03) | 0.29(0.03) | 0.43(0.03) |
| SB3.3 | 0.34(0.07) <.001 | 0.22(0.05) <.001 | −0.04(0.04) 0.37 | 0.01(0.03) 0.857 | 0.03(0.03) 0.239 | 0.04(0.04) 0.276 |
| MB 2 | 0.07(0.05) 0.186 | 0.01(0.04) 0.862 | −0.03(0.04) 0.432 | −0.09(0.03) 0.007 | 0.01(0.03) 0.751 | −0.02(0.03) 0.59 |
| MB 3 | −0.05(0.06) 0.427 | −0.1(0.04) 0.008 | −0.09(0.04) 0.024 | −0.09(0.03) 0.001 | −0.03(0.03) 0.346 | −0.06(0.03) 0.049 |
| MB 4 | 0.02(0.05) 0.669 | −0.11(0.04) 0.003 | −0.1(0.04) 0.007 | −0.06(0.03) 0.026 | −0.03(0.03) 0.271 | −0.07(0.03) 0.007 |
| MB 6 | −0.08(0.05) 0.119 | −0.17(0.04) <.001 | −0.12(0.04) 0.002 | −0.1(0.03) 0.001 | −0.05(0.03) 0.032 | −0.07(0.03) 0.032 |
| MB 8 | −0.31(0.05) <.001 | −0.32(0.04) <.001 | −0.19(0.03) <.001 | −0.13(0.03) <.001 | −0.08(0.02) 0.001 | −0.14(0.02) <.001 |
| MB 9 | −0.3(0.05) <.001 | −0.34(0.04) <.001 | −0.23(0.03) <.001 | −0.14(0.03) <.001 | −0.1(0.02) <.001 | −0.17(0.03) <.001 |
| MB 12 | −0.36(0.05) <.001 | −0.44(0.03) <.001 | −0.21(0.03) <.001 | −0.18(0.02) <.001 | −0.16(0.02) <.001 | −0.25(0.03) <.001 |
| Thalamus - 9p+bp | Putamen - 9p+bp | Cerebellum - 9p+bp | Executive - 9p+bp | Salience - 9p+bp | DMN - 9p+bp | |
| Int. | 0.52(0.06) | 0.59(0.06) | 0.31(0.04) | 0.39(0.04) | 0.26(0.04) | 0.43(0.04) |
| SB3.3 | 0.47(0.07) <.001 | 0.31(0.05) <.001 | −0.02(0.04) 0.637 | 0.04(0.04) 0.249 | 0.08(0.03) 0.01 | 0.11(0.04) 0.006 |
| MB 2 | 0.22(0.05) <.001 | 0.1(0.05) 0.036 | −0.01(0.04) 0.814 | −0.06(0.04) 0.167 | 0.05(0.03) 0.115 | 0.04(0.03) 0.172 |
| MB 3 | 0.22(0.07) 0.001 | 0.09(0.05) 0.051 | 0(0.06) 0.98 | −0.03(0.04) 0.417 | 0.05(0.04) 0.201 | 0.04(0.03) 0.228 |
| MB 4 | 0.33(0.06) <.001 | 0.18(0.04) <.001 | −0.01(0.04) 0.87 | 0.04(0.04) 0.362 | 0.07(0.03) 0.032 | 0.03(0.03) 0.287 |
| MB 6 | 0.29(0.06) <.001 | 0.14(0.06) 0.012 | −0.02(0.05) 0.746 | −0.02(0.04) 0.543 | 0.06(0.03) 0.052 | 0.1(0.04) 0.008 |
| MB 8 | 0.07(0.05) 0.207 | 0.07(0.05) 0.133 | −0.09(0.04) 0.021 | −0.03(0.04) 0.342 | 0.07(0.03) 0.038 | 0.06(0.03) 0.054 |
| MB 9 | 0.09(0.07) 0.151 | 0.06(0.06) 0.276 | −0.08(0.05) 0.133 | −0.03(0.04) 0.433 | 0.06(0.03) 0.071 | 0.01(0.04) 0.712 |
| MB 12 | 0.04(0.06) 0.442 | −0.12(0.05) 0.025 | −0.1(0.05) 0.081 | −0.02(0.04) 0.677 | −0.02(0.03) 0.604 | −0.04(0.03) 0.246 |
Web Supplement Figure S.9 also reveals a large degree of inter-subject variation in correlations, as well as some degree of inter-subject variation in g*-factors. For example, in the thalamus at MB 6, participants’ g*-factors vary from 1.31 to 7.57, where the g*-factors are more variable in regions that on average have higher g*-factors.
As was the case for the full set of edges, correlations were in general more similar across MB acquisitions for the 9p+bandpass processed data, but there were some notable differences in subcortical regions (Table 2). In the thalamus, SB 3.3 mm was much higher and MB 2 to 6 notably higher than SB 2 mm (p ≤ 0.001). In the putamen, SB 3.3 mm and MB 4 were higher than SB 2 mm (p < 0.001). The correlations across acquisitions in the cerebellum were generally similar to SB 2 mm with a trend of lower correlations in MB 8, MB 9, and MB 12 (p = 0.02, p = 0.13, p = 0.08, respectively). Correlations were similar to SB 2 mm within executive control. In salience, SB 3.3 mm tended to have higher correlations (0.08 on Fisher z-scale, p = 0.01). In the default mode network (DMN), SB 3.3 mm and MB 6 tended to have higher correlations (0.1 on Fisher z-scale, p < 0.01). Boxplots with participant data colored by g*-factor appear in Web Supplement Figure S.10, which illustrates that correlations overall are similar across acquisitions, with the notable exception of higher correlations at SB 3.3 mm and MB 4 compared to other acquisitions in the thalamus and putamen.
In the 9p+spatial smoothing and 9p+bandpass+spatial smoothing, the patterns were similar to the 9p and 9p+bandpass, respectively (Web Supplement Table S.1). Overall, the correlations tended to be higher in smoothed data compared to the unsmoothed data.
4.3.2. Impacts on edge density
The number of significant correlations (edge density) with 9p preprocessing tended to be higher in MB 6, MB 4, and MB 8, with the relative ranking of SB 3.3 mm depending on the community, and SB 2 mm, MB 2, MB 3, MB 9, and MB 12 tending to perform worse (Figure 7A). MB 6 had the greatest edge density across all edges, and MB 8 was nearly equal (difference between MB 6 and MB 8=0.006, p = 0.46; all differences and p-values hereafter are relative to MB 8, Web Supplement Table S.2), and MB 4 also nearly equal (difference=0.001, p = 0.95). The next highest density was MB 3 (difference=−0.011, p = 0.15) followed by SB 3.3 mm (difference=−0.014, p = 0.05), with lower densities in MB 9, MB 2, SB 2 mm, and MB 12 (p < 0.004). Edge density was somewhat higher in MB 4 and MB 6 than MB 8 for edges with a subcortical node (difference=0.026, p = 0.06, and difference=0.028, p = 0.07, respectively) and for fronto-parietal task control (p = 0.06, p = 0.01, respectively). The ranking of the proportion of significant correlations in SB 3.3 mm varied by community, with lower densities for default mode and visual compared to MB 8 (difference=−0.043, p = 0.001 and diff=−0.023, p = 0.01, respectively), while in subcortical, the density in SB 3.3 mm was close to MB 4 and MB 6 (Figure 7A) with a trend of higher density than MB 8 (difference=0.023, p = 0.10). Note the power of the permutation test is impacted by the size of the community (e.g., 31 nodes in visual versus 13 nodes in subcortical).
Figure 7:
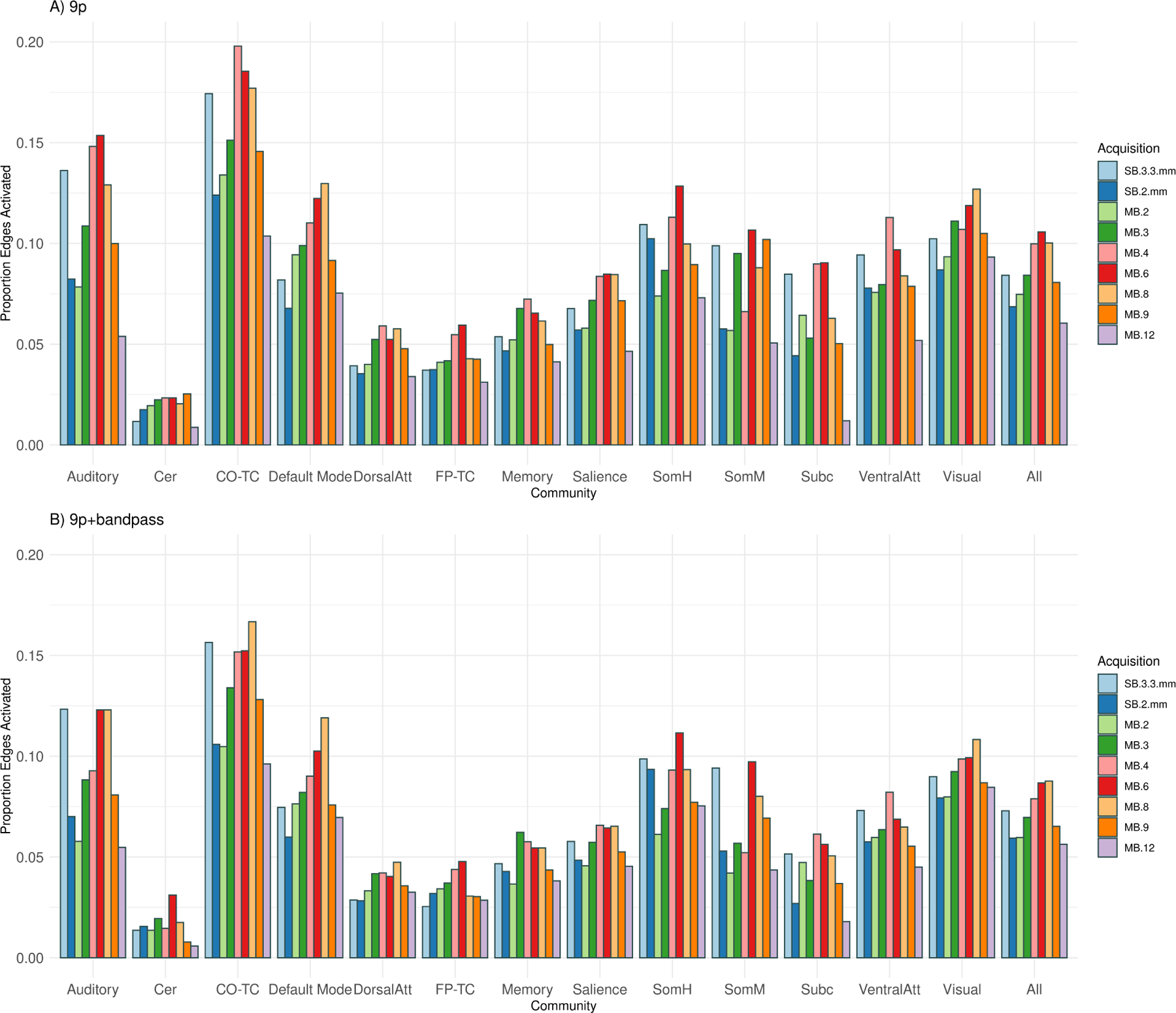
Edge density (number of significant correlations) for thirteen communities (auditory, cerebellum, cingulo-opercular task control, default mode, dorsal attention, fronto-parietal task control, memory, salience, somatomotor hand, somatomotor mouth, subcortical, ventral attention, and visual) and across all edges (all). The edge density for a community is defined as the proportion of significant one-sample t-statistics (using the Bonferroni-corrected α-level) for the Fisher z-transformed correlations for each edge in which at least one of the nodes is in the community. A) The number of significant correlations with 9p preprocessing tended to be higher in MB 6, MB 4, and MB 8, with the relative ranking of SB 3.3 mm depending on the community, and SB 2 mm, MB 2, MB 3, MB 9, and MB 12 tending to perform worse. Permutation tests of significant differences between MB factors appear in Web Supplement Table S.2. Similar results were obtained with 9p+spatial smoothing, shown in Web Supplement Table S.3. B) The rankings with 9p+bandpass were similar to 9p, with MB 8, 6 and 4 tending to be higher than others and SB 2 mm, MB 2, MB 9, and MB 12 lower. Permutation tests of significant differences between MB factors appear in Web Supplement Table S.4. Overall, 9p+bandpass had lower edge density compared to 9p, with significant differences displayed in Web Supplement Table S.5.
Overall, spatial smoothing did not impact the relative rankings of the MB factors. Permutation tests for 9p+spatial smoothing were similar to 9p (Web Supplement Table S.3). The overall pattern is that MB4, MB 6, and MB 8 outperform SB 2 mm, MB 2, and MB 12.
The number of significant correlations with 9p+bandpass across all edges was highest in MB 8, with approximately equal density in MB 6 (p = 0.92) and similar density in MB 4 (p = 0.49) (Figure 7, Web Supplement Table S.4). Across all edges, the rankings were similar to 9p, in which SB 3.3 mm and MB 3 were somewhat lower than MB 8 (difference=−0.012, p = 0.08 and difference=−0.012, p = 0.10), and SB 2 mm, MB 2, MB 9, and MB 12 lower (differences larger than −0.02, p < 0.003). In contrast to the trends in 9p, subcortical density was similar in MB 8 versus SB 3.3 mm, MB 4, and MB 6 (p ≥ 0.30).
There were fewer significant edges in 9p+bandpass compared to 9p across most communities and acquisitions (Web Supplement Table S.5). This included the densities across all edges (p < 0.001 for all acquisitions except MB 8 and MB 12, where p = 0.02 and p = 0.26, respectively). The overall reduced edge density in 9p+bandpass may be due to removing signal (decrease in power) and/or removing physiological confounding (decrease in false positives, where here we consider a true positive if the connection is due to neural signal); see Section 5.3 Temporal filtering decreases noise amplification and physiological signal but may remove neural signal.
Plots of the matrices of Cohen’s d illustrate that effect size matrices look somewhat similar across many acquisitions with some notable differences (Figure 8). The subcortical to salience connections tend to be stronger in MB 4 and MB 6, particularly when compared to MB 3 and MB 9. Visually, Cohen’s d in 9p and 9p+bandpass look more comparable. In fact, the effect sizes tend to be higher with 9p preprocessing; as discussed above, the number of significant correlations was higher in 9p than 9p+bandpass in nearly all communities and MB factors (Web Supplement Table S.5).
Figure 8:
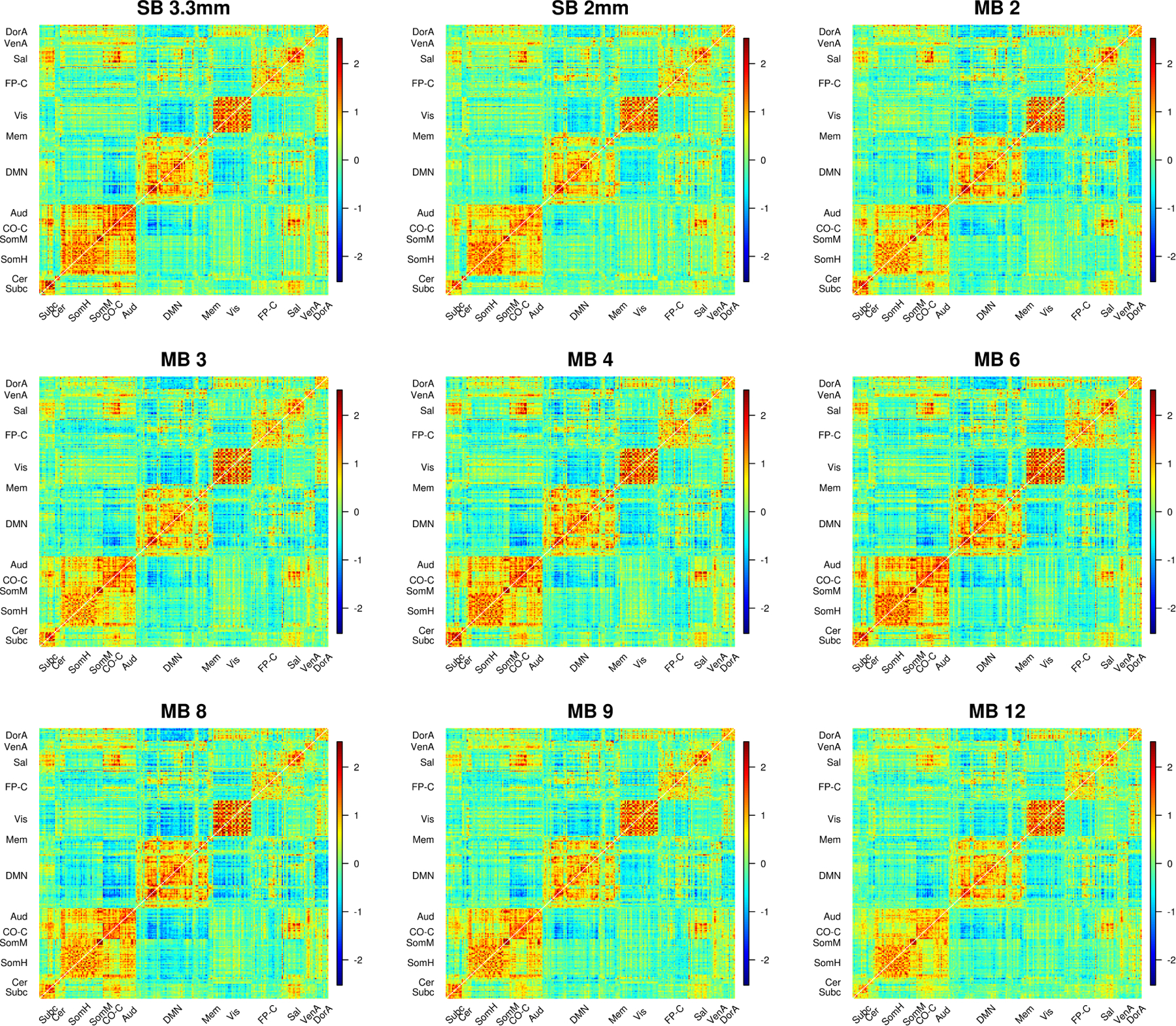
Cohen’s d for SB and MB acquisitions. Cohen’s d statistic is formed for the one-sample t-test of the null hypothesis that the Fisher z-transformed correlation is equal to zero. Cohen’s d for 9p preprocessing is above the diagonal and 9p+bandpass below the diagonal. Compared to the correlations in Figure 6, effect size matrices in 9p and 9p+bandpass look more similar. A close examination reveals some differences. For example, the subcortical to salience connections tend to be stronger in MB 4 and MB 6 than MB 3 and MB 9 in 9p, and these effect sizes tend to be reduced in 9p+bandpass. In general, there were some significant differences between MB factors, as illustrated in Web Supplement Tables S.2 and S.4, and 9p+bandpass tended to have lower effect sizes than 9p, as illustrated in Web Supplement Table S.5.
4.4. Impacts in independent datasets
4.4.1. Evaluation of a third scanner using a 64-channel head coil
In the three subjects collected with the 64-channel head coil and scanner at the University of Rochester, we observed similar patterns of noise amplification as in the Emory cohort (Web Supplement S.12). In particular, we do not see any clear evidence of large differences due to different head coils.
In the seed maps for the right dorsal rostral putamen, we again see the general pattern that correlations decrease as MB factor increases, and temporal filtering reduces these biases (Web Supplement S.13). An exception to the decreasing trend in correlations with MB factor is that MB 4 had higher correlations than MB 3. In this small sample, these patterns are more clearly illustrated with the spatially smoothed data (panels C and D). In 9p+spatial smoothing, correlations with the left putamen appear stronger in SB 3.3 mm, MB 2, and MB 4 compared to the other acquisitions. In 9p+bandpass+spatial smoothing, MB 4 appears to most clearly reveal right-left connectivity.
In the correlation matrices, we also see a trend of decreasing correlations with increasing multiband factor with 9p processing, whereas acquisitions appear more similar with 9p+bandpass processing (Web Supplement Figure S.14).
4.4.2. Evaluation of pairwise correlations in the preprocessed Young Adult Human Connectome Project data
In the ICA-FIX rs-fMRI data from the HCP (collected using MB 8), we see that many subcortical to subcortical and subcortical to cortical correlations appear weak in the correlation matrix. In contrast, functional connectivity between these regions is more prominent in the Cohen’s d matrix (Web Supplement S.4.2).
5. Discussion
We evaluated the impact of multiband acceleration on correlation-based functional connectivity using MB factors of 2, 3, 4, 6, 8, 9, and 12 with 2 mm isotropic voxels, and additionally 2 mm and 3.3 mm single-band acquisitions. Our contributions are the following:
In seed maps, putamen connectivity and motor-thalamic connectivity were both higher in the single-band 3.3 mm acquisition (both with and without bandpass), with MB 4 performing well among 2 mm acquisitions.
Noise amplification from multiband acceleration creates large spatial biases in correlations, suggesting underestimated subcortical-cortical connectivity, particularly at high MB factors (8 and higher).
Bandpass filtering decreases spatial biases but in some settings reduces effect sizes.
Effect sizes or test statistics should be used for multiband studies, and correlations without noise removal should not be reported.
MB 4, 6 and 8 have a greater number of significant correlations across a functional atlas (both with and without bandpass), with lower edge density in SB 2 mm, MB 2, MB 9, and MB 12.
We discuss our recommendations and study limitations below.
5.1. Recommendations
In our seed-based analysis, we examined functional connectivity between locations where we expect true functional connectivity based on anatomy and previous studies. Our recommendation is to use SB 3.3 mm for seed-based connectivity studies where the regions of interest fall in high g-factor areas, and we recommend MB 4 for 2 mm acquisitions. For a seed in the right putamen (high g-factor), bilateral putamen connectivity and connections to the insula, cingulate, and thalamus were clearly more prominent in SB 3.3 mm than other acquisitions, and bandpass filtering did not impact this conclusion (Figure 2). Among the 2 mm acquisitions, connectivity in MB 4 was higher than others, particularly for putamen-thalamic connectivity. For the correlations between a seed in the motor cortex (low g-factor) and the thalamus (high g-factor), this pathway is also best captured using the SB 3.3 mm acquisition (Figure 3). In particular, MB 8 and higher do not robustly reveal this thalamocortical connectivity. The pathway between the motor cortex and cerebellum (moderate g-factor) is best captured using MB 4 (Web Supplement Figure S.7).
In the analyses of correlations between regions in a functional atlas, our results indicate that the number of significant correlations is on average higher in MB 6, MB 8, and MB 4 compared to other acquisitions (Figure 7, Web Supplement Table S.2). All acquisitions have a decreased number of significant correlations in 9p+bandpass compared to 9p. Overall, we prefer MB 4 compared to MB 6 and MB 8 because it performs comparably in the functional atlas analysis, and it has benefits in subcortical seed-based analyses.
We recommend reporting effect sizes, or similarly, test statistics, in resting-state studies utilizing multiband data, including secondary analyses of existing data. Correlations are reduced in regions with noise amplification in multiband (Figures 2, 3, 4; Web Supplement Figures S.8, S.9.) If correlations (rather than effect sizes or test statistics) are reported, noise removal, e.g., temporal filtering, can reduce spatial biases, but may also have costs. We discuss temporal filtering in Section 5.3 Temporal filtering decreases noise amplification and physiological signal but may remove neural signal.
This study used young, healthy subjects and one-sample tests. We expect that these results also apply to comparing groups, e.g., disease versus healthy. In disease versus healthy, g-factors will attenuate the differences in a manner parallel to the one-sample analysis (see Section 2.1 Noise amplification and functional connectivity). Thus we also recommend MB 4 for whole-brain group comparisons, and SB 3.3 mm for seed-based analyses of subcortical functional connectivity.
5.2. Generalizability
Decisions at every step in the study design process could potentially impact our findings, but we made these decisions in a way to improve the generalizability of our recommendations. First, the combination of scanner model and head coil used in our Emory cohort (Siemens PrismaFit, 32-channel head coil) are amongst the most commonly used in recent rs-fMRI studies. Thus our findings are widely applicable to many other research labs. Secondly, we chose to use standard, popular preprocessing pipelines commonly found in the literature (Ciric et al., 2017; Parkes et al., 2018), rather than specialized or less common processing pipelines, which arguably improves the generalizability of the results.
The spatial biases in correlations are a general issue in multiband acquisitions that is expected to be problematic across scanner types and head coils. This includes secondary analyses of the UK BioBank (Miller et al., 2016a), HCP (Glasser et al., 2013; Howell et al., 2019), ABCD (Hagler et al., 2019), ADNI-3 (Weiner et al., 2017b), and other public datasets. Noise amplification is a cost of multiband acquisition (Setsompop et al., 2012; Xu et al., 2013; Todd et al., 2017; Risk et al., 2018). Consistent with the theoretical arguments in (3), we empirically showed correlations were reduced in regions with high noise amplification. This was true for the expected connection between LM1 and the thalamus in our seed map analysis (Figure 3). It emerged as a general pattern when we examined the impact of g*-factors on correlation magnitude using the Power 264-node functional atlas (Figure 5). We also saw this pattern in the 64-channel head coil used in the University of Rochester cohort (Web Supplement Figures S.13 and S.14). We again observed evidence that effect sizes may capture functional connectivity involving subcortical areas in our secondary analysis of the HCP data (Web Supplement Figure S.15).
5.3. Temporal filtering decreases noise amplification and physiological signal but may remove neural signal
Temporal filtering in multiband acquisitions has three impacts: 1) a reduction in noise amplification; 2) a reduction in physiological sources of correlation; and 3) a possible introduction of bias due to the removal of neural signal. Figure 1 shows temporal filtering results in dramatic reductions in noise amplification, which increases correlations. However, the increase in correlations does not result in an increase in power because of the loss of residual degrees of freedom, resulting in the same degrees of freedom across MB factors (Table 1). We implement bandpass filtering during nuisance regression in the temporal domain using AFNI’s 3dTproject. Lindquist et al. (2019) and Hallquist et al. (2013) found that implementing temporal filtering and nuisance regression in separate steps led to biased results. Intuitively, low-pass filtering removes all the high frequency content from data, which renders it more similar to slower acquisitions. This includes a removal of some of the effects of noise amplification, as well as some cardiac and respiratory effects because most of their power resides outside the passband.
The reduction in variance due to physiological sources is depicted in Figure 1, in which the contributions of physiological noise steadily decline with increase in MB factor. The overall number of significant edges decreased when using temporal filtering (Web Supplement Table S.5, Figure 7). An important limitation in our brain-wide analysis is that we do not distinguish between true positives and false positives, where false positives include high correlations from motion and physiology. However, our seed-based analysis provides some insight into neural effects that may be reduced by bandpass filtering. Tract-tracing studies have established the existence of cortical projections between the dorsal anterior cingulate and the striatum, including the putamen (Haber et al., 2006). Consistent with this anatomical evidence, we observed weak, but notable, correlations between the putamen and cingulate in SB 3.3 mm data, but these correlations were decreased by bandpass filtering (Figure 2). Tract-tracing and physiological experiments have also revealed the presence of projections from the thalamus to the putamen (Haber and Calzavara, 2009), but in the present study, functional connectivity evidence of these projections appears to have been reduced by bandpass filtering in MB 6 and MB 8. Feinberg et al. (2010) and Lee et al. (2013) suggest there is neural signal in the high-frequency content of MB acquisitions, which may be discarded by bandpass filtering. Jahanian et al. (2019) also found benefits of MB 6 without temporal filtering in their study comparing MB 6 to SB. Chen et al. (2019) caution that temporal filtering is a not a catch-all for cardiac and respiratory effects, as these effects are not sinusoidal and contain higher order harmonics.
5.4. Preprocessing pipelines and strategies for artifact and noise removal
We examined four preprocessing pipelines in which all pipelines included a popular and effective approach to nuisance regression (white matter, CSF, global signal, and the 6 parameters from motion regression) (Ciric et al., 2017; Parkes et al., 2018; Fox et al., 2005, 2009), and we compared results with and without temporal filtering, as well as with and without spatial smoothing. The possible benefits of multiband with alternative preprocessing pipelines is an important avenue for future research. Data from this study are available on OpenNeuro (https://openneuro.org/datasets/ds003540) to facilitate studies on the impacts of preprocessing.
While GSR is effective at minimizing respiratory as well as motion-related artifacts, more targeted physiological noise removal strategies may help leverage the benefits of higher sampling rates. Fair et al. (2020) found that notch filters to target the respiratory rate improved fMRI data quality, particularly in multiband data. For studies that collect respiratory and cardiac data, RETROICOR may allow more targeted removal of physiological impacts to decrease false positives (Glover et al., 2000; Bollmann et al., 2018).
A greater number of time points in multiband may allow more aggressive retrospective motion correction using derivatives and quadratic terms of the motion parameters, scrubbing, and/or other approaches (Ciric et al., 2017; Power et al., 2014). However, many of these methods can not be combined with simultaneous bandpass regression as the number of predictors in the design matrix approaches or exceeds the number of time points. For example, in our six minute acquisitions, including the 9 regressors, their derivatives, quadratic terms, and squares of derivatives (36 p, Satterthwaite et al. 2013) leaves 10 or fewer residual degrees of freedom for all acquisitions (see Table 1). Although the more aggressive noise removal strategies can remove distance-dependent motion artifacts, the 9p pipeline had the best network modularity quality (Ciric et al., 2017), which may be related to possible over-fitting in aggressive approaches. Additionally, recent evidence suggests that changes in the magnetic field caused by respiratory effects can falsely appear to be motion artifacts, which results in overly aggressive frame censoring and data loss and can corrupt nuisance regressors (Fair et al., 2020). We chose to use the same pipelines for all acquisitions to isolate the effect of MB factor, rather than more aggressive noise removal strategies that are facilitated by the acquisition of a larger number of volumes, but which may be removing false positives and false negatives.
While retrospective image post-processing methods are commonly used to reduce motion effects, prospective motion correction methods can be used to mitigate spin history effects. Methods for multislice-to-volume registration that do not require external hardware have been developed for real-time motion monitoring in multiband studies (Hoinkiss et al., 2019). Higher temporal resolution associated with higher MB factor could carry additional benefits in prospective motion correction but potentially have higher computational costs.
ICA-based artifact removal approaches may be more effective in multiband acquisitions; however, noise amplification is a separate issue. ICA-AROMA can be used to estimate the time courses of motion (Pruim et al., 2015), and ICA-FIX additionally estimates physiology and some multiband artifacts (Griffanti et al., 2014). Multiband artifacts identified using ICA-FIX have a “checkerboard” pattern (Griffanti et al., 2017). The corresponding independent component time courses appear to correspond to motion and the interaction with the slice-GRAPPA kernels. Mathematically, an IC component represents a spatial map with a single time course. This approach may not be suited to capturing noise amplification because the thermal noise time courses are not shared at different locations within the axial plane; the noise has high rank that is not captured by a low-rank structure. As shown in Risk et al. (2018), the ICA-FIX preprocessed resting-state fMRI in the Human Connectome Project still contains large noise amplification, particularly in subcortical regions. In the present work, correlations involving subcortical regions in the ICA-FIX HCP preprocessed data tended to be weak (Web Supplement Figure S.15). We speculate that ICA-based artifact removal can reduce motion and physiological artifacts, which can decrease spurious false positives, but would not greatly impact noise amplification.
PCA-based data reduction, in which a signal subspace is estimated and the many directions of low variation are discarded, is another alternative cleaning strategy. This approach may be similar to bandpass filtering. In particular, it may greatly reduce the noise but also reduce the benefits of higher sampling rates. Although we speculate ICA artifact removal would not address noise amplification, ICA-based functional connectivity analyses may reduce noise amplification, since ICA methods first apply a PCA-dimension reduction step. PCA noise reduction is an important avenue for future research.
Another possible concern in multiband acquisitions is slice leakage artifacts and spurious correlations. The original slice-GRAPPA algorithm resulted in signal leaking to aliased locations, but this appears to have been largely addressed by split slice-GRAPPA (leak block) reconstruction (Cauley et al., 2014; Todd et al., 2016; Risk et al., 2018). A related issue may occur with thermal noise. The thermal noise shared by aliased locations resulted in spurious correlations in the slice-GRAPPA reconstruction of rs-fMRI data in a simulation study (Setsompop et al., 2013). However, our analyses demonstrate that correlations decrease at higher multiband factors (Figure 5). Moreover, the correlations in Figure 2 are a single axial slice at the center of the seed ROI, and thus there is no aliasing between voxels within these seed maps. The impacts of slice separation on spurious correlations is understudied. In particular, the impacts should be evaluated in recently proposed reconstruction methods that are emerging as alternatives to split slice-GRAPPA (discussed below).
5.5. Voxel size and other considerations
In this study, our analysis used volume-based space with 2 mm MB data and 3.3 mm SB data, whereas a surface-based analysis may provide different insights. An important question raised by this is whether a 2 mm acquisition is beneficial when conducting volume-based analyses, particularly if the primary interest is to study subcortical connectivity. Our approach showed little advantage of smaller voxel size in the seed maps. There appears to be fair specificity in gray matter regions in the SB 3.3 mm acquisition; for example, the left and right insula are clearly delineated in the top row of Figure 3. The higher-resolution associated with 2-mm isotropic voxel size could allow a better parcellation of small anatomical structures such as sub-nuclei of the thalamus. Our analyses suggest these choices should be evaluated in light of the dramatic reduction in effect sizes in the putamen and the thalamus when using 2 mm compared to 3.3 mm. We elected to use a volume-based approach for our primary analyses, since volume-based analyses are used for subcortical analyses, and subcortical regions are prone to have lower SNR due to low coil sensitivity and high g-factor. It is unknown how an MB 6 3.3 mm acquisition would compare to the SB 3.3 mm. Note it is generally not feasible to map 3.3 mm voxels to the surface, and hence, a surface-based analysis would be restricted to the 2 mm acquisitions.
We also examined the correlations between regions in the surface parcellation from Glasser et al. (2016) using the surface-registered HCP data together with the nineteen non-cortical gray matter volume-based regions (Web Supplement Figure S.15). Many of the correlations involving subcortical regions were small. This is consistent with the hypothesis that noise amplification results in spatial biases in correlations, although in this analysis the size of the regions varied which can also impact the analysis. As in the Emory cohort, subcortical functional connectivity was more prominent in the Cohen’s d matrices. The costs and benefits of voxel size, as well as volume versus surface-based representations of BOLD signal, is also an important avenue for future research.
A comparison of the effect sizes in a 64-channel versus 32-channel head coil is not possible in our study due to the small size of the University of Rochester cohort. Seidel et al. (2020) found that temporal SNR was higher using a 64-channel versus 20-channel head coil and recommended MB 6 with no in-plane acceleration, but 32-channel head coils were not evaluated.
In line with the approach used in the HCP (Ugurbil et al., 2013; Xu et al., 2013), we did not use in-plane acceleration due to a concern with SNR loss and g-factor penalties. In-plane acceleration leads to substantial SNR decrease (Seidel et al., 2020). Studies interested in regions with severe magnetic-susceptibility induced distortion should cautiously balance the benefits of in-plane acceleration and the loss in power.
We utilized split-slice GRAPPA for reconstruction (Cauley et al., 2014) implemented by the CMRR sequences. However, recently introduced reconstruction methods may increase the benefits of acceleration. Methods using convolutional neural networks are being developed (Akçakaya et al., 2019; Mickevicius et al., 2019; Nencka et al., 2020). Chiew and Miller (2019) add a ridge penalty on the difference between time points to decrease noise amplification and improve multiband reconstruction. These new developments may allow the use of higher MB factors.
An important application of multiband acquisition is to studies of dynamic functional connectivity. The Nyquist frequencies for MB 4, 6 and 8 are 0.34 Hz, 0.52 Hz, and 0.68 Hz, respectively, suggesting MB 8 will facilitate the detection of brain dynamics. However, the ability of higher frequency data to resolve faster brain dynamics will also be impacted by the noise characteristics of those acquisitions. Moreover, the spatial biases of multiband acquisition may also impact dynamic connectivity studies.
6. Conclusions
In seed-based analyses of putamen functional connectivity and seed-based analyses of motor-thalamic connectivity, we recommend SB 3.3 mm. MB 4 2 mm also revealed subcortical connectivity, as well as motor-cerebellum connectivity, and is a good option for studies desiring smaller voxel size. In effect sizes from correlation matrices using a brain-wide functional atlas, MB 4, 6, and 8 had similar results. In general, MB 8 and higher did not have advantages over MB 4 or 6. Overall, MB 4 is a reasonable choice for studies examining both subcortical seed-based functional connectivity and brain-wide correlation matrices. We recommend reporting Cohen’s d or test statistics rather than correlations, as these measures were less sensitive to the biases created by spatially heterogeneous noise amplification. Correlations with 9p preprocessing without noise removal should not be reported. Bandpass filtering can reduce noise amplification but also effect sizes, with the caveat that we do not distinguish a reduction in physiology-based activation from a loss in neuronal activation in the atlas-based analysis.
Supplementary Material
Acknowledgments
The authors thank Dr. Gopinath Kaundinya, Emory University, Dr. David Reiter, Emory University, Dr. Allyson Mackey, University of Pennsylvania, and three anonymous reviewers for helpful comments and discussions. We would like to thank Sarah Basadre, Michael Larch, Sonny Roh, and Samira Yeboah for MRI acquisition and Lei Zhou for computational support. Data collection in this study was supported by the Dean’s Pilot and Innovation Grant of the Rollins School of Public Health at Emory University to B.B.R. and the Center for Systems Imaging Core Pilot Grant at Emory University to B.B.R. Analysis, interpretation, and writing of the report were supported by NIH R21AG066970 to B.B.R., Z.Z., and D.Q., K01MH109766 to M.B.N, and P50AG025688 and R21AG064405 to D.Q.
Appendix A. Power when comparing two groups
Let zavv′1 and zavv′2 denote the population Fisher z-transformed correlation for groups 1 and 2, respectively. Assume N subjects for each group: and . In the one-sided test H0 : zavv′1 ≤ zavv′2 and Ha : zavv′1 > zavv′2, the power is
| (A.1) |
By (3), zavv′1 and zavv′2 are attenuated by noise amplification, which can decrease statistical power.
Appendix B. Implications of autocorrelation on power
Recall that is the sample correlation between locations v and v′ for MB factor a in subject i. Also recall that . In the absence of autocorrelation, . Let , where favv′(·,·) is the function characterizing the impact of autocorrelation in the two time series and their population correlation zavv′ (here, Fisher z-transformed). Related results and special cases for the untransformed correlations are in Davey et al. (2013), Fiecas et al. (2017), and Arbabshirani et al. (2014), but in general, this is a complicated function. Under positive autocorrelation, f(Ta, zavv′) ⪅ Ta (where we use the notation “⪅” because this is an asymptotic result that holds for sufficiently large Ta), with f(Ta, zavv′) ≈ Ta when time series for both locations v and v′ have zero autocorrelation. Using (3), the population effect size (Cohen’s d) is
| (B.1) |
Then the power in (4) becomes .
Inspecting (B.1), the term can offset the increase in . Additionally, the function favv′(Ta, zavv′) may vary across space. Bollmann et al. (2018) found the autoregressive coefficients tend to be lower in subcortical regions in task fMRI. Then the term favv′(Ta, zavv′) may be closer to Ta in high noise amplification regions. Let and , and define the sample Cohen’s . In practice, we expect to be larger than even if there is no autocorrelation due to violations of the assumption that all participants’ Fisher z-transformed correlations are realizations of the same population parameter zavv′. To the extent that the model generating (B.1) captures key elements of the data, then may be a useful measure of functional connectivity in MB acquisitions. Insight into temporal filtering can also be gained with this model. Temporal filtering reduces the effective degrees of freedom (Davey et al., 2013), resulting in favv′(Ta, zavv′) ≪ Ta, but can also increase the magnitude of correlations by reducing and .
Accurate modeling of autocorrelation is important in single-subject analysis of multiband task fMRI studies with short TR, with relatively minor impacts in group studies (Olszowy et al., 2019). Similarly, studies on the distribution of correlations have focused on single-subject analysis (James et al., 2019; Davey et al., 2013) with autocorrelation corrections having little impact on group inference (Arbabshirani et al., 2014), although additional research in MB acquisitions would be useful. We note that prewhitening the time series, and closely related, using the residuals from models fitting the autocorrelation, can reduce , but it can also impact ψvv′ in (1). The underlying vascular response to neural activity is also autocorrelated, and the hemodynamic response function follows a temporal pattern (Lindquist et al., 2009). Hence, applying a pre-whitening matrix may be undesirable. Pre-whitening in functional connectivity was not used in a number of prominent studies of functional connectivity nor is it a standard preprocessing step (Finn et al., 2015; Smith et al., 2013; Esteban et al., 2019). Hence, in our data application, we adapted a preprocessing pipeline that did not include prewhitening (Section 3.2 FMRI data processing).
Appendix C. Supplementary Materials
GFactorTables264nodes.xlsx includes tables of the apparent g-factors for the 9p and 9p+bandpass pipelines for the 264-node atlas.
WebSupplement_RestingStateFMRI_Multiband.pdf includes Web Supplement Figures S.1–S.15 and Tables S.1–S.5, including results from the University of Rochester cohort and secondary analysis of the HCP dataset.
Footnotes
Data and code availability statement
The preprocessing and analysis pipelines used toolboxes and packages from FSL 6.0.3, AFNI 19.3.16, Matlab R2020a, and R 3.6.0, with details described in Section 3 Methods. Additionally, figures were created using wb_view in Connectome Workbench 1.4.2 (Marcus et al., 2011) and BrainNet viewer 1.7 (Xia et al., 2013).
The Emory Multiband Dataset is available on OpenNeuro: https://openneuro.org/datasets/ds003540. Bash preprocessing, Matlab, and R scripts are available at the Brain Research in Imaging Statistics Kit: https://github.com/thebrisklab/RestingStateMultiband.
Declaration of Competing Interest
None.
References
- Akçakaya M, Moeller S, Weingärtner S, and Uğurbil K (2019). Scan-specific robust artificial-neural-networks for k-space interpolation (RAKI) reconstruction: Database-free deep learning for fast imaging. Magnetic Resonance in Medicine, 81(1):439–453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andersson JL, Skare S, and Ashburner J (2003). How to correct susceptibility distortions in spin-echo echo-planar images: Application to diffusion tensor imaging. NeuroImage, 20(2):870–888. [DOI] [PubMed] [Google Scholar]
- Arbabshirani MR, Damaraju E, Phlypo R, Plis S, Allen E, Ma S, Mathalon D, Preda A, Vaidya JG, Adali T, and Calhoun VD (2014). Impact of autocorrelation on functional connectivity. NeuroImage, 102(P2):294–308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bastian AJ and Thach WT (1995). Cerebellar outflow lesions: A comparison of movement deficits resulting from lesions at the levels of the cerebellum and thalamus. Annals of Neurology. [DOI] [PubMed] [Google Scholar]
- Bhandari R, Kirilina E, Caan M, Suttrup J, de Sanctis T, De Angelis L, Keysers C, and Gazzola V (2019). Does higher sampling rate (Multiband + SENSE) benefit the detection of task correlated BOLD for cognitive neuroscience applications at 3T? bioRxiv, page 762831. [Google Scholar]
- Biswal B, Zerrin Yetkin F, Haughton VM, and Hyde JS (1995). Functional connectivity in the motor cortex of resting human brain using echo-planar mri. Magnetic Resonance in Medicine. [DOI] [PubMed] [Google Scholar]
- Biswal BB, Mennes M, Zuo XN, Gohel S, Kelly C, Smith SM, Beckmann CF, Adelstein JS, Buckner RL, Colcombe S, and others (2010). Toward discovery science of human brain function. Proceedings of the National Academy of Sciences, 107(10):4734–4739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bollmann S, Puckett AM, Cunnington R, and Barth M (2018). Serial correlations in single-subject fMRI with sub-second TR. NeuroImage, 166:152–166. [DOI] [PubMed] [Google Scholar]
- Boyaciouglu R, Schulz J, Koopmans PJ, Barth M, and Norris DG (2015). Improved sensitivity and specificity for resting state and task fMRI with multiband multi-echo EPI compared to multi-echo EPI at 7T. Neuroimage, 119:352–361. [DOI] [PubMed] [Google Scholar]
- Breuer FA, Kannengiesser SA, Blaimer M, Seiberlich N, Jakob PM, and Griswold MA (2009). General formulation for quantitative G-factor calculation in GRAPPA reconstructions. Magnetic Resonance in Medicine, 62(3):739–746. [DOI] [PubMed] [Google Scholar]
- Bright MG, Tench CR, and Murphy K (2017). Potential pitfalls when denoising resting state fMRI data using nuisance regression. NeuroImage, 154:159–168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buckner RL, Krienen FM, Castellanos A, Diaz JC, and Thomas Yeo BT (2011). The organization of the human cerebellum estimated by intrinsic functional connectivity. Journal of Neurophysiology, 106(5):2322–2345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cauley SF, Polimeni JR, Bhat H, Wald LL, and Setsompop K (2014). Interslice leakage artifact reduction technique for simultaneous multislice acquisitions. Magnetic Resonance in Medicine, 72(1):93–102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cerliani L, Mennes M, Thomas RM, Di Martino A, Thioux M, and Keysers C (2015). Increased functional connectivity between subcortical and cortical resting-state networks in Autism spectrum disorder. JAMA Psychiatry. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chand GB, Wu J, Hajjar I, and Qiu D (2017). Interactions of the Salience Network and Its Subsystems with the Default-Mode and the Central-Executive Networks in Normal Aging and Mild Cognitive Impairment. Brain Connectivity, 7(7):401–412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen JC, Forsyth A, Dubowitz DJ, and Muthukumaraswamy SD (2020). On the Quality, Statistical Efficiency, and Safety of Simultaneously Recorded Multiband fMRI/EEG. Brain Topography, 33(3):303–316. [DOI] [PubMed] [Google Scholar]
- Chen JE, Polimeni JR, Bollmann S, and Glover GH (2019). On the analysis of rapidly sampled fMRI data. NeuroImage, 188:807–820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen L, Vu AT, Xu J, Moeller S, Ugurbil K, Yacoub E, and Feinberg DA (2015). Evaluation of highly accelerated simultaneous multi-slice EPI for fMRI. Neuroimage, 104:452–459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chiew M and Miller KL (2019). Improved statistical efficiency of simultaneous multi-slice fMRI by reconstruction with spatially adaptive temporal smoothing. NeuroImage, 203:116165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ciric R, Wolf DH, Power JD, Roalf DR, Baum GL, Ruparel K, Shinohara RT, Elliott MA, Eickhoff SB, Davatzikos C, Gur RC, Gur RE, Bassett DS, and Satterthwaite TD (2017). Benchmarking of participant-level confound regression strategies for the control of motion artifact in studies of functional connectivity. NeuroImage, 154:174–187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox RW (1996). AFNI: Software for analysis and visualization of functional magnetic resonance neuroimages. Computers and Biomedical Research, 29(3):162–173. [DOI] [PubMed] [Google Scholar]
- Davey CE, Grayden DB, Egan GF, and Johnston LA (2013). Filtering induces correlation in fMRI resting state data. NeuroImage, 64(1):728–740. [DOI] [PubMed] [Google Scholar]
- Demetriou L, Kowalczyk OS, Tyson G, Bello T, Newbould RD, and Wall MB (2018). A comprehensive evaluation of increasing temporal resolution with multiband-accelerated protocols and effects on statistical outcome measures in fMRI. NeuroImage, 176:404–416. [DOI] [PubMed] [Google Scholar]
- Di Martino A, Kelly C, Grzadzinski R, Zuo XN, Mennes M, Mairena MA, Lord C, Castellanos FX, and Milham MP (2011). Aberrant striatal functional connectivity in children with autism. Biological Psychiatry, 69(9):847–856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dum RP and Strick PL (2003). An unfolded map of the cerebellar dentate nucleus and its projections to the cerebral cortex. Journal of Neurophysiology, 89(1):634–639. [DOI] [PubMed] [Google Scholar]
- Esteban O, Markiewicz CJ, Blair RW, Moodie CA, Isik AI, Erramuzpe A, Kent JD, Goncalves M, DuPre E, Snyder M, Oya H, Ghosh SS, Wright J, Durnez J, Poldrack RA, and Gorgolewski KJ (2019). fMRIPrep: a robust preprocessing pipeline for functional MRI. Nature Methods, 16(1):111–116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fair DA, Miranda-Dominguez O, Snyder AZ, Perrone A, Earl EA, Van AN, Koller JM, Feczko E, Tisdall MD, van der Kouwe A, Klein RL, Mirro AE, Hampton JM, Adeyemo B, Laumann TO, Gratton C, Greene DJ, Schlaggar BL, Hagler DJ, Watts R, Garavan H, Barch DM, Nigg JT, Petersen SE, Dale AM, Feldstein-Ewing SW, Nagel BJ, and Dosenbach NU (2020). Correction of respiratory artifacts in MRI head motion estimates. NeuroImage, 208:116400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feinberg DA, Moeller S, Smith SM, Auerbach E, Ramanna S, Glasser MF, Miller KL, Ugurbil K, and Yacoub E (2010). Multiplexed echo planar imaging for sub-second whole brain {fMRI} and fast diffusion imaging. PloS one, 5(12):e15710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feinberg DA and Setsompop K (2013). Ultra-fast MRI of the human brain with simultaneous multi-slice imaging. Journal of magnetic resonance, 229:90–100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fiecas M, Cribben I, Bahktiari R, and Cummine J (2017). A variance components model for statistical inference on functional connectivity networks. NeuroImage, 149:256–266. [DOI] [PubMed] [Google Scholar]
- Finn ES, Shen X, Scheinost D, Rosenberg MD, Huang J, Chun MM, Papademetris X, and Constable RT (2015). Functional connectome fingerprinting: identifying individuals using patterns of brain connectivity. Nature neuroscience, 18(11):1664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox MD, Snyder AZ, Vincent JL, Corbetta M, Van Essen DC, and Raichle ME (2005). The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proceedings of the National Academy of Sciences of the United States of America, 102(27):9673–9678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox MD, Zhang D, Snyder AZ, and Raichle ME (2009). The global signal and observed anticorrelated resting state brain networks. Journal of Neurophysiology, 101(6):3270–3283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glasser MF, Coalson TS, Robinson EC, Hacker CD, Harwell J, Yacoub E, Ugurbil K, Andersson J, Beckmann CF, Jenkinson M, and others (2016). A multimodal parcellation of human cerebral cortex. Nature, 536(7615):171–178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glasser MF, Sotiropoulos SN, Wilson JA, Coalson TS, Fischl B, Andersson JL, Xu J, Jbabdi S, Webster M, Polimeni JR, and others (2013). The minimal preprocessing pipelines for the Human Connectome Project. NeuroImage, 80:105–124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glover GH, Li T, and Ress D (2000). Image-based method for retrospective correction of physiological motion effects in fMRI: RETROICOR. Magnetic Resonance in Medicine, 44(1):162–167. [DOI] [PubMed] [Google Scholar]
- Greicius M (2008). Resting-state functional connectivity in neuropsychiatric disorders. Current Opinion in Neurology, 21(4):424–430. [DOI] [PubMed] [Google Scholar]
- Greicius MD, Flores BH, Menon V, Glover GH, Solvason HB, Kenna H, Reiss AL, and Schatzberg AF (2007). Resting-State Functional Connectivity in Major Depression: Abnormally Increased Contributions from Subgenual Cingulate Cortex and Thalamus. Biological Psychiatry, 62(5):429–437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Griffanti L, Douaud G, Bijsterbosch J, Evangelisti S, Alfaro-Almagro F, Glasser MF, Duff EP, Fitzgibbon S, Westphal R, Carone D, and others (2017). Hand classification of fMRI ICA noise components. Neuroimage, 154:188–205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Griffanti L, Salimi-Khorshidi G, Beckmann CF, Auerbach EJ, Douaud G, Sexton CE, Zsoldos E, Ebmeier KP, Filippini N, Mackay CE, and others (2014). ICA-based artefact removal and accelerated fMRI acquisition for improved resting state network imaging. NeuroImage, 95:232–247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haber SN and Calzavara R (2009). The cortico-basal ganglia integrative network: The role of the thalamus. [DOI] [PMC free article] [PubMed]
- Haber SN, Kim KS, Mailly P, and Calzavara R (2006). Reward-related cortical inputs define a large striatal region in primates that interface with associative cortical connections, providing a substrate for incentive-based learning. Journal of Neuroscience, 26(32). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hagler DJ, Hatton SN, Cornejo MD, Makowski C, Fair DA, Dick AS, Sutherland MT, Casey BJ, Barch DM, Harms MP, Watts R, Bjork JM, Garavan HP, Hilmer L, Pung CJ, Sicat CS, Kuperman J, Bartsch H, Xue F, Heitzeg MM, Laird AR, Trinh TT, Gonzalez R, Tapert SF, Riedel MC, Squeglia LM, Hyde LW, Rosenberg MD, Earl EA, Howlett KD, Baker FC, Soules M, Diaz J, de Leon OR, Thompson WK, Neale MC, Herting M, Sowell ER, Alvarez RP, Hawes SW, Sanchez M, Bodurka J, Breslin FJ, Morris AS, Paulus MP, Simmons WK, Polimeni JR, van der Kouwe A, Nencka AS, Gray KM, Pierpaoli C, Matochik JA, Noronha A, Aklin WM, Conway K, Glantz M, Hoffman E, Little R, Lopez M, Pariyadath V, Weiss SR, Wolff-Hughes DL, DelCarmen-Wiggins R, Feldstein Ewing SW, Miranda-Dominguez O, Nagel BJ, Perrone AJ, Sturgeon DT, Goldstone A, Pfefferbaum A, Pohl KM, Prouty D, Uban K, Bookheimer SY, Dapretto M, Galvan A, Bagot K, Giedd J, Infante MA, Jacobus J, Patrick K, Shilling PD, Desikan R, Li Y, Sugrue L, Banich MT, Friedman N, Hewitt JK, Hopfer C, Sakai J, Tanabe J, Cottler LB, Nixon SJ, Chang L, Cloak C, Ernst T, Reeves G, Kennedy DN, Heeringa S, Peltier S, Schulenberg J, Sripada C, Zucker RA, Iacono WG, Luciana M, Calabro FJ, Clark DB, Lewis DA, Luna B, Schirda C, Brima T, Foxe JJ, Freedman EG, Mruzek DW, Mason MJ, Huber R, McGlade E, Prescot A, Renshaw PF, Yurgelun-Todd DA, Allgaier NA, Dumas JA, Ivanova M, Potter A, Florsheim P, Larson C, Lisdahl K, Charness ME, Fuemmeler B, Hettema JM, Maes HH, Steinberg J, Anokhin AP, Glaser P, Heath AC, Madden PA, Baskin-Sommers A, Constable RT, Grant SJ, Dowling GJ, Brown SA, Jernigan TL, and Dale AM (2019). Image processing and analysis methods for the Adolescent Brain Cognitive Development Study. NeuroImage, 202:116091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halekoh U, Højsgaard S, and Yan J (2006). The R Package geepack for Generalized Estimating Equations. Technical Report 2.
- Hallquist MN, Hwang K, and Luna B (2013). The nuisance of nuisance regression: Spectral misspecification in a common approach to resting-state fMRI preprocessing reintroduces noise and obscures functional connectivity. NeuroImage, 82:208–225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoinkiss DC, Erhard P, Breutigam NJ, von Samson-Himmelstjerna F, Günther M, and Porter DA (2019). Prospective motion correction in functional MRI using simultaneous multislice imaging and multislice-to-volume image registration. NeuroImage, 200:159–173. [DOI] [PubMed] [Google Scholar]
- Howell BR, Styner MA, Gao W, Yap PT, Wang L, Baluyot K, Yacoub E, Chen G, Potts T, Salzwedel A, Li G, Gilmore JH, Piven J, Smith JK, Shen D, Ugurbil K, Zhu H, Lin W, and Elison JT (2019). The UNC/UMN Baby Connectome Project (BCP): An overview of the study design and protocol development. [DOI] [PMC free article] [PubMed]
- Jahanian H, Holdsworth S, Christen T, Wu H, Zhu K, Kerr AB, Middione MJ, Dougherty RF, Moseley M, and Zaharchuk G (2019). Advantages of short repetition time resting-state functional MRI enabled by simultaneous multi-slice imaging. Journal of Neuroscience Methods, 311:122–132. [DOI] [PubMed] [Google Scholar]
- James O, Park H, and Kim S (2019). Impact of sampling rate on statistical significance for single subject fMRI connectivity analysis. Human Brain Mapping, 40(11):3321–3337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jenkinson M, Bannister P, Brady M, and Smith S (2002). Improved Optimization for the Robust and Accurate Linear Registration and Motion Correction of Brain Images. NeuroImage. [DOI] [PubMed] [Google Scholar]
- Konova AB, Moeller SJ, Tomasi D, Volkow ND, and Goldstein RZ (2013). Effects of methylphenidate on resting-state functional connectivity of the mesocorticolimbic dopamine pathways in cocaine addiction. JAMA Psychiatry. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kravitz AV, Freeze BS, Parker PR, Kay K, Thwin MT, Deisseroth K, and Kreitzer AC (2010a). Regulation of parkinsonian motor behaviours by optogenetic control of basal ganglia circuitry. Nature. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kravitz AV, Freeze BS, Parker PRL, Kay K, Myo T, Deisseroth K, and Kreitzer AC (2010b). Control of Basal Ganglia Circuitry. Nature, 466(7306):622–626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee HL, Zahneisen B, Hugger T, LeVan P, and Hennig J (2013). Tracking dynamic resting-state networks at higher frequencies using MR-encephalography. NeuroImage, 65:216–222. [DOI] [PubMed] [Google Scholar]
- Lindquist MA, Geuter S, Wager TD, and Caffo BS (2019). Modular preprocessing pipelines can reintroduce artifacts into fMRI data. Human Brain Mapping, 40(8):2358–2376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindquist MA, Meng Loh J, Atlas LY, and Wager TD (2009). Modeling the hemodynamic response function in fMRI: efficiency, bias and mis-modeling. NeuroImage, 45(1 Suppl). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marcus DS, Harwell J, Olsen T, Hodge M, Glasser MF, Prior F, Jenkinson M, Laumann T, Curtiss SW, and Van Essen DC (2011). Informatics and Data Mining Tools and Strategies for the Human Connectome Project. Frontiers in Neuroinformatics, 5:4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mickevicius NJ, Paulson ES, Muftuler LT, and Nencka AS (2019). Application of a k-Space Interpolating Artificial Neural Network to In-Plane Accelerated Simultaneous Multislice Imaging.
- Miller KL, Alfaro-Almagro F, Bangerter NK, Thomas DL, Yacoub E, Xu J, Bartsch AJ, Jbabdi S, Sotiropoulos SN, Andersson JL, Griffanti L, Douaud G, Okell TW, Weale P, Dragonu I, Garratt S, Hudson S, Collins R, Jenkinson M, Matthews PM, and Smith SM (2016a). Multimodal population brain imaging in the UK Biobank prospective epidemiological study. Nature Neuroscience, 19(11):1523–1536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller KL, Alfaro-Almagro F, Bangerter NK, Thomas DL, Yacoub E, Xu J, Bartsch AJ, Jbabdi S, Sotiropoulos SN, Andersson JLR, and others (2016b). Multimodal population brain imaging in the UK Biobank prospective epidemiological study. Nature Neuroscience. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moeller S, Yacoub E, Olman CA, Auerbach E, Strupp J, Harel N, and Ugurbil K (2010). Multiband multislice GE-EPI at 7 tesla, with 16-fold acceleration using partial parallel imaging with application to high spatial and temporal whole-brain fMRI. Magnetic Resonance in Medicine, 63(5):1144–1153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nencka AS, Arpinar VE, Bhave S, Yang B, Banerjee S, McCrea M, Mickevicius NJ, Muftuler LT, and Koch KM (2020). Split Slice Training Augmentation and Hyperparameter Tuning of RAKI Networks for Simultaneous Multi-Slice Reconstruction. [DOI] [PubMed]
- Olszowy W, Aston J, Rua C, and Williams GB (2019). Accurate autocorrelation modeling substantially improves fMRI reliability. Nature Communications, 10(1):1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parkes L, Fulcher B, Yücel M, and Fornito A (2018). An evaluation of the efficacy, reliability, and sensitivity of motion correction strategies for resting-state functional MRI. NeuroImage, 171. [DOI] [PubMed] [Google Scholar]
- Pessiglione M, Seymour B, Flandin G, Dolan RJ, and Frith CD (2006). Dopamine-dependent prediction errors underpin reward-seeking behaviour in humans. Nature. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poldrack RA, Clark J, Pare-Blagoev EJ, Shohamy D, Creso Moyano J, Myers C, and Gluck MA (2001). Interactive memory systems in the human brain. Nature. [DOI] [PubMed] [Google Scholar]
- Power JD, Cohen AL, Nelson SM, Wig GS, Barnes KA, Church JA, Vogel AC, Laumann TO, Miezin FM, Schlaggar BL, and Petersen SE (2011). Functional Network Organization of the Human Brain. Neuron, 72(4):665–678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power JD, Lynch CJ, Adeyemo B, and Petersen SE (2020). A Critical, Event-Related Appraisal of Denoising in Resting-State fMRI Studies. Cerebral Cortex, 30(10):5544–5559. [DOI] [PubMed] [Google Scholar]
- Power JD, Lynch CJ, Gilmore AW, Gotts SJ, and Martin A (2019). Reply to Spreng et al.: Multiecho fMRI denoising does not remove global motion-associated respiratory signals. [DOI] [PMC free article] [PubMed]
- Power JD, Mitra A, Laumann TO, Snyder AZ, Schlaggar BL, and Petersen SE (2014). Methods to detect, characterize, and remove motion artifact in resting state fMRI. NeuroImage, 84:320–341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power JD, Plitt M, Laumann TO, and Martin A (2017). Sources and implications of whole-brain fMRI signals in humans. NeuroImage, 146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Preibisch C, Bührer M, Riedl V, and others (2015). Evaluation of multiband EPI acquisitions for resting state fMRI. PloS one, 10(9):e0136961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pruim RH, Mennes M, van Rooij D, Llera A, Buitelaar JK, and Beckmann CF (2015). ICA-AROMA: A robust ICA-based strategy for removing motion artifacts from fMRI data. NeuroImage, 112:267–277. [DOI] [PubMed] [Google Scholar]
- Risk B, Kociuba M, and Rowe D (2018). Impacts of simultaneous multislice acquisition on sensitivity and specificity in fMRI. NeuroImage, 172. [DOI] [PubMed] [Google Scholar]
- Satterthwaite TD, Elliott MA, Gerraty RT, Ruparel K, Loughead J, Calkins ME, Eickhoff SB, Hakonarson H, Gur RC, Gur RE, and others (2013). An improved framework for confound regression and filtering for control of motion artifact in the preprocessing of resting-state functional connectivity data. Neuroimage, 64:240–256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seidel P, Levine SM, Tahedl M, and Schwarzbach JV (2020). Temporal Signal-to-Noise Changes in Combined Multislice- and In-Plane-Accelerated Echo-Planar Imaging with a 20- and 64-Channel Coil. Scientific Reports, 10(5536). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Setsompop K, Gagoski BA, Polimeni JR, Witzel T, Wedeen VJ, and Wald LL (2012). Blipped-controlled aliasing in parallel imaging for simultaneous multislice echo planar imaging with reduced g-factor penalty. Magnetic Resonance in Medicine, 67(5):1210–1224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Setsompop KP, Polimeni JR, Bhat H, and Wald LL (2013). Characterization of artifactual correlation in highly-accelerated simultaneous multi-slice (SMS) fMRI acquisitions. Abstract 0410. In ISMRM Proceedings. [Google Scholar]
- Smith SM, Beckmann CF, Andersson J, Auerbach EJ, Bijsterbosch J, Douaud G, Duff E, Feinberg DA, Griffanti L, Harms MP, and others (2013). Resting-state fMRI in the human connectome project. Neuroimage, 80:144–168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, Jenkinson M, Woolrich MW, Beckmann CF, Behrens TE, Johansen-Berg H, Bannister PR, De Luca M, Drobnjak I, Flitney DE, Niazy RK, Saunders J, Vickers J, Zhang Y, De Stefano N, Brady JM, and Matthews PM (2004). Advances in functional and structural MR image analysis and implementation as FSL. In NeuroImage, volume 23. Neuroimage. [DOI] [PubMed] [Google Scholar]
- Todd N, Josephs O, Zeidman P, Flandin G, Moeller S, and Weiskopf N (2017). Functional sensitivity of 2D simultaneous multi-slice echo-planar imaging: effects of acceleration on g-factor and physiological noise. Frontiers in Neuroscience, 11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Todd N, Moeller S, Auerbach EJ, Yacoub E, Flandin G, and Weiskopf N (2016). Evaluation of 2D multiband EPI imaging for high-resolution, whole-brain, task-based fMRI studies at 3T: Sensitivity and slice leakage artifacts. NeuroImage, 124:32–42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsay RS (2010). Analysis of Financial Time Series Second Edition. Wiley, 3rd edition. [Google Scholar]
- Ugurbil K, Xu J, Auerbach EJ, Moeller S, Vu AT, Duarte-Carvajalino JM, Lenglet C, Wu X, Schmitter S, de Moortele PF, and others (2013). Pushing spatial and temporal resolution for functional and diffusion MRI in the Human Connectome Project. NeuroImage, 80:80–104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weiner MW, Veitch DP, Aisen PS, Beckett LA, Cairns NJ, Green RC, Harvey D, Jack CR, Jagust W, Morris JC, Petersen RC, Salazar J, Saykin AJ, Shaw LM, Toga AW, and Trojanowski JQ (2017a). The Alzheimer’s Disease Neuroimaging Initiative 3: Continued innovation for clinical trial improvement. [DOI] [PMC free article] [PubMed]
- Weiner MW, Veitch DP, Aisen PS, Beckett LA, Cairns NJ, Green RC, Harvey D, Jack CR, Jagust W, Morris JC, Petersen RC, Salazar J, Saykin AJ, Shaw LM, Toga AW, and Trojanowski JQ (2017b). The Alzheimer’s Disease Neuroimaging Initiative 3: Continued innovation for clinical trial improvement. [DOI] [PMC free article] [PubMed]
- Wood S (2017). Generalized additive models: an introduction with R. CRC Press. [Google Scholar]
- Woodward ND and Heckers S (2016). Mapping Thalamocortical Functional Connectivity in Chronic and Early Stages of Psychotic Disorders. Biological Psychiatry, 79(12):1016–1025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xia M, Wang J, and He Y (2013). BrainNet Viewer: A Network Visualization Tool for Human Brain Connectomics. PLoS ONE, 8(7). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu J, Moeller S, Auerbach EJ, Strupp J, Smith SM, Feinberg DA, Yacoub E, and Ugurbil K (2013). Evaluation of slice accelerations using multiband echo planar imaging at 3T. NeuroImage, 83:991–1001. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


