Genomic basis of parallel adaptation varies with divergence in Arabidopsis and its relatives

Significance

Repeated evolution tends to be more predictable. The impressive spectrum of recent reports on genomic parallelism, however, revealed that the fraction of the genome that evolves in parallel varies greatly, possibly reflecting different evolutionary scales investigated. Here, we demonstrate divergence-dependent parallelism using a comprehensive genome-wide dataset comprising 12 cases of parallel alpine adaptation and identify decreasing probability of adaptive re-use of genetic variation as the major underlying cause. This finding empirically demonstrates that evolutionary predictability is scale dependent and suggests that availability of preexisting variation drives parallelism within and among populations and species. Altogether, our results inform the ongoing discussion about the (un)predictability of evolution, relevant for applications in pest control, nature conservation, or the evolution of pathogen resistance.

Abstract

Parallel adaptation provides valuable insight into the predictability of evolutionary change through replicated natural experiments. A steadily increasing number of studies have demonstrated genomic parallelism, yet the magnitude of this parallelism varies depending on whether populations, species, or genera are compared. This led us to hypothesize that the magnitude of genomic parallelism scales with genetic divergence between lineages, but whether this is the case and the underlying evolutionary processes remain unknown. Here, we resequenced seven parallel lineages of two Arabidopsis species, which repeatedly adapted to challenging alpine environments. By combining genome-wide divergence scans with model-based approaches, we detected a suite of 151 genes that show parallel signatures of positive selection associated with alpine colonization, involved in response to cold, high radiation, short season, herbivores, and pathogens. We complemented these parallel candidates with published gene lists from five additional alpine Brassicaceae and tested our hypothesis on a broad scale spanning ∼0.02 to 18 My of divergence. Indeed, we found quantitatively variable genomic parallelism whose extent significantly decreased with increasing divergence between the compared lineages. We further modeled parallel evolution over the Arabidopsis candidate genes and showed that a decreasing probability of repeated selection on the same standing or introgressed alleles drives the observed pattern of divergence-dependent parallelism. We therefore conclude that genetic divergence between populations, species, and genera, affecting the pool of shared variants, is an important factor in the predictability of genome evolution.

Evolution is driven by a complex interplay of deterministic and stochastic forces whose relative importance is a matter of debate (1). Being largely a historical process, we have limited ability to experimentally test for the predictability of evolution in its full complexity (i.e., in natural environments) (2). Distinct lineages that independently adapted to similar conditions by similar phenotype (termed parallel,” considered synonymous to “convergent” here) can provide invaluable insights into the issue (3, 4). An improved understanding of the probability of parallel evolution in nature may inform on constraints on evolutionary change and provide insights relevant for predicting the evolution of pathogens (5–7), pests (8, 9), or species in human-polluted environments (10, 11). Although the past few decades have seen an increasing body of work supporting the parallel emergence of traits by the same genes and even alleles, we know surprisingly little about what makes parallel evolution more likely and, by extension, what factors underlie evolutionary predictability (1, 12).

A wealth of literature describes the probability of “genetic” parallelism, showing why certain genes are involved in parallel adaptation more often than others (13). There is theoretical and empirical evidence for the effect of pleiotropic constraints, availability of beneficial mutations or position in the regulatory network all having an impact on the degree of parallelism at the level of a single locus (3, 13–18). In contrast, we know little about causes underlying “genomic” parallelism (i.e., what fraction of the genome is reused in adaptation and why). Individual case studies demonstrate large variation in genomic parallelism, ranging from absence of any parallelism (19), similarity in functional pathways but not genes (20, 21), and reuse of a limited number of genes (22–24) to abundant parallelism at both gene and functional levels (25, 26). Yet, there is little consensus about what determines variation in the degree of gene reuse (fraction of genes that repeatedly emerge as selection candidates) across investigated systems (1).

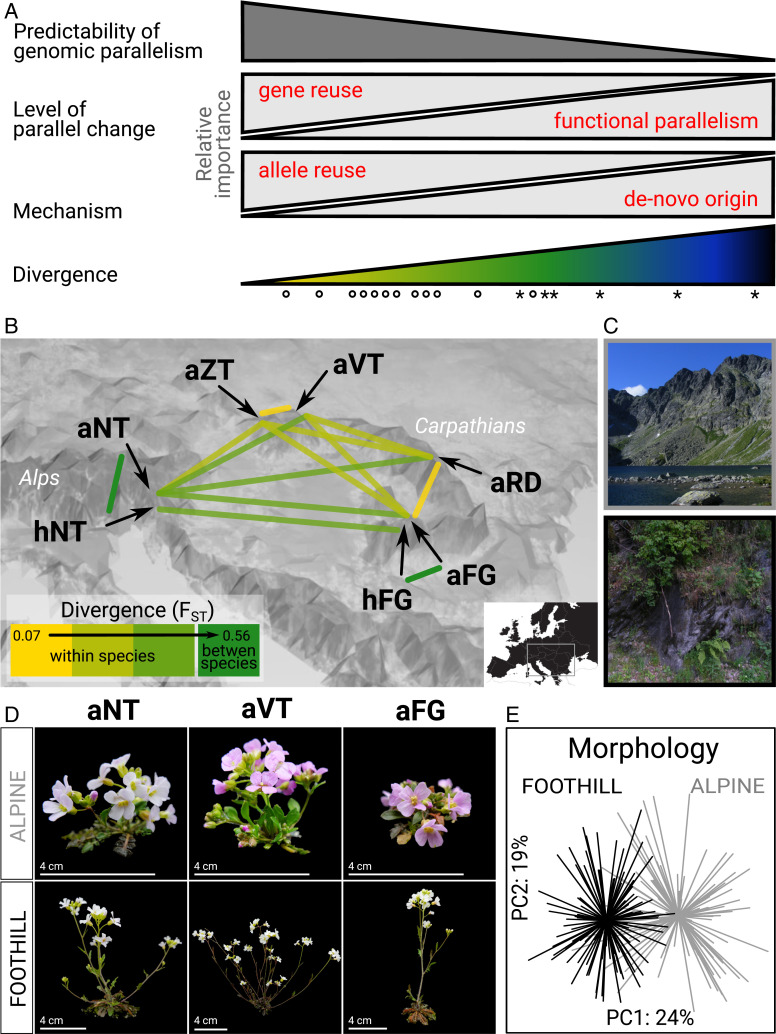
Divergence (the term used here to consistently describe both intra- and interspecific genetic differentiation) between the compared instances of parallelism appears as a potential driver of the variation in gene reuse (14, 27, 28). Phenotype-oriented meta-analyses suggest that both phenotypic convergence (28) and genetic parallelism underlying phenotypic traits (14) decrease with increasing time to the common ancestor. Although a similar targeted multiscale comparison is lacking at the genomic level, our brief review of published studies (29 cases, Dataset S1) suggests that also gene reuse tends to scale with divergence (Fig. 1A and SI Appendix, Fig. S1). Moreover, allele reuse (repeated sweep of the same haplotype that is shared among populations either via gene flow or from standing genetic variation) frequently underlies parallel adaptation between closely related lineages (29–32), while parallelism from independent de novo mutations at the same locus dominates between distantly related taxa (13). Similarly, previous studies reported a decreasing probability of hemiplasy (apparent convergence resulting from gene tree discordance) with divergence in phylogeny-based studies (33, 34). This suggests that the degree of allele reuse may be the primary factor underlying the hypothesized divergence-dependency of parallel genome evolution, possibly reflecting either weak hybridization barriers, widespread ancestral polymorphism between closely related lineages (35), or ecological reasons (lower niche differentiation and geographical proximity) (36, 37). However, the generally restricted focus of individual studies of genomic parallelism on a single level of divergence does not lend itself to a unified comparison across divergence scales. Although different ages of compared lineages affect a variety of evolutionary–ecological processes such as diversification rates, community structure, or niche conservatism (37), the hypothesis that genomic parallelism scales with divergence has not yet been systematically tested, and the underlying evolutionary processes remain poorly understood.

Fig. 1.

Hypotheses regarding relationships between genomic parallelism and divergence and the Arabidopsis system used to address these hypotheses. (A) Based on our literature review, we propose that genetically closer lineages adapt to a similar challenge more frequently by gene reuse, sampling suitable variants from the shared pool (allele reuse), which makes their adaptive evolution more predictable. Color ramp symbolizes rising divergence between the lineages (∼0.02 to 18 Mya in this study); the symbols denote different divergence levels tested here using resequenced genomes of 22 Arabidopsis populations (circles) and meta-analysis of candidates in Brassicaceae (asterisks). (B) Spatial arrangement of lineages of varying divergence (neutral F_ST; bins only aid visualization; all tests were performed on a continuous scale) encompassing parallel alpine colonization within the two Arabidopsis outcrossers from central Europe: A. arenosa (diploid: aVT; autotetraploid: aNT, aZT, aRD, and aFG) and A. halleri (diploid: hNT and hFG). Note that only two of the ten between-species pairs (dark green) are shown to aid visibility. The color scale corresponds to the left part of the color ramp used in A. (C) Photos of representative alpine and foothill habitat. (D) Representative phenotypes of originally foothill and alpine populations grown in common garden demonstrating phenotypic convergence. Scale bar corresponds to 4 cm. (E) Morphological differentiation among 223 A. arenosa individuals originating from foothill (black) and alpine (gray) populations from four regions after two generations in a common garden. Principal component analysis was run using 16 morphological traits taken from ref. 45.

Here, we aimed to test this hypothesis and investigate whether allele reuse is a major factor underlying the relationship. We analyzed replicated instances of adaptation to a challenging alpine environment, spanning a range of divergence from populations to tribes within the plant family Brassicaceae (38–43) (Fig. 1A). First, we took advantage of a unique naturally multireplicated setup in the plant model genus Arabidopsis that was so far neglected from a genomic perspective (Fig. 1B). Two predominantly foothill-dwelling Arabidopsis outcrossers (A. arenosa, A. halleri) exhibit scattered, morphologically distinct alpine occurrences at rocky outcrops above the timberline (Fig. 1C). These alpine forms are separated from the widespread foothill population by a distribution gap spanning at least 500 m of elevation. Previous genetic and phenotypic investigations and follow-up analyses presented here showed that the scattered alpine forms of both species represent independent alpine colonization in each mountain range, followed by parallel phenotypic differentiation (Fig. 1 D and E) (44–46). Thus, we sequenced genomes from seven alpine and adjacent foothill population pairs, covering all European lineages encompassing the alpine ecotype. We discovered a suite of 151 genes from multiple functional pathways relevant to alpine stress that were repeatedly differentiated between foothill and alpine populations. This points toward a polygenic, multifactorial basis of parallel alpine adaptation.

We took advantage of this set of well-defined parallel selection candidates and tested whether the degree of gene reuse decreases with increasing divergence between the compared lineages (Fig. 1A). By extending our analysis to five additional alpine Brassicaceae species, we further tested whether there are limits to gene reuse above the species level. Finally, we inquired about possible underlying evolutionary processes by estimating the extent of allele reuse using a designated modeling approach. Overall, our empirical analysis provides a perspective to the ongoing discussion about the variability in the reported magnitude of parallel genome evolution and identifies allele reuse as an important evolutionary process shaping the extent of genomic parallelism between populations, species, and genera.

Results

Parallel Alpine Colonization by Distinct Lineages of Arabidopsis.

We retrieved whole-genome sequences from 11 alpine and 11 nearby foothill populations (174 individuals in total, seven to eight per population) covering all seven mountain regions with known occurrence of A. arenosa or A. halleri alpine forms (a set of populations from one mountain region is further referred to as a “lineage”; Fig. 1B and SI Appendix, Fig. S2 and Tables S1 and S2). Within each species, population structure analyses based on genome-wide fourfold degenerate (4d) synonymous single nucleotide polymorphisms (SNPs) demonstrated clear grouping according to lineage but not alpine environment, suggesting parallel alpine colonization of each mountain region by a distinct genetic lineage (SI Appendix, Figs. S3 and S4). This was in line with separation histories between diploid populations of A. halleri estimated in Relate (SI Appendix, Fig. S5) and previous coalescent simulations on broader population sampling of A. arenosa (45). The only exception was the two spatially closest lineages of A. arenosa (aVT and aZT) for which alpine populations clustered together, keeping the corresponding foothill populations paraphyletic. Due to considerable pre- (spatial segregation) and postzygotic (ploidy difference) barriers between the alpine populations from these two lineages (47), we left aZT and aVT as separate units in the following analyses for the sake of clarity (exclusion of this pair of lineages did not lead to qualitatively different results; SI Appendix, Text S1).

We observed a gradient of neutral differentiation among the seven lineages, quantified as average pairwise 4d-F_ST between foothill populations from each lineage, ranging from 0.07 to 0.56 (SI Appendix, Table S3). To control for potential effects of linked selection on our divergence estimates, we also calculated F_ST differentiation using noncoding sites that are distant from selectively constrained sites (Materials and Methods). These F_ST values strongly correlated with 4d-F_ST (Pearson’s r = 0.93, P value < 0.001). Further, 4d-F_ST values correlated with absolute neutral divergence (4d-D_XY, Pearson’s r = 0.89, P < 0.0001), and we further refer to them consistently as “divergence.” All populations showed high levels of 4d-nucleotide diversity (mean = 0.023, SD = 0.005), as expected for strict outcrossers, and no remarkable deviation from neutrality [the range of 4d-Tajima’s D was −0.16 tp 0.6, well within the neutrality interval −2 to 2 proposed by Tajima (48); SI Appendix, Table S4]. We found no signs of severe demographic change that would be associated with alpine colonization (similar 4d-nucleotide diversity and 4d-Tajima’s D of alpine and foothill populations; Wilcoxon rank test, P = 0.70 and 0.92, respectively; n = 22). Coalescent-based demographic inference further supported a no-bottleneck model even for the outlier population with the highest 4d-Tajima’s D value (population LAC of aFG lineage, SI Appendix, Fig. S6).

Genomic Basis of Parallel Alpine Adaptation.

Leveraging whole-genome resequencing data of the seven natural replicates, we identified a set of genes showing signatures of parallel directional selection associated with alpine colonization. We used a conservative approach taking the intersection of F_ST-based divergence scans designed to control for potential confounding signal of local selection within each ecotype (Materials and Methods) and candidate detection under a Bayesian framework that accounts for neutral processes (BayPass) and identified from 100 to 716 gene candidates in the seven lineages. Of these, we identified 196 gene candidates that were shared between at least two lineages and further tested whether they are consistent with parallel adaptation using neutral simulations in the Distinguishing Modes of Convergence (DMC) maximum composite likelihood framework (49) (Materials and Methods). Out of the 196 shared gene candidates, we identified 151 genes showing significantly higher support for the parallel alpine selection model as compared to a neutral model assuming no selection in DMC (further referred to as “parallel gene candidates”). This set of genes contains an enrichment of differentiated nonsynonymous SNPs (SI Appendix, Table S5), and we did not find any evidence that this was explained by weaker selective constraint compared to the rest of the genome (approximated by ratio of their nonsynonymous-to-synonymous diversity; SI Appendix, Table S6 and Fig. S7 and Text S2). Further, F_ST values calculated for the 5% outlier windows do not correlate with recombination rate (Pearson’s r = 0.037, P = 0.67), and such genes do not tend to cluster in regions of low recombination rates (SI Appendix, Figs. S8 and S9).

Functional annotations of the parallel gene candidates using The Arabidopsis Information Resource (TAIR) database and associated publications (Dataset S2), protein–protein interaction database STRING (SI Appendix, Fig. S10), and gene onthology (GO) enrichment analysis (Dataset S3) suggest a complex polygenic basis of alpine adaptation, involving multiple major functional categories, well-matching expectations for a response to a multifactorial environmental stress (SI Appendix, Text S3). Six of the physiological adaptations to alpine environment, encompassing both abiotic and biotic stress, stand out (broadly following ref. 50), both in terms of number of associated parallel candidate genes and functional pathways (Fig. 2). We further discuss these putative alpine adaptations and their functional implications in (SI Appendix, Text S3).

Fig. 2.

Physiological responses to alpine stresses in A. arenosa and A. halleri, identified based on functional annotation of parallel gene candidates (circle) and signatures of parallel directional selection at the corresponding loci (surrounding dotplots). The circle scheme is based on the annotated list of 151 parallel gene candidates (Dataset S2) and corresponding enriched GO terms within the biological process category (Dataset S3). For purposes of functional interpretation and visualization, we also classified the enriched GO terms in the context of major alpine stressors following ref. 50, and list a subset of corresponding 47 well-annotated parallel gene candidates in the outer circle. For the complete list of all genes, refer to Dataset S2, and for more details on functional interpretations, refer to SI Appendix, Text S3. Dotplots show allele frequency difference (AFD) at SNPs between foothill and alpine populations summed over all lineages showing a parallel differentiation in a given gene (blue arrow). The lineage names are listed on the sides. Loci with two independently differentiated haplotypes likely representing independent de novo mutations (AT5G65750 and ATL12) are represented by peaks of black and gray dots, corresponding with the two parallel lineages. Red circles highlight nonsynonymous variants.

Ubiquitous Gene and Function-Level Parallelism and Their Relationship with Divergence.

Using the set of parallel gene candidates identified in Arabidopsis lineages, we quantified the degree of parallelism at the level of genes and gene functions (biological processes). We overlapped the seven lineage-specific candidate gene lists across all 21 pairwise combinations of the lineages and identified significant parallelism (nonrandom number of overlapping genes, P < 0.05, Fisher’s exact test, Fig. 3A) among 15 (71%) lineage pairs (SI Appendix, Table S7). Notably, the overlaps were significant for 10 out of 11 pairwise comparisons among the lineages within a species but only in five out of 10 pairwise comparisons across species (Dataset S4). We then annotated the functions of gene candidates using “biological process” GO terms in each lineage, extracted only significantly enriched functions, and again overlapped them across the seven lineages. Of these, we found significant overlaps (P < 0.05, Fisher’s exact test) among 17 (81%) lineage pairs, and the degree of overlap was similar within and across species (82 and 80%, respectively, Fig. 3B and SI Appendix, Table S7 and Dataset S5).

Fig. 3.

Variation in gene and function-level parallelism and their relationship with divergence in A. arenosa and A. halleri (A–D) and across species from Brassicaceae family (E and F). (A and B) Number of overlapping candidate genes (A) and functions (B; enriched GO terms) for alpine adaptation colored by increasing divergence between the compared lineages. Only overlaps of >2 genes and >1 function are shown (for a complete overview, refer to Datasets S4–S7). Numbers in the bottom-right corner of each panel show the total number of candidates in each lineage. Categories indicated by an asterisk exhibited higher than random overlap of the candidates (P < 0.05, Fisher’s exact test). For lineage codes, see Fig. 1B. Categories with overlap over more than two lineages are framed in bold and filled by a gradient. (C and D) Proportions of parallel genes (C; gene reuse) and functions (D) among all candidates identified within each pair of lineages (dot) binned into categories of increasing divergence (bins correspond to Fig. 1B and only aid visualization; size of the dot corresponds to the number of parallel items). Significance of the association was inferred by Mantel test over continuous divergence scale. (E and F) Same as A and B but for species from Brassicaceae family, spanning higher divergence levels. Codes: aar: our data on A. arenosa; ahe: our data on A. halleri combined with A. halleri candidates from Swiss Alps (39); ahj: Arabidopsis halleri subsp. gemmifera from Japan (38); aly: A. lyrata from Northern Europe (40); ath: A. thaliana from Alps (43); chi: Crucihimalaya himalaica (42); and lme: Lepidium meyenii (41).

Then, we quantified the degree of parallelism for each pair of Arabidopsis lineages as the proportion of overlapping gene and function candidates out of all candidates identified for these two lineages. The degree of parallelism was significantly higher at the function level (mean proportion of parallel genes and functions across all pairwise comparisons = 0.045 and 0.063, respectively, D = 437.14, degrees of freedom [df] = 1, P < 0.0001, generalized linear model [GLM] with binomial errors). Importantly, the degree of parallelism at the gene level (i.e., gene reuse) significantly decreased with increasing divergence between the lineages (negative relationship between Jaccard’s similarity in candidate gene identity among pairs of lineages and 4d-Fst; Mantel rM = −0.71, P = 0.001, 999 permutations, Fig. 3C). In contrast, the degree of parallelism by function did not correlate with divergence (rM = 0.06, P = 0.6, 999 permutations, n = 21, Fig. 3D).

We further tested whether the relationship between the degree of parallelism and divergence persists at deeper phylogenetic scales by complementing our data with candidate gene lists from six genome-wide studies of alpine adaptation from the Brassicaceae family (38–43) [involving five species diverging 0.5 to 18 Mya (51, 52), SI Appendix, Supplementary Methods and Tables S8 and S9]. While we still found significant parallelism both at the level of candidate genes and functions (Fig. 3 E and F and Datasets S6 and S7), their relationship with divergence was nonsignificant (Mantel rM = −0.52/−0.22, for genes/functions respectively, P = 0.08/0.23, 999 permutations, n = 21). However, the degree of gene reuse was significantly higher for comparisons within a genus (Arabidopsis) than between genera (D = 15.37, df = 1, P < 0.001, GLM with binomial errors) while such a trend was absent for parallel function candidates (D = 0.38, df = 1, P = 0.54), suggesting that there are limits to gene reuse at above-genus–level divergences. Taken together, these results suggest that there are likely similar functions associated with alpine adaptation among different lineages, species, and even genera from distinct tribes of Brassicaceae. However, the probability of reusing the same genes within these functions decreases with increasing divergence among the lineages, thus reducing the chance to identify parallel genome evolution.

Probability of Allele Reuse Underlies the Divergence Dependency of Gene Reuse.

Repeated evolution of the same gene in different lineages could either reflect repeated recruitment of the same allele from a shared pool of variants (“allele reuse”) or adaptation via alleles representing independent mutations in each lineage (“de novo origin”) (49). To ask whether varying prevalence of these two evolutionary processes could explain the observed divergence-dependency of gene reuse, we quantified the contribution of allele reuse versus de novo origin to the gene reuse in each pair of A. arenosa and A. halleri lineages and tested whether it scales with divergence.

For each of the 151 parallel gene candidates, we inferred the most likely source of its candidate variant(s) by using a designated likelihood-based modeling approach that investigates patterns of shared hitchhiking from allele frequency covariance at positions surrounding the selected site [DMC method (49)]. We contrasted three models of gene reuse, involving 1) selected allele acquired via gene flow, 2) sourced from ancestral standing variation (both 1 and 2 representing allele reuse), and 3) de novo origin of the selected allele. In line with our expectations, the degree of allele reuse decreased with divergence (D = 34.28, df = 16, P < 0.001, GLM with binomial errors; Fig. 4A). In contrast, the proportion of variants sampled from standing variation remained relatively high even at the deepest interspecific comparison (43%; Fig. 4A and SI Appendix, Fig. S11). The absolute number of de novo–originated variants was low across all divergence levels investigated (Dataset S8). This corresponds to predictions about a substantial amount of shared variation between related species with high genetic diversity (35) and frequent adaptive transspecific polymorphism in Arabidopsis (10, 53–55). Absence of interspecific parallelism sourced from gene flow was in line with the lack of genome-wide signal of recent migration between A. arenosa and A. halleri inferred by coalescent simulations (SI Appendix, Fig. S12).

Fig. 4.

Decreasing probability of allele reuse with increasing divergence in A.arenosa and A. halleri. (A) Proportion of parallel candidate gene variants shared via gene flow between alpine populations from different lineages or recruited from ancestral standing variation (together describing the probability of allele reuse) and originated by independent de novo mutations within the same gene. Percentages represent mean proportions for lineages of a particular divergence category (color ramp; total number of parallel gene candidates is given within each plot). (B) Explained variation in gene reuse between lineages partitioned by divergence (green circle), allele reuse (orange circle), and shared components (overlaps between them). (C) Maximum composite log-likelihood estimate (MCLE) of median time (generations) for which the allele was standing in the populations prior to the onset of selection. (D–F) Examples of SNP variation and MCL estimation of the evolutionary scenario describing the origin of parallel candidate allele. Two lineages in light and dark gray are compared in each plot. Shown is the entire region of each parallel candidate gene. (D) Parallel selection on variation shared via gene flow on gene ALA3, affecting vegetative growth and acclimation to temperature stresses (87). (E) Parallel recruitment of shared ancestral standing variation at gene AL730950, encoding heat shock protein. (F) Parallel selection on independent de novo mutations at gene PKS1, regulating phytochrome B signaling (88); here, de novo origin was prioritized over standing variation model based on very high MCLE of standing time (Materials and Methods). Note that each sweep includes multiple highly differentiated nonsynonymous SNPs (in C and D at the same positions in both population pairs, in line with reuse of the same allele). Dotplot (left y-axis): AFD between foothill and alpine population from each of the two lineages (range 0 to 1 in all plots). Lines (right y-axis): MCL difference from a neutral model assuming no parallel selection (all values above dotted gray line show the difference, higher values indicate higher support for the nonneutral model, and the final model selection is based on the genomic position with the highest likelihood within the gene).

Importantly, allele reuse covered a dominant fraction of the variation in gene reuse that was explained by divergence (Fig. 4B), suggesting allele reuse is the major factor contributing to the observed divergence-dependency of gene reuse. We also observed a strong correlation between divergence and the maximum composite likelihood estimate of the amount of time the allele was standing in the populations between their divergence and the onset of selection (Pearson’s r = 0.83, P < 0.0001, Fig. 4C). This suggests that the onset of selection pressure (assuming a similar selection strength) likely happened at a similar time point in the past. Altogether, the parallel gene candidates (Fig. 4 D–F) in the two Arabidopsis species likely experienced selection at comparable time scales in all lineages, but the degree of reuse of the same alleles decreased with increasing divergence between parallel lineages, which explained most of the divergence-dependency of gene reuse.

Discussion

By analyzing genome-wide variation over 12 instances of alpine adaptation across Brassicaceae, we found that the degree of gene reuse decreased with increasing divergence between compared lineages. This relationship was largely explained by the decreasing role of allele reuse in a subset of seven thoroughly investigated pairs of Arabidopsis lineages. These findings provide empirical support for earlier predictions on genetic parallelism (14, 28) and present a general mechanism that may help explain the tremendous variability in the extent of parallel genome evolution that was recorded across different case studies (1, 13). The decreasing role of allele reuse with divergence agrees with theoretical and empirical findings that the evolutionary potential of a population depends on the availability of preexisting (standing or introgressed) genetic variation (56–58) and that the extent of ancestral polymorphism and gene flow decreases with increasing differentiation between gradually diverging lineages (35, 59). In contrast, the overall low contribution of de novo–originated parallel alleles and generally large and variable outcrossing Arabidopsis populations suggest a minor role of mutation limitation, at least within our genomic Arabidopsis dataset. In general, our study demonstrates the importance of a quantitative understanding of divergence for the assessment of evolutionary predictability (60) and brings support to the emerging view of the ubiquitous influence of divergence scale on different evolutionary and ecological mechanisms (37).

There are potentially additional, nonexclusive explanations for the observed divergence-dependency of gene reuse, although presumably of much lower impact given the large explanatory power of allele reuse in our system. First, theory predicts that the degree of conservation of gene networks, their functions, and developmental constraints decrease with increasing divergence (14, 28). Diversification of gene networks, however, typically increases at higher divergence scales than addressed here [millions of years of independent evolution (28)] and affects parallelism caused by independent de novo mutations (18). We also did not find any evidence that our gene reuse candidates were under weaker selective constraint than other genic loci genome-wide. Nevertheless, we cannot exclude that changes in constraint contribute to the decreasing probability of gene reuse across Brassicaceae, as was also reported in ref. 61. Second, protein evolution studies reported patterns of diminishing amino acid convergence over time due to the decreasing probability of hemiplasy (i.e., the gene tree discordance caused by incomplete lineage sorting and introgression) (33, 34, 62). As such a pattern reflects neutral processes and is expected to decrease with time, it can confound the assessment of the level of adaptive convergence (33, 34). However, we accounted for this bias in our sampling and analysis design by considering only genes identified as selection candidates in separate divergence scans that contrasted derived alpine populations by their control foothill counterparts. Third, as genetic divergence often corresponds to the spatial arrangement of lineages (63), external challenges posed by the alpine environment at remote locations may differ. Such risk is, however, mitigated at least in our Arabidopsis dataset, as the genomically investigated alpine populations share very similar niches (45).

In contrast, no relationship between the probability of gene reuse and divergence was shown in experimental evolution of different populations of yeast (64), raising a question about the generality of our findings. Our study addresses a complex selective agent [a multihazard alpine environment (50)] in order to provide insights into an ecologically realistic scenario relevant for adaptation in natural environments. Results might differ in systems with a high degree of self-fertilization or recent bottlenecks, as these might decrease the probability of gene reuse even among closely related lineages by reducing the pool of shared standing variation (65, 66). Although this is not the case in our Arabidopsis outcrossers, encompassing highly variable and demographically stable populations, drift might have contributed to the low number of overlaps in comparisons involving the less-variable selfer Arabidopsis thaliana (43) in our meta-analysis (Fig. 3E). However, considering the supporting evidence from the literature (Fig. 1A and SI Appendix, Fig. S1) and keeping the aforementioned restrictions in mind, we predict that our findings are widely applicable. In summary, our study demonstrates divergence-dependency of parallel genome evolution between different populations, species, and genera and identifies allele reuse as the underlying mechanism. This indicates that the availability of genomic variation preexisting in the species may be essential for (repeated) local adaptation and consequently also for the predictability of evolution, a topic critical for pest and disease control as well as for evolutionary theory.

Materials and Methods

Sampling.

A. arenosa and A. halleri are biennial to perennial outcrossers closely related to the model A. thaliana. Both species occur primarily in low to mid elevations (to ∼1,000 m above sea level) across Central and Eastern Europe, but scattered occurrences of morphologically distinct populations have been recorded from treeless alpine zones (>1,600 m) in several distinct mountain regions in Central–Eastern Europe (44, 67) that were exhaustively sampled by us (Fig. 1, details provided in SI Appendix, Supplementary Methods).

Here, we sampled and resequenced genomes of foothill (growing in elevations 460 to 980 m a.s.l.) as well as adjacent alpine (1,625 to 2,270 m a.s.l.) populations from all known foothill–alpine contrasts. In total, we sequenced genomes of 111 individuals of both species and complemented them with 63 published whole-genome sequences of A. arenosa (68) totaling 174 individuals and 22 populations (SI Appendix, Table S1). Ploidy of each sequenced individual was checked using flow cytometry following (69).

Sequencing, Raw Data Processing, Variant Calling, and Filtration.

Samples were sequenced on Illumina HiSeq X Ten, mapped to reference genome A. lyrata (70), and processed following ref. 68. Details are provided in SI Appendix, Supplementary Methods.

Population Genetic Structure.

We calculated genome-wide 4d within- [nucleotide diversity {π} and Tajima’s D (48)] and between- [F_ST (70)] population metrics using python3 ScanTools_ProtEvol pipeline (https://github.com/mbohutinska/ScanTools_ProtEvol) (71). ScanTools_ProtEvol is a customized version of ScanTools, a toolset specifically designed to analyze diversity and differentiation of diploid and autotetraploid populations using SNP data (68). To overcome biases caused by unequal population sizes and to preserve the most sites with no missing data, we randomly subsampled genotypes at each position to six individuals per population.

We quantified divergence between pairs of lineages as average pairwise 4d-F_ST between the foothill populations as they likely represent the ancestral state within a given lineage. To control for potential effects of linked selection on our divergence estimates, we also extracted all putatively neutral sites that are unlinked from the selected sites (i.e., sites >5 kb outside genic and conserved regions and sites >1 Mb away from the centromere). As both F_ST estimates strongly correlated (Pearson’s r = 0.93, P value < 0.001), we used only 4d-F_ST in further analyses of population structure.

Next, we inferred relationships between populations using allele frequency covariance graphs implemented in TreeMix v. 1.13 (72). We ran TreeMix allowing a range of migration events and presented two and one additional migration edges for A. arenosa and A. halleri, as they represented points of log-likelihood saturation (SI Appendix, Fig. S4). To obtain confidence in the reconstructed topology, we bootstrapped the scenario with zero events (the tree topology had not changed when considering the migration events), choosing a bootstrap block size of 1,000 bp, equivalent to the window size in our selection scan, and 100 replicates. Finally, we displayed genetic relatedness among individuals using principal component analysis as implemented in adegenet (73).

We further investigated particular hypotheses regarding the demographic history of our system using coalescent simulations implemented in fastsimcoal2 (74). We calculated joint allele frequency spectra (AFS) of selected sets of populations from genome-wide 4d-SNPs and compared their fit to the AFS simulated under different demographic scenarios using the Poisson random field model likelihood. We used wide range of initial parameters (effective population size, divergence times, migration rates; see attached est file, Dataset S10).

Population structure inference was based on a complete dataset of all populations as all the above used methods allow for a combined analysis of diploid and autotetraploid data (further explained in SI Appendix, Supplementary Methods).

Genome-Wide Scans for Directional Selection.

To infer SNP candidates, we worked with the full set of SNPs which passed variant filtration (SI Appendix, Table S2). We used a combination of two different divergence scan approaches, both of which are based on population allele frequencies and allow analysis of diploid and autopolyploid populations.

First, we calculated pairwise window-based F_ST between foothill and alpine population pairs within each lineage and used minimum sum of ranks to find the candidates. For each population pair, we calculated F_ST (75) for 1 kb windows along the genome. Based on the average genome-wide decay of genotypic correlations (150 to 800 bp, SI Appendix, Fig. S13 and Supplementary Methods), we designed windows for the selection scans to be 1 kb (i.e., at least 200 bp larger than the estimated average linkage disequilibrium [LD]). All calculations were performed using ScanTools_ProtEvol and custom R scripts (https://github.com/mbohutinska/ProtEvol/). Our F_ST-based detection of outlier windows was not largely biased toward regions with low recombination rate [as estimated based on the available A. lyrata recombination map (40) and also from our diploid population genomic data; SI Appendix, Figs. S8 and S9]. This corresponds well with outcrossing and high nucleotide diversity that aids divergence outlier detection in our species (76).

Whenever two foothill and two alpine populations were available within one lineage (i.e., aFG, aNT, aVT and aZT populations of A. arenosa), we designed the selection scan to account for changes which were not consistent between the foothill and alpine populations (i.e., rather reflected local changes within one environment). Details are provided in SI Appendix, Supplementary Methods. Finally, we identified SNPs which were 5% outliers for foothill–alpine allele frequency differences in the above-identified outlier windows and considered them SNP candidates of selection associated with the elevational difference in the lineage.

Second, we used a Bayesian model–based approach to detect significantly differentiated SNPs within each lineage, while accounting for local population structure as implemented in BayPass (SI Appendix, Supplementary Methods) (77).

Finally, we overlapped SNP candidate lists from F_ST and BayPass analysis within each lineage and considered only SNPs which were outliers in both methods as directional selection candidates. We annotated each SNP candidate and assigned it to a gene using SnpEff 4.3 (78) following A. lyrata version 2 genome annotation (79). We considered all variants in 5′ untranslated regions (UTRs), start codons, exons, introns, stop codons, and 3′ UTRs as genic variants. We further considered as gene candidates only genes containing more than five SNP candidates to minimize the chance of identifying random allele frequency fluctuation in few sites rather than selective sweeps within a gene.

For both selection scans, we used relatively relaxed 95% quantile threshold as we aimed to reduce the chance of getting false negatives (i.e., undetected loci affected by selection) whose extent would be later magnified in overlaps across multiple lineages. At the same time, we controlled for false positives by accepting only gene candidates fulfilling criteria of the two complementary selection scans. Using a more stringent threshold of 1% did not lead to qualitatively different results in regard to the relationship between parallelism and divergence (SI Appendix, Text S4).

GO Enrichment Analysis.

To infer functions significantly associated with foothill–alpine divergence, we performed gene ontology enrichment of gene candidates in the R package topGO (80), using A. thaliana orthologs of A. lyrata genes obtained using biomaRt (81). We used the conservative “elim” method, which tests for enrichment of terms from the bottom of the GO hierarchy to the top and discards any genes that are significantly enriched in descendant GO terms while accounting for the total number of genes annotated in the GO term (80). We used “biological process” ontology and accepted only significant GO terms with more than five and less than 500 genes as very broad categories do not inform about the specific functions of selected genes (false discovery rate [FDR] = 0.05, Fisher’s exact test). Reanalysis with “molecular function” ontology led to qualitatively similar results (SI Appendix, Fig. S14).

Quantifying Parallelism.

At each level (gene candidates, enriched GO categories), we considered parallel candidates all items that overlapped across at least one pair of lineages. To test for a higher-than-random number of overlapping items per each set of lineages (pair, triplet, etc.), we used Fisher’s exact test [SuperExactTest (82) package in R]. Next, we calculated the probability of gene-level parallelism (i.e., gene reuse) and functional parallelism between two lineages as the number of parallel candidate items divided by the total number of candidate items between them (i.e., the union of candidate lists from both lineages). We note that the identification of parallel candidates between two alpine lineages does not necessarily correspond to adaptation to alpine environments as it could also reflect an adaptation to some other trigger or to foothill conditions. However, our sampling and selection scans, including multiple replicates of alpine populations originating from their foothill counterparts, were designed in order to make such an alternative scenario highly unlikely.

Model-Based Inference of the Probability of Allele Reuse.

For all parallel gene candidates, we identified whether they indeed support the parallel selection model and the most likely source of their potentially adaptive variant(s). We used the newly developed composite likelihood–based method DMC (49) which uses patterns of hitchhiking at sites linked to a selected locus to distinguish among the neutral model and three different models of parallel selection (considering different sources of parallel variation): 1) on the variation introduced via gene flow, 2) on ancestral standing genetic variation, and 3) on independent de novo mutations in the same gene (at the same or distinct positions). In lineages having four populations sequenced (aVT, aZT, aFG, and aNT), we subsampled to one (best-covered) foothill and one alpine population to avoid combining haplotypes from subdivided populations.

We estimated maximum composite log-likelihoods (MCLs) for each selection model and a wide range of the parameters (SI Appendix, Table S10). We placed proposed selected sites (one of the parameters) at eight locations at equal distance apart along each gene candidate sequence. We analyzed all variants within 25 kb of the gene (both upstream and downstream) to capture the decay of genetic diversity to neutrality with genetic distance from the selected site. We used Ne = 800 000 inferred from A. thaliana genome-wide mutation rate (83) and nucleotide diversity in our sequence data (SI Appendix, Table S4) and a recombination rate of 3.7 × 10⁻⁸ determined from the closely related A. lyrata (40). To determine whether the signal of parallel selection originated from adaptation to the foothill rather than alpine environment, we ran the method assuming that parallel selection acted on 1) two alpine populations or 2) two foothill populations. For the model of parallelism from gene flow, we allowed either of the alpine populations to be the source of admixture.

For each pair of lineages and each gene candidate, we identified the model which best explained our data as the one with the highest positive difference between its MCL and that of the neutral model at the position within each gene with the highest likelihood.

We further simulated data under the neutral model to find out which difference in MCLs between the parallel selection and neutral model is significantly higher than expected under neutrality. For details, reference SI Appendix, Supplementary Methods.

The R code to run the DMC method over a set of parallel population pairs and multiple gene candidates is available at https://github.com/mbohutinska/DMCloop.

Statistical Analysis.

As a metric of neutral divergence between the lineages within and between the two sequenced species (A. arenosa and A. halleri), we used pairwise 4d-F_ST values calculated between foothill populations. These values correlated with absolute differentiation (D_XY, Pearson’s r = 0.89, P < 0.001) and geographic separation within species (rM = 0.86 for A. arenosa, P = 0.002, Fig. 1B) and thus reasonably approximate between-lineage divergence.

To test for a significant relationship between the probability of parallelism and divergence at each level, we calculated the correlation between Jaccard’s similarity in the identity of gene/function candidates in each pair of lineages and 1) the 4d-F_ST distance matrix (Arabidopsis dataset) or (2) the time of species divergence (Brassicaceae meta-analysis). For each pair of lineages, the Jaccard’s similarity was calculated as the ratio of intersection in their candidate gene/function lists over their union. Jaccard’s similarities calculated for all 21 possible lineage pairs resulted in a similarity matrix which was then correlated with the corresponding matrix of interlineage divergence using Mantel test with 999 replications [ade4 (83) package in R]. We also performed similar test for candidates found in three lineages instead of two and found congruent results showing significant divergence-dependence for gene reuse (Pearson’s r = −0.71, P < 0.001) but not for parallelism by function (Pearson’s r = 0.04, P = 0.82, n = 35; taking average 4d-F_ST over the three lineage pairs as a divergence measure).

Then, we tested whether the relative proportion of the two different evolutionary mechanisms of parallel variation (allele reuse versus de novo origin) relate to divergence using GLMs [R package stats (84)] with a binomial distribution of residual variation. We used the 4d-F_ST as a predictor variable and counts of the parallel candidate genes assigned to either mechanism as the explanatory variable. Finally, we used multiple regression on distance matrices [R package ecodist (85)] and calculated the fraction of variation in gene reuse that was explained by similarity in allele reuse, divergence, and by their shared component using the original matrices of Jaccard’s similarity in gene and allele identity, respectively, following ref. 86.

Data Availability

Sequence data that support the findings of this study have been deposited in the Sequence Read Archive (SRA; https://www.ncbi.nlm.nih.gov/sra) with the study codes SRP156117 and SRP233571 (see Dataset S9 for individual codes).