Nonparametric coalescent inference of mutation spectrum history and demography

Significance

Population histories are encoded by genomic variation among modern individuals. Population genetic inference methods, all theoretically rooted in probabilistic population models, can recover complex demographic histories from genomic variation data. However, the mutation process is treated very simply in these models—usually as a single constant. Recent empirical findings show that the mutation process is complex and dynamic over a range of evolutionary timescales and thus, deserving of richer descriptions in population genetic models. Here, we show that complex mutation spectrum histories can be accommodated by extending classical theoretical tools. We develop mathematical optimization methods and software to infer both demographic history and mutation spectrum history, revealing human mutation signatures varying through time and global divergence of mutational processes.

Abstract

As populations boom and bust, the accumulation of genetic diversity is modulated, encoding histories of living populations in present-day variation. Many methods exist to decode these histories, and all must make strong model assumptions. It is typical to assume that mutations accumulate uniformly across the genome at a constant rate that does not vary between closely related populations. However, recent work shows that mutational processes in human and great ape populations vary across genomic regions and evolve over time. This perturbs the mutation spectrum (relative mutation rates in different local nucleotide contexts). Here, we develop theoretical tools in the framework of Kingman’s coalescent to accommodate mutation spectrum dynamics. We present mutation spectrum history inference (mushi), a method to perform nonparametric inference of demographic and mutation spectrum histories from allele frequency data. We use mushi to reconstruct trajectories of effective population size and mutation spectrum divergence between human populations, identify mutation signatures and their dynamics in different human populations, and calibrate the timing of a previously reported mutational pulse in the ancestors of Europeans. We show that mutation spectrum histories can be placed in a well-studied theoretical setting and rigorously inferred from genomic variation data, like other features of evolutionary history.

Over the past decade, population geneticists have developed many sophisticated methods for inferring population demography and have consistently found that simple isolated populations of constant size are far from the norm (reviewed in refs. 1–3). Population expansions and founder events, as well as migration between species and geographic regions, have been inferred from virtually all high-resolution genetic datasets. We now recognize that inferring these nonequilibrium demographies is often essential for understanding the histories of adaptation and global migration. Population genetics has uncovered many features of human history that were once virtually unknowable by other means, revealing a complex series of migrations, population replacements, and admixture networks among human groups and extinct hominoids.

Although demographic inference methods can model complex population histories, the germline mutation process that creates variation has long received a comparatively simple treatment. A single parameter, $\mu$, is used to represent the mutation rate per generation at all loci, in all individuals, and at all times. In humans, $\mu$ is estimated from parent–child trio sequencing studies, and modest variation in $\mu$ can have major effects on the interpretation of inferred parameters, such as times of admixture and population divergence. In other organisms, for which trio sequence data are usually unavailable, $\mu$ is estimated from sequence divergence between species with a fossil-calibrated divergence time, and these estimates come with still higher uncertainty.

A growing body of evidence indicates that simple, constant mutation rate models may not adequately describe how variation accumulates on either inter- or intraspecific timescales (4–7). Germline mutation rates appear to have evolved during the speciation of great apes and the divergence of modern human populations (reviewed in ref. 8). Much of this evolution might be caused by nearly neutral drift (9), but a contributing factor could be selection on traits, like life history and chromatin structure, that indirectly affect mutation accumulation. Because mutation is intimately tied to the basic housekeeping process of cell division, gamete production, and embryonic development, the accumulation of mutations is likely to be complexly coupled to other biological processes (10–12).

It is difficult to disentangle past changes in mutation rate from past changes in effective population size, which modulate levels of polymorphism even when the mutation rate stays constant. However, evolution of the mutation process can be indirectly detected by measuring its effects on the mutation spectrum: the relative mutation rates among different local nucleotide contexts. Hwang and Green (13) modeled the triplet context dependence of the substitution process in a mammalian phylogeny, finding varying contributions from replication errors, cytosine deamination, and biased gene conversion and showing that the relative rates of these processes varied between different mammalian lineages. Many cancers also exhibit somatic hypermutability of certain triplet motifs due to different DNA damage agents and failure points in the DNA repair process (14, 15). Harris (6) and Harris and Pritchard (7) examined the variation of triplet spectra between closely related populations, counting single-nucleotide variants in each triplet mutation type as a proxy for mutational input. They found that human triplet spectra distinctly cluster by continental ancestry group and that historical pulses in mutation activity influence the distribution of allele frequencies in certain mutation types. The divergence of mutation spectra among human continental groups has been replicated in independently generated datasets (7, 16), and similar patterns have been observed in other species, including great apes (17), mice (18), and yeast (19). Some of the mutation spectrum divergence between mice and yeast lineages has been mapped to mutator alleles (19, 20).

Emerging from the literature is a picture of a mutation process evolving within and between populations, anchored to genomic features and accented by spectra of local nucleotide context. If probabilistic models of population genetic processes are to keep pace with these empirical findings, mutation deserves a richer treatment in state-of-the-art inference tools. In this paper, we build on classical theoretical tools to introduce fast nonparametric inference of population-level mutation spectrum history (MuSH)—the relative mutation rate in different local nucleotide contexts across time—alongside inference of demographic history. Whereas previous work has uncovered mutation spectrum evolution using summary statistics of standing variation, we shift perspective to focus on inference of the MuSH, which we model on the same footing as demography.

Demographic inference requires us to invert the map that takes population history to the patterns of genetic diversity observable today. This task is often simplified by first compressing these genetic diversity data into a summary statistic such as the sample frequency spectrum (SFS), the distribution of derived allele frequencies among sampled haplotypes. The SFS is a well-studied population genetic summary statistic that is sensitive to demographic history. Inverting the map from demographic history to SFS is a notoriously ill-posed problem, in that many different population histories can have identical expected SFS (21–25). One way to deal with the ill posedness of demographic inference is to specify a parametric model of population size change, usually piecewise linear or piecewise exponential. An alternative, which generalizes to other inverse problems, is to allow a more general space of solutions but to regularize by penalizing histories that contain biologically unrealistic features (e.g., high-frequency population size oscillations). Both approaches shrink the set of feasible solutions to the inverse problem so that it becomes well posed and can be thought of as leveraging prior knowledge. In particular, regularization constrains the population size from changing on arbitrarily small timescales since significant population size change usually takes at least a few generations.

In this paper, we extend a coalescent framework for demographic inference to accommodate inference of the MuSH from an SFS that is resolved into different local $k$-mer nucleotide contexts. This is a richer summary statistic that we call the $k$-SFS where, for example, $k=3$ means triplet context. We show using coalescent theory that the $k$-SFS is related to the MuSH by a linear transformation while depending nonlinearly on the demographic history. We infer both demographic history and MuSH by optimizing a cost that balances a data-fitting term using the forward map from coalescent theory, along with regularization terms that favor solutions with low complexity. Our open-source software mushi (mutation spectrum history inference) is available in ref. 26 as a Python package with extensive documentation. Using default settings and modest hardware, mushi takes only a few seconds to infer histories from population-scale sample frequency data.

The recovered MuSH is a rich object that illuminates dimensions of population history and addresses biological questions about the evolution of the mutation process. After validating with data simulated under known histories, we use mushi to independently infer histories for each of the 26 populations (from 5 superpopulations defined by continental ancestry) from the 1000 Genomes Project (1KG) Consortium (27) using recent high-coverage sequencing data (28). We demonstrate that mushi is a powerful tool for demographic inference that has several advantages over existing demographic inference methods and then go on to describe the illuminated features of human MuSH.

We recover demographic features that are robust to regularization parameter choices, including the out-of-Africa event and the more recent bottleneck in the ancestors of modern Finns, and we find that effective population sizes converge ancestrally within each superpopulation, despite being inferred independently. Decomposing human MuSH into mutation signatures varying through time in each population, we see global divergence in the mutation process that impacts many mutation types and reflects population and superpopulation relatedness. Finally, we revisit the timing of a previously reported ancient pulse of elevated TCC $\to$ TTC mutation rate, active primarily in the ancestors of Europeans and absent in East Asians (6, 7, 29, 30). We find that the extent of the pulse into the ancient past is sensitive to the choice of demographic history model but that all demographic models that fit the $k$-SFS yield a pulse timing that is significantly older than previously thought, seemingly arising near the divergence time of East Asians and Europeans.

With mushi, we can quickly reconstruct demographic history and MuSH without strong model specification requirements. This adds an approach to the toolbox for researchers interested only in demographic inference. For researchers studying the mutation spectrum, demographic history is necessary for time calibration of events in mutation history, so we expect that jointly modeling demography and MuSH will be important for studying mutational spectrum evolution in population genetics.

Model Summary

Augmenting the SFS with Nucleotide Context Information.

The SFS is a summary statistic of population variation that counts variants partitioned by the number of sampled individuals who carry the derived allele. Since rare variants tend to be younger than common variants, this summary preserves considerable information about the distribution of allele age, which can reflect temporal variation in either the mutation rate or the intensity of genetic drift. To disentangle these two causal factors, we leverage the fact that genetic drift affects all mutations uniformly, whereas mutation rate changes may depend on genomic sequence context.

By default, we classify mutation types by their derived allele and ancestral $k$-mer nucleotide context, with $k$ odd and the variant centered. There are $K=2\times 3\times 4^{k-1}$ mutation types after collapsing by strand symmetry (e.g., considering C $>$ T mutations and their complementary G $>$ A mutations to be identical). When $k=3$, there are $K=96$ triplet mutation types, of which TCC $\to$ TTC is one. For a sample of $n$ genomes, the standard SFS is an $\left(n-1\right)$-dimensional vector of the number of variants present in exactly $i$ genomes, with $i$ ranging from 1 to $n-1$. The $k$-SFS is an $\left(n-1\right)\times K$-dimensional matrix, where the $\left(i,j\right)$th entry is the number of variants of mutation-type $j$ that are present in exactly $i$ individuals.

Our goal is to sequentially infer demographic history and then MuSH by inferring histories that optimize a composite likelihood of an observed $k$-SFS data matrix $\mathbf{X}$. This requires computing $\mathbf{\Xi }\equiv \mathbb{E}\left[\mathbf{X}\right]$, the expected $k$-SFS as a function of effective population size and context-dependent mutation rate over time. Our main theoretical result, Theorem in Materials and Methods, shows that $\mathbf{\Xi }$ is a linear functional of the $K$-element MuSH $\mathit{\mu }\left(t\right)$ given the haploid effective population size history $\eta \left(t\right)$ [where $\eta \left(t\right)=2N\left(t\right)$ for diploid populations]: $\mathbf{\Xi }=\mathcal{L}\left(\eta \right){\mathit{\mu }}^{⊺}$. The linear operator $\mathcal{L}\left(\eta \right)$ transforms the unknown MuSH into a matrix of observed allele frequencies across mutation types.

Regularization to Select Parsimonious Population Histories.

Demographic inference—the recovery of population size history $\eta \left(t\right)$ from SFS summary data—is complicated by the fact that different population size histories can have identical expected SFSs. This nonidentifiability problem has been extensively explored in the literature (21–25). Although many different population size histories can optimally fit an SFS, it has been proven that uniquely good (identifiable) fits are available when excluding biologically unrealistic histories that contain rapid oscillations. Here, we introduce a mathematical framework that expresses histories nonparametrically (approximating infinite-dimensional functions), but it prefers sparse solutions that consist of simple pieces and disfavors histories that fit the $k$-SFS equally well with more erratic features.

Inference of the MuSH introduces a second identifiability problem of a different nature. The effective population size $\eta \left(t\right)$ and the mutation rate $\mu \left(t\right)$ are mutually nonidentifiable for all $t$, meaning that the expected SFS $\mathit{\xi }$ is invariant under a modification of $\eta \left(t\right)$ as long as a compensatory modification is made in $\mu \left(t\right)$. The nonidentifiability of $\eta$ and $\mu$ can be understood intuitively by considering two histories that can be tuned to have the same expected SFS: one where the mutation rate increases over an interval of time in the past while the effective population size stays constant and the other with a constant mutation rate where population size increases, dilating coalescence times on the same branches affected in the first scenario.

While the total mutation rate is confounded with demography, the composition of the mutation spectrum—the relative mutation rate of each mutation type—reveals itself in the $k$-SFS. This can also be understood intuitively; an excess of variants of a given frequency in only a single mutation type (one column of the $k$-SFS) cannot be explained by an historical population boom because all mutation types are associated with the same demographic history. In this case, we would infer a period of increased relative mutation rate for this mutation type. We cannot discern changes in total mutation rate, so mushi assumes a constant total rate ${\mu }_0$, and time variation in the rate of drift is modeled only in $\eta \left(t\right)$. We handle this constraint using a transformation technique from the field of compositional data analysis (Materials and Methods).

Even with this compositional constraint on the total mutation rate, many different population histories may be equally consistent with an empirical $k$-SFS. As mentioned before, we overcome this with regularization methods to select simple demographies and MuSHs. We penalize the model for three different types of irregularity. One penalty is motivated by the demographic inference literature; histories that feature rapid oscillations over time are disallowed in favor of similarly likely histories that change less rapidly and less often and are composed of a few simple (low-order polynomial) trends. The second penalty favors models in which the MuSH $\mathit{\mu }\left(t\right)$ is composed of a few mutation signatures that vary in their intensity over time for each mutation type and represent a sparse vocabulary of mutagenic processes. The third regularization penalty is a classical ridge (or Tikhonov) penalty, which speeds up convergence of the optimization without significantly affecting the solution. Detailed formulation of our optimization problems and regularization strategies are in Materials and Methods.

The strength of all three regularizations can be tuned by changing the values of user-specified hyperparameters. Stronger regularization yields simpler histories, but eventually, this will result in a poor fit to $k$-SFS data. Users should tune the regularization parameters to select histories that are simple while still fitting well, perhaps considering prior knowledge about the natural history of their study population. This process is designed to be flexible and more straightforward than specifying an explicit parametric model.

Quantifying Goodness of Fit to the Data.

The probability distribution of an empirical SFS given an expected SFS is often specified using a Poisson random field (PRF) approximation (31), which stipulates that, neglecting linkage, the observed number of sites with derived allele count $i$ is Poisson distributed around the expected number of sites of this frequency. This PRF approximation is easily generalizable to $k$-SFS data. Recall that $\mathbf{X}$ is the observed $k$-SFS matrix, so the SFS is $\mathbf{x}\equiv \mathbf{X}\mathbf{1}$ (row sums over mutation types). In Materials and Methods, we show that the generalized PRF factorizes as $\mathbb{P}\left(\mathbf{X}\mid \eta ,\mathit{\mu }\right)=\mathbb{P}\left(\mathbf{x}\mid \eta \right)\hspace{0.17em}\mathbb{P}\left(\mathbf{X}\mid \mathbf{x},\eta ,\mathit{\mu }\right)$, with the first factor given by a Poisson distribution and the second by a multinomial distribution. We also show that the SFS $\mathbf{x}$ is a sufficient statistic for the demographic history $\eta$ with respect to the $k$-SFS $\mathbf{X}$. This means that estimation of $\eta$ can be done by fitting the total SFS, which maximizes the first factor as a likelihood for $\eta$. Then, the MuSH can be estimated by fitting the $k$-SFS, maximizing the second factor as a likelihood for $\mathit{\mu }$, conditioned on the $\eta$ estimate.

Results

Reconstructing Simulated Histories.

We investigated mushi’s ability to recover histories in simulations where known histories are used to generate $k$-SFS data. Instead of simulating under the mushi forward model itself, we used msprime (32) to simulate a tree sequence describing the genealogy for 200 haplotypes of human chromosome 1 across all loci. This is a more difficult test, as it introduces linkage disequilibrium that violates our model assumptions.

We used the human chromosome 1 model implemented in the stdpopsim package (33), which includes a realistic recombination map (34). We used a difficult demography consisting of a series of exponential crashes and expansions, variously referred to as the “sawtooth,” “oscillating,” or “zigzag” history. This pathological history has been widely used to evaluate demographic inference methods (29, 35–37) and is available in the stdpopsim package as the Zigzag_1S14 model. Our simulated tree sequence contained about 250,000 marginal trees.

We defined a MuSH with 96 mutation types, 2 of which are dynamic: 1 undergoing a pulse and 1 undergoing a monotonic increase. Since estimates of mutation spectra in real data are often confounded by misidentification of some ancestral alleles as derived, we modeled an ancestral misidentification rate of 0.01, with the two dynamic mutation types as misidentification partners. The total mutation rate varies slightly over time due to these two components—introducing another model misspecification since inference assumes a constant total mutation rate. We placed mutations on the simulated tree sequence according to the historical relative rate function for each mutation type and computed the $k$-SFS.

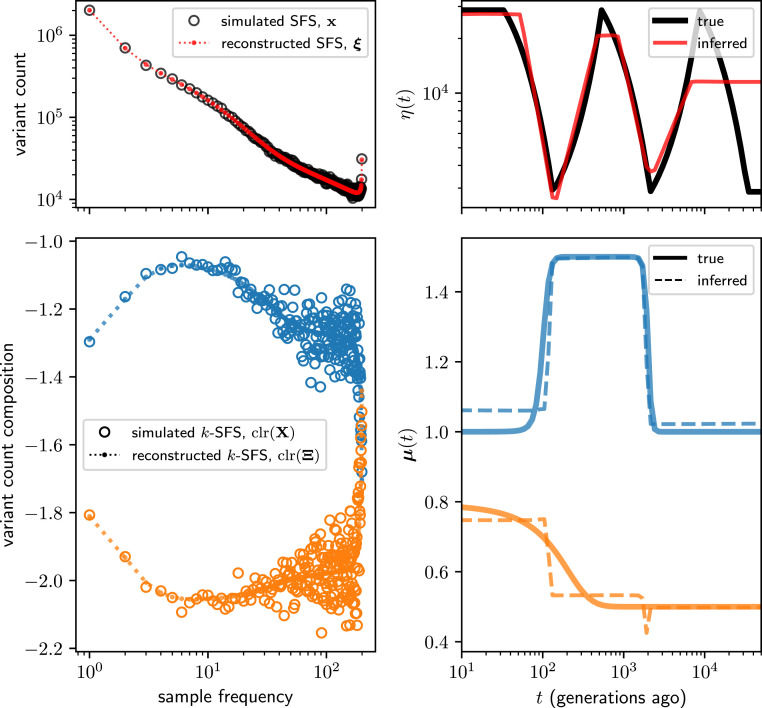
Fig. 1 depicts inference results for this simulation. We find that mushi accurately recovers the difficult sawtooth demography for most of its history but oversmooths beyond the third population bottleneck because little information about this time survives in the SFS. The MuSH is accurately reconstructed as well, with both the pulse and ramp signatures recovered. The timing of the features in the MuSH also appears accurate, despite demographic misspecification that has the potential to distort the diffusion timescale. In SI Appendix, Figs. S1 and S2, we explore various hyperparameter choices and how they impact inferences of the demographic history and of the different trends in the two variable mutation types. We find that demographic model selection does not significantly impact inference of MuSH, and that different MuSH penalty hyperparameters recover the two distinct components of the MuSH with varying fidelity. The folded SFS can also be used for demographic inference in mushi, and in SI Appendix, Fig. S3, we show that inference results are similar.

Fig. 1.

Simulation study of mushi performance. The sawtooth demography (Upper Right) and a MuSH with 96 mutation types (Lower Right; with two nonconstant components shown) were used to simulate 3-SFS data for $n=200$ sampled haplotypes. The MuSH has a total mutation rate of about ${\mu }_0=95.8$, generating about 9.5 million segregating variants. Upper Left shows the SFS, and Lower Left shows the two variable components of the $k$-SFS as a composition among mutation types at each allele frequency. Time was discretized with a logarithmic grid of 100 points. Inference was performed using a mixture of order 0 and order 1 trends for demography, and order 0 trends for MuSH (Materials and Methods and SI Appendix, Figs. S1 and S2).

One noteworthy feature of our fit to the sawtooth demography is the tendency of mushi to smooth older demographic oscillations without smoothing younger oscillations as aggressively. In contrast to methods such as the pairwise sequential Markov coalescent (PSMC) (38) that tend to infer runaway population sizes in the ancient past, mushi’s history flattens in the limit of the ancient past. The same constraint underlies both PSMC’s ancient oscillations and mushi’s ancient flattening; genomic data sampled from modern individuals cannot contain information about history older than the time to most recent common ancestor of the sample since mutations that occurred before then will be fixed, rather than segregating, in the sample. For example, we expect that population bottlenecks erase information about history since they accelerate the fixation of variant sites that predate the bottleneck. While this information loss intuition holds for very general coalescent processes (39), the linearity in Theorem enables us to make these statements precise for mutation rate history via spectral analysis of the operator $\mathcal{L}\left(\eta \right)$. This is explored in detail for the case of a simple bottleneck demography in SI Appendix, section F and Fig. S9.

Reconstructing the Histories of Human Populations.

We next inferred the histories of human populations from large publicly available resequencing data. We computed a $k$-SFS for each of the 26 human populations from five continental ancestries sequenced in the 1KG (27) using an unphased variant call set (mapped to human genome assembly GRCh38 [hg38]) from the recent high-coverage (30×) resequencing data of 1KG samples from the New York Genome Center (28). Our bioinformatic pipeline for computing the $k$-SFS for each 1KG population is detailed in Materials and Methods. Briefly, we augment autosomal biallelic single-nucleotide polymorphisms by adding triplet mutation-type ($k=3$) annotations, masking for strict callability and ancestral triplet identifiability. Across 1KG populations, the resulting number of segregating variants ranged from $\sim$7.5 million (population Finland [FIN]) to $\sim$15 million (population Luhya in Webuye, Kenya). We also computed the genomic target sizes for each ancestral triplet, resulting in a total ascertained genome size of $\sim$2.0 Gb.

We use a de novo mutation rate estimate of ${\mu }_0=1.25\times 10^{-8}$ per site per generation (40), which corresponds to $\sim$24.9 mutations per $\sim$2.0 Gb masked haploid genome per generation. For time calibration, we assume a generation time of 29 y (41). To discretize the time axis for our numerical implementation, we use a logarithmically spaced grid of 200 points, with the most recent at 1 generation ago and the oldest at 200,000 generations (5.8 My) ago.

Human demographic history.

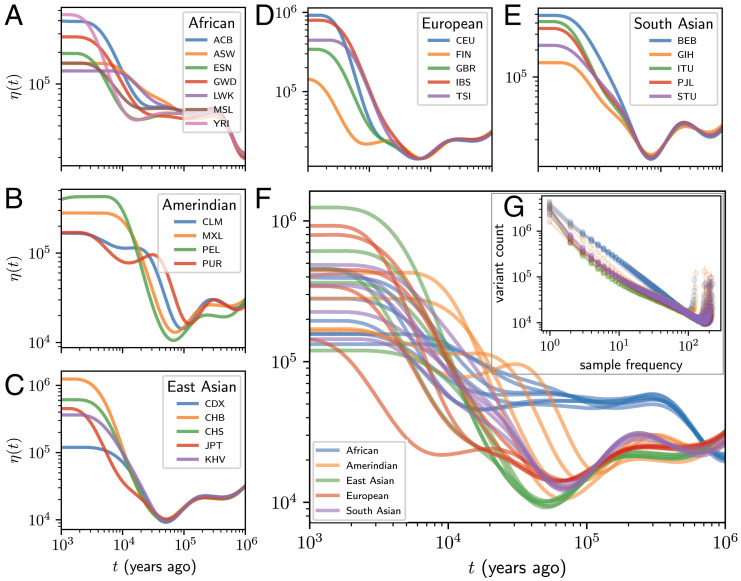
We used mushi to infer demographic history $\eta \left(t\right)$ independently for each 1KG population. Fig. 2 shows results grouped by superpopulation: African, Amerindian, East Asian, European, and South Asian. Broadly, we recover many previously known features of human demographic history that are highly robust to regularization parameters: a $\sim$100-kya (thousand years ago) out-of-Africa bottleneck in non-Africans, a second contraction $\sim$10 kya due to a founder event in FIN, and recent expansion of all populations. Histories ancestrally converge within each superpopulation. SI Appendix, Fig. S4, Upper shows similar histories inferred using the folded SFS.

Fig. 2.

Effective population size histories estimated from high-coverage 1KG data. (A–E) Estimated demographic history $\eta \left(t\right)$ for all populations grouped by continental ancestry. Inference was performed using a mixture of order 0 and order 3 trends (Materials and Methods and SI Appendix, Fig. S6). African populations: African Caribbeans in Barbados (ACB); Americans of African ancestry from the southwestern United States (ASW); Esan in Nigeria (ESN); Gambian in western divisions in the Gambia (GWD); Luhya in Webuye, Kenya (LWK); Mende in Sierra Leone (MSL); and Yoruba in Ibadan, Nigeria (YRI). Amerindian populations: Colombians from Medellin (CLM); Mexican ancestry from Los Angeles (MXL); Peruvians from Lima (PEL); and Puerto Rican (PUR). East Asian populations: Chinese Dai in Xishuangbanna (CDX); Han Chinese from Beijing (CHB); Han Chinese from Shanghai (CHS); Japanese from Tokyo (JPT); and Kinh in Ho Chi Minh City (KHV). European populations: Utah residents with Northern and Western European ancestry (CEU); Finnish in FIN; British in England and Scotland (GBR); Iberian population in Spain (IBS); and Toscani in Italia (TSI). South Asian populations: Bengali from Bangladesh (BEB); Gujarati Indian from Houston (GIH); Indian Telugu from the United Kingdom (ITU); Punjabi from Lahore (PJL); and Sri Lankan Tamil from the United Kingdom (STU). (F) The same $\eta \left(t\right)$ estimates on common axes to allow comparison of superpopulations. (G) SFS data (open circles) for all populations grouped by continental ancestry, as well as fits based on the expected SFS from the estimated demographic history (points connected by lines).

Human MuSH.

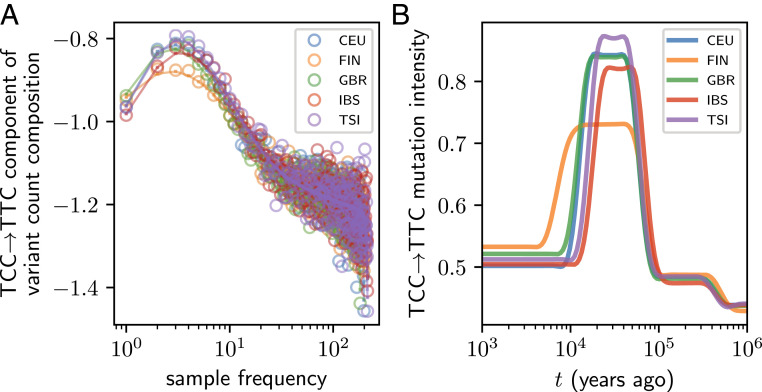
An estimated demographic history induces a mapping of allele frequency onto a distribution of allele ages. With these distributions encoded in our model, we next used mushi to infer time-calibrated MuSHs for each population. First, to highlight the time calibration capabilities of mushi, we focus on the specific triplet mutation-type TCC $\to$ TTC, which was previously reported to have undergone an ancient pulse of activity in the ancestors of Europeans and is absent in East Asians (6, 7, 29, 30). To produce sharp estimates of the timing of this TCC pulse, we used regularization that prefers histories with a minimum number of change points (Materials and Methods). Fig. 3A shows our fit to this component of the $k$-SFS for each European population, and Fig. 3B shows the corresponding estimated component of the MuSH. With the consistent joint estimation performed by mushi, we find that the TCC pulse is much older than previously reported, beginning $\sim$80 kya.

Fig. 3.

Timing of the TCC $\to$ TTC pulse in Europeans. (A) The relative composition of TCC $\to$ TTC variants (centered log ratio transform) (Materials and Methods) in each frequency class for each European population (open circles) shows an excess at intermediate frequencies. The expected values fit using the inferred MuSH are shown as points connected by lines. (B) The inferred TCC $\to$ TTC mutation rate histories (in units of mutations per ascertained genome per generation); MuSH inference was performed using a mixture of order 0 and order 3 trends (Materials and Methods and SI Appendix, Figs. S6–S8) for both demography and MuSH. CEU, Utah residents with Northern and Western European ancestry; GBR, British in England and Scotland; IBS, Iberian population in Spain; TSI, Toscani in Italia.

It is also possible to run mushi without estimating a new demographic history from the input data but instead, assuming a prespecified demography. When we use the Tennessen et al. (42) history, which was assumed by Harris and Pritchard (7) in their estimate of the timing of the TCC pulse, we recover a pulse that reaches a maximum around $\sim$20 to 30 kya, similar to that initial estimate (SI Appendix, Fig. S5, Upper). However, this demography fits the SFS poorly, indicating that demographic misspecification may be distorting mushi’s time calibration. Indeed, a global-scale shift in the SFS arises from inconsistency in the phylogenetically calibrated mutation rate used by Tennessen et al. (42) ($2.36\times 10^{-8}$) and the more recent de novo rate used in mushi ($1.25\times 10^{-8}$). This inconsistency also distorted the estimate reported by Harris and Pritchard (7) since their Monte Carlo procedure used the more recent de novo mutation rate. To resolve this, we next rescaled the Tennessen demography to the de novo mutation rate [as done by Amorim et al. (43)] and inferred the TCC pulse with mushi again. This resulted in a better fit to the SFS and a clear shift to an older TCC pulse (SI Appendix, Fig. S5, dotted lines in Upper), consistent with the pulse inferred using the mushi demographies.

We estimated another set of TCC pulses in Europeans conditioned on demographic histories that were inferred using the method Relate (29), which used the phase three 1KG data to infer demographic histories for each population by first pruning the population genealogy from an inferred whole-genome genealogy of all 1KG samples and then, independently inferring a coalescence rate history for each extracted genealogy. Conditioning on the Relate demographies yields younger estimates of the TCC pulse timing, similar to the estimate under the inconsistent Tennessen model (SI Appendix, Fig. S5, Lower). The Relate demographic histories for each 1KG population are shown in SI Appendix, Fig. S4, Lower, with SFS fits.

SI Appendix, Fig. S6 shows that our inference of the TCC pulse is highly robust to demographic model selection among demographic histories that fit the SFS. SI Appendix, Fig. S7 shows that TCC pulse timing is robust to regularization strength. SI Appendix, Fig. S8 indicates the stability of our history estimates under bootstrap resampling of the variant data (but we caution this does not provide confidence bounds on histories since our penalized likelihood approach is strongly biased toward simple solutions).

After our focused study of the TCC pulse, we aimed to more broadly characterize how human MuSH decomposes into mutational signatures varying through time in each population. This is inspired by the use of nonnegative matrix factorization to infer mutational signatures associated with mutagenic processes in cancer genomes, which represent a set of tumor mutational spectra as mixtures of a small set of mutational signatures, although our problem is more complex due to the time dimension. To capture this additional dimension, we designed a mutational signature extraction method that factorizes a three-dimensional (3D) tensor of MuSHs for all populations, rather than a two-dimensional (2D) matrix of mutation spectra from static samples.

We first ran mushi on all 1KG populations using stronger order 3 (cubic) trend penalties that favor smoother variation over time compared with the discontinuous jumps of order 0 penalties that were needed to fit the TCC pulse (Materials and Methods). This resulted in an estimated MuSH for each population of the 26 populations in the 1KG data. We then normalized each MuSH by the genomic target size for each triplet mutation type, so that mutation rate is rendered sitewise, and stacked the populationwise MuSHs to form an order 3 tensor. This tensor is a 3D numerical array with dimensions (no. of populations) $\times$ (no. of time points) $\times$ (no. of mutation types) = 26 $\times$ 200 $\times$ 96. When we slice the array along the time axis, we obtain a series of matrices whose rows are the inferred mutation spectra of each 1KG population at a past time $t$. The numerical value of an entry in the tensor indicates the mutation rate (in units of mutations per site per generation) in a given population at a given time and for a given mutation type.

We used nonnegative canonical polyadic tensor factorization (NNCP) (reviewed in ref. 44) to extract factors in the population, time, and mutation-type domains. Since NNCP generalizes nonnegative matrix factorization to tensors of arbitrary order, this is analogous to extracting mutation signatures that form a sparse vocabulary for explaining the mutation spectrum variation between tumor mutational profiles but adds the dimension of time variation. The addition of the time dimension means that each mutational signature is associated with a dosage that can jointly increase or decrease over the histories of all populations.

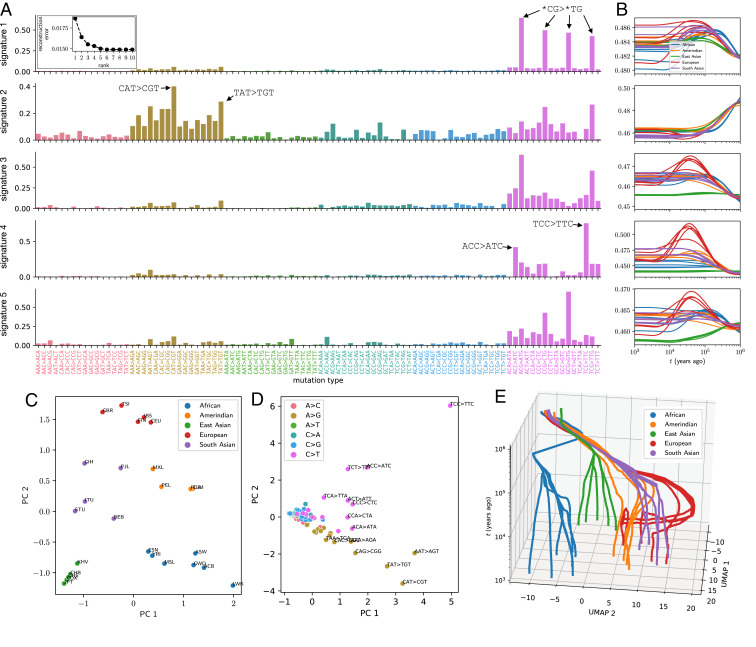
Briefly, we hypothesize that the MuSH tensor can be approximated by a sum of a few rank 1 tensors, implying that most evolving mutational processes are shared across multiple populations, possibly with different relative intensities over time. A tensor of rank 5, which describes a set of five mutation signatures, accurately represents the 1KG MuSH tensor (Fig. 4 A, Inset). The NNCP decomposition results in $26\times 5$, $200\times 5$, and $96\times 5$ factor matrices for population, time, and mutation type, respectively. Fig. 4 C and D projects population and mutation-type factors from five dimensions to two principal components for visualization. The population factors clearly cluster by superpopulation. The mutation-type factors show a number of mutation types with distinct outlier behavior, including TCC $\to$ TTC, as expected.

Fig. 4.

Decomposing MuSHs for 1KG populations into mutation signatures varying through time and between populations. (A) Triplet mutation signatures, shown as loading into triplet mutation types for each signature (rows). Inset shows tensor reconstruction error over a range of ranks for NNCP decomposition, indicating rank 5 as a good approximation. (B) Historical dynamics of each mutation signature’s intensity in each 1KG population (panels correspond to rows in A). SI Appendix, Fig. S10 shows the same intensity histories separately for each superpopulation. (C) Five-dimensional population factors projected to the first two principal components (PCs). (D) Five-dimensional mutation signature factors projected to the first two PCs. (E) UMAP embedding of mutation signature histories, initialized using the first two PCs of the time domain factors and then performed with default parameters.

We next recast the MuSH for each population in terms of the five mutation signatures that comprise the tensor factors, capturing covariation among the set of 96 triplet mutation types with the smaller set of signatures. This allows us to characterize and biologically interpret the time dynamics of each mutation signature in each population. Fig. 4A shows the five mutation signatures as loadings in each triplet mutation type. Fig. 4B shows how each of these five signatures varies through time in each 1KG population (computed by projecting 96-dimensional spectra to the five mutational signatures in each population at each time). Signature 4 fits the profile of the TCC pulse that affects Europeans, South Asians, and European-admixed Amerindians, containing the previously reported minor component ACC $\to$ ATC. It does not, however, contain the minor component CCC $\to$ CTC, which was previously inferred from the low-coverage 1KG data to be one of the mutation types associated with the TCC pulse. Signatures 1 and 3 are dominated by C $\to$ T mutations at CpG sites, the signature of error-prone repair of deaminated methylcytosines. These signatures are consistently enriched in rare (young) variants across populations. Some of this frequency bias is likely caused by purifying selection against mutations that disrupt the gene-regulatory function of methylated CpG sites. Another contributing factor is likely biased gene conversion, which disfavors the increase in frequency of C/G $\to$ A/T mutations (also called strong to weak mutations). Signature 2 is enriched for common (old) variants and has high loadings of A $\to$ G, which is consistent with the action of biased gene conversion to select for the retention of weak to strong mutations.

Although the time profiles of these five signatures appear to be modulated by biased gene conversion, they also vary between populations at recent times and cannot be explained by a selective force acting uniformly on all non–GC-conservative mutations. We note that we do not see evidence of the profile of a signature reported to be enriched specifically in the Japanese population (7). This signature was thought to stem from a subtle cell line artifact affecting the Japanese HapMap Consortium samples (45) and apparently is not a prominent feature of the new high-coverage 1KG data, whose genotypes were called without imputation. Signature 5, which is dominated by C $\to$ T transitions, is notably depleted in East Asians.

Finally, we used uniform manifold approximation and projection (UMAP) (46) to compute a 2D embedding of mutation signature histories (after initially decomposing the MuSHs into five mutation signatures as described) of each 1KG population at each time point. Fig. 4E shows this embedding with the time coordinate added as a third dimension. Despite performing independent inferences for each population’s MuSH, we see tree structure that reflects population and superpopulation ancestry and convergence toward an ancestral MuSH in the distant past.

Discussion

It is becoming clear that mutation spectrum variation is a common feature of genetically diverse populations. Initial reports on the existence of such variation were mostly qualitative in nature, focused on enumerating which populations exhibit robust variation and putting bounds on the possible contributions of bioinformatic error. Here, we have introduced a quantitative framework for inferring how this variation arose over time, utilizing variation of all ages from unphased whole-genome data to resolve a time-varying portrait of germline mutagenesis. Our method mushi can decompose context-augmented SFSs into time-varying mutational signatures, regardless of whether those signatures are sparse and obvious like the European TCC pulse or represent more subtle concerted perturbations of mutation rates in many sequence contexts. Previous estimates of the timescale of mutation spectrum change were restricted to pulse-like signatures that are more obvious but less ubiquitous than diffuse signatures appear to be (7, 29).

Not all of the temporal structure unveiled by mushi can be interpreted as time variation in the germline mutational processes. Some time variation in signature dosage is consistent with biased gene conversion, and signatures may also be affected by cell line artifacts (45). The strengths of mushi are to automate the visualization of deviations from mutation spectrum uniformity and localize them to particular populations, frequency ranges, and time periods. It is possible that profiles of germline signatures we report here will need to be revised as higher-quality human datasets are published and inference methods are refined.

Although mushi’s most notable feature is the ability to infer mutation spectrum variation over time, it includes a demographic inference subroutine with some advantages over existing methods. We infer population size changes nonparametrically from SFS data with state-of-the-art regularization methods that yield population size histories with some more desirable properties than other methods. The method fastNeutrino (47) uses a piecewise exponential parameterization to infer demographic histories and locuswise mutation rate from SFS data, and it does not use regularization. The method SMC++ (36) uses smoothing spline regularization for demographic inference in a model that combines the efficiency of SFS models with a coalescent hidden Markov model. The method CubSFS (48) uses cubic smoothing spline regularization to infer demographic history from the SFS. The sparse trend filtering used in mushi has been shown to have superior local adaptivity properties over the related spline methods (49).

The use of sample allele frequencies rather than phased whole genomes should make mushi broadly useful to researchers working on nonmodel organisms, which are still beyond the scope of many state-of-the-art methods that require long sequence scaffolds and phased data. The software is also very fast, returning results in seconds to minutes on a modest computer, and is designed for researchers familiar with scripting in Python.

The mushi model calibrates the times at which mutational signatures wax and wane using a demographic model inferred from the same input allele frequency data from which the signatures themselves are extracted. We estimated a surprisingly old start time to the TCC pulse, around 80 kya, which is older than any estimates of European/East Asian divergence times and is robust to demographic models that maintain good fit to the SFS. However, mushi can also calibrate its timescale using a user-specified demographic history, which reveals that the timing of transient events like the TCC pulse in Europe are sensitive to underlying assumptions about effective population size that fit the SFS poorly. When we input the demographic history used in the initial report of the TCC pulse (7), we similarly find that the TCC pulse began 20 to 30 kya, comfortably later than Europeans’ divergence from East Asians, who were not affected by the TCC pulse. However, it became apparent that the initially reported timing of the TCC pulse was distorted by a scaling issue between recent human de novo mutation rate and the older phylogenetically calibrated mutation rate used for inferring the demographic history that was used (42). Rescaling this demography to the de novo rate resulted in a strikingly older TCC pulse, matching the estimate that was obtained using the self-consistent demographic inference from mushi.

We also inferred TCC pulse timing using demographic histories that were inferred with the Relate method from whole-genome genealogies (29) instead of allele frequency data and found a younger TCC pulse, matching the initially reported timing that was obtained with inconsistent demographic history scaling. These demographic histories also yield poor fits to the 1KG SFS data, with more deviation at lower frequencies. However, we note that inferred demographic histories are notoriously poor at predicting the distributions of genomic summary statistics other than the ones that were used to fit the models (50), and of course, mushi would be unable to recapitulate haplotype structure, for example. We cannot rule out the possibility that another MuSH with a similar SFS, different haplotype structure, and more recent TCC pulse might fit the data better than the MuSH we infer.

If the older TCC pulse timing is correct, complex patterns of ancient gene flow are likely essential for reconciling it with other knowledge about human population history. Ancient DNA evidence suggests that the divergence of East and West Eurasians occurred gradually over a period that began more than 40,000 y ago (51), possibly beginning with the divergence of a basal Eurasian population before the interbreeding of other Eurasians with Neanderthals around 50,000 y ago (52). Speidel et al. (30) recently discovered that the proportion of TCC $\to$ TTC mutations is highly correlated across populations with the proportion of ancestry from Neolithic Anatolia, a finding that underscores the need for future work modeling mutation spectrum evolution jointly with more complex demographic history involving substructure and migration between populations. It also points to the tantalizing possibility that the distribution of mutational signatures could provide extra information about hard to resolve substructure and gene flow between populations that lived in the distant past.

Although powerful new methods for inferring ancestral recombination graphs (ARGs) ultimately have the potential to estimate more accurate histories than can be accomplished by fitting compressed SFS data, these methods are still in a relatively early stage of development. In the method Relate (29), mutation rate history is approximately inferred from an ARG using independent marginal estimates for each epoch in a piecewise-constant history. This avoids joint inference over all epochs—which can also be formulated as a linear inverse problem—by ignoring mutation rate variation within branches.

Until further developments make it possible to infer histories that fit both haplotype structure and site frequency spectra, our results underscore the importance of using more compressed summary statistics to validate inference results. The differences between our SFS-inferred histories and Relate-inferred histories imply that none of these histories yet capture the joint distribution of allele age and allele frequency, which could affect claims about the timing of gene flow and selection in addition to the claims about the timing of the TCC pulse that we focus on in this paper. Until demographic inference methods are able to infer histories compatible with all features of modern datasets, it will be important for researchers to infer histories from different data summaries, including classical compressed statistics like the SFS, in order to understand the sensitivity of various biological and historical claims to methodological eccentricities.

Materials and Methods

The Expected SFS Is a Linear Transform of the Mutation Intensity History.

We work in the setting of Kingman’s coalescent (53–56), with all of the usual niceties: neutrality, infinite sites, linkage equilibrium, and panmixia (57, 58). In SI Appendix, section A, we retrace the derivation by Griffiths and Tavaré (59) of the frequency distribution of a derived allele conditioned on the demographic history while generalizing to a time inhomogeneous mutation process. We make use of the results of Polanski and coworkers (60, 61) to facilitate computation. We use the time discretization of Rosen et al. (25) and adopt their notation. Detailed proofs can be found in SI Appendix.

With $n$ denoting the number of sampled haplotypes, denote the expected SFS column vector $\mathit{\xi }={\left[{\xi }_1\hspace{0.17em}\dots \hspace{0.17em}{\xi }_{n-1}\right]}^{⊺}$, where ${\xi }_i$ is the expected number of variants segregating in $i$ out of $n$ haplotypes. Let $\eta \left(t\right)$ denote the haploid effective population size history, with time measured retrospectively from the present in Wright–Fisher generations. Note that $\eta \left(t\right)=2N\left(t\right)$ for diploid populations. Let $\mu \left(t\right)$ denote the mutation intensity history, in units of mutations per ascertained genome per generation, understood to apply uniformly across individuals in the population at any given time. Under these model assumptions, we obtain the following theorem.Theorem. Fix the number of sampled haplotypes $n$. Then, for all bounded functions $\eta :{\mathbb{R}}_{\ge 0}\to {\mathbb{R}}_{>0}$ and $\mu :{\mathbb{R}}_{\ge 0}\to {\mathbb{R}}_{\ge 0}$, the expected SFS is $\mathit{\xi }=\mathcal{L}\left(\eta \right)\mu$, where $\mathcal{L}\left(\eta \right)$ is a finite-rank bounded linear operator parameterized by $\eta$ that maps mutation intensity histories $\mu$ to $\left(n-1\right)$ -dimensional SFS vectors $\mathit{\xi }$. Viewed as a nonlinear operator on $\eta$, $\mathcal{L}\left(\eta \right)$ is also bounded. In particular, $\mathcal{L}\left(\eta \right)\mu \equiv \mathbf{C}\hspace{0.17em}\mathbf{d}\left(\eta ,\mu \right)$, where $\mathbf{C}$ is an $\left(n-1\right)\times \left(n-1\right)$ constant matrix with elements that can be computed recursively, and $\mathbf{d}\left(\eta ,\mu \right)$ is an $\left(n-1\right)$ vector with elements

$$d_j\left(\eta ,\mu \right)\equiv {\int }_0^{\infty }\exp \left[-\left(\genfrac{}{}{0.0pt}{}{j}{2}\right){\int }_0^t\frac{d{t}^{\prime }}{\eta \left(t^{\prime }\right)}\right]\mu \left(t\right)dt,\hspace{0.17em}for\hspace{0.17em}j=1,\dots ,n-1,$$ [1]

which is linear in $\mu$ and nonlinear in $\eta$.

Theorem is proved in SI Appendix, section A. Recursions for computing $\mathbf{C}$ can be procedurally generated as described in SI Appendix, section B.

In order to partition the expected SFS $\mathit{\xi }$ by $k$-mer mutation type, we promote the $\left(n-1\right)$-element expected SFS vector $\mathit{\xi }$ to the $\left(n-1\right)\times K$ expected $k$-SFS matrix $\mathbf{\Xi }$. Similarly, the mutation intensity history function $\mu \left(t\right)$ is promoted to the $K$-element MuSH $\mathit{\mu }\left(t\right)$, a column vector with each element giving the mutation intensity history function for one mutation type. Then, Theorem generalizes to

$$\mathbf{\Xi }=\mathcal{L}\left(\eta \right){\mathit{\mu }}^{⊺}.$$ [2]

As in Theorem, the time coordinate is integrated over by the action of the operator $\mathcal{L}$.

Empirical SFS data contain a characteristic “smile” at high frequencies. As detailed in SI Appendix, section G, we account for this by modeling ancestral state misidentification rates for each mutation type and inferring them jointly with the history functions $\eta \left(t\right)$ and $\mathit{\mu }\left(t\right)$.

We use the notation $\mathbf{X}$ to denote a sampled $k$-SFS matrix [i.e., the $\left(n-1\right)\times K$ matrix containing the sample counts for each mutation type]. By construction, $\mathbf{\Xi }\equiv \mathbb{E}\left[\mathbf{X}\right]$.

Compositional Modeling Leads to Identifiable MuSHs.

As mentioned in the summary methods, the effective population size $\eta \left(t\right)$ and the mutation intensity $\mu \left(t\right)$ are nonidentifiable for all $t$, meaning that the expected SFS $\mathit{\xi }$ is invariant under a modification of $\eta$ as long as a compensatory modification is made in $\mu$. We now demonstrate this formally by introducing a change of variables that measures time in expected number of coalescent events since the present (i.e., the diffusion timescale) (21, 25). Let $R_{\eta }\left(t\right)\equiv {\int }_0^t\frac{d{t}^{\prime }}{\eta \left(t^{\prime }\right)}$, and substitute $\tau \equiv R_{\eta }\left(t\right)$ in Eq. 1 to give

$$d_j\left(\eta ,\mu \right)={\int }_0^{\infty }\exp \left[-\left(\genfrac{}{}{0.0pt}{}{j}{2}\right)\tau \right]\tilde{\eta }\left(\tau \right)\tilde{\mu }\left(\tau \right)d\tau ,$$ [3]

where $\tilde{\eta }\left(\tau \right)\equiv \eta \left(R^{-1}\left(\tau \right)\right)$ and $\tilde{\mu }\left(\tau \right)\equiv \mu \left(R^{-1}\left(\tau \right)\right)$. In this timescale, we see that $\eta$ and $\mu$ appear as a product on the right of Eq. 3. This means we cannot jointly infer $\eta$ and $\mu$ since only their product influences the data. This nonidentifiability is similarly manifest by a change of variables to measure time in the expected number of mutations.

Because we cannot discern changes in total mutation rate, we assume a constant total rate ${\mu }_0$, so that time variation in the rate of drift is modeled only in $\eta \left(t\right)$. A MuSH with $K$ mutation types can then be written as $\mathit{\mu }\left(t\right)={\mu }_0\mathit{\nu }\left(t\right)$, where $\mathit{\nu }\left(t\right)\in {\mathcal{S}}^K$ for all $t$, and ${\mathcal{S}}^K\equiv \left\{\mathbf{x}\in {\mathbb{R}}_{>0}^K:{\sum }_{j=1}^K{x}_j=1\right\}$ denotes the standard simplex. We call the relative MuSH $\mathit{\nu }\left(t\right)$ a composition and employ techniques from compositional data analysis (62–64).

To avoid difficulties arising from optimizing directly over the simplex, we represent compositions using Aitchison geometry. Briefly, analogs of vector–vector addition, scalar–vector multiplication, and an inner product are defined for compositions, and the simplex is closed under these operations. It is then possible to construct an orthonormal basis in the simplex ${\mathit{\psi }}_1,\dots ,{\mathit{\psi }}_{K-1}$ using the Gram–Schmidt orthogonalization. We first introduce the centered log ratio transform of some $\mathbf{x}\in {\mathcal{S}}^K$, defined as

$$\mathrm{c}\mathrm{l}\mathrm{r}\left(\mathbf{x}\right)\equiv {\left[\log \frac{x_1}{\overline{x}},\dots ,\log \frac{x_K}{\overline{x}}\right]}^{⊺},$$ [4]

where $\overline{x}$ denotes the geometric mean. The inverse transform ${\mathrm{c}\mathrm{l}\mathrm{r}}^{-1}$ is the softmax function.

The isometric log ratio transform and its inverse allow us to transform back and forth between the simplex and a Euclidean space in which we will cast our optimization problem. The transform $\mathrm{i}\mathrm{l}\mathrm{r}:{\mathcal{S}}^K\to {\mathbb{R}}^{K-1}$ and its inverse are defined as

$$\mathrm{i}\mathrm{l}\mathrm{r}\left(\mathbf{x}\right)\equiv {\mathbf{\Psi }}^{⊺}\mathrm{c}\mathrm{l}\mathrm{r}\left(\mathbf{x}\right),\mathbf{x}\in {\mathcal{S}}^K$$ [5]

$${\mathrm{i}\mathrm{l}\mathrm{r}}^{-1}\left.\left(\mathbf{y}\right)\equiv {\mathrm{c}\mathrm{l}\mathrm{r}}^{-1}\left(\mathbf{\Psi }\mathbf{y}\right)\right),\mathbf{y}\in {\mathbb{R}}^{K-1},$$ [6]

where $\mathbf{\Psi }\equiv \left[{\mathit{\psi }}_1\hspace{0.17em}\dots \hspace{0.17em}{\mathit{\psi }}_{K-1}\right]$ is the $K\times \left(K-1\right)$ matrix of basis vectors. To build intuition about this transformation, which is an isometric isomorphism, we highlight the following behaviors. First, the center of the simplex maps to the origin in the Euclidean space. Second, approaching a corner of the simplex (where a component of the composition vanishes) corresponds to diverging to infinity in the Euclidean space. Finally, a ball in the Euclidean space maps to a convex region in the simplex that is more distorted the farther the ball is from the origin.

We use the convention that the $\mathrm{c}\mathrm{l}\mathrm{r}$ and $\mathrm{i}\mathrm{l}\mathrm{r}$ act rowwise on matrices. Finally, we introduce the ilr-transformed MuSH $\mathbf{z}\left(t\right)\equiv \mathrm{i}\mathrm{l}\mathrm{r}\left(\mathit{\mu }\left(t\right)\right)$ and write Eq. 2 as

$$\mathbf{\Xi }={\mu }_0\mathcal{L}\left(\eta \right)\hspace{0.17em}{\mathrm{i}\mathrm{l}\mathrm{r}}^{-1}{\left(\mathbf{z}\right)}^{⊺}.$$ [7]

Again, the time coordinate is integrated over by the action of the linear operator. Although the forward model is nonlinear in $\mathbf{z}\left(t\right)$, it is convex given the convexity of the softmax function that appears in ${\mathrm{i}\mathrm{l}\mathrm{r}}^{-1}\left(\cdot \right)$.

Formulating and Solving the Inverse Problem for Population History Given Genomic Variation Data.

The inverse problem Eq. 8 is ill posed, meaning that many very different and erratic histories can be equally consistent with the data (65). We deal with this problem using regularization, seeking solutions that are constrained in their complexity without sacrificing data fit. We use optimization algorithms to find regularized demographies and MuSHs.

Time discretization.

For numerical implementation, we need finite-dimensional representations of $\eta \left(t\right)$ and $\mathbf{z}\left(t\right)$. We use piecewise constant functions of time on $m$ segments $\left[t_0,t_1\right),\left[t_1,t_2\right),\dots ,\left[t_{m-1},t_m\right)$ where the grid $0=t_0<t_1<\dots <t_{m-1}<t_m=\infty$ is common to $\eta \left(t\right)$ and $\mathbf{z}\left(t\right)$. We take the boundaries of the segments as fixed parameters and in practice, use a logarithmically spaced dense grid of hundreds of segments to approximate infinite-dimensional histories. Let the $m$-vector $\mathbf{y}={\left[y_1,\dots ,y_m\right]}^{⊺}$ denote the population size $\eta \left(t\right)$ during each segment, and define the $m\times \left(K-1\right)$ matrix $\mathbf{Z}$ as the constant ilr-transformed MuSH $\mathbf{z}\left(t\right)$ during each segment. In SI Appendix, section C, we show that Eq. 7 discretizes to the following matrix equation:

$$\mathbf{\Xi }={\mu }_0\mathbf{L}\left(\mathbf{y}\right)\hspace{0.17em}{\mathrm{i}\mathrm{l}\mathrm{r}}^{-1}\left(\mathbf{Z}\right),$$ [8]

where the $\left(n-1\right)\times m$ matrix $\mathbf{L}\left(\mathbf{y}\right)$ is fixed given a fixed demographic history $\mathbf{y}$. The transformation ${\mathrm{i}\mathrm{l}\mathrm{r}}^{-1}\left(\mathbf{Z}\right)$ is applied to each time point (i.e., row of $\mathbf{Z}$) independently.

Regularization.

We implement three different regularization criteria: sparsity of trends in the solutions $\mathbf{y}$ and $\mathbf{Z}$ [hypothesizing that the time variation of $\eta \left(t\right)$ and $\mathbf{z}\left(t\right)$ is not excessively erratic], sparsity of the singular value spectrum of the matrix $\mathbf{Z}$ (hypothesizing that the number of independently evolving mutational signatures is much less than the number $K$ of distinct mutation types), and improved numerical conditioning of the problem. These goals are in some cases overlapping, but we add a regularization term for each one. Before computing the penalties on the demography $\mathbf{y}$, we apply a log transform because variation over orders of magnitude is expected from population crashes and exponential expansions. This also has the benefit of enforcing nonnegative solutions. We now explain the regularizations in detail.

Our first regularization imposes simplicity in the time domain by preferring solutions with a small number of piecewise polynomial trends. This is achieved by penalizing the variation of $\log \eta \left(t\right)$ and $\mathbf{z}\left(t\right)$ via the ${\ell }_1$ norm of their time derivatives. Penalizing the $\left(\kappa +1\right)$ th-order time derivative encourages piecewise $\kappa$th-order polynomial solutions since the ${\ell }_1$ norm favors sparse derivatives in time. For example, $\kappa =0$ results in piecewise constant solutions, $\kappa =1$ results in piecewise linear solutions, and so on. Penalties with different $\kappa$ can be combined to obtain mixed trends (e.g., using $\kappa =0$ and $\kappa =3$ will allow solutions with both constant and cubic pieces). In the discretized model, the $\left(\kappa +1\right)$ th-order derivative operator corresponds to a matrix ${\mathit{D}}^{\left(\kappa +1\right)}$ of finite differences. This leads to the penalties ${‖{\mathit{D}}^{\left(\kappa +1\right)}\log \mathbf{y}‖}_1$ and ${‖{\mathit{D}}^{\left(\kappa +1\right)}\mathbf{Z}‖}_{\mathrm{1,1}}$ (penalizing the MuSH columnwise). In the least-squares setting, this regularization is called trend filtering (49, 66) and is one of many generalizations of the Lasso method (67). We later describe how we perform optimization with trend penalties in the setting of a more complex likelihood. Many demographic inference methods fit models composed of a small number of constant or exponential epochs that are motivated by prior knowledge about population histories. Although our histories are represented on a dense time grid, our regularization fuses the history at neighboring time points to discover epochs within which behavior is simple, while remaining flexible to capture more complicated behavior if the data justify it.

Second, because specific mutation processes may affect multiple mutation types, it is reasonable to assume that a small number of latent processes drives the majority of the variation across mutation types. We thus hypothesize that $\mathbf{Z}$ can be approximated by a low-rank matrix and propose two regularizations to enforce this. Let $\mathit{\sigma }$ be the vector of singular values of $\mathbf{Z}-{\mathbf{Z}}_{\mathrm{r}\mathrm{e}\mathrm{f}}$, where ${\mathbf{Z}}_{\mathrm{r}\mathrm{e}\mathrm{f}}$ is a reference, or baseline, MuSH taken to be the maximum likelihood estimate (MLE) constant solution by default. We use the nuclear norm ${\Vert \mathbf{Z}-{\mathbf{Z}}_{\mathrm{r}\mathrm{e}\mathrm{f}}\Vert }_{*}={\Vert \mathit{\sigma }\Vert }_1$ as a soft rank penalty, as it is the convex envelope of the rank function (68). The soft rank penalty constrains the number of nonzero singular values while also shrinking them toward zero. As an alternative to the soft rank penalty, we also implement a hard rank penalty, which directly penalizes $\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}\left(\mathbf{Z}-{\mathbf{Z}}_{\mathrm{r}\mathrm{e}\mathrm{f}}\right)={\Vert \mathit{\sigma }\Vert }_0$, equal to the number of nonzero singular values. The hard rank penalty results in a singular value thresholding step without shrinkage in the resulting algorithm, and it is not convex. Either of these rank regularizations assures that $\mathbf{Z}$ is a low-rank perturbation of the constant solution ${\mathbf{Z}}_{\mathrm{r}\mathrm{e}\mathrm{f}}$. Although the MuSH represents the history of each of $K$ mutation types, this attempts to explain them using a smaller set of mutation signatures.

Finally, we include classical ${\ell }_2$ (also called ridge or Tikhonov) penalties on both $\log \mathbf{y}$ and $\mathbf{Z}$. A small amount of this kind of regularization speeds up convergence without significantly influencing the solution. For the ridge penalty on the demography $\mathbf{y}$, we use a Tikhonov term ${‖\log \mathbf{y}-\log {\mathbf{y}}_{\mathrm{r}\mathrm{e}\mathrm{f}}‖}_2^2$ that shrinks toward a reference demography ${\mathbf{y}}_{\mathrm{r}\mathrm{e}\mathrm{f}}$. By default, we use the MLE constant history for ${\mathbf{y}}_{\mathrm{r}\mathrm{e}\mathrm{f}}$ to speed the convergence of the $\mathbf{y}$ problem. Similarly, the ridge penalty on the MuSH is a Tikhonov term for each mutation type, the squared Frobenius norm ${‖\mathbf{Z}-{\mathbf{Z}}_{\mathrm{r}\mathrm{e}\mathrm{f}}‖}_{\mathrm{F}}^2$.

Likelihood factorization: The SFS is a sufficient statistic for the demographic history with respect to the $k$-SFS.

The PRF approximation neglects linkage disequilibrium to model the probability of the SFS $\mathbf{x}$ given the expected SFS $\mathit{\xi }$ as independent Poisson random variables for each sample frequency

$$\mathbb{P}\left(\mathbf{x}\mid \mathit{\xi }\right)={\prod }_{i=1}^{n-1}\mathbb{P}\left(x_i\mid {\xi }_i\right)={\prod }_{i=1}^{n-1}\frac{e^{-{\xi }_i}{\xi }_i^{x_i}}{x_i!}.$$ [9]

We model the $k$-SFS as generated by independent mutational targets for each mutation type. We then show that a constant total mutation rate allows us to factorize the joint likelihood for $\eta$ and $\mathit{\mu }$ into a sequential inference procedure for $\eta$ then $\mathit{\mu }$.Proposition. The PRF, when generalized to the 2D grid of sample frequency and mutation type, factorizes as $\mathbb{P}\left(\mathbf{X}\mid \mathbf{\Xi }\right)=\mathbb{P}\left(\mathbf{x}\mid \mathit{\xi }\right)\hspace{0.17em}\mathbb{P}\left(\mathbf{X}\mid \mathbf{x},\widehat{\mathbf{\Xi }}\right)$, where $\mathbb{P}\left(\mathbf{x}\mid \mathit{\xi }\right)$ is the standard PRF Eq. 9 and $\mathbb{P}\left(\mathbf{X}\mid \mathbf{x},\widehat{\mathbf{\Xi }}\right)$ is independent multinomial for each sample frequency $i$, with multinomial parameter ${\widehat{\mathrm{\Xi }}}_{i,j}\equiv \frac{{\mathrm{\Xi }}_{i,j}}{{\xi }_i}$.

Proposition is proved via a Poissonization argument in SI Appendix, section D.

Next, we restore the $\eta$ and $\mathit{\mu }$ dependence of $\mathit{\xi }$ and $\mathbf{\Xi }$ (with fixed total mutation rate ${\mu }_0$), so Proposition gives the factorization

$$\mathbb{P}\left(\mathbf{X}\mid \eta ,\mathit{\mu }\right)=\mathbb{P}\left(\mathbf{x}\mid \eta \right)\hspace{0.17em}\mathbb{P}\left(\mathbf{X}\mid \mathbf{x},\eta ,\mathit{\mu }\right).$$ [10]

Lemma. If the total mutation rate is a constant $\mathit{\mu }\left(t\right)={\mu }_0\in {\mathbb{R}}_{>0}$, then the SFS $\mathbf{x}$ is a sufficient statistic for $\eta$ with respect to the $k$-SFS $\mathbf{X}$.

Lemma is proved via a Poisson thinning argument in SI Appendix, section E. The result is intuitively obvious because information about historical coalescence rates recorded in the SFS does not change if we further specify how mutation counts are partitioned into different mutation types; this only adds information about relative mutation rates for alleles with a given age distribution. Although $\eta$ appears in the second factor of Eq. 10, this only serves to map the MuSH rendered on the natural diffusion timescale $\tilde{\mathit{\mu }}\left(\tau \right)$ to time measured in Wright–Fisher generations. Because this map is one to one, there is no statistical information about $\eta$ in $\mathbf{X}$ not already present in $\mathbf{x}$. That is, $\mathbb{P}\left(\mathbf{X}\mid \mathbf{x},\eta ,\mathit{\mu }\right)=\mathbb{P}\left(\mathbf{X}\mid \mathbf{x},\tilde{\mathit{\mu }}\right)$.

This sufficiency is important from an inference perspective because it means we can sequentially infer demography from the SFS and then infer the MuSH from the $k$-SFS with the demography fixed from the previous step. Sufficiency implies that the negative log likelihood factors into the sum of two losses. We thus formulate two sequential optimization problems using negative log likelihoods from the factors Eq. 10 as loss functions for assessing data fit. Recall that $\mathbf{y}$ and $\mathbf{Z}$ are the discrete forms of $\eta$ and $\mathit{\mu }$, respectively; $\mathbf{\Xi }$ is given by Eq. 8; and $\mathit{\xi }$ is given by the row sums of $\mathbf{\Xi }$ and thus, independent of $\mathbf{Z}$. Neglecting constant terms, the two loss functions are

$${\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}_1\left(\log \mathbf{y}\right)={\sum }_{i=1}^{n-1}\left({\xi }_i-x_i\log {\xi }_i\right)$$ [11]

and

$${\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}_2\left(\mathbf{Z};\mathbf{y}\right)=-{\sum }_{i=1}^{n-1}{\sum }_{j=1}^K{X}_{ij}\log {\mathrm{\Xi }}_{ij}.$$ [12]

As with regularization, we parameterize in terms of $\log \mathbf{y}$.

Optimization problems for mushi.

We infer demography and MuSH by minimizing cost functions that combine the loss functions above, which measure error in fitting the data, with regularization. This may be considered a penalized likelihood method and, from a Bayesian perspective, may be interpreted as introducing a prior distribution over histories. Inference of $\log \mathbf{y}$ and $\mathbf{Z}$ is performed sequentially. We first initialize $\log \mathbf{y}={\mathbf{y}}_{\mathrm{r}\mathrm{e}\mathrm{f}}$ using the elementary formula for the MLE constant demography $\frac{S}{2{\mu }_0{H}_{n-1}}$ where $S\equiv {\sum }_{i=1}^{n-1}{x}_i$ is the number of segregating sites and $H_{n-1}$ denotes the $n$th harmonic number. We then minimize

$$\begin{array}{ll}\hfill f_1\left(\log \mathbf{y}\right)={\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}_1\left(\log \mathbf{y}\right)& +{\alpha }_{\kappa }{‖{\mathit{D}}^{\left(\kappa +1\right)}\log \mathbf{y}‖}_1\hfill \\ \hfill & +\frac{{\alpha }_{\mathrm{r}\mathrm{i}\mathrm{d}\mathrm{g}\mathrm{e}}}{2}{‖\log \mathbf{y}-\log {\mathbf{y}}_{\mathrm{r}\mathrm{e}\mathrm{f}}‖}_2^2\hfill \end{array}$$ [13]

over $\log \mathbf{y}\in {\mathbb{R}}^m$ to obtain the demographic history. Here, the ${\alpha }_{\kappa }$ hyperparameter controls the trend penalty strength and determines the number of $\kappa$th-order polynomial pieces in the solution (a larger penalty results in fewer pieces). The ${\alpha }_{\mathrm{r}\mathrm{i}\mathrm{d}\mathrm{g}\mathrm{e}}$ hyperparameter controls the strength of shrinkage toward ${\mathbf{y}}_{\mathrm{r}\mathrm{e}\mathrm{f}}$ and is intended to improve convergence without strongly biasing the solution.

Having fixed $\mathbf{y}$ from the previous step, we next infer $\mathbf{Z}$. We initialize $\mathbf{Z}={\mathbf{Z}}_{\mathrm{r}\mathrm{e}\mathrm{f}}$ to the MLE constant MuSH; mutation-type $j$ has the constant rate ${\mu }_0\frac{S_j}{S}$, where $S_j\equiv {\sum }_{i=1}^{n-1}{X}_{i,j}$ is the number of segregating sites in mutation-type $j$. Using the default soft rank penalty, we then minimize

$$\begin{array}{ll}\hfill f_2\left(\mathbf{Z}\right)={\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}_2\left(\mathbf{Z};\mathbf{y}\right)& +{\beta }_{\kappa }{‖{\mathit{D}}^{\left(\kappa +1\right)}\mathbf{Z}‖}_{\mathrm{1,1}}+{\beta }_{\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}}{\Vert \mathbf{Z}-{\mathbf{Z}}_{\mathrm{r}\mathrm{e}\mathrm{f}}\Vert }_{*}\hfill \\ \hfill & +\frac{{\beta }_{\mathrm{r}\mathrm{i}\mathrm{d}\mathrm{g}\mathrm{e}}}{2}{‖\mathbf{Z}-{\mathbf{Z}}_{\mathrm{r}\mathrm{e}\mathrm{f}}‖}_{\mathrm{F}}^2\hfill \end{array}$$ [14]

over $\mathbf{Z}\in {\mathbb{R}}^{m\times \left(K-1\right)}$ to obtain the ilr-transformed MuSH. Using the hard rank penalty instead of the default soft rank penalty, we would replace the nuclear norm ${\Vert \cdot \Vert }_{*}$ with the rank function $\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}\left(\cdot \right)$. The ${\beta }_{\kappa }$ and ${\beta }_{\mathrm{r}\mathrm{i}\mathrm{d}\mathrm{g}\mathrm{e}}$ hyperparameters are analogous to ${\alpha }_{\kappa }$ and ${\alpha }_{\mathrm{r}\mathrm{i}\mathrm{d}\mathrm{g}\mathrm{e}}$, respectively. The ${\beta }_{\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}}$ hyperparameter controls the rank of $\mathbf{Z}$ (a larger penalty results in smaller rank). We note that the trend order $\kappa$ can be different for demography and MuSH inference, and each can use mixed trends, adding more terms if desired.

We now briefly cover the methods used for optimization. The cost function Eq. 13 is nonconvex due to the nonlinear dependence of $\mathit{\xi }$ on $\mathbf{y}$, while the cost function Eq. 14 is convex. The trend penalties on both Eqs. 13 and 14 are nonsmooth, as is the soft rank penalty on Eq. 14. If the hard rank penalty is used instead of the soft rank penalty, Eq. 14 is also nonconvex. Although we cannot guarantee convergence to the global minimum for the demographic history ($\mathbf{y}$) problem, we have found that proximal gradient methods rapidly converge to good solutions that are robust to initialization. Briefly, in proximal methods the cost is split into differentiable and nondifferentiable parts, gradient descent steps are taken using the smooth part of the cost, and then, the proximal operator (or prox) of the nondifferentiable piece is applied. The prox projects to a nearby point, which ensures that the nonsmooth part of the cost is small and can be computed for the trend filtering and hard or soft rank penalties. For the $\mathbf{y}$ problem, we use the Nesterov accelerated proximal gradient method with adaptive line search (69, 70). For the MuSH ($\mathbf{Z}$) problem, we use a three-operator splitting method to deal with the two nonsmooth terms (71). We implemented a specialized alternating direction method of multipliers trend filtering algorithm to compute the prox for our mixed trend penalties (72). Our optimization algorithms are implemented very generally as a Python submodule in the mushi package (73).

Hyperparameter tuning.

Although mushi does not require a parametric model to be specified, it requires the user to tune a few key regularization hyperparameters to target reasonable solutions. Rather than treat the ridge penalties as adjustable hyperparameters, we fix them to ${\alpha }_{\mathrm{r}\mathrm{i}\mathrm{d}\mathrm{g}\mathrm{e}}={\beta }_{\mathrm{r}\mathrm{i}\mathrm{d}\mathrm{g}\mathrm{e}}=10^{-4}$ to improve convergence without noticeably influencing solutions. This leaves the trend penalty ${\alpha }_{\kappa }$ (or penalties for mixed trends) for demographic inference. Inferring demography from SFS data requires strong priors on the simplicity of solutions, so there can be no general recipe for selecting optimal hyperparameters. It is generally advisable to explore a few trend orders $\kappa$ and their strengths.

Small trend penalties give erratic, unregularized solutions. Increasing ${\alpha }_{\kappa }$ limits the number of $\kappa$th-order pieces in the solution and can be set to produce solutions that are consistent with known features of population history. Overregularization is indicated when the fit to the SFS becomes poor and can be seen in an “elbow plot” of the loss with increasing penalization. Mixing a zeroth-order term with higher-order models helps flatten the end points of the time domain, which may be desired.

We take a similar approach for the MuSH inference step. The two hyperparameters in this case are the trend hyperparameter ${\beta }_{\kappa }$ and the rank hyperparameter ${\beta }_{\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}}$. With $\kappa =0$, pulse-like histories can be recovered, while for higher orders (e.g., $\kappa =3$), smoothly varying histories are recovered (but do not fit pulse components as well). Again, oversmoothing is indicated by poor fit to the $k$-SFS. We set ${\beta }_{\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}}$ to select a rank (number of latent histories) between three and six. If ${\beta }_{\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}}$ is too large, the rank will be too small to fit all components of the $k$-SFS well. If it is too small, it is more difficult to find common features in different populations. By default, we prefer the soft rank penalty for its convexity but can choose the hard rank penalty if the former results in undesirable shrinkage.

Software Implementation Methods

The Open-Source mushi Python Package.

The mushi software is available as a Python 3 package in ref. 26 with extensive documentation. We use the JAX package (74) for automatic differentiation and just-in-time compilation of our optimization methods and the ProxTV package (75) for fast computation of the total variation prox. We modified the compositional data analysis module in the scikit-bio package (http://scikit-bio.org) to allow JAX compatibility. Using default parameters, inferring the demography and MuSH for a population of hundreds of individuals takes a few seconds on a laptop with a modest hardware configuration.

Reproducible Analysis.

All of the analyses and figures for this paper can be reproduced using Nextflow pipelines (76) and Jupyter notebooks (https://jupyter.org) available in ref. 77. We used msprime (32) and stdpopsim (33) for simulations, TensorLy (78) for NNCP tensor decomposition, umap-learn (46) for UMAP embedding, and several other standard Python packages. We used the Mathematica package fastZeil (79) to procedurally generate recursion formulas for the combinatorial matrix $\mathbf{C}$ in Theorem (SI Appendix, section B).

We generated $k$-SFS data for each 1KG population using mutyper (80, 81) and BCFtools (82, 83). High-coverage 1KG variant call data (27) were accessed from ref. 84, with sample manifest available in ref. 85. Ancestral state estimates for hg38 were accessed from ref. 86 (see also ref. 87), and the strict callability mask was accessed from ref. 88. Relate coalescence rate histories were accessed from ref. 89.

Data Availability

All study data are included in the article and/or SI Appendix.