Evolutionary design of magnetic soft continuum robots

Significance

Magnetic soft continuum robots (MSCRs) capable of magnetic field–controllable steering offer great promise for the endovascular treatment of cardiovascular diseases. However, existing MSCRs are often limited to small workspaces because of the lack of efficient design and optimization tools. In this work, we introduce an evolutionary design strategy by integrating theoretical modeling and the genetic algorithm. Enabled by this strategy, the proposed MSCR achieves an optimal workspace much larger than those of the state-of-the-art MSCRs. The proposed design strategy also offers a potent tool for efficient design and optimization of future magnetic soft robots and actuators.

Abstract

Worldwide cardiovascular diseases such as stroke and heart disease are the leading cause of mortality. While guidewire/catheter-based minimally invasive surgery is used to treat a variety of cardiovascular disorders, existing passive guidewires and catheters suffer from several limitations such as low steerability and vessel access through complex geometry of vasculatures and imaging-related accumulation of radiation to both patients and operating surgeons. To address these limitations, magnetic soft continuum robots (MSCRs) in the form of magnetic field–controllable elastomeric fibers have recently demonstrated enhanced steerability under remotely applied magnetic fields. While the steerability of an MSCR largely relies on its workspace—the set of attainable points by its end effector—existing MSCRs based on embedding permanent magnets or uniformly dispersing magnetic particles in polymer matrices still cannot give optimal workspaces. The design and optimization of MSCRs have been challenging because of the lack of efficient tools. Here, we report a systematic set of model-based evolutionary design, fabrication, and experimental validation of an MSCR with a counterintuitive nonuniform distribution of magnetic particles to achieve an unprecedented workspace. The proposed MSCR design is enabled by integrating a theoretical model and the genetic algorithm. The current work not only achieves the optimal workspace for MSCRs but also provides a powerful tool for the efficient design and optimization of future magnetic soft robots and actuators.

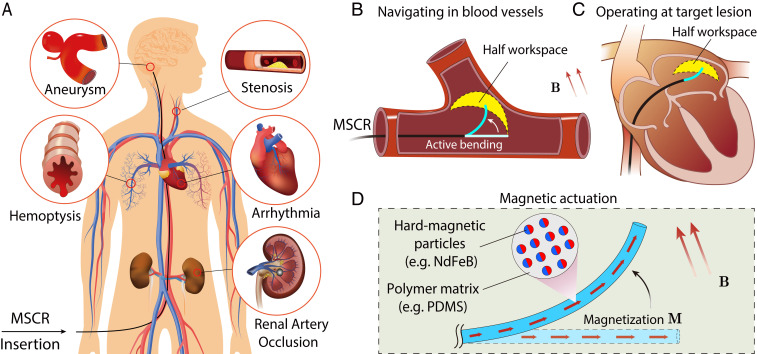
Cardiovascular diseases such as stroke and heart disease are the leading cause of long-term disability and death worldwide, with an annual cost of over $300 billion in the United States alone (1, 2). Diverse cardiovascular diseases are treated with minimally invasive surgery (Fig. 1A), which is less traumatic and more effective than open surgery (3–6). The conventional minimally invasive treatments of cardiovascular diseases typically employ a passive guidewire and catheter with a preshaped tip that is manually operated under radioscopic imaging. For example, in mechanical thrombectomy, a surgeon usually inserts a guidewire/catheter combination from the patient’s femoral artery over the leg and navigates this combination using fluoroscopic imaging through the aorta into the target occluded artery (usually in the brain or lungs) for mechanical clot removal (7). As another example, in atrial fibrillation ablation, a surgeon usually threads a catheter into the patient’s heart, where the catheter’s tip applies high or low temperature to disrupt heart conduction that generates faulty electrical signals (8). This manual operation of passive guidewires and catheters, however, is often limited by low steerability through complex vasculatures, difficulty in accessing small branches, long operation times, and/or increased accumulated imaging-related radiation to both patients and operating surgeons (9). To overcome these challenges, immense efforts have been committed to exploring robotic-assisted minimally invasive treatments in a remotely operated manner. In particular, because of the untethered and biocompatible nature of magnetic fields, a promising robotic-assisted minimally invasive platform has recently emerged based on magnetic field–controllable elastomeric fibers—magnetic soft continuum robots (MSCRs) (10–13).

Fig. 1.

MSCRs for minimally invasive treatments. (A) Cardiovascular diseases in hard-to-reach areas across the human body where MSCRs can find utility. (B) Schematic illustration of the active bending of the MSCR navigating in a complex blood vessel. The workspace is defined as the area of attainable locations by the MSCR’s end effector via tuning the actuation magnetic field. (C) Schematic illustration of operating the MSCR at lesion tissues in atrial fibrillation ablation. (D) Schematic illustration of the distal portion of an MSCR in which hard-magnetic particles (e.g., NdFeB) are dispersed in the polymer matrix (e.g., silicone).

An MSCR typically consists of a magneto-active distal portion that can be actively bent by tuning the actuation magnetic field and a nonmagnetized body that can be advanced or retracted by controlling the motor connected to the MSCR’s proximal end. In a typical minimally invasive treatment, a surgeon remotely controls the motor to advance the MSCR up to locations that require active steering, such as in front of branches of blood vessels (Fig. 1B) or lesion tissues (Fig. 1C) (14, 15). At these locations, the surgeon needs to remotely apply a magnetic field to bend the distal portion of the MSCR so that the MSCR’s end effector reaches the desired location. Thereafter, the surgeon further advances or operates the MSCR actively steered by the actuation magnetic field. Evidently, the steerability of an MSCR is largely determined by the set of attainable locations by its end effector via tuning the actuation magnetic field named the workspace of the MSCR (16, 17). A larger workspace gives a higher steerability of the MSCR in minimally invasive treatments.

Existing MSCRs are mostly fabricated by embedding one or more permanent magnets in the distal portion of the MSCR (18–25). More recently, a new type of MSCR has been developed by uniformly dispersing hard-magnetic particles in elastomeric fibers (16) (Fig. 1D). However, the workspaces of MSCRs with both embedded magnets and uniformly distributed hard-magnetic particles are still limited, mainly because of the lack of efficient design and optimization tools for MSCRs. Indeed, existing designs of MSCRs heavily rely on experimental trial and error or numerical simulations (26, 27) that are not ideal for design or optimization with a large number of design parameters. Hence, an efficient design strategy capable of maximizing the workspaces of MSCRs remains an important, yet unresolved, challenge in the field.

Here, we report an evolutionary design strategy to maximize the workspaces of MSCRs by integrating theoretical modeling (17, 28) and the genetic algorithm (29) to identify the optimal magnetization and rigidity patterns within the MSCRs (Fig. 2A). We first develop a hard-magnetic elastica theory to calculate the deflections of an MSCR with a specific magnetization and rigidity pattern under uniform magnetic fields up to 40 mT applied along various directions in one plane (17) (SI Appendix, Fig. S1). Notably, 40 mT is a typical magnetic-field strength for operating MSCRs (16, 30). We then calculate the area of the workspace for this MSCR and repeat the calculations for MSCRs with various random magnetization and rigidity patterns. Thereafter, we only select the MSCRs with relatively large workspaces, mutate and cross over their magnetization and rigidity patterns to give a new generation of MSCRs, and then calculate the workspaces of the new generation of MSCRs (29). By repeating this evolutionary process over a few generations, we can achieve an optimal design of the MSCR with an unprecedented workspace. We further validate this evolutionary design of the MSCR by both finite element simulations and experiments.

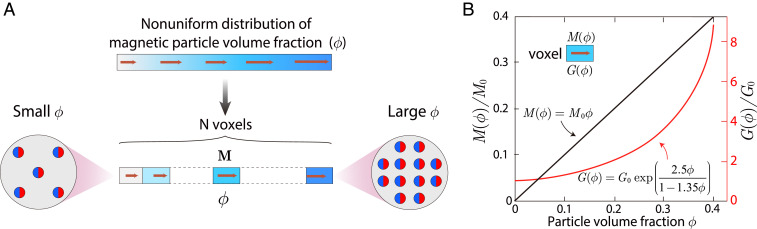
Fig. 2.

Designing MSCRs by programming their magnetization and rigidity pattern in the distal portion. (A) Each voxel is encoded with a specific remanent magnetization M by tuning its magnetic particle volume fraction $\varphi$. The direction of the remanent magnetization of all voxels is along the axial direction pointing to the distal tip. (B) The normalized magnetization strength $M\left(\varphi \right)/M_0$ (Left, black) and shear modulus $G\left(\varphi \right)/G_0$ (Right, red) of the MSCR as a function of particle volume fraction $\varphi$.

Results and Discussion

MSCR and Its Workspace.

In the current study, the magneto-active portion of the MSCR is composed of hard-magnetic particles dispersed in a polymer matrix (26). Hard-magnetic materials refer to a class of materials with intrinsic magnetic dipoles that have coercivity larger than 10⁶ A/m (31). The widely used hard-magnetic particles in MSCRs are based on neodymium-iron-boron (NdFeB) (16, 32–34), and the common polymer matrices for MSCRs include polyurethane and silicone. Once saturated by a strong magnetic field, the hard-magnetic particles in the MSCR can retain remanent magnetization along the direction of the saturation magnetic field (SI Appendix, Fig. S2). Thereafter, when subjected to an actuation magnetic field much lower than the saturation field, the MSCR tends to bend because of the collective torques and/or forces applied by the actuation field on the hard-magnetic particles.

In the current study, we apply uniform actuation fields up to 40 mT along different directions in one plane to bend the MSCR into different shapes in the plane accordingly. Consequently, the end effector of the MSCR can reach a set of attainable locations in the plane, giving the two-dimensional (2D) workspace of the MSCR (SI Appendix, Fig. S1). Notably, rotating the actuation fields around the axis of the undeformed MSCR will give a three-dimensional (3D) workspace. However, we will focus on the 2D workspace in the current study because the 3D workspace is simply a revolution of the 2D workspace (SI Appendix, Fig. S3). In addition, because the 2D workspace is symmetric about the axis of the undeformed MSCR (SI Appendix, Fig. S1), we only need to analyze half of the workspace in the rest of the paper.

Design Parameters for MSCRs.

We aim to optimize the workspace of an MSCR by tuning its magnetization and rigidity pattern. Without losing generality, the MSCR’s magneto-active portion can be segmented into $N$ voxels, where each voxel is encoded with a specific volume fraction of the hard-magnetic particles. This volume fraction is denoted as $\varphi$ (Fig. 2A). By applying a strong impulse of magnetic fields along the axial direction of the MSCR, the hard-magnetic particles in the MSCR are magnetized to saturation, giving rise to remanent magnetization $\mathbf{M}$ for each voxel (SI Appendix, Fig. S2). Note that $\mathbf{M}$ is a vector indicating both the strength (denoted as $M$) and direction of the remanent magnetization.

The $\varphi$ value of a voxel has two effects on its remanent magnetization and rigidity. On the one hand, the remanent magnetization of the voxel is linearly proportional to $\varphi$ (i.e., $\mathbf{M}={\mathbf{M}}_0\varphi$, where ${\mathbf{M}}_0$ is the remanent magnetization of the hard-magnetic particles) (16) (Fig. 2B). Therefore, increasing $\varphi$ will increase the remanent magnetization of the voxel. On the other hand, because the hard-magnetic particles have a much higher rigidity than the polymer matrix, increasing $\varphi$ will increase the shear modulus of the voxel, following the Mooney model (i.e., $G\left(\varphi \right)=G_0\exp \left[2.5\varphi /\left(1-1.35\varphi \right)\right]$, where $G$ and $G_0$ are the shear moduli of the voxel and the polymer matrix, respectively) (35). Furthermore, the upper limit of $\varphi$ is found to be around 40%, above which the MSCR cannot be consistently fabricated (16). Overall, to achieve a maximum workspace for the MSCR, we need to optimize the $\varphi$ values of all voxels of the MSCR within the range of $0\le \varphi \le 0.4$. Therefore, the $\varphi$ values of all voxels and the corresponding remanent magnetization and shear moduli of the voxels are the design parameters for the MSCR.

Theory of Hard-Magnetic Elastica.

The driving force for bending the magneto-active portion of the MSCR originates from the interaction between the actuation magnetic field and the hard-magnetic particles dispersed in the polymer matrix (Fig. 1D). In a uniform magnetic field, the driving force is the distributed magnetic torque. Since the actuation magnetic field is much smaller than the saturation magnetic field, the magnetization of the voxel is independent of the actuation magnetic field (34). Therefore, as the MSCR deforms, the magnetization of the voxel in the deformed configuration is only a function of the deformation gradient tensor (17, 26) denoted as $\mathbf{F}$. Due to the incompressibility of the voxel (17, 26), the magnetization of the voxel in the deformed configuration can be expressed as $\mathbf{F}\mathbf{M}$, indicating that the deformation gradient tensor maps the magnetization in the reference configuration to the magnetization in the deformed configuration.

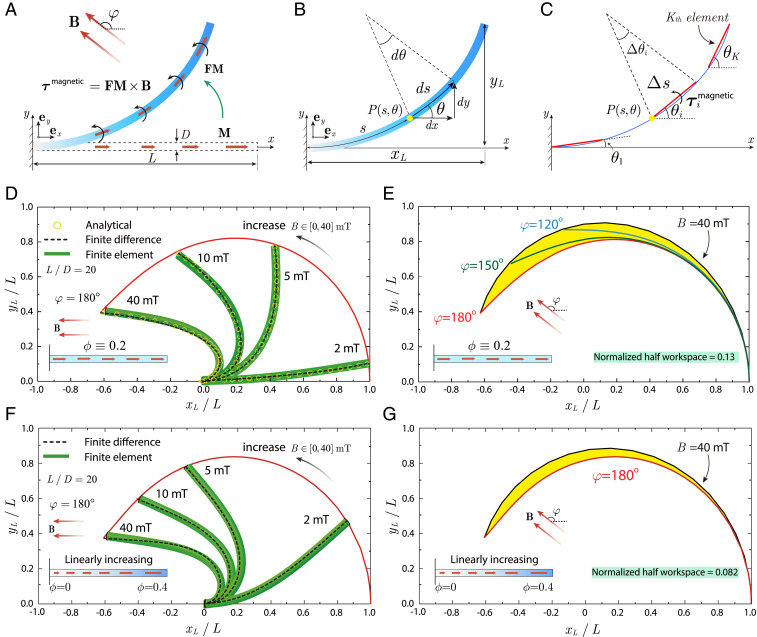
Fig. 3A depicts a typical bending configuration of the distal portion of an MSCR under a uniform actuation magnetic field. The actuation magnetic field can be expressed as $\mathbf{B}=B\left(\cos \phi {\mathbf{e}}_x+\sin \phi {\mathbf{e}}_y\right)$, where $B$ is the magnetic field strength; $\phi$ denotes the field direction; and ${\mathbf{e}}_x,{\mathbf{e}}_y$ are the basis vectors of the 2D Cartesian coordinate system. Therefore, the distributed magnetic torque per unit volume of the voxel can be expressed as ${\mathbf{\tau }}^{\text{magnetic}}=\mathbf{F}\mathbf{M}\times \mathbf{B}$, where × denotes the cross-product operation between two vectors.

Fig. 3.

Theoretical modeling of the distal portion of an MSCR. (A) Schematic illustration of the distal portion of a MSCR with remanent magnetization $\text{M}$ along its axial direction deflecting toward the direction of the uniform actuation magnetic field B. The length and diameter of the distal portion are denoted as $L$ and $D$, respectively. (B) The deformed distal portion is characterized by a parameterized spatial curve $\theta \hspace{0.17em}=\hspace{0.17em}\theta \left(s\right)$, referred to as an elastica, where $s$ and $\theta$ represent the arc length and tangential angle at the spatial point $P\left(s,\theta \right)$, respectively. The Cartesian coordinates of the distal tip are $\left(x_L,y_L\right)$. (C) The finite difference method discretizes the elastica into $K$ elements in which the infinitesimal arc $ds$ is approximated by a straight line $\mathrm{\Delta }s=L/K$. (D) Comparison of the deformation of the distal portion with uniform magnetic particle distribution $\varphi =0.2$ under 180° magnetic field from the analytical solution, finite difference method, and finite element simulation. (E) The normalized half workspace of the MSCR with uniform magnetic particle distribution $\varphi =0.2$ is 0.13. (F) Comparison of the deformation of the distal portion with linearly increasing particle concentration from 0 to 0.4 under 180° magnetic field from the finite difference method and finite element simulation. (G) The normalized half workspace of the MSCR with linearly increasing magnetic particle concentration from 0 to 0.4 is 0.082.

MSCRs are usually in the form of a slender cylindrical fiber (16). We denote the length and cross-sectional diameter of the distal portion as $L$ and $D$, respectively (Fig. 3A). Because of the slender nature of MSCRs ($L\gg D$), we adopt the elastica theory to describe the large deflection of MSCRs (17). The elastica theory assumes that the cross sections remain perpendicular to the axial centerline during deformation and that the length of the axial centerline remains unchanged during deformation (36–38). Therefore, for a planar motion of the elastica shown in Fig. 3B, the curvature of the centerline can be expressed as $\kappa \left(s\right)=d\theta /ds$, where $s$ represents the arc length from the origin to an arbitrary point$P$ on the elastica and $\theta$ denotes the angle between the tangent to the curve at point $P$ and the reference direction (i.e., x-axis). The deformation gradient of the voxel can be written as $\mathbf{F}=\cos \theta {\mathbf{e}}_x\otimes {\mathbf{e}}_x-\sin \theta {\mathbf{e}}_x\otimes {\mathbf{e}}_y+\sin \theta {\mathbf{e}}_y\otimes {\mathbf{e}}_x+\cos \theta {\mathbf{e}}_y\otimes {\mathbf{e}}_y+{\mathbf{e}}_z\otimes {\mathbf{e}}_z\mathbf{ },$ where $\otimes$ denotes dyadic product between two vectors. Such a deformation gradient suggests that the voxel undergoes a pure rotation. Then the internal bending moment in the distal portion can be calculated as $EI\kappa \left(s\right)$, where $EI=3\pi G{D}^4/64$ is the bending rigidity of the distal portion (17). At equilibrium, the bending moment at point $P$ is balanced by the summation of distributed magnetic torques from point $P$ to the load-free end effector (17)

$$\begin{array}{c}EI\kappa \left(s\right)=\underset{s}{\overset{L}{{\displaystyle \int }}}{\tau }^{\text{magnetic}}Ads\end{array},$$ [1]

where $A=\pi D^2/4$ is the cross-section area of the elastica. Solving Eq. 1 with the clamped boundary condition at $s=0$ [i.e., $\theta \left(0\right)=0$at $s=0$] yields the tangential angle $\theta \left(s\right)$ of the elastica. Then the Cartesian coordinates of point $P$ in the deformed configuration can be found using $x=\underset{0}{\overset{s}{{\displaystyle \int }}}\cos \theta \left(\eta \right)d\eta$ and $y=\underset{0}{\overset{s}{{\displaystyle \int }}}\sin \theta \left(\eta \right)d\eta$. When the hard-magnetic particles are uniformly distributed in the distal portion of the MSCR (i.e., constant$\varphi$), Eq. 1 can be analytically solved (17) (SI Appendix, section 1). However, when $\varphi$ is not a constant, one usually needs to adopt a numerical approach to solve Eq. 1.

Finite Difference Method.

For a distal portion with nonuniform $\varphi$ (Fig. 2A), we can solve Eq. 1 using the finite difference method. We first discretize the entire elastica into $K$ elements of equal length and approximate the infinitesimal arc length using a straight segment (i.e., $ds\approx \mathrm{\Delta }s=L/K$ as illustrated in Fig. 3C). Then the curvature at point $P$ can be approximated as $\kappa \left(s\right)=d\theta /ds\approx \left({\theta }_i-{\theta }_{i-1}\right)/\mathrm{\Delta }s$, where ${\theta }_i$ is the slope of the $i_{\text{th}}$ element ($i=\mathrm{1,2}\dots K$). By properly setting a large number for $K$, we can ensure that the magnetization of each element is constant. Therefore, the distributed magnetic torque density on the $i_{\text{th}}$ element can be found as ${\mathbf{\tau }}_i^{\text{magnetic}}=\mathbf{F}{\mathbf{M}}_i\times \mathbf{B}=M_{i}B\sin \left(\phi -{\theta }_i\right){\mathbf{e}}_z$, where $M_i=M_0{\varphi }_i$ is the magnetization strength of the $i_{\text{th}}$ element. As a result, Eq. 1 can be recast as

$$\begin{array}{c}{\left(EI\right)}_i\frac{{\theta }_i-{\theta }_{i-1}}{\mathrm{\Delta }s}={\displaystyle \sum }_{q=i}^{K}AB{M}_q\sin \left(\phi -{\theta }_q\right)\mathrm{\Delta }s,\hspace{0.17em}i=\mathrm{1,2}\dots K\end{array}.$$ [2]

The clamped boundary condition at $s=0$ requires that ${\theta }_0=0$. Substituting $q=i-1$ into Eq. 2, we have

$$\begin{array}{c}{\left(EI\right)}_{i-1}\frac{{\theta }_{i-1}-{\theta }_{i-2}}{\mathrm{\Delta }s}={\displaystyle \sum }_{q=i-1}^{K}AB{M}_q\sin \left(\phi -{\theta }_q\right)\mathrm{\Delta }s,\hspace{0.17em}i=\mathrm{2,3}\dots K\end{array}.$$ [3]

By subtracting Eq. 2 from Eq. 3, we can solve

$$\begin{array}{c}{\theta }_{i-2}=\frac{1}{{\left(EI\right)}_{i-1}}\left\{\left[{\left(EI\right)}_i+{\left(EI\right)}_{i-1}\right]{\theta }_{i-1}-{\left(EI\right)}_i{\theta }_i-AB{M}_{i-1}{\left(\mathrm{\Delta }s\right)}^2\sin \left(\phi -{\theta }_{i-1}\right)\right\}\end{array},$$ [4]

where ${\left(EI\right)}_i=3\pi G_i{D}^4/64$ is the bending rigidity, $G_i=G_0\exp \left[2.5{\varphi }_i/\left(1-1.35{\varphi }_i\right)\right]$ is the shear modulus, and $M_i=M_0{\varphi }_i$ is the magnetization strength of the $i_{th}$ element (Fig. 2B). Assuming a trial solution of ${\theta }_K$, we can solve ${\theta }_{K-1}$ with Eq. 2. Then Eq. 4 can be iteratively invoked to eventually yield ${\theta }_0$. The admissible solution of ${\theta }_i$ should give ${\theta }_0=0$ so that the clamped boundary condition at $s=0$ is satisfied. After solving ${\theta }_i$, the Cartesian coordinate of an arbitrary point $P$ on the deformed elastica can be calculated by $x=\sum _{q=1}^{i-1}\cos {\theta }_q\mathrm{\Delta }s$ and $y=\sum _{q=1}^{i-1}\sin {\theta }_q\mathrm{\Delta }s$, and the bending angle of the distal tip is ${\theta }_K$.

We validate the developed finite difference method by comparing its results with both the analytical solutions and finite element simulations for an MSCR with uniformly distributed hard-magnetic particles. We choose a representative MSCR in which the polymer matrix is polydimethylsiloxane (PDMS) with shear modulus $G_0=200$ kPa and the hard-magnetic particles are based on NdFeB with remanent magnetization $M_0=640$ kA/m (16). The length-to-diameter aspect ratio of the distal portion is taken to be $L/D=20$, and the hard-magnetic particle volume fraction is taken to be $\varphi =0.2$. Under actuation magnetic fields $B=2,\hspace{0.17em}5,\hspace{0.17em}10,\hspace{0.17em}40$ mT with field direction $\phi =180°$, the configurations of the deformed elastica are presented in Fig. 3D. The analytical solutions are adopted from ref. 17 (SI Appendix, section 1), the finite element results are given by Abaqus with 3,000 user-defined elements (26), and the finite difference results are obtained with 100 elements. The results from the three approaches agree well with one another, validating the accuracy of the finite difference method. The normalized half workspace of the MCRS with uniformly dispersed magnetic particle $\varphi =0.2$ is calculated as 0.13 (Fig. 3E). Next, we analyze an MSCR with a linearly increasing particle concentration from 0 to 0.4. Under actuation magnetic fields $B=2,\hspace{0.17em}5,\hspace{0.17em}10,\hspace{0.17em}40$ mT with field direction $\phi =180°$, configurations of the deformed elastica by the finite difference method agree well with finite element results (Fig. 3F). By varying the actuation field, the normalized half workspace of such an MSCR is 0.082 (Fig. 3G).

Evolutionary Design and Optimization by Genetic Algorithm.

The developed hard-magnetic elastica theory and finite difference method offer an effective approach for solving the large deformation and the workspaces of MSCRs. We next employ the genetic algorithm to calculate the optimal magnetization and rigidity pattern that maximizes the workspace. The genetic algorithm resembles the process of natural selection, in which the fittest individuals survive to produce the offspring of the next generation (29). Different from gradient-based algorithms that may provide only locally optimized results, the genetic algorithm has been widely used in many fields because of its remarkable efficiency in seeking near-global optimum in large search spaces (39–43).

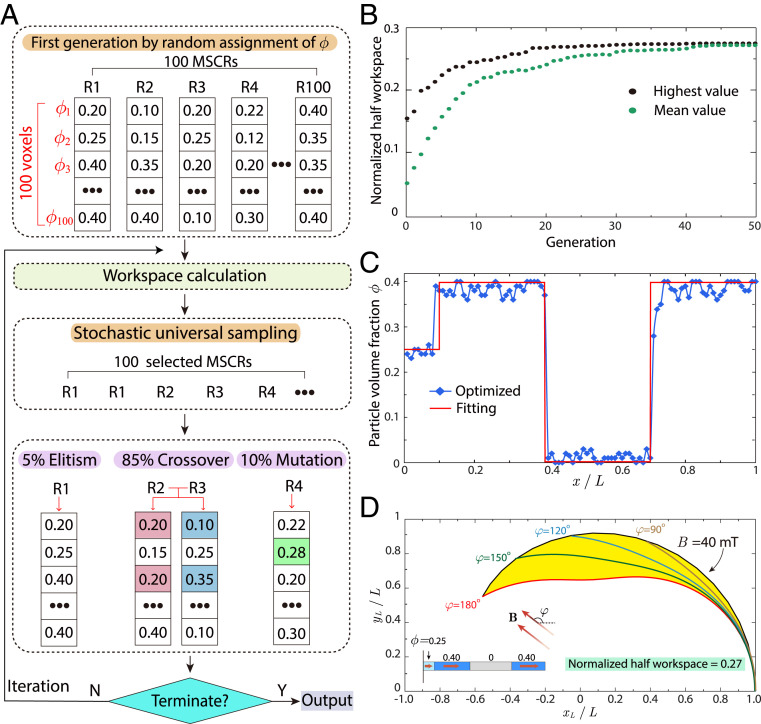
The design and optimization process of the MSCR is schematically depicted in Fig. 4A. The distal portion of the MSCR is equally divided into 100 voxels, where the $\varphi$ of each voxel is between 0 and 0.4. We create the first generation of 100 MSCRs with random magnetization and rigidity patterns by assigning a random $\varphi$ value between 0 and 0.4 to each voxel of the MSCR, and then we calculate their workspaces. Thereafter, we adopt the stochastic universal sampling method (44) to select 100 MSCRs (SI Appendix, section 2 and Fig. S4). Notably, in stochastic universal sampling (44), the MSCR with a larger workspace has a higher chance to be selected (even multiple times) than the MSCR with a smaller workspace. The selected 100 MSCRs will reproduce the second generation of 100 MSCRs by 5% elitism, 85% crossover, and 10% mutation (45) (Fig. 4A). The 5% elitism means that the five first-generation MSCRs with the highest workspaces will directly propagate to the second generation without changing their magnetization and rigidity patterns. The 85% crossover means that, in the remaining 95 first-generation MSCRs, we randomly select 85 MSCRs and exchange some of their voxels to form 85 new MSCRs. The 10% mutation means that, in the remaining 10 first-generation MSCRs, each MSCR will generate a new MSCR by randomly altering some of its voxels. Thereafter, we iterate the abovementioned process of the stochastic universal sampling followed by elitism, crossover, and mutation to create future generations of MSCRs in an evolutionary manner. This evolutionary process should be repeated over multiple generations until the difference between the largest workspace and the mean value of all workspaces in a certain generation of MSCRs is smaller than the tolerance.

Fig. 4.

Design and optimization of MSCRs by the genetic algorithm. (A) The schematic flowchart of the optimization process. MSCRs with a larger workspace may be selected multiple times by stochastic universal sampling to reproduce the next generation via elitism, crossover, and mutation. (B) The highest and mean values of the normalized half workspaces of 100 MSCRs over generations. The normalized half workspaces of all MSCRs reach the maximum and optimal value, ∼0.27, after 40 generations. (C) The hard-magnetic particle distribution (blue marker) and its fitted function (red line) of the optimized MSCR at generation 40. (D) The normalized half workspaces of the optimized MSCR with the fitted magnetization and rigidity pattern (red line in C) is 0.27.

Fig. 4B shows the evolution of the highest and mean areas of the half workspaces of MSCRs over generations. It can be seen that, after 40 generations, the normalized half workspaces of all MSCRs reach the maximum or optimal value, ∼0.27. The optimized magnetization and rigidity pattern given by the genetic algorithm is plotted in Fig. 4C with blue markers. Considering the ease of experimental fabrication, we further fit the optimized magnetization and rigidity pattern with the red line in Fig. 4C. Toward the tip of the optimized MSCR, the volume fraction of hard-magnetic particles follows a pattern of $\varphi =[0.25,0.4,0.4,0.4,\mathrm{0,0,0,0.4},0.4,0.4]$, where each number represents the volume fraction in 10 consecutive voxels. It is worth noting that such an optimized result is independent of the initial 100 MSCRs in the first generation (SI Appendix, Fig. S5), suggesting a near-global optimum achieved by the genetic algorithm. Applying the magnetic field up to 40 mT along various directions, the end effector sweeps different trajectories (Fig. 4D). The collection of all trajectories indeed gives the optimized MSCR a half workspace with a normalized area of 0.27.

Comparison of Workspaces.

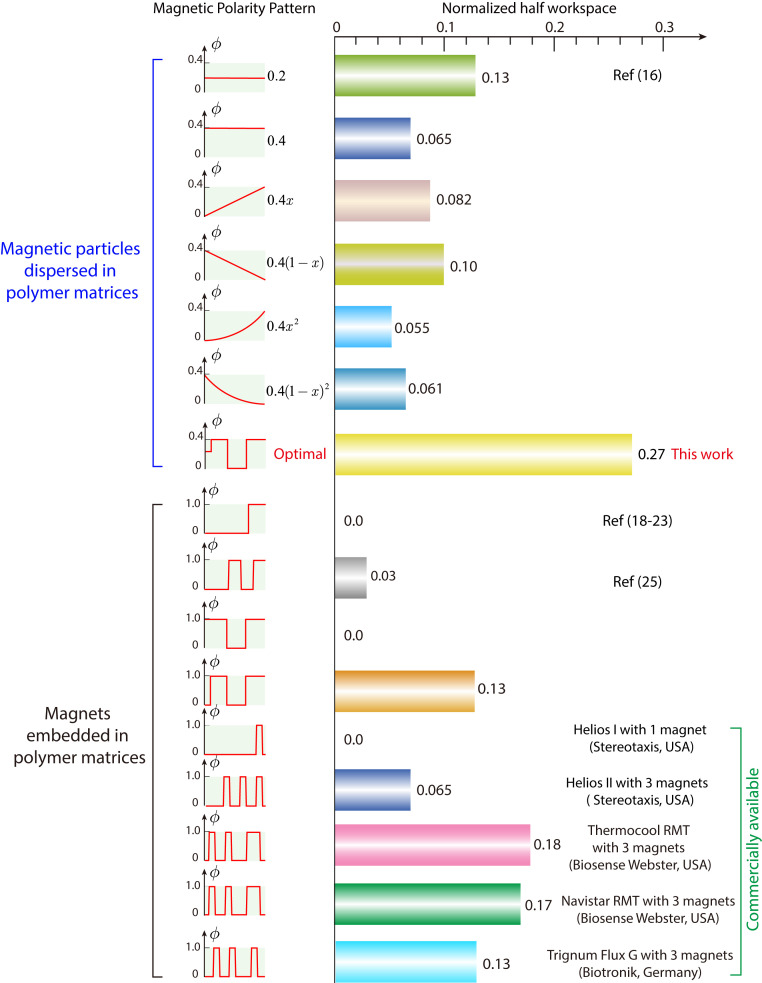
Next, we compare the workspaces of the optimized MSCR, the state-of-the art MSCRs, and guidewire/catheters with embedded magnets (Fig. 5). We first analyze the workspaces of MSCRs by uniformly dispersing hard-magnetic particles in polymer matrices. We find that the state-of-the-art design with constant $\varphi =0.2$ (16) shows a normalized half workspace of 0.13, while the design with constant $\varphi =0.4$ exhibits a lower normalized half workspace of 0.065 (Fig. 5 and SI Appendix, Fig. S6). We further calculate the workspaces of four MSCRs with nonuniform particle distributions. The MSCR with linearly increasing particle concentration from 0 to 0.4 has a normalized half workspace of 0.082, while the MSCR with linearly decreasing particle concentration from 0.4 to 0 shows a normalized half workspace of 0.10 (Fig. 5 and SI Appendix, Fig. S6). The MSCR with parabolically increasing particle concentration from 0 to 0.4 has a normalized half workspace of 0.055, while the MSCR with parabolically decreasing particle concentration from 0.4 to 0 has a normalized half workspace of 0.061 (Fig. 5 and SI Appendix, Fig. S6). In contrast, enabled by the genetic algorithm, the optimized MSCR has a normalized half workspace of 0.27—much higher than that of the state-of-the-art MSCRs (0.13).

Fig. 5.

Comparison of the normalized half workspaces between the optimized MSCR, the state-of-the-art MSCRs, and guidewires/catheters with embedded magnets. The optimized MSCR produces the largest normalized half workspace of 0.27.

Thereafter, we analyze the workspaces of guidewires/catheters with embedded magnets. We first consider guidewires/catheters with a single magnet embedded at the distal tip (SI Appendix, Fig. S7). While guidewires/catheters with different single magnets have been fabricated (18–23), their half workspaces are always a curve with an area of 0 (Fig. 5 and SI Appendix, section 3). We then analyze the guidewire with two permanent magnets embedded in the distal portion according to ref. 25 and find its normalized half workspace is 0.03 (Fig. 5 and SI Appendix, Fig. S8). Notably, if we change the voxels with $\varphi =0.4\hspace{0.17em}\text{and}\hspace{0.17em}\varphi =0.25$ in the optimized design into permanent magnets ($\varphi =1$) and elastomer ($\varphi =0$), respectively, the resultant MSCR will still yield a low normalized half workspace of 0.13 (Fig. 5 and SI Appendix, Fig. S8). If we change the voxels with $\varphi =0.4\hspace{0.17em}\text{and}\hspace{0.17em}\varphi =0.25$ in the optimized design into permanent magnets ($\varphi =1$), the resultant MSCR will have a normalized half workspace of 0 (SI Appendix, Fig. S8).

Next, we calculate the normalized half workspaces of five commercially available catheters with embedded magnets (SI Appendix, Table S1). The Helios I catheter (Stereotaxis) has a rigid magnet at the tip, and thus, it shows a normalized half workspace of 0. The Helios II (Stereotaxis), Thermocool RMT (Biosense Webster), Navistar RMT (Biosense Webster), and Trignum Flux G (Biotronik) catheters have three magnets, and their normalized half workspaces are calculated as 0.065, 0.18, 0.17, and 0.13, respectively (SI Appendix, Fig. S9). In summary, the normalized half workspaces of the state-of-the-art MSCRs and guidewires/catheters with embedded magnets are much lower than that of the optimized MSCR (0.27). This contrast highlights the importance of the optimization of the remanent magnetization and rigidity of voxels in achieving a high workspace, which is enabled by our design and optimization method.

Experimental Validation.

To experimentally validate the design and optimization of MSCRs, we fabricated a distal portion of the optimized MSCR and measured its deformation under uniform magnetic fields (SI Appendix, Fig. S10). The length and diameter of the distal portion were set to be $L=4$ cm and $D=2$ mm, respectively, in accordance with the condition $L/D=20$ in the design and optimization. Uniform magnetic fields up to 40 mT were generated by an electromagnet. The deformed MSCR configurations from the theoretical modeling and finite element simulations under $\phi =180°$ and $B=5,\hspace{0.17em}20,\hspace{0.17em}40$ mT are shown in SI Appendix, Fig. S10A; the deformed MSCR configurations by fixing $B=40$ mT while varying $\phi$ are presented in SI Appendix, Fig. S10B. In comparison, the corresponding experimental results are given on the right panel in SI Appendix, Fig. S10 A and B, respectively. Overlaying the theoretical and experimental results demonstrates an excellent agreement between them. These experimental results also validate the large half workspace of the optimized MSCR (SI Appendix, Fig. S10C). Furthermore, we also fabricated the distal portion of an MSCR with a permanent-magnet tip and experimentally validated its normalized half workspace of 0 (SI Appendix, Fig. S11).

Conclusions

In summary, we report an evolutionary strategy for the design and optimization of MSCRs to achieve the largest workspace. Distinct from the existing MSCRs based on embedding permanent magnets or uniformly dispersing magnetic particles in polymer matrices, we propose to design MSCRs with a nonuniform hard-magnetic particle distribution. We have developed a theoretical model to calculate the large deflections and the workspaces of MSCRs actuated by uniform magnetic fields. With this method, we have further adopted the genetic algorithm for the design and optimization of the MSCR in an evolutionary manner. The optimized MSCR gives a workspace much larger than those of the state-of-the-art MSCRs, implying the superior steerability of the optimized MSCR in minimally invasive treatments.

While we focus on the magnetization and rigidity patterns of the MSCR as the design parameters in the current study, the current design and optimization method can readily incorporate other design parameters such as the magnetization direction and coercivity of the hard-magnetic particles and the diameter of the MSCR. In addition, we believe the proposed design strategy, by incorporating theoretical modeling and the genetic algorithm, will potentially offer more opportunities for the design and optimization of future magnetic soft robots and actuators.

Materials and Methods

Finite Element Simulation.

Finite element simulations of MSCRs actuated in uniform magnetic fields were performed by implementing a user-defined element (UEL) in a commercial package Abaqus/Standard 2017. The driving force for bending the MSCR is interpreted as microscopic magnetic Cauchy stresses, defined as $\mathbf{\sigma }=-\mathbf{B}\otimes \mathbf{F}\mathbf{M}$, where $\mathbf{F}$ is the deformation gradient and the ⊗ operation denotes the dyadic product, which takes two vectors to yield a second-order tensor. The constitutive model of the material and the UEL to quantify the microscopic magnetic Cauchy stresses have been developed by Kim et al. (34) and Zhao et al. (26). In all simulations, the bulk modulus was set to be 1,000 times the shear modulus to approximate the material incompressibility, and the total number of UEL was 3,000 with convergence checked. The strength and direction of actuation magnetic fields and the magnetization of each voxel were defined as additional input parameters. A supplementary video showing the finite element simulation of the optimized MSCR under various actuation magnetic fields is given in Movie S1.

Sample Preparation.

The magneto-active portion of the optimized MSCR was fabricated by dispersing NdFeB particles (average diameter ∼5 μm) in PDMS matrix (base-to-curing agent mass ratio 20:1, SYLGARD 184 silicone, Dow Corning). Following the magnetic polarity pattern of the optimized MSCR, NdFeB particles with a prescribed volume fraction (0, 25, or 40 vol%) were first dispersed in the uncured PDMS resin using a planetary mixer (RWD100) at 800 rpm for 3 min. Novocs gloss solvent (Smooth-On) was used for thinning the PDMS resin with 40 vol% particles. Then the composite was injected into a cylindrical mold with a diameter of 2 mm and cured in an oven at 37 °C for 48 h. Novocs gloss solvent evaporated during the curing. After curing, a 4-mm fiber with 25 vol%, a 12-mm fiber with 40 vol%, a 12-mm fiber with 0 vol%, and a 12-mm fiber with 40 vol% were cut and glued contiguously to form the distal portion of the optimized MSCR. Thereafter, the distal portion was magnetized along its axial direction to saturation by impulse magnetic fields (about 3.8 T) generated by a digital pulse magnetizer. For MSCRs with a permanent magnet at the distal tip, a cylindrical NdFeB magnet (diameter 2 mm, length 4 mm) was glued to the tip of a 36-mm PDMS fiber.

Data Availability

All study data are included in the article and/or supporting information.