Significance
Using food web models that account for juvenile and adult individuals of species, I show that commonly observed differences between juveniles and adults in foraging capacity and predation risk result in larger, more complex communities than predicted by models without stage structure. Based on their species interaction networks these complex and diverse communities would be expected to be unstable, but these destabilizing effects of species interactions are overruled by stabilizing changes in juvenile–adult stage structure. Differences between juvenile and adult individuals hence offer a natural resolution to the diversity–stability enigma of ecological communities.
Keywords: food webs, community dynamics, community complexity, population stage structure, resilience
Abstract
Natural ecological communities are diverse, complex, and often surprisingly stable, but the mechanisms underlying their stability remain a theoretical enigma. Interactions such as competition and predation presumably structure communities, yet theory predicts that complex communities are stable only when species growth rates are mostly limited by intraspecific self-regulation rather than by interactions with resources, competitors, and predators. Current theory, however, considers only the network topology of population-level interactions between species and ignores within-population differences, such as between juvenile and adult individuals. Here, using model simulations and analysis, I show that including commonly observed differences in vulnerability to predation and foraging efficiency between juvenile and adult individuals results in up to 10 times larger, more complex communities than observed in simulations without population stage structure. These diverse communities are stable or fluctuate with limited amplitude, although in the model only a single basal species is self-regulated, and the population-level interaction network is highly connected. Analysis of the species interaction matrix predicts the simulated communities to be unstable but for the interaction with the population-structure subsystem, which completely cancels out these instabilities through dynamic changes in population stage structure. Common differences between juveniles and adults and fluctuations in their relative abundance may hence have a decisive influence on the stability of complex natural communities and their vulnerability when environmental conditions change. To explain community persistence, it may not be sufficient to consider only the network of interactions between the constituting species.
Ecological communities have traditionally been conceptualized as collections of species that are connected with each other through a network of positive and negative interactions. This species-based paradigm adopts the population as the fundamental unit of measurement or modeling, altogether ignores differences between individuals within populations, and hence considers the vital rates of all conspecific individuals to be identical. Yet, it is individuals, not species, that interact. Furthermore, in real populations no two individuals are alike, mostly because of differences in their developmental stage (1). And vital rates are definitely not the same for all individuals as only juveniles grow and mature, while only adults reproduce. This raises the question of to what extent current theoretical insights about dynamics of ecological communities are robust or, alternatively, are artifacts of the species-level scale of study of ecological communities (2).
One of the core elements of the theory about ecological community dynamics pertains to the relationship between community complexity, diversity, and stability, which has been explored at length through dynamic simulations of the network of species interactions (3, 4) or through analysis of the community matrix (5), the elements of which measure how strongly the species in a community affect each other’s growth rate. Using community matrices, Robert May (6, 7) theoretically predicted almost half a century ago that large, complex ecological communities are less stable than simpler ones, refuting prevailing ideas that complexity begets stability (8, 9). He challenged ecologists to “…elucidate the devious strategies which make for stability in enduring natural systems” (p. 174 in ref. 7). May’s findings initiated the diversity–stability debate in ecology (10) and the search for special characteristics and constraints on natural communities promoting stability (11). Analysis of different types of community matrices (12) has uncovered a range of mechanisms that benefit community stability, such as weak interaction strength (13); adaptive foraging (14); allometric scaling of interaction strength (15); and omnivorous (16), mutualistic (17), or high-order interactions (18). The diversity–stability conundrum seems, however, far from resolved, given that a recent review concluded that for community stabilityo occur “at least half—and possibly more than 90%—of species must be subject to self-regulation to a substantial degree” (p. 1873 in ref. 19), even though clear empirical evidence for self-regulation is lacking and the extent to which it occurs in natural populations is debated (16, 20–22). Paradoxically therefore, while competitive and predatory interactions between species are considered the two most important, structuring forces of ecological communities (23), direct, negative effects of species on their own growth rate seem crucial for community stability (19).
The network of population-level interactions between species in the community, its topology, the nature of these interactions, and their strength have been the conceptual foundation of virtually all existing studies on ecological community stability (24). Even studies assessing stability of real-life communities (25) aim at estimating how species in a community affect each other’s population-level growth rate to construct the community matrix (5). But within populations individuals by definition differ and not only because juveniles grow and mature while adults reproduce. Juveniles and adults also differ in their body size and therefore in their ecology (26, 27). Because juveniles are smaller, they generally feed at lower rates (28), are more food limited (29), and are more vulnerable to predation (30, 31). These body size-dependent differences translate into an asymmetry in foraging and predation risk between juveniles and adults, which has been shown to affect structure and dynamics of ecological communities (32).
To study the impact of these asymmetries in foraging and predation risk between juvenile and adult individuals on community diversity and stability I simulated dynamics of randomly constructed, stage-structured model food webs, in which juveniles were more food limited and more exposed to predation than adults, and compared them with dynamics of an analogous model without stage structure (Materials and Methods). Species in the food web differed in body weight with only the smallest—basal—species following self-regulating population dynamics. Foraging interactions between all nonbasal species were modeled based on their difference in body weight (Materials and Methods). To focus exclusively on differences between juveniles and adults in foraging rate and predation mortality and to allow comparison between models with and without population structure, I assumed juveniles and adults to forage at different rates on the same range of prey species with the same preferences and thus have overlapping diets. Juveniles and adults are furthermore preyed upon by the same predator species but at different rates. Asymmetry in resource foraging is represented phenomenologically by a foraging asymmetry factor , ranging between 0 and 2, with juvenile and adult resource ingestion rate taken proportional to and , respectively (Fig. 1). Asymmetry in vulnerability to predation is represented analogously by a predation asymmetry factor , also ranging between 0 and 2, with predation mortality of juveniles and adults taken proportional to and , respectively (Fig. 1). For juveniles and adults hence forage at the same rate, such that maturation and reproduction are limited by food to the same extent. If in addition , juveniles and adults do not differ in their rates of predation mortality either. Juvenile and adult dynamics were modeled using a juvenile–adult structured model (33) in terms of numerical abundances that explicitly accounts for maintenance requirements, which cause maturation and reproduction to halt at low food availabilities. For and this stage-structured food web model can be shown to be identical to a food web model without stage structure (SI Appendix, Model simplification in case of ontogenetic symmetry). Community dynamics were simulated until density fluctuations of the persisting species had stabilized (Materials and Methods).
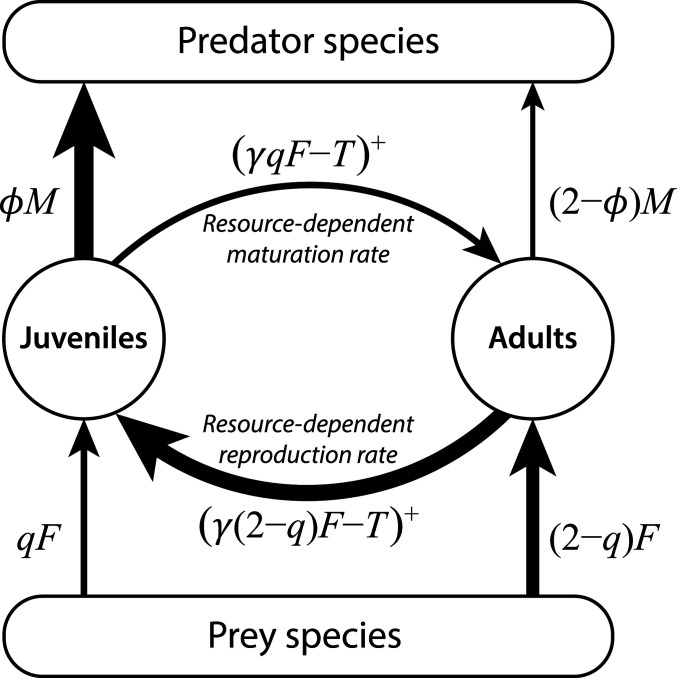
Fig. 1.
Basic juvenile–adult structured food web module. Juveniles and adults are assumed to forage with identical preferences on the same prey species at per-capita rate and , respectively, where represents the juvenile–adult ingestion asymmetry and the functional response of the species. Juveniles and adults are preyed upon by the same predator species, dying from predation at per-capita rates and , respectively, where represents the juvenile–adult asymmetry in vulnerability to predation and represents the species-specific predation pressure. Per-capita maturation and reproduction rates equal and , respectively, where the superscript indicates restriction of these rates to nonnegative values. Maturation and reproduction stop when food availability drops below and , respectively, and all ingestion is used to cover maintenance requirements. Default parameter values are and , reflecting that maturation is more resource limited than reproduction and juveniles are more vulnerable to predation than adults (graphically represented by arrows of different thickness). See Materials and Methods for more details.
Generally, juvenile individuals are far more vulnerable to predation than adults (30, 31). Empirical observations on predator–prey body size ratios have revealed that this ratio is roughly an order of magnitude smaller when it is computed on the basis of the average body size in the predator and prey population than when it is computed as the average body-size ratio between individual predators and the individual prey in their gut (34, 35). This order of magnitude difference suggests that small individuals in a prey population are up to 10 times more likely to be preyed upon than large individuals. Furthermore, per-capita reproduction rates are for most species less limited by food than juvenile maturation rates, in particular because offspring sizes are small compared to adult body sizes (32). A competitive asymmetry between juveniles and adults is further supported by the occurrence of stunted populations in fish (36, 37), shellfish (38), and dragonflies (39) and the asymmetry observed in intraspecific competition experiments (29, 40, 41). Therefore, and are adopted as default values for the juvenile–adult ingestion and predation asymmetry parameter (but see SI Appendix, Fig. S1 for the effect of varying and ).
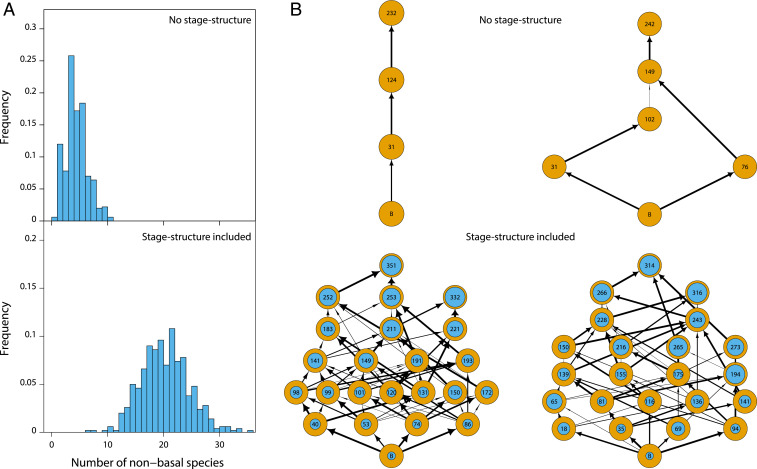
When juveniles are more limited by food and are more predator sensitive than adults (, ), the structured model results in communities with on average 20 or more nonbasal species persisting on the single basal species (Fig. 2). In contrast, food web simulations with the corresponding unstructured model result in persistence of on average 3 to 4 nonbasal species (Fig. 2 and SI Appendix, Fig. S1). This increase in community diversity due to juvenile–adult asymmetry is larger at higher system productivity (SI Appendix, Fig. S2). In addition to increasing community diversity juvenile–adult asymmetry also increases the complexity of the food web that structures the community. Food webs resulting from model simulations without stage structure are simple, mostly linear food chains, with most species foraging on a single prey and vulnerable to a single predator (Fig. 2 and SI Appendix, Fig. S3). In contrast, food webs resulting from simulations with juvenile–adult asymmetry are complex with most species foraging on multiple prey species and exposed to predation by multiple consumer species (Fig. 2 and SI Appendix, Fig. S3). Diverse and complex communities occur in particular when predation on juveniles is 8 to 10 times larger than on adults and is less dependent on foraging differences (SI Appendix, Figs. S1 and S7).
Fig. 2.
Juvenile–adult stage structure increases community size and complexity. (A) Frequency distribution of community sizes (nonbasal species only) and (B) examples of food webs resulting from 500 replicate food web simulations without stage structure (Top) and including stage structure with foraging and predation asymmetry between juveniles and adults (Bottom). In B vertical positions indicate trophic level. Inner circles in Bottom row indicate the density of juveniles as fraction of total population density. Arrow widths indicate the relative feeding preference of consumers for a particular prey species.
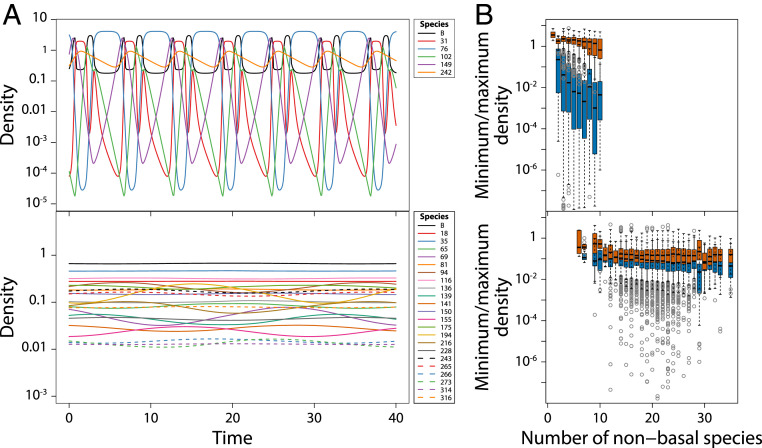
Temporal dynamics of food webs that result from model simulations without stage structure are characterized by large-amplitude fluctuations in species abundances reminiscent of classical predator–prey cycles (Fig. 3). The cycle amplitudes moreover increase with increasing community size especially because minimum species densities during the cycle decrease (Fig. 3), ultimately leading to species extinction and reductions in community diversity. In contrast, the complex food webs resulting from the structured model with juvenile–adult asymmetry either are stable or exhibit small-amplitude fluctuations in total species densities (Fig. 3). Furthermore, if fluctuations in total species densities occur, their amplitude is unaffected by community size (Fig. 3).
Fig. 3.
Juvenile–adult stage structure stabilizes community dynamics. (A) Examples of dynamics of all species in food web simulations without stage structure (Top) and including stage structure with foraging and predation asymmetry between juveniles and adults (Bottom). Corresponding food web structures are shown in Fig. 2 B, Right. (B) Boxplot of minimum (blue bars) and maximum (red bars) total densities of all populations as a function of community size for all persisting species in 500 replicate food web simulations without (Top) and with stage structure and foraging and predation asymmetry between juveniles and adults (Bottom).
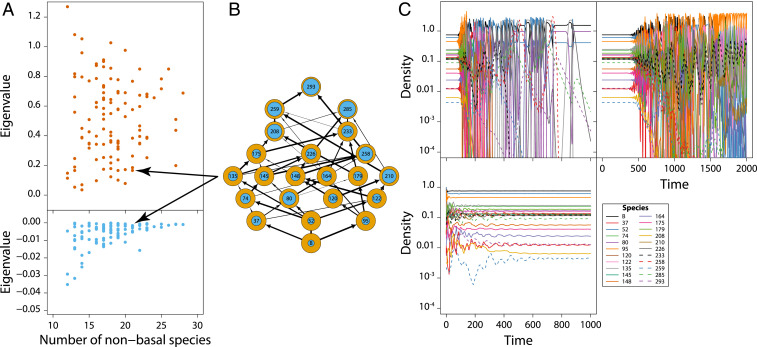
When juveniles are more limited by food and more predator sensitive than adults, 22% of the food webs generated by the structured model approach a stable community equilibrium (Materials and Methods and SI Appendix, Computing eigenvalues of the stage-structured model). These stable communities allow for disentangling how food web interactions and population structure together affect community stability. The structured model in terms of juvenile and adult abundances can be transformed into an equivalent model, in which each species is represented by its total density and the fraction of juveniles in it. The transformation separates the model into a “total species-density subsystem” and a complementary “species-structure subsystem.” Community stability is now determined by the stability of each of these two subsystems on their own and their interactions (Materials and Methods). The stability of the species-density subsystem on its own is determined by the usual community matrix, measuring the per-capita effect of species on each other’s growth rate. For all stable communities resulting from the structured model in the case of juvenile–adult asymmetry the dominant eigenvalue of this community matrix is positive and large (Fig. 4A). The community matrix hence predicts these communities to be highly unstable, which mostly results because only the basal species is regulated by a negative self-effect, top predators have no self-effect, and all other nonbasal species exhibit positive self-effects (Materials and Methods and SI Appendix, Fig. S5). The dominant eigenvalue of the Jacobian matrix determining the stability of the coupled subsystems of species density and species structure, however, has a negative real part for all stable communities (Fig. 4A) mostly because the species-density subsystem is connected to and interacts with the species-structure subsystem and the dominant eigenvalue of the matrix determining the stability of this species-structure subsystem on its own has a negative real part. The large differences between the dominant eigenvalues of the community and Jacobian matrices indicate that the dynamic nature of the fraction of juveniles of the species is key to community stability.
Fig. 4.
Adaptive stage structure stabilizes community dynamics. (A) Real part of the dominant eigenvalue of the community matrix (Top) and the Jacobian matrix determining community stability (Bottom) as a function of community size for all stable communities resulting from simulations with the stage-structured model and foraging and predation asymmetry between juveniles and adults (Materials and Methods). (B) Example of a stable community with 21 nonbasal species. (C) Dynamics of the community shown in B with a constant juvenile–adult density ratio equal to its equilibrium value for each species and initial densities equal to their equilibrium densities (Top Left), with a constant juvenile maturation rate equal to its equilibrium value for each species and initial densities equal to their equilibrium densities (Top Right, model equivalent with an analogous age-structured model), and with dynamic juvenile–adult stage structure following a disturbance event that reduces the densities of all species in the community by 50% (Bottom) (Materials and Methods).
Simulations of community dynamics starting from stable community states confirm the stabilizing impact of dynamic population structure and how it increases the resilience of the community: Even after a disturbance that reduces the density of all species by 50% the complete model involving the coupled species-density and species-structure subsystems predicts a rapid return to the stable community equilibrium (Fig. 4C). The reduction in density at most results in the extinction of a few species (SI Appendix, Fig. S6). In contrast, when starting in the undisturbed community equilibrium and simulating dynamics using only the species-density subsystem with for each species the fraction of juveniles constant and equal to its equilibrium value, species densities soon start to fluctuate wildly (Fig. 4C). Consequently, most species eventually go extinct and the community ends up being of similar size to the communities predicted by the food web model without population structure (SI Appendix, Fig. S6). Similar results were obtained with an alternative method (42) to represent the stage structure of each species by a single measure of species density. Likewise, starting in the undisturbed community equilibrium and simulating dynamics using a corresponding, age-structured model, in which the juvenile maturation rate is set constant in time and equal to its equilibrium value, wild fluctuations in species density soon develop (Fig. 4C) and the community eventually ends up being of similar size to the communities predicted by the food web model without population structure (SI Appendix, Fig. S6).
Stability of these model communities therefore depends on the dynamic changes in juvenile–adult ratio in the population and on the food dependence of both the maturation and the reproduction rate. The dynamics of the juvenile fraction in each of the species dampen density fluctuations in the community in various ways. For example, increases in reproduction of one particular species have more limited effects on its prey species and are more quickly quenched by its predators, when juveniles forage at lower rates and are more vulnerable to predation, than in the absence of any population structure. Increases in food availability for a particular focal species will lead to modulation of the interaction strength with its prey, as higher prey densities will speed up maturation, increase the fraction of adults, and thus increase the average per-capita impact of the species on its prey. Furthermore, a dynamic population stage structure also buffers against fluctuations in predation pressure, as increases in predation will primarily affect the juveniles that are limited most by food availability. Higher mortality under these conditions has been shown to relax possible bottlenecks in juvenile maturation and to increase the efficiency with which resources are used for population growth as opposed to being used for somatic maintenance (33, 43). Thus, dynamic population stage structure leads to adaptive modulation of the average interaction strength between species that counters fluctuations in bottom-up and top-down effects.
The presented results are robust to changes in the population stage structure as well as the model describing dynamics of each of the species. Similar results regarding community diversity, complexity, and dynamics are obtained under even wider parameter ranges when populations are represented by the biomass densities in three life history stages (small juveniles, larger immatures, and adults) as opposed to numerical abundances of juveniles and adults only and the dynamics of each population are modeled using a stage-structured biomass model that approximates the dynamics of a complete population body size distribution (Materials and Methods and SI Appendix, Stage-structured biomass model of species dynamics and Figs. S7–S9). The communities resulting from this more detailed model tend to be even larger with on average 25 to 30 species coexisting on a single basal species.
The topology of the interaction network between species in a community, which forms the theoretical foundation of existing studies on community stability, may hence provide only partial insight into the mechanisms stabilizing complex communities and may even suggest necessary conditions for stability, such as ubiquitous self-regulation, that might prove too restrictive once the dynamics of population stage structure are taken into account. As shown here, the dynamic population structure can simply overrule the destabilizing effects of the species interaction network. This within-species mechanism thus breaks up in a realistic and natural way the constraints on community complexity that were originally identified by May (6, 7) and extends the range of mechanisms and constraints on community interactions that have been identified to promote stability using species-based approaches (13–18). If we are to model the impact of environmental change on complex ecological communities, we need models that can fully capture the diversity, complexity, stability, and vulnerability of these systems—this study represents a major advance on existing approaches that consider only species-level interaction networks.
Materials and Methods
Food Web Construction.
Model food webs are constructed by assigning each of an initial species random niche values between 0 and 1. Niche values are related to body size following with minimum and maximum species body size equal to and g, respectively (SI Appendix, Fig. S10). To represent documented prey–predator body size ratios (35, 44) more faithfully than in the niche model (45) the center of the feeding niche of consumer species is uniformly distributed between and , resulting in median prey–predator body size ratios between and . The width of the feeding niche equals , such that consumer species feeds on prey species with body sizes ranging between and . The relative preference of consumer for prey follows a piecewise continuous hump-shaped distribution with finite range (Bates distribution of order 3):
| [1] |
Food Web Dynamics without Stage Structure.
Species are ranked according to their niche value (i.e., body size) and their numerical abundances are indicated with . The basal species (with index 1) is assumed to forage on its own exclusive resource , the dynamics of which are described by
| [2] |
with the productivity of the resource and its turnover rate, while scales the predation pressure of the basal species on its resource. The resource dynamics are assumed to be in pseudo-steady state, such that at all times. The (linear) functional response of the basal species, indicated with , is consequently assumed to equal the pseudo-steady-state value of :
| [3] |
Nonbasal species are assumed to forage following a type II functional response on all other species in the community at a relative rate (Eq. 1) determined by the species body size ratio. The encounter rate of a consumer species with index with all its prey species (indexed with ) therefore equals
| [4] |
and its functional response (scaled between 0 and 1) equals
| [5] |
with the consumer’s half-saturation density. Because the prey–predator body size ratio is assumed to be strictly smaller than 1, consumer species can only forage on all species with index .
The dynamics of all species densities are now described by
| [6] |
where and represent the value of the food encounter rate and the scaled functional response of species , respectively. The parameter relates the growth rate of species to its functional response , while scales the predation pressure of species on its prey species. The parameters and represent the population loss rate through somatic maintenance costs and background mortality, respectively. Note that all species are ordered according to their body size and hence only species with an index can feed on species .
Food Web Dynamics with Stage Structure.
Numerical abundances of juvenile and adult individuals of consumer species are indicated with and , respectively. Juveniles and adults are assumed to feed on the same range of prey species, have the same prey preferences, and thus have overlapping diets. However, juveniles and adults feed at different rates, such that the foraging rates of juveniles and adults of species equal and , respectively, with proportionality constants and the functional response of species .
Juveniles and adults are also assumed to differ in their sensitivity to predation, such that the predation mortality experienced by juveniles and adults of species equals and , respectively, where represents the predation pressure exerted on species by all of its predators. The parameters and are referred to as the foraging and predation asymmetry between juveniles and adults.
The functional response for the basal species is defined analogously to the model without stage structure, taking into account the foraging asymmetry between juveniles and adults,
| [7] |
while the encounter rate with prey for nonbasal species equals
| [8] |
The expression for the functional response of nonbasal species remains the same (Eq. 5). In addition to decreasing through background mortality the numerical abundances of juvenile and adult individuals change through reproduction and maturation. These processes are described by a stage-structured model (33) that assumes maturation and reproduction to stop when food availability drops below a threshold level and food intake is not sufficient to cover basic maintenance costs. In particular, maturation of juveniles of species depends on its functional response , following
| [9] |
while reproduction by adults follows
| [10] |
Analogous to the model without stage structure the parameter relates maturation and reproduction to the food availability, and , for juveniles and adults, respectively. The maximum functions in the expressions for and ensure that maturation and reproduction halt whenever food availability drops below and , respectively. The parameter hence determines in a phenomenological manner whether maturation () or reproduction () is more limited by food availability.
Dynamics of the juvenile–adult structured food web model are described by
| [11] |
| [12] |
with
| [13] |
the predation pressure exerted on species by all of its predators.
Model Parameterization.
Parameter values were randomly selected, but constrained by default scaling relationships with species body size as presented by de Roos and Persson (ref. 32, boxes 3.3 and 3.4), except that the time variable and hence all rate parameters have been scaled by a factor of 10 to speed up numerical computations. The default parameter scaling relationships with body size reflect documented generalities (28, 46, 47) that maximum ingestion rates are roughly an order of magnitude larger than maintenance rates, that conversion efficiency is roughly 60%, and that losses through background mortality are 7 to 10 times smaller than losses through maintenance. More specifically, for each nonbasal species, the half-saturation density occurring in its functional response was sampled uniformly from the interval [0.5,2.5]. The parameters , , , and were assumed to scale with . For each species the values of these parameters were generated using the equations
with , , , and the default mean values of the species-specific parameters (32). The species-specific parameters , , , and were for each species randomly selected from a Bates distribution of degree 3 around these mean values. The Bates distribution is the continuous probability distribution of the mean, , of three independent uniformly distributed random variables on the unit interval. Random values from this distribution range between 0 and 1 with mean value of . The quantities are independent realizations of the random variable , while , , , and represent the one-sided, relative width of the distributions of the species-specific parameters , , , and , respectively, around their mean values. Default values for these relative widths equal 0.1, such that all species-specific parameters range between 0.9 and 1.1 times their default, mean value and follow hump-shaped distributions within these ranges. Finally, the productivity and turnover rate of the exclusive resource for the basal species were taken equal to 60 and 2.0, respectively, in all computations, unless stated otherwise. The two remaining parameters in the model, the foraging asymmetry parameter and the predation asymmetry parameter , were varied between the different computations to assess their effect on community dynamics.
Numerical Simulation Procedure.
Numerical integrations of the food web with species were carried out using an adaptive Runge–Kutta method implemented in C. Relative and absolute tolerances during the integration were set to and , respectively. During the first time units no species were removed from the community, even if they attained very low density. For each species, whose total density dropped below , was removed from the community. This persistence threshold ensures that the product of the relative tolerance () and the lowest species density () is larger than the machine precision (equal to according to the Institute of Electrical and Electronics Engineers (IEEE) 754-2008 standard in the case of double precision). During numerical computations mean and variance as well as the maximum and minimum values of the total species density were continuously monitored for all species. The values of these measured statistics are reset whenever the community structure changes as one or more species in the community go extinct. Numerical integrations are halted whenever the community structure has not changed for time units and no change has occurred from one time unit to the next in the values of these statistics (mean, minimum, maximum, and variance of total species density) for all species in the community.
Sources of Community Stability.
Through analytical manipulations the model in terms of juvenile abundances and adult abundances can be recast into an equivalent model in terms of total species abundance and the fraction of juveniles in a population . In terms of these alternative model variables the functional response value for the basal species can be written as
| [14] |
while the encounter rate with prey for nonbasal species equals
| [15] |
The dynamics of total species density and fraction of juveniles in all populations are then described by
| [16] |
| [17] |
with
| [18] |
the predation pressure exerted on species by all of its predators.
The resulting system of differential equations can hence be written as
| [19] |
| [20] |
in which and indicate vectors of all total species abundances and fractions of juveniles in all populations, respectively. The vector-valued functions and contain the right-hand side of the differential equations for the species-density subsystem and for the species-structure subsystem, respectively. For a system with species the Jacobian matrix of the ordinary differential equations above is a matrix of the form
| [21] |
Each of the four parts of is a matrix containing the partial derivatives of the functions and with respect to the total species densities and fractions of juveniles . Expressions for these partial derivatives are provided in SI Appendix, Computing eigenvalues of the stage-structured model.
All communities resulting from the stage-structured model with asymmetry in feeding and predation between juveniles and adults (, ) for which the minimum and maximum values of the total species density differ less than for all species are classified as stable. Communities for which minimum and maximum values of total density of at least one species differed more than from each other are considered unstable (cycling). For both stable and unstable communities the average total abundance and fraction of juveniles observed in the simulation were used as starting values to numerically solve for the equilibrium state using the package “rootSolve” (48, 49) in R (50). For all 115 stable communities the equilibrium community state was successfully located and was numerically indistinguishable from the average densities and juvenile fractions observed in the numerical simulations. For 147 communities that were considered unstable (cycling) the numerical solution procedure also converged to an equilibrium community state with all species present, while for 238 unstable communities the numerical solution procedure did not converge to such an equilibrium state. For all equilibrium community states found, the Jacobian matrix is evaluated by substituting for all species the equilibrium value for total abundance and fraction of juveniles as well as all general and species-specific parameters into the expressions for the elements of . The eigenvalues of the Jacobian matrix are subsequently computed using the routine eigen() in R (Fig. 4 A, Bottom, for stable communities only; see SI Appendix, Fig. S4 for both stable and unstable communities).
To evaluate how dynamic changes in population stage structure (i.e., changes in the juvenile–adult ratio) affect community stability, the eigenvalues of the Jacobian matrix of stable communities are compared with the eigenvalues of the top-left submatrix of , the matrix . The latter matrix determines the stability of the species-density subsystem on its own with the juvenile fraction of each species equal to its equilibrium value. This matrix also corresponds to the community matrix with elements capturing the per-capita effect of the species in the community on each other’s growth rate. The community matrix determines the stability of a model, in which the dynamics of total species densities follow the same set of equations as in the full model, but the fraction of juveniles in the populations is constant over time and equals the fraction of juveniles of the species at equilibrium (Fig. 4 A, Top). Comparing the eigenvalues of the Jacobian matrix and the community matrix reveals the impact of dynamic changes in the population structure of the species on the stability of the community equilibrium (SI Appendix, Computing eigenvalues of the stage-structured model).
To further assess the differences between constant and dynamic juvenile fractions in the populations, for all stable communities resulting from the stage-structured model with asymmetry in feeding and predation between juveniles and adults (, ) community dynamics were computed starting from the equilibrium community state using the reduced model including the differential equations for the species-density subsystem only, with the juvenile fraction in each of the populations taken equal to its equilibrium value inferred from the stable community state (Fig. 4 C, Top Left and SI Appendix, Sources of community stability and Fig. S6). Similarly, community dynamics were computed with an age-structured analogue of the full model including differential equations for the species-density subsystem and for the species-structure subsystem, but with the juvenile maturation rate for each of the species in the community taken constant in time and equal to the maturation rate in the equilibrium community state. These simulations were also started from the equilibrium community state (Fig. 4 C, Top Right and SI Appendix, Sources of community stability and Fig. S6). Finally, community dynamics were computed with the full model including the differential equations for the species-density subsystem and for the species-structure subsystem and dynamic changes in the juvenile maturation rates starting from a community state in which the initial density of each species was exactly 50% of its equilibrium value as inferred from the stable community state (Fig. 4 C, Bottom and SI Appendix, Fig. S6).
Extent of Self-Regulation.
For stable communities the extent of self-regulation of species is assessed with the diagonal elements of the community matrix, the matrix , which measures the positive or negative effect of the total species abundance on its own rate of change (SI Appendix, Fig. S5).
Supplementary Material
Acknowledgments
I thank Bernd Blasius, Jennifer Dunne, Jacopo Grilli, Bob Holt, Kevin Lafferty, Ben Martin, Lennart Persson, Axel Rossberg, and Peter de Ruiter for stimulating discussions and their comments on the manuscript and the Santa Fe Institute for the hospitality while carrying out this research.
Footnotes
The author declares no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2023709118/-/DCSupplemental.
Data Availability
All code, data files, and R scripts used to generate the figures are available in Bitbucket at https://bitbucket.org/amderoos/structuredfoodweb/.
References
- 1.Schoener T. W., “Resource partitioning” in Community Ecology Pattern and Process, Kilkkawa J., Anderson D. J., Eds. (Blackwell Scientific, Boston, MA, 1986), pp. 91–126. [Google Scholar]
- 2.Wiens J. A., Spatial scaling in ecology. Funct. Ecol. 3, 385–397 (1989). [Google Scholar]
- 3.Chen X., Cohen J. E., Transient dynamics and food-web complexity in the Lotka-Volterra cascade model. Proc. Biol. Sci. 268, 869–877 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Williams R. J., Martinez N. D., Stabilization of chaotic and non-permanent food-web dynamics. Euro. Phys. J. B 38, 297–303 (2004). [Google Scholar]
- 5.Levins R., Evolution in Changing Environments: Some Theoretical Explorations (Princeton University Press, Princeton, NJ, 1968). [Google Scholar]
- 6.May R. M., Will a large complex system be stable? Nature 237, 413–414 (1972). [DOI] [PubMed] [Google Scholar]
- 7.May R. M., Stability and Complexity in Model Ecosystems (Princeton University Press, Princeton, NJ, 1973). [Google Scholar]
- 8.MacArthur R., Fluctuations of animal populations and a measure of community stability. Ecology 36, 533–536 (1955). [Google Scholar]
- 9.Paine R. T., Food web complexity and species diversity. Am. Nat. 100, 65–75 (1966). [Google Scholar]
- 10.McCann K. S., The diversity-stability debate. Nature 405, 228–233 (2000). [DOI] [PubMed] [Google Scholar]
- 11.Namba T., Multi-faceted approaches toward unravelling complex ecological networks. Popul. Ecol. 57, 3–19 (2015). [Google Scholar]
- 12.Allesina S., Tang S., The stability–complexity relationship at age 40: A random matrix perspective. Popul. Ecol. 57, 63–75 (2015). [Google Scholar]
- 13.Neutel A. M., Heesterbeek J. A. P., De Ruiter P. C., Stability in real food webs: Weak links in long loops. Science 296, 1120–1123 (2002). [DOI] [PubMed] [Google Scholar]
- 14.Kondoh M., Foraging adaptation and the relationship between food-web complexity and stability. Science 299, 1388–1391 (2003). [DOI] [PubMed] [Google Scholar]
- 15.Brose U., Williams R. J., Martinez N. D., Allometric scaling enhances stability in complex food webs. Ecol. Lett. 9, 1228–1236 (2006). [DOI] [PubMed] [Google Scholar]
- 16.Pimm S. L., Lawton J. H., On feeding on more than one trophic level. Nature 275, 542–544 (1978). [Google Scholar]
- 17.Thébault E., Fontaine C., Stability of ecological communities and the architecture of mutualistic and trophic networks. Science 329, 853–856 (2010). [DOI] [PubMed] [Google Scholar]
- 18.Grilli J., Barabás G., Michalska-Smith M. J., Allesina S., Higher-order interactions stabilize dynamics in competitive network models. Nature 548, 210–213 (2017). [DOI] [PubMed] [Google Scholar]
- 19.Barabás G., Michalska-Smith M. J., Allesina S., Self-regulation and the stability of large ecological networks. Nat. Ecol. Evol. 1, 1870–1875 (2017). [DOI] [PubMed] [Google Scholar]
- 20.Yodzis P., The stability of real ecosystems. Nature 289, 674–676 (1981). [Google Scholar]
- 21.Sterner R. W., Bajpai A., Adams T., The enigma of food chain length: Absence of theoretical evidence for dynamic constraints. Ecology 78, 2258–2262 (1997). [Google Scholar]
- 22.Pimm S. L., Food Webs (University of Chicago Press, Chicago, IL, 2002). [Google Scholar]
- 23.Chase J. M., et al. , The interaction between predation and competition: A review and synthesis. Ecol. Lett. 5, 302–315 (2002). [Google Scholar]
- 24.Pascual M., Dunne J. A., “From small to large ecological networks in a dynamic world” in Ecological Networks Linking Structure to Dynamics in Food Webs, Pascual M., Dunne J. A., Eds. (Oxford University Press, New York, NY, 2006), pp. 3–24. [Google Scholar]
- 25.Jacquet C., et al. , No complexity-stability relationship in empirical ecosystems. Nat. Commun. 7, 12573–12578 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Werner E. E., Gilliam J. F., The ontogenetic niche and species interactions in size structured populations. Annu. Rev. Ecol. Syst. 15, 393–425 (1984). [Google Scholar]
- 27.Miller T. E. X., Rudolf V. H. W., Thinking inside the box: Community-level consequences of stage-structured populations. Trends Ecol. Evol. 26, 457–466 (2011). [DOI] [PubMed] [Google Scholar]
- 28.Peters R. H., The Ecological Implications of Body Size (Cambridge Studies in Ecology, Cambridge University Press, Cambridge, UK, 1983). [Google Scholar]
- 29.Potter T., King L., Travis J., Bassar R. D., Competitive asymmetry and local adaptation in Trinidadian guppies. J. Anim. Ecol. 88, 330–342 (2018). [DOI] [PubMed] [Google Scholar]
- 30.Sogard S. M., Size-selective mortality in the juvenile stage of teleost fishes: A review. Bull. Mar. Sci. 60, 1129–1157 (1997). [Google Scholar]
- 31.Woodward G., Speirs D. C., Hildrew A. G., Quantification and resolution of a complex, size-structured food web. Adv. Ecol. Res. 36, 85–135 (2005). [Google Scholar]
- 32.de Roos A. M., Persson L., Population and Community Ecology of Ontogenetic Development (Monographs in Population Biology, Princeton University Press, Princeton, NJ, 2013), vol. 51. [Google Scholar]
- 33.de Roos A. M., When individual life history matters: Conditions for juvenile-adult stage structure effects on population dynamics. Theor. Ecol. 11, 397–416 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Woodward G., Warren P. H., “Body size and predatory interactions in freshwaters: Scaling from individuals to communities” in Body Size: The Structure and Function Of Aquatic Ecosystems, Hildrew A. G., Raffaelli D. G., Edmonds-Brown R., Eds. (Cambridge University Press, Cambridge, UK, 2007), pp. 98–117. [Google Scholar]
- 35.Nakazawa T., Ushio M., Kondoh M., Scale dependence of predator–prey mass ratio: Determinants and applications. Adv. Ecol. Res. 45, 269–302 (2011). [Google Scholar]
- 36.Roff D. A., The Evolution of Life Histories (Chapman & Hall, New York, NY, 1992). [Google Scholar]
- 37.Chizinski C. J., Pope K. L., Wilde G. R., Strauss R. E., Implications of stunting on morphology of freshwater fishes. J. Fish. Biol. 76, 564–579 (2010). [DOI] [PubMed] [Google Scholar]
- 38.Saunders T. M., Mayfield S., Hogg A. A., A simple, cost-effective, morphometric marker for characterizing abalone populations at multiple spatial scales. Mar. Freshw. Res. 59, 32–40 (2008). [Google Scholar]
- 39.Van Buskirk J., Population consequences of larval crowding in the dragonfly Aeshna Juncea. Ecology 74, 1950–1958 (1993). [Google Scholar]
- 40.Narvaez C. A., Sainte-Marie B., Johnson L. E., Intraspecific competition in size-structured populations: Ontogenetic shift in the importance of interference competition in a key marine herbivore. Mar. Ecol. Prog. Ser. 649, 97–110 (2020). [Google Scholar]
- 41.Nelson W. A., Joncour B., Pak D., Bjørnstad O. N., Asymmetric interactions and their consequences for vital rates and dynamics: The smaller tea tortrix as a model system. Ecology 100, e02558–15 (2019). [DOI] [PubMed] [Google Scholar]
- 42.Rossberg A. G., Farnsworth K. D., Simplification of structured population dynamics in complex ecological communities. Theor. Ecol. 4, 449–465 (2010). [Google Scholar]
- 43.de Roos A. M., et al. , Food-dependent growth leads to overcompensation in stage-specific biomass when mortality increases: The influence of maturation versus reproduction regulation. Am. Nat. 170, E59–E76 (2007). [DOI] [PubMed] [Google Scholar]
- 44.Brose U., et al. , Body sizes of consumers and their resources. Ecology 86, 2545 (2005). [Google Scholar]
- 45.Williams R. J., Martinez N. D., Simple rules yield complex food webs. Nature 404, 180–183 (2000). [DOI] [PubMed] [Google Scholar]
- 46.Yodzis P., Innes S., Body size and consumer resource dynamics. Am. Nat. 139, 1151–1175 (1992). [Google Scholar]
- 47.McCoy M. W., Gillooly J. F., Predicting natural mortality rates of plants and animals. Ecol. Lett. 11, 710–716 (2008). [DOI] [PubMed] [Google Scholar]
- 48.Soetaert K., RootSolve: Nonlinear Root Finding, Equilibrium and Steady-State Analysis of Ordinary Differential Equations (R package 1.6, 2009).
- 49.Soetaert K., Herman P. M., A Practical Guide to Ecological Modelling. Using R as a Simulation Platform (Springer, Dordrecht, The Netherlands, 2009). [Google Scholar]
- 50.R Core Team , R: A Language and Environment for Statistical Computing (R Foundation for Statistical Computing, Vienna, Austria, 2020). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All code, data files, and R scripts used to generate the figures are available in Bitbucket at https://bitbucket.org/amderoos/structuredfoodweb/.