Combining primary cohort data with external aggregate information without assuming comparability

Summary:

In comparative effectiveness research (CER) for rare types of cancer, it is appealing to combine primary cohort data containing detailed tumor profiles together with aggregate information derived from cancer registry databases. Such integration of data may improve statistical efficiency in CER. A major challenge in combining information from different resources however, is that the aggregate information from the cancer registry databases could be incomparable with the primary cohort data, which are often collected from a single cancer center or a clinical trial. We develop an adaptive estimation procedure, which uses the combined information to determine the degree of information borrowing from the aggregate data of the external resource. We establish the asymptotic properties of the estimators and evaluate the finite sample performance via simulation studies. The proposed method yields a substantial gain in statistical efficiency over the conventional method using the primary cohort only, and avoids undesirable biases when the given external information is incomparable to the primary cohort. We apply the proposed method to evaluate the long-term effect of trimodality treatment to inflammatory breast cancer (IBC) by tumor subtypes, while combining the IBC patient cohort at The University of Texas MD Anderson Cancer Center and the external aggregate information from the National Cancer Data Base (NCDB).

1. Introduction

Comparative effectiveness research (CER) in oncology has attracted substantial attention because of its potential to provide timely treatment comparisons and improve health outcomes (Hahn and Schilsky, 2012). However, a major research challenge in CER is how to best use multiple sources of data to assemble quality evidence, especially for rare cancers. Inflammatory breast cancer (IBC) is a rare (less than 5% of breast cancer diagnoses annually) but aggressive breast cancer subtype, with 5-year survival rates of only 35% to 40% (Rueth et al., 2014). Because of the rarity of the disease, there have been no prospective randomized clinical trials to assess various treatment options and to identify the optimal ones (Robertson et al., 2010). The current IBC treatment guideline recommended by the National Comprehensive Cancer Network is trimodality, defined as neoadjuvant chemotherapy followed by modified radical mastectomy and post-mastectomy radiation therapy to the chest wall and draining lymphatics. It would be medical value to evaluate IBC patients’ long-term prognosis by treatment and their tumor subtype.

The IBC patient cohort at The University of Texas MD Anderson Cancer Center, denoted as the primary cohort, contains valuable individual patient information, including demographic variables, tumor biology and tumor cell proliferation markers, and detailed systematic adjuvant therapies and surgery management (Masuda et al., 2014). This primary cohort, with a median follow-up of 5.17 years (range 0.06 to 19 years), is ideal for better understanding the treatment effects for these patients by tumor subtype. Although MD Anderson is the largest cancer center in the world, the sample size of the primary cohort is not large enough to have adequate power and efficiency to characterize treatment effects by tumor subtype, due to the rarity of IBC. Complementary data sources, such as population-based cancer registry databases, denoted as external data, are being used increasingly for CER in oncology (Lyman and Levine, 2012). However, the large population-based databases, such as the Surveillance, Epidemiology and End Results (SEER) database and the National Cancer Data Base (NCDB), do not capture detailed tumor biology information, such as tumor cell proliferation markers. Hence, it is not possible to rely only on population-based databases to investigate treatment effects on disease prognosis by tumor subtype. Most uses of such databases have focused on monitoring national trends in the disease incidence, pattern of treatments, and mortality. Our goal is to facilitate a more accurate statistical estimation and inference by combining individual-level data from the primary cohort (e.g., the MD Anderson IBC cohort) with aggregate survival information (e.g., 5-year survival rates) from NCDB to improve evidence-based treatment guidelines for IBC patients by tumor subtypes.

In recent statistical and econometrical literature, combining information from a primary cohort with a published external aggregate has drawn considerable interest (Qin, 2017). Qin and Lawless (1994) and Qin (2000) developed the empirical-likelihood framework to borrow aggregate information from external resources, using the constraints imposed to the likelihood. Imbens and Lancaster (1994) discussed how to define constraints on regression parameters in econometrical survey sampling. Qin et al. (2015) used stratum-specific probabilities from external resources to increase the estimation efficiency of logistic regression model fitting, given case-control data. Recently, Chatterjee et al. (2016) and Huang et al. (2016) developed extensions to accommodate data from complex stratified sampling designs and right-censored data. One essential assumption of the aforementioned methods is that the aggregate information from the external databases is comparable with those of the primary cohort. If the aggregate information was obtained from a different population, such information borrowing may result in misleading conclusions, and any efficiency gain could be spurious.

The penalized likelihood has been successfully used for variable selection purposes in regression analysis, in which penalty terms and tuning parameters shrink certain regression coefficients towards zero or exactly to zero, if needed. For example, Tibshirani (1996) proposed a least absolute shrinkage and selection operator (LASSO), and Fan and Li (2001) developed a non-concave penalized likelihood method with a smoothly clipped absolute deviation (SCAD) penalty. In the context of our applications, we propose a penalized constraint maximum likelihood to combine the primary cohort data and external aggregate information. A penalty function with additional parameters is included to characterize the potential discrepancy in the aggregate information from the primary cohort and external resources.

The remainder of this article is organized as follows. In Section 2, we introduce the notations and the Cox proportional hazards model for the data from the primary cohort with constraints to integrate the external information. In Section 3, we propose a penalized constraint maximum likelihood to control the degree of borrowing information from the external resources, which is determined by the magnitude of comparability. We develop a computational algorithm to obtain the estimators of unknown parameters. We also establish the asymptotic properties of the proposed estimators. In Section 4, we assess the empirical performance of the proposed estimators under various scenarios. We apply the proposed method to analyze the MD Anderson IBC cohort with aggregate survival information from NCDB in Section 5. We provide concluding remarks in Section 6. The detailed proofs are deferred to the online Supporting Information.

2. Notation and Model

Let T be the survival time from an initial event to an event of interest, and C be its censoring time. Denote the covariates of interest by the p-dimensional vector X with a cumulative density function (CDF) of G(·). Conditional on X, we assume that censoring time C and survival time T are independent, and T is absolutely continuous. Denote the conditional density function and the conditional survival function of T given X = x as f(t|x) and S(t|x). The observed data are represented by n independent copies, (Y_i, Δ_i, X_i),i = 1, ⋯ ,n, where Y_i = min{T_i, C_i}, Δ_i = I(T_i ⩽ C_i), and I(·) is the indicator function.

We assume the survival time T follows the proportional hazards model (Cox, 1972): λ(t|x) = λ(t) exp(x^Tβ), where β is a p–dimensional vector of regression coefficients and λ(t) is an unspecified baseline hazard function. Let $\Lambda (t)={\int }_0^t\lambda (u)du$ be the corresponding cumulative baseline hazard function. Under the proportional hazards model, the full log-likelihood function for the observed data including covariate information is, up to a constant,

$$l_F=\sum _{i=1}^n\left[{\Delta }_i\left[X_i^T\beta +\text{log}\left\{d\Lambda \left(Y_i\right)\right\}\right]-\Lambda \left(Y_i\right)\text{exp}\left(X_i^T\beta \right)+\text{log}\left\{dG\left(X_i\right)\right\}\right].$$ (1)

Following the empirical likelihood principle (Owen, 1988; Qin and Lawless, 1994), let λ_i be the jump of Λ at Y_i and p_i be the jump of G at X_i. The log-likelihood function can be rewritten as the sum of the conditional likelihood of (Y, Δ) given X (denoted as l₁) and log marginal likelihood of X (denoted as l₂), where

$$l_1=\sum _{i=1}^n{\Delta }_i\left\{X_i^T\beta +\text{log}\left({\lambda }_i\right)\right\}-n\sum _{i=1}^n{\lambda }_i{S}^{(0)}\left(Y_i,\beta \right),$$

$$l_2=\sum _{i=1}^n\text{log}\left(p_i\right),\text{and,}{S}^{(0)}(t,\beta )=n^{-1}\sum _{j=1}^{n}I\left(Y_j⩾t\right)\text{exp}\left(X_j^T\beta \right).$$

Suppose that in addition to individual-level data from the primary cohort, some aggregate information from the external resources is available. For example, the survival rates at time t* by subgroups are commonly reported using data from large population-based registries,

$$P\left(T>t^{*}\mid X\in {\Omega }_k\right)={\varphi }_k,k=1,2,\cdots ,K.$$ (2)

We want to use such external information appropriately to improve the estimating efficiency for unknown parameters for the primary cohort under the proportional hazards model.

3. Method

For the primary cohort, we define the survival rate of the subgroup Ω_k, as ${\varphi }_k^{*}$, i.e.,

$$Pr\left(T>t^{*}\mid X\in {\Omega }_k\right)={\varphi }_k^{*},k=1,\cdots ,K.$$ (3)

When integrating the aggregate information with the primary cohort, one necessary assumption for the existing methods is that the survival information should be comparable between the different resources, i.e., ${\varphi }_k^{*}={\varphi }_k$, k = 1, ⋯ , K, referred to as the comparability assumption by some authors (Huang et al., 2016). We briefly review the work of Huang et al. (2016) in Section 3.1, and then present our proposed method to accommodate the potential violation of the comparability assumption, i.e., there exists at least one k such that ${\varphi }_k^{*}\ne {\varphi }_k$, in Section 3.2.

3.1. Comparable aggregate information from external resources

Under the assumption of comparability, we review the double empirical likelihood with constrains by Huang et al. (2016). The external aggregate information only depends on parameters of β and Λ(t*). As noted in Huang et al. (2016), the Breslow-type estimator of $\widehat{\Lambda }\left(t^{*},\beta \right)$ yields biased estimation, since it involves the unknown parameter β. The solution is to introduce an additional parameter, defined as α = Λ(t*), whose sample analogue is

$$\sum _{i=1}^n{\lambda }_{i}I\left(Y_i⩽t^{*}\right)-\alpha =0.$$ (4)

Under constraint (4) and by the method of Lagrange multipliers, the objective function to be maximized is

$$\sum _{i=1}^n{\Delta }_i\left\{X_i^T\beta +\text{log}\left({\lambda }_i\right)\right\}-n\sum _{i=1}^n{\lambda }_i{S}^{(0)}\left(Y_i,\beta \right)-n\nu \left\{\sum _{i=1}^n{\lambda }_{i}I\left(Y_i⩽t^{*}\right)-\alpha \right\}.$$ (5)

Taking a derivative of (5) with respect to λ_i, and letting the derivative be 0, they have

$${\lambda }_i=\frac{{\Delta }_i}{n\left\{S^{(0)}\left(Y_i,\beta \right)+\nu I\left(Y_i⩽t^{*}\right)\right\}},$$ (6)

where ν is determined by $\sum _{i=1}^n\left[{\Delta }_{i}I\left(Y_i⩽t^{*}\right)/\left\{S^{(0)}\left(Y_i,\beta \right)+\nu I\left(Y_i⩽t^{*}\right)\right\}-\alpha \right]=0$. After plugging Equation (6) into (5), they have the double empirical log-likelihood,

$$l=\sum _{i=1}^n{\Delta }_i\left[X_i^T\beta -\text{log}\left\{S^{(0)}\left(Y_i,\beta \right)+\nu I\left(Y_i⩽t^{*}\right)\right\}\right]+n\nu \alpha +\sum _{i=1}^n\text{log}\left(p_i\right).$$ (7)

Given the external aggregate information, the estimators of β, α, and ν can be derived by maximizing the likelihood function (7) with the following constraints:

$$p_i⩾0,\sum _{i=1}^n{p}_i=1,\sum _{i=1}^n{p}_i{\Psi }_k\left(X_i;\beta ,\alpha ,{\varphi }_k\right)=0,k=1,\cdots ,K,$$ (8)

where ${\Psi }_k\left(X_i;\beta ,\alpha ,{\varphi }_k\right)=I\left(X_i\in {\Omega }_k\right)\left[\text{exp}\left\{-\alpha \text{exp}\left(X_i^T\beta \right)\right\}-{\varphi }_k\right]$. We denote the corresponding estimators of β, α, and ν here as ${\widehat{\beta }}_C$, ${\widehat{\alpha }}_C$ and ${\widehat{\nu }}_C$, respectively. Using the combined information, the baseline cumulative hazard function Λ(t) can be estimated by:

$${\widehat{\Lambda }}_C(t)=\frac{1}{n}\sum _{i=1}^n\frac{{\Delta }_{i}I\left(Y_i⩽t\right)}{S^{(0)}\left(Y_i,{\widehat{\beta }}_C\right)+{\widehat{\nu }}_{C}I\left(Y_i⩽t^{*}\right)}.$$

3.2. Potentially incomparable information from external resources

Cohorts with subjects enrolled in a single institution (e.g., MD Anderson) may not be comparable to the aggregate survival information, which is derived from a different population. Note that Equation (3) can be expressed equivalently to

$$E\left[I\left(X\in {\Omega }_k\right)\left[\text{exp}\left\{-\Lambda \left(t^{*}\right)\text{exp}\left(X^T\beta \right)\right\}-{\varphi }_k^{*}\right]\mid X\in {\Omega }_k\right]=0,k=1,\cdots ,K.$$

We introduce a K-dimensional vector parameter τ = (τ₁,·⋯ , τ_K)^T to incorporate the potential incomparable information for ${\varphi }_k^{*}:E\left\{{\Psi }_k\left(X_i;\beta ,\alpha ,{\varphi }_k\right)\mid X_i\in {\Omega }_k\right\}={\tau }_k$, for k = 1, ⋯ , K. When the information from the two resources are comparable, we have ${\tau }_k={\varphi }_k^{*}-{\varphi }_k=0$, k = 1, ⋯ , K. Otherwise, there exists at least one k such that. We need to estimate τ and identify non-zero τ_ks to adaptively combine the aggregate information from the external resources.

We propose a penalized empirical likelihood with extra constraints, which includes the log-likelihood specified in (7) and a penalty term with a tuning parameter γ on the potential differences characterized by τ,

$$l_{Pe}=l-n\sum _{k=1}^K{p}_{\gamma }\left(\left|{\tau }_k\right|\right),$$ (9)

under constraints ${\sum }_{i=1}^n{p}_i=1$, p_i ⩾ 0 and ${\sum }_{i=1}^n{p}_i\left\{{\Psi }_k\left(X_i;\beta ,\alpha ,{\varphi }_k\right)-I\left(X_i\in {\Omega }_k\right){\tau }_k\right\}=0$, for k = 1,·⋯ , K. Here, we use the smoothly clipped absolute deviation (SCAD) penalty, defined as

$$p_{\gamma }(t)=\gamma |t|I(|t|⩽\gamma )-\frac{t^2-2a\gamma |t|+{\gamma }^2}{2(a-1)}I(\gamma <|t|⩽a\gamma )+\frac{(a+1){\gamma }^2}{2}I(|t|>a\gamma ),$$

with the first derivative of

$$p_{\gamma }^{\prime }(t)=\gamma \left\{I(t⩽\gamma )+\frac{{(a\gamma -t)}_{+}}{(a-1)\gamma }I(t>\gamma )\right\},$$

where γ > 0, and the parameter a is set to be 3.7, as recommended by Fan and Li (2001). The SCAD penalty has been well studied in the literature and has many desirable properties, including continuity, sparsity, and oracle property (Fan and Li, 2001; Fan and Peng, 2004).

Denote Ψ(X_i; β, α) = (Ψ₁(X_i; β, α, ϕ₁), ⋯ , Ψ_K(X_i; β, α, ϕ_K))^T and I_i = (I(X_i ∈ Ω₁), ⋯ , I(X_i ∈ Ω_K))^T. Applying the method of Lagrange multipliers to the penalized log-likelihood, we have

$$p_i=\frac{1}{n}\times \frac{1}{1+\xi {(\beta ,\alpha ,\tau )}^T\left\{\Psi \left(X_i;\beta ,\alpha \right)-I_i○\tau \right\}},$$ (10)

where ○ is the Hadamard product and ξ(β, α, τ) is determined by

$$\frac{1}{n}\sum _{i=1}^n\frac{\Psi \left(X_i;\beta ,\alpha \right)-I_i○\tau }{1+\xi {(\beta ,\alpha ,\tau )}^T\left\{\Psi \left(X_i;\beta ,\alpha \right)-I_i○\tau \right\}}=0,$$

with a constraint 1+ξ(β, α, τ)^T{Ψ(X_i; β, α)−I_i◦τ} ⩾ 1/n to satisfy 0 ⩽ p_i ⩽ 1 for any given β, α, and τ. By substituting (10), the maximization of the log-likelihood l_Pe with the extra constraints can be achieved by maximizing the following penalized profile log-likelihood:

$$l_{Pro}(\beta ,\alpha ,\tau )=\sum _{i=1}^n{\Delta }_i\left[X_i^T\beta -\text{log}\left\{S^{(0)}\left(Y_i,\beta \right)+\nu (\beta ,\alpha ,\tau )I\left(Y_i⩽t^{*}\right)\right\}\right]+n\nu (\beta ,\alpha ,\tau )\alpha -\sum _{i=1}^n\text{log}\left[1+\xi {(\beta ,\alpha ,\tau )}^T\left\{\Psi \left(X_i;\beta ,\alpha \right)-I_i○\tau \right\}\right]-n\sum _{k=1}^K{p}_{\gamma }\left(\left|{\tau }_k\right|\right),$$ (11)

where $\nu (\beta ,\alpha ,\tau )=\frac{1}{n}{\sum }_{i=1}^n\left\{\xi {(\beta ,\alpha ,\tau )}^T\partial \Psi \left(X_i;\beta ,\alpha \right)/\partial \alpha \right\}/\left[1+\xi {(\beta ,\alpha ,\tau )}^T\left\{\Psi \left(X_i;\beta ,\alpha \right)-I_i○\tau \right\}\right]$.

To maximize (11), we design a stable and efficient algorithm based on the method of profile likelihood. For any given τ, we can apply the estimation procedure in Huang et al. (2016) to obtain the estimators $\widehat{\beta }(\tau )$, $\widehat{\alpha }(\tau )$, and $\widehat{\nu }(\tau ):=\nu (\widehat{\beta }(\tau ),\widehat{\alpha }(\tau ),\tau )$. We then maximize $l_{Pro}(\widehat{\beta }(\tau ),\widehat{\alpha }(\tau ),\widehat{\nu }(\tau ))$ to obtain the estimator $\widehat{\tau }$, and finally update all estimators by $\widehat{\beta }=\widehat{\beta }(\widehat{\tau })$, $\widehat{\alpha }=\widehat{\alpha }(\widehat{\tau })$, and $\widehat{\nu }=\widehat{\nu }(\widehat{\tau })$. Given these estimators, the cumulative baseline hazard function Λ(t) can be estimated by

$$\widehat{\Lambda }(t)=\frac{1}{n}\sum _{i=1}^n\frac{{\Delta }_{i}I\left(Y_i⩽t\right)}{S^{(0)}\left(Y_i,\widehat{\beta }\right)+\widehat{\nu }I\left(Y_i⩽t^{*}\right)}.$$

We call the proposed estimators the adaptive double empirical likelihood (ADEL) estimators from now on. In the estimating procedure, we choose the tuning parameter γ, such that it minimizes the Bayesian information criterion (BIC)-like criterion (Wang et al., 2007, 2009; Kai et al., 2011; Chen et al., 2014).

3.3. Asymptotic Properties

We establish asymptotic properties of $(\widehat{\beta },\widehat{\tau },\widehat{\Lambda })$, where true values of these parameters are denoted as (β₀, τ₀, Λ₀). Technical challenges arise due to the infinite dimension of Λ(·), as well as the variability from the estimated τ. Under the mild regularity conditions given in the online Supporting Information, we apply the empirical process techniques to prove the consistency and asymptotic normality of $\widehat{\beta }$, consistency of $\widehat{\tau }$, and weak convergence of $\widehat{\Lambda }$. We respectively summarize the asymptotic properties of estimators under two settings in which the aggregate information are comparable or incomparable with the primary cohort. The proofs of the following Theorems are found in the online Supporting Information.

Theorem 3.1:

When the external information is comparable (τ₀ = 0), under the regularity assumptions specified in the online Supporting Information, as n → ∞, $P(\widehat{\tau }=0)\to 1$; $\sqrt{n}\left(\widehat{\beta }-{\beta }_0\right)$ converges to a multivariate normal distribution with a zero mean and covariance matrix ${\Gamma }^{-1}={\left(\Sigma +\tilde{B}{\tilde{Q}}^{-1}{\tilde{B}}^T\right)}^{-1}$, where Σ⁻¹ is the asymptotic covariance matrix of the partial likelihood estimator of β; $\tilde{B}$ and $\tilde{Q}$ are defined in the online Supporting Information, and $\sqrt{n}\left\{\widehat{\Lambda }(t)-{\Lambda }_0(t)\right\}$ converges to a zero-mean Gaussian process.

Remark 1.

When τ₀ = 0, Theorem 3.1 shows that $\sqrt{n}\left(\widehat{\beta }-{\beta }_0\right)$ has the same asymptotic normal distribution as $\sqrt{n}\left({\widehat{\beta }}_C-{\beta }_0\right)$. This implies that the proposed estimator achieves the same efficiency as that by Huang et al. (2016). Similarly, at any t > 0, $\sqrt{n}\left\{\widehat{\Lambda }(t)-{\Lambda }_0(t)\right\}$ has the same asymptotic distribution as $\sqrt{n}\left\{{\widehat{\Lambda }}_C(t)-{\Lambda }_0(t)\right\}$. Hence, we do not have any efficiency loss for the estimation of Λ(·) compared with the method of Huang et al. (2016).

When the external information is incomparable with the primary cohort (τ₀ ≠ 0), let ${\tau }_0^T=\left({\tau }_{01}^T,{\tau }_{02}^T\right)$. Without loss of generality, we assume τ₀₁ ≠ 0 and τ₀₂ = 0.

Theorem 3.2:

Under the regularity assumptions specified in the online Supporting Information,, as n → ∞ ${\widehat{\tau }}_1{\to }^p{\tau }_{01}$; $P\left({\widehat{\tau }}_{02}=0\right)\to 1$; $\sqrt{n}\left(\widehat{\beta }-{\beta }_0\right)$ converges to a zero mean multivariate normal distribution with covariance matrix Γ*⁻¹ = (Σ + BQ⁻¹B^T)⁻¹, where Γ* is nonsingular, and B and Q are defined in the online Supporting Information; and $\sqrt{n}\left\{\widehat{\Lambda }(t)-{\Lambda }_0(t)\right\}$ converges to a zero-mean Gaussian process.

Remark 2.

Note that (Σ + BQ⁻¹B^T)⁻¹ ⩽ Σ⁻¹ and $B{Q}^{-1}{B}^T⩽\tilde{B}{\tilde{Q}}^{-1}{\tilde{B}}^T$. This implies Γ⁻¹ ⩽ Γ*⁻¹ ⩽ Σ⁻¹, confirming that the proposed estimator is more efficient than the partial likelihood estimator by using the primary cohort only. On the other hand, the estimating equations in Huang et al. (2016) have non-zero expectations in the presence of non-zero τ₀, thus the corresponding estimator is not consistent (Struthers and Kalbfleisch, 1986). Although the asymptotic variance of ${\widehat{\beta }}_C$ is smaller than that of $\widehat{\beta }$, the non-consistency of ${\widehat{\beta }}_C$ could bring misleading statistical inferences.

4. Simulation

We conducted simulation studies to evaluate the finite sample performance of the proposed ADEL. We further compared the performance of ADEL estimators with those of the standard Cox regression model with the partial likelihood (PL), and those of the double empirical likelihood (DEL) method by Huang et al. (2016) and its extended DEL (DEL-E) for handling a special case of the violation of the comparability assumption.

4.1. Simulation set up

For the primary cohort, we considered two covariates: X₁ was a continuous covariate following the standard normal distribution and X₂ was a binary variable with Pr(X₂ = 1) = 0.5. The survival times were generated from a Cox model with a hazard function of λ(t|X₁, X₂) = 2t exp(X₁β₁ + X₂β₂). Here, we set β₁ = −0.5 and β₂ = 0.5. The censoring times were generated from a uniform distribution with varying upper boundaries to have different censoring percentages. Sample sizes of 100 and 200 were used, and each scenario had 500 repetitions.

The aggregate information consisted of survival rates at t* = 0.5 for two subgroups classified by the covariate information: Ω₁ = {(X₁, X₂) : X₁ ⩽ 0, X₂ = 0} and Ω₂ = {(X₁, X₂) : X₁ > 0, X₂ = 0}. Under the Cox model for the primary cohort, the survival information was specified as ${\varphi }_1^{*}=Pr\left(T>t^{*}\mid X\in {\Omega }_1\right)=0.68$, and ${\varphi }_2^{*}=Pr\left(T>t^{*}\mid X\in {\Omega }_2\right)=0.84$, respectively. We considered different settings in terms of magnitudes of discrepancy, representing four realistic relationships between the primary cohort and external aggregate information.

• Setting 1. The external aggregate information were matched with those of the primary cohort, i.e., $\left({\varphi }_1,{\varphi }_2\right)=\left({\varphi }_1^{*},{\varphi }_2^{*}\right)=(0.68,0.84)$ and (τ₁, τ₂) = (0, 0).

• Setting 2. The external aggregate survival rates of the two subgroups were 0.64 and 0.88, i.e., (τ₁, τ₂) = (0.04, −0.04). Under this setting, although the aggregate survival rates of the two subgroups were not exactly comparable, the “marginal” aggregate survival rate of the subgroup X₂ = 0 was comparable (=0.76) between the primary cohort and external information.

• Setting 3. The external aggregate survival rates of the two subgroups were 0.65 and 0.81, i.e., (τ₁, τ₂) = (0.03, 0.03). In other words, the survival rates of the two subgroups in the primary cohort were higher when compared with the rates from the external resource.

• Setting 4. The external aggregate survival rates of the two subgroups were 0.62 and 0.78, i.e., (τ₁, τ₂) = (0.06, 0.06). This setting was similar to Setting 3, but with larger disparities between the primary cohort and external data.

4.2. Simulation results

In the settings of our simulation studies, we found that $\widehat{\tau }=0$ when γ >= 2. Our proposed penalized empirical likelihood became the empirical likelihood in Huang et al. (2016) when $\widehat{\tau }=0$. This implied that a reasonable range of the tuning parameter was [0, 2], otherwise the imposed penalty on τ was too large, such that $\widehat{\tau }=0$. We therefore chose the value of the tuning parameter γ by minimizing the BIC-like criterion (Wang et al., 2007, 2009; Kai et al., 2011; Chen et al., 2014) over γ ∈ [0, 2].

Tables 1–4 summarize simulation results of the estimated regression coefficients under four settings, respectively. The summary statistics are the empirical biases, empirical standard deviation (SD), estimated standard errors (SE), square root of mean squared errors (RMSE), and coverage probabilities (CP) of 95% Wald-type confidence intervals for the estimated regression coefficients β. Tables S1 and S2 in the Supporting Information show simulation results for the estimated cumulative baseline hazard function. To report the overall performance of $\widehat{\Lambda }(t)$, we used a sequence of 100 equidistant time points within the interquartile range of the simulated survival time, denoted as (t₁, ⋯ , t₁₀₀). We then summarized the mean of the estimators, standard errors, and converge probabilities over these time points, and used these statistics to compare performance of the four methods. We also calculated the empirical mean of the integrated squared error (EMISE) to summarize the accuracy and efficiency of all estimates of Λ(·) as follows: $\text{EMISE}(\widehat{\Lambda })={\sum }_{q=1}^{500}{\sum }_{l=1}^{100}\left\{{\widehat{\Lambda }}^{(q)}\left(t_l\right)-\Lambda \left(t_l\right)\right\}/50000$, where ${\widehat{\Lambda }}^{(q)}(\cdot )$ was the estimator of Λ(·) using the qth data set, for q = 1, … , 500.

Table 1.

Simulation results (all the entries are multiplied by 100) under Setting 1. PL, the standard Cox regression with the partial likelihood; DEL and DEL-E, the double empirical likelihood method and its extension by Huang et al. (2016); ADEL, the proposed adaptive double empirical likelihood method.

PC	Method	β 1						β2
		Bias	SD	SE	RMSE	CP	RE	Bias	SD	SE	RMSE	CP	RE
Sample Size=100
0%	PL	−1.27	11.09	11.56	11.15	95.4	–	1.93	21.69	21.25	21.76	95.4	–
	DEL	−0.68	4.92	4.90	4.96	95.4	0.44	−0.76	17.62	17.48	17.62	94.8	0.81
	DEL-E	−0.80	5.02	4.96	5.08	95.0	0.46	1.61	21.07	21.02	21.11	95.4	0.97
	ADEL	−1.29	9.65	8.73	9.73	95.0	0.87	0.72	18.96	18.91	18.96	94.6	0.87
15%	PL	−1.53	12.28	12.43	12.36	95.2	–	1.17	26.29	23.05	26.29	92.0	–
	DEL	−0.31	5.03	4.87	5.04	95.2	0.41	−0.95	20.33	18.72	20.33	92.4	0.77
	DEL-E	−0.38	5.07	4.91	5.08	95.2	0.41	0.72	25.95	22.80	25.93	92.0	0.99
	ADEL	−1.65	10.68	9.67	10.80	96.6	0.87	0.33	22.42	20.55	22.40	93.0	0.85
30%	PL	−1.97	13.27	13.68	13.40	95.4	–	2.11	29.04	25.44	29.08	92.2	–
	DEL	−0.32	5.09	4.94	5.10	95.0	0.38	−0.80	21.44	20.20	21.43	92.8	0.74
	DEL-E	−0.41	5.14	4.98	5.15	95.6	0.38	1.51	28.67	25.15	28.68	91.8	0.99
	ADEL	−2.04	11.34	10.90	11.51	96.6	0.86	0.84	23.35	22.81	23.34	93.8	0.80
Sample Size=200
0%	PL	−0.18	8.15	8.00	8.15	95.4	–	0.44	15.17	14.78	15.16	95.2	–
	DEL	−0.35	3.48	3.44	3.49	94.4	0.43	−1.09	12.50	12.26	12.54	95.2	0.83
	DEL-E	−0.42	3.51	3.47	3.53	94.0	0.43	0.23	14.92	14.68	14.91	94.6	0.98
	ADEL	−0.44	7.19	6.29	7.20	93.8	0.88	−0.28	13.52	13.06	13.51	94.8	0.89
15%	PL	−1.10	8.87	8.66	8.92	95.0	–	−0.76	15.84	15.99	15.84	94.2	–
	DEL	−0.39	3.53	3.51	3.55	95.0	0.40	−1.05	12.59	13.14	12.62	95.2	0.80
	DEL-E	−0.39	3.53	3.52	3.55	94.8	0.40	−1.17	15.62	15.88	15.65	95.0	0.99
	ADEL	−1.17	7.98	6.89	8.05	94.2	0.90	−0.54	13.85	14.14	13.85	95.0	0.87
30%	PL	−1.12	9.60	9.49	9.66	95.4	–	−0.71	18.11	17.59	18.11	93.6	–
	DEL	−0.37	3.60	3.56	3.61	95.8	0.37	−1.22	14.25	14.17	14.28	94.4	0.79
	DEL-E	−0.38	3.61	3.57	3.62	95.4	0.37	−1.17	17.86	17.47	17.88	93.4	0.99
	ADEL	−1.09	8.73	7.10	8.80	94.6	0.91	−0.65	15.91	15.50	15.91	94.8	0.88

Table 4.

Simulation results (all the entries are multiplied by 100) under Setting 4. PL, the standard Cox regression with the partial likelihood; DEL and DEL-E, the double empirical likelihood method and its extension by Huang et al. (2016); ADEL, the proposed adaptive double empirical likelihood method.

PC	Method	β 1						β 2
		Bias	SD	SE	RMSE	CP	RE	Bias	SD	SE	RMSE	CP	RE
Sample Size=100
0%	PL	−1.27	11.09	11.56	11.15	95.4	–	1.93	21.69	21.25	21.76	95.4	–
	DEL	7.36	4.30	4.29	8.52	55.8	0.76	−15.73	16.18	16.97	22.55	87.8	1.04
	DEL-E	6.81	4.50	4.42	8.16	59.8	0.73	0.30	20.72	20.98	20.70	96.4	0.95
	ADEL	−1.68	10.79	10.82	10.91	92.2	0.98	−3.27	19.48	20.43	19.73	95.8	0.91
15%	PL	−1.53	12.28	12.43	12.36	95.2	–	1.17	26.29	23.05	26.29	92.0	–
	DEL	7.84	4.34	4.23	8.95	51.8	0.72	−16.65	18.64	18.17	24.98	85.2	0.95
	DEL-E	7.40	4.45	4.33	8.64	56.0	0.70	−0.48	25.46	22.76	25.44	92.6	0.97
	ADEL	−2.04	11.71	11.78	11.87	93.2	0.96	−3.41	22.61	22.32	22.85	94.4	0.87
30%	PL	−1.97	13.27	13.69	13.40	95.4	–	2.11	29.04	25.44	29.08	92.2	–
	DEL	7.94	4.36	4.25	9.06	49.6	0.68	−17.62	19.67	19.62	26.40	86.6	0.91
	DEL-E	7.55	4.47	4.35	8.77	54.0	0.65	0.37	28.00	25.11	27.98	92.4	0.96
	ADEL	−2.39	12.44	13.11	12.66	95.0	0.94	−2.92	23.70	24.63	23.85	95.6	0.82
Sample Size=200
0%	PL	−0.18	8.15	8.00	8.15	95.4	–	0.44	15.17	14.78	15.16	95.2	–
	DEL	7.62	3.04	3.01	8.20	30.2	1.01	−15.91	11.44	11.90	19.60	73.0	1.29
	DEL-E	7.13	3.12	3.09	7.78	37.2	0.95	−1.05	14.57	14.65	14.60	96.0	0.96
	ADEL	−0.95	8.12	7.82	8.17	92.0	1.00	−4.12	13.78	14.48	14.37	94.8	0.95
15%	PL	−1.10	8.87	8.66	8.92	95.0	–	−0.76	15.84	15.99	15.84	94.2	–
	DEL	7.74	3.04	3.04	8.31	28.4	0.93	−16.52	11.54	12.75	20.15	78.6	1.27
	DEL-E	7.35	3.10	3.10	7.97	33.2	0.89	−2.25	15.29	15.86	15.44	95.2	0.97
	ADEL	−1.71	8.77	8.42	8.93	91.8	1.00	−4.88	14.15	15.57	14.95	94.4	0.94
30%	PL	−1.12	9.60	9.49	9.66	95.4	–	−0.71	18.11	17.59	18.11	93.6	–
	DEL	7.88	3.09	3.06	8.46	26.2	0.88	−17.70	13.14	13.76	22.04	78.4	1.22
	DEL-E	7.53	3.14	3.12	8.15	30.2	0.84	−2.18	17.51	17.45	17.63	94.8	0.97
	ADEL	−1.79	9.37	9.20	9.53	92.6	0.99	−4.92	16.08	17.12	16.80	94.6	0.93

Under Setting 1, all four methods performed well and the empirical biases of the four estimates were negligible. The censoring degree did not affect the estimation bias much, but increased the estimation variation of all four methods. Since the external information was the same as survival probabilities of the primary cohort, the DEL estimators had the smallest SDs and RMSEs, as expected. Although the proposed method posed two additional parameters to account for the potential disparities between the primary cohort and external information, it was more efficient than the PL method, with smaller SDs and RMSEs. The estimated standard errors agreed well with the standard deviations, and the coverage probabilities were close to the nominal value. These observations confirm that the analytical variance estimation procedure can capture the true variation of the estimation procedure.

Under Setting 2, the external aggregate survival rates of the two subgroups (Ω₁ and Ω₂) did not match well with those of the primary cohort (τ₁, τ₂) = (0.04, −0.04). The proposed method still performed well in terms of estimating the regression coefficients β and Λ(t). The DEL and DEL-E methods produced larger biases for both the estimated β and Λ(t), due to incorporating incomparable external information without any adjustment. For example, the biases of the regression coefficient corresponding to X₁ were at least three times larger than the related standard deviations, regardless of the censoring percentages, which could lead to misleading inferences with < 5% coverage probabilities. As noted, despite the discrepancy between the primary cohort and external information within the subgroups Ω₁ and Ω₂, the marginal survival rate of the subgroup X₂ = 0 was comparable (=0.76). As shown in Table 2, the biases of ${\widehat{\beta }}_2$ related to the covariate X₂ by the DEL and DEL-E methods were smaller compared with those of ${\widehat{\beta }}_1$. Due to the same reason, the efficiency gain of our proposed estimators over the PL method for β₂ was larger than that for β₁.

Table 2.

Simulation results (all the entries are multiplied by 100) under setting 2. PL, the standard Cox regression with the partial likelihood; DEL and DEL-E, the double empirical likelihood method and its extension by Huang et al. (2016); ADEL, the proposed adaptive double empirical likelihood method.

PC	Method	β 1						β2
		Bias	SD	SE	RMSE	CP	RE	Bias	SD	SE	RMSE	CP	RE
Sample Size=100
0%	PL	−1.27	11.09	11.56	11.15	95.4	–	1.93	21.69	21.25	21.76	95.4	–
	DEL	−21.30	6.34	5.94	22.22	3.0	1.99	3.28	19.25	17.72	19.51	92.6	0.90
	DEL-E	−21.45	6.48	6.09	22.40	4.0	2.01	5.34	22.74	21.15	23.34	93.2	1.07
	ADEL	−2.80	10.92	11.04	11.26	93.0	1.01	1.17	19.29	20.21	19.30	95.6	0.89
15%	PL	−1.53	12.28	12.43	12.36	95.2	–	1.17	26.29	23.05	26.29	92.0	–
	DEL	−21.90	6.70	6.09	22.90	4.2	1.85	2.62	22.31	19.00	22.44	90.4	0.85
	DEL-E	−21.98	6.71	6.23	22.98	4.8	1.86	4.25	27.97	22.96	28.27	88.6	1.08
	ADEL	−2.70	11.81	12.06	12.10	93.2	0.98	1.49	22.70	21.86	22.73	94.0	0.86
30%	PL	−1.97	13.27	13.68	13.40	95.4	–	2.11	29.04	25.44	29.08	92.2	–
	DEL	−22.83	6.94	6.35	23.86	3.6	1.78	2.46	23.72	20.52	23.82	89.8	0.82
	DEL-E	−22.98	6.97	6.49	24.02	4.2	1.79	4.99	31.03	25.33	31.40	89.2	1.08
	ADEL	−3.01	12.35	12.90	12.70	92.0	0.95	1.99	23.87	23.96	23.93	95.6	0.82
Sample Size=200
0%	PL	−0.18	8.15	8.00	8.15	95.4	–	0.44	15.17	14.78	15.16	95.2	–
	DEL	−20.57	4.61	4.23	21.07	0.2	2.59	3.13	13.80	12.44	14.14	91.8	0.93
	DEL-E	−20.60	4.72	4.33	21.12	0.6	2.59	3.87	16.42	14.75	16.86	92.2	1.11
	ADEL	−1.34	8.41	7.86	8.51	93.0	1.04	0.84	13.80	14.34	13.81	95.6	0.91
15%	PL	−1.10	8.87	8.66	8.92	95.0	–	−0.76	15.84	15.99	15.84	94.2	–
	DEL	−21.59	4.82	4.43	22.11	0.4	2.48	2.49	13.92	13.35	14.13	93.6	0.89
	DEL-E	−21.49	4.83	4.53	22.02	0.4	2.47	1.95	17.18	15.95	17.27	91.8	1.09
	ADEL	−2.33	8.85	8.48	9.15	92.4	1.03	0.31	14.23	15.14	14.22	95.6	0.90
30%	PL	−1.12	9.60	9.49	9.66	95.4	–	−0.71	18.11	17.59	18.11	93.6	–
	DEL	−22.50	4.97	4.61	23.04	0.4	2.39	1.94	15.62	14.40	15.73	92.2	0.87
	DEL-E	−22.46	5.00	4.71	23.01	0.4	2.38	1.82	19.50	17.55	19.56	90.4	1.08
	ADEL	−2.09	9.38	9.33	9.60	94.2	0.99	0.24	16.10	16.99	16.09	95.2	0.89

Under Setting 3, although there was discrepancy in the survival rates between the external resources and the primary cohort (τ₁, τ₂) = (0.03, 0.03), the proposed method could adaptively determine the degree of information integration, resulting in reasonable estimators and inference results. In contrast, the biases of the DEL and DEL-E estimators were not ignorable, and they did not decrease with increasing sample sizes. With more discrepant information between the external resources and primary cohort (Setting 4), the proposed method still had comparable performance with the PL method, while the DEL and DEL-E estimators again had substantial biases that could lead to misleading conclusions.

We also conducted simulation studies to evaluate the finite sample performance of the proposed method when the external aggregate survival rate P(T > t*|X₂ = 0) was comparable with the primary cohort, but P(T > t*|X₂ = 1) was not, i.e., (τ₁, τ₂) = (0, 0.06). Table S3 in the online Supporting Information summarizes the simulation results. Under this setting, our proposed method was more efficient than the standard Cox regression (PL), and had smaller estimation biases and more accurate inference conclusions than DEL and its extension (DEL-E) by Huang et al. (2016).

Note that the DEL-E method is proposed to handle a special case of the violation of the comparability assumption. Specifically, the hazard function of the external survival data is assumed to follow a Cox model λ(t|x) = λ*(t) exp(x^Tβ). The survival difference between the two resources is assumed to be caused by different baseline hazard functions via a constant ρ, i.e., λ*(t) = ρλ(t). In contrast to this special case, our proposed method considers a more general scenario without imposing such model assumptions. Under Settings 2–4, the information discrepancy did not follow the specific model required by the DEL-E method. Therefore, the DEL and DEL-E methods had similar performance, although DEL-E slightly outperformed the DEL method.

Figure 1 displays the means of estimated cumulative baseline hazard functions with 95% empirical confidence intervals by the aforementioned four methods for Setting 2. As expected, the proposed method outperformed the PL method with narrower confidence intervals, although both can capture the true cumulative baseline hazard curve with negligible biases. It was not surprising that the DEL method estimated curve was biased, underestimating the risk of developing the event of interest. This was due to the incomparable information between different resources. We observed the same pattern in the estimated cumulative baseline hazard functions under Settings 3 and 4.

Figure 1:

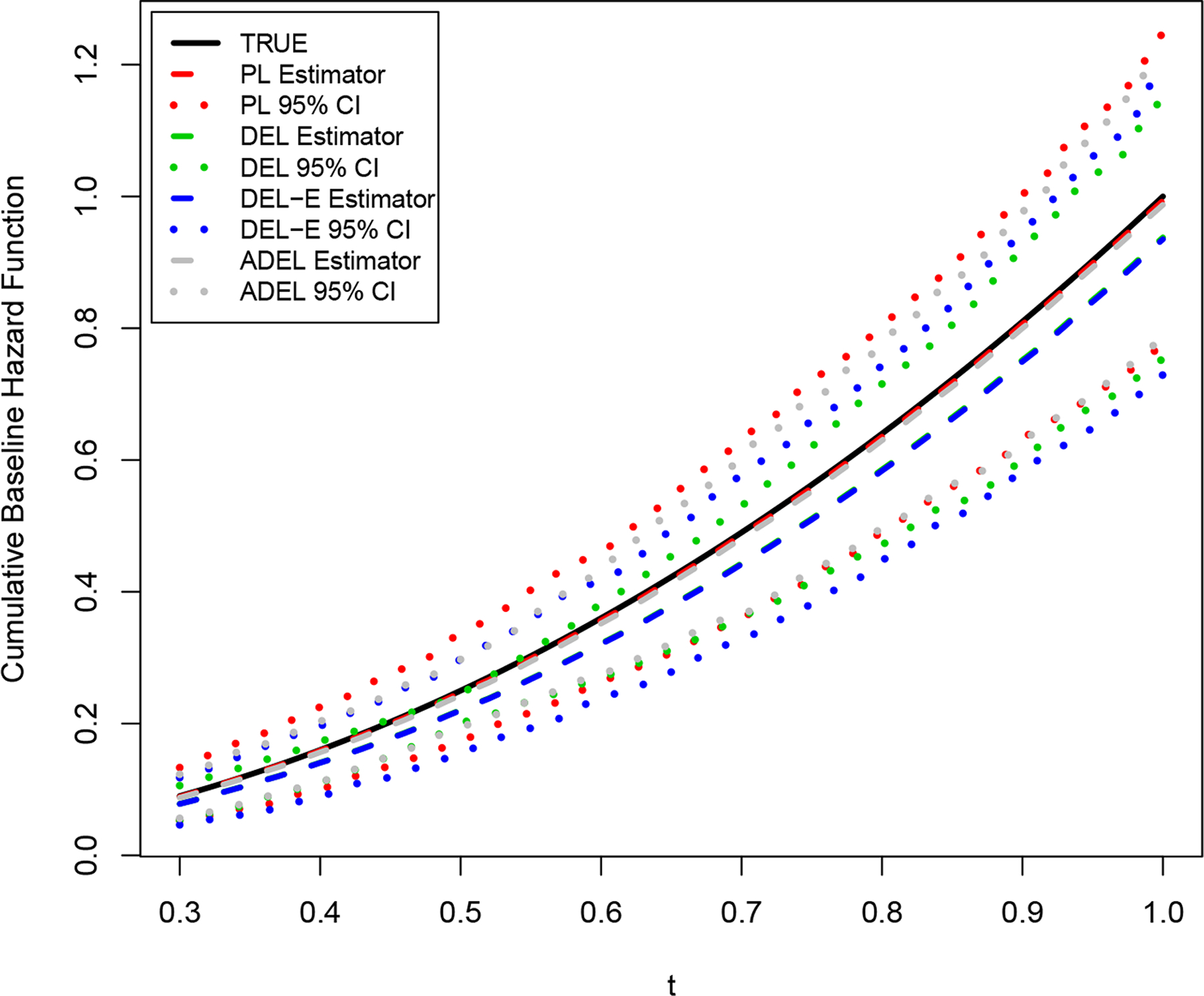
Estimated cumulative baseline hazard functions under Setting 2 with a sample size of n = 200: true curve (black solid), estimated curve (gray dashed) with 95% confidence intervals (CIs) (gray dotted) by the proposed method, estimated curve (red dashed) with 95% CIs (red dotted) by PL method, estimated curve (green dashed) with 95% CIs (green dotted) by DEL method, and estimated curve (blue dashed) with 95% CIs (blue dotted) by DEL-E method.

We further calculated the relative efficiency (RE) of the three methods compared with the PL method, defined as the RMSE from each of the three methods divided by that of the PL method, respectively. In general, the REs of the proposed method were less than one, supporting the systemic efficiency gain regardless of whether the external information was comparable or not to the primary cohort. With an increase in the sample size of the primary cohort, the REs of the proposed method increased and the efficiency gains via integrating the external information decreased, as expected.

5. Application

5.1. IBC data cohort and aggregate survival information

IBC is a rare but aggressive form of breast cancer that accounts for < 5% of all breast cancer diagnoses (Rueth et al., 2014). Although the use of the recommended therapy, trimodality treatment, has shown a survival advantage for the IBC patients, there is limited research to reveal how the molecular biology of IBC tumors might be associated with the trimodality treatment effects.

Ki-67, one of tumor cell proliferation markers, has received increasing attention in the precision treatment for breast cancer patients. The evaluation of Ki-67 has been integrated into emerging prognostic tools, such as the Immunohistochemical 4 score for predicting disease recurrence in early breast cancer (Lakhanpal et al., 2016). We analyzed the IBC cohort data from the Morgan Welch Inflammatory Breast Cancer Research Program and Clinic at MD Anderson. We focused on a cohort of patients who had been diagnosed with non-metastatic IBC between 1992 and 2012, with a median follow-up of 5.17 years and a censoring rate of 58%. After excluding patients who had missing information regarding the Ki-67 status of their tumor, our cohort included 257 IBC patients.

NCDB is a collaborative effort of the American College of Surgeons, the American Cancer Society, and the Commission on Cancer. NCDB collects patient demographics, treatments and survival data from hospitals across the USA (Raval et al., 2009). The aggregate survival information of IBC patients has been reported using NCDB data. In the paper by Rueth et al. (2014), the authors identified a cohort of 10,197 patients with non-metastatic IBC diagnosed from 1998 to 2010, and evaluated the impact of trimodality treatment on survival. Although this NCDB cohort had a much larger sample size than that of the MD Anderson cohort, it did not capture detailed information on tumor markers such as Ki-67. Hence, it is not possible to only rely on NCDB data to investigate the prognostic or predictive value of Ki-67 on IBC patients.

Our goal is to combine the MD Anderson IBC cohort (primary cohort) with the external aggregate information from NCDB. As reported by Rueth et al. (2014), the 5-year survival rates among IBC patients with and without the use of trimodality treatment were 0.554 and 0.401, respectively. As noted, there is a potential referral bias for large cancer centers, such as MD Anderson, and it is unlikely that IBC patients treated at MD Anderson will represent IBC patients within USA (Al-Hasan et al., 2011). Accordingly, we should not directly use aggregate information from NCDB under the comparability assumption to improve the estimating efficiency.

5.2. Analysis results

We fitted a Cox model on the overall survival by including the Ki-67 status (negative vs. positive), the use of trimodality treatment, and the interaction term of Ki-67 status and trimodality treatment. The same strategy applied in the simulation studies was used to identify the value of the tuning parameter in the IBC data. Specifically, we first identified a possible range for the turning parameter and then used a finer grid search for the minimizer of BIC-like criterion within the range. Table 5 shows the estimated regression coefficients and cumulative baseline hazard functions at 3 years and 5 years with their standard errors and p-values from Wald-type tests.

Table 5.

Analysis results of the inflammatory breast cancer study.

	Treatment	Ki67	Treatment*Ki67	Treatment*Ki67+Treatment	Λ(3)	Λ(5)
Standard Cox regression with the partial likelihood (PL)
Estimate	0.282	1.516	−1.299	−1.017	0.249	0.383
Standard error	0.641	0.607	0.679	0.228	0.155	0.237
Wald p-value	0.660	0.013	0.056	<0.001
Double empirical likelihood (DEL)
Estimate	0.744	1.628	−1.417	−0.673	0.157	0.235
Standard error	0.629	0.659	0.725	0.127	0.102	0.155
Wald p-value	0.236	0.014	0.051	<0.001
Extended Double empirical likelihood (DEL-E)
Estimate	0.701	1.587	−1.355	−0.653	0.177	0.271
Standard error	0.622	0.645	0.712	0.118	0.136	0.208
Wald p-value	0.260	0.014	0.057	<0.001
Adaptive double empirical likelihood (ADEL)
Estimate	0.369	1.552	−1.341	−0.972	0.224	0.342
Standard error	0.646	0.620	0.690	0.210	0.137	0.210
Wald p-value	0.568	0.012	0.052	<0.001

All four methods resulted in similar overall conclusions: the IBC patients with positive Ki-67 status had the highest risk of death and the effect of trimodality treatment differed by Ki-67 status. The trimodality treatment significantly improved the overall survival for patients with positive Ki-67 status, but showed little benefit for patients with negative Ki-67 status. Specifically, by the proposed method, the log hazard ratio of the use of trimodality treatment was −0.972 (standard error = 0.210, p-value <0.001) for IBC patients with positive Ki-67 status, and was 0.369 (standard error = 0.646, p-value = 0.568) for IBC patients with negative Ki-67 status. However, the magnitudes of the treatment effects estimated by the DEL and DEL-E methods were substantially larger than those by the other two methods, suggesting the potential incomparability on the external information against the primary cohort. The estimated values of τ₁ and τ₂ by our proposed method were −0.1125 and 0. Specifically, the 5-year survival rate of IBC patients without receiving the trimodality treatment at MD Anderson was lower than that of the NCDB cohort, although the 5-year survival rates of IBC patients receiving the trimodality treatment were comparable between the two resources. This observation is not surprising, because MD Anderson treated many referred IBC patients, who had received their initial treatment elsewhere, which may not be the standard recommended therapy.

For the cumulative baseline hazard function (see Figure 2), by adaptively incorporating external survival information, the proposed method had similar point estimates, but narrower confidence intervals compared with the PL method. On the other hand, the baseline hazard functions estimated by the DEL and DEL-E methods showed a substantial underestimation compared to that from the standard PL method, due to ignoring the incomparability on the survival information.

Figure 2:

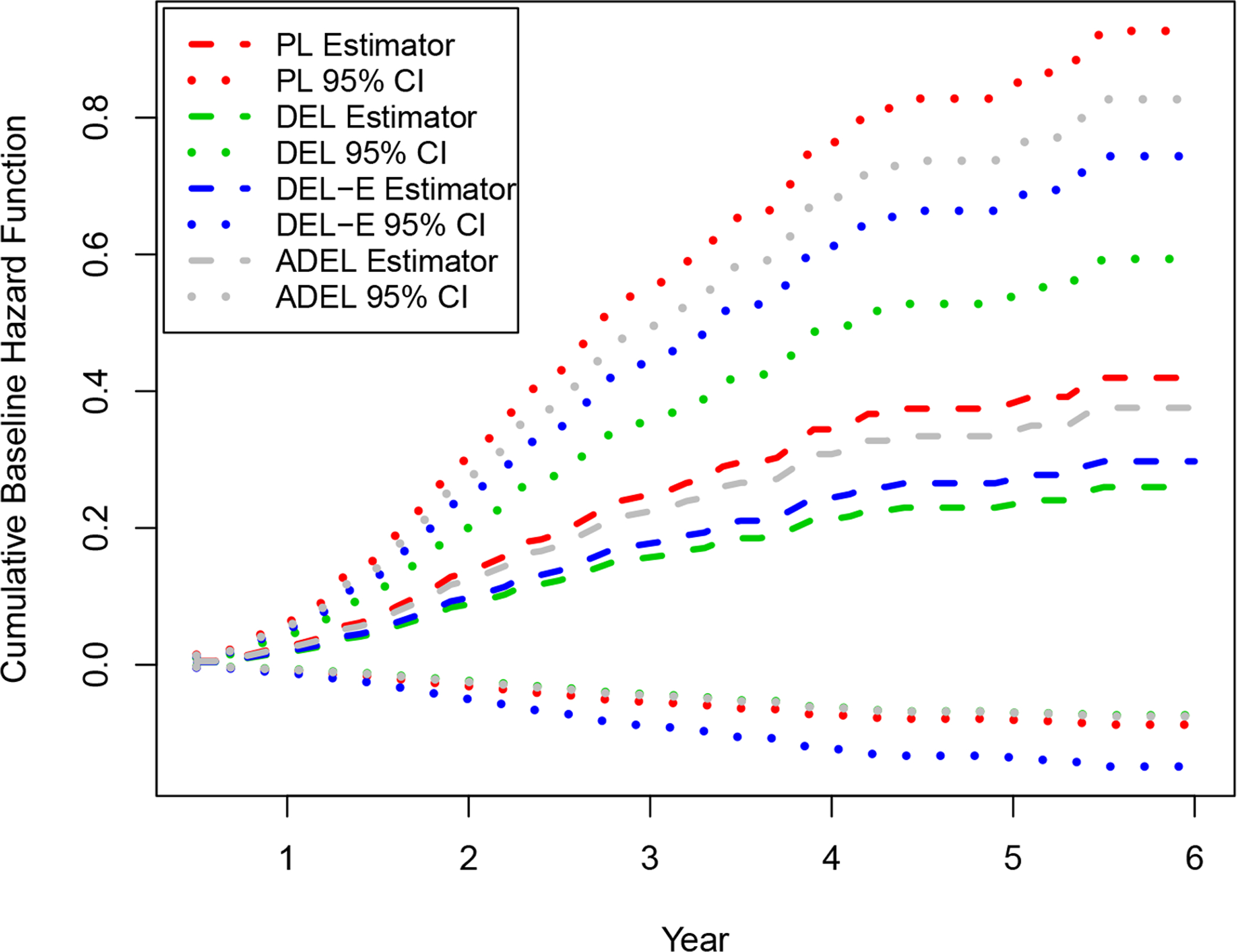
The estimated cumulative baseline hazard function Λ(t) of the inflammatory breast cancer study.

6. Discussion

We have proposed a penalized empirical likelihood approach to accommodate the potential discrepancy between the primary cohort data and external aggregate information, when combining the two resources for efficiency improvement. The primary cohort with detailed tumor information is the target population of interest (e.g., IBC patients at MD Anderson), and the primary purpose is to evaluate the treatment effects by tumor subtype for hypothesis generating. The large population-based databases unfortunately do not capture detailed tumor biology information, such as tumor cell proliferation markers. Therefore, the propensity-score based approaches cannot be directly applied here to improve statistical efficiency. Developing personalized medicines is a long journey. If the treatment heterogeneity by tumor subtype can be pinpointed by combining the primary cohort (an observation study) and large population-based databases, confirmation of such findings would require further evaluation through randomized clinical trials (RCTs). Then evaluating the results observed from the RCTs in the general patient population, represented by large population-based databases such as NCDB, would be the next step to advise the clinical practice. Our work is focused on the first step of the process.

The proposed penalized likelihood allows us to determine the degree of information borrowing from the external resources by making use of the parameter τ_k and the penalty function. Although the value of τ_k may not be a rigorous indicator for measuring comparability, the proposed method is to use such a modeling structure to adaptively adjust the utility of the external ancillary information, regardless of whether they are comparable or not to the primary cohort.

Although we have assumed the Cox regression model for the primary cohort, due to its popularity in survival analysis, the proposed estimation and inference method can be readily extended to other types of semiparametric models, such as the proportional odds model and accelerated failure time model. We have focused on the scenario in which the external information is aggregate survival rates at a single time point. In practice, aggregate survival information may be available at multiple time points (e.g., 1-year and 3-year survival rates). The proposed method can be readily generalized to accommodate such information. Please see online Supporting Information for more details.

In our data application, the external survival rates obtained from NCDB had a negligible variation, and thus they can be integrated as estimating constraints in the likelihood. However, in other applications, such information may be estimated with non-negligible uncertainties from an external dataset. The proposed method is not directly applicable for such a case. Developing rigorous tools that account for the uncertainty of the aggregate information in the estimation and inference procedures is beyond the scope of this paper, though worthy of future research.

Table 3.

Simulation results (all the entries are multiplied by 100) under setting 3. PL, the standard Cox regression with the partial likelihood; DEL and DEL-E, the double empirical likelihood method and its extension by Huang et al. (2016); ADEL, the proposed adaptive double empirical likelihood method.

PC	Method	β 1						β 2
		Bias	SD	SE	RMSE	CP	RE	Bias	SD	SE	RMSE	CP	RE
Sample Size=100
0%	PL	−1.27	11.09	11.56	11.15	95.4	–	1.93	21.69	21.25	21.76	95.4	–
	DEL	3.79	4.58	4.57	5.94	79.4	0.53	−8.54	16.84	17.20	18.86	94.2	0.87
	DEL-E	3.40	4.74	4.67	5.83	81.4	0.52	0.88	20.86	21.00	20.86	96.2	0.96
	ADEL	−1.06	10.17	9.94	10.21	92.8	0.92	−1.25	18.75	19.69	18.77	95.8	0.86
15%	PL	−1.53	12.28	12.43	12.36	95.2	–	1.17	26.29	23.05	26.29	92.0	–
	DEL	4.23	4.65	4.52	6.28	77.0	0.51	−9.11	19.41	18.42	21.42	92.4	0.81
	DEL-E	3.93	4.73	4.60	6.15	78.2	0.50	0.05	25.67	22.78	25.64	92.2	0.98
	ADEL	−1.62	11.47	11.01	11.57	93.2	0.94	−1.62	22.23	21.44	22.27	95.0	0.85
30%	PL	−1.97	13.27	13.69	13.40	95.4	–	2.11	29.04	25.44	29.08	92.2	–
	DEL	4.29	4.69	4.57	6.36	76.2	0.47	−9.52	20.49	19.88	22.58	92.6	0.78
	DEL-E	4.02	4.77	4.64	6.23	78.2	0.46	0.86	28.35	25.12	28.33	92.4	0.97
	ADEL	−1.95	12.08	12.22	12.23	94.4	0.91	−0.85	23.50	23.66	23.49	95.4	0.81
Sample Size=200
0%	PL	−0.18	8.15	8.00	8.15	95.4	–	0.44	15.17	14.78	15.16	95.2	–
	DEL	4.07	3.24	3.21	5.20	70.6	0.64	−8.79	11.92	12.06	14.80	91.2	0.98
	DEL-E	3.75	3.30	3.26	4.99	73.6	0.61	−0.48	14.72	14.66	14.71	95.8	0.97
	ADEL	−0.57	7.89	7.54	7.90	93.0	0.97	−1.98	13.59	14.11	13.72	95.4	0.91
15%	PL	−1.10	8.87	8.66	8.92	95.0	–	−0.76	15.84	15.99	15.84	94.2	–
	DEL	4.14	3.26	3.26	5.27	72.2	0.59	−9.09	12.01	12.93	15.05	90.8	0.95
	DEL-E	3.89	3.29	3.30	5.10	75.4	0.57	−1.77	15.42	15.87	15.51	94.6	0.98
	ADEL	−1.12	8.31	7.74	8.38	92.2	0.94	−2.82	13.95	14.89	14.21	95.2	0.90
30%	PL	−1.12	9.60	9.49	9.66	95.4	–	−0.71	18.11	17.59	18.11	93.6	–
	DEL	4.23	3.32	3.29	5.37	71.2	0.56	−9.79	13.64	13.95	16.78	89.0	0.93
	DEL-E	4.01	3.35	3.33	5.22	74.4	0.54	−1.73	17.65	17.46	17.72	94.6	0.98
	ADEL	−1.12	9.03	8.57	9.09	92.4	0.94	−2.75	15.83	16.38	16.05	95.4	0.89