Acoustic cavities in 2D heterostructures

Abstract

Two-dimensional (2D) materials offer unique opportunities in engineering the ultrafast spatiotemporal response of composite nanomechanical structures. In this work, we report on high frequency, high quality factor (Q) 2D acoustic cavities operating in the 50–600 GHz frequency (f) range with f × Q up to 1 × 10¹⁴. Monolayer steps and material interfaces expand cavity functionality, as demonstrated by building adjacent cavities that are isolated or strongly-coupled, as well as a frequency comb generator in MoS₂/h-BN systems. Energy dissipation measurements in 2D cavities are compared with attenuation derived from phonon-phonon scattering rates calculated using a fully microscopic ab initio approach. Phonon lifetime calculations extended to low frequencies (<1 THz) and combined with sound propagation analysis in ultrathin plates provide a framework for designing acoustic cavities that approach their fundamental performance limit. These results provide a pathway for developing platforms employing phonon-based signal processing and for exploring the quantum nature of phonons.

Here, authors report on acoustic cavities in 2D materials operating in the 50–600 GHz range and show that quality factors approach the limit set by lattice anharmonicity. Functionality expanded by heterogeneities (steps and interfaces) is demonstrated through coupled cavities and frequency comb generation.

Introduction

Acoustic cavities capable of providing spatial confinement for high frequency (1–10 GHz) elastic waves embody a vital part of optomechanical signal processing^1–6. The ongoing search for implementations of high quality factor (Q) acoustic cavities operating in the extremely high frequency range (EHF, 30–300 GHz) is strongly motivated by the promise that nanomechanical devices invoking quantum behavior^1,2,7,8 will allow for an extended temperature range suitable for reaching zero-point motion. Coupling EHF mechanical strain to an embedded nanoscale quantum system (e.g., quantum emitter)^9–11 is another area where the extended frequency range may enable devices suitable for interfacing phonons with two-level systems. However, the low phonon speed that is advantageous for 1–10 GHz devices³ (and is much celebrated for enabling small device footprints), becomes a challenge as the operational frequency exceeds ~100 GHz. In this frequency regime, the longitudinal phonon wavelength enters the nanometer size range and the critical dimensions fall beyond the limits of electron-beam-based microfabrication methods, thus necessitating a different approach in cavity design.

Two-dimensional (2D) materials enable the fabrication of single-crystal, suspended mechanical structures as thin as a single monolayer and represent a promising platform for confining EHF longitudinal acoustic (LA) phonons where free surfaces are utilized as acoustic mirrors. The ultrafast mechanical response of transition metal dichalcogenide (TMD) films was shown to include coherent LA phonons in the frequency range extending up to 1 THz^12–15 as the film thicknesses decrease to a few monolayers. The mismatch in acoustic impedance between clamped exfoliated layers and their underlying substrate allow for trapping of optically-generated elastic waves with quality factors on the order of Q ≈5 at frequencies up to 200 GHz^12,14,15. Significantly longer lifetimes for LA phonons (τ_ph = 0.36 ns at 100 GHz) were reported for suspended MoSe₂ films where radiative acoustic losses were excluded¹³. The corresponding improvement in quality factor (Q_{MoSe2 at 100GHz} ≈ 100) puts 2D material-based cavities on a par with implementations based on acoustic distributed Bragg reflectors (DBR) grown by molecular beam epitaxy (MBE) in systems like GaAs/AlGaAs^16–18. A drastic reduction in cavity modal volume intrinsic to suspended 2D devices represents a significant advantage over DBR cavity implementations, where limited acoustic contrast attainable for MBE-compatible materials (e.g., Z_GaAs/Z_AlAs = 1.2) causes the elastic strain to extend over 10–20 acoustic wavelengths, even for fine-tuned DBRs (e.g., ref. ¹⁹). In view of these developments, the fundamental factors that define the highest Q-values attainable in 2D-based acoustic cavities become of prime importance, as well as the prospects of engineering the ultrafast mechanical response of composite 2D devices in order to extend acoustic cavity functionality.

In this work, we present an experimental study and theoretical analysis of LA phonon lifetimes in MoS₂ and h-BN that are chosen as an exemplary set of 2D materials with distinct optomechanical properties. We demonstrate that at room temperature (RT), LA phonon lifetimes attainable in MoS₂-based EHF acoustic cavities (τ_MoS2 ≈ 2 ns at 100 GHz, Q ≈ 600) are the highest reported to date for 2D materials and provide a comparison with h-BN based cavities (τ_hBN ≈ 0.2 ns). The high spectral purity of MoS₂ devices allows us to study the effects of a unique structural feature for layered materials —monolayer steps—introduced in cavities as a functionality-enabling heterogeneity. We demonstrate laterally-abutted, step-detuned 2D acoustic cavities that behave independently, while being simultaneously accessible for optical excitation and readout. In compound laminar structures, where the heterogeneity is implemented as a MoS₂/h-BN interface, we exploit cross-plane strain patterns to build a frequency comb generator with nine overtones in the frequency range extending up to 300 GHz. This concept is further extended to a tri-layer MoS₂/h-BN/MoS₂ structure, where we show that the acoustic spectrum of the laminar structure is related to vibrational modes of two vertically stacked MoS₂ cavities coupled through a more compliant thin h-BN layer. An estimate for the coupling strength of Γ = 47 GHz greatly exceeds the linewidth of the cavity and indicates strong coupling, which offers opportunities in phonon-based signal processing. Finally, the anharmonicity-limited acoustic phonon lifetimes in these systems are evaluated using first-principles density functional theory (DFT) calculations. Given the highly anisotropic nature of 2D materials and the fact that the period of mechanical vibrations of interest is commensurate with the lifetimes of thermal phonons at RT (ωτ_th ≈ 1), our atomistic approach provides higher confidence in assessing the fundamental loss contributions in these systems. We use quantum perturbation theory, i.e., Fermi’s golden rule, to determine phonon–phonon scattering rates in which the phonon dispersions and the scattering interactions between phonons are obtained from DFT. These calculations highlight the difference in EHF LA phonon lifetimes between MoS₂ and h-BN and are in good agreement with measurements, indicating that the performance of RT 2D acoustic cavities in the 100–200 GHz frequency range approaches the fundamental limit.

Results

Experimental approach

The acoustic structures examined here were assembled using a rapidly developing set of fabrication tools^20–22 that enable the formation of 2D laminates with material quality comparable to MBE films, while alleviating the restrictions intrinsic to MBE (e.g., lattice matching, thermal expansion). MoS₂ and MoS₂/h-BN structures were prepared using either one-step direct mechanical exfoliation or sequential stamping and transfer of flakes onto gold-coated substrates with pre-etched wells (see Fig. 1a, METHODS, and Supplementary Figs. 1, 2).

Fig. 1. Mechanical response of acoustic cavities implemented as suspended 2D films.

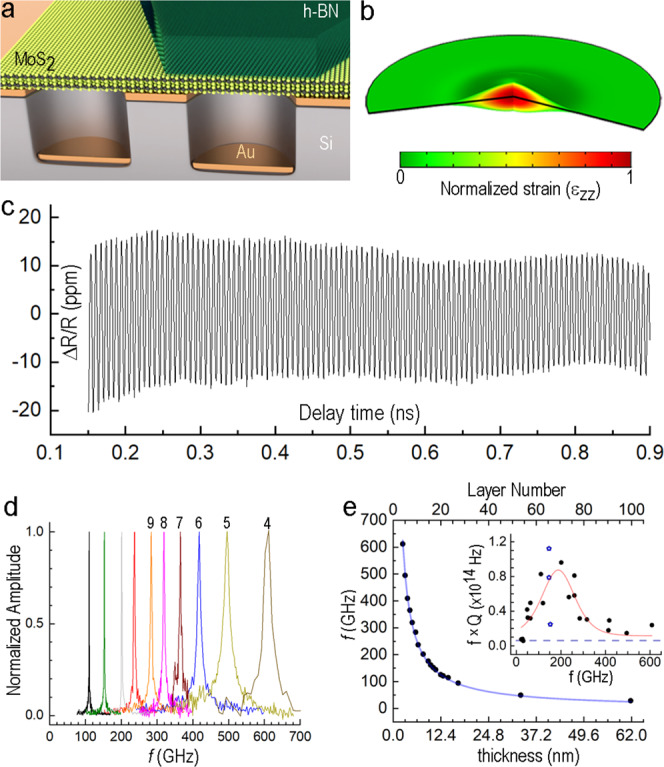
a Schematic showing MoS₂ and MoS₂/h-BN films on a Ti/Au-coated substrate with pre-etched circular wells. b Snapshot of the normalized ε_ZZ mechanical strain (color coded) in the vibrating part of the MoS₂ suspended plate as predicted by time-dependent FEM analysis. The pump beam is modeled as Gaussian with radius 0.5 μm. The part of the plate included in the model is limited by the radius 2 μm with low-reflecting outer boundaries. c Time-dependent reflectivity of a suspended MoS₂ film, shown for delay time between 0.15 and 0.9 ns in parts per million (ppm). d Examples of normalized FFT spectra of the time-dependent reflectivity taken from different MoS₂ cavities. The high frequency peaks are labeled with the corresponding MoS₂ film thicknesses in layer number as extracted from Raman spectroscopy data (see frequency vs. layer number dependence in Supplementary Fig. 2). The peaks are displayed in different colors to help readability. e Frequency versus layer number for a range of MoS₂ acoustic cavities. (inset) f × Q of MoS₂ cavities as a function of frequency. The dashed line shows the value required for ground state cooling (6 × 10¹² Hz). The red curve is added as a guide-to-the-eye and was obtained as a fit using a logistic distribution. Variability in f × Q values for different cavities in the vicinity of 150 GHz is illustrated by the blue star points with f × Q_average = 0.7 × 10¹⁴.

An ultrafast near infrared (NIR) optical pump-probe setup with spatial resolution of about 1 μm was used to evaluate the local, time-resolved mechanical response of the suspended structures. We refer to the portions of the 2D structures undergoing optically-generated thickness-mode vibrations as “acoustic cavities,” and consider these as an extension of the trapped energy resonator concept²³. Given the semiconducting nature of MoS₂, the deformation potential is likely to be the dominant mechanism for generating optically-induced elastic strain^24,25. The large penetration depth for the pump laser (770 nm) in MoS₂ ensures uniform excitation and thus homogeneous initial stress along the normal component. Optical readout for the mechanical response is provided by delayed probe pulse (830 nm wavelength), as its reflectivity is modulated by both film dilation (Fig. 1b) and photoelastic effects^26,27, also magnified by interferometric effects via a Fabry–Perot optical cavity (see METHODS). Finite element modeling (FEM)²⁸ was used to analyze and to interpret the outcome of pump-probe experiments. Calculations fully account for the anisotropy of bulk TMD materials and h-BN. In accord with Greener et al.¹⁵, continuum elasticity-based models were consistent with the experimental results in the sub-THz frequency range.

MoS₂ acoustic cavities

The normalized reflectivity (ΔR/R) of a suspended MoS₂ film, after subtracting a slowly varying background, is shown in Fig. 1c as a function of delay time between the pump and probe laser pulses (raw data is shown in Supplementary Fig. 3). A pronounced modulation is attributed to the thickness-mode vibrations since the single peak in the FFT spectrum (e.g., Fig. 1d) matches the expected resonance frequency for a sound wave where a half-wavelength fits across the film thickness (146.25 GHz for the 18-layer (18 L), 11.2 nm film in Fig. 1c). The variation of the FFT spectra with the film thickness measured in number of monolayers N (0.62 nm per layer for MoS₂²⁹) is shown in Fig. 1e and follows the expected trend of f ∼N⁻¹ (see for example ref. ¹³). Fitting the data in Fig. 1e provides an average value for the cross-plane LA sound speed c_LA = 3170 m/s in our MoS₂ films.

The slow decay of the pump-induced vibrations (Fig. 1c) indicates minimal energy losses and highlights a low internal friction of crystalline MoS₂, as well as negligible “phonon leaking” (caused by lateral spreading of pump-driven elastic excitations) in the 100 GHz-range TMD cavities. A ring-down time of τ ≈ 1.6 ns that is extracted via fitting an exponentially-decaying time dependence to the vibrational amplitude in Fig. 1c corresponds to a cavity quality factor Q = 730 at f  = 146.25 GHz. For this cavity, the resulting f × Q = 1.1 × 10¹⁴ Hz is the highest measured in our experiments and also the highest reported to date for a 2D material system (to our knowledge). The physical mechanisms that define the fundamental limits attainable for Q values (i.e., phonon lifetimes) in different 2D materials will be discussed below. While differences in the performance of individual cavities can be 5× (attributed to variability in manual exfoliation), the f × Q product for our MoS₂ devices remains at or above that required for ground state laser cooling (f × Q = 6 × 10¹² Hz)³⁰. Figure 1d, e inset highlight the frequency dependence of energy losses and suggest that the 100–200 GHz frequency range is favorable for maximizing the f  × Q product in this measurement geometry at RT. Therefore, we focus on the corresponding range in film layer number, centered at about 10 nm (N ~16 layers), and demonstrate that the layered nature of 2D materials enables introduction of well-controlled heterogeneities that can alter the underlying elastic-strain patterns and expand cavity functionality by modifying the ultrafast mechanical response.

Step-detuned cavities in MoS₂

Toward the goal of employing heterogeneities as acoustic tools, we consider discrete thickness variations, or steps, between atomically-flat regions on a 2D material surface as a reproducible and well-controlled feature for altering the ultrafast response. The high Q value of our MoS₂ cavities allows us to resolve perturbations in the mechanical response of 100 GHz devices induced by the presence of even a single monolayer step. Figure 2a shows the time-dependent reflectivity acquired for a suspended MoS₂ film with a 1 L step positioned at the center of the coinciding pump/probe beams (optical image in Supplementary Fig. 4).

Fig. 2. Horizontally-abutted cavities divided and detuned by a monolayer step.

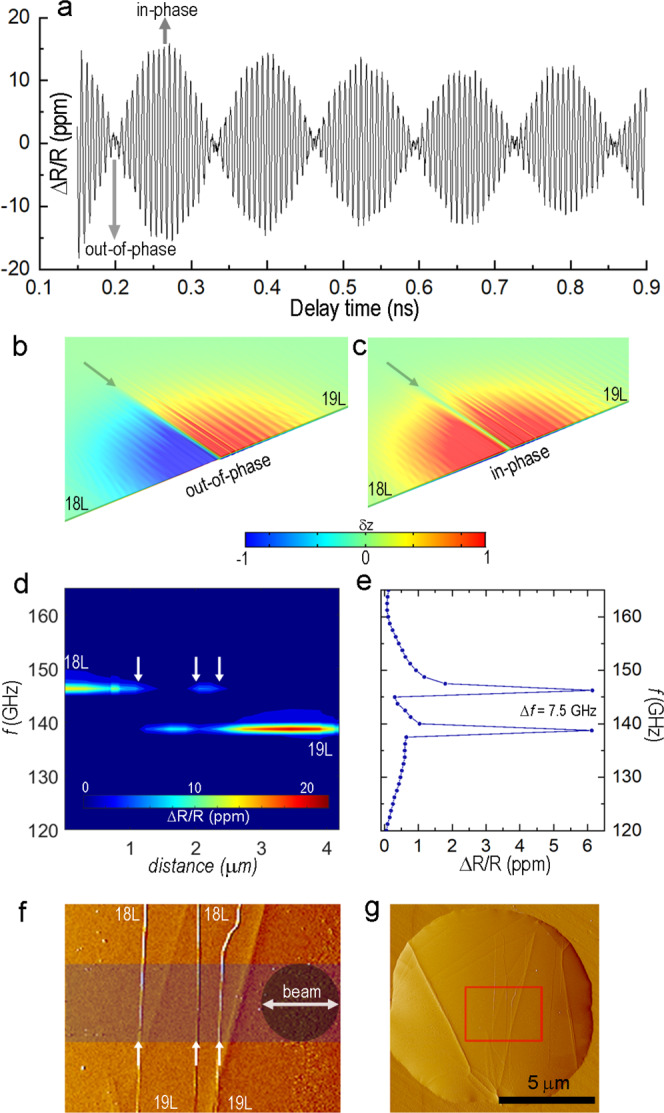
a Time-dependent reflectivity taken at a monolayer step boundary on an 18-layer (18 L)/19-layer (19 L) MoS₂ suspended film. The in-phase and out-of-phase labels show the timing for the snap-shots in b, c. FEM-generated snapshots of normalized vertical displacement maps (δz) highlighting the out-of-phase (b) and in-phase (c) vibrations of the abutted cavities at the monolayer step. Additional information for the time-domain FEM analysis are included in the Supplementary Information (Supplementary Note 2 and Supplementary Movie 1). d 2D plot showing color-coded FFT spectra of the probe reflectivity acquired at different positions while stepping the beam across the monolayer steps shown in f. e FFT spectrum of time-dependent reflectivity from a, which is taken approximately at the 2.2 μm position in d. f AFM phase-image showing the region where the spectra in a and d were acquired. The monolayer steps run vertically across the image. The horizontal darkened band shows the path where the 1 μm diameter beam was scanned across the surface. g Low magnification AFM phase-image showing the MoS₂ drum (see Supplementary Fig. 4 for optical image). The red box highlights the region imaged in f.

Pronounced beats observed during the ring-down (Fig. 2a) manifest as two distinct peaks in the FFT spectrum (see below), in striking contrast to the monochromatic response of homogeneous cavities in Fig. 1d. The split Δf ≈ 7.5 GHz between the experimentally observed peaks in the spectrum of the “step-cavity” closely matches the detuning expected from a monolayer change in thickness and suggests that the excited parts of the film on each side of the step behave as co-vibrating, but nearly isolated acoustic cavities. Such interpretation implies that the experimentally observed beats in the intensity of the reflected probe pulse arise when the photodetector sums up the contributions from two concurrent but frequency-shifted vibrational modes (Fig. 2b, c). If we assume that some degree of coupling is present between the half-cavities, these vibrational modes could be considered as mixed modes (ω_±) of coupled resonators (see for example ref. ³¹ and Supplementary Note 1). In the weak coupling limit κ_coupling → 0, the frequencies of the mixed modes are expected to approach those corresponding to flat plates (18 L and 19 L).

To evaluate the coupling strength, we compare the vibrational spectra acquired on the step with the response far away from the step. Figure 2d shows a filled contour plot of the spatially varying FFT spectra (see example of a single spectra in Fig. 2e) as coinciding pump/probe beams are moved laterally across the monolayer steps imaged in Fig. 2f, g. Regardless of the measurement position (“on step” or “away from step”) we only observe a set of discrete frequencies, each corresponding to a whole number of MoS₂ monolayers. There is no evidence of frequency deviation for the mixed modes in the vicinity of the steps, at least not within the signal-to-noise ratio available in our experiments. This result indicates that despite the cavities being formed mostly by the same atomic planes, the lateral coupling between the abutted cavities does not exceed the halfwidth of the resonance (≈0.2 GHz). Employing a one degree-of-freedom (1DOF) model for two coupled and nearly identical oscillators³¹ (Supplementary Equation 3), this result provides an upper boundary estimate for the spring constant ratio κ_coupling/k_oscillator ≈ 2 × 10⁻³, implying nearly independent cavities. This estimate confirms that in contrast to “acoustic molecules”³², the energy transfer between laterally abutted 2D cavities is negligible, at least within the pump repetition period in our experiments. Therefore, the low frequency envelope in Fig. 2a provides the frequency difference between the abutted half-cavities (ω₊–ω₋, Fig. 2a), where each can be viewed as independent. We emphasize that such a differential readout is enabled by the nature of well-defined monolayer steps in 2D materials and note that recently developed transfer methods allow for controlled placement of such steps in top-down lithographical approaches (e.g., adding a monolayer film on half of a uniformly thick slab³³).

Simultaneous optical response from the adjacent acoustic cavities can enable frequency down-conversion, where one of the half-cavities acts as a local oscillator for the other half-cavity. Recent progress in developing nonlinear optical detectors³⁴ opens the possibility for mixing intensity-modulated optical signals coming from the abutted-cavities directly at the photodetector. An estimated bandwidth of ~0.5 THz for the graphene-based mixer-detector³⁴ could allow real-time down-conversion with the output electric signal from the photodetector modulated at the beat frequency of adjoined TMD cavities. We also note that although our experiments do not show cyclic energy exchange between the half-cavities, a step on the area of the plate that undergoes thickness-mode vibrations can generate a steady energy outflow (i.e., leakage) by launching slow propagating longitudinal elastic waves known as Lamb waves^23,35. These waves are manifested as the ripples seen in Fig. 2b, c and for a nanostructure embedded in the plate, they can make a remote, high-Q, pulse-driven step-cavity to appear as a narrow-band Lamb wave generator with the frequency defined by the plate thickness. While beyond the scope of this work, this concept can open opportunities for in-plane (“on-chip”) EHF acoustics. Unfortunately, within our experimental approach, these effects are muted by the disparity between the lateral extent of the diffraction-limited probe laser spot and the much shorter in-plane wavelengths of step-generated elastic excitations.

h-BN/MoS₂ bilayer: Frequency comb and h-BN phonon lifetime

To provide stronger coupling for our optical readout system, we explore heterogeneities that span the full laser spot diameter, such as those formed at the boundaries of dissimilar materials in laminar structures. Modifications to an acoustic cavity that enable access to high-frequency overtones can be implemented by invoking highly nonuniform strain patterns for the cavity excitation. To ensure such a nonuniformity in a laminated stack of 2D materials, we assembled devices composed of a relatively thick h-BN layer (44 nm) van der Waals (vdW) bonded to a thinner MoS₂ layer (8.7 nm or 14 L; optical image in Supplementary Fig. 4). The large disparity in material bandgaps (h-BN ≈ 6 eV and bulk MoS₂ ≈ 1.2 eV) limits optical absorption of the pump beam to the MoS₂ layer alone, thereby making the TMD a thin transducer that drives the full 53 nm thick stack.

Figure 3a shows the time-dependent reflectivity from a h-BN/MoS₂ heterostructure, which is notably different from both the homogenous cavities in Fig. 1 and the “step-cavities” in Fig. 2. Despite the complex appearance, the temporal behavior is straightforward to interpret in the frequency domain, where a pronounced frequency comb emerges with a series of nearly equidistant peaks with separation Δf ≈ 34 GHz (Fig. 3b). Using eigenfrequency numerical analysis, we find that the center frequency for each experimentally observed peak coincides with that of corresponding high-order overtones (red ticks) in the laminated h-BN/MoS₂ structure. Examples of the spatial configuration of the strain for the high-order overtones can be seen in Fig. 3c. The frequency comb extends to the ninth-order overtone and spans nearly four octaves, which is unattainable for a uniformly excited homogeneous film (e.g., Fig. 1d). The larger amplitudes of high-order overtones in Fig. 3b are directly related to the highly inhomogeneous strain generated across the h-BN/MoS₂ stack by the pump pulse. Figure 3d shows snapshots of strain patterns calculated using time-domain FEM analysis (see Supplementary Note 3 for details of the modeling approach). Expansion of the MoS₂ film is driven by the deformation potential²⁵ and generates a succession of nearly rectangular strain pulses launched into the h-BN layer, which then propagate at the speed of the longitudinal sound waves (c_LA ≈ 3.4 × 10³ m/s for h-BN; the snap-shots of the spatial distribution for the out-of-plane strain in the bilayer are shown in Supplementary Figs. 6, 7 and Supplementary Movie 2). The envelope of the comb in the experimentally acquired spectrum (Fig. 3b) peaks at about 200 GHz and is defined by the sample geometry. An overtone is prominent when the wavelength of the standing wave, λ_s (see Fig. 3c) closely matches that of the elastic wave launched by the MoS₂ transducer in response to pulse excitation (Fig. 3d). Here, the sixth overtone (~200 GHz, strain pattern in Fig. 3c) has the closest overlap since the MoS₂ layer thickness approaches the half-wavelength, λ_s/2. Accordingly, the inverse round-trip time for sound within the MoS₂ is commensurate with the overtone’s frequency.

Fig. 3. Frequency comb generator implemented in a h-BN/MoS₂ bilayer.

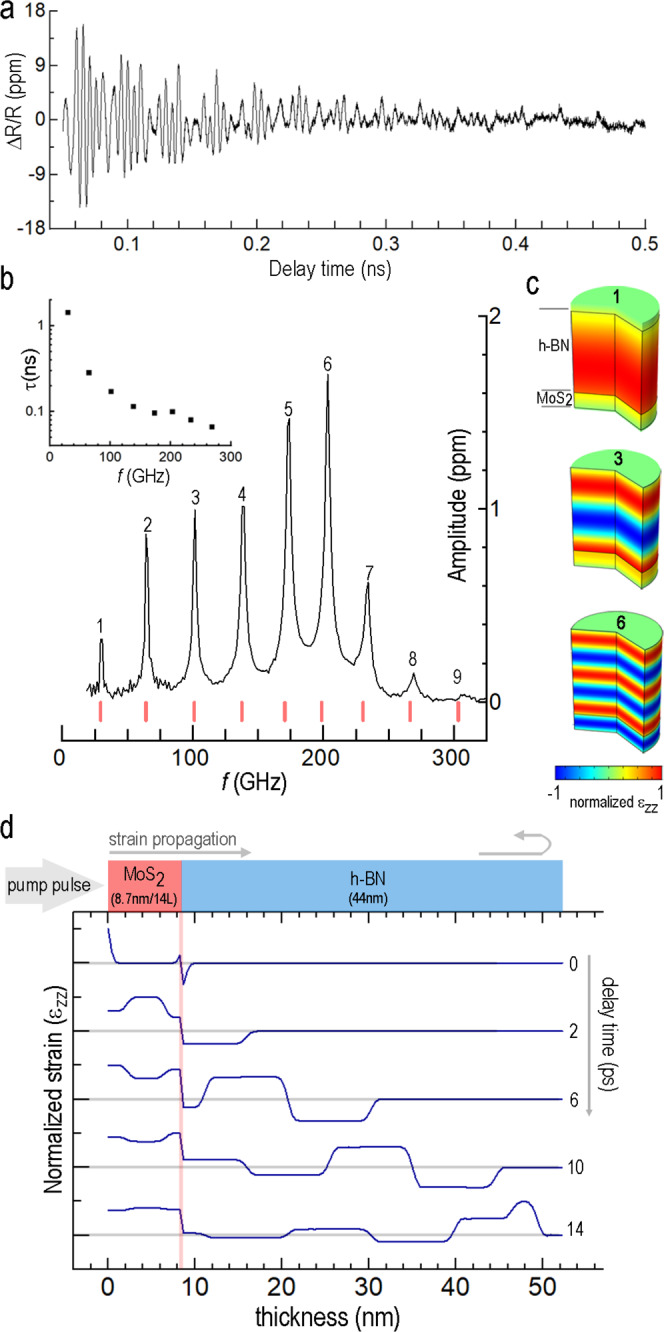
a Time-dependent reflectivity for a h-BN (44 nm)/MoS₂ (8.7 nm/14 L) suspended film. b FFT spectrum of the signal shown in a. The red tick marks along the bottom of the plot show positions of the bilayer overtones as predicted by FEM eigenfrequency analysis. The peaks are numerically labeled from lowest to highest frequency. (inset) Extracted lifetimes for h-BN (τ_hBN) versus frequency for peaks in b (see Supplementary Note 4 for details of the extraction method). c Spatial configuration of the normalized ε_ZZ strain for three different modes (labeled) in the h-BN/MoS₂ heterostructure (eigenfrequency FEM analysis, 1D model). d Snapshots of the ε_ZZ strain distribution generated by optically-excited MoS₂ are shown across the thickness of the bilayer at early delay times (for details of time-domain axisymmetric FEM analysis, see Supplementary Note 3).

The bilayer h-BN/MoS₂ geometry used here provides a point of comparison with a similar transduction approach based on spatially-inhomogeneous optical absorption that has been used to generate a broadband frequency comb in GaAs/AlGaAs/InGaAs systems^36,37. A distinct advantage offered by 2D materials is the higher level of spatial confinement, which is illustrated by comparing our 53 nm thick h-BN/MoS₂ stack versus the combined 407 nm thick multiple quantum well structures (plus 3.76 μm for the DBR reflector) in ref. ³⁷. More importantly, given the wide frequency range of excited overtones, our measurement provides experimental evaluation for the frequency dependence of the longitudinal phonon lifetimes in h-BN (Fig. 3b inset), as the energy dissipation in our bilayer structure can be separated into individual contributions from h-BN and MoS₂ (see for example ref. ³⁸ and Supplementary Note 4 with the elastic energy distribution for different vibrational modes in the bilayer shown in Supplementary Fig. 8, and energy partitioning coefficients listed in Supplementary Table 1). These results are enabled by the high-quality, low-loss MoS₂ transducer layer since h-BN alone would be inaccessible for a NIR wavelength pump-probe setup. While a metal transducer evaporated on a semiconductor film can also be used to generate a frequency comb^39,40, the use of a crystalline 2D material-based transducer with low internal friction and diminished surface roughness can reduce the overall energy losses and make the estimates for the phonon lifetimes more reliable. Importantly, a wide variety of high-contrast bilayer structures with atomically-sharp interfaces can be built using 2D materials. The transfer approach mitigates problems inherent to physical vapor deposition, such as island growth modes (due to dissimilar surface energies) or interdiffusion, as well as built-in stress associated with many evaporated/epitaxial films. Our control experiments with stacked MoS₂/MoS₂ slabs indicate that the adopted method for flake transfer, including exposure to ambient air does not increase the mechanical losses considerably (see Supplementary Note 5 and frequency dependence of the quality factor Q for MoS₂/MoS₂ stacks shown in Supplementary Fig. 9). Similar low-loss behavior is projected on MoS₂/h-BN boundaries based on transmission electron microscopy (TEM) results that find pristine interfaces between h-BN and MoS₂⁴¹. Close values of interface adhesion energy (0.3 J/m² for MoS₂/h-BN versus 0.4 J/m² for MoS₂/MoS₂ interfaces) also imply commonalities in vdW self-cleansing mechanism for these interfaces⁴² and therefore, similar losses.

Coupled cavities in MoS₂/h-BN/MoS₂ tri-layer

In the implementation of the frequency comb described above, we centered our analysis on energy dissipation within individual cavity components and on relative intensities of the excited overtones in the bilayer h-BN_(44 nm)/MoS_{2 (8.7 nm)} cavity. Building on this assessment, we extend the multilayer design approach in an effort to reengineer the cavity vibrational modes themselves. To illustrate mode alteration, we sandwich a thin h-BN film between two MoS₂ layers (MoS_2(17L)/ h-BN_(5L)/ MoS_2(15L)) in an effort to tailor the strain patterns and the corresponding spatial redistribution of the elastic energy across a tri-layer laminar structure (optical images of the tri-layer structures and elastic energy distribution for selected vibrational modes are shown in Supplementary Figs 10, 11).

Figure 4 compares the measured vibrational spectrum for a tri-layer MoS_2(17L)/h-BN_(5L)/ MoS_2(15L) sample (Fig. 4a) with the spectrum of a control bi-layer MoS_2(17L)/ MoS_2(15L) sample (Fig. 4b). A significant increase in the intensity of the third overtone (215 GHz, Fig. 4a) is a notable outcome of introducing the h-BN middle layer. However, even more important is the fact that the position of the second overtone in the tri-layer structure (158 GHz, Fig. 4a) becomes far detuned from the doubled frequency of the fundamental mode (70.3 GHz). The fundamental mode frequencies for both devices match the FEM-predicted values (Fig. 4c), which provides confidence that the material interfaces behave as “ideal boundaries” with no softening due to interlayer contamination¹⁵. Dotted lines in Fig. 4c show the calculated frequencies for the first three vibrational modes of the tri-layer stack as function of the h-BN thickness. The salient feature is the progression from equidistant harmonics in the monolithic MoS₂ film (at h-BN = 0 nm) to a set of second and third overtones (red and blue lines, Fig. 4c) that converge towards the resonant frequency for an isolated 17L-thick MoS₂ layer (154 GHz). Such a tendency is governed by the strain patterns arising from the presence of the h-BN layer (Fig. 4d, e). For the second overtone (anti-symmetric, ≈ 158 GHz) the location of h-BN layer coincides with the strain node. As a result, the reduced material stiffness (C₃₃ = 27 GPa in h-BN⁴³ versus C₃₃ = 54 GPa in MoS₂⁴⁴) becomes inconsequential in the elastic response. On the contrary, the third overtone (symmetric, 216 GHz) applies maximum strain to the h-BN layer, which leads to a reduced restoring force and lower resonant frequency. The overtones moving closer to each other invoke a model where two MoS₂ slabs can be considered as distinct acoustic cavities coupled through the h-BN barrier. The third overtone is then interpreted as ω₊ (symmetric) mode, while the second overtone is assigned as ω₋ mode (see refs. ^30,31 and Supplementary Notes 1, 6). Experimental data for the overtones’ positions in our tri-layer stack are shown by open symbols in Fig. 4c and demonstrate a clear step toward a coupled-cavity implementation. A 1DOF model for two coupled mechanical oscillators (see Supplementary Equations 3, 4) applied to our tri-layer system produces coupling strength Γ ≈ 47 GHz and κ_coupling/k_oscillator ≈ 0.35, implying very strong coupling.

Fig. 4. Strongly coupled acoustic cavities constructed as a vertically-stacked heterostructure.

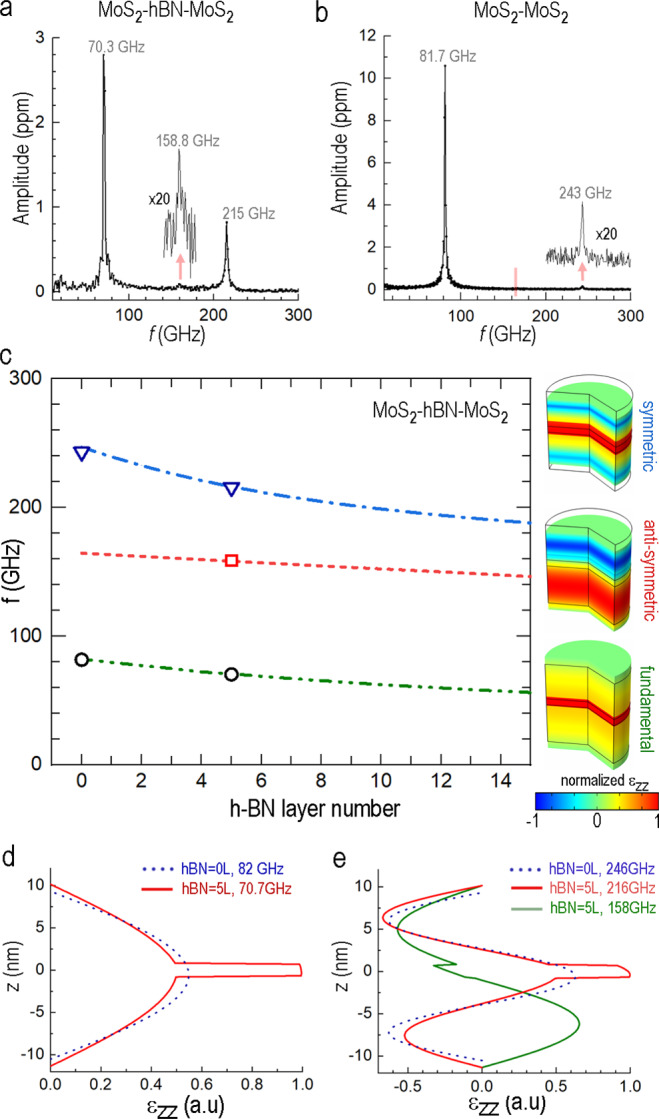
a Spectrum for the MoS₂/h-BN/MoS₂ tri-layer; b Spectrum of the neighboring MoS₂/MoS₂ control area. The red tick in b highlights the location of the non-active second harmonic peak. Only odd modes are excited with the homogeneous pump excitation here. c FEM-predicted frequencies for the three lowest vibrational modes of the tri-layer system as function of the spacer h-BN layer thickness. Experimental data (open symbols) are included for the tri-layer (h-BN thickness = 5 L, normalized ε_ZZ strain configurations are shown on the right) and for the control sample (h-BN thickness = 0 L). d, e The normalized ε_ZZ strain profiles for vibrational modes in monolithic MoS₂ (dotted lines) are shown in comparison with strain in the tri-layer system (solid lines) at the labeled frequencies.

Apart from the interplay between the high-frequency overtones, the fundamental vibration mode in our tri-layer system is of prime interest since it features a large and nearly uniform strain profile within the h-BN layer (Fig. 4d). Known to be a good host for RT quantum photon sources^45–48, the h-BN spacer layer sandwiched between MoS₂ “hammer and anvil” represents a promising configuration for coupling embedded optical emitters to coherent LA phonons confined in the tri-layer cavity. Importantly, both the maximum attainable strain, as well as the spectral purity of the elastic stimulus delivered to embedded nanostructures are defined by the quality factor of the overall cavity. Energy losses in both the h-BN “device layer” and surrounding MoS₂ structures affect the total phonon lifetime in the cavity. The experimental values for the tri-layer ring-down time τ_Total = 0.65 ns fall between our previously extracted values for τ_hBN = 0.24 ns and τ_MoS2 = 2.8 ns at 70 GHz and agree to within 10% with the prediction 1/τ_Total = α₁/τ_hBN + α₂/τ_MoS2 where α_1, α₂ are energy partition coefficients for the tri-layer structure (see Supplementary Table 2). We view this agreement as a strong indicator that losses related to the MoS₂/h-BN interfaces do not limit the phonon lifetime in the cavity.

Discussion

Developing a toolbox for building high-performance acoustic cavities in 2D materials requires a quantitative understanding of the fundamental mechanisms that govern phonon lifetimes, including both frequency and temperature dependences. It is also necessary to account for both material-specific internal friction, as well as extrinsic effects (e.g., surfaces and imperfections, confinement losses, etc.). Intrinsic losses in the nonmetallic materials studied here (at RT) arise mainly from phonon–phonon scattering, often referred to as anharmonic effects. Until recently only semiquantitative models, developed primarily for sound attenuation in isotropic materials and intended for frequency limits ωτ_th << 1 or ωτ_th >> 1, have been available for fitting measured data (ω is the frequency of the sound wave and τ_th is the lifetime of thermal phonons, see for example refs. ^49,50). Advancements in the development of first-principles techniques now allow for fully microscopic treatments of phonon lifetimes^51,52 (see Supplementary Notes 7, 8 for description of theoretical approach), which do not invoke uncertainties resulting from experimentally-derived empirical constants within the model (e.g., average Grüneisen parameters). Relatively little work of this kind has been done in predicting phonon lifetimes for low frequency acoustic phonons^51,52, particularly in comparing with measured data in low dimensional and vdW layered systems.

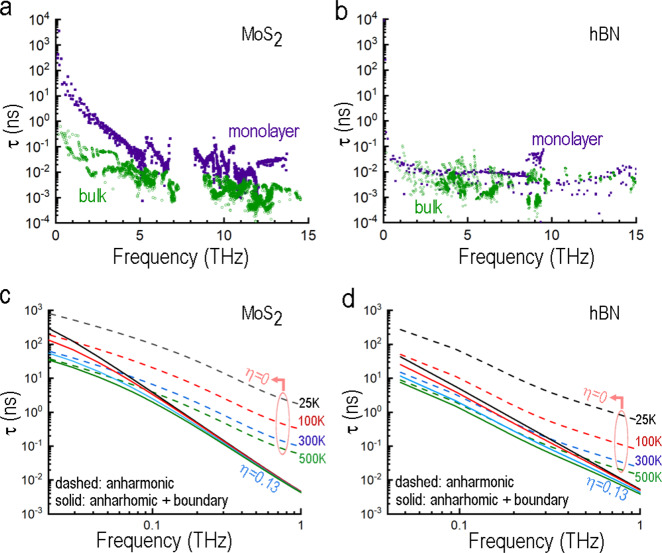
Our calculated phonon lifetimes for all polarizations due to anharmonic three-phonon scattering alone through the Brillouin zones for bulk and monolayer MoS₂ and h-BN are shown in Fig. 5a, b (see METHODS; also see Supplementary Figs. 12–14 for schematics of the theoretical setup and Supplementary Figs. 15, 16 for phonon lifetimes projected onto the phonon dispersion curves, as well as full Brillouin zone data). They vary widely in magnitude across each Brillouin zone and become considerably longer at low frequencies. For thermal phonons (f_th = k_BT/(2 π ħ) ≈ 6.25 THz at RT) the predicted lifetime is close to τ_th ≈ 1–3 ps for both bulk h-BN and MoS₂. The ability to cover seamlessly the entire low frequency range (ħω < k_BT), including the crossover at ω_cτ_th ≈ 1 (which is of prime interest here at ω_c ≥ 2π × 55 GHz), is a major advantage of our DFT-based approach. The lifetimes in MoS₂ and MoSe₂ (see Supplementary Figs. 15, 16) were found to be similar in overall magnitude, and those in h-BN are somewhat shorter, especially near the f ≈ 1 THz range. To illustrate the versatility of the microscopic approach, we also present the phonon lifetimes calculated for monolayers of MoS₂, h-BN and MoSe₂ (see Supplementary Fig. 16). The enhanced phonon lifetimes predicted for the TMD monolayers MoS₂ and MoSe₂ (though not so for h-BN) suggest that the intrinsic anharmonic losses are less significant in these materials as layer thicknesses are reduced. At lower frequencies in particular, out-of-plane flexure vibrations with quadratic dispersions in monolayer materials tend to have long lifetimes. These modes are not present in their bulk counterparts.

Fig. 5. Phonon lifetimes due to anharmonic phonon–phonon scattering for bulk and monolayer systems.

Phonon lifetimes through the Brillouin zones for all polarizations and propagation directions at room temperature in a MoS₂ and b h-BN. For h-BN, phonon lifetimes are truncated at 15 THz. Lifetimes over the entire frequency range are shown in Supplementary Fig. 16. Low-frequency plot (log-log) showing temperature dependences of lifetimes for cross-plane LA phonons in c MoS₂ and d h-BN from anharmonic scattering (dashed curves, η = 0) and from the sum of anharmonic scattering and surface losses (solid curves, η = 0.13). η is the root mean square variation of the surface height (i.e., rms roughness in nanometers).

In order to represent acoustic vibrations in films with varying thicknesses h we use calculations for bulk LA modes polarized perpendicular to the surfaces with wave vectors q_z and with half wavelengths equal to the layer thicknesses, h = λ_z/2 = π/q_z. Their frequencies as functions of thickness are found to agree well with the corresponding measurements in Fig. 1e. The phonon lifetimes due to anharmonic phonon scattering alone in the THz regime for MoS₂ and h-BN are given by the dashed curves in Fig. 5c, d, where they are seen to decrease with frequency. The temperature dependences of the anharmonic contributions to phonon lifetimes for MoS₂ (Fig. 5c) and h-BN (Fig. 5d) are pronounced and arise from the phonon population factors in the phonon–phonon scatterings. Lower temperatures can reduce anharmonic scattering losses considerably.

To represent the extrinsic contributions to the vibration lifetimes, a simple model for surface losses due to scattering from randomly varying surface or boundary heights⁵³ is used (solid lines Fig. 5c, d). This gives a scattering contribution in the form

$$1/{\tau }_{\mathrm{surface}}=\frac{1-p}{1+p}\frac{∣v_z∣}{h},p=e^{-{\left(4\pi \eta /{\lambda }_z\right)}^2}$$ 1

where p is the specularity of the surface, v_z is the group velocity, λ_z is the acoustic wavelength and η is the root mean square variation of the surface height (i.e., rms roughness). Recent measurements on freshly cleaved MoS₂ surfaces give an estimated η = 0.23 nm⁵⁴, which could be even smaller for clean MoS₂ surfaces with fewer sulfur vacancies and adsorbed species.

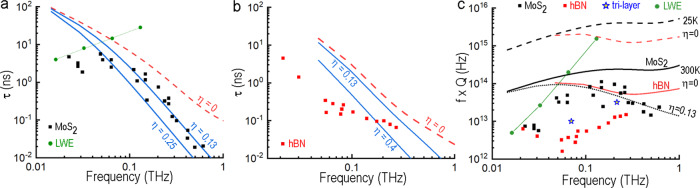
To assess how well these microscopic calculations compare with our measured data, Fig. 6a shows the experimental ring-down times for the monolithic MoS₂ cavities described earlier (see Fig. 1). The sum of the anharmonic and surface roughness losses are in very good agreement with experiment for the frequencies f ≥ 100 GHz, both for magnitude and for frequency dependence. Two different values of η are provided to illustrate the effects of varying surface roughness. The two solid blue curves in Fig. 6a give the sum of these surface losses and the anharmonic scattering for MoS₂ for η = 0.25 nm and for η = 0.13 nm, where the latter is fit to the measured data here (black squares).

Fig. 6. Experimental and theoretical results for the lifetimes of LA phonons polarized perpendicular to the basal plane.

Frequency dependence predicted for the room temperature phonon lifetimes in a MoS₂ and b h-BN as defined by anharmonic scattering alone (dashed curves; η = 0) and by the combination of anharmonic scattering with surface losses (solid curves; η > 0) for two values of rms surface roughness (η) in nanometers. Values extracted from experimentally measured cavity ring-down times are shown by the black (a) and red (b) square points. The green points in a and c show the FEM-calculated time for Lamb waves escape LWE (see Supplementary Note 9 for details). c Comparison of calculated and measured f × Q product as a function of frequency. The black lines show f × Q values calculated for MoS₂ cavities and the red lines correspond to h-BN structures at the labeled temperatures and η. Experimental data for cavities studied in the present work are given by the square and star symbols as labeled. The tri-layer data points represent the MoS₂/h-BN/MoS₂ heterostructure (see Fig. 4).

A broad frequency range comparison of our microscopic calculations and experimental data against the well-accepted models for absorption of sound in insulators⁵⁵, based on Landau–Rumer and Akhiezer approach, shows that ab initio predictions for τ in the intermediate range (i.e., ωτ_th ≈ 1) are an order of magnitude larger (see Supplementary Fig. 17 for the comparison of ab initio calculations, experimental data, and asymptotic theoretical models). We emphasize that in the absence of the DFT-based results any quantitative analysis of dissipation above 50 GHz (ωτ_th ≈1) would be challenging and assumption-driven (see for example ref. ⁵⁰). That frequency range is of prime importance here, since at 100 GHz the performance of our MoS₂-based cavities is within a factor of three from the fundamental limit defined by the intrinsic anharmonicity-based losses (Fig. 6a). Unexpectedly, the experimental ring-down times deviate down from our theoretical predictions at f < 100 GHz. While some limitations of the measuring technique can be a contributor, we attribute most of this divergence to another extrinsic loss mechanism only recently considered in ultrathin photoexcited semiconductor plates⁵⁶ —the lateral spreading of pump-generated elastic waves that propagate outward from the probe-beam spot as Lamb waves²³ (see Supplementary Note 9). The escape rate of these waves, as opposed to a phonon lifetime, can be a limiting factor in the experimentally-measured ring-down at lower frequencies. Given the absence of any structurally-defined lateral confinement in our films (e.g., walls or steps), the escape time is governed by the details of Lamb wave dispersion (see Supplementary Note 10) and scales approximately as a ratio of pump spot size, R_pump, to film thickness, h, τ_Lamb ~ R_pump/h, which makes the runaway more pronounced for thicker films. The analytical approach developed by Photiadis et al.⁵⁶ is consistent with FEM modeling for MoS₂ films (see Lamb wave dispersion calculated using eigenfrequency analysis and ring-down time extracted from time-domain simulations in Supplementary Figs. 18, 19). The estimates for the Lamb waves escape times (LWE) produced by numerical modeling are shown by green points/line in Fig. 6a and agree well with the low frequency leveling-off of our experimentally measured ring-down times.

It is evident from comparing Figs. 1c and 3a that the ring-down time measured for h-BN-based structures is significantly shorter than that exhibited by monolithic MoS₂ films. Figure 6b shows that the phonon lifetimes in h-BN (extracted from Fig. 3b and additional h-BN/MoS₂ cavities) is consistently lower than the theoretical limit defined by phonon–phonon scattering. The dashed line in Fig. 6b is for anharmonic phonon scattering alone (η = 0) while two solid curves show the cumulative effects of phonon–phonon as well as boundary scattering. Comparison with the experimental data shows that even the upper-bound value for h-BN surface roughness reported in the literature η = 0.1–0.4^57,58 does not fully account for the extra dissipation in our devices. The presence of the h-BN/MoS₂ interface cannot explain the extra dissipation since the ring-down times from our tri-layer structure MoS₂/h-BN/MoS₂ (which contains two identical interfaces with a very thin h-BN layer) is actually longer than the decay in the h-BN/MoS₂ bilayer with a single interface (Fig. 6c, blue stars). This discrepancy implies the presence of an additional dissipation mechanism, possibly related to inter-mode coupling or material quality. We anticipate that future low temperature measurements will provide insights into various loss mechanisms in h-BN.

Finally, to gain a broader picture of how these results project the ultimate performance of 2D material-based acoustic cavities, we employ f × Q products as a figure of merit. Figure 6c compares experimental data with the f × Q values calculated for bulk MoS₂ and h-BN at two different temperatures. For anharmonicity-limited systems the predicted f × Q product increases slightly with frequency (in a qualitative agreement with the Landau–Rumer model⁵⁵), and for a given material represents the highest achievable performance for an acoustic cavity. With the boundary scattering term included for MoS₂ (η = 0.13) the f × Q product decreases with increasing frequency (dotted line Fig. 6c), and fits our experimental f × Q values for MoS₂ (black squares Fig. 6c). The order of magnitude increase in f × Q projected at low temperature is highly desirable, but will only become attainable if boundary scattering can be mitigated (see for example ref. ²¹).

The presence of a “goldilocks zone” centered near f ≈ 100–200 GHz, where currently available materials and fabrication techniques yield the highest f × Q products, is an important takeaway from Fig. 6c. Being flanked by the dominance of lateral spreading of elastic waves at low frequency (green points/line) and by surface scattering at higher frequencies (black dotted line), the f × Q product at the 100–200 GHz range exceeds that required for ground state laser cooling (f × Q = 6 × 10¹²) by more than order of magnitude. Data from the tri-layer cavity in Fig. 4 (blue stars in Fig. 6c) offers an example of how a relatively lossy material (h-BN) can be added judiciously to the acoustic device to expand functionality, while maintaining high overall cavity performance (see f × Q ≈ 3 × 10¹³ for the 200 GHz mode of the tri-layer). We view this approach as a path toward integrated optomechanical systems where the cavity couples high-frequency elastic waves to embedded quantum systems (e.g., optical emitters in h-BN), while the acoustic interaction with the quantum system can be further tuned using advanced methods of laser cooling⁵⁹ or coherent phonon manipulation (e.g., refs. ^60–62).

In summary, we have shown how heterogeneities within high-quality 2D material structures extend the functionality of acoustic cavities operating in the GHz to THz frequency range. We demonstrated differential readout for adjacent MoS₂ cavities detuned by a monolayer step, as well as a frequency comb generator in a heterostructured h-BN/MoS₂ cavity. By employing MoS₂ as a thin transducer for h-BN, we successfully extracted the longitudinal phonon lifetimes for optically transparent h-BN. Strain engineering within tri-layer MoS₂/h-BN/MoS₂ laminar structures resulted in strongly coupled acoustic cavities with coupling strengths of Γ ≈ 47 GHz. Our first-principles theoretical analysis provides a benchmark for the highest attainable, material-limited performance for 2D acoustic cavities at different temperatures. We find that the currently available 2D material quality and fabrication techniques can produce acoustic devices that operate within a factor of three of their fundamental anharmonic limit at RT, where we measure f × Q products in excess of 1 × 10¹⁴ in vicinity of 100–200 GHz frequency range. We anticipate that by extending the palette of 2D materials and by invoking different types of heterogeneities within 2D acoustic cavities, numerous acoustic devices will become available for advanced phonon-based sensing and signal processing.

Methods

Sample fabrication

In order to mitigate extrinsic contributions to the acoustic losses, we fabricated 2D material structures with minimal exposure to wet chemistry agents. To fabricate samples, we first lithographically patterned and etched wells and trenches into a Si or SiO₂/Si substrate (e.g., Fig. 1a, well diameter: 1–10 μm; well depth: 250–425 nm). Then a Ti (5 nm)/Au (40 nm) film was evaporated on the surface, which served two purposes: (i) facilitating the exfoliation of large-area samples (e.g., ref. ⁶³) and (ii) to enhance the optical cavity formed between the bottom of the wells and the suspended films. Bulk MoS₂ crystals were directly exfoliated onto these substrates, leaving behind suspended flakes ranging in thickness from monolayer to bulk (see Supplementary Fig. 1). Measurements were performed on flakes ranging in thickness from 2.5 nm (4 L) up to 60 nm. Heterostructures (h-BN/MoS₂ and MoS₂/h-BN/MoS₂) were fabricated using a PPC/PDMS stamping technique²⁰ where h-BN and MoS₂ films were exfoliated onto different SiO₂ substrates. The PPC/PDMS stamp was then used to sequentially pick up the predetermined layers. Afterwards the heterostructure stacks were thermally released on the well-etched substrate described above. To determine film thicknesses for MoS₂ flakes under ten layers, we use a combination of optical microscopy and Raman spectroscopy (e.g., peak positions of the interlayer breathing and shear modes of MoS₂⁶⁴, see Supplementary Fig. 2). For MoS₂ films >10 layers and for all h-BN layers we used atomic force microscopy (AFM) to measure film thickness.

Pump-probe measurements

An ultrafast optical pump-probe setup with micrometer-scale spatial resolution was used to study longitudinal vibrations in both MoS₂ and MoS₂/h-BN suspended films. Two femtosecond Ti:Sapphire lasers with repetition rate ~960 MHz provided pump (750 nm wavelength, 3–10 mW power) and probe (830 nm, ≤1 mW) pulses with variable time delay governed by asynchronous optical sampling (ASOPS)^65,66. The detuning between the pump and probe repetition rate was set at 2.5 kHz. Both beams were focused using 50× objective lens and independently positioned with respect to structures of interest. The same objective also provided optical imaging of the sample and was used to collect the reflected probe light.

In order to facilitate optical readout, the wells in the substrate were pre-etched to a depth that approximately equals one-half the wavelength of the probe beam (λ_probe ~830 nm), which forms an optical cavity between the suspended flake and bottom mirror. This configuration in combination with a high repetition rate allows us to use relatively low pulse energy in order to provide acceptable signal-to-noise ratio while mitigating overheating and ensuring linear response of the mechanical structure. Typical acquisition mode included 50,000 sweeps averaged over accumulation time of 20 s. All the measurements were done at RT in ambient conditions.

Phonon lifetime calculations

For first-principles calculations, the strength of each scattering is determined by matrix elements built from third-order anharmonic perturbations, frequencies, and eigenvectors of the phonons^51,53,67 derived from DFT. Phonon scattering due to point defects, such as isotopic variation, is negligible for the frequency range considered here, particularly around RT. This method has been found to give good agreement with measured data in a wide range of bulk materials for phonon dispersions^68–70 and for thermal conductivities^67,71,72, where the latter are governed by phonon scattering. Details are given in the Supplementary Notes 7, 8.

Author contributions

M.K.Z. and J.T.R. conceived the experiments. J.J.F., S.W.L., C.D.C. and J.T.R. fabricated samples. M.K.Z. performed pump-probe experiments. J.J.F., J.T.R. and J.C.C. performed Raman spectroscopy measurements. L.R.L., T.P. and T.L.R. performed first-principle study of phonon–phonon interactions and energy dissipation. D.M.P., B.H.H. and M.K.Z. performed elasticity-based analysis of 2D material heterostructures. The manuscript was written with contributions of all authors. All authors have given approval to the final version of the manuscript.

Data availability

The authors declare that the data supporting this study are available within the article and its Supplementary Information files. Further information is available from the corresponding authors upon reasonable requests.

Code availability

Data for Figs. 5 and 6 were produced using publicly available software (Quantum Espresso). Relevant input and harmonic and anharmonic force constant files can be available upon request.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-021-23359-7.