Connecting Rodent and Human Pharmacokinetic Models for the Design and Translation of Glucose-Responsive Insulin

Abstract

Despite considerable progress, development of glucose-responsive insulins (GRIs) still largely depends on empirical knowledge and tedious experimentation—especially on rodents. To assist the rational design and clinical translation of the therapeutic, we present a Pharmacokinetic Algorithm Mapping GRI Efficacies in Rodents and Humans (PAMERAH) built upon our previous human model. PAMERAH constitutes a framework for predicting the therapeutic efficacy of a GRI candidate from its user-specified mechanism of action, kinetics, and dosage, which we show is accurate when checked against data from experiments and literature. Results from simulated glucose clamps also agree quantitatively with recent GRI publications. We demonstrate that the model can be used to explore the vast number of permutations constituting the GRI parameter space and thereby identify the optimal design ranges that yield desired performance. A design guide aside, PAMERAH more importantly can facilitate GRI’s clinical translation by connecting each candidate’s efficacies in rats, mice, and humans. The resultant mapping helps to find GRIs that appear promising in rodents but underperform in humans (i.e., false positives). Conversely, it also allows for the discovery of optimal human GRI dynamics not captured by experiments on a rodent population (false negatives). We condense such information onto a “translatability grid” as a straightforward, visual guide for GRI development.

Introduction

Diabetes is a growing condition affecting upwards of 425 million people worldwide, with a health care burden of U.S. $727 billion in 2017 (1). In the U.S. alone, the total estimated cost of diagnosed diabetes exceeds $320 billion yearly, which saw a 26% increase from 2012 to 2017 (2). The condition is marked by high blood glucose levels, or hyperglycemia, resulting from either impaired insulin production (type 1 diabetes [T1DM]) or insulin resistance (type 2 diabetes). If left unchecked, hyperglycemia can result in organ damage, disabilities, and other life-threatening complications (1). Insulin, the 51–amino acid hormone secreted from pancreatic β-cells, remains a mainstay therapeutic for all people with diabetes.

Conventionally, glycemic control is accomplished by scheduled insulin injections and regular blood glucose monitoring. The open-loop nature of such a dosing scheme renders substantial patient compliance a requirement. Alarmingly, three-quarters of physicians have reported nonadherence to the prescribed regimen in their patients, which can be attributed to both the uncomfortable and the time-consuming nature of the traditional therapy (3). The intrinsic drawbacks of an open-loop therapy are further highlighted by factors such as interindividual variations, the lag between blood glucose measurement and insulin administration, delayed absorption, and the conservatism in dosing as a result of hypoglycemia concerns (4,5). Resnick et al. (6) estimated that the desired glycemic control was not achieved by one-half of the patients with diabetes surveyed. Efforts have thus been aimed toward a closed-loop, automated system in which insulin dosing is modulated in accordance with the real-time glucose concentration in the patient’s bloodstream, akin to a functional pancreas (7). Recently, integration of continuous glucose sensing and insulin pumps has shown promise in hypoglycemia reduction and sustained blood glucose suppression, although it is currently still expensive and associated with increased risks of complications such as infection, inflammation, and scarring (8).

An alternative is the concept of a glucose-responsive insulin (GRI). In the absence of external devices, these therapeutics achieve controlled insulin activity in response to the local environment through their glucose-binding chemistries and subsequent triggered insulin release or potency enhancement (9). A multitude of GRI constructs have been reported over the years, often relying on glucose-mediated degradation, swelling, gelling, or disassembly of insulin-encapsulating carriers, which can be reversible or irreversible (10). Recently, freely circulating GRIs, not polymer-encapsulated formations, have been designed by Chou et al. (11) with simplified chemical kinetics, echoing the first GRI concept conceived by Brownlee and Cerami in 1979 (12).

GRIs are shown to enforce tighter glycemic control, reduce the incidence of hypoglycemic episodes, and lessen the burden of multiple daily injections in a multitude of experimental studies (4,10), yet efforts toward a mathematical framework for their rational design have been limited to date (9). While the localized release kinetics from certain GRIs have been modeled before, they have not been translated into therapeutic efficacy for design purposes. Specifically, GRI models were not pieced together with the underlying insulin-glucose-glucagon metabolism (13,14). Our previous work (5) established the first framework that linked GRI designs to their therapeutic effectiveness through pharmacokinetic modeling of patients with T1DM.

However, the majority of GRI research relies on substantial testing in animal models and specifically rodents (11,15). We identify the critical importance of extending this said mathematical framework to bridge the gap between widely used animal models and the prediction of human clinical observations so as to expedite the search for viable drug candidates. Given that pharmacokinetics cannot be simply scaled between organisms in general (16) and that almost all therapeutics are inevitably tested on animal models such as rodents, as a start, the rational design of GRIs may therefore greatly benefit from a mathematical approach specifically developed for predicted testing in mice and rats. In this work, we present a Pharmacokinetic Algorithm Mapping GRI Efficacies in Rodents and Humans (PAMERAH). This in silico modeling framework couples GRI kinetics to the first full-body physiology-based model describing murine glycemic control and maps rodent physiology to that of humans for therapeutic design.

PAMERAH can serve as a standardized platform for GRI construction, candidate screening, design optimization, and preclinical trial planning. Prior to any experimentation, the model is able to predict average GRI performances and narrow down the vast parameter space to a set of optimal combinations of design variables for the user-defined population and GRI mode of action. Such model-aided preclinical research would alleviate the burden of many trials and errors required in the traditional drug development workflow, an implication for not just GRIs.

Moreover, our mathematical formulation allows for a cross-comparison among mice, rats, and humans, highlighting their commonalities and differences. PAMERAH shows that the optimal GRI parameter spaces overlap, but not to a large extent, among the species, echoing the frequent difficulty of replicating animal studies in humans (17,18): the long-standing practice of informing clinical trials with animal data is now coming under scrutiny, as wittily described by Mak et al. (19) as “lost in translation.” PAMERAH further allows a zoned grid to be drawn on which GRI candidates are sectioned by their predicted viabilities along the train of medicinal translation. We expect the so-called “translatability grid” to serve as a straightforward visual guide for planning animal testing and clinical trials.

Research Design and Methods

Modeling the Full-Body Glucoregulatory System

A physiological model simulating a rodent’s full-body pharmacokinetics of glucose, insulin, and glucagon is first constructed, followed by its integration with GRI kinetics. The overall workflow is summarized in Supplementary Fig. 4.

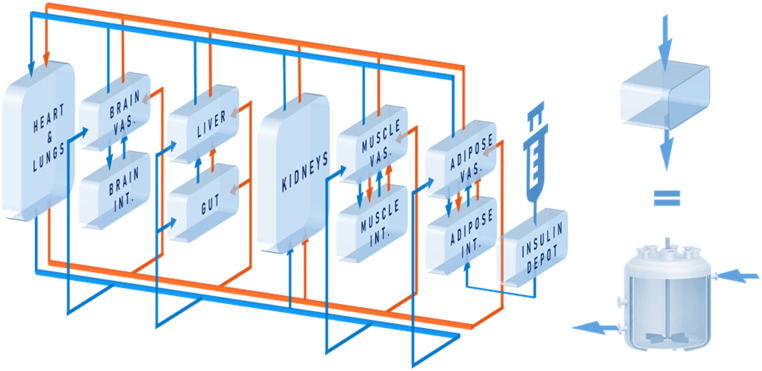
Mathematical modeling of the human glucoregulatory system has attracted sustained attention from the diabetes community over the years. While semimechanistic parsimonious models have seen some success (20,21), their compartmentalization is not based on physiology, which renders GRI integration difficult. This is contrasted by the whole-body model by Sorensen (22) and its variants. The Sorensen-like models (23–25) explicitly consider the physiology, taking into account the blood flow rates, volumes, and connectivity of organs. This allows dynamic concentrations to be probed and the glucose-hormone metabolism to be altered at the organ, rather than the organism, level (26). As with our prior physiological model of humans (5,26), PAMERAH is divided into well-mixed compartments symbolizing participating body parts, each equivalent numerically to an ideal continuous stirred-tank reactor (CSTR), as illustrated by Fig. 1. Blood circulates through vascular compartments of gut, liver, kidneys, brain, muscle, and adipose tissues, carrying glucose, insulin, and glucagon; the composition in the outlet of a vascular volume is approximated to be identical to that within the compartment—just like a CSTR. The solutes diffuse freely between the vascular and interstitial compartments as well where applicable, dictated by the concentration gradients. Naturally then, each solute s in each organ k is described as:

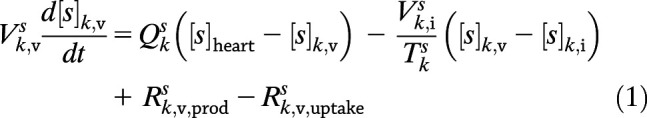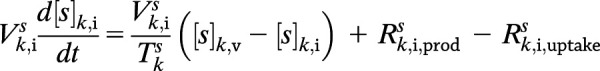where subscripts v and i denote the vascular and interstitial volumes, respectively. V represents the compartmental volume, [s] the solute concentration, Q the arterial flow rate through the organ, and T the characteristic transcapillary time of mass transfer. The production and uptake rates, R_prod and R_uptake, when applicable, are modulated by the compartment’s glucose, insulin, and glucagon concentrations through logistic transfer functions. As with our prior work (5), the subcutaneous injection depot is described by a hexamer-dimer-monomer equilibrium of which only the dimeric/monomeric insulins (or GRIs), lumped as a single state, are absorbed (Supplementary Table 2).

Figure 1.

Schematic of the model structure. Glucose (blue) circulates around the body along with blood, which is pumped by the heart and flows through vascular compartments of gut, liver, kidneys, brain, muscle, and adipose tissues. For the latter three, transcapillary diffusion of glucose into interstitial spaces is captured by the interstitial compartments. Insulin or GRI (orange), introduced into the circulation via the subcutaneous injection depot, flows through all but the brain interstitial compartment, into which insulin is unable to penetrate. Each compartment is equivalent to a CSTR (as shown on the right), where perfect mixing is assumed. INT., interstitial; VAS., vascular.

As the existing Sorensen-like mathematical models are parameterized based on the physiology of a healthy 70-kg man, the parameters have to be reexamined meticulously during the model’s extension to rats and mice. While exponential scaling laws are followed for interspecies adaptation of parsimonious compartmental models (27), the allometric exponents are empirical and bear little physical meaning. On the other hand, for a physiology-backed model like PAMERAH, a priori animal anatomical measurements are used to adjust the physiological parameters accordingly, such as the organ sizes, cardiac outputs, arterial flows, and blood volumes (Supplementary Table 1). As the transfer functions, which characterize the organs’ responsiveness to glucoregulation, are not directly adaptable to rodents, these metabolic parameters are estimated numerically from blood glucose time trajectories measured in rats and mice. The same method is applied to the base generation/clearance rates, which lack consistent measured values in the published literature. The insulin response data for rats and mice are collected experimentally and from literature (11) (male Lewis rats and C57BL/6J mice, healthy or with streptozotocin [STZ]-induced diabetes; also see Supplementary Material Text 1). To avoid overfitting, sensitivity analyses (28,29) are performed for dimension reduction. The model reduction is shown to yield consistent results for mice and rats (Supplementary Fig. 1). The most impactful 15 unknown parameters identified, out of >120, are subsequently fitted to data while keeping the remainder fixed (Supplementary Table 2). The dimension of estimated parameters is minimal compared with published physiology-based models (24,30,31). Parameter estimation is performed in MATLAB R2017a (The MathWorks, Inc.) with a pattern search algorithm.

The Sorensen model and its many extensions treat a patient with T1DM simply as a healthy individual with the pancreatic parameters negated and starting concentrations modified (5,22). In addition to introducing these distinctions between T1DM and healthy rodents, we also acknowledge the more subtle differences reported between the two populations, such as the changes in glucose/hormonal sensitivities and organ-specific base metabolic rates upon diabetes development (32–34). These interpopulation distinctions are addressed by estimating the eight relevant parameters separately for the T1DM and healthy rodents (Supplementary Table 2), consistent with current published works (21,24,35). In fact, attempts to simulate both groups with a single, unified set of values do not render satisfactory predictions that globally match experiments, thus highlighting the need of the distinguishing parameterization. Such was concurred and discussed in detail by Schaller et al. (24), who differentiated the healthy and diabetic populations by 26 separately fitted variables.

Modeling the GRI

GRIs of different working mechanisms, once expressed in mathematical terms, can be integrated with the as-constructed full-body physiological model, assembling into PAMERAH. Of all GRIs, the freely circulating class presents the simplest chemical kinetics. An example was reported by Chou et al. (11), who introduced responsiveness into their insulin analog by chemical modification with phenylboronic acid as a glucose-sensing element. Note that although Chou et al. also demonstrated a long-lasting activity with the GRI by incorporation of an aliphatic domain, our model focuses on the glucose responsiveness for now.

Action of the said class of GRIs can be condensed into the following two-state kinetics, where a dormant GRI (D) is reversibly activated by glucose (G), turning into the active form (I):

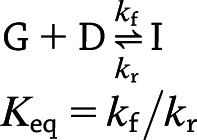where k_f is the forward rate constant, k_r is the reverse rate constant, and K_eq is the equilibrium constant. Consequently, for any solute s—where s can now be glucose, insulin, glucagon, or dormant GRI, each with a stoichiometric coefficient (ν) of −1, 1, 0, and −1, respectively—the defining Eqs. 1 and 2 in compartment k become:

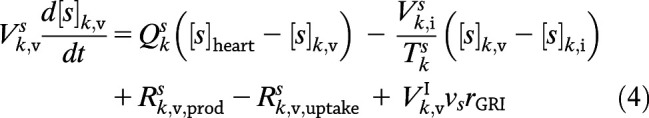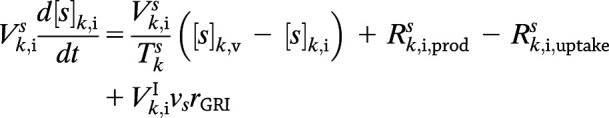where 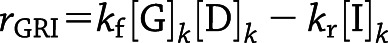for freely circulating GRIs described by Eq. 3. We adopt the kinetics of these GRIs for all PAMERAH simulations presented hereafter in this report for the mathematical simplicity and recent attention attracted. Of note, it is assumed throughout this report that the dormant GRI does not perturb the metabolic or hormone kinetics, while the activated GRI behaves identically as native insulin. For scenarios where the activated analog differs in potency from insulin, the assumption may be relaxed by treating them as separate solutes, each with a distinct set of ordinary differential equations.

The complete system of ordinary differential equations for all compartments and all solutes concerned can be constructed from the simple general Eqs. 4 and 5. A comprehensive tutorial is provided in the Supplementary Material Text 2 to walk the reader through the process. Note that the equations are given in a generalizable form, not just specific to the current model architecture, so that a reader attempting to modify or to supplement the model may follow exactly the same procedures outlined in the tutorial.

Simulating GRI in a Clamp

In addition to tracking the response of the blood glucose concentration to a single GRI injection, clamp studies (36) are an alternative standard technique to assess glucose responsiveness. We program PAMERAH to also simulate glucose clamps, the results of which are compared with recent GRI experiments as a further validation of the model. We follow the two-period pancreatic clamp protocol outlined in Moore et al. (37), illustrated in Supplementary Fig. 6. The glucose concentration is clamped for 150 min at 110 mg/dL (period 1) and for another 150 min at 240 mg/dL (period 2) by continuous infusion via the peripheral vascular compartment. The variable glucose infusion rate is adjusted by a simple feedback control. Meanwhile, either insulin lispro (1.2 mU/min) or GRI (24 mU/min) is infused continuously throughout the 300-min clamp, together with glucagon at its basal rate. The rates are consistent with prior reports (37,38). In Moore et al., pancreatic endocrine release was completely suppressed by somatostatin, simulated as the corresponding differential equations bypassed in PAMERAH. Therefore, all circulating insulin and glucagon is accounted for by external infusion, except during the short initial equilibration. The hepatic glucose load (HGL) is calculated as 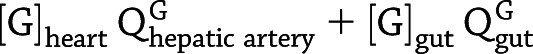, and the net hepatic glucose balance (NHGB) is defined as .

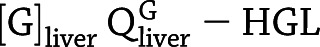Elucidating the GRI Design Space

PAMERAH provides valuable assistance to the GRI development process by assessing the GRI’s therapeutic efficacy in mice and rats on the basis of its material and molecular design. Intuitively, an adequate GRI should reduce hyperglycemia in a patient with diabetes for a prolonged period (with a single bolus), while not incurring any additional risk of hypoglycemia (9). Sometimes fatal, the latter is referred to as the “limiting factor” in glycemic management (39). The mathematical expression for said criteria is below:

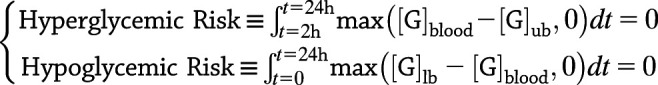in which t = 0 marks the time of GRI administration. [G]_ub and [G]_lb are the upper and lower bounds of the normoglycemic range, set to 240 and 75 mg/dL, respectively, for rats (40) and 250 and 40 mg/dL for mice (41). As described by Eq. 6, normoglycemia should be maintained for a GRI design to be qualified: the blood glucose level should not deviate from the normal range within 24 h of the single GRI bolus, except for the first 120 min allowed for the hyperglycemia to be put under control.

The properties of freely circulating GRIs are modulated by three design variables: k_f, K_eq, and the dosage. We term each distinct permutation of the three a potential GRI design or a candidate, with its own hyper- and hypoglycemic risks. By probing the k_f-K_eq-dosage parameter space, the in silico preclinical simulations identify regions free from the said risks. Finally, this simulation study is repeated for humans as well using the model of Bakh et al. (5). An interspecies cross-comparison reveals the similarities and dissimilarities among humans, rats, and mice and provides insights on drug translatability.

Data and Resource Availability

The data used in this study are available from the corresponding author upon request. No applicable resources were generated or analyzed.

Results

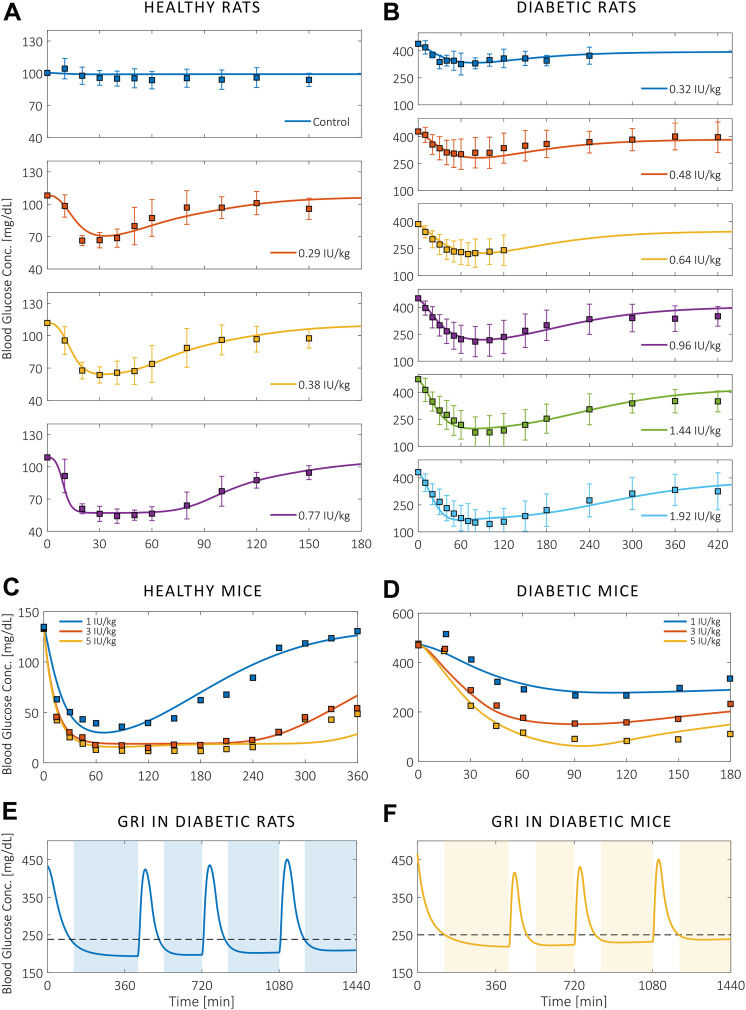
Blood glucose responses to an initial insulin injection, as predicted by the parameterized full-body physiological models, are presented in Fig. 2A–D alongside murine in vivo data collected experimentally and from the published literature (11). We show that the temporal profiles match between model and animal data for various doses of subcutaneous insulin administration to healthy and T1DM rodents alike. Trajectories in Fig. 2A–D also reveal how the effect of unmodified insulin decreases quickly despite large injection doses. In Fig. 2E and F, we present as an example the simulated action profiles of a freely circulating GRI in average diabetic rats and mice. PAMERAH predicts that in addition to suppressing the blood glucose levels, this particular GRI candidate is also able to arrest three postprandial glycemic excursions within 120 min, each resultant from a 1 g/kg oral glucose meal (42), over the course of 24 h. The corresponding insulin release patterns (Supplementary Fig. 5) resemble published results (15).

Figure 2.

Blood glucose responses in rodents to a single insulin injection. A–D: The agreement between murine in vivo data (squares) and the predicted glycemic responses (curves) to various doses of nonresponsive insulin administered at t = 0. PAMERAH predictions match well with experimental measurements from healthy (A) and T1DM rats (B) as well as healthy (C) and T1DM mice (D). Curves for rats are presented individually to avoid overlapping of data points and confidence limits, which indicate ±1 SD. Data were collected from male Lewis rats, the diabetes of which was induced by STZ (Supplementary Material Text 1). Measurements on mice (male C57BL/6J, STZ) are extracted from Chou et al. (11). The corresponding error bars are absent because they were undefined in Chou et al., and the clustered error bars cannot be precisely digitized from the original figures. E and F: The 24-h action profiles of a GRI example (k_f = 0.1 L/mol-min, K_eq = 0.02 L/mol, dosage = 300 μg/kg) in average diabetic rats (E) and mice (F). The blood glucose concentration drops to the normoglycemic range within 120 min after the initial injection at t = 0 and each of the three meal ingestions (1 g/kg glucose at t = 420, 720, and 1,080 min), periods represented by the unshaded areas. The peak postprandial concentrations are respectively 423.8, 434.9, and 450.2 mg/dL for diabetic rats and 415.2, 430.5, and 450.4 mg/dL for diabetic mice. The dashed lines indicate the upper bounds of normoglycemic ranges. Conc., concentration.

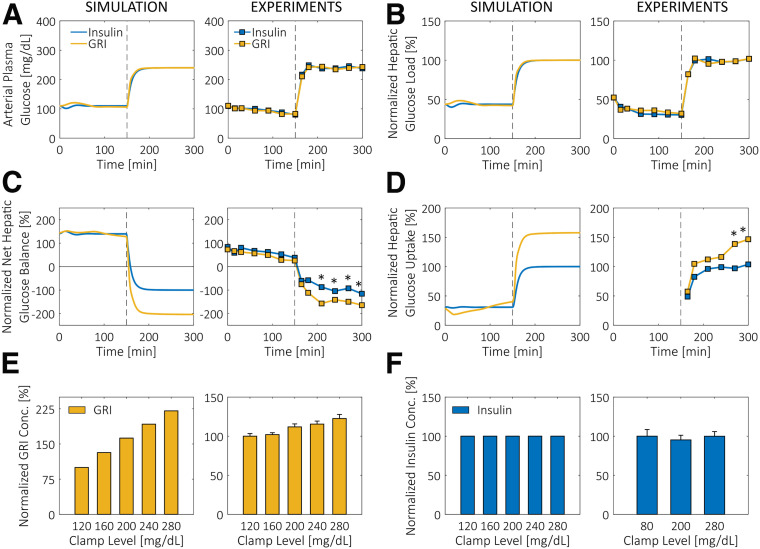
The validity of PAMERAH is further supported by the agreement between simulated clamp results and experimental data. In their two-period pancreatic clamp study, Moore et al. (37) found that while the hepatic glucose loads were comparable between the GRI and insulin groups (Fig. 3B), both the net and the unidirectional hepatic glucose uptakes (HGUs) (Fig. 3C and D, respectively) for the GRI study were significantly higher than the nonresponsive insulin control at the hyperglycemic clamp level (period 2). All these findings are matched by PAMERAH simulation in rats (Fig. 3A–D) in addition to correctly predicting the relative changes in each quantity after the clamp level shift. Curiously, the simulated and actual time courses of HGL, NHGB, and HGU agree quantitatively once normalized, despite the fact that the GRI of Moore et al. was of a different working principle and tested on dogs. This seems to suggest a universal signature of glucose responsiveness: under hyperglycemic conditions, a GRI would enhance the liver glucose uptake more effectively than a dose of nonresponsive insulin.

Figure 3.

Glucose clamp results simulated by PAMERAH compared with experiments. A: Glucose is clamped at 110 mg/dL (period 1) and 240 mg/dL (period 2) for 150 min each with constant infusion of either nonresponsive insulin or GRI, as described in research design and methods. B–D: Consistent with the published experimental data (37), the HGLs (B) for insulin and GRI do not differ at either clamp level. While the NHGBs (C) are positive in period 1, they switch signs at the higher clamp level, indicating a change from net glucose production to consumption in the liver. As with experiments (right), GRI induces a larger change than the nonresponsive control in period 2. Similarly, while both the GRI and the insulin groups trigger a surge in unidirectional HGU (D) at t = 150 min, GRI is more effective, a feature captured by the simulation. Data in B–D are normalized by the respective period 2 steady-state values for the insulin group due to the differences in GRI mechanisms and test animals. *P < 0.05 for GRI vs. control. E and F: Responsiveness of GRI and insulin to various glucose levels is shown alongside data from clamps (43). While the amount of active GRI released is increasing with the clamp level (E), the concentration of nonresponsive insulin (F) shows no dependence. Note that in the clamps described, GRI is solely responsible for the observed responsiveness because the pancreatic insulin production is inhibited by somatostatin. The concentrations in E and F are normalized by the corresponding values at 120 mg/dL. The prenormalization GRI concentrations ranged from 165.8 mU/L (at 120 mg/dL) to 290.4 mU/L (at 280 mg/dL) for simulations in rats and from 761.5 to 933.3 mU/L for MK-2640 in dogs. All experimental data are digitized from published figures. Conc., concentration.

PAMERAH simulation is shown to also match a separate set of data provided by Kaarsholm et al. (43), who investigated the active GRI/insulin concentrations at various clamp levels following a similar protocol outlined above. Both our simulation and the data clearly show that a larger amount of active GRI is made available at a higher glucose level (Fig. 3E), while such a dependence is absent in the control study (Fig. 3F). The quantitative discrepancies are attributed to the different GRI mechanisms, to be addressed further in the discussion.

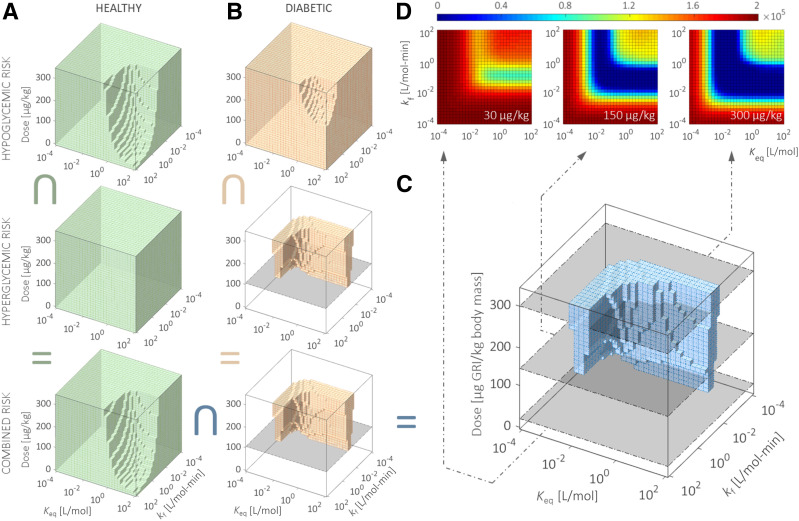
Following its validation with experimental results, PAMERAH is subsequently applied to systematically screen the freely circulating GRI candidates by simulating the murine glycemic responses to each. The varied design parameters therefore form a three-dimensional GRI Design Space (GRIDS), shown as the boxes in Fig. 4 and probed by PAMERAH. Each point in GRIDS represents a unique combination of k_f, K_eq, and dosage, which we term as one design. Our mathematical model gauges the hypo- and hyperglycemic risks associated with each such design and thereby identifies the qualified GRI candidates free of the risks (i.e., those predicted to maintain normoglycemia over at least 24 h, as governed by Eq. 6). The qualified designs within GRIDS constitute what we call optimal design regions (ODRs), represented as the shaded geometries in Fig. 4A–C, which are respectively ODRs of healthy rats, T1DM rats, and the intersection. Those for mice and humans are found in Supplementary Fig. 7. We observe that the diabetic ODR is bounded from beneath by a global minimum effective dose of 115 ± 5 μg/kg (marked by the gray planes in Fig. 4B), below which no design is able to contain hyperglycemia for a day (Fig. 4D). The global minimum doses for mice and humans are 105 ± 5 and 12.25 ± 0.25 μg/kg, respectively. The latter is of a reduced uncertainty because the low-dosage portion of the human GRIDS is explored with a refined resolution (Supplementary Fig. 7C).

Figure 4.

Exploring the optimal combinations of GRI design parameters for efficacy in rodents. PAMERAH explores the GRIDS and evaluates the hypo- and hyperglycemic risks associated with each GRI candidate for both healthy (A) and diabetic (B) rats. The shaded areas in GRIDS are the ODRs, which represent those combinations of k_f, K_eq, and dosage free of hypoglycemic (top), hyperglycemic (middle), or both (bottom, intersection of the other two single-risk ODRs) risks. The gray planes in B mark the global minimum effective dosage in diabetic rats. The GRI designs, which incur neither risk in normal and diabetic rats alike, are shaded blue (C). The characteristic L shape is consistent with prior reports (5), better visualized by contour plots (D) sliced at fixed GRI dosages (30, 150, and 300 μg/kg) (marked gray in the GRIDS). The colors in D correspond to the sum of all hypo- and hyperglycemic risks combined, with dark blue representing desirable GRI constructs that maintain normoglycemia over 24 h. ODRs and GRIDS for mice and humans are found in Supplementary Fig. 7. The inverted U symbol indicates intersection.

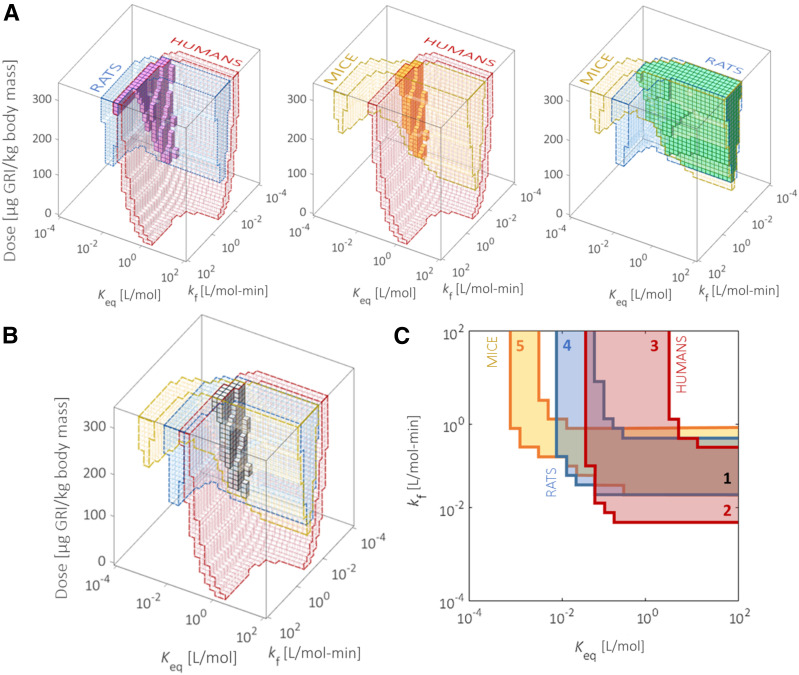
A cross-comparison among the ODRs of rats, mice, and humans (Fig. 5A and B) reveals the interspecies commonalities and distinctions. While the ODRs for rats and mice overlap to a moderate extent, a fairly limited subset of optimal GRI designs in rodents is predicted to be also acceptable to humans. Acknowledging the GRI dosage as an easily adjustable design parameter neglecting solubility, we relax the corresponding dimension (Fig. 5C). The three-dimensional GRIDS is thereby collapsed into a two-dimensional plane on which combinations of k_f and K_eq are zoned by their performances in different species: we are able to identify designs effective in rodents only, humans only, neither, or both, each respectively constituting 12.0%, 14.1%, 60.3%, and 13.6% of all designs within the particular variable bounds. This zoning scheme can serve as a simple guideline for GRI translation as discussed in more detail below.

Figure 5.

Evaluating the GRI translatability from rodents to humans. A: The commonalities (solid) between ODRs (colored and outlined) of humans and rats (left), humans and mice (middle), and rats and mice (right). B: The ODR intersection (solid) is marked among all three species. The limited overlap between human and rodent ODRs forecasts the difficulties in interspecies translation of the therapeutic. C: By relaxing the dosage variable (0–330 μg/kg) and allowing it to assume flexible values for different species, we project the three-dimensional GRIDS onto a two-dimensional k_f-K_eq plot. We call the plot a translatability grid on which GRI designs are zoned according to their translatability. GRI constructs in zone 1 are predicted to be effective in both rodents and humans. They therefore translate well among species with appropriate dosages. Zones 2 and 3 represent the false-negative designs eliminated in rodent studies yet potentially clinically viable. Zones 4 and 5 are examples of false positives that appear effective in rat/mouse trials but do not translate well into humans. They will likely meet attrition at the clinical stage.

Discussion

In this work, we developed the modeling framework PAMERAH as a platform relating a GRI’s design to its therapeutic efficacy in rats and mice. On the basis of the full-body physiology, the pharmacokinetic model simulates the absorption, circulation, uptake, generation, and clearance of glucose, glucagon, as well as GRI or nonresponsive insulin by treating each organ as a well-mixed CSTR. With key parameters calibrated by in vivo data, we demonstrate that PAMERAH predicts the dynamic blood glucose responses and clamp results in rodents for insulin as well as for GRIs of user-specified kinetics (Figs. 2 and 3). In the following discussion, we highlight how PAMERAH aids the rational design process of GRI and its translation to the clinic.

Model-Aided GRI Design

PAMERAH is able to explore the parameter space and predict the average performance of each combination of design variables, thus narrowing down the vast pool of GRI candidates in silico, thereby providing directions to GRI preclinical research as evidenced by GRIDS and ODRs in Fig. 4. The ODR geometries also strengthen validity of the model predictions. We observe that the diabetic rat ODR assumes a signature L shape (Fig. 4B, bottom) and, consequently, so does the ODR for normal and diabetic populations combined (Fig. 4C). Concurring with prior reports (5), the L geometry results from the balance between rapid action and sustained control. On one hand, GRI candidates of slow kinetics, marked by a small k_f or K_eq, are unable to reduce blood glucose concentration in time to the normoglycemic range (Fig. 4B, middle). On the other hand, GRIs of large k_f and K_eq rapidly convert to active insulin; consequently, they either deplete prematurely, unable to sustain the potency over 24 h (Fig. 4B, middle), or overcorrect the hyperglycemia, thus triggering hypoglycemic episodes (Fig. 4B, top). The latter also explains the missing corner in Fig. 4A, which characterizes the ODR of the healthy population, for which the hyperglycemic risk is absent. Consistent with mouse and human GRIDS probed as well (Supplementary Fig. 7), the observations above suggest a good agreement between PAMERAH predictions and qualitative expectations.

We envisage the PAMERAH-aided rational design of GRI boosting the productivity of drug developers by (partially) substituting the conventional workflow, where each empirically designed and often laboriously synthesized candidate is experimented in vitro and in vivo for its efficacy evaluation (11,44). The same evaluation may now be performed in silico at effectively no cost, even before the physical existence of any GRI prototype, a benefit enjoyed only by mechanistic, physiological models like PAMERAH and not data-driven empirical models (45). The medicinal chemists may then proceed, focusing on just the optimized, most promising lot—the ODRs (46). This would be especially helpful to GRI researchers without access to automated combinatorial chemistry or screening. The facilitated designing process aside, PAMERAH also provides information on the minimum effective doses and may potentially lighten the dependency on animal testing, to which the model supplies a rational starting point. Furthermore, such a physiological model for preclinical species, supported by in vivo measurements, promotes the confidence in the corresponding human models, as argued by Jones et al. (47,48): simulations in rodents are an essential intermediate step toward accurate predictions of human pharmacokinetics at the clinical stage, as concluded from a PhRMA initiative (45).

Model-Aided GRI Translation

Cross-comparing the optimal designs for different species is shown to reveal the commonalities and distinctions among rats, mice, and humans (Fig. 5) and, therefore, the potential interspecies translatability of drug candidates. While the ODRs for diabetes all assume the characteristic L geometry, the minimal overlaps between rodent and human ODRs (Fig. 5A and B) hint that a large portion of GRI designs, again each defined by a combination of k_f, K_eq, and dosage in this report, would render adequate, sustained glycemic control in rodents yet fail clinically, which we call false-positive preclinical results. In other words, PAMERAH predicts a high attrition rate if GRI constructs are translated to the clinical trial stage with the same parameters as in rodents, hence echoing the published poor rates of successful translation (18,49): the well-known estimate of Hackam and Redelmeier (17) was that only 37% of animal studies were successfully replicated in human trials. A Tufts University investigation further communicated that the clinical translation of antidiabetic drugs is even riskier compared with other pharmaceuticals (50). For instance, Merck’s MK-2640, the only GRI we know of that entered the clinical trial stage, did not achieve the same level of glucose responsiveness in humans as in preclinical models (43,51).

In addition to the false positives, the overlaid GRIDSs in Fig. 5 by the same token identify the GRI candidates deemed unsuitable in rodents but potentially effective in humans (i.e., the false negatives). While many agree that the opportunity cost of the false negative is greater than the false positive (52), little is known about the extent to which we wrongly discontinue a viable drug design on the basis of negative preclinical outcomes because such a candidate is usually eliminated from further confirmation. The available analyses on this topic target false negatives at a single clinical stage, which is more of a decision variable controllable by the trial sample size (52)—conceptually distinct from the false negatives pertaining to rodent model translatability. PAMERAH predictions on “what should have passed,” in addition to “what should not have,” therefore adds helpful new knowledge. We further note that the same methodology is applicable to therapeutics beyond GRIs. For example, Jones et al. (48) simulated pharmacokinetic actions of several small-molecule candidates in both preclinical animals and humans; while the compounds had been finalized before the said study, the physiology-based models could have assisted the design and translation processes, akin to PAMERAH, were they available at the earlier stages of drug development.

We acknowledge that in contrast to kinetic variables k_f and K_eq, the GRI dosage is a more flexible dimension. Figure 5C displays the outcome when the dosage dimension is relaxed and allowed to assume different values (per body mass) for different species. Projecting the three-dimensional GRIDS along the dosage axis onto the k_f-K_eq plane issues a graphic (Fig. 5C) loosely analogous to a Clarke error grid (53) but with zones representing the design’s translatability instead of a measurement’s clinical accuracy. We see that each three-dimensional ODR is now compressed to a two-dimensional L shape, inside which a GRI design (of a certain k_f-K_eq combination) is effective within some dosage range. The overlap between ODRs of humans and either rodent (mice or rats) marks the true-positive designs predicted to translate well into the clinic: they are effective regardless of species (Fig. 5C, zone 1). They, nevertheless, only make up 13.6% of the total plane, comparable to the identified false positives (12.0%; zones 2 and 3): The numbers are roughly interpreted as an attrition rate of almost one-half for the candidates successful in rodents. On the other hand, it is surprising that 14.1% of possible GRI constructs are wrongly disqualified (false negative; zones 4 and 5), equivalent to approximately one-half of the clinically adequate designs being excluded from potentially entering the human trials. This observation highlights the need for predictive tools such as PAMERAH since animal models can possess parametric regions that do not map to human performance. We note that the exact area percentages depend on the GRIDS bounds (Supplementary Fig. 8), and a reasonable upper dosage bound should be set based on, say, solubility limitations (54). Although the attrition in developing a GRI may also result from nonefficacy-related factors, such as toxicity and commercial unprofitability (46), and that certain combinations of k_f-K_eq may be more attainable than the others, the idea of this translatability grid, drawn from model predictions, is widely applicable and offers a straightforward visualization for early-stage decision making just like the Clarke error grid. The translatability grid makes possible a modified paradigm in medicinal translation: a higher priority to clinical evaluation may now be granted to the true positives over the false positives, and the false negatives identified proceed to further trials in preclinical models closer to humans (e.g., pigs, nonhuman primates).

Outlook and Summary

The approach that we describe is of considerable flexibility. To start with, the application space is not constrained to just freely circulating GRIs taken as a proof of concept here since GRI kinetics in PAMERAH are independent from the organism physiology and are therefore adaptable to reflect alternative glucose-responsive mechanisms, established or hypothetical. For example, one of our ongoing projects is to model the aforementioned MK-2640, which responds to glucose via a competitive clearance mechanism (43) illustrated in Supplementary Fig. 2. We have already demonstrated that the predicted hepatic impacts of a freely circulating GRI match that of MK-2640 well and that their trends of active GRI concentrations versus clamp levels agree qualitatively (Fig. 3). It is therefore reasonable to argue that PAMERAH can be extended to describe the MK-2640 action with an updated set of chemical kinetics. Although MK-2640’s glucose responsive activity is considerably more involved, we have shown that the competitive receptor binding and subsequent clearance can be modeled equally well as the simpler kinetics explored earlier (Supplementary Material Text 3), supported by the convincing fit to in vitro binding assay measurements (Supplementary Fig. 3). Ultimately, mapping MK-2640’s animal and human design spaces can possibly reveal why the translation was difficult (51).

Along the same lines, PAMERAH may be built upon non-Sorenson–like physiology as well, such as the acclaimed Dalla Man, or UVA/Padova, model (55), the adaptability of which is demonstrated in our prior work on human pharmacokinetics (5). Similar procedures may be taken to develop mathematical models of other animal species as well. From a model customization perspective, the GRIDS can be subject-tailored by updating the parameter estimation with any new data available (45), alongside a priori parameterization of the individual physiology (24) discussed in detail by Peters (16). Such will supplement the future studies on intrapopulation variabilities (56) in GRI responses and the associated implications on ODRs. We acknowledge that, while information on population averages suffices for early GRI design and screening as in the case of this report, the capability to predict the variabilities will form the basis of individualized health care and fine-tuning of the drug. Such capability is lacking in the current iteration of PAMERAH and will be addressed. As described in Cobelli et al. (57), joint probability distribution of free parameters can be reconstructed from population data, after which a pool of virtual individuals can be generated.

Future iterations of the model will also take into account additional factors that affect the overall GRI performance, such as pH, temperature, and exercises. Physical activities, for instance, redistribute the blood flow and modify the glucose production/uptake (25). From the modeling perspective, the corresponding variables can be correlated to the exercise intensity, following methodologies outlined previously (25,58). Finally, we envision PAMERAH being used for planning GRI regimens in the future: will a recipe involving multiple kinetics be even superior to a single GRI?

GRIs represent “a new horizon in therapeutic technology” that offers a closed-loop control strategy alternative to continuous insulin infusion (9). However, their design and screening, largely at the early preclinical research stage, have been reliant on empirical knowledge and repeated experimentation. We present a modeling platform, PAMERAH, that predicts a GRI’s efficacy in rats and mice from its properties. It is therefore able to explore the targeted GRIDS and identify the pool of optimal candidates before any experiments, thereby providing some rational guidance to the preclinical GRI research. Built upon prior human physiological models, our platform is shown to gauge a design’s translatability from animal subjects to clinical patients and thereby generate the translatability grid. We hope PAMERAH helps to establish an improved drug development workflow and accelerate the development of GRIs for individuals with T1DM.