Abstract
In this article we analyze the linear parabolic partial differential equation with a stochastic domain deformation. In particular, we concentrate on the problem of numerically approximating the statistical moments of a given Quantity of Interest (QoI). The geometry is assumed to be random. The parabolic problem is remapped to a fixed deterministic domain with random coefficients and shown to admit an extension on a well defined region embedded in the complex hyperplane. The stochastic moments of the QoI are computed by employing a collocation method in conjunction with an isotropic Smolyak sparse grid. Theoretical sub-exponential convergence rates as a function to the number of collocation interpolation knots are derived. Numerical experiments are performed and they confirm the theoretical error estimates.
Keywords: Parabolic PDEs, Stochastic PDEs, Uncertainty Quantification, Stochastic Collocation, Complex Analysis, Smolyak Sparse Grids
1. Introduction
Mathematical modeling forms an essential part for understanding many engineering and scientific applications with physical domains. These models have been widely used to predict the QoI of any particular problem when the underlying physical phenomenon is well understood. However, in many cases the practicing engineer or scientist does not have direct access to the underlying geometry and uncertainty is introduced. Quantifying the effects of the stochastic domain on the QoI will be critical.
In this paper a numerical method to efficiently solve parabolic PDEs with respect to stochastic geometrical deformations is developed. Application examples include subsurface aquifers with geometric variability diffusion problems [13], acoustic energy propagation with geometric uncertainty [27], chemical diffusion with uncertain geometries [26], among others.
Several methods have been developed to quantify uncertainty of elliptic PDEs with stochastic domains. The perturbation approaches [21, 46, 18] are accurate for small stochastic domain deformations. In contrast, the collocation approaches in [9, 14, 45] allow the computation of the statistics of the quantity of interest for larger domain deviations, but lack a full error analysis. In [8], the authors present a collocation approach for elliptic PDEs based on Smolyak grids with a detailed analyticity and convergence analysis. Similar results where also developed in [20, 22]..
For stationary Stokes and Navier-Stokes Equations for viscous incompressible flow in [10], a regularity analysis of the solution is studied with respect to the deformation of the domain. This approach is similar to the mapping technique proposed in this paper i.e. the stochastic domain is assumed to be transformed from a fixed reference domain. The authors establish shape holomorphy with respect to the transformations of the shape of the domain.
In [25] the authors perform a shape holomorphy analysis for time-harmonic, electromagnetic fields arising from scattering by perfect conductor and dielectric bounded obstacles. This approach falls under the class of asymptotic methods for arbitrarily close random perturbations of the geometry. However, the authors show dimension-independent convergence rates for shape Taylor expansions of linear and higher order moments.
A fictitious domain approach combined with Wiener expansions was developed in [7], where the elliptic PDE is solved in a fixed domain. In [38, 37] the authors introduce a level set approach to the stochastic domain problem. In [40] a multi-level Monte Carlo has been developed. This approach is well suited for low regularity of the solution with respect to the domain deformations. Related work on Bayesian inference for diffusion problems and electrical impedance tomography on stochastic domains is considered in [16, 23].
The work developed in this paper is a extension of the analysis and error estimates derived in [8] to the parabolic PDE setting with Neumann and Dirichlet boundary conditions. Moreover, the stochastic domain deformation representation is extended to a larger class of geometrical perturbations. This class of perturbations was originally introduced in [20, 18].
The stochastic domain is assumed to be parameterized by a valued random vector. Complex analytic regularity of the solution with respect to the random vector is shown. A detailed mathematical convergence analysis of the collocation approach based on isotropic Smolyak grids is presented. The error estimates are shown to decay sub-exponentially as a function of the number of interpolation nodes of the sparse grid. This approach can be extended to anisotropic sparse grids [35].
In Section 2 the problem formulation is discussed. The stochastic domain parabolic PDE problem is remapped onto a deterministic domain with a matrix valued random coefficients. In Section 3 the solution of the parabolic PDE is shown that an analytic extension exists in region in . In Section 4 isotropic sparse grids and the stochastic collocation method are described. In Section 5 an error analysis of the QoI as a function of the number of sparse grid knots and a truncation approximation Ns < N of the random vector are derived. In section 6 numerical examples confirm the theoretical sub-exponential convergence rates of the sparse grids, and the truncation approximation.
2. Problem setting
Let be an open bounded domain that is dependent upon a random parameter , where is a complete probability space, Ω is the set of outcomes, is the σ-algebra of events and is a probability measure. The corresponding is assumed to be Lipschitz.
Suppose that the boundary is split into two disjoints sections and . Consider the following boundary value problem such that the following equations hold almost surely:
| (1) |
where T > 0. Let , then the functions , and are defined over the region of all the stochastic perturbations of the domain in . Similarly, let , then the boundary conditions are defined over all the stochastic perturbations of the boundary .
Before the weak formulation is posed, some notation and definitions are established. If , let be defined as follows
where is strongly measurable. For valued vector functions , , let
In addition, defined the following space
and denote by the dual space of .
Suppose that , where for all is a compact connected domain or unbounded. Let be the Borel σ–algebra with respect to and suppose that is a valued random vector measurable in .
Consider the induced measure on . Let for all . Suppose that the is absolutely continuous with respect to the Lebesgue measure defined on , then from the Radon–Nikodym theorem [5] for any event there exists a density function such that . In addition, the expected value is defined as for any measurable function .
For define the following spaces
We now pose the weak formulation of equation (1) (See Chapter 7 in [11] and Chapter 7 in [30]):
Problem 1.
Given that and find , with Neumann boundary conditions on s.t.
| (2) |
almost surely, and
Through out the paper, we restrict our attention to linear parabolic PDE with Neumann boundary conditions. Recall that the Neumann boundary condition is defined over . Problem 1 has a unique solution if the following assumption is satisfied (See Chapter 7 of [11], Chapter 7 of [30], and Chapter 4 of [32] in Volume II):
Assumption 1.
Let and , and assume that .
Remark 1.
In Problem 1 vanishing Dirichlet boundary conditions are assumed to simplify the presentation. We can also consider nonzero Dirichlet boundary condition e.g. . If the boundary condition is time independent, i.e. , then set , where agrees with on . It follows the solution satisfies the following weak form on :
Hence we translate the nontrivial Dirichlet boundary condition into the standard Dirichlet boundary condition with an alternative inhomogeneous term. The analyticity analysis in Section 3 can be easily extended by following similar assumptions and arguments for as shown in [8]. However, it may also require a compatibility condition between gD and gN on .
On the other hand, if gD is a function of t, and agrees with some - function on for each t, then the setup will result in an extra time dependent term in the weak sense:
In this case, the analytic extension for the term becomes time dependent and the analysis is significantly more complicated.
2.1. Reformulation on a reference domain
To simplify the analysis of Problem 1 we remap the solution onto a non-stochastic fixed domain. This approach has been applied in [14, 8, 20, 22, 18] and we can then take advantage of the extensive theoretical and practical work of PDEs with stochastic diffusion coefficients.
The idea now is to remap the domain onto a reference domain almost surely with respect to Ω. Suppose there exist a reference domain with Lipschitz boundary and a bijection that maps into U almost surely with respect to Ω. The map, is written as
where β are the coordinates for the reference domain U. See the cartoon example in Figure 1.
Figure 1:
Bijection map graphic example of the reference domain U and the domain with respect to the realization . The drawing is rendered from a TikZ modification of the code provided in [43].
Assumption 2.
Denote by the Freéhet derivative (Jacobian) of the bijective map . Furthermore, let and be respectively the minimum and maximum singular value of . Suppose there exist constants such that and a.e. in U and a.s. in Ω.
Remark 2.
The previous assumption implies that the Jacobian almost surely.
From the Sobolev chain rule (see Theorem 3.35 in [1] or page 291 in [11]) it follows that for any
| (3) |
where refers to the gradient on the domain , ∇ is the gradient on the reference domain U, and . Let
where ∂U is the boundary of is the range of F−1 with respect to the boundary is the range of F−1 with respect to the boundary and . Furthermore, denote by V* the dual space of V.
We can now show that:
Lemma 1.
Under Assumptions 2 the following pairs of spaces are isomorphic
Proof.
i)–iv) From the Sobolev chain rule it is not hard to prove. These results can be found in either [8], or similarly in [9].
v) Suppose we have a disjoint finite covering of the boundary ∂U such that for each there exists a Lipschitz bijective mapping (c.f. trace theorem proof, p. 258 in [11] for details and [39]), where and is a ball of radius r. In the following proof the Lipschitz mappings , are assumed to be differentiable. From the Radamacher Theorem [12] every Lipschitz function is differentiable almost everywhere. Therefore without loss of generality we can replace the Lipschitz mappings , with an equivalent differentiable version except for sets of measure zero. For simplicity we shall perform the following analysis with respect to a single open set τ and mapping , then for any
| (4) |
Now, covers a portion of the boundary of , then
where . It is not hard to show that for any vector , where ,
The result follows.
-
vi) Suppose that , then is equal toThe positive constant C > 0 is due to the fact that . Let , then
The converse is similarly proven.
vii)The result follows by using ii), the Trace Theorem and inverse Trace Theorem (Theorems 2.21 and 2.22 in [44]).
Note that analogous lemmas are proved in [8, 20].
From this point on the terms a.s. and a.e. will be dropped unless emphasis or disambiguation is needed. For any
With a change of variables the boundary value problem is remapped.
Problem 2.
Given that , and find , with Neumann boundary condition on ∂UN s.t.
almost surely, where
where is a linear bounded operator such that , satisfies . The weak solution is obtained as .
Now we have to be a little careful. The existence theorems from [11], Chapter 7, do not apply directly to Problem 2 due to the term. Although the existence proof in [11] can be modified to incorporate this extended term, we direct our attention to Theorem 10.9 in [6] from J. Lions [32].
Let H (with norm ) and W (with norm ) be Hilbert spaces with the associated dual spaces H* and W* respectively. It is assumed that with dense and continuous injection so that
For a.e. suppose the bilinear form satisfies the following properties:
For every the function is measurable,
For all for a.e.
For all for a.e. .
where α > 0, M and C are constants.
Theorem 1.
(J. Lions) Given a bounded linear functional and , there exists a unique function satisfying
for a.e. , and .
Proof.
See Chapter 4 of Volume II of [32].
We can now use Theorem 1 to show that there exists a unique solution to Problems 1 and 2. Let and then from Theorem 1 there exists a unique solution for Problem 1 such that . From Lemma 1 there is an isomorphic map between and u. Since there is a unique solution for Problem 1, we conclude there exists a solution for Problem 2 such that . The last step is to confirm that it is unique solution. This is done by checking is the solution whenever the inhomogeneous term vanishes and the boundary conditions are trivial.
2.2. Stochastic domain deformation map
The next step is to build a parameterization of the map from a set of random variables with probability density function . One objective is to build a parameterization such that a large class of stochastic domain deformations are represented. Following the same approach as in [18, 20], without loss of generality we assume that the map has the finite noise model
From the Doob-Dynkin Lemma the solution to Problem 2 will be a function of the random variables .
This is a very general representation of the stochastic domain deformation. For example, such representation may be achieved by a truncation of a Karhunen-Loéve (KL) expansion of vector random fields [20]. In general, the KL eigenfunctions , which presents a problem, as the KL expansion of the random domain may lead to large spikes and thus most likely Problem 2 will be ill-posed. However, under stricter regularity assumptions of the covariance function the eigenfunctions will have higher regularity (see [15] for details). We thus make the following assumption:
Assumption 3.
For
. decreasing.
The Jacobian can be similarly written as
| (5) |
3. Analyticity of the boundary value problem
In this section we show that the solution to Problem 2 can be analytically extended on a region in with respect to stochastic variable . The larger the complex analytic domain is the higher the regularity of the solution with respect to . This provides us a path to estimate the convergence rates of the stochastic moments by using a sparse grid approximation. In particular, the larger the size of the region , the faster the convergence rate of the sparse grid approximation will be.
Remark 3.
To simplify the analysis assume that is bounded in . Without loss of generality it can also be assumed that . However, can be extended to the non-bounded case by following the approach described in [2].
We formulate the region by making the following assumption:
Assumption 4.
1. There exists such that for all .
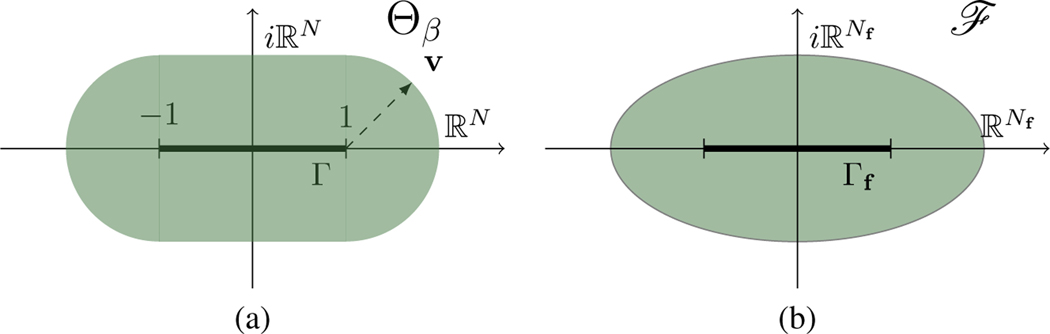
For any define the region (as shown in Figure 2 (a)):
| (6) |
Figure 2:
Graphical representation of the sets Γ and Γf. (a) is the extension of the set Γ as a function of the parameter β. (b) Extension of Γf into the region .
Now, we can extend the mapping , with , to by simply replacing y with . It is clear due to linearity that the entries of the maps F and ∂F are holomorphic in . Moreover, denote by the image of .
Since then the matrix inverse of can be written as . Furthermore, since then the holomorphic expansion of can be written as the series
The sum is pointwise convergent . We conclude that for all the entries of the matrix are analytic.
Up to this point we have assumed that only the geometry is stochastic but have made no assumptions on further randomness in the forcing function, the boundary conditions or the initial condition in Problems 1 and 2. These terms can also be extended with respect to other stochastic spaces.
Assumption 5.
-
Suppose that the Nf valued random vector takes values on with the probability density . The domains can be assumed to be closed intervals in . Now, assume that the random vector f is independent of y and write the forcing function as
where for , and . Since is defined on we can remap with pullback onto the reference domain asWe shall now make analytic extension assumptions of the coefficients cn(t, f) and for . The coefficients are defined over the domain . Since the solution from Problem 2 is dependent on the coefficient cn(t, f) certain analyticity assumptions have to be made. In particular, suppose there exists an analytic extension of onto the set , where (See Figure 2 for a graphical representation). The size of the region will directly depend on the coefficients on a case by case basis. Furthermore, for the following assumptions are made:- can be analytically extended on .
- where refers to the the Wirtinger derivative along the nth dimension.
The initial condition has an analytic extension on . Moreover, it is assumed that for all .
Assumption 6.
We make the following assumptions on the Neumann boundary conditions: It is also assumed that can be analytically extended on Θβ, and that , . Furthermore, assume that is analytic for all z in some region for all .
Remark 4.
Since is analytic everywhere then is analytic in . Thus is analytic if . The region can be synthesized by placing the restriction on . This can be achieved by placing restrictions on for all . This is, however, a little involved and is left for a future publication. Thus, to simplify the rest of the discussion in this paper we assume that there exists a constant such that and .
To show that an analytic extension of the solution to Problem 2 exists certain assumptions on the diffusion coefficient a(x) are made. This assumption is left quite general and should be checked on a case by case basis.
Assumption 7.
Suppose that the diffusion coefficient is a deterministic map defined over the domain . Furthermore, assume there exists an analytic extension of a(x) such that if then
where and .
Let for all , we can now conclude that G(z) is analytic for all .
The following lemma shows under what conditions the matrix Re G(z) is positive definite and provides uniform bounds for the minimum eigenvalue of Re G(z). This lemma is key to showing that there exists an analytic extension of on . Note that this is an extension of Lemma 5 in [8].
Lemma 2.
Whenever
where then for all Re G(z) is positive definite. Furthermore, we have the following uniform bounds:
- where
and , - where
- where
Proof.
(a) From the proof in Lemma 5 in [8] and Assumption 4 we have that if then
| (7) |
Furthermore, for all ,
| (8) |
thus
where with a slight abuse of notation and .
It is simple to check that and are Hermitian. Let and . For the next step the dual Lidskii inequality is applied. Suppose that are Hermitian, then . Assuming that it follows from the dual Lidskii inequality that
| (9) |
The next step is to place sufficient conditions on and such that in Equation (9).
From Assumption 7 it follows that if .
From I) - II) it follows that since the angle of is less than π/4 for all . However, an explicit expression can be derived:
where and . We observe from Assumption 7 that
It follows that . Apply the same argument to , we have . It follow that
| (11) |
Since , we obtain
In particular, substituting equations (7) and (8) in equation (9) we obtain that for all
Since is uniformly bounded by below it follows from From London’s Lemma [33] that for all is positive definite.
(b) From the proof in Lemma 5 in [8] and Assumption 4 we have that
| (12) |
From Assumption 7 we have that for all . From Lemma 4 in [8] for all . We then have that
| (13) |
Applying the Lidskii inequality (if are Hermitian then and substituting equations (7), (8), (12) and (13)
(c) Similarly to (b), as shown in [8], it can be shown that
| (14) |
and
| (15) |
From equations (13), (14) and (15) it follows that
Lemma 3.
For all and whenever
Then , where is equal to
Proof.
The proof essentially follows Lemma 6 in [8]. The main result of this section can now be proven.
Theorem 2.
Let then can be analytically extended on if
Proof.
Suppose that V is a vector valued Hilbert space equipped with the inner product , where and , such that for all
Consider the extension of on . Let and consider the extension on , where and . Let , then the extension of on is posed in the weak form as: Find such that
| (16) |
for all , where ,
, , , , , , , , , , and The system of equations (16) has a unique solution if GR is uniformly positive definite since this implies that uniformly. From Lemma 2 this condition is satisfied if . Moreover, coincides with whenever and thus making it a valid extension of on .
The analytic regularity of the solution with respect to variables in z is now analyzed. However, it is not necessary to perform the analysis with respect to all the variables z jointly. It is sufficient to show that is analytic with respect to each variable , separately. As shown at the end of the proof it can be concluded that is analytic in .
First, we concentrate on the zn variable of the vector z. Let and w = Im zn. Analogous to [8], we would like to take derivatives on (16) with respect to w and s, but we cannot do this directly since we do not know whether is differentiable in w or s. Due to Lemma 8, and do exist on . Furthermore, we also conclude from Lemma 8 that:
- uniquely satisfies
in U × (0, T) for all v ∈ V and(17) - uniquely satisfies
in U × (0, T) for all v ∈ V and(18)
In the following argument we show that Φ is analytic with respect to zn for all by using the Cauchy-Riemann equations. Consider the two functions and . First, let us write out explicitly equation (18) for the first term:
| (19) |
Second, for equation (17) exchange with , and with (Note, that this is valid since equations (16) and (17) are satisfied for all v ∈ V), then the first term can written explicitly as
| (20) |
Adding Equations (19) and (20) we obtain
Following for the rest of the terms we obtain the following weak problem: Find , with , s.t.
in U × (0, T) for all v ∈ V and
Since is holomorphic in and c(z) and G(z) are holomorphic in Θβ then from the Cauchy Riemann equations we have that
Observe that zero solved the above equation above, and hence due to uniqueness we have that Q(z) = P(z) = 0 and therefore Φ(z, q, t) is holomorphic in along the nth dimension. From Hartogs’ Theorem (Chap1, p32, [31]) and Osgood’s Lemma (Chap 1, p 2, [19]) Φ(z, q, t) is holomorphic in Θβ whenever .
Since is holomorphic in then Φ(z, q, t) is also holomorphic in whenever . Applying Hartogs’ Theorem and Osgood’s Lemma it follows that Φ(z, q, t) is holomorphic in .
4. Stochastic polynomial approximation
Consider the problem of approximating a function on the domain Γ. Our goal is to seek an accurate approximation of ν in a suitably defined finite dimensional space. To this end the following spaces are defined:
We first define the space of tensor product polynomials , where controls the degree along each dimension. Let , and form the space .
Suppose that , is a series of Lagrange polynomials that form a basis for . An approximation of ν, know as the Tensor Product (TP) representation, can be constructed as
where yk are evaluation points from an appropriate set of abscissas. However, this is a poor choice for approximating ν as the dimensionality of the index set is . Thus the computational burden quickly becomes prohibitive as the number of dimensions N increases. This motivates us to choose a reduced polynomial basis while retaining good accuracy.
Consider the univariate Lagrange interpolant along the nth dimension of Γ:
In the above equation i ≥ 0 is the level of approximation and is the number of evaluation points at level where m(0) = 0, m(1) = 1 and m(i) ≤ m(i + 1) if i ≥ 1. Note that by convention .
An interpolant can now be constructed by taking tensor products of along each dimension n. However, the dimensionality of increases as with N. Thus even for a moderate size of dimensions the computational cost of the Lagrange approximation becomes intractable. In contrast, given sufficient regularity of ν with respect to the stochastic variables defined on Γ, the application of Smolyak sparse grids is better suited [42, 4, 3, 36]).
Consider the difference operator along the nth dimension of Γ
We can now construct a sparse grid from a tensor product of the difference operators along every dimension. Denote , as the approximation level. Let be a multi-index and given the user defined function , which is considered to be strictly increasing along each argument. Note that the function g imposes a restriction along each dimension such that a small subset of the polynomial tensor is selected. More precisely, the sparse grid approximation of ν is constructed as
The sparse grid with respect to formulas (m, g) and level w can also be written as
Let vector and the define the following index set with respect to (m, g, w) as
The indices in form the set of allowable polynomial moments restricted by (m, g, w). Specifically this polynomial set is defined as
We have different choices for m and g. One of the objectives is to achieve good accuracy while restricting the growth of dimensionality of the space . The well known Smolyak sparse grid [36] can be constructed with the following formulas:
For this choice the index set where
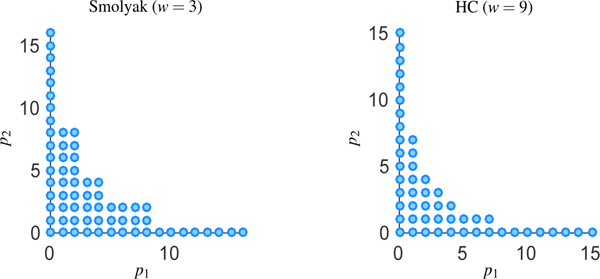
This selection is known as the Smolyak sparse grid. Other choices include the Total Degree (TD) and Hyperbolic Cross (HC), which are described in [8]. See Figure 4 for a graphical representation of the index sets Λm,g(w) for N = 2.
Figure 4:
Embedding of the polyellipse in . Each ellipse is embedded in for .
The Smolyak sparse grid combined with Clenshaw-Curtis abscissas form a sequence of nested one dimensional interpolation formulas and a sparse grid with a highly reduced number of nodes compared to the corresponding tensor grid. For any choice of m(i) > 1 the Clenshaw-Curtis abscissas, which are formed from the extrema of Chebyshev polynomials, are given by
We finally remark that not all of the stochastic dimensions have to be treated equally. In particular, some dimensions will have more of a contribution to the sparse grid approximation that others. By adapting the restriction function g to the input random variables yn for a more accurate anisotropic sparse grid can be obtained [41, 35]. For the sake of simplicity in the rest of this paper we restrict ourselves to isotropic sparse grids. However, an extension to the anisotropic setting is not difficult.
5. Error analysis
In this section we analyze the error contributions of the sparse grid approximation to the mean and variance estimates of the QoI. In addition, an error analysis is also performed with respect to a truncation of the stochastic model to the first Ns dimensions. Note that the error contributions from the finite element and implicit solvers are neglected since there are many methods that can be used to solve the parabolic equation (e.g. [30]) and the analysis can be easily adapted. First, we establish some notation and assumptions:
- Split the Jacobian matrix:
and let , then the domain .(21) Assume that is a bounded linear functional on L2(U) with norm .
Refer to Q(ys) as Q(y) restricted to the stochastic domain Γs and similarly for G(ys). It is clear also that Q(ys, yκ) = Q(y) and G(ys, yκ) = G(y) for all y ∈ Γs × Γκ, ys ∈ Γs, and yκ ∈ Γκ.
- Suppose that the Ng < Nf valued random vector matches with f from the first to Nf entry and takes values on . The truncated forcing function can now be written as
It is not difficult to show that the variance error and mean error are less or equal to (see [8])
where CT R, CF T R and CSG are positive constants and . We now derive error estimates for the truncation (I) and sparse grid (II) errors.
5.1. Truncation error (I)
We study the effect of truncating the stochastic Jacobian matrix to the first Ns stochastic dimensions. Consider the bounded linear functional , then
It follows that for
The objective now is to control the error term . But first we establish some notation. If W is a Banach space defined on U then let define the following spaces
and
With a slight abuse of notation let for all and . From Theorem 2 it follows that
We can now bound the error due to the truncation of the stochastic variables. However, due to the heavy density of the notation, we first prove several lemmas that will be useful to the truncation analysis.
Lemma 4.
Let
then
for some positive constant .
- For all
where
and
Proof.
(a) - (c) Follow the same arguments as in Theorem 10 in [8]. (d) To prove this last inequality, we use Theorem 2.12 in [24] ( then . For any let and , where
then
The result follows.
Lemma 5.
Let
then
Proof.
Lemma 6.
Let , and CT (U) the trace constant defined in [11] then
Proof.
From Lemma 4 (a) it follows that
By using the trace theorem [11] we have that where CT (U). From equation (4), Jensen’s inequality and the fact that all are disjoint then
Lemma 7.
Let then
Proof.
Following the same arguments as in the proof of Lemma 6
From the mean value theorem
The result follows from Lemma 4 (d).
Theorem 3.
Suppose that satisfies
| (22) |
for all , where . Let then for , it follows that
where .
Proof.
Consider the solution to equation (22)
where the matrix of coefficients G(ys) depends only on the variables . Following an argument similar to Strang’s Lemma it follows that
| (23) |
where and CP(U) is the Poincaré constant. Recall that and note that
We conclude that
for all t ∈ (0; T), f ∈ Γf and y ∈ Γ, where
.
From Gronwall’s inequality we have that for t ∈ (0, T), y ∈ Γ, and f ∈ Γf
and thus
| (24) |
We will now obtain bounds for , , , and .
- . The first term in equation (24) is bounded as
for all f ∈ Γf and y ∈ Γ. From equation (25) and Lemma 4 (a)(25) - The third term is bounded as
By using the Schwartz inequality is less or equal to -
. The last term
is more complex and it can be bounded by
for all t ∈ (0, T), f ∈ Γf and y ∈ Γ. From Lemma 5 (b) and Lemma 7 we have thatNote that C refers to some generic non-negative constant with the respective dependen cies.
-
Combining the bounds for , , , and inserting them in equation (24) we obtain that
The constant depends on the coefficients andSimilarly, depends on the coefficients T, d,
Remark 5.
Note that for Theorem 3 to be valid, a bound to the terms and is needed. Clearly,
By modifying the energy estimates in Chapter 7 [11] to take into account the domain mapping on the reference domain U the terms and can be bounded.
5.2. Forcing function truncation error (II)
Since Q is a bounded linear functional the error due to (II) is controlled by . Recall that satisfies the following equation
| (26) |
for all and , where . It is clear then that satisfies
| (27) |
for all and , where .
Theorem 4.
Let
and
then
Proof.
| (28) |
∀v ∈ V. Recall that
Let and substitute in (28), then
Applying the Poincaré and Cauchy’s inequalities we obtain
From Gronwall’s inequality it follows that
We have that
thus
5.3. Sparse grid error (III)
In this section convergence rates for the isotropic Smolyak sparse grid with Clenshaw Curtis abscissas are derived. The convergence rates can be extended to a larger class of abscissas and anisotropic sparse grids following the same approach.
Given the bounded linear functional it follows that
for all and . The sparse grid operator is defined on the domain . The next step it to bound the term
for . The error term , where
is directly affected by (i) the number of interpolation knots η, (ii) the sparse grid formulas (m(i), g(i)), (iii) the level of approximation w of the sparse grid and from (iv) the size of an embedded polyellipse in . Recall that from Theorem 2 the solution admits an analytic extension in for all .
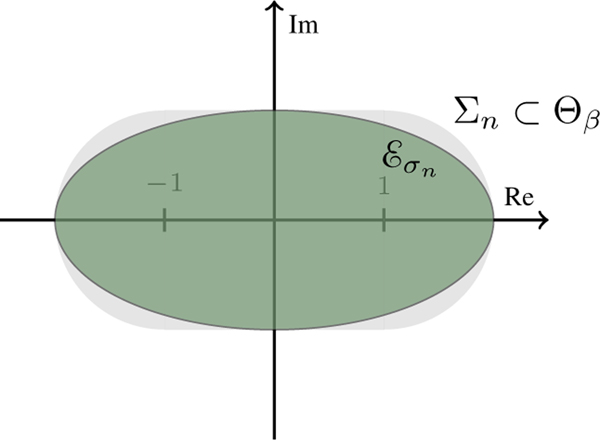
Consider the Bernstein ellipses
where σn > 0 and . From each of these ellipses form the polyellipse , such that . From Theorem 2 the solution admits an extension .
For given Clenshaw-Curtis or Gaussian abscissas, the isotropic (or anisotropic) Smolyak sparse grid error decays algebraically or sub-exponentially as function of the number of interpolation nodes η and the level of approximation w (see [35, 36]). In the rest of the discussion we concentrate on isotropic sparse grids.
Since for a isotropic sparse grids all the dimensions are considered of equally, the overall convergence rate will be controlled by the smallest width of the polyellipse, i.e.
Then the goal is to choose the largest such that is embedded in . To thus end, for , let
and
We can now construct a the set that is embedded in . By setting we conclude that (see Figure 4).
The second step is to form a polyellipse such that . This, of course, depends on the size of the region . For simplicity we assume that , for some constant . The constant is chosen such that . Finally, the polyellipse is embedded in by setting .
We now establish some notation before providing the final result. Suppose , and and let
Furthermore, define the following constants:
Suppose that we use a nested CC sparse grid. If then From Theorem 3.11 [36], the following sub-exponential estimate holds:
| (29) |
otherwise the following algebraic estimate holds:
| (30) |
Remark 6.
Note that for the convergence rate given by equation (29) there is an implicit assumption that the constant , for , is equal to one. This assumption was introduced in [36] to simplify the overall presentation of the convergence results. This constant for can be easily reintroduced in equations (29) and (30). However, it will not change the overall convergence rate.
6. Numerical results
In this section numerical examples are executed that elucidate the truncation and Smolyak sparse grid convergence rates for parabolic PDEs. Define the reference domain to be the unit square U := (0, 1) × (0, 1) and is stochastically reshaped according to the following rule:
where c > 0. This deformation rule only stretches (or compresses) the upper half of the domain and fixes the button half. For the top part of the square, the Dirichlet boundary condition is set to zero. The rest of the border is set to Neumann boundary conditions with (See Figure 5 (a)). Furthermore, the diffusion coefficient is set as , and the forcing function f = 0. The stochastic model is defined as
where are independent uniform distributed in . Note that through a rescaling of the random variables the random vector can take values on Γ. Thus the analyticity theorems and convergence rates derived in this article are valid.
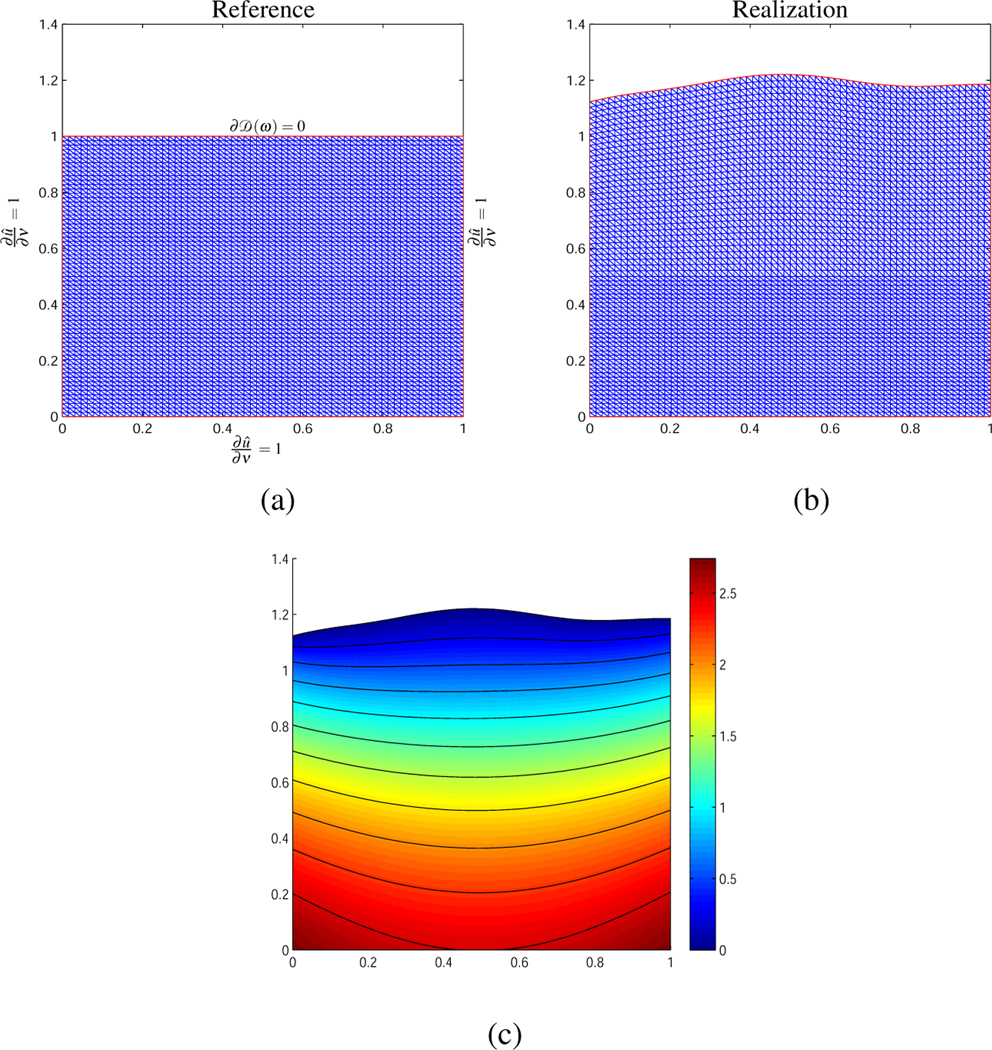
Figure 5:
Random shape deformation of the reference U. (a) Reference square domain with Dirichlet and Neumann boundary conditions. (b) Realization according the deformation rule. (c) Contours of the solution of the parabolic PDE for T = 1 on the stochastic deformed domain realization.
To make comparison between the theoretical decay rates and the numerical results the gradient terms are set to decay linearly as , where k = 1 or k = 1/2, thus for , and
With this choice , for , is bounded by a constant, which depends on N, and gradient of the deformation map decays linearly.
The QoI is defined on the non-stochastic part of the domain as
where . The chosen QoI Q can, for example, represent the weighed total chemical concentration in the region defined by (0, 1) × (0, 1/2) given uncertainty in the region. Other useful applications include sub-surface aquifers with soil variability, heat transfer, etc.
To solve the parabolic PDE a finite element semi-discrete approximation is used for the spatial domain. For the time evolution an implicit second order trapezoidal method with a step size of td and final time T.
For each realization of the domain the mesh is perturbed by the deformation map F. In Figure 5 the original reference domain (a) is shown. An example realization of the deformed domain from the stochastic model and the contours of the solution for the final time T = 1 are shown in Figure 5 (a) & (b). Notice the significant deformation of the stochastic domain.
Remark 7.
For N = 15 dimensions, k = 1 and k = 1/2 the mean and variance are computed with a dimensional adaptive sparse grid method collocation with collocation points and a Chebyshev abscissa [17]. For the linear decay, k = 1, the computed normalized mean value is 0.9846 and variance is 0.0342 (0.1849 std). This indicates that the variance is non-trivial and shows significant variation of the QoI with respect to the domain perturbation.
6.1. Sparse Grid convergence numerical experiment
In this section numerically analyze the convergence rate of the Smolyak sparse grid error without without the truncation error. The purpose is to validate the regularity of the solution with respect the stochastic parameters.
For N = 3, 4, 5 dimensions, the mean and variance var[Q] calculated with an isotropic Smolyak sparse grid (Clenshaw-Curtis abscissas) using the software package Sparse Grid Matlab Kit [3]. In addition, for comparison, and var[Q] are also calculated for N = 3, 4, 5 using a dimension adaptive sparse grid algorithm from the (Sparse Grid Toolbox V5.1 [17, 29, 28]). The abscissas are set to Chebyshev-Gauss-Lobatto.
In addition the following parameters and experimental conditions are set to:
Let for all and set the stochastic model parameters to L = 19/50, LP = 1, c = 1/2.175, N = 15,
The reference domain is discretized with a triangular mesh. The number of vertices are set in a 513 × 513 grid pattern. Recall that for the computation of the stochastic solution the fixed reference domain numerical method is used with the stochastic matrix G(y). Thus it is not necessary to re-mesh the domain for each perturbation.
The step size is set to td := 1/1000 and final time T := 1.
The QoI is normalized by Q(U ) with respect the reference domain.
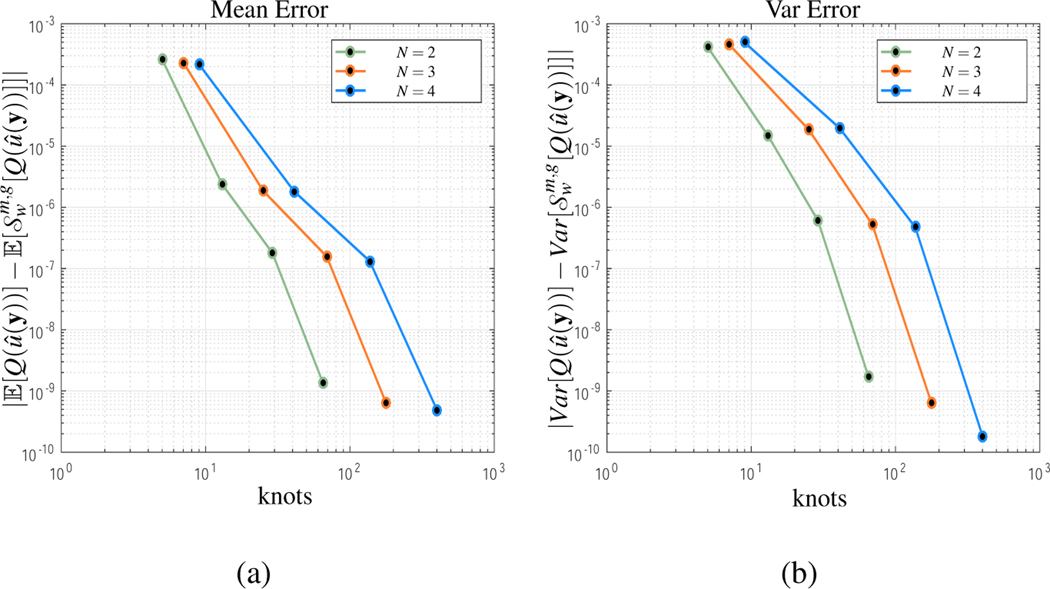
In Figure 6, for Ns = 2, 3, 4, the normalized mean and variance errors are shown. Each black marker corresponds to a sparse grid level up to w = 4. For (a) we observe a faster than polynomial convergence rate. Theoretically, the predicted convergence rate should approach sub-exponential. This is not quite clear from the graph as a higher level (w ≥ 5) is needed to confirm the results. However, this places the simulation beyond the computational capabilities of the available hardware. In contrast, for (b), the variance error convergence rate is clearly sub-exponential, as the theory predicts.
Figure 6:
Isotropic Smolyak sparse grid stochastic collocation convergence rates for N = 2, 3, 4 with k = 1 (linear decay). (a) Mean error: Notice that the convergence rate is faster than polynomial. (b) Variance error: From the graph the convergence rate appears to be subexponential.
Remark 8.
In this work for simplicity we only demonstrate the application of isotropic sparse grids to the stochastic domain problem. However, a significant improvement in error rates can be achieved by using an anisotropic sparse grid. By adapting the number of knots across each dimension to the decay rate of λn, a higher convergence rate can be achieved. In particular, if the decay rate of λn is relative fast it will be not necessary to represent all the dimensions of Γ to high accuracy.
6.2. Truncation experiment
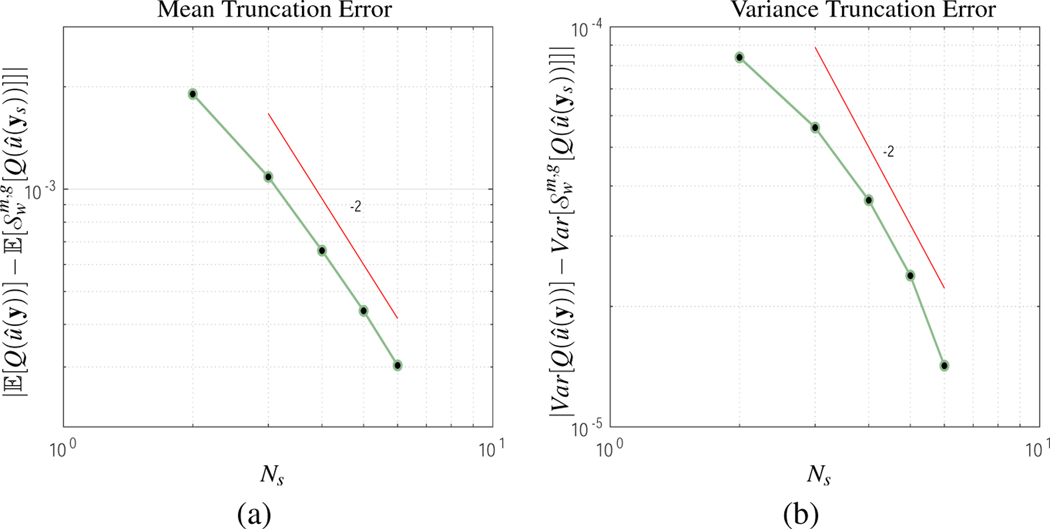
The truncation error as a function of Ns is analyzed and compared with respect to for N = 15 dimensions, k = 1 and k = 1/2. The coefficient c is changed to 1/4.35. In Figure 7 the truncation error is plotted for the mean and variance as a function of Ns. The decay is set to linear (k = 1).
Figure 7:
Truncation error results with linear decay stochastic model i.e. k = 1. (a) From the mean error graph, the truncation error decays quadratically. This is twice the theoretical truncation convergence rate. (b) The variance error also show at least a quadratic convergence rate.
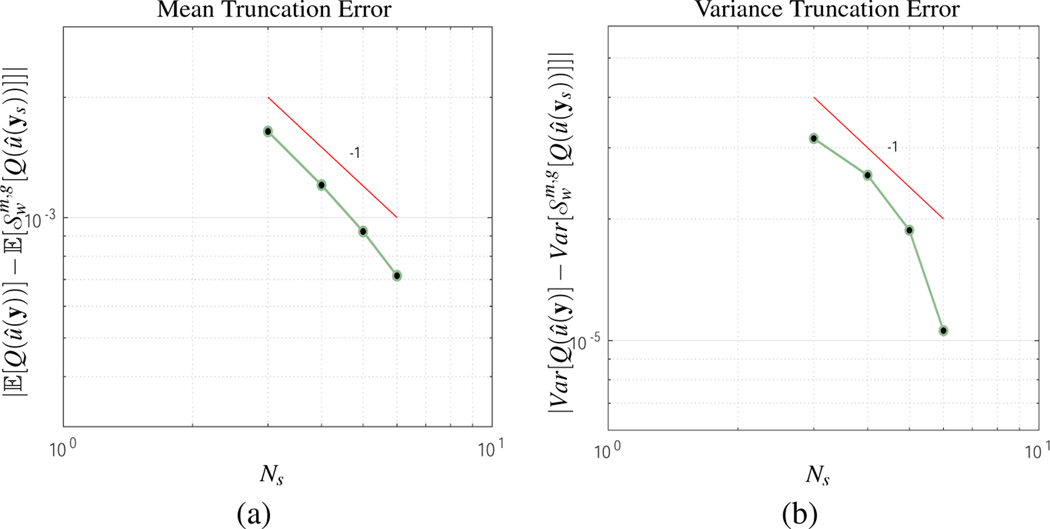
From these plots observe that the convergence rates are close to quadratic, which is at least one order of magnitude higher than the predicted theoretical truncation error rate. In addition, in Figure 8 the mean and variance error are shown for k = 1/2. As observed, the decay rate appears at least linear, which is at least twice the decay rate of the theoretical convergence rate. The numerical results shows that in practice a higher convergence rate is achieved than what the theory predicts.
Figure 8:
Truncation Error with sqrt decay k = 1/2 of stochastic model coefficients. (a) Mean error. (b) Variance error. In both cases, the mean and variance decay linearly, which at twice the theoretical convergence rate. This result is consistent with the linear decay k = 1 truncation error experiment.
6.3. Forcing function truncation experiment
For the last numerical experiment the decay of the forcing function truncation error (II) is tested with respect to the number of dimensions Ng. The mean and variance errors of Q(g, ys) with respect to Q(f, ys) are compared, where
and Nf > Ng. The maps ξn : , n = 1,...,N, are defined as
where σ = 0.001. The coefficients are given such that ξn are centered in a 4 by 4 grid. Let , then for and let . Furthermore,
For , fn are independent and uniformly distributed in , and (linear decay of the coefficients).
The stochastic PDE is solved on the domain with a 513 × 513 triangular mesh.
Nf = 12, Ns = 2, Ng = 2, …, 7 and c = 1/4.35.
and are computed with a dimensional adaptive sparse grid with collocation points and a Chebyshev abscissa [17].
For and are calculated with the Sparse Grid Matlab Kit [3]. An isotropic Smolyak sparse grid with Clenshaw-Curtis abscissas is chosen.
By setting the coefficients to we have a non-linear mapping from the forcing function to the solution. From Theorem 4 the errors and decay as
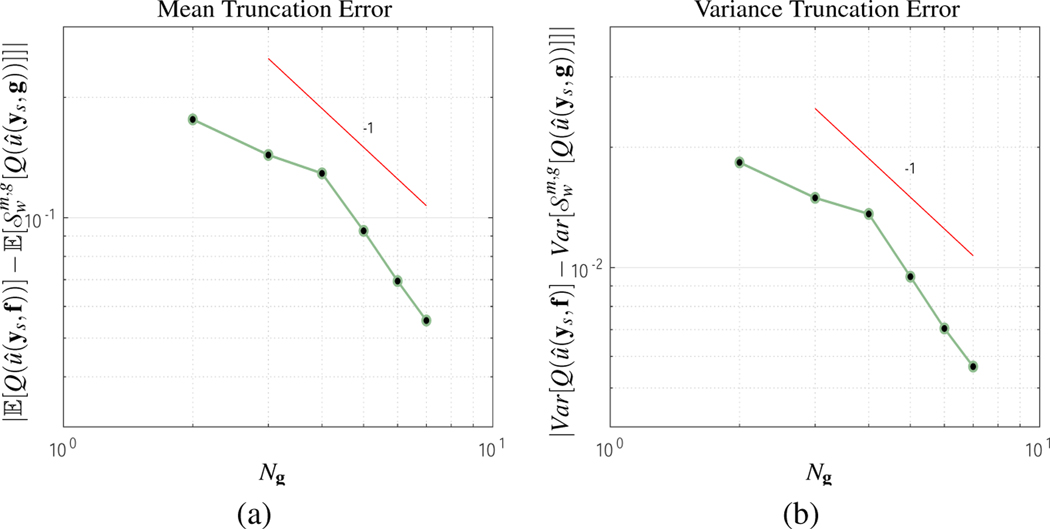
In Figure 9 the error of the mean and variance are plotted as a function of the number of dimensions Ng. The error decay appears to be faster than the theoretically derived rate of ∼ 1/Ng.
Figure 9:
Forcing function truncation error vs the number of dimensions Ng. The decay of the coefficients cn(t, fn), for are set to 1/n. The decay of the (a) Mean truncation error and the (b) Variance truncation error appears to be faster than linear, which is at least twice the forcing function theoretically predicted rate.
7. Conclusions
A detailed mathematical convergence analysis is performed in this article for a Smolyak sparse grid stochastic collocation method for the numerical solution of parabolic PDEs with stochastic domains. The following contributions are achieved in this work:
An analysis of the regularity of the solution of the parabolic PDE with respect to the random variables shows that an analytic extension onto a well defined region exists.
Error estimates in the energy norm for the solution and the QoI are derived for sparse grids with Clenshaw Curtis abscissas. The derived subexponential convergence rate of the sparse grid is consistent with numerical experiments.
A truncation error with respect to the number of random variables is derived. Numerical experiments show a faster convergence rate.
From the numerical experiments and theoretical convergence rates of an isotropic Smolyak sparse grid is efficient for medium size stochastic domain problems. Due to the curse of dimensionality, as shown from the derived theoretical convergence rates, it is impractical for larger dimensional problems. However, the approach described in this paper can be easily broaden to the anisotropic setting [41, 35]. Moreover, new approaches, such as quasi-optimal sparse grids [34], are shown to have exponential convergence.
Figure 3:
Index sets for Smolyak (SM) sparse grid for N = 2 and w = 3. The Hyperbolic Cross (HC) index set is also shown for N = 2 and w = 9, see [8] for details.
Acknowledgements
We are grateful for the invaluable feedback from the reviewer of this paper. We also appreciate the help and advice from Fabio Nobile and Raul Tempone.
This material is based upon work supported by the National Science Foundation under Grant No. 1736392. Research reported in this technical report was supported in part by the National Institute of General Medical Sciences (NIGMS) of the National Institutes of Health under award number 1R01GM131409-01.
Appendix
In the proof of Theorem 2, we take derivatives with respect to w and s respectively on (16) and pass derivatives through integration and exchange with other derivatives. In order to do this, we need the to be differentiable with respect to w and s. In the following lemma, we show that under the same assumption as in Theorem 2, if solves (16), then there exist a couple of functions and (which solves equations (32) and (33) below respectively) such that within the region
Remark 9.
For Lemma 8 to be valid extra conditions on have to be placed beyond analyticity in that follows from Assumptions 5, 6, 7. Now, extend from to all by letting f, g, G, C approach to zero if any Re zi, . Note that this extension beyond Θβ does not have to be analytic, thus we are free to choose such an extension. Thus assumption does not affect the uniqueness of analytic extension within the bounded domain .
Lemma 8.
Let be defined the same as in Theorem 2. Let C, G, f, g satisfy the assumption in Remark 9. Suppose is the unique solution of
| (31) |
for all v ∈ V and is the unique solution of
| (32) |
in U × (0, T) for all v ∈ V and
Furthermore, if is the unique solution of
| (33) |
in U × (0, T) for all v ∈ V and
Then we conclude that within the region is differentiable in w, s in the sense that
Proof.
The main strategy of this proof is the application of the Fundamental Theorem of Calculus (FTC) and the Dominated Convergence Theorem (DCT). The existence and uniqueness of the solutions of (31) and (33) are given by Theorem 1 in Section 2, since G(z) is uniformly positive definite then (31) - (33) have a unique solution whenever .
We prove first. Note that in equations (31) - (33), the gradient is in β direction. Note also that due to Remark 4, we know that Θβ is a bounded set. So for any point , we integrate (32) in Re zn direction from to w, we have
| (34) |
Now, compare (34) with (31) and conclude that
| (35) |
One choice of ζ such that (35) is satisfied is
| (36) |
To check this, we observe that by plugging in the expression (36) and using the First FTC on the first term in the left side can be written as
Now, by applying the Second FTC and the DCT to exchange the integral limits with the derivatives ∂t and ∂w we have that
which is exactly the same as the first term in right side of equation (35). This is also true for the second term on both sides, respectively.
Note that by Remark 9, does vanish when and hence the FTC gives us the desired result.
We now show that this choice is unique. Notice that any choice
for satisfies equation (35). Thus we must show that the only choice is K = 0. This follows by the uniqueness of equation (35) by using the standard argument.
Taking derivatives with respect to w on both sides of (36), we conclude that within that
By the same argument, we conclude also that in .
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- [1].Adams RA: Sobolev Spaces. Academic Press; (1975) [Google Scholar]
- [2].Babuska I, Nobile F, Tempone R: A stochastic collocation method for elliptic partial differential equations with random input data. SIAM Review 52(2), 317–355 (2010). DOI 10.1137/100786356 [DOI] [Google Scholar]
- [3].Bäck J, Nobile F, Tamellini L, Tempone R: Stochastic spectral Galerkin and collocation methods for PDEs with random coefficients: A numerical comparison. In: Hesthaven JS, Rønquist EM (eds.) Spectral and High Order Methods for Partial Differential Equations, Lecture Notes in Computational Science and Engineering, vol. 76, pp. 43–62. Springer Berlin Heidelberg; (2011) [Google Scholar]
- [4].Barthelmann V, Novak E, Ritter K: High dimensional polynomial interpolation on sparse grids. Advances in Computational Mathematics 12, 273–288 (2000) [Google Scholar]
- [5].Billingsley P: Probability and Measure, third edn. John Wiley and Sons; (1995) [Google Scholar]
- [6].Brezis H: Functional Analysis, Sobolev Spaces and Partial Differential Equations, 1st edn. Springer; (2010) [Google Scholar]
- [7].Canuto C, Kozubek T: A fictitious domain approach to the numerical solution of PDEs in stochastic domains. Numerische Mathematik 107(2), 257 (2007) [Google Scholar]
- [8].Castrillón-Candás J, Nobile F, Tempone R: Analytic regularity and collocation approximation for PDEs with random domain deformations. Computers and Mathematics with applications 71(6), 1173–1197 (2016) [Google Scholar]
- [9].Chauviere C, Hesthaven JS, Lurati L: Computational modeling of uncertainty in time-domain electromagnetics. SIAM J. Sci. Comput. 28, 751–775 (2006) [Google Scholar]
- [10].Cohen A, Schwab C, Zech J: Shape Holomorphy of the Stationary Navier–Stokes Equations. SIAM Journal on Mathematical Analysis 50(2), 1720–1752 (2018) [Google Scholar]
- [11].Evans LC: Partial Differential Equations, Graduate Studies in Mathematics, vol. 19. American Mathematical Society, Providence, Rhode Island: (1998) [Google Scholar]
- [12].Federer H: Geometric measure theory. Grundlehren der mathematischen Wissenschaften. Springer (1969) [Google Scholar]
- [13].Feng D, Passalacqua P, Hodges BR: Innovative approaches for geometric uncertainty quantification in an operational oil spill modeling system. Journal of Marine Science and Engineering 7(8) (2019) [Google Scholar]
- [14].Fransos D: Stochastic numerical methods for wind engineering. Ph.D. thesis, Politecnico di Torino (2008) [Google Scholar]
- [15].Frauenfelder P, Schwab C, Todor RA: Finite elements for elliptic problems with stochastic coefficients. Computer Methods in Applied Mechanics and Engineering 194(2–5), 205–228 (2005). Selected papers from the 11th Conference on The Mathematics of Finite Elements and Applications [Google Scholar]
- [16].Gantner R, Peters M: Higher order quasi-Monte Carlo for Bayesian shape inversion. SIAM/ASA Journal on Uncertainty Quantification 6(2), 707–736 (2018) [Google Scholar]
- [17].Gerstner T, Griebel M: Dimension-adaptive tensor-product quadrature. Computing 71(1), 65–87 (2003) [Google Scholar]
- [18].Guignard D, Nobile F, Picasso M: A posteriori error estimation for the steady Navier-Stokes equations in random domains. Computer Methods in Applied Mechanics and Engineering 313, 483–511 (2017) [Google Scholar]
- [19].Gunning R, Rossi H: Analytic Functions of Several Complex Variables. American Mathematical Society (1965) [Google Scholar]
- [20].Harbrecht H, Peters M, Siebenmorgen M: Analysis of the domain mapping method for elliptic diffusion problems on random domains. Numerische Mathematik 134(4), 823–856 (2016) [Google Scholar]
- [21].Harbrecht H, Schneider R, Schwab C: Sparse second moment analysis for elliptic problems in stochastic domains. Numerische Mathematik 109, 385–414 (2008) [Google Scholar]
- [22].Hiptmair R, Scarabosio L, Schillings C, Schwab C: Large deformation shape uncertainty quantification in acoustic scattering. Advances in Computational Mathematics (2018) [Google Scholar]
- [23].Hyvönen N, Kaarnioja V, Mustonen L, Staboulis S: Polynomial collocation for handling an inaccurately known measurement configuration in electrical impedance tomography. SIAM Journal on Applied Mathematics 77(1), 202–223 (2017) [Google Scholar]
- [24].Ipsen I, Rehman R: Perturbation bounds for determinants and characteristic polynomials. SIAM Journal on Matrix Analysis and Applications 30(2), 762–776 (2008) [Google Scholar]
- [25].Jerez-Hanckes C, Schwab C, Zech J: Electromagnetic wave scattering by random surfaces: Shape holomorphy. Mathematical Models and Methods in Applied Sciences 27(12), 2229–2259 (2017) [Google Scholar]
- [26].Jha AK, Bahga SS: Uncertainty quantification in modeling of microfluidic t-sensor based diffusion immunoassay. Biomicrofluidics 10(1), 014,105–014,105 (2016) [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Jing Y, Xianga N: A modified diffusion equation for room-acoustic predication. The Journal of the Acoustical Society of America 121, 3284–3287 (2007) [DOI] [PubMed] [Google Scholar]
- [28].Klimke A: Sparse Grid Interpolation Toolbox – user’s guide. Tech. Rep. IANS report 2007/017, University of Stuttgart; (2007) [Google Scholar]
- [29].Klimke A, Wohlmuth B: Algorithm 847: spinterp: Piecewise multilinear hierarchical sparse grid interpolation in MATLAB. ACM Transactions on Mathematical Software 31(4) (2005) [Google Scholar]
- [30].Knabner P, Angermann L: Discretization methods for parabolic initial boundary value problems. In: Numerical Methods for Elliptic and Parabolic Partial Differential Equations, Texts in Applied Mathematics, vol. 44, pp. 283–341. Springer New York; (2003) [Google Scholar]
- [31].Krantz SG: Function Theory of Several Complex Variables. AMS Chelsea Publishing, Providence, Rhode Island: (1992) [Google Scholar]
- [32].Lions J, Magenes E: Non-homogeneous boundary value problems and applications. Non-homogeneous Boundary Value Problems and Applications. Springer-Verlag; (1972). (3 volumes) [Google Scholar]
- [33].London D: A note on matrices with positive definite real part. Proceedings of the American Mathematical Society 82(3), pp. 322–324 (1981) [Google Scholar]
- [34].Nobile F, Tamellini L, Tempone R: Convergence of quasi-optimal sparse-grid approximation of Hilbert-space-valued functions: application to random elliptic pdes. Numerische Mathematik 134(2), 343–388 (2016) [Google Scholar]
- [35].Nobile F, Tempone R, Webster C: An anisotropic sparse grid stochastic collocation method for partial differential equations with random input data. SIAM Journal on Numerical Analysis 46(5), 2411–2442 (2008) [Google Scholar]
- [36].Nobile F, Tempone R, Webster C: A sparse grid stochastic collocation method for partial differential equations with random input data. SIAM Journal on Numerical Analysis 46(5), 2309–2345 (2008) [Google Scholar]
- [37].Nouy A, Clément A, Schoefs F, Moës N: An extended stochastic finite element method for solving stochastic partial differential equations on random domains. Computer Methods in Applied Mechanics and Engineering 197(51), 4663–4682 (2008) [Google Scholar]
- [38].Nouy A, Schoefs F, Moës N: X-sfem, a computational technique based on x-fem to deal with random shapes. European Journal of Computational Mechanics 16(2), 277–293 (2007) [Google Scholar]
- [39].Sauter SA, Schwab C: Boundary Element Methods, pp. 183–287. Springer Berlin Heidelberg, Berlin, Heidelberg; (2011) [Google Scholar]
- [40].Scarabosio L: Multilevel Monte Carlo on a high-dimensional parameter space for transmission problems with geometric uncertainties. ArXiv e-prints (2017) [Google Scholar]
- [41].Schillings C, Schwab C: Sparse, adaptive Smolyak quadratures for Bayesian inverse problems. Inverse Problems 29(6), 065,011 (2013) [Google Scholar]
- [42].Smolyak S: Quadrature and interpolation formulas for tensor products of certain classes of functions. Soviet Mathematics, Doklady 4, 240–243 (1963) [Google Scholar]
- [43].Stacey A: Smooth map of manifolds and smooth spaces. URL http://www.texample.net/tikz/examples/smooth-maps/ [Google Scholar]
- [44].Steinbach O: Numerical Approximation Methods for Elliptic Boundary Value Problems: Finite and Boundary Elements. Texts in applied mathematics. Springer; New York: (2007) [Google Scholar]
- [45].Tartakovsky D, Xiu D: Stochastic analysis of transport in tubes with rough walls. Journal of Computational Physics 217(1), 248–259 (2006). Uncertainty Quantification in Simulation Science [Google Scholar]
- [46].Zhenhai Z, White J: A fast stochastic integral equation solver for modeling the rough surface effect computeraided design. In: IEEE/ACM International Conference ICCAD-2005, pp. 675–682 (2005) [Google Scholar]