Dynamics of Drug Resistance: Optimal Control of an Infectious Disease

Abstract

Antimicrobial resistance is a significant public health threat. In the U.S. alone, 2 million people are infected and 23,000 die each year from antibiotic resistant bacterial infections. In many cases, infections are resistant to all but a few remaining drugs. We examine the case where a single drug remains and solve for the optimal treatment policy for an SIS infectious disease model incorporating the effects of drug resistance. The problem is formulated as an optimal control problem with two continuous state variables, the disease prevalence and drug’s “quality” (the fraction of infections that are drug-susceptible). The decision maker’s objective is to minimize the discounted cost of the disease to society over an infinite horizon. We provide a new generalizable solution approach that allows us to thoroughly characterize the optimal treatment policy analytically. We prove that the optimal treatment policy is a bang-bang policy with a single switching time. The action/inaction regions can be described by a single boundary that is strictly increasing when viewed as a function of drug quality, indicating that when the disease transmission rate is constant, the policy of withholding treatment to preserve the drug for a potentially more serious future outbreak is not optimal. We show that the optimal value function and/or its derivatives are neither C¹ nor Lipschitz continuous suggesting that numerical approaches to this family of dynamic infectious disease models may not be computationally stable. Furthermore, we demonstrate that relaxing the standard assumption of constant disease transmission rate can fundamentally change the shape of the action region, add a singular arc to the optimal control, and make preserving the drug for a serious outbreak optimal. In addition, we apply our framework to the case of antibiotic resistant gonorrhea.

1. Introduction

Antimicrobial resistance—bacteria, viruses, fungi, and parasites that are no longer susceptible to some or all available treatments—is an urgent public health concern (Hayden 2006; CDC 2013; Laxminarayan et al. 2013; Spellberg et al. 2013; Laxminarayan 2014; WHO 2014). Infections that were once easily cured are becoming more difficult to treat, requiring more intensive care and more expensive therapies (Williams and Heymann 1998; Arias and Murray 2009). Reports of infections with pathogens that are resistant to all but a few remaining drugs are increasing in frequency (CDC 2013, WHO 2014). Though inappropriate use of treatment is often cited as driving antimicrobial resistance, even the appropriate use of treatment contributes to resistance (Spellberg et al. 2013). Therefore, treatment policies must consider both the benefit of treating current patients and the impact of increased resistance on the treatment benefits for future patients.

In this paper, we seek to establish general, analytical insights into whether or not, or specifically under what conditions, the last available drug for a given infectious disease should be reserved for future use. We study an established family of susceptible–infected–susceptible (SIS) infectious disease models, which generally represents diseases such as tuberculosis, H. pylori, and sexually transmitted diseases such as gonorrhea, chlamydia, and syphilis, expanded to include drug resistance (see Spicknall et al. 2013). We examine the problem of minimizing the cost of an infectious disease when only one drug remains. The problem is formulated as an optimal control problem with two continuous state variables: disease prevalence and drug “quality” (the fraction of infections that are drug-susceptible). Treatment with the drug expedites recovery (if the infecting strain is not resistant to the drug), but recovered individuals are subject to reinfection. These dynamics incorporate the spread of drug resistance through natural selection; use of the drug reduces the prevalence of the drug-susceptible strain and allows the drug-resistant strain to become the dominant type. We analytically identify the optimal treatment policy and properties of the optimal value function providing generalizable insights for this class of models.

Addressing the key policy question, we prove that when the disease transmission rate is constant, the optimal prescription policy is of bang-bang type with a single switching time. In plain language, this means that it is optimal to use the drug for everyone, regardless of disease prevalence, until the level of resistance is so high that it is no longer economical to treat anyone. However, in practice, it is not uncommon for the disease transmission rate to be a (decreasing) function of prevalence, as higher prevalence and awareness of the disease may lead to social distancing, increased adoption of prevention behaviors, or higher-intensity cleaning procedures at health care facilities (Nigmatulina and Larson 2009; Aleman et al. 2009; Gilchrist et al. 2015; Ambrosch and Rockmann 2016; Manfredi and D’Onofrio 2013). If the disease transmission rate is not constant, we find that it is optimal to reserve the drug for relatively larger outbreaks and in some cases to use the drug to treat some, but not all, infected individuals. These findings have policy implications for antimicrobial stewardship and the reservation of last-line drugs as a national and international health priority (WHO 2017b). In addition, these findings indicate that it is critically important to incorporate non-constant disease transmission rates, when they exist, into models as they can structurally change the optimal policy.

We also provide a semi-closed form expression for the social planner’s optimal value function characterizing sets of conditions under which SIS infectious disease models (or their variants) are not amenable to numerical analysis. Specifically, we show that the optimal value function is not C¹ (continuously differentiable) and, depending on the discount rate, may not be Lipschitz continuous, indicating that numerical approaches to this family of infectious disease models may not be computationally stable. This is an important warning for analysts seeking to use detailed disease-specific simulation models to guide real-world policy. Computational error caused by the numerical instability of the model in certain regions propagates to the whole state space and can cause a particular type of policy to be identified as optimal when it is not. Thus, Lipschitz continuity of control problems based on SIS dynamics with drug-resistance cannot be assumed and should be verified. From a technical perspective, this paper makes significant contributions to the optimal control literature. Control problems with more than one continuous state variable are rarely analytically solvable. The arguments presented in our proofs can be generalized to other deterministic or stochastic control problems. We prove the optimality of our policy by verifying that its value function satisfies the Hamilton-Jacobi-Bellman (HJB) equation. This task must be carried out in both the action and inaction regions implied by the candidate value function. Although straightforward in the inaction region, verifying that the HJB equation holds in the action region is often challenging because it requires ruling out the possible existence of an inaction region within the candidate action region. In our case, this means eliminating the possibility of a second switching time or singular arc in the optimal policy. The proof argument of our main result streamlines this task by proving that the HJB equation holds inside the action region if it holds on the boundary of the action region. Our proof argument is by contradiction and is readily adaptable to other control problems.

Finally, we apply our framework to extensively drug resistant gonorrhea to gain disease-specific policy insights. Gonorrhea is a non-fatal sexually transmitted disease affecting nearly 1 million Americans each year (CDC 2017a). Though gonoccocal infections are rarely fatal, patients who receive no or delayed treatment may experience costly and life-altering complications (CDC 2017a). Gonorrhea infections can be treated with antibiotics; however, gonorrhea has progressively developed resistance to the antibiotics used to treat it (reviewed in Unemo and Shafer 2014). Due to high levels of resistance across multiple classes of antibiotics, current treatment guidelines recommend a combination of two antibiotics from different classes (CDC 2012). Still, strains of gonorrhea exhibiting high-level clinical resistance to nearly all available antibiotics have been reported in several countries and the reality of untreatable gonorrhea is on the near-term horizon (Bolan et al. 2012; Unemo and Nicholas 2012; Unemo and Shafer 2014; Papp et al. 2017; Lefavre et al. 2018). We apply our framework to identify the threshold level of resistance at which it is no longer economical to treat anyone with a gonorrhea infection and the expected time to reach this threshold for the general US population.

1.1. Literature Review

1.1.1. Antimicrobial resistance

Antibiotic resistance occurs naturally in bacteria, but the high levels of antibiotic use in both healthcare and agriculture create a selective pressure that increases the prevalence of resistance above natural equilibrium levels (Spellberg et al. 2008). Disastrously high levels of antibiotic resistance have been described in numerous pathogens across varying contexts, including antibiotic-resistant S. aureus, S. pneumoniae, N. gonorrhoeae,M. tuberculosis, E. coli, and V. cholerae (see Spellberg et al. 2008; Ohnishi et al. 2011; Bolan et al. 2012; Laxminarayan et al. 2013; CDC 2013; Vasoo et al. 2015; Tadesse et al. 2016, among others). Antibiotic-resistant bacterial infections are estimated to be responsible annually for more than 23,000 deaths in the U.S., 25,000 deaths in Europe, and many more in the developing world (Laxminarayan et al. 2013; Laxminarayan and Bhutta 2016). Antibiotic-resistant bacterial infections are generally associated with greater healthcare costs, longer hospital stays, and higher mortality compared to antibiotic-susceptible infections (Cosgrove 2006; Neidell et al. 2012; Laxminarayan et al. 2013; CDC 2013).

Non-bacterial infectious pathogens also exhibit antimicrobial resistance. Treatment use propagates drug-resistance in parasites, such as malaria (Kim and Schneider 2013) and parasitic worms (Furtado et al. 2016), and in viruses such as HIV (Deeks 2003; Cane et al. 2005) and influenza (Hayden 2006; Moscona 2009). Influenza viruses develop resistance particularly rapidly (Hayden 2006; Hayden and Pavia 2006; Moscona 2009). For example, resistance to oseltamivir in influenza H1N1 strains increased from 10% during the 2007–2008 U.S. influenza season to virtually 100% in the 2008–2009 influenza season without a loss of virulence (Moscona 2009; Dharanet al. 2009).

Compounding the problem of antimicrobial resistance and, in particular, antibiotic resistance, there has been very little development or new investment in the development of new antibiotics for more than 25 years (Spell-berg et al. 2008). In the case of some pathogens (bacterial and viral), only one treatment option remains (CDC 2013; WHO 2014; Laxminarayan and Bhutta 2016). Currently available antibiotics are thus a limited resource; however, individual patients, doctors, and hospitals have little incentive to use antibiotics judiciously and it is estimated that thirty to fifty percent of antibiotic prescriptions are inappropriate (Laxminarayan 2014; CDC 2013; Fleming-Dutra et al. 2016; Silverman et al. 2017). Strategies to mitigate antibiotic resistance include establishing antibiotic stewardship programs in healthcare facilities; restricting access to antibiotics for example by requiring a prescription; limiting drug advertisement; and standardizing infection control policies, including quarantining individuals with resistant infections (Laxminarayan et al. 2013; CDC 2013).

1.1.2. Mathematical models of infectious disease

Deterministic mathematical models of infectious disease have been used for decades to understand the dynamics of infectious diseases and to evaluate control policies including quarantine, treatment, and vaccination. Much of the literature consists of either numerical analyses using complex, realistic models to evaluate specific treatment or prevention policies (Garnett and Anderson 1996; Lipsitch et al. 2003; Larson 2007; Nigmatulina and Larson 2009; Lizon et al. 2010; González-Parra et al. 2011; Teytelman and Larson 2012) or analytical derivations of epidemiological properties of uncontrolled disease dynamics (Anderson et al. 1992; Keeling and Rohani 2008; Long et al. 2008). A small number of studies have established analytical results for the optimal control of an infectious disease using deterministic infectious disease models. Sethi (1974) identifies the optimal treatment control to minimize the total social cost for an SIS model and shows that, depending on the initial value of the state variables, it is either a bang-bang policy or it includes a singular control arc. Morton and Wickwire (1974), Wickwire (1975), and Sethi and Staats (1978) extend these analytical findings to SIR and SEIR models¹ with vaccination for which they identify that a bang-bang policy with a single switching point is optimal when the discount rate is set to zero. Behncke (2000) considered several intervention types in an SIR model, such as vaccination or treatment, and identify that the optimal control is to put maximum effort into the intervention immediately. From a mathematical perspective, a key difference between these models and ours is the incorporation of resistance.

1.1.3. Mathematical models of infectious disease with resistance

Primarily using numerical methods, mathematical models that incorporate antimicrobial resistance have identified resistance as an important factor influencing the total number of infected individuals over the course of an epidemic and the duration of an outbreak (e.g., Lipsitch et al. 2007; Alexander et al. 2007; Moghadas et al. 2008; Brockmann et al. 2008; Spicknall et al. 2013; Xiao et al. 2016). However, these analyses have not resulted in generalizable insights. For example, different models evaluating treatment strategies in response to pandemic influenza incorporating antiviral resistance found different optimal policies due to, at least in part, different parameterizations (e.g., Stilianakis et al. 1998; McCaw et al. 2008; Eichner et al. 2009).

A small number of papers have attempted to partially characterize the optimal control of an infectious disease in the presence of treatment resistance. Using an SIS model, Bonhoeffer et al. (1997) demonstrate through steady-state analysis that the oft-cited policy idea of cycling between two antibiotics is inferior to a policy of treating equal fractions of the infected population with two antibiotics even in the presence of high resistance fitness costs (the rate at which the treatment-resistant bacteria lose the resistance genes and regress to susceptibility in the absence of antibiotic treatment). Laxminarayan and Brown (2001) consider a similar model where the two antibiotic treatments have different monetary costs and rates of losing effectiveness and the social planner’s objective is to maximize the net benefit of treatment options over an infinite horizon. Consistent with the strategy taken in many papers studying the optimal control of infectious disease, they identify the necessary optimality conditions using the Pontryagin maximum principle (PMP). However, since the transversality conditions of the PMP often do not generalize to an infinite horizon formulation (see for example Weber 2011 on page 114), the obtained PMP’s boundary value problem on state and costate, in combination with the optimization conditions, lacks some of its initial or end point conditions to uniquely identify a candidate policy. Since these conditions are not sufficient, all candidate policies that satisfy the necessary optimality conditions must be systematically evaluated for optimality. This is often difficult and it is common to numerically examine the optimality of one or a limited number of candidate solutions. Using a numerical approach, Laxminarayan and Brown (2001) posit that, on the optimal path, the lower cost (higher quality) drug should be used exclusively until its cost, incorporating the present value of downstream costs associated with its loss of quality, is equal to that of the higher cost drug, at which time, the two drugs should be used simultaneously in a ratio that maintains equal cost. Laxminarayan (2001) examines the case when the treatment-resistant strain faces a fitness cost of resistance, in which case antibiotics can be considered a renewable resource. When choosing between two otherwise identical drugs, they suggest that the optimal policy is to use the drug with the lower fitness cost of resistance (the one that holds onto the resistance genes more strongly) until both drugs have the same quality to fitness-cost ratio. In contrast to Bonhoeffer et al. (1997), Laxminarayan (2001) suggest that cycling can be an optimal policy when treatment costs are not convex and there are costs associated with switching between drugs.

In this paper, we extend this literature substantially in proving the optimality of our candidate treatment policy by verifying that its value function satisfies the HJB equation (a sufficient optimality condition). Unlike prior work, we provide a semi-closed form solution for the optimal value function and fully characterize the optimal treatment policy, i.e., the conditions under which it is optimal to use the drug, the fraction of the infected population that should be treated, and the time when the drug should not be used anymore due to effective obsolescence.

2. Model

Consider a social planner who is charged with developing a treatment policy for an infectious disease affecting a population using the last-remaining effective drug. To formulate the social planner’s problem, we start with establishing a mathematical framework of disease spread in the absence of any intervention. We will then introduce the treatment option and model its impact on the dynamics of the disease and the “quality” of the drug. Our base formulation follows the classic epidemic SIS model by Kermack and McKendrick (1927) with treatment resistance incorporated consistent with the formulation presented in Laxminarayan and Brown (2001). After presenting this formulation, the social planer’s problem is stated. In this paper, variables that are functions of time are capitalized. We provide a summary of notation in Table D1.

2.1. Disease Dynamics in the Absence of Treatment

In a closed population of fixed size, consider two major classes of individuals: susceptible individuals and infected individuals. Infected individuals may spread the disease to susceptible individuals via contact at a rate determined by the pathogen’s infectiousness and expressed by the transmission rate β > 0. At any time t ≥ 0, we denote the size of the infected population as a percentage of the total population size by P (t) ∈ [0, 1] and the size of the susceptible population by 1 − P (t). We further divide the infected population into two subclasses: individuals infected with a strain of the pathogen that responds to treatment (denoted by P₁(t)) and individuals infected with a strain that does not respond to treatment (denoted by P₀(t)) such that P (t) = P₀(t) + P₁(t). All infected individuals can recover naturally through their own immune response at a rate r ≥ 0. We assume that all individuals who recover (with or without treatment) return to the susceptible state, which restricts our analysis to infections with negligible mortality rates that do not confer immunity. Examples of relevant infections include gonorrhea (CDC 2017a), chlamydia (Geisler 2010; Geisler et al. 2013), conjunctivitis (Jefferis et al. 2011; Sheikh et al. 2006), and streptococcal pharyngitis (Spinks et al. 2013). In the absence of any treatment, the above dynamics can be captured by adapting the following SIS-type system of ODE’s:

$${\dot{P}}_i(t)=\left({\beta }_i(1-P(t))-r_i\right)P_i(t),t\ge 0,$$ (1)

where i is an element of {0, 1}. Note that the first term in the above differential equations, i.e., β_iP_i(t)(1 − P (t)), represents the disease spread dynamics while the second term, i.e., r_iP_i(t), models the natural recovery dynamics. It is assumed that the drug-sensitive and drug-resistant strains have the same rate of recovery, i.e., r₀ = r₁ = r, and transmission rate, i.e., β₀ = β₁ = β. While drug-resistant strains may be initially less virulent or infectious, equal virulence and infectiousness are acquired rapidly without loss of resistance (Andersson and Levin 1999; Hughes and Andersson 2015; Björkman et al. 1998; Dharan et al. 2009; Beceiro et al. 2013). This assumption is consistent with our case study disease, gonorrhea (Unemo and Shafer 2014), and many other pathogens (Andersson and Levin 1999; Hughes and Andersson 2015; Roux et al. 2015). The above system of ODE’s is a Riccati differential equation and its solution for any given initial condition P_i(0) = p_i, when β_i = β and r_i = r, i ∈ {0, 1}, can be written as

$$P_i(t)=\frac{p_i(\beta -r)e^{(\beta -r)t}}{p\beta \left(e^{(\beta -r)t}-1\right)+\beta -r},t\ge 0,$$ (2)

where p = p₀ + p₁ is the initial size of the infected population. Note that in the absence of any external intervention, the ratio of drug-sensitive and drug-resistant infected populations P₁(t)/P₀(t) remains fixed. Moreover, the size of the infected population

$$P(t)=\frac{p(\beta -r)e^{(\beta -r)t}}{p\beta \left(e^{(\beta -r)t}-1\right)+\beta -r},t\ge 0,$$ (3)

converges to p_∞ = 1 − r/β. To avoid degenerate cases, in the rest of this document, we assume that r < β and p < p_∞.

2.2. Treatment Policy

The drug prescription policy is denoted by $W:{ℝ}_{+}\to [0,1]$ and represents the percentage of the infected population that will be prescribed the drug. Since in most cases it is not possible to identify drug-resistance before treatment begins, W states the prescription policy regardless of infection type (drug-sensitive or drug-resistant). For example, if W (t) is set to one, every infected individual will be treated with the drug irrespective of the infection’s type. Incorporating treatment, the dynamics of P_i(t), i ∈ {0,1}, are governed by the following ODE’s:

$${\dot{P}}_i(t)=(\beta (1-P(t))-i\delta W(t)-r)P_i(t),t\ge 0,$$ (4)

where δ > 0 is the drug strength. Drug strength is the additional rate at which individuals who receive the drug recover due to treatment. Note that the prescription policy W puts a direct negative pressure on the size of the drug-sensitive infected population P₁(t). It also indirectly increases the growth of the size of drug-resistant infected population P₀(t), through its impact on the magnitude of P(t). As such, when the drug is prescribed, the relative size of drug-sensitive infected population with respect to the size of total infected population, i.e., P₁(t)/P(t), decreases. We denote this ratio by Q(t) and refer to it as drug “quality”. Rewriting the above system of ODE’s in terms of P(t) and Q(t), we obtain

$$\dot{P}(t)=(\beta (1-P(t))-\delta W(t)Q(t)-r)P(t),$$ (5)

$$\dot{Q}(t)=\delta W(t)Q(t)(Q(t)-1),$$ (6)

which capture the same dynamics but can be interpreted and measured with greater ease.² It is evident from the new system of ODE’s that the higher the consumption rate W(t), the faster P(t) decreases (or the slower P(t) increases) and the faster the quality of the drug Q(t) decreases. This captures the fundamental trade-off between drug consumption and conservation. Our formulation focuses on the spread of resistance through natural selection. As such we assume the pre-existence of drug-resistant strains and hence assume that the initial drug quality q can be only in [0, q_m] where q_m < 1. Extensive drug resistance, generally indicating resistance to at least one agent in almost all antimicrobial categories (Magiorakos et al. 2012), already exists in circulating strains of many pathogens including N. gonorrhoeae, S. pneumoniae, Salmonella, Shigella, M. tuberculosis, and many healthcare associated infections (CDC 2013; WHO 2017a).

2.3. Economics

Denoting the marginal cost of treatment by c₁ > 0, the treatment cost will accumulate at the rate c₁W(t)P(t). Besides the cost of the drug, we also consider the costs associated with infection c₂ > 0 which can include, for example, the cost of symptom relief, hospitalizations, long-term complications of the infection, and lost productivity. Effective treatment reduces the disease prevalence by shortening the duration of infection and, consequently, decreases these costs associated with infection. The objective of the social planner is to minimize the total cost of the disease. That is, she wants to identify a prescription policy W* that solves

$$\underset{W:{ℝ}_{+}\to [0,1]}{\text{inf}}{\int }_0^{\infty }\left(c_{1}W(t)P(t)+c_{2}P(t)\right)e^{-\rho t}dt$$ (P)

subjected to the dynamics (5) and (6), where ρ > 0 is the discount rate.

Remark 1. In many practical settings, not all infected individuals receive treatment even when the adopted policy is to treat everyone. Reasons for this may include challenges in accessing care (due to cost, or because it is only available from a specialist) or asymptomatic disease presentation. This effectively restricts the set of feasible values for W(t) to $[0,\overline{w}]$ where $\overline{w}\le 1$. This scenario can be captured in our formulation by simply multiplying δ and c₁ by $\overline{w}$, essentially changing the strength and cost of treatment to “effective” strength and cost.

3. Optimal Treatment Policy

In this section we fully characterize the optimal prescription policy W* that solves the social planner’s control problem (P). We start by establishing a sufficient optimality condition for problem (P) and characterizing the system’s trajectory for any given prescription policy. The latter allows us to establish regularity results in the form of first- and second-order monotonicity properties over the social planner’s optimal value function. We then show that the optimal prescription policy is of bang-bang form and can have at most one switching time. In order to establish this result we must consider two separate cases: the case of a short-term focused planner who discounts the future at a rate ρ > β − r, and the case of a long-term focused planner that discounts the future at a rate ρ ≤ β − r. We show that under the latter, the social planner’s optimal value function is not Lipschitz continuous when the initial infected population size p is close to zero. Because of this, some steps in the proofs must be adjusted to ensure validity of calculations that involve infinity.

To aid in visualizing the results in this section, we provide the solution of problem (P), when the model parameters (β, r, δ, c₁, c₂, q_m) are set to (0.17, 0.04, 1, 15, 5, 0.9) and ρ ∈ {0.1, 0.15, 0.25}. The parameters were chosen such that each case captures the features of an important scenario and are otherwise arbitrary.³ In particular the three discount rates, denoted in increasing order by ρ_j, for j ∈ {1, 2, 3}, are chosen such that: (a) β − r − ρ₁ > 0 (a small ρ representing a long-term focused social planner); (b) β − r − ρ₂ < 0 where 2(β − r) −ρ₂ > 0; and (c) β − r − ρ₃ < 0 where 2(β − r) −ρ₃ < 0. Cases (b) and (c) fall under the specifications of a short-term focused social planner and therefore their corresponding optimal value functions are Lipschitz continuous. However, even when ρ > β − r, higher derivatives of the optimal value function can still be non-Lipschitz. This does not have any material impact on our proofs, but it influences the shape of the action/inaction boundary (resulting in the visual differences between case (b) and case (c)). When case (c) differs materially from case (b), the results for case (c) are presented in the appendix. We briefly discuss challenges in implementing numerical analysis in Appendix B.

3.1. Sufficient Optimality Condition

For any measurable prescription policy $W:{ℝ}_{+}\to [0,1]$ and initial state (p, q), denote the trajectory that is obtained by implementing W by (P (t; p, q, W), Q(t; q, W)). Moreover, let v(p, q; W) denote the value of the social planner’s objective function in the control problem (P). Note that the integral in problem (P) converges for any W as the integrand is bounded; hence, v(p, q; W) is not only well defined, but it is also bounded. The following sufficient optimality condition is obtained by following the standard argument.

Proposition 1 (HJB Equation). Let $v^{*}:[0,1]\times [0,1]\to ℝ$ be a bounded, continuous function that is almost everywhere (a.e.) differentiable on any trajectory (P(t; p, q; W), Q(t; q,W)), t ≥ 0, and that satisfies the Hamilton-Jacobi-Bellman (HJB) equation

$$0=\underset{{}_{w\in [0,1]}}{\text{min}}\left\{c_{1}wp+c_{2}p+{\partial }_1{v}^{*}(p,q)(\beta (1-p)-\delta wq-r)p+{\partial }_2{v}^{*}(p,q)\delta wq(q-1)-\rho v^{*}(p,q)\right\}.$$ (7)

Then v* is the optimal value function of the social planner problem (P).

In words, the HJB equation examines a value function obtained by following a prescription policy W, starting at an initial point (p, q), for optimality by searching for any feasible improvement. Specifically, if v(p, q; W) does not satisfy the HJB equation on the current trajectory (P(t; p, q,W), Q(t; q,W)) when t is in a nonzero measure set $\mathcal{T}\subset {ℝ}_{+}$, or there is an alternative policy $\widehat{W}$ such that v(p, q; W) does not satisfy the HJB equation on the trajectory obtained by following this alternative policy, i.e., $(P(t;p,q,\widehat{W}),Q(t;q,\widehat{W}))$, when t is in a non-zero measure set $\widehat{\mathcal{T}}\subset {ℝ}_{+}$, it is possible to identify a new policy such that its value function is strictly smaller than v(p; q;W). The details of how to achieve such an improvement are used in the appendix to prove the optimality of our candidate policy by showing that the feasibility of any improvement leads to a contradiction.

3.2. System Trajectory and Value Function Properties

For any given prescription policy W, the differential equation (6) is separable and can be solved. Moreover, for any admissible functions W and Q, the differential equation (5) is again a Riccati differential equation and has a closed form solution. The following proposition characterizes the dynamics of the system’s trajectory.

Proposition 2 (System Trajectory). For any prescription policy $W:{ℝ}_{+}\to [0,1]$ and initial condition (p, q) ∈ [0, 1] × [0, 1], it can be verified that

$$P(t;p,q,W)=\frac{p{e}^{-{\int }_0^t(\delta W(s)Q(s;q,W)-\beta +r)ds}}{\beta p{\int }_0^t{e}^{-{\int }_0^s(\delta W(\sigma )Q(\sigma ;q,W)-\beta +r)d\sigma }ds+1},$$ (8)

$$Q(t;q,W)=\frac{q}{(1-q)e^{{\int }_0^t\delta W(s)ds}+q},$$ (9)

solve the system of ODE’s (5)–(6). Furthermore, for any t ≥ 0:

1. Q(t; q, W) is increasing and convex in q.

2. P(t; p, q, W) is a complete Bernstein function in p. Moreover, it is decreasing and concave with respect to q.

The above proposition plays a major role in establishing regularity properties for the optimal value function and it facilitates our calculations by allowing us to exchange the order of the limit and the integral. Note that as is shown in the proof of the proposition, P(t; p, q, W) is strictly increasing and strictly concave in p. These two properties, along with monotonicity and concavity in q, are preserved under infimum (see for example Theorem 5.5 of Rockafellar 1970); hence, the optimal value function inherits them all. We formalize this statement in the following theorem.

Theorem 1 (Value Function Properties). The optimal value function v* is (i) strictly increasing and strictly concave with respect to p and (ii) decreasing and concave with respect to q.

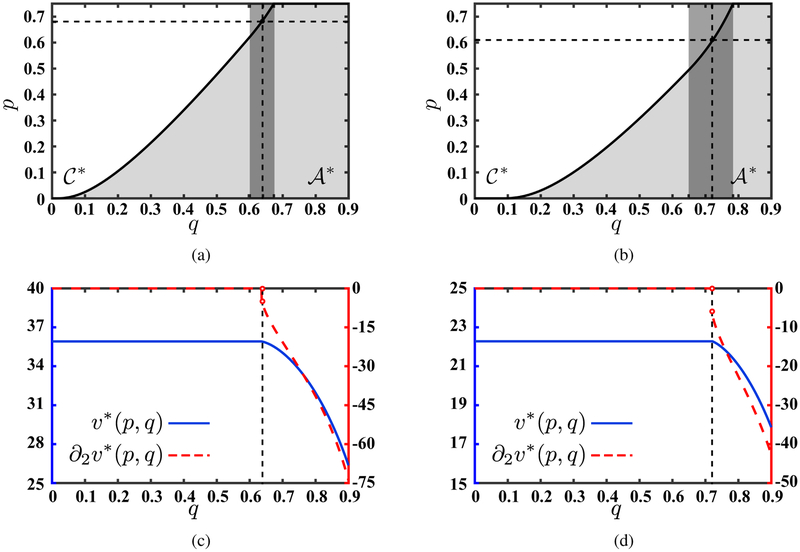
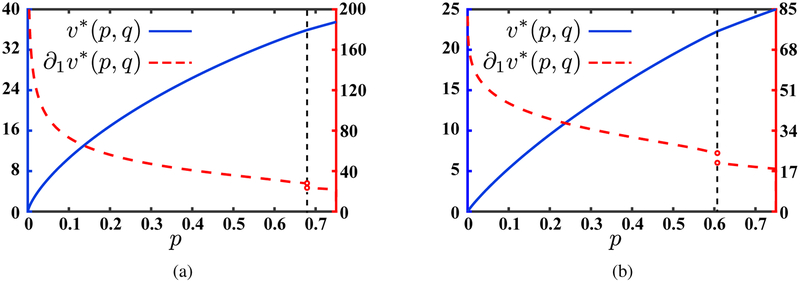
Intuitively, Thm. 1 shows that the lower the initial size of the infected population or the higher the quality of the drug, the lower the discounted cost of the disease will be. Moreover, the marginal cost of the disease decreases as the infection level increases, primarily because it reduces the duration of the optimal intervention. However, the marginal benefit of drug quality increases as the quality of the drug increases. These properties are illustrated in Fig. 3 and 4.

Figure 3:

Action/Inaction regions for (a) long-term focused planner (ρ₁ ≤ β − r) and (b) short-term focused planner (ρ₂ > β − r). In these two panels ${\mathcal{Q}}_n$ is indicated by gray the dark rectangle. The white area denotes the optimal inaction (continuation) region while the gray shading on the right-hand side of the solid line denotes the optimal action region. The optimal value function as a function of q and its first derivative when ρ₁ ≤ β − r and p = 0.68 (the horizontal dashed line in panel (a)) as well as when ρ₂ > β − r and p = 0.61 (the horizontal dashed line in panel (b)) are shown in panels (c) and (d), respectively. In panels (c) and (d), the left vertical axis represents v* and the right vertical axis represents its first derivative. In these panels a vertical dashed line has been added (at q = 0.64 and q = 0.72, respectively) drawing attention to the the non-differentiability of v* with respect to q at these points. Moreover, in panels (c) and (d) v*(0.68, q) and v*(0.61, q) are constant when q ≤ 0.64 and q ≤ 0.72 respectively as in the inaction (continuation) region ${\mathcal{C}}^{*}$, v*(p, q) = v_c(p).

Figure 4:

The optimal value function as a function of p and its first derivative for (a) long-term focused planner (ρ₁ ≤ β − r) when q = 0.64 (vertical line in Fig. 3a) and (b) short-term focused planner (ρ₂ > β − r) when q = 0.72 (vertical line in Fig. 3b). In each panel, the left vertical axis represents v* and the right vertical axis represents its first derivative. On each panel a vertical dashed line has been added (at p_b (0.64) = 0.68 and p_b (0.72) = 0.61, respectively) drawing attention to the the non-differentiability of v* with respect to p at (p_b(q); q), with $q\in {\mathcal{Q}}_n$. Note that when ρ₁ ≤ β − r, the derivative of v*(p, q) with respect to p is unbounded when p is equal to zero. In contrast, when ρ₂ > β − r, the derivative of v*(p, q) remains bounded when p = 0.

3.3. Optimality of Bang-Bang Policy with a Single Switching Time

For (p, q) ∈ [0, p_∞] × [0, q_m] and any time τ ≥ 0, consider a policy that prescribes treatment for every infected individual for any t ≤ τ and no treatment for any t > τ, i.e., $W(t)=1_{\{t\le \tau \}},t\in {ℝ}_{+}$. To simplify the notation, we denote the value function associated with this policy by v_s(p, q; τ). In addition, we denote the trajectories P(t; p, q, W) and Q(t; q, W) by P_a(t; p, q) and Q_a(t; q) when $W(t)=1,t\in {ℝ}_{+}$, and by P_c(t; p) and Q_c(t; q) when $W(t)=0,t\in {ℝ}_{+}$.⁴ Note that in the latter case, i.e., when no treatment is offered, the quality of the drug will not change with time and remains at its initial level q. Moreover, the dynamics of the disease spread does not depend on q. Given this notation we can write

$$v_s(p,q;\tau )={\int }_0^{\tau }\left(c_1+c_2\right)P_a(s;p,q)e^{-\rho s}ds+e^{-\rho \tau }{v}_c\left(P_a(\tau ;p,q)\right),$$ (10)

where $v_c(p)\triangleq {\int }_0^{\infty }{c}_2{P}_c(s;p)e^{-\rho s}ds$ is the autonomous value function, i.e., when no treatment is offered. It is easy to see that v_c coincides with the optimal value function v^* when q is zero; hence it is strictly increasing and strictly concave. The following proposition further characterizes v_c.

Proposition 3 (Autonomous Value Function). Fixing $(\beta ,r)\in {ℝ}_{++}^2$, the autonomous value function v_c is a complete Bernstein function. Specifically, it is strictly increasing and strictly concave. Moreover, it (i) solves the differential equation

$$c_{2}p+{\partial }_{1}v(p,q)(\beta (1-p)-r)p-\rho v(p,q)=0.$$ (11)

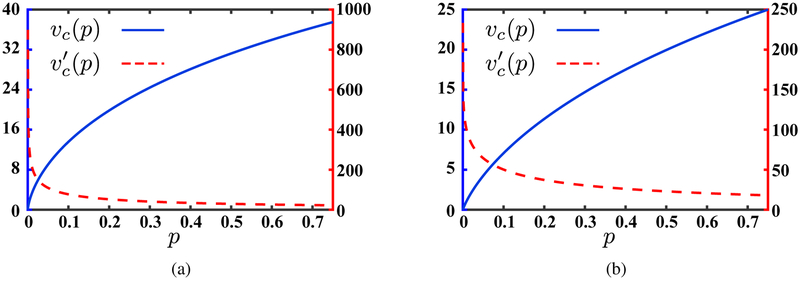
In addition, (ii) for ρ ≤ β − r, it is not Lipschitz continuous in any neighborhood of p = 0 since ${\text{lim}}_{p\downarrow 0}{v}_c^{\prime }(p)=\infty$, while (iii) for ρ > β − r, it is Lipschitz continuous because $v_c^{\prime }(0)=-c_2/(\beta -r-\rho )$.

The claims of Prop. 3 are illustrated in Figure 10 in Appendix B. The dynamics that cause v_c (and similarly v^*) not to be Lipschitz continuous in any neighborhood of p = 0 when ρ ≤ β − r have a profound impact on the form of the optimal treatment policy. The same dynamics are present when ρ > β − r. Note that when ρ > β − r, the social planner puts more emphasis on present costs and benefits as she discounts the future at higher rate relative to the other case (when ρ ≤ β − r). We consider these two cases separately.

Figure 10:

The autonomous value function and its first derivative when (a) long-term focused planner (ρ₁ ≤ β − r), and (b) short-term focused planner (ρ₂ > β − r). In each panel, the left vertical axis represents v_c(p) and the right vertical axis represents its first derivative.

3.3.1. Short-term Focused Planner

Consider the case where ρ > β − r. Focusing on the class of policies described above, we define

$$v_s^{*}(p,q)\triangleq \underset{\tau \ge 0}{\text{inf}}{v}_s(p,q;\tau ),(p,q)\in \left[0,p_{\infty }\right]\times \left[0,q_m\right].$$ (12)

Note that an argument similar to the one in the proof of Thm. 1 allows us to conclude that $v_s^{*}(p,q)$ is strictly increasing and strictly concave in p and decreasing and concave in q. In addition, since for c₁ > 0, it is lim_τ→∞ v_s (p, q; τ) > v_c(p), the infimum is achieved, and the above optimization problem has a finite solution. For (p, q) ∈ [0, p_∞] × [0, q_m] such that the optimal switching time, the time at which it is no longer economical to treat the population via the drug given the initial starting point (p, q), is strictly positive, it satisfies the first-order optimality condition

$$\left(c_1+c_2\right)P_a(\tau ;p,q)e^{-\rho \tau }-{\rho e}^{-\rho \tau }{v}_c\left(P_a(\tau ;p,q)\right)+e^{-\rho \tau }{v}_c^{\prime }\left(P_a(\tau ;p,q)\right){\dot{P}}_a(\tau ;p,q)=0.$$

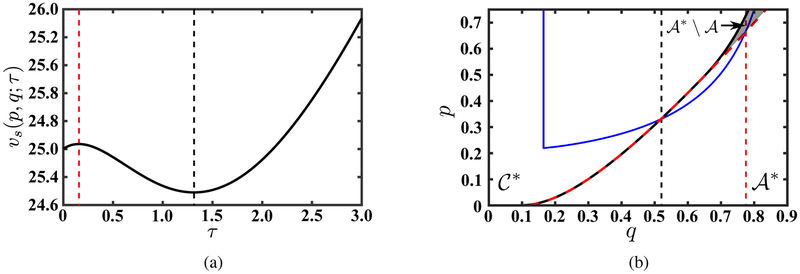
Given that v_c solves the differential equation (11), the above optimality condition simplifies to

$$c_1-\delta q{v}_c^{\prime }(p)=0.$$ (13)

Note that since v_c is strictly increasing and concave, if this equation has a solution, that solution is unique. Specifically, as $v_c^{\prime }(0)=-c_2/(\beta -r-\rho )$ is finite, for any $q<\underset{\_}{q}\triangleq -(\beta -r-\rho )c_1/\left(\delta c_2\right)$, the left-hand side of Eq. (13) is strictly positive and hence it does not have any solution. This allows us to conclude that for $q<\underset{\_}{q}$, $v_s^{*}(p,q)=v_c(p)$ and the optimal switching time is zero (see Fig. 1b). Given that $v_c^{\prime }\left(p_{\infty }\right)=c_2/(\beta -r+\rho )$, for $\underset{\_}{q}\le q\le \text{min}\left(q_m,(\beta -r+\rho )c_1/\left(\delta c_2\right)\right)$, the first-order optimality condition has a unique solution $\overline{p}(q)$ which is strictly increasing, it is zero at $q=\underset{\_}{q}$, and it is p_∞ at q = (β − r + ρ)c₁/(δc₂) if (β − r + ρ)c₁/(δc₂) < q_m. Defining $\overline{p}(q)=p_{\infty }$ for q ∈ ((β − r + ρ)c₁/(δc₂), q_m] when (β − r + ρ)c₁/(δc₂) < q_m, we can conclude that for any $(p,q)\in [0,\overline{p}(q)]\times \left[\underset{\_}{q},q_m\right]$, $v_s^{*}(p,q)\le v_c(p)$. Note that for any $(\overline{p}(q),q),q\ge \underset{\_}{q}$, such that

$$\underset{w\in [0,1]}{\text{max}}\frac{(\beta (1-\overline{p}(q))-r-\delta wq)\overline{p}(q)}{\delta wq(q-1)}=\frac{(\beta (1-\overline{p}(q))-r-\delta q)\overline{p}(q)}{\delta q(q-1)}>\frac{d}{dq}\overline{p}(q),$$ (14)

the optimal τ is not zero. This is because the trajectory $\left(P_a(t;\overline{p}(q),q),Q_a(t;q)\right)$ enters

$$\mathcal{A}\triangleq \left\{(p,q)\in \left[0,p_{\infty }\right]\times \left[0,q_m\right]:\underset{\_}{q}\le q\text{ and }p\le \overline{p}(q)\right\},$$

and therefore there is a strictly positive ϵ for which $v_s(\overline{p}(q),q;\tau )$ is decreasing for τ ∈ [0, ϵ]. Consequently, for $(\overline{p}(q),q),q\ge \underset{\_}{q}$ such that condition (14) holds, $v_s^{*}(\overline{p}(q),q)<v_c(p)$.⁵

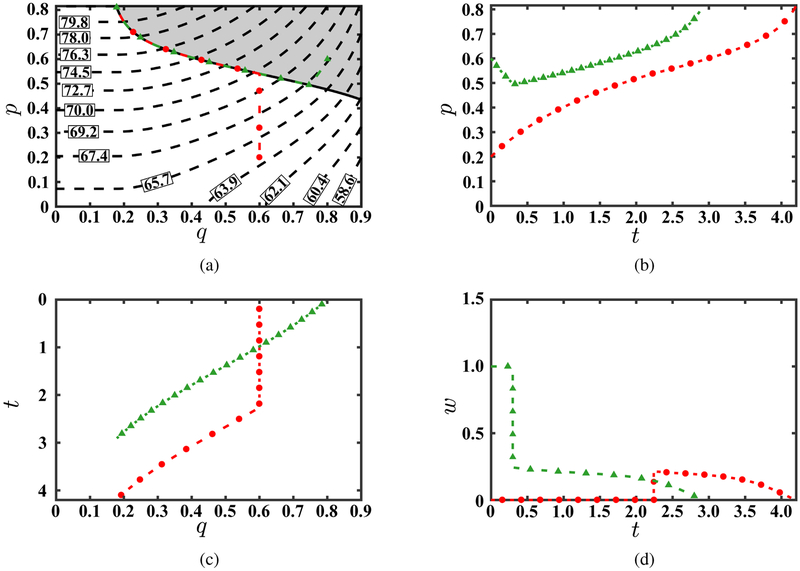
Figure 1:

Action/Inaction boundary p_b along with the solution to the first-order optimality condition, i.e., $\overline{p}$, for (a) long-term focused planner (ρ₁ ≤ β − r) and (b) short-term focused planner (ρ₂ > β − r). Gray arrows indicate the vector field defined in the system of ODE’s (5)–(6) when W (t) = 1, t ≥ 0. In panel (a) where ρ₁ > β − r, observe that the infimum of the set of drug qualities for which it is economical to prescribe the drug for some p > 0 is zero (i.e., $\underset{\_}{q}=0$). In addition, since ${\overline{p}}^{\prime }(q)=-v_c^{\prime }(\overline{p}(q))/q{v}_c^{\prime \prime }(\overline{p}(q))$ converges to zero when $\overline{p}(q)$ is close to zero, $\overline{p}$ is tangent to the q axis. In contrast, in panel (b) where ρ₂ > β − r, it is $\underset{\_}{q}>0$. Similar to panel (a), since ρ₂ > 2β − 2r, the second derivative of v_c to diverges infinity when p approaches to zero. This causes ${\overline{p}}^{\prime }(\underset{\_}{q})=0$ leading to the tangency of $\overline{p}$ to the q-axis When ρ = ρ₃, however however, the second derivative of v_c is infinite at p = 0 and hence ${\overline{p}}^{\prime }(\underset{\_}{q})>0$. This case is shown in Fig. 9a in Appendix A.

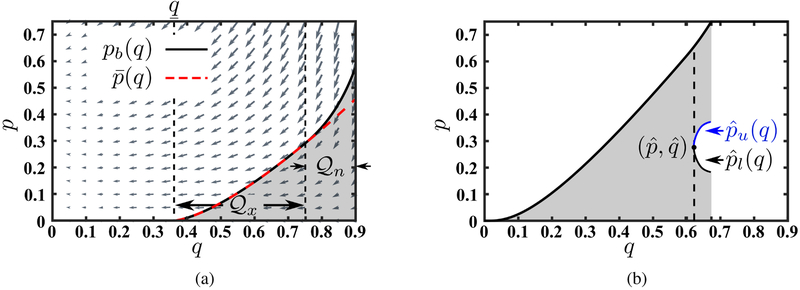
Motivated by the above observation, for any $q>\underset{\_}{q}$, we define p_b(q) as the smallest p ∈ (0, p_∞] for which $v_s^{*}(p,q)=v_c(p)$.⁶ Similar to the definition of $\overline{p}$, for any q such that $v_s^{*}(p,q)<v_c(p)$ for all p ∈(0, p_∞], we extend the definition of p_b by setting p_b(q) = p_∞ and denote the minimum $q\in \left[\underset{\_}{q},q_m\right]$ for which p_b(q) = p_∞ by $\overline{q}$.⁷ In addition, for $q=\underset{\_}{q}$ we define $p_b\left(\underset{\_}{q}\right)=0$. Note that since $v_s^{*}(p,q)$ is decreasing in q, it follows that p_b : [q, q_m] → [0, p_∞] is an increasing function (see Fig. 1b). Given this definition for p_b, we define the action region—a subset of [0, p_∞] × [0, q_m] where treatment is offered to all infected individuals—as

$${\mathcal{A}}^{*}\triangleq \left\{(p,q)\in \left[0,p_{\infty }\right]\times \left[0,q_m\right]:\underset{\_}{q}\le q\text{ and }p\le p_b(q)\right\},$$ (15)

and the inaction (continuation) region—a subset of [0, p_∞] × [0, q_m] where no treatment is offered—as

$${\mathcal{C}}^{*}\triangleq \left\{(p,q)\in \left[0,p_{\infty }\right]\times \left[0,q_m\right]:q<\underset{\_}{q},\text{ or }\underset{\_}{q}\le q\text{ and }{p}_b(q)<p\right\}.$$ (16)

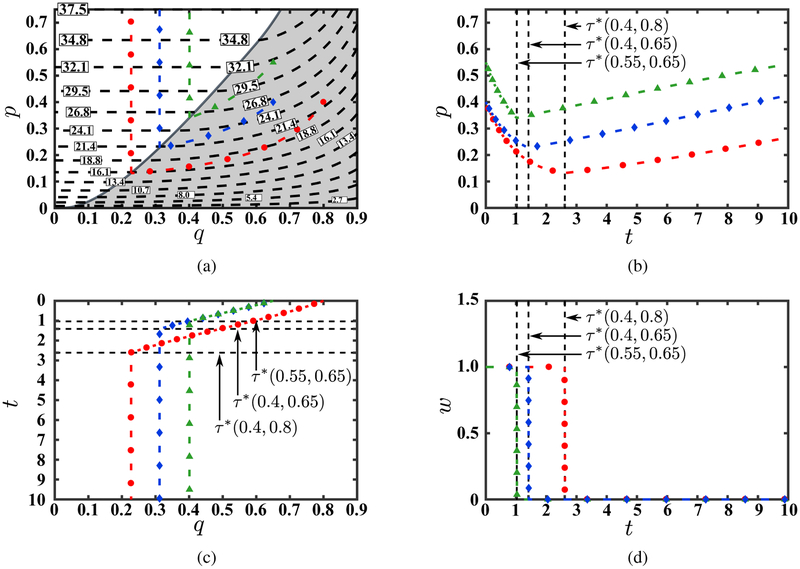
In addition, for any point $(p,q)\in {\mathcal{A}}^{*}$, we denote τ*(p, q) as the first time the trajectory (P_a(t; p, q), Q_a(t; q)) exits the action region ${\mathcal{A}}^{*}$ (see Fig. 11 in Appendix B). For any point $(p,q)\in {\mathcal{C}}^{*}$, we extend the definition of τ* by setting τ*(p, q) = 0. Although we have not proved it yet, τ* is the unique solution of the optimization problem in Eq. (12). The proof is not trivial since upon departure from ${\mathcal{A}}^{*}$, it may be possible to enter the action region again; however as we show in what follows, this will not be optimal. Moreover, for any fixed $q\ge \underset{\_}{q}$ it is possible that $v_s^{*}$ and v_c cross multiple times. This possibility is also ruled out by the following results.

Figure 11:

The optimal state trajectory for three different starting points from four perspectives: (a) in the state space; (b) in the p-dimension as a function of time; (c) in the q-dimension as a function of time; and (d) of the optimal control as a function of time. Panel (a) also illustrates iso-curves of the optimal value function. To enable comparison, p-axis and q-axis in panels (b) and (c) are kept parallel to these axes in panel (a).

Proposition 4 (Action/Inaction Regions). The interior of $\mathcal{A}$, i.e., $\mathcal{A}°$, is a subset of ${\mathcal{A}}^{*}$.

Since both $\mathcal{A}$ and ${\mathcal{A}}^{*}$ are closed, it follows that $\mathcal{A}\subset {\mathcal{A}}^{*}$. This inclusion is shown in Fig. 1. The following definitions enables us to further characterize $\overline{p}$ and p_b.

Definition 1 (Weakly/Strongly Entering/Exiting Points). (i) A point on the boundary of the action region ${\mathcal{A}}^{*}$, i.e., $\left(p_b(q),q\right),q\in \left[\underset{\_}{q},\text{min}\left(\overline{q},q_m\right)\right]$, is called weakly entering if there exists ϵ > 0 such that $\left(P_a\left(t;p_b(q),q\right),Q_a(t;q)\right)\in {\mathcal{A}}^{*}$ for any t ∈ [0, ϵ] and (P_a(ϵ; p_b(q), q), Q_a(ϵ; q)) is in the interior of ${\mathcal{A}}^{*}$. Such a point is called strongly entering if there exists ϵ > 0 such that (P_a(t; p_b(q), q), Q_a(t; q)) is in the interior of ${\mathcal{A}}^{*}$ for any t ∈ (0, ϵ]. (ii) Denoting the closure of ${\mathcal{C}}^{*}$ by $\overline{{\mathcal{C}}^{*}}$, we can define weakly exiting and strongly exiting by replacing ${\mathcal{A}}^{*}$ with $\overline{{\mathcal{C}}^{*}}$ in the above definition.

Similar definitions can be provided for points on the boundary of $\mathcal{A}$. The concepts of entering and exiting points on the boundary of ${\mathcal{A}}^{*}$ and $\mathcal{A}$ are defined relative to the trajectory obtained by setting W (t) = 1 for all t ≥ 0, i.e., by adopting the strongest treatment policy. These two concepts are geometric interpretation of the second-order optimality condition of the optimization problem (12). In particular, if the trajectory $\left(P_a(t;\overline{p}(q),q),Q_a(t;q)\right)$ is entering at $(\overline{p}(q),q)$ on the boundary of $\mathcal{A}$, then for t ∈ [−ϵ, 0] for some ϵ > 0 the state of the system is in $\mathcal{C}\triangleq \left[0,p_{\infty }\right]\times \left[0,q_m\right]\backslash \mathcal{A}$, where the derivative of v_s(p, q; τ) with respect to τ is positive (left-hand side of Eq. (13)), while for t ∈ [0, ϵ], the state of the system is in $\mathcal{A}$ where the derivative of v_s(p, q; τ) with respect to τ is negative. Consequently, an entering point on the boundary of $\mathcal{A}$ is a local maximum v_s(p, q; τ) (See Fig. 2). Characterizing the weakly/strongly entering/exiting points of the boundary of $\mathcal{A}$ or ${\mathcal{A}}^{*}$ enables us to determine how many times the trajectory (P_a(t; p, q), Q_a(t; q)) crosses this boundary for an arbitrary starting point (p, q). This, in turn, allows us to characterize the solution of the optimization problem (12) and determine the count of the optimal switching times of a bang-bang policy. In addition, it enables us to rigorously rule out the possibility of having an optimal treatment policy that consists of a singular control (which must necessarily remain on the boundary of ${\mathcal{A}}^{*}$ for a non-zero measure set).

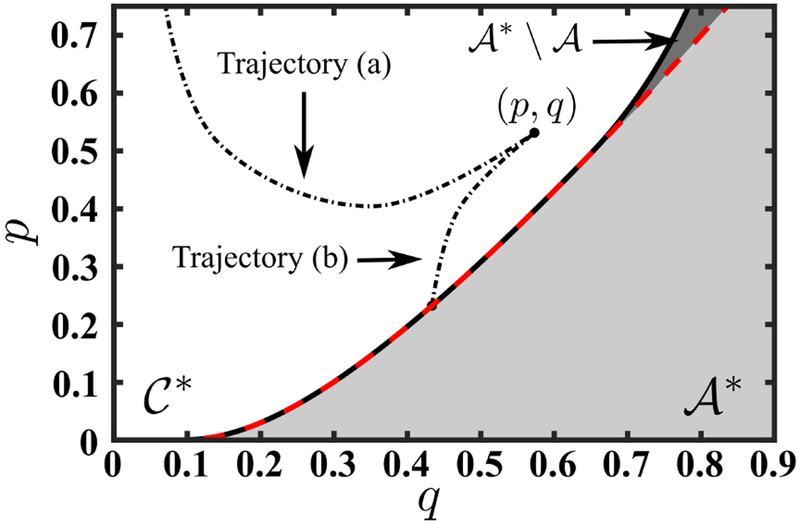
Figure 2:

(a) The value function for an arbitrary switching time τ when the initial point (p, q) is (0.75, 0.8) and(b) the system trajectory when the switching time τ = 3. For any switching time τ < 3, the state of the system remains on the blue line for t ≤ τ after which moves vertically toward p_∞ = 0.75, i.e., Q(t) = Q_a(τ; 0.8) and P (t) = P_c(t − τ; P_a(τ; 0.75, 0.8)), t > τ. The two vertical dashed lines indicate the time when the state of the system enters $\mathcal{A}$ and exits $\mathcal{A}$. Panel (a) and (b) together illustrate that although initially v_s(0.75, 0.8; τ) is increasing in τ, it will eventually decrease as the system trajectory is “strongly entering”.

We denote the set of $q\in \left[\underset{\_}{q},\text{min}\left(\overline{q},q_m\right)\right]$ for which (p_b(q), q) is weakly exiting by ${\mathcal{Q}}_x$ and the set of $q\in \left[\underset{\_}{q},\text{min}\left(\overline{q},q_m\right)\right]$ for which (p_b(q), q) is weakly entering by ${\mathcal{Q}}_n$.⁸ Note that by definition we have $\left[\underset{\_}{q},\text{min}\left(\overline{q},q_m\right)\right]={\mathcal{Q}}_n\cup {\mathcal{Q}}_x$. The vector field in Fig. 1 identifies the points on $\overline{p}$ that are strongly entering (those in the ${\mathcal{Q}}_n$ region). These points reside in the interior of ${\mathcal{A}}^{*}$ (denoted in these panels by the gray shading). In addition, $\overline{p}$ overlaps with the action/inaction regions boundary p_b when $(\overline{p}(q),q)$ is strongly exiting (the ${\mathcal{Q}}_x$ region). Note that when p is close to zero, the derivative of P_a(t) with respect to time diminishes, while the derivative of Q_a(t) with respect to time does not change with p and remains negative. Consequently, the vector field when p is close to zero is aligned with vector (−1, 0). This suggests that the segment of the action/inaction boundary (i.e., p_b) that is close to q-axis is strongly exiting. Since p_b is strictly increasing, ${\mathcal{Q}}_x$ resides on the left-side of ${\mathcal{Q}}_n$. These observations are formally proved in the following proposition.

Proposition 5 (Action Boundary). (i) For any $q\in {\mathcal{Q}}_n$, we have $\overline{p}(q)<p_b(q)$. (ii) Moreover, if $q\in {\mathcal{Q}}_x$, it follows that $\overline{p}(q)=p_b(q)$. (iii) In addition, for any $q\in {\mathcal{Q}}_x$, (p_b(q), q) is strongly exiting and, for any $q\in {\mathcal{Q}}_n$, (p_b(q), q) is strongly entering. (iv) Finally, p_b is increasing on $\left[\underset{\_}{q},\text{min}\left(\overline{q},q_m\right)\right]$ and there is no subinterval of $\left[\underset{\_}{q},\text{min}\left(\overline{q},q_m\right)\right]$ over which the graph of p_b is either horizontal (i.e., p_b is constant) or vertical (i.e., p_b is discontinuous).

Proposition 5 rules out the optimality of remaining on the boundary of ${\mathcal{A}}^{*}$. In particular, it is infeasible to remain on this boundary for $q\in {\mathcal{Q}}_x$ since the boundary is strongly exiting. Although it is feasible to remain on the boundary of ${\mathcal{A}}^{*}$ when $q\in {\mathcal{Q}}_n$, this segment resides strictly inside of $\mathcal{C}$ and therefore the argument presented in step 1 of the proof indicates that such a policy is strictly suboptimal. After proving Thm. 2 and Thm. 3, this observation formally rules out the possibility having a singular arc as part of the optimal policy. Given the above definitions, let

$$v_s\left(p,q;{\tau }^{*}(p,q)\right)=\{\begin{array}{ll}{v}_c(p),\hfill & (p,q)\in {\mathcal{C}}^{*},\hfill \\ {\int }_0^{{\tau }^{*}(p,q)}\left(c_1+c_2\right)P_a(s;p,q)e^{-\rho s}ds+e^{-\rho {\tau }^{*}(p,q)}{v}_c\left(P_a\left({\tau }^{*}(p,q);p,q\right)\right),\hfill & (p,q)\in {\mathcal{A}}^{*}.\hfill \end{array}$$ (17)

The following proposition characterizes v_s(p, q; τ*(p, q)).

Proposition 6 (Value Function of a Bang-bang Policy with a Single Switching Time). (i) For any (p, q) ∈ [0, p_∞] × [0, q_m], $v_s\left(p,q;{\tau }^{*}(p,q)\right)=v_s^{*}(p,q)$. (ii) Moreover, for any (p, q) ≠ (p_b(q), q) when $q\in {\mathcal{Q}}_n$ and any (p, q) ≠ (0, q), τ*(p, q) is the unique minimizer of the optimization problem (12). (iii) For any $(p,q)\in {\mathcal{A}}^{*}$, $v_s^{*}$ solves

$$c_{1}p+c_{2}p+{\partial }_{1}v(p,q)(\beta (1-p)-r-\delta q)p+{\partial }_{2}v(p,q)\delta q(q-1)-\rho v(p,q)=0.$$ (18)

(iv) For any (p_b(q), q) with $q\in {\mathcal{Q}}_n$, $v_s^{*}$ is not differentiable. (v) The value function $v_s^{*}$ is strictly increasing and strictly concave in p and is strictly decreasing and concave in q when $(p,q)\in {\mathcal{A}}^{*}$.

Figures 3 and 4 illustrate the claim in part (iv) and (v) of Prop. 6. Given the above results, we can now prove that $v_s^{*}(p,q)$ is the social planner’s optimal value function and, hence, ${\mathcal{A}}^{*}$ and ${\mathcal{C}}^{*}$ are the optimal action and inaction regions, respectively.

Theorem 2 (Optimality of a Bang-bang Policy with a Single Switching Time). For any (p, q) ∈ [0, p_∞] × [0, q_m] the value function $v_s^{*}(p,q)$ solves the HJB equation (7) and hence is the optimal value function of the social planner’s problem (P).

3.3.2. Long-term Focused Planner

Consider the case where ρ ≤ β − r. As was pointed out in Prop. 3 and depicted in Fig. 10a in Appendix B, v_c is not Lipschitz continuous as ${\text{lim}}_{p\downarrow 0}{v}_c^{\prime }(p)=\infty$. We show that in this setting, a policy similar to the one in subsection 3.3.1 is optimal. Specifically, defining $v_s^{*}(p,q)$ as in subsection 3.3.1, first- and second-order monotonicity of $v_s^{*}(p,q)$ in p and q along with the fact that the infimum in Eq. (12) is obtained follows from the same arguments. A major difference in this setting is that since ${\text{lim}}_{p\downarrow 0}{v}_c^{\prime }(p)=\infty$, it follows that q = 0 (see Fig. 1a). Defining $\overline{p}:\left[0,q_m\right]\to \left[0,p_{\infty }\right]$, p_b : [0, q_m] → [0, p_∞], $\mathcal{A}$, ${\mathcal{A}}^{*}$, and ${\mathcal{C}}^{*}$ in a similar manner, Prop. 4–6 remain valid.⁹ Using these results, we prove that $v_s^{*}(p,q)$ is the social planner’s optimal value function.

Theorem 3 (Optimality of a Bang-bang Policy with a Single Switching Time). For any (p, q) ∈ [0, p_∞]×[0, q_m] the value function $v_s^{*}(p,q)$ solves the HJB equation (7) and hence is the optimal value function of the social planner’s problem (P).

Similar to the case where ρ > β − r, panels (a) and (c) in Fig. 3 and panel (a) in Fig. 4 illustrate the properties of the optimal value function when ρ ≤ β − r. Fig. 11 in Appendix B shows the evolution of the system’s state on the optimal path and hitting times for three example initial conditions.

Finally, comparing figures 1a, 1b, and 9a (in Appendix A) reveals that increasing the social planner’s discount rate ρ reduces the size of the optimal action region. Intuitively, this is because the cost of the drug is incurred immediately, but the benefits of treatment materialize over time. Specifically, prescribing the drug either causes P(t) to decrease or slows the rate at which it increases depending on the quality and strength of the drug. Increasing the discount rate reduces the present value of these future benefits and, therefore, decreases the size of the optimal action region.

Figure 9:

(a) Action/Inaction boundary p_b along with the solution to the first-order optimality condition, i.e., $\overline{p}$, for 2(β − r) < ρ. (b) Illustration of step 2, part (a) and (b) of the proof of Thm. 2.

4. Policy Insights

Our analytical results in section 3 have immediate implications for our main policy question. The solution to the social planner’s problem (P) indicates that (for at least some q) it is optimal to prescribe the drug for all patients even when the percentage of the population that is infected is close to zero. Specifically, Thm. 2 and 3 indicate that reserving the last drug for future use is not optimal. In this section, we apply our analytical results to the case of extensively resistant gonorrhea in the United States, a sexually transmitted infection which has seen a number of cases resistant to the last available treatment (Bolan et al. 2012; Unemo and Nicholas 2012; Terkelsen et al. 2017). Given current levels of infection and resistance, we compare treatment stopping times under the optimal policy identified by our analysis to antibiotic treatment norms presented in the policy literature and the resulting economic impacts of these policies.

4.1. Case Study: Extensively Resistant Gonorrhea

Gonorrhea is a sexually transmitted infection caused by the bacterium N. gonorrhoeae that annually affects approximately 820,000 Americans and 78–106 million people globally (CDC 2017a; Newman et al. 2015; Unemo and Shafer 2014). Gonoccocal infections are often asymptomatic which contributes to the persistence of the disease (CDC 2017a). Though gonoccocal infections are rarely fatal, patients who do not receive treatment, or in whom treatment is delayed, may experience complications including pelvic inflammatory disease (PID), infertility, ectopic pregnancy, epididymitis, arthritis, and cellulitis (CDC 2017a).

Gonorrhea can be cured with antibiotics; however, gonorrhea has progressively developed resistance to the antibiotics used to treat it (reviewed in Unemo and Shafer 2014). Forty-four percent of gonorrhea infections in the US are resistant to at least one antibiotic, including penicillin (18%), tetracycline (22%), ciprofloxacin (27%) (CDC 2017b). Due to these high levels of resistance, gonorrhea treatment guidelines were updated to recommended a combination of two antibiotics from different classes: ceftriaxone (an injected third-generation cephalosporin) with azithromycin (a macrolide) (CDC 2012).

Current levels of resistance to ceftriaxone and azithromycin are low (0.3% and 3.6%, respectively, in 2016; see CDC 2017b), but a handful of untreatable infections have been identified (Allen et al. 2014; Bolan et al. 2012; Unemo and Nicholas 2012; Terkelsen et al. 2017; Papp et al. 2017; Lefavre et al. 2018). Furthermore, the antibiotic drug development pipeline is sparse and it is unclear when or if the few antibiotics currently in clinical trials will be successfully brought to market (Alirol et al. 2017). As a result, antibiotic-resistant gonorrhea has been declared an urgent public health threat by US Centers for Disease Control and Prevention (CDC) and a high priority pathogen by the World Health Organization (WHO) (CDC 2013; WHO 2017a). Discussions of the potential costs and health consequences of widespread untreatable gonorrhea, clearly on the horizon, are routinely present in the medical literature (Bolan et al. 2012; Kidd et al. 2012; Barbee 2014; Tuddenham and Ghanem 2015) and in the popular press (Stein 2007; Greenfield 2011; Rudd 2017). Generally, the WHO recommends changing treatment guidelines when more than 5% of infections are resistant to a recommended drug regimen (Tapsall 2001; Alirol et al. 2017); however, it is not clear that this recommendation is either feasible or optimal for gonorrhea in particular since no alternative regimens currently exist.

We applied our analytical approach to the question of optimal management for gonorrhea in the context of antibiotic resistance to the last remaining treatment. Parameter values used in our analysis are summarized in Table 1 with a more detailed description of assumptions and inputs provided in Appendix C. Treatment-related parameters account for the fact that even under a 100% treatment policy, not all patients will receive treatment due to asymptomatic infections and imperfect access to medical care (see remark 1).

Table 1:

Summary of input parameter values and ranges (corresponding to 2.5% and 97.5% quantiles) for the numerical case study of the optimal treatment policy of gonorrhea. All parameter values are presented on an annual basis and costs are presented in 2016 USD.

Parameter	Base Value	Range	Description
β	1.69	0.96 – 2.86	Rate of infection
r	1.41	0.80 – 2.37	Rate of recovery without treatment
δ	0.27	0.13 – 0.54	Incremental increase in rate of recovery with treatment (i.e., effective drug strength)
c2	$454	$231.88 – $475.05	Healthcare costs associated with gonorrhea complications
c1	$99	$40.12 – $285.74	Effective cost of treatment
ρ	0.03	-	Discount rate

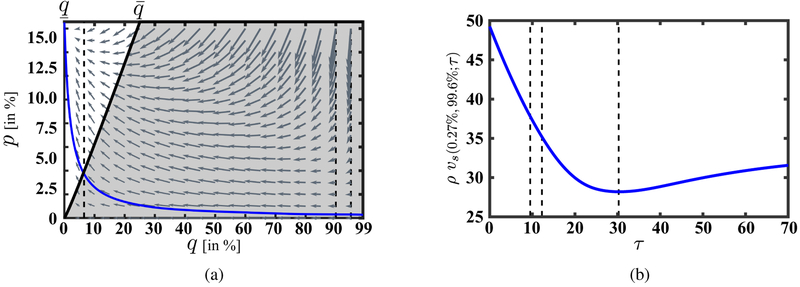
The action/inaction boundary along with the vector field defined by the ODE’s (5)–(6) with W (t) = 1, t ≥ 0, is shown in Fig. 5a for the base case values of our model parameters. At the current gonorrhea prevalence of 0.27% in the general population and drug quality q > 99% (less than 1% resistance), the optimal policy is to treat all infections, as we would expect. Furthermore, it is clear that it is optimal to use the current treatment regimen for gonorrhea resistance levels far higher than the 5% threshold (q < 95%) generally recommended by WHO. Figure 5b shows the projected annualized gonorrhea-related total expenditures over an infinite time horizon, ρv_s(0.27%, 99.6%; τ), for various stopping times τ. In particular, the system’s trajectory when W(t) = 1 for t ≥ 0 is shown by a blue line in Fig. 5a. For our base case parameters, it takes 9.53 years for the treatment quality to drop to 95% (denoted by τ₉₅) and 12.30 years for quality to fall to 90% (denoted by τ₉₀). However, these points remain strictly inside the optimal action region. In fact, it is economical to use the last-line treatment until the treatment quality drops to 6.4% (resistance level of 93.6%) which corresponds to an economic lifetime of 30.31 years. These stopping times are marked in Fig. 5b by vertical dashed lines and the projected annualized per-person cost of the corresponding policies are $37.78, $35.15, and $28.19 respectively. Note that in the absence of resistance (i.e., if the current effectiveness of the last-line treatment could be preserved in perpetuity), the annualized per-person cost of gonorrhea would remain at its current value of $1.50. Thus, the minimum annualized per-person cost of resistance is $26.69 for gonorrhea, which makes a compelling case for investments in new drug development projects. We have summarized some of these results in Table 2. If a new drug for gonorrhea becomes available after the time when it is no longer economical to treat patients with the current drug combination, our model can be used to identify the action/inaction boundary for the new drug which determines the optimal action based on the prevalence of gonorrhea at that time and the initial level of resistance to the new treatment. If a new drug becomes available while it is still economical to use the current treatment regimen, the new optimal treatment policy would depend on the prevalence of gonorrhea, as well as the levels of resistance, strengths (i.e., δ), and costs of both the existing and the new treatment. This setting requires its own comprehensive analysis as policies that are not optimal when only a single drug remains could become optimal. For example, when the prevalence of gonorrhea is low, withholding the new treatment completely to preserve its effectiveness or restricting use of the new treatment as second-line therapy could be optimal.

Figure 5:

(a) The action/inaction boundary for the gonorrhea case study. The shaded area indicates the region in which it is optimal to treat all patients and the unshaded area indicates the region in which it is optimal to treat no one (because the treatment is effectively obsolete due to high resistance levels). Consistent with our main analysis in section 3, it is never optimal to only treat a subset of infected individuals. The gray arrows depict the vector field for the gonorrhea case study when W (t) = 1, t ≥ 0, indicating the direction of the movement in the state space when treatment is offered to all infected individuals. The solid blue line represents the state trajectory for the initial point (p, q) = (0.27%, 99.6%) when treatment is provided to all patients (W (t) = 1, t ≥ 0), even after it is no longer optimal to provide treatment to anyone. The three dashed vertical lines correspond to q = 95%, q = 90%, and q = 6.4%. (b) Projected annualized gonorrhea total expenditures over an infinite time horizon for W (t) = 1_{t≤τ} as the function of τ. The three dashed vertical lines mark the times when Q_a(t; 99.6%) = 95%, Q_a(t; 99.6%) = 90%, and Q_a(t; 99.6%) = 6.4%.

Table 2:

The time (in years) it takes for the last-line treatment of gonorrhea to reach 95% (denoted by τ₉₅), and 90% (denoted by τ₉₀) effectiveness as well as the time at which this treatment ceases to be economical (i.e., τ*). The last row indicates the annualized total cost of gonorrhea per person (ρv*) for an infinite time horizon when the discount rate ρ is 3%. All policy-relevant quantities were evaluated with an initial gonorrhea prevalence of 0.27% and drug quality of 99.6%. The range corresponds to 2.5% and 97.5% quantiles of each quantity.

Policy Relevant Quantities	Base Value	Range	Description
τ95	9.53	4.75 – 19.09	Years until drug quality reduces to 95%
τ90	12.30	6.13 – 24.63	Years until drug quality reduces to 90%
τ*	30.31	14.11 – 61.79	Years until treatment is no longer economical (optimal stopping time)
ρv*	$28.19	$6.34 – $46.38	Annualized per-person cost of gonorrhea under the optimal policy

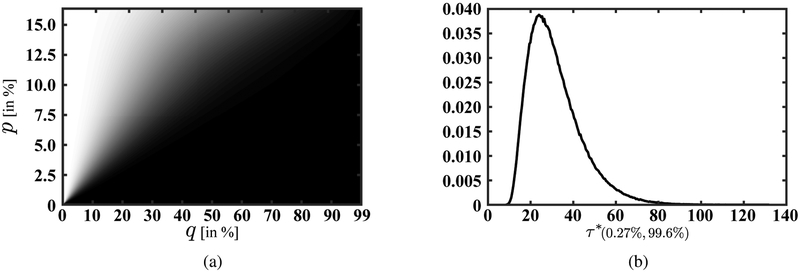
We examined the sensitivity of the action/inaction boundary as well as other policy-relevant quantities to uncertainty in the available data through a probabilistic sensitivity analysis. We sampled from appropriate distributions over our model parameters 750,000 times. Details of these distributions and sampling process are included in Appendix C. Fig. 6a illustrates the sensitivity of the optimal action/inaction regions to the uncertainty in our data. This figure demonstrates greater uncertainty in the location of the action/inaction boundary at higher disease prevalence. However, given the current disease prevalence and treatment quality, the optimal system trajectory crosses the action/inaction boundary at a relatively low disease prevalence where uncertainty in this boundary is also low (see Fig. 5a). Figure 6b depicts the distribution of the stopping time that corresponds to the optimal treatment policy (i.e., τ*).

Figure 6:

(a) Sensitivity of the optimal action/inaction region to the uncertainty in the model primitives for the gonorrhea case study. The shading represents the likelihood of a point being in the optimal action region with solid black representing 100% and solid white 0%. (b) The distribution of the stopping time corresponding to the optimal treatment policy.

5. Structural Sensitivity Analysis

In our original formulation, we considered a constant disease transmission rate β. Assuming a constant disease transmission rate is consistent with convention, representative of transmission for some diseases (e.g., gonorrhea discussed in section 4.1), and often considered a good first-order approximation otherwise. However, there are reasons to consider a non-constant transmission rate. Higher prevalence (and awareness) of the disease may lead to social distancing, increased hygiene behaviours (i.e, hand washing), or higher-intensity cleaning procedures at health care facilities which reduces the transmission rate as the prevalence increases (Nigmatulina and Larson 2009; Aleman et al. 2009; Gilchrist et al. 2015; Ambrosch and Rockmann 2016; Manfredi and D’Onofrio 2013). In addition, even when the number of infections has remained low for many years, the possibility of resurgence remains, as eradication of many diseases is very difficult (e.g., Singh et al. 2007; Moran-Gilad et al. 2016). This may be due, in part, to a relaxation of prevention behaviors as a disease becomes more rare (e.g., Kalichman et al. 2017; Manfredi and D’Onofrio 2013). In a real-world setting, locally-eradicated diseases can be reintroduced (e.g., Barrett 2004; Moran-Gilad et al. 2016).

We incorporate a non-constant transmission rate that captures the spirit of these forces into our formulation by replacing β with B(p) = βp^γ with γ ≤ −1. In this case B(p) converges to infinity when p approaches to zero, ensuring that the disease cannot be eradicated from the population even with treatment.¹⁰ Use of the drug which reduces B(P(t)) (1 − P(t)) − r by at most δ will not impact the evolution of P(t) when P(t) is close to zero. Thus, a non-constant transmission rate of this form creates a situation where the drug is ineffective at controlling the dynamics when the disease prevalence is low. Although infected individuals do benefit from the prescription of the drug, their numbers relative to the size of society is too small to justify the loss in drug quality. Therefore, incorporating a non-constant transmission rate creates the situation in which a policy of reserving the last drug for future use can be optimal.

Figure 7 illustrates the above dynamics when γ is set to −1.5. In this section, parameter values were selected to illustrate features of the optimal policy. They are the same as in section 3, except for c₁ and c₂, which are now set to 5 and 10 respectively. We changed these costs in order to ensure that the action region is nonempty since the disease spreads much faster when γ ≤ −1. We only consider one discount rate ρ = ρ₁ = 0.1 because the optimal value function is Lipschitz continuous for any discount rate ρ > 0. Moreover, P (t) will not stay at zero when p = 0 since there is a positive (and unbounded) force pushing it into the positive region.¹¹ Consequently, unlike in our base model, v*(0, q) is strictly positive. Another change that is caused by introducing γ is the size of the long-run value of P (t). In our example, this value, i.e., the solution of β(1 − p)p^γ − r = 0, is equal to 0.82.

Figure 7:

(a) The state space partition to action/inaction region when γ = −1.5 along with two optimal state trajectories. (b, c) The optimal state trajectory as a function of time for two initial starting points. (d) The optimal control as a function of time for two different starting points. To enable comparison, p-axis and q-axis in panels (b) and (c) are kept parallel to these axes in panel (a).

Fig. 7a demonstrates the partition of the state space to action and inaction regions. In addition, it includes the contour levels of the optimal value function along with two optimal trajectories: one starting in the optimal action region and one starting from the optimal inaction (continuation) region. There are several notable differences between the optimal policies in this case and in the base case with constant β. First, we see that the action-inaction boundary does not intersect the x-axis, indicating that for some (relatively lower) values of p it is not optimal to treat infected individuals in the population at any value of q. This means that, for some values of p, the optimal policy is to preserve the drug for a potentially more serious outbreak. Second, as it is evident from this picture, it is possible to remain on the optimal action/inaction boundary. This suggests that the optimal control (prescription policy) consists of a singular arc. Specifically, starting from an initial condition in the inaction region, it is optimal to preserve treatment quality and let the size of the infected population increase until it reaches a quality-dependant prevalence threshold. At that point, the drug is prescribed to a fraction of the infected population in such a way that the growth rate of the disease is optimally managed. This management balances treatment-associated reductions in prevalence with reductions in drug quality and the effect of prevalence on self-protective behaviors. In practice, the fraction who receives treatment can be chosen based on considerations such as contact network structure and membership in specific risk groups. For an initial condition starting from the interior of the action region, it is optimal to prescribe the drug to every infected individual until the size of this population is reduced to the level of the drug-quality dependent prevalence threshold. At that point, similar to the previous case, the drug is then prescribed to a fraction of the infected population to keep the growth rate of the disease under control.

6. Conclusion

We considered the problem of minimizing the total cost of an infectious disease using a single available drug from a social planner’s perspective. Our base formulation is a classic SIS model with the additional incorporation of a drug-resistant strain. Drug resistance and its spread through natural selection in response to disease treatment is a key feature of our model. The social planner’s objective is to identify the prescription policy, essentially the rules by which the useful life of the drug should be consumed, that minimizes the total costs of the disease over an infinite horizon.

While stylized, our model represents a class of non-fatal SIS infectious diseases for which treatment expedites recovery, infection does not confer immunity (i.e., recovered individuals can be re-infected), and drug resistance exists. This represents a number of sexually transmitted bacterial infections, including gonorrhea, and some viral conditions for which there is no vaccine and recovery does not confer immunity, such as the common cold and hepatitis C virus. We provide a detailed case study of one such example, extensively drug-resistant gonorrhea, which has been declared an urgent public health threat by US Centers for Disease Control and Prevention (CDC) and a high priority pathogen by the World Health Organization (WHO) (CDC 2013; WHO 2017a). Without effective antibiotic treatment, gonoccocal infections can cause costly and life-altering complications (CDC 2017a). Our analysis indicates that resistance to the last-line of treatment will reach 5% of all infections in 9.5 years (95%CI 4.8–19.1 years) but that treatment will continue to provide cost effective benefits until the optimal stopping time, which we estimate will occur in 30.3 years (95%CI 14.1–61.8 years). Even though treatment will continue to be useful for many years, resistance increases the total cost of gonorrhea infections in the US from a per-person cost of $1.50 per year to $28.19 per year under our optimal policy.

In addition to policy insights specific to our case study on gonorrhea, this paper makes multiple significant contributions to the operations research literature. First, to our knowledge, this is the first paper that provides a complete solution to an optimal control problem for an SIS model of an infectious disease with resistance. We prove that the optimal prescription policy is of bang-bang type with a single switching time. We characterize the optimal action/inaction regions and provide a semi-closed form for the social planner’s optimal value function. We show that the optimal value function is not C¹ and, depending on the magnitude of the discount rate, may not be Lipschitz continuous when the prevalence of the disease is low. This has important consequences for numerical evaluations of infectious disease control problems with detailed disease-specific dynamics, as it showcases potential numerical instability.

Second, we demonstrate the importance of the disease transmission rate in determining the shape of the action region and the form of the optimal policy. With a non-constant disease transmission rate, we demonstrate it is sometimes optimal to reserve the drug for a more severe outbreak. In the context of antimicrobial stewardship these results indicate that reserving last-line treatment options may be an appropriate component of infectious disease and resistance control programs for diseases with high population- or system-level responses to high prevalence situations and for which low prevalence can diminish self-protective behaviors and system-level vigilance. For diseases with a constant transmission rate, which may include diseases for which changes in prevalence are not widely visible (e.g., sexually transmitted diseases) or for which protective behaviors are costly resulting in slow uptake, greater emphasis on other elements of an antimicrobial stewardship program may provide more social value. These efforts may include reducing inappropriate medical, veterinary, and non-medical antimicrobial use; public awareness campaigns to decrease infection rates generally; other community or health facility-based infection control efforts; and investments in the development of new antimicrobials. Our results also have important implications for policy modelers as these findings reveal that, if relevant to the disease of interest, it is critically important to incorporate a non-constant disease transmission rates into detailed disease-specific models.

On the technical side, we develop a new generalizable method for proving the optimality of a candidate value function. Our approach verifies the validity of the HJB equation in the action and inaction regions implied by the candidate value function. Verifying that the HJB equation holds in the inaction region is often straightforward and can be carried out directly. We prove that the HJB equation holds in the action region by contradiction. Our argument relies only on the assumption that the HJB equation holds at the boundary of the action region. This greatly facilitates the verification step, as verifying the latter assumption is often straightforward. The key elements of our method can be readily adapted to other control problems, specifically those with piecewise deterministic dynamics (see Davis 1984 for further detail).

It should be noted that while our model formulation reflects an important class of SIS infectious diseases exhibiting resistance, there are a number of infectious pathogens and treatment resistance patterns that our model formulation does not represent. For example, our model does not represent infections for which treatment does not result in recovery (e.g., HIV), death is a likely outcome (e.g., malaria), recovery confers immunity (e.g., influenza, measles), or vaccination is available (e.g., influenza, measles). Our framework also assumes that the infection is transmitted directly between infected and susceptible individuals and would not be suitable for addressing policy questions related to managing infections that result from overgrowths of microbes that are part of the normal flora of the body (i.e., S. aureus, S. pneumoniae, and C. albicans), or where transmission is via contaminated water or food (e.g., Salmonella, V. cholerae, or E. coli) or via a vector such as mosquitoes (e.g., malaria, dengue, or Lyme disease). Each of these variations requires different system dynamics, with additional state variables, and different policy considerations (e.g., vaccination strategies for the prevention of influenza, water treatment response after a natural disaster for the prevention of cholera). Antimicrobial resistance affects many pathogens with significant impacts on human health and we intend to consider some of these challenges in future work.

Appendix A. Proofs

The following Lemma is used in the proof of Prop. 1.

Lemma 1. Fix (p, q) ∈ [0, 1] × [0, 1], and let $v^{*}:[0,1]\times [0,1]\to {ℝ}_{+}$ be a bounded function. For any t ≥ 0 and measurable policy $W:{ℝ}_{+}\to [0,1]$ define

$$H(t;W)\triangleq {\int }_0^t{e}^{-\rho s}\left(c_{1}W(s)P(s)+c_{2}P(s)\right)ds+e^{-\rho t}{v}^{*}(P(t),Q(t)),$$

where (P (t), Q(t)) is the solution of ODE’s (5)–(6) for initial conditions (p, q) and prescription policy W. If v* is such that (i) H(t; W) is nondecreasing in t for any admissible policy W and (ii) there is an admissible policy W* for which H(t; W*) is constant with respect to t, then

$$v^{*}(p,q)=\underset{W:{ℝ}_{+}\to [0,1]}{\text{inf}}{\int }_0^{\infty }\left(c_{1}W(s)P(s)+c_{2}P(s)\right)e^{-\rho s}ds,$$

and W* attains the infimum.

Proof of Lemma 1.

Note that since v* is bounded, we have ${\text{lim}}_{t\to \infty }H(t;W)={\int }_0^{\infty }\left(c_{1}W(s)P(s)+c_{2}P(s)\right)e^{-\rho s}ds$. Moreover, since for any admissible W, H(t; W) is nondecreasing, we have H(0; W) = v*(p, q) ≤ H(t; W) ≤ lim_t→∞ H(t; W). Consequently, we can write

$$v^{*}(p,q)\le \underset{W:{ℝ}_{+}\to [0,1]}{\text{inf}}{\int }_0^{\infty }{e}^{-\rho s}\left(c_{1}W(s)P(s)+c_{2}P(s)\right)ds.$$

Since for W*, H(t; W*) is constant with respect to t, i.e., H(0; W*) = v*(p, q) = H(t; W*), t ≥ 0, the infimum is obtained at W = W* which completes the proof. ■

Proof of Proposition 1.

It is sufficient to show that v* satisfies the conditions of lemma 1. Note that for any t ≥ 0, we can write

$$\begin{gathered} H(t;W)-H(0;W)={\int }_0^t\left[c_{1}W(s)P(s)+c_{2}P(s)\right]e^{-\rho s}ds+e^{-\rho t}{v}^{*}(P(t),Q(t))-v^{*}(p,q) \\ ={\int }_0^t\left[c_{1}W(s)P(s)+c_{2}P(s)-\rho v^{*}(P(s),Q(s))+{\partial }_1{v}^{*}(P(s),Q(s))(\beta (1-P(s))-\delta W(s)Q(s)-r)P(s)+{\partial }_2{v}^{*}(P(s),Q(s))\delta W(s)Q(s)(Q(s)-1)\right]e^{-\rho s}ds. \end{gathered}$$ (19)

Since by Eq. (7), the integrand in the above equation is nonnegative, it follows that H(t; W) is nondecreasing. Moreover, since Eq. (7) is linear in w (and hence is continuous), for any (P(s), Q(s)) it has at least a solution (by the extreme value theorem) which sets the integrand of the above equation equal to zero. Hence conditions of lemma 1 holds for v* and the proof is complete. ■

Proof of Proposition 2.

Part (i). Monotonicity and convexity of Q(t; q, W) can be verified by direct calculation. Specifically,

$$\frac{d}{dq}Q(t;q,W)=\frac{e^{{\int }_0^t\delta W(s)ds}}{{\left((1-q)e^{{\int }_0^t\delta W(s)ds}+q\right)}^2}>0,$$ (20)

$$\frac{d^2}{d{q}^2}Q(t;q,W)=\frac{2e^{{\int }_0^t\delta W(s)ds}\left(e^{{\int }_0^t\delta W(s)ds}-1\right)}{{\left((1-q)e^{{\int }_0^t\delta W(s)ds}+q\right)}^3}\ge 0.$$ (21)

Part (ii). The fact that P(t; p, q, W) is a complete Bernstein function in p follows from its algebraic form (see Schilling et al. 2012, page 304). Moreover, taking the first and second derivative of P(t; p, q, W), we obtain

$$\begin{gathered} \frac{d}{dp}P(t;p,q,W)=\frac{e^{-{\int }_0^t(\delta W(s)Q(s;q,W)-\beta +r)ds}}{{\left(\beta p{\int }_0^t{e}^{-{\int }_0^s(\delta W(\sigma )Q(\sigma ;q,W)-\beta +r)d\sigma }ds+1\right)}^2}>0, \\ \frac{d^2}{d{p}^2}P(t;p,q,W)=-\frac{2\beta e^{-{\int }_0^t(\delta W(s)Q(s;q,W)-\beta +r)ds}{\int }_0^t{e}^{-{\int }_0^s(\delta W(\sigma )Q(\sigma ;q,W)-\beta +r)d\sigma }ds}{{\left(\beta p{\int }_0^t{e}^{-{\int }_0^s(\delta W(\sigma )Q(\sigma ;q,W)-\beta +r)d\sigma }ds+1\right)}^3}<0. \end{gathered}$$ (22)

Similarly, the first derivative of P(t; p, q, W) with respect to q can be written as

$$\frac{d}{dq}P(t;p,q,W)=-\left[p{e}^{-{\int }_0^t(\delta W(s)Q(s;q,W)-\beta +r)ds}(-\beta p{\int }_0^t\left({\int }_0^s\delta W(\sigma )\frac{d}{dq}Q(\sigma ;q,W)d\sigma \right)e^{-{\int }_0^s(\delta W(\sigma )Q(\sigma ;q,W)-\beta +r)d\sigma }ds+{\int }_0^t\delta W(s)\frac{d}{dq}Q(s;q,W)ds\left(\beta p{\int }_0^t{e}^{-{\int }_0^s(\delta W(\sigma )Q(\sigma ;q,W)-\beta +r)d\sigma }ds+1\right))\right]/{\left(\beta p{\int }_0^t{e}^{-{\int }_0^s(\delta W(\sigma )Q(\sigma ;q,W)-\beta +r)d\sigma }ds+1\right)}^2\le 0.$$ (23)

The above inequality follows since Q(σ; q, W) is increasing in q and therefore ${\int }_0^s\delta W(\sigma )\frac{d}{dq}Q(\sigma ;q,W)d\sigma$ is positive and increasing in s. This allows us to conclude

$${\int }_0^t\left({\int }_0^s\delta W(\sigma )\frac{d}{dq}Q(\sigma ;q,W)d\sigma \right)e^{-{\int }_0^s(\delta W(\sigma )Q(\sigma ;q,W)-\beta +r)d\sigma }ds\le \left({\int }_0^t\delta W(s)\frac{d}{dq}Q(s;q,W)ds\right){\int }_0^t{e}^{-{\int }_0^s(\delta W(\sigma )Q(\sigma ;q,W)-\beta +r)d\sigma }ds,$$

which provides us with the result. Similar to the first derivative, we can obtain

$$\frac{d^2}{d{q}^2}P(t;p,q,W)=p{e}^{-{\int }_0^t(\delta W(s)Q(s;q,W)-\beta +r)ds}\left\{2{\beta }^2{p}^2{\left({\int }_0^t\left({\int }_0^s\delta W(\sigma )\frac{d}{dq}Q(\sigma ;q,W)d\sigma \right)e^{-{\int }_0^s(\delta W(\sigma )Q(\sigma ;q,W)-\beta +r)d\sigma }ds\right)}^2-2\beta p{\int }_0^t\left({\int }_0^s\delta W(\sigma )\frac{d}{dq}Q(\sigma ;q,W)d\sigma \right)e^{-{\int }_0^s(\delta W(\sigma )Q(\sigma ;q,W)-\beta +r)d\sigma }ds{\int }_0^t\delta W(s)\frac{d}{dq}Q(s;q,W)ds\left(\beta p{\int }_0^t{e}^{-{\int }_0^s(\delta W(\sigma )Q(\sigma ;q,W)-\beta +r)d\sigma }ds+1\right)+\left(\beta p{\int }_0^t{e}^{-{\int }_0^s(\delta W(\sigma )Q(\sigma ;q,W)-\beta +r)d\sigma }ds+1\right)\left[\left({\left({\int }_0^t\delta W(s)\frac{d}{dq}Q(s;q,W)ds\right)}^2-{\int }_0^t\delta W(s)\frac{d^2}{d{q}^2}Q(s;q,W)ds\right)\left(\beta p{\int }_0^t{e}^{-{\int }_0^s(\delta W(\sigma )Q(\sigma ;q,W)-\beta +r)d\sigma }ds+1\right)-\beta p{\int }_0^t\left({\left({\int }_0^s\delta W(\sigma )\frac{d}{dq}Q(\sigma ;q,W)d\sigma \right)}^2-{\int }_0^s\delta W(\sigma )\frac{d^2}{d{q}^2}Q(\sigma ;q,W)d\sigma \right)e^{-{\int }_0^s(\delta W(\sigma )Q(\sigma ;q,W)-\beta +r)d\sigma }ds\right]\right\}/{\left(\beta p{\int }_0^t{e}^{-{\int }_0^s(\delta W(\sigma )Q(\sigma ;q,W)-\beta +r)d\sigma }ds+1\right)}^3.$$

First, note that the denominator of the above expression is positive. Moreover, we have

$${\left({\int }_0^t\left({\int }_0^s\delta W(\sigma )\frac{d}{dq}Q(\sigma ;q,W)d\sigma \right)e^{-{\int }_0^s(\delta W(\sigma )Q(\sigma ;q,W)-\beta +r)d\sigma }ds\right)}^2\le \left({\int }_0^t\left({\int }_0^s\delta W(\sigma )\frac{d}{dq}Q(\sigma ;q,W)d\sigma \right)e^{-{\int }_0^s(\delta W(\sigma )Q(\sigma ;q,W)-\beta +r)d\sigma }ds\right)\left({\int }_0^t\delta W(s)\frac{d}{dq}Q(s;q,W)ds\right)\left({\int }_0^t{e}^{-{\int }_0^s(\delta W(\sigma )Q(\sigma ;q,W)-\beta +r)d\sigma }ds+\frac{1}{\beta p}\right).$$

Hence, the sum of the first two terms is negative. Now consider the coefficient of the third term, i.e., the expression inside the square bracket, which depends on

$$\left({\left({\int }_0^s\delta W(\sigma )\frac{d}{dq}Q(\sigma ;q,W)d\sigma \right)}^2-{\int }_0^s\delta W(\sigma )\frac{d^2}{d{q}^2}Q(\sigma ;q,W)d\sigma \right),s\in [0,t].$$

Taking the derivative of this expression with respect to s we obtain

$$\frac{d}{ds}\left({\left({\int }_0^s\delta W(\sigma )\frac{d}{dq}Q(\sigma ;q,W)d\sigma \right)}^2-{\int }_0^s\delta W(\sigma )\frac{d^2}{d{q}^2}Q(\sigma ;q,W)d\sigma \right)=2\delta W(s)\frac{d}{dq}Q(s;q,W)\left({\int }_0^s\delta W(\sigma )\frac{d}{dq}Q(\sigma ;q,W)d\sigma \right)-\delta W(s)\frac{d^2}{d{q}^2}Q(s;q,W)=\delta W(s)\frac{d}{dq}Q(s;q,W)\left(2{\int }_0^s\delta W(\sigma )\frac{d}{dq}Q(\sigma ;q,W)d\sigma -\frac{\frac{d^2}{d{q}^2}Q(s;q,W)}{\frac{d}{dq}Q(s;q,W)}\right).$$

Substituting for the first and second derivatives of Q(s; q, W) with respect to q using Eq. (20) and Eq. (21), we obtain

$$\left(2{\int }_0^s\delta W(\sigma )\frac{d}{dq}Q(\sigma ;q,W)d\sigma -\frac{\frac{d^2}{d{q}^2}Q(s;q,W)}{\frac{d}{dq}Q(s;q,W)}\right)=2{\int }_0^s\delta W(\sigma )\frac{e^{{\int }_0^{\sigma }\delta W\left(s^{\prime }\right)d{s}^{\prime }}}{{\left((1-q)e^{{\int }_0^{\sigma }\delta W\left(s^{\prime }\right)d{s}^{\prime }}+q\right)}^2}d\sigma -\frac{2\left(e^{{\int }_0^s\delta W(\sigma )d\sigma }-1\right)}{(1-q)e^{{\int }_0^s\delta W(\sigma )d\sigma }+q}=0.$$

Consequently,

$$\left({\left({\int }_0^s\delta W(\sigma )\frac{d}{dq}Q(\sigma ;q,W)d\sigma \right)}^2-{\int }_0^s\delta W(\sigma )\frac{d^2}{d{q}^2}Q(\sigma ;q,W)d\sigma \right)=0,$$

for any s ∈ [0, t]. This allows us to conclude P(t; p, q, W) is concave with respect to q. ■

Proof of Theorem 1.

The claim follows since for any admissible W, P(t; p, q, W) is strictly increasing¹² and strictly concave in p and decreasing and concave in q. These properties are preserved under infimum/minimum (see for example Theorem 2.1 or Theorem 5.5 of Rockafellar 1970). ■

Proof of Proposition 3.

Part (i). The fact that v_c is a complete Bernstein function follows from Prop. 2 and since the property is preserved under positive weighted sum. Using integration by parts we can write

$$\begin{gathered} v_c(p)=\frac{c_2}{\rho }p+\frac{c_2}{\rho }{\int }_0^{\infty }{\dot{P}}_c(s;p)e^{-\rho s}ds \\ =\frac{c_2}{\rho }p+\frac{c_2}{\rho }{\int }_0^{\infty }\left[\beta \left(1-P_c(s;p)\right)-r\right]P_c(s;p)e^{-\rho s}ds \\ =\frac{c_2}{\rho }p+\frac{c_2}{\rho }{\int }_0^{\infty }\frac{{(\beta -r)}^2[(\beta (1-p)-r)p]e^{(\beta -r)s}}{{\left(p\beta \left(e^{(\beta -r)s}-1\right)+\beta -r\right)}^2}{e}^{-\rho s}ds. \end{gathered}$$

where the last equality is obtained using Eq. (3). Moreover, we have

$$\begin{gathered} v_c^{\prime }(p)={\int }_0^{\infty }{c}_2{\partial }_2{P}_c(s;p)e^{-\rho s}ds \\ ={\int }_0^{\infty }{c}_2\frac{{(\beta -r)}^2{e}^{(\beta -r)s}}{{\left(p\beta \left(e^{(\beta -r)s}-1\right)+\beta -r\right)}^2}{e}^{-\rho s}ds \end{gathered}$$ (24)

where the exchange of the derivative and integral is warranted by Leibniz’s rule (or monotone convergence theorem as P_c(s; p) is complete Bernstein in p). Substituting the above expressions into the differential equation (11) provides us with the results.

Part (ii) and (iii). Using Eq. (24) we have

$$\begin{gathered} \underset{p\downarrow 0}{\text{lim}}{v}_c^{\prime }(p)={\int }_0^{\infty }\underset{p\downarrow 0}{\text{lim}}{c}_2{\partial }_2{P}_c(s;p)e^{-\rho s}ds \\ ={\int }_0^{\infty }{c}_2{e}^{(\beta -r-\rho )s}ds, \end{gathered}$$ (25)

where the integral and the limit can be exchanged by monotone convergence theorem (P(t; p, q; W) is concave with respect to p). Therefore, since v_c is increasing and concave, the claim follows immediately. ■

Proof of Proposition 4.

For any (p, q) in the interior of $\mathcal{A}$, i.e., $(p,q)\in {\mathcal{A}}^{°}$, there exists ϵ > 0 such that $\left(P_a(t;p,q),Q_a(t;q)\right)\in {\mathcal{A}}^{°}$, for t ∈ [0, ϵ]. Since for any $(p,q)\in {\mathcal{A}}^{°}$ we have $c_1-\delta q{v}_c^{\prime }(p)<0$, it follows that v_s(p, q; τ) is strictly decreasing for τ ∈ [0, ϵ]. Hence it is $v_s^{*}(p,q)<v_c(p)$. Since if $(p,q)\in {\mathcal{A}}^{°}$ then $(\widehat{p},q)\in {\mathcal{A}}^{°}$ where $0<\widehat{p}\le p$, it follows that p ≤ p_b(q). This completes the proof. ■

Proof of Proposition 5.

We prove the claims in multiple steps.

Step 0. We first show that if $(p,q)\in \overline{{\mathcal{C}}^{*}}$, and there is ϵ > 0 such that the trajectory $\left(P_a(t;p,q),Q_a(t;q)\right)\in {\mathcal{C}}^{*}$ for t ∈ (0, ϵ), then $v_s^{*}(p,q)=v_s(p,q;0)=v_c(p)$ (see Fig. 8). Consider the case where ϵ is infinity (trajectory (a) in Fig. 8), i.e., (P_a(t; p, q), Q_a(t; q)) can never reach the action region boundary (i.e., it remains in ${\mathcal{C}}^{*}$ for any t ≥ 0). Since $\mathcal{A}\subset {\mathcal{A}}^{*}$, we can conclude that

$$\left[c_1-\delta Q_a(t;q)v_c^{\prime }\left(P_a(t;p,q)\right)\right]P_a(t;p,q)=\left(c_1+c_2\right)P_a(t;p,q)+v_c^{\prime }\left(P_a(t;p,q)\right)\left[\beta \left(1-P_a(t;p,q)\right)-r-\delta Q_a(t;q)\right]P_a(t;p,q)-\rho v_c\left(P_a(t;p,q)\right)>0,$$

for any t ≥ 0, where the equality follows from Prop. 3. Multiplying the above expression by e^−ρt and integrating over [0, τ], τ > 0, we obtain

$$v_c(p)<{\int }_0^{\tau }\left(c_1+c_2\right)P_a(t;p,q)e^{-\rho t}dt+e^{-\rho \tau }{v}_c\left(P_a(\tau ;p,q)\right)=v_s(p,q;\tau ).$$ (26)

Figure 8:

Action/Inaction boundary p_b, denoted with a solid black line; the solution to the first-order optimality condition, i.e., $\overline{p}$, denoted by a dashed red line; optimal action region ${\mathcal{A}}^{*}$ marked by gray shading; optimal inaction (continuation) region ${\mathcal{C}}^{*}$ in white; set ${\mathcal{A}}^{*}\backslash \mathcal{A}$ marked by dark gray shading; and two hypothetical trajectories (P_a(t; p, q), Q_a(t; q)) staring from point a (p, q) in the interior of $\overline{{\mathcal{C}}^{*}}$

Consequently, it follows that under conditions of this case, $v_s^{*}(p,q)=v_c(p)$. Now consider the case where the trajectory (P_a(t; p, q), Q_a(t; q)) can reach the action region boundary (trajectory (b) in Fig. 8), and define ϵ > 0 as the first hitting time. Similar to the above, for any 0 < τ < ϵ, the inequality in Eq. (26) is valid. For τ = ϵ we have

$$\begin{gathered} v_c(p)<{\int }_0^{ϵ}\left(c_1+c_2\right)P_a(t;p,q)e^{-\rho t}dt+e^{-\rho ϵ}{v}_c\left(P_a(ϵ;p,q)\right) \\ ={\int }_0^{ϵ}\left(c_1+c_2\right)P_a(t;p,q)e^{-\rho t}dt+e^{-\rho ϵ}{v}_s^{*}\left(P_a(ϵ;p,q),Q_a(ϵ;q)\right), \end{gathered}$$

where the last equality follows since (P_a(ϵ; p, q), Q_a(ϵ; q)) is on the action region boundary. Therefore, we can conclude that $v_s^{*}(p,q)=v_c(p)$. Note that it follows from the above argument that for any p > p_b(q), $q\in \left[\underset{\_}{q},\text{min}\left(\overline{q},q_m\right)\right]$, we have $v_s^{*}(p,q)=v_c(p)$. This rules out the possibility of $v_s^{*}(p,q)$ hitting v_c(p) multiple times.

Step 1. For any (p, q) in the interior of ${\mathcal{A}}^{*}\backslash \mathcal{A}$ there exists ϵ > 0 such that $\left(P_a(t;p,q),Q_a(t;q)\right)\in {\mathcal{A}}^{*}$ for any t ∈ [0, ϵ] and $\left(P_a(ϵ;p,q),Q_a(ϵ;q)\right)\in {\mathcal{A}}^{°}$. This is so since if for any t ∈ [0, τ*(p, q)], (P_a(t; p, q), Q_a(t; q)) never enters ${\mathcal{A}}^{°}$, the inequality in Eq. (26) is valid for any τ ∈ [0, τ*(p, q)] and by the argument presented in step 0, it follows that v_s(p, q; t) > v_c(p) for any t > 0. This contradicts with our assumption that (p, q) in the interior of ${\mathcal{A}}^{*}\backslash \mathcal{A}$. Therefore by continuity of (P_a(t; p, q), Q_a(t; q)) with respect to (p, q), it follows that any $\left(p_b(q),q\right)\in {\mathcal{A}}^{*}\backslash \mathcal{A}$ is weakly entering. Specifically, if (P_a(t; p_b(q), q), Q_a(t; q)) cannot enter ${\mathcal{A}}^{*}$, for any point in the interior of ${\mathcal{A}}^{*}\backslash \mathcal{A}$ that is sufficiently close to (p_b(q), b), it wouldn’t be possible to reach the interior of $\mathcal{A}$.¹³ This, as shown in the above, is in contradiction with $v_s^{*}(p,q)=v_c(p)$.

Finally, the fact that $\left(p_b(q),q\right)\in {\mathcal{A}}^{*}\backslash \mathcal{A}$ is strongly follows step 0. In particular, if there is some ϵ > 0 such that (P_a(t; p_b(q), q),Q_a(t; q)) = (p_b(Q_a(t; q)), Q_a(t; q)) for t ϵ [0, ϵ], i.e., the state trajectory remains on the boundary, then for any τ > 0 and 0 < ϵ′ < min(τ, ϵ) we have

$$\begin{gathered} v_c\left(p_b(q)\right)<{\int }_0^{{ϵ}^{\prime }}\left(c_1+c_2\right)P_a\left(t;p_b(q),q\right)e^{-\rho t}dt+e^{-\rho {ϵ}^{\prime }}{v}_c\left(P_a\left({ϵ}^{\prime };p_b(q),q\right)\right) \\ ={\int }_0^{{ϵ}^{\prime }}\left(c_1+c_2\right)P_a\left(t;p_b(q),q\right)e^{-\rho t}dt+e^{-\rho {ϵ}^{\prime }}{v}_s^{*}\left(P_a\left({ϵ}^{\prime };p_b(q),q\right),Q_a\left({ϵ}^{\prime };q\right)\right) \\ \le {\int }_0^{{ϵ}^{\prime }}\left(c_1+c_2\right)P_a\left(t;p_b(q),q\right)e^{-\rho t}dt+e^{-\rho {ϵ}^{\prime }}{v}_s\left(P_a\left({ϵ}^{\prime };p_b(q),q\right),Q_a\left({ϵ}^{\prime };q\right);\tau -{ϵ}^{\prime }\right)=v_s\left(p_b(q),q;\tau \right), \end{gathered}$$

where the first inequality follows since ${\mathcal{A}}^{*}\backslash \mathcal{A}\subset \mathcal{C}$, the first equality follows by the definition of p_b and since by assumption (P_a(t; p_b(q), q),Q_a(t; q)) = (P_b(Q_a(t; q)),Q_a(t; q)) for t ∈ [0, ϵ], the last inequality follows by the definition of $v_s^{*}$, and the last equality follows from the definition of v_s. This is in contradiction with the fact that $v_s^{*}(p,q)=v_c(p)$ for (p, q) in the interior of ${\mathcal{A}}^{*}\backslash \mathcal{A}$, which indicates that elements of arg min_{τ ≥ 0} v_s(p, q; τ) are strictly positive and bounded away from zero (i.e., arg min_{τ ≥ 0} v_s(p_b(q), q; τ) cannot only consists of τ = 0; see Berge maximum theorem).

Note that the above argument will allow us to conclude that $(\overline{p}(q),q),q\in \left[\underset{\_}{q},q_m\right]$ that are in the interior are ${\mathcal{A}}^{*}$ are weakly entering in the same sense defined in Def. 1 when p_b is replaced with $\overline{p}$.

Step 2. Any $(\overline{p}(q),q),q\in \left[\underset{\_}{q},q_m\right]$ that is weakly entering, i.e., there exists ϵ > 0 such that $\left(P_a(t;\overline{p}(q),q),Q_a(t;q)\right)\in \mathcal{A}$ for any t ∈ [0, ϵ] and $\left(P_a(\in ;\overline{p}(q),q),Q_a(\in ;q)\right)$ is in the interior of $\mathcal{A}$, resides in the interior of ${\mathcal{A}}^{*}$. This follows since $c_1-\delta Q_a(t;q)v_c^{\prime }\left(P_a(t;\overline{p}(q),q)\right)\le 0$ for t ∈ [0, ϵ], where the inequality is strict in a neighborhood of ϵ. Therefore, it follows that

$$v_c(\overline{p}(q))>{\int }_0^{ϵ}\left(c_1+c_2\right)P_a(t;\overline{p}(q),q)e^{-\rho t}dt+e^{-\rho ϵ}{v}_c\left(P_a(ϵ;\overline{p}(q),q)\right)\ge \underset{\tau \ge 0}{\text{min}}{v}_s(\overline{p}(q),q;\tau )$$

and consequently, $v_c(\overline{p}(q))>v_s^{*}(\overline{p}(q),q)$.

Step 3. Using steps 1 and 2 and the fact that $\mathcal{A}\subset {\mathcal{A}}^{*}$, it follows that for any $q\in \left[\underset{\_}{q},\text{min}\left(\overline{q},q_m\right)\right]$ such that $\left(p_b(q),q\right)\in \mathcal{A}\cap \overline{{\mathcal{C}}^{*}}$, $p_b(q)=\overline{p}(q)$, and (p_b(q), q) is weakly exiting.

Step 4. We now show that for any $q\in {\mathcal{Q}}_x$, (p_b(q), q) is strongly exiting. Since the algebraic steps of this part are quite involved and only mechanical, we include only the major steps. Suppose the claim is not true, i.e., there exists ϵ > 0 such that (P_a(t; p_b(q), q), Q_a(t; q)) = (p_b(Q_a(t; q)), Q_a(t; q)) for any t ∈ [0, ϵ]. Since on [Q_a(ϵ; q), q], p_b and $\overline{p}$ overlap, and Eq. (13) holds, we have

$$\begin{gathered} c_1-\delta q{v}_c^{\prime }(p)=0, \\ \delta (1-q)v_c^{\prime }(p)-v_c^{\prime \prime }(p)(\beta (1-p)-r-\delta q)p=0, \\ {c}_2+v_c^{\prime \prime }(p)(\beta (1-p)-r)p+v_c^{\prime }(p)(\beta (1-2p)-r-\rho )=0, \end{gathered}$$

where the second ODE is obtained by taking the derivative of Eq. (13) with respect to time on (P_a(t; p_b(q), q), Q_a(t; q)), t ∈ [0, ϵ], and the third ODE is obtained by taking the derivative of ODE (11) with respect to p when v_c(p) is substituted for v(p, q). Solving for q and $v_c^{\prime \prime }(p)$ we obtain

$$-(\beta (1-p)-r)(\beta (1-2p)-r-\rho +\delta ){\left(v_c^{\prime }(p)\right)}^2+\left(2c_1(\beta (1-p)-r)-c_2(\beta (1-p)-r)-c_1(\beta p+\rho )\right)v_c^{\prime }(p)+c_1{c}_2=0.$$ (27)

Since the above equation holds for any p ∈ [p_b(Q_a(ϵ; q)), p_b(q)], taking its derivative with respect to p and substituting for $v_c^{\prime \prime }(p)$ provides us with a different quadratic equation for $v_c^{\prime }(p)$. Using the second quadratic equation, we can eliminate ${\left(v_c^{\prime }(p)\right)}^2$ and obtain an expression for $v_c^{\prime }(p)$. Substituting this expression back into Eq. (27), we obtain a fraction whose numerator is a polynomial of degree six in p. Since the coefficient of p⁶, i.e., $4c_2\left(18c_1^3+13c_2{c}_1^2+4c_2^2{c}_1+c_2^3\right){\beta }^6$ is strictly positive, it follows that Eq. (27) cannot hold for any p ∈ [p_b(Q_a(ϵ; q)), p_b(q)]. This contradiction allows us to conclude that for any $q\in {\mathcal{Q}}_x$, (p_b(q), q) is strongly exiting. Note that this argument also allows us to conclude that for any $q\in {\mathcal{Q}}_n$, $(\overline{p}(q),q)$ is strongly entering.

Step 5. It is already shown in the main text that p_b is nondecreasing. Therefore, it only remains to show that the graph of p_b does not have a horizontal or vertical segment. Note that any vertical segment (i.e., jump discontinuity in p_b) will be strongly exiting, and hence it overlaps with $\overline{p}$. Since $\overline{p}$ is continuous, i.e., does not have any vertical segment, this part of the claim follows immediately.

Now consider an interval $I\subset \left[\underset{\_}{q},\text{min}\left(\overline{q},q_m\right)\right]$ such that for any q ∈ I, p_b(q) is constant. Note that since $\overline{p}$ is strictly increasing, it follows that $p_b(q)>\overline{p}(q)$ for q ∈ I and (p_b(q), q), q ∈ I are strongly entering. Since for q_i ∈ I, i ∈ {1, 2} with q₂ > q₁, we have Q_a(t; q₂) > Q_a (t; q₁), P_a(t; p_b(q₂), q₂) < P_a(t; p_b(q₁), q₁), and p_b(q₁) = p_b(q₂), and since τ*(p_b(q₂), q₂) > τ*(p_b(q₁), q₁) because $\overline{p}(q)$ is strictly increasing (see the red and blue curves in Fig. 11 in Appendix B), it follows that v_s(p_b(q₁), q₁; τ*(p_b(q₁), q₁)) > v_s(p_b(q₂), q₂; τ*(p_b(q₁), q₁)). This contradicts our assumption that $v_c\left(p_b\left(q_1\right)\right)=v_s^{*}\left(p_b\left(q_1\right),q_1\right)=v_s^{*}\left(p_b\left(q_2\right),q_2\right)=v_c\left(p_b\left(q_2\right)\right)$. This completes the proof. ■

Proof of Proposition 6.

Part (i) and (ii). We only focus on the case where p > 0. For (0, q), q ∈ [0, q_m], any admisible policy W, including 1_{{t ≤ τ*(0, q)}} is optimal as P(t; 0, q, W) = 0, t ≥ 0. By the argument in step 0 of the proof of Prop. 5 it follows that for any $(p,q)\in {\mathcal{C}}^{*}$, $v_s^{*}(p,q)=v_s(p,q;0)=v_c(p)$ and τ = 0 is the unique minimizer of min_τ≥0 v_s(p, q; τ). Consequently, we only need to prove the statement for $(p,q)\in {\mathcal{A}}^{*}$. Note that step 0 of the proof of Prop. 5 also shows that for $(p,q)\in {\mathcal{A}}^{*}$, when (P_a(t; p, q), Q_a(t; q)) exits ${\mathcal{A}}^{*}$, it is never optimal to return to ${\mathcal{A}}^{*}$ again. This allows us to limit our attention to only τ ∈ [0, τ*(p, q)] since (P_a(τ*(p, q); p, q), Q_a(τ*(p, q); q)) = (p_b(Q_a(τ*(p, q); q)), Q_a(τ* (p, q); q)) is strongly exiting. By Prop. 5, since (P_a(t; p, q), Q_a(t, q)), t ∈ [0, τ*(p, q)) can cross $(\overline{p}(\widehat{q}),\widehat{q}),\widehat{q}\in [\underset{\_}{q},q]$ at most once, the derivative of v_s(p, q; τ) with respect to τ, τ ∈ [0, τ*(p, q)), is either initially nonnegative and then negative, when $(p,q)\in {\mathcal{A}}^{*}\backslash \mathcal{A}$, or it is entirely negative. Therefore, the optimal switching time that leads to $v_s^{*}(p,q)$ belongs to {0, τ*(p, q)} (see Fig. 2). Since for $(p,q)\in {\mathcal{A}}^{*}$ that is not on (p_b(q), q), $q\in \left[\underset{\_}{q},\text{min}\left(\overline{q},q_m\right)\right]$, it is $v_s^{*}(p,q)<v_c(p)=v_s(p,q;0)$ we can conclude that $v_s^{*}(p,q)=v_s\left(p,q;{\tau }^{*}(p,q)\right)$. For $\left(p_b\left(q\right),q\right),q\in {\mathcal{Q}}_x$, we have τ*(p, q) = 0, hence $v_s^{*}(p,q)=v_s(p,q;0)=v_c(p)$. For $\left(p_b\left(q\right),q\right),q\in {\mathcal{Q}}_n$, we have τ*(p_b(q), q) ≠ 0; however since both v_s(p, q; τ) and τ*(p, q) are continuous, approaching (p_b(q), q) from the interior of ${\mathcal{A}}^{*}$ allows us to conclude $v_s^{*}\left(p_b(q),q\right)=v_c\left(p_b(q)\right)=v_s\left(p_b(q),q;0\right)=v_s\left(p_b(q),q;{\tau }^{*}\left(p_b(q),q\right)\right)$. Therefore, the minimum is obtained at τ = τ*(p, q) and the minimizer is unique if (p, q) ≠ (p_b(q), q) when $q\in {\mathcal{Q}}_n$.

Part (iii). The claim can be verified by direct calculation. Alternatively, for any $(p,q)\in {\mathcal{A}}^{*}$, multiplying PDE (18) by exp(−ρs) and integrating on (P_a(s; p, q), Q_a(s; q)) over [0, t], one obtains

$${\int }_0^t\left[\left(c_1+c_2\right)P_a(s;p,q)+{\partial }_{1}v\left(P_a(s;p,q),Q_a(s;q)\right)\left[\beta \left(1-P_a(s;p,q)\right)-r-\delta Q_a(s;q)\right]+{\partial }_{2}v\left(P_a(s;p,q),Q_a(s;q)\right)\delta Q_a(s;q)\left(Q_a(s;q)-1\right)-\rho v\left(P_a(s;p,q),Q_a(s;q)\right)\right]e^{-\rho s}ds={\int }_0^t\left[\left(c_1+c_2\right)P_a(s;p,q)e^{-\rho t}+\frac{d}{ds}\left[v\left(P_a(s;p,q),Q_a(s;q)\right)e^{-\rho s}\right]\right]ds=0.$$

Hence, any v that solves PDE (18) can be written as

$$v(p,q)={\int }_0^t\left(c_1+c_2\right)P_a(s;p,q)e^{-\rho s}ds+e^{-\rho t}v\left(P_a(t;p,q),Q_a(t;q)\right).$$

Therefore, setting t = τ*(p, q) and v(P_a(τ*(p, q); p, q), Q_a(τ*(p, q); q)) = v_c(P_a(τ*(p, q); p, q)), it follows that $v_s^{*}(p,q)$ solves PDE (18) for any $(p,q)\in {\mathcal{A}}^{*}$.

Part (iv). Note that since v_c, P_a, Q_a, $\overline{p}$, and hence τ* are C^∞, it follows that $v_s^{*}$ is C^∞ in the interior of the action and inaction (continuation) regions. By the envelope theorem and Leibniz’s rule, for any (p, q) in the interior of ${\mathcal{A}}^{*}$, we have

$${\partial }_1{v}_s^{*}(p,q)={\int }_0^{{\tau }^{*}(p,q)}\left(c_1+c_2\right){\partial }_2{P}_a(s;p,q)e^{-\rho s}ds+e^{-\rho {\tau }^{*}(p,q)}{v}_c^{\prime }\left(P_a\left({\tau }^{*}(p,q);p,q\right)\right){\partial }_2{P}_a\left({\tau }^{*}(p,q);p,q\right).$$ (28)

$${\partial }_2{v}_s^{*}(p,q)={\int }_0^{{\tau }^{*}(p,q)}\left(c_1+c_2\right){\partial }_3{P}_a(s;p,q)e^{-\rho s}ds+e^{-\rho {\tau }^{*}(p,q)}{v}_c^{\prime }\left(P_a\left({\tau }^{*}(p,q);p,q\right)\right){\partial }_3{P}_a\left({\tau }^{*}(p,q);p,q\right),$$ (29)

where using Eq. (22) and (23) we can obtain

$$\frac{d}{dp}{P}_a(t;p,q)=\frac{e^{-{\int }_0^t\left(\delta Q_a(s;q)-\beta +r\right)ds}}{{\left(\beta p{\int }_0^t{e}^{-{\int }_0^s\left(\delta Q_a(\sigma ;q)-\beta +r\right)d\sigma }ds+1\right)}^2},$$ (30)

$$\frac{d}{dq}{P}_a(t;p,q)=-\left[p{e}^{-{\int }_0^t\left(\delta Q_a(s;q)-\beta +r\right)ds}\left(-\beta p{\int }_0^t\left({\int }_0^s\delta {\partial }_2{Q}_a(\sigma ;q)d\sigma \right)e^{-{\int }_0^s\left(\delta Q_a(\sigma ;q)-\beta +r\right)d\sigma }ds+{\int }_0^t\delta {\partial }_2{Q}_a(s;q)ds\left(\beta p{\int }_0^t{e}^{-{\int }_0^s\left(\delta Q_a(\sigma ;q)-\beta +r\right)d\sigma }ds+1\right)\right)\right]/{\left(\beta p{\int }_0^t{e}^{-{\int }_0^s\left(\delta Q_a(\sigma ;q)-\beta +r\right)d\sigma }ds+1\right)}^2<0.$$ (31)

Since for any ${\left({\widehat{p}}_n,{\widehat{q}}_n\right)}_{n=1}^{\infty }\in {\mathcal{A}}^{*}$ that approaches the boundary $\left(p_b(q),q\right),q\in {\mathcal{Q}}_x,{\tau }^{*}(p,q)$ converges to zero, i.e., ${\text{lim}}_{n\to \infty }{\tau }^{*}\left({\widehat{p}}_n,{\widehat{q}}_n\right)=0$, we have

$$\begin{gathered} \underset{n\to \infty }{\text{lim}}{\partial }_2{P}_a\left({\tau }^{*}\left({\widehat{p}}_n,{\widehat{q}}_n\right);{\widehat{p}}_n,{\widehat{q}}_n\right)=1, \\ \underset{n\to \infty }{\text{lim}}{\partial }_3{P}_a\left({\tau }^{*}\left({\widehat{p}}_n,{\widehat{q}}_n\right);{\widehat{p}}_n,{\widehat{q}}_n\right)=0. \end{gathered}$$

Consequently, it follows that ${\text{lim}}_{n\to \infty }{\partial }_1{v}_s^{*}\left({\widehat{p}}_n,{\widehat{q}}_n\right)=v_c^{\prime }\left(p_b(q)\right)$ and ${\text{lim}}_{n\to \infty }{\partial }_2{v}_s^{*}\left({\widehat{p}}_n,{\widehat{q}}_n\right)=0$. Since for any $(p,q)\in {\mathcal{C}}^{*}$, $v_s^{*}(p,q)=v_c(p)$ we can conclude that $v_s^{*}(p,q)$ has continuous first-order derivatives on $\left(p_b(q),q\right),q\in {\mathcal{Q}}_x$

Unlike the previous case, τ*(p, q) is strictly positive when ${\left({\widehat{p}}_n,{\widehat{q}}_n\right)}_{n=1}^{\infty }\in {\mathcal{A}}^{*}$ converges to $\left(p_b(q),q\right),q\in {\mathcal{Q}}_n$. Consequently, it follows from Eq. (29) that ${\text{lim}}_{n\to \infty }{\partial }_2{v}_s^{*}\left({\widehat{p}}_n,{\widehat{q}}_n\right)<0$ while ${\partial }_2{v}_s^{*}(p,q)=0$ for any $(p,q)\in {\mathcal{C}}^{*}$. Therefore, $v_s^{*}(p,q)$ is not differentiable with respect to q at $\left(p_b(q),q\right),q\in {\mathcal{Q}}_n$. Note that since $v_s^{*}(p,q)<v_c(p)$ in the interior of ${\mathcal{A}}^{*}$, it follows that ${\text{lim}}_{n\to \infty }{\partial }_1{v}_s^{*}\left({\widehat{p}}_n,{\widehat{q}}_n\right)\ge v_c^{\prime }\left(p_b(q)\right)$. We prove that this inequality is strict by contradiction. Specifically, suppose ${\partial }_1{v}_s^{*}\left({\widehat{p}}_n,{\widehat{q}}_n\right)$ converges to $v_c^{\prime }\left(p_b(q)\right)$. Since $\left(p_b(q),q\right),q\in {\mathcal{Q}}_n$ is in the interior of

$$\mathcal{C}=\left\{(p,q)\in \left[0,p_{\infty }\right]\times \left[0,q_m\right]:q<\underset{\_}{q},\text{ or }\underset{\_}{q}\le q\text{ and }\overline{p}(q)<p\right\},$$

by the strict concavity property of v_c, it follows

$$c_1{p}_b(q)-v_c^{\prime }\left(p_b(q)\right)\delta q{p}_b(q)>0.$$

Consequently, because $v_s^{*}\left(p_b(q),q\right)=v_c\left(p_b(q)\right)$, v_c solves ODE (11), and $v_s^{*}$ solves PDE (18),

$$c_1{p}_b(q)-v_c^{\prime }\left(p_b(q)\right)\delta q{p}_b(q)+{\partial }_2{v}_s^{*}\left(p_b(q),q\right)\delta q(q-1)=0.$$

The above equation is a contradiction since ${\partial }_2{v}_s^{*}\left(p_b(q),q\right)\le 0$ and hence ${\partial }_2{v}_s^{*}\left(p_b(q),q\right)\delta q(q-1)\ge 0$.

Therefore, $v_s^{*}(p,q)$ is not differentiable with respect to p at $\left(p_b(q),q\right),q\in {\mathcal{Q}}_n$.

Part (v). The first, second and last property follows since $v_s\left(p,q;{\tau }^{*}(p,q)\right)=v_s^{*}(p,q)$. The fact that $v_s^{*}(p,q)$ is strictly decreasing in q when $(p,q)\in {\mathcal{A}}^{*}$ follows from the argument used in part (iv) of Prop. 5. ■

Proof of Theorem 2.

We only need to show that for any $(p,q)\in {\mathcal{C}}^{*}$.

$$c_{1}p-{\partial }_1{v}_s^{*}(p,q)\delta qp+{\partial }_2{v}_s^{*}(p,q)\delta q(q-1)\ge 0,$$ (32)

and for any $(p,q)\in {\mathcal{A}}^{*}$,

$$c_{1}p-{\partial }_1{v}_s^{*}(p,q)\delta qp+{\partial }_2{v}_s^{*}(p,q)\delta q(q-1)\le 0.$$ (33)

For any $(p,q)\in {\mathcal{C}}^{*}$, $v_s^{*}(p,q)=v_c(p)$, therefore, Eq. (32) simplifies to

$$c_1-v_c^{\prime }(p)\delta q\ge 0.$$

The inequality holds by definition of $\overline{p}(q)$, concavity of v_c, and since by Prop. 5, ${\mathcal{C}}^{*}\subset \mathcal{C}$. It only remains to show that for $(p,q)\in {\mathcal{A}}^{*}$, inequality in Eq. (33) holds, or alternatively it is

$$c_{2}p+{\partial }_1{v}_s^{*}(p,q)[\beta (1-p)-r]p-\rho v_s^{*}(p,q)\ge 0.$$ (34)

We prove this by contradiction. The argument requires multiple steps.

Step 1. Defining $f(p,q)\triangleq c_{2}p+{\partial }_1{v}_s^{*}(p,q)[\beta (1-p)-r]p-\rho v_s^{*}(p,q)$, we first show that close to top, bottom, and left segments of the boundary of ${\mathcal{A}}^{*}$, i.e., (p_∞, q) with $q>\text{min}\left(\overline{q},q_m\right),\left(p_b(q),q\right)$, (p_b(q), q) with $q\in \left[\underset{\_}{q},\text{min}\left(\overline{q},q_m\right)\right]$ and (0, q) with $q\ge \underset{\_}{q},f(p,q)$, positive.

Part (a). Note that at p = p_∞, the coefficient of the second term in the definition of f is zero. Moreover, by the definition of $v_s^{*}$, for any $q>\text{min}\left(\overline{q},q_m\right)$, $v_s^{*}\left(p_{\infty },q\right)=v_s\left(p_{\infty },q;{\tau }^{*}\left(p_{\infty },q\right)\right)<v_s\left(p_{\infty },q;0\right)=v_c\left(p_{\infty }\right)=c_2{p}_{\infty }/\rho$. Therefore, the claim is true for $\left(p_{\infty },q\right),q>\text{min}\left(\overline{q},q_m\right)$ and by continuity when $(p,q)\in (p_{\infty }-{ϵ}_1,p_{\infty }]\times \left[\text{min}\left(\overline{q},q_m\right)+{ϵ}_2,q_m\right]$, for some ϵ₁ > 0 and any ϵ₂ > 0.

Part (b). As was shown in Prop. 6, for any (p_b(q), q) with $q\in {\mathcal{Q}}_n$, we have ${\partial }_1{v}_s^{*}\left(p_b(q),q\right)>v_c^{\prime }\left(p_b(q)\right)$ and $v_s^{*}\left(p_b(q),q\right)=v_c\left(p_b(q)\right)$. Hence, since $c_2{p}_b(q)+v_c^{\prime }\left(p_b(q)\right)\left(\beta \left(1-p_b(q)\right)-r\right)p_b(q)-\rho v_c\left(p_b(q)\right)=0$, it follows that f(p_b(q), q) > 0.

Consider (p_b(q), q) with $q\in {\mathcal{Q}}_x$. Since ${\partial }_1{v}_s^{*}\left(p_b(q),q\right)=v_c^{\prime }\left(p_b(q)\right)$ and $v_s^{*}\left(p_b(q),q\right)=v_c\left(p_b(q)\right)$ it follows that f(p_b(q), q) = 0. Taking the derivative of f(p, q) with respect to p,

$${\partial }_{1}f(p,q)=c_2+{\partial }_{11}{v}_s^{*}(p,q)[\beta (1-p)-r]p+{\partial }_1{v}_s^{*}(p,q)[\beta (1-2p)-r-\rho ],$$ (35)

we show that ∂₁f(p_b(q), q) < 0. This allows us to conclude that for any ϵ₁ > 0 there is ϵ₂ > 0 such that f(p, q) ≥ 0 for any $(p,q)\in \left(p_b(q)-{ϵ}_2,p_b(q)\right]\times \left[\underset{\_}{q}+{ϵ}_1,\text{min}\left(\overline{q},q_m\right)\right]$, where the inequality is strict for any (p, q) in the interior of ${\mathcal{A}}^{*}$ or $\left(p_b(q),q\right),q\in {\mathcal{Q}}_n$.

Using Liebniz’s rule and Eq. (28), for $(p,q)\in {\mathcal{A}}^{*}$, the second derivative of $v_s^{*}(p,q)$ with respect to p can be written as

$${\partial }_{11}{v}_s^{*}(p,q)=\left(c_1+c_2\right){\partial }_2{P}_a\left({\tau }^{*}(p,q);p,q\right)e^{-\rho {\tau }^{*}(p,q)}{\partial }_1{\tau }^{*}(p,q)+{\int }_0^{{\tau }^{*}(p,q)}\left(c_1+c_2\right){\partial }_{22}{P}_a(s;p,q)e^{-\rho s}ds-\rho e^{-\rho {\tau }^{*}(p,q)}{v}_c^{\prime }\left(P_a\left({\tau }^{*}(p,q);p,q\right)\right){\partial }_2{P}_a\left({\tau }^{*}(p,q);p,q\right){\partial }_1{\tau }^{*}(p,q)+e^{-\rho {\tau }^{*}(p,q)}{v}_c^{\prime \prime }\left(P_a\left({\tau }^{*}(p,q);p,q\right)\right){\partial }_2{P}_a\left({\tau }^{*}(p,q);p,q\right)\left({\dot{P}}_a\left({\tau }^{*}(p,q);p,q\right){\partial }_1{\tau }^{*}(p,q)+{\partial }_2{P}_a\left({\tau }^{*}(p,q);p,q\right)\right)+e^{-\rho {\tau }^{*}(p,q)}{v}_c^{\prime }\left(P_a\left({\tau }^{*}(p,q);p,q\right)\right)\left({\partial }_2{\dot{P}}_a\left({\tau }^{*}(p,q);p,q\right){\partial }_1{\tau }^{*}(p,q)+{\partial }_{22}{P}_a\left({\tau }^{*}(p,q);p,q\right)\right).$$ (36)

Note that using the definition of τ*(p, q), Eqs. (30)–(31), and the fact that $q\in {\mathcal{Q}}_n$, for any sequence ${\left({\widehat{p}}_n,{\widehat{q}}_n\right)}_{n=1}^{\infty }\in {\mathcal{A}}^{*}$ that converges to $\left(p_b(q),q\right),q\in {\mathcal{Q}}_x$, we have

$$\begin{gathered} \underset{n\to \infty }{\text{lim}}{P}_a\left({\tau }^{*}\left({\widehat{p}}_n,{\widehat{q}}_n\right);{\widehat{p}}_n,{\widehat{q}}_n\right)=p_b(q),\underset{n\to \infty }{\text{lim}}{\partial }_2{P}_a\left({\tau }^{*}\left({\widehat{p}}_n,{\widehat{q}}_n\right);{\widehat{p}}_n,{\widehat{q}}_n\right)=1, \\ \underset{n\to \infty }{\text{lim}}{\tau }^{*}\left({\widehat{p}}_n,{\widehat{q}}_n\right)=\underset{n\to \infty }{\text{lim}}{\partial }_{22}{P}_a\left({\tau }^{*}\left({\widehat{p}}_n,{\widehat{q}}_n\right);{\widehat{p}}_n,{\widehat{q}}_n\right)=0, \\ \underset{n\to \infty }{\text{lim}}{\dot{P}}_a\left({\tau }^{*}\left({\widehat{p}}_n,{\widehat{q}}_n\right);{\widehat{p}}_n,{\widehat{q}}_n\right)=\left(\beta \left(1-p_b(q)\right)-r-\delta q\right)p_b(q), \\ \underset{n\to \infty }{\text{lim}}{\partial }_2{\dot{P}}_a\left({\tau }^{*}\left({\widehat{p}}_n,{\widehat{q}}_n\right);{\widehat{p}}_n,{\widehat{q}}_n\right)=\beta \left(1-2p_b(q)\right)-r-\delta q. \end{gathered}$$ (37)

Hence, in the limit we have

$$\underset{n\to \infty }{\text{lim}}{\partial }_{11}{v}_s^{*}\left({\widehat{p}}_n,{\widehat{q}}_n\right)=\left[c_1+c_2-\rho v_c^{\prime }\left(p_b(q)\right)+v_c^{\prime \prime }\left(p_b(q)\right)\left(\beta \left(1-p_b(q)\right)-r-\delta q\right)p_b(q)+v_c^{\prime }\left(p_b(q)\right)\left(\beta \left(1-2p_b(q)\right)-r-\delta q\right)\right]{\partial }_1{\tau }^{*}\left(p_b(q),q\right)+v_c^{\prime \prime }\left(p_b(q)\right)=\left[c_2-\rho v_c^{\prime }\left(p_b(q)\right)+v_c^{\prime \prime }\left(p_b(q)\right)\left(\beta \left(1-p_b(q)\right)-r-\delta q\right)p_b(q)+v_c^{\prime }\left(p_b(q)\right)\left(\beta \left(1-2p_b(q)\right)-r\right)\right]{\partial }_1{\tau }^{*}\left(p_b(q),q\right)+v_c^{\prime \prime }\left(p_b(q)\right)=-v_c^{\prime \prime }\left(p_b(q)\right)\delta q{p}_b(q){\partial }_1{\tau }^{*}\left(p_b(q),q\right)+v_c^{\prime \prime }\left(p_b(q)\right),$$ (38)

where the second equality is obtained since for $q\in {\mathcal{Q}}_x$ it is $c_1-\delta q{v}_c^{\prime }\left(p_b(q)\right)=0$, and the third equality is obtained since by Prop. 3, v_c solves

$$c_{2}p+v_c^{\prime }(p)(\beta (1-p)-r)p-\rho v_c(p)=0;$$ (39)

therefore,

$$c_2+v_c^{\prime \prime }(p)(\beta (1-p)-r)p+v_c^{\prime }(p)(\beta (1-2p)-r))-\rho v_c^{\prime }(p)=0.$$ (40)

Since by Prop. 6, for any $(p,q)\in {\mathcal{A}}^{*}$, τ* (p, q) satisfies

$$c_1-\delta Q_a\left({\tau }^{*}(p,q);q\right)v_c^{\prime }\left(P_a\left({\tau }^{*}(p,q);p,q\right)\right)=0,$$ (41)

it follows that

$${\partial }_1{\tau }^{*}(p,q)=-\frac{v_c^{\prime \prime }\left(P_a\left({\tau }^{*}(p,q);p,q\right)\right)Q_a\left({\tau }^{*}(p,q);q\right){\partial }_2{P}_a\left({\tau }^{*}(p,q);p,q\right)}{v_c^{\prime }\left(P_a\left({\tau }^{*}(p,q);p,q\right)\right){\dot{Q}}_a\left({\tau }^{*}(p,q);q\right)+v_c^{\prime \prime }\left(P_a\left({\tau }^{*}(p,q);p,q\right)\right)Q_a\left({\tau }^{*}(p,q);q\right){\dot{P}}_a\left({\tau }^{*}(p,q);p,q\right)}.$$

Taking the limit when ${\left({\widehat{p}}_n,{\widehat{q}}_n\right)}_{n=1}^{\infty }\in {\mathcal{A}}^{*}$ converges to $\left(p_b(q),q\right),q\in {\mathcal{Q}}_x$, the above expression simplifies to

$${\partial }_1{\tau }^{*}\left(p_b(q),q\right)=\frac{-1/(\delta q(q-1))}{\frac{v_c^{\prime }\left(p_b(q)\right)}{q{v}_c^{\prime \prime }\left(p_b(q)\right)}+\frac{\left(\beta \left(1-p_b(q)\right)-r-\delta q\right)p_b(q)}{\delta q(q-1)}}<0,$$

where the inequality is obtained since

$$\frac{\left(\beta \left(1-p_b(q)\right)-r-\delta q\right)p_b(q)}{\delta q(q-1)}<-\frac{v_c^{\prime }\left(p_b(q)\right)}{q{v}_c^{\prime \prime }\left(p_b(q)\right)}=p_b^{\prime }(q),$$ (42)

because $\left(p_b(q),q\right),q\in {\mathcal{Q}}_x$ is strongly exiting. Consequently, it follows that ${\partial }_{11}{v}_s^{*}\left(p_b(q),q\right)<v_c^{\prime \prime }\left(p_b(q)\right)<0$ for $q\in {\mathcal{Q}}_x\backslash \left\{\underset{\_}{q}\right\}$. The claim will then follow from Eq. (40).

Part (c). Now consider lim_p↓0 f(p; q)/p. Since f(0; q) = 0; q ∈ [0; q_m], this limit is ∂1f(0, q) = lim_p↓0 ∂₁f(p, q). Using the definition of f(p; q), for any $q\ge \underset{\_}{q}$ we can write

$$\begin{gathered} \underset{p\downarrow 0}{\text{lim}}f(p,q)/p=\underset{p\downarrow 0}{\text{lim}}\left(c_2+{\partial }_1{v}_s^{*}(p,q)[\beta (1-p)-r-\rho ]-\rho \left(v_s^{*}(p,q)/p-{\partial }_1{v}_s^{*}(p,q)\right)\right) \\ =c_2+{\partial }_1{v}_s^{*}(0,q)(\beta -r-\rho ), \end{gathered}$$ (43)

where the last equality is obtained since ${\partial }_1{v}_s^{*}(0,q)$ is finite and $v_s^{*}(0,q)=0$, hence the last parentheses converges to zero. If we show that ${\partial }_{12}{v}_s^{*}(0,q)<0$, for $q\ge \underset{\_}{q}$, it follows that there exist ϵ₁ > 0 and ϵ₂ > 0 such that for $(p,q)\in \left[0,{ϵ}_2\right]\times \left[\underset{\_}{q}+{ϵ}_1,q_m\right]$, it is f(p, q) ≥ 0 because ${\partial }_1{v}_s^{*}(0,\underset{\_}{q})=v_c^{\prime }(\underset{\_}{q})=-c_2/(\beta -r-\rho )$. Comparing Eq. (43), with Eq. (35) when p converges to zero, provides us with ${\text{lim}}_{p\downarrow 0}{\partial }_{11}{v}_s^{*}(p,q)p=0$. Moreover, by Prop. 6, we have

$$c_1+c_2+{\partial }_{11}{v}_s^{*}(p,q)[\beta (1-p)-r-\delta q]p+{\partial }_1{v}_s^{*}(p,q)[\beta (1-2p)-r-\rho -\delta q]+{\partial }_{12}{v}_s^{*}(p,q)\delta q(q-1)=0.$$ (44)

These two together let us conclude that ${\partial }_1{v}_s^{*}(0,q)$ solves

$$c_1+c_2+{\partial }_1{v}_s^{*}(0,q)(\beta -r-\rho -\delta q)+{\partial }_{12}{v}_s^{*}(0,q)\delta q(q-1)=0,$$ (45)

For any $q\ge \underset{\_}{q}$ with boundary condition ${\partial }_1{v}_s^{*}(0,\underset{\_}{q})=v_c^{\prime }(0)=-c_2/(\beta -r-\rho )$.¹⁴ Consequently, we can write

$${\partial }_1{v}_s^{*}(0,q)=\frac{1}{(\beta -r-\rho )(\beta -r-\rho -\delta )}\left[-\left(c_1+c_2\right)(\beta -r-\rho +\delta (q-1))+c_1\delta (\underset{\_}{q}-1){\left(\frac{1-\underset{\_}{q}}{1-q}\right)}^{\frac{\beta -r-\rho -\delta }{\delta }}{\left(\frac{q}{\underset{\_}{q}}\right)}^{\frac{\beta -r-\rho }{\delta }}\right],$$ (46)

whose first and second derivatives with respect to q can also be written as

$${\partial }_{12}{v}_s^{*}(0,q)=\frac{1}{(\beta -r-\rho )(\beta -r-\rho -\delta )}\left[-\delta \left(c_1+c_2\right)-c_1{\left(\frac{1-\underset{\_}{q}}{1-q}\right)}^{\frac{\beta -r-\rho }{\delta }}{\left(\frac{q}{\underset{\_}{q}}\right)}^{\frac{\beta -r-\rho }{\delta }}\left(\frac{\beta -r-\rho -\delta q}{q}\right)\right],$$ (47)

and

$${\partial }_{122}{v}_s^{*}(0,q)=\frac{c_1{\left(\frac{1-\underset{\_}{q}}{1-q}\right)}^{\frac{\beta -r-\rho }{\delta }}{\left(\frac{q}{\underset{\_}{q}}\right)}^{\frac{\beta -r-\rho }{\delta }}}{\delta q^2(q-1)}.$$ (48)

Since ${\partial }_{12}{v}_s^{*}(0,\underset{\_}{q})=0$ and ${\partial }_{122}{v}_s^{*}(0,q)<0$ for $q>\underset{\_}{q}$, the claim follows.

Part (d). It only remains to show that there is a ball at $(0,\underset{\_}{q})$ with radius ϵ > 0, i.e., ${\mathcal{B}}_{(0,\underset{\_}{q})}(ϵ)$, such that for any (p, q) in the interior of ${\mathcal{B}}_{(0,\underset{\_}{q})}(ϵ)\cap {\mathcal{A}}^{*}$, f(p, q) is positive. First, note that the action boundary around $(0,\underset{\_}{q})$ is strictly exiting, hence $p_b(q)=\overline{p}(q)$ for $q\in [\underset{\_}{q},\underset{\_}{q}+ϵ]$ some ϵ > 0. Taking the derivative of f(p, q) with respect to q we obtain

$${\partial }_{2}f(p,q)={\partial }_{12}{v}_s^{*}(p,q)(\beta (1-p)-r)p-\rho {\partial }_2{v}_s^{*}(p,q).$$

Note that since $v_s^{*}(p,q)$ is nonincreasing in q, the last term is nonnegative. In addition, the cross partial derivative of $v_s^{*}(p,q)$ is positive when (p, q) converges to the action boundary $\left(p_b(q),q\right),q\in (\underset{\_}{q},\underset{\_}{q}+ϵ]\subset {\mathcal{Q}}_x$. This is so since using Eq. (28) we can write

$${\partial }_{12}{v}_s^{*}(p,q)=\left(c_1+c_2\right){\partial }_2{P}_a\left({\tau }^{*}(p,q);p,q\right)e^{-\rho {\tau }^{*}(p,q)}{\partial }_2{\tau }^{*}(p,q)+{\int }_0^{{\tau }^{*}(p,q)}\left(c_1+c_2\right){\partial }_{23}{P}_a(s;p,q)e^{-\rho s}ds-\rho e^{-\rho {\tau }^{*}}(p,q)v_c^{\prime }\left(P_a\left({\tau }^{*}(p,q);p,q\right)\right){\partial }_2{P}_a\left({\tau }^{*}(p,q);p,q\right){\partial }_2{\tau }^{*}(p,q)+e^{-\rho {\tau }^{*}(p,q)}{v}_c^{\prime \prime }\left(P_a\left({\tau }^{*}(p,q);p,q\right)\right){\partial }_2{P}_a\left({\tau }^{*}(p,q);p,q\right)\left({\dot{P}}_a\left({\tau }^{*}(p,q);p,q\right){\partial }_2{\tau }^{*}(p,q)+{\partial }_3{P}_a\left({\tau }^{*}(p,q);p,q\right)\right)+e^{-\rho {\tau }^{*}(p,q)}{v}_c^{\prime }\left(P_a\left({\tau }^{*}(p,q);p,q\right)\right)\left({\partial }_2{\dot{P}}_a\left({\tau }^{*}(p,q);p,q\right){\partial }_2{\tau }^{*}(p,q)+{\partial }_{23}{P}_a\left({\tau }^{*}(p,q);p,q\right)\right).$$ (49)

Similar to part (b), using the definition of τ*(p; q), Eqs. (30)–(31), and the fact that $q\in {\mathcal{Q}}_x$, for any sequence ${\left({\widehat{p}}_n,{\widehat{q}}_n\right)}_{n=1}^{\infty }\in {\mathcal{A}}^{*}$ that converges to $\left(p_b(q),q\right),q\in {\mathcal{Q}}_x$, we have

$$\begin{gathered} \underset{n\to \infty }{\text{lim}}{\tau }^{*}\left({\widehat{p}}_n,{\widehat{q}}_n\right)=\underset{n\to \infty }{\text{lim}}{\partial }_3{P}_a\left({\tau }^{*}\left({\widehat{p}}_n,{\widehat{q}}_n\right);{\widehat{p}}_n,{\widehat{q}}_n\right)=\underset{n\to \infty }{\text{lim}}{\partial }_{23}{P}_a\left({\tau }^{*}\left({\widehat{p}}_n,{\widehat{q}}_n\right);{\widehat{p}}_n,{\widehat{q}}_n\right)=0, \\ \underset{n\to \infty }{\text{lim}}{P}_a\left({\tau }^{*}\left({\widehat{p}}_n,{\widehat{q}}_n\right);{\widehat{p}}_n,{\widehat{q}}_n\right)=p_b(q),\underset{n\to \infty }{\text{lim}}{\partial }_2{P}_a\left({\tau }^{*}\left({\widehat{p}}_n,{\widehat{q}}_n\right);{\widehat{p}}_n,{\widehat{q}}_n\right)=1, \\ \underset{n\to \infty }{\text{lim}}{\dot{P}}_a\left({\tau }^{*}\left({\widehat{p}}_n,{\widehat{q}}_n\right);{\widehat{p}}_n,{\widehat{q}}_n\right)=\left(\beta \left(1-p_b(q)\right)-r-\delta q\right)p_b(q), \\ \underset{n\to \infty }{\text{lim}}{\partial }_2{\dot{P}}_a\left({\tau }^{*}\left({\widehat{p}}_n,{\widehat{q}}_n\right);{\widehat{p}}_n,{\widehat{q}}_n\right)=\beta \left(1-2p_b(q)\right)-r-\delta q. \end{gathered}$$

Hence, for $q\in (\underset{\_}{q},\underset{\_}{q}+ϵ]$, it is

$$\underset{n\to \infty }{\text{lim}}{\partial }_{12}{v}_s^{*}\left({\widehat{p}}_n,{\widehat{q}}_n\right)=\left[c_1+c_2-\rho v_c^{\prime }\left(p_b(q)\right)+v_c^{\prime \prime }\left(p_b(q)\right)\left(\beta \left(1-p_b(q)\right)-r-\delta q\right)p_b(q)+v_c^{\prime }\left(p_b(q)\right)\left(\beta \left(1-2p_b(q)\right)-r-\delta q\right)\right]{\partial }_2{\tau }^{*}\left(p_b(q),q\right)=\left[c_2-\rho v_c^{\prime }\left(p_b(q)\right)+v_c^{\prime \prime }\left(p_b(q)\right)\left(\beta \left(1-p_b(q)\right)-r-\delta q\right)p_b(q)+v_c^{\prime }\left(p_b(q)\right)\left(\beta \left(1-2p_b(q)\right)-r\right)\right]{\partial }_2{\tau }^{*}\left(p_b(q),q\right)=-v_c^{\prime \prime }\left(p_b(q)\right)\delta q{p}_b(q){\partial }_2{\tau }^{*}\left(p_b(q),q\right).$$ (50)

Similar to part (b), we can obtain

$${\partial }_2{\tau }^{*}(p,q)=-\frac{v_c^{\prime }\left(P_a\left({\tau }^{*}(p,q);p,q\right)\right){\partial }_2{Q}_a\left({\tau }^{*}(p,q);q\right)+v_c^{\prime \prime }\left(P_a\left({\tau }^{*}(p,q);p,q\right)\right)Q_a\left({\tau }^{*}(p,q);q\right){\partial }_3{P}_a\left({\tau }^{*}(p,q);p,q\right)}{v_c^{\prime }\left(P_a\left({\tau }^{*}(p,q);p,q\right)\right){\dot{Q}}_a\left({\tau }^{*}(p,q);q\right)+v_c^{\prime \prime }\left(P_a\left({\tau }^{*}(p,q);p,q\right)\right)Q_a\left({\tau }^{*}(p,q);q\right){\dot{P}}_a\left({\tau }^{*}(p,q);p,q\right)}.$$

Taking the limit provides us with

$$\underset{n\to \infty }{\text{lim}}{\partial }_2{\tau }^{*}\left({\widehat{p}}_n,{\widehat{q}}_n\right)=\frac{-\frac{v_c^{\prime }\left(p_b(q)\right)}{v_c^{\prime \prime }\left(p_b(q)\right)q}}{\frac{v_c^{\prime }\left(p_b(q)\right)}{v_c^{\prime }\left(p_b(q)\right)q}\delta q(q-1)+\left(\beta \left(1-p_b(q)\right)-r-\delta q\right)p_b(q)}>0,$$

where the inequality follows from Eq. (42). Consequently, for $q\in (\underset{\_}{q},\underset{\_}{q}+ϵ]$, ∂₂f(p_b(q), q) is strictly positive. Now consider the value of ∂₂f(p_b(q), q) at $q=\underset{\_}{q}$. Since $v_s^{*}(0,q)={\partial }_2{v}_s^{*}(0,q)={\partial }_{22}{v}_s^{*}(0,q)=0$ for any q ∈ [0, q_m], it follows that. ∂₂f(0, q) = ∂₂₂f(0,q) = 0. Using this observation, we can write

$$\begin{gathered} \underset{n\to \infty }{\text{lim}}\frac{{\partial }_{22}f\left({\widehat{p}}_n,{\widehat{q}}_n\right)}{{\widehat{p}}_n}=\underset{n\to \infty }{\text{lim}}{\partial }_{122}{v}_s^{*}\left({\widehat{p}}_n,{\widehat{q}}_n\right)\left(\beta \left(1-{\widehat{p}}_n\right)-r\right)-\rho \underset{n\to \infty }{\text{lim}}\frac{{\partial }_{22}{v}_s^{*}\left({\widehat{p}}_n,{\widehat{q}}_n\right)-{\partial }_{22}{v}_s^{*}(0,\underset{\_}{q})}{{\widehat{p}}_n} \\ ={\partial }_{122}{v}_s^{*}(0,\underset{\_}{q})(\beta -r-\rho )>0, \end{gathered}$$

where the inequality follows from Eq. (48). This will allow us to conclude that there is a ball at $(0,\underset{\_}{q})$ with radius ϵ > 0 such that f(p, q) ≥ 0 when $(p,q)\in {\mathcal{B}}_{(0,\underset{\_}{q})}(ϵ)\cap {\mathcal{A}}^{*}$.

Step 2. Let’s assume that, contradictory to our claim, there is a non-measure zero region in ${\mathcal{A}}^{*}$, within which f(p, q) is strictly negative. Let $\widehat{q}>0$ be the smallest $q\in \left[\underset{\_}{q},q_m\right]$ such that $f(p,\widehat{q})\ge 0$ for every p ∈ [0, p_b(q)] and for any ϵ > 0 small enough, $f(p,\widehat{q}+ϵ)<0$ for a non-measure zero subset of $\left[0,p_b(\widehat{q}+ϵ)\right]$ (see Fig. 9b). By continuity of f there is $\widehat{p}\in \left(0,p_b(\widehat{q})\right)$ such that $f(\widehat{p},\widehat{q})=0$.¹⁵ Such $\widehat{p}$ is a local minimum for $f(\widehat{p},\widehat{q})$, and hence ${\partial }_{1}f(\widehat{p},\widehat{q})=0$.

Part (a). Consider the case where ${\partial }_{2}f(\widehat{p},\widehat{q})=0$ as well. We have

$$\begin{gathered} c_2\widehat{p}+{\partial }_1{v}_s^{*}(\widehat{p},\widehat{q})[\beta (1-\widehat{p})-r]\widehat{p}-\rho v_s^{*}(\widehat{p},\widehat{q})=0, \\ {c}_2+{\partial }_{11}{v}_s^{*}(\widehat{p},\widehat{q})[\beta (1-\widehat{p})-r]\widehat{p}+{\partial }_1{v}_s^{*}(\widehat{p},\widehat{q})[\beta (1-2\widehat{p})-r]-\rho {\partial }_1{v}_s^{*}(\widehat{p},\widehat{q})=0, \\ {\partial }_{12}{v}_s^{*}(\widehat{p},\widehat{q})[\beta (1-\widehat{p})-r]\widehat{p}-\rho {\partial }_2{v}_s^{*}(\widehat{p},\widehat{q})=0, \\ {c}_1\widehat{p}+c_2\widehat{p}+{\partial }_1{v}_s^{*}(\widehat{p},\widehat{q})[\beta (1-\widehat{p})-\delta \widehat{q}-r]\widehat{p}+{\partial }_2{v}_s^{*}(\widehat{p},\widehat{q})\delta \widehat{q}(\widehat{q}-1)-\rho v_s^{*}(\widehat{p},\widehat{q})=0 \\ {c}_{1,}+c_2+{\partial }_{11}{v}_s^{*}(\widehat{p},\widehat{q})[\beta (1-\widehat{p})-\delta \widehat{q}-r]\widehat{p}+{\partial }_1{v}_s^{*}(\widehat{p},\widehat{q})[\beta (1-2\widehat{p})-\delta \widehat{q}-r]+{\partial }_{12}{v}_s^{*}(\widehat{p},\widehat{q})\delta \widehat{q}(\widehat{q}-1)-\rho {\partial }_1{v}_s^{*}(\widehat{p},\widehat{q})=0, \\ {\partial }_{12}{v}_s^{*}(\widehat{p},\widehat{q})[\beta (1-\widehat{p})-\delta \widehat{q}-r]\widehat{p}-{\partial }_1{v}_s^{*}(\widehat{p},\widehat{q})\delta \widehat{p}+{\partial }_{22}{v}_s^{*}(\widehat{p},\widehat{q})\delta \widehat{q}(\widehat{q}-1)+{\partial }_2{v}_s^{*}(\widehat{q},\widehat{q})\delta (2\widehat{q}-1)-\rho {\partial }_2{v}_s^{*}(\widehat{p},\widehat{q})=0, \end{gathered}$$

where the first three equations are simply $f(\widehat{p},\widehat{q})=0$, ${\partial }_{1}f(\widehat{p},\widehat{q})=0$, and ${\partial }_{2}f(\widehat{p},\widehat{q})=0$, and the last three are Eq. (18) and its derivatives with respect to p and q evaluated at $(\widehat{p},\widehat{q})$ respectively.

Solving for the six unknowns $v_s^{*}(\widehat{p},\widehat{q})$, ${\partial }_1{v}_s^{*}(\widehat{p},\widehat{q})$, ${\partial }_2{v}_s^{*}(\widehat{p},\widehat{q})$, ${\partial }_{11}{v}_s^{*}(\widehat{p},\widehat{q})$, ${\partial }_{12}{v}_s^{*}(\widehat{p},\widehat{q})$and ${\partial }_{22}{v}_s^{*}(\widehat{p},\widehat{q})$, we obtain and as

$$v_s^{*}(\widehat{p},\widehat{q})=\frac{c_2\delta \widehat{q}(\beta -r)+c_1(\beta (1-\widehat{p})-r)(\beta (1-\widehat{p})-r-\rho )}{\beta \rho \delta \widehat{q}},$$ (51)

$${\partial }_1{v}_s^{*}(\widehat{p},\widehat{q})=\frac{c_1(\beta (1-\widehat{p})-r-\rho )+c_2\delta \widehat{q}}{\beta \widehat{p}\delta \widehat{q}},$$ (52)

$${\partial }_2{v}_s^{*}(\widehat{p},\widehat{q})=\frac{c_1(\beta (1-2\widehat{p})-r-\rho )+c_2\delta \widehat{q}}{\beta \delta \widehat{q}(\widehat{q}-1)},$$ (53)

$${\partial }_{11}{v}_s^{*}(\widehat{p},\widehat{q})=-\frac{(\beta (1-\widehat{p})-r-\rho )\left(c_1(\beta (1-2\widehat{p})-r-\rho )+c_2\delta \widehat{q}\right)}{\beta {\widehat{p}}^2\delta \widehat{q}(\beta (1-\widehat{p})-r)},$$ (54)

and

$${\partial }_{22}{v}_s^{*}(\widehat{p},\widehat{q})=-\left[c_1\widehat{q}\left(-3\beta \widehat{p}(\beta (1-\widehat{p})-r-\rho )-\beta \widehat{p}(\beta -r)+{(\beta -r-\rho )}^2\right)+c_1\beta \widehat{p}(\beta (1-\widehat{p})-r)+c_2\delta {\widehat{q}}^2(\beta (1-\widehat{p})-r-\rho )\right]/\left(\beta \delta {(\widehat{q}-1)}^2{\widehat{q}}^2(\beta (1-\widehat{p})-r)\right).$$ (55)

Note that since β− r − ρ < 0, it follows that $\beta (1-\widehat{p})-r-\rho <0$. In addition, we have $\beta (1-\widehat{p})-r>0$ as $\widehat{p}<p_{\infty }$. Moreover, since ${\partial }_2{v}_s^{*}(\widehat{p},\widehat{q})<0$ and ${\partial }_1{v}_s^{*}(\widehat{p},\widehat{q})>0$, we obtain $c_1(\beta (1-2\widehat{p})-r-\rho )+c_2\delta \widehat{q}>0$ and $c_1(\beta (1-\widehat{p})-r-\rho )+c_2\delta \widehat{q}>0$. Therefore, ${\partial }_{11}{v}_s^{*}(\widehat{p},\widehat{q})>0$ which is a contradiction as $v_s^{*}(p,q)$ is concave in p.

Part (b). Consider the case where ${\partial }_{2}f(\widehat{p},\widehat{q})\ne 0$. Therefore, by the Implicit Function Theorem, the level set f(p, q) = 0 has a C¹ representation (as a function of p) that is tangent to the vertical line at $(p,\widehat{q}),p\in \left[0,p_{\infty }\right]$ (see Fig. 9b).¹⁶ Hence, it necessarily follows that ${\partial }_{2}f(\widehat{p},\widehat{q})<0$. We show that this leads to a contradiction. In particular, we have

$$\begin{gathered} c_2\widehat{p}+{\partial }_1{v}_s^{*}(\widehat{p},\widehat{q})[\beta (1-\widehat{p})-r]\widehat{p}-\rho v_s^{*}(\widehat{p},\widehat{q})=0, \\ {c}_2+{\partial }_{11}{v}_s^{*}(\widehat{p},\widehat{q})[\beta (1-\widehat{p})-r]\widehat{p}+{\partial }_1{v}_s^{*}(\widehat{p},\widehat{q})-r]-\rho {\partial }_1{v}_s^{*}(\widehat{p},\widehat{q})=0, \\ {c}_1\widehat{p}+c_2\widehat{p}+{\partial }_1{v}_s^{*}(\widehat{p},\widehat{q})[\beta (1-\widehat{p})-\delta \widehat{q}-r]\widehat{p}+{\partial }_2{v}_s^{*}(\widehat{p},\widehat{q})\delta \widehat{q}(\widehat{q}-1)-\rho v_s^{*}(\widehat{p},\widehat{q})=0, \\ {c}_1+c_2+{\partial }_{11}{v}_s^{*}(\widehat{p},\widehat{q})[\beta (1-\widehat{p})-\delta \widehat{q}-r]\widehat{p}+{\partial }_1{v}_s^{*}(\widehat{p},\widehat{q})[\beta (1-2\widehat{p})-\delta \widehat{q}-r]+{\partial }_{12}{v}_s^{*}(\widehat{p},\widehat{q})\delta \widehat{q}(\widehat{q}-1)-\rho {\partial }_1{v}_s^{*}(\widehat{p},\widehat{q})=0, \end{gathered}$$

where similar to the previous case, the first two equations are simply $f(\widehat{p},\widehat{q})=0$, and ${\partial }_{1}f(\widehat{p},\widehat{q})=0$, and the last two are Eq. (18) and its derivative with respect to p evaluated at $(\widehat{p},\widehat{q})$ respectively.

Solving for the four unknowns ${\partial }_1{v}_s^{*}(\widehat{p},\widehat{q}),{\partial }_2{v}_s^{*}(\widehat{p},\widehat{q})$, ${\partial }_{11}{v}_s^{*}(\widehat{p},\widehat{q})$, and ${\partial }_{12}{v}_s^{*}(\widehat{p},\widehat{q})$ as a function of $v_s^{*}(\widehat{p},\widehat{q})$, we obtain

$${\partial }_1{v}_s^{*}(\widehat{p},\widehat{q})=\frac{\rho v_s^{*}(\widehat{p},\widehat{q})-c_2\widehat{p}}{\widehat{p}(\beta (1-\widehat{p})-r)}>0,$$ (56)

$${\partial }_2{v}_s^{*}(\widehat{p},\widehat{q})=\frac{-c_1\widehat{p}(\beta (1-\widehat{p})-r)+\delta \widehat{q}\left(\rho v_s^{*}(\widehat{p},\widehat{q})-c_2\widehat{p}\right)}{\delta \widehat{q}(\widehat{q}-1)(\beta (1-\widehat{p})-r)}\le 0,$$ (57)

$${\partial }_{11}{v}_s^{*}(\widehat{p},\widehat{q})=\frac{\rho v_s^{*}(\widehat{p},\widehat{q})(2\beta \widehat{p}-\beta +\rho +r)-c_2\widehat{p}(\beta \widehat{p}+\rho )}{{\widehat{p}}^2{(\beta (1-\widehat{p})-r)}^2}\le 0,$$ (58)

$${\partial }_{12}{v}_s^{*}(\widehat{p},\widehat{q})=\frac{\rho v_s^{*}(\widehat{p},\widehat{q})\delta \widehat{q}(\beta \widehat{p}+\rho )-c_1\widehat{p}{(\beta (1-\widehat{p})-r)}^2-c_2\delta \widehat{q}\widehat{p}(\beta -r+\rho )}{\delta \widehat{q}(\widehat{q}-1)\widehat{p}{(\beta (1-\widehat{p})-r)}^2},$$ (59)

Noting that − β + ρ + r > 0, the first and the third inequality provide us with

$$\rho v_s^{*}(\widehat{p},\widehat{q})\le \frac{c_2\widehat{p}(\beta \widehat{p}+\rho )}{(2\beta \widehat{p}-\beta +\rho +r)},$$ (60)

$${\partial }_1{v}_s^{*}(\widehat{p},\widehat{q})\le \frac{c_2}{(2\beta \widehat{p}-\beta +\rho +r)}.$$ (61)

Moreover, using the above and the second inequality, i.e., Eq. (57), we can obtain

$$\delta \widehat{q}\ge \frac{c_1\widehat{p}(\beta (1-\widehat{p})-r)}{\rho v_s^{*}(\widehat{p},\widehat{q})-c_2\widehat{p}}\ge \frac{c_1}{c_2}(2\beta \widehat{p}-\beta +\rho +r).$$ (62)

Substituting for ${\partial }_2{v}_s^{*}(\widehat{p},\widehat{q})$ and ${\partial }_{12}{v}_s^{*}(\widehat{p},\widehat{q})$ in ${\partial }_{2}f(\widehat{p},\widehat{q})={\partial }_{12}{v}_s^{*}(\widehat{p},\widehat{q})[\beta (1-\widehat{p})-r]\widehat{p}-\rho {\partial }_2{v}_s^{*}(\widehat{p},\widehat{q})$, we obtain

$${\partial }_{2}f(\widehat{p},\widehat{q})=-\frac{c_1\widehat{p}(\beta (1-\widehat{p})-r)(\beta (1-\widehat{p})-r-\rho )-\delta \widehat{q}\widehat{p}\left[\beta \left(\rho v_s^{*}(\widehat{p},\widehat{q})-c_2\widehat{p}\right)-c_2(\beta (1-\widehat{p})-r)\right]}{\delta \widehat{q}(\widehat{q}-1)(\beta (1-\widehat{p})-r)}.$$ (63)

Since ${\partial }_{2}f(\widehat{p},\widehat{q})<0$, we can conclude that the numerator of the above expression is strictly negative. However, we have

$$c_1\widehat{p}(\beta (1-\widehat{p})-r)(\beta (1-\widehat{p})-r-\rho )-\delta \widehat{q}\widehat{p}\left[\beta \left(\rho v_s^{*}(\widehat{p},\widehat{q})-c_2\widehat{p}\right)-c_2(\beta (1-\widehat{p})-r)\right]\ge c_1\widehat{p}(\beta (1-\widehat{p})-r)(\beta (1-\widehat{p})-r-\rho )-\delta \widehat{q}\widehat{p}\left[\frac{c_2\beta \widehat{p}(\beta (1-\widehat{p})-r)}{(2\beta \widehat{p}-\beta +\rho +r)}-c_2(\beta (1-\widehat{p})-r)\right]=c_1\widehat{p}(\beta (1-\widehat{p})-r)(\beta (1-\widehat{p})-r-\rho )-\delta \widehat{q}\widehat{p}\left[c_2(\beta (1-\widehat{p})-r)\frac{(\beta (1-\widehat{p})-r-\rho )}{(2\beta \widehat{p}-\beta +\rho +r)}\right]\ge c_1\widehat{p}(\beta (1-\widehat{p})-r)(\beta (1-\widehat{p})-r-\rho )-\frac{c_1}{c_2}(2\beta \widehat{p}-\beta +\rho +r)\widehat{p}\left[c_2(\beta (1-\widehat{p})-r)\frac{(\beta (1-\widehat{p})-r-\rho )}{(2\beta \widehat{p}-\beta +\rho +r)}\right]=0,$$ (64)

where the first inequality is obtained from Eq. (60), and the second inequality is obtained via Eq. (62) since the term in the square bracket is negative. Consequently, it follows that the numerator of Eq. (63) is nonnegative which is a contradiction. This completes the proof. ■

Proof of Theorem 3.

The proof structure is identical to the proof of Thm. 2. We only need to provide a new argument for step 1, parts (c) and (d) as well as step 2 since ${\text{lim}}_{p\downarrow 0}{v}_c^{\prime }(p)$ a ${\text{lim}}_{p\downarrow 0}{\partial }_1{v}_s^{*}(p,q)$ nd are not finite and β − r − ρ ≥ 0.

Step 1.

Part (c) and (d). Note that since v(p, q; W) is bounded for any (p, q) ∈ [0, p_∞] × [0, q_m] and any admissible control W, the optimal value function of the finite horizon formulation of the social planner problem (P), i.e.,

$${\widehat{v}}^{*}(p,q;h)=\underset{W:[0,h]\to [0,1]}{\text{inf}}{\int }_0^h\left(c_{1}W(t)P(t)+c_{2}P(t)\right)e^{-\rho t}dt,$$ (65)

converges (uniformly) to the infinite horizon value function v*(p, q). The same statement is valid for the first-order derivatives of ${\widehat{v}}^{*}(p,q;h)$ when p > 0. Consequently, if for any $(q,h)\in \left[0,q_m\right]\times {ℝ}_{++}$, we show that $\widehat{f}(p,q;h)\triangleq c_{2}p+{\partial }_1{\widehat{v}}^{*}(p,q;h)(\beta (1-p)-r)p-\rho {\widehat{v}}^{*}(p,q;h)$ is nonnegative for p ∈ (0, ϵ) for some ϵ > 0, the claim would follow. This statement can be shown in exactly the same manner as in part (c) of Thm. 2. Specifically, we have

$$\underset{p\downarrow 0}{\text{lim}}\frac{\widehat{f}(p,q;h)}{p}={\partial }_1\widehat{f}(0,q;h)=c_2+{\partial }_1{\widehat{v}}^{*}(0,q;h)(\beta -r-\rho )>0,$$

where the inequality follows since ${\partial }_1{\widehat{v}}^{*}(0,q;h)>0$ as P (t; p, q, W) is increasing for any W (see Prop. 2) and (β − r − ρ) ≥ 0 by our assumption. Hence, since $\widehat{f}(0,q;h)=0$, it follows that $\widehat{f}(p,q;h)$ is nonnegative when p ∈ (0, ϵ) for some ϵ > 0. Taking the limit with respect to h provides us with the result.

Step 2.

Part (a). Using Eqs. (51)–(55) and the fact that ${\partial }_2{v}_s^{*}(\widehat{p},\widehat{q})<0$, ${\partial }_1{v}_s^{*}(\widehat{p},\widehat{q})>0$, and ${\partial }_{11}{v}_s^{*}(\widehat{p},\widehat{q})\le 0$ it follows that $c_1(\beta (1-2\widehat{p})-r-\rho )+c_2\delta \widehat{q}>0$, $c_1(\beta (1-\widehat{p})-r-\rho )+c_2\delta \widehat{q}>0$, and $(\beta (1-\widehat{p})-r-\rho )\ge 0$. The last inequality allows us to conclude $\widehat{p}\le p_{\infty }-\rho /\beta$. Note that $v_s^{*}(\widehat{p},\widehat{q})$ is quadratic and convex in $\widehat{p}$. Moreover, for $\widehat{p}\le p_{\infty }-\rho /\beta$, $v_s^{*}(\widehat{p},\widehat{q})$ is decreasing since

$$\frac{d}{d\widehat{p}}\left(\frac{c_2\delta \widehat{q}(\beta -r)+c_1(\beta (1-\widehat{p})-r)(\beta (1-\widehat{p})-r-\rho )}{\beta \rho \delta \widehat{q}}\right)=\frac{-c_1(2\beta (1-\widehat{p})-2r-\rho )}{\rho \delta \widehat{q}}<0.$$ (66)

Hence, substituting p_∞ − ρ/β for $\widehat{p}$ in Eq. (51) we obtain

$$v_s^{*}(\widehat{p},\widehat{q})\ge c_2\frac{p_{\infty }}{\rho }.$$ (67)

This is a contradiction since ${\text{max}}_{p\in \left[0,p_{\infty }\right]}{v}_c(p)=c_2{p}_{\infty }/\rho >v_s^{*}(\widehat{p},\widehat{q})$.

Part (b). An identical analysis leads to a contradiction if we assume that $\beta \widehat{p}-\beta +\rho +r>0$. Consider the case where $\beta \widehat{p}-\beta +\rho +r\le 0$. From Eq. (63), it follows that the term in square bracket has to be positive (the numerator has to be strictly negative, but the first term is nonnegative). This allows us to obtain

$$\beta \rho v_s^{*}(\widehat{p},\widehat{q})-c_2(\beta -r)=\beta \rho \left[v_s^{*}(\widehat{p},\widehat{q})-c_2\frac{p_{\infty }}{\rho }\right]>0.$$ (68)

Similar to part (a), this is a contradiction. ■

Appendix B. Supplemental Results

Note on Numerical Analysis

In principle, in the absence of the results we present section 3, the social planner’s problem (P) can be solved numerically using the HJB equation (7). Specifically, since any trajectory (P (t; p, q, W), Q(t; q, W)) converges to either the left or the top of the state space boundary, i.e., (p, 0) with p ∈ [0, p_∞], or (p_∞, q) with q ∈[0, q_m], provided that v*(p, 0) = v_c(p) and v*(p_∞, q) can be approximated, these boundary approximations can be extended to the whole state space region by solving

$${\tilde{v}}^{*}(p,q)\approx \underset{w\in [0,1]}{\text{min}}{\int }_0^{\text{Δ}t}\left(c_{1}w+c_2\right)P(s;p,q,w)e^{-\rho s}ds+e^{-\rho \text{Δ}t}{\tilde{v}}^{*}(P(\text{Δ}t;p,q,w),Q(\text{Δ}t;q,w)),$$ (69)

where ${\tilde{v}}^{*}$ is an approximation of v*, and Δt is small enough to justify the approximation of W (s), s ∈ [0, Δt], by a constant w ∈ [0, 1]. However, since the value function is not always Lipschitz continuous, a naive implementation of the HJB equation can lead to numerical instability and erroneous results. In order to avoid such problems, an extremely fine grid is required when p approaches zero. This can increase the run time of the numerical implementation to the point that it becomes impractical. For example, for the cases we present in section 3, the run time of the above scheme on a server with 32 cores and 128GB RAM is more than one month. Knowing that the optimal policy is of bang-bang type (i.e., there is no singular arc) with, at most, one switching time (i.e., the action region can be described by a single boundary), the run time of the above algorithm can be reduced significantly. For us, this reduced the run time for the cases we present in section 3 to about 10 minutes. Computational efficiency is possible because it is not necessary to solve the optimization problem in Eq. (69) at (p, q) if at (p, q − Δq) with Δq > 0 the solution of the problem is w* = 1. This is an immediate consequence of the fact that the action region can be described by a single boundary and the boundary is such that if (p, q − Δq) is in the action region, then (p, q) is also in the action region.

The autonomous value function

Figure 10 illustrates the claims of Prop. 3. As we proved in Prop. 3, v_c is strictly increasing and strictly concave.

Evolution of system state on the optimal path

Figure 11 shows the evolution of the system’s state on the optimal path when ρ ≤ β − r for three different starting points: (p, q) = (0.4, 0.65) plotted in blue with diamond marks, (p, q) = (0.4, 0.8) plotted in red with circle marks, and (p, q) = (0.55, 0.65) plotted in green with triangle marks. All these starting points reside in the action region and hence the optimal control is initially equal to one, meaning that the drug is prescribed for all infected individuals. This causes the drug quality to decrease as the resistant strain prevails and becomes the dominant type. The strength of the drug affects whether the size of the infected population decreases or its growth is only slowed through its influence on the sign and the magnitude of β(1 − P (t)) − r − δQ(t). For the case we are studying in Fig. 11 the former holds; therefore, the optimal path in the state space moves in a south west direction (see Fig. 11a). This dynamic holds until the state trajectory crosses the action region boundary and moves into the continuation region. At that time, it is no longer economical to prescribe the drug. These hitting times are marked in panels (b)–(d) and are the unique solutions of optimization problem (12). In the absence of any consumption, drug quality does not decline, but the size of the infected population grows. This dynamic continues forever since the state trajectory will never again enter the action region.

We would like to use Fig. 11 to point out some properties of the state trajectory that played a major role in our proofs. First, comparing the blue (with diamond marks) and green (with triangle marks) trajectories, it is evident that on the optimal trajectory disease prevalence will remain higher when the initial disease prevalence is higher (i.e., for p₂ > p₁ and q₁ = q₂ = q, P(t; p₂, q, W*) > P (t; p₁, q, W*)). Similarly, comparing the blue (with diamond marks) and red (with circle marks) trajectories, disease prevalence will be lower for t > 0 on the optimal trajectory when the initial drug quality is higher (i.e., for q₂ > q₁ and p₁ = p₂ = p, it is P(t; p, q₁, W*) > P(t; p, q₂, W*)). Prop. 2 shows that both of these observations are also true for any (fixed) W. Furthermore, since p_b is an increasing function of q, lower initial disease prevalence and greater initial drug quality result in a longer economic life of the drug, (i.e., for p₂ > p₁ and q₁ = q₂ = q, it is τ*(p₂, q) < τ*(p₁, q), and for q₂ > q₁ and p₁ = p₂ = p, it is τ*(p, q₂) > τ*(p, q₁)). This can be observed in Fig. 11d.

Appendix C. Parameter Calculations for Gonorrhea Case Study

Steady-state prevalence

An analysis by Satterwhite et al. (2013) provides the most recent estimate of gonorrhea prevalence in the United States using data from 1999–2008 waves of the National Health and Nutrition Examination Survey (NHANES). They estimated the prevalence of gonorrhea among 15–39 year-old men and women to be 0.21% and 0.32%, respectively. These estimates include both symptomatic and asymptomatic infections. Assuming that the proportion of adult men and women in the US population are roughly equal, the overall prevalence among 15–39 year-olds is 0.27%, of which 40% of infections occurred in men and 60% of infections occurred in women. We assumed that these estimates reflect the steady-state prevalence of gonorrhea in the US under current treatment policies. We will use the steady-state prevalence to calculate some disease dynamics parameters, as outlined below.

Natural recovery rate

We calculated the natural recovery rate of gonorrhea infection by taking the inverse of the average duration of infection in the absence of treatment.¹⁷ Historical data suggest that the time to recovery for an untreated gonococcal infection differs by symptom status: sources estimate that a symptomatic infections lasts an average of 2 months (0.17 years) while an asymptomatic infection last an average of 1 year (Garnett and Bowden 2000; Wiesner and Thompson 1980). Furthermore, the likelihood that a gonococcal infection produces symptoms is greater in men than in women, though asymptomatic infections are common for both sexes. We used estimates provided by Owusu-Edusei et al. (2013) that 50% of men and 25% of women infected with gonorrhea experience symptoms. This results in an average duration of untreated infection of 0.50×0.17 (years)+0.50×1.0 (years) = 0.58 (years) in men and 0.25×0.17 (years)+0.75×1.0 (years) = 0.79 (years) in women. The overall average duration of infection in the absence of treatment, assuming 60% of infections occur in women, is thus 0.71 years. This corresponds to an annual recovery rate of r = 1.41.

Recovery with treatment

The current policy for managing gonorrhea is to treat all patients with antibiotics. However, not all individuals who become infected will seek treatment, due to challenges in accessing care or because they are asymptomatic. We calculated the proportion of men and women who seek care using estimates compiled by Owusu-Edusei et al. (2013). They estimated that 89% of symptomatic individuals seek treatment. Asymptomatic infections may also end up being detected and treated due to contact tracing of the recent sexual partners of infected individuals and through routine STI screening at preventive health exams; Owusu-Edusei et al. (2013) estimated that 9% of asymptomatic men and 40% of asymptomatic women would be treated. Women are much more likely to be routinely screened for STIs than men which is why more asymptomatic women are treated. Owusu-Edusei et al. (2013) also provided estimates of the average duration of treated infections: 0.08 years (approximately 1 month) for symptomatic infections and 0.38 and 0.58 years for asymptomatic men and women, respectively.

Combining these values, we calculate the average duration of infection under the current treatment policy for men (assuming 50% of infections are symptomatic (Owusu-Edusei et al. 2013))

$$0.5\times [0.89\times 0.09(\text{ years })+0.11\times 0.17(\text{ years })]+0.5\times [0.09\times 0.38(\text{ years })+0.91\times 1.0(\text{ years })]=0.52(\text{ years })$$

as and for women (assuming 25% of infections are symptomatic Owusu-Edusei et al. 2013) as

$$0.25\times \left[0.89\times 0.09(\text{ years })+0.11\times 0.17(\text{ years })]+0.75\times [0.40\times 0.58(\text{ years })+0.60\times 1.0(\text{ years)}\right]=0.65(\text{ years }).$$

Weighting by the proportion of infections that occur among men and women, we calculate the average overall duration of infection under the current treatment policy to be 0.60 years. This corresponds to a recovery rate of 1.68 per year. In our numerical analysis, we implement the impact of treatment as an incremental increase in the rate of recovery, δq, compared to no treatment. Based on our estimates, for the current drug quality q > 99%, it is δ = (1.68 − 1.41)/0.99 = 0.27.

Infection rate

We estimated the infection rate by calculating the necessary value for β that, in combination with the estimated recovery rate of 1.68 under the current treatment policy, would yield a “steady-state” disease prevalence of 0.27%. For a susceptible-infected-susceptible (SIS) model, the prevalence of disease in steady-state is equal to 1 − (r + δq)/β. Re-arranging, we calculate β = 1.68/(1 − 0.0027) = 1.69.

Costs

We estimated the average cost of an untreated gonorrhea infection by calculating the probability of sequelae arising from an untreated infection and multiplying that by the expected cost of medical care to address that sequelae. Owusu-Edusei et al. (2013) estimated the probability of the most common gonorrhea-associated complications to be a 2% risk of epididymitis for untreated men and a 15% risk of pelvic inflammatory disease (PID) for untreated women. They also estimated the cost of these complications to be $313 for a case of epididymitis and $3,202 for a case of PID in 2010 USD (inflated to $344.51 and $3,524.34 in 2016 USD, respectively). The expected cost of an untreated infection is therefore 0.02 × $344.51 = $6.89 for men and 0.15 × $3524.34 = $528.65 for women. The overall average cost of an untreated infection, again assuming 60% of infections occur in women, is $322 in 2016 USD. This is the cost per infection; however, the model formulation involves a cost per unit time infected, c₂. To adjust our estimate, we divide the per-infection cost by the expected duration of an untreated infection (0.71 years) for an annualized cost of $454.¹⁸ A discount rate of 3% per year was selected in accordance with recommendations from the Second Panel on Cost-Effectiveness in Health and Medicine (Sanders et al. 2016).

In the case of treatment, we included the cost of treating a gonorrhea infection (including a physician visit, diagnostic tests, and drug costs) as well as the (lower) expected costs of complications. Owusu-Edusei et al. (2010) used insurance claims data to estimate the medical costs associated with a gonorrhea diagnosis and treatment. They found an average total cost of $210 in 2007 USD (inflated to $243.13 in 2016 USD) for visits with a primary diagnosis of gonorrhea when an antibiotic was prescribed. Owusu-Edusei et al. (2013) estimated the risk of sequelae to be zero for men and symptomatic women who receive treatment; they estimated that 8% of treated asymptomatic women would still develop PID owing to a delay in diagnosis and treatment. Using the estimated probability of treatment by symptom status and the probability of sequelae with and without treatment, we estimate that under a treat-all policy, 49% of men and 52% of women would be treated, resulting in an expected 1% risk of epididymitis in men and 10% risk of PID in women. The total expected cost per infection is then 0.49×$243.13+0.01×$344.51 = $122.65 for men and 0.52×$243.13+0.10×$3524.34 = $464.05 for women, for an overall per-infection cost of $329. We calculate the annualized cost of an infection under a treat-all policy by dividing by the average duration of an infection under treatment (0.60 years), resulting in a cost of $553 per year. In the model, the cost of treatment is included as an incremental cost, so we calculate c₁ = $553 − c₂ = $99.

Probabilistic sensitivity analysis

Whenever possible, we used distributions consistent with the analysis carried out in our sources and best practices guidelines for incorporating uncertainty into medical decision making models (Briggs et al. 2012; Sanders et al. 2016). These distributions are summarized in Table C1. The samples for each category were generated independently and correlation were imposed by rejecting infeasible realizations. For example, since the average recovery period with treatment must be no larger than the average recovery period without treatment, any realization for which this was not true was dropped. Similarly, the probability of sequelae with and without treatment were obtained from the average disease duration via a linear map as higher sickness period should imply higher probability of sequelae.

Table C1:

Gonorrhea’s base parameters, 95% confidence intervals, and assumed distributions. [1]: Satterwhite et al. (2013), [2]: Farley et al. (2003), [3]: Owusu-Edusei et al. (2013), [4]: Owusu-Edusei et al. (2010), [5]: Wiesner and Thompson (1980), [6]: Garnett and Bowden (2000)

	Base Case	Range	Distribution
Prevalence
Male[1]	0.21%	0.09% – 0.48%	Lognormal(−6.19, 0.18)
Female[1]	0.32%	0.17% – 0.60%	Lognormal(−5.75, 0.10)
Symptomatic infection
Male[1],[2],[3]	50%	35% – 65%	Normal(50%, 0.56%)
Female[1],[2],[3]	25%	10% – 40%	Normal(25%, 0.56%)
Seeking treatment
Symptomatic infection[2],[3]	89%	80% – 100%	Uniform(80%, 100%)
Asymptomatic infection
Male[3]	9%	4% – 14%	Uniform(4%, 14%)
Female[3]	40%	25% – 55%	Uniform(25%, 55%)
Average recovery time (yrs) without treatment
Symptomatic infection[5],[6]	0.17	0.07 – 0.44	Lognormal(−1.74, 0.21)
Asymptomatic infection[5],[6]	1	0.5 – 2	Lognormal(0, 0.12)
Average recovery time (yrs) with treatment
Symptomatic infection[1]	0.08	0.04 – 0.19	Lognormal(−2.50, 0.17)
Asymptomatic infection
Male[1]	0.38	0.20 – 0.71	Lognormal(−0.97, 0.10)
Female[1]	0.58	0.32 – 1.1	Lognormal(−0.54, 0.09)
Probability of sequelae without treatment
Male[3]	2%	0% – 4%	Obtained via a linear map using the corresponding average recovery time
Female[2],[3]	15%	5% – 25%
Probability of sequelae with treatment
Male[3]	0%	0% – 2%	Obtained via a linear map using the corresponding average recovery time
Female
Symptomatic Infection[2],[3]	0%	0% – 2%
ASymptomatic Infection[2],[3]	8%	2% – 14%
Average unit costs (2016USD)
Sequelae in males[2],[3]	$345	$200 – $620	Lognormal(5.84, 0.08)
Sequelae in female[2],[3]3’	$3524	$2400 – $4750	Lognormal(8.17, 0.03)
Treatment cost[4]	$243	$243 – $243	Deterministic

Appendix D. Summary of Notation

Table D1:

Summary of notation.

Symbol	Description	Range
t	Time	${ℝ}_{+}$
P(t)	Percentage of the population infected with the disease at time t without its dependence on the prescription policy W and initial condition (p, q) made explicit	[0, 1]
P1(t)	Percentage of the population infected with the drug-susceptible strain of the disease at time t without its dependence on the prescription policy W and initial condition (p, q) made explicit	[0, 1]
Q(t)	Drug quality at time t without its dependence on the prescription policy W and initial condition (p, q) made explicit	[0, 1]
W(t)	Drug prescription policy at time t	[0, 1]
β	Disease transmission rate	${ℝ}_{++}$
r	Natural recovery rate	${ℝ}_{+}$
δ	Drug strength	${ℝ}_{++}$
ρ	Social planner’s discount rate	${ℝ}_{++}$
p∞	Long-run prevalence of the disease in the population	[0, 1]
p	Percentage of the population infected with the disease	[0, p∞]
qm	Maximum drug quality	[0, 1)
q	Drug quality	[0, qm]
c1	Cost of treatment	${ℝ}_{++}$
c2	Cost of infection	${ℝ}_{++}$
v*(p, q)	Social planner’s optimal value function	${ℝ}_{+}$
P(t; p, q, W)	Percentage of the population infected with the disease at time t for policy W and initial condition (p, q)	[0, 1]
Q(t; q, W)	Drug quality at time t for policy W and initial condition (p, q)	[0, 1]
v(p, q; W)	Social planner’s value function for policy W and initial condition (p, q)	${ℝ}_{+}$
Pa(t; p, q)	Percentage of the population infected with the disease at time t for initial condition (p, q) when the drug is prescribed for all infected individuals	[0, 1]
Qa(t; q)	Drug quality at time t and initial condition (p, q) when the drug is prescribed for all infected individuals	[0, 1]
Pc(t; p, q)	Percentage of infected population at time t for initial condition (p, q) when the drug is not prescribed to anyone	[0, 1]
vc(p)	Social planner’s autonomous value function	${ℝ}_{+}$
vs(p, q; r)	Social planner’s value function for a bang-bang policy with switching time τ ≥ 0	${ℝ}_{+}$
$\underset{\_}{q}$	Minimum drug quality for which it is economical to prescribe the drug for at least some p ≥ 0	[0, qm]
$\overline{q}$	Minimum drug quality for which it is economical to prescribe the drug for any p ≤ p∞	[0, qm]
$\overline{p}(q)$	Solution of the first-order optimality condition (13)	[0, p∞]
pb(q)	The boundary of the optimal action region	[0, p∞]
${\mathcal{Q}}_n$	q-coordinate of points on the optimal action/inaction boundary that are entering	$\left[\underset{\_}{q},\text{min}\left(\overline{q},q_m\right)\right]$
${\mathcal{Q}}_x$	q-coordinate of points on the optimal action/inaction boundary that are exiting	$\left[\underset{\_}{q},\text{min}\left(\overline{q},q_m\right)\right]$
$\mathcal{A}$	Action region implied by the first-order optimality condition (13)	[0, p∞] × [0, qm]
${\mathcal{A}}^{*}$	Optimal action region	[0, p∞] × [0, qm]
${\mathcal{C}}^{*}$	Optimal inaction (continuation) region	[0, p∞] × [0, qm]