Abstract
Treating macaques with an anti-α4β7 antibody under the umbrella of combination antiretroviral therapy (cART) during early SIV infection can lead to viral remission, with viral loads maintained at < 50 SIV RNA copies/ml after removal of all treatment in a subset of animals. Depletion of CD8+ lymphocytes in controllers resulted in transient recrudescence of viremia, suggesting that the combination of cART and anti-α4β7 antibody treatment led to a state where ongoing immune responses kept the virus undetectable in the absence of treatment. A previous mathematical model of HIV infection and cART incorporates immune effector cell responses and exhibits the property of two different viral load set-points. While the lower set-point could correspond to the attainment of long-term viral remission, attaining the higher set-point may be the result of viral rebound. Here we expand that model to include possible mechanisms of action of an anti-α4β7 antibody operating in these treated animals. We show that the model can fit the longitudinal viral load data from both IgG control and anti-α4β7 antibody treated macaques, suggesting explanations for the viral control associated with cART and an anti-α4β7 antibody treatment. This effective perturbation to the virus-host interaction can also explain observations in other nonhuman primate experiments in which cART and immunotherapy have led to post-treatment control or resetting of the viral load set-point. Interestingly, because the viral kinetics in the various treated animals differed—some animals exhibited large fluctuations in viral load after cART cessation—the model suggests that anti-α4β7 treatment could act by different primary mechanisms in different animals and still lead to post-treatment viral control. This outcome is nonetheless in accordance with a model with two stable viral load set-points, in which therapy can perturb the system from one set-point to a lower one through different biological mechanisms.
Author summary
Some macaques treated with an anti-α4β7 monoclonal antibody along with antiretroviral therapy during the early stages of simian immunodeficiency virus infection had their viral load become undetectable (below 50 SIV RNA copies/ml) after all treatment was stopped, whereas animals not given the antibody all had their viral loads rebound to high levels. Using a mathematical model, we examined four potential ways in which the antibody could have altered the balance between viral growth and immune control to maintain an undetectable viral load. We show that a shift to controlled infection can occur through multiple biologically reasonable mechanisms of action of the anti-α4β7 antibody.
Introduction
Combination antiretroviral therapy (cART) can effectively suppress the viremia in people living with HIV. However, successful viral suppression requires life-long treatment, and no cure for HIV infection is currently available. The integrin α4β7 antibody has become a target for the development of a novel HIV therapy [1–4], as its expression at the cell surface increases the susceptibility of CD4+ T cells to HIV infection [5,6]. Intravenous infusion of an anti-α4β7 antibody can decrease the viral load both in plasma and in the gastrointestinal tract during primary simian immunodeficiency virus (SIV) infection [3,4], while prophylactic administration can substantially reduce the risk of SIV infection [3]. Treating SIV nef-stop infected macaques with a 90-day course of cART initiated at five weeks post-infection (p.i.) supplemented by the intravenous administration of a primatized monoclonal anti-α4β7 antibody started at nine weeks p.i. has been shown to result in plasma viral loads ultimately being maintained below 50 RNA copies/ml for more than nine months following the cessation of all treatment [2]. This sustained effect has raised the prospect of using anti-α4β7 antibodies as an adjunct to HIV preventive therapy and treatment.
Here, we provide a potential explanation for how the addition of a monoclonal anti-α4β7 antibody to cART could lead to long-term viral control after treatment cessation. A follow-up study on a subset of the eight controller macaques from Byrareddy et al. [2] showed that SIV was still present in those animals as their virus transiently rebounded when CD8+ lymphocytes were depleted (S2 Text). This transient rebound in viremia suggests that long-term control was immune-mediated. Conway and Perelson [7] developed a viral kinetic model containing an effector cell response to explain the observation of post-treatment control in the VISCONTI study, where 14 HIV-infected individuals who started cART during primary infection were able to control virus levels to low or undetectable levels for years following cessation of treatment [8]. Here, we expand this model by including potential mechanisms by which anti-α4β7 antibodies may act. The mechanisms that we consider are described below and in Fig 1.
Fig 1. A visualization of the four different mechanisms of action of the anti-α4β7 antibody and corresponding model diagram.
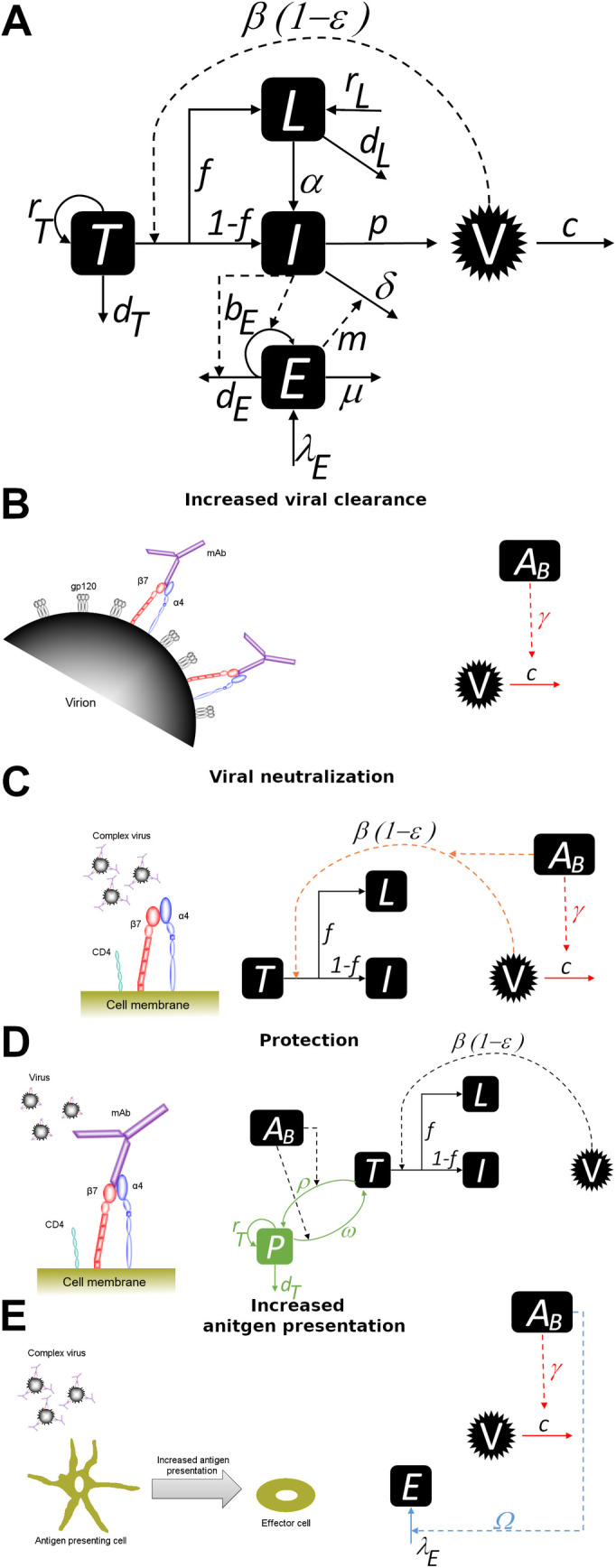
A) Model schematic in the absence of the anti-α4β7 antibody. Target cells (T) proliferate logistically at rate rT, die at rate dT and become infected at rate (1- ε)V, where β is the transmission rate, ε is the efficacy of cART, and V is the viral concentration. Once target cells are infected, a fraction f become latent cells (L) and the remaining become productively infected cells (I). Latent cells proliferate at rate rL, die at rate dL, and activate at rate α. Infected cells produce virus at rate p, die due to viral cytopathic effects at rate δ, and are killed at rate mE by effector cells (E). Effector cells are produced at rate λE, proliferate at a maximum rate bE, become exhausted at a maximum rate dE, and die at rate μ. Virus is cleared in the absence of the anti-α4β7 antibody at rate c. B) Increased viral clearance. The anti-α4β7 monoclonal antibody (purple) (AB) binds to α4β7 integrin (red and blue) expressed on the viral membrane and opsonizes the virus, increasing the clearance rate γ-fold or less depending on the AB concentration. C) Viral neutralization. The anti-α4β7 monoclonal antibody (purple) binds to the α4β7 integrin (red and blue) expressed on the viral membrane, causing increased viral clearance and viral neutralization, i.e. inhibition of infection, while also contributing to increased viral clearance. D) Protection from infection. The anti-α4β7 monoclonal antibody binds to α4β7 integrin expressed on the surface of uninfected CD4+ T cells and protects them from infection. Target cells enter a protected state (P) at a maximum rate ρ, with protection waning at a maximum rate ⍵. E) Increased antigen presentation. Antibody-virus complexes are picked up by antigen presenting cells resulting in increased antigen presentation. We assume that this increased antigen presentation increases the effector cell source rate dependent on the AB concentration and the parameter Ω. The formation of antibody-virus complexes may also contribute to increased viral clearance.
The α4β7 integrin is incorporated into the membrane of viruses produced by SIV-infected α4β7+ T cells and is functionally active [9]. It has been hypothesized that the anti-α4β7antibody can bind the α4β7 integrin and lead to increased viral opsonization and increased viral clearance [9] (Fig 1B) and possibly virus neutralization (Fig 1C).
Blocking of SIV infection might occur when the anti-α4β7 antibody binds to α4β7+ CD4+ T cells [4,10] (Fig 1D). We define this mechanism as protection, to differentiate it from neutralization in which the anti-α4β7 antibody binds to the virus to prevent infection. The anti-α4β7 antibody is known to restrict the trafficking of lymphocytes to the gut [2,4], as it inhibits the interaction of the α4β7 integrin expressed on the lymphocyte with MAdCAM-1 expressed on gut endothelial cells [11]. The gut is a region of high viral replication and cellular activation during HIV infection. Thus, limiting the number of α4β7+ CD4+ T cells that traffic to that region will offer some level of protection from infection—a reduction that is implicitly captured by the protection mechanism.
Giving an anti-α4β7 antibody could improve immune responses due to increased antigen presentation, as there would be a greater uptake of opsonized virus by antigen presenting cells [9] (Fig 1E).
Because obtaining virological control using anti-α4β7 monoclonal antibody adjunctive therapy carries a level of importance to the field of HIV treatment and cure, the original experiment was repeated by two different groups using the same viral stock. Neither experiment led to long-term viral control [12,13]. Byrareddy et al. [2] used a SIV nef-stop virus to better replicate chronic HIV infection [14]. After an animal is infected, mutation can remove the stop codon and subsequent selection can change the dominant viral species, leading to stochastic effects. We highlight the effects of a nef-stop in our results, as well as elaborate on several other possible explanations for the discrepancy between the original and repeat experiments [12,13,15], in the Discussion.
Distinguishing among the four mechanisms—each of which could plausibly lead to viral suppression—is challenging because it is an outcome of complex viral-immune system interactions. The interaction between the virus, infected cells and the immune system is critical in determining whether the virus rebounds to a high viral set-point or remains below the limit of detection (< 50 SIV RNA copies/ml) after the removal of all treatment. If the viral suppression induced by the anti-α4β7 antibody were too strong, the resulting levels of viral replication might not be sufficient to stimulate an effective antiviral response, enabling the virus to escape the immune system after the anti-α4β7 antibody dissipates. Conversely, if the effects of the antibody were too weak, then the virus-host interaction might not be perturbed enough to suppress viral replication after the removal of all therapy. A systematic understanding of how cART and anti-α4β7 antibody affects the viral immune system interactions to achieve viral suppression in the absence of treatment is critical to the design and implementation of new therapeutic strategies and to understand the mechanisms operating in different repeat studies.
Methods
Ethics statement
The experimental protocols were reviewed and approved by the Emory University Institutional Animal Care and Use Committee. The animals were bred and maintained at Yerkes National Primate Research Center (Emory University, Atlanta, Georgia) in their nonhuman primate facilities. The diets of the macaques consisted of a monkey diet (Purina, Gray Summit, Missouri), along with daily fresh fruit and/or vegetables and water ad libitum. To ensure to social enhancement and their well-being, macaques were housed in a temperature controlled indoor facility with a 12-hour light/dark cycle and caged with socially compatible same sex pairs. The Yerkes enrichment staff oversaw and provided appropriate safe toys for further social enrichment. Animal health was closely monitored, with veterinary staff directing treatment for any signs of distress or disease. If symptoms could not be alleviated by the directed treatment, the macaque was humanely euthanized according to the directed guidelines of the American Veterinary Medical Association.
Mathematical model
To reproduce both the post-treatment high viral load set-point observed in the control IgG treated macaques and the maintained low viral load seen in the anti-α4β7 antibody treated macaques (S1 Fig), we adapted a previously developed mathematical model by Conway and Perelson that allows for multiple viral load set-points [7]. We incorporated the various anti-α4β7 antibody mechanisms of action into this model (Eqs (1)–(8)), which includes uninfected CD4+ T cells, productively infected cells, latently infected cells, cytotoxic effector cells, and virus.
First, we describe the base model that applies to the IgG control macaques, who did not receive the anti-α4β7 antibody, AB. We then describe the additional model terms involving the proposed anti-α4β7 antibody mechanisms of action. Lastly, we introduce a pharmacokinetic model to describe the time-dependent changes in the anti-α4β7 antibody concentration, which for ease of notation we denote AB rather than AB(t).
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
We define target cells, T, to be uninfected activated/proliferating CD4+ T cells [16–18]. Target cells proliferate logistically at maximum rate rT [16,17,19], have a carrying capacity k and die at per capita rate dT.
Target cells become infected through cell-free virus infection at rate βVT, where β is the infection rate constant and V is the virus concentration, i.e., plasma SIV RNA/ml. A fraction 1-f of infected target cells become productively infected cells, I, while the remaining proportion f become latently infected cells, L. In the Byrareddy et al. [2] study, all macaques received an integrase inhibitor and two reverse transcriptase inhibitors between five and 19-weeks p.i. These antiretroviral drugs interfere with the infection process. More complex models have been used to describe the action of integrase inhibitors [20] but this level of detail is not needed here due to the infrequent viral sampling. Thus, we assume cART reduces the SIV infection rate by the factor ε, where ε ∈ [0,1] is the efficacy of cART.
Productively infected cells, I, produce virions at rate p per cell, which are naturally cleared at rate c per virion. Productively infected cells die due to viral cytopathic effects at per capita rate δ and are killed at rate mE by cytotoxic effector cells, E. Thus, the overall death rate of a productively infected cell is δ + mE. We consider only cytotoxic effector cells that contribute to infected cell death, which can consist of both natural killer (NK) and SIV-specific cytotoxic T cells.
The generation of a cell that is productively infected can also occur by activation of a latently infected cell, which occurs at rate α. There is no evidence indicating that latently infected cells have a carrying capacity to allow for homeostatic control, as seen in the total CD4 memory population. Thus, we assume latently infected cells proliferate at per capita rate rL and die at per capita rate dL. The half-life of the latent cell population is then ln (2)/(α+dL-rL).
As described previously by Conway and Perelson [7], cytotoxic effector cells are produced at rate λE and die at per capita rate μ. The presence of infected cells leads to their proliferation at rate bEEI/(I+KB), with bE denoting the maximum proliferation rate and KB being a half-saturation constant for proliferation. During viral infection, effector cells can become exhausted [21–23] causing the cells to lose effector function [24]. Exhaustion of cytotoxic effector cells occurs at rate dEEI/(I+KD), where dE represents the maximum rate of exhaustion, and KD is the half-saturation constant for cytotoxic effector cell exhaustion.
Conway and Perelson used a constant source of effector cells [7]. As effector CD8+ T cell differentiate from naïve CD8+ T cells, we also examined two alternative models for the source of effector cells (S1 and S2 Texts).
Mechanism 1: Anti-α4β7 antibody increases viral clearance
The anti-α4β7 antibody can increase the clearance of the virus through opsonization of the α4β7-coated viruses [9]. We assume that the kinetics of anti-α4β7 antibody binding to α4β7+ virus is much faster than the changes in viral load so that equilibrium binding relations apply. We further assume antibody binding enhances the viral clearance rate a maximum of γ-fold compared to the viral clearance rate of antibody-free virus and that the clearance rate depends on the amount of antibody bound. Thus, the overall viral clearance rate in the presence of anti-α4β7 is c(1 + (γ−1)ψCAB / (1 + ψCAB)) (S1 Text), where 1/ψC is the half-maximal effective antibody concentration (Fig 1B). As the antibody is infused multiple times, the antibody concentration changes during the experiment and thus an antibody concentration dependent clearance rate needs to be used in the model.
Mechanism 2: Anti -α4β7antibody reduces the infection rate by neutralizing the virus
With the anti-α4β7antibody having the potential to bind to α4β7+ virus, neutralization could be an additional mechanism of antibody action. We test this by setting the indicator variable 𝕀N = 1 if we assume viral neutralization is present and 𝕀N = 0 if we assume neutralization is absent in Eqs (1)–(3). The maximum neutralizing efficacy of the anti-α4β7 antibody is assumed to be 100%. As we assume anti-α4β7 antibody binding rapidly reaches equilibrium, we use (1- 𝕀N ψN AB/ (1 + ψN AB)) (S1 Text) as the factor by which antibody reduces the infection rate, where 1/ψN is the antibody concentration for 50% neutralization. Since neutralization requires the anti-α4β7 antibody to bind to the virus, we account for increased viral clearance in addition to the inhibition of infection when we model this mechanism of action (Fig 1C). To limit the number of free parameters, we assumed that ψN = ψC.
Mechanism 3: Anti-α4β7 antibody can bind to α4β7+ CD4+ T cells and protect them from infection
The anti-α4β7 antibody can block infection of α4β7+ CD4+ T cells [4,10]. Also, the anti-α4β7 antibody decreases trafficking of CD4+ T cells to the gut [2,4]. As the gut is a site of high viral replication, reducing the trafficking of α4β7+ CD4+ T cells to this site could also contribute to the inhibition of infection. Not all CD4+ T cells express α4β7. During acute SIV infection, the maximum percentage of peripheral blood CD4+ T cells that express α4β7 is approximately 73% [1]. Thus, we restrict the fraction of target cells protected from infection by an anti-α4β7 antibody to be less than the fraction of α4β7+ CD4+ T cells—denoted by kα4β7. To limit the number of target cells in the protected state (P) to those that are α4β7+, we used a logistic function, in Eqs (1) and (6), where ρ is the maximum rate target cells enter the protected state and EC50 is the antibody concentration needed for half-maximal effect. After anti-α4β7 treatment the antibody concentration wanes and protected cells can become target cells, as the antibody reversibly binds to cell-associated α4β7 and will dissociate. We assume the rate that protected cells become target cells again is dependent on the plasma concentration of the anti-α4β7 antibody according to ,with protection waning at maximum rate ⍵ (Eqs (1) and (6)) (Fig 1D).
Mechanism 4: Anti- α4β7 antibody increases antigen presentation
The anti-α4β7 antibody could increase antigen presentation due to greater uptake of α4β7+ virus by antigen presenting cells and lead to a more robust adaptive immune response [9]. We test this by setting the indicator variable 𝕀A = 1 if we assume an increase in antigen presentation and 𝕀A = 0 if we assume this mechanism is absent in Eq (5). We account for this improvement in the presence of the anti-α4β7 antibody by increasing the source rate λE by a factor of 1 + , where Ω is the half-saturation constant for the antibody effect that enhances antigen presentation to generate more cytotoxic effector cells (Fig 1E). To limit the number of free parameters, we assume that the source rate is at most double based on in vitro experiments [25]. Also, this approach assumes that in the presence of the anti-α4β7 antibody, antigen presenting cells increase the rate effector cell precursors become activated, consistent with the observation that blocking the β7 integrin with a monoclonal antibody enhances MHC-I presentation [25].
In the supplementary material (S2 Text), we consider a version of this mechanism that requires the antibody to bind to the virus. We include the effects of increased viral clearance when studying mechanism 4 in this alternative scenario (Fig 1E and S2 Text). For the effector cell source model that includes antigen presenting cells, we explicitly model the interaction between virus in complex with the antibody and antigen-presenting cells within mechanism 4 (S1 Text).
Pharmacokinetics of the anti-α4β7 antibody
To describe the pharmacokinetics of the anti-α4β7 antibody, we used a two-compartment pharmacokinetic (PK) model [26] in which the anti-α4β7 antibody is infused into the bloodstream at rate Aα4β7(t), and disseminates to the tissue at rate k12. Once in the tissue, the antibody either re-enters the bloodstream at rate k21 or is eliminated at rate k0 (S1 Text). The equations describing the PK dynamics are
| (7) |
| (8) |
where XB and XT are the total amounts of antibody in the blood and tissues, respectively, vB is the volume of blood, and thus the concentration of the antibody in the blood is AB = XB/vB.
Model parameters
We fixed many parameters with estimates from the literature (Table 1) and others were determined by fitting to the viral load data in Byrareddy et al. [2] and to macaque pharmacokinetic data [3] using maximum likelihood methods (S14–S19 Tables) (S1 Text).
Table 1. Parameter definitions and values.
| Parameter | Description | Value | Units | Reference |
|---|---|---|---|---|
| dT | Uninfected CD4+ T-cell death rate | 0.01 | per day | [18,53] |
| rT | CD4+ T-cell proliferation rate | per day | Estimated for individual macaques | |
| κ | Carrying capacity for the CD4+ T cell population | a | cells/ml | Calculated |
| α | Latent cell activation rate | 0.001 | per day | [7] |
| dL | Latent cell death rate | b | per day | Calculated |
| rL | Latent cell proliferation rate | b | per day | Calculated |
| dL+ α -rL | Decay rate of the latent cell reservoir | 0.0182b | per day | [32] |
| f | Fraction of infections resulting in latency | 10−5 | Calibratedc | |
| m | Rate cytotoxic effector cells kill infected cell | ml/cell per day | Estimated for individual macaques | |
| δ | Infected cell death rate due to viral cytopathic effects in baseline model | 0.60 | per day | Calibrated |
| p | Viral production rate | RNA copies per cell per day | Estimated for individual macaques | |
| c | Viral clearance rate | 23 | per day | [54–56] |
| λE | Effector cell source rate | 103 | cells / ml per day | Calibratedd |
| μ | Death rate of cytotoxic effector cells | 0.32 | per day | [30] |
| bE | Maximum proliferation rate for cytotoxic effector cells | 1.62 | per day | [30,31] |
| dE | Maximum exhaustion rate for cytotoxic effector cells in baseline model | 1.35 | per day | Calibrated |
| KB | Saturation constant for cytotoxic effector cell expansion | cells/ml | Estimated for individual macaques | |
| KD | Saturation constant for cytotoxic effector cell exhaustion | 55 KB | cells/ml | [32] |
| ε | Efficacy of cART | 0.90 | Assumed | |
| T(0)β | Free virus infection rate | 5 ⨉ 10−3 | cells/SIV RNA per day | Assumed |
| Aα4β7 | Total amount of anti-α4β7 antibody infused | 805 | μg/ml | 50 mg/kg for a 5.3 kg [57] macaque with 329 ml of blood |
| V(0) | Initial virus concentration | 413 | SIV RNA copies/ml | Estimated |
| k0 | Elimination rate of anti-α4β7 antibody | 0.048 | per day | Estimated |
| k12 | Distribution rate of anti-α4β7 antibody to tissue | 0.165 | per day | Estimated |
| k21 | Distribution rate of anti-α4β7 antibody to blood from tissue | 0.008 | per day | Calibratede |
| κα4β7 | Fraction of CD4+ T cells that are α4β7+ | 0.73 | [1] | |
| EC50 | Half-maximal concentration for anti-α4β7 antibody binding to CD4 T cells | 2.76 ⨉ 10-2 | μg/ml | [58] |
| KP | Saturation constant for the source of effector cells in the saturated source model | cell/ml | Estimated for individual macaques | |
| γ | Fold increase in viral clearance rate | Estimated for individual treated macaques | ||
| 1/ψC | Antibody concentration of half-maximal effect for increased viral clearance | μg/ml | Estimated for individual treated macaques | |
| 1/ψN | Antibody concentration of half-maximal effect for neutralization | 1/ψN = 1/ψC | μg/ml | Estimated for individual treated macaques |
| 𝕀N | Indicator variable for the presence of the effect of viral neutralization from the anti-α4β7 antibody | 1 when present; 0 otherwise | ||
| 𝕀A | Indicator variable for the presence of the effect of an increase in the effector cell source rate from the anti-α4β7 antibody | 1 when present; 0 otherwise | ||
| ⍵ | Maximum rate protection wanes | per day | Estimated for individual treated macaques | |
| ⍴ | Maximum rate target cells become protected | per day | Estimated for individual treated macaques | |
| Ω | Half-saturation constant for the effect the anti-α4β7 antibody has on increasing antigen presentation | μg/ml | Estimated for individual treated macaques |
a The carrying capacity was calculated such that in the absence of productively infected and latently infected cells the CD4+ T cell population would be in steady state at the initial target cell concentration.
b Specifying the latent cell activation rate, the difference between the latent cell death rate and the latent cell proliferation rate is such that the half-life of the latent cell reservoir is 38 days.
c The fraction of infections resulting in latency was calibrated during the initial stages of fitting such that the viral load under cART was greater than 1 SIV RNA copies/ml during chronic HIV infection.
d The source rate of effector cells was chosen such that the effector cell concentration in the baseline model was relatively comparable to the concentration of HIV specific CD8+ T cells during HIV infection.
e The distribution rate of the antibody to the blood from the tissue was calibrated at 0.001 intervals to maximize the likelihood of the antibody dynamics from the pharmacokinetic model.
According to Sachsenberg et al [19], 1.1% of the total CD4+ T cell population (106 cells/ml) in an HIV individual is Ki67+ and likely in cell cycle. Thus, we assume the initial number of target cells, T(0) = 1.1 x 104 cells/ml. We specify βT(0) = 5 × 10−3 cells/day, as estimates of the HIV infection rate β tend to vary between 10−7 and 10−8 ml/day [18,27,28]. To obtain an effector cell concentration in the absence of all therapy that was relatively comparable in scale to empirical estimates of HIV-specific CD8+ T -cell concentrations [29], we set the effector cell source rate λE = 103 cells/ml/day. We set the maximum expansion rate of the effector cells bE = 1.62/day based on past SIV studies [30,31] and the effector cell death rate μ = 0.32/day [30]. We specified the fraction of infections resulting in latency f = 10-5, so that the predicted viral load while on cART during chronic infection was that observed in chronic HIV infected patients on cART, where we assumed that the efficacy of cART is 90%. These values were later varied in a sensitivity study. Starting five weeks after infection, macaques were given cART for up to 14 weeks. As cART was given during acute SIV infection and for a short time, we used the prior estimate of a 38-day half-life of the SIV latent cell reservoir [32] based on a study in which reservoir decay was measured in pigtail macaques given four antiretroviral drugs starting at 12 days post infection for approximately 23 weeks [33].
Parameter estimation
To determine the maximum effector cell exhaustion rate, dE, and the infected cell death rate due to viral cytopathic effects, δ, we conducted a primary grid search on these two parameters across the seven control macaques. The values of these two parameters that maximized the combined likelihood across the seven control macaques were used in the model fitting of the treated macaques and model simulations of the control and treated macaques (S1–S3 Tables).
According to the mathematical model, each of the eight anti-α4β7 treated macaques (henceforth referred to as treated macaques) has one viral load set-point above 50 SIV RNA copies/ml and another other below 50 SIV RNA copies/ml (Fig 2 and S1–S3 Figs). The achievement of post-treatment control after the removal of cART was not observed in the seven IgG control macaques, and there is only moderate variability in viral dynamics among these animals after stopping cART (S6–S8 Figs). The viral dynamics among the treated macaques after the removal of cART is highly variable. Our fitting approach for integrating the IgG control viral load data and accounting for the individual heterogeneity in the treated macaques, is motivated by methods used in population sciences to identify heterogeneous treatment effects [34]. We paired each treated macaque with a control macaque that received normal IgG, simultaneously fitting the model to the viral load data of the two macaques, provided the opportunity to disentangle the effects of the effector cell response and the mechanism of action of the antibody. This fitting process using the one-to-one pairing was repeated for each IgG control macaque, such that all the treated macaque were paired with every IgG control macaque (S1 Text). We assumed that the IgG control macaques are a well-representative population of macaques who did not receive the anti-α4β7 antibody. Thus, we assume the viral dynamics of each of the eight treated macaques would approach the viral steady state above 50 SIV RNA copies/ml and resemble that of an IgG control macaque after cART was stopped and if the anti-α4β7 antibody were not given.
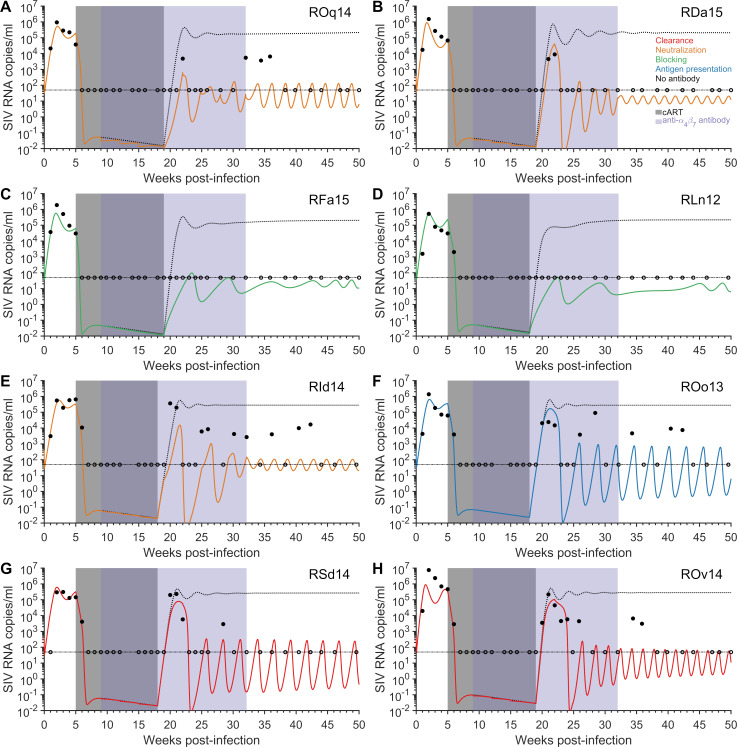
Fig 2. Fit of the model to the data.
The measured (≥50 SIV RNA copies/ml solid circles and <50 SIV RNA copies/ml open circles) and model predicted viral loads (solid line) using the best-fit parameter estimates and model variation with the greatest AIC weight for each of the treated macaques and predicted viral dynamics in the absence of the anti-α4β7antibody (dotted black line), panels A)–H). The limit of detection is 50 SIV RNA copies/ml (thin horizontal dashed black line). Treatment with cART occurred between five weeks and 18/19 weeks post-infection (gray area), while eight infusions of the anti-α4β7antibody occurred between nine weeks post-infection and 32 weeks post-infection (purple area). The mechanisms considered include increased viral clearance (red line), virus neutralization (orange line), target cell protection (green line), and increased antigen presentation (blue line). Parameters for these simulations are in Tables 1 and S14–S18, for the AIC selected model (Table 2).
We computed the 95% confidence intervals using the profile likelihoods of the estimated parameters and a threshold for the log-likelihood based on half the value of the 95% percentile of a χ2distribution with k degrees of freedom [35], where k is the number of estimated parameters (S1 Text).
Model selection
For model selection, we calculated the Akaike information criterion (AIC) weight [36]. The small sample size corrected AIC score for model i and macaque j is
where Li,j is the likelihood for model i and macaque j, nj is the number of observations, and ki is the number of parameters for model i [37]. The AIC weight for model i and macaque j is
where ΔAICi,j = AICi,j−mink{AICk,j} [36]. As the AIC weight of a model (i.e., mechanism) can be viewed as the probability that the model is the best one, we averaged the weights across all the macaques for each model to evaluate the relative importance of the model (i.e., mechanism) in explaining the observed dynamics.
Sensitivity
As in other viral dynamic models, many of the estimated parameters are correlated [38,39]. The estimated value of the effector cell killing rate, m, scales with the assumed values of the effector cell source rate, λE, and the rate antigen presenting cells encounter antigen, bD, for the model presented in S1 Text. The free-virus infection rate, βT(0), is correlated with the estimated value of the viral production rate, p. We performed a sensitivity analysis for the efficacy of cART, ε, the fraction of new infections that are latent, f, and the rate latent cells are activated (with the latent cell reservoir half-life fixed at 38 days), a, and the impact these parameters have on the average viral load dynamics in the IgG control and treated macaques.
We also conducted an extensive sensitivity analysis, on the fraction of new infections that are latent, f, the rate latent cells are activated, a (which influences the half-life of the latent cell reservoir because we keep the latent cell proliferation rate, rL, fixed), the efficacy of cART, ε, the maximum rate of effector cell expansion, bE, the ratio of KD to KB, the effector cell death rate, μ, the percentage of CD4+ T cells that are targets, T(0) (which influences β as βT(0) = 5 × 10−3 cells/day), the initial viral inoculum, V(0), and the effector source rate, λE, based on changes in the log-likelihood value (S3 Text).
Simulating nef-competent SIV
In Byrareddy et al. [2], SIVmac239 nef-stop was used to infect the macaques. Major histocompatibility complex (MHC) class I molecules on the surface of SIV and HIV-infected cells are downregulated by nef [40,41], allowing infected cells to evade CD8+ T effector cell responses to some degree. Since peptide-MHC class I molecules are recognized by the T cell receptor on CD8+ T cells, we speculate that cells infected with a nef-competent virus will not stimulate effector cell expansion as well as the nef-defective virus used by Byrareddy et al. [2]. Therefore, to model a nef-competent virus, such as in the repeat experiment by Abbink et al. [15], we reduced the effector cell killing rate m and increased the half-saturation constant for effector cell proliferation KB, while fixing the remaining best-fit parameters for each treated macaque (i.e., the half-saturation constant for effector cell proliferation KD remains fixed and is not increased with KB) (S1 Text). We implemented a grid search for the perturbation of these two parameters within fixed ranges that would give rise to viral rebound (S1 Text).
Results
The achievement of post-treatment virologic control after the removal of treatment is dependent upon obtaining a balance between viral growth and the immune control. Models that differed by the mechanism of action of the anti-α4β7 antibody were able to attain post-treatment control with the administration of the anti-α4β7 antibody, with most reproducing the observed viral dynamics (Figs 2 and 3 and S2–S5). In addition, the model could portray the viral dynamics in the IgG control macaques (S6–S8 Figs). With multiple models fitting the viral load after the removal of cART in both the IgG control and anti-α4β7 antibody treated macaques, we next determined which models gave the best fit for each individual animal.
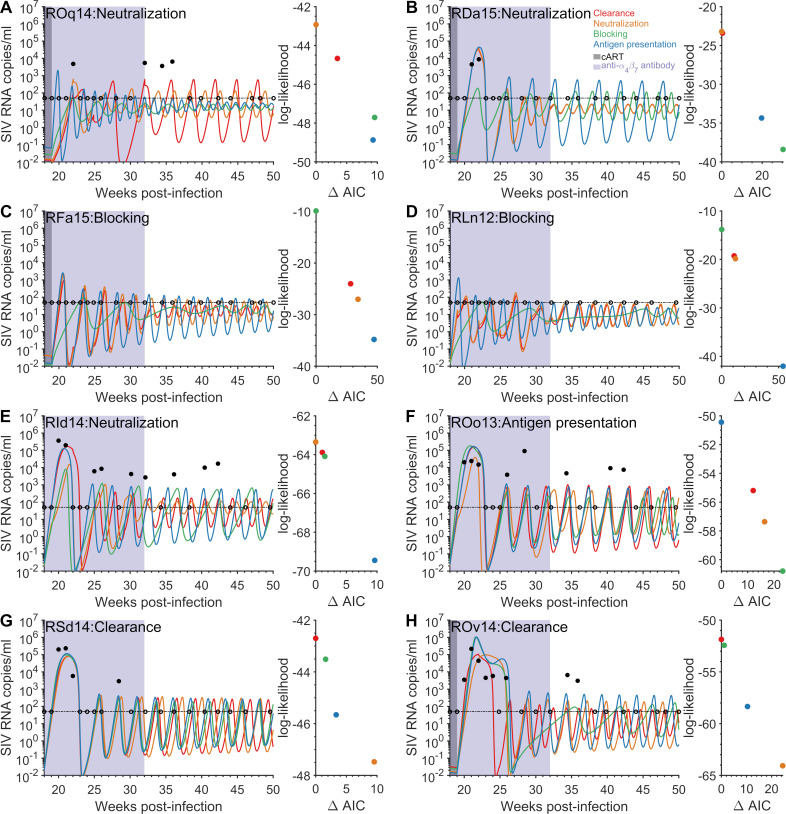
Fig 3. Viral dynamics after the removal of cART for the four anti-α4β7 antibody mechanisms of action.
The measured (≥50 SIV RNA copies/ml solid circles and <50 SIV RNA copies/ml open circles) and model predicted viral loads for the AIC selected model (indicated after macaque) and three remaining models using the best-fit parameter estimates for the mechanisms of increased viral clearance (red line), viral neutralization (orange line), target cell protection (green line), and increased antigen presentation (blue line), panels A)–H). For each macaque, a scatter plot of the ΔAIC and the log-likelihood for each mechanism, panels A)–H). The limit of detection is 50 SIV RNA copies/ml (thin horizontal dashed black line). Treatment with cART occurred between five weeks and 18/19 weeks post-infection (gray area), while eight infusions of the anti-α4β7antibody occurred between nine weeks post-infection and 32 weeks post-infection (purple area). The mechanisms considered include parameters for these simulations are in Tables 1 and S14–S18.
Viral load dynamics best reproduced with baseline source of effector cells
As described in the Supplemental Information (S1 Text), we tested three different models for the source of effector cells in the absence of anti-α4β7 antibody therapy: a baseline model where the source rate is independent of infected cells, virus, or antigen presenting cells; a saturated source dependent on the infected cell concentration or equivalently the virus concentration as the virus and infected cell levels rapidly establish a quasi-steady state in which they are proportional to each other; and a more mechanistic model where the source is dependent on the concentration of antigen presenting cells. We examined which model best fit the viral load dynamics of the IgG control and treated macaques using AIC weight, where models with the larger weights (lower AIC score) are selected [36]. Given an effector source model, the best mechanism of action of the anti-α4β7antibody based on AIC was used for each treated macaque in the model comparison (S5–S12 Tables). Overall, we found that the baseline model was the best option to generate the viral load dynamics seen in both the treated and IgG control macaques (S4 Table), showing that adding more biological complexity does not improve the fits enough to justify the inclusion of additional parameters. Given this finding, we only discuss the results obtained with the baseline model below. We note that this AIC selected model is not universally favored across the different mechanisms for the individual macaques (S5–S13 Tables).
Viral dynamics in the treated group is best explained by the protection mechanism
We considered four mechanisms by which the anti-α4β7 antibody perturbs the balance between viral replication and immune control (Fig 1). To determine which mechanism best explains the viral load dynamics for the treated macaques, we fit the model to the viral load data from each monkey and compared the mechanisms using the AIC weight (Table 2 and Figs 2 and 3). We found that the protection mechanism provides the overall largest AIC weight on average for the treated macaques (Table 2), while some individual macaques have different optimal mechanisms (Table 2). Increased viral clearance and viral neutralization follow second and third, respectively, for explaining the observed viral load dynamics in the eight treated macaques.
Table 2. The AIC weight* for increased viral clearance, viral neutralization, protection, and improved antigen presentation mechanisms for the baseline source model.
| Mechanism | ROq14 | RDa15 | RFa15 | RLn12 | RId14 | ROo13 | RSd14 | ROv14 | Average |
|---|---|---|---|---|---|---|---|---|---|
| Viral clearance | 0.147 | 0.452 | 0.000 | 0.004 | 0.282 | 0.002 | 0.609 | 0.637 | 0.267 |
| Virus neutralization | 0.838 | 0.548 | 0.000 | 0.002 | 0.484 | 0.000 | 0.005 | 0.000 | 0.235 |
| Protection | 0.007 | 0.000 | 1.000 | 0.993 | 0.230 | 0.000 | 0.271 | 0.360 | 0.358 |
| Antigen presentation | 0.008 | 0.000 | 0.000 | 0.000 | 0.004 | 0.997 | 0.115 | 0.003 | 0.141 |
* AIC weights are rounded and as a result some columns may not sum to one.
The protection mechanism still had the largest average AIC weight when including increased viral clearance into the increased antigen presentation mechanism (Table A in S2 Text). The average AIC weight of increased antigen presentation improved slightly with the addition of increased viral clearance to this mechanism (Table A in S2 Text).
We examined the viral load dynamics predicted by each mechanism post-cART and compared them to the AIC selected mechanism for the individual macaque (Fig 3). For most macaques, the rebound dynamics are qualitatively similar for the different mechanisms. For the two macaques that had no detectable viremia post-cART (RFa15 and RLn12), the protection mechanism was more able to suppress the initial rebound immediately after cART was removed compared to the other four mechanisms which produced peaks slightly above detection. For macaque RId14, which had highly oscillatory viral load dynamics after cART was stopped, the four mechanisms produced qualitatively different oscillatory patterns. For macaque ROo13, the difference in the mechanisms were more apparent in capturing the initial viral load peak after cART was stopped, with relatively similar dynamics afterwards. Although some mechanisms may qualitatively be similar during the phase once cART is removed, the reduced log-likelihood can be attributed to i) poor representation of the viral load dynamics prior to the initiation of cART or ii) a substandard portrayal of the viral load dynamics in the absence of the anti-α4β7 antibody.
Area under viral load curve post-treatment correlated with the level at which effector cells proliferate
We calculated the area under the predicted log10 viral load curve (AUC) for the 30 weeks after cART was removed. The time period of 30 weeks after cART was removed was used instead of a specified time post-infection because cART was stopped at either week 18 or 19 p.i., which would result in different durations in which the AUC is calculated. The estimated half-saturation constant for effector cell proliferation, KB, was a strong predictor of the predicted AUC for the treated macaques (r = 0.77, p = 0.025) (S9 Fig), suggesting that treated macaques with a faster responding effector cell response were better able to control the virus than those with a delayed effector cell response. A strong correlation was also found between the estimated KB and the model predicted AUC for the 30 weeks following the last infusion of the antibody (r = 0.63, p = 0.096), although it was not statistically significant (S9 Fig).
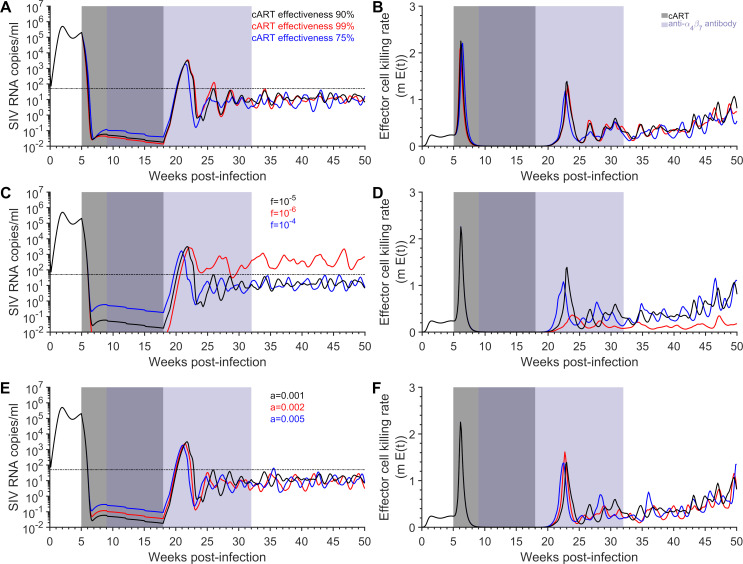
Sensitivity analysis
Conducting one-way sensitivity analysis on the efficacy of cART, the fraction of infections resulting in latency and the activation rate of latent cells, the viral load dynamics and the infected cell death rate for the treated macaques are only moderately affected (Fig 4). Increasing the half-maximal concentration (EC50) associated with the protection mechanism increases both the breadth and magnitude of the viral peak after the removal of cART (S10 Fig).
Fig 4. Sensitivity of the viral load dynamics and effector cell killing rate in the treated macaques predicted by the model.
The geometric mean of the model predicted viral load (left panels) and the per day effector cell killing rate (right panels) using the best-fit parameter estimates under the baseline source model with the greatest AIC weight for each of the treated macaques. The sensitivity of the viral load and per day effector cell killing rate with respect to changing the A)-B) effectiveness of cART from 90% (black) to 99%(red) and 75% (blue), C)-D) the fraction of infections resulting in latency from 10−5 (black) to 10−6 (red) and 10−4 (blue), and E)-F) the activation rate of latent cells from 10−3 (black) to 2 ×10−3 (red) and 5×10−3 (blue). The limit of detection is 50 SIV RNA copies/ml (thin dashed black line, left panels). Treatment with cART occurred between 5 weeks and 18/19 weeks p.i. (gray area), while eight infusions of the anti-α4β7antibody occurred between nine weeks p.i. and 32 weeks p.i. (purple area). Parameters for these simulations are in Table 1 and S14–S18 Tables, for the AIC selected mechanism (Table 2).
Through analysis of the profile likelihood, we found that the value of log-likelihood was sensitive to small changes in the value of our best estimates of the viral production rate, p, and the effector cell killing rate, m (S3 Text). Moderate changes in parameters associated with the anti-α4β7 antibody mechanism can also produce rapid changes in the log-likelihood (S3 Text). In addition, small changes in fixed parameters pertaining to the effector cell response (ratio of KD to KB, maximum rate of proliferation bE, and effector cell death rate μ) can also produce rapid changes in the log-likelihood (S3 Text). These results are somewhat expected, given the delicate balance between viral growth and immune control for the system to attain post-treatment control after the anti-α4β7 antibody is removed. We conducted similar sensitivity analysis for the IgG control macaques (S11 Fig and S3 Text).
We found that for most of the scenarios that were considered with different effector source models (Table C–H in S2 Text), the protection mechanism was found to be the dominant mechanism when explaining the population level viral dynamics (i.e., greatest average of AIC model weights). We found that increased antigen presentation was the other dominant mechanism in the instances that it performed equally well or outperformed the protection mechanism (Table F in S2 Text).
Model simulation of nef-competent SIV
Abbink et al. [15] tried to replicate the Byrareddy et al. [2] experiment using a nef-competent virus rather than a nef-deficient virus, but found that when all treatment was stopped virus rebounded in their experimental animals. Since the presence of nef can affect the parameters governing the effector cell response in our model, particularly the effector killing rate constant m and the effector cell 50% maximum proliferation constant KB (see Methods), we systematically varied these parameters for each of the eight treated macaques in the Byrareddy experiment. By changing these parameters, we converted the post-treatment control dynamics to viral rebound dynamics in all eight macaques (S12 and S13 Figs), as observed in the Abbink et al. experiment [15]. We also found that viral rebound occurs across a broader range of perturbations to the effector cell killing rate and the 50% maximum proliferation constant (S13 Fig).
Discussion
We expanded a viral kinetic model previously used to explain the phenomenon of post-treatment control observed in the VISCONTI study [7,8]. Our generalization incorporated four possible mechanisms of action of the anti-α4β7 antibody: increased viral clearance, virus neutralization, protection of CD4+ T cells from infection, and increased antigen presentation. To examine the role of these mechanisms in explaining the viral dynamics seen in eight rhesus macaques treated with cART plus an anti-α4β7 antibody, we fit our mathematical model to the viral load data from these eight macaques as well as the viral load data from seven control macaques treated with normal IgG and cART [2]. Our mathematical model with best-fit parameters was largely able to reproduce the observed viral dynamics as well as the viral suppression observed in the treated macaques after cessation of all therapy.
Through our analysis, we determined the protection mechanism best explained the population level viral dynamics in all eight macaques treated with the anti-α4β7 antibody. However, there was substantial heterogeneity in the dominant mechanisms across individual animals, as at least one of the four mechanisms were suggested to be the dominant in at least one of the animals. In retrospect, this heterogeneity of mechanism may not be surprising if we view anti-α4β7 antibody treatment as a perturbation of the interactions between the virus and its host that leads to viral suppression and the strengthening of the host immune response so that in the absence of all therapy viral suppression can be maintained. In addition, the macaques were not genetically identical which would lead to differences in the immune responses they developed. Our results reflect these differences, as the model predicted log10 viral load AUC after cART and the last anti-α4β7 antibody infusion was strongly correlated with the half-saturation constant in the effector cell proliferation rate function. The individual heterogeneity also suggests that the anti-α4β7 antibody likely has multiple mechanisms of action by which it ultimately suppressed viral rebound. Also, our analysis showed that in some macaques there are secondary mechanisms of anti-α4β7 antibody action that should not be ignored, as they have some explanatory power for the observed viral dynamics (Tables 2 and S5–S12). The individual heterogeneity of the selected mechanism among the treated macaques suggests that less dominant mechanisms could also be present.
These multiple mechanisms likely affect viral replication in overlapping ways. For example, the increased viral clearance mechanism reduces the viral concentration, which subsequently produces fewer infected cells, which in turn could increase effector cell concentrations due to the lack of immune exhaustion. Therefore, the antibody will likely have both direct and indirect effects on viral replication that may not be appropriately quantified.
The characteristics of the viral dynamics post-cART were highly heterogeneous across the eight treated macaques. After removal of cART, two macaques experienced no viremia above the limit of detection, two exhibited viral peaks only while the antibody was administered, two had a broad viral peak after the last infusion of the anti-α4β7 antibody, and the remaining two exhibited large oscillations in the viral load. Some of the variability of these dynamics may be due to stochastic reactivation of cells in the latent reservoir, which was not accounted for in our deterministic model. Rather, our model produces the observed dynamics through the perturbation of the system and the complex interaction between target cells, the virus, and the effector cell response. The objective of the model was not to provide precise estimates of mechanistic parameters of the anti-α4β7 antibody, as we were limited by the frequency of viral sampling, but rather to show that post-treatment control can be achieved through multiple mechanisms of action.
The four mechanisms considered perturb the balance between viral growth and immune control in different ways. The protection mechanism allows for the accumulation of protected CD4+ T cells during cART, which can produce a lower viral peak that may be below the limit of detection when cART is removed. This buildup of protected CD4+ T cells slows viral expansion after cART is removed, allowing the effector response to quickly suppress viral replication. The effects of the increased viral clearance and the virus neutralization mechanisms during cART can further suppress the viral load and the level of infected cells. During the continued presence of the anti-α4β7 antibody after the removal of cART, these two mechanisms will reduce the rate of de novo infections which will aid the immune response in controlling infection but also indirectly influence effector cell dynamics. The increased antigen presentation mechanism perturbs the source of effector cells, which depending on the model is either constant or dependent on the infected cell concentration in the absence of the antibody. The temporal change in the effector cell source rate in the presence of the antibody has the potential to induce oscillations in the effector cell population as the antibody concentration fluctuates due to its periodic infusion, contributing to the variable viral concentrations observed after the removal of cART.
Within the model, post-treatment control is achieved through the combined effect of cART, the anti-α4β7 antibody, and the effector cell response. HIV treatment interruption studies revealed that lower viral load set-points after stopping cART could be attributed to an increased response from HIV-specific CD8+ T cells [42]. The effector-cell response is a critical component in maintaining viral suppression, as there was a large transient rebound of viremia when CD8α expressing NK cells, NK T cells, and classic CD8 T cells were depleted in the treated macaques (Fig A in S2 Text). After the effector cell population was restored in the macaques, control of viremia was regained (Fig A in S2 Text). Additionally, Cartwright et al. showed that the responses of CD8+ T cells are critical to the suppression of viremia in SIV-infected animals treated with short-term cART [43]. CD8 depletion of SIV-infected animals while still on cART lead to viral rebound and subsequent control of viremia when the CD8+ T cells repopulated the animals. Interestingly, the viral dynamics observed in that experiment could be reproduced by a generalization of the Conway-Perelson model [32]. A limitation of our model is that we only considered the cytolytic response of effector cells, even though CD8 T cells can also use non-cytolytic mechanisms to limit infection. This was done to avoid adding extra unknown parameters and over-fitting the data. Cao et al [32] modeled the Cartwright et. al. [43] experiment using a variant of the Conway and Perelson model and found that non-cytolytic mechanisms were unlikely to be the sole mechanism of CD8 control [32].
The anti-α4β7 antibody has been hypothesized to enhance antigen presentation, resulting in a better immune response [9]. Broadly neutralizing antibodies may also induce a potent effector cell response by a mechanism in which immune complexes activate antigen presenting cells [44]. Prior studies in mice have shown that passive administration of monoclonal anti-CD20 antibodies to treat melanoma can induce a vaccinal effect, whereby the antibody aids in the development of long-term durable anti-tumor T cell responses [45]. It is hypothesized that this vaccinal effect is a result of the antibody generating immune complexes that activate antigen presenting dendritic cells which then stimulate a cell-mediated immune response [45]. The critical component of the vaccinal effect is the presence of a long-term effective memory response after the antibody has been eliminated from the body. One can speculate that the anti-α4β7 antibody induces a vaccinal effect, as macaques not only maintain long-term suppression of viremia but also viremia rebounds after the depletion of CD8+ T cells (Fig A in S2 Text).
One action of an anti-α4β7 antibody is to reduce the trafficking of lymphocytes to the gut [2,4], a site where much viral replication occurs during primary infection [46]. Our results are consistent with this hypothesis, as the protection mechanism best explained population level viral dynamics. To keep our model tractable, we did not explicitly consider trafficking. However, the protection mechanism that we did study can capture the effect of reduced CD4+ T-cell trafficking to the gut. Thus, part of the protection mechanism could be viewed as being a consequence of changes in lymphocyte trafficking due to anti-α4β7 antibody administration.
Second to the protection mechanism, both increased viral clearance and virus neutralization were the next set of mechanisms to best explain the data. The Iwamoto et al. study [13] shows that an anti-α4β7 antibody may have little to no neutralizing capabilities. However, cell cultures not treated with retinoic acid (which induces expression of α4β7) can result in cultures producing substantially lower amounts of α4β7 integrated into virions than cell cultures treated with retinoic acid [9]. Girard et al [47] observed limited viral replication in retinoic acid treated α4β7+ CD4+ T cells when preincubated with an anti-α4β7 antibody, suggesting neutralization may be feasible mechanism. From a model mechanistic standpoint, the virus neutralization mechanism could be representative of both the increased viral clearance mechanism and the protection mechanism. Increased viral clearance is encompassed within the virus neutralization mechanism, which limits infection of target cells, albeit in a different manner than the protection mechanism. We further see a role of increased viral clearance when considering a combined role with the increased antigen presentation mechanism, as the average AIC weight increased for the latter mechanism (S2 Text). This evidence strengthens the suggestion that multiple mechanisms of action from the anti-α4β7 antibody could be perturbing the balance between viral growth and immune control to obtain post-treatment control.
Although there is substantial supportive evidence targeting the α4β7 integrin to alter the course of HIV infection [14], there has been concern about the robustness of the Byrareddy et al. [2] study as other groups were unable to replicate the outcome of the original experiment [12,13,15,48]. The virus used in the original experiment contained a stop codon in nef, which upon in vivo inoculation in rhesus macaques is stochastically repaired to generate wildtype virus. The stochastic nature of the nef-stop repair over the course of infection has been suggested as one potential reason the experiment might not have been replicated [14].
We can only speculate about the reasons underlying the failure to replicate the Byrareddy et al. [2] results. The repeat study by Abbink et al. used a different SIV strain, SIVmac251, and a different route of virus infection that was not optimized to determine the effect of anti-α4β7 on SIV infection and control [15]. Further, this virus is not nef-deficient and is more pathogenic than the virus used by Byrareddy et al. [2]. To understand whether nef-competence may have played a role in the inability to repeat the original experiment, we asked whether the ability of the model to achieve post-treatment control is sensitive to changes in parameters that nef is most likely to influence. Since the presence of nef leads to down-regulation of MHC class I, we expect that the effector cell killing rate constant, m, would be decreased and that the proliferation of CD8 T cells driven by interaction with infected cells through their T cell receptor would be decreased, i.e., the parameter KB controlling the amount of stimulation by infected cells needed to induce 50% maximal proliferation would be increased. We showed using our model and best-fit parameters for each macaque that if we decreased m and increased KB that instead of post-treatment control we would get viral rebound when all treatment was stopped as found in the experiment by Abbink et al. [15].
The Iwamoto et al. study [13] also failed to achieve virologic control observed in the Byrareddy et. al. [2] experiment. This failure could be attributed to the use of a different integrase inhibitor. When cART was applied in this system, the decline in the viral load was significantly slower than in the original study. As a result, cART was administered for an extra six weeks to obtain viral suppression before starting anti-α4β7 antibody administration. The authors speculated that more rapid repair of nef in this virus could explain the slower virologic control after cART was initiated. As we argued above for the Abbink et al. [15] experiment, having nef-competent virus could easily lead to viral rebound instead of post-treatment control.
This study also examined the effect of antibodies against the V2-loop of the SIV envelope protein on viral replication after the removal of cART. They observed that the broadly neutralizing antibody ITS103.01 delayed the rebound of viremia longer than the anti-α4β7 antibody and the non-neutralizing antibody ITS12.01. Unlike the original Byrareddy et al. [2] experiment, all animals rebounded [13]. These antibodies targeting the V2 loop likely would not influence the trafficking of CD4+ T cells to the gut and not interact with non-infected cells that express α4β7 [2]. As a result, the effects of these V2 antibodies might not induce the protection mechanism included in our model of anti-α4β7 antibody action. Further, not all virions express α4β7 and their concentration is likely reduced in later stages of the experiment due to preferential infection and subsequent loss of α4β7 expressing cells. Thus, even if anti-α4β7 antibody has neutralizing ability it would not be as broad as that of ITS103.01. Moreover, ITS103.01 is directed against the CD4 binding site on Env and shows complete neutralization against tier 1, 2 and 3 SIV, including the highly neutralization-resistant SIVmac239 [49]. These factors may explain why the ITS103.01 antibody led to a greater delay in viral rebound than the anti-α4β7 antibody.
The third study by Di Mascio et al. [12] also had issues in attaining post-treatment control. In addition to the stochastic nature of reversion of the nef-stop mutation, discussed by Di Mascio et al [12], this experiment was performed using monkeys housed at the NIH Animal Care Center that were fed either 5038-Monkey Diet Jumbo or 5045-High Protein Monkey Diet [12], while the Byrareddy et al. [2] animals were housed at the Yerkes National Primate Research Center and were fed a monkey diet supplemented by fresh fruits and vegetables [2]. This leads us to speculate that the microbiomes of the animals at the two facilities were different. As the composition of the microbiome can affect immune responses and the reliability of an animal model to mimic human immune responses [50] this could be another factor in the differing outcomes. Also, the genetics of the animals might have played a role. The animals used by Di Mascio et al. [12] were obtained from Morgan Island and were genetically typed for a limited number of MHC alleles whereas the animals utilized by Byrareddy et al. [2] were bred in the facilities at the Yerkes Primate Center, Emory University. These macaques were typed for detailed MHC alleles, KIR alleles, FcR polymorphisms and TRIM5alpha genes and the animals assigned to the experimental and control groups to preclude any of these genetic biases. It is also possible that there are other genetic polymorphisms that contribute to the control of viremia, a subject under current study.
In summary, treating acute SIV infection with cART and an anti-α4β7 antibody has led to post-treatment control with viremia levels maintained below 50 SIV RNA copies/ml in an experiment by Byrareddy et al. [2]. No matter what the detailed mechanisms of action of the antibody are, the critical feature of this experiment was that after all treatment was removed, in a majority of animals the virus was controlled to below the level of detection of the assay after an initial high burst of viral replication. A model that yields two stable viral set-points, one where the viral load is below the limit of detection, explains how the antibody can perturb the viral-host system in such a way that it moves the system from the basin of attraction of the high-viral-load set-point to that of the low-viral-load set-point. Based on our analysis, which involved fitting the observed viral load data to models incorporating different mechanisms of antibody action, it appears that multiple mechanisms of antibody action can generate this type of perturbation. Alternatively, one can say that the antibody is generating a vaccinal effect, as the long-term control of the virus in the absence of all therapy ultimately depends on having an effector-cell response in the model. The involvement of effector cells in maintaining virologic control was also shown experimentally using CD8 depletion experiments.
The work presented here introduced new models for four different possible mechanisms by which a monoclonal antibody against the α4β7 integrin could modulate immune responses. These models, although needing further validation, may prove useful in exploring the mechanism of action of other antibodies, such as broadly neutralizing antibodies [51,52], in generating long-term virologic control of SIV/HIV.
Supporting information
(DOCX)
(DOCX)
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
The intervals specify the range of the set of intervals to approximate the 95% confidence intervals (S1 and S3 Texts).
(PDF)
The intervals specify the range of the set of intervals to approximate the 95% confidence intervals (S1 and S3 Texts).
(PDF)
The intervals specify the range of the set of intervals to approximate the 95% confidence intervals (S1 and S3 Texts).
(PDF)
The intervals specify the range of the set of intervals to approximate 95% confidence intervals (S1 and S3 Texts).
(PDF)
The intervals specify the range of the set of intervals to approximate the 95% confidence intervals (S1 and S3 Texts).
(PDF)
The intervals specify the range of the set of intervals to approximate the 95% confidence intervals (S1 and S3 Texts).
(PDF)
The viral load set points predicted by the model using the best-fit parameter estimates and the mechanism with the greatest AIC weight from A) and B) with the baseline cell source model; C) and D) the model with a saturated source of effector cells; E) and F) a model where the source of effector cells is dependent on the concentration of antigen presenting cells. The maximum and minimum viral load equilibrium points predicted by the model (left column) and estimated by the predicted viral load at 81 weeks p.i. (right column). Parameters for these simulations are in Tables 1 and S14–S18, for the AIC selected mechanism (S5–S12 Tables). We do not consider the alternative mechanism of increased antigen presentation with increased viral clearance in this analysis.
(PDF)
The measured (≥50 SIV RNA copies/ml solid circles and <50 SIV RNA copies/ml open circles) and model predicted viral loads (solid line) using the best-fit parameter estimates and model variation with the greatest AIC weight for each of the treated macaques and predicted viral dynamics in the absence of the anti-α4β7antibody (dotted black line), panels A)–H). The limit of detection is 50 SIV RNA copies/ml (thin horizontal dashed black line). Treatment with cART occurred between five weeks and 18/19 weeks post-infection (gray area), while eight infusions of the anti-α4β7antibody occurred between nine weeks post-infection and 32 weeks post-infection (purple area). The mechanisms considered include increased viral clearance (red line), viral neutralization (orange line), target cell protection (green line), and increased antigen presentation (without increased viral clearance) (blue line). Parameters for these simulations are in Tables 1 and S14–S18 and S2 Text, for the AIC selected mechanism (S5–S12 Tables).
(PDF)
The measured (≥50 SIV RNA copies/ml solid circles and <50 SIV RNA copies/ml open circles) and model predicted viral loads (solid line) using the best-fit parameter estimates and model variation with the greatest AIC weight for each of the treated macaques and predicted viral dynamics in the absence of the anti-α4β7antibody (dotted black line), panels A)–H). The limit of detection is 50 SIV RNA copies/ml (thin horizontal dashed black line). Treatment with cART occurred between five weeks and 18/19 weeks post-infection (gray area), while eight infusions of the anti-α4β7antibody occurred between nine weeks post-infection and 32 weeks post-infection (purple area). The mechanisms considered include increased viral clearance (red line), viral neutralization (orange line), target cell protection (green line), and increased antigen presentation (without increased viral clearance) (blue line). Parameters for these simulations are in Tables 1and S14–S18 and S2 Text, for the AIC selected mechanism (S5–S12 Tables).
(PDF)
The measured (≥50 SIV RNA copies/ml solid circles and <50 SIV RNA copies/ml open circles) and model predicted viral loads for the AIC selected model (indicated after macaque) and three remaining models using the best-fit parameter estimates for the mechanisms of increased viral clearance (red line), viral neutralization (orange line), target cell protection (green line), and increased antigen presentation (without increased viral clearance) (blue line), panels A)–H). For each macaque, a scatter plot of the ΔAIC and the log-likelihood for each mechanism, panels A)–H). The limit of detection is 50 SIV RNA copies/ml (thin horizontal dashed black line). Treatment with cART occurred between five weeks and 18/19 weeks post-infection (gray area), while eight infusions of the anti-α4β7antibody occurred between nine weeks post-infection and 32 weeks post-infection (purple area). The mechanisms considered include parameters for these simulations are in Tables 1 and S14–S18 and S2 Text.
(PDF)
The measured (≥50 SIV RNA copies/ml solid circles and <50 SIV RNA copies/ml open circles) and model predicted viral loads for the AIC selected model (indicated after macaque) and three remaining models using the best-fit parameter estimates for the mechanisms of increased viral clearance (red line), viral neutralization (orange line), target cell protection (green line), and increased antigen presentation (without increased viral clearance) (blue line), panels A)–H). For each macaque, a scatter plot of the ΔAIC and the log-likelihood for each mechanism, panels A)–H). The limit of detection is 50 SIV RNA copies/ml (thin horizontal dashed black line). Treatment with cART occurred between five weeks and 18/19 weeks post-infection (gray area), while eight infusions of the anti-α4β7antibody occurred between nine weeks post-infection and 32 weeks post-infection (purple area). The mechanisms considered include Parameters for these simulations are in Tables 1and S14–S18 and S2 Text.
(PDF)
The observed (black dots) and model predicted viral load dynamics (solid line) using the best-fit parameter estimates for A)–G) each of the macaques. Parameters for these simulations are in Tables 1 and S19.
(PDF)
The observed (black dots) and model predicted viral load dynamics (solid line) using the best-fit parameter estimates for A)–G) each of the macaques. Parameters for these simulations are in Tables 1and S19 and S2 Text.
(PDF)
The observed (black dots) and model predicted viral load dynamics (solid line) using the best-fit estimates for A)–G) each of the macaques. Parameters for these simulations are in Tables 1 and S19.
(PDF)
The correlation between the best parameter estimates for the half-saturation constant for effector cell proliferation for the AIC selected mechanism of the baseline model for each treated macaque and the area under the predicted log10 viral load curve for the 30 weeks following A) the removal of cART and B) the last infusion of the anti-α4β7antibody.
(PDF)
The model predicted viral load (solid line) using the best-fit parameter estimates and the baseline source model for the treated macaques A) RSd14, B) ROv14, C) RLn12, and D) RFa15 using the baseline half-maximal concentration, EC50, (black), 100-fold higher EC50 (red), and 1000-fold higher EC50 (blue). The limit of detection is 50 SIV RNA copies/ml (thin dashed black line, left panels). E) The area under the log10 predicted viral load curve for the 30 weeks after cART was stopped for the treated macaques RSd14 (black), ROv14 (red), RLn12 (blue), and RFa15 (purple). Treatment with cART occurred between five weeks and 18/19 weeks post-infection (gray area). Parameters for these simulations are in Tables 1 and S16.
(PDF)
The average model predicted viral load (left panels) and the per day effector cell killing rate (right panels) using the best-fit parameter estimates under the baseline source model with the greatest AIC weight for each of the treated macaques (solid line). The sensitivity of the viral load and per day effector cell killing rate with respect to changing A)−B) the effectiveness of cART from 90% (black) to 99%(red) and 75% (blue); C)−D) the fraction of infections resulting in latency from 10−5 (black) to 10−6 (red) and 10−4 (blue); E)−F) the activation rate of latent cells from 10−3 (black) to 2 ×10−3 (red) and 5×10−3 (blue). The limit of detection is 50 SIV RNA copies/ml (thin dashed black line, left panels) and the minimum infected cell death rate is the death rate due to viral cytopathic effects (thin dashed line, right panels). Treatment with cART occurred between five weeks and 18/19 weeks post-infection (gray area). The average was calculated using the geometric mean for the seven IgG control macaques. Parameters for these simulations are in Tables 1 and S19.
(PDF)
The model predicted viral loads for SIV nef-competent virus with anti-α4β7antibody therapy (black) and without anti-α4β7antibody therapy (red) using the best-fit parameter estimates and model variation with the greatest AIC weight for each of the treated macaques, panels A)–H). The limit of detection is 50 SIV RNA copies/ml (thin dashed black line). Treatment with cART occurred between five weeks and 18/19 weeks post-infection (gray area), while eight infusions of the anti-α4β7antibody occurred between nine weeks post-infection and 32 weeks post-infection (purple area). Parameters for these simulations are in Tables 1 and S14–S18, for the AIC selected model (Table 2). The effector cell killing rate (m) and the saturation constant for effector cell proliferation was adjusted for each treated macaque for the nef-competent virus (S13 Fig).
(PDF)
The proportion of macaques whose viral load rebounded after the removal of cART (color gradient) for various reductions in the effector cell killing rate (m) and increases in the half-saturation constant for effector cell proliferation (KB). Parameters for these simulations are in Tables 1 and S14–S18, for the AIC selected model (Table 2). Viral rebound was characterized by the model viral load not dropping below 50 RNA copies/ml any time after week 40 post-infection and had a viral load that exceeded 10,000 RNA copies/ml at week 81-post infection.
(PDF)
Data Availability
All relevant data are within the manuscript and its Supporting Information files.
Funding Statement
Portions of this work were done under the auspices of the US Department of Energy under contract 89233218CNA000001 and NIH grants R01-OD011095, R01-AI028433 and P01-AI131365 (ASP) and R01-AI29745 (SNB). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Pereira LE, Onlamoon N, Wang X, Wang R, Li J, Reimann KA, et al. Preliminary in vivo efficacy studies of a recombinant rhesus anti-alpha(4)beta(7) monoclonal antibody. Cell Immunol. 2009;259: 165–176. doi: 10.1016/j.cellimm.2009.06.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Byrareddy SN, Arthos J, Cicala C, Villinger F, Ortiz KT, Little D, et al. Sustained virologic control in SIV+ macaques after antiretroviral and α4β7 antibody therapy. Science. 2016;354: 197–202. doi: 10.1126/science.aag1276 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Byrareddy SN, Kallam B, Arthos J, Cicala C, Nawaz F, Hiatt J, et al. Targeting α4β7 integrin reduces mucosal transmission of simian immunodeficiency virus and protects gut-associated lymphoid tissue from infection. Nat Med. 2014;20: 1397–1400. doi: 10.1038/nm.3715 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ansari AA, Reimann KA, Mayne AE, Takahashi Y, Stephenson ST, Wang R, et al. Blocking of α4β7 gut-homing integrin during acute infection leads to decreased plasma and gastrointestinal tissue viral loads in simian immunodeficiency virus-infected rhesus macaques. J Immunology. 2011;186: 1044–1059. doi: 10.4049/jimmunol.1003052 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Arthos J, Cicala C, Martinelli E, Macleod K, Van Ryk D, Wei D, et al. HIV-1 envelope protein binds to and signals through integrin alpha4beta7, the gut mucosal homing receptor for peripheral T cells. Nat Immunol. 2008;9: 301–309. doi: 10.1038/ni1566 [DOI] [PubMed] [Google Scholar]
- 6.Cicala C, Martinelli E, McNally JP, Goode DJ, Gopaul R, Hiatt J, et al. The integrin a4b7 forms a complex with cell-surface CD4 and defines a T-cell subset that is highly susceptible to infection by HIV-1. Proc Nat Acad Sci USA. 2009;106: 20877–20882. doi: 10.1073/pnas.0911796106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Conway JM, Perelson AS. Post-treatment control of HIV infection. Proc Natl Acad Sci USA. 2015;6: 4–9. doi: 10.1073/pnas.1419162112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Sáez-Cirión A, Bacchus C, Hocqueloux L, Avettand-Fenoel V, Girault I, Lecuroux C, et al. Post-treatment HIV-1 controllers with a long-term virological remission after the interruption of early initiated antiretroviral therapy ANRS VISCONTI Study. PLoS Pathog. 2013;9: e1003211. doi: 10.1371/journal.ppat.1003211 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Guzzo C, Ichikawa D, Park C, Phillips D, Liu Q, Zhang P, et al. Virion incorporation of integrin α4β7 facilitates HIV-1 infection and intestinal homing. Science Immunology. 2017;2: eaam7341. doi: 10.1126/sciimmunol.aam7341 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Goes LR, Sajani A, Sivro A, Olowojesiku R, Ray JC, Perrone I, et al. The V2 loop of HIV gp120 delivers costimulatory signals to CD4 T cells through Integrin αβ and promotes cellular activation and infection. Proc Natl Acad Sci U S A. 2020;117: 32566–32573. doi: 10.1073/pnas.2011501117 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Soler D, Chapman T, Yang L-L, Wyant T, Egan R, Fedyk ER. The binding specificity and selective antagonism of vedolizumab, an anti-alpha4beta7 integrin therapeutic antibody in development for inflammatory bowel diseases. J Pharmacol Exp Ther. 2009;330: 864–875. doi: 10.1124/jpet.109.153973 [DOI] [PubMed] [Google Scholar]
- 12.Di Mascio M, Lifson JD, Srinivasula S, Kim I, DeGrange P, et al. Evaluation of an antibody to α4β7 in the control of SIVmac239-nef-stop infection. Science. 2019. pp. 1025–1029. doi: 10.1126/science.aav6695 [DOI] [PubMed] [Google Scholar]
- 13.Iwamoto N, Mason RD, Song K, Gorman J, Welles HC, Arthos J, et al. Blocking α4β7 integrin binding to SIV does not improve virologic control. Science. 2019;365: 1033–1036. doi: 10.1126/science.aaw7765 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Berg J. Editorial expression of concern. Science. 2019;365: 991–991. [DOI] [PubMed] [Google Scholar]
- 15.Abbink P, Mercado NB, Nkolola JP, Peterson RL, Tuyishime H, McMahan K, et al. Lack of therapeutic efficacy of an antibody to α4β7 in SIVmac251-infected rhesus macaques. Science. 2019;365: 1029–1033. doi: 10.1126/science.aaw8562 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kepler TB, Perelson AS. Drug concentration heterogeneity facilitates the evolution of drug resistance. Proc Natl Acad Sci U S A. 1998;95: 11514–11519. doi: 10.1073/pnas.95.20.11514 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.De Boer RJ, Perelson AS. Target cell limited and immune control models of HIV infection: a comparison. J Theor Biol. 1998;190: 201–214. doi: 10.1006/jtbi.1997.0548 [DOI] [PubMed] [Google Scholar]
- 18.Stafford MA, Corey L, Cao Y, Daar ES, Ho DD, Perelson AS. Modeling plasma virus concentration during primary HIV infection. J Theor Biol. 2000;203: 285–301. doi: 10.1006/jtbi.2000.1076 [DOI] [PubMed] [Google Scholar]
- 19.Sachsenberg N, Perelson AS, Yerly S, Schockmel GA, Leduc D, Hirschel B, et al. Turnover of CD4+ and CD8+ T lymphocytes in HIV-1 infection as measured by Ki-67 antigen. J Exp Med. 1998;187: 1295–1303. doi: 10.1084/jem.187.8.1295 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Fabian Cardozo E, Andrade A, Mellors JW, Kuritzkes DR, Perelson AS, Ribeiro RM. Treatment with integrase inhibitor suggests a new interpretation of HIV RNA decay curves that reveals a subset of cells with slow integration. PLoS Pathog. 2017;13: e1006478. doi: 10.1371/journal.ppat.1006478 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Hoffmann M, Pantazis N, Martin GE, Hickling S, Hurst J, Meyerowitz J, et al. Exhaustion of activated CD8 T cells predicts disease progression in primary HIV-1 infection. PLoS Pathog. 2016;12: e1005661. doi: 10.1371/journal.ppat.1005661 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Norris S, Coleman A, Kuri-Cervantes L, Bower M, Nelson M, Goodier MR. PD-1 expression on natural killer cells and CD8(+) T cells during chronic HIV-1 infection. Viral Immunol. 2012;25: 329–332. doi: 10.1089/vim.2011.0096 [DOI] [PubMed] [Google Scholar]
- 23.Schafer JL, Müller-Trutwin MC, Reeves RK. NK cell exhaustion: bad news for chronic disease? Oncotarget. 2015;6: 21797–21798. doi: 10.18632/oncotarget.5490 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wherry EJ, John Wherry E, Kurachi M. Molecular and cellular insights into T cell exhaustion. Nat Rev Immunol. 2015;15: 486–499. doi: 10.1038/nri3862 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Tjomsland V, Ellegård R, Burgener A, Mogk K, Che KF, Westmacott G, et al. Complement opsonization of HIV-1 results in a different intracellular processing pattern and enhanced MHC class I presentation by dendritic cells. Eur J Immunol. 2013;43: 1470–1483. doi: 10.1002/eji.201242935 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Yates JWT, Arundel PA. On the Volume of Distribution at Steady State and Its Relationship with Two-Compartmental Models. Journal of Pharmaceutical Sciences. 2008; 97; 111–122. doi: 10.1002/jps.21089 [DOI] [PubMed] [Google Scholar]
- 27.Vaidya NK, Rong L, Marconi VC, Kuritzkes DR, Deeks SG, Perelson AS. Treatment-mediated alterations in HIV fitness preserve CD4+ T cell counts but have minimal effects on viral load. PLoS Comput Biol. 2010;6: e1001012. doi: 10.1371/journal.pcbi.1001012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Conway JM, Perelson AS. Residual Viremia in Treated HIV+ Individuals. PLoS Comput Biol. 2016;12: e1004677. doi: 10.1371/journal.pcbi.1004677 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Elemans M, al Basatena N-KS, Asquith B. The efficiency of the human CD8+ T cell response: How should we quantify it, what determines it, and does it matter? PLoS Comput Biol. 2012;8: e1002381. doi: 10.1371/journal.pcbi.1002381 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Davenport MP, Ribeiro RM, Perelson AS. Kinetics of virus-specific CD8+ T cells and the control of human immunodeficiency virus infection. J Virol. 2004;78: 10096–10103. doi: 10.1128/JVI.78.18.10096-10103.2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Davenport MP, Zhang L, Bagchi A, Fridman A, Fu T-M, Schleif W, et al. High-potency human immunodeficiency virus vaccination leads to delayed and reduced CD8+ T-cell expansion but improved virus control. J Virol. 2005;79: 10059–10062. doi: 10.1128/JVI.79.15.10059-10062.2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Cao Y, Cartwright EK, Silvestri G, Perelson AS. CD8+ lymphocyte control of SIV infection during antiretroviral therapy. PLoS Pathog. 2018;14: e1007350. doi: 10.1371/journal.ppat.1007350 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Dinoso JB, Rabi SA, Blankson JN, Gama L, Mankowski JL, Siliciano RF, et al. A simian immunodeficiency virus-infected macaque model to study viral reservoirs that persist during highly active antiretroviral therapy. J Virol. 2009;83: 9247–9257. doi: 10.1128/JVI.00840-09 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Xie Y, Brand JE, Jann B. Estimating heterogeneous treatment effects with observational data. Sociol Methodol. 2012;42: 314–347. doi: 10.1177/0081175012452652 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Meeker WQ, Escobar LA. Teaching about Approximate Confidence Regions Based on Maximum Likelihood Estimation. The American Statistician. Feb1995;49: 48–53. [Google Scholar]
- 36.Johnson JB, Omland KS. Model selection in ecology and evolution. Trends Ecol Evol. 2004;19: 101–108. doi: 10.1016/j.tree.2003.10.013 [DOI] [PubMed] [Google Scholar]
- 37.Symonds MRE, Moussalli A. A brief guide to model selection, multimodel inference and model averaging in behavioural ecology using Akaike’s information criterion. Behavioral Ecology and Sociobiology. 2011. pp. 13–21. doi: 10.1007/s00265-010-1037-6 [DOI] [Google Scholar]
- 38.Smith AM, Adler FR, McAuley JL, Gutenkunst RN, Ribeiro RM, McCullers JA, et al. Effect of 1918 PB1-F2 expression on influenza A virus infection kinetics. PLoS Comput Biol. 2011;7: e1001081. doi: 10.1371/journal.pcbi.1001081 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Hadjichrysanthou C, Cauët E, Lawrence E, Vegvari C, de Wolf F, Anderson RM. Understanding the within-host dynamics of influenza A virus: from theory to clinical implications. J R Soc Interface. 2016;13. doi: 10.1098/rsif.2016.0289 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Minang JT, Trivett MT, Coren LV, Barsov EV, Piatak M, Ott DE, et al. Nef-mediated MHC class I down-regulation unmasks clonal differences in virus suppression by SIV-specific CD8 T cells independent of IFN-γ and CD107a responses. Virology. 2009. pp. 130–139. doi: 10.1016/j.virol.2009.06.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Basmaciogullari S, Pizzato M. The activity of Nef on HIV-1 infectivity. Frontiers in Microbiology. 2014. doi: 10.3389/fmicb.2014.00232 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Rosenberg ES, Altfeld M, Poon SH, Phillips MN, Wilkes BM, Eldridge RL, et al. Immune control of HIV-1 after early treatment of acute infection. Nature. 2000;407: 523. doi: 10.1038/35035103 [DOI] [PubMed] [Google Scholar]
- 43.Cartwright EK, Spicer L, Smith SA, Lee D, Fast R, Paganini S, et al. CD8(+) lymphocytes are required for maintaining viral suppression in SIV-infected macaques treated with short-term antiretroviral therapy. Immunity. 2016;45: 656–668. doi: 10.1016/j.immuni.2016.08.018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Caskey M, Klein F, Nussenzweig MC. Broadly neutralizing anti-HIV-1 monoclonal antibodies in the clinic. Nat Med. 2019;25: 547–553. doi: 10.1038/s41591-019-0412-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.DiLillo DJ, Ravetch JV. Differential Fc-receptor engagement drives an anti-tumor vaccinal effect. Cell. 2015. pp. 1035–1045. doi: 10.1016/j.cell.2015.04.016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Veazey RS. Gastrointestinal tract as a major site of CD4 T cell depletion and viral replication in SIV infection. Science. 1998;280: 427–431. doi: 10.1126/science.280.5362.427 [DOI] [PubMed] [Google Scholar]
- 47.Girard A, Jelicic K, Van Ryk D, Rochereau N, Cicala C, Arthos J, et al. Neutralizing and Targeting Properties of a New Set of α4β7-Specific Antibodies Are Influenced by Their Isotype. J Acquir Immune Defic Syndr. 2017;75: 118–127. doi: 10.1097/QAI.0000000000001307 [DOI] [PubMed] [Google Scholar]
- 48.Berg J. Replication challenges. Science. 2019;365: 957–957. doi: 10.1126/science.aaz2701 [DOI] [PubMed] [Google Scholar]
- 49.Iwamoto N, Mason R, Hu J, Ransier A, Welles H, Song K, et al. A high throughput lentivirus sieving assay identifies neutralization resistant Envelope sequences and predicts in vivo sieving. J Immunol Methods. 2019;464: 64–73. doi: 10.1016/j.jim.2018.10.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Rosshart SP, Herz J, Vassallo BG, Hunter A, Wall MK, Badger JH, et al. Laboratory mice born to wild mice have natural microbiota and model human immune responses. Science. 2019;365. doi: 10.1126/science.aaw4361 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Nishimura Y, Gautam R, Chun T-W, Sadjadpour R, Foulds KE, Shingai M, et al. Early antibody therapy can induce long-lasting immunity to SHIV. Nature. 2017;543: 559–563. doi: 10.1038/nature21435 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Desikan R, Raja R, Dixit NM. Modeling how early passive immunization with broadly neutralizing antibodies elicits lasting control of SHIV infection. bioRxiv. 2019. p. 548727. doi: 10.1101/548727 [DOI] [Google Scholar]
- 53.De Boer RJ, Perelson AS. Quantifying T lymphocyte turnover. J Theor Biol. 2013;327: 45–87. doi: 10.1016/j.jtbi.2012.12.025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Chen HY, Di Mascio M, Perelson AS, Ho DD, Zhang L. Determination of virus burst size in vivo using a single-cycle SIV in rhesus macaques. Proc Natl Acad Sci U S A. 2007;104: 19079–19084. doi: 10.1073/pnas.0707449104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Ramratnam B, Bonhoeffer S, Binley J, Hurley A, Zhang L, Mittler JE, et al. Rapid production and clearance of HIV-1 and hepatitis C virus assessed by large volume plasma apheresis. Lancet. 1999;354: 1782–1785. doi: 10.1016/S0140-6736(99)02035-8 [DOI] [PubMed] [Google Scholar]
- 56.De Boer RJ, Ribeiro RM, Perelson AS. Current estimates for HIV-1 production imply rapid viral clearance in lymphoid tissues. PLoS Comput Biol. 2010;6: e1000906. doi: 10.1371/journal.pcbi.1000906 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Fooden J. Comparative review of fascicularis-group species of macaques (primates: Macaca). Fieldiana. 2006; 1–43. [Google Scholar]
- 58.Haanstra KG, Hofman SO, Lopes Estêvão DM, Blezer ELA, Bauer J, Yang L-L, et al. Antagonizing the α4β1 integrin, but not α4β7, inhibits leukocytic infiltration of the central nervous system in rhesus monkey experimental autoimmune encephalomyelitis. J Immunol. 2013;190: 1961–1973. doi: 10.4049/jimmunol.1202490 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(DOCX)
(DOCX)
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
The intervals specify the range of the set of intervals to approximate the 95% confidence intervals (S1 and S3 Texts).
(PDF)
The intervals specify the range of the set of intervals to approximate the 95% confidence intervals (S1 and S3 Texts).
(PDF)
The intervals specify the range of the set of intervals to approximate the 95% confidence intervals (S1 and S3 Texts).
(PDF)
The intervals specify the range of the set of intervals to approximate 95% confidence intervals (S1 and S3 Texts).
(PDF)
The intervals specify the range of the set of intervals to approximate the 95% confidence intervals (S1 and S3 Texts).
(PDF)
The intervals specify the range of the set of intervals to approximate the 95% confidence intervals (S1 and S3 Texts).
(PDF)
The viral load set points predicted by the model using the best-fit parameter estimates and the mechanism with the greatest AIC weight from A) and B) with the baseline cell source model; C) and D) the model with a saturated source of effector cells; E) and F) a model where the source of effector cells is dependent on the concentration of antigen presenting cells. The maximum and minimum viral load equilibrium points predicted by the model (left column) and estimated by the predicted viral load at 81 weeks p.i. (right column). Parameters for these simulations are in Tables 1 and S14–S18, for the AIC selected mechanism (S5–S12 Tables). We do not consider the alternative mechanism of increased antigen presentation with increased viral clearance in this analysis.
(PDF)
The measured (≥50 SIV RNA copies/ml solid circles and <50 SIV RNA copies/ml open circles) and model predicted viral loads (solid line) using the best-fit parameter estimates and model variation with the greatest AIC weight for each of the treated macaques and predicted viral dynamics in the absence of the anti-α4β7antibody (dotted black line), panels A)–H). The limit of detection is 50 SIV RNA copies/ml (thin horizontal dashed black line). Treatment with cART occurred between five weeks and 18/19 weeks post-infection (gray area), while eight infusions of the anti-α4β7antibody occurred between nine weeks post-infection and 32 weeks post-infection (purple area). The mechanisms considered include increased viral clearance (red line), viral neutralization (orange line), target cell protection (green line), and increased antigen presentation (without increased viral clearance) (blue line). Parameters for these simulations are in Tables 1 and S14–S18 and S2 Text, for the AIC selected mechanism (S5–S12 Tables).
(PDF)
The measured (≥50 SIV RNA copies/ml solid circles and <50 SIV RNA copies/ml open circles) and model predicted viral loads (solid line) using the best-fit parameter estimates and model variation with the greatest AIC weight for each of the treated macaques and predicted viral dynamics in the absence of the anti-α4β7antibody (dotted black line), panels A)–H). The limit of detection is 50 SIV RNA copies/ml (thin horizontal dashed black line). Treatment with cART occurred between five weeks and 18/19 weeks post-infection (gray area), while eight infusions of the anti-α4β7antibody occurred between nine weeks post-infection and 32 weeks post-infection (purple area). The mechanisms considered include increased viral clearance (red line), viral neutralization (orange line), target cell protection (green line), and increased antigen presentation (without increased viral clearance) (blue line). Parameters for these simulations are in Tables 1and S14–S18 and S2 Text, for the AIC selected mechanism (S5–S12 Tables).
(PDF)
The measured (≥50 SIV RNA copies/ml solid circles and <50 SIV RNA copies/ml open circles) and model predicted viral loads for the AIC selected model (indicated after macaque) and three remaining models using the best-fit parameter estimates for the mechanisms of increased viral clearance (red line), viral neutralization (orange line), target cell protection (green line), and increased antigen presentation (without increased viral clearance) (blue line), panels A)–H). For each macaque, a scatter plot of the ΔAIC and the log-likelihood for each mechanism, panels A)–H). The limit of detection is 50 SIV RNA copies/ml (thin horizontal dashed black line). Treatment with cART occurred between five weeks and 18/19 weeks post-infection (gray area), while eight infusions of the anti-α4β7antibody occurred between nine weeks post-infection and 32 weeks post-infection (purple area). The mechanisms considered include parameters for these simulations are in Tables 1 and S14–S18 and S2 Text.
(PDF)
The measured (≥50 SIV RNA copies/ml solid circles and <50 SIV RNA copies/ml open circles) and model predicted viral loads for the AIC selected model (indicated after macaque) and three remaining models using the best-fit parameter estimates for the mechanisms of increased viral clearance (red line), viral neutralization (orange line), target cell protection (green line), and increased antigen presentation (without increased viral clearance) (blue line), panels A)–H). For each macaque, a scatter plot of the ΔAIC and the log-likelihood for each mechanism, panels A)–H). The limit of detection is 50 SIV RNA copies/ml (thin horizontal dashed black line). Treatment with cART occurred between five weeks and 18/19 weeks post-infection (gray area), while eight infusions of the anti-α4β7antibody occurred between nine weeks post-infection and 32 weeks post-infection (purple area). The mechanisms considered include Parameters for these simulations are in Tables 1and S14–S18 and S2 Text.
(PDF)
The observed (black dots) and model predicted viral load dynamics (solid line) using the best-fit parameter estimates for A)–G) each of the macaques. Parameters for these simulations are in Tables 1 and S19.
(PDF)
The observed (black dots) and model predicted viral load dynamics (solid line) using the best-fit parameter estimates for A)–G) each of the macaques. Parameters for these simulations are in Tables 1and S19 and S2 Text.
(PDF)
The observed (black dots) and model predicted viral load dynamics (solid line) using the best-fit estimates for A)–G) each of the macaques. Parameters for these simulations are in Tables 1 and S19.
(PDF)
The correlation between the best parameter estimates for the half-saturation constant for effector cell proliferation for the AIC selected mechanism of the baseline model for each treated macaque and the area under the predicted log10 viral load curve for the 30 weeks following A) the removal of cART and B) the last infusion of the anti-α4β7antibody.
(PDF)
The model predicted viral load (solid line) using the best-fit parameter estimates and the baseline source model for the treated macaques A) RSd14, B) ROv14, C) RLn12, and D) RFa15 using the baseline half-maximal concentration, EC50, (black), 100-fold higher EC50 (red), and 1000-fold higher EC50 (blue). The limit of detection is 50 SIV RNA copies/ml (thin dashed black line, left panels). E) The area under the log10 predicted viral load curve for the 30 weeks after cART was stopped for the treated macaques RSd14 (black), ROv14 (red), RLn12 (blue), and RFa15 (purple). Treatment with cART occurred between five weeks and 18/19 weeks post-infection (gray area). Parameters for these simulations are in Tables 1 and S16.
(PDF)
The average model predicted viral load (left panels) and the per day effector cell killing rate (right panels) using the best-fit parameter estimates under the baseline source model with the greatest AIC weight for each of the treated macaques (solid line). The sensitivity of the viral load and per day effector cell killing rate with respect to changing A)−B) the effectiveness of cART from 90% (black) to 99%(red) and 75% (blue); C)−D) the fraction of infections resulting in latency from 10−5 (black) to 10−6 (red) and 10−4 (blue); E)−F) the activation rate of latent cells from 10−3 (black) to 2 ×10−3 (red) and 5×10−3 (blue). The limit of detection is 50 SIV RNA copies/ml (thin dashed black line, left panels) and the minimum infected cell death rate is the death rate due to viral cytopathic effects (thin dashed line, right panels). Treatment with cART occurred between five weeks and 18/19 weeks post-infection (gray area). The average was calculated using the geometric mean for the seven IgG control macaques. Parameters for these simulations are in Tables 1 and S19.
(PDF)
The model predicted viral loads for SIV nef-competent virus with anti-α4β7antibody therapy (black) and without anti-α4β7antibody therapy (red) using the best-fit parameter estimates and model variation with the greatest AIC weight for each of the treated macaques, panels A)–H). The limit of detection is 50 SIV RNA copies/ml (thin dashed black line). Treatment with cART occurred between five weeks and 18/19 weeks post-infection (gray area), while eight infusions of the anti-α4β7antibody occurred between nine weeks post-infection and 32 weeks post-infection (purple area). Parameters for these simulations are in Tables 1 and S14–S18, for the AIC selected model (Table 2). The effector cell killing rate (m) and the saturation constant for effector cell proliferation was adjusted for each treated macaque for the nef-competent virus (S13 Fig).
(PDF)
The proportion of macaques whose viral load rebounded after the removal of cART (color gradient) for various reductions in the effector cell killing rate (m) and increases in the half-saturation constant for effector cell proliferation (KB). Parameters for these simulations are in Tables 1 and S14–S18, for the AIC selected model (Table 2). Viral rebound was characterized by the model viral load not dropping below 50 RNA copies/ml any time after week 40 post-infection and had a viral load that exceeded 10,000 RNA copies/ml at week 81-post infection.
(PDF)
Data Availability Statement
All relevant data are within the manuscript and its Supporting Information files.