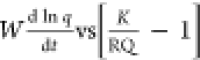Langmuir Adsorption Kinetics in Liquid Media: Interface Reaction Model

Abstract

Adsorption kinetic equation has been derived assuming that the process follows the behavior of a heterogeneous chemical reaction at the solid–liquid interface. This equation is converted into the Langmuir isotherm at equilibrium and describes well the unsteady-state adsorption process. Based on that, a working equation has been developed, which gives adsorption-rate-constant independent of operating parameters including concentration. Also, a kinetic model expressed as a sum of first- and second-order systems available in the literature has been applied (modified with the interface reaction concept) to determine the adsorption rate constant. Both methods gave similar results. Three dimensionless numbers have been developed to determine and distinguish pseudo-first-order and pseudo-second-order kinetics justified from the viewpoint of chemical kinetics. It is shown that curve-fitting with a high correlation coefficient could validate an empirical kinetic model, but the fitted model parameters could not automatically be related to chemical kinetic parameters if the model itself is not grounded on well-defined chemical kinetics. Finally, it is concluded that the currently applied empirical approach could not provide reliable data for comparison among similar systems, while the Langmuir kinetic equation developed based on the concept of heterogeneous reaction would be a good basis for standardization of the method for adsorption system characterization.

1. Introduction

Rapid industrialization has led to the production of a devastating amount of wastewater. Adsorption process seems to be an effective method to manage this problem. In the last few decades, an enormous number of papers have been published on wastewater treatment by adsorption process using locally available, naturally abundant, and practically noncommercial products (with a few exceptions for commercial activated carbon) such as tea-waste,^1,2 leaves,^3,4 agricultural residues,^5,6 biomasses,⁷⁻¹⁰ waste minerals,^11,12 etc. The task of these works consists mainly of the search for suitable adsorbents characterized by equilibrium and kinetic parameters. Most of the adsorption systems dealing with wastewater treatment follow the well-known Langmuir adsorption equilibrium model, but for studying the adsorption kinetics, the authors use some pseudo-first-order (PFO) or pseudo-second-order (PSO) empirical models, and the fitted values (pseudo-rate constants) appear to be dependent on operating parameters (initial concentration, adsorbent amount, W, and solution volume V) and they are not correlated to the Langmuir parameters at all. We must recognize that for conducting an adsorption process in an optimal regime, the adsorption rate constants (like those of a chemical reaction) must be known to be independent of operating parameters, and the equilibrium equation must be a special case of the kinetic equation. This is the element to which the decade-long research on developing an adsorbent system for wastewater treatment, with a few exceptions,¹³⁻²⁹ has not been paid the deserved attention.

Islam et al.¹³ developed an adsorption kinetic model based on the Langmuir adsorption concept, in which for a given adsorption dosage, w_a = W/V, three parameters, namely, maximum adsorption density (adsorption capacity) (q_∞) and concentration-independent adsorption and desorption rate constants (k_a and k_d), completely described both adsorption kinetics and equilibrium simultaneously.

The research group of Azizian^14−17,19 is the most active one in the experimental work equipped with a theoretical interpretation of adsorption data. In ref (14), the author concluded that the system followed PFO kinetics for high initial adsorbate concentration and PSO kinetics for low initial adsorbate concentration and sufficiently small reaction times. In ref (15), they concluded that the correlation coefficient could not be the only criterion to distinguish between the PFO and the PSO kinetics. In ref (16), the author introduced a two-site PSO adsorption model for the heterogeneous surface. In ref (17), the authors developed further a geometric approach initially proposed by Kuan et al.¹⁸ to determine the adsorption rate constant and also proposed a mixed Langmuir–Freundlich model, for which the reaction became of n-th order with respect to the active site. In ref (19), the authors applied extended geometric methods and claimed to have obtained a concentration-independent adsorption constant. But still the adsorption and desorption rate constants remained adsorption dosage-dependent.

Extensive theoretical works on adsorption kinetics have been reported by a research team in refs (20−24). In ref (20), they propose a general kinetic equation based on the statistical rate theory (SRT), which is transformed into the PFO and PSO kinetic equations for surface-reaction-controlled adsorption processes. In ref (21), they conclude that the PFO and PSO equations are simple approximations of different theoretical approaches. In ref (22), they show that the PSO kinetic equation describes the process efficiently close to equilibrium. In ref (23), they proposed a two-resistance model for sorption kinetics controlled simultaneously by intraparticle diffusion and surface reaction. In ref (24), they express the PSO constant as a function of the initial sorbate concentration, the progress of the sorption process, and the solid/solution ratio.

Liu and Shen²⁵ made excellent rearrangement of the adsorption kinetic equation as a sum of the first- and second-order kinetic components. The rate constants corresponding to the PFO and PSO components (k_H1 and k_H2) were dependent on operating parameters.

Marczewski²⁶ proposed a new integrated kinetic Langmuir (IKL) equation to describe the general kinetic behavior of the adsorption process. In a further work, the author made vigorous and complicated mathematical treatment to determine pure PSO kinetics.²⁷

Salvestrini²⁸ developed a method for the determination of the concentration-independent adsorption rate constant, k_a, but that method required highly complicated estimations. Also, the adsorption constant, k_a, is again dependent on operating parameters, as the starting equation does not take into proper account the solid–liquid-phase mass balance (interface reaction). Guo and Wang²⁹ chose a mixed-order model to describe Langmuir adsorption kinetics and solved the equation with a 4–5-order Runge–Kutta method using a MatLab program.

As mentioned above, the models describing adsorption kinetics in aqueous media are becoming more and more complicated. In refs (13, 19, 28), it has already been established that by applying the conventional Langmuir kinetic model, one could estimate concentration-independent adsorption constants. Search for some correlation between pseudo-rate constants and adsorption rate constants might merely satisfy scientific curiosity. Discussion on pseudo-order kinetics, however, is necessary to convince research teams active in the field to abandon the empirical approach in treating adsorption kinetic data. Moreover, the PFO and PSO kinetics are distinguished based on some data and methods of treatment, which have been disputed by Canzano et al.³⁰ and Simonin.³¹ Since the last four decades, a huge number of adsorbent–adsorbate systems have been studied, but since the pseudo-rate constants are operating-parameter-dependent, there is no scope of comparing the adsorption kinetics. To design and operate a plant in an optimal regime, the rate constants should be available as independent of operating parameters. The formulations described in refs (13, 19, 28) give concentration-independent adsorption constants, but they are dependent on the adsorption amount, W, and solution volume, V. This would mean that different researchers would obtain the same concentration-independent value of rate constants for themselves, but these values would differ from one another, as they would design the batch experiments independently with different W and V. Thus, for a given adsorption system, different researchers would report different concentration-independent rate constants.

The method of determination of adsorption constants might be standardized by fixing the adsorbent dosage, but such fixation might not be optimum for different adsorbents as they might show largely varying adsorption capacities. To avoid such disadvantages, the Langmuir adsorption kinetics may be described as an interface reaction. With the interface reaction model, the adsorption rate constant will appear independent of operating parameters. The prime task of this study is to develop a simple methodology for determining the adsorption rate constant, k_a, which, together with the Langmuir equilibrium parameters—namely, (i) maximum adsorption capacity conventionally denoted q_∞ (kg adsorbate/kg adsorbent) and (ii) Langmuir equilibrium constant, K (m³/kg)—will characterize the equilibrium as well as the kinetic state of an adsorption system. A set of these three parameters would serve as a basis for comparing the adsorption efficiencies of different adsorbent–adsorbate systems.

The secondary task of the work is (i) to derive a working equation to determine the “rate constants of the first- and the second-order components” of the “hybrid-order” kinetic equation and to relate them to the Langmuir constants in terms of operating parameters, and (ii) finally, to find well-defined conditions under which Langmuir kinetics is reduced to “true” PFO and PSO kinetics. Dimensionless numbers will be defined to determine the conditions under which the adsorption processes could be described by the true pseudo-first-order and pseudo-second-order kinetics justified from the viewpoint of chemical kinetics. The secondary task is undertaken only to establish the findings of the prime task as the simplest and most reliable method for characterizing adsorbate–adsorbent systems. The theoretical ground and the procedure for determining the rate constants defined through the mentioned kinetic models have been discussed in detail and illustrated through the same data available in the literature.

2. Theoretical

2.1. Langmuir Model for Equilibrium Adsorption and Independent Empirical Model for Kinetics: Empirical Approach (EA)

This is the approach that has been applied indiscriminately in the literature, where the kinetic model is separately treated from the equilibrium one. To distinguish it from the others, this approach will be called the “Empirical Approach (EA)” henceforth.

2.1.1. Langmuir Adsorption Equilibrium Model

The Langmuir model adapted to the liquid system is represented by the following relation

1

where q_e is the adsorption density at equilibrium (kg adsorbate A/kg adsorbent), q_∞ is the adsorption capacity of the adsorbent or the maximum achievable adsorption density (kg adsorbate A/kg adsorbent), C_A,e is the equilibrium adsorbate concentration in the liquid phase (kg/m³), and K is the Langmuir equilibrium constant (m³/kg). Equation 1 can be linearized as follows

2

A C_A,e/q_e vs C_A,e plot will give the Langmuir parameters, q_∞ and K. In fact, the determination of these two equilibrium parameters is a mandatory step in the analysis of Langmuir adsorption kinetics for all three approaches to be discussed in the following section.

2.1.2. Kinetic Model of EA

In EA, the kinetic models are expressed as PFO³² and PSO³³ equations in terms of (q_e – q), where q is the adsorption density at any time, t. The PFO equation is expressed as follows

3

where k_E1 (s^–1) is the apparent adsorption rate constant for the PFO adsorption process (as per EA).

Integrating eq 3 for t = 0, q = 0, one obtains

4

If a −ln(1 – q/q_e) vs t plot gives a straight line, the value of k_E1 is determined from the slope. In fact, with q vs t data available at hand, the derivative of q could be estimated graphically or numerically and eq 3 itself could be applied to determine k_E1 on a dq/dt vs (q_e – q) plot. This option, however, is not practiced. Since the correlation coefficient for linear fit is the only criterion for the assertion of the pseudo-rate order, the change in the reference frame for linear fit might also be used to diffuse any confusion distinguishing pseudo-rate orders. In this study, both options will be applied.

The PSO adsorption kinetics³³ is represented by the following relation

5

where k_E2 (s^–1) is the apparent rate constant for a PSO adsorption process as per EA.

Integrating eq 5 for t = 0, q = 0 and rearranging, one derives

6

Equation 6 is the most popular form of the integrated adsorption kinetic equation for determining the rate constant of PSO adsorption kinetics. If a t/q vs t plot gives a straight line, the value of k_E2 is determined from the intercept of the plot. Similar to the PFO kinetics, the value of k_E2 could also be determined from a dq/dt vs (q_e – q)² plot described by eq 5.

The q vs t curves are of saturation type. The adsorption density q gradually increases with a continuously decreasing slope until it attains an ultimate value, q_e, depending on the initial concentration, adsorbent mass, and solution volume. Such curves can be described empirically as follows

7

and/or

8

Equations 7 and 8 are standard empirical equations for describing saturation-type curves. The PFO kinetic equation (eq 3) and its linearized form (eq 4) are virtually the differential and the linearized form, respectively, of eq 7 with a = k_E1. Moreover, the PSO kinetic equation (eq 5) and its linearized form (eq 6) are virtually the same for eq 8 with b = k_E2q_e (for details, see Appendix A in the Supporting Information SI). Both a and b (and consequently, k_E1 and k_E2) depend on the initial concentration (and also on operating parameters).

Although both eqs 7 and 8 generally describe the saturation curves well, in many adsorption kinetic experiments, saturation is reached within a short time, and there are very few data recorded in the steep-rising zone and the other data are available only in the near-equilibrium zone.³⁴⁻³⁶ It might be expected that eq 7 (which corresponds to eq 3) containing an exponential term would describe the adsorption curves reaching the equilibrium with a very steep slope comparatively better. The reverse picture, however, is observed in reality. All such curves are undisputedly fitted to eq 6, which is derived from eq 8, and the kinetics is recognized as PSO. Canzano et al.,³⁰ however, have excellently demonstrated that the fit of the near-equilibrium data to eq 6 is a straight line irrespective of the sorption kinetics. Simonin³¹ also concludes that the inclusion of several data points from the near-equilibrium zone might lead to an erroneous decision that the adsorption kinetics follows the PSO model. For a good adsorbent, the equilibrium is reached very quickly and data points far from equilibrium are rare, and more data points are taken from near-equilibrium. Despite the conclusive finding of Canzano et al.³⁰ and Simonin³¹ that near-equilibrium data have to be avoided in determining the order of kinetics, most of the authors still have been concluding about kinetics based on such data. Also, there are cases when both PFO and PSO models describe the adsorption kinetic data equally well, but again with curve-fittings with a higher coefficient of correlation, usually, it is concluded to be PSO kinetics. In this study, both the differential and integral forms of the pseudo-order kinetic equation will be tested for cross-checking. In chemical kinetics, there must be some well-defined demarcation line between the PFO and PSO reaction kinetics. Discussion on such a demarcation line will be discussed later in Section 2.4.

2.2. Adsorption–Desorption as a Physicochemical Interface Reaction: Interface Reaction Approach (IRA)

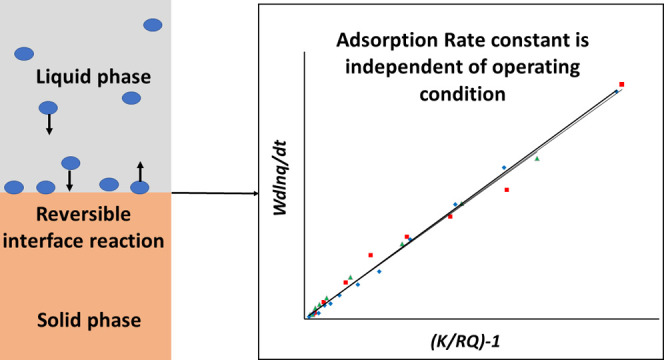
The subject matter of this subsection is related to the prime task of this work, i.e., to work out a simple method to characterize the adsorption–adsorbate system. For this purpose, a theoretical model will be developed considering the adsorption process as a physicochemical interaction at the solid–liquid interface following the laws of chemical kinetics, and this approach will be termed the “Interface Reaction Approach (IRA)” in this work.

In a batch adsorption process, a preweighed amount of adsorbent, W (kg), is added to an adsorbate solution of volume V and initial concentration C_A,0. The system is kept under vigorous stirring to keep the adsorbate concentration, C_A, uniform throughout the liquid phase. At some predetermined time intervals, samples are collected from the vessel/reactor to control the remaining adsorbate in the liquid phase.

Assuming that there is no diffusion layer, and the interface represents a sharp boundary between the solid and liquid phases (i.e., the process is adsorption kinetics-limited), the adsorption kinetics is represented by a reversible interface reaction of the type

9

where k_a (m³/s) and k_d (kg/s) are the adsorption and desorption rate constants, respectively, the suffixes (l) and (s) denote the liquid and solid phases, respectively, and S represents the active site or “a collection of sites” capable of hosting a single molecule of the adsorbate. It should be mentioned that the Langmuir model was initially proposed to describe adsorption in the gas–solid system with an assumption of a 1:1 ratio for the adsorbate molecules and the active sites. When the model is adapted to the solid–liquid system, due to the large size of the adsorbate, S might not represent a single site but rather a collection of sites performing the same function as a single site does in the gas–liquid system.

In the differential form, the mass-balance equation concerning the adsorbate mass in the whole solid–liquid system is as follows

10

Referring to the physicochemical interaction at the solid–liquid interface in eq 9, the sorption–desorption kinetics can be described as follows

11

or

12

where C_A (kg/m³) and C_AS (kg/kg) are the adsorbate concentrations at time t in the liquid and solid phases, respectively, and C_S represents the unoccupied site concentration in the solid phase and is expressed as the amount of adsorbate (kg) that could still be accommodated in 1 kg of adsorbent. Although the adsorption takes place at the solid surface, the concentration in the solid phase is expressed in terms of the mass of the adsorbent (assuming that the surface area is proportional to the mass of the adsorbent). It is worth mentioning that the form of writing kinetics of a chemical reaction by multiplying the rate of change in concentration by weight or volume (as done in eqs 11 or 12) is not much common in the analysis of chemical kinetics. However, this is the key to finding operating-condition-independent adsorption rate constants, which have been so desired by all researchers in the field of intensive adsorption kinetics studies since the last four decades. Interface reaction is the rate of transfer of a species from one phase to another.³⁷ The first term on the right-hand side of eqs 11 or 12 is the rate of transfer of species A (kg/s) from the liquid to the solid phase, and the second term is the rate for the reverse course. This exchange of mass is manifested in the change of concentration of the species in both phases simultaneously. On the left-hand side of eq 11, dC_AS/dt represents the rate of change of concentration (kg/kg) of species A in the solid phase, while in eq 12, dC_A/dt represents the rate of change of concentration (kg/m³) of species A in the liquid phase. Therefore, multiplying the rate of change of adsorbate concentration in the solid phase (i.e., the rate of adsorption) by W on the left-hand side of eq 11 or multiplying the rate of change of adsorbate concentration in the liquid phase by V on the left-hand side of eq 12 is mandatory to define the adsorption and desorption constants independent of operating parameters, and this makes eqs 11 and 12 different from all other formulations available in the literature studying adsorption kinetics in waste treatment. In an adsorption experiment, the rate of change in adsorbate concentration is not monitored on the adsorbent surface but rather in the liquid volume. Therefore, one can also apply eq 12 for analysis and will get the same values for the rate constants.

Using conventional symbols used in the adsorption process, C_AS ≡ q and C_s ≡ q_∞ – q, eq 11 takes the form

13

At equilibrium, C_A = C_A,e, q = q_e, and dq/dt = 0, and after some algebraic manipulations, eq 13 is converted into the Langmuir isotherm equation (eq 1) with k_a/k_d = K, and eq 13 itself is the corresponding Langmuir adsorption kinetic equation.

2.2.1. Derivation of the Working Equation for Studying Adsorption Kinetics in IRA

Integrating the mass-balance equation (eq 10) for the adsorbate in the solid–liquid system, one has

14

where w_a is the adsorption dosage (kg/m³) and C_A,0 is the initial concentration of the adsorbate in the liquid phase.

Equation 14 is substituted in eq 13, and then the adsorption kinetic equation takes the following form

15

Equation 15 can now be integrated for q analytically by a conventional method, and fitting the experimental data to the solution equation and knowing that K = k_a/k_d, one can determine the values of k_a and k_d. For details, the readers are referred to ref (10). To make a better analogy with eqs 3 or 5, eq 15 is rearranged as follows

16

or

17

where RQ is called the “reaction quotient.” The linearity of the 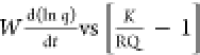plot will validate the Langmuir kinetic model, and from the slope of the line, one will get k_d (and subsequently, k_a). In fact, with the application of the equilibrium relation in eq 1 and the working equation of adsorption kinetics (eq 17), the three basic Langmuir parameters, namely, q_∞, K, and k_a, will be known, and the adsorbent–adsorbate system is well-characterized.

2.3. Adsorption Kinetic Equation in the Hybrid-Order Approach (HOA)

The subject matter of this subsection is related to the secondary task of this work. For this purpose, the adsorption kinetics described by eq 13 will be presented as a sum of the first-and second-order reaction components, and a methodology will be developed to determine the adsorption rate constant. This approach of data analysis will be termed “HOA” in this work, and then, the results from IRA will be compared with those obtained by EA and HOA.

2.3.1. Derivation of the Kinetic Equation as a Sum of the First- and Second-Order Reaction Components

Rewriting eq 15 for the equilibrium condition, one obtains

18

Equation 18 is a quadratic one, and solving it for q_e, two probable expressions are obtained (eq 19 with a ± sign).

19

with

20

From the two expressions for q_e in eq 19, that one is accepted for which it has got physical significance. Thus, for a given batch adsorption system, with the known Langmuir parameters, K, and adsorption capacity, q_∞, the equilibrium adsorption density, q_e, can be predicted by eq 19 for a given adsorbent mass, initial adsorbate concentration, and liquid volume. Both the signs (positive and negative) in eq 19 give a positive value for q_e (which are justified as a mathematical solution), but with a positive sign, it will give an unacceptable value in the physical sense (e.g., higher than q_∞ or some other irrational value like that corresponding to the adsorbed amount higher than the total adsorbate amount in the system). Only the negative sign will give a value that is acceptable in the physical sense. Thus, the acceptable option of eq 19 is eq 21.

21

Combining eqs 15, 18, and 21, we have

22

with

23–25

The derivation of eq 22 along with the expressions for k_H1 and k_H2 is available in refs (25, 29). As in this work, the adsorption process is viewed as a solid–liquid interface reaction (eq 9) and the adsorption kinetics is described in conformity with changes of the adsorbate concentration in the liquid and solid phases (eqs 11 and 12); for ease of the readers, the derivation of the equation and the modified expressions for k_H1 and k_H2 with the correction for material balance in the solid–liquid system are given in details in Appendix B (Supporting Information).

As seen in eq 23, the “so-called rate constants” k_H1 and k_H2, respectively, for the first- and second-order components of the reaction kinetics are related to the adsorption rate constants of the Langmuir kinetic model and also depend on the operating parameters. Thus, these rate constants could be considered as technological rate constants for the adsorbate–adsorbent system valid for given initial concentrations and operating parameters (adsorbent amount W and liquid volume V). Equation 22, however, could be used as an indirect method for estimating the adsorption rate constant, k_a. It can be noted that the ratio k_H1/k_H2 in eq 23 does not depend on the adsorption rate constant but rather depends on Δ (i.e., on the equilibrium and the operating parameters of the process) (eq 20).

2.3.2. Determination of the Technological Rate Constant, k_H1

Equation 22 can be rearranged as follows

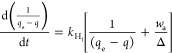26

A d(1/(q_e – q))/dt vs 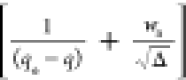plot will give the value of k_H1. Finally, the value of k_a will be estimated following the relation expressed by eq 23.

2.4. PFO or PSO Kinetics in IRA

In subsection 2.1, we have already introduced the PFO (eq 3) and PSO (eq 5) kinetic models as per the empirical approach (EA), in which the pseudo-rate constants are not correlated to the rate constants that define the equilibrium process. The chemical kinetics of a complex process could reduce to some pseudo-first-order or pseudo-second-order kinetics under some special operating conditions, but in such cases, the rate constants preserve their significance as those in the complex processes, i.e., the pseudo-rate constants remain closely related to the rate constant of the precursor complex processes. Tien and Ramarao³⁸ and Zhang³⁹ have discussed in detail the conditions under which the Langmuir kinetic equation is reduced to PFO and PSO order models and shown the errors made in this approximation. In the following subsection, we shall find out the conditions under which the adsorption kinetic equation (eq 15) will be converted into pseudo-first-order and pseudo-second-order equations from the viewpoint of interface reaction kinetics.

2.4.1. Condition 1 for PFO Kinetics in IRA

Combining eqs 15 and 18, and making some algebraic manipulation, one obtains

27

As q increases from 0 to q_e, the term w_aq/C_A,0 assumes the value from 0 to N₁ = w_aq_e/C_A,0, and now if N₁ is much less than unity, eq 27 is approximated to

28

with

29

where k_I,a is the rate constant of true PFO adsorption kinetics in IRA under the condition N₁ = w_aq_e/C_A,0 ≪ 1, and this PFO rate constant (unlike k_E1 in the empirical approach, EA) is well-correlated with k_a through eq 29. Practically, k_E1 is averaged over the whole range of θ (=q/q_e) from 0 to 1 to satisfy an empirical relation representing a saturation curve. Note that two different symbols (k_I and k_E with additional subscripts a, 1, etc.) have been used in this work to denote pseudo-rate constants. This has been done deliberately to differentiate the pseudo-order reactions from the viewpoints of IRA and EA. Under the condition of N₁ ≪1, k_E1 in EA coincides with k_I,a in IRA.

2.4.1.1. Physical Significance of the Dimensionless Number, N₁

As defined, N₁ is equal to w_aq_e/C_A,0 = (Wq_e)/(VC_A,0). Thus, N₁ is the ratio between the amount (kg) of adsorbate in the solid phase at equilibrium and that in the liquid phase dissolved initially (which is virtually the total amount of adsorbate in the whole system). In other words, at equilibrium, it is the part of the adsorbate in the solid phase in a solid–liquid system. Under a given operating condition (W, V, C_A,0), N₁ assumes a constant value independent of the degree of completion, θ (=q/q_e), of the adsorption process.

2.4.2. Condition 2 for PFO Kinetics in IRA

Again combining eqs 15 and 18, we have

30

As q increases from 0 to q_e, the term q/q_∞ assumes the value from 0 to N₂ = q_e/q_∞, and now if N₂ is much less than unity, eq 30 is approximated to

31

with

32

where k_I,b is also the rate constant of PFO adsorption kinetics in IRA under the condition N₂ = q_e/q_∞ ≪ 1. Under this condition, k_E1 in EA coincides with k_I,b in IRA.

2.4.2.1. Physical Significance of the Dimensionless Number N₂

As defined, N₂ is equal to q_e/q_∞. Thus, it is the ratio between the amount of adsorption at equilibrium and the adsorption capacity of the adsorbent. In terms of active sites, it is the degree of occupation of active sites at equilibrium. Under a given operating condition (W, V, C_A,0), N₂ assumes a constant value independent of the degree of completion, θ, of the adsorption process.

2.4.3. Reaction-Order-Determining Common Dimensionless Number in IRA

Equation 15 can also be rewritten as follows

33

with

34, 35

Comparing eq 34 with eq 21, we have

36, 37

Substituting eq 36 into eq 33 and after some simple algebraic manipulation, we have

38

Let us define a reaction-order-determining dimensionless number, N_OD, such that

39

The value of N_OD will depend on N_OD,0 and a factor f_θ. For a change of θ from 0 to 0.9 (keeping a 10% margin to reach q_e), the factor f_θ varies from 1 to 10.

2.4.3.1. Physical Significance of the Dimensionless Number, N_OD

The value of N_OD depends on two factors: N_OD,0 and f_θ. The dimensionless number, N_OD,0, is defined in eq 39, and combining eqs 39, 21, and 1, it can be expressed as follows

40

The derivation of eq 40 is given in details in Appendix C in the Supporting Information. As seen in eq 40, N_OD,0 is a complex function of the dimensionless numbers, N₁ and N₂, and under a given operating condition (W, V, C_A,0), N_OD,0 will also assume a constant value independent of the degree of completion, θ, of the adsorption process. N_OD, however, depends on the factor, f_θ, as well, which varies with θ. In terms of the dimensionless number, N_OD, one can rewrite eq 38 as follows

41

If N_OD ≫ 1 in the θ-range of (0, 0.9), eq 41 is approximated to eq 42

42

where k_Ic is also a rate constant of PFO adsorption kinetics in IRA. For N_OD ≫ 1, k_I,c in IRA coincides with k_H1 in HOA and also with k_E1 in EA.

If N_OD ≪ 1 in the θ-range of (0, 0.9), then eq 41 is approximated to eq 43

43

where k_II is the rate constant of PSO adsorption kinetics in IRA under the condition N_OD ≪ 1 for θ in the range of (0, 0.9). For N_OD ≪ 1, k_II in IRA coincides with k_H2 in HOA and also with k_E2 in EA.

Thus, the three dimensionless numbers will determine under what conditions the adsorption reaction will follow true PFO or PSO kinetics (justified from the viewpoint of chemical kinetics), and the adsorption rate constant could be estimated from the pseudo- rate constants in EA.

2.4.4. Pseudo-Rate Constants of EA in the Light of the Dimensionless Number NOD

As discussed in the preceding three subsections, the PFO and PSO adsorption processes are well-defined in the IRA and are characterized by the corresponding rate constants (k_Ia, k_Ib, or k_Ic for PFO, and k_II for PSO), and these pseudo-rate constants have a well-defined correlation with k_a. Then, the question arises as to what do the PFO and PSO adsorption kinetics in EA with the corresponding rate constants, k_E1 and k_E2, stand for? What information could one get from these rate constants?

Since the 1980s, enormous numbers of papers have been published in scientific journals on adsorption in aqueous media, in which adsorption kinetics have been treated as PFO or PSO (as per EA). In subsection 2.1, it has been mentioned that the saturation-type experimental curves could almost always be described with some approximation with eqs 7 or 8, and the PFO (eq 3) and PSO (eq 5) equations in EA are derived from these equations.

The three dimensionless numbers, N₁, N₂, and N_OD, can determine under what conditions an adsorption kinetic equation can be transformed into the PFO or the PSO equation. If such conditions are not met, the adsorption rate constant has to be determined from the general equation (eq 17). In EA, there is no buffer zone, and the kinetic data must satisfy either the PFO or PSO model. Thus, the corresponding rate constants, k_E1 and k_E2, could be related to k_a only when the PFO or PSO is justified by chemical kinetics (in terms of the dimensionless numbers). Beyond that, there is no theoretical ground to correlate k_E1 and k_E2 to k_a.

The adsorption kinetic data could be fitted to PFO kinetics (eq 4) for N₁ ≪ 1, N₂ ≪ 1, or N_OD ≫ 1, and the fitted value of k_E1 could be equated to k_I,a, k_I,c, or k_I,c (whatever applies), respectively, and k_a can be evaluated. Compromising with the condition, N₁ ≪ 1, N₂ ≪ 1, or N_OD ≫ 1, will result in a k_a value with more and more uncertainty. For N_OD ≪ 1, the adsorption kinetic data could be fitted to PSO kinetics (eq 6), and the fitted value of k_E2 could be evaluated, and finally, by equating k_E2 to k_II, k_a can be evaluated.

The choice of a maximum value as “much less than unity” or a minimum value as “much higher than unity” determines the preciseness of the analysis. The value of N_OD depends on the factor f_θ, which increases from 0 to 10 for an increase in θ from 0 to 0.9 (eq 39). That will mean, if N_OD,0 = 8 (for example), the value of N_OD will increase from 8 to 80 in the θ-range of 0–0.9. Also, if N_OD,0 = 0.02, the value of N_OD will increase from 0.02 to 0.2 for the same θ-range. Avoiding any discussion on experimental errors in kinetic data acquisition, for the present analysis, we accept that for N₁ < 0.2, N₂ < 0.2, or N_OD,0 > 8, the process will follow PFO kinetics, and for N_OD,0 < 0.02, the process will follow PSO kinetics.

3. Results and Discussion

3.1. Validation of the Model Generated from IRA and HOA

Before stepping up into the application of any form of adsorption kinetics model, it must be remembered that the acquisition of data for equilibrium analysis (eq 1) is much easier and more precise than that of the data for kinetics analysis. This is because the samples for equilibrium data could be collected and analyzed at the end of the experiment after an undetermined period of time to ensure that equilibrium has been reached. This is not the case with the collection of adsorption kinetics data. Distinguishable q vs t data is collected easily for slow adsorption processes when the sampling time interval is much smaller than the time for reaching the equilibrium. Each sample undergoes centrifuging for some time (2–3 min) to separate the adsorbent particles from the sample solution (during that time the adsorption continues, but not counted) before being analyzed with a UV spectrometer. Thus, from sampling to analysis, it always requires some time, and the sampling is necessary at some reasonable time interval to acquire well-distinguishable data points.

When the adsorption process is very fast, it may not be possible to collect an adequate number of well-distinguishable q vs t data points. In that case, the analysis has to be done with very few numbers of data points. The data points near equilibrium may be appealing for some theoretical analyses,⁴⁰ but those experienced in the experimental work on adsorption must admit that near equilibrium, the data are sometimes a bit fluctuating, the increment rate is very low, and sometimes confusion may arise about whether or not the changes are within the experimental error. Such data are not much suitable for precise kinetic studies. Canzano et al.³⁰ and Simonin³¹ have made a thorough analysis of the consequence of the inclusion of data near equilibrium and concluded that such inclusion may lead to a confusing conclusion about the order of adsorption kinetics. The data near equilibrium are acquired for a long period of time only to ascertain the value of equilibrium adsorption, and not to follow the kinetics. Consequently, the treatment of equilibrium data with eq 1 is more precise than that of the kinetics ones.

3.2. Illustration of IRA and HOA with Literature Data and the Determination of k_a

Four absorbent–adsorbate systems (each designated by a number from 1 to 4, and each system is subdivided into groups “a–c” based on the variation in operating conditions) under investigation have been presented in Table 1 along with their equilibrium parameters. The data have been collected from the plots of the source materials using the software WebPlotDigitizer and retreated to verify the preciseness of the collection. As seen in Table 1, the equilibrium values reported in the source and those determined in this work are satisfactory in the same range.

Table 1. Absorbent–Adsorbate Systems under Investigation along with the Langmuir Equilibrium Parameters.

designation	adsorption system	W × 104 (kg)	V × 104 (m3)	CA,0 (kg/m3)	T (K)	q∞ (q∞)	K (m3/kg) (K)	source
system 1a	aGAC-MV	0.8	0.5	0.001	298.15	0.095 (0.093)	380.76 (378.5)	(19)
system 1b				0.002
system 1c				0.003
system 2a	aCA-B_AC composite beads-MB	2	2	0.20	303.15	0.756 (0.755)	21.5 (21.0)	(41)
system 2b				0.30
system 2c				0.50
system 3a	Durian shell-MB	6	1	0.20	303.15	0.289 (0.283)	19.7 (21.2)	(42)
system 3b				0.25
system 3c				0.30
system 4a	Cadmium II-C. vulgaris	0.75	1	0.10	303.15	0.091 (0.089)	22 (21.4)	(43)
system 4b					313.15	0.083 (0.085)	15 (14.1)
system 4c					323.15	0.077 (0.077)	9.5 (9.3)

^aAbbreviations: GAC, granular activated carbon; MV, methyl violet; CA_B_AC, calcium alginate–bentonite–activated carbon; MB, methylene blue. In parentheses are the values re-estimated in the present work.

3.3. Determination of k_a as per IRA and HOA

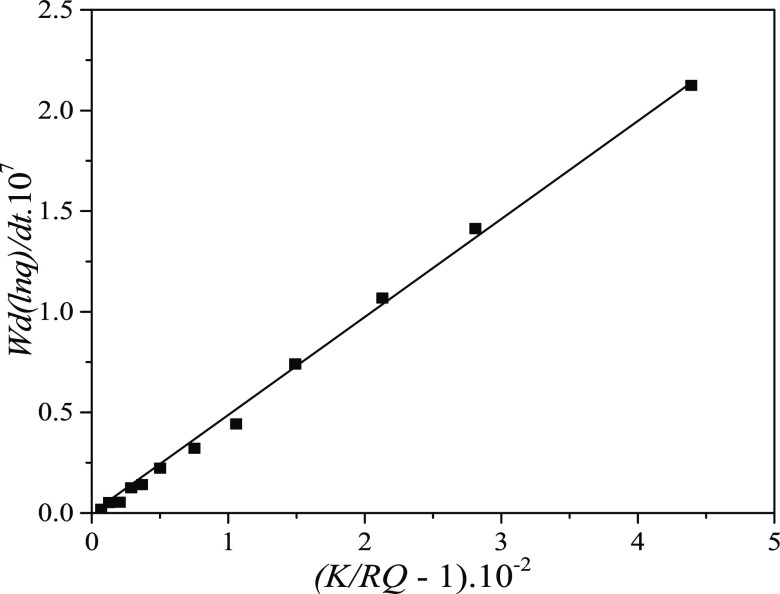
The adsorption kinetic data of all four systems in Table 1 have been fitted to eq 17 as per IRA and to eq 26 as per HOA to determine the adsorption/desorption rate constants, k_d and k_a (from the relation K = k_a/k_d). Figures 1 and 2 present the W(d ln q/dt) vs (K/RQ – 1) and the d(1/(q_e – q))/dt vs 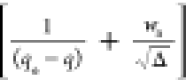plots with kinetic data of the system 1c. For the economy of spaces, similar plots for some representative systems have been presented in Appendix D (Supporting Information). The results from the curve-fittings for the validation of IRA and HOA are presented in Table 2.

Figure 1.

IRA validation (eq 17): plot for the system 1c.

Figure 2.

HOA validation (eq 26): d(1/(q_e – q))/dt vs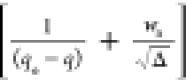 plot for the system 1c.

Table 2. Adsorption and Desorption Rate Constants, k_a and k_d, of the Adsorption Systems Determined by IRA and HOA.

		parameters as per IRA		parameters as per HOA
adsorption system	characteristic change in operating condition	ka × 109 (m3/s)	kd × 109 (kg/s)	kH1 × 105 (s–1)	ka × 109 (m3/s)	kd × 109 (kg/s)
system 1a	CA,0 = 0.001 kg/m3	182	0.48	35.1	183	0.48
system 1b	CA,0 = 0.002 kg/m3	181	0.48	35.6	187	0.49
system 1c	CA,0 = 0.003 kg/m3	185	0.49	35.0	184	0.48
system 2a	CA,0 = 0.20 kg/m3	18.4	0.86	6.37	20.1	0.94
system 2b	CA,0 = 0.30 kg/m3	16.6	0.77	4.58	16.5	0.77
system 2c	CA,0 = 0.50 kg/m3	15.4	0.71	3.63	16.9	0.79
system 3a	CA,0 = 0.20 kg/m3	5.97	0.30	1.57	5.90	0.30
system 3b	CA,0 = 0.25 kg/m3	5.93	0.30	1.58	6.11	0.31
system 3c	CA,0 = 0.30 kg/m3	6.21	0.31	1.61	6.42	0.33
system 4a	T = 303.15 K	334	15.2	70.3	389	17.7
system 4b	T = 313.15 K	390	26.0	79.7	360	24.2
system 4c	T = 323.15 K	440	46.3	104	363	38.3

As seen in Table 2, the adsorption and desorption rate constants, k_a and k_d, of a given system determined by the two approaches, IRA and HOA (corrected with material balance), are satisfactorily close to each other. Obtaining of the close values for k_a and k_d is quite expected as both approaches have their origin in the interface reaction kinetic equation (eq 13). The working equation in IRA (eq 17) is formed directly from eq 13, while that in HOA (eq 26) is formed from eq 22, which was derived again from eq 13.

The adsorption rate constants of system 1 (determined at three different initial concentrations but at a constant temperature) are close to one another and could be averaged as (1.83 ± 0.06) × 10^–07 m³/s and (4.8 ± 0.2) × 10^–10 kg/s, respectively, in IRA and (1.85 ± 0.05) × 10^–07 and (4.9 ± 0.2) × 10^–10 kg/s, respectively, in HOA. Similar is the case with systems 2 and 3, the k_a values of which could be averaged to consider them as concentration-independent parameters. “The rate constant of a chemical reaction does not depend on concentration” is described even in textbooks of physical chemistry.⁴⁴ As the adsorption process is viewed as a physicochemical interaction and its kinetics is described by the law of chemical kinetics, the adsorption (also desorption) rate constant must be concentration-independent, and it has become such within data treatment (also acquisition) error. The rate constant determined in this method could be a basis for comparison with other similar systems

With an increase in temperature, both the adsorption and desorption rate constants increase simultaneously (see k_a and k_d values for system 4 in columns 3 and 4, Table 2), but the equilibrium constant K gradually decreases (see column 8, Table 1). Obviously, the increment rate of the desorption process is higher than that of the adsorption process, and the whole adsorption process is an exothermic one.

Figure 3a,b presents the temperature dependence, respectively, of the adsorption constant, k_a (m³/s), and the equilibrium constant K (recalculated into the SI unit, m³/mol) of system 4. The data are fitted to eqs 44 and 45, respectively.⁴⁴

44, 45

where k_a,0 is a constant for the system, R (kJ/(mol K)) is the universal gas constant, E_A (kJ/mol) is the energy of activation, ΔH (kJ/mol) is the enthalpy, and ΔS (kJ/(mol K)) is the entropy of the process.

Figure 3.

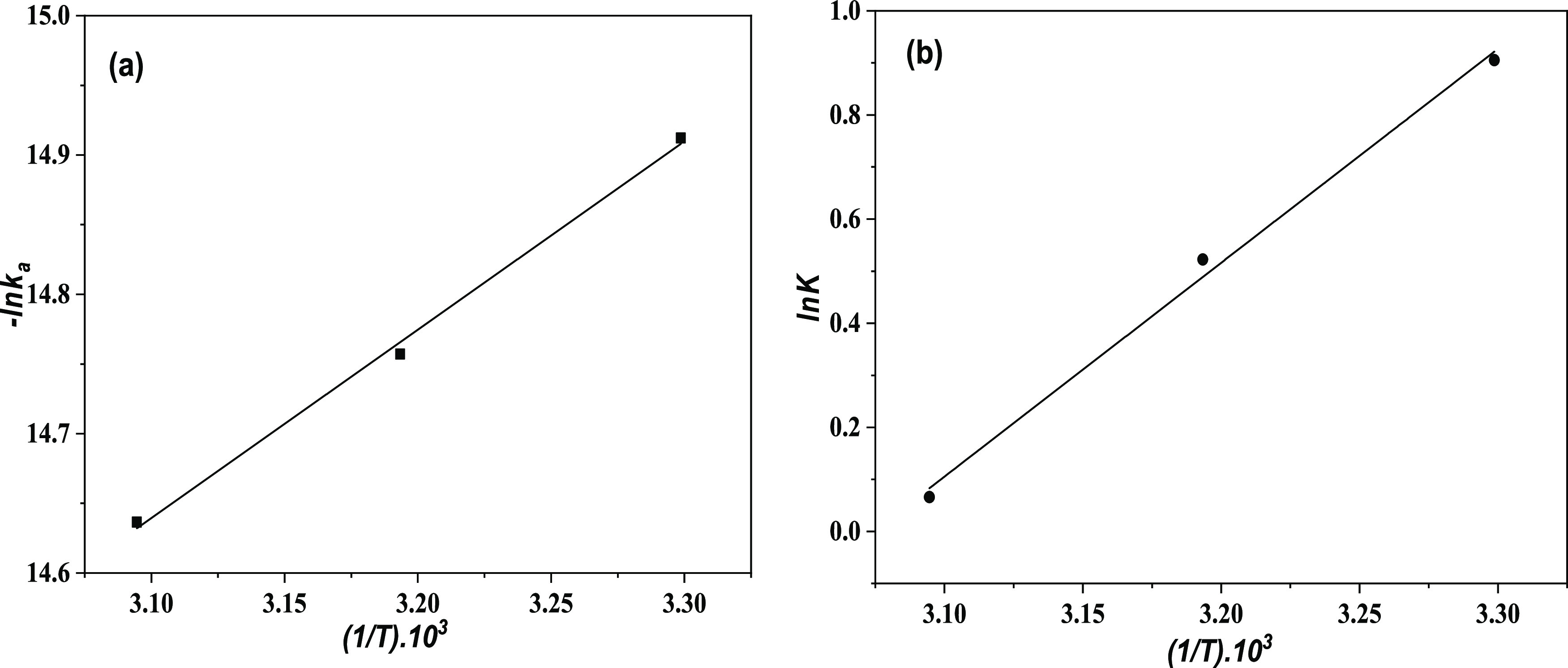
Temperature dependence of (a) k_a (m³/s) and (b) K (in m³/mol).

From the slope and intercept of the lines in Figure 3a,b, the energy parameters are estimated as follows: E_A = 11.2 kJ/mol, ΔH = −34.2 kJ/mol, and ΔS = −105.0 kJ/(mol K). The evaluated parameters confirm that the process is exothermic and takes place with a decrease in entropy. However, in the temperature range of 303–323 K, the change in Gibb’s energy, ΔG, is negative and the process is spontaneous.

3.4. Validation of PFO and PSO Kinetics in EA

For the validation of the PFO and PSO models in EA, four plots, namely, (i) dq/dt vs (q_e – q) (eq 3) and (ii) −ln(1 – q/q_e) vs t (eq 4) for the PFO, and (iii) dq/dt vs (q_e – q)² (eq 5) and (iv) t/q vs t (eq 6) for the PSO kinetics, have been drawn for each of the systems. The fitted values of k_E1 and k_E2 from these plots along with the correlation coefficients of the fittings are presented in Table S1 (Supporting Information). The same for −ln(1– q/q_e) vs t (eq 4) and t/q vs t (eq 6) reported in the source materials have also been inserted in Table S1 for comparison.

As seen in Table S1 (Supporting Information), for some subsystems, the difference in the estimated k_E1 and k_E2 values between the source and the present work is a bit high, indicating that the collection of kinetic data from the plots of the source material might not always be precise enough (the collection of equilibrium data was more precise). However, as an illustrative material, it does not have much impact on the analysis as the analysis is performed based on the values retreated in this work. From the data treatment in this work, it is found that in PFO kinetics, the fitted value of k_E1 and also the correlation coefficient for model validation do not differ much for a change in the form of the model equation from eq 4 to eq 3 (see the R² values for all subsystems in columns 3 and 4 in Table S1). This, however, could not be said for PSO, in which the correlation coefficient for model validation shows substantial changes for a change in the form of the model equation from eq 6 to eq 5. With poor curve-fitting, the fitted value of k_E2 is also not much reliable (see the R² values for subsystems 2a–c, 3a–c, and 4b,c in columns 6 and 7 in Table S1). Thus, the application of cross-checking especially for PSO kinetics with eq 5 against eq 6 is quite justified. Cross-checking gives the opportunity to decide with more confidence whether a system is empirically more inclined to PFO or PSO kinetics. There are systems that satisfy both PFO and PSO kinetic models with good correlation coefficients (e.g., see correlation coefficients for systems 1c, 3a, and 4a). Such cases in IRA are quite absurd, as in a chemical reaction, the transformation of a complex kinetic equation into both the PFO and PSO forms simultaneously is mutually excluding. On the contrary, in EA, it is quite acceptable that a kinetic equation may be described in some cases by both the PFO and PSO models satisfactorily because a saturation-type curve could be described by both eqs 7 and 8 simultaneously. Satisfactory curve-fitting to an empirical equation, however, is not adequate to help determine the adsorption rate constants. For this purpose, the requirements to dimensionless numbers for defining PFO or PSO kinetics have to be satisfied.

3.5. Reliability of Application of Pseudo-Rate Constants, k_E1 and k_E2, in EA for the Estimation of Adsorption Rate Constants k_a

As proposed in subsection 2.4.4, for practical purposes, we shall accept that for N₁ < 0.2, N₂ < 0.2, or N_OD,0 > 8 (theoretically, N₁ ≪1, N₂ ≪ 1, or N_OD ≫ 1) the process will follow PFO kinetics, and for N_OD,0 < 0.02 (correspondingly, N_OD,max < 0.2, and theoretically, N_OD ≪ 1), the process will follow PSO kinetics. Such a compromise with the limiting values of the dimensionless numbers N₁, N₂, and N_OD will bring some uncertainty in the estimated value of k_a. The higher the compromise we make, the higher will be the uncertainty in the k_a value.

Table 3 presents the dimensionless numbers N₁ (column 3), N₂ (column 5), and N_OD,0 (column 7) for all systems (column 1) under investigation along with the k_a value determined by IRA (column 2) for comparison. Whether the condition N₁ < 0.2, N₂ < 0.2, or N_OD,0 > 8 is maintained or not, the corresponding k_a values for PFO kinetics have been estimated by eq 29 (with k_I,a = k_E1), eq 32 (with k_I,b = k_E1), or eq 42 (with k_I,c = k_E1), whatever applies, and put in columns 4, 6, and 8, respectively. The values of k_E1 and k_E2 are determined from dq/dt vs (q_e – q) (eq 3) and dq/dt vs (q_e – q)² (eq 5) plots, respectively, which were used in estimating the k_a values. The systems under discussion were all of PFO type (although in source articles some of them were recognized as PSO type). Thus, whether the condition N_OD,0 < 0.02 is maintained or not, the k_a value has been estimated with eq 43 (with k_II = k_E2) and put in column 9. The k_a values estimated by maintaining the conditions imposed on the dimensionless numbers are underlined.

Table 3. k_a-Values Estimated from k_E1 and k_E2 in EA, with or without Fulfillment of the Requirements to Dimensionless Numbers as Indicators for PFO or PSO Kinetics^a.

		PFO kinetics: N1 < 0.2		PFO kinetics: N2 < 0.2		PFO kinetics: NOD,0 > 8 PSO kinetics: NOD,0 < 0.02
system no.	ka × 109 from IRA	N1	ka × 109	N2	ka × 109	NOD,0	*ka,1 × 109	**ka,2 × 109
1a	182	0.96	8460	0.01	203	146.5	205	37 450
1b	181	0.98	6630	0.01	199	76.9	202	22 200
1c	185	0.94	5407	0.01	195	54.8	198	14 900
2a	18.4	0.93	58.3	0.25	18.0	3.4	22.8	43.2
2b	16.6	0.95	31.9	0.38	13.8	1.9	20.0	68.8
2c	15.4	0.87	20.5	0.58	14.0	0.98	26.2	43.2
3a	5.97	0.97	42.35	0.11	5.95	8.25	6.65	71.8
3b	5.93	0.97	34.7	0.14	5.85	6.4	6.73	56.7
3c	6.21	0.97	31.3	0.17	6.15	5.2	7.29	48.9
4a	334	0.37	375	0.55	481	3.6	403	2270
4b	390	0.32	441	0.51	569	5.2	442	4690
4c	440	0.23	515	0.41	649	8.9	493	9210

^a*k_a,1 and **k_a,2 values were calculated from k_E1 and k_E2, respectively.

As we see in Table 3, no system satisfies the condition N₁ < 0.2, and consequently, k_a could not be predicted for any system from k_E1 under this criterion. The subsystems 1a–c and 3a–c satisfy the condition N₂ < 0.2 and hence follows condition 2 for PFO kinetics in IRA. Consequently, the k_a values estimated for the systems (column 5) from k_E1 values agree satisfactorily with the corresponding ones in column 2 determined by IRA.

Again, subsystems 1a–c, 3a, and 4c satisfy the condition N_OD,0 > 8 and hence follow condition 3 for PFO kinetics in IRA. Consequently, k_a values estimated for the systems (column 8) from k_E1 values agree satisfactorily with the corresponding ones in column 2 determined by IRA. No subsystem satisfies the condition for PSO kinetics in IRA, and the k_a value estimated for the systems (column 9) from k_E2 values is abnormally high and not acceptable.

It is interesting to observe that although most of the subsystems do not satisfy condition N_OD,0 > 8, still the k_a values estimated for the systems (column 8) from k_E1 values are well within the acceptable range of the corresponding k_a values in column 2 determined by IRA. It should be remembered that N_OD depends on θ, and if N_OD,0 = 3.5 (for example), N_OD varies from 3.5 to 35 for a change in θ from 0 to 0.9 with N_OD = 7 for θ = 0.5. Thus, if EA is applied for kinetic data in the θ-range of 0.5–0.9, the requirements to N_OD for PFO kinetics will be fulfilled. However, it will be a very exhaustive job to sort out the kinetic data from a suitable θ-range, while a simple but chemical kinetics-justified method has been worked out in IRA for determining k_a.

From the exhaustive analysis and discussion, it has become quite clear that the EA applied by researchers will give k_a values if the pseudo-rate constants are correlated with k_a within a defined range of the dimensionless number, N_OD. The question arises, does it deserve to treat the adsorption kinetic data with EA at all, while through proper scrutiny, it might be found that most of the previously accepted PSO kinetics are wrongly recognized. With the inclusion of the interface reaction concept, the adsorption rate constant has become concentration- as well as operating-parameter-independent, and thus, although tested only for four adsorption systems, the IRA appears to be very perspective for the characterization of adsorbents operating in liquid media. In developing the present model, no diffusion layer is considered and the system is considered surface-reaction-controlled. It is curious to verify to what extent the model could describe systems with micro- and mesoporous adsorbents and how the IRA could supplement the intraparticle diffusion model. Now, it is high time to standardize the characterization method of the adsorbent–adsorbate system in an aqueous medium. The characterization should be such that one system could be comparable to a similar one in terms of equilibrium and kinetic parameters. The empirical approach as it has been implemented in practice could not serve the comparison purpose. Both IRA and HOA (with correction of material balance, eq 10) could serve the purpose for surface-reaction-controlled processes, but the IRA is a comparatively straightforward method for determining k_a, while HOA is an indirect method passing through the determination of the technological rate constants. Further research on adsorbent materials with different porosities would definitely lead to the standardization of characterization methods for adsorbent–adsorbate systems.

4. Conclusions

• (1)Both the interface reaction kinetics and the hybrid-order approaches considering mass balance in the solid–liquid system give reliable operating-parameter-independent adsorption rate constants. The first approach provides a straightforward way to obtain that, while the second, although justified from the viewpoint of chemical kinetics, follows a somewhat tortuous path to achieve the goal.
• (2)The empirical approach, which was widely practiced in the last few decades, in the form of a pseudo-first-order or pseudo-second-order kinetic model, does not provide significant information and could not be correlated to the adsorption rate constant reliably.
• (3)Three dimensionless numbers have been proposed to identify whether the adsorption kinetics could be described by the pseudo-first-order and the pseudo-second-order models. Applying one of these numbers, namely, the “order-determining dimensionless number,” it is established that none of the four systems under investigation followed pseudo-second-order kinetics, while in the source literature, three of them were recognized as such.
• (4)A standardized method of characterizing the kinetic behavior of adsorption systems is the demand of the time when effective adsorbents are expected to be in operation for wastewater treatment. For this purpose, systematic intensive studies are recommended on various adsorbent–adsorbate systems and to find conditions to correlate IRA and the intraparticle diffusion model.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.1c01449.

• Conversion of standard equations for saturation type curves into PFO and PSO kinetic equations; derivation of the kinetic equation (eq 22) in HOA; derivation of the expression for the dimensionless number, N_OD,0 (eq 40); validation of IRA and HOA for systems 2c, 3a, and 4a; validation of PFO and PSO kinetics in EA for systems 2c, 3a, and 4a; and table with data for pseudo-rate constants obtained from linear fit to eqs 3–6 (PDF)

Author Contributions

This manuscript was written through contributions from all authors. All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.