Abstract
We present improvements to the hydropathy scale (HPS) coarse‐grained (CG) model for simulating sequence‐specific behavior of intrinsically disordered proteins (IDPs), including their liquid–liquid phase separation (LLPS). The previous model based on an atomistic hydropathy scale by Kapcha and Rossky (KR scale) is not able to capture some well‐known LLPS trends such as reduced phase separation propensity upon mutations (R‐to‐K and Y‐to‐F). Here, we propose to use the Urry hydropathy scale instead, which was derived from the inverse temperature transitions in a model polypeptide with guest residues X. We introduce two free parameters to shift (Δ) and scale (µ) the overall interaction strengths for the new model (HPS‐Urry) and use the experimental radius of gyration for a diverse group of IDPs to find their optimal values. Interestingly, many possible (Δ, µ) combinations can be used for typical IDPs, but the phase behavior of a low‐complexity (LC) sequence FUS is only well described by one of these models, which highlights the need for a careful validation strategy based on multiple proteins. The CG HPS‐Urry model should enable accurate simulations of protein LLPS and provide a microscopically detailed view of molecular interactions.
Keywords: coarse‐grained model, hydropathy scales, liquid‐liquid phase separation, molecular simulation, physics‐based model
1. INTRODUCTION
Liquid–liquid phase separation (LLPS) of intrinsically disordered proteins (IDPs) has been shown to be the fundamental mechanism driving the formation of membraneless organelles in the cell, which are crucial for organizing and maintaining spatiotemporal balances of protein concentrations. 1 , 2 , 3 , 4 , 5 Recent experimental 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 and computational studies 15 , 16 , 17 , 18 , 19 , 20 , 21 have indicated that nonspecific interactions between amino acids driven by their hydrophobic, aromatic, or electrostatic character play the leading role in driving the protein LLPS. To study how these various interactions come into play for a specific IDP sequence one must conduct extensive experimental studies and use computational methods for gaining an in‐depth understanding of the phase separation mechanism at the molecular level. 9 , 11 , 22 All‐atom simulations can provide detailed information on molecular interactions 16 , 23 but cannot be used currently to study the LLPS of IDPs.
Coarse‐grained (CG) modeling techniques have been quite successful in assisting and leading studies on drivers of phase separation and assembly of IDPs previously. 8 , 17 , 19 , 20 , 21 , 24 , 25 , 26 , 27 , 28 , 29 The CG simulations can be conducted with off 21 , 30 , 31 , 32 , 33 or on lattice 19 models with varying resolutions 33 , 34 and the interactions between the CG amino acids can be informed by physics‐ or knowledge‐based potentials. 35 We have previously proposed a one bead per amino acid CG model 30 using the Kapcha‐Rossky (KR) hydropathy scale 36 referred to as the HPS‐KR model hereafter which has been successfully used in numerous previous studies of IDP LLPS. 8 , 9 , 17 , 26 , 27 , 28 , 37 , 38 Specifically, the transferable HPS‐KR model has been used to study the phase separation of several IDP sequences like the intrinsically disordered region (IDR) of DEAD‐box helicase LAF‐1 protein also referred to as LAF‐1 RGG, 9 the low complexity (LC) domain of the Fused in Sarcoma (FUS) protein 8 , 28 , 38 , 39 , 40 and disordered C‐terminal domain (CTD) of the TAR DNA binding protein (TDP‐43). 26 We also recently extended the HPS‐KR model to capture thermoresponsive LLPS behavior of IDPs, 31 the role of post‐translational modifications in perturbing LLPS, 37 and the multicomponent LLPS of IDP and polynucleotide mixtures 17 ; the simulations results were in very good agreement with the experimental observations. 39 , 41 , 42
Although the HPS‐KR model (in tandem with experimental studies) has advanced our understanding of the sequence‐dependent LLPS of IDPs, several potential shortcomings in the model have also been identified. 43 , 44 For example, the radius of gyration (Rg) of many IDPs in this model is significantly different from their values estimated from experimental observables. 43 Also, this model is not able to account for qualitative differences in LLPS when mutating Arg and Tyr residues to Lys and Phe, respectively. 6 , 7 , 9 , 45 It was proposed that the nonbonded interactions parameters in the HPS‐KR model can be refined using a combination of maximum entropy optimization and least‐squares regression to better capture experimental Rg values. 43 Recently, Das et al. 44 also proposed another parameter refinement strategy focusing on modifying interaction strengths of certain residue pairs based on the expected behavior from experimental studies and guided by bioinformatics‐based potentials such as the Kim‐Hummer (KH) model which uses the statistical contact potential derived by Miyazawa and Jernigan (hereafter referred to as MJ). 46
In this paper, we use a different model refinement strategy to address the aforementioned issues, while preserving the transferability of our CG framework by avoiding overfitting of parameters based on limited experimental data. To accomplish this, we replace the hydropathy scale used to inform nonbonded interactions between the CG beads from KR to the Urry scale. 47 As the Urry scale was derived based on the LLPS of elastin‐like model polypeptides, we believe it is more appropriate for parameterizing a CG model to study protein phase separation. We also use a modified approach to tune the free parameters of the CG model to obtain an excellent match between the simulated and experimental Rg values for 42 IDPs covering an extensive range of sequence properties. Furthermore, the new model termed as HPS‐Urry can provide near‐quantitative prediction of coexistence densities for well‐studied IDP sequences, FUS LC and DDX4 at room temperature.
2. RESULTS AND DISCUSSION
2.1. Comparison between the KR and Urry hydropathy scales
There are over 100 hydropathy scales of 20 naturally occurring amino acids reported in the literature. 48 Although straightforward, it is time and resource consuming to examine all the hydropathy scales for building an IDP CG model. Instead, in this study, we focus only on two hydropathy scales, namely the KR scale, 36 which was used in the previous models, 17 , 30 , 37 and the scale proposed by Urry et al. 47 (hereafter denoted as the Urry scale). We also compared the ability of these hydropathy scales to estimate single‐chain IDP properties with the 210 parameters MJ statistical contact potential used in the KH model we used previously to capture IDP phase behavior. The KR hydropathy scale is an atomistic scale that assigns each atom as hydrophilic or hydrophobic depending on their partial charges based on an all‐atom forcefield and it has one advantage over other scales since it is straightforward to account for nonnatural amino acids or amino acids modified via post‐translational modifications. The HPS model with the KR scale has also been applied to study the effects of posttranslational modifications on IDP phase behavior. 37 On the other hand, the Urry hydropathy scale is based on the inverse transition temperature of a polypeptide (VPGXG)n with n = 11, where X stands for the guest residue to be evaluated. This polypeptide was derived from the repeat elastin‐like sequence VPGVG (where the second valine residue is replaced by a guest residue) that undergo the lower critical solution temperature (LCST) transition in which the proteins transition from water‐soluble state to self‐assembled state upon increasing the temperature. The inverse transition temperature is defined as the temperature at which the polypeptide undergoes the LCST transition. This temperature depends on the hydrophobicity of constituent amino acid residues, and thus is well correlated to the hydrophobicity of the guest residue X.
Figure 1 presents the KR and Urry hydropathy scales rescaled from zero for the least hydrophobic residue to unity for the most hydrophobic residue. The biggest difference between the two scales occurs for Arg where it is the least hydrophobic (0) in the KR scale but is in the middle (0.56) for the Urry scale. It has been pointed out that the KR scale enhances the LLPS of IDPs upon replacing Arg by Lys (R2K mutation) in contrast to experimental observations. 44 This is due to the increase in the interaction strength for the modified IDPs since the hydropathy scale of Lys (0.51) is larger than that of Arg. In fact, this short‐coming of the KR scale has led us to examine the Urry scale, since it can be expected that the Urry scale would predict the weakening of the LLPS for such modified IDPs in agreement with experiments as the hydropathy scale of Lys (0.38) is smaller than that of Arg. Other residues that exhibit significant differences (Table S2) between the two scales are Glu (0.46 for KR vs. 0 for Urry), Pro (1.0 for KR vs. 0.76 for Urry), Leu (0.97 for KR vs. 0.72 for Urry), and Ile (0.97 for KR vs. 0.71 for Urry).
FIGURE 1.
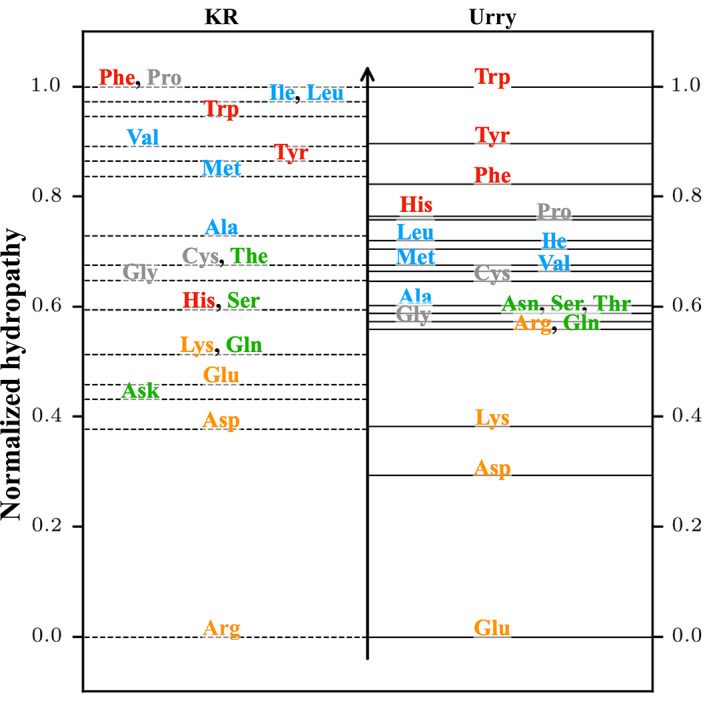
The normalized (0 to 1) Kapcha‐Rossky (KR) and Urry hydropathy scales used in the HPS CG modeling framework for IDPs. Aromatic residues (Trp, Tyr, Phe, and His) are colored red, Hydrophobic residues (Leu, Ile, Met, Val, and Ala) are colored blue, Polar residues (Asn, Ser, Thr, and Gln) are colored green, other residues (Pro, Cys, and Gly) are colored gray and charged residues (Arg, Lys, Asp, and Gln) are colored yellow
2.2. Optimization of interaction parameters
The LJ interaction model contains two free parameters, μ and Δ, that account for the strength of non‐electrostatic contributions and the affinity between amino acids relative to that of solvent, respectively. To obtain the optimal values for these parameters, we first determine the optimal Δ value for a given μ by simulating R g values for 42 IDP sequences (compared with 12 sequences previously used 30 ) listed in Table S1. The scoring function to be minimized is given by the standard chi‐square function
| (1) |
where and are experimental and simulated R g values for an ith IDP sequence. Figures 2a and S1 show the behavior of χ 2 for the Urry scale as a function of the offset parameter Δ for four different μ values. For a given μ, χ 2 exhibits a minimum close to 0.02, which suggests that the simulated R g values deviate overall less than ~14% from the experimental R g values at this parameter value. Interestingly, the minimum χ 2 values are almost independent of the scale parameter μ, remaining close to 0.02 for 0.5 ≤ μ ≤ 2. For the KR hydropathy scale and MJ contact potentials, similar trends are observed with minimum χ 2 between 0.015 and 0.02. The set of optimal (μ, Δ) values, at which χ 2 is minimum, is then obtained by fitting the scoring function via polynomial curve and is shown in Figure 2b. For all three scales considered (KR, Urry, and MJ), the optimal μ and Δ exhibit a linear relationship given by
| (2) |
where a Urry = 0.58, a KR = 0.69, and a MJ = 0.39, while b = − 0.5 independent of scales used.
FIGURE 2.
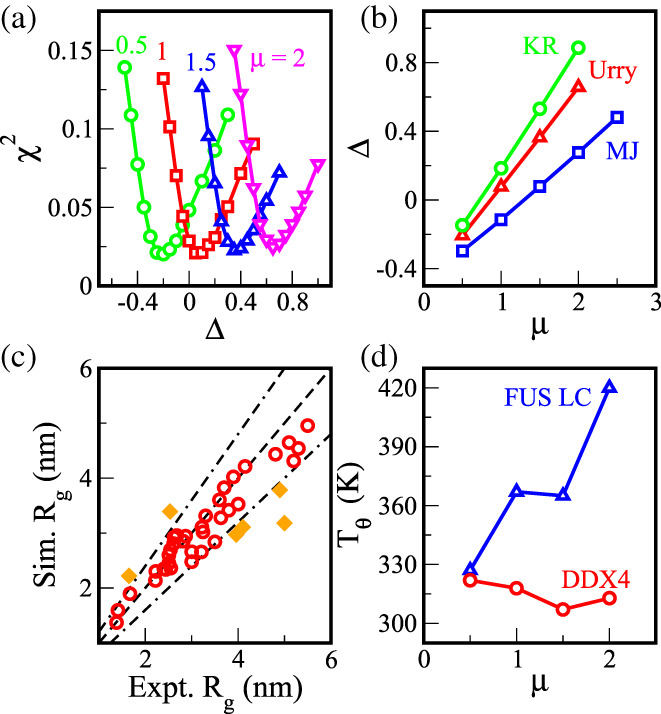
(a) Fits to chi‐square values (χ2) from comparison of experimental and simulated Rg data on 42 IDP sequences on a range of shift (Δ) for a selected scale (μ) allows for locating the offset providing minimum chi square value. (b) Scale and offset for optimum chi‐square change linearly with respect to each other for Urry, Kapcha Rossky (KR), and Miyazawa Jernigan (MJ) interaction parameters. (c) Scatter plot of experimental and simulated Rg for 42 IDPs using an optimal model, Black (dot‐dash) lines represent 20% deviation in Rg. (scale (μ) = 1.0, offset (Δ) = 0.08) (d) T θ versus scale (μ) for FUS LC and DDX4 sequences shows a scenario where unique sequences might show drastic changes in behavior between different optimal models (μ, Δ)
Figure 2c shows the comparison between simulated and experimental R g values for an optimal parameter set of μ = 1.0 and Δ = 0.08 for the Urry scale. The model shows excellent agreement between simulated and experimental R g values for many IDP sequences. For most sequences the simulated R g values lie within 20% of the experimental values (dot‐dashed lines). The largest discrepancy occurs for an16 (5.0 nm for experiment vs. 3.2 nm for simulation), where the model predicts more compact structures compared with the experimental observation. For protein‐L and hcyp, the trend is opposite where the simulated R g values are about 35% higher than the experimental values (Figure S2). Comparing the amino acid compositions of these IDP sequences with the entire set, we do not observe any significant differences that could explain these discrepancies (Figure S3). However, in the absence of explicit backbone potentials, such as pseudo‐angle potential between three neighboring beads and pseudo‐dihedral angle potential between four neighboring beads, as well as considering possible differences in simulation and experimental conditions, the Urry scale captures the configurations of many IDP sequences very well. The KR and MJ scales after appropriate optimization based on Equation (8) also give the R gvalues with similar accuracy to the experimental values (data not shown).
2.3. Effects of interaction parameters on IDP single‐chain properties
The optimal set of parameters μ and Δ shows high degeneracy in the (μ, Δ) parameter space where the scoring function, χ 2, has minima of similar magnitude along a “critical” line. In order to narrow the range of the parameters for the model, we investigate the effects of the parameters along the critical line on the phase behavior of two IDPs, DDX4 IDR 49 and FUS LC proteins. 6 , 8 , 16 They are quite different in their amino acid compositions (Figure 3a,c, sequences in Supporting Information) and have been well studied for their phase separation making them excellent candidates for testing the model's ability to predict the IDP phase behavior. It has been shown that the coil‐to‐globule transition temperature, T θ, of a single‐chain IDP is highly correlated with its critical temperature of phase separation, T c. 15 Since computing T θ is computationally less expensive, we calculated T θ as a first step for these IDPs using REMD simulations along the critical line in the parameter space. Figure 2d presents T θ values for the DDX4 and FUS LC at different μ values along the critical line from the Urry scale. The coil‐to‐globule transition temperature of the DDX4 depends weakly on μ, while that of FUS LC increases sharply from ~330 K at μ = 0.5 to ~420 K at μ = 2.
FIGURE 3.
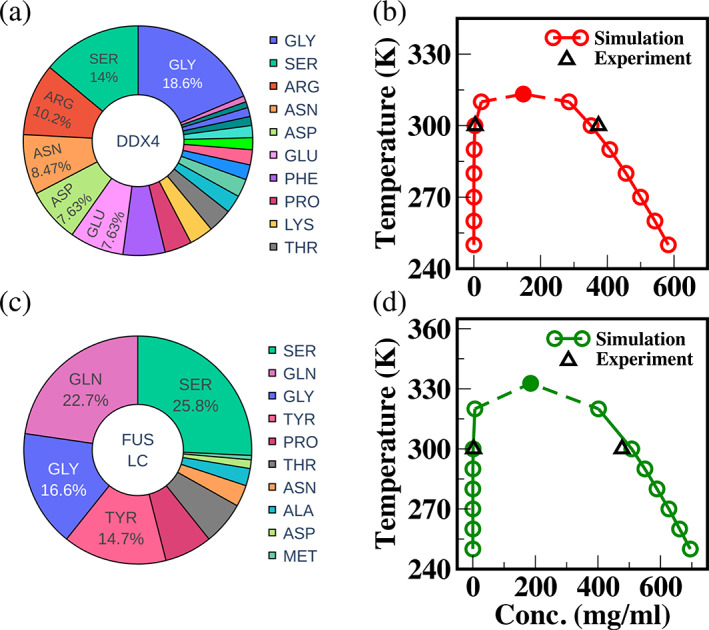
(a) Amino acid composition of DDX4 sequence used for this simulation. (b) Coexistence concentrations of DDX4 at 100 mM salt and room temperature from simulations (Red, circles) and experiments (Black, triangles). (c) Amino acid composition of FUS LC sequence used for this simulation. (d) Coexistence concentrations of FUS LC at 100 mM salt and room temperature from simulations (Green, circles), and experiments (Black, triangles)
The large difference in the behavior of these two sequences arises from their amino acid compositions. Using Equations (7) and (1), one can express λ ij in terms of the optimal μ opt as
| (3) |
where, as μ opt increases, λ ij increases for , but decreases for . For the Urry scale with a Urry = 0.58, the amino acids, Glu, Asp, and Lys, contribute to the decrease in the interaction energy when μ opt increases, while Trp, Tyr, Phe, Pro, His, Ile, Leu, Met, and Val contribute to the increase in the interaction energy. Since the DDX4 contains a significant number of Asp, Glu, Phe, Met, and Pro residues, the competition between opposing contributions from these residues leads to the fact that T θ is almost independent of μ opt. On the other hand, FUS LC is a protein mostly consisting of Ser, Gln, Gly, and Pro residues. The normalized hydropathy scales of Ser, Gln, and Gly are about 0.57 resulting in λ ij among themselves remaining close to 0.49 for 0.5 ≤ μ opt ≤ 2. On the other hand, λ ij for Pro‐Pro varies from 0.58 at μ opt = 0.5 to 0.86 at μ opt = 2. Also λ ij between Pro and other residues (Ser, Gln, and Gly) increases, albeit to a lesser degree, as μ opt increases. Consequently, the intramolecular interactions for FUS LC become more attractive as μ opt increases, resulting in the increase of T θ values.
For the KR scale, the hydropathy scales of most residues lie below a KR = 0.69, resulting in T θ decreasing for both DDX4 and FUS LC as μ opt increases (see Figure S4). For the MJ scale, the T θ of both DDX4 and FUS LC also decreases with increasing μ opt. Since T θ is highly correlated with the critical temperature of LLPS, these observations suggest that the KR and MJ scales predict undesirably low T c values for these two proteins.
2.4. Urry scale captures the IDP phase behavior
The single‐chain properties of DDX4 and FUS LC (see Figure 2d) suggest that the Urry scale may be more appropriate to study the phase behavior of these IDPs. Recently, experimentally derived coexistence densities were used to scale the interaction strengths in the MARTINI CG forcefield 34 for capturing the LLPS of the FUS LC sequence. 50 We want to test if our optimized Urry scale‐based CG model above can capture the concentrations of coexisting phases of FUS LC and DDX4 without any further modifications. We simulated the coexistence densities of these two proteins using the Urry scale with the optimal parameter set of μ = 1, and Δ = 0.08. Figure 3b,d show the temperature‐concentration phase diagrams of DDX4 and FUS LC together with the experimentally measured coexisting concentrations at 300 K. We see excellent agreement between simulated and experimental coexistence densities of both DDX4 49 (Figure 3b) and FUS LC 8 (Figure 3d) with the differences at condensed phases less than 7% for both DDX4 and FUS LC. Upon varying model parameters, we observe large fluctuations in the coexistence concentrations for FUS LC at 300 K (Figure S5) which corresponds to the higher sensitivity of FUS LC phase behavior on model parameters observed earlier with the coil‐to‐globule transition temperature in the previous section. Hence, this warrants a careful validation strategy for model parameters in our CG framework as certain sequences based on their amino acid composition could be more prone to dramatic changes in phase behavior between various model parameters which were deemed optimal for capturing IDP phase behavior based solely on only comparing R g values. Using the same parameter set (μ = 1, Δ = 0.8), we then investigated the model's ability to capture the effect of certain bulk mutations to the IDP sequence (sequences in SI) on its phase separation propensity. As mentioned earlier, the Urry scale would predict that the replacement of arginine residues with Lysine residues (R2K) on a protein sequence reduces phase separation propensity since the hydropathy value of Arg is larger than that of Lys. Figure 4a shows this anticipated behavior for the bulk R2K mutation of DDX4 showing the loss in phase separation propensity for two sequences DDX4 (Figure 4a, R2K, red lines joining ∆) and LAF‐1 RGG (Figure 4b, R2K, red lines joining ∆). We see the phase boundary shrinking and the critical temperature decreasing for the mutated sequences compared with the wild type (WT) (Figure 4a,b, WT, black lines joining O) in agreement with experimental observations. 49 On the other hand, the KR scale yielded the opposite trend on phase separation upon this mutation, which led to the proposed modifications in the interaction strengths of Arg and Lys residues based on experimental and bioinformatics studies. 44
FIGURE 4.
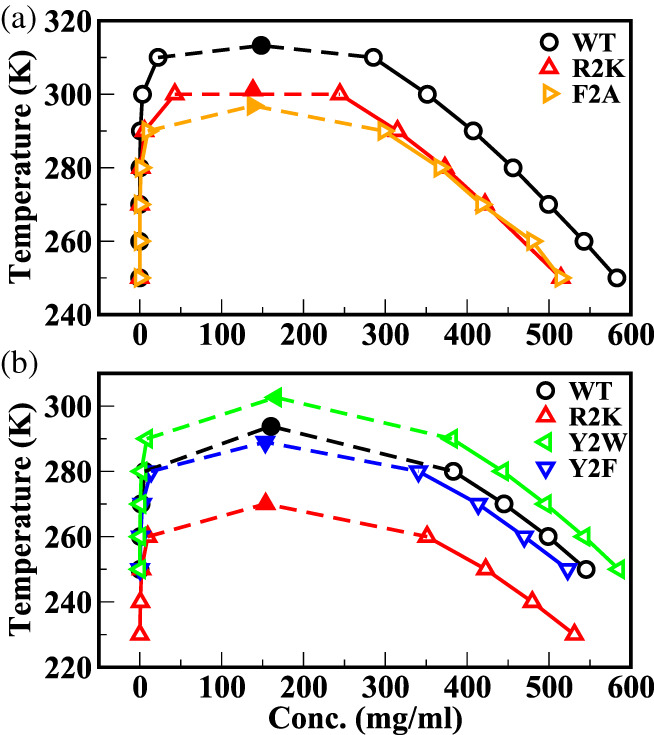
Phase diagrams for DDX4 (a) and LAF‐1 RGG (b) sequence variants show shifts in phase separation propensity upon bulk mutations as expected from experimental data
In addition to studying the effects of the Arg to Lys (R2K) mutation, we also tested the model for the effects of mutations of aromatic residues on phase separation propensity, for example, the Phe to Ala (F2A) mutation, which is also supposed to reduce phase separation propensity according to experimental studies. 6 , 7 , 45 , 49 For the DDX4 sequence we see the F2A mutation reducing phase separation propensity in agreement with experimental studies (Figure 4a, F2A, orange lines joining ⊲). The model was also able to predict the decrease in phase separation propensity upon replacement of Tyr with Phe (Y2F) residues for the LAF‐1 RGG sequence (Figure 4b, Y2F, blue lines joining ∇) as seen in experiments, which is not captured in the KR and the MJ scales. 32 Other mutations such as Tyr to Trp (Y2W) in LAF‐1 RGG (Figure 4b, Y2W, green lines joining ⊲) showed increased phase separation propensity in agreement with the experimental data for the LAF‐1 RGG sequence. 9
3. CONCLUSION
We propose a new CG model for studying IDP phase behavior, called the HPS‐Urry model which attempts to improve the previous HPS‐KR model using the hydropathy scale proposed by Urry et al. 47 We also apply a rigorous parameterizing and testing strategy to tune the parameters by comparing easily measurable quantities like the radius of gyration and coexistence densities with their known experimental values. The use of the Urry hydropathy scale for informing nonbonded interactions between amino acids to study liquid–liquid phase separation is supported by the fact that this scale was derived from the transitions of polypeptides from a water‐soluble state to an assembly of proteins into a condensed phase. We are able to capture experimentally observed phase behavior of IDPs and effects of bulk mutations without requiring any additional parameter refinements to the HPS‐Urry model. Future work will focus on extending this model to capture sequence‐dependent LCST and UCST transitions in IDPs, similar to what was proposed earlier for the HPS‐KR model. 31
4. METHODS
In the HPS modeling framework developed earlier, 30 each amino acid of an IDP is represented by a spherical bead that is connected to neighboring beads via a harmonic spring. The total interaction energy is given by
| (4) |
where , and are the short‐range van der Waals (vdW) and long‐range electrostatic interactions between residues i and j, while r i,i + 1 is the distance between two neighboring residues, i and i + 1, with the spring constant k b = 20 kJ/Å2 and an equilibrium bond length r 0 = 3.82 Å. The vdW interaction between residues i and j is modeled using the Ashbaugh and Hatch functional form given by 51
| (5) |
where is the standard Lennard‐Jones (LJ) potential shown below:
| (6) |
Here ϵ is set to 0.2 kcal/mol and σ ij = (σ i + σ j)/2 where σ i is the van der Waals radius of residue i, while λ ij controls the interaction strength between residues i and j and is adapted from hydropathy scales or contact potentials.
The long‐range electrostatic interactions between charged residues are described by a simple Debye‐Hückel potential,
| (7) |
where q i is the charge of residue i located at the center of the corresponding bead, D is the dielectric constant of the solvent medium, and κ is the inverse Debye screening length. Here we set D = 80, the dielectric constant of water and κ = 1 nm−1, the inverse Debye length at physiological salt concentrations of ~100 mM. Residue charges are set according to pH 7, such that q i = + e for Arg and Lys, and −e for Asp and Glu, where e is the elementary charge. Here the charge of His is set to zero instead of +0.5e adapted by the KH model. 32
In the previous model, λ ij values were fixed from the KR hydropathy values scaled from 0 (Arg) to 1 (Phe, Pro) while ϵ was optimized. In this study, λ ij values are optimized against the experimentally measured radius of gyration (R g) of IDPs 52 from hydropathy scales or contact potentials. Specifically, we set
| (8) |
where values are contact potentials or hydropathy scales scaled from 0 to 1, while μ and Δ are free parameters. For hydropathy scales of 20 amino acids, the arithmetic sum was used to obtain the cross‐interaction parameters, that is, , where λ i is the rescaled (from 0 to 1) hydropathy value of residue i. The parameter μ scales the strength of the vdW potentials compared with the physical electrostatic interactions, while Δ is the offset parameter that balances the preference of residue–residue interactions relative to residue‐solvent interactions. These two parameters are optimized using the experimental R g values of 42 IDP sequences (see Table S1).
Replica Exchange Molecular Dynamics (REMD) simulations of single chain IDPs were performed to compute R gvalues and coil‐to‐globule transition temperatures (T θ) using the LAMMPS 53 software package. A total of 16 replicas were used with the temperature ranging from 200 to 600 K for IDPs with chain length less than 200. For longer IDP sequences, a total of 36 replicas with the temperature ranging from 170 to 640 K were used. In addition, coexistence simulations of several IDPs were conducted to map their phase diagrams using the HOOMD‐Blue 2.9.3 software package 54 , 55 following the protocol proposed in our previous work. 30 , 56 A python code is provided for readers to setup and simulate a given IDP sequence with the optimized model using HOOMD‐Blue at the following location (https://bitbucket.org/jeetain/hoomd_slab_builder).
AUTHOR CONTRIBUTIONS
Roshan Regy: Data curation; formal analysis; investigation; validation; writing‐original draft. Jacob Thompson: Data curation; formal analysis; investigation. Youngchan C. Kim: Conceptualization; data curation; formal analysis; investigation; methodology; project administration; software; supervision; validation; writing‐review & editing. Jeetain Mittal: Conceptualization; data curation; formal analysis; investigation; methodology; project administration; supervision; writing‐review & editing.
Supporting information
Appendix S1: Supporting Information
ACKNOWLEDGMENTS
Research reported in this publication was supported by the National Institute of General Medical Sciences of the National Institutes of Health under Award Number R01GM136917. Research was also supported in part by NINDS and NIA R01NS116176 and NSF 2004796. Y. C. K. is supported by the Office of Naval Research via the U.S. Naval Research Laboratory base program. Use of the high‐performance computing capabilities of the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by the NSF grant TG‐MCB‐120014, is gratefully acknowledged. We thank Prof. Wenwei Zheng for providing his analysis of the experimental radius of gyration data.
Regy RM, Thompson J, Kim YC, Mittal J. Improved coarse‐grained model for studying sequence dependent phase separation of disordered proteins. Protein Science. 2021;30:1371–1379. 10.1002/pro.4094
Funding information Division of Materials Research, Grant/Award Number: 2004796; National Institute of General Medical Sciences, Grant/Award Numbers: R01GM136917, R01NS116176; National Science Foundation, Grant/Award Number: TG‐MCB‐120014; U.S. Naval Research Laboratory; Office of Naval Research
Contributor Information
Young C. Kim, Email: youngchan.kim@nrl.navy.mil.
Jeetain Mittal, Email: jeetain@lehigh.edu.
REFERENCES
- 1. Banani SF, Rice AM, Peeples WB, et al. Compositional control of phase‐separated cellular bodies. Cell. 2016;166:651–663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Alberti S, Gladfelter A, Mittag T. Considerations and challenges in studying liquid‐liquid phase separation and biomolecular condensates. Cell. 2019;176:419–434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Riback JA, Zhu L, Ferrolino MC, et al. Composition‐dependent thermodynamics of intracellular phase separation. Nature. 2020;581:209–214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Lee CYS, Putnam A, Lu T, He S, Ouyang JPT, Seydoux G. Recruitment of mRNAs to P granules by condensation with intrinsically‐disordered proteins. elife. 2020;9:e52896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Klosin A, Oltsch F, Harmon T, et al. Phase separation provides a mechanism to reduce noise in cells. Science. 2020;367:464–468. [DOI] [PubMed] [Google Scholar]
- 6. Wang J, Choi JM, Holehouse AS, et al. A molecular grammar governing the driving forces for phase separation of prion‐like RNA binding proteins. Cell. 2018;174:688–699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Vernon RM, Chong PA, Tsang B, et al. Pi‐Pi contacts are an overlooked protein feature relevant to phase separation. elife. 2018;7:e31486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Murthy AC, Dignon GL, Kan Y, et al. Molecular interactions underlying liquid−liquid phase separation of the FUS low‐complexity domain. Nat Struct Mol Biol. 2019;26:637–648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Schuster BS, Dignon GL, Tang WS, et al. Identifying sequence perturbations to an intrinsically disordered protein that determine its phase‐separation behavior. Proc Natl Acad Sci U S A. 2020;117:11421–11431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Yang Y, Jones HB, Dao TP, Castañeda CA. Single amino acid substitutions in stickers, but not spacers, substantially alter UBQLN2 phase transitions and dense phase material properties. J Phys Chem B. 2019;123:3618–3629. [DOI] [PubMed] [Google Scholar]
- 11. Martin EW, Holehouse AS, Peran I, et al. Valence and patterning of aromatic residues determine the phase behavior of prion‐like domains. Science. 2020;367:694–699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Elbaum‐Garfinkle S, Kim Y, Szczepaniak K, et al. The disordered P granule protein LAF‐1 drives phase separation into droplets with tunable viscosity and dynamics. Proc Natl Acad Sci U S A. 2015;112:7189–7194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Qamar S, Wang GZ, Randle SJ, et al. FUS phase separation is modulated by a molecular chaperone and methylation of arginine cation‐π interactions. Cell. 2018;173:720–734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Muiznieks LD, Sharpe S, Pomès R, Keeley FW. Role of liquid–liquid phase separation in assembly of elastin and other extracellular matrix proteins. J Mol Biol. 2018;430:4741–4753. [DOI] [PubMed] [Google Scholar]
- 15. Dignon GL, Zheng W, Best RB, Kim YC, Mittal J. Relation between single‐molecule properties and phase behavior of intrinsically disordered proteins. Proc Natl Acad Sci U S A. 2018;115:9929–9934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Zheng W, Dignon GL, Jovic N, et al. Molecular details of protein condensates probed by microsecond long atomistic simulations. J Phys Chem B. 2020;124:11671–11679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Regy RM, Dignon GL, Zheng W, Kim YC, Mittal J. Sequence dependent phase separation of protein‐polynucleotide mixtures elucidated using molecular simulations. Nucleic Acids Res. 2020;48:12593–12603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Shea J, Best RB, Mittal J. Physics‐based computational and theoretical approaches to intrinsically disordered proteins. Curr Opin Struct Biol. 2021;67:219–225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Choi JM, Dar F, Pappu RV. LASSI: A lattice model for simulating phase transitions of multivalent proteins. PLoS Comput Biol. 2019;15:e1007028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Lin YH, Brady JP, Forman‐Kay JD, Chan HS. Charge pattern matching as a “fuzzy” mode of molecular recognition for the functional phase separations of intrinsically disordered proteins. New J Phys. 2017;19:225003. [Google Scholar]
- 21. Baul U, Chakraborty D, Mugnai ML, Straub JE, Thirumalai D. Sequence effects on size, shape, and structural heterogeneity in intrinsically disordered proteins. J Phys Chem B. 2019;123:3462–3474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Murthy AC, Fawzi NL. The (un)structural biology of biomolecular liquid‐liquid phase separation using NMR spectroscopy. J Biol Chem. 2020;295:2375–2384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Paloni M, Bailly R, Ciandrini L, Barducci A. Unraveling molecular interactions in liquid‐liquid phase separation of disordered proteins by atomistic simulations. J Phys Chem B. 2020;124:9009–9016. [DOI] [PubMed] [Google Scholar]
- 24. Levine ZA, Shea JE. Simulations of disordered proteins and systems with conformational heterogeneity. Curr Opin Struct Biol. 2017;43:95–103. [DOI] [PubMed] [Google Scholar]
- 25. McCarty JJ, Delaney KT, Danielsen SPO, Fredrickson GH, Shea J‐E. Complete phase diagram for liquid‐liquid phase separation of intrinsically disordered proteins. J Phys Chem Lett. 2019;10:1644–1652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Conicella AE, Dignon GL, Zerze GH, et al. TDP‐43 α‐helical structure tunes liquid–liquid phase separation and function. Proc Natl Acad Sci U S A. 2020;117:5883–5894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Espinosa JR, Joseph JA, Sanchez‐Burgos I, Garaizar A, Frenkel D, Collepardo‐Guevara R. Liquid network connectivity regulates the stability and composition of biomolecular condensates with many components. Proc Natl Acad Sci U S A. 2020;117:201917569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Krainer G, Welsh TJ, Joseph JA, et al. Reentrant liquid condensate phase of proteins is stabilized by hydrophobic and non‐ionic interactions. Nat Commun. 2021;12:1085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Chakraborty D, Straub JE, Thirumalai D. Differences in the free energies between the excited states of Aβ40 and Aβ42 monomers encode their aggregation propensities. Proc Natl Acad Sci U S A. 2020;117:19926–19937. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Dignon GL, Zheng W, Kim YC, Best RB, Mittal J. Sequence determinants of protein phase behavior from a coarse‐grained model. PLoS Comput Biol. 2018;14:e1005941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Dignon GL, Zheng W, Kim YC, Mittal J. Temperature‐controlled liquid‐liquid phase separation of disordered proteins. ACS Cent Sci. 2019;5:821–830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Kim YC, Hummer G. Coarse‐grained models for simulations of multiprotein complexes: Application to ubiquitin binding. J Mol Biol. 2008;375:1416–1433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Wu H, Wolynes PG, Papoian GA. AWSEM‐IDP: A coarse‐grained force field for intrinsically disordered proteins. J Phys Chem B. 2018;122:11115–11125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. De Jong DH, Singh G, Bennett WFD, et al. Improved parameters for the martini coarse‐grained protein force field. J Chem Theory Comput. 2013;9:687–697. [DOI] [PubMed] [Google Scholar]
- 35. Kmiecik S, Gront D, Kolinski M, Wieteska L, Dawid AE, Kolinski A. Coarse‐grained protein models and their applications. Chem Rev. 2016;116:7898–7936. [DOI] [PubMed] [Google Scholar]
- 36. Kapcha LH, Rossky PJ. A simple atomic‐level hydrophobicity scale reveals protein interfacial structure. J Mol Biol. 2014;426:484–498. [DOI] [PubMed] [Google Scholar]
- 37. Perdikari TM, Jovic N, Dignon GL, Kim YC, Fawzi NL, Mittal J. A predictive coarse‐grained model for position‐specific effects of post‐translational modifications. Biophys J. 2021;120:1187–1197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Berkeley RF, Kashefi M, Debelouchina GT. Real‐time observation of structure and dynamics during the liquid‐to‐solid transition of FUS LC. Biophys J. 2021;120:1276–1287. 10.1016/j.bpj.2021.02.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Alshareedah I, Moosa MM, Raju M, Potoyan DA, Banerjee PR. Phase transition of RNA−protein complexes into ordered hollow condensates. Proc Natl Acad Sci U S A. 2020;117:15650–15658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Kaur T, Raju M, Alshareedah I, Davis RB, Potoyan DA, Banerjee PR. Sequence‐encoded and composition‐dependent protein‐RNA interactions control multiphasic condensate morphologies. Nat Commun. 2021;12:273748. 10.1101/2020.08.30.273748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Banerjee PR, Milin AN, Moosa MM, Onuchic PL, Deniz AA. Reentrant phase transition drives dynamic substructure formation in ribonucleoprotein droplets. Angew Chem Int Ed Engl. 2017;56:11354–11359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Wei MT, Elbaum‐Garfinkle S, Holehouse AS, et al. Phase behaviour of disordered proteins underlying low density and high permeability of liquid organelles. Nat Chem. 2017;9:1118–1125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Latham AP, Zhang B. Maximum entropy optimized force field for intrinsically disordered proteins. J Chem Theory Comput. 2020;16:773–781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Das S, Lin Y‐H, Vernon RM, Forman‐Kay JD, Chan HS. Comparative roles of charge, π, and hydrophobic interactions in sequence‐dependent phase separation of intrinsically disordered proteins. Proc Natl Acad Sci U S A. 2020;117:28795–28805. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Fisher RS, Elbaum‐Garfinkle S. Tunable multiphase dynamics of arginine and lysine liquid condensates. Nat Commun. 2020;11:4628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Miyazawa S, Jernigan RL. Residue–residue potentials with a favorable contact pair term and an unfavorable high packing density term, for simulation and threading. J Mol Biol. 1996;256:623–644. [DOI] [PubMed] [Google Scholar]
- 47. Urry DW, Gowda DC, Parker TM, et al. Hydrophobicity scale for proteins based on inverse temperature transitions. Biopolymers. 1992;32:1243–1250. [DOI] [PubMed] [Google Scholar]
- 48. Palliser CC, Parry DAD. Quantitative comparison of the ability of hydropathy scales to recognize surface β‐strands in proteins. Proteins. 2001;42:243–255. [DOI] [PubMed] [Google Scholar]
- 49. Brady JP, Farber PJ, Sekhar A, et al. Structural and hydrodynamic properties of an intrinsically disordered region of a germ‐cell specific protein upon phase separation. Proc Natl Acad Sci U S A. 2017;114:E8194–E8203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Benayad Z, von Bülow S, Stelzl LS, Hummer G. Simulation of FUS protein condensates with an adapted coarse‐grained model. J Chem Theory Comput. 2021;17:525–537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Ashbaugh HS, Hatch HW. Natively unfolded protein stability as a coil‐to‐globule transition in charge/hydropathy space. J Am Chem Soc. 2008;130:9536–9542. [DOI] [PubMed] [Google Scholar]
- 52. Zheng W, Zerze GH, Borgia A, Mittal J, Schuler B, Best RB. Inferring properties of disordered chains from FRET transfer efficiencies. J Chem Phys. 2018;148:123329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Plimpton S. Fast parallel algorithms for short‐range molecular dynamics. J Comput Phys. 1995;117:1–19. [Google Scholar]
- 54. Anderson JA, Glaser J, Glotzer SC. HOOMD‐blue: A python package for high‐performance molecular dynamics and hard particle Monte Carlo simulations. Comput Mater Sci. 2020;173:109363. [Google Scholar]
- 55. Howard MP, Panagiotopoulos AZ, Nikoubashman A. Efficient mesoscale hydrodynamics: Multiparticle collision dynamics with massively parallel GPU acceleration. Comput Phys Commun. 2018;230:10–20. [Google Scholar]
- 56. Mammen Regy R, Zheng W, Mittal J. Using a sequence‐specific coarse‐grained model for studying protein liquid–liquid phase separation. Methods Enzymol. 2021;646:1–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix S1: Supporting Information


