Biomolecular phase separation through the lens of sodium‐23 NMR

Abstract

Phase separation is a fundamental physicochemical process underlying the spatial arrangement and coordination of cellular events. Detailed characterization of biomolecular phase separation requires experimental access to the internal environment of dilute and especially condensed phases at high resolution. In this study, we take advantage from the ubiquitous presence of sodium ions in biomolecular samples and present the potentials of ²³Na NMR as a proxy to report the internal fluidity of biomolecular condensed phases. After establishing the temperature and viscosity dependence of ²³Na NMR relaxation rates and translational diffusion coefficient, we demonstrate that ²³Na NMR probes of rotational and translational mobility of sodium ions are capable of capturing the increasing levels of confinement in agarose gels in dependence of agarose concentration. The ²³Na NMR approach is then applied to a gel‐forming phenylalanine‐glycine (FG)‐containing peptide, part of the nuclear pore complex involved in controlling the traffic between cytoplasm and cell nucleus. It is shown that the ²³Na NMR together with the ¹⁷O NMR provide a detailed picture of the sodium ion and water mobility within the interior of the FG peptide hydrogel. As another example, we study phase separation in water‐triethylamine (TEA) mixture and provide evidence for the presence of multiple microscopic environments within the TEA‐rich phase. Our results highlight the potentials of ²³Na NMR in combination with ¹⁷O NMR in studying biological phase separation, in particular with regards to the molecular properties of biomolecular condensates and their regulation through various physico‐ and biochemical factors.

1.

Significance.

Many cellular events occur inside phase‐separated biomolecular condensates. It is not clear how the microscopic properties of the crowded interior of condensates are affected by regulatory factors. Here, we exploit the ubiquitous presence of sodium ions in bimolecular samples and utilize NMR probes of sodium ion mobility for monitoring the properties of condensates. Our data demonstrates the potentials of sodium NMR combined with oxygen NMR in detailed characterization of biomolecular condensates formed through phase separation.

2. INTRODUCTION

Spatial organization of entities and activities within distinct compartments is a fundamental feature of living matter. The role of phase separation in the spatial organization of cells is highlighted in a quote from Sir Frederick G. Hopkins in 1913, that the living cell is “not a mass of matter composed of a congregation of like molecules, but a highly differentiated system of co‐existing phases of different constitution.” ¹ In recent years, the interest in biological phase separation has re‐emerged as its underlying role in the formation and dissolution of different cellular bodies is increasingly appreciated. ²

The chemical composition and physical properties of phase separated cellular bodies exhibit remarkable diversity and vary in response to a broad range of regulatory signals in cells. ³ Different biophysical and micro‐rheological techniques based on (translational) diffusion and fusion timescale analysis are currently used to provide an overall picture of the physical properties of biomolecular condensates. ⁴ , ⁵ Detailed understanding of biological phase separation however requires experimental access to the internal environment of biomolecular condensates at higher sensitivity and resolution, ⁶ enabling monitoring alterations in their microscopic properties in dependence of subtle biochemical events such as small molecule, proteins or RNA recruitment, mutations, and posttranslational modifications. ⁷

NMR spectroscopy is a powerful technique allowing experimental access to biomolecular structure and dynamics at a broad range of time and length scales in different environments, including the liquid‐ and gel‐like biomolecular condensates. ⁸ , ⁹ Several recent studies have utilized high‐resolution NMR to monitor the structural dynamics of proteins and other biomolecules within condensed phases. ¹⁰ , ¹¹ , ¹² , ¹³ Recently, natural abundance ¹⁷O relaxation of water molecules has been utilized as a reliable proxy to report the internal fluidity of phase‐separated biological hydrogels and the ordering of water molecules across lipid nanodiscs. ¹⁴ , ¹⁵ The use of additional NMR probes could however provide complementary molecular‐level information on the local environment of biomolecular condensates.

In this article, we present sodium‐23 (²³Na) NMR probes of biomolecular mobility in phase separating systems. ²³Na is an NMR‐active nucleus with half‐integer spin quantum number I of 3/2 ubiquitously present in biological tissues and bimolecular samples. This, in addition to natural abundance of 100% and gyromagnetic ratio of ca. 26% of ¹H nuclei, makes ²³Na an attractive candidate for NMR studies of biomolecular phase separation. ¹⁶ Besides, sodium ions minimally perturb the structure of surrounding water molecules, a feature that makes them a reasonably inert probe for the water structure. ¹⁷ The NMR relaxation of ²³Na has been extensively studied in a broad range of motional regimes from fast (“extreme narrowing”) to slow and ultra‐slow motions. ¹⁸ , ¹⁹ , ²⁰ , ²¹ Here, the ²³Na longitudinal relaxation rates (R ₁) and translational diffusion coefficient (D _tr) are presented as reporters of local restriction in rotational and translational mobility of sodium ions within dilute and condensed phases. We first show how ²³Na R ₁ rates could be utilized to determine effective viscosity in dilute phases. The method will then be applied to two phase separating systems: first, an FG peptide of nucleoporin (Nup), part of the nuclear pore complex (NPC), which undergoes phase transition to gel‐like materials and acts as a permeability barrier in controlling the traffic between cell nucleus and cytoplasm, ²² and second, the water‐triethylamine (TEA) mixture, as a model system. ²³

3. RESULTS

3.1. Temperature‐dependence of ²³NaCl NMR

To probe sodium ion mobility in dependence of temperature, we first measured 1D ²³Na NMR spectra of 100 mM sodium chloride at different temperatures varying from 278 to 333 K. As shown in Figure 1a, the increase in temperature caused gradual displacement of ²³Na signals from ca. 0.43 ppm at 278 K to 0.18 ppm at 298 K and − 0.34 ppm at 333 K. The ²³Na chemical shifts were referenced based on HDO deuterium chemical shifts (4.700 ppm). When temperature dependence of the HDO deuterium chemical shifts was taken into consideration, the temperature variation of ²³Na chemical shifts became more prominent: it varied from ca. 0.69 ppm at 278 K to 0.24 ppm at 298 K and − 0.65 ppm at 333 K. In addition, the ²³Na signals exhibited strong temperature‐dependent broadening: the ²³Na resonance linewidth decreased from 12.18 ± 0.05 Hz at 278 K to 5.72 ± 0.04 Hz at 298 K and 3.33 ± 0.01 Hz at 333 K. As expected, the heating‐induced (partial) dehydration of sodium ions was represented by the upfield, that is, more shielded, ²³Na chemical shift changes, while the higher rotational mobility of sodium ions at higher temperatures was reflected in ²³Na signal narrowing.

FIGURE 1.

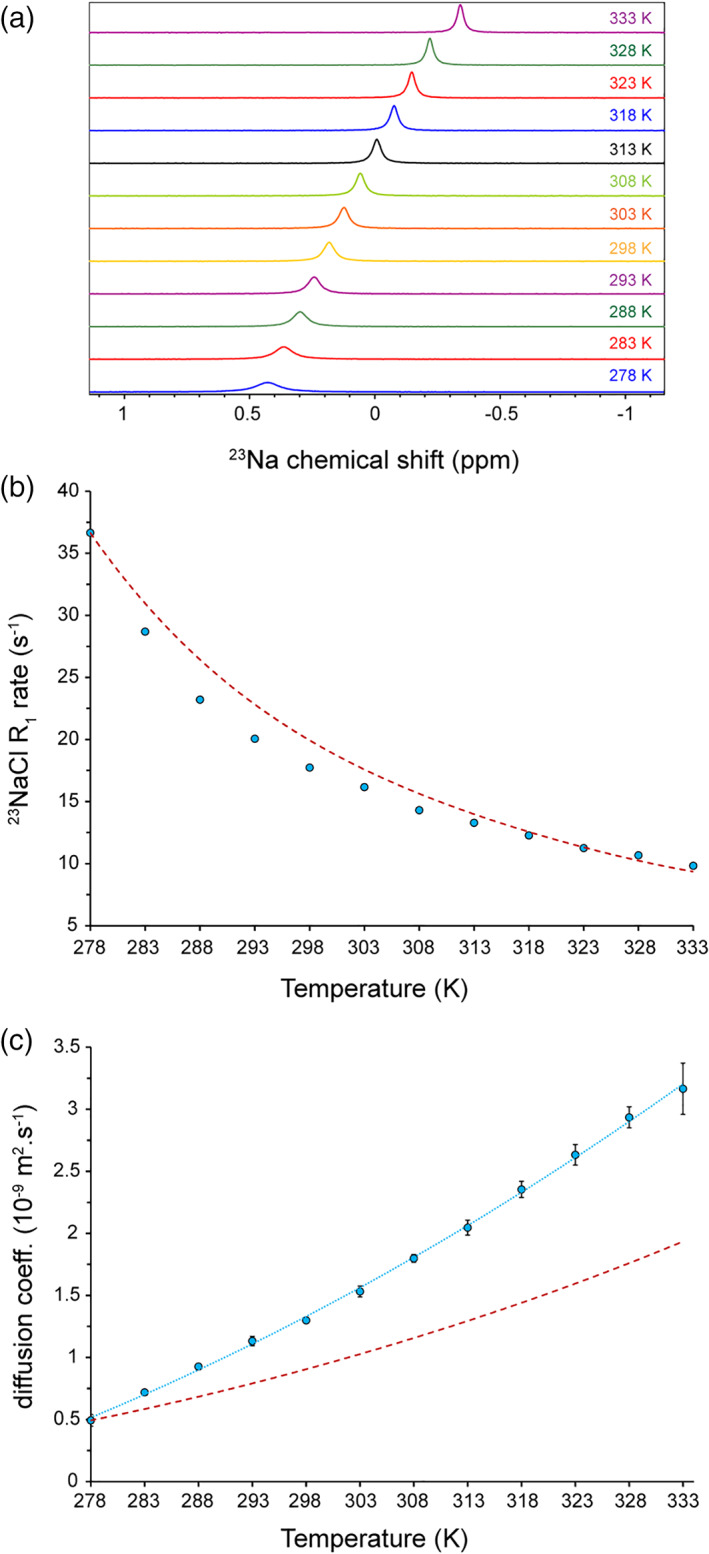
Temperature dependence of ²³Na NMR in 100 mM NaCl solution. (a) 1D ²³Na NMR spectra reveal temperature‐dependent ²³Na chemical shift changes and broadening. (b) The ²³Na longitudinal relaxation (R ₁) rates obtained from inversion‐recovery data at different temperatures (shown in Figure S1). The dashed line (dark red) shows the expected trend of R1 changes calculated based on the η/T ratio variation. The error bars are smaller than the symbol size. (c) Temperature dependence of ²³NaCl translational diffusion coefficients (Dtr) obtained through PFG‐NMR diffusion experiments. The temperature‐dependent changes in Dtr is more pronounced than the expected trend calculated based on the T/η ratio variation (dashed line in dark red). PFG, pulse field gradient

Then, we measured ²³Na longitudinal relaxation rates (R ₁) through standard inversion‐recovery experiments at different temperatures. Consistent with sodium ions at fast motion regime, single‐exponential recovery curves were observed over the studied range of temperatures (Figure S1). The obtained ²³Na R ₁ rates exhibited temperature‐dependent decrease from 36.7 ± 0.2 s⁻¹ at 278 K to 17.7 ± 0.2 s⁻¹ at 298 K and 9.8 ± 0.1 s⁻¹ at 333 K (Figure 1b). The obtained value at 298 K is in excellent agreement with previous reports. ¹⁷ Interestingly, the apparent transverse relaxation rates (R _2,app) estimated through ²³Na linewidths and the ²³Na R ₁ rates matched very well (Figure S2), as expected for the fast motion regime, further indicating that the contribution from (B ₀) field and sample inhomogeneity to ²³Na R ₂ rates were negligible compared to its quadrupole relaxation.

Next, we monitored the temperature‐dependent variation of translational diffusion coefficient (D _tr) of sodium ions through standard pulse field gradient (PFG)‐NMR diffusion experiments. The ²³Na D _tr increased from ca. 0.5 × 10⁻⁹ m²s⁻¹ at 278 K to 1.3 × 10⁻⁹ m²s⁻¹ at 298 K and 3.3 × 10⁻⁹ m²s⁻¹ at 333 K. Interestingly, the temperature dependence of ²³Na D _tr was more pronounced than the temperature dependence of the T/η ratio (Figure 1c), further supporting the heating‐induced (partial) dehydration of sodium ions and its consequent enhancement in translational mobility. The ²³Na R ₁ (and R _2,app, see above) rates more closely followed the temperature dependence of the η/Τ ratio (Figure 1b), suggesting that the partial dehydration of sodium ions in the outer hydration layers did not strongly alter the rotational mobility of sodium ions, and despite changes in the shielding tensor largely determined by inner water molecules, as indicated from ²³Na chemical shift changes (Figure 1a), the electric field gradient (EFG) tensor at the site of ²³Na quadrupolar nuclei was only slightly affected.

3.2. Viscosity‐dependence of ²³NaCl NMR in glycerol‐water mixtures

To investigate the response of sodium ion mobility to solution viscosity, glycerol‐water mixtures were studied. The solution viscosity of glycerol‐water mixtures is known in a broad range of glycerol concentrations and temperatures. ²⁴ More importantly, it has been shown that both the translational and rotational diffusion in glycerol‐water mixtures exhibit viscosity‐dependent decrease in accord with classical Stokes‐Einstein and Stokes‐Einstein‐Debye laws. ²⁵ The ²³Na NMR experiments were performed in samples containing 0 to ca. 40% (vol/vol) glycerol, each containing 100 mM sodium chloride, at 298 K, where the solution viscosity ranged from 0.89 to 4.01 cP. The range of viscosity in the present study is considerably larger than the previous report, where viscosity ranged between 0.89 and 2.01 cP. ¹⁷

In 1D ²³Na spectra, addition of glycerol led to a gradual displacement of ²³Na signals toward lower chemical shifts (Figure S3), consistent with glycerol‐dependent dehydration of sodium ions. Interestingly, the ²³Na chemical shift displacements induced by temperature increase (faster dynamic) and glycerol addition (slower dynamic) followed the same direction, that is, they both moved upfield (Figure 1a and Figure S3). This suggests that the chemical shift perturbations caused by altered sodium hydration are dominant over any potentially existing quadrupolar “dynamic frequency shifts.” ²¹ , ²⁶ The linewidth of ²³Na signals increased by ca. 3.5‐fold from 5.79 ± 0.19 Hz at 0% glycerol to 20.15 ± 0.92 Hz at 40% glycerol. Following a similar trend, the ²³Na R ₁ rates increased from 17.7 ± 0.2 s⁻¹ at 0% glycerol to 62.3 ± 0.1 s⁻¹ at 40% glycerol (Figure 2a,b), which are in excellent agreement with the previous report. ¹⁷ Again, the R _2,app estimated through ²³Na linewidths and the ²³Na R ₁ closely matched (Figure S4), indicating fast motion regime and negligible contribution of field and sample inhomogeneity to ²³Na transverse relaxation.

FIGURE 2.

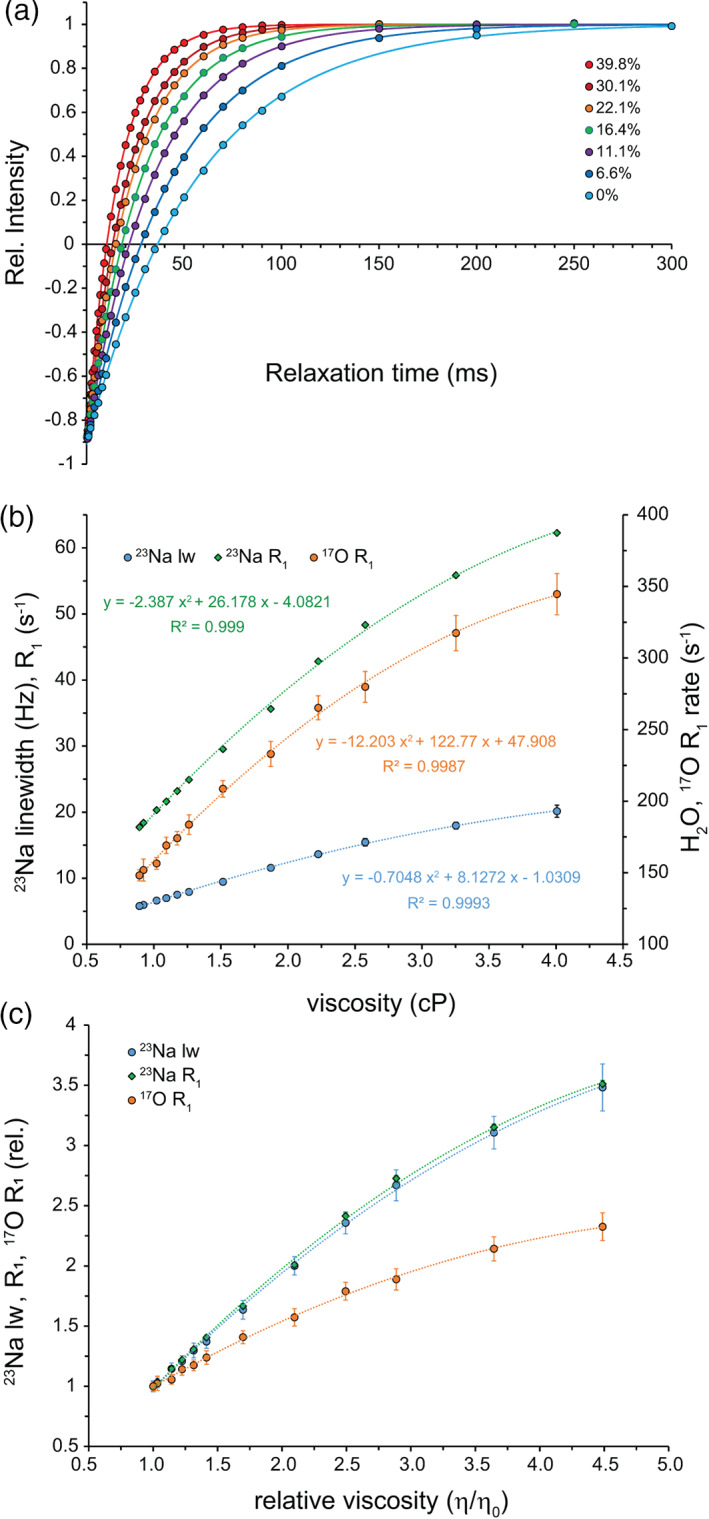
Viscosity dependence of ²³Na NMR in glycerol‐water mixtures containing 100 mM NaCl solution. (a) ²³Na signal intensity recovery following 180° inversion, showing faster recovery at higher glycerol concentrations. (b) Viscosity dependence of ²³Na longitudinal relaxation (R ₁) obtained from inversion‐recovery data, shown along with the ²³Na resonance linewidth and the H2¹⁷O R ₁ rates (secondary axis). (c) Relative change in ²³Na linewidth and R ₁ rates or H2¹⁷O R ₁ rates versus relative viscosity, showing the larger sensitivity of ²³Na NMR probes to viscosity variation

Subsequently, the translational mobility of sodium ions in glycerol‐water mixtures was determined. Upon addition of glycerol, the ²³Na D _tr gradually decreased from 1.3 × 10⁻⁹ m²s⁻¹ at 0% glycerol to ca. 0.5 × 10⁻⁹ m²s⁻¹ at 40% glycerol, in line with previously published data. ¹⁷ The decrease in translational diffusion fell behind the glycerol concentration‐dependent decrease in 1/η ratio (Figure S5), suggesting (partial) dehydration of sodium ions upon glycerol addition and the consequent (partial) compensation of viscosity effects on their translational mobility. Overall, glycerol addition to water slowed down the rotational, and to lesser extent, translational mobility of sodium ions and perturbed their hydration.

3.3. Viscosity determination through ²³NaCl NMR

Based on the viscosity dependence of ²³Na NMR probes of dynamics in glycerol‐water mixtures, empirical relations between ²³Na resonance linewidths (lw) or R ₁ rates and viscosity were defined (Figure S6). The ²³Na lw or R ₁ rates versus viscosity data fitted better to cubic relations, as follow respectively,

$$\eta \left(\mathit{cP}\right)=7.13\left(\pm 0.76\right)*{10}^{-4}*{\left(\mathit{lw}\right)}^3-2.1\left(\pm 0.3\right)*{10}^{-2}*{\left(\mathit{lw}\right)}^2+0.365\left(\pm 0.035\right)*\mathit{lw}-0.67\left(\pm 0.13\right)$$ (1)

$$\eta \left(\mathit{cP}\right)=2.76\left(\pm 0.41\right)*{10}^{-5}*{\left(R_1\right)}^3-2.55\left(\pm 0.49\right)*{10}^{-3}*{\left(R_1\right)}^2+0.128\left(\pm 0.018\right)*R_1-0.755\left(\pm 0.203\right)$$ (2)

when compared to linear and quadratic relations (p‐values < .001). However, in the range from 0 to ca. 22% (vol/vol) glycerol, across which viscosity varies from 0.89 to 1.87 cP, linear relations were sufficient to describe the data. This behavior is similar to the viscosity dependence of ¹⁷O R ₁ rates of water molecules (Figure S7; see also Reference 14), however, the larger slope of the linear part of ²³Na R ₁ rates versus viscosity curve indicates the higher sensitivity of ²³Na R ₁ rates of sodium ions to subtle viscosity changes when compared to ¹⁷O R ₁ rates of water molecules (Figure 2c).

With the viscosity dependence of ²³Na R ₁ rates established, we employed ²³Na R ₁ rates to determine (effective) viscosity through Equation (2). As a test case, the ubiquitin sample at 2.67 mM concentration containing 100 mM sodium chloride was measured, where the volume occupancy was around 3.5%. The ¹⁷O R ₁ rate of water was 157 ± 3 s⁻¹, corresponding to a viscosity of 0.99 ± 0.04 cP and relative viscosity of 1.11 ± 0.04 in close agreement with the predicted relative viscosity of 1.10 ± 0.01 based on hydrodynamic calculations. The ²³Na chemical shift was very close to the value observed in the buffer solution (the difference was <0.01 ppm), suggesting that the chemical environment of sodium ions was largely unaffected. The ²³Na R ₁ rates was 19.9 ± 0.1 s⁻¹, which yielded viscosity of 1.01 ± 0.01 cP and relative viscosity of 1.13 ± 0.01, highly similar to the ¹⁷O R ₁‐based and predicted viscosities. Considering experimental uncertainties in protein concentration determination, the close agreement between the ²³Na‐ and ¹⁷O‐derived and predicted viscosities supports the validity of ²³Na NMR in viscosity determination of concentrated protein solutions, where sodium ion hydration is not expected to be significantly perturbed.

3.4. ²³NaCl NMR in crowded media

Molecularly crowded solutions are frequently used to mimic the highly crowded interior of cells. ²⁷ To address whether ²³Na NMR could be used in viscosity determination within such crowded environments, we examined sucrose as the crowding agent at 200 g L⁻¹ concentration. The ¹⁷O R ₁ rate of water was 206 ± 7 s⁻¹, corresponding to the relative viscosity of 1.70 ± 0.09, consistent with previous reports. ¹⁴ , ²⁸ On the other hand, the ²³Na R ₁ rate was 39.8 ± 0.2 s⁻¹, which yielded much larger relative viscosity of 2.28 ± 0.01. A similar discrepancy was observed in 200 g L⁻¹ Ficoll solution, where the ¹⁷O R ₁ rate of 230 ± 7 s⁻¹ and ²³Na R ₁ rate of 57.6 ± 0.5 s⁻¹ corresponded to relative viscosities of 2.01 ± 0.10 and 3.85 ± 0.06 respectively. The ²³Na chemical shifts in sucrose and Ficoll were respectively ca. 0.08 and 0.04 ppm smaller than the value observed in the control solution. The ²³Na chemical shift differences point to the potential effect of sucrose and Ficoll on sodium ion hydration and suggest that the resultant alterations in the EFG tensor at ²³Na nuclei may be the origin of the observed discrepancy between ¹⁷O and ²³Na‐based viscosities.

3.5. ²³NaCl NMR in confined media

Next, we investigated the potentials of ²³Na NMR probes for dynamics as a proxy to monitor the interior of biological confined media such as hydrogels and condensed phases. We started with agarose gels, ranging from 0 to 6% agarose concentrations, containing 100 mM sodium chloride. In line with our previous report, ¹⁴ the ¹⁷O R ₁ rates of water increased from 149 ± 2 s⁻¹ in the control solution to 152 ± 4, 156 ± 4, 160 ± 7, 166 ± 4, 174 ± 7, 179 ± 4 and 218 ± 14 s⁻¹, respectively at 0.5, 1, 1.5, 2, 3, 4.5, and 6% agarose gels, reflecting agarose concentration‐dependent restriction in the rotational mobility of water molecules (Figure 3a). In ²³Na NMR spectra, the ²³Na chemical shifts did not show any significant variation among different gels, however significant signal broadening was observed in dependence of agarose concentration (Figure S8). Similarly, the ²³Na R ₁ rates rose from 17.8 ± 0.1 s⁻¹ in the control solution to 18.3 ± 0.1, 18.8 ± 0.1, 19.1 ± 0.1, 20.8 ± 0.1, 22.6 ± 0.1, 23.4 ± 0.3, and 27.4 ± 0.3, respectively at 0.5, 1, 1.5, 2, 3, 4.5, and 6% agarose gels (Figure 3b). Interestingly, when the ²³Na R ₁ and the linewidth‐based R _2,app rates were compared, clear difference was observed at all the studied agarose gels (Figure 3c). Comparing the ²³Na R ₁ rates obtained from agarose gels with those from glycerol‐water mixtures (Figure 2b), the discrepancy between ²³Na R ₁ and R _2,app rates does not seem to have its origin in a deviation from fast motion regime. Instead, it is likely to reflect the considerable level of sample inhomogeneity in agarose gels especially at high‐agarose concentrations. In regards to the translational mobility of ²³Na ions, the effect of agarose gels was less pronounced: the D _tr of sodium ions at 6% agarose gels was 1.2 × 10⁻⁹ m²s⁻¹, only slightly lower than the value of 1.3 × 10⁻⁹ m²s⁻¹ in the control solution (Figure S9). Overall, ²³Na NMR captured the agarose concentration‐dependent restrictions in the rotational and translational mobility of sodium ions within the gels and provided a way of evaluating the gel inhomogeneity.

FIGURE 3.

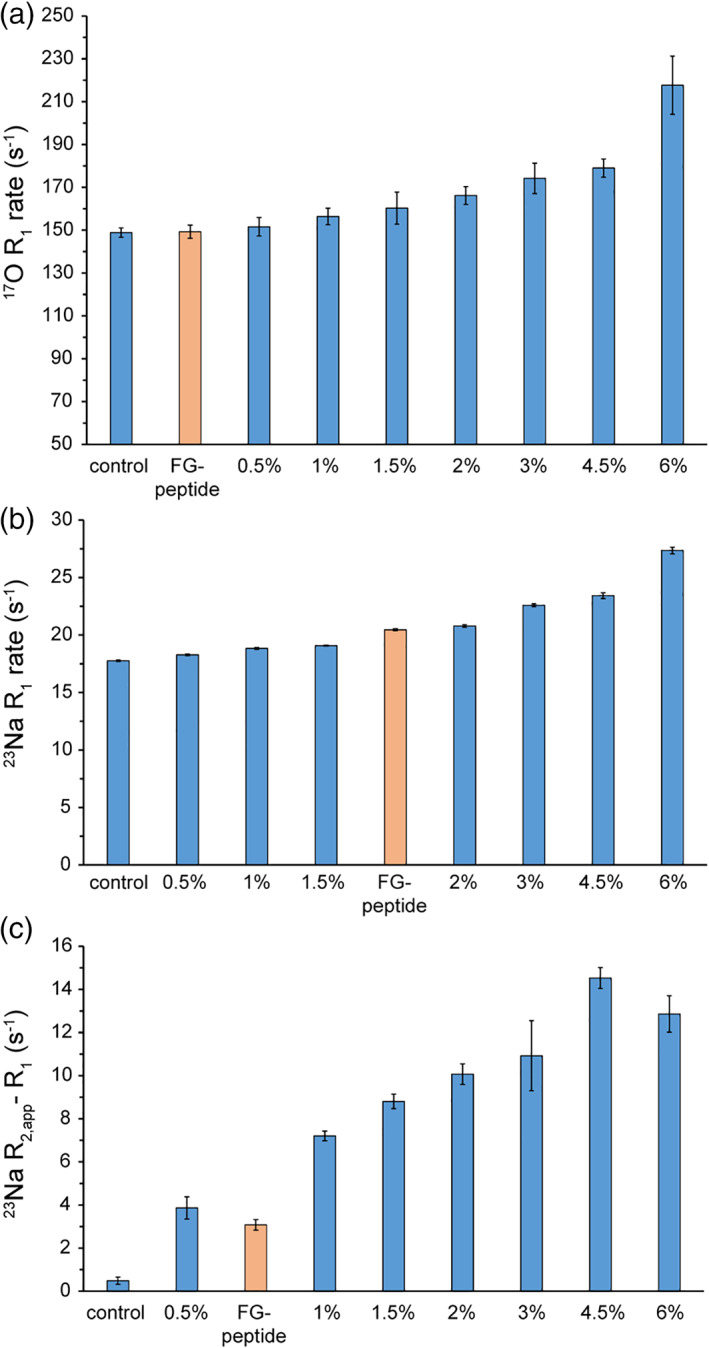
²³NaCl and H2¹⁷O NMR probes of confinement level in biological hydrogels. The (a) H2¹⁷O and (b) ²³NaCl longitudinal relaxation (R ₁) rates capture the agarose concentration‐dependent restriction in rotational mobility of water molecules and sodium ions. In (c), the difference between ²³Na linewidth‐based R _2,app and R ₁ reveals the extent that sample inhomogeneity contributes to ²³Na R _2,app rates

3.6. ²³NaCl NMR‐based characterization of FG‐rich protein hydrogels

Next, we utilized ²³Na and ¹⁷O NMR to characterize the gel‐like material formed by an FG peptide, which is part of the NPC and controls the traffic between cell nucleus and cytoplasm. ²⁹ The ¹⁷O R ₁ rate of water was 149 ± 3 s⁻¹, indicating that the (rotational) mobility of water molecules within the FG peptide gel was even larger than that of the 0.5% agarose gel (Figure 3a). On the other hand, the ²³Na R ₁ rate of sodium ions was 20.5 ± 0.1 s⁻¹. The ²³Na chemical shift in the FG‐based gel was indistinguishable from the control sample, thus the increased ²³Na R ₁ rate was largely caused by the significantly restricted rotational mobility of sodium ions within the FG gel (Figure 3b). Interestingly, the comparison between ²³Na R ₁ and the linewidth‐based R _2,app revealed some degrees of sample inhomogeneity in the FG peptide gel (Figure 3c). Finally, the D _tr of sodium ions indicated a high level of translational mobility within the FG gel comparable to 4.5–6% agarose gels (Figure S9). Taken together, the combined use of ²³Na and ¹⁷O NMR provided a detailed picture of the interior of FG‐based gel regarding the mobility of sodium ions and water molecules, as well as the degree of its inhomogeneity.

3.7. ²³NaCl NMR in phase separation of TEA‐water mixture

To further explore the potentials of ²³NaCl NMR in characterizing phase separation, we studied a water‐TEA mixture (5%/95% vol/vol), which spontaneously separates into two phases: a less‐dense TEA‐enriched phase and a more‐dense water‐enriched phase (Figure 4a). The sample contained 300 mM NaCl to enable probing the internal environment of the two phases. The 1D ²³Na spectrum of the whole sample spanning both phases showed a complex peak, consisted of at least three overlapped peaks at ca. 1.06, 0.53, and 0.19 ppm (Figure 4a). After putting the lower water‐enriched phase outside the detection coil, the 1D ²³Na spectrum was simplified with the leftmost peak at 1.06 ppm almost entirely removed from the spectrum. This observation confirmed that the leftmost peak was largely originated from the water‐enriched phase, while the middle and the rightmost peaks had their origins in the TEA‐enriched phase. The ²³Na R ₁ rate of the peak from water‐enriched phase was 35.4 ± 0.6 s⁻¹, while the collective ²³Na R ₁ rate of the two peaks originated from the TEA‐enriched phase was slightly larger: 38.3 ± 1.0 s⁻¹. The corresponding D _tr coefficients were 0.6 × 10⁻⁹ and 1.1 × 10⁻⁹ m²s⁻¹, respectively.

FIGURE 4.

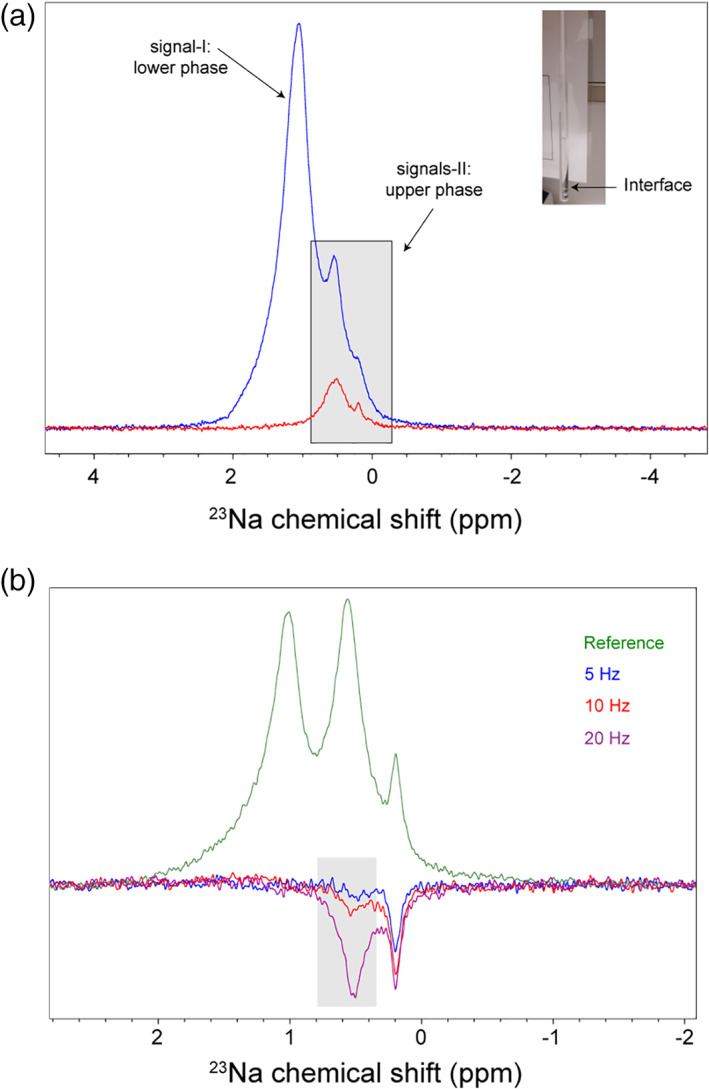
Phase separation in water‐triethylamine (5%/95% vol/vol) mixture, studied by ²³NaCl NMR. (a) The mixture undergoes a rapid phase separation to an upper triethylamine‐rich phase and a lower (relatively) water‐rich phase separated by the “Interface.” 1D ²³Na NMR spectrum of the whole sample encompassing both phases (blue) is superimposed with the spectrum of only the upper phase (red), showing that the leftmost signal is originated from the lower phase, while the two rightmost signals are from the upper phase. (b) 1D difference spectra with selective saturation of the resonance at 0.19 ppm revealed saturation transfer to the resonance at 0.53 ppm, that increased in dependence of the irradiation strength. The selective saturation of the resonance at 0.19 ppm was achieved using continuous‐wave (cw) irradiation at the strengths of 5 (blue), 10 (red) or 20 Hz (purple). The reference spectrum was obtained with irradiation frequency set far off‐resonance (50 ppm)

The presence of more than one ²³Na signal in the TEA‐enriched phase points to the existence of distinct chemical microenvironments within that phase. The 1D spectrum with selective excitation at 0.19 ppm revealed a negative peak at ca. 0.53 ppm (Figure 4b), suggesting the presence of chemical exchange between the two sites. The alternative explanation of through‐space magnetization transfer through cross‐relaxation (NOE) is unlikely, considering the ²³Na R ₁ rates that propose sodium ions dynamics occurring at fast motion regime.

4. DISCUSSION

²³Na NMR measurements of sodium chloride solutions at different temperatures and viscosities established how ²³Na linewidth and R ₁ rates could be utilized as probes of effective viscosity in sodium‐containing biomolecular samples (Figure 2 and Figure S6). In the confined media of agarose gels, ²³Na NMR relaxation and diffusion coefficient were capable of capturing the increasing confinement level in dependence of agarose concentration and its resultant restriction in the rotational and translational mobility of sodium ions (Figure 3 and Figures S8, S9). The use of ²³Na NMR together with ¹⁷O NMR provided a detailed picture of the mobility of sodium ions and water molecules inside an FG peptide hydrogel. In addition, ²³Na NMR was used to detect microscopic inhomogeneity in a model system undergoing phase separation (Figure 4).

The use of ²³Na NMR relaxation and diffusion as probes of solution viscosity and confinement level in biomolecular samples benefits from the advantageous properties of ²³Na nuclei, for example their relatively large gyromagnetic ratio and their 100% natural abundance, increasing the sensitivity of NMR experiments. ¹⁶ , ³⁰ Besides, the high degree of symmetry of the sodium ion and its hydration layer dramatically reduces the EFG tensor at the site of ²³Na nuclei and the consequent reduction in the quadrupolar relaxation rate of ²³Na further improves the sensitivity and resolution of ²³Na NMR spectra. ¹⁷ , ³¹ Our data revealed that the ²³Na NMR relaxation of sodium ions has the further advantage of being more sensitive to subtle changes in the viscosity when compared with ¹⁷O NMR relaxation of water molecules (Figure 2c). On the other hand, the use of ²³Na NMR relaxation in determining solution viscosity is limited to the conditions where the sodium ion hydration especially in the inner layer and therefore the EFG tensor at the site of ²³Na nuclei are not significantly perturbed. In our data, a drastic example of this limitation was observed in crowded sucrose and Ficoll solutions, where the use of ²³Na NMR relaxation led to a significant overestimation of the solution viscosity. Another potential limitation would be that the change in the motional regime of sodium ions significantly alters the relaxation behavior complicating the interpretation of ²³Na NMR relaxation data. ¹⁸ , ¹⁹ For example, at ²³Na Larmor frequency of ~106 MHz in our study, if the tight binding to proteins or other relatively large biomolecules slows down the rotational correlation time (τ_c) of sodium ions to ~1.6 ns or longer, the NMR relaxation of sodium ions in this so‐called “slow” regime will obey a double‐exponential behavior. Further complications could also arise when the sodium ions experience significant heterogeneity in their immediate microenvironments or interact with the various components of the system at different affinities. This may again cause a deviation from single‐exponential relaxation behavior if the exchange rate between different states is slow with respect to the NMR relaxation timescale. However, despite all these potential complications, our data suggest that in a broad range of conditions relevant to biomolecular samples studied through solution NMR, the sodium ions remain within the fast motion regime inside an effectively homogeneous environment and therefore follow single‐exponential NMR relaxation.

Brownian rotational and translational diffusion of biomolecules in solution is influenced by the local “molecular drag” experienced by them. Consequently, the “effective viscosity” determined from NMR measurements of molecular diffusion is not necessarily identical to the viscosity of the bulk solution measured through conventional methods. ²⁵ This is represented in the nonlinear relation between ²³Na NMR probes of solute diffusion and bulk viscosity (Equation (1), (2))). In line with the recently reported nonlinear relation between ¹⁷O NMR relaxation of water molecules and the bulk viscosity, ¹⁴ our ²³Na NMR results indicate that the bulk viscosity is a collective property of solutions not reducible at a first‐order approximation to the dynamics of individual solute molecules.

Biological phase separation leads to the formation of condensed phases, where biomolecular structure and dynamics are potentially altered by the crowded and confined environment inside the condensates. The microscopic physical properties of biological condensates may be altered through the intrinsic maturation process of the condensates, or extrinsic regulatory factors such as recruitment of small molecules, proteins, RNA, and posttranslational modifications. ³ , ⁷ The maturation of condensed phases from liquid‐like to gel‐ or solid‐like droplets could influence the ²³Na NMR relaxation rates by slowing down the rotational dynamics of sodium ions and/or providing a highly anisotropic environment for (partially) dehydrated sodium ions. These alterations manifest themselves in the changes in ²³Na relaxation rates, or potentially in more extreme cases, in transition from “fast” single‐exponential relaxation regime to slower regimes. In agarose gels as an example of confined media, our data showed that the agarose concentration‐dependent increase in mobility restriction is clearly reflected in the ²³Na NMR probes of rotational and translational mobility of sodium ions, along with the ¹⁷O NMR probe of the mobility of water molecules. In addition, the phase transition of the FG peptide into a gel‐like material was mirrored in the ¹⁷O and particularly ²³Na NMR probes of the mobility of water molecules and sodium ions inside the FG‐rich hydrogel. Accordingly, our results support the potential of ²³Na NMR as a sensitive molecular probe of the local environment of biomolecular condensates, allowing detection of subtle changes in the microscopic properties of the condensates in dependence of various physicochemical and biochemical factors. Besides, the capability of ²³Na NMR in detecting microscopic heterogeneity and the corresponding exchange processes was demonstrated in the phase separating TEA‐water mixture (Figure 4).

The traffic between cell nucleus and cytoplasm is controlled by NPCs via gel forming FG‐rich domains of Nups acting as permeability barriers. ²² , ³² Generally, the FG‐rich domains form hydrogels in a wide range of concentrations, however, their transport selectivity may be achieved only at sufficiently high concentrations where the small pore size of the FG hydrogels sets a size limit for the mobile species. ³³ The sieving effect of the FG hydrogels is fine‐tuned through sequence variations, for example, by changing the number of FG repeats or posttranslational modifications. ²² , ³⁴ , ³⁵ When compared with agarose gels as the reference, our data revealed that the rotational and translational mobility of sodium ions and water molecules are variably restricted within the FG hydrogel. Accordingly, we recommend the combined use of ²³Na and ¹⁷O NMR probes of the mobility of sodium ions and water molecules in order to provide a more complete picture of the microscopic environment of the interior of aqueous biological condensates.

5. CONCLUSION

To summarize, we provide experimental support for the potentials of ²³Na NMR in probing the microscopic properties of phase separated biomolecular condensates, enabling monitoring their changes in dependence of various regulatory factors.

6. MATERIALS AND METHODS

Sodium chloride, glycerol, and sucrose were from Merck, Ficoll 400 from Calbiochem, TEA from Sigma‐Aldrich and agarose from Invitrogen. Deionized Milli‐Q water was used for all aqueous solutions. ¹⁵N,¹³C‐labeled ubiquitin was prepared recombinantly, as described in References 36 and 37. The FG‐based peptide (sequence: Acetyl‐GGGGGGLFGGNNNQQTNPTA‐Amid) capped at both N‐ and C‐termini, was obtained from Peptide Specialty Laboratory (PSL, Heidelberg, Germany). The FG‐based peptide solution in 100 mM sodium chloride was prepared at 3 mM concentration and immediately transferred to a 3 mm NMR tube.

6.1. ²³Na NMR

²³Na has spin quantum number I of 3/2. The quadrupole moment (Q) of ²³Na is 12 fm², which represents a prolate‐like charge distribution interacting with the EFG present at the site of ²³Na nuclei. ¹⁶ As a nucleus with spin I = 3/2, the NMR spectrum of ²³Na is generally comprised of a superposition of one central (−1/2 – > 1/2) and two satellite (−3/2 – > −1/2 and 1/2 – > 3/2) transitions, which in solution become degenerate due to the traceless character of the nuclear quadrupolar interaction and its averaging out due to fast unrestrained molecular motions. ¹⁶ , ³⁰ According to Redfield's relaxation theory, the quadrupolar interaction‐induced transverse relaxation of ²³Na contains two components: one for the central transition and the other for two satellite transitions. ¹⁸ , ¹⁹ However, under fast motion regime (“extreme narrowing” condition, which is relevant in the current study unless specified otherwise) where ω ₀ τ _c ≪ 1 (ω₀: Larmor's frequency, τ_c: rotational correlation time), all the components share the same relaxation rate, as follows:

$$R_1=R_2=\frac{3{\pi }^2}{10}\left(\frac{2I+3}{I^2\left(2I-1\right)}\right){\chi }^2\left(1+\frac{{\eta }^2}{3}\right){\tau }_c$$ (3)

where I = 3/2 is the spin quantum number of ²³Na, $\chi =\frac{e^{2}Q{q}_{\mathit{zz}}}{h}$ is quadrupole coupling constant (C_Q) and η is the asymmetry parameter, describing the deviation of EFG tensor, q, from axial symmetry. It is however notable that the bi‐exponential relaxation of ²³Na nuclei is recovered in the slow motion regime where ω ₀ τ _c ≥ 1, ¹⁸ , ¹⁹ and the ²³Na relaxation deviates from Redfield's theory predictions when molecular motion is further slowed down and the systems enters the so‐called ultraslow motion regime where ${\omega }_0{\tau }_c>{\left(\frac{{\omega }_0}{{\omega }_Q}\right)}^2$ (ω_Q is quadrupolar coupling constant C_Q in angular frequency units). ²⁰ , ²¹

6.2. NMR measurements

²³Na NMR experiments were performed at a Bruker spectrometer with proton Larmor frequency of 400.13 MHz. The spectrometer was equipped with a room‐temperature triple resonance broadband (TBO) probe, where for the ²³Na‐detected experiments the inner coil of the probe was tuned and matched at ²³Na Larmor frequency of ~105.84 MHz. The temperature was controlled to ±0.05 K using the Bruker VT unit calibrated through a standardized thermocouple. The NMR samples contained H₂O/D₂O at a ratio of 90%/10% (vol/vol), unless specified otherwise, and the deuterium signal was used for frequency locking. The water‐TEA (5%/95% vol/vol) sample in a 3‐mm NMR tube was placed inside a 5‐mm NMR tube filled with D₂O for frequency locking. Instead of calibrating against 1 M ²³NaCl as the external reference (0.000 ppm), the ²³Na spectra are shown using the frequency of H²DO lock signal as the chemical shift reference (4.700 ppm). In this way, the temperature‐dependent variation of ²³NaCl chemical shifts (e.g., because of changes in sodium ion dehydration) were more visible and could be more easily compared with the ²³NaCl chemical shift changes in dependence of glycerol concentration (Figure 1 and Figure S3). When needed, the actual frequency of H²DO lock signal was calculated from the known temperature dependence of water proton/deuterium resonance:

$$\delta \left(H2O\right)=7.83-T\left(K\right)/96.9\mathrm{ppm}$$ (4)

and utilized for the indirect chemical shift referencing of ²³Na (and other) nuclei.

²³Na longitudinal relaxation (R ₁) rates were measured through standard inversion‐recovery (d ₁‐180°‐t‐90°‐acq) pulse sequence, where duration of recovery time, t, varied from 0.25 to 500 ms. A total of 26 to 34 recovery data points were collected. A total recycle delay (d ₁ + acq) of ca. 1 s was used. The ²³Na signal intensity followed single‐exponential recovery curves, as expected in the “extreme narrowing” regime of motion for sodium ions. The data were fitted to a three‐parameter single‐exponential recovery function, as follows:

$$I=a\left(1-2b{e}^{-R_{1}t}\right).$$ (5)

The fit to a five‐parameter double‐exponential recovery function did not show any considerable improvement, even at the sample with highest ²³Na R ₁ rate in this study (Figure S10). The natural linewidths (lw) of ²³Na resonances were obtained through single‐Lorentzian fitting of peaks in 1D ²³Na spectra processed without apodization. The apparent transverse relaxation (R_2,app) rates were then estimated through the following equation:

$$R_{2,\mathrm{app}}=\pi .\mathit{lw}.$$ (6)

Translational diffusion coefficient (D _tr) of sodium ions were measured through standard PFG stimulated‐echo (STE) diffusion experiments with diffusion gradient length (δ) of 5 ms and diffusion delay (Δ) of 40 ms and 12 or 16 gradient strength levels linearly ranging from 5 to 95% of the maximal gradient strength. Gradient calibration was performed using the known diffusion coefficient of residual HDO in 99.8% D₂O at 298.14 K (1.9 × 10⁻⁹ m²s⁻¹, Figure S11). The absence of significant convection was confirmed through diffusion measurements of the control sample (100 mM NaCl in 10% D₂O, 90% H₂O) at 3‐ and 5‐mm NMR tubes, using two diffusion delays of 40 and 100 ms.

The natural abundance ¹⁷O R ₁ rates of water molecules were measured as described in Reference 14.

AUTHOR CONTRIBUTIONS

Juan Carlos Fuentes‐Monteverde: Investigation; visualization; writing‐review and editing. Stefan Becker: Resources; writing‐review and editing. Nasrollah Rezaei‐Ghaleh: Conceptualization; formal analysis; funding acquisition; investigation; methodology; project administration; resources; supervision; visualization; writing‐original draft; writing‐review and editing.

CONFLICTS OF INTEREST

The authors declare no potential conflict of interest.

Supporting information

Appendix S1: Supplementary Information

Fuentes‐Monteverde JC, Becker S, Rezaei‐Ghaleh N. Biomolecular phase separation through the lens of sodium‐23 NMR. Protein Science. 2021;30:1315–1325. 10.1002/pro.4010