Abstract
We demonstrate quantitatively how values of electron densities in GaAs extracted from Raman spectra of two samples depend on models used to describe electric susceptibility and band structure. We, therefore, developed a theory that is valid for any temperature, doping level, and energy ratio proportional to q2=(ω + iγ) (where q is the magnitude of wave vector, ω is Raman frequency, and γ is plasmon damping). We use a full Mermin–Lindhard description of Raman line shape and compare n-type GaAs spectra obtained from epilayers with our simulated spectra. Our method is unique in two ways: (1) we do a sensitivity analysis by employing four different descriptions of the GaAs band structure to give electron densities as functions of Fermi energies and (2) one of the four band structure descriptions includes bandgap narrowing that treats self-consistently the many-body effects of exchange and correlation in distorted-electron densities of states and solves the charge neutrality equation for a two-band model of GaAs at 300 K. We apply these results to obtain electron densities from line shapes of Raman spectra and thereby demonstrate quantitatively how the values of electron densities extracted from Raman spectra of n-type GaAs depend of various models for susceptibility and band structure.
I. INTRODUCTION
The semiconductor and chemical industries require equipment that more accurately, non-destructively, and cost-effectively measures carrier densities.1–3 The carrier density characterization relates to device performance and to process control and is critical for determining whether compound semiconductor materials meet specifications and are worthy of further processing. Such measurements enable manufacturers to produce next-generation devices with improved figures of merit such as switching speeds, low power, and other operating efficiencies to reduce the cost per unit area and the cost per function, and to increase yield and productivity. The carrier concentration is a key figure of merit associated with a go–no–go decision for determining whether a wafer meets specifications and should undergo further processing. Non-destructive, optical measurements of carrier densities are crucial in the characterization of nanoscale semiconductors.4–10
As devices shrink in size to nanometers, performing experimental measurements becomes more costly and time-consuming. This trend means that computer simulations will be more essential for advances in future nanotechnologies.
Raman spectroscopy is an attractive non-destructive method for material acceptance tests and process validation. Our proposed Raman technique11 will allow process engineers in the semiconductor industry to
Go from what they can measure to what they need to know for process control, even though they cannot measure directly what they need to know.
Extract transport properties from Raman spectra of compound semiconductors. Raman spectroscopy requires minimal sample preparation and is particularly useful as a non-destructive technique.
The interpretation of Raman spectra to determine the electron density in n-type semiconductors is an interdisciplinary effort involving Raman experiments, theory, and computer-based simulations. Because most of the necessary input data for GaAs exist and the physics of the phonon–plasmon coupled modes in this system is well understood,12,13 we implement numerically here the theory11 for the calculation of Raman spectra and investigate how the Raman spectra vary as functions of the Fermi energy, plasmon damping, and temperature in zinc blende, n-type GaAs for donor densities between 1016 cm−3 and 1019 cm−3. We demonstrate quantitatively as illustrative examples how the values of electron densities in GaAs extracted from the Raman spectra of two samples depend on the models used to describe the electric susceptibility and band structure. Our goal is not to compare quantitatively the electron densities extracted from interpreting Raman spectra with those values extracted from interpreting Hall effect measurements. The numerical implementation of the algorithm, previously published in Ref. 11, enables the practical extraction of electron densities non-destructively from Raman spectra of very thin layers, e.g., epilayers, of compound semiconductors. The algorithm combines numerical results from validated, robust theoretical models that are based upon detailed quantum mechanical calculations and Raman spectra to give a method for determining electron densities in n-type compound semiconductors.
The algorithm has two independent input parameters, namely, the Raman excitation energy or frequency and the temperature and consists of the following four steps:
Simulation of Raman Spectra. Calculate the shapes of peaks in Raman spectra due to the coupling between longitudinal optic phonons and plasmons from the real and imaginary parts of the electric susceptibility as a function of the Fermi energy.
Determination of Fermi energy. Model Raman spectra for different Fermi energies. From among the many calculated Raman spectra, determine the Fermi energy for which the calculated Raman spectra agree best with the measured Raman spectra.
Computation of carrier density as a function of the Fermi energy. Solve the charge neutrality equation self-consistently with one of the four band structure models to calculate the carrier density as a function of the Fermi energy at a given temperature.
Determination of electron density. Obtain the carrier density from the Fermi energy identified in step 2 and the result in step 3.
The theory assumes that a sufficient number of atoms exists to define an appropriate wave vector space in two- or three-dimensions for the material of interest and for performing the foregoing steps 1 and 3. The present algorithm uses for illustrative purposes a three-dimensional wave vector space appropriate for the zinc blende lattice to describe the band structure models and perturbed–distorted densities of states due to many-body effects in n-type GaAs.
Unlike many models for step 3 that are based on using variations in parameters to fit experimental data, the Bandgap Narrowing (BGN) model, one of the four band structure models presented below in Sec. III, is based on quantum mechanical calculations with no fitting parameters to account for dopant ion effects and many-body physics effects. The calculations for the BGN model include the effects of high carrier concentrations and dopant densities on the distorted–perturbed densities of states used to calculate the Fermi energy as a function of temperature, bandgap narrowing due to dopant ion carrier interactions, and the many-body quantum effects due to both carrier exchange and correlation interactions. The algorithm given here for the BGN model is unique because all other reported treatments for the electric susceptibility do not treat these many-body effects self-consistently. Several of the reported treatments for the electric susceptibility in compound semiconductors consider approximate forms that result from expansions in either q or the ratio q2/(ω + iγ), where q is the magnitude of the wave vector, ω is the Raman frequency, and γ is the plasmon damping. For instance, the treatment for the electric susceptibility of GaInAsSb reported in Ref. 14 considers the hydrodynamic and the Lindhard–Mermin (LM) models, and the authors note that the latter leads to a simplified Drude-like model, with a wave-vector-dependent plasma frequency, when expansions in small q are considered. We will adopt the Lindhard–Mermin model in our calculations.
We describe in Sec. II the experimental measurements for the Raman spectra. We present in Sec. III the theoretical models used to calculate Raman line shapes. Finally, we show quantitatively in Sec. IV a proof-of-concept for extracting electron densities from Raman line shapes.
II. EXPERIMENTAL MEASUREMENTS
We measured Raman spectra on three samples of n-type GaAs. Samples A and B were 2 μm thick epilayers doped with silicon and grown by metal organic chemical vapor deposition. Sample C was a bulk single crystal. Samples A and B had electron concentrations of nHall−A = 1:4 × 1018 cm−3 and nHall−B = 5:8 × 1018 cm−3, respectively, as determined from the Hall effect measurements performed by the supplier. Sample C was doped as-grown with a reported electron concentration between 5.2 and 8:4 × 106 cm−3 and was used as a reference sample for the purposes of this investigation. Uncertainity in the electron densities were not reported by the manufacturer.
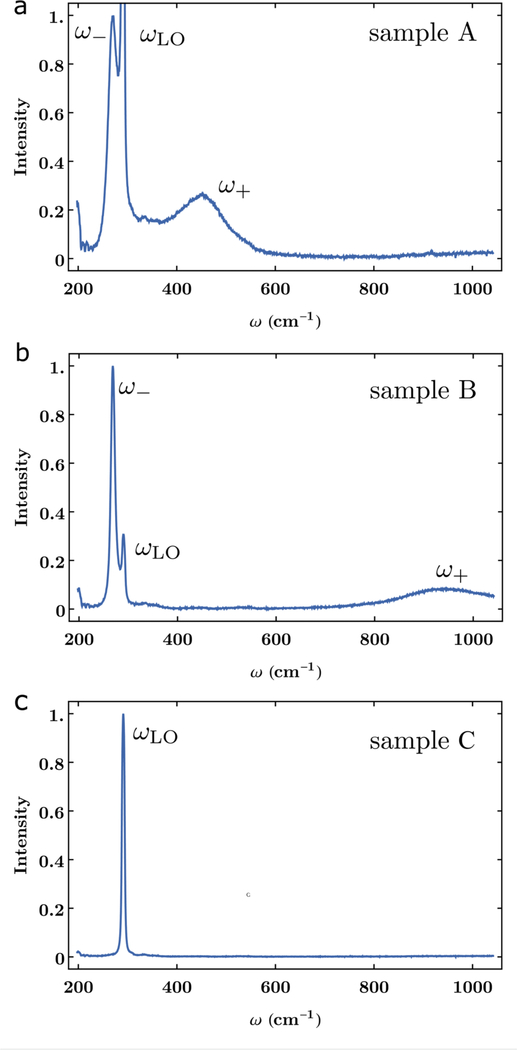
We performed Raman spectroscopic measurements at room temperature in a backscattering geometry described by , where x, y, z, and denote the [100], [010], [001], and directions, respectively, and using 514.5 nm excitation radiation. We used a single-grating imaging spectrograph equipped with a back-illuminated charge coupled device camera system to collect the scattered radiation. The instrumental bandpass (FWHM) was approximately 4:7 cm−1. We corrected the Raman scattering intensities for the wavelength-dependent response of the optical system using a white-light source of known relative irradiance. Figures 1(a)–1(c) contain, respectively, the measured Raman spectra for samples A, B, and C that we obtained in a dark laboratory with no ambient lighting.
FIG. 1.
Experimental Raman line shapes measured on samples of GaAs with nominal values on the electron densities Ne. (a) Ne = 1:4 × 1018 cm−3. (b) Ne = 5:8 × 1018 cm−3. (c) Ne = 5.2 − 8:4 × 106 cm−3 The line shape in (c), corresponding to a sample with low electron density, reveals a single peak for the longitudinal optical mode ωLO in GaAs. As the electron density increases, local plasmons develop, which couple to the LO mode. The resulting coupled states appear as two additional peaks in the Raman spectra ω− and ω+ in (a) and (b). We notice that the frequencies ω− and ω+, as well as their broadening, are sensitive to the dopant concentration of the sample. The intensity is normalized to the maximum signal in ωLO for (c) and ω− in (a) and (b).
III. THEORY
A. Step 1—Raman spectra
In the relaxation time approximation, the full longitudinal dielectric response function ε(q, ω) at an angular frequency ω and scattering wave vector q is
| (1) |
where the dielectric susceptibility χVE is the contribution from valence electrons, χL (ω) is the contribution from the polar lattice phonons, and χe(q, ω) is the contribution from the conduction electrons. We define the high frequency dielectric constant by such that for a binary semiconductor, Eq. (1) becomes
| (2) |
The contribution of the polar lattice phonons is15
| (3) |
where we neglect the phonon damping and ωLO and ωTO are the longitudinal (LO) and transverse (TO) phonon angular frequencies.
Utilizing the relaxation time approximation, the Lindhard expression16 gives the electronic contribution to the zero order17 dielectric response function that describes light scattering by the conduction electrons in doped semiconductors,
| (4) |
where f (E) = (1 + exp{β(E − EF)})−1 is the Fermi–Dirac distribution function, E(k) is the energy dispersion of the conduction band, EF is the Fermi energy, β = (kBT)−1 and T is the absolute temperature. To account for the losses associated with electron-phonon and electron–dopant interactions, we introduce the collision relaxation time τ and the corresponding angular collision frequency γ = τ−1. Mermim18 demonstrated that within the relaxation time approximation, the electron–dopant and electron–phonon interactions relax the electron density matrix to a local equilibrium density matrix18–20 and derived the following expression for the electronic susceptibility χe(q, ω) that incorporates γ:
| (5) |
Equation (5) constitutes the Lindhard–Mermin (LM) model for the electronic susceptibility.
Next, we obtain a simplified form for the LM model in Eq. (5). First, note that the integrand in Eq. (4) is independent of the azimuthal angle ϕ. We, therefore, integrate with respect to this degree of freedom and introduce a new variable μ = cos θ in terms of the polar angle θ such that the integral element transforms as , and q · k = qkμ. Also, we introduce the following dimensionless normalized quantities: Q = qaB, K = kaB, , and , where is the Rydberg energy. As a result, Eq. (4) takes the form
| (6) |
The longitudinal optical (LO) phonons and plasmons interact in GaAs, a polar semiconductor, to form LO phonon–plasmon hybrid modes. The line shape function LA(q, ω) of the Raman spectrum that contains longitudinal optical (LO) phonon–plasmon hybrid modes present in GaAs is15
| (7) |
where is a parameter with angular frequency units, and CFH is the dimensionless Faust–Henry coefficient that accounts for the longitudinal/transverse optical phonon scattering ratio. Equation (7) includes the deformation potential and the electro-optic mechanisms.
Here, we use the command NIntegrate from Mathematica21 to numerically evaluate the double integral in Eq. (6) at room temperature and obtain the exact result. The function LA(q, ω) in Raman spectra then becomes
| (8) |
where
| (9) |
and
| (10) |
We note that approximate analytical forms, similar to the Drude model, can be derived as expansions in terms of the ratio of Eqs. (4) and (5). See the supplementary material section for further details.
B. Step 3—Charge neutrality: Relate electron density to Fermi energy
The interpretations of Raman measurements on compound semiconductors such as GaAs require physical models and associated input parameters that describe how carrier densities vary with dopant concentrations and Fermi energies. We introduce two main classes of models that relate carrier concentrations to the Fermi energy for a given temperature and donor dopant density: Bandgap narrowing (BGN) models and Parabolic densities of states (PDOS) models.
Because the Fermi energy EF and the damping γ are the variables for calculating the Raman spectra, we have to select from among those band structure models in the charge neutrality equation appropriate to the system of interest, those models that are amenable to numerical solutions. The charge neutrality equation connects the electron density and its Fermi energy. Reference 11 contains, for illustrative purposes, self-consistent solutions for the charge neutrality equation utilizing an iterative procedure with carrier densities of states (DOS) for the conduction subbands and the valence subbands at high symmetry points in the wave-vector space. We present here the charge neutrality solutions for the BGN and the PDOS models of n-type GaAs for donor densities between 1016 cm−3 and 1019 cm−3 at 300 K.
1. BGN model
The bandgap narrowing (BGN) model is a two-band model with one equivalent conduction band and one equivalent valence band at the Γ point in the Brillouin space. The BGN model is related to the earlier work (Ref. 22) on n-type GaAs and incorporates modifications to the densities of states due to high concentrations of dopants, bandgap narrowing, and many-body effects associated with carrier–carrier interactions (carrier–carrier exchange and correlation). This model has the following characteristics:
Fermi–Dirac statistics for the electron distribution at any temperature,
Many-body quantum effects such as carrier–carrier and carrier–dopant–ion interactions, bandgap narrowing, and distorted–perturbed DOS for the carriers,
Iterative and self-consistent solutions of the coupled charge neutrality equation and Klauder’s fifth level of approximation for the renormalized self-energy propagator from which we obtain the distorted–perturbed DOS, and
Statistical analyses to obtain analytic expressions from large simulated data for carrier densities as a functions of the Fermi energy.
Tables S2 and S3 in the supplementary material contain the input parameters for the BGN calculations in Ref. 22 and for the BGN model given here.
In the thermal equilibrium, the corresponding electron n and hole h concentrations in units of cm−3 are
| (11) |
| (12) |
where ρC(E) and ρV(E) are the corresponding electron DOS for the equivalent conduction band and the hole DOS for the equivalent valence band. The BGN model invokes the charge neutrality condition NI = n − h and implements the Thomas–Fermi expression for the screen radius rs to compute in a self-consistent form the Fermi energy EF and rs for given values of the ionized dopant concentration NI at any temperature. The results reported here are for the n-type material (NI positive), when that each dopant is ionized. We do not report the results for the screening radius rs here because they are not needed to extract carrier concentrations from Raman scattering measurements.
The BGN model for extracting electron densities from Raman spectra is unique in two respects. First, we include the many-body effects from Ref. 22. That is, the BGN model used here includes self-consistently the many-body effects of carrier–dopant–ion interactions on the conduction and valence bands and their densities of states and the effects of carrier–carrier interactions (majority-carrier exchange and minority-carrier correlation). Second, the BGN as well as the PDOS models are valid at room temperature. Reference 23 included the bandgap narrowing effect due only to the electron–electron exchange interaction for k·p calculations of n-type InP.
We compare our methods with the methods reported in Ref. 24 for GaSb and in Ref. 23 for InP. Reference 24 for GaSb treats conduction band minimum as a nonparabolic band with spherical constant energy surfaces and an isotropic effective mass, while the L conduction band minimum is treated as a parabolic band with four equivalent ellipsoidal constant energy surfaces and an anisotropic effective mass; but it does not include any bandgap narrowing because it assumes that Γ and L are independent of the doping level.
Reference 23 for InP includes the nonparabolicity of the conduction band from a 14 × 14 k·p model that accounts for interactions among the Γ7 split-off valence band, the Γ8 valence band, and the Γ6, Γ7, and Γ8 conducting bands, as well as the bandgap narrowing due to the carrier–carrier exchange interactions given by Ref. 25.
2. PDOS models
All three PDOS models (PDOS2, PDOS2NPG, and PDOS4) incorporate an equivalent valence band with heavy hole mass mhh and light hole mass mlh for the two degenerate subbands at the top of the valence band. mhh and mlh are combined into an effective mass
| (13) |
for the valence top most subband, which then becomes the equivalent valence band with a hole energy dispersion .
These PDOS models use parabolic densities of states for all equivalent bands and subbands. In contrast with the BGN model introduced above, the PDOS models do not include modifications to the DOS due to many-body effects and high concentrations of dopants and carriers. This is, in part, due to the computational cost associated with treating a four-band model in the context of the Klauder self-energy method.
PDOS2 model.
The PDOS2 model uses one equivalent conduction band and one equivalent valence band at the Γ symmetry point in the Brillouin space. The electron energy dispersion for the equivalent conduction band is .
PDOS2NPG model.
The PDOS2NPG model is a two-band model with one equivalent conduction band and one equivalent valence band at the Γ point in the Brillouin space. This model does not include bandgap narrowing, but it includes the nonparabolicity for the electron energy dispersion in the equivalent conduction band at Γ. Following Ref. 26, we can add non-quadratic terms |k|l to the electron energy dispersion EcΓ(k) for the conduction Γ subband in GaAs if k is small, that is,
| (14) |
where ζ is the non-parabolicity factor. In this work, we implement the Kane three level k · p model,27 which does not consider the conduction subbands at L and X, and include quartic terms in E(k) (i.e., we set l = 4).
PDOS4 model.
The PDOS4 model incorporates three conduction subbands at the respective Γ, L, and X symmetry points in the Brillouin space and one equivalent valence band at the Γ symmetry point. For the PDOS4, we modify here the PDOS model for GaSb in Ref. 28 so that it is valid for GaAs. It uses the parabolic electron energy dispersion EcΓ(k) for the conduction Γ subband in GaAs when k is small, namely, .
We adopt the following form29 for the temperature dependence of conduction subband minima relative to the top of the valence band at Γ:
| (15) |
where i = Γ, L, or X. The coefficients Ei0, Ai, and Bi are listed in Table S4 in the supplementary material. Since there are eight equivalent permutations of the wave vector in the (111) direction, we find eight L subband ellipsoids with centers located near the boundary of the first Brillouin zone. The six equivalent permutations of the wave vector in the (100) direction imply that the system has six X subband ellipsoids with centers located close to the boundary of the first Brillouin zone. Since half of each ellipsoid is in the neighboring zone, the number of equivalent subbands NcL for the EcL is four, and the number of equivalent subbands NcX for the X subband is three.
The full DOS ρc(E) in the four-band PDOS4 model for the majority-carrier electrons in n-type GaAs is, therefore,
| (16) |
where ρcΓ(E), ρcL(E), and ρcX(E) are the DOS for the conduction Γ, L, and X subbands with corresponding effective masses of mcΓ, mcL, and mcX. On the other hand, the DOS for the minority-carrier holes with an effective mass of mνΓ is
| (17) |
The quantitative significances that the relative effects of electrons in the upper level sub-conduction bands have on the Fermi energy vary with the particular n-type semiconductor. For example, the few electrons in L and X sub-conduction bands of n-type GaAs have a negligible effect on the Fermi energy. However, this is not the case for some other zinc blende, semiconductors such as n-type GaSb and InP as discussed in many papers such as Refs. 23, 28, 30, 31 and 32.
Interpreting experiments for GaSb and InP requires at least a three-band model and under some conditions may require a four-band model (see Ref. 28), even though GaSb and InP are intrinsically direct semiconductors, electrons for n-type GaSb and InP in the vicinity of their Fermi surfaces will have some characteristics that are similar to those for electrons in indirect semiconductors.
IV. NUMERICAL IMPLEMENTATIONS
Step 1. Simulation of Raman spectra
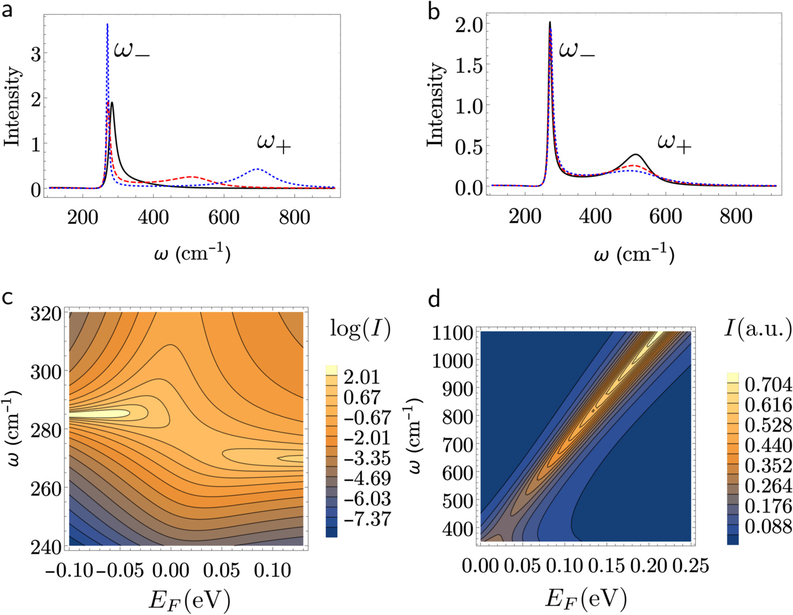
We iterate the calculated Raman line shape function Eq. (8) with the Fermi energy EF and the plasmon damping γ as variation parameters to give the best self-consistent fit to the measured Raman line shape (peaks). Then, after selecting an appropriate band structure model from among various band structure models, such as those suggested in Sec. III B, we determine the carrier density from the Fermi energy. Numerical Raman line shapes that we obtain from Eq. (8) with parameters representative of n-type GaAs are presented in Fig. 2. The line shape reveals two peaks, corresponding to two coupled phonon–plasmon states with corresponding frequencies ω− and ω+, which differ from the frequency of the uncoupled (longitudinal) phonon ωLO such that ω− < ωLO < ω+. The frequencies for the coupled modes are sensitive to the Fermi energy and, therefore, to the carrier concentration. Figure 2(a) shows the line shape for three values in EF (EF = 0, 0:05, and 0:10 eV) and a significant change in the frequency for the second peak ω+. The peak for the ω+ mode shows a significant linewidth increase with γ [see Fig. 2(b)]. The dispersion curve in Fig. 2(c) confirms that these peaks correspond to coupled states. Figure 2(d) displays in a contour plot on how the frequency ω+ drifts for larger values with increasing Fermi energy EF.
FIG. 2.
Raman scattering line shapes obtained from Eq. (8) for model systems. (a) Line shape as a function of the incident frequency ω for three different values of the Fermi energy EF at a fix damping rate of γ = 7 meV, EF = 0 eV (black, solid), EF = 0:05 eV (red, dashed), and EF = 0:10 eV (blue, dotted). (b) line shape for different values in the damping energy γ at a fix value Fermi energy EF = 0:05 eV, γ = 3:5 meV (black, solid), γ = 7 meV (red, dashed), and γ = 10:5 meV (blue, dotted). (c) and (d) present, respectively, in the logarithmic and normal scale, contour plots for the Raman Spectra I, in atomic units, as a function of the Raman frequency ω and the Fermi energy EF. (c) Reveals the formation of hybrid plasmon–phonon states with characteristic frequencies ω− and ω+. Due to thermal broadening and the plasmon damping, the avoided crossing in the dispersion curve is shadowed. (d) shows how the frequency ω+ shifts with Fermi energy EF. Although the intensity of the ω+ branch increases with EF, in real Raman scattering measurements the intensity of this branch decreases as the electron density increases due to the increase of plasmon damping arising from ionized impurity scattering. Other parameters are CFH = −0:28, ωLO = 284.7 cm−1, ωTO = 267:8 cm−1, meff = 0:067mo, ε∞ = 10.9.
We report experimental Raman measurements in Fig. 1 for three samples with different carrier concentrations. The intensity is normalized to the maximum of the ωLO in Fig. 1(c), and ω− peak in Figs. 1(a) and 1(b). For low carrier concentrations the Raman peaks display a single peak, corresponding to the free longitudinal phonon. For larger electron densities, the Raman line shape consists of three peaks that we identify with the two coupled phonon–plasmon modes, and the uncoupled longitudinal phonon in the depletion region. The anticipated shift in the position of the second peak ω+ as a function of carrier densities is experimentally observed in Figs. 1(a) and 1(b).
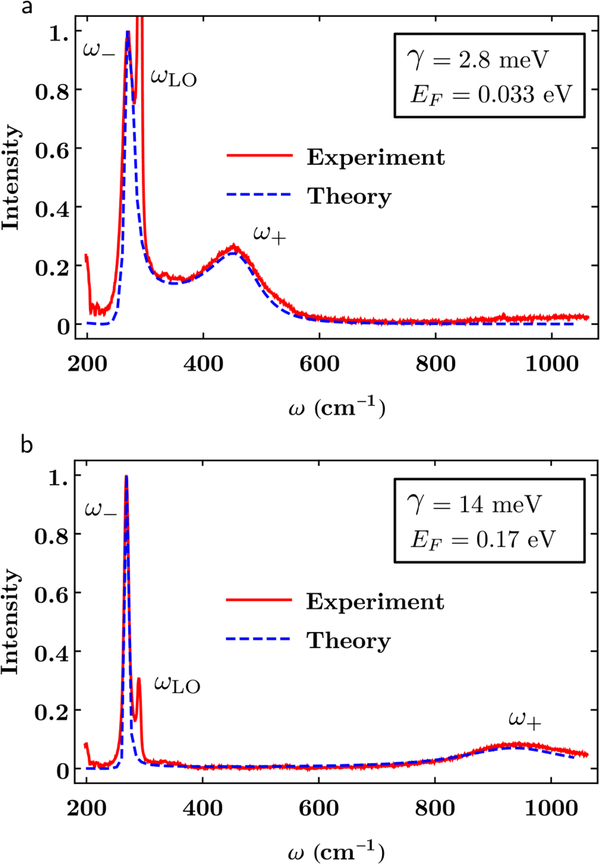
Step 2. Determination of Fermi energy
We fit the measured line shapes in Figs. 1(a) and 1(b) to the form in Eq. (8) utilizing as variational parameters EF and γ. The results are presented in Fig. 3, where the intensity of the theoretical line shape has also been normalized. We notice that both the Fermi energy and the damping are different between samples, and while the theory does not account for the contribution of uncoupled phonon to the total line shape, one can remove this contribution from the spectra by subtracting the intensity for samples at low carrier densities [e.g., Fig. 1(c)]. However, we notice that this additional step is not required in the interpretation and numerical fitting of the Raman signals. These completes step 2 of our algorithm.
FIG. 3.
Numerical fit of the theoretical line shape in Eq. (8) to the experimentally measured Raman spectra reported in Fig. 1. The intensity is normalized to the maximum of the ω− peak. The Fermi energy EF and the damping γ are the fitting parameters. In (a) EF = 33 meV and γ = 2.8 meV and (b) EF = 0.17 eV and γ = 14 meV. Other parameters are as in Fig. 1.
Step 3. Computation of carrier density as a function of the Fermi energy
Obtaining the carrier density requires an analytic representation of the band structure for the GaAs. We refer readers to Ref. 11 for more complete, detailed discussions about the analytic fits to the theoretical results given by the four models labeled therein as BGN and PDOS models (PDOS2, PDOS2NPG, and PDOS4). In each case, the numerical prediction for the logarithm of the electron density nM (M = BGN, PDOS, PDOS2NPG, PDOS4) is fitted to a fourth order polynomial in the Fermi energy of the form
| (18) |
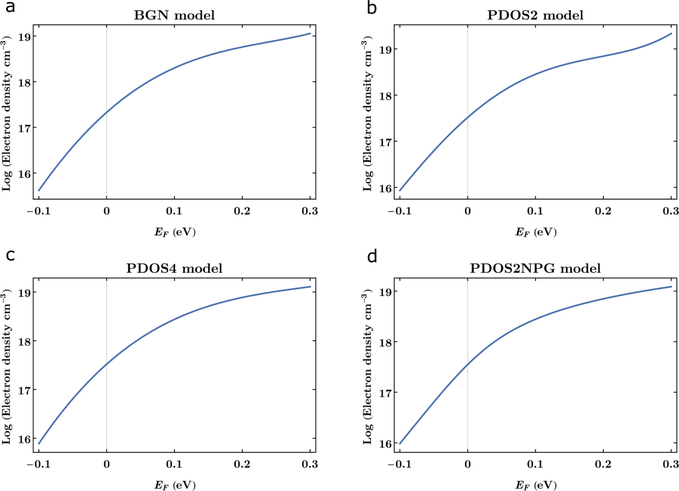
with coefficients aMi. Figure 4 presents the result of Eq. (18) for the four models analyzed here for Fermi energies ranging from −0.1 eV to 0:3 eV. We note that unlike GaSb, most of the electrons for GaAs are in the conduction subband at Γ, the conduction subband at L is only weakly populated at the highest Fermi energies, and the conduction subband at X is negligibly populated. This explains why there is very little difference between the PDOS2 and PDOS4 models for GaAs.
FIG. 4.
Determination of electron densities nM in GaAs from the Fermi energy identified in the Raman line shapes. The logarithm of the electron densities for (a) BGN, (b) PDOS2, (c) PDOS4, and (d) PDOS2NPG models as a function of Fermi energy are shown.
Step 4. Determination of electron density
We can finally determine with the results in Fig. 4, the electron densities for the samples A nd B in Figs. 1(a) and 1(b) and corresponding Figs. 3(a) and 3(b). We interpolate in Fig. 4 from the Fermi energies obtained in the numerical fitting in Fig. 4 the electron densities for each model. We report in Table I the electron densities nM in GaAs from the Fermi energy identified in the Raman line shapes. The logarithm of the electron densities for (a) BGN, (b) PDOS2, (c) PDOS4, and (d) PDOS2NPG models as a function of Fermi energy is calculated utilizing the fitting coefficients reported in Table S5 in the supplementary material. We conclude that the present approach provides reasonable predictions of the electron densities in GaAs. The theoretically predicted electron densities depend on the choice for the values of GaAs material properties and the density of states models used to compute the electron density from the Fermi energy. The predicted values among the four models (BGN, PDOS2, PDOS2NPG, and PDOS4) span a range of about 30% for both samples. We used whenever possible well-established values for GaAs materials properties given in the supplementary material section. The authors of Ref. 24 estimate that the statistical variation for nHall in GaSb is 10% based on measurement reproducibility for the decade of 1018 cm−3. Considering the similarities between GaAs and GaSb for some of their respective Hall effect parameters, we would expect that the statistical variation for the measurement reproducibility of nHall in GaAs to be also 10% for the decade of 1018 cm−3. However, considering the eight sources of error for Hall effect measurements listed by Thurber,33 we estimate that those eight sources of error contribute to a larger than 10% uncertainty in the nominal electron densities reported for samples A and B. As we state in the foregoing, our goal is to show quantitatively how the values of electron densities extracted from Raman spectra depend on both electric susceptibility models and band structure models. We consider the Raman spectra of sample A and B to be representative of GaAs spectra in the decade of 1018 cm−3. Our goal is not to compare quantitatively Raman and Hall effect determinations of electron densities for samples A and B. Improved values are possible if other parameters, such as effective masses, are adjusted for samples with known electron densities. This method can also be extended to other semiconductors if adequate models for the band structure near symmetry points such as the Γ point are available.
TABLE I.
Comparison between theoretically predicted and nominal electron densities for the samples A and B on Figs. 3(a) and 3(b).
| Sample | A | B |
|---|---|---|
| Fit to ω+ peak (cm−1) | 450 | 940 |
| EF (eV) | 0.033 | 0.17 |
| γ (meV) | 2.8 | 14 |
| CFH | −0.28 | −0.28 |
| nBGN (1018 cm−3) | 0.53 | 4.4 |
| nPDOS2 (1018 cm−3) | 0.80 | 5.6 |
| nPDOS2NPG (1018 cm−3) | 0.86 | 5.5 |
| nPDOS4 (1018 cm−3) | 0.78 | 6.0 |
| nHall (1018 cm−3) | 1.4 | 5.8 |
V. CONCLUSION
We introduced an algorithm for the extraction of carrier densities in compound semiconductors, which includes simulation of Raman spectra as a function of Fermi energy, and band structure calculations. We applied this methodology to different samples of n-type GaAs of known electron doping to provide a proof of concept. Our theoretical analysis for extracting electron densities from Raman spectra is unique in two ways: (1) one of the four physical models, the BGN physical model treats the many-body effects self-consistently and (2) all four physical models are valid at any temperature, e.g., room temperature. When high concentrations of carriers exist, this theory and its associated numerical procedures for determining carrier concentrations from Fermi energies are necessary for interpreting room temperature Raman spectra self-consistently.
Supplementary Material
ACKNOWLEDGMENTS
The authors acknowledge many discussions with their colleagues at the National Institute of Standards and Technology, especially Angela Hight-Walker, Garnett Bryant, Adam Bianchi, and Thuc Mai and thank their respective NIST managers for continued support of our Raman project. One of the authors, H.S.B., thanks Alan Heckert for guidance in using DATAPLOT and James Filliben for help in obtaining the closed-form analytic expressions for carrier densities from numerical tabulations of theoretical calculations. M.A.O. acknowledges support under the Cooperative Research Agreement between the University of Maryland and the National Institute of Standards and Technology Physical Measurement Laboratory (Award No. 70NANB14H209) through the University of Maryland.
Certain commercial equipment, instruments, or materials are identified in this paper in order to specify the experimental procedure adequately. Such identification is not intended to imply recommendation or endorsement by the National Institute of Standards and Technology, University of Maryland, and AltaTech Strategies LLC, nor is it intended to imply that the materials or equipment identified are necessarily the best available for the purpose.
Footnotes
DATA AVAILABILITY
The data that support the findings of this study are available from the corresponding author upon reasonable request.
SUPPLEMENTARY MATERIAL
See the supplementary material for additional tables that include data parameters used in the calculation of the coefficients in Eq. (18) for each model and an expanded discussion on approximate forms to the susceptibility.
REFERENCES
- 1.Bennett HS, J. Res. Natl. Inst. Stand. Technol 112, 25 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Bennett HS, Andres H, and Pellegrino J, J. Res. Natl. Inst. Stand. Technol 114, 237 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Garlapati SK, Divya M, Breitung B, Kruk R, Hahn H, and Dasgupta S, Adv. Mater 30, 1707600 (2018). [DOI] [PubMed] [Google Scholar]
- 4.Spirkoska D, Abstreiter G, and I Morral AF, Nanotechnology 19, 435704 (2008). [DOI] [PubMed] [Google Scholar]
- 5.Jeganathan K, Debnath R, Meijers R, Stoica T, Calarco R, Grützmacher D, and Lüth H, J. Appl. Phys 105, 123707 (2009). [Google Scholar]
- 6.Bhattacharya S, Datta A, Dhara S, and Chakravorty D, J. Raman Spectrosc 42, 429 (2011). [Google Scholar]
- 7.Ho C-H, Varadhan P, Wang H-H, Chen C-Y, Fang X, and He J-H, Nanoscale 8, 5954 (2016). [DOI] [PubMed] [Google Scholar]
- 8.Madapu KK, Polaki S, and Dhara S, Phys. Chem. Chem. Phys 18, 18584 (2016). [DOI] [PubMed] [Google Scholar]
- 9.Robins LH, Horneber E, Sanford NA, Bertness KA, Brubaker M, and Schlager J, J. Appl. Phys 120, 124313 (2016). [Google Scholar]
- 10.Parida S, Patsha A, Bera S, and Dhara S, J. Phys. D: Appl. Phys 50, 275103 (2017). [Google Scholar]
- 11.Bennett HS, J. Res. Natl. Inst. Stand. Technol 112, 209 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Pinczuk A, Abstreiter G, Trommer R, and Cardona M, Solid State Commun 21, 959 (1977). [Google Scholar]
- 13.Abstreiter G, Trommer R, Cardona M, and Pinczuk A, Solid State Commun 30, 703 (1979). [Google Scholar]
- 14.Cuscó R, Alarcón-Lladó E, Artús L, Hurst WS, and Maslar JE, Phys. Rev. B 81, 195212 (2010). [Google Scholar]
- 15.Abstreiter G, Cardona M, and Pinczuk A, in Light Scattering in Solids IV (Springer, 1984), pp. 5–150. [Google Scholar]
- 16.Lindhard J, Dan. Vid. Selsk Mat. Fys. Medd 28, 8 (1954). [Google Scholar]
- 17. The susceptibility in Eq. (4) is the limit form for the Lindhard–Mermim susceptibility in Eq. (5) when γ vanishes. In this respect, Eq. (4) is a zero order approximation.
- 18.Mermin ND, Phys. Rev. B 1, 2362 (1970). [Google Scholar]
- 19.Ernst S, Goni A, Syassen K, and Cardona M, Phys. Rev. B 53, 1287 (1996). [DOI] [PubMed] [Google Scholar]
- 20.Röpke G, Selchow A, Wierling A, and Reinholz H, Phys. Lett. A 260, 365 (1999). [Google Scholar]
- 21.W. R. Inc., Mathematica, Version 11.3 (W. R. Inc., Champaign, IL, 2018). [Google Scholar]
- 22.Bennett HS, J. Appl. Phys 83, 3102 (1998). [Google Scholar]
- 23.Artús L, Cuscó R, Ibáñez J, Blanco N, and González-Díaz G, Phys. Rev. B 60, 5456 (1999). [Google Scholar]
- 24.Maslar JE, Hurst WS, and Wang C, J. Appl. Phys 104, 103521 (2008). [Google Scholar]
- 25.Bugajski M and Lewandowski W, J. Appl. Phys 57, 521 (1985). [Google Scholar]
- 26.Blakemore J, J. Appl. Phys 53, R123 (1982). [Google Scholar]
- 27.Richter W, Nowak U, Jürgensen H, and Rössler U, Solid State Commun 67, 199 (1988). [Google Scholar]
- 28.Bennett HS and Hung H, J. Res. Natl. Inst. Stand. Technol 108, 193 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Levinshtein M and Rumyantsev S, in Handbook Series on Semiconductor Parameters: Volume 1: Si, Ge, C (Diamond), GaAs, GaP, GaSb, InAs, InP, InSb (World Scientific, 1996), p. 1. [Google Scholar]
- 30.Baraldi A, Colonna F, Ghezzi C, Magnanini R, Parisini A, Tarricone L, Bosacchi A, and Franchi S, Semicond. Sci. Technol 11, 1656 (1996). [Google Scholar]
- 31.Chin V, Solid State Electron 38, 59 (1995). [Google Scholar]
- 32.Ibáñez J, Cuscó R, and Artús L, Phys. Status Solidi B 223, 715 (2001). [Google Scholar]
- 33.Thurber R, see https://www.nist.gov/pml/nanoscale-device-characterizationdivision/popular-links/hall-effect/resistivity-and-hall/hall for “Hall Effect Measurements Sources of Error.”
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.