Developmental influence on evolutionary rates and the origin of placental mammal tooth complexity

Significance

Interactions during development among genes, cells, and tissues can favor the more frequent generation of some trait variants compared with others. This developmental bias has often been considered to constrain adaptation, but its exact influence on evolution is poorly understood. Using computer simulations of development, we provide evidence that molecules promoting the formation of mammalian tooth cusps could help accelerate tooth complexity evolution. Only relatively small developmental changes were needed to derive the more complex, rectangular upper molar typical of early placental mammals from the simpler triangular ancestral pattern. Development may therefore have enabled the relatively fast divergence of the early placental molar dentition.

Abstract

Development has often been viewed as a constraining force on morphological adaptation, but its precise influence, especially on evolutionary rates, is poorly understood. Placental mammals provide a classic example of adaptive radiation, but the debate around rate and drivers of early placental evolution remains contentious. A hallmark of early dental evolution in many placental lineages was a transition from a triangular upper molar to a more complex upper molar with a rectangular cusp pattern better specialized for crushing. To examine how development influenced this transition, we simulated dental evolution on “landscapes” built from different parameters of a computational model of tooth morphogenesis. Among the parameters examined, we find that increases in the number of enamel knots, the developmental precursors of the tooth cusps, were primarily influenced by increased self-regulation of the molecular activator (activation), whereas the pattern of knots resulted from changes in both activation and biases in tooth bud growth. In simulations, increased activation facilitated accelerated evolutionary increases in knot number, creating a lateral knot arrangement that evolved at least ten times on placental upper molars. Relatively small increases in activation, superimposed on an ancestral tritubercular molar growth pattern, could recreate key changes leading to a rectangular upper molar cusp pattern. Tinkering with tooth bud geometry varied the way cusps initiated along the posterolingual molar margin, suggesting that small spatial variations in ancestral molar growth may have influenced how placental lineages acquired a hypocone cusp. We suggest that development could have enabled relatively fast higher-level divergence of the placental molar dentition.

Whether developmental processes bias or constrain morphological adaptation is a long-standing question in evolutionary biology (1–4). Many of the distinctive features of a species derive from pattern formation processes that establish the position and number of anatomical structures (5). If developmental processes like pattern formation are biased toward generating only particular kinds of variation, adaptive radiations may often be directed along developmental–genetic “lines of least resistance” (2, 4, 6, 7). Generally, the evolutionary consequences of this developmental bias have been considered largely in terms of how it might influence the pattern of character evolution (e.g., refs. 1, 2, 8–10). But development could also influence evolutionary rates by controlling how much variation is accessible to natural selection in a given generation (11).

For mammals, the dentition is often the only morphological system linking living and extinct species (12). Correspondingly, tooth morphology plays a crucial role in elucidating evolutionary relationships, time calibrating phylogenetic trees, and reconstructing adaptive responses to past environmental change (e.g., refs. 13–15). One of the most pervasive features of dental evolution among mammals is an increase in the complexity of the tooth occlusal surface, primarily through the addition of new tooth cusps (16, 17). These increases in tooth complexity are functionally and ecologically significant because they enable more efficient mechanical breakdown of lower-quality foods like plant leaves (18).

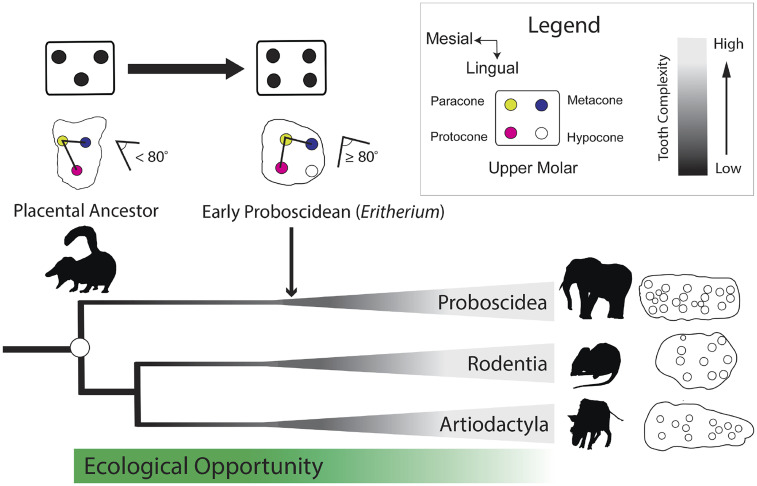
Placental mammals are the most diverse extant mammalian group, comprising more than 6,000 living species spread across 19 extant orders, and this taxonomic diversity is reflected in their range of tooth shapes and dietary ecologies (12). Many extant placental orders, especially those with omnivorous or herbivorous ecologies (e.g., artiodactyls, proboscideans, rodents, and primates), convergently evolved a rectangular upper molar cusp pattern from a placental ancestor with a more triangular cusp pattern (19–21). This resulted from separate additions in each lineage of a novel posterolingual cusp, the "hypocone'' [sensu (19)], to the tritubercular upper molar (Fig. 1), either through modification of a posterolingual cingulum (“true” hypocone) or another posterolingual structure, like a metaconule (pseudohypocone) (19). The fossil record suggests that many of the basic steps in the origin of this rectangular cusp pattern occurred during an enigmatic early diversification window associated with the divergence and early radiation of several placental orders (20, 21; Fig. 1). However, there remains debate about the rate and pattern of early placental divergence (22–24). On the one hand, most molecular phylogenies suggest that higher-level placental divergence occurred largely during the Late Cretaceous (25, 26), whereas other molecular phylogenies and paleontological analyses suggest more rapid divergence near the Cretaceous–Paleogene (K–Pg) boundary (21, 24, 27–29). Most studies agree that ecological opportunity created in the aftermath of the K–Pg extinction probably played an important role in ecomorphological diversification within the placental orders (30, 31). But exactly how early placentals acquired the innovations needed to capitalize on ecological opportunity remains unclear. Dental innovations, especially those which facilitated increases in tooth complexity, may have been important because they would have promoted expansion into plant-based dietary ecologies left largely vacant after the K–Pg extinction event (32).

Fig. 1.

Placental mammal lineages separately evolved complex upper molar teeth with a rectangular cusp pattern composed of two lateral pairs of cusps from a common ancestor with a simpler, triangular cusp pattern. Many early relatives of the extant placental orders, such as Eritherium, possessed a hypocone cusp and a more rectangular primary cusp pattern. Examples of complex upper molars are the following: Proboscidea, the gomphothere Anancus; Rodentia, the wood mouse Apodemus; and Artiodactyla, the suid Nyanzachoerus.

Mammalian tooth cusps form primarily during the “cap” and “bell” stage of dental development, when signaling centers called enamel knots establish the future sites of cusp formation within the inner dental epithelium (33, 34). The enamel knots secrete molecules that promote proliferation and changes in cell–cell adhesion, which facilitates invagination of the dental epithelium into an underlying layer of mesenchymal cells (34, 35). Although a range of genes are involved in tooth cusp patterning (36–38), the basic dynamics can be effectively modeled using reaction–diffusion models with just three diffusible morphogens: an activator, an inhibitor, and a growth factor (39–41). Candidate activator genes in mammalian tooth development include Bmp4, Activin A, Fgf20, and Wnt genes, whereas potential inhibitors include Shh and Sostdc, and Fgf4 and Bmp2 have been hypothesized to act as growth factors (38, 40–43). In computer models of tooth development, activator molecules up-regulated in the underlying mesenchyme stimulate differentiation of overlying epithelium into nondividing enamel knot cells. These in turn secrete molecules that inhibit further differentiation of epithelium into knot cells, while also promoting cell proliferation that creates the topographic relief of the cusp (40). Although many molecular, cellular, and physical processes have the potential to influence cusp formation, and thereby tooth complexity (35, 37), parameters that control the strength and conductance of the activator and inhibitor signals, the core components of the reaction–diffusion cusp patterning mechanism (39, 40) are likely to be especially important.

Here, we integrate a previous computer model of tooth morphogenesis called ToothMaker (41), with simulations of trait evolution and data from the fossil record (Fig. 2), to examine the developmental origins of tooth complexity in placental mammals. Specifically, we ask the following: 1) What developmental processes can influence how many cusps form? 2) How might these developmental processes influence the evolution of tooth cusp number, especially rates? And 3) what developmental changes may have been important in the origins of the fourth upper molar cusp, the hypocone, in placental mammal evolution?

Fig. 2.

Workflow for simulations of tooth complexity evolution. (A) Tooth shape is varied for five signaling and growth parameters in ToothMaker. (B) From an ancestral state, each parameter is varied in 2.5% increments up to a maximum of ± 50% of the ancestral state. (C) Tooth complexity and enamel knot (EK) pattern were quantified for each parameter combination. Tooth complexity was measured using cusp number/EK number and OPC. ToothMaker and placental upper second molars were classified into categories based on EK/cusp pattern. (D) The parameter space was populated with pattern and tooth complexity datums to build a developmental landscape. (E) Tooth complexity evolution was simulated on each developmental landscape. (F) Resulting diversity and pattern of tooth complexity was compared with placental mammal molar diversity.

Results

Developmental Variation in Tooth Pattern and Complexity.

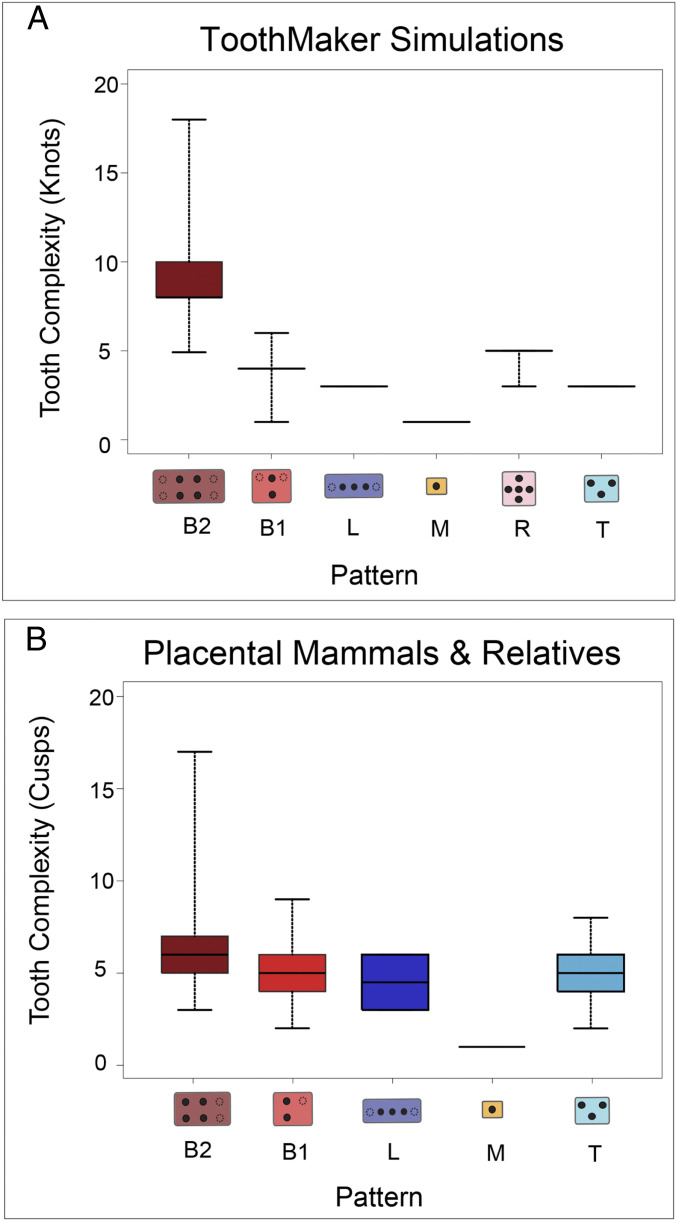
From the ToothMaker simulations, five basic patterns of knot formation were identified: a lateral (buccolingual) pattern (B), a triangular pattern (T), a longitudinal pattern (L), a single knot pattern (M), and a radial or hemiradial pattern (R) (Fig. 2 and SI Appendix, Fig. S1). We distinguished two subcategories of pattern B: the formation of a single lateral knot pair (B1) or more than one lateral pair of knots (B2). The earliest patterning event was the formation of a primary knot on a largely flat sheet of epithelial cells (SI Appendix, Fig. S1), followed by formation of either a single secondary knot (L, M, R, and T) or a lateral pair of secondary knots (B; SI Appendix, Fig. S1). Apart from small differences in the position of the late-forming secondary knots, there was little difference in tooth shape between T, L, and R patterns (SI Appendix, Fig. S2), and these can be conceptualized as a spectrum of mesiodistal knot patterns. In terms of frequency, the M and T patterns were present on all 10 landscapes, the B and L patterns were present on 7 and 6 landscapes, respectively, and the R pattern was present on 3 landscapes.

Tooth surface complexity, measured as orientation patch count (OPC), increased through in silico development (SI Appendix, Fig. S3). However, the rate at which tooth surface complexity accumulated varied depending on the knot pattern and developmental parameters (i.e., the “landscape”; SI Appendix, Table S2), tending to accumulate more rapidly on landscapes with increased activator up-regulation (Act/activation, SI Appendix, Fig. S3). Although the initiation of a knot always predicted sites of cusp formation, not all knots formed cusps, especially when knots initiated late or near the flank of the tooth bud. Overall, there was a positive relationship between the number of knots and the patch count score (r score 0.69; SI Appendix, Fig. S4), although this varied depending on the parameter combination, being strongest for landscapes with high levels of activation. Knot number varied substantially between landscapes (range: 1 to 18; SI Appendix, Fig. S5), being more disparate where activation was varied. Landscapes with variation in activation generated tooth shapes with 1.8 times as many knots and 2 times as many patches as landscapes without variation in activation. Landscapes with activator variation tended to be more rugged, with regions of complex teeth interspersed by regions of simpler teeth (SI Appendix, Figs. S5 and S6). Tooth complexity varied between knot patterns, with B knot patterns being associated with increased enamel knot number compared with other patterns (Fig. 3A), primarily because elevated activation favored the formation of this pattern. However, teeth with a B pattern were also generated on landscapes where activation was not varied, although these tended to have somewhat lower knot numbers (SI Appendix, Fig. S7).

Fig. 3.

Tooth complexity and enamel knot/cusp pattern variation in ToothMaker and among 93 fossil and extant placental mammals and their relatives. (A) Pooled variation in enamel knot number and pattern across developmental landscapes. (B) Tooth cusp number and pattern variation across mammalian taxa. Black filled circles in tooth digrams denote the fundamental cusp arrangement for each pattern. Note more symmetrical patterns for simulated teeth.

Developmental Influence on Simulated Tooth Complexity Evolution.

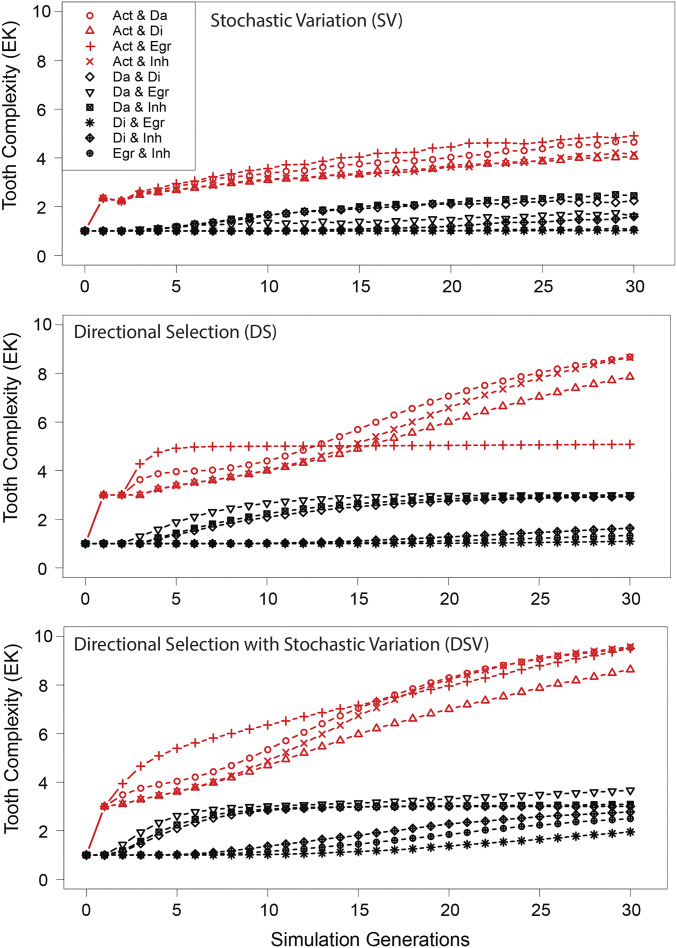
Simulations under stochastic variation (SV), directional selection (DS), and directional selection with stochastic variation (DSV) showed substantial variation in rates and trajectories across landscapes (Fig. 4 and SI Appendix, Fig. S8). Models including a selection component (DS and DSV) had faster rates than the stochastic model (SV). Disparity and rates for all models was greater where activation was varied (Fig. 4). Among the selection-based models, variation in rates was also influenced by the extent of “exploration” of the landscape. For instance, DSV exhibited the broadest distribution of lineages across the landscape as well as the fastest evolutionary rates compared with the other models (SI Appendix, Fig. S8). Compared with SV, lineages evolving under DS and (especially) DSV moved on average further from the ancestral developmental state. Tracking the sequence of knot pattern evolution under each model showed that as tooth complexity increased, the range of unique evolutionary sequences decreased dramatically (SI Appendix, Fig. S9). For instance, when complexity increased from more than 1 to more than 5 knots, the number of unique paths under SV decreased by 50%, and by 66% and 24% for the DS and DSV models, respectively (SI Appendix, Fig. S9). Under SV, the number of unique paths leading to a tooth with more than five cusps (304 paths) was substantially higher than under either the DSV (119 paths) or the DS (46 paths) models. The type of evolutionary model was also associated with shifts in the frequency distribution of possible evolutionary transitions. Under SV, the distribution was more uniform, whereas it was strongly skewed under DS and DSV (SI Appendix, Fig. S9). In both these selection-based models, the skew overwhelmingly favored a single evolutionary sequence of patterning changes (M > T > B1 > B2).

Fig. 4.

Simulations of tooth complexity evolution across 10 developmental landscapes under different models of evolution. Lines are means of 10,000 evolutionary simulations, each run for a maximum of 30 generations. Red denotes landscapes where activation (Act) was varied. Evolutionary models were the following: 1) stochastic variation (SV), 2) directional selection (DS) for enamel knot (EK) number, and 3) directional selection with stochastic variation (DSV). The parameter abbreviations are the following: activator self-regulation (Act), activator diffusion rate (Da), inhibitor diffusion rate (Di), epithelial growth rate (Egr), and strength of inhibition (Inh).

Comparison of ToothMaker and Placental Tooth Complexity.

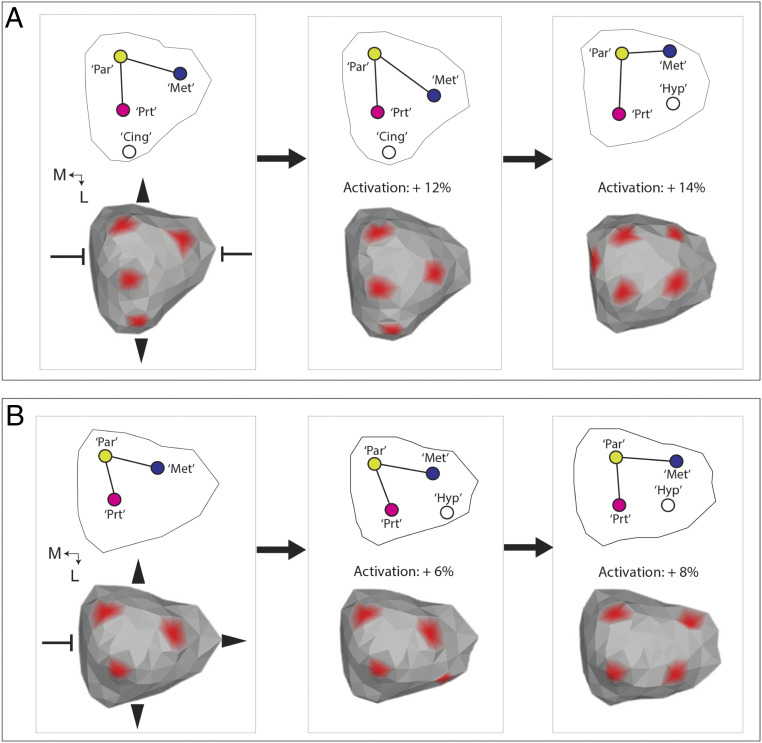
Four of the five major knot patterns present in ToothMaker simulations were also present among the sample of 93 fossil and extant mammal taxa (SI Appendix, Table S3). The R pattern was absent. There was a similar relationship between cusp number/knot number and pattern among the pairwise ToothMaker simulations and the mammalian dataset (Fig. 3). In both instances, the B pattern (especially B2) was associated with teeth with higher complexity compared with other patterns (Fig. 3). Enamel knot numbers comparable to the most complex mammalian teeth only evolved on landscapes where activation was elevated (e.g., Fig. 4). Still, there were important differences between the pairwise ToothMaker simulations and the realized tooth shapes. For instance, the simulated tooth shapes tended to be more elongated and possess relatively symmetrical cusp patterns, especially about the lateral axis (SI Appendix, Fig. S1). The simulated tooth shapes also displayed much less disparity in cusp number within a pattern than did the realized tooth shapes (Fig. 3). To create tooth shapes more similar to the tritubercular pattern expected for the placental common ancestor, it was necessary to strongly reduce anterior (Abi) and posterior (Pbi) growth and increase the lingual expression bias of the activator (Fig. 5 and SI Appendix, Table S4). This created a much more acutely triangulated primary knot pattern (comparable to the protocone, paracone, and metacone cusps) than was present in the T pattern teeth generated through the pairwise simulations (e.g., SI Appendix, Fig. S1). It was also associated with formation of a cingulum-like ridge lingual of the “protocone” knot (Fig. 5A). This knot pattern was relatively invariant to increases in activation up to 14% (SI Appendix, Fig. S10A), except for lingual deflection of the “metacone” knot (Fig. 5A). Above this level, a knot emerged along the posterolingual (and anterior) margin, and the most lingual knot disappeared, creating a basically rectangular knot pattern. A different pattern formed when an ancestral tooth was simulated with more posterior growth (Fig. 5B). Under this scenario, only a 6% increase in activation was required to create a knot along the posterolingual margin (Fig. 5B). Increasing activation by 8% (SI Appendix, Fig. S10B) increased the size of this knot and displaced the metacone knot buccally and the protocone knot slightly anteriorly, also creating a rectangular knot pattern (Fig. 5B). The in silico patterning histories showed that the primary difference between the respective paths to a rectangular knot pattern was the later initiation of the posterolingual knot when Pbi was increased (SI Appendix, Fig. S11).

Fig. 5.

Changes in ancestral growth pattern lead to divergent origins of a hypocone-like cusp in ToothMaker simulations. (A) Changes in the cusp pattern associated with increases in activation in a molar with restricted anterior and posterior growth and a lingual bias in activator expression. Note the presence of cingulum-like ridge along the lingual margin (Cing) expressing growth factor. (B) Changes in the cusp pattern on a molar with increased posterior molar growth resulted in formation of a more posterobuccally forming marginal knot. Abbreviations are the following: “Par” = paracone-like, “Prt” = protocone-like, “Met” = metacone-like, and “Hyp” = hypocone-like. Directions are mesial (M) and lingual (L). Red denotes growth factor concentration at view threshold = 0.2.

Phylogenetic Pattern of Placental Tooth Complexity.

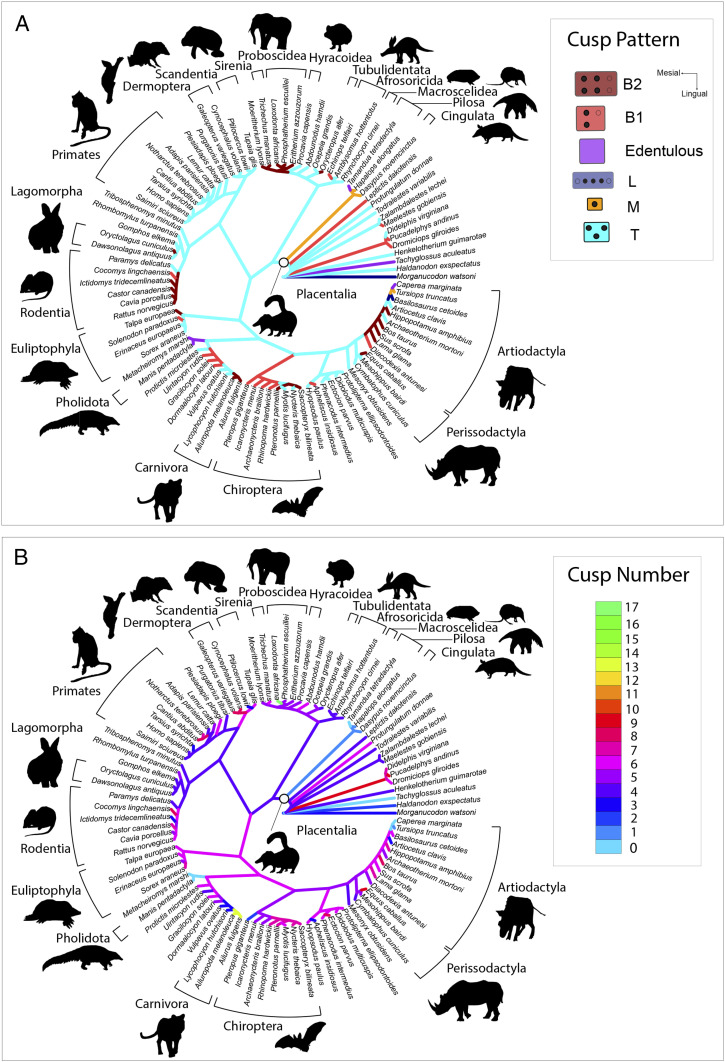
Ancestral state reconstruction recovered the placental ancestor as possessing an upper molar with a T cusp pattern (Fig. 6B). This T cusp pattern was reconstructed as plesiomorphic for mammals extending back at least as far as the last common ancestor with Haldanodon. Multiple gains in tooth cusp number occurred across most extant placental orders, although there was substantial variation in how much tooth cusp number increased (Fig. 6B). In most groups, increases were relatively modest, involving the addition of a single posterolingual cusp (i.e., the hypocone) or several small stylar cusps along the buccal upper molar margin. Among predominantly omnivorous or insectivorous clades like primates, chiropterans, and euliptophylans, the increases in cusp number were primarily associated with expression of these stylar cusps. In predominantly herbivorous clades like proboscideans, rodents, perissodactyls, and artiodactyls, basal increases in cusp number were linked with the addition of both posterolingual and stylar cusps or other conules. There were five examples of upper molar simplification across the tree, among xenarthrans, artiodactyls (cetaceans), carnivorans, pholidotans, and chiropterans. Increases in cusp number generally accompanied shifts to a more lateralized protocone–paracone arrangement (Figs. 1 and 6). Across placental phylogeny there were at least 10 origins of this B cusp pattern (Fig. 6A), with additional origins among metatherian and nonplacental eutherians. The shift from a T to a B cusp pattern, and initial increases in cusp number, were generally localized near the base of the ordinal crown group, especially among chiropterans, artiodactyls, rodents, and proboscideans (Fig. 6A). Among primates, euliptophylans, and phenacodontids the increases in cusp number occurred primarily on T cusp patterns rather than where the protocone–paracone arrangement was fully lateral (i.e., B).

Fig. 6.

Ancestral state reconstruction of tooth cusp pattern (A) and tooth cusp number (B) across a phylogeny of 93 species of fossil and extant placental mammals and closely related taxa. All data collected from the upper second molar. Tree modified after the phylogeny of ref. 21. (Clockwise from Top Left) images credit: Wikimedia Commons/Nina Holopaninen/Stavenn/Joey Makalintal/birdphotos/PD-USGov/Thomas Hardwicke.

Discussion

Developmental Drivers of Tooth Complexification.

Our results reveal similarities between simulated and realized mammalian tooth shapes, especially in terms of how cusp pattern and tooth complexity covary (Fig. 3). In particular, our results suggest that lateral patterning of cusps is more likely to be associated with complex tooth shapes than other patterns, suggesting that cusp number and pattern are to some extent developmentally connected. However, there were also differences between the simulated and realized tooth shapes, such as the absence of acutely triangulated patterns, low levels of intrapattern variation in complexity, and a predominance of more-symmetrical patterns in the simulated tooth shapes. We interpret these differences as reflecting the missing influence of tooth shape parameters, especially growth biases, from the pairwise simulations. These findings reinforce experimental evidence that some aspects of tooth shape, like the cusp pattern, are likely to be multifactorial (44). They also suggest that while tooth cusp patterning may be fundamentally a reaction–diffusion process (39, 40), tissue growth parameters may be important for building the “correct” tooth shape. Still, despite the evidence for the multifactorial basis of the cusp pattern, our results suggest that tooth cusp number may have a simpler developmental basis, being closely linked to molecular activation. This is consistent with the role that activator molecules play in promoting the differentiation of dental epithelium into the specialized nondividing knot cells that initiate cusp formation (45). Experiments in mice have shown that manipulating a range of signaling pathways (sonic hedgehog, activin bA, and ectodysplasin) can produce teeth with increased tooth cusp number, and it has been suggested that synchronous modulation of these pathways may be necessary for gains in tooth complexity (16). Our results suggest that activator-related parameters, especially activation, may exert a disproportionate influence on tooth complexification. This hypothesis is consistent with evidence that euarchontan mammals with molar proportions expected to form under a relatively high activator–inhibitor balance have relatively more complex molar tooth surfaces (46). Additional parameters like the strength of inhibition (Inh), a parameter analogous to sonic hedgehog signaling, a pathway whose suppression can add cusps to mouse molars (16, 47), had relatively little influence on the trajectory of tooth complexification in our simulations (e.g., SI Appendix, Fig. S8D). This may be because activation needs to be relatively high (as in rodents; e.g., refs. 17 and 41) for inhibition to strongly influence tooth complexity. While our results suggest that increases in activation are critical for adding tooth cusps, other parameters may be important for modulating other aspects of tooth complexity. For instance, combined with increased activation, high epithelial growth rates (Egr) generated high tooth surface complexities (SI Appendix, Fig. S4), which probably reflects the influence of Egr on the prominence of tooth cusps (40). Likewise, mechanical factors like the resistance of the mesenchyme to downgrowth of the epithelium and cell adhesion—important factors in the folding of the inner enamel epithelium (35, 48)—may be important influences on tooth surface complexity through their effects on the curvature of the basement membrane. Given the evidence from the simulations for the important role of activation in tooth complexification, mutations which up-regulate the activity of activator genes like Bmp4, Activin A, Fgf20, and Wnt (38, 40–43) may be important molecular “hotspots” for tooth complexity evolution.

Rate of Tooth Complexity Adaptation on the Developmental Landscape.

Evolutionary simulations on the developmental landscapes provide evidence that developmental parameters could strongly influence both the rate (Fig. 4) and pattern of tooth complexity evolution (SI Appendix, Fig. S8). Landscapes with high levels of activation enabled accelerated evolution of tooth complexity (Fig. 4), especially when relatively smooth gradients connected simple and complex teeth. The evidence for increases in the rate of tooth complexity evolution alongside some developmental parameters contrasts with the historical emphasis on development as a negative “constraint” on adaptation (1, 3, 4, 6). The simulations support the idea that rate slowdowns because of such constraint is only one possible influence of development on adaptation (1, 4), with the balance between slowdowns and accelerations depending on the structure of the developmental landscape and the amount of stochastic variation (assuming selection pressure is constant). As a result, when the landscape was rugged, with many “hills” and “valleys,” a structure predicted when growth and patterning overlap during morphogenesis (49), lineages risked becoming trapped on local optima far from the global peak. Previous analysis has suggested that such landscapes may limit adaptation because lineages cannot find the global trait optimum (50). Although our simulations show that such “trapping” of lineages is a plausible outcome (SI Appendix, Fig. S8 C and F), they also suggest that if there is sufficient stochastic variation available (e.g., via mutation or recombination), or if selection pressures are intermittently relaxed, development may be more likely to bias rather than stall adaptation. Supporting this, introducing a stochastic variation term alongside selection pressure enabled lineages to explore a wider region of the landscape, undergo more adaptation (longer trajectories, SI Appendix, Fig. S8), and evolve faster (Fig. 4). These findings support Simpson’s hypothesis (51) that phenotypic drift is critical for complex traits to traverse adaptive valleys and escape constraints. The connection between the simulated rates of tooth complexity evolution and how lineages traverse the landscape also highlights the inseparability of “tempo” and “mode” in evolution (52) and the important link provided by the developmental landscape. The results raise questions about the extent to which it is possible to accurately predict the rate or pattern of trait evolution without information about the structure of the developmental landscape. Potentially, integration of mechanistic models of development with phylogenetic trait modeling approaches could help improve reconstructions of evolutionary rates for complex traits.

Developmental Evolution of Early Placental Tooth Complexity.

To understand more about the specific developmental changes involved in the diversification of early placental tooth complexity, we tinkered with signaling and growth parameters to produce a cusp pattern more similar to the tritubercular condition ancestral to placental mammals (19–21). We found that to create a more acutely triangulated protocone–paracone–metacone (PPM) arrangement it was necessary to establish a pronounced lingual bias in activator expression and strongly reduce anterior and posterior molar growth (Fig. 5A). A byproduct of this was the formation of a ridge-like structure lingual of the protocone, reminiscent of the cingulum (Fig. 5A) sometimes present on the upper molars of basal placental and closely related eutherian mammals (53, 54). Relatively little is known about signaling and growth processes within the upper molar of tritubercular mammals compared to mammals with quadritubercular molars like the mouse. In tritubercular bats, the upper molar initially grows longitudinally before shifting to buccolingual expansion (55). Quantitative genetic evidence from primates suggests that the genetic control of this expansion in the width of the molars is independent from factors controlling molar elongation (56–58). Based on the ToothMaker modeling here and previous evidence (39), a possible developmental mechanism for this buccolingual expansion of the upper molar could be a bud stage lingual bias in activator expression which establishes a buccolingual growth axis. This might explain the pronounced lingual slope on the tall and likely early forming protocone (i.e., ref. 59) of some "protoplacentals" like Protungulatum and Purgatorius (53, 54). Similar spatial biases in the expression of activators such as bone morphogenetic protein (BMP) molecules have been hypothesized to create slanted cusps on the scales of some sharks (60). There is also evidence for buccolingual variation in the expression of activator genes (e.g., Bmp4) in the dental lamina of mammals (38, 61). Transcription factor genes like Osr2 and Msx are thought to regulate the buccolingual expression domains of BMPs in the dental mesenchyme of mammals (33, 38), and changes in the expression of these genes, as well as the mechanical forces that shape the direction of tooth growth (44), may have been important factors in establishing the triangular architecture of the tritubercular upper molar.

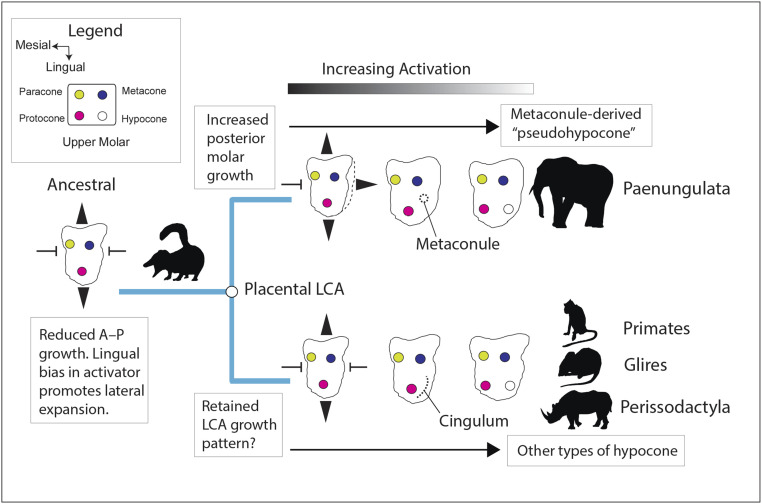
Interestingly, we found that in silico activation only needed to be increased by around 14% on this “ancestral” tritubercular geometry to create a posterolingual cusp (Fig. 5A) topologically similar to the hypocone, a cusp which evolved numerous times in placental evolution (19). The mammalian hypocone originated in several different ways, being separately derived from a range of structures including the metacone, metaconule, protocone, postprotocingulum, and postprotocrista (19, 20, 62, 63). We found that increasing the amount of posterior growth in silico shifted the site of marginal knot initiation more posterobuccally (Fig. 5B), compared with when posterior growth was restricted (Fig. 5A). Correspondingly, relatively small ancestral variations in growth biases in the rear of the upper molar could provide a developmental mechanism for the divergent origins of the hypocone and its strong phylogenetic signature (19–21, 63; Fig. 7). Additionally, given that lower levels of activation were needed to initiate a posterolingual cusp when the posterior growth of the molar was increased (SI Appendix, Fig. S10B), growth biases may also have modulated how rapidly different types of hypocone could evolve in placental evolution.

Fig. 7.

Parallel increases in molecular activation facilitate convergent evolution of rectangular cusp patterns in lineages diverging from the placental last common ancestor (LCA). Increasing posterior molar growth is hypothesized to create a more posterobuccally derived hypocone, as in the paenungulate metaconule (so-called “pseudohypocone”), whereas reduced posterior molar growth may have favored a more lingually derived hypocone as in other groups.

Irrespective of the specific ancestral upper molar growth pattern, relatively small, progressive increases in activation favored formation of a rectangular cusp pattern (SI Appendix, Fig. S10 A and B). This convergence may arise because, as more knots initiate, a lateral knot pattern offers a relatively stable self-organizing arrangement (44). This tendency of high levels of activation to create both more cusps and a more lateral cusp pattern offers a developmental explanation for the nonindependence of tooth complexity and pattern in the developmental simulations. It also could help explain the rampant convergent evolution of lateral cusp arrangements across placentals (Fig. 6) as well as metatherian, monotreme, multituberculate, and even crocodylomorph dentitions (64, 65). In some groups like early chiropterans, carnivoraforms, and euliptophylans, more lateral arrangements of the protocone and paracone also formed, although in the absence of a hypocone, perhaps driven more by changes in tooth bud growth than activation. Although other developmental parameters were undoubtedly involved, because only relatively small increases in activation (8 to 14%; SI Appendix, Fig. S10) were needed in silico to create a rectangular cusp pattern, it appears plausible that higher-level dental divergence within placental mammals could have occurred fairly rapidly, as would be expected under accelerated models of early placental diversification (i.e., refs. 21, 24, and 27).

Materials and Methods

ToothMaker Overview.

The dynamics of ToothMaker (and related models) have previously been described (39–41), but here, we provide a brief overview. ToothMaker simulates inductive interactions between adjacent epithelial and mesenchymal tissue layers from the bud stage to the bell stage. Initially, a cluster of epithelial cells overlays two rows of mesenchymal cells. Cells can undergo nonreversible differentiation into enamel knot cells or undergo proliferation in the case of nonsignaling epithelium and mesenchyme. Molecules include an “activator,” which promotes localized differentiation of epithelial cells into knot cells; an “inhibitor,” which prevents differentiation of epithelial cells into knot cells; and a diffusible “growth factor,” which modulates proliferation within the epithelium and mesenchyme. Whether cells differentiate or proliferate is determined by thresholds in activator and inhibitor concentration. ToothMaker includes parameters to modulate the initial conditions, diffusion rate, secretion rate, and responsiveness of cells to the diffusible morphogens (SI Appendix, Table S1). In the case of the activator, a buccal and lingual mesenchymal expression bias can also be parameterized. Mechanical behaviors of the epithelium and mesenchyme can be regulated by parameters controlling cell–cell adhesion, the stiffness of cells, traction forces, and the mechanical resistance of the mesenchyme to invagination (SI Appendix, Table S1). The propensity of the epithelium to grow in the anterior and posterior direction can be influenced by growth bias parameters. Likewise, initial size and shape of the tooth bud can be regulated by changing parameters that control the dimensions of the bud (SI Appendix, Table S1). The output from ToothMaker is the shape of the epithelial–mesenchymal boundary and the concentration of the activator, inhibitor, and growth factor within three-dimensional space at time intervals of the simulation.

ToothMaker Simulations.

Using ToothMaker 0.6.4 (dead.cthulhu.fi/ToothMaker), we simulated tooth shapes by varying five parameters in a pairwise fashion (Fig. 2A and SI Appendix, Table S2). Because of the large number of possible parameters within ToothMaker (26 in total; SI Appendix, Table S1), we focused on five signaling and growth parameters that directly regulate tooth cusp patterning and have been shown to closely match natural variation in seal dentitions (40). These parameters were the following: the self-regulation of the activator (Act), strength of inhibition (Inh), the diffusion rate of the activator (Da), the diffusion rate of the inhibitor (Di), and the epithelial growth rate (Egr). Pairwise combinations of these parameters produced 10 unique developmental landscapes (SI Appendix, Table S2), each with the same dimensions and each sharing a common starting state that generated a tooth with a single cusp (SI Appendix, Table S1). From this starting point, each parameter was varied in 2.5% increments of this ancestral state up to a maximum value of ± 50% of the ancestral parameter state (Fig. 2B). This resulted in each of the 10 developmental landscapes consisting of 21 × 21 grid cells. The “scan parameter” function was used to export the tooth surface shape at each time point spanning from the initial iteration (0 iteration steps) to the final iteration (14,000 iteration steps) at 500 step intervals (28 total). As a result, the in silico development of each simulated tooth shape was characterized by 28 surface files (*.off format). ToothMaker was implemented with a virtual Linux machine (Ubuntu 16.04.3) mounted on a Windows host machine using the software VMware Workstation 15 Player.

Tooth Complexity and Pattern.

Simulated tooth complexity was measured by quantifying the number of enamel knots (Fig. 2C), a developmental predictor of tooth cusp number on fully formed teeth (45). Knot number was computed using a macro implemented with Image J (1.52a) on occlusal snapshots of the fully formed tooth shapes (14,000 iterations). The macro thresholds regions of differentiated cells marking the position of knots and computes the number of islands. To compare this metric of tooth complexity with tooth surface complexity, we calculated the OPC (18) for each simulated tooth shape (Fig. 2C). OPC groups contiguous regions of the tooth surface falling within one of eight directional bins into “patches.” The total number of patches on the tooth surface provides an index of surface complexity, with more complex tooth shapes having a higher patch count score than simpler tooth shapes. The OPC analysis was implemented with “molar_Batch” in the “R” package “molaR” (66) with “OPC_minimum_faces = 3” and all other parameters run as default. For each grid cell in the parameter space, the series of *.off files containing the tooth surface geometry at a given time point was converted to *.ply surface file format in “R” (67) using the “vcgPlyWrite” function in “rvcg” (68). To capture differences in cusp patterning, we classified enamel knot patterns into five categories based on occlusal snapshots exported from ToothMaker (Fig. 2C). These patterns were the following: B, enamel knots formed as a buccolingual pair; L, enamel knots formed along the longitudinal tooth axis; T, enamel knots formed in a triangular arrangement along the longitudinal axis; R, enamel knots formed in a radial/hemiradial arrangement; and M, formed into a single enamel knot. In addition, we further subdivided the B pattern into the following: B1 (enamel knots formed only a single lateral pair) and B2 (enamel knots formed more than one lateral pair). For simplicity, we did not differentiate between lingual and buccal sides when classifying the ToothMaker knot patterns.

Evolutionary Simulations.

To examine how different developmental factors might influence tooth complexity evolution, we simulated trait evolution on the landscapes using three simple evolutionary models. To begin, we first mapped tooth complexity and tooth cusp pattern datums across parameter space to build a developmental landscape (Fig. 2D). Next, we ran simulations (Fig. 2E) under the following models: 1) a stochastic variation (SV) model, 2) a model of directional selection (DS) for higher knot number, and 3) a model combining the selection for higher knot number with stochastic variation (DSV). Under SV, an “evolving” lineage moves randomly across the morphospace, with the grid position in the next generation determined by randomly sampling the eight immediately adjacent grid cells using the “sample” function in “R." Under DS, the grid position of the lineage in the subsequent generation is determined by which of the eight neighboring grid cells has the highest knot number. Ties between cells with the same complexity were randomly resolved, which introduces some stochasticity into this model. Under DSV, the ancestral position in the landscape is randomly varied, and the adjacent grid cell with the highest knot number is selected. In each of the three evolutionary models, the starting state for each lineage was the same simple monocuspid tooth with identical developmental parameters. Simulations were run for up to 30 generations and each was repeated 10,000 times on each landscape. Lineages that reach the edge of the landscape exit the simulation and do not reenter. Using the x and y coordinates at the end of each generation, the sequence of patterning changes needed to cross the developmental landscape was reconstructed. To characterize the range of possible evolutionary transitions, we pooled all the lineage simulations across the 10 landscapes for each evolutionary model. All evolutionary simulations were performed in “R” (67).

Phylogenetic Analysis of Placental Tooth Complexity.

To reconstruct the pattern of tooth cusp number and cusp pattern evolution across placental phylogeny, we scored cusp number and cusp pattern for 93 species of fossil and extant mammal (SI Appendix, Table S3). This was done based on occlusal images in published sources and from data on morphobank (https://morphobank.org/). Tooth cusp number and pattern was scored only for the upper second molar. The PPM angle was measured to provide an empirical basis for cusp pattern classification. Teeth with a PPM angle greater or equal to 80° were scored as B (a “lateral” or “buccolingual” arrangement of the protocone and paracone) and those with an angle less than 80° were scored as T (Fig. 1). For zalambdodont taxa, in which the metacone was absent, we measured the angle connecting the metastyle, parastyle, and paracone. The B pattern was further subdivided into B1 and B2 patterns based on the protocone–hypocone–metacone (PHM) angle. The pattern was scored as B1 if no hypocone was present or if the PHM angle was greater or equal to 135° and B2 if the PHM angle was less than 135°. Some derived placental mammals (e.g., artiodactyls and proboscideans) have highly modified upper molars where the cusps have been specialized into crests or ridges. In these cases, we used the ancestral cusp pattern in these clades to conservatively estimate tooth cusp number and pattern. All clearly identifiable cusps were counted.

A phylogenetic tree of placental mammals and their relatives was built based on the combined molecular and morphological topology of ref. 21. However, we modified some branches to reflect updated views on key relationships, as well as to add important fossil and extant taxa to the tree. These changes included positioning Protungulatum and Leptictis as eutherian lineages just outside the placental crown following refs. 22, 27, and 29. Although Purgatorius is sometimes recovered as outside the placental crown group (i.e., ref. 29), we include it here as a basal primatomorph following refs. 22 and 69. Representatives of the basal carnivoraform genera Uintacyon, Gracilocyon, Protictis, Lycophocyon, and Miacis were added following the phylogeny of ref. 70. Basal fossil afrotherian taxa were positioned following ref. 20. The platypus (Ornithorhynchus anatinus) was excluded from the analysis because of its highly degenerate upper molars. Using the resulting phylogeny (without branch lengths), we performed a parsimony ancestral state reconstruction of tooth cusp number and cusp pattern as discrete characters using “castor” (71) and “ape” (72) in “R."

Data Availability

Data and code are available on Dryad (https://doi.org/10.5061/dryad.mgqnk98zf) (73) and in the SI Appendix.