Agonist efficiency from concentration-response curves: Structural implications and applications

Abstract

Agonists are evaluated by a concentration-response curve (CRC), with a midpoint (EC₅₀) that indicates potency, a high-concentration asymptote that indicates efficacy, and a low-concentration asymptote that indicates constitutive activity. A third agonist attribute, efficiency (η), is the fraction of binding energy that is applied to the conformational change that activates the receptor. We show that η can be calculated from EC₅₀ and the asymptotes of a CRC derived from either single-channel or whole-cell responses. For 20 agonists of skeletal muscle nicotinic receptors, the distribution of η-values is bimodal with population means at 51% (including acetylcholine, nornicotine, and dimethylphenylpiperazinium) and 40% (including epibatidine, varenicline, and cytisine). The value of η is related inversely to the size of the agonist’s headgroup, with high- versus low-efficiency ligands having an average volume of 70 vs. 102 Å³. Most binding site mutations have only a small effect on acetylcholine efficiency, except for αY190A (35%), αW149A (60%), and those at αG153 (42%). If η is known, the EC₅₀ and high-concentration asymptote can be calculated from each other. Hence, an entire CRC can be estimated from the response to a single agonist concentration, and efficacy can be estimated from EC₅₀ of a CRC that has been normalized to 1. Given η, the level of constitutive activity can be estimated from a single CRC.

Significance

Receptors are molecular machines that convert chemical energy from agonist binding into mechanical energy of a global conformational change that generates a cell response. Agonists are distinguished by their potency (proportional to affinity) and efficacy but also by the efficiency at which their binding energy is applied to receptor activation. Here, we show that agonist efficiency can be estimated from a single concentration-response curve (CRC) and estimate efficiencies of 20 nicotinic receptor agonists. These have a bimodal distribution with larger agonists belonging to the lower efficiency population. We further show that mutations of some binding site residues alter efficiency and that knowledge of agonist efficiency simplifies and extends dose-response curve analysis.

Introduction

Nicotinic acetylcholine (ACh) receptors (AChRs) are members of the cys-loop, ligand-gated receptor family that in mammals also comprise GABA_A, glycine, 5-HT₃, and zinc-activated receptors (1). They are 5-subunit, liganded-gated ion channels with agonist binding sites in the extracellular domain, far from a narrow region of the pore in the transmembrane domain that regulates ion conductance (2,3).

AChRs switch between global closed-channel (C) and open-channel (O) conformations (“gating”) to produce transient membrane currents. Agonists promote channel opening because they bind more strongly to the O conformation. Importantly, the energy (structure) of the binding site at the gating transition state resembles that of O (4). Hence, when a receptor begins its journey from C to O, extra (favorable) binding energy eases the pathway, thereby increasing the probability of reaching and residing in O (P_O) (5,6).

AChRs are the primary receptors at vertebrate neuromuscular synapses, where they initiate muscle membrane depolarization and contraction. Neuromuscular AChRs have two α1 subunits and one each of β, δ, and either ε (adult) or γ (fetal). There are two neurotransmitter binding sites located at α1-δ and α1-δ/γ subunit interfaces (7) that are approximately equivalent for ACh in adult-type AChRs (5). AChRs switch conformation spontaneously (only under the influence of temperature), with the presence of neurotransmitters at both adult sites increasing the opening rate constant by a factor of ∼5 million and the lifetime of the O conformation by a factor of ∼5.

Agonists are typically characterized by a potency (proportional to affinity) and an efficacy. Affinity is a measure of how strongly the ligand binds to its target site and is the inverse of an equilibrium dissociation constant. The constants K_dC and K_dO correspond to low-affinity (weak) binding to the C conformation and high-affinity (strong) binding to the O conformation. (The logarithm of an equilibrium dissociation constant is proportional to binding energy.)

The high-concentration asymptote of a CRC, or the maximal response elicited by the ligand, is called P_O^max in single-channel or I^max in whole-cell currents. This limit gives the agonist’s efficacy and depends only on the fully liganded gating equilibrium constant. The midpoint (EC₅₀) of a CRC or the agonist concentration that produces a half-maximal response is proportional to K_dC but also depends on the gating equilibrium constant.

The low-concentration asymptote of a CRC, which gives the level of activity in the absence of agonists (P_O^min or I^min), depends on the unliganded gating equilibrium constant that is typically small and difficult to measure. However, it is important to know the exact value of this constant because it multiplies the fully liganded gating equilibrium constant to influence potency, efficacy, and synaptic current profiles. Allosteric modulators and AChR mutations (8), including some that cause slow-channel myasthenic syndromes (9), alter EC₅₀, I^max, and the time course of synaptic currents simply by increasing or decreasing the unliganded gating equilibrium constant, without making a noticeable change in baseline activity.

Recently, efficiency (η) was defined as the fraction of an agonist’s chemical binding energy that is converted into the mechanical (kinetic) energy for gating (10). Efficiency reports the strength of the link between binding and gating. As shown previously (and again below by using a different approach), η is a function of the resting/active binding energy ratio, logK_dC/logK_dO. Direct, independent measurements of these two equilibrium dissociation constants obtained by detailed kinetic modeling of single-channel currents indicated that at adult-type human AChR neurotransmitter binding sites, ACh and three related agonists on average apply ∼50% of their binding energy to gating, whereas at the α1-δ binding site, the frog toxin epibatidine and three related agonists on average apply only ∼40% (10).

Here, we show that agonist efficiency can be estimated from the asymptotes and midpoint of a single CRC constructed from either single-channel or whole-cell responses. Given two agonists with the same EC₅₀, the one with the larger I^max has the greater η. We provide separate efficiency estimates for 20 agonists of mouse adult AChRs and show that knowledge of agonist efficiency broadens our understanding of receptor activation and drug action.

Materials and methods

Experimental design

Expression

Human embryonic kidney 293 cells were maintained in Dulbecco’s minimal essential medium supplemented with 10% fetal bovine serum and 1% penicillin-streptomycin (pH 7.4). For single-channel experiments, AChRs were expressed by transient transfection of 3 μg mouse α1, β, δ, and ε subunits in the ratio 2:1:1:1 (TransIT 293 transfection reagent; Mirus Bio, Madison, WI). Electrophysiological experiments started ∼48 h posttransfection. For whole-cell recording, human embryonic kidney 293 cells were transiently transfected with adult-type mouse AChRs using calcium phosphate precipitation. 20 μg of cDNA was added in the ratio of 2:1:1:1 (α1-GFP encoded between M3-M4,β,δ and ε) to a T75 flask at ∼60% confluence. Cells were incubated for ∼16 h at 37°C, replenished with fresh medium, and harvested after ∼20 h of washing. GFP-positive cells were sorted by using an ABD FACS Fusion four-laser Cell Sorter (Becton Dickinson, Franklin Lakes, NJ). Cells were excited with laser at 488 nm, and the GFP signal was collected in the green channel through a 530/40 filter. A light scatter gate was drawn in the side scatter versus forward scatter plot to exclude debris and to include viable single cells. No animals were used in this study.

Electrophysiology

Single-channel currents were recorded in the cell-attached patch configuration at 23°C. The bath solution was (in mM) 142 KCl, 5.4 NaCl, 1.8 CaCl₂, 1.7 MgCl₂, and 10 HEPES/KOH (pH 7.4). Patch pipettes were fabricated from borosilicate glass and fire polished to a resistance of ∼10 MΩ when filled with the pipette solution that was Dulbecco’s phosphate-buffered saline (in mM): 137 NaCl, 0.9 CaCl₂, 2.7 KCl, 1.5 KH₂PO₄, 0.5 MgCl₂, and 8.1 Na₂HPO₄ (pH 7.3/NaOH). Currents were recorded using a PC505 amplifier (Warner Instruments, Hamden, CT), low-pass filtered at 20 kHz, and digitized at a sampling frequency of 50 kHz using a data acquisition board (SCB-68; National Instruments, Austin, TX). Agonists were added to the pipette solution at the desired concentration.

Whole-cell currents were recorded using an IonFlux 16 automated patch-clamp system (Fluxion Biosciences, Alameda, CA) on 96-well IonFlux microfluidic ensemble plates that give a cumulative whole-cell current from up to 20 cells. GFP-positive cells were resuspended in extracellular solution containing (in mM) 138 NaCl, 4 KCl, 1.8 CaCl₂, 1 MgCl₂, 5.6 glucose, and 10 HEPES, pH adjusted to 7.4 with NaOH. Cells were captured in the trapping wells with intracellular solution containing 60 KCl, 70 KF, 15 NaCl, 5 HEPES, and 5 EGTA, pH adjusted to 7.2 using KOH. Cells clamped at −80 mV were exposed to a 2-s agonist application followed by 90-s wash between applications to allow recovery from desensitization. IonFlux software (ver.4.5) was used for cell capture, seal formation, compound application, and data acquisition.

Analysis

Scheme 1 (Fig. 1) shows the main states of AChR activation/deactivation. First, we estimated η from single-channel current CRCs. When agonist binding and channel opening rate constants are sufficiently large, openings occur in clusters (Fig. 2 A; Fig. S1–S4; (11)). Shut intervals within clusters represent mainly agonist binding to C and channel opening (bold in Fig. 1), whereas shut intervals between clusters represent mainly long-lived desensitization (not shown in Fig. 1; for connections, see (6)). We selected for analysis clusters that appeared by eye to arise from a homogeneous P_O population and, to exclude sojourns in desensitized states, limited our analyses to intracluster interval durations.

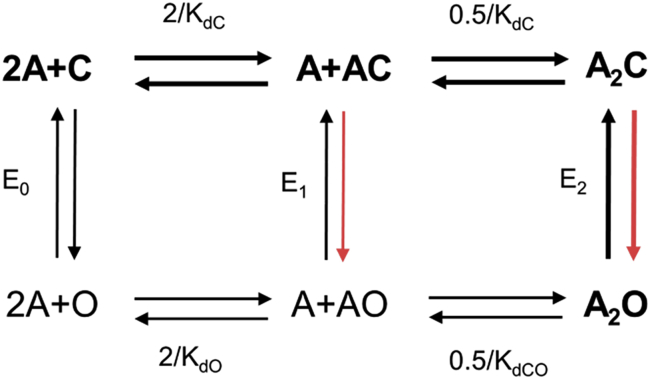
Figure 1.

Cyclic activation of AChRs (scheme 1). Receptors switch between closed-channel (C) and open-channel (O) conformations spontaneously (influenced only by temperature) with or without agonists (A). Equilibrium constants are as follows: E_n, gating with n bound agonists, and K_dC and K_dO, dissociation constants to C (low affinity) and to O (high affinity). The adult-type, endplate AChR binding sites are approximately equivalent and independent with regards to the agonists used in this study. From experiments and microscopic reversibility, E₂/E₀ = (K_dC/K_dO)². Agonists increase activity above the baseline level because they bind more strongly to the C-O transition state, with the extra binding energy serving to increase the channel-opening rate constant (red arrows). Thick arrows and bold letters mark the physiological activation-deactivation pathway. To see this figure in color, go online.

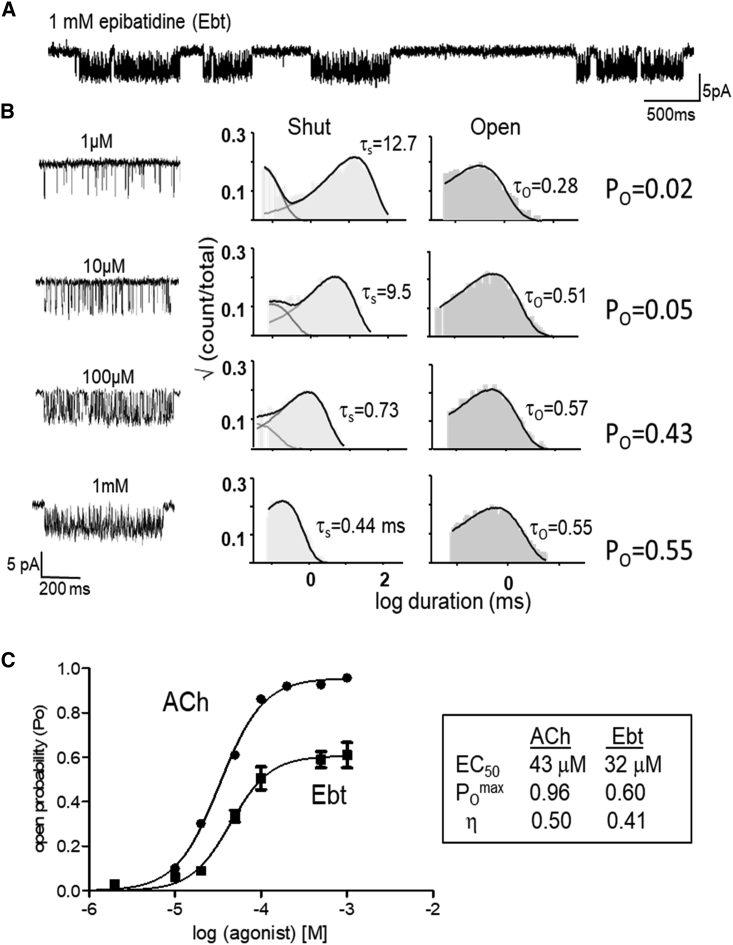
Figure 2.

Single-channel current CRCs. (A) Low-resolution view of cell-attached, single-channel currents activated by epibatidine (Ebt; open is down). Clusters of open/shut intervals from one AChR separated by silent periods in which all AChRs in the patch are desensitized. (B) Left, high-resolution views of example clusters at different Ebt concentrations. Right, corresponding intracluster interval-duration histograms are shown. τ_s and τ_o are predominant shut- and open-interval time constants (in ms). O probability (P_O) at each agonist concentration is τ_o/(τ_s + τ_o). (C) Each CRC was fitted by Eq. 1 to estimate EC₅₀ and P_O^max (symbols, mean ± SE). Efficiency (η) was calculated by using (2), (3), (4), (5). It is apparent that ACh is more efficient than Ebt because the same EC₅₀ is associated with a greater P_O^max.

Because of the high extracellular [K⁺], the cell membrane potential (V_m) was 0 mV. The AChR agonists we examined also are channel blockers. To both generate measurable currents and reduce the effect of channel block on P_O, the membrane was depolarized to +70 mV by holding the pipette at −70 mV. This effectively eliminated agonist binding to the channel block site in the transmembrane domain but did not affect agonist binding to the neurotransmitter sites in the extracellular domain.

Analyses of the single-channel (outward) currents were performed by using QUB software (12). A cluster was defined as a group of openings flanked by shut intervals longer than a duration that depended on the agonist concentration (range, 7–20 ms). Open and shut currents within clusters were idealized into noise-free intervals by using the segmental k-means algorithm after digitally low-pass filtering the data at 10 kHz (13). Idealized interval durations were fitted by multiple exponential components using a maximal interval likelihood algorithm (14). Cluster P_O at each agonist concentration was calculated from the time constants of the predominant components of the shut- (τ_s) and open-time distributions (τ_o): τ_o/(τ_s + τ_o) (Fig. 2 B). The single-channel CRC was a plot of the absolute P_O (not normalized) versus the agonist concentration.

We also estimated η from whole-cell current CRCs. The currents were digitized using a sampling frequency of 10 kHz and were analyzed using IonFlux Data Analyzer v5.0. Peak currents were normalized to a maximal response (I/I^max), where I^max was the response to 300 μM ACh. The 20–80% rise time to a step to 300 μM ACh was ∼400 ms, a time we attribute to solution exchange.

The rate of entering a long-lived desensitized state is proportional to cluster P_O and occurs with a rate constant of ∼5 s⁻¹ (15). Hence, under conditions in which P_O is ∼1, a whole-cell current will decline with a time constant of ∼200 ms. As a consequence, the peaks of whole-cell currents elicited by high concentrations of high-efficacy agonists are truncated because of the solution exchange time. This has the effect of shifting EC₅₀ to lower concentrations. Responses at lower agonist concentrations or from lower efficacy agonists were unaffected by desensitization.

Voltage, E₀, and background mutations

Depolarization to V_m = +70 mV reduces channel block by the agonist but has the undesired consequence of shortening τ_o to make single-channel current detection and idealization difficult. To compensate, we added the background mutation εS450W (in the M4 transmembrane segment of the ε subunit) that has the equal-but-opposite effect on the unliganded gating equilibrium constant E₀ as does depolarization by +140 mV but has no effect on agonist binding (16). With this mutation, τ_o and E₀ at +70 mV were the same as in wild-type (wt) adult AChRs at V_m = −70 mV. E₀ at −100 mV is 7.4 × 10⁻⁷ and is reduced e-fold by a 60-mV depolarization (17). Hence, we estimate that in our experiments at V_m = +70 mV and with εS450W, E_o was 5.2 × 10⁻⁷. In the whole-cell experiments, no background mutations were used and V_m = −80 mV, so we estimate E₀ was 5.9 × 10⁻⁷.

With the low-efficacy agonists varenicline, tetraethylammonium (TEA), and tetramethylphosphonium (TMP), single-channel clusters generated by wt AChRs were poorly defined because the channel opening rate constant was small. For these ligands, P_O could not be estimated accurately using wt AChRs. To increase the diliganded opening rate constant and generate better-defined, higher-P_O clusters, we added two background mutations in the ε subunit, εL269F (in the M2 helix) and εE181W (in strand β9), without εS450W. Together, these two substitutions increase E₀ by 1084-fold (making it 4.9 × 10⁻⁴), without affecting agonist binding (18,19). From the uncorrected CRC, we estimated an E₂ value from the P_O^max (Eq. 4) and K_dC from EC₅₀. We divided this E₂ by 1084 to arrive at a corrected E₂, from which we calculated corrected P_O^max and EC₅₀ values that pertain to wt AChRs (Table 1).

Table 1.

Efficiencies from single-channel CRCs

	Measured Values					Calculated values
s.no	Agonist	EC50 ± SE (μM)	POmax ± SE	nH	n	E2	KdC (μM)	KdO (nM)	log KdC	log KdO	ƞ	volume (A3)
1	ACha	43	0.96	1.7	ND	23.4	174	24	−3.76	−7.62	0.50	77
ND	AChc	ND	ND	ND	ND	ND	130	18	−3.89	−7.74	0.50	ND
ND	AChd	22	0.96	ND	ND	24	90	12	−4.04	−7.91	0.49	ND
2	Norb	72	0.92	1.0	ND	12	200	38	−3.70	−7.41	0.50	69
3	CCha	320	0.84	1.6	ND	5.25	542	159	−3.27	−6.80	0.52	77
4	Anab	524	0.78	1.2	ND	3.63	719	253	−3.14	−6.60	0.52	70
5	TMAa	1200	0.75	1.1	ND	3	1480	574	−2.83	−6.24	0.54	77
6	DMTa	4200	0.42	0.8	ND	0.72	2730	2150	−2.56	−5.67	0.54	58
7	DMPa	6700	0.26	1.1	ND	0.35	3570	4040	−2.45	−5.39	0.54	56
8	Cho	4013	0.05	ND	ND	0.05	4100	15,100	−2.39	−4.82	0.50	77
9	DMPP$	246 ± 81	0.87 ± 0.09	1.3	3	6.69	480	134	−3.32	−6.87	0.52	59
10	4OH-B$	2171 ± 77	0.29 ± 0.04	0.9	3	0.41	1270	1350	−2.92	−5.87	0.50	77
11	3OH-P$	3485 ± 10	0.15 ± 0.02	0.6	4	0.18	1660	2840	−2.78	−5.55	0.50	77
12	Ebt$	32 ± 2	0.60 ± 0.6	1.9	4	1.50	28	16	−4.55	−7.78	0.41	88
13	Ebx$	90 ± 4	0.74 ± 0.02	1.6	3	2.85	108	46	−3.96	−7.33	0.46	88
14	Cyt$	137 ± 5	0.18 ± 0.01	1.3	4	0.22	67	104	−4.17	−6.99	0.40	114
15	Var∗	135 ± 12	0.015 ± 0.002	4.8	3	0.02	57	331	−4.25	−6.48	0.35	102
16	TEA∗	4200 ± 130	0.002 ± 0.0007	1.1	3	0.002	174	26,800	−2.76	−4.57	0.40	136
17	TMP∗	844 ± 32	0.03 ± 0.002	2.5	3	0.031	360	1473	−3.44	−5.83	0.41	87
18	Atxe	ND	ND	ND	ND	ND	115	247	−3.94	−6.61	0.40	114
19	Azae	ND	ND	ND	ND	ND	934	6053	−3.03	−5.22	0.42	88
20	Nicb	ND	ND	ND	ND	0.87	1000	920	−3.00	−6.04	0.50	84

E₂, diliganded gating equilibrium constant; K_dC, equilibrium dissociation constant to C; K_dO, equilibrium dissociation constant to O (see Fig. 1); n, number of CRCs; ND, not determined.

EC₅₀, P_O^max, and n_H were obtained by using Eq. 1. The unliganded gating equilibrium constant E₀ was 5.2 × 10⁻⁷. η efficiency was calculated using Eq. 5; volume is of the agonist’s headgroup volume (Fig. S5). All entries pertain to wt adult AChRs.

^aPreviously published values are from (20).

^bPreviously published values are from (21).

^cPreviously published values are from (5).

^dPreviously published values are from (22).

^ePreviously published values are from (10).

Equations

Single-channel CRCs were constructed from P_O values after eliminating extraneous events arising from channel block, desensitization, and modal activity (23). Whole-cell CRCs were constructed directly from peak currents. EC₅₀ and P_O^max (or I^max) the Hill coefficient (n_H) were estimating by fitting the CRC,

$$P_O=\frac{P_O^{max}}{1+{\left(\frac{E{C}_{50}}{\left[agonist\right]}\right)}^{n_H}}.$$ (1)

Scheme 1 (Fig. 1) was used to derive expressions for η. Because microscopic reversibility is satisfied,

$$\frac{E_2}{E_0}={\left(\frac{K_{dC}}{K_{dO}}\right)}^2,$$ (2)

where E₂ and E₀ are the diliganded and unliganded gating equilibrium constants, and K_dC and K_dO are the equilibrium dissociation constants for binding to C and O. The exponent reflects the fact that in adult-type AChRs, there are two neurotransmitter sites that are approximately equivalent and independent with regards to the agonists used in this study. Eq. 2 has been confirmed by experiment (5).

Constitutive and monoliganded activity are both rare, so in wt AChRs, the only significant pathway that generates current is the clockwise, linear activation route highlighted in Fig. 1. Transitions between these four states determine P_O and, hence, the experimental values of EC₅₀ and P_O^max (or I^max).

Accordingly, EC₅₀ depends on both binding and gating equilibrium constants,

$$E{C}_{50}=\frac{K_{dC}\sqrt{E_2+2}}{E_2+1},$$ (3)

whereas P_O^max (I^max) depends only on the gating equilibrium constant,

$$P_O^{max}=\frac{E_2}{E_2+1}.$$ (4)

This equation also can be used to relate P_O^min (I^min) and E₀.

Agonist efficacy depends on the diliganded gating equilibrium constant that, from Eq. 2, is a function of the affinity ratio, K_dC/K_dO. Taking the log of Eq. 2, we see that efficacy is determined by the difference between the binding energies, log(K_dC) − log(K_dO). Partial agonists experience smaller increases in O versus C binding energy compared to full agonists, antagonists experience no change in binding energy, and inverse agonists experience a decrease in favorable binding energy upon receptor activation.

In contrast, η depends on the ratio of these binding energies, log(K_dC)/log(K_dO), as shown previously (10) and as follows. Agonist activation of a resting, unliganded AChR entails connecting the resting-unliganded state C to the diliganded-active state A₂O (Fig. 1). The product of the equilibrium constants (or sum of the energy changes) for steps linking these states in the clockwise direction (the highlighted, physiological activation route) is the same as in the rarely taken, counterclockwise direction. The product of the counterclockwise constants is E₀/K_dO², the negative log of which is proportional to the total energy required for constitutive gating and binding to O at two sites, 2log(K_dO) − logE₀. The product of the equilibrium dissociation constants connecting C with A₂C is 1/K_dC², the negative log of which is proportional to the energy for just the binding part of clockwise activation, 2log(K_dC). We are interested only in the agonist component of the total energy and, because E_o is agonist independent, it can be ignored. Hence, the fraction of the total agonist energy that is used in binding is 2logK_dC/2logK_dO, so efficiency, or the fraction of this total that is applied to gating, is

$$\eta =1-\frac{\log {\text{K}}_{\text{dC}}}{\log {\text{K}}_{\text{dO}}}.$$ (5)

Efficacy and efficiency are distinct, but related, agonist attributes. In terms of energy, efficiency is equal to efficacy (logK_dO − logK_dC) divided by logK_dO (Eq. 5). An agonist can be high efficacy and low efficiency (epibatidine) or low efficacy and high efficiency (choline) but within limits. If an agonist has P_O^max = 0.75 (about the same as tetramethylammonium (TMA)) and η = 30%, it would have unreasonably small equilibrium dissociation constants, K_dC = 27 nM and K_dO = 15 pM. In practice, high-efficacy agonists will also have high efficiencies.

Except for Fig. 8 A, we calculated efficiency from EC₅₀, P_O^max, and P_O^min using a stepwise approach: 1) E₂ from P_O^max (Eq. 4), 2) K_dC from E₂ and EC₅₀ (Eq. 3), 3) K_dO from E₂ and K_dC using a known value of E₀ (Eq. 2), and finally, 4) η from the equilibrium dissociation constant ratio (Eq. 5). In Fig. 8 A only, an approximate value of η was calculated directly using Eq. 10 with A = 0.

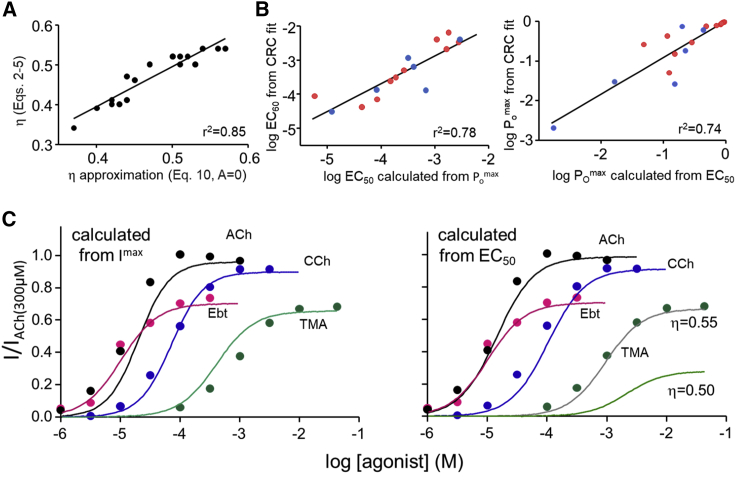
Figure 8.

Using efficiency to calculate CRC parameters. (A) Approximate efficiencies calculated in a single step (Eq. 10, with A = 0) match efficiencies calculated in multiple steps ((2), (3), (4), (5)). (B) If ƞ and E₀ are known, EC₅₀ and I^max (P_O^max) can be calculated from each other. Left, calculated versus measured EC₅₀ from single-channel CRCs is shown. η for each agonist is given in Table 2. Right, calculated versus measured P_O^max using η = 50% (red) or 40% (blue) is shown. (C) Left, CRCs drawn using calculated EC₅₀ and measured I^max (Table 2, left) superimposed on whole-cell current responses (Fig. 6A). Right, CRCs are drawn using calculated I^max and measured EC₅₀ (Table 2, right) using η = 50% for ACh, CCh, and TMA and 40% for Ebt. With TMA, η = 55% improves the match. To see this figure in color, go online.

Four prior results enabled us to estimate η from a CRC. First, adult AChR binding sites have approximately the same affinity, so only single values of the equilibrium dissociation constants needed to be estimated for each ligand. Second, scheme 1 and microscopic reversibility have been proved experimentally. Third, the unliganded gating equilibrium constant has been measured. In an “efficiency” plot for a group of ligands (10), E₀ is estimated from the y-intercept (see Eq. 8, below). However, prior knowledge of I^min (∼E₀) is required to estimate efficiency from a single CRC. I^min is the same for all agonists and so needs to be estimated only once for each receptor (at a given membrane potential).

Statistical analyses

For both single-channel and whole-cell CRCs, the midpoint, maximum, and slope (EC₅₀, P_O^max or I^max, and n_H) were estimated by fitting by Eq. 1 using GraphPad Prism 6 (GraphPad). Eq. 9 was solved numerically for E₂ using the symbolic math program Wolfram Alpha.

The goodness of fit for the efficiency frequency distribution (Fig. 5 A) was estimated using Prism. The F-test rejects the null hypothesis (Gaussian fit) over a sum of two Gaussian with an F-value (F = 3.9) and significance (p-value <0.05). A k-means cluster analysis algorithm (MATLAB; The MathWorks, Natick, MA) was used to define agonist groups for two-dimensional (2D) cluster analysis, both efficiency and headgroup volume (Fig. 5 B). Correlation significance between log EC₅₀ or log P_O^max, measured from CRCs or calculated from each other (Fig. 8 A), was by Pearson’s correlation test using Prism software. The p-value (two-tail) <0.0001 and r² = 0.78 or 0.74 imply that there is a significant correlation.

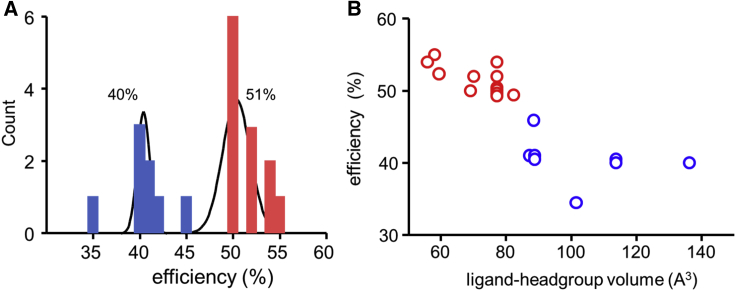
Figure 5.

Distribution of agonist efficiency. (A) Distribution of efficiencies for 20 agonists, fitted by the sum of two Gaussians. There are two populations at η = 51 ± 2% and 40 ± 4% (mean ± SD). (B) 2-D scatter plot of efficiency versus headgroup volume (v). Cluster analysis (k-means) shows that there are two populations with η/v centroids at 52%/70.4 A³ (red) and 41%/102.2 A³ (blue). To see this figure in color, go online.

Agonists

Agonist structures are shown in Fig. 3, Fig. 4, and Fig. S5. Agonist headgroup volumes (Fig. 5 B) were calculated using Chimera (24). The following agonists were used: ACh, nornicotine (Nor), nicotinic, carbamylcholine (CCh), anabasine, TMA, dimethylthiazolidinium (DMT), dimethylpyrrolidium (DMP), choline (Cho), 3-hydroxypropyltrimethylammonium, 4-hydroxybutyltrimethylammonium, anatoxin (Atx), azabicycloheptane (Aza), TEA, epibatidine (Ebt), epiboxidine (Ebx), varenicline (Var), cytisine (Cyt), dimethylphenylpiperazinium (DMPP), and TMP. Cyt, Var, TEA, and TMP were from Sigma (St. Louis, MO). The sources for other agonists are given in previous publications (10,25).

Figure 3.

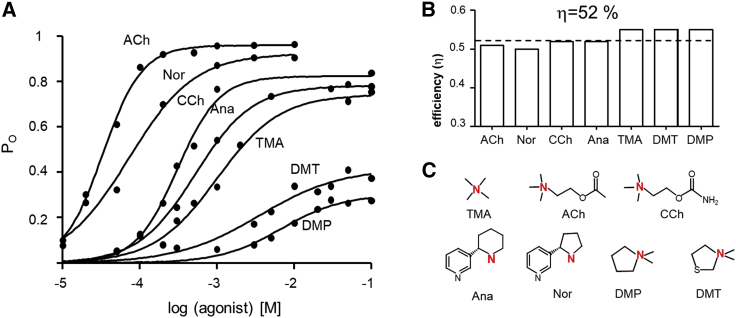
Efficiencies from single-channel CRCs. (A) CRCs of seven agonists in adult-type mouse AChRs (replotted from (20)). There is an inverse correlation between EC₅₀ and P_O^max (Table 1). (B) Agonist efficiencies calculated from EC₅₀ and P_O^max. All agonists have a similar efficiency (average, 52%; dashed line). (C) Agonist structures (see Materials and methods for abbreviations). Red represents the key nitrogen atom in the agonist’s headgroup. To see this figure in color, go online.

Figure 4.

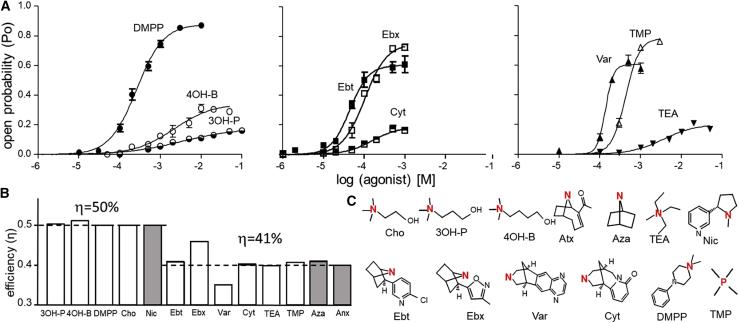
Efficiencies from more single-channel CRCs. (A) Single-channel CRCs of nine agonists in adult-type mouse AChRs (symbols, mean ± SE). In some cases, background mutations were used to increase constitutive gating and, hence, increase P_O^max and left-shift EC₅₀ (εS450W, left and middle; εL269F + εE181W, right). EC₅₀ and P_O^max values in Table 1 have been corrected for these backgrounds and pertain to wt AChRs. (B) Efficiencies calculated from the CRCs (open bars) or from previously reported measurements of K_dC and K_dO obtained by kinetic modeling (gray bars (5,21)). There are two populations with average efficiencies of 50 and 41% (dashed lines). (C) Agonist structures. Red represents key nitrogen or phosphorous atom in the agonist’s headgroup. To see this figure in color, go online.

Results

ACh efficiency

Fig. 2 shows example single-channel currents and CRCs. For the neurotransmitter ACh, P_O^max and EC₅₀ estimated by fitting the CRC by Eq. 1 are 0.96 and 43 μM (Table 1). From P_O^max, we calculate the diliganded gating equilibrium constant, E₂ = 23.4 (Eq. 4). From this value and EC₅₀, we calculate the low-affinity equilibrium dissociation constant, K_dC = 174 μM (Eq. 3). The unliganded gating equilibrium constant at +70 mV is 5.2 × 10⁻⁷ (see Materials and methods), so we calculate the high-affinity equilibrium dissociation constant is K_dO = 26 nM (Eq. 2). Finally, from the ratio of the logs of the two equilibrium dissociation constants, we calculate the efficiency of the neurotransmitter, η_ACh = 50% (Eq. 5).

We also calculated η_ACh from published values of K_dC and K_dO obtained either from wild-type mouse AChRs (20) or from individual α−δ and α−ε human AChR binding sites (5), in both instances estimated by kinetic modeling of single-channel currents. The efficiencies calculated from these independent data sets are both 50% (Table 1).

At adult AChR binding sites, half of the neurotransmitter binding energy is applied to the gating conformational change. That is, at each of the two binding sites, the energy change when ACh binds to the C conformation is approximately equal to the increase in binding energy that happens within the C-to-O transition.

Efficiency of other agonists

We fitted other previously published, single-channel CRCs (20) to estimate EC₅₀ and P_O^max and, from these, calculated agonist η-values as described above (Fig. 3; Table 1). Despite the wide ranges in both EC₅₀ (43 μM to 6.7 mM) and P_O^max (0.26–0.96), all eight of these agonists (including ACh) have a similar efficiency, η = 52 ± 2% (mean ± SD) (Fig. 3 B). The efficiency of the lowest-efficacy agonist in this group, DMP, was greater than that of the highest-efficacy agonist, ACh. This highlights the distinction between efficiency (that depends on the binding energy ratio) and efficacy (that depends on the binding energy difference).

Next, we measured efficiencies for agonists that were not studied previously by CRCs (Fig. 4). Choline (Cho) has two methylenes between its quaternary nitrogen and hydroxyl (OH) group versus 3 and 4 for 3-hydroxybutyltrimethylammonium and 4-hydroxypropyltrimethylammonium (4OH-PTMA). Cho is a low-affinity, low-efficacy agonist (26) that K_dC and K_dO values estimated by modeling single-channel kinetics at the human α−ε site indicate has a similar efficiency as does ACh (10). Simulations of binding site structures suggest that an H-bond between the terminal OH and the backbone carbonyl of αW149 serves to position the charged nitrogen of choline away from the aromatic rings that line the cavity to reduce favorable binding energy (27,28). Inserting additional methylenes reduces the probability of this H-bond and allows a more-optimal position that increases binding energy relative to Cho.

The CRCs and associated P_O^max and EC₅₀ values for 3-hydroxybutyltrimethylammonium and 4OH-PTMA are shown in Fig. 4 A (left). From the calculated equilibrium dissociation constants, we estimate η is 50% for both agonists (Table 1). Despite the substantial range in affinity and efficacy afforded by the different H-bond propensities, all three of the choline agonists have the same efficiency that is similar to the efficiencies of the agonists shown in Fig. 3. The similarity in the C versus O binding energy ratio (but not the difference) for these three ligands suggests that the effect of the H-bond on the position of the nitrogen atom applies equally to C and O binding cavities.

Fig. 4 A (left) also shows the CRC of DMPP, a nicotinic receptor agonist that is selective for the α3β4 (ganglionic) subtype (29). The result was η_DMPP = 52% (Table 1).

Overall, the mean ± SD efficiency calculated from CRCs for the 11 agonists described so far (ACh, nornicotine, CCh, anabasine, TMA, DMP, DMT, Cho, 4-hydroxybutyltrimethylammonium, 4OH-PTMA, and DMPP) is 52 ± 2%. For this entire group of ligands, that covers a huge range in potency and efficacy; the binding energy ratio logK_dC/logK_dO is 0.48. Hence, for all of these agonists, binding energy increases by a factor of 2.1 (the inverse of this ratio) when the liganded sites switch from low to high affinity at the beginning of the global, channel opening transition.

Fig. 4 A (middle) shows CRCs for three agonists that have a bridge in their headgroup. The efficiency values for epibatidine, Ebx, and cytisine calculated from P_O^max and EC₅₀ were η_ebt = 41%, η_ebx = 46%, and η_cyt = 40%. The first two values are similar to those estimated previously by kinetic modeling at the human α1-δ binding site (10).

Fig. 4 A (right) shows CRCs for three agonists that have extraordinarily low efficacies and affinities. To study these, we added background mutations that did nothing more than increase E₀ and, hence, increase P_O^max and left-shift EC₅₀ ((2), (3), (4)). After correcting for the effects of the background mutations, from the CRC parameters, we estimate that in wt AChRs, η_TEA = 40%, η_TMP = 41%, and η_var = 35%.

For the group of six ligands shown in Fig. 4 A (middle and right) (Ebt, Ebx, Cyt, Var, TEA, and TMP), the average efficiency was 41 ± 4% (Fig. 4 B). For all these ligands, the binding energy ratio (logK_dC/logK_dO) is ∼0.60, indicating that binding energy increases by a factor of ∼1.7 when the sites switch from C to O.

Fig. 5 A shows a histogram of efficiency values for 17 agonists estimated from single-channel CRCs plus three agonists estimated from single-channel kinetic modeling (Atx, Aza, and nicotine; Fig. 4 C) (10,21). A goodness of fit test indicates that a bimodal (sum of two Gaussians) frequency distribution is a better fit than a single Gaussian (F (3,16) = 3.37, p = 0.044). The two populations have efficiencies of 51 ± 2% and 40 ± 1% (mean ± SD), which is comparable to the mean efficiencies discussed above.

We also estimated the volumes of the headgroup of the agonists (Fig. S5; Table 1) and plotted these versus efficiency (Fig. 5 B). A 2D cluster analysis again shows two populations with efficiencies of η₁ = 52% (n = 12) and η₂ = 41% (n = 8) with corresponding volumes of v₁ = 70.4 ± 8.8 and v₂ = 102.2 ± 17.8 Å³ (centroid ± SD). There is an inverse relationship between agonist efficiency and headgroup volume.

CRCs from whole-cell currents

Single-channel CRCs may offer an accurate method for estimating K_dC and E₂, but CRCs constructed from whole-cell responses are more common. To ascertain the extent to which η estimated from whole-cell CRCs might be influenced by slow perfusion (that allows desensitization to reduce some peak amplitudes) and heterogeneous receptor properties, we measured whole-cell current amplitude as a function of concentration using four agonists, three from the high-efficiency group (ACh, CCh, and TMA) and one from the low-efficiency group (Ebt).

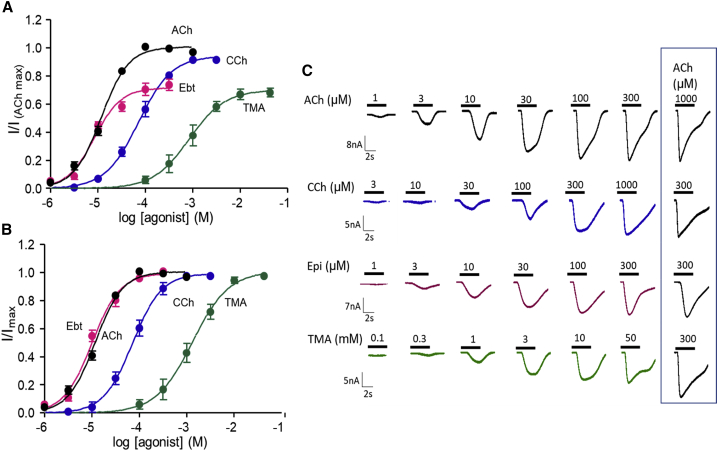
In whole-cell CRCs with maximums normalized to the response to 300 μM ACh response (Fig. 6 A), EC₅₀ values were left-shifted compared to those in single-channel CRCs by an amount that increased with agonist efficacy (Table 2, left). For example, the left-shift was more substantial for ACh (12.2 vs. 43 μM) than for TMA (0.84 vs. 1.2 mM). An independent whole-cell CRC measurement, also made using an automated patch-clamp and adult-type AChRs, was 22 μM for EC₅₀ for ACh (22). We attribute this left-shift to desensitization (see Materials and methods). Despite this error, for all four agonists, the efficiency values estimated from whole-cell CRCs were only slightly smaller than those estimated from single-channel measurements.

Figure 6.

Whole-cell current CRCs. (A) Each current response was normalized to that of 300 μM ACh (P_O = 0.93). I^max and EC₅₀ values are in Table 2 (left). (B) CRCs normalized to I^max = 1. EC₅₀ values are in Table 2 (right). (symbols, mean ± SE) (C) Example currents. To see this figure in color, go online.

Table 2.

Whole-cell CRC parameters and efficiency (η) estimates

Agonist	Imax = response to 300 μM ACh				Imax = 1	n
	EC50 ± SE (μM)	Imax ± SE	nH	η	EC50 ± SE (μM)
ACh	12.2 ± 0.7	0.96	1.5	0.47	12.2 ± 0.7	6
CCh	72.2 ± 11	0.91 ± 0.04	1.2	0.50	72.4 ± 6	6
TMA	843 ± 110	0.70 ± 0.04	1.2	0.52	1328 ± 160	4
Ebt	8.42 ± 1.0	0.72 ± 0.02	1.5	0.39	10 ± 1.2	8

n, number of trials (up to 20 cells each).

Left, EC₅₀, I^max, and n_H from CRCs normalized by the response to 300 μM ACh (Fig. 6A; I^max for ACh determined from single-channel currents; I^min, 5.9 × 10⁻⁷). Right, EC₅₀ from CRCs internally normalized to I^max = 1 (Fig. 6B).

Because the number of receptors contributing to responses varies from cell to cell and with time, whole-cell CRCs are often normalized so that the maximal response for each agonist is 1. We did this for the four whole-cell CRCs to estimate new values for EC₅₀ (Fig. 6 B; Table 2, right). It was not possible to estimate efficiency from these plots because information regarding efficacy was removed, but below, we show that with knowledge of η and I^min, I^max can be recovered from EC₅₀ of a CRC that has been normalized to 1.

Binding site mutations

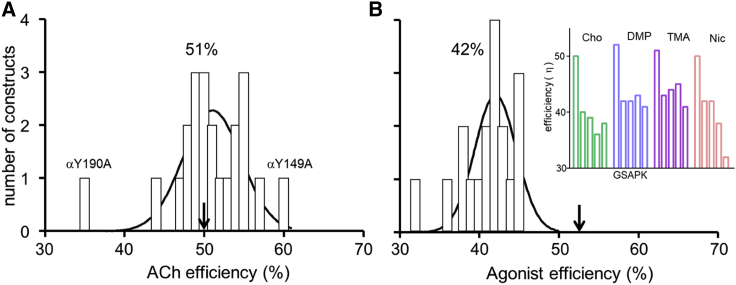
K_dC and K_dO have been measured by kinetic modeling of single-channel currents from mouse, adult-type AChRs having a mutation at one of the five aromatic residues at each of the two binding sites (30). We calculated from these values η_ACh for 21 different mutants (Table S1). Fig. 7 A shows that the distribution is Gaussian with η_ACh = 51 ± 4% (mean ± SD), which is the same as in wt AChRs. The exceptions were αY190A (in loop C) that decreased η_ACh to 35% and mutations of αW149 (in loop B) that increased η_ACh by up to 60% in αW149A. Removal of the αY190 side chain results in a ∼30% decrease in efficiency, whereas removal of the αW149 side chain results in a ∼20% increase in efficiency.

Figure 7.

Effect of binding site mutations on agonist efficiency. Mutations were at both adult-type binding sites. (A) Mutations of aromatic amino acids and εP121 (agonist, ACh) (Table S1). Arrow marks wt efficiency. The only substitutions to alter efficiency significantly are αY190A and αW149A. Gaussian fit of frequency distribution for 21 mutants (excluding αY190A) gives η = 51 ± 4% (mean ± SD). (B) Mutations of αG153 activated by four high-efficiency agonists (Table S2 and inset) (21). Gaussian fit of frequency distribution for all 16 mutation/agonist combinations gives η = 42 ± 3%. To see this figure in color, go online.

Mutations of a residue on the complementary side of the binding site, εP121, had little effect on ACh efficiency except, perhaps, for the slow-channel myaesthenic syndrome mutation εP121L (31).

Binding and gating equilibrium constants have also been reported for AChRs having a mutation of αG153 (21). This amino acid is in loop B and close to αW149 but does not appear to contact the agonist directly. However, αG153 is interesting because so far it is the only binding site amino acid we know of in which mutations decrease K_dC (increase binding energy) and increase significantly E₀. We calculated efficiencies from K_dC, E₂, and E₀ values for 16 different αG153 mutant/agonist combinations using agonists from the high-efficiency population (Table S2).

The distribution of these efficiencies is shown in Fig. 7 B. With a αG153 mutation, η 42 ± 3%, which is ∼20% smaller than the wt. This is the same efficiency as the low-efficiency agonist population in wt AChRs. αG153 mutations that increase affinity also decrease efficiency. The extent of the reduction in η was similar for all agonists and side-chain substitutions, with the exception of αG153K + nicotine. In summary, it appears that a glycine at position α153 allows high efficiency for small-volume agonists that otherwise take on the low-efficiency characteristic of large-volume agonists.

Putting efficiency to use

In this section, we show how knowledge of η can simplify and extend CRC analysis. The same efficiency for a group of agonists means that for all, the logK_dC/logK_dO ratio is the same. Hence, the two equilibrium dissociation constants are related by an exponent,

$${\text{K}}_{\text{dC}}{=\text{K}}_{\text{dO}}^{1-\eta }.$$ (6)

With knowledge of η, only one of the equilibrium dissociation constants needs to be measured. The value of the exponent in Eq. 6 in wt AChRs is ∼0.5 for the high-efficiency group of agonists and ∼0.6 for the low-efficiency group. Accordingly, Eq. 2 becomes

$$\left({\text{E}}_2/{\text{E}}_{\text{0}}\right)={\text{K}}_{\text{dC}}^{\text{p}},$$ (7)

where

$$\mathrm{p}=2\eta /\left(\eta -1\right).$$

The two reflect the number of equivalent binding sites. For the higher efficiency group (η = 0.5), p = −2.00, and for the lower efficiency group (η = 0.4), p = −1.33.

Taking the log of Eq. 7 and rearranging,

$$\log {\mathrm{E}}_2=\mathrm{p}\log {\mathrm{K}}_{\mathrm{d}\mathrm{C}}+\log {\mathrm{E}}_0.$$ (8)

This equation describes an “efficiency” plot, with the x axis being proportional to agonist binding energy (logK_dC) and the y axis being proportional to gating energy (log E₂). For a group of agonists having the same efficiency, a log-log plot of gating versus binding equilibrium constants is a straight line with a slope (p) that depends on efficiency and a y-intercept that gives the unliganded gating equilibrium constant (Eq. 8). Previously, these constants determined from kinetic modeling were used to estimate average η-values for four ACh- and Ebt-class agonists at individual AChR binding sites (10). In addition, values of these constants obtained from the literature were fitted by Eq. 8 to estimate E₀ and average η-values for agonists of other receptors, with off-line points reflecting agonists having other efficiencies.

The clustering of AChR efficiency values into two populations that correlate with agonist size (Fig. 5) suggests that it may someday be possible to predict approximately an agonist’s efficiency a priori from its structure and that of the binding cavity. For example, it is reasonable to guess that in adult-type muscle AChRs, other choline or nicotine derivatives will have η∼50% and that congeners of Ebt and TEA will have η∼40%. More experiments are needed to test the hypothesis that headgroup volume and binding site structure in combination can be used to estimate η. We again note that E₀ (I^min) is agonist independent and needs to be measured only once, so perhaps in the future, this important constant will be known for many different receptors.

Given prior knowledge of agonist η and receptor I^min, the CRC parameters EC₅₀ and I^max (the response at a single, high agonist concentration) can be estimated from each other, as follows.

First, we calculate EC₅₀ from I^max (whole-cell CRCs normalized to an ACh response; Table 2, left). The procedure is to solve E₂ from I^max (Eq. 4), K_dC (Eq. 7; η equal to the value shown in Table 2), and then EC₅₀ (Eq. 3). Fig. 8 B (left) shows that calculated and experimental EC₅₀ values are correlated (Pearson’s correlation, r² = 0.78, p < 0.0001). Fig. 8 C (left) shows that there is a good match between experimental current amplitudes normalized to an ACh response (Fig. 6 A) and those calculated from η according to Eq. 1 using the new EC₅₀ estimates. E₂ has been measured for many AChR agonists (28). Using the above procedure, we estimated corresponding EC₅₀ values assuming η = 51% and E₀ = 7.4 × 10⁻⁷ (Table S3). CRCs for these agonists have not been measured but doing so would test further the ability to use η and E₀ to calculate EC₅₀ from P_O^max.

Second, we calculate I^max from EC₅₀ values (whole-cell CRCs normalized to 1; Table 2, right). Solving Eqs. 7 and 3 for K_dC and setting them equal yields

$$\frac{E{C}_{50}\left(E_2+1\right)}{\sqrt{\left({\text{E}}_2+2\right)}}={\left(\frac{E_2}{E_0}\right)}^{\left(1/\text{p}\right)}.$$ (9)

E₂ and E₀ can be calculated from I^max and I^min (Eq. 4). We solved Eq. 9 for I^max using known values for η and I^min and EC₅₀ from normalized CRCs. Fig. 8 B (right) is a plot of calculated versus experimental P_O^max values from single-channel CRCs using an approximate value for η, either 50% (ACh, CCh, and TMA) or 40% (Ebt). Again, there is rough agreement (Pearson’s correlation, r² = 0.74, p < 0.0001). Next, these calculated I^max values were used to generate CRCs (Eq. 1) that were compared to experimental ones that were not normalized to 1 (Fig. 8 C, right). The match is good for ACh, CCh, and Ebt but not for TMA. Increasing η_TMA from 0.50 to 0.55 makes the calculated and experimental curves match more closely. The I^max value calculated from EC₅₀ by using Eq. 9 is sensitive to the value of η (Fig. S6). Nonetheless, knowledge of agonist efficiency allows efficacy information to be recovered approximately from a CRC that has been normalized to a maximal response of 1.

In addition, knowledge of η allows the estimation of E₀ from a single CRC. E₀ is of critical importance because it sets the baseline level from which agonists increase P_O, but it is often small and difficult to measure directly (8,32,33). However, a fold change in E₀ caused by a mutation or a modulator will produce the same fold change in E₂ (Eq. 2) and, hence, a change in both EC₅₀ and P_O^max (Eqs. 3 and 4).

The procedure we used to estimate E₀ (I^min) from a CRC of a wt receptor is first to solve for E₂ and K_dC from P_O^max and EC₅₀ as described above and then solve for E₀ by using Eq. 8. Fig. S7 shows E₀ values so calculated from single-channel CRC parameters. The mean result is reasonably close to the experimentally determined value (17).

Finally, it is possible to gain an approximate estimate of η from CRC parameters in a single step. Taking the log of Eq. 9 and rearranging

$$p=\frac{\log E_2-log{E}_0}{\log E{C}_{50}-A}$$

$$\mathrm{A}=0.5\log \left({\mathrm{E}}_2+2\right)-\log \left({\mathrm{E}}_2+1\right),$$ (10)

$$\eta =\mathrm{p}/\left(\mathrm{p}-2\right)$$

where E₂ = I^max/(1-I^max) and E₀ = I^min. For many AChR agonists, E₂ < 25 and EC₅₀ < 10⁻³ M, so A will usually be much less than log(EC₅₀). Hence, a reasonable approximation for agonist efficiency can be obtained simply by using Eq. 10 with A equal to zero. Fig. 8 A shows that η-values calculated using this shortcut indeed approximate the more-exact values calculated stepwise using (2), (3), (4), (5).

Discussion

The notion of agonist efficiency arose from an experimental observation—in neuromuscular AChRs, the binding energy ratio logK_dC/logK_dO is the same for many different nicotinic agonists (20). Later, this ratio was associated with the efficiency at which agonist binding energy is converted into receptor gating energy (10). Here, we show that agonist efficiency can be estimated from the asymptotes and midpoint of a CRC. Below, we discuss the nature and distribution of efficiency values obtained from single-channel and whole-cell CRCs, some structural implications of efficiency, and applications of efficiency to CRC analysis.

Efficiency

Agonist efficiencies are the same whether obtained from single-channel or whole-cell currents and from a CRC or by detailed kinetic modeling. They are the same in wild-type AChRs that have two binding sites or in crippled AChRs that have just one operational site. Efficiency values are the same in mouse and human AChRs and with many mutations at the binding sites (exceptions discussed below) or in distant regions that do not affect binding. In AChRs, efficiency is a robust agonist attribute. At adult neuromuscular synapses, half of the available neurotransmitter binding energy is converted into kinetic energy of the channel opening conformational change.

In AChRs, there are two populations of η-values, at 51 ± 2% and 40 ± 4% (Fig. 5 A). Despite the small SDs, we suspect that the variance within each group arises from actual, ligand-specific differences rather than from measurement errors for the following reasons. 1) Efficiency is a ratio of logarithms and therefore is not sensitive to errors in the measured values of EC₅₀ and P_O^max. For example, changing EC₅₀ or P_O^max (Table 1) by ±10% changes the calculated η-value by <1%. 2) The order of η-values within the high-efficiency group is the same in single-channel and whole-cell experiments (TMA > CCh > ACh), and 3) a small difference in efficiency leads to a large difference in efficacy calculated from EC₅₀ (Fig. S6). The single-channel η-value for TMA predicts the experimental, whole-cell CRC more accurately than does the group value (Fig. 8 C, right). We hypothesize that the efficiency difference between, for example, ACh and TMA is meaningful (Fig. 3 B).

The observation that mutations of αG153 shift η for four agonists from the high- to the low-efficiency population supports the existence of two discrete η-populations. Although the distribution of agonist efficiency appears to be modal rather than continuous, the high accuracy of experimental η-estimates must be considered. More experiments might reveal if other η-populations exist or if small differences between agonists or mutations are meaningful. For example, the observations that η is modestly lower with εP121 substitutions (Table S1), higher with most nonaromatic substitutions of αY198 (Table S1), and usually lowest with a K substitution at αG143 (Table S2) might prove to be meaningful. Likewise, experiments might show that the 35% efficiency values for varenicline and ACh + αY190A indicate the existence of a third population.

Structural implications

That a group of agonists have the same efficiency means that all members have the same binding energy ratio, logK_dC/logK_dO (Eq. 5). Below, we discuss implications of this result with regards to 1) rearrangements at the binding site, 2) agonist volume, 3) the bimodal efficiency distribution, and 4) binding site mutations.

The energy of low-affinity binding is proportional to logK_dC and is determined mainly not by diffusion but rather by a local rearrangement at the binding site called “catch.” The energy of the switch from low to high affinity is proportional to (logK_dO-logK_dC), occurs at the beginning of the global channel opening isomerization, and is called “hold” (30,34). As discussed elsewhere (34), “hold” is related to, and possibly the same as, an intermediate (preopening) gating state called “flip” that has been detected directly (35,36). “Flip” refers to a brief shut state that is high affinity, and “hold” refers to the rearrangement of the binding site that generates such a state (37). Regardless, a group efficiency implies that for all members, the energy change in hold is 1/(1 − η) times that of catch. This factor is ∼2 for high- and ∼1.7 for low-efficiency agonists.

This linear relationship between catch-and-hold energy changes suggests that the associated structural changes too are related. Accordingly, the observation that many agonists have the same efficiency suggests that the binding site rearrangements in catch and in hold can be considered as two stages of a single conformational sweep. Although “binding” and “gating” have long been considered to be distinct processes (38), a group efficiency implies that they are components of a multipart structural-change cascade. In AChRs, this cascade begins with a “touch” by the agonist that takes place after the ligand has diffused to its target but before binding site rearrangements that form the low-affinity complex and ends when ions begin to cross the membrane. The “catch-and-hold” sweep of the binding sites is the first part of this cascade, with η quantifying the strength of the connection between the binding (catch) and gating (hold) components.

It remains to be determined whether or not a shared binding energy ratio for a group of related agonists is a general feature of receptor activation. It appears that in some receptors other than neuromuscular AChRs, there is a linear relationship between log gating and log binding equilibrium constants for related ligands and that association to C is slower than diffusion. These results raise the possibility that a shared logK_dC/logK_dO ratio and a correlation between structural changes in low- and high-affinity complex formation are not exclusive to AChRs (10).

Members of both efficiency populations can have a quaternary amine (TMA and TEA) or a secondary amine (DMPP and Ebt). Hence, it does not appear that the bimodal distribution in efficiency reflects this aspect of the agonist’s headgroup. The inverse correlation between agonist headgroup volume and efficiency is more relevant (Fig. 5 B). Simulations of AChR structures suggest that the agonist binding cavity is smaller in O compared with C, and hence, that binding site contraction is a structural correlate of “hold” (27). In addition, kinetic analyses of AChR gating indicate that in the channel opening isomerization, “hold” is followed by a rearrangement of the extracellular domain (4,34,39,40).

These results lead us to hypothesize that large-volume, low-efficiency agonists encounter steric hindrance when the binding cavity contracts in “hold” to limit the shrinkage and, hence, the mechanical force applied to the next element in the gating sequence, the extracellular domain. We imagine that small, high-efficiency ligands fit comfortably into both C and O pockets but that large, low-efficiency agonists do not fit easily into the smaller O cavity and so support a smaller contraction. According to this hypothesis, large ligands transfer less energy to the next step in the conformational cascade and thus have low efficiencies.

In support of this idea, the smallest agonists we tested, DMP, DMT, and TMA, have the largest efficiencies (Fig. 3 B). Further, simulations show that compared to ACh, the binding cavity is smaller with TMA, and the extent of cavity contraction is smaller with the low-efficiency agonist Ebx (27). However, the relationship between agonist volume and efficiency is not simple because Ebt and TEA have similar efficiencies despite a substantial difference in volume (Table 1).

There are two efficiency populations (Fig. 5 A). One possible explanation is that each efficiency group reflects a different “hold” binding site conformation. In this view, the high-affinity cavity can adopt only a limited number (so far, two) of “preset” structures and is not malleable or able to adapt its shape to each agonist. Perhaps, small versus large agonists allow the pocket to adopt alternative contracted shapes, with all agonists larger than some threshold forcing the less-efficient shape. Another hypothesis for the bimodal distribution of η is that there are two discrete energy transfer pathways that supply energy for activating the extracellular domain. Both paths are activated with smaller agonists but one (or both) is compromised when the pocket is “stretched” by a large ligand. Both of these hypotheses are speculations that can be tested experimentally.

Aromatic side chains at the binding site govern agonist affinity. Although most mutations of these have little or no effect on η, another clue regarding the structural basis of efficiency is that the efficiency of ACh is reduced by 30% by the mutation αY190A (in loop C) and increased by 20% by the mutation αW149A (in loop B). αY190 appears to be the most-important aromatic side chain with regards to the propagation of structural changes from the binding site in channel opening (25,41). That the mutations αY190F and αY190W have little effect on ACh efficiency suggests that the key interaction here is with the aromatic ring rather than with the OH group.

All four mutations of αG153 (in loop B) reduced the efficiency of all four tested agonists. Again, the drop appeared to be modal, reducing the average efficiency from 51 to 42%. At this juncture, we do not have a hypothesis for the structural basis for this decrease in efficiency. Perhaps, molecular dynamics simulations can test if flexibility of the loop B backbone promotes high efficiency. It will be worthwhile to ascertain experimentally the extent to which the αW149A and αG153 mutations are correlated.

Efficiency estimates for the two populations are the same whether measured in whole receptors (that have α-δ and α-ε binding sites) or in receptors having only one functional site (10). This indicates that the energy changes that contribute to efficiency are determined mainly by local ligand-protein interactions at each binding site, with little or no energy transfer between sites. The efficiency of Ebx is somewhat higher in whole receptors compared with α-δ alone, so it is possible that the efficiency of this agonist is modestly greater at one site (α-ε) compared with the other. Agonist affinity is greatest at the fetal (α1-γ) neurotransmitter binding sites (56% for ACh), and it is possible that the some of the small, agonist-dependent differences in η between adult sites are meaningful.

Applications

Because η-values are modal, efficiency can be used to classify agonists. Someday, efficiency may stand alongside affinity and efficacy as a core agonist attribute. An approximate value for agonist efficiency can be calculated from CRC parameters by using Eq. 10, with A = 0 (Fig. 8 A). To make the calculation even easier, Eq. 10 can be rearranged to express η directly in terms of CRC parameters,

$$\frac{1}{\eta }\approx \left(1-\frac{n\log \left(E{C}_{50}\right)}{\log \left(\frac{I^{max}}{1-I^{max}}\right)-\text{log}\left(I^{min}\right)}\right),$$ (11)

where n is the number of agonist binding sites and is proportional to n_H (42). Eq. 11 offers an easy way to estimate approximately an agonist’s efficiency from a CRC. If I^min is not known, it may be possible to compare efficiencies of different agonists by using a common value, for instance 10⁻⁶.

We know η is useful because it allows EC₅₀ and I^max to be estimated from each other. With knowledge of η, EC₅₀ and an entire CRC can be calculated knowing only the responses at the low- and high-concentration asymptotes (Fig. 8 C). Given η and I^min, the response at just one agonist concentration, that which produces I^max, needs to be measured to estimate EC₅₀. Having this ability could facilitate drug screening.

It is common practice in CRCs to normalize I^max to one and lose information regarding agonist efficacy. We have shown that given prior knowledge of η and I^min and an experimental estimate of EC₅₀, Eq. 9 can be solved numerically for E₂ and, hence, I^max. The ability to compute an absolute CRC from a normalized one could be useful once the values of the agonist’s efficiency and the receptor’s constitutive activity are established. The main caveat is that the calculated efficacy is very sensitive to the value of η.

Author contributions

D.C.I. designed and performed research and analyzed data. A.A. conceptualized and designed research and analyzed data and wrote the manuscript.

Editor: Vasanthi Jayaraman.