Abstract
During clathrin-mediated endocytosis, a patch of flat plasma membrane is deformed into a vesicle. In walled cells, such as plants and fungi, the turgor pressure is high and pushes the membrane against the cell wall, thus hindering membrane internalization. In this work, we study how a patch of membrane is deformed against turgor pressure by force and by curvature-generating proteins. We show that a large amount of force is needed to merely start deforming the membrane and an even larger force is needed to pull a membrane tube. The magnitude of these forces strongly depends on how the base of the membrane is constrained and how the membrane is coated with curvature-generating proteins. In particular, these forces can be reduced by partially, but not fully, coating the membrane patch with curvature-generating proteins. Our theoretical results show excellent agreement with experimental data.
Significance
Yeast cells have been widely used as a model system to study clathrin-mediated endocytosis. The mechanics of membrane during endocytosis has been extensively studied mostly in low turgor pressure condition, which is relevant for mammalian cells, but not for yeast cells. It has been suggested that as a result of high turgor pressure in yeast cells, a large amount of force is needed to drive the progress of the membrane invagination. In this work, we investigated mechanisms to reduce the force requirement. We highlight the role of boundary conditions at the membrane base, which is a factor that has been largely ignored in previous studies. We also show that a large protein coat does not necessarily reduce the force barrier.
Introduction
Clathrin-mediated endocytosis (CME) is an active process eukaryotic cells use to transport materials from their outside environment to inside of the cell (1, 2, 3, 4, 5, 6). During CME, a patch of flat plasma membrane is bent into the cell and severed to release a vesicle (Fig. 1 a). Deforming the membrane toward the cytoplasm is opposed by membrane’s resistance to bending and membrane tension (8,9). In walled cells such as plants and fungi, the inward deformation is also opposed by turgor pressure, which pushes the membrane against the cell wall (10, 11, 12). In yeast cells, the inner pressure can be up to 1.5 MPa (13,14). It is conjectured that as a consequence of this high turgor pressure, the membrane invagination exhibits a narrow tubular shape with a diameter of ∼30 nm in yeast cells (4,7), whereas in mammalian cells, the invagination exhibits a spherical shape with a diameter of ∼100 nm because of relatively low pressure (∼1 kPa) (15).
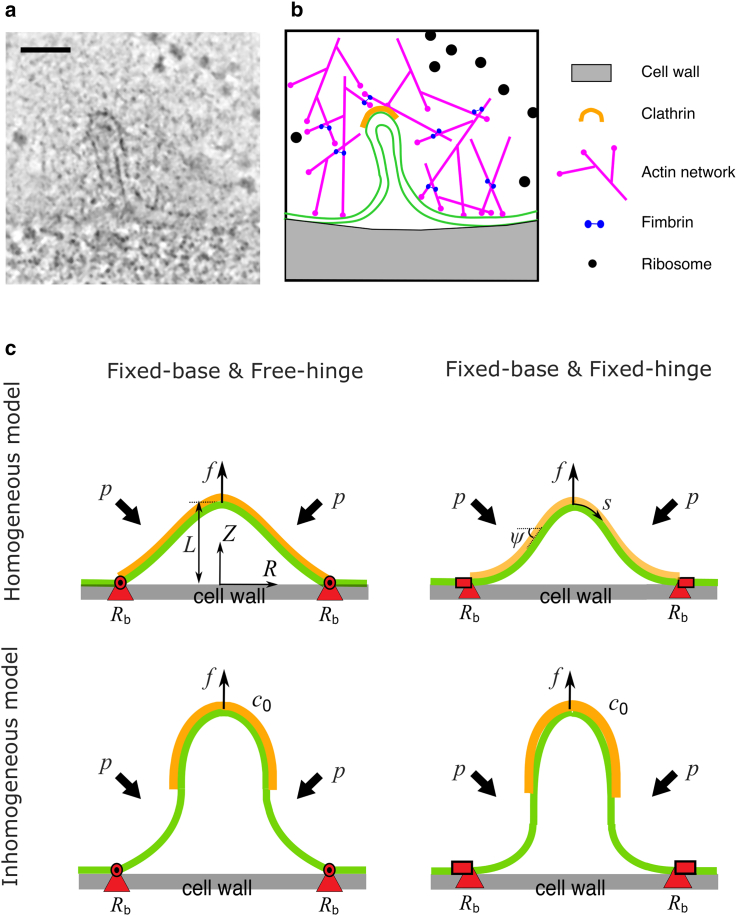
Figure 1.
CME in yeast and membrane models for CME. (a) Electron micrograph of a membrane tube formed during CME in budding yeast. The image was obtained from https://www.embl.de/download/briggs/endocytosis.html and adapted under the permission of the authors of (7). The scale bar represents 50 nm. (b) Schematic illustration of the membrane and key endocytoic proteins shown in (a). The actin network surrounding the membrane tube is depicted as a meshwork of branched and cross-linked filaments, though their precise organization cannot be resolved in the electron micrograph and the meshwork appears as a zone from which ribosomes are excluded. A clathrin coat covering the tip of the membrane tube is also depicted, though the specific spatial distribution of clathrin molecules cannot be resolved in (a). (c) Illustration of the membrane models. The membrane (green layer) is pulled up by a point force f against osmotic pressure p. The membrane is coated with proteins (orange layer) that locally change the spontaneous curvature of the membrane c0. The position of the base (red triangles) is maintained at a constant value Rb. We consider a homogeneous model (top) in which the membrane is fully coated or fully uncoated with curvature-generating proteins and an inhomogeneous model (bottom) in which the membrane is partially coated. We consider two types of BCs, the free-hinge BC (left) in which the membrane is allowed to freely rotate at the base and the fixed-hinge BC (right) in which the membrane angle is fixed. To see this figure in color, go online.
In the past decade, several theoretical models have been proposed to account for the membrane shape evolution during CME (16, 17, 18, 19, 20, 21). Most of these models have assumed conditions relevant to mammalian cells, i.e., low turgor pressure (<1 kPa) and focused on the role of membrane tension. Such tension-dominant membrane deformations have also been extensively studied in in vitro experiments in which membrane tethers are pulled from giant liposomes (22, 23, 24). In contrast, the pressure-dominant regime of membrane deformations, which is relevant to endocytosis in walled cells, has been rarely studied (18). The role of turgor pressure in shaping the membrane has been extensively studied in the case of closed vesicles (25, 26, 27). The typical force barrier to invaginate a membrane tube against a membrane tension of 0.01 pN/nm is only 10–100 pN, whereas a substantial force (∼1000 pN or more) seems to be required to overcome a turgor pressure of 1 MPa (5,28,29).
The cytoskeleton protein actin is essential for generating the forces required for CME in yeast cells (11,30, 31, 32, 33, 34, 35, 36). However, the exact organization of actin filaments around the membrane invagination remains elusive. Actin filaments are likely organized into a tight meshwork because ribosomes are excluded from the endocytic sites and actin filaments are heavily cross-linked (Fig. 1, a and b; (37)). How the actin machinery produces force to bend the membrane remains unclear. The most commonly accepted hypothesis is that polymerization of actin filaments is converted into a pulling force acting on the tip of the invagination through a push-pull mechanism (28,38, 39, 40). In this mechanism, actin filaments are nucleated on a ring around a patch of clathrin and adaptor proteins. Polymerization of actin filaments at the ring, which is the base of the invagination, pushes the actin meshwork away from the plasma membrane and, in turn, pulls the invagination inwards thanks to the adaptor proteins that link actin filaments to the membrane tip.
Membrane can also be bent by proteins that induce membrane curvature. Clathrin molecules can assemble into a cage-like icosahedral lattice composed of hexagons and pentagons in vitro (41,42). The clathrin lattice alone is able to induce spherical buds from membrane in reconstituted experiments (43). In yeast cells, the clathrin lattice acts as a scaffold linked to the plasma membrane via adaptor proteins, and together, they form a rigid coat at the membrane invagination tip (44,45). Based on measurements of the copy number of clathrin molecules in yeast cells, this coat is expected to form a hemispherical cap (46). Many clathrin-associated proteins, such as BAR-domain proteins and epsin, have also shown the capacity to induce membrane curvature and might help with CME (47,48).
In this work, we study CME under conditions of high turgor pressure and low membrane tension by investigating a theoretical model, which describes how a membrane patch is deformed by a point force and by proteins that induce membrane curvature. In the absence of coat proteins, we show that as a result of high turgor pressure (1 MPa), a large amount of force is needed to merely start deforming the membrane and an even larger force is needed to pull a membrane tube. We also show that the magnitude of these forces strongly depends on the constraints at the base of the membrane patch. In particular, the force to start deforming the membrane increases with the base radius, whereas the force barrier to pull a membrane tube decreases with the base radius. The forces also depend on whether the angle of the membrane at the base can freely rotate or not.
When the membrane is coated with curvature-generating proteins, we show that the forces to deform partially coated membranes are quantitatively and qualitatively different from the forces to deform fully coated membranes. By partially coating the membrane, the force barrier that is usually present for fully coated membranes can be dramatically reduced to zero, which implies that the membrane can be spontaneously curved up into a vesicular shape.
We find excellent agreement between our theory and experiments. With a single set of parameters for the partially coated membrane model, we can fit geometric features of the membrane shape obtained via electron tomography across different stages of CME. From the comparison, we estimate that the force required for CME in yeast cells is ∼2500 pN if the membrane angle at the base is free to rotate and almost 5000 pN if the angle is fixed to be in parallel with the cell wall. This result suggests that actin polymerization alone is insufficient to provide the force to drive the membrane invagination during CME.
Methods
Model of the membrane patch at the endocytic site
We model the membrane patch at the endocytic site as an axisymmetric two-dimensional surface. The shape of the membrane is parameterized with its meridional coordinates [R(s), Z(s)], where s is the arclength along the meridional direction (Fig. 1 c). The angle ψ(s) spans between the tangential direction and the horizontal direction. The actin polymerization force is modeled as a point force f acting at the symmetry center of the membrane, which is lifted to a height L relative to the cell wall (Fig. 1 c). The membrane patch is in contact with the cell wall at a base radius of Rb, which is covered by a ring of proteins as observed in recent experiments (28). We assume the proteins serve as anchors that fix the base of the membrane to the cell wall, therefore Rb is a constant. Outside of Rb, there is a lipid reservoir such that the membrane tension σ is kept constant at the base points. An isotropic turgor pressure p is exerted on the membrane, which possesses a bending rigidity κ and spontaneous curvature c0 due to protein coating. Here, we assume the turgor pressure p is a constant and neglect the concentration change caused by volume reduction upon endocytosis because the reduced volume of the membrane invagination only occupies a tiny fraction (1/106) of the total cell volume. The free energy of the membrane, which takes into account the influence of curvature-generating proteins, can be written as
| (1) |
where c1 and c2 denote the two principal curvatures of the membrane surface (49), A denotes the surface area, and V denotes the volume between the membrane and the cell wall. The reference state for the free energy G in Eq. 1 is a vertically flat and horizontally circular shape. We consider both a homogeneous model in which the spontaneous curvature c0 is spatially uniform—such as a bare membrane or a membrane fully coated with curvature-generating proteins—and an inhomogeneous model in which c0 is spatially varied—such as a membrane partially coated by curvature-generating proteins (Fig. 1 c).
Because of rotational symmetry about the z axis, the free energy of the membrane in Eq. 1 can be expressed as a functional
| (2) |
where and denote their derivatives with respect to the arclength s, S denotes the total arclength from the tip to the base, and γ is a Lagrangian multiplier that enforces the geometric relation = cosψ (see Appendix for the explicit form of ). The shape of the membrane is determined by minimization of the free energy G with respect to small variations of the membrane shape variables δψ and δR. Proper boundary conditions (BCs) at the base, where the ring of proteins is formed and the membrane is in contact with the cell wall, are also needed to determine the membrane shape. The exact BCs require knowledge of the microscopic interactions between the membrane, the cell wall, and the ring of proteins. Because these microscopic interactions are unclear, we choose to derive the BCs in the following way. The small variations of δψ and δR result in variation of the free energy δG, which consists of boundary terms like and . Four types of BCs at the base can be identified by letting these boundary terms vanish (Table 1). Physically, they correspond to the combination of whether the base radius is fixed or variable and whether the angle of the membrane at the base is fixed or free to rotate. We focus on the two BCs for which the base radius is fixed (R = Rb) and refer them as free-hinge BC (BC1 in Table 1) if the membrane angle is free to rotate ( = 0) and fixed-hinge BC (BC2 in Table 1) if the membrane angle is fixed to zero (ψ = 0). We also compare our results with a previous work (18), which studied the homogeneous model with a BC in which the base is free to move and the membrane angle is fixed (BC4 in Table 1).
Table 1.
Possible BCs at the base of the endocytic membrane
| Base radius | Membrane angle at the base | Mathematical definition | |
|---|---|---|---|
| BC1a | fixed | free | R = Rb, = 0 |
| BC2b | fixed | fixed | R = Rb, ψ = 0 |
| BC3 | free | free | = 0, = 0 |
| BC4c | free | fixed | = 0, ψ = 0 |
Referred to as the free-hinge BC.
Referred to as the fixed-hinge BC.
BC4 has been studied in (18) for a fully coated membrane.
Results
The characteristic forces to elongate a membrane tube are different between pressure-dominant and tension-dominant conditions
To demonstrate the distinct physics of CME between pressure-dominant and tension-dominant conditions, we approximate the elongated endocytic invagination (as in Fig. 1 a, for example) as a cylindrical tube of radius R and length L and derive analytic formulas for the forces to elongate a membrane tube. The free energy (Eq. 1) under this approximation becomes
| (3) |
Without considering the effect of the spontaneous curvature (c0 = 0), in the case of pressure-dominant condition (σ = 0), by minimization of Ftube with respect to R and L, we obtain the characteristic tube radius Rp and the corresponding force fp (18):
| (4) |
Note that the tube radius scales with the turgor pressure as Rp ∝ p−1/3, but the force obeys fp ∝ p1/3. This means a higher turgor pressure results in a narrower tube but needs larger forces to elongate. In the case of the tension-dominant condition, the characteristic tube radius Rσ and force fσ read (50)
| (5) |
As for endocytosis in yeast cells, σ ≈ 0.01 pN/nm (19), p ≈ 1 MPa (13,14), and κ ≈ 300kBT (44). These numbers lead to a rough estimation of Rp ≈ 8.5 nm, fp ≈ 700 pN and Rσ ≈ 250 nm, fσ ≈ 30 pN. The radius of long endocytic invaginations observed experimentally is about 15 nm (7), which is much closer to the estimated Rp than the estimated Rσ, thus supporting the statement that the turgor pressure, but not the membrane tension, is the dominant factor that opposes endocytosis in yeast cells. For the rest of the study, we assume σ = 0.002pRp such that Rσ = 22Rp ≫ Rp, and therefore, the turgor pressure always dominates over the surface tension in shaping the membrane. We measure the length in units of the characteristic radius Rp and the force in units of the characteristic force fp. The pressure is nondimensionalized with κ/ to a constant 0.5. The mechanics of the system is then determined by only a few dimensionless parameters, including the rescaled base radius Rb/Rp, the rescaled spontaneous curvature c0Rp, and the rescaled coating area a0/(2π) and rescaled edge sharpness parameter α2π when considering the inhomogeneous model (see Eq. 6).
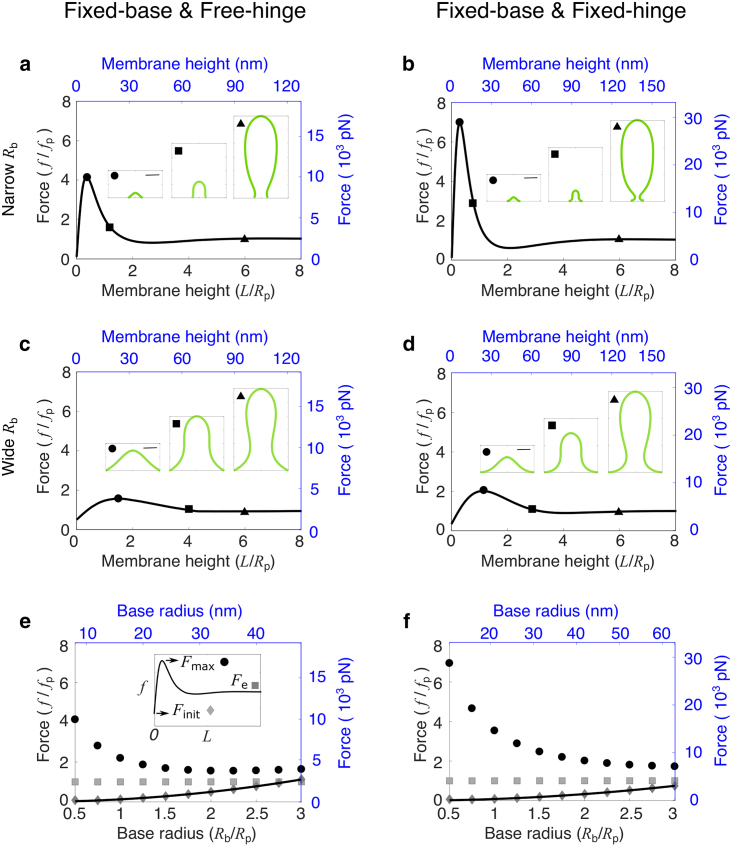
A large base radius lowers the force barrier to pull a membrane tube against turgor pressure
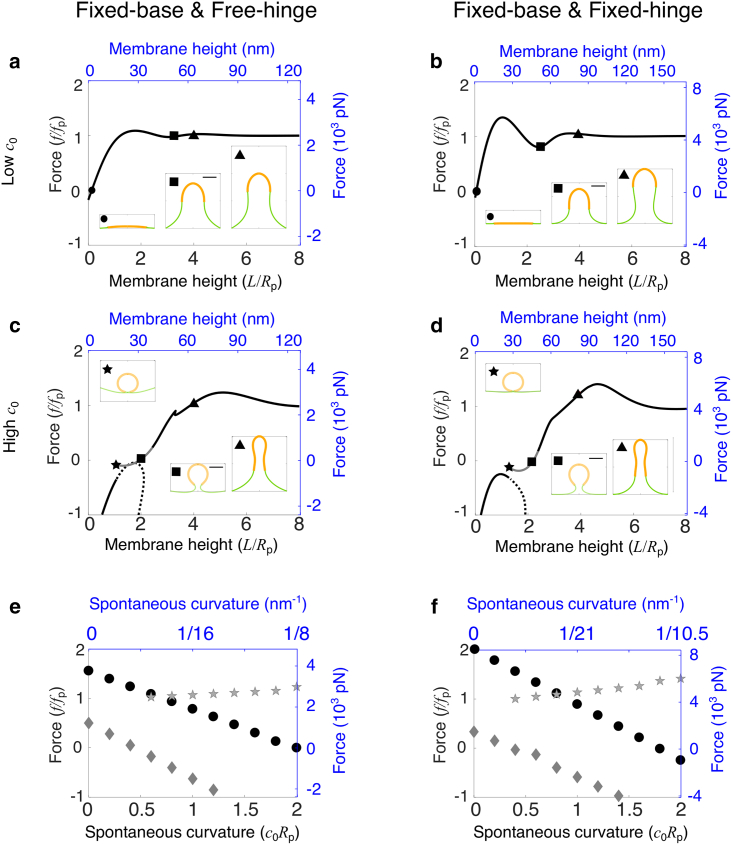
We first consider the case of a membrane at the endocytic site void of any curvature-generating proteins (i.e., c0Rp = 0) and study the effect of base radius on the required forces to pull a membrane tube. The effect of forces on the membrane deformation is characterized by the force-height (f-L) curve, which in general is nonmonotonic (Fig. 2, a–d). A force barrier Fmax appears at a relatively low height L when the membrane is dome shaped (Fig. 2, a–d, inset, labeled by circles). As the membrane is lifted further up, the membrane changes from a dome shape to an Ω-shape, when a narrow neck appears (signaled by the tangential angle ψ = π/2 at an intermediate arclength). The force f then decreases with L and approaches the elongation force Fe limL→∞f(L), which equals fp in the case of a bare membrane as expected by Eq. 4. The existence of a force barrier in the f-L curve is similar to that in the tension-dominant condition (50). However, two striking differences should be noted: 1) in the pressure-dominant condition discussed here, a nonzero initiation force Finit f(L = 0) is needed to merely start deforming the membrane, i.e., to lift the membrane just off the cell wall (Fig. 2, e and f, diamonds), whereas in the tension-dominant condition, Finit = 0 is independent of Rb (50); and 2) when pressure dominates, the force barrier Fmax significantly varies with the base radius Rb (Fig. 2, e and f, circles), whereas in the tension-dominant condition, Fmax always overshoots 13% relative to the equilibrium force fσ (50), independent of Rb.
Figure 2.
Effect of the base radius Rb on the membrane shape and force requirement. (a–d) Force-height relationship f-L of membrane deformations for a fixed base radius Rb/Rp = 0.5 in (a) and (b) and Rb/Rp = 2 in (c) and (d), where Rp is the characteristic tube radius (Eq. 4). The spontaneous curvature c0Rp = 0. Insets show membrane shapes at the points indicated by the corresponding symbols on the f-L curve. The square indicates the critical shape where the membrane is about to form a neck. The scale bar corresponds to the characteristic tube radius Rp. (e and f) Force barrier Fmax (circle), initiation force Finit (diamond), and elongation force Fe (square) for varying base radii Rb. The solid curve represents the analytical solution for Finit. (a–f) In the left column (a, c, and e), the free-hinge BC is imposed at the base points R = Rb, and in the right column (b, d, and f), the fixed-hinge BC is imposed. On the left and bottom axes (black), nondimensionalized quantities are used, and on the right and top axes (blue), quantities are measured in their physical units. The parameters are listed in Table 2 except Rb = 8 nm in (a) and Rb = 10.5 nm in (b). To see this figure in color, go online.
When comparing the differences between the f-L curves for the two BCs, we notice that 1) the initiation force Finit scales with the base radius Rb as Finit = 3/8πp for the free-hinge BC, whereas Finit = 1/4πp for the fixed-hinge BC (Fig. 2, e and f, solid curves; see Supporting materials and methods for the derivation); 2) though the initiation force Finit is smaller for the fixed-hinge BC than for the free-hinge BC, the opposite trend is observed for the force barrier Fmax. The difference in Fmax is more pronounced for smaller base radii. For instance, when Rb = 0.5Rp, the force barrier Fmax is about 4fp for the free-hinge BC, whereas it is 7fp for the fixed-hinge BC (Fig. 2, a and b, labeled by circles); and 3) the membrane neck appears at a smaller membrane height for the fixed-hinge BC than for the free-hinge BC. For instance, when Rb = 2Rp, the neck appears at a height of 3Rp for the fixed-hinge BC but 4Rp for the free-hinge BC (Fig. 2, c and d, labeled by squares).
When the membrane is pulled up above the height of 6Rp, the force to elongate the tube remains almost unchanged (Fe = fp), regardless of the BCs and the base radii. However, the shape of the membrane can be quite different for different radii Rb. If Rb < Rp, the membrane exhibits a balloon shape with a narrower base than the tubular body (Fig. 2, a and b, inset, labeled by triangles), whereas when Rb > Rp, a wider base connected to a narrower body is observed (Fig. 2, c and d, inset, labeled by triangles), which is more consistent with experimental observations (7).
For both BCs, the force barrier Fmax is significantly reduced with increasing base radius Rb. When the base radius is increased from 0.5Rp to 3Rp, the force barrier is reduced from 4fp to 1.5fp for the free-hinge BC and from 7fp to 2fp for the fixed-hinge BC (Fig. 2, e and f, circles). These results suggest that a relatively wide base facilitates CME in yeast cells. With the parameters listed in Table 2, the force barrier to pull a membrane tube against a turgor pressure of 1 MPa can be reduced to 3500 pN for the free-hinge BC and 8000 pN for the fixed-hinge BC when the base radius Rb is greater than 30 nm (Fig. 2, e and f, circles). For the rest of the study, we fix the base radius at Rb = 2Rp and study the other factors that influence the membrane shape and the force to pull a membrane tube.
Table 2.
Fitting parameters to compare with experimental data
| Symbols | Physical meaning | Values for the free-hinge BC | Values for the fixed-hinge BC |
|---|---|---|---|
| P | turgor pressure | 1 MPa | 1 MPa |
| Rp | characteristic tube radius | 16 nm | 21 nm |
| c0 | spontaneous curvature of the membrane induced by the protein coat | 0.063 nm−1 | 0.048 nm−1 |
| a0 | coating area of proteins | 1609 nm2 | 2771 nm2 |
| Rb | base radius of the membrane patch | 32 nm | 42 nm |
| σ | surface tension at the base | 0.032 pN/nm | 0.042 pN/nm |
| α | control parameter for the sharpness of the coating edge | 0.006 nm−2 | 0.004 nm−2 |
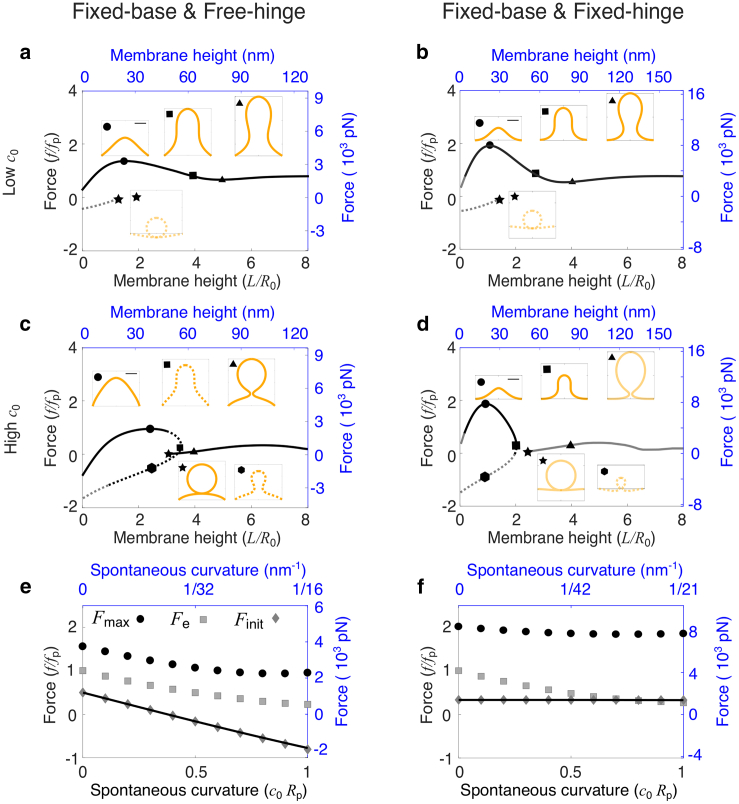
The ability of a fully covered protein coat to reduce the force barrier and the initiation force depends on BCs
In this section, we consider the effect of a uniform coat of curvature-generating proteins on membrane deformations. The ability of curvature-generating proteins to induce membrane curvature is characterized by the spontaneous curvature c0 in the model. When the spontaneous curvature c0 is small, e.g., c0Rp = 0.2, the f-L curves show similar trends as a fully uncoated membrane. However, a new branch of solutions with negative forces emerges (Fig. 3, a and b, dashed line). On this branch, the membrane exhibits a highly curved Ω-shape and has part of the shape lying below the plane z = 0. The membrane, therefore, may interact with the cell wall. This interaction is not considered in our model. The branch terminates at a limiting shape of a closed spherical vesicle budding off from the base (Fig. 3, a and b, inset, labeled by stars). The free energy of the membrane on this negative-force branch is significantly higher than that on the positive-force branch (Fig. S1), thus being energetically unfavorable. Hereafter, the free energy refers to Eq. 1 excluding the contribution −fL from the external pulling force.
Figure 3.
Effect of the spontaneous curvature c0 on membrane shape and force requirement for a fully coated membrane. (a–d) Force-height (f-L) relationship of membrane deformations for a fixed spontaneous curvature c0Rp = 0.2 in (a) and (b) and c0Rp = 1 in (c) and (d). Insets show membrane shapes at the points indicated by the corresponding symbols on the f-L curve. The square indicates the critical shape where the membrane is about to form a neck. The scale bar corresponds to Rp. In (a)–(d), the solid line indicates shapes of the lowest free energy, and the dashed line indicates shapes of relatively high free energy. The dark color indicates membrane shapes that are all above z = 0, and the gray color indicates shapes that have parts below z = 0. (e and f) Force barrier Fmax (circle), initiation force Finit (diamond), and elongation force Fe (square) for varying c0. The solid curve represents the analytical solution for Finit. (a–f) In the left column (a, c, and e), the free-hinge BC is imposed at the base points Rb = 2Rp, and in the right column (b, d, and f), the fixed-hinge BC is imposed. On the left and bottom axes (black), nondimensionalized quantities are used, and on the right and top axes (blue), quantities are measured in their physical units. The parameters are listed in Table 2. To see this figure in color, go online.
When the spontaneous curvature c0 is large, e.g., c0Rp = 1, the f-L curve breaks into two branches, each branch only covering part of the membrane height (Fig. 3, c and d). In the small-L branch, one L has two corresponding forces f. The larger f corresponds to a solution with a dome shape (Fig. 3, c and d, inset, labeled by circles), and the smaller f corresponds to a solution with an Ω-shape (Fig. 3, c and d, inset, labeled by hexagons). The dome shape has lower free energy than the Ω-shape for the same membrane height L and therefore is energetically more stable (Fig. S1, c and d). The large-L branch starts from a point at which the force f is slightly above zero, and the shape of the membrane is shown as a vesicle budding off from the base (Fig. 3, c and d, inset, labeled by stars). This shape has the lowest free energy in the large-L branch, which implies that if a long tube is pulled up and maintained by a force, when the force is gradually released, the tube retracts, and a vesicle spontaneously forms and detaches from the base of the membrane.
For a fully coated membrane, increasing the spontaneous curvature c0 is able to reduce the elongation force Fe. With increasing c0Rp from 0 to 1, Fe shows exactly the same dependence on c0 for both BCs and drops from fp to about 0.2fp (Fig. 3, e and f, squares). However, the impact of the spontaneous curvature c0 on the initiation force Finit and the force barrier Fmax shows qualitative differences between the two BCs: 1) under the free-hinge BC, the initiation force Finit drops down with increasing c0 and becomes negative for c0Rp > 0.5 (Fig. 3 e, diamonds and solid line). This negative Finit implies that the membrane is spontaneously bent off the cell wall without external forces. By contrast, under the fixed-hinge BC, the initiation force Finit remains positive and almost constant (Fig. 3 f, diamonds and solid line); and 2) the force barrier Fmax noticeably decreases from 1.5fp to fp with increasing c0 under the free-hinge BC, whereas Fmax remains almost constant at 2fp under the fixed-hinge BC (Fig. 3, e and f, circles).
In biological terms, our results suggest that for a membrane fully coated with curvature-generating proteins, the protein coat might significantly reduce the forces to start deforming the membrane if the membrane angle at the base is free to rotate. However, the protein coat has little impact on the forces if the membrane angle is fixed to zero. With the parameters listed in Table 2, the force barrier to pull a membrane tube for the fixed-hinge BC can be reduced from 3500 pN for a fully uncoated membrane to 2500 pN for a fully coated membrane (Fig. 3 e, circles), but the force barrier is kept at 8000 pN for the fixed-hinge BC, regardless of the spontaneous curvature (Fig. 3 f, circles).
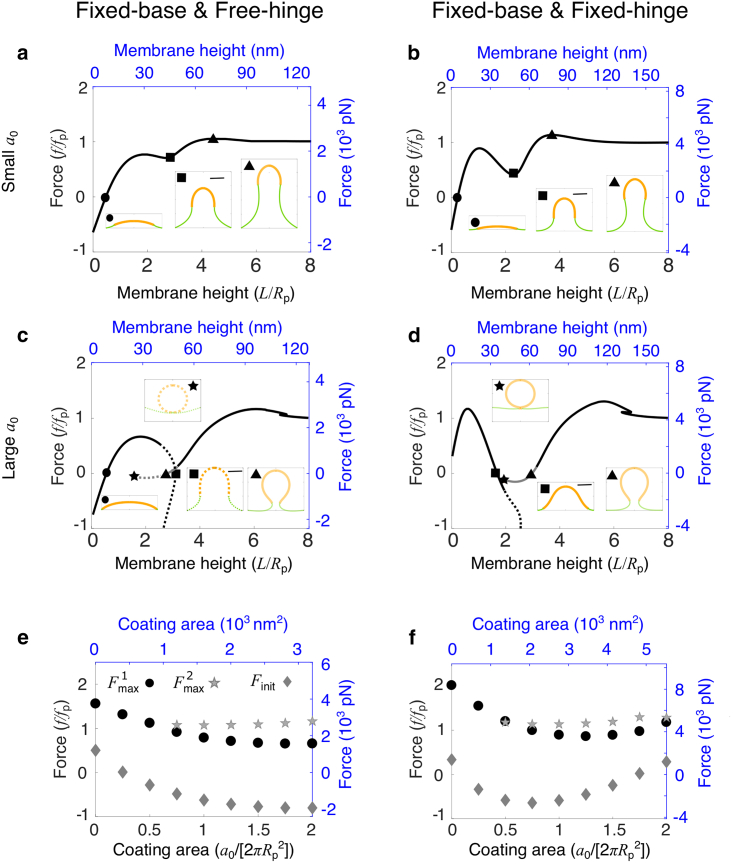
Partially coating the membrane with curvature-generating proteins can reduce the initiation force and the force barrier, but not the elongation force
In this section, we study the inhomogeneous model in which the membrane is coated with curvature-generating proteins only around the tip, thus mimicking the distribution of clathrin and other adaptor proteins. The spontaneous curvature in our model spatially varies as
| (6) |
where a(s) is the surface area calculated from the tip to the position of arclength s. The parameter α controls the sharpness of the coating edge. The coating area of proteins is denoted by a0, and these proteins induce a spontaneous curvature of c0 in the coated region of the membrane. This form of spontaneous curvature has been used in many previous studies (16,17,19,20).
We first vary the coating area a0 while fixing the spontaneous curvature at c0Rp = 1. When a0 is small, the f-L curves are nonmonotonic with a single force barrier at a low membrane height, similar to that of a bare membrane (data not shown). However, when a0 is above a critical value, a second force barrier emerges on the f-L curve at a higher membrane height at which the membrane exhibits an Ω-shape (Fig. 4, a and b, inset, labeled by triangles). For a0/(2π) = 1, the protein coat forms a hemispherical cap when the membrane is pulled up into a tubular shape (Fig. 4, a and b, inset, labeled by triangles). The initiation forces are negative for both BCs, and the zero force f = 0 intersects with the f-L curve at a positive membrane height (Fig. 4, a and b, inset, labeled by circles). For a very large coating area (a0/(2π) = 2), the membrane is almost fully coated with proteins when the membrane is flat (Fig. 4 c, inset, labeled by circles). The f-L curve is broken into two branches, each branch only covering part of the membrane height (Fig. 4, c and d), similar to the f-L curve of a fully coated membrane. The two branches might overlap in some intermediate membrane heights. For the free-hinge BC, the zero force f = 0 intersects with the f-L curve at three points, two of them lying on the small-L branch and the third one on the large-L branch (Fig. 4 c, inset, labeled by circles and squares in the small-L branch and triangles in the large-L branch). The two points on the small-L branch correspond to a dome shape of low free energy and a tubular shape of high free energy (Document S1. Supporting materials and methods and Figs. S1–S8, Document S2. Article plus supporting material c, circles and squares). Therefore, in the absence of forces, the membrane adopts a dome shape, spontaneously curved off from the cell wall. The one point on the large-L branch corresponds to a highly curved Ω-shape with a narrow neck (Fig. 4 c, inset, labeled by triangles), which is the final shape of a long membrane tube when it retracts upon force release. The large-L branch starts with a limiting membrane shape that is a closed vesicle budding off from the base (Fig. 4 c, inset, labeled by stars). In contrast with the fully coated membrane, the force at this point is negative, which means that a downward force is further needed to push the membrane into a budding vesicle when the membrane tube retracts. Under the fixed-hinge BC, the f-L curve for a0/(2π) = 2 shows similar features with that of the free-hinge BC, except that the dome-shaped solution at f = 0 does not exist (Fig. 4 d). This is because the initiation force Finit is positive and the membrane cannot be spontaneously curved off from the cell wall.
Figure 4.
Effect of the coating area a0 of curvature-generating proteins on membrane shape and force requirement for a partially coated membrane. (a–d) Force-height (f-L) relationship of membrane deformations for a fixed coating area a0/(2π) = 1 in (a) and (b) and a0/(2π) = 2 in (c) and (d). Insets show membrane shapes at the points indicated by the corresponding symbols on the f-L curve. The orange part represents the area of the membrane coated with proteins, and the green part represents the bare membrane. The scale bar corresponds to Rp. In (a)–(d), the solid line indicates shapes of the lowest free energy, and the dashed line indicates shapes of relatively high free energy. The dark color indicates membrane shapes that are all above z = 0, and the gray color indicates shapes that have parts below z = 0. (e and f) Low-height force barrier (circle), high-height force barrier (star), and initiation force Finit (diamond) for varying a0. (a–f) In the left column (a, c, and e), the free-hinge BC is imposed at the base points Rb = 2Rp, and in the right column (b, d, and f), the fixed-hinge BC is imposed. On the left and bottom axes (black), nondimensionalized quantities are used, and on the right and top axes (blue), quantities are measured in their physical units. The parameters are listed in Table 2. To see this figure in color, go online.
Despite some common features in the f-L curves for both BCs, differences also exist: 1) under the free-hinge BC, the initiation force Finit decreases and remains negative with increasing a0, whereas under the fixed-hinge BC, Finit is negative for intermediate values of a0 and becomes positive for larger a0 (Fig. 4, e and f, diamonds); 2) a similar difference is also observed for the low-height force barrier , which is monotonically decreasing with a0 under the free-hinge BC, whereas it is nonmonotonic under the fixed-hinge BC (Fig. 4, e and f, circles).
For a partially coated membrane, the low-height force barrier can be significantly reduced to below fp for some coating areas (Fig. 4, e and f, circles), whereas the high-height force barrier increases with a0 and remains above fp (Fig. 4, e and f, stars). This is because the force barrier must be greater than the elongation force Fe, which equals fp for both BCs and any coating areas. This tradeoff between the two force barriers implies there is an optimum coating area that minimizes the overall force barrier. With the parameters listed in Table 2, the optimum coating area is about 1200 nm2 for the free-hinge BC and 2000 nm2 for the fixed-hinge BC. The minimal force barrier is about 2500 pN for the free-hinge BC and about 4000 pN for the fixed-hinge BC. Compared with the force barrier of 8000 pN for a fully coated membrane under the fixed-hinge BC, partially coating the membrane significantly reduces the force barrier.
Increasing the spontaneous curvature of a partially coated membrane leads to a sharp transition of the membrane shape
In this section, we vary the spontaneous curvature c0 while fixing the coating area (a0/(2π) = 1) to study how c0 influences the f-L curves for a partially coated membrane. Upon gradually increasing c0, the f-L curve shows similar trends to what we observed when increasing the coating area. Above a critical value of c0, a high-height force barrier appears on the f-L curve in addition to the low-height force barrier (Fig. 5, a and b). Further increasing the spontaneous curvature c0 splits the f-L curve into two branches, a small-L branch and a large-L branch (Fig. 5, c and d). A striking new feature is that when c0Rp = 2, the force for the entire small-L branch falls below zero (Fig. 5, c and d). The zero force f = 0 intersects with the f-L curve on the long-L branch at only one point, which corresponds to a highly curved Ω-shape (Fig. 5, c and d, inset, labeled by squares). This shape has the lowest free energy (Fig. S3, c and d, labeled by squares), which implies that even in the absence of forces, increasing the spontaneous curvature c0 can lead to a transition of the membrane from the dome shape in the small-L branch to the Ω-shape in the large-L branch. The membrane height has a sharp increase during this transition.
Figure 5.
Effect of the spontaneous curvature c0 of curvature-generating proteins on membrane shape and force requirement for a partially coated membrane. (a–d) Force-height (f-L) relationship of membrane deformations for a fixed spontaneous curvature c0Rp = 0.6 in (a) and (b) and c0Rp = 2 in (c) and (d). Insets show membrane shapes at the points indicated by the corresponding symbols on the f-L curve. The orange part represents the area of the membrane coated with proteins and the green part represents the bare membrane. The scale bar corresponds to Rp. In (a)–(d), the solid line indicates shapes of the lowest free energy, and the dashed line indicates shapes of relatively high free energy. The dark color indicates membrane shapes that are all above z = 0, and the gray color indicates shapes that have parts below z = 0. (e and f) Low-height force barrier (circle), high-height force barrier (star), and initiation force Finit (diamond) for varying c0. (a–f) In the left column (a, c, and e), the free-hinge BC is imposed at the base points Rb = 2Rp, and in the right column (b, d, and f), the fixed-hinge BC is imposed. On the left and bottom axes (black), nondimensionalized quantities are used, and on the right and top axes (blue), quantities are measured in their physical units. The parameters are listed in Table 2. To see this figure in color, go online.
The spontaneous curvature c0 not only influences the forces but also the morphology of the clathrin coat. When c0Rp = 2, the clathrin coat tends to bend the membrane to a narrow radius of ∼0.5Rp, and the coated area exhibits a pearl-like structure when elongated (Fig. 5, c and d, triangles). However, for c0Rp = 1, the clathrin coat maintains a roughly hemispherical cap (Fig. 4, a and b, triangles).
Both the low-height force barrier and the initiation force Finit linearly decrease with increasing c0 (Fig. 5, e and f, circles and diamonds), and they become negative when c0 is beyond a critical value. By contrast, the high-height force barrier linearly increases with c0 (Fig. 5, e and f, stars) and remains above fp. The optimum spontaneous curvature, which has the minimal force barrier, is about 0.8 for both BCs. The corresponding force barrier is as much as fp, which is the lowest force barrier one can achieve by partially coating the membrane with curvature-generating proteins. With the parameters listed in Table 2, the optimum spontaneous curvature corresponds to a preferred radius of about 40 nm for the free-hinge BC and 50 nm for the fixed-hinge BC. The force barrier for the free-hinge BC is about 2500 pN and for the fixed-hinge BC is about 4000 pN.
Our theory agrees well with experiments
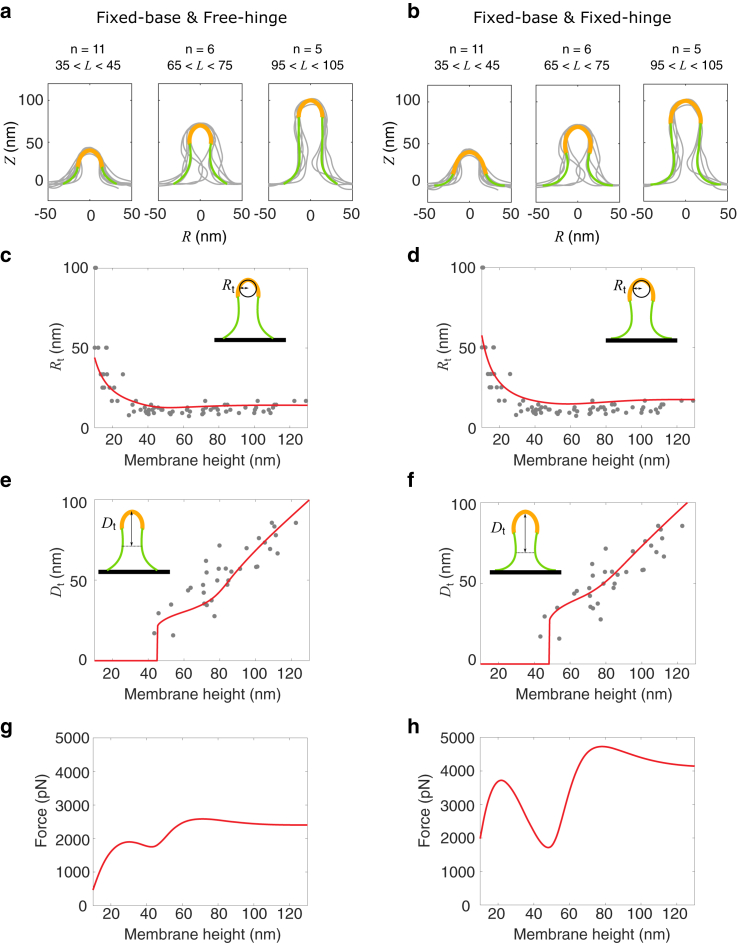
The shapes of endocytic invaginations in budding yeast have been imaged with electron tomography (7). These shapes typically do not have perfect axisymmetry assumed in our model (Fig. 6, a and b). However, from these images one can numerically fit the membrane shape and extract geometric features of the shape, which typically include the tip radius Rt, the tip-neck distance Dt, and the membrane height L (7). The tip radius Rt is defined as the reciprocal of the meridian curvature averaged over an arc that extends over 15 nm from the endocytic invagination tip. The tip-neck distance Dt is defined as the distance from the center of the neck to the most distant profile point from the neck. The membrane height L is defined as the maximal height of the fitted profile above the base. The experimental data sets Rt vs. L and Dt vs. L contain the shape information of the endocytic invagination across different stages of CME. We use the two data sets as the fitting data to compare our theory with experiments. The fitting procedure is elaborated in the Appendix, in which we use the characteristic radius Rp as the single parameter to fit the data. We find the optimum that minimizes the fitting error for the two data sets. For the free-hinge BC, the optimum = 16 nm, and for the fixed-hinge BC, = 21 nm (Fig. S4). The fitting errors at the optimum are comparable for the two BCs, and we cannot distinguish which BC fits the experimental data better (Fig. S4).
Figure 6.
Comparison between our theory and experiments. (a and b) Membrane shapes obtained by electron tomography are grouped according to their heights and overlaid at the tip. The data come from the database https://www.embl.de/download/briggs/endocytosis.html maintained by the authors of (7). The membrane shapes obtained by our model are represented by solid curves. The orange part represents the area of the membrane coated with proteins, and the green part represents the bare membrane. (c and d) Comparison of the tip radius Rt between results obtained with our theory (line) and measured experimentally (dots). (e and f) Comparison of the neck to tip distance Dt between results obtained with our theory (line) and measured experimentally (dots). (g and h) Prediction of the force-height (f-L) relationship from our theory using the parameters listed in Table 2 that fit the experimental shapes in (a) and (b). (a–h) In the left column (a, c, e, and g), the free-hinge BC is imposed at the base points Rb = 32 nm, and in the right column (b, d, f, and h), the fixed-hinge BC is imposed at the base points Rb = 42 nm. To see this figure in color, go online.
Using the optimum , our calculated membrane shapes agree well with the experimental profiles, particularly in the early stage when the membrane height is low (Fig. 6, a and b). For membrane shapes that are higher than 65 nm, experimental membrane shapes are typically asymmetric and exhibit a narrower neck than the calculated ones, probably because of the presence of other membrane proteins that arrive later during CME and impose a cylindrical curvature at the neck of the invagination (e.g., amphiphysins). These effects are not considered in our model.
As for the geometric features, experimental data show that the tip radius Rt drops from 50–100 to 15 nm as the membrane height increases. Our theory matches the trend of the experimental data, particularly for the part where Rt < 40 nm (Fig. 6, c and d). The fitting for the tip radius with the free-hinge BC is slightly better than that with the fixed-hinge BC. For the tip-neck distance Dt, our theory predicts that Dt grows slowly with the membrane height L when L is less than 65 nm. Beyond this point, Dt scales almost linearly with L with a larger slope than the initial phase. This theoretical prediction again matches well with the experimental data (Fig. 6, e and f). The fitting for the tip-neck distance with the fixed-hinge BC is slightly better than that with the fixed-hinge BC.
We stress that the different optimum -values for the two BCs result in a large difference in the magnitude of forces in the f-L curve (Fig. 6, g and h). This is because the unit of the force is the characteristic force fp, which scales with the characteristic radius Rp as fp ∝ . As a result, the force barrier is about 2500 pN for the free hinge, whereas it is about 4000 pN for the fixed hinge.
Fixed base is a more proper BC than freely moving base
We have focused on BCs for which the base radius of the membrane is fixed. For a membrane fully coated with curvature-generating proteins, the initiation force Finit either decreases with the intrinsic curvature c0 under the free-hinge BC or is independent of c0 under the fixed-hinge BC (Fig. 3, e and f, diamonds and solid lines). A previous work (18) studied a similar homogeneous model but used the free-base and fixed-hinge BC (BC4 in Table 1). This BC led to the surprising conclusion that the initiation force Finit of a fully coated membrane is proportional to the spontaneous curvature c0, which implies that increasing the spontaneous curvature c0 hinders CME because it raises the force required to lift the membrane off the cell wall. In addition, as a result of the freely moving base, the model predicted that the base radius Rb approaches zero when the membrane height is low. This result is inconsistent with experimental observations that the base radius of membrane invaginations remains roughly the same during the entire course of CME, from shallow invaginations to long tubes (Fig. 6, a and b). Therefore, the experimental data support our assumption that the base of the membrane is maintained at a fixed radius by endocytic proteins or by attachment to the cell wall. A recent systematic study of proteins involved in endocytosis by super-resolution microscopy revealed that many proteins are organized in concentric rings around the clathrin coat (28). These proteins may serve as anchors and may fix the base radius of the endocytic membrane. In addition, the actin network around the endocytic invagination can also impose constraints on the extent the membrane base can spread. Furthermore, we fix the surface tension at the fixed base radius. It implies the assumption that the lipids can flow past any structures that fix the membrane to the cell wall.
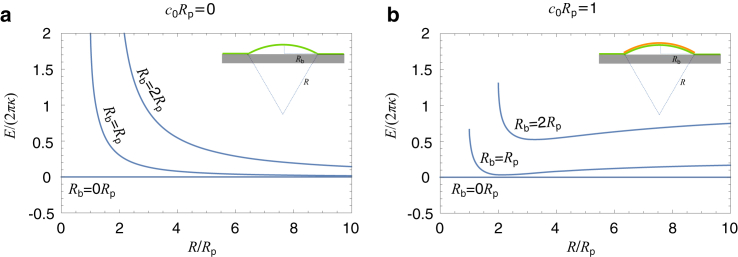
The different dependence of the initiation force Finit on c0 between the fixed-base BC and the free-base BC can be clarified with a simple example. Because Finit is only related to the early stage of CME when the membrane is almost flat, we approximate the dome-shaped membrane as a spherical cap and calculate its free energy E(R; c0, Rb) as a function of the sphere radius R for different spontaneous curvatures c0 and base radii Rb (Fig. 7). For the fixed-base BC, the base radius Rb is a constant. When c0 is small, E(R; c0, Rb) decreases monotonically with R and has its minimum at R = ∞, which implies that a flat shape is more favorable than a curved one (Fig. 7 a). When c0 becomes large, E(R; c0, Rb) has a nontrivial minimum at a finite radius R (Fig. 7 b, Rb = 2Rp), which implies that the membrane spontaneously bends into a curved shape. However, for the free-base BC assumed in the work of (18), the base radius Rb becomes a free parameter and the free energy E(R, Rb; c0) is a function of both R and Rb. No matter how large c0 is, the energy E(R, Rb; c0) always admits a trivial minimum at Rb = 0, which represents a solution without any deformation (Fig. 7, a and b, Rb = 0Rp). If a force f is applied, a nontrival minimum of the total free energy F(R, Rb; f, c0) = E(R, Rb; c0) − fL(R, Rb) may exist for a positive force f (Fig. S5). However, the base radius for this nontrivial minimum is unrealistically narrow (∼0.02 nm; see Supporting materials and methods); therefore, a freely moving base is probably not a proper BC to model CME in yeast.
Figure 7.
Free energy of membrane deformations under spherical cap approximation. (a and b) Free energy of the membrane as a function of the sphere radius R for c0Rp = 0 in (a) and c0Rp = 1 in (b). For different base radii Rb, the range of R is [Rb, ∞], where R = Rb corresponds to a hemispherical cap and R = ∞ corresponds to a flat shape. To see this figure in color, go online.
Discussion
Free hinge versus fixed hinge
Our analysis of the experimental data favors the BC with a fixed base radius over that with a freely moving base. However, we cannot directly distinguish whether the angle of the membrane at the base is free to rotate (free hinge) or fixed to zero (fixed hinge) because both BCs show good agreements with the experimental data (Fig. 6, a–f). Under the free-hinge BC, the membrane shape has a kink at the base points. We stress that this discontinuity in the membrane angle is physically and biologically plausible. First, for a membrane fully coated with curvature-generating proteins, the membrane’s spontaneous curvature can change abruptly at the base points and such discontinuity of the mechanical properties of the membrane will result in a kink. Second, for a partially coated membrane whose mechanical properties smoothly change across the base points, the kink can be induced by external factors. Though it is hypothetical, early-arriving endocytic proteins, such as myosin-I motors and BAR-domain proteins Syp1p, Cdc15p, and Bzz1p, form a ring-like structure around the clathrin-coated pit (28). The microscopic interactions between the ring, the membrane, and the cell wall determine the exact BCs. At the macroscopic level, the phenomenological method of membrane mechanics used in this work allows the presence of a kink as long as the underlying microscopic interactions permit it. The free-hinge BC is only one of the many possible BCs that form a kink. Even for the fixed-hinge BC, the fixed angle is not necessarily zero but determined by the microscopic interactions. When tuning the membrane angle at the base for the fixed-hinge BC, we notice that the force barrier to pull a bare membrane into a tube can be reduced by increasing the base angle (Fig. S6).
Our calculations assume a single type of BCs for the entire stage of CME. We have shown that the free-hinge BC and the fixed-hinge BC might lead to dramatically different f-L curves. These results suggest a new way to regulate CME by tuning the BCs. By changing the BC from the fixed hinge to the free hinge, the force barrier is typically reduced. If at an early stage, the BC is fixed hinge, switching to free hinge permits the accumulated force to drive the transformation of the membrane from a dimple shape to a tubular shape, providing the force is larger than the force barrier determined by the free-hinge BC but smaller than the force barrier determined by the fixed-hinge BC.
Homogeneous model versus inhomogeneous model
We have studied not only the homogeneous model, i.e., a fully coated (or fully uncoated) membrane, but also the inhomogeneous model, i.e., a partially coated membrane. Comparing the two models, we noted the following differences: 1) in the inhomogeneous model, two force barriers in the f-L curve emerge as the spontaneous curvature c0 increases, and the low-height force barrier can be significantly reduced, even to values below zero, with increasing c0 (Fig. 5, e and f, circles). However, in the homogeneous model, there is only one force barrier, which can hardly be reduced with increasing c0, especially in the fixed-hinge BC (Fig. 3, e and f, circles). 2) The elongation force Fe can be reduced with c0 in the homogeneous model (Fig. 3, e and f, squares), whereas in the inhomogeneous model, it remains at a constant value of fp regardless of BCs and parameter values of a0 and c0. These differences suggest that a partially coated membrane can be spontaneously lifted up to a significant height via the curvature-generating protein coat, whereas it is impossible to do so when the membrane is fully coated.
Actin polymerization alone is insufficient to overcome the force barrier for CME in yeast cells even with the help of proteins that induce membrane curvature
One of the key questions we aimed to address in this work is how much force is needed to pull a membrane tube against high turgor pressure during CME. We have assumed a turgor pressure of 1 MPa and estimated that the force barrier is about 2500 pN for the free-hinge BC but 4000 pN for the fixed-hinge BC (Fig. 6, g and h). In this calculation, we have assumed a point force acting on the membrane, which is a good approximation if the forces produced by actin filaments are concentrated near the tip of the membrane because the point force is the limit of a concentrated force distribution. We expect the point force is the most efficient way to deform a flat membrane into a tubular shape because it minimizes the total amount of force necessary to deform the membrane. Indeed, let us consider a concentrated force distribution acting on the membrane such that the normal stress is larger than the turgor pressure at the stress-applied area. The stress is able to overcome the turgor pressure and therefore pulls the membrane up locally, and the stress-free parts of the membrane are raised up correspondingly. If the same amount of force is distributed on a larger area, the resulting stress is reduced and might be smaller everywhere on the membrane than the turgor pressure and therefore could not pull the membrane up. As an attempt to test this idea, we calculated the f-L curve assuming the forces are distributed within an area of af near the membrane tip and pointing in the normal direction. In agreement with our expectation, when the forces are distributed on a larger area af, a larger magnitude of the total force f is needed to pull up the membrane, and the increase in the magnitude of the force barrier can be more than twofold (Fig. S8, a and b). Nevertheless, the z-component of the total force remains the same with the value calculated with the point force assumption when the membrane height is large (Fig. S8, c and d). Based on this argument, we expect our results provide a lower bound for the magnitude of the force barrier and a good estimation for the z-component of the elongation force. However, even 2500 pN is still beyond the force (<200 pN) that can be generated by polymerization alone of 150–200 actin filaments at the endocytic site (46,51) given that the measured polymerization force for a single filament is only 1 pN, the force generated by a group of filaments is usually smaller than the sum of each individual ones, and a large fraction of the filaments are capped (52). Investigating non-polymerization-based force production by the actin machinery will be our future work. A possible way is to release the elastic energy stored in geometrically frustrated cross-linkers, such as fimbrin (53,54). There are some important factors about CME in yeast cells we do not consider in our model. The clathrin coat in general is stiffer than the plasma membrane (44). Therefore, the clathrin-coated part of the membrane should have a larger bending rigidity κ than the uncoated part. There are also BAR proteins that bind to the side of the membrane invagination, and they impose an anisotropic curvature on the membrane. Investigating these missing factors will help us provide a more accurate estimation of the force requirement to pull the membrane up against turgor pressure for CME in yeast cells.
Conclusions
We have studied membrane deformations driven by a point force and by curvature-generating proteins in the presence of a high turgor pressure. A significant amount of force is required to deform the membrane as a result of the high turgor pressure. We have investigated possible ways to reduce the force requirement. This includes fully or partially coating the membrane with curvature-generating proteins and letting the membrane angle at the base freely rotate. By comparing with experimental data, we have shown that the BC with a fixed base radius is more appropriate than the freely moving base in describing membrane invaginations at the endocytic sites. The minimal force barrier predicted by our theory is about 2500 pN.
Author contributions
R.M. and J.B. designed the research. R.M. carried out all simulations and analyzed the data. R.M. and J.B. wrote the article.
Acknowledgments
We thank Wanda Kukulski, Marko Kaksonen, and John Briggs for kindly sharing the micrograph of Fig. 1 a. We thank Dr. Pablo Sartori for critical reading of the manuscript.This research is supported by National Institutes of Health/National Institute of General Medical Sciences Grant R01GM115636.
Editor: Markus Deserno.
Footnotes
Supporting material can be found online at https://doi.org/10.1016/j.bpj.2021.02.033.
Contributor Information
Rui Ma, Email: ruima@xmu.edu.cn.
Julien Berro, Email: julien.berro@yale.edu.
Appendix
Derivation of the membrane shape equations
The membrane shape is parameterized with its meridional coordinates [R(s), Z(s)], which are related to the tangent angle ψ(s) via the geometrical relation
| (7) |
and
| (8) |
To obtain the Euler-Lagrange equation associated with the free energy Eq. 1, we express in Eq. 2 explicitly as
| (9) |
Here, we introduce the rescaled Lagrangian multiplier 2πγ(s) and 2πη(s) to impose the geometric constraints set by Eqs. 7 and 8 The variation of the functional G in Eq. 2 reads
| (10) |
which contains both the bulk terms (first line) and the boundary terms (second line). The Euler-Lagrange equations can be obtained by the vanishing bulk terms, which are reduced to
| (11) |
| (12) |
and
| (13) |
For the homogeneous model, the spontaneous curvature c0 is uniform and is explicitly independent of the arclength s. This symmetry leads to a conserved quantity (55)
| (14) |
For the inhomogeneous model, the spontaneous curvature c0[a(s)] is spatially varied over the arclength s as depicted by Eq. 6. The variation of the functional G in Eq. 10 needs to change to include a spatially varied surface tension σ(s) to ensure that the membrane area is locally unstretchable. The detailed derivation can be found in (16). The equation for σ reads
| (15) |
In addition to the varied surface tension, Eq. 11 for the membrane angle ψ needs to change to include a new term c0,
| (16) |
It is easy to verify that the new Eqs. 15 and 16, together with Eqs. 12 and 13, ensure that is conserved, i.e., = 0.
When considering the effect of distributed forces, we assume the forces are localized in an area of af near the membrane tip and pointing in the normal direction. Specifically, we express the normal stress (force per unit area) gn as the following form:
| (17) |
where denotes the magnitude of the normal stress within the area af where forces are loaded, and αf controls the sharpness of the force drop at af. In this case, Eqs. 12 and 13 need to make the following changes:
| (18) |
and
| (19) |
The total force f is calculated as the surface integral of the normal stress
| (20) |
The z-component of the force reads
| (21) |
Derivation of the BCs
To get proper BCs, we set the boundary terms in Eq. 10 to zero. At the membrane tip (s = 0), R = 0 by definition, and we choose ψ = 0 to avoid any singularity. As a result, δR = 0 and δψ = 0, and the boundary terms automatically vanish.
At the base of the invagination (s = S), as a result of the product of two conjugate variables and δψ, we have the freedom to let either = 0, i.e., the membrane can be freely rotate (free-hinge BC), or δψ = 0, i.e., the angle of the membrane is fixed (fixed-hinge BC). Similarly, we can choose = 0, i.e., the base can freely move, or δR = 0, i.e., the base radius is fixed. The combination of the two choices makes up the four possible BCs listed in Table 1.
Numerical methods to calculate the force-height (f-L) relationships
For the homogeneous model with a uniform spontaneous curvature c0, Eqs. 7, 11, and 12 and η = 0 constitute a complete system of equations, which are numerically solved by a shooting method that has been widely used in Helfrich models (18,50). The idea is to numerically integrate the three equations from the membrane tip s = 0 with MATLAB solver ode45 (The MathWorks, Natick, MA) until the free-hinge BC or the fixed-hinge BC is met. The numerical integration needs input of the initial values of R(s = 0), ψ(s = 0), (s = 0), and γ(s = 0). The radius R(s = 0) should be zero at the membrane tip. However, Eqs. 11 and 12 have a singular point at R = 0. To avoid the singular point, we set R(s = 0) = ɛRp, where ɛ = 0.001 is chosen to be a small number such that values smaller than 0.001 do not produce numerically distinguishable results. The initial angle ψ(s = 0) = 0 is to ensure continuity of the membrane shape at the tip. The derivative (s = 0) is the tuning parameter to match the BCs. For any given (s = 0), γ(s = 0) is solved via Eq. 14. Once the four initial values are set, the numerical integration continues until the free-hinge BC or the fixed-hinge BC is met. This is achieved by setting the termination event function in the ode45 solver. The membrane height L = sinψds is then obtained via Eq. 8. Note that for different trials, the final arclength S when the solver terminates are different. The shooting method is to find a proper pair of ((s = 0), f) such that when the integration terminates, i.e., the free-hinge BC or the fixed hinge has been satisfied, the other BCs R = Rb and L = L0 are fulfilled for a particular membrane height L0. To construct the f-L curve, once we get the solution of (∗(s = 0), f∗) for a particular L0, we extend the membrane height L with a small increment to L0 + ΔL. The solution (∗(s = 0), f∗) for L = L0 is then used as the initial trial for searching the solution for L = L0 + ΔL.
For the inhomogeneous model with a spatially varied spontaneous curvature c0(s) defined by Eq. 6, Eqs. 7, 12, 15, and 16 and = 2πR and η = 0 constitute a complete system of equations. In addition to the four initial values required by the homogeneous model, a(s = 0) and σ(s = 0) are needed to numerically integrate the equations. We set a(s = 0) = 0 and tune the combination of ((s = 0), σ(s = 0), f) to match R = Rb, L = L0, and σ = σ0 when the solver terminates. The f-L curve is constructed in a similar way by gradually extending the membrane height L with small increment of ΔL.
When considering the effect of distributed forces on a homogeneous membrane, Eqs. 7, 11 (with f = 0), 18, and 19, and = 2πR constitute a complete system of equations. In addition to the four initial values required by the homogeneous model, a(s = 0) and η(s = 0) are needed to numerically integrate the equations. We set a(s = 0) = 0 and η(s = 0) = 0 and tune the combination of to match R = Rb and L = L0 when the solver terminates. The total force is calculated with (20).
Numerical procedure to fit the experimental data
We have seven parameters in the inhomogeneous model listed in Table 2. The turgor pressure p is fixed at p = 1 MPa. For the remaining six parameters, we express five of them as the function of the characteristic radius Rp and use Rp as the single parameter to fit the experimental data. The surface tension at the base σ is set to be 0.002pRp such that the surface tension σ plays a much less important role than the turgor pressure p in determining the tube radius because = 22Rp ≫ Rp. The base radius Rb is fixed at Rb = 2Rp such that for a bare membrane, the force barrier Fmax as a function of Rb is close to the plateau and not sensitive to the variation of base radius (see Fig. 2, e and f). Based on the experimental observation that the copy number of clathrin molecules stays small and almost constant during the assembly and disassembly of actin meshwork (46) and the measured copy number of 30–40 implies a hemispherical cap of the clathrin coat, we assume the coating area a0 = 2π and the spontaneous curvature c0 = 1/Rp. The sharpness of the coating edge is controlled by the parameter α, which is set to be 10/(2π). Values of α greater than 10/(2π) do not make a difference on the resulting f-L curve (Fig. S7).
We use the geometric features Rt and Dt vs. membrane height L as our fitting data. For the data points of {(Li, )}, i = 1, …, M in Fig. 6, c and d, the corresponding theoretical prediction of the tip radius ThR(Li) is calculated for a given Rp. The fitting error then reads
| (22) |
Similarly, the fitting error for the distance from neck to tip Dt reads
| (23) |
where ThD(Li) denotes the theoretical prediction of Dt at L = Li. When plotting err1 + err2 as a function of the fitting parameter Rp, we find the optimum that minimizes the sum err1 + err2 (Fig. S4).
Supporting material
references
- 1.McMahon H.T., Boucrot E. Molecular mechanism and physiological functions of clathrin-mediated endocytosis. Nat. Rev. Mol. Cell Biol. 2011;12:517–533. doi: 10.1038/nrm3151. [DOI] [PubMed] [Google Scholar]
- 2.Sorkin A., Puthenveedu M.A. Clathrin-mediated endocytosis. In: Yarden Y., Tarcic G., editors. Vesicle Trafficking in Cancer. Springer; 2013. pp. 1–31. [Google Scholar]
- 3.Lu R., Drubin D.G., Sun Y. Clathrin-mediated endocytosis in budding yeast at a glance. J. Cell Sci. 2016;129:1531–1536. doi: 10.1242/jcs.182303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kaksonen M., Roux A. Mechanisms of clathrin-mediated endocytosis. Nat. Rev. Mol. Cell Biol. 2018;19:313–326. doi: 10.1038/nrm.2017.132. [DOI] [PubMed] [Google Scholar]
- 5.Lacy M.M., Ma R., Berro J. Molecular mechanisms of force production in clathrin-mediated endocytosis. FEBS Lett. 2018;592:3586–3605. doi: 10.1002/1873-3468.13192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Mettlen M., Chen P.-H., Schmid S.L. Regulation of clathrin-mediated endocytosis. Annu. Rev. Biochem. 2018;87:871–896. doi: 10.1146/annurev-biochem-062917-012644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kukulski W., Schorb M., Briggs J.A. Plasma membrane reshaping during endocytosis is revealed by time-resolved electron tomography. Cell. 2012;150:508–520. doi: 10.1016/j.cell.2012.05.046. [DOI] [PubMed] [Google Scholar]
- 8.Boulant S., Kural C., Kirchhausen T. Actin dynamics counteract membrane tension during clathrin-mediated endocytosis. Nat. Cell Biol. 2011;13:1124–1131. doi: 10.1038/ncb2307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Wu X.-S., Elias S., Wu L.-G. Membrane tension inhibits rapid and slow endocytosis in secretory cells. Biophys. J. 2017;113:2406–2414. doi: 10.1016/j.bpj.2017.09.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Low P.S., Chandra S. Endocytosis in plants. Annu. Rev. Plant Biol. 1994;45:609–631. [Google Scholar]
- 11.Aghamohammadzadeh S., Ayscough K.R. Differential requirements for actin during yeast and mammalian endocytosis. Nat. Cell Biol. 2009;11:1039–1042. doi: 10.1038/ncb1918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Basu R., Munteanu E.L., Chang F. Role of turgor pressure in endocytosis in fission yeast. Mol. Biol. Cell. 2014;25:679–687. doi: 10.1091/mbc.E13-10-0618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Minc N., Boudaoud A., Chang F. Mechanical forces of fission yeast growth. Curr. Biol. 2009;19:1096–1101. doi: 10.1016/j.cub.2009.05.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Atilgan E., Magidson V., Chang F. Morphogenesis of the fission yeast cell through cell wall expansion. Curr. Biol. 2015;25:2150–2157. doi: 10.1016/j.cub.2015.06.059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Avinoam O., Schorb M., Kaksonen M. ENDOCYTOSIS. Endocytic sites mature by continuous bending and remodeling of the clathrin coat. Science. 2015;348:1369–1372. doi: 10.1126/science.aaa9555. [DOI] [PubMed] [Google Scholar]
- 16.Agrawal A., Steigmann D.J. Modeling protein-mediated morphology in biomembranes. Biomech. Model. Mechanobiol. 2009;8:371–379. doi: 10.1007/s10237-008-0143-0. [DOI] [PubMed] [Google Scholar]
- 17.Walani N., Torres J., Agrawal A. Endocytic proteins drive vesicle growth via instability in high membrane tension environment. Proc. Natl. Acad. Sci. USA. 2015;112:E1423–E1432. doi: 10.1073/pnas.1418491112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Dmitrieff S., Nédélec F. Membrane mechanics of endocytosis in cells with turgor. PLoS Comput. Biol. 2015;11:e1004538. doi: 10.1371/journal.pcbi.1004538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hassinger J.E., Oster G., Rangamani P. Design principles for robust vesiculation in clathrin-mediated endocytosis. Proc. Natl. Acad. Sci. USA. 2017;114:E1118–E1127. doi: 10.1073/pnas.1617705114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Alimohamadi H., Vasan R., Rangamani P. The role of traction in membrane curvature generation. Mol. Biol. Cell. 2018;29:2024–2035. doi: 10.1091/mbc.E18-02-0087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Napoli G., Goriely A. Elastocytosis. J. Mech. Phys. Solids. 2020;145:104133. [Google Scholar]
- 22.Koster G., Cacciuto A., Dogterom M. Force barriers for membrane tube formation. Phys. Rev. Lett. 2005;94:068101. doi: 10.1103/PhysRevLett.94.068101. [DOI] [PubMed] [Google Scholar]
- 23.Cuvelier D., Derényi I., Nassoy P. Coalescence of membrane tethers: experiments, theory, and applications. Biophys. J. 2005;88:2714–2726. doi: 10.1529/biophysj.104.056473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Dimova R., Aranda S., Lipowsky R. A practical guide to giant vesicles. Probing the membrane nanoregime via optical microscopy. J. Phys. Condens. Matter. 2006;18:S1151–S1176. doi: 10.1088/0953-8984/18/28/S04. [DOI] [PubMed] [Google Scholar]
- 25.Zhong-can O.Y., Helfrich W. Instability and deformation of a spherical vesicle by pressure. Phys. Rev. Lett. 1987;59:2486–2488. doi: 10.1103/PhysRevLett.59.2486. [DOI] [PubMed] [Google Scholar]
- 26.Seifert U., Berndl K., Lipowsky R. Shape transformations of vesicles: phase diagram for spontaneous- curvature and bilayer-coupling models. Phys. Rev. A. 1991;44:1182–1202. doi: 10.1103/physreva.44.1182. [DOI] [PubMed] [Google Scholar]
- 27.Seifert U. Configurations of fluid membranes and vesicles. Adv. Phys. 1997;46:13–137. [Google Scholar]
- 28.Mund M., van der Beek J.A., Ries J. Systematic nanoscale analysis of endocytosis links efficient vesicle formation to patterned actin nucleation. Cell. 2018;174:884–896.e17. doi: 10.1016/j.cell.2018.06.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Carlsson A.E. Membrane bending by actin polymerization. Curr. Opin. Cell Biol. 2018;50:1–7. doi: 10.1016/j.ceb.2017.11.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kübler E., Riezman H. Actin and fimbrin are required for the internalization step of endocytosis in yeast. EMBO J. 1993;12:2855–2862. doi: 10.1002/j.1460-2075.1993.tb05947.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Engqvist-Goldstein Å.E., Drubin D.G. Actin assembly and endocytosis: from yeast to mammals. Annu. Rev. Cell Dev. Biol. 2003;19:287–332. doi: 10.1146/annurev.cellbio.19.111401.093127. [DOI] [PubMed] [Google Scholar]
- 32.Yarar D., Waterman-Storer C.M., Schmid S.L. A dynamic actin cytoskeleton functions at multiple stages of clathrin-mediated endocytosis. Mol. Biol. Cell. 2005;16:964–975. doi: 10.1091/mbc.E04-09-0774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Sun Y., Martin A.C., Drubin D.G. Endocytic internalization in budding yeast requires coordinated actin nucleation and myosin motor activity. Dev. Cell. 2006;11:33–46. doi: 10.1016/j.devcel.2006.05.008. [DOI] [PubMed] [Google Scholar]
- 34.Kaksonen M., Toret C.P., Drubin D.G. Harnessing actin dynamics for clathrin-mediated endocytosis. Nat. Rev. Mol. Cell Biol. 2006;7:404–414. doi: 10.1038/nrm1940. [DOI] [PubMed] [Google Scholar]
- 35.Mooren O.L., Galletta B.J., Cooper J.A. Roles for actin assembly in endocytosis. Annu. Rev. Biochem. 2012;81:661–686. doi: 10.1146/annurev-biochem-060910-094416. [DOI] [PubMed] [Google Scholar]
- 36.Goode B.L., Eskin J.A., Wendland B. Actin and endocytosis in budding yeast. Genetics. 2015;199:315–358. doi: 10.1534/genetics.112.145540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Berro J., Pollard T.D. Local and global analysis of endocytic patch dynamics in fission yeast using a new “temporal superresolution” realignment method. Mol. Biol. Cell. 2014;25:3501–3514. doi: 10.1091/mbc.E13-01-0004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Carlsson A.E., Bayly P.V. Force generation by endocytic actin patches in budding yeast. Biophys. J. 2014;106:1596–1606. doi: 10.1016/j.bpj.2014.02.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Wang X., Galletta B.J., Carlsson A.E. Actin-regulator feedback interactions during endocytosis. Biophys. J. 2016;110:1430–1443. doi: 10.1016/j.bpj.2016.02.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Tweten D.J., Bayly P.V., Carlsson A.E. Actin growth profile in clathrin-mediated endocytosis. Phys. Rev. E. 2017;95:052414. doi: 10.1103/PhysRevE.95.052414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Kirchhausen T., Harrison S.C. Protein organization in clathrin trimers. Cell. 1981;23:755–761. doi: 10.1016/0092-8674(81)90439-6. [DOI] [PubMed] [Google Scholar]
- 42.Fotin A., Cheng Y., Walz T. Molecular model for a complete clathrin lattice from electron cryomicroscopy. Nature. 2004;432:573–579. doi: 10.1038/nature03079. [DOI] [PubMed] [Google Scholar]
- 43.Dannhauser P.N., Ungewickell E.J. Reconstitution of clathrin-coated bud and vesicle formation with minimal components. Nat. Cell Biol. 2012;14:634–639. doi: 10.1038/ncb2478. [DOI] [PubMed] [Google Scholar]
- 44.Jin A.J., Prasad K., Nossal R. Measuring the elasticity of clathrin-coated vesicles via atomic force microscopy. Biophys. J. 2006;90:3333–3344. doi: 10.1529/biophysj.105.068742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Lherbette M., Redlingshöfer L., Dannhauser P.N. The AP2 adaptor enhances clathrin coat stiffness. FEBS J. 2019;286:4074–4085. doi: 10.1111/febs.14961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Sirotkin V., Berro J., Pollard T.D. Quantitative analysis of the mechanism of endocytic actin patch assembly and disassembly in fission yeast. Mol. Biol. Cell. 2010;21:2894–2904. doi: 10.1091/mbc.E10-02-0157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Gallop J.L., Jao C.C., McMahon H.T. Mechanism of endophilin N-BAR domain-mediated membrane curvature. EMBO J. 2006;25:2898–2910. doi: 10.1038/sj.emboj.7601174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Henne W.M., Kent H.M., McMahon H.T. Structure and analysis of FCHo2 F-BAR domain: a dimerizing and membrane recruitment module that effects membrane curvature. Structure. 2007;15:839–852. doi: 10.1016/j.str.2007.05.002. [DOI] [PubMed] [Google Scholar]
- 49.Helfrich W. Elastic properties of lipid bilayers: theory and possible experiments. Z. Naturforsch. C. 1973;28:693–703. doi: 10.1515/znc-1973-11-1209. [DOI] [PubMed] [Google Scholar]
- 50.Derényi I., Jülicher F., Prost J. Formation and interaction of membrane tubes. Phys. Rev. Lett. 2002;88:238101. doi: 10.1103/PhysRevLett.88.238101. [DOI] [PubMed] [Google Scholar]
- 51.Berro J., Sirotkin V., Pollard T.D. Mathematical modeling of endocytic actin patch kinetics in fission yeast: disassembly requires release of actin filament fragments. Mol. Biol. Cell. 2010;21:2905–2915. doi: 10.1091/mbc.E10-06-0494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Footer M.J., Kerssemakers J.W.J., Dogterom M. Direct measurement of force generation by actin filament polymerization using an optical trap. Proc. Natl. Acad. Sci. USA. 2007;104:2181–2186. doi: 10.1073/pnas.0607052104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Ma R., Berro J. Structural organization and energy storage in crosslinked actin assemblies. PLoS Comput. Biol. 2018;14:e1006150. doi: 10.1371/journal.pcbi.1006150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Ma R., Berro J. Crosslinking actin networks produces compressive force. Cytoskeleton (Hoboken) 2019;76:346–354. doi: 10.1002/cm.21552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Jülicher F., Seifert U. Shape equations for axisymmetric vesicles: a clarification. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 1994;49:4728–4731. doi: 10.1103/physreve.49.4728. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.