Abstract
During actin-based cell migration, the actin cytoskeleton in the lamellipodium both generates and responds to force, which has functional consequences for the ability of the cell to extend protrusions. However, the material properties of the lamellipodial actin network and its response to stress on the timescale of motility are incompletely understood. Here, we describe a dynamic wrinkling phenotype in the lamellipodium of fish keratocytes, in which the actin sheet buckles upward away from the ventral membrane of the cell, forming a periodic pattern of wrinkles perpendicular to the cell’s leading edge. Cells maintain an approximately constant wrinkle wavelength over time despite new wrinkle formation and the lateral movement of wrinkles in the cell frame of reference, suggesting that cells have a preferred or characteristic wrinkle wavelength. Generation of wrinkles is dependent upon myosin contractility, and their wavelength scales directly with the density of the actin network and inversely with cell adhesion. These results are consistent with a simple physical model for wrinkling in an elastic sheet under compression and suggest that the lamellipodial cytoskeleton behaves as an elastic material on the timescale of cell migration despite rapid actin turnover.
Significance
Many adherent cells crawl using a thin and flat protrusive structure known as a lamellipodium. Because the lamellipodium is so thin and dynamic, it has been difficult to determine whether it has the mechanical properties of a viscous fluid or an elastic solid, which is important for understanding the mechanical workings of cell motility. We observed that lamellipodia in fish epidermal cells buckle into a periodic pattern of wrinkles. This pattern is shown to be consistent with a physical model in which the lamellipodium behaves as an elastic sheet compressed by myosin motor activity. These results imply that the lamellipodium can store mechanical energy and maintain its integrity over length scales and timescales relevant to cell migration.
Introduction
The actin cytoskeleton is essential for force generation and mechanosensing in many different contexts, including the regulation of cell migration, division, shape, and differentiation (1). The types of F-actin structures found within cells are often heterogeneously distributed and diverse, ranging from the highly branched, dense, and thin sheet of F-actin found in lamellipodia, to the bundled structures in filopodia and stress fibers, to the looser network that makes up the cell cortex (2). The lamellipodium is of particular interest because it is the structure responsible for many forms of actin-based motility, and it both generates and responds to force that is related to its function. Specifically, the force of actin polymerization is responsible for pushing out the membrane (3), whereas myosin motors pull on the actin network to restrain protrusion (4). Thus, to understand actin-based motility, it is important to understand the mechanical properties of the lamellipodial actin network and especially its mechanical response to stress on the timescale of cell migration.
However, the mechanical properties of the lamellipodial actin cytoskeleton have proved to be difficult to measure directly using standard microrheology techniques because the network is too dense to permit the entry of tracer particles and too thin for atomic force microscopy. Studies of in vitro reconstituted actin networks have found that pure polymerized actin behaves as a viscoelastic material whose elastic and viscous properties can be affected by various actin binding proteins (5, 6, 7, 8, 9). In addition, in vitro dendritic networks nucleated by Arp2/3, which most resemble lamellipodial network structure, have been shown to have an elastic response to force (10, 11, 12). However, actin turnover is known to occur at a much faster rate in the lamellipodia of living cells than can be reproduced in vitro (13, 14, 15, 16, 17), suggesting that the living lamellipodial cytoskeleton is rapidly rearranging and might thus behave more like a viscous fluid than the highly cross-linked, largely elastic networks observed in vitro. Indeed, measurements of the local properties of the cortical cytoskeleton in living cells have shown that, on micron length scales, the cortex behaves largely like a fluid (18,19), but it is not clear whether the same is true for the lamellipodial cytoskeleton, which is both denser and more highly cross-linked than the cell cortex (20). Furthermore, the mechanical properties of the cytoskeleton might be scale dependent and more solid-like on longer length scales in which small local rearrangements due to turnover might play less of a role.
Although rheological measurements have been difficult to perform on lamellipodia, the mechanical properties of the lamellipodial actin cytoskeleton can be inferred from its large-scale morphodynamics in certain cell types. Specifically, fish epidermal keratocytes, which have a single large lamellipodium with relatively uniform cytoskeletal structure (20), have been observed to have an apparently periodic pattern of lamellipodial wrinkles that are oriented perpendicular to the leading edge and are visible in phase-contrast or differential interference contrast microscopy (21, 22, 23, 24).
The formation of a stable pattern of wrinkles is expected of elastic but not of viscous materials. Regular periodic patterns of wrinkles in thin elastic sheets under lateral stress or strain are generally formed when the minimal energy configuration of the sheet corresponds to buckling at an optimal wavelength (i.e., buckling with either too short or too long a wavelength would have a higher potential energy) (25, 26, 27, 28, 29, 30). For a given lateral strain, the wavelength and amplitude of a periodic wrinkling pattern are inter-related, with the amplitude proportional to the wavelength. At a fixed lateral strain, wrinkling with small wavelengths corresponds to higher curvature of the elastic sheet, with the bending energy proportional to the inverse square of the wavelength (31). Long wavelengths, on the other hand, give rise to higher amplitude deformations for a given strain. The physical mechanisms that penalize wrinkling with large wavelength and amplitude are diverse and can include the vertical stretching of an elastic foundation to which the thin sheet is glued (31), gravity (32), or tension along the wrinkles (26). Importantly, in all these cases, the characteristic wavelength of the wrinkle pattern scales directly with the bending modulus of the elastic sheet, penalizing small wavelengths, and inversely with the strength of the specific forces, penalizing large amplitudes and, hence, large wavelengths.
Here, we characterize the geometry and dynamics of the lamellipodial wrinkles in zebrafish embryonic keratocytes and demonstrate that the wrinkles can be explained by a simple physical model in which the compressive force from myosin contractility leads to buckling of the lamellipodial F-actin network that behaves as a thin elastic sheet. These results suggest that, on the timescale of cell migration, even in rapidly moving cells with a high rate of F-actin turnover, the lamellipodial F-actin behaves largely as an elastic material.
Materials and methods
Cell culture and reagents
Keratocytes were cultured from zebrafish embryos at 2 days postfertilization (dpf) as described (33). Briefly, embryos were treated with cell dissociation buffer (Gibco, Waltham, MA) for 30 min, followed by 0.1% trypsin supplemented with 0.9 mM EDTA for 10 min to dissociate the epithelium. The dissociated cell suspension was transferred to a collagen-coated coverslip and allowed to adhere for 1 h before imaging. Cells were imaged in Leibovitz’s media (L-15; Gibco) supplemented with 10% fetal bovine serum, 14.2 mM HEPES (pH 7.4), and 1% antibiotic-antimycotic. The cytoplasmic RFP-expressing cells are from a transgenic krt4-RFP zebrafish line (34), which was a kind gift from A. Sagasti. The membrane GFP-expressing cells are from a transgenic bactin-EGFP-CAAX zebrafish line previously described (33). All experimental protocols were approved by the Stanford University Administrative Panel on Laboratory Animal Care under protocol no. 10240. Pharmacological agents included blebbistatin (Sigma, St. Louis, MO), latrunculin A (Molecular Probes, Eugene, OR), and ER Tracker Blue-White DPX (Invitrogen, Carlsbad, CA). Media pH was adjusted by replacing the HEPES in regular culture media with either 15 mM MES (pH 6.0) or Tris (pH 9.0).
Immunofluorescence and phalloidin staining
Indirect immunofluorescence for adhesions was performed using a mouse monoclonal phospho-tyrosine antibody at 1:50 (no. 9411; Cell Signaling Technology, Danvers, MA). Indirect immunofluorescence for myosin was performed using polyclonal rabbit anti-pS19 myosin light chain antibody (ab2480; Abcam, Cambridge, UK) at 1:100 dilution. The secondary antibodies were AF546 goat anti-rabbit (no. A-11035; Life Technologies, Carlsbad, CA) and AF405 goat anti-mouse (no. A-31553; Life Technologies), each at 1:1000 dilution. Cells were fixed in 4% formaldehyde and 0.32 M sucrose in fixation buffer (234 mM KCl, 6 mM MgCl2, 4 mM EGTA, and 10 mM MES (pH 6.1)) for 15 min, permeabilized with 0.5% Triton X-100 for 10 min, and blocked with phosphate-buffered saline (PBS) BT (3% bovine serum albumin, 0.1% Triton X-100, and 0.02% sodium azide) for 30 min before incubation with primary antibody and secondary antibody diluted in PBS-BT. F-actin was labeled with 0.2 μM fluorescently conjugated phalloidin (Molecular Probes).
Microscopy
For phase-contrast microscopy, live cells were imaged on an inverted microscope (TiEclipse; Nikon, Tokyo, Japan) using a 100× NA 1.4 Plan-Apo oil objective (Nikon). Images were collected with a cooled back-thinned EM-CCD camera (iXon + DU888; Andor Technology, Belfast, UK) with a 1× or 1.5× optovar using MicroManager 1.4 software (35). For total internal reflection fluorescence (TIRF) microscopy, live cells were imaged on a ZEISS AxioObserver TIRF3 system using a 100× NA 1.46 Plan-Apo oil objective (ZEISS, Jena, Germany). Images were collected with a cooled back-thinned EM-CCD camera (ImagEM-1k; Hamamatsu Photonics, Hamamatsu City, Japan) using AxioVision software (ZEISS). For three-dimensional (3D) structured illumination microscopy (SIM) experiments, fixed cells were mounted in SlowFade Gold mounting media (Invitrogen) and imaged on a DeltaVision OMX (GE Healthcare, Chicago, IL) microscope using DeltaVision software (GE Healthcare) with a 100× NA 1.4 UPlan-Apo oil objective (Olympus, Tokyo, Japan) using 0.125-μm z-slices at room temperature. Images were collected with a cooled back-thinned EM-CCD camera (Evolve; Photometrics, Tucson, AZ). Registration of multichannel images was achieved with multicolor fluorescence fiduciary beads (Tetraspeck; Thermo Fisher Scientific, Waltham, MA). 3D structured illumination reconstructions were created with the softWoRx imaging suite (GE Healthcare). All images were collected at room temperature. For ER Tracker experiments, cells were incubated in 1 μM of ER Tracker dye for 30 min in Hank’s Balanced Salt Solution with calcium and magnesium, and then media was replaced with the L15 solution described above.
Electron microscopy
Cell fixation and staining was based in part on a protocol designed to preferentially preserve and stain actin-based structures (36). Cells were fixed at room temperature for 30 min in Buffer A (100 mM sodium phosphate, 50 mM KCl, and 5 mM MgCl2 (pH 7.0)) containing 1% fresh glutaraldehyde (Electron Microscopy Sciences, Hatfield, PA), 2% paraformaldehyde (EMS), 0.5 mg/mL saponin, and 2 mg/mL tannic acid (no. 1764; Mallinckrodt, Staines-upon-Thames, UK). Cells were then stained with 1% OsO4 in Buffer A (pH 6.0) for 20 min at room temperature, followed by en bloc staining with 1% uranyl acetate in water for over 2 h at 4°C. Samples were dehydrated over 90 min with ethanol (50, 70, and 95% and twice with absolute) and propylene oxide and then infiltrated with increasing concentrations of Epon 812 in propylene oxide (1:1, 2:1, and then 100% Epon, each for 1 h). Coverslips were polymerized in a thin layer of Epon overnight at 65°C and then were placed onto a plug of fresh Epon (cells facing the plug) and baked again.
Once polymerized, excess Epon was removed to expose the back side of the coverslip, and the mount was immersed in 50% hydrofluoric acid for 20 min or until the coverslip was dissolved. A region of interest was trimmed, and silver-gold, 70-nm serial sections were taken (parallel to the substrate) with an ultramicrotome and mounted on formvar carbon-coated slots.
Sections were poststained with 3.5% uranyl acetate in acetone for 30 s and Reynold’s lead citrate for 3 min and imaged with a JEOL JEM-1400 microscope at an accelerating voltage of 120 kV using a Gatan Orius 832 CCD camera. Micrographs were analyzed using the TrakEM2 plugin for ImageJ (37, 38, 39).
Wrinkle characterization
To create the actin height map from a 3D structured illumination z-stack, for every pixel in the xy-plane, we calculated the height to be the weighted average of the z-steps, using actin intensity at each z-position as the weight. We assumed that most of the fluorescence signal from a given xy-location is coming from a lamellipodial actin sheet, whose thickness (z axis dimension) is small (substantially smaller than the ∼300 nm z axis resolution of the SIM) and relatively uniform over the xy-plane. This assumption was corroborated with electron microscopy (Fig. 2 e). This approach, which is analogous to how photoactivated localization microscopy (PALM) achieves superresolution, allows us to estimate the z-position with an accuracy better than the optical resolution of SIM. To measure the wrinkle profile in the image along a swath at a fixed distance from the leading edge, we used Celltool, an open source program for quantifying cell shape (40). The input cell outlines for Celltool were manually created using Photoshop (Adobe). To measure wrinkle wavelength, for each cell, the wrinkle profile was smoothed with a Gaussian filter, and peaks were detected using the argrelextrema function in scipy’s signal package. Average wavelength per cell was computed to be the mean of the peak-to-peak distances of detected peaks. The same calculation was performed for live cell phase microscopy experiments, except wrinkle peaks are represented by minima rather than maxima in the wrinkle profile.
Figure 2.
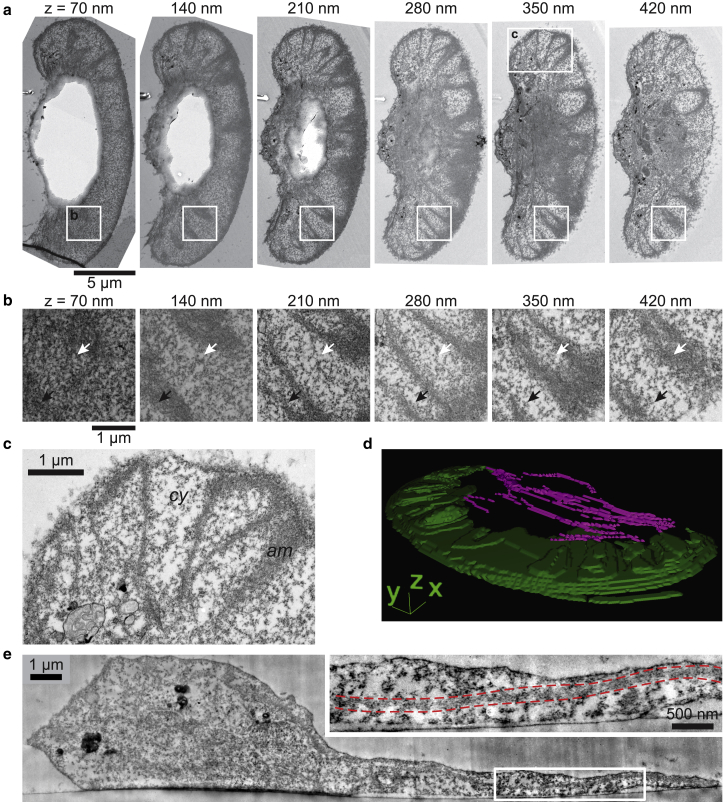
Lamellipodial ultrastructure supports interpretation of wrinkles as buckling of the actin network. (a) Serial electron micrographs of a single keratocyte, sectioned parallel to the coverslip. Sections are 70 nm; height from the ventral cell surface is indicated above each image. Actin-based structures stain strongly in this protocol (see Materials and methods), and dark staining in the lamellipodium resembles the phalloidin staining pattern in 3D SIM, suggesting that this is the lamellipodial actin network. Insets are magnified in (b) and (c). (b) Magnification of lamellipodial region for each section in (a) shows changes in staining consistent with wrinkles. Wrinkle troughs are indicated by dark staining in lower sections that disappears in higher sections (black arrow); conversely, peaks are indicated by lighter staining in lower sections that darkens in higher sections (white arrow). The cytoplasm beneath the wrinkles stains weakly and is not suggestive of familiar structures, actin-based or otherwise. (c) High-resolution image of a lamellipodial region specified in (a) shows the texture of the actin network (am) and diffusely stained surrounding cytoplasm (cy). (d) 3D reconstruction of actin network and actin cable staining for the cell in (a), segmented manually. Staining suggestive of actin cables is in magenta, and actin network staining is in green. (e) Transverse section of a keratocyte. Actin network in the lamellipodium appears as an electron-dense line ∼100 nm in thickness. Inset shows a portion of the lamellipodium in greater detail, with red dashed lines as a guide to the eye for actin network. The distance of the actin network to the coverslip changes more over the extent of the lamellipodium than the membrane-coverslip distance.
Fluorescence speckle microscopy
To visualize the actin network, we electroporated cells with Alexa Fluor (AF) 546-phalloidin (Molecular Probes), as previously described (24). Movement of the actin network was measured using an adaptive multiframe correlation algorithm (41), except we used three-frame averaging (6 s) and a correlation template between 11 × 11 and 21 × 21 pixels.
Traction force microscopy
Silicone gel substrates were prepared in glass-bottomed 50-mm dishes (GWSB-5040 with no. 1.5 coverglass bottoms from WillCo Wells, Amsterdam, The Netherlands). Tracer particles and 40-nm carboxylated dark red fluorescent beads (Invitrogen) were deposited on the coverglass bottoms at a low concentration to serve as fiduciaries of the glass surface. Gel prepolymer was prepared by mixing the A and B components of the CY 52–276 silicone gel (Dow Corning, Midland, MI) at a ratio of 1.2:1. The prepolymer was spin coated onto the coverglass bottoms at 2500 rpm for 30 s and then baked overnight in an 80°C oven, producing ∼30 μm-thick layers of cured gels. The gels were then treated with (3-aminopropyl)triethoxysilane to functionalize their surfaces. The same 40-nm carboxylated far red fluorescent beads were covalently linked to the gel surfaces by incubating the gels under a suspension of the beads (1:10,000 dilution from the 5% stock suspension) in 20 mM HEPES (pH = 8), with 0.01% 1-ethyl-3-(3-dimethylaminopropyl)carbodiimide (EDC) as a catalyst. Before cell attachment, the substrates were functionalized with 0.1 mg/mL collagen I (Advanced BioMatrix, Carlsbad, CA) with 0.01% EDC as a catalyst.
The elastic modulus of the gels was measured at 1.0 kPa with a microfluidic technique (42) by assessing the deformation of an ∼70 μm-thick layer of the gel on a 35 × 50 mm no. 1.5 microscope coverglass under a controlled shear flow. To minimize the experimental uncertainty, the ∼70 μm measurement sample was prepared from the same batch of the gel prepolymer and cured together with the ∼30 μm-thick gels used in experiments on cells.
To collect bead displacement images, cells were imaged every 10 s on an inverted microscope (TiEclipse; Nikon) using a 60× NA 1.4 Plan-Apo oil objective (Nikon). The unstressed image was acquired after the cell had migrated from the field of view. Bead displacements were quantified using the PIV ImageJ plugin (43) and converted to traction stress using Fourier transform traction cytometry (44).
Preparation of variable RGD surfaces
Surfaces were prepared as previously described (24). Briefly, plasma-cleaned coverslips were incubated with PLL-PEG-RGD solutions for 20 min at room temperature and then thoroughly washed with ddH2O and allowed to dry before use. For the 50% RGD substrates, coverslips were incubated in 0.5 mg/mL PLL-PEG-RGD (50%) (i.e., 50% of the PEG is functionalized with RGD; kind gift from E. Barnhart) solubilized in PBS. For 5% RGD surfaces, coverslips were incubated with 0.05 mg/mL PLL-PEG-RGD (50%) and 0.45 mg/mL PLL-PEG (PEG 2 kDa; SuSoS, Dübendorf, Switzerland) solubilized in PBS. Coverslips were always prepared fresh the same day each experiment was performed.
Results
Lamellipodial wrinkles represent the F-actin network bending away from the ventral surface of the cell
Ever since their initial description (21), fish epidermal keratocytes from a variety of species have occasionally been observed to have lamellipodial stripes, visible in phase-contrast or differential interference contrast microscopy, although the prevalence and prominence of these stripes may depend on the fish species and cell culture conditions (21, 22, 23, 24). We found that all motile keratocytes derived from zebrafish embryos at 2 dpf display these stripes, which are oriented perpendicular to the leading edge and appear to be periodic thickenings of the lamellipodium that stain more intensely for a volume marker (Fig. 1 a). Correlation of phase-contrast and volume marker fluorescence intensity indicates that the stripes of higher phase density correspond to thicker regions of the lamellipodium (Fig. 1 b). We note that the orientation of these lamellipodial thickenings perpendicular to the leading edge makes them distinct from the dorsal membrane ruffles that have been observed in fibroblasts, which are typically oriented parallel to the cell leading edge (45,46). We also note that the stripes in the phase-contrast images reflect thickenings of the cytoplasm itself and should not be confused with the stripe patterns reported for keratocytes plated on highly deformable substrates (25) because those patterns correspond to deformation of the substrate rather than of the cells.
Figure 1.
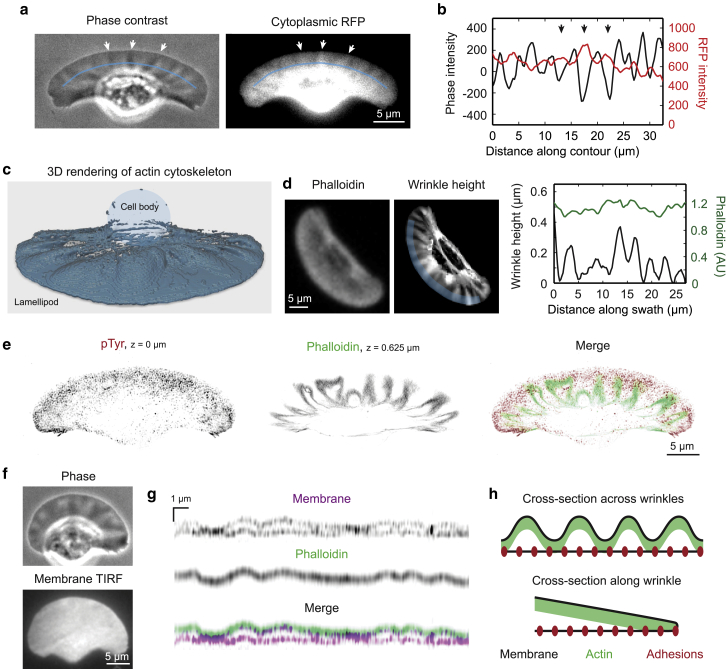
The lamellipodial actin cytoskeleton in keratocytes forms wrinkles by buckling up off the ventral membrane. (a) Wrinkles are visible as phase-dense stripes in phase contrast microscopy (left), which correspond to thickenings of the cytoplasm (right) visible when imaging cytoplasmic RFP as a volume marker. Arrows indicate example phase-dense wrinkles that are also brighter in the RFP channel. Blue line indicates the contour along which a profile was taken in (b). (b) Intensity profile along the blue line was indicated in (a) for both the phase contrast and RFP channels. Intensity values are background subtracted. Peaks of RFP intensity correspond to minima in phase contrast. Arrows indicate the same three example wrinkles as in (a). (c) 3D rendering of a cell fixed and stained with AF488-phalloidin, imaged with 3D structured illumination microscopy (SIM). Shaded oval represents the position of the cell body, which is relatively devoid of F-actin. (d) Representative cell fixed and stained with AF488-phalloidin is imaged first on a widefield microscope with a 20× objective (left) and later using 3D SIM to show wrinkle height (center). Right panel shows mean 20× phalloidin intensity (green) and mean wrinkle height (black) measured in a 2 μm-deep swath across the leading edge, as indicated by the shaded blue region in the center panel. (e) 3D SIM imaging of adhesion distribution in a fixed cell stained with a phospho-tyrosine antibody (red) compared with AF488-phalloidin-stained actin filaments (green) in a higher z-plane, which indicate the positions of wrinkle peaks. (f) A representative cell expressing EGFP-CAAX was imaged using TIRF microscopy. The ventral membrane appears flat. (g) A representative cell expressing EGFP-CAAX was fixed and stained with AF546-phalloidin and imaged using 3D SIM. Shown is a cross-sectional profile (i.e., x-z projection) across the front of the cell 2 μm from the leading edge. The actin appears as a single sheet (green), with the dorsal membrane closely associated on top and the ventral membrane on bottom (purple). (h) Diagram of lamellipodium geometry when wrinkles are present. Top panel represents a cross section across the width of the lamellipodium, and bottom panel shows a cross section from the front to back of the lamellipodium along the top of a wrinkle.
To determine the detailed structure of keratocyte lamellipodial periodic cytoplasmic thickenings, we used 3D SIM to assess the relative localization of the membrane, adhesions, and actin cytoskeleton. To our surprise, it appeared that the thickenings of the lamellipodium are not caused by additional actin polymerization in the z-direction (Fig. 1, c and d; Video S1) but rather result from the curving of a single sheet of F-actin of apparently uniform thickness out of contact with the ventral surface of the cell (Fig. 1 g).
3D rendering of the AF488-phalloidin-stained actin cytoskeleton in a representative cell as imaged by 3D structured illumination microscopy. Movie shows the rendering rotated around the x and z axes. This video corresponds to Fig. 1 c.
Structured illumination and TIRF imaging of the membrane confirmed that the ventral membrane has a much smaller amplitude of undulations than either the dorsal membrane or the actin sheet (Fig. 1, g and f). There are occasional undulations in the ventral membrane near the leading edge (Video S2), and their locations appear to be correlated with wrinkle position. These observations are consistent with previously reported variations in the distance from the glass substratum to the ventral membrane over the range of 15–100 nm as measured by interference reflection microscopy (47). We also noted that the adhesions are evenly distributed throughout the ventral membrane, including regions where the dense layer of actin is more than 0.5 μm above the substratum (Fig. 1 e). Because these periodic lamellipodial thickenings appear to be caused by a single sheet of F-actin bending in and out of proximity with the ventral membrane (Fig. 1 h), we believe the term “wrinkles” to be an apt description of the phenomenon by analogy to the wrinkles displayed by thin elastic sheets under compression (48). Notably, anucleate cytoplasmic fragments can form these structures as well (Fig. S1).
Time-lapse phase contrast and TIRF microscopy movie of the representative cell expressing membrane-localized EGFP-CAAX shown in Fig. 1 f. Time stamp (upper right) is in the format minutes:seconds. Frames were acquired every 3 seconds for 3:21 minutes. Scale bar is 10 microns.
To confirm our results from SIM, we also examined wrinkle morphology using thin-section transmission electron microscopy. We observed a dense staining pattern in the lamellipodium, consistent with F-actin (36), which formed undulating patterns similar to what we observed with phalloidin (Fig. 2, a–c). Manual segmentation of the dense staining pattern yielded a wrinkled structure reminiscent of that reconstructed from 3D SIM (Fig. 2 d, cf. Fig. 1 c). Viewed in cross section, the ventral membrane showed much smaller variations in height than the actin network (Fig. 2 e). The actin network maintained a constant thickness of ∼100 nm despite variation in the height of the lamellipodium, consistent with 3D structured illumination. Overall electron microscopic analysis confirmed the presence and specific features of wrinkles as visualized in 3D SIM (cf. Fig. 1).
Electron microscopy clearly demonstrated the presence of cytoplasmic space in the lamellipodium, which had a more diffuse staining, suggesting the absence of dense F-actin (Fig. 2 c). Emphasizing the extent of this cytoplasmic “free space,” we were able to observe small vesicles and other membrane-bound structures underneath wrinkles in electron micrographs (Fig. S2, a–d). In live imaging experiments, we also observed that larger organelles like endoplasmic reticulum could transiently penetrate into the lamellipodial space, either above or below the actin network (Fig. S2 e; Video S3). This suggests that there is more space available within the keratocyte lamellipodium than is conventionally assumed (49).
Side-by-side views of phase contrast (magenta, left) and widefield fluorescence microscopy (green, center) of a representative cell whose endoplasmic reticulum is stained with the dye ER Tracker. The right panel shows the two channels merged together. As the wrinkle pattern changes over time, the infiltration of the ER into the lamellipodium follows the wrinkles. Frames were acquired every 4 seconds for 160 seconds. Scale bar is 10 μm. This video corresponds to Fig. S2 e.
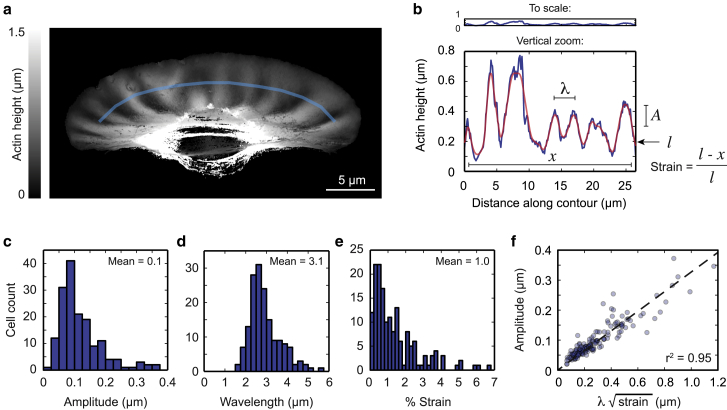
To measure wrinkle morphology, we developed a method to quantify the height of the lamellipodial F-actin at any given position (see Materials and methods) from 3D structured illumination reconstructions of phalloidin-stained fixed cells (Fig. 3 a). By tracing the height of the F-actin at a fixed distance from the leading edge, we measured wrinkle properties, including wavelength, amplitude, and effective strain. The effective strain is defined to be the difference between the actual arc length along the curved layer of dense F-actin and the in-plane distance it spans, normalized by the actual arc length (Fig. 3 b). Mathematically, if the arc length of the lamellipodium is l and spans a horizontal distance x, then the strain is defined by (l−x)/l. On average, keratocytes derived from 2 dpf zebrafish embryos have wrinkles with an amplitude ∼0.1 μm (Fig. 3 c), wavelength ∼3.1 μm (Fig. 3 d), and ∼1% strain (Fig. 3 e) when measured 2.5 μm from the leading edge. Average measurements at other distances from the leading edge are shown in Fig. S3. To confirm the self-consistency of our measurements, we checked the dependence of the measured root mean-squared amplitude on the product of the measured mean wavelength and square root of the strain (Fig. 3 f). This dependence is expected to be linear for all approximately sinusoidal curves (26). A linear dependence is observed in our data set (Fig. 3 f), indicating that our measurements of different geometrical properties of the wrinkles are self-consistent.
Figure 3.
Wrinkles exhibit regular geometry. (a) From 3D structured illumination z-stacks of cells fixed and stained with AF488-phalloidin, the average height of the lamellipodial actin can be estimated from a weighted average of pixel intensities in each slice (see Materials and methods). Blue line indicates the contour along which the height profile in (b) was taken. (b) Raw (blue line) and Gaussian-smoothed (red line) height profile was taken along the light blue line in (a). Top panel shows the height profile scaled such that the x and y axes are equal. Bottom panel zooms the y axis to show wrinkles in more detail. Gaussian-smoothed height profiles can be quantified as follows: mean amplitude A is measured as the root mean-squared deviation of the height profile; mean wavelength l is measured as the mean peak-to-peak distance; and mean strain was defined as the difference between the total arc length of the height profile l, and the flat line distance along the contour x, normalized by the arc length. (c–e) Histograms of mean amplitude (c), wavelength (d), and percentage of strain (e) measured in a population of 163 cells. All measurements were made from Gaussian-smoothed height profiles taken 2.5 μm in from the leading edge. (f) Amplitude is proportional to the product of wavelength and the square root of the strain, as predicted geometrically, indicating that the measurements are self-consistent. Dashed line shows best-fit line with the intercept set to zero.
Wrinkles are dynamic structures
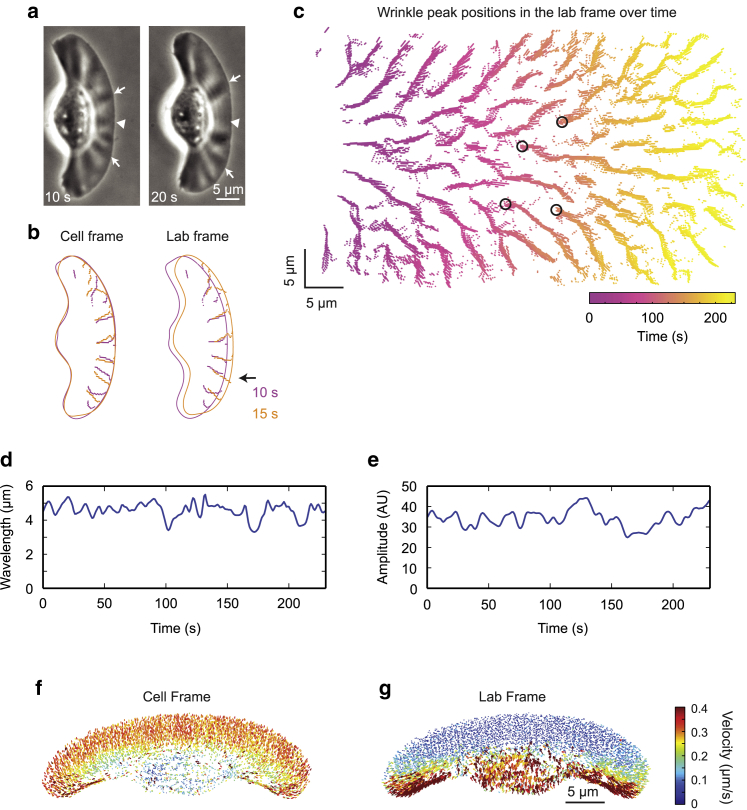
We note that the apparent positions and phase densities of the wrinkles evolve in time, indicating that wrinkles are dynamic structures (Fig. 4 a). The plots of the positions of local maxima in phase density versus time show how wrinkle position moves relative to both the cell and lab frames of reference (Fig. 4, b and c; Video S4). The wrinkles are largely stationary in the lab frame of reference, especially in the front region of the lamellipodium. In other words, the wrinkles (once formed) tend to maintain their position and orientation in the lab frame of reference, and in the strip of newly polymerized actin at the leading edge, wrinkles tend to form exactly where one would expect if the existing wrinkles were extended (Fig. 4 b, arrow).
Figure 4.
Wrinkles are dynamic. (a) Phase-contrast images of a representative cell over time. Arrows indicate wrinkles that travel laterally in the cell frame of reference. Arrowhead indicates a wrinkle that decreases in amplitude. (b and c) Cell outlines (b) and a plot of wrinkle peak positions in the lab frame of reference over the course of 232 s (b and c) for the cell shown in (a). See also Video S4. Time is encoded by color as indicated by the legend (b) or color bar (c). Arrow indicates an example wrinkle that is extended in its preexisting orientation as the cell moves. Circles indicate examples of new wrinkle formation. (d and e) Mean wavelength (d) and amplitude (e) for the cell are shown in (a) over time. (f and g) Actin flow velocity as measured with fluorescence speckle microscopy is shown in both the cell frame (f) and lab frame (g) of reference for a representative cell. Flow vectors are shown at 2× scale. Flow vector magnitude is indicated by color according to the color bar at right.
Time-lapse phase microscopy movie of a representative cell where wrinkle peaks as detected by our algorithm are continuously overlaid over the movie. Images were acquired with a widefield microscope. Time stamp (upper left) is in the format minutes:seconds. Frames were acquired every 2 seconds for 4 minutes. Scale bar is 10 microns. This video corresponds to Fig. 4 c.
The wrinkles are oriented radially at an angle to the direction of cell migration. As the cell continues to polymerize actin and extend existing wrinkles, the wrinkles appear to move laterally away from the cell midline in the moving frame of reference tied to the cell’s leading edge (Fig. 4 a, arrows). This lateral movement accelerates with increasing distance from the midline and is a natural consequence of radial extension for the wrinkles, whereas the leading edge as a whole moves directly forward. The observation that wrinkles move laterally in the cell frame was previously reported and was used to help establish the graded radial extension model for shape maintenance during motility (22). The lateral movement of the wrinkles away from the midline would continuously increase their mean wavelength if no new wrinkles were formed. However, the cells are able to maintain an approximately constant wavelength and amplitude (Fig. 4, d and e), suggesting that the cells have a preferred or characteristic wavelength, and indeed, new wrinkles can be observed to form whenever the local wavelength becomes substantially greater than the preferred one (Fig. 4 c, circles).
To determine if new wrinkles were forming through local variations in actin polymerization or flow rates, we performed fluorescence speckle microscopy on actin in wrinkled cells and found that the lamellipodial F-actin sheet is largely stationary in the lab frame of reference with no obvious local variations in actin polymerization or flow rates (Fig. 4 g), just as has been previously observed in nonwrinkled keratocytes (24,41). In addition, actin flow in the cell frame of reference is uniform and parallel to the direction of cell migration despite the presence of radial wrinkles (Fig. 4 f). The fact that wrinkled cells appear to form new wrinkles to maintain a constant wrinkle wavelength in the absence of variations in actin polymerization or flow suggests that the wrinkles may be formed by a mechanical process.
Myosin contractility provides compressive stress for wrinkling
Prior work on wrinkling of thin elastic sheets has suggested that the basic requirements for wrinkling are as follows: 1) some source of stress, 2) an elastic sheet with nonzero bending modulus, and 3) some mechanism penalizing large amplitude and large wavelength wrinkles (26,31). We wished to identify the physical basis for each of these three features in our experimental system.
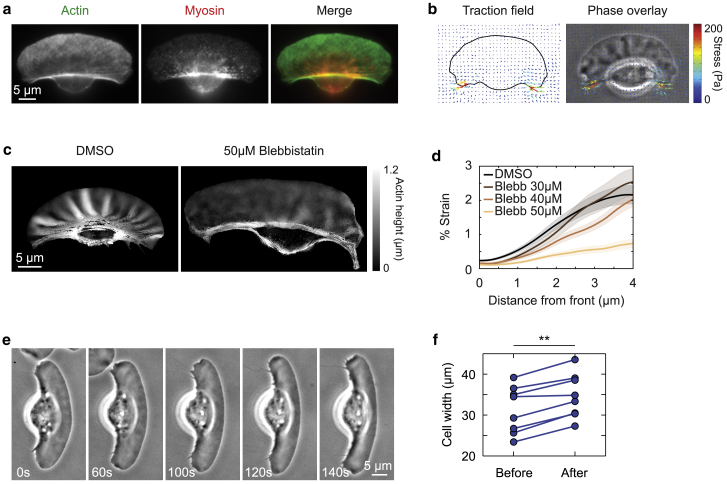
For the wrinkles we observe in keratocyte lamellipodia, myosin II contractility is an obvious candidate to provide compressive stress. Myosin II minifilaments are found throughout the lamellipodium in discrete clusters (20,41) but are swept toward the rear of the cell by the net retrograde movement of the actin network in the cell frame of reference to eventually localize on the actin bundle that runs parallel to the retracting edge (Fig. 5 a). Traction force microscopy reveals that the cells exert strong contractile forces on the substrate near the rear actomyosin bundle in the inward direction (Fig. 5 b; (25,50,51)). We note that the direction of the forces is correlated with the direction of inward actin flow seen in fluorescence speckle microscopy (Fig. 4, f and g). These forces are myosin dependent and dissipate upon myosin inhibition (50). It should be noted that the traction forces are perpendicular to the direction of the wrinkles, consistent with the hypothesis that the wrinkles form because of elastic buckling under compression.
Figure 5.
Myosin contractility drives wrinkle formation. (a) Example image of a cell fixed and stained with AF488 phalloidin (green) and pS19-MLC (red). (b) Traction stress exerted on the substrate by a typical wrinkled cell. Vectors are colored by stress magnitude, as shown in the color bar. (c) Representative actin height maps of cells fixed after treatment with either DMSO control or 50 μM blebbistatin for 5 min. Actin height is represented according to the grayscale bar. (d) Percentage of strain as a function of distance from the leading edge was measured in cell populations treated with DMSO control (n = 59) or 30, 40, or 50 μM blebbistatin (n = 24, 27, and 20, respectively). Shaded regions represent standard error. (e) Example phase-contrast time series of a cell treated with 50 μM blebbistatin. Time stamps indicate time since drug addition. (f) Cell width was measured in n = 8 cells before and 5 min after 50 μM blebbistatin treatment. ∗∗p < 0.01, as measured by paired-sample t-test.
To test if myosin-driven contractility is providing the compressive stress for wrinkle formation, we inhibited myosin with the small molecule blebbistatin (52). If wrinkles are forming mechanically because of myosin compression, release of myosin stress should both reduce the overall strain and cause the cell to widen along the direction of compression as the material relaxes. Both of these predictions are validated by the results we observe after blebbistatin treatment of cells (Fig. 5, c–f). Note that blebbistatin has no effect on wrinkle wavelength or actin filament density (Fig. S4, a–c). Conversely, the small molecule calyculin is a phosphatase inhibitor that has been shown to increase myosin activity (53). It appears to have a weak effect on strain (Fig. S4 d). We speculate this could be due to already near-maximal activation of myosin in untreated cells.
The lamellipodial actin cytoskeleton acts as the thin sheet
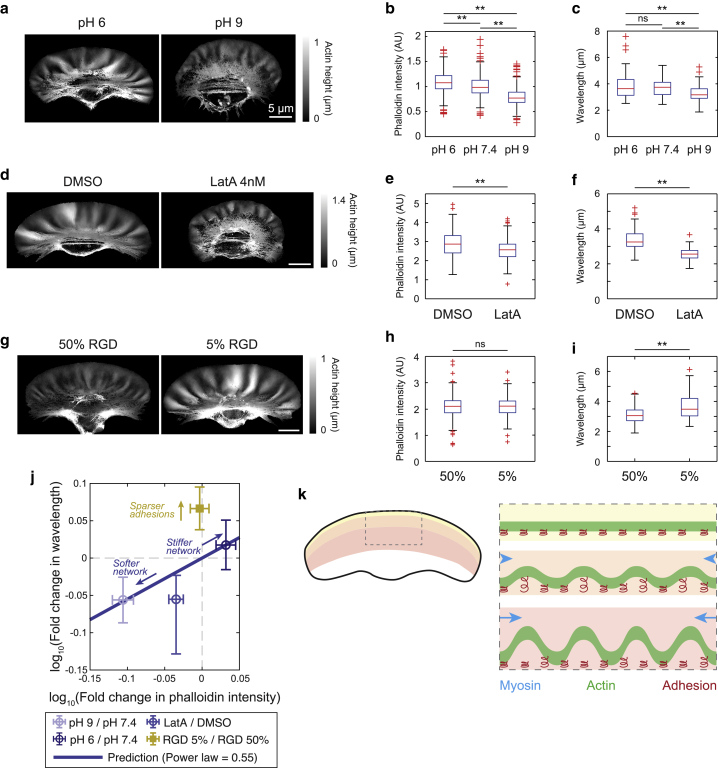
Given that myosin II, which binds to and exerts force directly on F-actin (54,55), is providing the compressive stress for wrinkling, we wondered if the lamellipodial F-actin itself could be acting as the thin elastic sheet that is the second required element for wrinkle formation. In our proposed mechanical model for wrinkling, a reduction in the bending modulus of the thin sheet leads to a decrease in the wavelength because it reduces the energetic cost of forming wrinkles with small wavelength and high curvature. The bending modulus of the network has been shown to be determined by F-actin density (56, 57, 58). We used two different perturbations to decrease F-actin density (Fig. 6, b and e): elevated pH, which has been previously shown to enhance cofilin activity (59,60), and the small molecule latrunculin, which sequesters G-actin and inhibits actin polymerization (61). Both perturbations result in a decrease in the population mean wavelength of the wrinkles (Fig. 6, a, c, d, and f), in agreement with the model.
Figure 6.
Actin density and adhesivity affect wrinkle wavelength. (a, d, and g) Actin height maps of representative cells cultured at pH 6 and pH 9 (a), with DMSO and 4 nM Latrunculin A (d) or on substrates coated with 50% RGD and 5% RGD (g). All scale bars 5 μm. (b, e, and h) Box plots of average phalloidin intensity per cell, normalized for cell area for the indicated cell populations. All box plots are standard Tukey style, with the box boundaries marking the 1st and 3rd quartiles and the whiskers extending up to 1.5× the interquartile range. N = 541, 267, and 433 cells, respectively, for pH 6, 7.4, and 9 (b). N = 319 and 261 for DMSO and latrunculin (e). N = 365 and 402 for 50% RGD and 5% RGD (h). ns = p > 0.05 and ∗∗p < 0.01 as measured by two-sided t-test. (c, f, and i) Box plots of mean wavelength per cell measured 2.5 μm from the leading edge for the indicated cell populations. N = 60, 64, and 48 cells, respectively, for pH 6, 7.4, and 9 (c). N = 54 and 57 for DMSO and latrunculin (f). N = 70 and 83 for 50% RGD and 5% RGD (i). (j) Power law scaling between actin density and wavelength. Data are from (b, c, e, f, h, and i), normalized by the indicated control. Error bars represent bootstrap 95% confidence intervals. Solid line shows the prediction of power law scaling because of changing network stiffness, with exponent 0.55 (see main text and Supporting materials and methods). Arrows guide the eye for two distinct scaling relationships because of changing network stiffness or adhesion density. Note that actin intensity could not be directly plotted against wavelength because of batch-to-batch variation in phalloidin fluorescence. (k) Model for wrinkle formation. Diagram on the right is a schematic for lamellipodium geometry in a segment (indicated by the gray box on the cell, left), with the different regions of the lamellipodium indicated by the colored zones.
Adhesion acts as the constraint penalizing long wavelength deformations
If the actin cytoskeleton is acting as the thin sheet being buckled up from the bottom plane by myosin contractility, adhesions are an obvious candidate for the constraint that resists deformations with large wavelength and amplitude. Adhesions are known to couple the actin cytoskeleton to the substratum and can sustain large forces before breaking (62, 63, 64). Therefore, lowering the density of adhesions should reduce the energetic cost of wrinkles with long wavelength and large amplitude, shifting the minimum of energy to longer wavelengths. We modulated adhesion density by plating cells on substrata with two different surface densities of the peptide integrin ligand RGD (24,65), which resulted in measurable differences in cell adhesivity (Fig. S5). The wrinkles on a substrate with a reduced adhesivity indeed had longer wavelengths (Fig. 6, g and i). Notably, F-actin density is not affected by changing the adhesivity of the surface (Fig. 6 h).
A mechanical model for wrinkle formation in keratocytes
Our results thus far indicate that wrinkle wavelength scales directly with actin network density and inversely with adhesion density. The direct scaling with actin network density is consistent with a mechanical model in which the actin network is represented by a thin elastic sheet whose bending modulus is a direct function of actin density. The inverse scaling of wrinkle wavelength with adhesion density can be explained by the fact that, at a given lateral strain generated by myosin contractility, the amplitude of the wrinkles is proportional to their wavelength. Greater density of adhesions increases the number of molecular bonds between the substrate and the actin network that are stretched or broken when the actin sheet buckles. Hence, a greater density of adhesions increases the energetic costs of wrinkle patterns with large amplitude and has a net effect of reducing the amplitude and wavelength of wrinkle patterns at a given lateral strain.
We constructed a simple mechanical model as a framework for explaining the experimentally observed trends in the dependence of wrinkle wavelength on the densities of adhesions and of F-actin. The thin elastic sheet representing the actin network is supported by an array of springs with a density proportional to the site density of the adhesion complexes, and compressive lateral strain is applied continuously and uniformly to the sheet by myosin II. Note that although myosin II is not distributed uniformly in the lamellipodium (Fig. 5 a), the assumption of continuously applied strain is justified because we found no correlation between myosin cluster localization and wrinkle positions, suggesting that the integrated strain of myosin II throughout the network is more relevant for wrinkling than small-scale heterogeneities in myosin localization (Fig. S6). This model predicts that the dependence of the wrinkle wavelength on actin density is a power law with an exponent of 0.55 (see Supporting materials and methods). Aggregated data from the pH and latrunculin perturbations that modulate actin density show reasonable agreement with this predicted scaling behavior, without any free parameters (Fig. 6 j). This model quantitatively supports the hypothesis that, on cellular length scales and on the timescales of cell migration, the actin network in lamellipodium behaves as a thin elastic sheet under lateral compression.
Although our model is able to capture observed trends in wrinkle wavelength, the amplitude of the wrinkles appears to be too large to be readily reconciled with the model and with what is known about the cytoskeleton. In particular, previous studies indicate that the typical height of an adhesion complex is less than 100 nm (66), whereas we observe that at 3–5 μm from the leading edge, the actin can buckle over 400 nm away from the adhesions and ventral surface of the cell (Figs. 1, d and g and 2 e). We do not have a clear molecular candidate for springs connecting adhesions with the actin sheet that would remain intact when stretched to 400 nm—although it is possible there is a sparse actin network filling the gap that, in principle, could play this role (see Supporting materials and methods for additional elaboration). Therefore, we propose a dynamical model for wrinkle formation. In a moving cell, the newly polymerized actin sheet at the leading edge is initially flat and strain-free (Fig. 6 k). As that particular strip of actin moves rearward in the cell frame of reference, myosin contractility leads to a gradual buildup of compressive lateral stress, which leads to wrinkling. Wrinkle wavelength may be selected at a relatively early stage, when the strain is still low, such that the wrinkles are of sufficiently small amplitude, and the actin sheet remains attached to the adhesions. Further back, more myosin accumulation increases network strain, resulting in larger amplitude wrinkles that begin to cause delamination of the actin network from the adhesions. However, we speculate that this delamination process is slow, so the troughs remain attached and the wavelength is unchanged despite increasing wrinkle amplitude, at least over the timescale required for that strip of actin to move from the front to the back of the lamellipodium in the cell frame of reference, typically 30–60 s.
Discussion
In summary, we find that keratocyte lamellipodia can form remarkably regular wrinkle patterns in which the F-actin network periodically buckles away from the ventral membrane. This wrinkling is perhaps surprising given previous observations that actin polymerization is required for adhesion assembly and maintenance (67). However, the composition of adhesion complexes in zebrafish keratocytes is quite different from the cell types in which these prior findings were made. For example, vinculin is not expressed in embryonic zebrafish keratocytes (33). In addition, we cannot exclude the possibility that, even when the dense F-actin network separates from the adhesions, there might be a sparse actin network remaining associated with the adhesions and ventral membrane.
The lamellipodial actin network is well known to form a thin sheet with a uniform thickness of 100–200 nm, regardless of cell type (49,68,69), but the mechanism maintaining this uniform thickness is not clear. Our results suggest that close apposition of the membrane on both ventral and dorsal surfaces is not required, ruling out one possible mechanism for maintaining lamellipodial actin thickness.
We show that wrinkle formation is dependent on myosin contractility and that modulation of actin density or cell adhesion strength alters the characteristic wavelength of the wrinkles. These results are consistent with a constrained buckling physical model in which the wavelength is determined by the energetic costs of bending the actin sheet and of stretching or breaking the molecular bonds connecting the actin sheet to adhesions. Note that buckling instabilities have previously been observed in actin bundles and branched networks under compression (11,70). Actin networks have also been observed to buckle parallel to the leading edge in response to contractile stress generated during cell-substrate traction (46), and myosin contractility has been shown to be sufficient to cause buckling of single actin filaments in vitro (54,55).
Because the wrinkles we observe are consistent with a mechanical model, in which the actin network in the lamellipodium is represented by a thin elastic sheet that resists bending, our results suggest that, on the timescale of cell migration, the lamellipodial F-actin network behaves as an elastic material. If the actin were instead behaving largely as a fluid, the force of myosin contractility would be rapidly dissipated by rearrangements in the network, and the network would not resist bending. This result may be surprising given the previous literature on the mechanical properties of the cortical cytoskeleton in living cells, which shows that the cytoskeleton behaves largely as a fluid on timescales as short as a second, as evidenced by the movement of small beads through the network (18,19). In addition, it is known that in lamellipodia, actin turnover and cross-linker rebinding is fast, occurring on a timescale of 1–10 s (13,71) as compared with tens of seconds timescale for cell motility. These results led to the assumption that, in the context of cell motility, the lamellipodium behaves as a viscous fluid (24,72).
We see no evidence that the potential fluid-like behavior of actin due to turnover plays a role in setting wrinkle wavelength. Because the actin network is nearly stationary in the lab frame of reference (Fig. 4 g) and actin disassembly rates are not correlated with cell velocity (13), we can assume that the actin network in slower cells has more time to remodel. If the relaxation of strain (or stress) resulting from actin remodeling on the timescale of cell migration had a significant influence upon the mechanical response of the actin network, we would expect both the amplitude and wavelength of the wrinkles to correlate with the cell speed. However, neither correlation is observed (Fig. S7).
Multiple experiments have suggested that locally—at the length scale of a few filaments or cross-links—regions of the cytoskeleton can in fact behave elastically. For example, actin bundled into stress fibers will spring apart when severed (73,74), suggesting that elastic tension can be stored in the network, although turnover rates are typically an order of magnitude slower in stress fibers than in lamellipodia (75). In addition, force applied to integrins at the surface of the cell can induce structural rearrangements and signaling events deep inside the cell within 1 s (76,77), which is at least as consistent with force propagating along an elastic network as with triggering of a biochemical signal transduction pathway. Finally, it has been shown that microtubules form periodic buckles when embedded in the actin cytoskeleton (27), which can be described with the same type of mechanical model we use. However, these results were limited to characterization of particular structures within a heterogeneous cytoskeleton.
Our results provide the first evidence, to our knowledge, that the native lamellipodial cytoskeleton behaves as an elastic material globally—on cellular length scales. This is not to say that the actin network in the keratocyte lamellipodium cannot exhibit a fluid-like behavior, because actin turnover is clearly occurring rapidly compared to the timescale of cell migration (13,78), but rather that the structural integrity of the network can be maintained for longer than the turnover time of the constituent individual proteins, so that the overall response to myosin compression is elastic. Importantly, the elastic behavior of the lamellipodium suggests that it is mechanically coupled such that forces acting on one region can propagate over long distances, which could contribute to large-scale coordination of motility. Although we believe our results point to an elastic model of the lamellipodium through converging lines of indirect evidence, direct measurement of the elasticity of the lamellipodium is an important next step.
Intriguingly, a similar wrinkling phenomenon has been observed in vitro using cross-linked actomyosin gels that buckle during isotropic compression arising from myosin contractility (79). This wrinkling was rationalized using a physical model of the actomyosin gel as a thin elastic sheet under compression in which an increase in actin density at the periphery of the gel provided a stiff boundary that resisted compression in the bulk, leading to out-of-plane wrinkling. Such a density gradient is present in the lamellipodium, in which the actin network is most dense at the leading edge and decreases in density further back in the lamellipodium (80). However, wrinkling of the in vitro gels occurred in experimental conditions in which adhesion of the gel to the substrate was minimized, and so this model is not able to explain the dependence of wrinkle wavelength on substrate adhesivity that we observe (Fig. 6, g–i). Furthermore, the model proposed in (79) predicts that the wavelength of wrinkles scales with the inverse square root of the effective strain, whereas our model predicts that wavelength and strain are independent. Consistent with our model, we do not observe any relationship between wavelength and strain (Fig. S8), suggesting that the wrinkling observed in actomyosin gels in vitro and lamellipodia in living cells are distinct phenomena.
Finally, although zebrafish keratocytes derived from embryos at 2 dpf all display this wrinkling phenotype, the proportion of keratocytes displaying this wrinkling behavior substantially varies depending on the species of fish and cell-substrate interactions. For example, it has previously been shown that nearly all cichlid keratocytes display wrinkles on surfaces with low adhesivity, whereas only a small proportion of cichlid keratocytes have wrinkles on surfaces with moderate adhesivity (24). This phenotypic difference can be explained by molecular differences within the context of our model if we assume that cells with either weak myosin contractility or strong adhesions may not be able to produce sufficient compressive stress to induce the buckling instability. It would be very interesting to explore the effects of quantitative changes in cytoskeletal and focal adhesion composition on wrinkle appearance or wavelength as a proxy for how these molecular changes affect the mechanical properties of a living lamellipodium.
Author contributions
S.S.L. and J.A.T. conceived and designed the research. S.S.L. and A.S.K. conducted the experiments and analyzed the data. E.F.K. and A.G. developed the mathematical model. E.G. and A.G. contributed reagents. S.S.L., E.F.K., A.S.K., A.G., and J.A.T. wrote the manuscript.
Acknowledgments
We are grateful to L. Mahadevan and D. Fisher for helpful discussion on the mechanical model, W. Talbot and members of the Talbot lab for zebrafish training and access to their fish facility, J. Perrino for advice and training on the electron microscope, E. Barnhart for PLL-PEG-RGD, A. Sagasti for the krt4-RFP fish line, G. Danuser for the fluorescence speckle microscopy tracking code, and B. Sabass for the Fourier transform traction cytometry program.
Use of the OMX 3D SIM microscope was provided through the Stanford Cell Sciences Imaging Facility and partially funded by award 1S10OD01227601 from the National Center for Research Resources; use of the electron microscope was also provided through the Imaging Facility and partially funded by award 1S10RR02678001 from the National Center for Research Resources. This work was supported by the Stanford Medical Scientist Training Program National Institutes of Health (NIH) T32-GM007365 (S.S.L.), the James S. McDonnell Foundation Postdoctoral Fellowship Award in Studying Complex Systems (E.F.K.), NIH T32-GM008294 (Molecular Biophysics, A.S.K.), NIH PO1-GM098412 (E.G. and A.G.), the Stanford Center for Systems Biology NIH P50-GM107615, and the Howard Hughes Medical Institute (J.A.T.).
Editor: Kinneret Keren.
Footnotes
Sunny S. Lou and Andrew S. Kennard contributed equally to this work.
Supporting material can be found online at https://doi.org/10.1016/j.bpj.2021.02.022.
Supporting references
Reference (81) appears in the Supporting material.
Supporting material
References
- 1.Miller C.J., Davidson L.A. The interplay between cell signalling and mechanics in developmental processes. Nat. Rev. Genet. 2013;14:733–744. doi: 10.1038/nrg3513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Le Clainche C., Carlier M.-F. Regulation of actin assembly associated with protrusion and adhesion in cell migration. Physiol. Rev. 2008;88:489–513. doi: 10.1152/physrev.00021.2007. [DOI] [PubMed] [Google Scholar]
- 3.Theriot J.A. The polymerization motor. Traffic. 2000;1:19–28. doi: 10.1034/j.1600-0854.2000.010104.x. [DOI] [PubMed] [Google Scholar]
- 4.Vicente-Manzanares M., Ma X., Horwitz A.R. Non-muscle myosin II takes centre stage in cell adhesion and migration. Nat. Rev. Mol. Cell Biol. 2009;10:778–790. doi: 10.1038/nrm2786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Janmey P.A., Hvidt S., Stossel T.P. The mechanical properties of actin gels. Elastic modulus and filament motions. J. Biol. Chem. 1994;269:32503–32513. [PubMed] [Google Scholar]
- 6.Shin J.H., Gardel M.L., Weitz D.A. Relating microstructure to rheology of a bundled and cross-linked F-actin network in vitro. Proc. Natl. Acad. Sci. USA. 2004;101:9636–9641. doi: 10.1073/pnas.0308733101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Gardel M.L., Nakamura F., Weitz D.A. Prestressed F-actin networks cross-linked by hinged filamins replicate mechanical properties of cells. Proc. Natl. Acad. Sci. USA. 2006;103:1762–1767. doi: 10.1073/pnas.0504777103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Koenderink G.H., Dogic Z., Weitz D.A. An active biopolymer network controlled by molecular motors. Proc. Natl. Acad. Sci. USA. 2009;106:15192–15197. doi: 10.1073/pnas.0903974106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.McCall P.M., MacKintosh F.C., Gardel M.L. Cofilin drives rapid turnover and fluidization of entangled F-actin. Proc. Natl. Acad. Sci. USA. 2019;116:12629–12637. doi: 10.1073/pnas.1818808116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.van der Gucht J., Paluch E., Sykes C. Stress release drives symmetry breaking for actin-based movement. Proc. Natl. Acad. Sci. USA. 2005;102:7847–7852. doi: 10.1073/pnas.0502121102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Chaudhuri O., Parekh S.H., Fletcher D.A. Reversible stress softening of actin networks. Nature. 2007;445:295–298. doi: 10.1038/nature05459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Dayel M.J., Akin O., Mullins R.D. In silico reconstitution of actin-based symmetry breaking and motility. PLoS Biol. 2009;7:e1000201. doi: 10.1371/journal.pbio.1000201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Theriot J.A., Mitchison T.J. Actin microfilament dynamics in locomoting cells. Nature. 1991;352:126–131. doi: 10.1038/352126a0. [DOI] [PubMed] [Google Scholar]
- 14.Watanabe N., Mitchison T.J. Single-molecule speckle analysis of actin filament turnover in lamellipodia. Science. 2002;295:1083–1086. doi: 10.1126/science.1067470. [DOI] [PubMed] [Google Scholar]
- 15.Ponti A., Machacek M., Danuser G. Two distinct actin networks drive the protrusion of migrating cells. Science. 2004;305:1782–1786. doi: 10.1126/science.1100533. [DOI] [PubMed] [Google Scholar]
- 16.Lai F.P.L., Szczodrak M., Rottner K. Arp2/3 complex interactions and actin network turnover in lamellipodia. EMBO J. 2008;27:982–992. doi: 10.1038/emboj.2008.34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Lewalle A., Fritzsche M., Charras G. A phenomenological density-scaling approach to lamellipodial actin dynamics. Interface Focus. 2014;4:20140006. doi: 10.1098/rsfs.2014.0006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kole T.P., Tseng Y., Wirtz D. Intracellular mechanics of migrating fibroblasts. Mol. Biol. Cell. 2005;16:328–338. doi: 10.1091/mbc.E04-06-0485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Wottawah F., Schinkinger S., Käs J. Optical rheology of biological cells. Phys. Rev. Lett. 2005;94:098103. doi: 10.1103/PhysRevLett.94.098103. [DOI] [PubMed] [Google Scholar]
- 20.Svitkina T.M., Verkhovsky A.B., Borisy G.G. Analysis of the actin-myosin II system in fish epidermal keratocytes: mechanism of cell body translocation. J. Cell Biol. 1997;139:397–415. doi: 10.1083/jcb.139.2.397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Goodrich H.B. Cell behavior in tissue cultures. Biol. Bull. 1924;46:252–262. [Google Scholar]
- 22.Lee J., Ishihara A., Jacobson K. Principles of locomotion for simple-shaped cells. Nature. 1993;362:167–171. doi: 10.1038/362167a0. [DOI] [PubMed] [Google Scholar]
- 23.Small J.V., Herzog M., Anderson K. Actin filament organization in the fish keratocyte lamellipodium. J. Cell Biol. 1995;129:1275–1286. doi: 10.1083/jcb.129.5.1275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Barnhart E.L., Lee K.-C., Theriot J.A. An adhesion-dependent switch between mechanisms that determine motile cell shape. PLoS Biol. 2011;9:e1001059. doi: 10.1371/journal.pbio.1001059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Burton K., Park J.H., Taylor D.L. Keratocytes generate traction forces in two phases. Mol. Biol. Cell. 1999;10:3745–3769. doi: 10.1091/mbc.10.11.3745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Cerda E., Mahadevan L. Geometry and physics of wrinkling. Phys. Rev. Lett. 2003;90:074302. doi: 10.1103/PhysRevLett.90.074302. [DOI] [PubMed] [Google Scholar]
- 27.Brangwynne C.P., MacKintosh F.C., Weitz D.A. Microtubules can bear enhanced compressive loads in living cells because of lateral reinforcement. J. Cell Biol. 2006;173:733–741. doi: 10.1083/jcb.200601060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Savin T., Kurpios N.A., Tabin C.J. On the growth and form of the gut. Nature. 2011;476:57–62. doi: 10.1038/nature10277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Asally M., Kittisopikul M., Süel G.M. Localized cell death focuses mechanical forces during 3D patterning in a biofilm. Proc. Natl. Acad. Sci. USA. 2012;109:18891–18896. doi: 10.1073/pnas.1212429109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Trejo M., Douarche C., Raspaud E. Elasticity and wrinkled morphology of Bacillus subtilis pellicles. Proc. Natl. Acad. Sci. USA. 2013;110:2011–2016. doi: 10.1073/pnas.1217178110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Groenewold J. Wrinkling of plates coupled with soft elastic media. Phys. A Stat. Mech. Appl. 2001;298:32–45. [Google Scholar]
- 32.Pocivavsek L., Dellsy R., Cerda E. Stress and fold localization in thin elastic membranes. Science. 2008;320:912–916. doi: 10.1126/science.1154069. [DOI] [PubMed] [Google Scholar]
- 33.Lou S.S., Diz-Muñoz A., Theriot J.A. Myosin light chain kinase regulates cell polarization independently of membrane tension or Rho kinase. J. Cell Biol. 2015;209:275–288. doi: 10.1083/jcb.201409001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.O’Brien G.S., Rieger S., Sagasti A. Coordinate development of skin cells and cutaneous sensory axons in zebrafish. J. Comp. Neurol. 2012;520:816–831. doi: 10.1002/cne.22791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Edelstein A., Amodaj N., Stuurman N. Computer control of microscopes using μManager. Curr. Protoc. Mol. Biol. 2010;92:14.20.1–14.20.17. doi: 10.1002/0471142727.mb1420s92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Maupin P., Pollard T.D. Improved preservation and staining of HeLa cell actin filaments, clathrin-coated membranes, and other cytoplasmic structures by tannic acid-glutaraldehyde-saponin fixation. J. Cell Biol. 1983;96:51–62. doi: 10.1083/jcb.96.1.51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Saalfeld S., Cardona A., Tomančák P. As-rigid-as-possible mosaicking and serial section registration of large ssTEM datasets. Bioinformatics. 2010;26:i57–i63. doi: 10.1093/bioinformatics/btq219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Saalfeld S., Fetter R., Tomancak P. Elastic volume reconstruction from series of ultra-thin microscopy sections. Nat. Methods. 2012;9:717–720. doi: 10.1038/nmeth.2072. [DOI] [PubMed] [Google Scholar]
- 39.Cardona A., Saalfeld S., Douglas R.J. TrakEM2 software for neural circuit reconstruction. PLoS One. 2012;7:e38011. doi: 10.1371/journal.pone.0038011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Pincus Z., Theriot J.A. Comparison of quantitative methods for cell-shape analysis. J. Microsc. 2007;227:140–156. doi: 10.1111/j.1365-2818.2007.01799.x. [DOI] [PubMed] [Google Scholar]
- 41.Wilson C.A., Tsuchida M.A., Theriot J.A. Myosin II contributes to cell-scale actin network treadmilling through network disassembly. Nature. 2010;465:373–377. doi: 10.1038/nature08994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Gutierrez E., Groisman A. Measurements of elastic moduli of silicone gel substrates with a microfluidic device. PLoS One. 2011;6:e25534. doi: 10.1371/journal.pone.0025534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Tseng Q., Duchemin-Pelletier E., Théry M. Spatial organization of the extracellular matrix regulates cell-cell junction positioning. Proc. Natl. Acad. Sci. USA. 2012;109:1506–1511. doi: 10.1073/pnas.1106377109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Sabass B., Gardel M.L., Schwarz U.S. High resolution traction force microscopy based on experimental and computational advances. Biophys. J. 2008;94:207–220. doi: 10.1529/biophysj.107.113670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Felder S., Elson E.L. Mechanics of fibroblast locomotion: quantitative analysis of forces and motions at the leading lamellas of fibroblasts. J. Cell Biol. 1990;111:2513–2526. doi: 10.1083/jcb.111.6.2513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Giannone G., Dubin-Thaler B.J., Sheetz M.P. Lamellipodial actin mechanically links myosin activity with adhesion-site formation. Cell. 2007;128:561–575. doi: 10.1016/j.cell.2006.12.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Lee J., Jacobson K. The composition and dynamics of cell-substratum adhesions in locomoting fish keratocytes. J. Cell Sci. 1997;110:2833–2844. doi: 10.1242/jcs.110.22.2833. [DOI] [PubMed] [Google Scholar]
- 48.Chung J.Y., Nolte A.J., Stafford C.M. Surface wrinkling: a versatile platform for measuring thin-film properties. Adv. Mater. 2011;23:349–368. doi: 10.1002/adma.201001759. [DOI] [PubMed] [Google Scholar]
- 49.Abraham V.C., Krishnamurthi V., Lanni F. The actin-based nanomachine at the leading edge of migrating cells. Biophys. J. 1999;77:1721–1732. doi: 10.1016/S0006-3495(99)77018-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Oliver T., Dembo M., Jacobson K. Separation of propulsive and adhesive traction stresses in locomoting keratocytes. J. Cell Biol. 1999;145:589–604. doi: 10.1083/jcb.145.3.589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Jurado C., Haserick J.R., Lee J. Slipping or gripping? Fluorescent speckle microscopy in fish keratocytes reveals two different mechanisms for generating a retrograde flow of actin. Mol. Biol. Cell. 2005;16:507–518. doi: 10.1091/mbc.E04-10-0860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Cheung A., Dantzig J.A., Straight A.F. A small-molecule inhibitor of skeletal muscle myosin II. Nat. Cell Biol. 2002;4:83–88. doi: 10.1038/ncb734. [DOI] [PubMed] [Google Scholar]
- 53.Ishihara H., Ozaki H., Hartshorne D.J. Calcium-independent activation of contractile apparatus in smooth muscle by calyculin-A. J. Pharmacol. Exp. Ther. 1989;250:388–396. [PubMed] [Google Scholar]
- 54.Lenz M., Thoresen T., Dinner A.R. Contractile units in disordered actomyosin bundles arise from F-actin buckling. Phys. Rev. Lett. 2012;108:238107. doi: 10.1103/PhysRevLett.108.238107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Murrell M.P., Gardel M.L. F-actin buckling coordinates contractility and severing in a biomimetic actomyosin cortex. Proc. Natl. Acad. Sci. USA. 2012;109:20820–20825. doi: 10.1073/pnas.1214753109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Hinner B., Tempel M., Frey E. Entanglement, elasticity and viscous relaxation of actin solutions. Phys. Rev. Lett. 1998;81:2614–2617. [Google Scholar]
- 57.Gisler T., Weitz D.A. Scaling of the microrheology of semidilute F-actin solutions. Phys. Rev. Lett. 1999;82:1606–1609. [Google Scholar]
- 58.Gardel M.L., Shin J.H., Weitz D.A. Elastic behavior of cross-linked and bundled actin networks. Science. 2004;304:1301–1305. doi: 10.1126/science.1095087. [DOI] [PubMed] [Google Scholar]
- 59.Hawkins M., Pope B., Weeds A.G. Human actin depolymerizing factor mediates a pH-sensitive destruction of actin filaments. Biochemistry. 1993;32:9985–9993. doi: 10.1021/bi00089a014. [DOI] [PubMed] [Google Scholar]
- 60.Frantz C., Barreiro G., Barber D.L. Cofilin is a pH sensor for actin free barbed end formation: role of phosphoinositide binding. J. Cell Biol. 2008;183:865–879. doi: 10.1083/jcb.200804161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Coué M., Brenner S.L., Korn E.D. Inhibition of actin polymerization by latrunculin A. FEBS Lett. 1987;213:316–318. doi: 10.1016/0014-5793(87)81513-2. [DOI] [PubMed] [Google Scholar]
- 62.Gallant N.D., Michael K.E., García A.J. Cell adhesion strengthening: contributions of adhesive area, integrin binding, and focal adhesion assembly. Mol. Biol. Cell. 2005;16:4329–4340. doi: 10.1091/mbc.E05-02-0170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Hu K., Ji L., Waterman-Storer C.M. Differential transmission of actin motion within focal adhesions. Science. 2007;315:111–115. doi: 10.1126/science.1135085. [DOI] [PubMed] [Google Scholar]
- 64.Chan C.E., Odde D.J. Traction dynamics of filopodia on compliant substrates. Science. 2008;322:1687–1691. doi: 10.1126/science.1163595. [DOI] [PubMed] [Google Scholar]
- 65.VandeVondele S., Vörös J., Hubbell J.A. RGD-grafted poly-L-lysine-graft-(polyethylene glycol) copolymers block non-specific protein adsorption while promoting cell adhesion. Biotechnol. Bioeng. 2003;82:784–790. doi: 10.1002/bit.10625. [DOI] [PubMed] [Google Scholar]
- 66.Kanchanawong P., Shtengel G., Waterman C.M. Nanoscale architecture of integrin-based cell adhesions. Nature. 2010;468:580–584. doi: 10.1038/nature09621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Oakes P.W., Gardel M.L. Stressing the limits of focal adhesion mechanosensitivity. Curr. Opin. Cell Biol. 2014;30:68–73. doi: 10.1016/j.ceb.2014.06.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Abercrombie M., Heaysman J.E., Pegrum S.M. The locomotion of fibroblasts in culture. I. Movements of the leading edge. Exp. Cell Res. 1970;59:393–398. doi: 10.1016/0014-4827(70)90646-4. [DOI] [PubMed] [Google Scholar]
- 69.Koestler S.A., Rottner K., Small J.V. F- and G-actin concentrations in lamellipodia of moving cells. PLoS One. 2009;4:e4810. doi: 10.1371/journal.pone.0004810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Leijnse N., Oddershede L.B., Bendix P.M. Helical buckling of actin inside filopodia generates traction. Proc. Natl. Acad. Sci. USA. 2015;112:136–141. doi: 10.1073/pnas.1411761112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Wachsstock D.H., Schwarz W.H., Pollard T.D. Cross-linker dynamics determine the mechanical properties of actin gels. Biophys. J. 1994;66:801–809. doi: 10.1016/s0006-3495(94)80856-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Rubinstein B., Fournier M.F., Mogilner A. Actin-myosin viscoelastic flow in the keratocyte lamellipod. Biophys. J. 2009;97:1853–1863. doi: 10.1016/j.bpj.2009.07.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Heidemann S.R., Kaech S., Matus A. Direct observations of the mechanical behaviors of the cytoskeleton in living fibroblasts. J. Cell Biol. 1999;145:109–122. doi: 10.1083/jcb.145.1.109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Kumar S., Maxwell I.Z., Ingber D.E. Viscoelastic retraction of single living stress fibers and its impact on cell shape, cytoskeletal organization, and extracellular matrix mechanics. Biophys. J. 2006;90:3762–3773. doi: 10.1529/biophysj.105.071506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Hotulainen P., Lappalainen P. Stress fibers are generated by two distinct actin assembly mechanisms in motile cells. J. Cell Biol. 2006;173:383–394. doi: 10.1083/jcb.200511093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Maniotis A.J., Chen C.S., Ingber D.E. Demonstration of mechanical connections between integrins, cytoskeletal filaments, and nucleoplasm that stabilize nuclear structure. Proc. Natl. Acad. Sci. USA. 1997;94:849–854. doi: 10.1073/pnas.94.3.849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Na S., Collin O., Wang N. Rapid signal transduction in living cells is a unique feature of mechanotransduction. Proc. Natl. Acad. Sci. USA. 2008;105:6626–6631. doi: 10.1073/pnas.0711704105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Raz-Ben Aroush D., Ofer N., Keren K. Actin turnover in lamellipodial fragments. Curr. Biol. 2017;27:2963–2973.e14. doi: 10.1016/j.cub.2017.08.066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Ideses Y., Erukhimovitch V., Bernheim-Groswasser A. Spontaneous buckling of contractile poroelastic actomyosin sheets. Nat. Commun. 2018;9:2461. doi: 10.1038/s41467-018-04829-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Ofer N., Mogilner A., Keren K. Actin disassembly clock determines shape and speed of lamellipodial fragments. Proc. Natl. Acad. Sci. USA. 2011;108:20394–20399. doi: 10.1073/pnas.1105333108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.MacKintosh F.C., Käs J., Janmey P.A. Elasticity of semiflexible biopolymer networks. Phys. Rev. Lett. 1995;75:4425–4428. doi: 10.1103/PhysRevLett.75.4425. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
3D rendering of the AF488-phalloidin-stained actin cytoskeleton in a representative cell as imaged by 3D structured illumination microscopy. Movie shows the rendering rotated around the x and z axes. This video corresponds to Fig. 1 c.
Time-lapse phase contrast and TIRF microscopy movie of the representative cell expressing membrane-localized EGFP-CAAX shown in Fig. 1 f. Time stamp (upper right) is in the format minutes:seconds. Frames were acquired every 3 seconds for 3:21 minutes. Scale bar is 10 microns.
Side-by-side views of phase contrast (magenta, left) and widefield fluorescence microscopy (green, center) of a representative cell whose endoplasmic reticulum is stained with the dye ER Tracker. The right panel shows the two channels merged together. As the wrinkle pattern changes over time, the infiltration of the ER into the lamellipodium follows the wrinkles. Frames were acquired every 4 seconds for 160 seconds. Scale bar is 10 μm. This video corresponds to Fig. S2 e.
Time-lapse phase microscopy movie of a representative cell where wrinkle peaks as detected by our algorithm are continuously overlaid over the movie. Images were acquired with a widefield microscope. Time stamp (upper left) is in the format minutes:seconds. Frames were acquired every 2 seconds for 4 minutes. Scale bar is 10 microns. This video corresponds to Fig. 4 c.