Abstract
Human challenge trials (HCTs) are a potential method to accelerate development of vaccines and therapeutics. However, HCTs for COVID‐19 pose ethical and practical challenges, in part due to the unclear and developing risks. In this article , we introduce an interactive model for exploring some risks of a severe acute respiratory syndrome coronavirus‐2 (SARS‐COV‐2) dosing study, a prerequisite for any COVID‐19 challenge trials. The risk estimates we use are based on a Bayesian evidence synthesis model which can incorporate new data on infection fatality risks (IFRs) to patients, and infer rates of hospitalization. The model estimates individual risk, which we then extrapolate to overall mortality and hospitalization risk in a dosing study. We provide a web tool to explore risk under different study designs. Based on the Bayesian model, IFR for someone between 20 and 30 years of age is 15.1 in 100,000, with a 95% uncertainty interval from 11.8 to 19.2, while risk of hospitalization is 130 per 100,000 (100–160). However, risk will be reduced in an HCT via screening for comorbidities, selecting lower‐risk population, and providing treatment. Accounting for this with stronger assumptions, we project the fatality risk to be as low as 2.5 per 100,000 (1.6–3.9) and the hospitalization risk to be 22.0 per 100,000 (14.0–33.7). We therefore find a 50‐person dosing trial has a 99.74% (99.8–99.9%) chance of no fatalities, and a 98.9% (98.3–99.3%) probability of no cases requiring hospitalization.
Keywords: Bayesian meta‐analysis, COVID‐19, human challenge trial, informed consent, interactive models, risk communication
1. INTRODUCTION
As of February 1, 2021, severe acute respiratory syndrome coronavirus 2 (SARS‐CoV‐2) has led to over 100 million confirmed infections worldwide, and over 2 million deaths. Despite the recent approval of vaccines, McKinsey estimates that global vaccine production will reach 8 billion doses in 2021—and because the vaccines require two doses, this is only enough to vaccinate a bit over half of the global population (Agrawal, Conway, Heller, Sabow, & Tolub, 2020). However, now that vaccines are approved, testing of additional vaccines with large‐scale field trials is difficult and morally fraught. Not only that, but a variety of critical questions are emerging about the extant vaccines, including the effectiveness of single doses, and the effectiveness against novel strains of COVID.
Rapid answers have been, and will continue to be, critical in the management of disease burden and mitigating impacts of COVID‐19. Different paths to producing relevant clinical data exist, but field trials are slow and require large subject populations to discern therapeutic effects (Jamrozik & Selgelid, 2020b), while observational studies of effectiveness are similarly slow, and not randomized. In order to accelerate testing of vaccines, several authors and institutions have proposed intentionally exposing human subjects to SARS‐CoV‐2 to test novel interventions; to this date, nearly 40,000 people have expressed interest in volunteering for this task (1Day Sooner, 2020). Such human challenge trials (HCTs) have been useful in the past (Jamrozik & Selgelid, 2021) to develop vaccines and treatments for other infectious diseases such as malaria, cholera, respiratory syncytial virus (RSV) (Gómez‐Pérez et al., 2015; Roestenberg, Hoogerwerf, Ferreira, Mordmüller, & Yazdanbakhsh, 2018), influenza (Treanor et al., 1999), and dengue fever (Larsen, Whitehead, & Durbin, 2015). While the changing situation has led some to question the need for HCTs, others have defended their usefulness (Turk, 2021). The usefulness is because HCTs can be used to answer a variety of questions (Nguyen et al., 2021), including many not addressed by the availability of current vaccines (Ducarmon, Kuijper, & Olle, 2021; Steuwer, Jamrozik, & Eyal, 2021). However, two ethical problems have been raised which stand in the way of conducting HCTs for SARS‐CoV‐2 infection. First, given lack of rescue therapies and our limited understanding of COVID‐19's risks, it is difficult to weigh the likely impacts of these studies on volunteers against the benefit to society, or to obtain informed consent from volunteers (Palmer & Schuck, 2020). Second, we do not know what viral dose of SARS‐CoV‐2 should be given to volunteers.
To help address both concerns, we developed a model to help assess the risks participants will face in a hypothetical dosing study for COVID‐19, one similar to hVIVO's soon‐to‐be‐launched trial (Turk, 2021). This model uses data from a nonsystematic review of data on COVID‐19 risks (mortality and infection rates) and describes risks for individuals as well as the overall study risk. As both clarification on viral dose and infection risks are essential before starting HCTs, this work can help inform policymakers and potential volunteers about some risks concerning the process of using HCTs to accelerate vaccine and therapeutic development.
2. METHODOLOGY
We developed a three‐component tool to understand and explain the relevant risks. The first component quantifies risk of COVID‐19 mortality by using a Bayesian evidence synthesis model; the second uses that estimate, along with other data on gender‐specific mortality and hospitalization risks to simulate the risk of a study with given characteristics; the third is a front‐end tool for allowing interactive exploration of risks from a study or to an individual.
2.1. Bayesian Evidence Synthesis Model
We use a Bayesian meta‐analysis approach to obtain an estimate of mortality risk. This form of modeling combines different sources of evidence to characterize both mean and dispersion in a given statistic of interest. In our case, we use age‐specific, location‐specific death and prevalence data to generate an estimate of the infection fatality risk (IFR), i.e., the probability that a person infected with COVID‐19 will die, accounting for age; we also provide an estimate of hospitalization risk. These two estimates allow us to understand risk reduction in individuals who would participate in an HCT.
We use Bayesian methods because they allow us to best account for heterogeneity in IFRs across age groups, different countries, and regions. Characterizing this heterogeneity is crucial when our goal is not only characterizing historical data, but also assessing the possible reductions in IFRs. For example, it can be argued that an HCT can use screening and provide medical care to achieve a rate of IFRs which is at least as low as the region or country with the lowest IFRs in our data.1
Although existing statistical packages for meta‐analysis (both Bayesian and frequentist) could easily be used to model event rates such as IFR (Carpenter, 2016; Wiȩcek & Meager, 2020), these models may encounter problems or provide biased results when in a large proportion of studies no deaths are observed, as is sometimes the case for COVID‐19 in younger populations. To address this, we use death data and estimates of prevalence as inputs instead of IFRs, so that the model is generative, following best practice for such models (Betancourt, 2016; Gelman et al., 2020). We then construct a new, reproducible model for IFRs. Methodological details of the model are described in the Appendix.2 Crucially, we assume that the fixed effect of age and random effects of location on IFR are on logistic scale, as is typical for meta‐analysis models of binary data.
While our IFR estimates capture average risks within different age groups and even heterogeneity across regions or countries, they still refer to the general population (of a given age, in a given location). A prospective HCT participant would be screened for health issues and comorbidities, further reducing the risk in comparison to the members of general population. To account for this, we perform an additional analysis using OpenSAFELY (Williamson et al., 2020), a large observational data set on COVID‐19 mortality factors that includes comorbidity and age information, as well as data on gender, comparing the risk in general population to lower‐risk subpopulation.3 Similarly to adjustment for heterogeneity across general populations, the adjustment for screening can be turned on or off in our tool.
Input data for the Bayesian IFR model is based on a nonsystematic review of the literature and earlier meta‐analyses, particularly by Levin, Cochran, and Walsh (2020) but we have also opportunistically included other studies, and data from other official sources as detailed in the Appendix. However, the list of studies is not fixed, since new and better characterized data sets are becoming available over time. For this reason, we have made sure that incorporating additional prevalence and death data from newer studies and/or updated data sets is straightforward. We will continually update the model to assure that any estimates provided to participants or used for decisions include all relevant data, rather than only using data that was available when the analysis was first performed.
We use the age‐ and gender‐specific data from Salje et al. (2020) for the rate of death of hospitalized patients to impute the relative risk of hospitalization based on our meta‐analysis for mortality risk.
Our model is available publicly, together with input data and source code for the tool and under an open license, at https://github.com/1DaySooner/RiskModel (Manheim, Wiecek, Choi, & Wick, 2021).
2.2. Transforming Individual Risk into Study Risk
Once a suitable challenge virus is manufactured, itself a complex process (Catchpole et al., 2018), the risk of the individual from a challenge trial depends on the dose of virus given. The uncertainties about dose–response lead to a number of additional uncertainties about overall study risk. For other viruses, such as H1N1 and H3N2 influenza, a dose–response relationship has been found (Han et al., 2019; Memoli et al., 2015). The specific dose–response relationship, and its functional form must be determined experimentally, which is an outcome rather than an input of a dosing study like the one we are considering.4 This uncertainty is a key issue, so, as suggested by Morgan and Henrion, we advise that this structural uncertainty should not be treated as a probabilistic variable, and instead sensitivity analysis should be used to enable the consideration of a range of plausible outcomes (Morgan, Henrion, & Small, 1990).
Given the specifics of a study design, the relationship between individual risk and the risks in the overall study is straightforward, assuming independence of risk between individuals in the study.5 The risk to an individual of severe disease in the study given dose is , and the risk of mortality is . The probability that someone in a group of size experiences the corresponding outcome is and . By simulating the probability of impact for each dosed group and, in the case of more complex studies, conditioning the trial of later groups on the results of earlier ones, we can find the overall risk in more complex studies.
In the current version, we have restricted the tool to consider to a simple ‐person study. This means the tool provides an upper bound for risk of mortality and hospitalization, higher than in a more complex dose‐escalation study.6 However, the underlying model structure allows simulation of dose‐dependent and/or conditional study designs, as necessary, to accommodate dose–response information and allow for the simulation of more complex trials.
2.3. Interface
The web tool we built allows exploration of two related types of risk. The first allows individuals to explore their personal risk, for example, by gender and age, if they volunteer to participate in a study, while the second displays overall risk of a single round dosing study with a given number of participants. Assumptions on study design and the underlying risk can be adjusted to allow interactive exploration by policymakers and participants. In considering personal risk, the tool uses precalculated outputs from the risk model to calculate and display predictions for hospitalization rate and death rate for individuals as a function of age and sex.
Deaths are further translated into micromorts—the expected number of deaths per million events, a standard method of showing mortality risk often used for patient consent (Ahmad, Peterson, & Torella, 2015; Howard, 1980). Quantities which cannot be transformed into micromorts, are presented as probabilities.7
The tool allows both the public and policymakers to explore how overall risks change depending on differences in study design. This also helps maintain transparency into clinical trial design concerns, thereby better informing potential challenge trial volunteers. We also note that for trial designers and ethicists, the relationship between risk of different impacts and compensation is critical (Blumenthal‐Barby & Ubel, 2020; Grimwade et al., 2020; Palmer & Schuck, 2020).
The importance of transparency and public engagement has been widely noted in the literature on challenge trials (Jamrozik & Selgelid, 2020a). For this reason, the tool is available for public use, and is already being used to inform people who have volunteered to be contacted to potentially participate in a challenge trial (1Day Sooner, 2020).
3. RESULTS
The analysis data set for age‐specific IFRs contains 167 data points from 34 studies, with each containing between 2 and 11 different age groups; all data are presented in Tables 3 and 4 of the Appendix and are included in the code repository accompanying this article. A glance at available data also confirms the necessity of using a more complicated modeling approach: only 37 inputs contain individuals aged between 20 and 30; however, out of these 37, only three cover precisely the main age group of interest, that is, people between 20 and 30 years of age.
The basic evidence synthesis model, which includes all data, but does not adjust for health status, finds that average IFR in 20–29 age group for the studies included in this analysis is 15.1 per 100,000 cases (95% uncertainty interval8 11.8–19.2). Extending the HCT population to include 20–39‐year olds gives mean IFR of 26.5 per 100,000 (95% interval 20.6–33.5).
The model assumes a log‐linear relationship between age and IFR. As seen in Fig. 1, the assumption is met across the entire age range we considered, from children to people older than 80. The model estimates that IFR increases on average 3.06‐fold per each additional decade of age.
Fig 1.
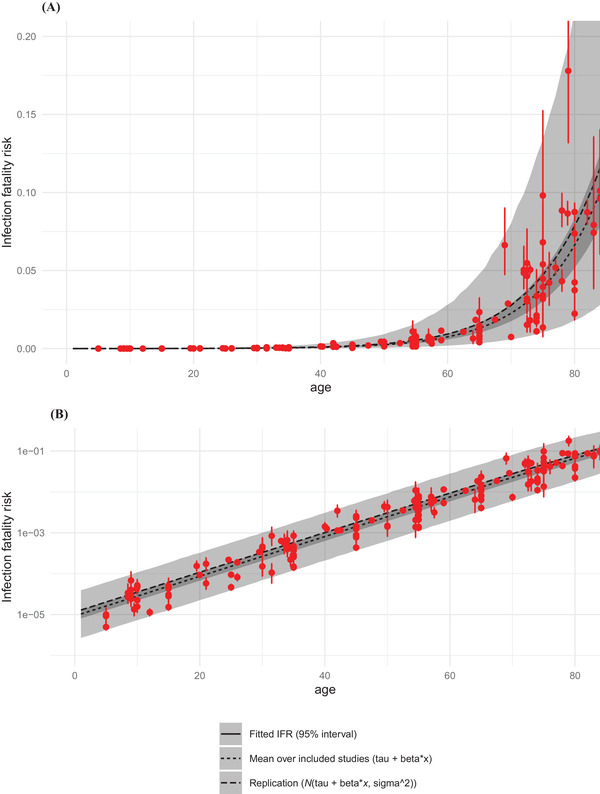
IFR as a function of age. Panel A is untransformed data. Panel B shows the same data on log 10 scale. Red points are data, i.e., model estimates of mean IFRs in particular studies, with bars representing 95% uncertainty intervals. Black and gray are modeled IFRs: lines are means, ribbons are 95% intervals: the narrower is average across all included studies, the wider takes into account heterogeneity between studies. Details and input values are given in the Appendix.
These results align with two recent meta‐analyses of IFRs (Brazeau et al., 2020; O'Driscoll et al., 2021). Both studies also show log‐linear relationships between age and IFR, as well as considerable variation in IFR by context. O'Driscoll et al. report median IFRs of 0.6 and 1.3 per 10,000 among those aged 20–24 and 25–29, respectively, while Brazeau et al. report 3 and 4 per 10,000, respectively.
Based on OpenSAFELY data, we estimate that in healthy population (defined as lack of any comorbidities listed above), the average mortality risk in 20–29‐year olds is 1.9 times lower than in the general population, with 95% interval from 1.3 to 2.8. Expanding to 20–39‐year olds only slightly increases the risk reduction factor, from 1.9 to 2.
We also note that there is large heterogeneity across the studies, due to treatment availability and other factors.9 The HCT volunteer population will receive the best available care, including the most up‐to‐date treatment options. They will also be screened based on socioeconomic and other population risk factors, trading off diversity for safety. For these reasons, we consider the population for an HCT to be akin to a best‐case scenario. In the current analysis, this is France, where the estimated risk for 20–29‐year olds is , approximately the mean risk across all populations.
It is unclear how much double‐counting occurs when adjusting for both available medical care and population screening, and for screening out comorbidities. However, using this estimate, we see that a simple 50‐person challenge trial has a 99.87% probability of having no induced fatalities, and a 98.9% probability of having no cases serious enough to require hospitalization. In other words, the probability of at least one death during a 50‐person trial is 0.13% and the probability of at least one hospitalization is 1.1%. This represents an upper bound of risk for the notional 50‐person trial, since the dosing study will escalate doses until a sufficient number of participants are infected, and therefore not everyone dosed is likely to develop an infection.
While the estimate is specific to a dosing study, it can also be useful for understanding the risk of later vaccine trials, though in that case other factors, including the possibility of vaccine‐enhanced infection, would need to be assessed.
Due to lack of reliable data, the current model does not include estimates of longer‐term impacts, and instead includes a more qualitative discussion of these risks (Smela, Kleinwaks, Sexton, & Schmit, 2020), but the model and interface will be updated with such estimates as they become available. The model interface can be used to explore how these uncertain factors can interact, as shown in Fig. 2.
Fig 2.
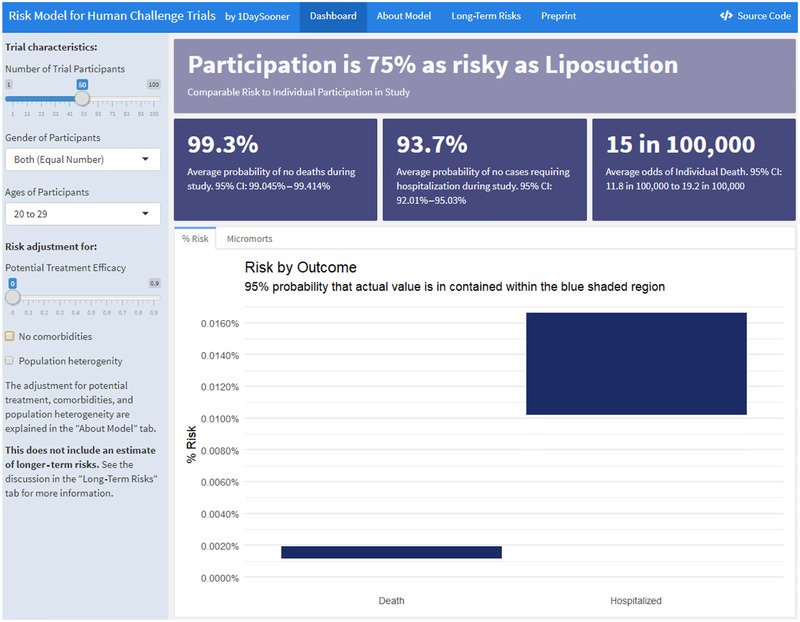
Interactive model interface.
4. DISCUSSION
We have demonstrated that we can model certain risks associated with HCTs. However, our model is incomplete, and considerable concerns remain about the risks of HCTs. While a full accounting of challenge trial ethics is beyond the scope of this article, we consider several factors below that inform our work on HCT design, especially unmodeled risks. For a more complete perspective on the ethics of COVID‐19 HCTs, we direct the reader to the World Health Organizations' (WHO) key considerations (Jamrozik et al., 2020) and the recent discussion in Lancet Infectious Disease (Jamrozik & Selgelid, 2020a; Manheim, 2020) on how these issues are being addressed.
Our model suggests that the risk of a dosage–response study is far lower than other risks that are typically widely viewed as acceptable. The risk for participants selected to be low risk is clearly far lower than the risk in the general population from comparable clinical infections. While modeling the difference between the two is not possible, we are confident that the risk in HCT would indeed be lower than in observational, general population data that we used, due to more intense monitoring and availability of immediate high‐priority medical care and pharmaceutical treatments, which we did not model here. We also note that HCTs have had historical precedent, showing promise for both less lethal human coronaviruses, and for yellow fever (Shah et al., 2017). They also provided early indications regarding the possible efficacy of a leading malaria vaccine candidate (Nielsen et al., 2018). The discussions about earlier trials show that the ethical challenges of HCTs should not be seen as unique, but rather as laying along a natural continuum of clinical studies (Franklin & Grady, 2001). That said, the initial HCTs should be held to high ethical standards, both for individual risks and to preserve public trust in scientific and medical progress. That includes emphasis on fully informed consent of the participants, and, as noted by the WHO, higher than typical ethical standards (Jamrozik et al., 2020).
4.1. Limitations
Our model has a number of limitations. First, hospitalizations and deaths for 20–30‐year olds are rare and may be subject to reporting bias. Second, we do not yet have enough information on long‐term damage caused by COVID‐19 and our model does not currently account for that risk, something we will discuss below. Third, although our model uses hospitalization as a proxy for the upper bound of serious nonfatal COVID‐19 cases, more data are required to see if this is an accurate assumption.
Our model also may not capture changes in COVID‐19 risks over time. It also does not estimate any indirect risks of the study. The model focuses on the risk due to the strain which will be used in an initial challenge trial. The model may not be appropriate for characterizing risk newer variants, including B.117. We stress that our model is not a comprehensive analysis of all available risks, but rather a tool quantifying certain known risks that can be used by trial participants and policymakers. We also limit our investigation to “risk” understood as probability of an event, as it is used in the medical literature (Kelly & Cowling, 2013), rather than a broader and more sociological understanding of risk.
Finally, this model captures only absolute risk. Relative risk assessment, comparing the risk of HCTs to other methods of finding the same information, is not intended. Any relative risk assessment would need to be combined with an assessment of relative benefits of each design, including speed and accuracy, as well as considering the ethical benefits of HCTs like the voluntary nature and better understanding and control of risks due to disease compared to other forms of clinical trials.
4.2. Opportunity Cost
When evaluating clinical trial designs, it is not sufficient to evaluate whether the proposed model is good, or even whether benefits outweigh costs, but also whether the alternatives are better. The key benefit of a dosing study is to allow further research with challenge trials, and alternative clinical trial models have major practical difficulties and far higher costs in a variety of ways. While this is not relevant for the initial set of vaccines that have now been approved, the challenge of conducting large‐scale trials is magnified for later vaccines.
For example, typical clinical phase 3 efficacy trials for an ongoing novel pandemic would be field trials, which rely on high numbers of trial participants, and require that a large number of people are treated with a new vaccine or drug. Such trials are relatively expensive and expose more trial participants to negative side effects of a given treatment, so that in many scenarios HCTs have been shown to be superior (Berry et al., 2020). These trials are also difficult to pursue now that an initial vaccine is available, due to ethical and logistical constraints. At this point, it may not be possible to find enough willing participants for field trials to study additional, potentially more effective or safer, vaccines.
4.3. Nonmodeled Risks
We also note that there are several impacts we do not model in the study, most notably the concern about so‐called “long COVID,” which is a catch‐all term referring to a combination of persistent symptoms, slow recovery, and new postrecovery symptoms (Carfì et al., 2020). It is understood that for some cases, especially severe ones, recovery from COVID‐19 can take months. In other cases, there are longer‐term symptoms differing from those experienced during the infection, perhaps similar to Post‐SARS syndrome (Moldofsky & Patcai, 2011; Perrin et al., 2020). At the same time, COVID‐19 recovery has been found to be faster in younger, healthier patients (Tenforde et al., 2020), which may mean the risk is lower in this group. It seems clear that the risk is a subject of continuing scientific investigation, and as it becomes better understood and quantified, it will be incorporated into both the risk model, and the web tool. Until then, the model contains an embedded overview of what is currently understood and known or unknown about longer‐term risks (Smela et al., 2020).
We also note that vaccine‐induced disease enhancement is a critical concern for vaccine challenge trials, but is not relevant to dosing studies. Still, this risk must be considered in analyses of risks for later trials, and the current model would need to be adapted or supplemented to consider this if it were used to inform decisions regarding those later trials.
5. CONCLUSION
HCTs are not risk‐free, but the balance of risk and benefits seems to clearly favor allowing them, as a large group of experts has argued (Sooner et al., 2020). This conclusion is disputed by some, but all decisions are made despite uncertainties and debate—whether empirical or moral (Lockhart, 2000; MacAskill, Bykvist, & Ord, 2020). The question is whether the both empirical and moral balance of factors lead to the indicated conclusion. The alternative is a failure to act due to misguided risk aversion, or worse, using uncertainty and disputed moral claims as a positive stance to shut down further work, as has occurred in the debate about HCTs (Martinez et al., 2020).
It seems likely that HCTs are a viable way to rapidly test vaccine efficacy, which is particularly critical now for testing second‐generation vaccines, which are important in quickly expanding vaccine availability (Castillo et al., 2021) and may prove superior to first‐generation vaccines. A dosing study is an urgent first step, and the risk estimates and tools developed for this article can assist in planning such studies and informing volunteers.
Our model provides insight into the overall risk of a trial of a given size, and can better inform HCT participants about the dangers they face. Given that an HCT may help select the multiple vaccines necessary for global immunization while also assisting with therapeutic testing, the risk of an initial study into SARS‐CoV‐2 pathogenesis seems justified. If the dosing study is successful, future HCTs of COVID‐19 may provide a rapid and systematic way of screening vaccine candidates for efficacy and safety, which is a significant benefit.
The results presented here are a useful static estimate of risk. The model is already being used to inform potential volunteers (1Day Sooner, 2020) and can be adapted and expanded in the future. Given the evolving understanding of the disease, the model should be continually updated with additional data on mortality and hospitalization risks or other long‐term risks. This will contribute to the discussion of whether or not to pursue challenge trials, which can help with response to COVID‐19 in a variety of ways (Nguyen et al., 2021). Challenge trials may be an important tool for fighting COVID‐19 and our model is a step toward that goal.
Supporting information
Table 1. Main parameters in the sensitivity analysis models using subsets of data.
Figure 3. Comparison of model estimates (black) with data on observed fatality risk (FR, red), compared on logarithmic scale. FR is number of deaths divided by overall population size. Bars are 95% posterior interval; point is the mean. For better clarity, we grouped the plot into four panels according to observed FR X axes on each panel differ. For many low‐risk populations (upper‐left quadrant) no deaths were reported: we indicate this by plotting a red point on the left‐hand side of the panel plot.
Figure 4. IFR as a function of age. Narrower ribbon corresponds to the 95% posterior interval of average across all included studies (tau parameter in the meta‐analysis model), while the wider band takes into account heterogeneity (tau and sigma). Lines are means. Red points are model estimates of mean IFRs in partciular studies, with bars representing 95% posterior intervals. Panel A is untransformed data. Panel B shows the same data on log 10 scale.
Figure 5. Fatality risks as a function of age in OpenSAFELY data. Fatality risk is zero in the 0–10 and 10–20 age groups.
Table 2. Data from the OpenSAFELY database grouped by age.
Figure 6. Comparison of posterior predictive numbers of deaths from the fitted Bayesian model (mean and 95% uncertainty intervals) with data inputs (circles). For each age grouping we have 4 estimates: male/female and healthy vs general population.
Table 3. Complete table of studies used by the meta‐analysis model.
Figure 7. Comparison of model‐estimated prevalences (95% CI's reported by modelling studies) collected by Levin, Cochran, andWalsh (2020) and our distributional assumptions: additional circles show 95% CIs recreated by assuming logit‐normal distribution of prevalence. We group studies into 4 bands of mortality to mirror earlier figures. Please note that this approach produces discrepancies in a number of US estimates where the confidence intervals were skewed toward including 0. However, since we do not have access to source data, we decided to use the logit‐normal assumption for all estimates. This assumption may have an effect of overestimating mortality risk in settings where prevalence was very low.
Table 4. Complete table of inputs used by the meta‐analysis model and crude IFR's.
ACKNOWLEDGEMENTS
Thank you to Rouslan Karimov and Jupiter Adams‐Phipps for validating, updating, and collecting references for the data set used in the analysis. Thanks to Chris Choe, Sophie Rose, Kate Sheahan, Troy Yamaguchi, and Linchuan Zhang, who helped prepare and edit an early version of the article. We would like to thank Ed Choi and William Kahn, as well as two anonymous referees, for providing helpful comments, and Ben Goldacre and the OpenSAFELY team (https://opensafely.org/team/) for sharing data with us.
Footnotes
Since this is only an assumption, rather than a fact which we can derive directly from data, we will present both the overall estimate across studies, or the expected lower risk. Similarly, users of our tool can choose between different assumptions.
| (1) |
| (2) |
| (3) |
| (4) |
The lower‐risk group is defined as nonobese, nonsmoking, and without the following risk factors (following those used by Williamson et al., 2020): asthma, other chronic respiratory disease, chronic heart disease, diabetes mellitus, chronic liver disease, chronic neurological diseases, common autoimmune diseases (rheumatoid arthritis, systemic lupus erythematosus, or psoriasis), solid organ transplant, asplenia, other immunosuppressive conditions, cancer, evidence of reduced kidney function, and raised blood pressure or a diagnosis of hypertension.
There is an assumption implicit in the model that the trial uses dose escalation or other data to ensure that the dose given does not greatly exceed the typical natural dose, or that a larger than natural dose does not increase disease severity.
The assumed independence is conditional on the age and health status of participants, and for dose–response studies, also infection severity by dose.
This is equivalent to assuming that the risk of infection at each dose is above the threshold for infection to replace a dose–response curve.
See discussion below about incorporating other risks in the model as more data become available.
All intervals reported here are Bayesian posterior intervals. For brevity, we just refer to them as “x% interval” or “uncertainty interval” (Gelman, 2010).
Denoting by the hyperscale parameter in the hierarchical model, impact corresponds to 3.96‐fold mean decrease in IFR. That means we expect 2.5% of studies to have IFR more than four times lower than the average IFR.
REFERENCES
- 1Day Sooner . (2020). 1Day Sooner web site. Retrieved from https://1daysooner.org/ [Google Scholar]
- Agrawal, G. , Conway, M. , Heller, J. , Sabow, A. , & Tolub, G. (2020). On pins and needles: Will COVID‐19 vaccines save the world? (Tech. Rep.). Online: McKinsey & Company. https://www.mckinsey.com/~/media/mckinsey/industries/pharmaceuticals%20and%20medical%20products/our%20insights/on%20pins%20and%20needles%20will%20covid%2019%20vaccines%20save%20the%20world/july%202020/on‐pins‐and‐needles‐will‐covid‐19‐vaccines‐save‐the‐world‐v4.pdf. [Google Scholar]
- Ahmad, N. , Peterson, N. , & Torella, F. (2015). The micromort: A unit for comparing and communicating risk to patients. International Journal of Clinical Practice, 69(5), 515–517. [DOI] [PubMed] [Google Scholar]
- Berry Donald A., Berry Scott, Hale Peter, Isakov Leah, Lo Andrew W., Siah Kien Wei, Wong Chi Heem (2020). A cost/benefit analysis of clinical trial designs for COVID‐19 vaccine candidates. PLOS ONE, 15 (12), e0244418 10.1371/journal.pone.0244418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Betancourt, M. (2016). Logic, probability, and Bayesian inference: A conceptual introduction to the foundations of applied inference for scientists and engineers (Tech. Rep.). The Stan Development Team. Retrieved from https://github.com/betanalpha/stan_intro/ [Google Scholar]
- Blumenthal‐Barby, J. , & Ubel, P. (2020). Payment of COVID‐19 challenge trials: Underpayment is a bigger worry than overpayment. Journal of Medical Ethics. doi: 10.1136/medethics‐2020‐106901. Retrieved from https://jme.bmj.com/content/early/2020/10/11/medethics‐2020‐106901 [DOI] [PubMed] [Google Scholar]
- Brazeau, N. , Verity, R. , Jenks, S. , Fu, H. , Whittaker, C. , Winskill, P. , … Okell, L. (2020). Report 34: COVID‐19 infection fatality ratio: Estimates from seroprevalence (Report). Imperial College COVID‐19 response team. 10.25561/83545. Retrieved from http://spiral.imperial.ac.uk/handle/10044/1/83545 [Google Scholar]
- Carfì, A. , Bernabei, R. , Landi, F. , & Against COVID‐19 Post‐Acute Care Study Group ., (2020). Persistent symptoms in patients after acute COVID‐19. JAMA, 324(6), 603–605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carpenter, B. (2016). Hierarchical partial pooling for repeated binary trials. Retrieved from https://mc‐stan.org/users/documentation/case‐studies/pool‐binary‐trials.html [Google Scholar]
- Carpenter, B. , Gelman, A. , Hoffman, M. D. , Lee, D. , Goodrich, B. , Betancourt, M. , … Riddell, A. (2017). Stan: A probabilistic programming language. Journal of Statistical Software, 76(1), 1–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Castillo, J. C. , Ahuja, A. , Athey, S. , Baker, A. , Budish, E. , Chipty, T. , … Wiȩcek, W. (2021). Market design to accelerate COVID‐19 vaccine supply. Science, 10.1126/science.abg0889 [DOI] [PubMed] [Google Scholar]
- Catchpole, A. P. , Fullen, D. J. , Noulin, N. , Mann, A. , Gilbert, A. S. , & Lambkin‐Williams, R. (2018). The manufacturing of human viral challenge agents for use in clinical studies to accelerate the drug development process. BMC Research Notes, 11(1), 1–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ducarmon, Q. R. , Kuijper, E. J. , Olle, B. (2021). Opportunities and Challenges in Development of Live Biotherapeutic Products To Fight Infections. The Journal of Infectious Diseases, 10.1093/infdis/jiaa779. [DOI] [PubMed] [Google Scholar]
- Franklin, G. M. , & Grady, C. (2001). The ethical challenge of infection‐inducing challenge experiments. Clinical Infectious Diseases, 33(7), 1028–1033. [DOI] [PubMed] [Google Scholar]
- Gelman, A. (2010). Instead of “confidence interval,” let's say “uncertainty interval”. Retrieved from https://statmodeling.stat.columbia.edu/2010/12/21/lets_say_uncert
- Gelman, A. , Vehtari, A. , Simpson, D. , Margossian, C. C. , Carpenter, B. , Yao, Y. , … Modrák, M. (2020). Bayesian workflow. arXiv preprint arXiv:2011.01808.
- Gómez‐Pérez, G. P. , Legarda, A. , Muñoz, J. , Sim, B. K. L. , Ballester, M. R. , Dobaño, C. , … Alonso, P. L. (2015). Controlled human malaria infection by intramuscular and direct venous inoculation of cryopreserved Plasmodium falciparum sporozoites in malaria‐naive volunteers: Effect of injection volume and dose on infectivity rates. Malaria Journal, 14(1), 306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grimwade, O. , Savulescu, J. , Giubilini, A. , Oakley, J. , Osowicki, J. , Pollard, A. J. , & Nussberger, A.‐M. (2020). Payment in challenge studies: Ethics, attitudes and a new payment for risk model. Journal of Medical Ethics, 46(12), 815–826. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han, A. , Czajkowski, L. M. , Donaldson, A. , Baus, H. A. , Reed, S. M. , Athota, R. S. , … Memoli, M. J. (2019). A dose‐finding study of a Wild‐type Influenza A (H3N2) virus in a healthy volunteer human challenge model. Clinical Infectious Diseases, 69(12), 2082–2090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howard, R. A. (1980). On making life and death decisions. In Schwing R. C. & W. A. Albers, Jr. (Eds.), Societal risk assessment (pp. 89–113). New York: Springer. [Google Scholar]
- Jamrozik, E. , Littler, K. , Bull, S. , Emerson, C. , Kang, G. , Kapulu, M. , … World Health Organization Working Group for Guidance on Human Challenge Studies in COVID‐19 . (2020). Key criteria for the ethical acceptability of COVID‐19 human challenge studies (Tech. Rep.). Geneva, Switzerland: World Health Organization. [Google Scholar]
- Jamrozik, E. , & Selgelid, M. J. (2020a). COVID‐19 human challenge studies: ethical issues. Lancet Infectious Diseases, 20(8), E198–E203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jamrozik, E. , & Selgelid, M. J. (2020b). Human challenge studies in endemic settings: Ethical and regulatory issues. Cham: Springer Nature. [Google Scholar]
- Jamrozik, E. , & Selgelid, M. J. (2021). History of human challenge studies. Human challenge studies in endemic settings: Ethical and regulatory issues (pp. 9–23). Cham: Springer International Publishing. 10.1007/978-3-030-41480-1_2 [DOI] [Google Scholar]
- Kelly, H. , & Cowling, B. J. (2013). Case fatality: Rate, ratio, or risk? Epidemiology, 24(4), 622–623.Retrieved from https://journals.lww.com/epidem/Fulltext/2013/07000/case_Fatality__Rate,_Ratio,_or_Risk_.23.aspx [DOI] [PubMed] [Google Scholar]
- Larsen, C. P. , Whitehead, S. S. , & Durbin, A. P. (2015). Dengue human infection models to advance dengue vaccine development. Vaccine, 33(50), 7075–7082. [DOI] [PubMed] [Google Scholar]
- Levin, A. T. , Cochran, K. B. , & Walsh, S. P. (2020). Assessing the age specificity of infection fatality rates for COVID‐19: Meta‐analysis & public policy implications (Tech. Rep.). Cambridge, MA: National Bureau of Economic Research. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lockhart, T. (2000). Moral uncertainty and its consequences. New York: Oxford University Press. [Google Scholar]
- MacAskill, W. , Bykvist, K. , & Ord, T. (2020). Moral uncertainty. Oxford: Oxford University Press. [Google Scholar]
- Manheim, D. (2020). Evolving ethics of COVID‐19 challenge trials. Lancet Infectious Diseases. 10.1016/S1473-3099(20)30649-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manheim, D. , Wiecek, W. , Choi, B. , & Wick, T. (2021). https://github.com/1daysooner/riskmodel: Preprint. Retrieved from https://github.com/1DaySooner/RiskModel 10.5281/zenodo.4297248 [DOI]
- Martinez, I. , Manheim, D. , McPartlin, S. , Jewler, L. , Pedersen, K. , Rohrig, A. , … 1DaySooner Research Team . (2020). Incorporating participant preferences and accounting for power imbalances in human challenge trial ethics (tentative title). Journal of Practical Ethics, In Preparation. 10.5281/zenodo.4297248 [DOI] [Google Scholar]
- Memoli, M. J. , Czajkowski, L. , Reed, S. , Athota, R. , Bristol, T. , Proudfoot, K. , … Taubenberger, J. K. (2015). Validation of the wild‐type influenza A human challenge model H1N1pdMIST: An A (H1N1) pdm09 dose‐finding investigational new drug study. Clinical Infectious Diseases, 60(5), 693–702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moldofsky, H. , & Patcai, J. (2011). Chronic widespread musculoskeletal pain, fatigue, depression and disordered sleep in chronic post‐SARS syndrome; a case‐controlled study. BMC Neurology, 11(1), 37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morgan, M. G. , Henrion, M. , & Small, M. (1990). Uncertainty: A guide to dealing with uncertainty in quantitative risk and policy analysis. Cambridge: Cambridge University Press. [Google Scholar]
- Nguyen, L. C. , Bakerlee, C. W. , McKelvey, T. G. , Rose, S. M. , Norman, A. J. , Joseph, N. , … Morrison, J. (2021). Evaluating use cases for human challenge trials in accelerating SARS‐CoV‐2 vaccine development. Clinical Infectious Diseases, 72(4), 710–715.Retrieved from https://academic.oup.com/cid/advance‐article/doi/10.1093/cid/ciaa935/5868014. 10.1093/cid/ciaa935 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nielsen, C. , Vekemans, J. , Lievens, M. , Kester, K. , Regules, J. , & Ockenhouse, C. (2018). RTS, S malaria vaccine efficacy and immunogenicity during Plasmodium falciparum challenge is associated with HLA genotype. Vaccine, 36(12), 1637–1642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O' Driscoll, M. , Dos Santos, G. R. , Wang, L. , Cummings, D. A. T. , Azman, A. S. , Paireau, J. , … Salje, H. (2021). Age‐specific mortality and immunity patterns of SARS‐CoV‐2. Nature, 590, 140–145.Retrieved from https://www.nature.com/articles/s41586‐020‐2918‐0 10.1038/s41586-020-2918-0 [DOI] [PubMed] [Google Scholar]
- Palmer, A. , & Schuck, C. (2020). Establishing informed consent for SARS‐COV‐2 challenge trials (Tech. Rep.). Delaware, US: 1Day Sooner Research Team. https://drive.google.com/file/d/1lsFSBBJ_CFLCSvMZDwB7s_dK28w6cwOW/view [Google Scholar]
- Perrin, R. , Riste, L. , Hann, M. , Walther, A. , Mukherjee, A. , & Heald, A. (2020). Into the looking glass: Post‐viral syndrome post COVID‐19. Medical Hypotheses, 144, 110055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roestenberg, M. , Hoogerwerf, M.‐A. , Ferreira, D. M. , Mordmüller, B. , & Yazdanbakhsh, M. (2018). Experimental infection of human volunteers. Lancet Infectious Diseases, 18(10), e312–e322. [DOI] [PubMed] [Google Scholar]
- Salje, H. , Tran Kiem, C. , Lefrancq, N. , Courtejoie, N. , Bosetti, P. , Paireau, J. , … Cauchemez, S. (2020). Estimating the burden of SARS‐COV‐2 in france. Science, 369(6500), 208–211.Retrieved from https://science.sciencemag.org/content/369/6500/208. 10.1126/science.abc3517 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shah, S. , Kimmelman, J. , Lyerly, A. D. , Lynch, H. F. , McCutchan, F. , Miller, F. , … Zorrilla, C. (2017). Ethical considerations for Zika virus human challenge trials. National Institute of Allergy and Infectious Diseases. [Google Scholar]
- Smela, M. P. , Kleinwaks, G. , Sexton, N. , & Schmit, G. (2020). FAQ: Long‐term effects of COVID‐19. Retrieved from https://1daysooner.org/long‐term‐risks‐faq [Google Scholar]
- Sooner, D. , Aaronson, S. , Ahuja, A. , Anderson, C. , Berger, A. , Caplan, A. , … Wikler, D. (2020). Open letter: Challenge trials for COVID‐19. Retrieved from https://1daysooner.org/openletter
- Steuwer, B. , Jamrozik, E. , & Eyal, N. (2021). Prioritizing between second‐generation SARS‐COV‐2 vaccines through low‐dosage challenge studies. International Journal of Infectious Diseases, 105, 307–311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tenforde, M. W. , Kim, S. S. , Lindsell, C. J. , Rose, E. B. , Shapiro, N. I. , Files, D. C. , … CDC COVID‐19 Response Team. , (2020). Symptom duration and risk factors for delayed return to usual health among outpatients with COVID‐19 in a multistate health care systems network–United States, March–June 2020. Morbidity and Mortality Weekly Report, 69(30), 993–998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Treanor, J. J. , Kotloff, K. , Betts, R. F. , Belshe, R. , Newman, F. , Iacuzio, D. , … Bryant, M. (1999). Evaluation of trivalent, live, cold‐adapted (CAIV‐T) and inactivated (TIV) influenza vaccines in prevention of virus infection and illness following challenge of adults with wild‐type influenza A (H1N1), A (H3N2), and B viruses. Vaccine, 18(9‐10), 899–906. [DOI] [PubMed] [Google Scholar]
- Turk, V. (2021). The UK is infecting people with COVID‐19 for science. Is it worth it? Retrieved from https://www.wired.co.uk/article/covid‐..‐uk‐challenge‐trial‐vaccines [Google Scholar]
- Wiȩcek, W. & Meager, R. (2020, May). baggr: Bayesian Aggregate Treatment Effects package. Zenodo. Retrieved from https://zenodo.org/record/3813443 10.5281/zenodo.3813443 [DOI] [Google Scholar]
- Williamson, E. J. , Walker, A. J. , Bhaskaran, K. , Bacon, S. , Bates, C. , Morton, C. E. , … Goldacre, B. (2020). Factors associated with COVID‐19‐related death using OpenSAFELY. Nature, 584(7821), 430–436.Retrieved from https://www.nature.com/articles/s41586‐020‐2521‐4. 10.1038/s41586-020-2521-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Table 1. Main parameters in the sensitivity analysis models using subsets of data.
Figure 3. Comparison of model estimates (black) with data on observed fatality risk (FR, red), compared on logarithmic scale. FR is number of deaths divided by overall population size. Bars are 95% posterior interval; point is the mean. For better clarity, we grouped the plot into four panels according to observed FR X axes on each panel differ. For many low‐risk populations (upper‐left quadrant) no deaths were reported: we indicate this by plotting a red point on the left‐hand side of the panel plot.
Figure 4. IFR as a function of age. Narrower ribbon corresponds to the 95% posterior interval of average across all included studies (tau parameter in the meta‐analysis model), while the wider band takes into account heterogeneity (tau and sigma). Lines are means. Red points are model estimates of mean IFRs in partciular studies, with bars representing 95% posterior intervals. Panel A is untransformed data. Panel B shows the same data on log 10 scale.
Figure 5. Fatality risks as a function of age in OpenSAFELY data. Fatality risk is zero in the 0–10 and 10–20 age groups.
Table 2. Data from the OpenSAFELY database grouped by age.
Figure 6. Comparison of posterior predictive numbers of deaths from the fitted Bayesian model (mean and 95% uncertainty intervals) with data inputs (circles). For each age grouping we have 4 estimates: male/female and healthy vs general population.
Table 3. Complete table of studies used by the meta‐analysis model.
Figure 7. Comparison of model‐estimated prevalences (95% CI's reported by modelling studies) collected by Levin, Cochran, andWalsh (2020) and our distributional assumptions: additional circles show 95% CIs recreated by assuming logit‐normal distribution of prevalence. We group studies into 4 bands of mortality to mirror earlier figures. Please note that this approach produces discrepancies in a number of US estimates where the confidence intervals were skewed toward including 0. However, since we do not have access to source data, we decided to use the logit‐normal assumption for all estimates. This assumption may have an effect of overestimating mortality risk in settings where prevalence was very low.
Table 4. Complete table of inputs used by the meta‐analysis model and crude IFR's.


