Additive CHARMM36 Force Field for Nonstandard Amino Acids

Abstract

Nonstandard amino acids are both abundant in nature, where they play a key role in various cellular processes, and can be synthesized in laboratories, for example, for the manufacture of a range of pharmaceutical agents. In this work we have extended the additive all-atom CHARMM36 and CHARMM General force field (CGenFF) to a large set of 333 nonstandard amino acids. These include both amino acids with nonstandard side chains, such as post translationally modified and artificial amino acids as well as amino acids with modified backbone groups, such as chromophores composed of several amino acids. Model compounds representative of the nonstandard amino acids were parametrized for protonation states that are likely at the physiological pH of 7 and, for some more common residues, in both D- and L-stereoisomers. Considering all protonation, tautomeric, and stereoisomeric forms, a total of 406 nonstandard amino acids were parametrized. Emphasis was placed on the quality of both intra- and intermolecular parameters. Partial charges were derived using quantum mechanical (QM) data on model compound dipole moments, electrostatic potentials, and interactions with water. Optimization of all intramolecular parameters, including torsion angle parameters, was performed against information from QM adiabatic potential energy surface (PES) scans. Special emphasis was put on the quality of terms corresponding to PES around rotatable dihedral angles. Validation of the force field was based on molecular dynamics simulations of 20 protein complexes containing different nonstandard amino acids. Overall, the presented parameters will allow for computational studies of a wide range of proteins containing nonstandard amino acids, including natural and artificial residues.

Graphical Abstract

Introduction

Proteins are built from amino acids that are mostly incorporated biosynthetically into proteins during translation. The side chains of amino acids, defined by their distinct chemical characteristics, compose binding interfaces for partners in macromolecular complexes, create ligand binding sites, and assist chemical reactions occurring in enzyme catalytic sites. There are 20 amino acids in the standard genetic code and two additional amino acids that can be incorporated by special translation mechanisms.^1,2 Apart from these amino acids, however, there are many more nonstandard amino acids that are produced as a result of post-translational modifications (PTMs) in the cell, or can be synthesized and incorporated in laboratories.^3,4 PTMs of proteins significantly expand the chemical space, increase the complexity of the proteome, and play an important role in a wide range of functions in the cell.^5,6 PTMs not only can be incorporated by enzymes but also can arise as a consequence of oxidative stress.⁷ Beyond natural ways of nonstandard amino acid incorporation, there has been a remarkable advance in the synthesis of nonstandard amino acids with novel characteristics and their incorporation into proteins.^3,8 Site-specific incorporation of nonstandard amino acids has been used to study protein structure, dynamics, and function by unique IR, X-ray, and fluorescent probes.^3,8 Furthermore, incorporation of nonstandard amino acids opened the door to novel biomaterials, enzymes,⁹ and therapeutics.^10,11

Molecular mechanics (MM) based simulation methods have become the most popular computational techniques for computational studies of biomolecular systems owing the system size and time-scale that can be accessed.^12,13 The major requirement for such computer simulations is the existence of a MM force field that defines the energies and forces acting on the molecular system. As such, the MM force field largely dictates the quality of these atomistic simulations. A number of force fields for nonstandard amino acids were derived previously and tools for the development of such force fields were reported.^14,15 AMBER parameters for 32 frequently occurring post-translational modifications were derived¹⁶ which were later extended to include 147 noncanonical amino acids. Petrov et al. developed force field parameters for 256 different types of PTMs compatible with the GROMOS force field,¹⁷ and later provided a web tool to incorporate PTMs into a 3D protein structure.¹⁸ For the additive CHARMM force field a number of nonstandard amino acids were parametrized specifically in previous works.^19–21 17 artificial amino acids were parametrized in our previous work.¹⁵ CHARMM compatible topologies were created for 210 nonstandard alpha amino acid side chains²² and were made available as an online service.²³ The set of the nonstandard amino acids included only amino acids that differ from the canonical amino acids by modifications in the side chains. These topologies and parameters for unknown functional groups were generated using the SwissParam web service,²⁴ which provides topologies based on the Merck molecular force field (MMFF).²⁵ However, no optimization of parameters was performed and the force field model is incompatible with the additive all-atom CHARMM36 force field.

The present study represents a systematic extension of the CHARMM36 additive force field to nonstandard amino acids,^26–29 also representing an extension of the additive CHARMM General Force Field (CGenFF) for small molecules.³⁰ The force field parameters, including charges and intramolecular parameters, were derived for the physiologically important protonation states and are of similar quality to those for the standard amino acids. The parametrization method is based on the same protocol that is used to derive the CGenFF force field. The parametrization was done against quantum mechanical (QM) data, with a special emphasis on the dihedral terms corresponding to rotatable torsions. Results from MD simulations with the developed parameters of protein complexes containing nonstandard amino acids were then compared to the experimental structures for validation. To summarize, the extension of the CHARMM36 (C36) force field developed in this work is suitable to investigate interactions of nonstandard amino acids in the context of proteins.

METHODS AND MATERIALS

CHARMM potential energy function

The potential energy function of the non-polarizable all-atom CHARMM force field was adopted in this work for nonstandard amino acids.¹² This potential energy function is used for the remainder of the CHARMM36/CGenFF force field. The CHARMM potential energy is:

$$U=U_{\mathit{\text{inter}}}+U_{\mathit{\text{intra}}}$$ [Eq 1]

The intermolecular or non-bonded energy is due to electrostatic and van der Waals (vdW) interactions:

$$U_{\mathit{\text{inter}}}=\sum _{\begin{array}{c}\mathit{\text{nonbonded}}\\ \mathit{\text{elec}}\end{array}}\frac{q_i{q}_j}{4\pi {\epsilon }_0 r_{ij}}+\sum _{\begin{array}{c}\mathit{\text{nonbonded}}\\ vdW\end{array}}{\epsilon }_{ij}\left({\left(\frac{R_{min,ij}}{r_{ij}}\right)}^{12}-2{\left(\frac{R_{min,ij}}{r_{ij}}\right)}^6\right)$$ [Eq 2]

The electrostatic term is described by Coulomb’s law with q_i and q_j being the respective partial atomic charges on atoms i and j, and r_ij is the distance between atoms i and j. The vdW term is treated by the Lennard-Jones (LJ) 6–12 potential in which ε_ij is the well depth, R_min,ij is the radius at which the LJ potential has a minimum. In the additive CHARMM force field, the LJ parameters for pairs of atoms i and j are constructed using the Lorentz-Berthelot combination rule.³¹

$${\epsilon }_{ij}=\sqrt{{\epsilon }_i{\epsilon }_j} \text{and }{R}_{ij}=\frac{R_i+R_j}{2}$$ [Eq 3]

The intramolecular or bonded part of the potential energy function in Equation 1 is contributed by terms for the bonds, valence angles, dihedral angles, improper dihedral angles, and selected Urey–Bradley terms. In addition, the bonded energy function has been extended to include the CMAP cross-term applied to improve the conformational properties associated with the ϕ and ψ torsion angles of the peptide backbone. The intramolecular part is given by:

$$U_{\mathit{\text{intra}}}=\sum _{\mathit{\text{bonds}}}{K}_b{\left(b-b_0\right)}^2+\sum _{\mathit{\text{angles}}}{K}_{\theta }{\left(\theta -{\theta }_0\right)}^2+\sum _{\mathit{\text{Urey}}-\mathit{\text{Bradley}}}{K}_{UB}{\left(r_{1-3}-r_{1-3;0}\right)}^2+\sum _{\mathit{\text{dihedral}}}\sum _{n=1}^N{K}_n \left(1+\text{cos}\left(n\phi -{\delta }_n\right)\right)+\sum _{\mathit{\text{improper}}}{K}_{\phi }{\left(\phi -{\phi }_0\right)}^2+\mathit{\text{CMAP}}$$ [Eq 4]

where b₀, θ₀, r_1−3;0, and φ₀ are the bond, angle, Urey–Bradley, and improper dihedral angle equilibrium values, respectively; the K’s are the force constants; and n and δn are the dihedral multiplicity and phase. A dihedral term is represented as a Fourier series with N number of multiplicities, and the CMAP term is a special grid-based dihedral correction map applied to the protein backbone.²⁷ The current CHARMM force field uses less than seven multiplicities (N<7) for a dihedral term with only two possible values for phases: 0° or 180°. An improper dihedral angle is defined between four atoms, but in contrast to the dihedral angle, three of the atoms are bonded to the central atom and in the CHARMM force field φ₀ is typically set to zero.

Parametrization Protocol

The atom types were adapted from CGenFF.³⁰ The ParamChem web server (https://cgenff.umaryland.edu/) was used to assign existing atomic types and to obtain initial guesses of the partial atomic charges and bonded parameters for the model compounds.^32,33 Partial charges that were assigned a zero penalty by ParamChem, i.e., already optimized in CGenFF, were not considered for optimization in the present study with the exception of selected zero-penalty atoms covalently-linked to high-penalty atoms. Parameters of the LJ potential were taken from the CGenFF force field and were not further optimized in this work. We use the atom names from the Protein Data Bank for non-hydrogen atoms in residues, which itself uses the convention defined in the PDB Chemical Component Dictionary (CCD).^34,35 The atom names for hydrogens were assigned according to the parent heavy atom to which they are bonded. The parametrization protocol is shown in Figure 1.

Figure 1.

Workflow of force field parametrization. For anionic species, the MP2/6–311G(d) model chemistry was used for optimization and potential energy surface (PES) scans of the compounds.

Given a model compound, the protocol starts by defining bonded parameters that need to be optimized for this molecule. These parameters are those that do not explicitly exist in CGenFF, but are assigned based on analogy with known CGenFF parameters by the CGenFF program (see below). The initial geometry for the model compound is constructed using the available PDB coordinates for the corresponding nonstandard amino acid and by adding protons using the Babel software.³⁶ The geometry is further optimized at the MP2/6–31G(d) model chemistry, or MP2/6–311G(d) model chemistry for anionic molecules. The resulting QM geometry is then used to optimize atomic charges as described below. The MM model with optimized charges is used to optimize bonded terms in the next step. Adiabatic potential energy scans with QM, discussed in detail below, are performed along the degrees of freedom for high-penalty parameters, which are those not explicitly present in CGenFF. Those bonded parameters are optimized to minimize differences between QM and MM geometries and potential energy surfaces. In this work, we first optimized terms associated with dihedral angles including soft dihedral angles, along which large conformational fluctuations are possible; then bonded terms associated with other degrees of freedom were adjusted. The steps were repeated iteratively at least two times, and the optimization was stopped when no significant improvement was obtained in further iterations.

Choice of atom types and model compounds

The nonstandard amino acids parametrized in this work represent a broad and heterogeneous set of molecules. The set of nonstandard amino acids was divided into two groups of residues depending on the need to parametrize the backbone group. For the residues of the first group the backbone atom types and associated parameters from the C36 force field are used, while the side chains up to the Cβ atom have CGenFF atom types. The terms corresponding to the bond Cα-Cβ between the backbone group and side chain have both CGenFF and C36 atom types. This allows the use of well-developed parameters from the C36 force field for the backbone of these residues including the CMAP term. The amino acids with backbone groups different from the backbone of the standard amino acids have CGenFF atom types and parameters for all atoms of the nonstandard amino acid. For the residues in this group the bonded terms corresponding to the peptide bonds between the nonstandard residues and neighboring residues have both CGenFF and C36 atom types as represented in Figure S1. The CMAP term was not included for this class of residues; however, all dihedral angles including those associated with the backbone atoms were carefully parametrized using potential energy surface (PES) scans.

Charges and bonded parameters for nonstandard amino acids were optimized using model compounds. In the charge optimization for amino acids with the standard backbone atom types, the model compound included the side chain group up to Cα or Cβ to parametrize the bonded terms associated with the side chain. However, if it was possible, smaller compounds were used, and several compounds were included for large side chains. Such amino acids were further broken down into several parts with the cleavage sites chosen between two acyclic saturated carbons. A proton was added to the acyclic saturated carbon of the cleavage site to complete the chemical structure of the model compound. All the nonstandard amino acids and the associated model compounds are presented in the Supporting Information. For the bonded terms of the amino acids with the standard backbone group, the torsion terms corresponding to the rotation around the bond Cα-Cβ (χ1) were optimized using dipeptides as model compounds, which represented a modified residue with acetylated N-terminus and N-methylamide C-terminus. Dihedral angles φ and ψ of the backbone were constrained to −60° and −45°, respectively, corresponding to the ideal values in an α-helix. For nonstandard amino acids with backbone groups different from the standard backbone, tetrapeptides were used to optimize the parameters corresponding to the peptide bonds between the nonstandard residues and neighboring residues. The tetrapeptides had the sequence ALA-X-ALA with acetylated N-terminus and N-methylamide C-terminus, where X is a nonstandard amino acid, with the backbone groups of the flanking residues constrained to the ideal α-helix geometry.

Determination of the intermolecular force field parameters

The intermolecular energy is due to Coulomb and LJ terms. Consistent with the development of the CHARMM force field, atomic charges were optimized targeting interactions between the model compound and individual water molecules, and the dipole moment of the model compound. Quantum mechanical electrostatic potentials (ESP) have also been used as additional target data in the charge fitting similar to the other work.³⁷ However, the weighting of the ESPs was smaller than that used for water interactions (see below). The charge optimization was performed on the compound structures optimized with the MP2 level of theory³⁸ and 6–31G(d) basis set³⁹ and 6–311G(d) for anionic molecules. Gaussian09⁴⁰ was used for all QM calculations. All QM optimizations were performed to default tight tolerances. Since optimization is performed in vacuum, for model compounds containing carboxylic acid and amine fragments, and that can exist in zwitterionic forms in aqueous solvent, the distance between protons on the amine group and the amine nitrogen was constrained to prevent protonation of the carboxylic group by proton transfer from the protonated amine group.

Atoms of the model compound that can participate in hydrogen bonds were probed by individual water molecules placed in idealized linear orientations.²⁶ Different orientations of the water molecule were considered around the interaction axis: the complex was calculated every 45° or 90° of the water probe rotation for polar atoms, and one or two orientations for non-polar atoms. All model compound-water interaction orientations are presented in the Supporting Information. Each water-model compound complex was optimized by varying the interaction distance between the water and the model compound with the monomer geometries fixed to find the minimum interaction energy distance. The QM-optimized gas-phase geometry was used for the model compounds as described above, and TIP3P model geometry for the water molecule. The angle defining the orientation of the water molecule around the interacting axis was held fixed during the optimization. The interaction energy was calculated for the minimum interaction energy distance. Calculations were done at the HF/6–31G(d) level.^26,30 Following the CHARMM standard protocol, the ab initio interaction energies were scaled (made more favorable) by an empirical factor of 1.16 only for neutral polar compounds and the HF/6–31G(d) minimum interaction distance was corrected by subtracting 0.2 Å for all polar interactions involving neutral compounds.²⁶ In the case of sulfur atoms, the model compound-water interactions were calculated at the MP2/6–31G(d) level including the basis set superposition error (BSSE) correction of Boys and Bernardi⁴¹ and without applying standard scaling and offset rules.

The molecular dipole moment, which is defined by the charge distribution, was used to provide additional target data for the optimization of the atomic charges. The dipole moment was included only for the neutral compounds in the charge fitting.⁴² The dipole moment was calculated in vacuum at the MP2/6–31G(d) model chemistry using the QM-optimized conformation.³⁰ Following the standard CHARMM protocol, to account for the molecular polarizability implicitly, the MM optimization targeted dipole moments increased by 30% with respect to the QM values.³⁰ Both the magnitude and direction of the dipole moment were targeted.⁴²

QM water interaction data may not be sufficient to define partial charges on all atoms for large compounds, since only water interactions with a few hydrogen-bond donors and acceptors at the molecular surface are probed. Therefore, ESP calculations were performed at the MP2/6–31G(d) model chemistry and at MP2/6–311G(d) for anions,³⁷ with the resulting ESPs used in the charge optimization to facilitate the determination of charges on atoms not involved in hydrogen bond interactions with water. At each iteration during the charge optimization, the root mean square deviation (RMSD) between QM and MM ESPs was evaluated and added with the corresponding weight to the target function. However, the weight for the ESPs (the corresponding weight: 1.0 kcal⁻¹·mol·Å) was kept small relative to the weights for water-interaction (10.0 kcal⁻¹·mol) and dipole moment contributions (3.0 D⁻¹), as the reproduction of water-compound interaction energies and geometries is important to balance the solvent-solvent, solvent-solute, and solute-solute interactions.

The charge optimization was performed with the C++ program that was used to parametrize a large number of modified nucleotides in our previous work.⁴² The following terms were included with different weights in the target function: the RMS deviation between empirical and ab initio minimum interaction energies, the RMS deviation between ab initio and empirical minimum interaction distances, the absolute difference between the norms of the empirical and ab initio dipole moments, the angle between the empirical and ab initio dipole moments, the RMS deviation between ab initio and empirical ESPs, and a term associated with restraints on the charges. The latter term was introduced to prevent large deviations from the starting guess for the charges. Charges of symmetrical atoms had identical values during the charge optimization. The initial partial charges were obtained from the ParamChem online server (https://cgenff.umaryland.edu/). Charges that were already optimized in CGenFF, for example for benzene, were not further adjusted in this work. Charges of aliphatic hydrogen atoms were not optimized, in accord with the standard CHARMM method with aliphatic hydrogen atoms having a charge of +0.09e. The LJ parameters were not considered for optimization. For seven complex model compounds two local minimum geometries were used simultaneously in charge fitting. In each geometry different hydrogen-bond sites were probed by water interactions, which are not accessible in the other geometry due to interactions with other groups of the compound.

Optimization of flexible dihedral parameters

Dihedrals within a molecule can be classed in two groups, soft or rotatable versus stiff or non-rotatable. PES associated with non-rotatable dihedrals (e.g., dihedral angles about double bonds or in ring systems) are typically characterized by a single minimum and high energy for small deformations. Rotatable dihedrals have a shallow energy surface with relative small barriers between minima and, thus, may undergo large fluctuations during simulations. Since the molecule can undergo large conformational motions along rotatable dihedrals, accurate treatment of these dihedral terms is paramount. Each compound has 1 to N, {χ_i}, rotatable dihedrals. To parametrize these terms adiabatic PES scans were performed for each torsion, χ_k, in which the torsion angle was scanned in the range from −180° to 180° in 10° increments. During these scan calculations, the compound was energetically optimized along all degrees of freedom, except for the soft dihedral angles. The scanned soft dihedral χ_k was constrained to the target value, while all other soft dihedrals {χ_{i ≠ k}} were constrained to the values corresponding to the minimum energy geometry of the model compound. QM calculations were performed at the MP2/6–31G(d) model chemistry (MP2/6–311G(d) for anions). Each conformation for the MM calculations was extracted from the QM scan and minimized with a harmonic restraint with the force constant of 5·10⁴ kcal·mol⁻¹·radian⁻² on the target torsion. All other rotatable dihedrals were restrained with the same force constant to the values corresponding to the minimum energy geometry. Using these dihedral restraints, we ensure that the QM and MM structures for each dihedral PES scan are close to each other, i.e. that we compare the same region on QM and MM PES surfaces. The dihedral parameters were optimized to achieve a minimum deviation between the QM and MM surfaces only in the low-energy regions with energies <10 kcal·mol⁻¹ above the minimum energy.

Optimization of bonded harmonic energy terms

Parameters for the intramolecular terms described by harmonic potentials; bonds, valence angles, Urey‐Bradley terms, and improper dihedrals, as well as non-rotatable dihedral angles were optimized using the following protocol. The initial guess for force constants was provided by the ParamChem online server as described above. The initial equilibrium values for bonds, valence angles, and Urey-Bradley distances were taken directly from MP2/6–31G(d) geometries (MP2/6–311G(d) for anions). Only parameters with the ParamChem penalty >10 were considered for optimization. The equilibrium angle for improper terms was set to zero and was not optimized. An adiabatic PES scan for each degree of freedom that has adjustable parameters in the force field was performed. The same method was also used in CGenFF to determine force constants by three-point PES scans, when the assignment of contributions of the internal coordinates to the vibrations was ambiguous.^42,43 During the PES scans performed by varying one stiff degree of freedom the potential energy may become very high, even for relatively small deformations. Such high-energy regions of PES are not sampled during typical MD simulations. To ensure that only relevant regions of PES are parametrized we use the method from our previous work⁴⁴ to limit deformations and corresponding energies. In this method using initial values for distortions, force constants of energy terms are estimated. The initial values for the distortions are then corrected using the following equation:

$$\Delta x\text{'}=\sqrt{2 \Delta E_{max}/k},$$ [Eq 5]

where k = 2 (E(Δx) − E₀) / Δx². Δ and Δx′ are the initial and adjusted maximum distortions, respectively; E₀ and E(Δx) are the minimum energy and energy of the deformed structure. ΔE_max defines the highest energy on scanned PES. To optimize each bonded term seven points were used on PES equally spaced in the range of x ∈ [x₀ − Δx′, x₀ + Δx′], including the minimum energy structure at x = x₀. 2.0 kcal·mol⁻¹ was used for ΔE_max in Equation 5. All PES scans were performed at the MP2/6–31G(d) model chemistry and MP2/6–311G(d) for anions.

The equilibrium values of the MM parameters and force constants were adjusted simultaneously using a C++ program based on the Powell minimization algorithms from Numerical Recipes.⁴⁵ Each conformation for the MM calculation was extracted from the QM scan and minimized with a harmonic restraint force constant of 5·10⁴ kcal·mol⁻¹·Å⁻² or 5·10⁴ kcal·mol⁻¹·radian⁻² on the target bond and valence angle, respectively. At each optimization iteration of bonded parameters, PES adiabatic scans were performed with CHARMM using a new set of MM parameters. The target function included RMS deviation between QM and empirical PES energies; QM and MM geometries; and restraints to the initial set of parameters provided by the ParamChem server. In addition, the weighted RMS deviation between Cartesian components of QM and CHARMM forces was added to the target function. The MM parameters were adjusted until the target function could not be reduced further. MM calculations were performed with the CHARMM program.⁴⁶

Molecular Dynamics simulations

To evaluate the quality of the force field model for nonstandard amino acids, molecular dynamics (MD) simulations of 20 protein complexes were performed. The protein complexes are summarized in Table S1. The crystal structures with a high to medium resolution were retrieved from the Protein Data Bank (PDB). Each system contained all protein residues for small and medium size proteins and a spherical truncated model centered on the modified residue was used for large protein complexes. Protonation states of residues were assigned using PROPKA,^47,48 while protonation states of histidines were assigned by visual inspection and ideal stereochemistry. In addition to crystal waters, a cubic box of water was overlaid and waters overlapping the protein and crystal water molecules were removed based on a minimum distance of 3.5 Å between non-hydrogen atoms. The size of the water box was chosen so that the shortest distance between protein atoms and the box edges was 10 Å. Periodic boundary conditions were assumed and all long range electrostatic interactions were computed efficiently by the particle mesh Ewald method⁴⁹ using a real-space cutoff of 11 Å. The appropriate number of potassium or chloride counterions was included to render the system electrically neutral. A smooth switching function was used to truncate all van der Waals interactions at the distance of 11 Å. Long range electrostatic forces were evaluated every 4 steps, while short-range non-bonded interactions were computed at each step. MD simulations were performed at constant room temperature and pressure, after 200 ps of thermalization. Constant pressure was maintained using the Berendsen pressure bath coupling⁵⁰ with the relaxation of 500 fs, the compressibility parameter of liquid water. Constant temperature was maintained by coupling to a heat bath with a room temperature by correcting forces as implemented in the NAMD program.⁵¹ For truncated protein systems, the simulation setup was similar to previous studies.^52,53 In brief, the simulations included protein residues within a 24 Å sphere around the nonstandard amino acid. Protein atoms between 20 and 24 Å from the sphere’s center were harmonically restrained to their experimentally determined positions. The CHARMM36m force field was used for the protein^28,37 and the TIP3P model for water.^26,54,55 The nonstandard amino acid was modeled using the force field parameters specifically developed in this work. Calculations were done with the NAMD program running on GPUs for efficiency.⁵¹ MD simulations of the protein complexes were continued for 100 nanoseconds.

Results and Discussion

Set of parametrized molecules

In this work a total of 333 nonstandard amino acids were parametrized. Chemical structures and amino acid names are given in Figure S2 and Table S2 in Supporting Information. This set of residues includes 198 amino acids from the SwissSidechain database of nonstandard amino acids.²³ In addition, another 134 frequent nonstandard amino acids were considered, including 42 nonstandard amino acids with modified backbone moieties. The D- and L- stereoisomers were considered for 61 residues. To designate D-stereoisomers, the letter D was added at the beginning of three letter code of the residue. The pK_a’s and tautomeric states were predicted with MarvinSketch software version 19.19.⁵⁶ The most important protonation and tautomeric states at the physiological pH of 7 were considered. We use the three letter code for deprotonated forms of residues and the four letter code with the letter P at the end to designate the protonated form. These residues are: TPQ (TPQP), PHD (PHDP), MHS (MHSP), LLP (LLPP), IT1 (IT1P), HIC (HICP), DDE (DDEP), CYQ (CYQP), CGU (CGUP), and GGB (GGBP). For 2-fluoro-L-histidine (residue name: 2HF), two tautomeric forms were considered for the neutral state: protonated on Nε and protonated on Nδ, named 2HFE and 2HFD, respectively. Four amino acids, AYA, CXM, FME, and PR4 are present at the N-terminus as they appear in the PDB structures only in N-termini. Two residues, C2N and FLA, are present in the force field model only as standalone ligands as they are not present in polypeptides in the PDB. The set of amino acids with the standard C36 backbone group includes 358 residues and the set of amino acids with nonstandard backbone groups includes 42 residues. Overall, considering all protonation, tautomeric, and stereoisomeric forms, 406 nonstandard amino acids were parametrized based on a total of 188 model compounds.

Charge optimization

The CHARMM partial charges were derived targeting water-compound interactions, the dipole moment magnitude and its orientation, and ESP. The amino acids were broken down into smaller compounds as described in the Methods section, giving 188 model compounds that were not previously optimized in the CGenFF force field and required charge optimization. The model compounds include 52 ionized compounds and 136 neutral compounds. Atomic charges of these molecules were further optimized. One QM minimum-energy geometry was considered for 181 model compounds and two local-minimum geometries were considered for seven complex molecules. A total of 3857 monohydrate probe water-model compound interaction complexes were used as target data as explained in Methods. This includes 906 probe water-model compound interactions for ionized and 2951 for neutral compounds.

Figure 2 compares QM and MM interactions energies. The statistics for water-compound interactions for all compounds is given in Table 1. Empirical and ab initio interaction energies and distances are given in Table S3–S678 in Supplementary Information. The RMS deviation for interaction energies with the initial ParamChem and optimized charges is 1.79 kcal·mol⁻¹ and 0.46 kcal·mol⁻¹, respectively, while the mean absolute error (MAE) is 0.95 kcal·mol⁻¹ and 0.32 kcal·mol⁻¹, respectively. In this work, several probe water orientations were considered for a compound atom that can participate in H-bonds, in contrast to the C36 force field where usually one interaction was considered to probe each atomic site in the molecule. Some of these orientations have much higher interaction energies due to interactions with other groups in the molecule, and are more difficult to reproduce by the simple additive form of the force field. This explains why the RMS deviation between QM and MM interaction energies of 0.46 kcal·mol⁻¹ obtained in this work is slightly higher relative to 0.34 kcal·mol⁻¹.reported for the CGenFF force field.³⁰ The initial ParamChem charges assigned by analogy systematically overestimate interaction energies with probe water molecules in Figure 2 by 6%. However, with ParamChem charges interactions can be significantly underestimated or overestimated as demonstrated in Figure 2, if the analogous groups are not available in CGenFF. The slope for the interaction energies computed with both the initial guess and optimal charges is close to one, demonstrating that the force field model can reproduce solvent interactions for a wide range of the nonstandard amino acids. The RMS deviation for minimum-energy interaction distances is 0.28 Å with the initial ParamChem guess, which decreased to 0.16 Å with the optimized atomic charges. The agreement for interaction distances is comparable to that previously reported for CGenFF with the distance RMS deviation of 0.20 Å.³⁰

Figure 2.

Corrected QM and CHARMM water interaction energies for the compound-water monohydrates. A) The CHARMM energies were computed using the initial ParamChem charges and B) the optimized atomic charges. C) and D) Percentage of water interactions vs energy deviation in A) and B), respectively. Interaction energies are shown in red and black for ionized and neutral compounds, respectively. The linear regression line between QM and CHARMM data is shown by the solid line. The diagonal dashed lines represent deviations of ±1.0 kcal·mol⁻¹ from the regression line.

Table 1.

Statistics for intermolecular parameter development and agreement with respect to selected target data for all model compounds used to parametrize nonstandard amino acids.

Property	N points	RMSD	MAE
		optimal/initial	optimal/initial
anorm of μ	141	0.59/1.72	0.41/1.28
bdirection of μ	141	2.4/16.3	5.1/32.7
cwater-solute Eint	3857	0.46/1.79	0.32/0.95
dwater-solute dmin	3857	0.20/0.66	0.16/0.28
eφelec	195	2.38/4.19	1.96/3.39

^aThe magnitude of the dipole moment (μ) is given in D;

^bangle (°) between the ab initio and empirical dipole moment vectors, the numbers in the RMSD and MAE columns correspond to the average angle and the average dipole moment-weighted angle (using Σφ_i · p_i / Σp_i where p_i is the magnitude of the QM dipole moment and φ_i is the angle between the MM and QM dipole moments), respectively;

^c,dprobe water-model compound interaction energies and distances are in kcal·mol⁻¹ and Å, respectively;

^eelectrostatic potential is in kcal·mol⁻¹·Å⁻¹.

The statistics for empirical and ab initio dipole moments are given in Table 1. The dipole moment was included only for neutral compounds consistent with the standard CHARMM protocol. The CHARMM additive force field charge optimization targets systematically overestimated interactions with water to implicitly include the contribution of electronic polarization of molecules in an aqueous environment. Consistent with this, the empirical dipole moments should overestimate the gas phase dipole moments by ~30%.³⁰ The initial ParamChem charges yield dipole moments that are within 1 D of the target scaled QM values for the majority of compounds, though significant deviations are present in a number of cases (Figure 3 and Tables S3–S678). The dipole moments with the optimal charges are significantly improved relative to the dipole moments computed using the initial set of ParamChem charges. The RMS deviation between scaled QM and MM dipole moments averaged over all model compounds is 1.7 and 0.6 D computed with the initial ParamChem and optimal charges, respectively. The orientation of the dipole moment is also improved, and the angle between the QM and MM dipole moment averaged over the neutral model compounds is 32.7° and 5.0° with the initial and optimal set of charges, respectively. The RMSD for the dipole moment direction in this work is comparable to or better than the agreement of 8.5° obtained for the original CGenFF force field.³⁰ The angle between the QM and MM dipole moments for all model compounds except for three cases is smaller than 10°, and larger than 10° only for three molecules with a very small dipole moment (<0.5 D). Consistent with this, the average dipole moment-weighted angle between the QM and MM dipole moments (computed using Σφ_i · p_i / Σp_i where p_i is the magnitude of the QM dipole moment and φ_i is the angle between the MM and QM dipole moments) is 16.3° and 2.4° with the initial and optimal charges.

Figure 3.

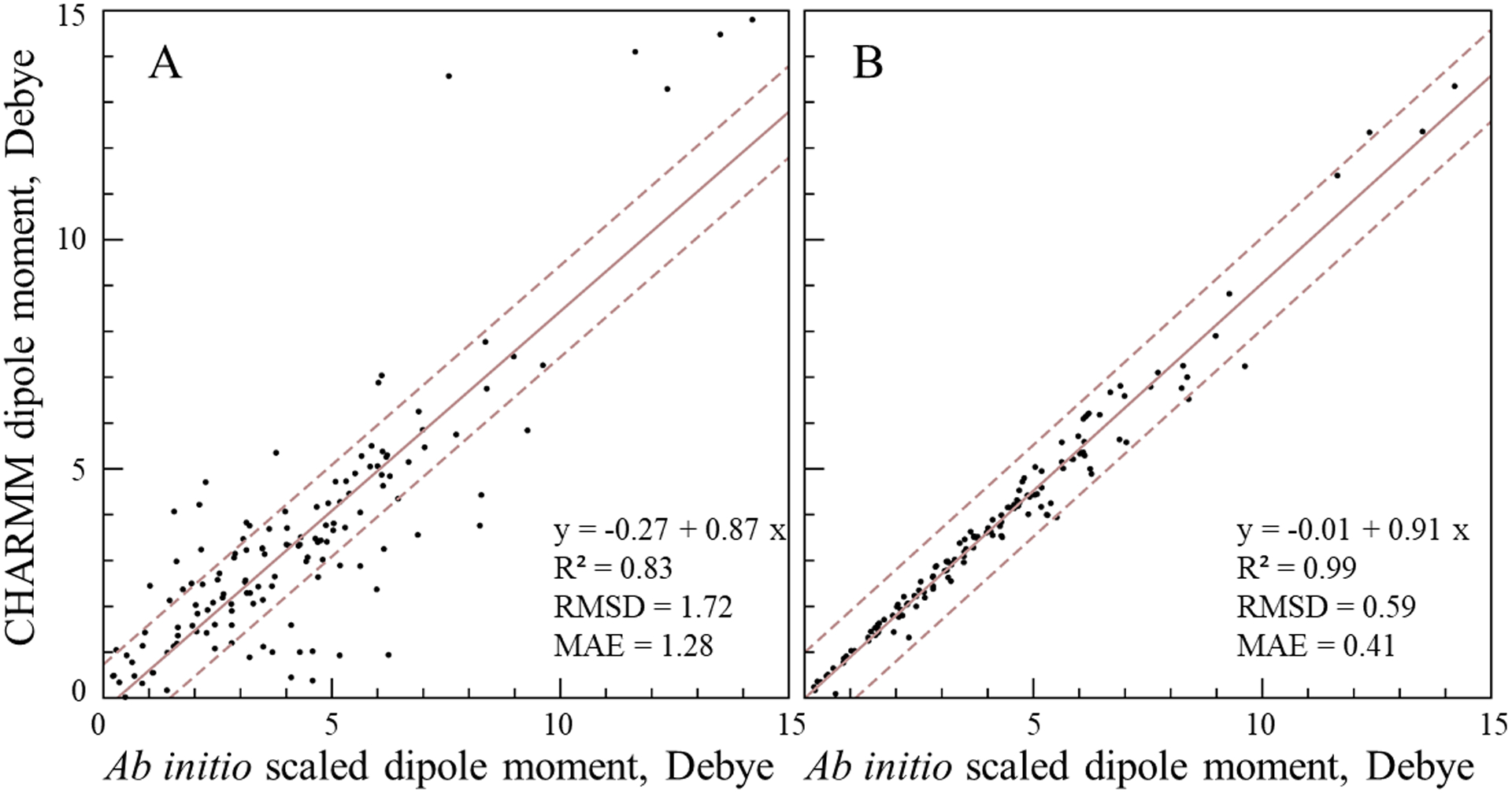
Comparison between the scaled QM (increased by 30%) and CHARMM dipole moments for 141 neutral model compounds. The CHARMM dipole moment was computed using A) the initial ParamChem charges and B) using the optimized atomic charges. The linear regression line is shown by the solid line; the dashed lines represent deviations of ±1 D from the regression line.

ESPs were included as an additional restraint to provide better charge distribution in the model compound as in a previous study.³⁷ However, the weight for the ESP potential was weak to achieve a better agreement for the water interactions. Nonetheless, for all model compounds, including ionized molecules, the ESPs are significantly improved relative to the initial values. The relative number of molecules vs ESP RMS deviation with the initial and optimal set of charges is shown in Figure S3. The RMS deviation between MM and QM electrostatic potential averaged over 195 compounds and geometries is 4.2 and 2.4 kcal·mol⁻¹·Å⁻¹ with the initial ParamChem and optimal set of charges, respectively. Targeting the QM ESP was found to be particularly important for ionized compounds, since the number of probe water interactions was fewer than for neutral compounds, due to the dominant contribution of the net charge to water interactions, as well as to the lack of the inclusion of dipole moments as target data.

The largest absolute difference between the initial ParamChem and optimized charges was observed for atoms in residues SUN (O-[(R)-(dimethylamino)(ethoxy)phosphoryl]-L-serine) and SVX (O-[(R)-ethoxy(methyl)phosphoryl]-L-serine). Both residues are similar: instead of the methyl group in SVX, SUN has the dimethylamino group bonded the phosphorous atom. In both cases, the largest difference (q_initial-q_optimal) was obtained for the phosphorus (P) atom charge, 1.14 e and 0.857 e in the SUN and SVX model compounds, respectively. The ParamChem penalty is relatively high, 31.6 and 83.9 for the P atom in the SUN and SVX model compounds, respectively, indicating that the initial charges should be optimized. With the initial ParamChem charges (the charge of the phosphorous atom of 2.154 e), the dipole moment in SUN is just 0.9 D versus 5.2 D computed with QM, while with the optimal charges (the charge of the phosphorous atom of 1.014 e) the MM dipole moment improves to 4.2 D. The RMS deviation for ESP also improves from 14.1 kcal·mol⁻¹·Å⁻¹ to 1.4 kcal·mol⁻¹·Å⁻¹. The interaction energies were also improved from 0.97 kcal·mol⁻¹ to 0.51 kcal·mol⁻¹. Similar improvements were observed for the SVX residue, its results can be found in Tables S571–S573. Overall, these results justify the need to adjust the charge of the phosphoryl group in these compounds.

Finally, to test the impact of the final CHARMM intramolecular geometry on the reproduction of the target water-model compound interactions and dipole moments, they were recomputed with the optimal charge set using the CHARMM optimized geometries. Model compound geometries were optimized using the optimal charges and optimized bonded parameters (see below). The RMS deviation between QM and CHARMM water-compound interaction energies is 0.50 kcal·mol⁻¹ very close to 0.46 kcal·mol⁻¹ computed using the QM optimized structures. The RMS deviation between QM and CHARMM dipole moments computed with the MM structures is 0.6 D practically identical to 0.6 D computed with the CHARMM optimized structures. The angle between QM and CHARMM dipole moments averaged over all model compounds is 5.0° and 7.7° computed with the MP2/6–31G(d) and CHARMM-optimized geometries, respectively. The RMS deviation between MM and QM ESPs averaged over all molecules is 2.4 and 2.6 kcal·mol⁻¹·Å⁻¹ with the QM and CHARMM optimized geometries, respectively. Accordingly, use of the QM gas phase geometries for optimization of the atomic charges yields parameters that are suitable for use with the CHARMM optimized geometries.

Case studies: Optimization of atomic charges for 4-fluorotryptophane (4FW), S-hydroxycystein (CSO), and S-(pyridin-3-ylcarbonyl)-L-cysteine (JJJ)

In this section the charge optimization is exemplified for three amino acids with nonstandard side chains: 4-fluorotryptophane (4FW), S-hydroxycystein (CSO), and S-(pyridin-3-ylcarbonyl)-L-cysteine (JJJ). 4FW is an artificial amino acid, which can be incorporated into proteins to probe thermodynamic and structural properties.^57,58 CSO (also known as sulfenic acid) is an important post-translational modification in proteins, which represents the critical intermediate oxoform in oxidative reactions leading to formation of disulfides, sulfenamides and higher order sulfinic or sulfonic acid species.^59,60 JJJ is a cysteine covalently bound to nicotinaldehyde, an inhibitor of nicotinamidase enzymes^61,62 used to study nicotinamidase function and structure.^63,64 These particular compounds were selected due to their different types of functional groups and, therefore, the presence of different types of interactions with water as well as different polarities. Currently, there are 804, 5, and 2 entries in the PDB for CSO, 4FW and JJJ, respectively. For the charge optimization the appropriate small model compounds were created. The model compounds include the side chain up to Cα for CSO and JJJ, and up to Cβ for 4FW as presented in Figure 4.

Figure 4.

Model compounds used to parametrize 4-fluorotryptophane (4FW), S-hydroxycystein (CSO), and S-(pyridin-3-ylcarbonyl)-L-cysteine (JJJ). The rotatable dihedral angles parametrized in this work are indicated by arrows.

The improvement for selected water interactions is demonstrated in Figure 5. In all cases the dipole moment with the optimized charges is strongly improved relative to the QM dipole moment both in the magnitude and direction. The QM and optimized MM dipole moments for 4FW are 4.5 D and 4.2 D, respectively, while the MM dipole moment with the initial charges is 3.0 D. This improvement was obtained by making the NE1 atom less negative from −0.58 e to −0.38 e, which also improved the water interaction with the HE1 atom from the absolute error of 0.56 kcal·mol⁻¹ to 0.32 kcal·mol⁻¹, with the initial and optimized charges, respectively. However, the charges for the 4FW compound needed only small adjustments, consistent with the small ParamChem penalty for the 4FW compound (the largest penalty of 13.8 is for atom CE3). Larger adjustments of charges were necessary for the CSO model compound. In the CSO model compound, the penalty for atoms OD and SG is very high, 235.7 in both cases, indicating that close analogous groups do not exist in CGenFF. Consistent with this, the water interaction energy computed with the initial charges is 2.95 and 3.60 kcal·mol⁻¹ off from the target QM interaction energy, for atoms OD and SG, respectively. The optimized charge for atom OD (-0.56 e) is more positive than the initial ParamChem charge (−0.74 e), while the charge for SG became more negative: 0.31 e against −0.05 e for the initial and optimized charge, respectively. The interaction energies with the optimized charges are strongly improved with the absolute deviation from the QM energy of 0.03 and 0.81 kcal·mol⁻¹ for atoms OD and SG, respectively. In the JJJ model compound, the dipole moment and angle were improved by making atom O7 less negative from −0.51 e to −0.39 e and by increasing the negative charge of atom SG from −0.01 e to −0.08 e, which also helped to improve the water interaction to absolute deviation of 0.11 kcal·mol⁻¹ and 0.10 kcal·mol⁻¹ for atoms O7 and SG, respectively, compared to the QM results. Atom N1 charge modification from −0.60 e to −0.56 e lowered the absolute water interaction energy error to 0.06 kcal·mol⁻¹ after optimization from initial 0.63 kcal·mol⁻¹.

Figure 5.

Selected water interactions with model compounds used to parametrize (A) 4FW, (B) CSO, and (C) JJJ. The water-compound interaction energies are given in the rectangular box: MM interaction energies computed with the initial and optimal charges, and QM interaction energies in blue, red and black, respectively. In the oval the ParamChem initial and optimized charges are in blue and red, respectively. The dipole moment computed with the ParamChem charges and optimized charges and the QM dipole moment, are shown as blue, red and black arrows, respectively.

Optimization of bonded terms

All bonded terms including harmonic terms were parametrized based on the reproduction of QM PES. Parameters with the ParamChem penalty > 10 were identified for each amino acid including all accessible protonation/tautomeric forms. A total of 189 model compounds were created to parametrize the bonded terms of 406 nonstandard amino acids. The same terms and associated parameters can be used in several compounds. In such cases, a representative model compound, normally with a fewer number of atoms and with a zero net charge, was chosen for optimization of a particular bonded term. The optimized parameters were then used for the other model compounds having the same term without further adjustments. Based on this hierarchal approach all model compounds were divided into four groups that contained 132, 24, 14, and 19 model compounds. The first group had all unique parameters, and the subsequent groups have decreasing numbers of free parameters to optimize with the remaining penalty > 10 parameters being optimized in the prior groups. For each term with missing parameters a PES scan was performed. To parametrize all the necessary bonded terms a total of 11194 QM optimizations were performed.

The phase and multiplicity of non-rotatable dihedral angles were taken from the ParamChem guess and were not further varied during optimization, with a few exceptions. In particular, for dihedral angles in conjugated systems the multiplicity was set to two and phase was set to 180°. For improper terms, the equilibrium values were set to zero. The results for bonded term parametrization are presented in this section except for rotatable dihedral angles. The results for empirical and ab initio structures and conformation energies are summarized in Table 2. The RMS deviation between the ab initio and CHARMM-optimized all Cartesian coordinates averaged over 189 model compounds is 0.18 Å (SD: 0.24 Å) and 0.14 (SD: 0.18 Å) Å for the initial and optimal and parameters, respectively. The values for bonds, valence angles, and torsion angles for the structures optimized with the MM model are in good agreement with the QM values. For bonds, the RMSD between bond distances in QM and MM optimized structures is 0.023 and 0.020 Å, with the initial and optimal parameters, respectively, with the values for valence angles being 1.6° and 1.4°, respectively. For torsions, the RMS deviation is 5.8° and 4.6° with the initial ParamChem and optimized parameters, respectively. Overall, with the optimized bonded parameters, the CHARMM model reproduces the QM geometries very well.

Table 2.

Comparison between empirical and ab initio optimized geometries for equilibrium structures.

Property	N points	MAE	RMSD
		optimal/initial	optimal/initial
aRMSD (Å)	189	0.14/0.18	0.18/0.24
bond (Å)	3519	0.015/0.016	0.020/0.023
angle (°)	5968	1.4/1.6	1.9/2.7
dihedral (°)	7133	4.6/5.8	9.6/11.7

^aRMS deviation between QM and MM optimized equilibrium structures for all atoms.

The RMS deviation between ab initio and optimized empirical energies for PES scans is 0.11, 0.31 and 0.43, kcal·mol⁻¹ for bond, angle, dihedral and improper angle terms, respectively. For non-rotatable dihedral angles the RMSD is 0.55 kcal·mol⁻¹. The MAE is 0.08, 0.16, 0.30 and 0.23 kcal·mol⁻¹ for bond, angle, dihedral and improper angle terms, respectively. Overall, good agreement between QM and MM energies was achieved with correlations between QM and MM relative energies of each data point in the PES of over 90%, except improper angles (86% correlation) as indicated in Table 3. It was found, in agreement with previous studies, that the force field model well reproduces energies for bonds, angles, but less accurately for dihedral angles.³⁰ Optimization of parameters improves the agreement between QM and MM energies for all terms. For example, the RMSD for bonds improves from 3.27 to 0.11 kcal·mol⁻¹ with the initial and optimal set of parameters, respectively. The significant improvement is explained by the fact that for stiff degrees of freedom even a small deviation in equilibrium values leads to significant deviations in energy. For rotatable dihedrals, the improvement is smaller relative to other degrees of freedom, from 2.29 kcal·mol⁻¹ to 0.72 kcal·mol⁻¹ with the initial and optimal sets of parameters, respectively.

Table 3.

Comparison between empirical and ab initio energies of PES scans

Term	aN terms	bN points	cRMSD	dMAE	eR
			optimal/initial	optimal/initial	optimal/initial
bond	57	399	0.11/3.27	0.08/1.59	99/17
angle	529	3703	0.31/3.50	0.16/1.39	93/22
stiff dihedral	516	3612	0.55/4.05	0.30/1.07	93/80
rotatable dihedral	212	7844	0.72/2.29	0.43/1.44	96/68
improper angle	24	168	0.43/1.72	0.23/0.78	86/56

^aNumber of terms parametrized in this work;

^bnumber of PES points used to optimize bonded parameters;

^c,d,eRMS deviation between QM and MM energies, mean absolute error, and linear correlation, R, respectively.

Rotatable dihedrals are degrees of freedom along which the molecule can undergo large structural fluctuations during MD simulations, hence accurate treatment of these dihedral PES is important to describe adequately the conformational space of molecules. Note that the dihedral terms associated with the rotation of the methyl group hydrogens with penalties > 10 were optimized in the present study, although the structural fluctuations due to the rotation of methyl groups are very small due to their being symmetric rotors. Thus, the dihedral terms associated with the rotation of methyl hydrogens were optimized using the method described in the previous section. The parameters of the rotatable dihedrals were determined based on points of PES scans to reproduce the complete rotation of 360° in 10° increments, with the exception of methyl groups which were subjected to a 7 point scan due to their symmetry. For all model compounds there were 212 rotatable dihedrals total. The PES points also included the local minimum geometry giving 36 points for each dihedral angle, yielding a total of 7632 QM optimizations to produce the QM target data, which contained 7844 data points.

For rotatable dihedral angles, in contrast to stiff torsion angles, additional Fourier terms (multiplicities or harmonics) were considered and phases were allowed to change from 0 to 180°. In particular, for the residues that have standard C36 parameters for the backbone, three multiplicities (n=1, 2, and 3) were introduced for the torsion terms associated with the rotation around the bond Cα-Cβ (χ1), since χ1 is particularly important for the conformation of the entire side chain. For all other dihedral angles, Fourier series were sought with a minimum number of multiplicities that could fit the energy profiles. However, if a satisfactory agreement was not possible additional multiplicities were tried. The RMS deviation between QM and CHARMM PES energies for all rotatable dihedral angles and all PES points (7844 total) is 0.72 kcal·mol⁻¹, while MAE is 0.43 kcal·mol⁻¹, demonstrating that the rotatable dihedrals are well reproduced by the force field model. Figure S4 shows the distribution of RMS energy deviation for local minima along PES against the number of molecules. RMS deviation for energy of local minima along PES is lower than 0.5 kcal mol⁻¹ for 57% and 80% of the soft dihedral PES scans with the initial and optimized parameters, respectively. As expected, due to the substantial impact of nonbond interactions on their PES the rotatable dihedrals were found the most difficult to fit and the largest RMS deviation with respect to the QM data was observed relative to other harmonic terms and stiff dihedral angles.

Case studies: Optimization of bonded terms for model compounds CSO and JJJ

Here we briefly illustrate the parametrization of bonded terms for CSO and JJJ. Model compounds for bonded term parametrization are shown in Figure 4, and the agreement for geometries is illustrated in Figure 6. In all cases, the MM geometry with the optimized parameters is very close to the QM geometry with the RMS deviation for the Cartesian coordinates of all atoms less than 0.1 Å. The geometries with the initial ParamChem parameters for these two residues are also close to the QM geometries, as can be seen in Figure 6, demonstrating that ParamChem provides a very good guess for these parameters.

Figure 6.

Comparison between QM and MM geometries of (A) CSO and (B) JJJ. The superposition of the QM structure and the structure optimized using the initial and optimal parameters is shown in the upper and bottom panels, respectively. The values for selected degrees of freedom are also given for the QM structure and the structure optimized with the initial and optimized parameters in black, blue and red, respectively.

The agreement between MM and QM energies is demonstrated in Figure 7 and Figure 8 for selected bonded terms in the CSO and JJJ model compounds, respectively, with the initial and optimal sets of bonded parameters. All energies for stiff degrees of freedom are within 2.0 kcal·mol⁻¹ of the minimum energy, as described in the Methods section. Overall, the models reproduce well the QM equilibrium conformations of the model compounds as well as QM energies of various deformations along parametrized degrees of freedom. Notable is agreement for rotatable dihedral angles of CSO model, which involve the rotation of the hydroxyl (C) and the sulfenic (D) groups shown in Figure 7. The position of the local minima and energy barrier heights are well reproduced in both cases. However, the force field model does not reproduce asymmetry of QM PES scans relative to zero degree. In particular, for the rotation the sulfenic group the local minimum at −60° is ~0.4 kcal·mol⁻¹ higher in energy relative to the minimum at 60°, while with CHARMM both energy minima have the same energy. This is explained by the fact that in the current CHARMM force field, by convention, the dihedral phases are allowed to be 0° or 180°, so the parameters can be applied for different stereoisomers associated with that dihedral.³⁰ For the JJJ compound, the deformations along the angle shown in Figure 8 (B) has a non-harmonic energy profile due to the rearrangement of the rotatable dihedral during the PES scan. Similar to the CSO compound, for the JJJ model compound, the force field model well reproduces the PES surfaces associated with the rotatable dihedral angles involving the rotation of pyridine (C) and thiol (D) groups shown in Figure 8. Finally, we note that the positions of wells and barriers for PES in Figure 7 and Figure 8 are in a good agreement for QM energies and MM energies computed with the ParamChem parameters, demonstrating that ParamChem provides a good guess for this molecule.

Figure 7.

PES scans for selected degrees of freedom in the CSO model compound. The PES scan was performed for a bond (A), for a valence angle (B), and for the dihedral angles associated with the rotation of the hydroxyl group (C) and the sulfenic (D) group, respectively. The arrows and dotted lines indicate the corresponding degree of freedom along which the adiabatic PES scan is performed. The dashed and solid lines show PES energies obtained with the initial and optimal force field parameters, respectively, with the ab initio PES indicated by open circles.

Figure 8.

PES scans for selected degrees of freedom in the JJJ model compound. The PES scan was performed for a bond (A), for a valence angle (B), and for the two dihedral angles adjacent to the phenyl ring (C and D). The arrow and dotted lines indicate the corresponding degree of freedom along which the adiabatic PES scan is performed. The dashed and solid lines show PES energies obtained with the initial and optimal force field parameters, respectively, with the ab initio PES indicated by open circles.

Molecular Dynamics simulations of protein complexes

To illustrate the quality of the model, MD simulations of proteins containing nonstandard amino acids were performed. Twenty protein structures with a high-to-medium resolution were chosen for MD simulations of 100 ns. The information on the proteins is given in Table S1. Nine systems contained all protein atoms, which were not restrained during MD simulations. A spherical protein model was used with restrained atoms beyond 20 Å for 11 protein systems. Note that our goal was to assess the quality of the force field model for nonstandard amino acids, which should affect primarily the structure and dynamics of the nonstandard amino acid and adjacent residues. The superposition of structures observed in MD simulations on the experimental structures is shown in Figures 9 and 10. For each protein complex 10 snapshots taken every 10 ns from the 100 ns MD simulations were superimposed on the experimental structure based on protein backbone atoms within 10 Å of the nonstandard amino acid. Conformations observed in MD simulations in all protein simulations are very similar to the position of nonstandard amino acids in the crystal structures as shown in Figures 9 and 10. The RMS deviations between simulation and experimental structures are given in Table 4 and S870. The RMS deviation for non-hydrogen atoms within 10 Å of nonstandard amino acids in all MD simulations is in the range of 0.37 Å to 0.99 Å. The RMS deviation for nonstandard amino acids after superimposing on the crystal structure based on the non-hydrogen atoms of the nonstandard amino acid is in the range between 0.11 Å and 0.91 Å; however, the RMS deviation is small for all residues (the mean value for all proteins is 0.40 Å). The largest RMS deviation, 0.91 Å, was observed for carboxymethylated cysteine (residue CCS). CCS106 has a flexible carboxylate group, which rotates during MD simulations starting with the crystal structure 6E5Z.⁶⁵ The RMS deviation computed based on non-hydrogen atoms of CCS without the carboxylate oxygens is much lower 0.49 Å (SD: 0.12 Å), showing that the main contribution to the observed RMS deviation for CCS is due to rotation of the carboxylate moiety. Overall, the RMS deviation for the non-hydrogen atoms of the nonstandard amino acid in all cases is lower than the RMS deviation for unrestrained protein backbone atoms, demonstrating that the model performs as well as the standard CHARMM force field for proteins in protein simulations.

Figure 9.

Comparison of structures from MD simulations (in gray) with the experimental structures (in color). Ten snapshots were taken every 10 ns from 100 ns MD simulations and superimposed on the experimental structure using the protein backbone atoms.

Figure 10.

Comparison of structures from MD simulations (in gray) with the experimental structures (in black) for (A) 4FW, (B) CSO, and (C) MDO. (PDB access codes: 6SZZ, 6Q00, and 1IYF, respectively). Ten snapshots were taken every 10 ns from 100 ns MD simulations and superimposed on the experimental structure using the protein backbone atoms. Right panel: RMS deviation for backbone atoms within 10 Å of the nonstandard amino acids; the average RMS deviation is shown in gray.

Table 4.

Root Mean Square (RMSD) deviation in molecular dynamics simulations.

Amino	PDB		RMSD (Å)
acid	ref. code	aBackbone	bBackbone	cResidue
MDO	1IYF	0.54 (0.05)/0.49 (0.03)	0.58 (0.08)/0.49 (0.05)	0.33 (0.07)/0.24 (0.07)
4FW	6SZZ	0.72 (0.12)/0.70 (0.12)	0.81 (0.16)/0.78 (0.16)	0.18 (0.06)/0.18 (0.05)
CSO	6Q00	0.80 (0.13)/0.78 (0.12)	0.67 (0.11)/0.62 (0.11)	0.80 (0.12)/0.68 (0.24)

^aRMSD was computed for unrestrained backbone atoms after superposition on the experimental structure;

^bRMSD was computed based on backbone heavy atoms within 10 Å sphere around the nonstandard amino acid;

^cRMSD was computed for the heavy atoms of the nonstandard amino acid; the numbers are given for MD simulations with the initial and optimized parameters, respectively.

Table 5 and S871 summarize selected non-bond interaction distances. The RMS deviation for distances between non-hydrogen atoms implicated in hydrogen bonds is in the range between 0.0 and 0.59 Å. The largest deviation was observed for residues OCS between N of Lys42 and OD1 of OCS48. In the crystal structure (PDB code: 5IMV),⁶⁶ this distance is too short, 2.36 Å, for a hydrogen bond, while in MD simulations the distance between N of Lys42 and OD1 of OCS48 increases to 2.95 (SD: 0.27 Å) Å. The RMS deviation averaged over all distances in Table S871 is 0.18 Å. Thus, important hydrogen bonds between nonstandard amino acids and other protein residues are in very good agreement with the experimental X-ray structures. As an additional test, the rotatable dihedral angles parametrized in this work were further investigated. The torsion angles are given in Table S872. All dihedral angles are well reproduced in MD simulations with the mean absolute deviation from those in the experimental crystal structures of just 5.4° and the RMS deviation of 11.0 °. The largest deviation of 55.5° from the value in the crystal structure (PDB code: 4Y4G)⁶⁷ is observed for residue GGB along the dihedral angle defined by atoms Cα, Cβ, Cγ, and Oδ. Further analysis revealed that at the location of atoms Cγ and Oδ there are areas of poor electron density, suggesting that the position of these atoms was not well defined in the crystal model.⁶⁷ Indeed, in the crystal structure the distance between atoms CG and NH1 of residue GGB is short, 3.0 Å, so that the distance between their protons of just 1.7 Å creates a repulsion between these groups. In MD simulations this strain is relieved by the rotation around the bond Cβ-Cγ leading to the deviation in the dihedral angle.

Table 5.

Selected average non-bond distances (Å) in MD simulations of proteins with the nonstandard amino acids.

Residue	aAtom pair	X-Ray str.	b,c MD simulation	cAbs. diff.
MDO	N2MDO66-OVal61	2.89	3.04 (0.22)/2.84 (0.12)	0.15/0.05
MDO	O MDO66-NE2Gln94	4.19	4.06 (0.65)/3.98 (1.07)	0.13/0.21
MDO	O2 MDO66-NH2Arg96	2.75	2.91 (0.25)/2.88 (0.21)	0.16/0.13
4FW	FE34FW8-NAsn10	3.27	3.45 (0.31)/3.43 (0.28)	0.18/0.16
4FW	FE34FW8-NPhe9	2.94	3.18 (0.22)/3.13 (0.18)	0.24/0.19
CSO	NCSO29-OArg25	3.05	3.04 (0.21)/3.04 (0.20)	0.01/0.01
CSO	OCSO29-NAla33	2.93	2.95 (0.19)/2.98 (0.17)	0.02/0.05

^aProtein atoms (left) are labeled by their amino acid;

^bvalues in parenthesis are the RMS fluctuations;

^cMD simulations were performed with the initial and optimized parameters, respectively.

In the following, MD simulation results will be presented for three residues CSO, 4FW, and MDO in detail (PDB access codes 1IYF, 6SZZ, and 6Q00, respectively), while the results for simulations of other protein complexes are given in Supplementary Information. Details of the optimization of the parameters associated with CSO and 4FW were presented above. MDO, the 4-methylidene-imidazole-5-one prosthetic group present in phenylalanine-2,3-aminomutase proteins is formed by autocatalytic post-translational modifications of three amino residues (A-S-G) in the polypeptide chain.⁶⁸ The RMS deviation, given in Table 4, for the non-hydrogen atoms of the nonstandard amino acid is very low 0.45 (SD of RMSD: 0.03 Å) Å and 0.18 (SD: 0.05 Å) Å, for MDO and 4FW, respectively. For CSO the RMSD for the non-hydrogen atoms is higher 0.68 Å, which is explained by the fact that CSO, in contrast to MDO and 4FW, has two predominant conformations as demonstrated by the analysis of the dihedral angles below. The superposition of the experimental structures for ten snapshots is shown in Figure 10. In all simulations the nonstandard amino acids fluctuate in the vicinity of the experimental position.

Important distances between non-hydrogen atoms are given in Table 5 for MD simulations of MDO, 4FW, and CSO. All average distances observed in the MD simulations are within the RMS fluctuations of the corresponding distances observed in the experimental structures and all within 0.2 Å of the experimental distance. The torsion angles are within the RMS fluctuations from those in the experimental structure for all torsions and residues. Notable is the agreement for CSO. In the PDB structure 6Q00, two models for the side chain of CSO29 are present with χ1 of 63.6° and 164.3° (model A and B, respectively). Fluctuations around χ1 shown in Figure 11 demonstrate that there are two populated rotamers for CSO in the protein structure with χ1 of 63.2° and 176.1°, both are very close to the experimental values (see also Table 6). Thus, starting from model A, MD simulations with the force field model were able to reproduce both structural models A and B for the CSO side chain. With the initial parameters, the two conformations were also observed in MD simulations (64.6° and 170.1°), however, the conformation with χ1 of ~60° was much less populated, 5.9% and 32.6% with the initial and optimized parameters, respectively. This is due to overestimation of the energy of the conformation at 180 ° by 1.2 kcal·mol⁻¹ relative to 60° by CHARMM with the initial parameters shown in Figure 7D. MDO, which has a nonstandard backbone group has three rotatable torsion angles and does not have any associated CMAP term. All three torsions can be regarded as dihedral angles in the peptide backbone. The angles observed in MD simulations with MDO are again in very good agreement with those in the X-ray structure, which is important to reproduce the geometry of the entire polypeptide chain. For 4FW, both angles χ1 and χ2 are in excellent agreement with the experimental structure, which is also reflected in the very low RMS deviation between the experimental structure and those observed in the MD simulation. Overall, the model reproduces well the structure of the nonstandard amino acids and their interactions.

Figure 11.

Rotatable dihedral angles in MD simulations of protein complexes with 4FW, CSO, and MDO. (PDB access codes: 6SZZ, 6Q00 and 1IYF, respectively). The dihedral angle is shown by the arrow; the experimental value is shown by the solid gray line; the right panels show the distribution of the dihedral angle in MD simulations.

Table 6.

Rotatable dihedral angles observed in MD simulations and experimental structures. RMS fluctuations are given in parenthesis.

Residue	Dihedral	X-ray	aMD	aabs. diff
MDO	CB-CA1-C1-N3	−168.7	−160.9 (10.7)/−164.4 (10.3)	7.8/4.3
MDO	C1-N3-CA3-C	101.9	89.2 (9.1)/96.6 (11.1)	12.7/5.3
MDO	N3-CA3-C-NV68	−32.4	−86.5 (22.2)/−50.8 (28.4)	54.1/18.5
4FW	C-CA-CB CG (χ1)	−37.4	−37.7 (7.8)/−37.6 (8.6)	0.3/0.2
4FW	CA-CB-CG-CD1 (χ2)	−89.3	−86.1 (9.0)/−88.6 (8.6)	3.2/0.7
CSO	C-CA-CB-SD (χ1)	63.6/164.3	64.6/170.1/63.2/176.1	1.0/5.8/0.4/11.8
CSO	CA-CB-SD-OD (χ2)	−149.8	−186.4 (22.3)/−178.1 (40.7)	36.6/28.4

^aMD simulations were performed with the initial and optimized parameters, respectively.

To test the initial parameters, MD simulations were also performed using the initial CGenFF parameters for CSO, 4FW and MDO. The system setup was identical to the one described above, except the initial CGenFF parameters were used for the modified amino acid. The RMS deviations given Table 4 are systematically larger for the non-hydrogen atoms of the non-standard amino acids, but also for the protein backbone atoms within 10 Å of the modified amino acid. For example for MDO, the RMS deviation is 0.58 Å and 0.49 Å for the backbone atoms, with the initial and optimized parameters, respectively. For the non-hydrogen atoms of the modified amino acids the RMS deviation is also larger with the initial parameters: 0.33 Å vs 0.24 Å with the optimized parameters. Selected dihedral angles given in Table 6 are also systematically better with the optimized parameters. The average non-bond distances, given in Table 5, do not show larger deviations relative to distances in the experimental structures, demonstrating that the ParamChem online server provides a good guess for charges.

Conclusion

The present study represents a systematic development of a force field model for a large set of nonstandard amino acids in the most important protonation states. The parametrization was performed consistent with the standard method used to develop the CHARMM36 additive force field, and thus the model should be compatible with the other components in the CHARMM36 additive force field, including the CHARMM TIP3P water model, the C36 force field for macromolecules and CGenFF for small molecules. The initial guess for both charges and bonded parameters was provided by the ParamChem online server that assigns parameters by analogy from the CGenFF force field. The parameters of the empirical force field were optimized to reproduce QM data and validated against experimental structural data. The charges were adjusted to reproduce interactions of a large number of model compound-water monohydrate complexes, which was important to maintain the balance between interactions of nonstandard amino acids with solvent and other protein residues. In addition, the model reproduces the scaled magnitude and direction of the ab initio dipole moment for neutral compounds as well as the electrostatic potential. Importantly, charge optimization of the neutral species involved systematically overestimating the charges, and thus the dipole moment relative to gas-phase QM data, to introduce implicit electronic polarization corresponding to the condense phase. Including the QM electrostatic potential in the charge optimization, in accord with the previous studies,^37,44 was found useful to obtain a better charge distribution in ionized molecules. Finally, to test that the model well reproduces water interactions with empirical structures of model compounds, probe water interactions were recomputed using the CHARMM optimized structures, demonstrating practically the same level of agreement between force field model results and corresponding QM data.

Special emphasis was given to the quality of all bonded parameters, including soft torsions and stiff harmonic terms, which were adjusted using computationally intensive PES scans. Given the large set of nonstandard amino acids parametrized in this work (406 molecules and their accessible protonation and tautomeric forms) a hierarchical optimization approach, similar to the method used for CGenFF was used for bonded parameters. In this approach, only new parameters that had not been previously available in the force field were optimized, as each new model compound was added to the force field. The order of compounds for bonded parameter optimization was chosen so that the parameters were adjusted in compounds with the minimal possible number of atoms among molecules that share those parameters.

Model validation was based on MD simulations of 20 proteins containing selected nonstandard amino acids. The results demonstrate that the model reproduces very well conformations of nonstandard amino acids in the experimental structures, and in particular rotatable torsions, indicating the quality of both the optimized charges and dihedral parameters. Importantly, the force field model reproduces non-bonded interactions involving the nonstandard amino acids, demonstrating a good balance in the interactions with other components of the system: standard amino acids and water.

The presented parameters represent an extension of the CHARMM36 force field that will allow for reliable molecular simulations of proteins containing nonstandard amino acids. Beyond the parameters for nonstandard amino acids, the parameters developed in this work will be included in the CGenFF force field further expanding its coverage of chemical space. The presented parameters will be incorporated in the program CHARMM⁴⁶ and be available from the MacKerell lab web page (https://mackerell.umaryland.edu/) and the CHARMM-GUI (http://www.charmm-gui.org),^15,69 facilitating their utilization in a range of molecular simulation software packages.