A Benchmark of Electrostatic Method Performance in Relative Binding Free Energy Calculations

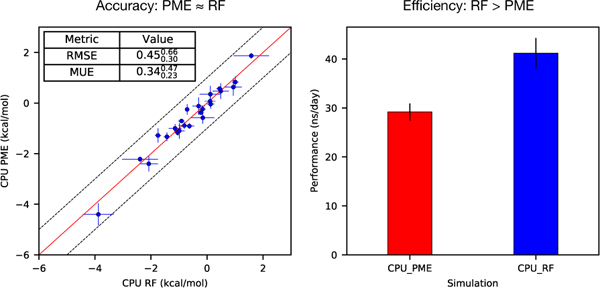
Abstract

Relative free energy calculations are fast becoming a critical part of early stage pharmaceutical design, making it important to know how to obtain the best performance with these calculations in applications which could span hundreds of calculations and molecules. In this work, we compared two different treatments of long-range electrostatics, Particle Mesh Ewald (PME) and Reaction Field (RF), in relative binding free energy calculations using a non-equilibrium switching protocol. We found simulations using RF achieve comparable results as those using PME but gain more efficiency when using CPU and similar performance using GPU. The results from this work encourage more use of RF in molecular simulations.

Graphical Abstract

INTRODUCTION

The lead optimization stage is an important part of pharmaceutical drug discovery, involving optimization of several key chemical and biophysical properties in order to ensure candidate compounds have adequate selective binding to their target while also having appropriate other properties to potentially become a new pharmaceutical. Lead optimization efforts always require adequate ligand binding affinity for the target, making this a critical design criterion, and one which is a target for predictive methods. Alchemical relative binding free energy (RBFE) calculations based on molecular dynamics (MD) simulations and statistical mechanics have shown promise in providing reliable predictions to guide experimental work in the context of real drug discovery projects.¹

RBFE calculations compare the potency of two structurally related ligands by transforming one ligand into another via an unphysical or alchemical pathway. This transformation is performed in both the protein-ligand complex and in the solution state to form a closed thermodynamic cycle. The RBFE of the ligands simulated can be calculated through two opposite legs in this cycle.²

To calculate free energies, these alchemical transformations can be performed via either an equilibrium or non-equilibrium protocol. In general, a number of intermediate simulations are conducted along an alchemical path between the two physical end states, with these simulations being either equilibrium or nonequilibrium depending on the approach chosen. While the free energy different of interest depends only on the physical end states in the limit of adequate sampling, these intermediate states serve to help obtain converged results and provide sampling which is hopefully adequate. Equilibrium free energy calculations run an equilibrium simulation at each intermediate state as well as the end states which are physically meaningful. In contrast, the non-equilibrium protocol simulates the end states at equilibrium, potentially spending considerably more time there, and only runs short simulations to switch between end states. However, running a large number of switching trials is critical in this case. It is still under debate which of the two protocols is more efficient, with different studies drawing different conclusions,^3,4 and the choice of protocol is beyond the scope of this paper. This work follows the protocol deployed in a previous work⁵ in which a non-equilibrium approach was used, though our results may generalize to equilibrium approaches as well.

Generally, modern MD engines (e.g., AMBER, GROMACS, CHARMM, etc) support different approaches for simulations, including RBFE calculations. Among these software packages, GROMACS is an open source package which is widely used for molecular simulations and reproduces calculated free energies within about 0.2 kcal/mol.⁶ Moreover, tools (e.g., pmx⁷) allow easy high-throughput applications of GROMACS RBFE simulations, providing a workflow spanning from initial coordinate files to final free energy estimates. This leads to relatively user-friendly RBFE calculations using GROMACS.

Long-range electrostatics interactions are critical in modeling molecular motions in simulations. Due to the computational complexity of such long-range interactions, it becomes challenging to design accurate and efficient methods to describe such interactions. An excellent review of methods for computing the long-range electrostatics interactions in biomolecular simulations can be found here.⁸

Among a number of existing methods, Particle Mesh Ewald (PME)^9,10 is perhaps the most broadly used. PME and other Particle-Mesh methods (e.g., particle-particle particle-mesh method (P3M)^11,12) are based on the Ewald approach which is a classic method to exactly calculate the electrostatic potential¹³ and is chosen as a starting point for further adjustments for better efficiency. Historically, the PME methods were inspired by the P3M method and the similarities and differences of the two methods are reviewed by previous work.^14,15 It is also somewhat controversial in the literature as to whether P3M and PME should be considered completely equivalent (and share the same name, e.g. P3M); here, however, we do not enter this debate and simply refer to the approach as PME, as this is how the implementation we use is described in the GROMACS documentation.

Another popular option to compute electrostatics interactions is Reaction Field (RF).^16,17 The RF method only computes the interactions up to a cutoff distance and implicitly treats any interactions beyond the cutoff in a mean-field manner using an appropriate dielectric constant. RF sees considerable use in the field and can be appealing for suitable system geometries.^18,19

Both Ewald based approaches (e.g., PME) and RF methods may introduce artifacts and lead to incorrect modeling of the system. Such artifacts have been extensively explored and summarized in previous work.²⁰

In this work, we compare the performance of PME and RF methods in RBFE calculations. There is extensive literature comparing RF and Particle-Mesh methods (e.g., PME, P3M) in plain MD simulations on different systems (e.g., liquids, proteins, etc) which is well summarized in the work of Reif and Oostenbrink.²¹ Our focus in this work is specifically on whether these methods yield equivalent relative binding free energies, given the tremendous industrial interest in such calculations. While both RF and PME methods are widely used in free energy calculations, ^5,18,19,22 they have not yet been compared head-to-head to see if they yield equivalent results in RBFE calculations, to our knowledge.

METHODS

Selected targets.

We selected the targets TYK2 and CDK2 which are part of several RBFE benchmark studies^23–25 including the set commonly referred to as Schrödinger’s “JACS set”²³ from a key paper in JACS on large-scale free energy calculations. Among all 8 target systems in the JACS set, TYK2 has a moderate system size (∼ 60000 atoms including water and ions) which yields representative results in performance. CDK2 is the largest system (∼ 110000 atoms including water and ions) among these targets and we selected it to verify the trends observed in TYK2 simulations. For TYK2, we used all 24 edges in our calculations and randomly selected 6 edges of CDK2. The ligands simulated in this work are neutral so no net charge change is involved in each perturbation. A table of successfully simulated perturbations can be found in Table S1, S2.

Molecular Dynamics Simulations.

The simulation protocol follows a previous work.⁵ Simulation details can be found in the Supporting Information.

Both CPU and GPU simulations were performed using PME or RF electrostatics. In the rest of the paper, we denote CPU-PME, CPU-RF, GPU-PME and GPU-RF to represent the hardware and methods for long-range electrostatic interactions treatment.

RESULTS AND DISCUSSION

Predicted relative binding free energies from simulations using RF show good agreement with those from PME.

The relative binding free energies (∆∆G) were calculated for a set of modification of TYK2 (24 ∆∆G values in total). Figure 1 summarizes the computed values using RF/PME on CPU/GPU. The uncertainty estimates were performed by 1000 bootstrapping trial and reported in Figure 1 as $x_{x_{low}}^{x_{high}}$ where x is the mean value, x_high and x_low indicate 95% confidence intervals. The averaged root-mean-square error (RMSE) and mean unsigned error (MUE) of ∆∆G for CPU-PME versus CPU-RF are 0.45 and 0.34 kcal/mol and for GPU-PME versus GPU-RF are 0.52, 0.40 kcal/mol, respectively (Figure 1a–b). A cross-platform (CPU vs GPU) comparison also shows essentially the same level of agreement between results using RF and PME (Figure 1c–d) suggesting the same trend holds true on both CPU and GPU.

Figure 1:

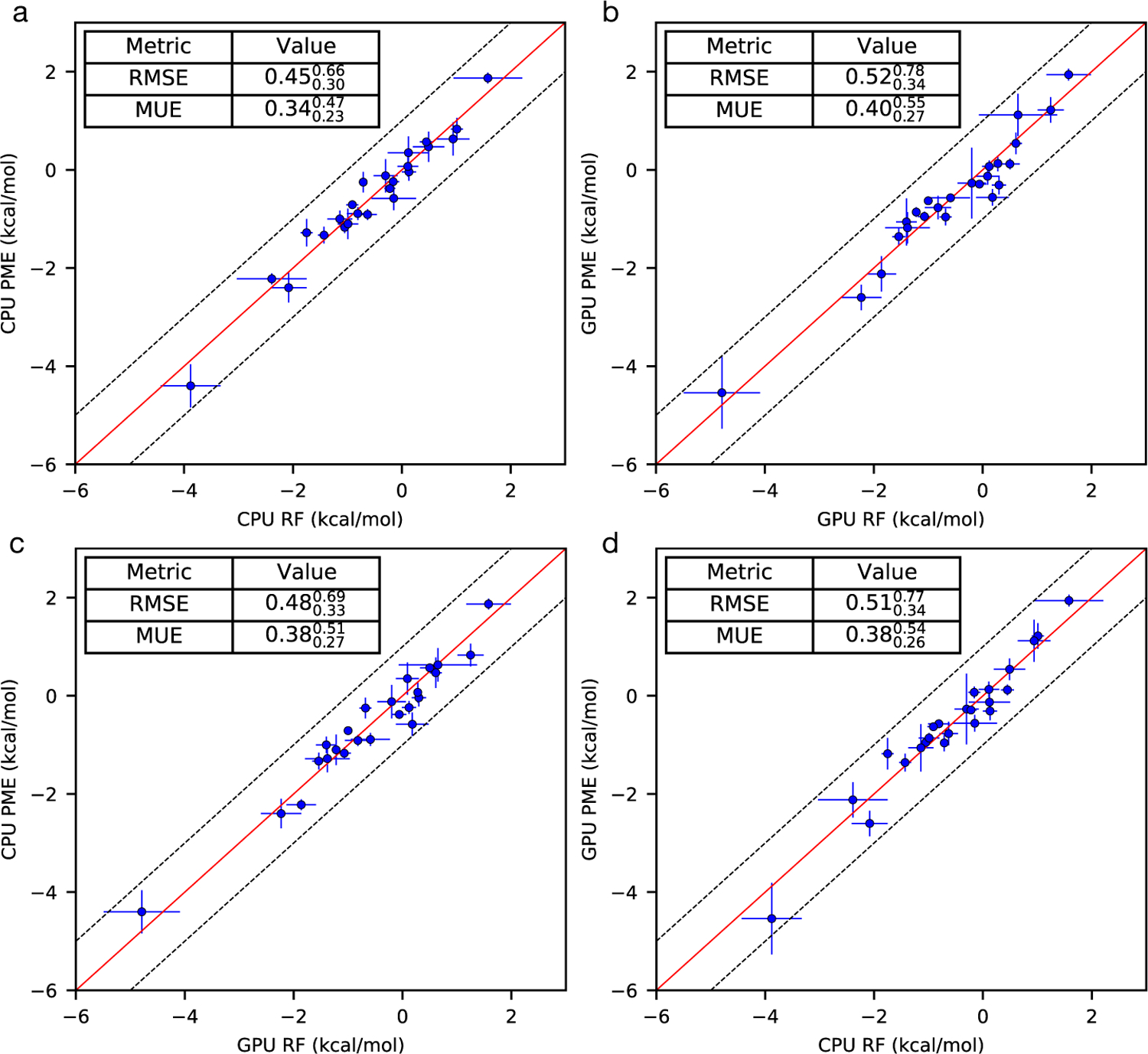
Calculated ∆∆G values of TYK2 ligands using RF/PME on CPU/GPU. Overall, a good agreement is achieved between using PME and RF on CPU/GPU. The uncertainty estimates are calculated by bootstrapping, using 100 bootstrap samples.

In this work, we are focused on the comparison between RF and PME methods on relative binding free energy calculations. While comparing calculated ∆∆G with experimental measured values is more important to benchmarking force field/methodologies, it is not the top interest in this work. However, we summarize our calculated values and the corresponding experimental results in Table S3. In conclusion, the calculated values of both methods are similarly accurate when compared to the experimental values.

Simulations using RF are more efficient than using PME.

Given that PME and RF achieve a good level of agreement of calculated ∆∆G values, our focus shifts to computational efficiency, where RF is generally less computationally demanding than using PME^26,27 when the same cut-off is used since more computational time is needed for PME in reciprocal space and tabulated interactions. The simulation performance (in the unit of ns/day) was analyzed from the 6-ns equilibrium NPT simulation and is summarized in Figure 2 where different colors represent using RF/PME on CPU/GPU. The uncertainties were estimated using the standard deviations across different edges. For the (less costly) in-solution ligand simulations, using RF on CPU is ∼30% faster than using PME on average (Figure 2a) and is similar to PME when simulated on GPU considering the uncertainties (Figure 2b). For the more costly bound state simulation, a similar trend is observed in CPU simulations (Figure 2c). However, using RF on GPU is ∼10% slower than using PME on average (Figure 2d). A summary of simulation wallclock time can be found in Table S4, S5.

Figure 2:

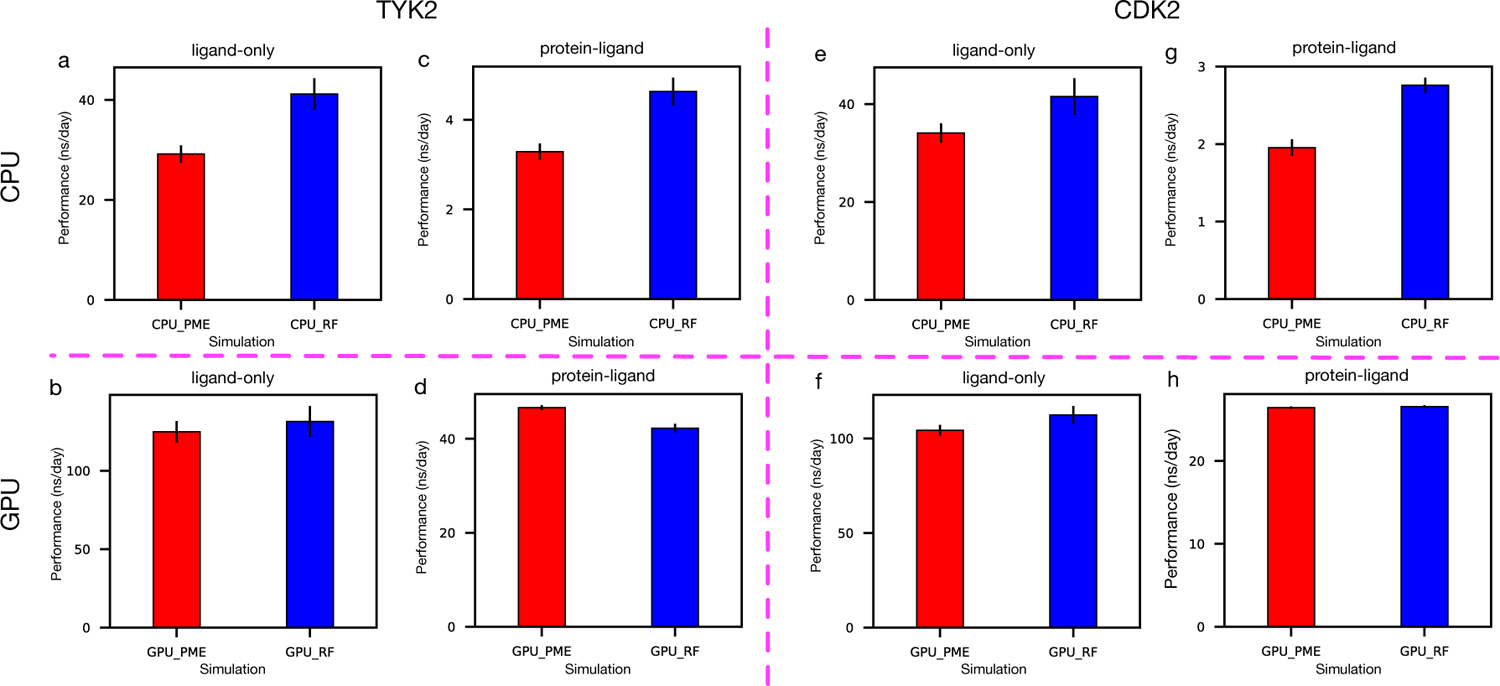
Performance different between using RF/PME on CPU/GPU in TYK2 simulations of (a–b) ligand-only in-solution, (c–d) protein-ligand complex and in CDK2 simulations of (e–f) ligand-only in-solution, (g-h) protein-ligand complex.

The results from Figure 2 show that using RF is faster than PME in most cases for the different system sizes and hardware tested here. It is notable that the GROMACS version used in these simulations was specifically optimized for PME performance on GPU. Thus, it is not surprising that PME outperformed RF on GPUs (slightly) in our tests here. However, the different between PME and RF on GPU performance is only minor (∼10%). Possibly a similar optimization of GROMACS for RF on GPUs could yield substantial performance gains.

To verify the observed trends in TYK2 simulations, 6 selected edges from CDK2 were simulated using the same protocol. Similar to the results of TYK2, simulations using RF are also faster (∼20–40%) than using PME on CPU (Figure 2e,g). Notably, GPU simulations using RF achieves a similar efficiency to PME (Figure 2f,h) which means even with optimizations, PME still cannot surpass RF in efficiency (Figure 2d).

We expect the results observed in this work will be generalizable to other simulation packages and force field in that results will not be highly dependent on PME vs RF, but (a) that is outside of scope for this work, and (b) details will depend on the exact implementation in those software packages. Previous work has shown that different simulation engines are able to take in the same force field and same systems and give identical free energies (with PME) within a reasonable tolerance, which would strongly suggest the implementations are equivalent or nearly so,^28,29 at least for PME. Meanwhile, the results observed here are with present-day force field and may not always be the case in future studies (i.e, optimized force field based on the choice of electrostatics treatment).

The conclusions presented in this work are true only for neutral perturbations and are not guaranteed in other perturbations (e.g., charge-changing mutations). When charged species are involved, different correction schemes must be applied to correct the bias induced by electrostatics finite-size effects depending on electrostatic treatment methods used (e.g., RF, PME).^30–33

CONCLUSION

The treatment of long-range electrostatic interactions is critical for a correct modeling of (bio)molecular systems in molecular dynamics simulations. Due to the long-range nature and N²-scaling of electrostatic interactions, they are computationally the most demanding terms in the force field evaluation. Given the results presented in this work, we suggest that RF may be a promising option for relative free energy simulations because, at least in GROMACS, it is less computationally demanding while retaining comparable accuracy to PME. This advantage may be particularly helpful in cases where a large number of simulations are needed (e.g., in the lead optimization stage of the drug discovery process). Thus we recommend free energy calculations with RF be considered as a viable option, at least for homogeneous systems.