A likelihood method for estimating present-day human contamination in ancient male samples using low-depth X-chromosome data

Abstract

Motivation

The presence of present-day human contaminating DNA fragments is one of the challenges defining ancient DNA (aDNA) research. This is especially relevant to the ancient human DNA field where it is difficult to distinguish endogenous molecules from human contaminants due to their genetic similarity. Recently, with the advent of high-throughput sequencing and new aDNA protocols, hundreds of ancient human genomes have become available. Contamination in those genomes has been measured with computational methods often developed specifically for these empirical studies. Consequently, some of these methods have not been implemented and tested for general use while few are aimed at low-depth nuclear data, a common feature in aDNA datasets.

Results

We develop a new X-chromosome-based maximum likelihood method for estimating present-day human contamination in low-depth sequencing data from male individuals. We implement our method for general use, assess its performance under conditions typical of ancient human DNA research, and compare it to previous nuclear data-based methods through extensive simulations. For low-depth data, we show that existing methods can produce unusable estimates or substantially underestimate contamination. In contrast, our method provides accurate estimates for a depth of coverage as low as 0.5× on the X-chromosome when contamination is below 25%. Moreover, our method still yields meaningful estimates in very challenging situations, i.e. when the contaminant and the target come from closely related populations or with increased error rates. With a running time below 5 min, our method is applicable to large scale aDNA genomic studies.

Availability and implementation

The method is implemented in C++ and R and is available in github.com/sapfo/contaminationX and popgen.dk/angsd.

1 Introduction

Having plagued the field since its inception (Zischler et al., 1995), contamination is one of the defining features of ancient DNA (aDNA). While DNA extracted from present-day specimens is mostly endogenous, aDNA extracts are a mixture of low levels of damaged and fragmented endogenous DNA often dwarfed by higher amounts of contaminant DNA (Orlando et al., 2015). In recent years, high-throughput sequencing technologies have substantially contributed to advancing the field by randomly retrieving DNA fragments present in the extract, i.e. including the shorter, damaged endogenous ones. Nevertheless, the problem of contamination has persisted, and affects all laboratories (Champlot et al., 2010; Der Sarkissian et al., 2015; Gilbert et al., 2005; Llamas et al., 2017; Pääbo et al., 2004; Sampietro et al., 2006; Wall and Kim, 2007; Willerslev and Cooper, 2005).

In human aDNA assays, contaminant DNA is expected to have either an environmental (e.g. soil microbes) or a common vertebrate and human origin, e.g. contaminated reagents or people involved in sample handling (Champlot et al., 2010; Deguilloux et al., 2011; Llamas et al., 2017; Sampietro et al., 2006). Since these efforts involve a single study organism for which a suitable reference genome is available, identifying environmental contamination—which usually represents the major source of contaminant DNA—is relatively straightforward. In this case, aDNA sequencing data is routinely mapped to the reference genome, thus retrieving potential endogenous reads through sequence identity (Schubert et al., 2012). However, human contamination in human samples, albeit less abundant than environmental contamination, can be particularly pernicious as endogenous and exogenous DNA molecules are highly similar. Moreover, this type of contamination is problematic as it could lead to spurious evolutionary inferences, especially when contamination and a given biological signal are similar in magnitude (Racimo et al., 2016; Wall and Kim, 2007). Consequently, a number of methods for quantifying contamination in aDNA data have emerged during the last decade. Existing methods often rely on either haploid chromosomes [e.g. the mitochondrial DNA (mtDNA) (Fu et al., 2013; Green et al., 2008; Renaud et al., 2015) and the X-chromosome in males (Rasmussen et al., 2011)] or diploid autosomes (Racimo et al., 2016).

1.1 MtDNA-based methods

Mitochondrial DNA is often present in multiple almost identical copies in a given cell and is considerably shorter than the nuclear genome. As such, mtDNA has been historically easier to target and sequence compared with the nuclear genome (Higuchi et al., 1984; Krings et al., 1997). Hence, the first computational methods to measure contamination were tailored to this short molecule for which a high depth of coverage (DoC) is often achieved. In general, methods based on haploid genomic segments (e.g. mtDNA) rely on the expectation that there is a single DNA sequence type per cell. Thus, multiple alleles at a given site would be the result of either contamination, postmortem damage, sequencing or mapping error.

Currently, there are three common mitochondrial DNA-based methods that require a high coverage mtDNA consensus sequence. Green et al. (2008) estimated mtDNA contamination in a Neanderthal sample by counting the number of reads that did not support the mtDNA consensus (assumed to be the endogenous sequence) at sites where the consensus differed from a worldwide panel of mtDNAs (‘fixed derived sites’). Later, Fu et al. (2013) introduced a method focused on modeling the observed reads as a mixture of the mtDNAs in a panel containing the endogenous sequence while co-estimating an error parameter. Importantly, these methods did not take into account the complexity of inferring the endogenous ‘consensus’ mtDNA sequence. Thus, a subsequent method (Schmutzi) sought to jointly infer the endogenous mitogenome while estimating present-day human contamination via the incorporation of the intrinsic characteristics of endogenous aDNA fragments into the model (Renaud et al., 2015).

1.2 Autosomes-based methods

Sequencing high depth ancient nuclear genomes remains challenging. Therefore, mtDNA-based contamination estimates have been used as a proxy for overall contamination (Allentoft et al., 2015). Yet, different mitochondrial-to-nuclear DNA ratios in the endogenous source and the human contaminant(s) may lead to inaccurate conclusions (Furtwängler et al., 2018). While the source of this difference has yet to be identified, accurate methods based on nuclear data are needed to estimate the level of human contamination which may have an impact on downstream analyses (Renaud et al., 2016). Indeed, most studies rely on nuclear data to answer key biological questions. A recent method (DICE) aims at estimating present-day human contamination for nuclear data (Racimo et al., 2016). It does so by co-estimating contamination, sequencing error and demography based on autosomal data. This method generally requires an intermediate DoC (at least 3×) and produces more accurate results when the sample and the contaminant are genetically distant (e.g. different species or highly differentiated populations).

1.3 X-chromosome-based methods and a novel approach

In 2011, Rasmussen et al. (2011) estimated the contamination level in whole-genome sequencing data from a male Aboriginal Australian based on the X-chromosome using a maximum likelihood method. Similar to mtDNA-based methods, this method relies on the fact that the X-chromosome is hemizygous in males. The mathematical details of the method used in that study were described in the supplementary information of Rasmussen et al. (2011). However, while this method could in principle also perform well for low depth data, its performance was not assessed in detail.

In this work, we propose a new maximum likelihood method (implemented in C++ and R) relying on ‘relatively long’ haploid chromosomes potentially sequenced at low DoC (such as the X-chromosome in human males). We present the mathematical details of our method, perform extensive simulations and analyze real data to compare it to existing nuclear-based methods. To do so, we also implement the method by Rasmussen et al. (2011) (see Sections 2.3 and 5 for a discussion on the fundamental differences between methods). We measure the performance of the methods for conditions typical of aDNA data by quantifying the accuracy of the contamination estimates and assess the effect of (i) varying levels of contamination; (ii) varying DoC; (iii) the ancestry of the endogenous and the contaminant populations and (iv) additional error in the endogenous data. We show that our method performs particularly well for low-depth data compared with other methods. It can accurately estimate present-day human contamination for male samples that are likely to be candidates for further evolutionary analysis (i.e. when contamination is <25%) when the X-chromosome DoC is as low as 0.5×. Moreover, our implementation is fast and scalable.

2 Methods

We assume we have collected high-throughput whole-genome sequence data from a sample that contains DNA from two different sources; DNA belonging to one individual of interest (the ‘endogenous’ DNA or ‘endogenous individual’), and DNA from contaminating individuals. We want to estimate the fraction c of DNA that belongs to the contaminant individuals versus the individual of interest. We assume that the individual of interest and the contaminants belong to the same species but they can belong to different populations. We denote the contaminating population by Pop_c. Given the high-throughput nature of the data, each site along the genome can be covered by multiple sequencing reads or alleles. The data has been mapped to a reference genome which includes a haploid chromosome (e.g. the X-chromosome for human males). Across all chromosomes, a fraction c of the reads belong to the contaminants while the rest ($1-c$) belong to the endogenous individual.

For haploid chromosome(s), we expect that the individual of interest will carry only one allele at each site, and we rely on this idea to estimate c, the contamination fraction. As discussed above, observing multiple alleles at a given site can be due to either sequencing error, postmortem DNA degradation, mapping errors or contamination.

2.1 Assumptions and notation

We rely on the availability of population genetic data (allele frequencies) from a ‘reference panel’ from a number of populations including Pop_c. We assume that (i) the panel includes data at L polymorphic sites; (ii) there are four possible bases (A, C, G and T) at every site but only two are naturally segregating across populations (we have bi-allelic sites); (iii) we know the population allele frequencies of Pop_c perfectly (see Section 5); (iv) the endogenous individual carries either naturally segregating alleles with equal probability (see Section 5); (v) there are no mapping errors, hence multiple alleles will only be due to error (sequencing or postmortem damage) or contamination; (vi) all observed sequencing reads are independent draws from a large pool of DNA sequences.

At every site i, we denote ${\alpha }_1^i,\hspace{0.17em}{\alpha }_2^i,\hspace{0.17em}{\alpha }_3^i$ and ${\alpha }_4^i$ the potential alleles that we can observe, with ${\alpha }_k^i\in \{A,C,G,T\},\hspace{0.17em}k\in \{1,2,3,4\}$ and $i\in \{1,\dots ,L\}$. To simplify the presentation, we will assume that at all sites ${\alpha }_1^i$ and ${\alpha }_2^i$ occur naturally in the population (bi-allelic sites), while ${\alpha }_3^i$ and ${\alpha }_4^i$ can be observed because of sequencing error or damage. For each site included in the reference panel, there is a single true allele carried by the individual of interest (the endogenous allele), where there could be also contaminant alleles. We call these the ‘endogenous allele’ ${\alpha }_E^i$ and the ‘contaminant allele(s)’ ${\alpha }_C^i$. The frequencies of the segregating alleles across sites in the contaminating population (Pop_c) will be denoted by the matrix $F=\{\overrightarrow{f^1},\dots ,\overrightarrow{f^L}\}$, where $\overrightarrow{f^i}=(f_1^i,f_2^i)$ are the frequencies of the alleles ${\alpha }_1^i$ and ${\alpha }_2^i$ in that population at site i.

We further assume that errors affect all bases equally and that they occur independently across reads and across bases within a read. The probability of having an error from base $a\in \{\mathrm{A}, \mathrm{C}, \mathrm{G}, \mathrm{T}\}$ to base $b\in \{\mathrm{A}, \mathrm{C}, \mathrm{G}, \mathrm{T}\}$ is given by the matrix $\Gamma =\left\{{\gamma }_{\mathit{ab}}\right\}$. While this can be easily generalized, in our current implementation, we will set ${\gamma }_{\mathit{ab}}=ϵ/3$ if $a\ne b$ and therefore ${\gamma }_{\mathit{aa}}=(1-ϵ)\hspace{0.17em}\forall \hspace{0.17em}a,b\in \{\mathrm{A}, \mathrm{C}, \mathrm{G}, \mathrm{T}\}$. In other words, we assume that all types of errors are equally likely. Although this assumption does not conform to known aDNA-characteristic error profiles (Briggs et al., 2007), we show through the simulations described below that despite it being unrealistic, it has little effect on the estimates. For instance, in Sections 3.5, 3.8 and 3.10 we show that our method performs well when estimating contamination in ancient samples. Furthermore, we explore and discuss the effect of differential error rates on the estimates in Section 3.9. As detailed in those sections, we expect our method to yield accurate estimates as long as error affects the sites that we use for contamination estimation and the sites that we use for error estimation equally (see Section 2.4 for details on the estimation of Γ).

Finally, we summarize the data by counting the total number of ${\alpha }_1^i,\hspace{0.17em}{\alpha }_2^i,\hspace{0.17em}{\alpha }_3^i$ and ${\alpha }_4^i$ alleles at every site and we label those counts $n_1^i,\hspace{0.17em}{n}_2^i,\hspace{0.17em}{n}_3^i$ and $n_4^i$ with $n_T^i=n_1^i+n_2^i+n_3^i+n_4^i$ and ${\vec{n}}^i$=$\{n_1^i,n_2^i,n_3^i,n_4^i\}$. We extend this notation to also keep track of multiple alleles, so for instance $n_{2,3,4}^i$ is the number of ${\alpha }_2^i,\hspace{0.17em}{\alpha }_3^i$ or ${\alpha }_4^i$ alleles. Note that $n_T^i$ represents the observed ‘DoC’ at a given segregating site (‘${\text{DoC}}_i$’); for the simulation study below, we control for the average DoC along the whole X-chromosome that we denote DoC.

2.2 Model description—a likelihood approach

Let us now assume that $X_1^i,\hspace{0.17em}{X}_2^i,\hspace{0.17em}{X}_3^i$ and $X_4^i$ are random variables keeping track of the number of ${\alpha }_1^i,\hspace{0.17em}{\alpha }_2^i,\hspace{0.17em}{\alpha }_3^i$ and ${\alpha }_4^i$ alleles that can be observed in the data at site i. We also write $X_{2,3,4}^i$, for instance, for the number of non-${\alpha }_1^i$ alleles. We can then denote $X=\{\overrightarrow{X^1},\dots ,\overrightarrow{X^L}\}$ the random variable summarizing the high-throughput data across polymorphic sites, with $\overrightarrow{X^i}=\{X_1^i,X_2^i,X_3^i,X_4^i\}$. Similarly, we denote $n=\{\overrightarrow{n^1},\dots ,\overrightarrow{n^L}\}$ the observed counts across polymorphic sites, with $\overrightarrow{n^i}=\{n_1^i,n_2^i,n_3^i,n_4^i\}$ the counts of each allele at site i. We would like to compute the probability of the data given the contamination rate, the error rates and the allele frequencies in the contaminating population. We will assume the data across sites are independent from each other given those parameters. In practice, this is true if we filter the panel so that a read only covers one polymorphic site. The likelihood function for the parameter c can then be written as:

$$\ell (c)=p(X=n|c,\Gamma ,F)=\prod _{i=1}^{L}p(\overrightarrow{X^i}=\overrightarrow{n^i}|c,\Gamma ,F).$$ (1)

The allele frequencies F are given as an input (from the reference panel) and we set the error rates Γ to the values we estimate below. We can therefore infer c from the likelihood function by finding the value c (${\widehat{c}}_{\mathit{mle}}$) that maximizes $\ell (c)$ (i.e. the maximum likelihood estimate, mle). Note that, if the sites are not independent (for instance, if the reference panel is not filtered to avoid having neighboring polymorphic sites covered by a single read), the likelihood will be a composite likelihood. In this case, our intuition is that the estimate ${\widehat{c}}_{\mathit{mle}}$ will converge asymptotically to the true c value, i.e. that we will have a consistent estimator (Wiuf, 2006).

We now explicit $p(\overrightarrow{X^i}|c,\Gamma ,F)$. There is a single true endogenous allele at each site. That allele (as discussed above) could be either ${\alpha }_1^i$ or ${\alpha }_2^i$ at every site i. We have assumed that each of those options is equally likely. We condition on either of those two options and rewrite the likelihood function:

$$\begin{array}{c}\ell (c)=\prod _{i=1}^L(p(\overrightarrow{X^i}=\overrightarrow{n^i}|c,\Gamma ,F,{\alpha }_E^i={\alpha }_1^i)p({\alpha }_E^i={\alpha }_1^i)\\ +p(\overrightarrow{X^i}=\overrightarrow{n^i}|c,\Gamma ,F,{\alpha }_E^i={\alpha }_2^i)p({\alpha }_E^i={\alpha }_2^i))\end{array}$$ (2)

 

$$\begin{array}{c}=\prod _{i=1}^L\frac{1}{2}(p(\overrightarrow{X^i}=\overrightarrow{n^i}|c,\Gamma ,F,{\alpha }_E^i={\alpha }_1^i)\hfill \\ +p((\overrightarrow{X^i})=(\overrightarrow{n^i})|c,\Gamma ,F,{\alpha }_E^i={\alpha }_2^i)).\hfill \end{array}$$ (3)

We now need to compute the probability of the counts at a given site i given the allele frequencies F in the contaminating population, the contamination rate c, the error matrix Γ, and a specific endogenous allele. We have assumed that the pool of sequencing reads we draw from is large (which is likely to be the case with high-throughput data). We therefore have that each draw is identically distributed for a given endogenous allele. We introduce a new random variable, $V_1^{i,h}$, which tracks whether we observe the allele α₁ in the hth draw at site i. We define:

$$V_1^{i,h}=\left\{\begin{array}{l}1, \text{with} \text{prob}. p_1^i, \text{when} \text{the} \text{drawn} \text{allele} \text{is} \text{an} {\alpha }_1 \text{allele},\\ 0, \text{with} \text{prob}. 1-p_1^i, \text{when} \text{the} \text{drawn} \text{allele} \text{is} \text{not} \text{an} {\alpha }_1\text{allele},\end{array}\right.$$ (4)

with $h\in 1,\mathrm{..},n_T^i$ (i.e. we have up to $n_T^i$ draws at site i). Note that since $p_1^i$ is constant for each h, $V_1^{i,h}$ is a Bernoulli random variable and $X_1^i=V_1^{i,1}+V_1^{i,2}+\cdots +V_1^{i,n_T^i}$ is binomially distributed. We can also drop the h subscript without loss of generality. Extending the notation to all four alleles, as above, we can define:

$$p_1^i:=p(V_1^i=1|c,F,\Gamma ,{\alpha }_E^i={\alpha }_1^i)$$ (5)

 

$$p_{2,3,4}^i:=p(V_{2,3,4}^i=1|c,F,\Gamma ,{\alpha }_E^i={\alpha }_1^i)=1-p_1^i$$ (6)

 

$$q_2^i:=p(V_2^i=1|c,F,\Gamma ,{\alpha }_E^i={\alpha }_2^i)$$ (7)

 

$$q_{1,3,4}^i:=p(V_{1,3,4}^i=1|c,F,\Gamma ,{\alpha }_E^i={\alpha }_2^i)=1-q_2^i,$$ (8)

where $p_k^i$ and $q_k^i$ are the probabilities of observing an allele α_k at site i, given an endogenous allele (${\alpha }_E^i={\alpha }_1^i$ or ${\alpha }_E^i={\alpha }_2^i$, respectively). With this new notation, we can rewrite the likelihood function as the product of a sum of binomial distributions:

$$\begin{array}{l}\ell (c)=\prod _{i=1}^L(p(\overrightarrow{X^i}|c,\Gamma ,F,{\alpha }_E^i={\alpha }_1^i)p({\alpha }_E^i={\alpha }_1^i)\\ +p(\overrightarrow{X^i}|c,\Gamma ,F,{\alpha }_E^i={\alpha }_2^i)p({\alpha }_E^i={\alpha }_2^i))\end{array}$$ (9)

 

$$\begin{array}{l}=\prod _{i=1}^L(\frac{1}{2}\left(\begin{array}{l}{n}_T^i\\ n_1^i\end{array}\right)\hspace{0.17em}{(p_1^i)}^{n_1^i}\hspace{0.17em}{(1-p_1^i)}^{n_{2,3,4}^i}\\ +\frac{1}{2}\left(\begin{array}{l}{n}_T^i\\ n_2^i\end{array}\right)\hspace{0.17em}{(q_2^i)}^{n_2^i}\hspace{0.17em}{(1-q_2^i)}^{n_{1,3,4}^i}).\end{array}$$ (10)

Indeed, the probability of seeing $n_1^i$ copies of the ${\alpha }_1^i$ allele in the data assuming the endogenous allele is ${\alpha }_1^i$ and that we have a total of $n_T^i$ sequenced reads at that site is given by:

$$p(X_1^i=n_1^i|c,F,\Gamma ,{\alpha }_E^i={\alpha }_1^i)=\left(\begin{array}{l}{n}_T^i\\ n_1^i\end{array}\right)\hspace{0.17em}{(p_1^i)}^{n_1^i}\hspace{0.17em}{(1-p_1^i)}^{n_{2,3,4}^i}.$$ (11)

Similarly, if the endogenous is ${\alpha }_2^i$, we have that

$$p(X_2^i=n_2^i|c,F,\Gamma ,{\alpha }_E^i={\alpha }_2^i)=\left(\begin{array}{l}{n}_T^i\\ n_2^i\end{array}\right)\hspace{0.17em}{(q_2^i)}^{n_2^i}\hspace{0.17em}{(1-q_2^i)}^{n_{1,3,4}^i}.$$ (12)

We now compute the probabilities $p_1^i$ and $q_2^i$. We will momentarily drop the i index to simplify the presentation. Let us first assume that the true endogenous allele is α₁ (i.e. we first compute p₁). By conditioning on the source of the observed allele being either the endogenous (‘endo’) or a contaminant (‘cont’) individual, we have that

$$\begin{array}{l}{p}_1=p(\text{cont})p(V_1=1|c,F,\Gamma ,\text{cont},{\alpha }_E={\alpha }_1)\\ +p(\text{endo})p(V_1=1|c,F,\Gamma ,\text{endo},{\alpha }_E={\alpha }_1)\end{array}$$ (13)

 

$$\begin{array}{l}=c\hspace{0.17em}p(V_1=1|c,F,\Gamma ,\text{cont})\\ +(1-c)\hspace{0.17em}p(V_1=1|c,F,\Gamma ,\text{endo},{\alpha }_E={\alpha }_1)\end{array}$$ (14)

In the contaminant case, we then condition on either of the naturally segregating alleles:

$$\begin{array}{l}p(V_1=1|c,F,\Gamma ,\text{cont})=p({\alpha }_C={\alpha }_1)p(V_1=1|c,F,\Gamma ,\text{cont},{\alpha }_C={\alpha }_1)\\ +p({\alpha }_C={\alpha }_2)p(V_1=1|c,F,\Gamma ,\text{cont},{\alpha }_C={\alpha }_2)\end{array}$$ (15)

 

$$=f_1{\gamma }_{11}+f_2{\gamma }_{21}.$$ (16)

While for an endogenous draw we have

$$p(V_1=1|c,F,\Gamma ,\text{endo},{\alpha }_E={\alpha }_1)={\gamma }_{11}.$$ (17)

By substituting the equations above into Equation (14) we have that

$$p_1=c(f_1{\gamma }_{11}+f_2{\gamma }_{21})+(1-c)({\gamma }_{11}).$$ (18)

There are indeed two ways to draw an α₁ allele. First, we could draw a read from a contaminating individual. This individual belongs to population Pop_c and there is therefore a probability f₁ that it carries that allele, and f₂ that it carries the alternative allele α₂. If it carries α₁, we would need no error to occur (γ₁₁). While if the contaminant carries α₂, it would need to change to α₁ through error (γ₂₁). Second, we could draw a read from the endogenous individual. Since we have assumed that the endogenous individual carries an α₁ allele, it should remain α₁, i.e. no error (γ₁₁). Note that we can obtain the other three equations for the probability of observing an α₂, α₃ or α₄ allele in a similar way:

$$p_2=c(f_1{\gamma }_{12}+f_2{\gamma }_{22})+(1-c)({\gamma }_{12})$$ (19)

 

$$p_3=c(f_1{\gamma }_{13}+f_2{\gamma }_{23})+(1-c)({\gamma }_{13})$$ (20)

 

$$p_4=c(f_1{\gamma }_{14}+f_2{\gamma }_{24})+(1-c)({\gamma }_{14}).$$ (21)

The equivalent expression for observing non-α₁ alleles is simply

$$\begin{array}{l}{p}_{2,3,4}=p(V_{2,3,4}=1)=p(V_2=1)+p(V_3=1)+p(V_4=1)\\ =1-p(V_1=1)=1-p_1\end{array}$$ (22)

since it is not possible to draw simultaneously two alleles. We then have that

$$\begin{array}{l}{p}_{2,3,4}=p(V_{2,3,4}=1|c,F,\Gamma ,{\alpha }_E={\alpha }_1)\\ =c(f_1({\gamma }_{12}+{\gamma }_{13}+{\gamma }_{14})+f_2({\gamma }_{22}+{\gamma }_{23}+{\gamma }_{24})+(1-c)({\gamma }_{12}+{\gamma }_{13}+{\gamma }_{14}).\end{array}$$ (23)

Conditioning on the endogenous allele being α₂ and following a similar logic, we have for the q_k equations:

$$q_1=c(f_1{\gamma }_{11}+f_2{\gamma }_{21})+(1-c)({\gamma }_{21})$$ (24)

 

$$q_2=c(f_1{\gamma }_{12}+f_2{\gamma }_{22})+(1-c)({\gamma }_{22})$$ (25)

 

$$q_3=c(f_1{\gamma }_{13}+f_2{\gamma }_{23})+(1-c)({\gamma }_{23})$$ (26)

 

$$q_4=c(f_1{\gamma }_{14}+f_2{\gamma }_{24})+(1-c)({\gamma }_{24})$$ (27)

 

$$\begin{array}{l}{q}_{1,3,4}=c(f_1({\gamma }_{11}+{\gamma }_{13}+{\gamma }_{14})+f_2({\gamma }_{21}+{\gamma }_{23}+{\gamma }_{24}))\\ +(1-c)({\gamma }_{21}+{\gamma }_{23}+{\gamma }_{24}).\end{array}$$ (28)

The first part of the q_k equations, corresponding to the contaminant read case, is identical to the first part of the p_k (Equations (18)−(21)). For the second part, which corresponds to the endogenous read case, we can simply invert indices 1 and 2 to recover the second part of the p_k equations. We can simplify all equations further since in our implementation we have ${\gamma }_{\mathit{aa}}=(1-ϵ)$ and ${\gamma }_{\mathit{ab}}=ϵ/3\hspace{0.17em}\forall \hspace{0.17em}a,b\in \{\mathrm{A}, \mathrm{C}, \mathrm{G}, \mathrm{T}\} \text{with} a\ne b$. With the i index, we have for the $p_k^i$:

$$p_1^i=c(f_1^i\hspace{0.17em}(1-\frac{4\hspace{0.17em}ϵ}{3})+\frac{4\hspace{0.17em}ϵ}{3}-1)+1-ϵ$$ (29)

 

$$p_2^i=c(f_1^i\hspace{0.17em}(\frac{4\hspace{0.17em}ϵ}{3}-1)+1-\frac{4\hspace{0.17em}ϵ}{3})+\frac{ϵ}{3}$$ (30)

 

$$p_3^i=\frac{ϵ}{3}$$ (31)

 

$$p_4^i=\frac{ϵ}{3}$$ (32)

 

$$p_{2,3,4}^i=c(f_1^i\hspace{0.17em}(\frac{4\hspace{0.17em}ϵ}{3}-1)+1-\frac{4\hspace{0.17em}ϵ}{3})+ϵ.$$ (33)

Note that we can further simplify those expressions by using $f_2^i=1-f_1^i$:

$$p_1^i=c{f}_2^i\hspace{0.17em}(\frac{4\hspace{0.17em}ϵ}{3}-1)+1-ϵ$$ (34)

 

$$p_2^i=c{f}_2^i\hspace{0.17em}(1-\frac{4\hspace{0.17em}ϵ}{3})+\frac{ϵ}{3}$$ (35)

 

$$p_3^i=\frac{ϵ}{3}$$ (36)

 

$$p_4^i=\frac{ϵ}{3}$$ (37)

 

$$p_{2,3,4}^i=c{f}_2^i\hspace{0.17em}(1-\frac{4\hspace{0.17em}ϵ}{3})+ϵ.$$ (38)

And for the $q_k^i$:

$$q_1^i=c{f}_1^i\hspace{0.17em}(1-\frac{4\hspace{0.17em}ϵ}{3})+\frac{ϵ}{3}$$ (39)

 

$$q_2^i=c{f}_1^i\hspace{0.17em}(\frac{4\hspace{0.17em}ϵ}{3}-1)+1-ϵ$$ (40)

 

$$q_3^i=\frac{ϵ}{3}$$ (41)

 

$$q_4^i=\frac{ϵ}{3}$$ (42)

 

$$q_{1,3,4}^i=c{f}_1^i\hspace{0.17em}(1-\frac{4\hspace{0.17em}ϵ}{3})+ϵ.$$ (43)

2.3 Previous related approach—‘One-consensus’

The method we propose above is related to one that was described in the supplementary material of Rasmussen et al. (2011). The key difference, beside the consideration that a contaminant allele may also have errors, is that Rasmussen et al. assumed that at each polymorphic site, the most prevalent allele in the sequencing data was the true endogenous allele. Without loss of generality, we can call this allele α₁. In other words, we assume that at every site $p({\alpha }_E={\alpha }_1)=1$ and $p({\alpha }_E={\alpha }_2)=0$. Denoting $Y_1^i$ the number of consensus α₁ alleles, $Y_{2,3,4}^i$ the number of non-consensus alleles and $W_1^i$ and $W_{2,3,4}^i$ the corresponding Bernoulli variables for each $k^{\text{th}}$ draw, we have that (dropping momentarily the i index):

$$p(W_1=1|c,F,\Gamma )=c(f_1{\gamma }_{11}+f_2{\gamma }_{21})+(1-c){\gamma }_{11}$$ (44)

Similarly, for $Y_{2,3,4}$, we have that

$$\begin{array}{l}p(W_{2,3,4}=1|c,F,\Gamma )=c(f_1({\gamma }_{12}+{\gamma }_{13}+{\gamma }_{14})+f_2({\gamma }_{22}+{\gamma }_{23}+{\gamma }_{24}))\\ +(1-c)({\gamma }_{12}+{\gamma }_{13}+{\gamma }_{14})\end{array}$$ (45)

Finally, denoting ${\varphi }_1=p(W_1=1|c,F,\Gamma )$ and ${\varphi }_{2,3,4}=p(W_{2,3,4}=1|c,F,\Gamma )$, and expressing the errors rates in terms of $ϵ$, we have as above:

$${\varphi }_1=c(f_1^i(1-\frac{4}{3}ϵ)+\frac{4}{3}ϵ-1)+1-ϵ$$ (46)

 

$${\varphi }_{2,3,4}=c(f_1^i(\frac{4}{3}ϵ-1)+1-\frac{4}{3}ϵ)+ϵ.$$ (47)

The likelihood function then becomes:

$$\begin{array}{l}\ell (c)=p(Y|c,\Gamma ,F)\\ =\prod _{i=1}^L\left(\begin{array}{l}{n}_T^i\\ n_1^i\end{array}\right)\hspace{0.17em}{({\varphi }_1^i)}^{n_1^i}\hspace{0.17em}{({\varphi }_{2,3,4}^i)}^{n_{2,3,4}^i}\end{array}$$ (48)

since $p({\alpha }_E={\alpha }_2)=0$. We call this approach the ‘One-consensus’ method since the ‘consensus’ allele is assumed to be the truth; accordingly, we will call our new approach the ‘Two-consensus’ method since we integrate over both segregating alleles and assume that either can be the true endogenous (consensus) allele at a particular site.

2.4 Estimating error rates

To infer the contamination rate c, we first obtain a point estimate of $ϵ$ by considering the flanking regions of the polymorphic sites following (Rasmussen et al., 2011). Specifically, we assume that the sites neighboring a polymorphic site i in the reference panel are fixed across all populations—including population Pop_c—and are given by the most prevalent allele at each of those sites. Without loss of generality we can assume ${\alpha }_1={\alpha }_C={\alpha }_E$ for all flanking sites. We label the flanking sites i_j where, e.g. $i_{-2}$ is the second site to the left of site i (i₀ is site i). We assume that non-α₁ alleles at those neighboring sites are solely due to error. In other words when $j\ne 0$, we have that $f_2^{i_j}=0$, and hence $p_1^{i_j}=1-ϵ$ and $p_{2,3,4}^{i_j}=cϵ+(1-c)ϵ=ϵ$ (Equations (34) and (38)). We consider the counts of non-α₁ alleles at s sites left and right of the polymorphic sites. Having assumed that (i) reads are independent of each other, (ii) bases within a read are independent from each other, we have

$$\ell (ϵ)=p((\sum _i\sum _{j=-s,j\ne 0}^s{X}_1^{i_j})={\nu }_1^s|ϵ)=\left(\begin{array}{l}{\nu }_T^s\\ {\nu }_1^s\end{array}\right){(1-ϵ)}^{{\nu }_1^s}{ϵ}^{{\nu }_T^s-{\nu }_1^s}$$

where ${\nu }_1^s=\sum _i\sum _{j=-s,j\ne 0}^s{n}_1^{i_j},\hspace{0.17em}{\nu }_T^s=\sum _i\sum _{j=-s,j\ne 0}^s{n}_T^{i_j}$. We choose s and filter the polymorphic sites such that error rate estimation is restricted to fixed sites (not polymorphic in the contaminant population). In practice, by default, we set s = 5 and exclude polymorphic sites located <10 bp away from another polymorphic site. To infer the contamination rate, we then substitute the error rate in Equation (10) by the maximum likelihood estimate of the error rate obtained at the flanking regions across polymorphic sites, which is simply: ${\widehat{ϵ}}_{\mathit{mle}}=\frac{{\nu }_1^s}{{\nu }_T^s}$.

2.5 Standard error

To compute the standard error for the inferred parameter, we consider a block jackknife approach. Specifically, we split the haploid chromosome into M blocks, each corresponding to one of the L sites (we have $M\le L$). For each $m=\mathrm{1\dots }M$ we leave one block m out and compute ${\widehat{c}}_{\mathit{mle}}^m$ over the remaining data. We estimate the standard error for the estimate using the following relationship:

$${\sigma }_c=\sqrt{\frac{M-1}{M}\sum _{m=1}^M{({\widehat{c}}_{\mathit{mle}}^m-{\widehat{c}}_{\mathit{mle}})}^2}.$$

Under some regularity conditions, the 95% confidence interval for our contamination rate is then $\widehat{c}\pm 2{\sigma }_c$.

2.6 Implementation

Our method is implemented as two separate steps. First, the counts of bases are tabulated for a sample provided by the user as a bam file of mapped reads. This is done within the software ANGSD (Korneliussen et al., 2014) which allows to filter the data efficiently and is implemented in c++. The contamination estimates are obtained in the second step based on the output from step one along with a file containing information about the reference population (polymorphism data from a reference panel). This step is implemented in R. The documentation along with a description and explanation of options and output are found on the following website: https://github.com/sapfo/contaminationX. The human reference population allele frequency panels used in this study are available there as well.

3 Performance assessment

To evaluate our method’s performance in practice, we carried out simulations with parameters typical of human aDNA experiments. Although we focused on humans, the method is in principle equally applicable to other species for which polymorphism data are available. In particular, we assessed the effect on the estimates of (i) the contamination fraction; (ii) the DoC (defined as the average number of reads covering each base of the X-chromosome); (iii) the genetic distance between the sample and the contaminant; (iv) the genetic distance between the contaminant and the reference panel assumed to be the contaminating population; and (v) the error rate. In addition, we compared our method with two existing methods based on nuclear data; namely, our implementation of the ‘One-consensus’ method by Rasmussen et al. (2011) and DICE by Racimo et al. (2016). In all cases, we simulated sequencing data by sampling and ‘mixing’ mapped reads from publicly available genomes in known proportions while controlling for the DoC. Our simulations do not match the model in all aspects – for instance we simulate a single contaminant individual – but they are meant to mimic typical real life conditions.

3.1 General simulation framework and settings

For all experiments described below we used our method with the following settings: −d 3, −e 20 (i.e. filtering for sites with a minimum DoC of 3 and a maximum of 20) and maxsites = 1000 (resampling at most 1000 blocks for the block jackknife procedure). To compare methods and parameter values, we computed the root mean square error (RMSE), the bias and the range for a set of k contamination estimates from simulated data $\widehat{C}=\{{\widehat{c}}_1,{\widehat{c}}_2,\dots ,{\widehat{c}}_k\}$ and an expected contamination fraction c_exp (where applicable) as follows:

1. $\mathit{RMSE}=\sqrt{\frac{{\sum }_{i=1}^k({\widehat{c}}_i-c_{\hspace{0.17em}\text{exp}\hspace{0.17em}}{)}^2}{k}}$

2. $\mathit{Bias}=\frac{{\sum }_{i=1}^k{\widehat{c}}_i}{k}-c_{\hspace{0.17em}\text{exp}\hspace{0.17em}}$

3. $\mathit{Range}=\max \left(\widehat{C}\right)-\min \left(\widehat{C}\right)$

For all experiments where we estimated RMSE, Bias and Range, we simulated 100 replicates for each parameter combination.

3.2 Test genomes and reference panels

We considered Illumina whole-genome sequencing data from a subset of the present-day individuals reported in Meyer et al. (2012). We included data from six male individuals ranging in DoC between 19.9× and 26.7×: a Yoruba (HGDP00927), a Karitiana (HGDP00998), a Han (HGDP00778), a Papuan (HGDP00542), a Sardinian (HGDP00665) and a French (HGDP00521). All data were pre-processed, mapped and filtered following (Malaspinas et al., 2014).

We considered ten populations from the HapMap project as potential proxies for Pop_c. Those populations represent broad scale worldwide variation (Altshuler et al., 2010). We filtered each panel by removing: (i) all sites located in the pseudoautosomal region of the human X chromosome (parameters −b 5000000 −c 154900000 discard the first 5 Mb and last ∼370 kb of the human X chromosome, following Ensembl GRCh37 release 95); (ii) all sites with a minor allele frequency lower than 0.05 (−m 0.05); (iii) all variable sites located <10 bp away from another variable site. The number of remaining sites after filtering each panel is shown in Table 1.

Table 1.

Reference allele frequency panels used for estimating contamination

Population	Number of sites	Number of sites (filtered)a	Number of individuals
HapMap_ASW	38 703	31 324	90
HapMap_CEU	73 562	58 190	180
HapMap_CHB	67 307	51 494	90
HapMap_GIH	34 158	26 098	100
HapMap_JPT	64 290	49 715	91
HapMap_LWK	39 992	31 119	100
HapMap_MEX	34 360	23 190	90
HapMap_MKK	37 935	29 612	180
HapMap_TSI	33 928	25 097	100
HapMap_YRI	89 604	72 546	180

^aNumber of single nucleotide polymorphism (SNPs) included for each population after applying the filtering described in the text. Data were downloaded from http://hapmap.ncbi.nlm.nih.gov/downloads/frequencies/2010-08_phaseII+III/allele_freqs_chrX_CEU_r28_nr.b36_fwd.txt.gz.

3.3 One- versus Two-consensus methods and reasonable parameter range for c

We first explored the contamination fractions for which our method yields informative estimates. To do so, we sampled 1× data from a Yoruba individual and ‘contaminated’ these with data from a French individual at increasing contamination rates {0.01, 0.05, 0.1,…, 0.45, 0.50}. For this exploratory analysis, we simulated five replicates for each contamination rate and used the HapMap_CEU reference panel as a proxy for the allele frequencies in the contaminant population. For each simulation, we estimated the contamination fraction using the ‘One-consensus’ (Rasmussen et al., 2011) and the ‘Two-consensus’ methods.

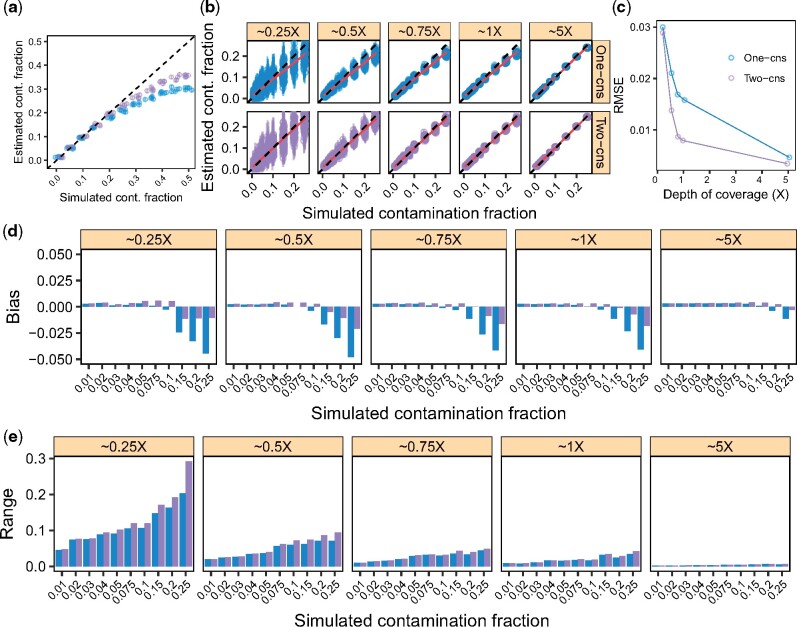
The results are shown in Figure 1a. We observed that the estimated contamination rates matched the simulated rates qualitatively for both methods as long as the contamination fraction was below $0.25$ (see below for a discussion relative to the bias). In addition, the ‘Two-consensus’ method provided more accurate results especially when contamination was high. Given both methods failed at estimating very large contamination fractions accurately, we simulate data with contamination rates between 0.01 and 0.25 for subsequent analyses.

Fig. 1.

Parameter range for c and effect of the DoC on the X-chromosome for the One- and Two-consensus methods. We simulated data as described in Sections 3.3 and 3.4 to explore the contamination fractions and DoC for which our method yields informative estimates: we ‘contaminated’ a Yoruba with a French individual with increasing contamination fractions while controlling for the DoC. (a, b) Contamination estimates for each replicate (points) and corresponding 95% confidence intervals (vertical bars). The dashed lines indicate the expected values and the red lines a linear regression. (c) RMSE for each DoC, combining the results across simulated contamination fractions in (b). (d) Bias for each DoC and contamination fraction combination. (e) Range for each DoC and contamination fraction combination. Results for the ‘One-consensus’ and ‘Two-consensus’ methods are shown in blue and purple, respectively, across all panels

3.4 One- versus Two-consensus methods and DoC

We carried out a similar simulation experiment to determine the broad effect of the DoC on the estimates of the ‘One-consensus’ and the ‘Two-consensus’ methods. In this case, we sampled sequencing data at varying DoC {0.25×, 0.5×, 0.75×, 1×, 5×} with increasing contamination rates {0.01, 0.02, 0.03, 0.04, 0.05, 0.075, 0.1, 0.2, 0.25}. Results are summarized in Figure 1b−e.

We found that both methods yielded estimates close to the truth, especially when the contamination fraction was within the simulation range [0.01, 0.25] and the DoC was $\ge$0.5× (Fig. 1b). As expected, the range of the estimates increased with lower DoC and higher contamination fractions (Fig. 1e). The RMSE also decreased with higher DoC, while we observed that this decrease slowed down between 0.75× and 1×.

We observed that both methods slightly overestimated contamination for true contamination fractions <0.1 and underestimated it for values >0.1. Importantly, the downward bias for large contamination fractions and the RMSE (especially between 0.5× and 5×) were substantially lower for the ‘Two-consensus’ method compared with the ‘One-consensus’ one. This difference in bias is intuitive and follows from the mathematical details of each of the methods (see also Section 5). Thus, since the ‘Two-consensus’ approach performed equally well for higher DoC and outperformed the previous method with lower DoC, we see no advantage in using the ‘One-consensus’ method and focus hereafter on characterizing the ‘Two-consensus’.

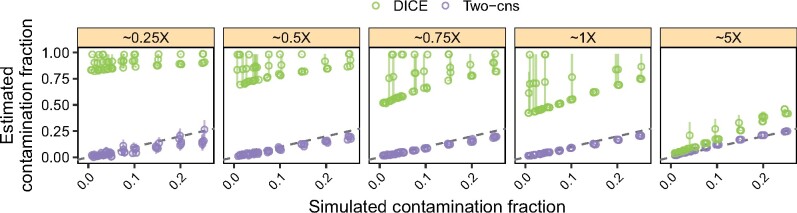
3.5 Comparison with DICE

We compared the performance of our method with DICE, an autosomal data-based method for co-estimating contamination, sequencing error and demography (Racimo et al., 2016). We carried out simulations as detailed above and we ‘contaminated’ an ancient Native American genome (Anzick1) (Rasmussen et al., 2014) with data from a present-day French individual. In this case, we used an ancient individual to favor DICE, which jointly estimates the error rate and contamination fraction. We ran DICE with the two-population model using the 1000 Genomes Project Phase III CEU allele frequencies as a proxy for the frequencies of the putative contaminant and the YRI frequencies to represent the ‘anchor’ population. We let the MCMC algorithm run for 100 000 steps and discarded as burn-in the first 10 000 steps. We used the coda R package to obtain 95% posterior credibility intervals. For our method we used the parameters detailed in Section 3.1. We summarize the results for this comparison in Figure 2.

Fig. 2.

Simulation results comparing our method to DICE. We simulated data as described in Section 3.5 and estimated contamination across five replicates using our method (purple) and DICE (green). We ‘contaminated’ the Anzick1 ancient Native American genome with a French individual at increasing contamination fractions while controlling for the DoC. Vertical bars correspond to 95% confidence intervals for the Two-consensus method and to 95% credible intervals for DICE. The dashed line indicates the expected values. Note that the simulated DoC corresponds to the autosomal DoC for DICE and the X-chromosome DoC for our method (i.e. autosomes and X-chromosomes were simulated independently)

In agreement with the simulations based on present-day data in the previous section, we observed that our method yielded accurate estimates for a DoC as low as 0.5× and for true contamination fractions below 0.25. In contrast, in most cases, we observed that DICE did not converge to a value close to the simulated contamination fraction for a DoC ≤1 but instead vastly overestimated contamination. Whereas DICE started to yield useful estimates at 5×, our method provided more accurate estimates than DICE for all simulated cases. These results suggest that for low depth data (≤5×) the ‘Two-consensus’ method should be used to estimate human−human contamination.

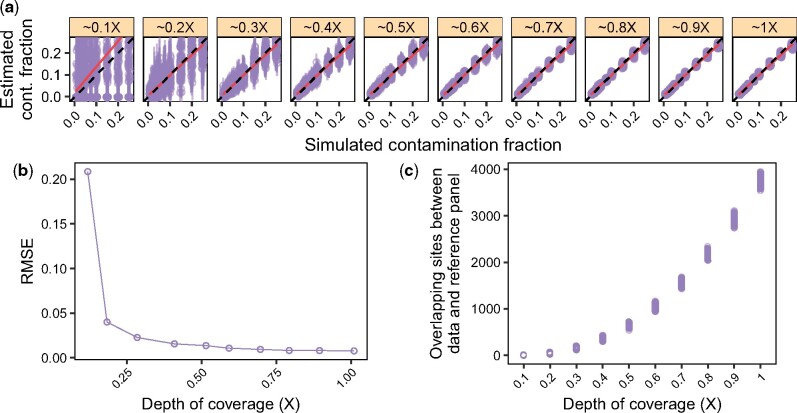
3.6 Lowest bound on DoC for the two-consensus method

To get a sense of the minimal amount of data necessary to obtain accurate estimates with our method, we carried out simulations for a more fine-grained range of DoC {0.1×, 0.2×, 0.3×, 0.4×, 0.5×, 0.6×, 0.7×, 0.8×, 0.9× and 1×}. Results are summarized in Figure 3. In agreement with results presented in Section 3.4, we observed that across simulations, the estimates closely matched the truth from 0.2× onward (see linear regression). Similarly, the RMSE sharply decreased at 0.2× while it qualitatively saturated from 0.5× onward. In other words, our estimates are already meaningful for a DoC as low as 0.2×, and become quite accurate for a DoC ≥0.5×. Based on these results, when the reference panel used for estimation is a close representative of the contaminant population (see also Section 3.8), we recommend the use of our method to determine if a sample or library is highly contaminated (contamination >25%), or to estimate the contamination fraction when contamination is between 0 and 25%.

Fig. 3.

Minimum required depth of coverage (DoC) on the X-chromosome. We simulated data as described in Section 3.4, but we considered an additional range of low DoC {0.01×, 0.02×,…, 1×}. (a) Contamination estimates for each replicate (points) and corresponding 95% confidence intervals (vertical bars). Dashed lines indicate the expected values and solid lines show a linear regression. (b) RMSE for each DoC, combining the results across contamination fractions from (a). (c) Number of overlapping sites between the simulated data and the contaminant population panel (HapMap_CEU in this case) after applying the filters detailed in Section 3.1

3.7 The effect of the genetic distance between the endogenous and the contaminant individuals

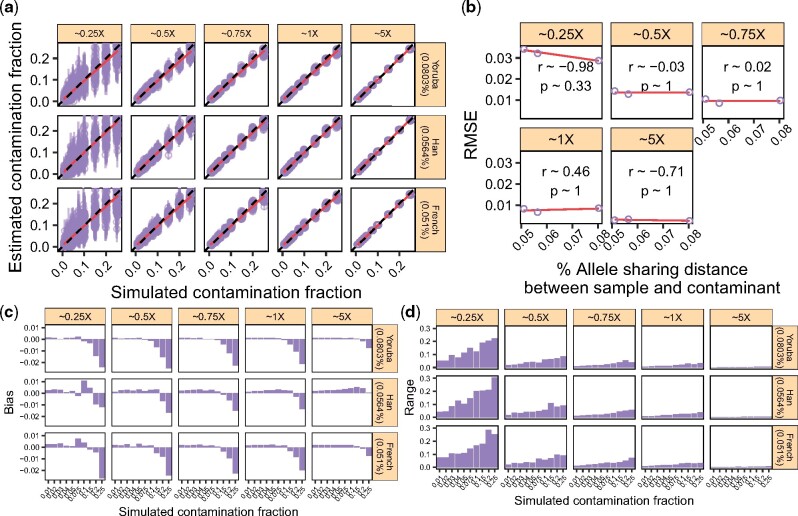
Intuitively, estimating the contamination fraction should be easier (e.g. will require less data) when the endogenous and contaminant individuals are more distantly related. To get further insights into this intuition, we sampled sequencing data from a Sardinian individual and contaminated them with data from three individuals (a Yoruba, a Han and a French). We used the same DoC and contamination fraction settings described in Section 3.4. In each case, we used the HapMap reference panel that best represented the ancestry of the contaminant individual to estimate the contamination fraction (HapMap_YRI for the Yoruba, HapMap_Han for the Han, and HapMap_CEU for the French). We explored the relationship of the contamination estimates and the ‘allele sharing distance’ between the X-chromosome consensus sequences from the five individuals and the French contaminant. We defined the allele sharing distance as the number of differences between the Sardinian and each contaminant individual’s consensus, divided by the number of non-missing sites for each pair.

Results are shown in Figure 4. We obtained a very similar picture across simulated contaminant individuals. Indeed, the RMSE, the bias and the range of the estimates vary as a function of the DoC with qualitatively little effect from the genetic distance between the contaminant and the endogenous individual. This observation makes sense given our model, where we do not consider the ancestry of the endogenous individual. As such, for the DoC we considered, our method seemingly performs equally well regardless of the ancestry of the contaminant individual, even for cases where contaminant and endogenous are closely related (e.g. a Sardinian individual contaminated with a French individual).

Fig. 4.

The effect of the genetic distance between the endogenous and the contaminant individuals. We considered three individuals (Yoruba, Han, French) and used them to ‘contaminate’ a Sardinian individual (Section 3.7). We simulated data with increasing contamination fractions while controlling for the DoC. (a) Contamination estimates for each replicate (points) and corresponding 95% confidence intervals (vertical bars). Dashed lines indicate the expected values and solid lines show a linear regression. The allele sharing distance between each sample and the contaminant is indicated in parentheses. (b) RMSE for each DoC as a function of the allele sharing distance between the five samples and the contaminant, combining the results across contamination fractions in (a). We show the Pearson correlation coefficient for each DoC. (c) Bias for each DoC, sample and contamination fraction combination. (d) Range for each DoC, sample and contamination fraction combination

3.8 The effect of the genetic distance between the simulated contaminant and the reference panel used for inferring contamination

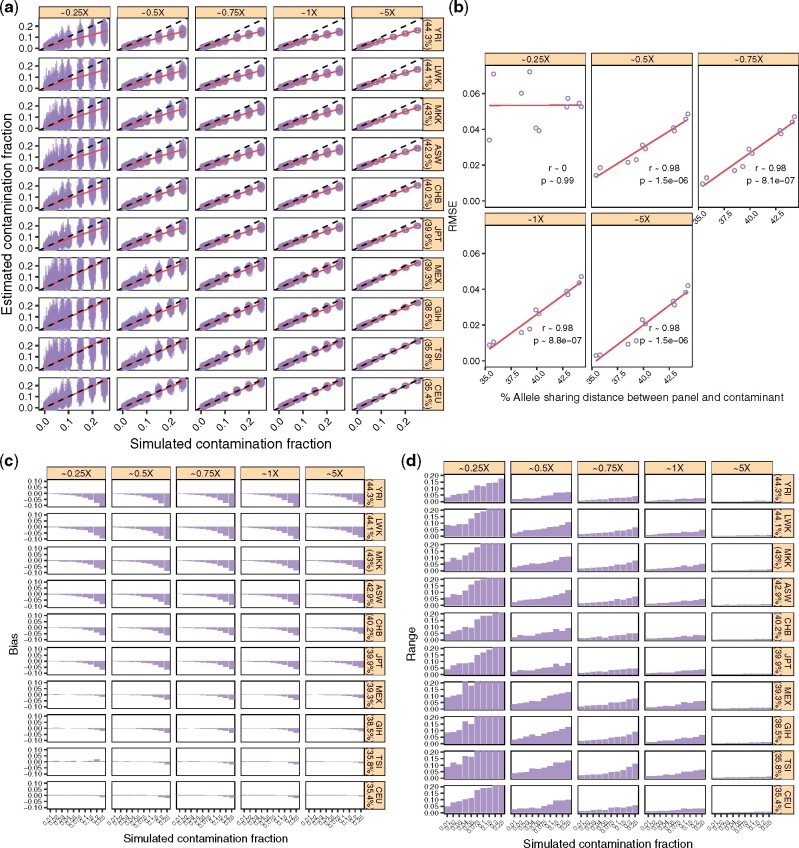
For this experiment, we sampled data from a Sardinian individual and contaminated it with data from a French individual. We applied the same DoC and contamination fraction settings from the above experiments and used 10 different reference populations from the HapMap project as proxies for Pop_c: ASW, CEU, CHB, GIH, JPT, LWK, MEX, MKK, TSI and YRI, to estimate the contamination fraction. To get an indicative value for the distance between the reference HapMap panel and the contaminant, we estimated the genetic distance between the X-chromosome consensus sequence from the contaminant French individual and each reference population. We defined this distance as $D_{X_{\mathit{French}}-\mathit{Po}{p}_c}=\frac{\sum _{i=1}^L{\psi }_i}{L}$ where L is the total number of sites included in the reference population Pop_c (assumed to be the contaminant) and ψ_i is the frequency of the allele carried by the contaminant individual X (French in this case), at locus i. Note that we only considered the sites that are included in all reference panels to compute this distance. Results are shown in Figure 5.

Fig. 5.

The effect of the distance between the reference population (Pop_c) and the contaminant. We simulated data as described in Section 3.7. We considered the ten reference populations described in Table 1 and ‘contaminated’ a Sardininan with a French individual. We simulated data with increasing contamination fractions while controlling for the DoC on the X-chromosome. (a) Contamination estimates for each replicate (points) and corresponding 95% confidence intervals (vertical bars). Dashed lines indicate the expected values and solid lines show a linear regression. The genetic distance between the reference panel ($D_{X-\mathit{Po}{p}_c}$) is indicated in parentheses. (b) RMSE for each DoC as a function of $D_{X-\mathit{Po}{p}_c}$, combining the results across contamination fractions in (a). We show the Pearson correlation coefficient for each DoC. (c) Bias for each DoC, sample and contamination fraction combination. (d) Range for each DoC, sample and contamination fraction combination

We found that mis-specifying the contaminant population led to an underestimation of the contamination fraction (Fig. 5a)—an effect that follows from the dependency of p_k and q_k on the allele frequencies of the contaminant population. In fact, as indicated by the strong correlation between the RMSE and the genetic distance $D_{X_{\mathit{French}}-\mathit{Po}{p}_c}$, worse ‘guesses’ of the contaminant ancestry resulted in worse estimates. This correlation was similar across all tested DoC but 0.25×. We observed a downward bias for larger simulated contamination fractions that increased with $D_{X-\mathit{Po}{p}_c}$. Although the overall effect could be deemed relatively small (e.g. RMSE <0.05 with the HapMap_YRI panel), if the contaminating population is not known, we recommend comparing results obtained through different reference populations.

We further explored the effect of using different contaminant populations in practice by estimating contamination in real data from Allentoft et al. (2015). We considered sequencing data from 14 male individuals for which the X-chromosome DoC is >0.3×, and used the CEU, CHB and YRI panels for estimation. In agreement with Allentoft et al. (2015), contamination estimates were low for all individuals (<5%) (Fig. 6a). Yet, we observed that estimates based on the CEU reference panel were, on average, slightly greater than those based on the other two panels: 0.3% when using CHB and 0.6% with YRI (Fig. 6b). This pattern is expected as the majority of the samples in Allentoft et al. (2015) have been handled by individuals with West Eurasian genetic ancestry. Whereas the observed difference is small, these estimates illustrate the potential effect of mis-specifying the ancestry of the contaminant(s). Notably, we expect this consideration to become more relevant as aDNA research becomes accessible to more researchers with different genetic ancestries around the world, since it will increase the diversity across the potential contaminating sources.

Fig. 6.

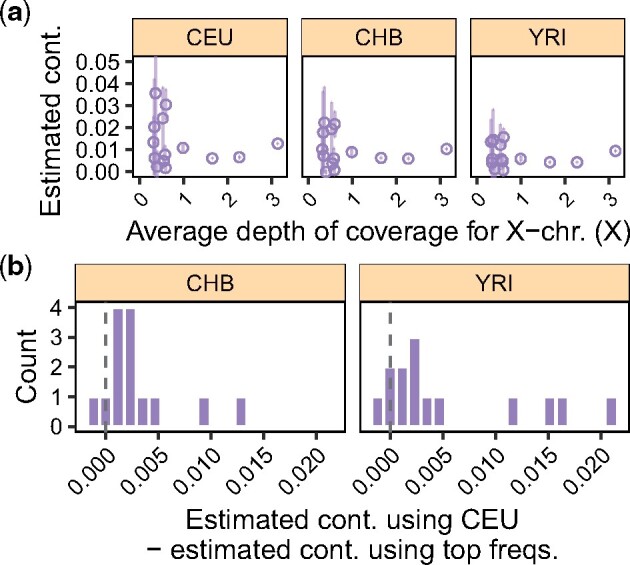
Contamination estimates for 14 > 0.3× male individuals from Allentoft et al. (2015). (a) Contamination estimates as a function of the DoC on the X-chromosome for each sample. Estimates obtained using the CEU, CHB and YRI panels are shown in each panel. (b) Histograms of the difference between the estimates obtained using CEU and the populations shown at the top of each panel

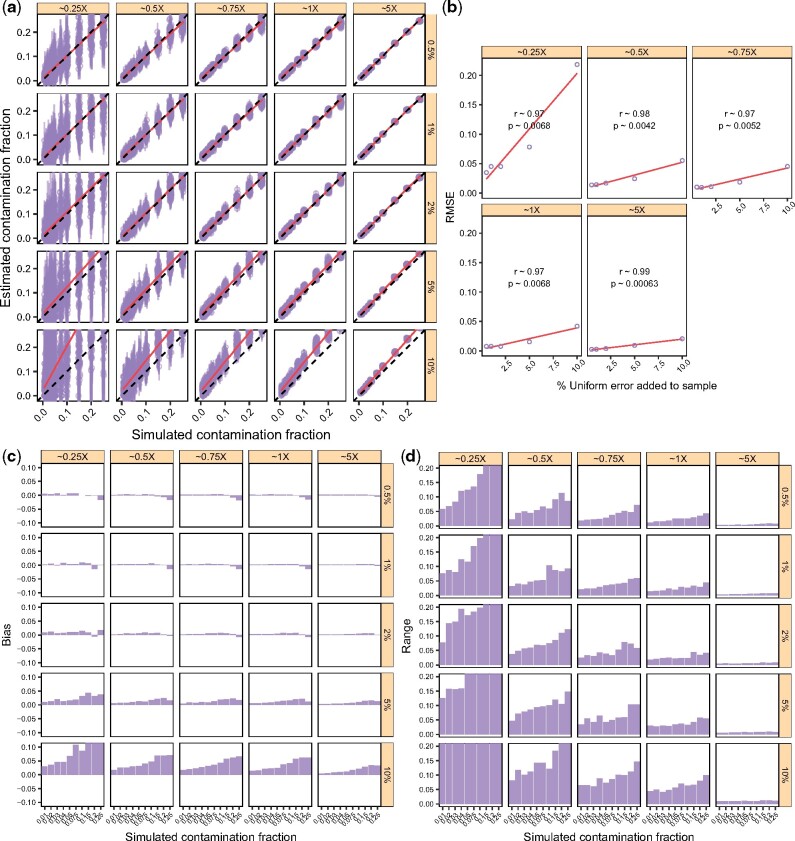
3.9 The effect of differential error rates in the endogenous and contaminant individuals

We assessed the effect of varying the error rates in the endogenous sequencing data by simulating data as detailed above. However, in this case, we added errors to the Yoruba reads at a constant rate $ϵ\in \{0.005,0.01,0.02,0.05,0.1\}$ by using a transition matrix $\Gamma ={\gamma }_{\mathit{ab}}$ analogous to the one used for error rate estimation. Results are summarized in Figure 7. Qualitatively, although there is a significant positive correlation between the RMSE and the error (Fig. 7b), the overall effect is small, except for the extreme cases of 5 and 10% added error, where we observe a systematic overestimation of contamination. Yet, we note that current second generation sequencing platforms such as the Illumina HiSeq, have substantially lower error rates, e.g. sequencing error rates in the modern human genome dataset from Meyer et al. (2012) have been estimated to be between 0.03 and 0.05% (Malaspinas et al., 2014). The apparent innocuousness of additional small amounts of error, is likely due to the fact that uniform error is accounted for in the first step of our procedure, and that the error rate is smaller than the explored range of contamination rate (except for 5 and 10% added error).

Fig. 7.

The effect of differential error rates in the endogenous individual. We simulated data as described in Section 3.4 and added error increasingly to the Yoruba individual. (a) contamination estimates for each replicate (points) and corresponding 95% confidence intervals (vertical bars). Dashed lines indicate the expected values and solid lines show a linear regression. Added error rates are indicated to the right of each panel. (b) RMSE for each DoC on the X-chromosome as a function of the added error. We show the Pearson correlation coefficient for each DoC. (c) Bias for each DoC, added error and contamination fraction combination. (d) Range for each DoC, added error and contamination fraction combination

We note that the observed error structure for aDNA is different from our simulations. In particular the error is not independent of the position across reads. For example, C to T and G to A misincorporations tend to accumulate towards the reads’ termini (Briggs et al., 2007). However, we expect damage-derived error to be uniform across polymorphic sites, in the sense that segregating and neighboring sites are equally likely to be damaged. Therefore, we do not expect aDNA damage to inflate contamination estimates differently from how uniform error does. We note, however, that if variable sites are more error-prone than neighboring sites due to sequence-intrinsic features, contamination may be overestimated. In Section 3.5, we showed that contamination estimates for simulations involving real aDNA data are qualitatively similar to those obtained for simulations with present-day data.

3.10 The effect of ‘ancient’ contamination

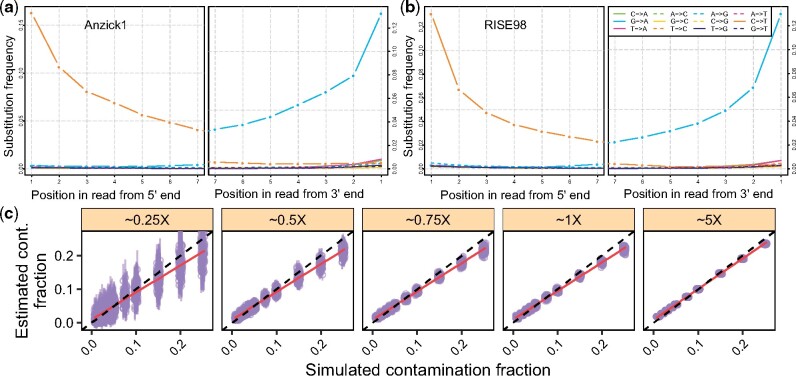
Laboratory best practices include measures to prevent sample cross-contamination (Llamas et al., 2017). However, the recent introduction of robotic technology to aDNA workflows where tubes are left open for substantial time periods has increased the concerns regarding cross-contamination. In this case, both the endogenous and contaminant DNA will have error patterns consistent with aDNA postmortem damage. Importantly, this scenario is similar to the case where contaminant DNA introduced with sample handling in the past accumulates damage over time, thus resembling aDNA (Sampietro et al., 2006). Therefore, we explored the performance of our method when the endogenous and contaminant individuals both have aDNA damage signatures. We ‘contaminated’ the Anzick1 genome (Rasmussen et al., 2014) with data from a Scandinavian Bronze Age individual (RISE98) (Allentoft et al., 2015), simulated data as detailed in Section 3.3 and used the CEU panel for estimation. We observed that the estimates matched the simulated contamination rates closely and improved with the DoC, in agreement with Section 3.3 (Fig. 8). Thus, we consider that our method will be able to detect sample cross-contamination and ‘ancient’ contamination, even if the endogenous and contaminant individuals carry aDNA-characteristic error patterns.

Fig. 8.

The effect of ‘ancient’ contamination. We simulated data as described in Section 3.10. (a, b) misincorporation frequencies with respect to the position from the 5′ (left) and 3′ (right) ends of the reads for the Anzick1 and RISE98 genomes. (c) Contamination estimates for each replicate (points) and corresponding 95% confidence intervals (vertical bars). Dashed lines indicate the expected values and red lines show a linear regression

3.11 The potential effect of contamination on evolutionary analysis

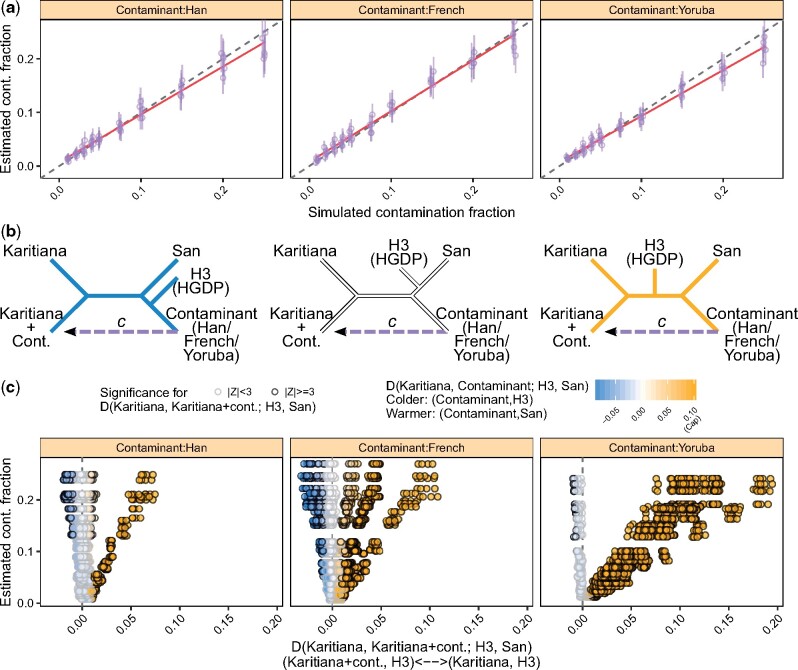
To illustrate the effect of contamination on evolutionary inference, we simulated contaminated whole-genome data and computed D-statistics, which are routinely used in paleogenomic studies to test for treeness and gene flow (Patterson et al., 2012). We simulated 1× whole-genome data (∼0.5× on the X-chromosome) from a Karitiana individual (Native American) and ‘contaminated’ these with data from a Han (East Asian), a French (European) and a Yoruba (African). We generated five replicates for each contamination rate (0.01−0.25) for each contaminant, and used the CHB, CEU and YRI reference panels for estimation, respectively. In Figure 9a, we show that the contamination estimates correspond closely to the simulated contamination fractions.

Fig. 9.

An example of the effect of contamination on evolutionary analysis. We simulated data as described in Section 3.11. We ‘contaminated’ ∼1× whole-genome data from a Karitiana with three different individuals (a Han, a French and a Yoruba), with increasing contamination fractions. We estimated contamination using the CHB, CEU and YRI panels, respectively. (a) Contamination estimates for each replicate (points) and corresponding 95% confidence intervals (vertical bars). Dashed lines indicate the expected values and red lines show a linear regression. (b) A schematic representation of the genetic relationships between the simulated datasets, the contaminant individuals and the HGDP test populations (H₃) considered in this experiment. Unrooted tree topologies are colored according to the three possible outcomes of D_cont [color scheme in (c)], which varies with the choice of H₃. $D_{\mathrm{cont}}\sim 0$: white, the Karitiana and the contaminant are symmetric with respect to H₃. $D_{\mathrm{cont}}<0$: colder, the contaminant shares more alleles with H₃ than the Karitiana do. $D_{\mathrm{cont}}>0$: warmer, the contaminant shares more alleles with the San than the Karitiana do. (c) D-statistics exploring the relationship between the simulated datasets and different populations in the HGDP panel (D_case), as a function of the estimated contamination fraction. D_case with $\left|Z\right|>3$ have a darker outline. The color scheme corresponds to D_cont, which summarizes the relationship between the Karitiana, the contaminant and a given H₃ population [see schematic representation in (b)]. For clarity, positive values of D_cont were capped at 0.1 when defining the color scale

For each replicate, we computed two D-statistics that we label: (a) the case D-statistic (D_case) and (b) the contaminant D-statistic (D_cont). D_case has the form D (Karitiana, Karitiana_cont; H₃, San), where Karitiana_cont represents the simulated dataset and Karitiana, H₃ and San are populations from the HGDP (Li et al., 2008)—a reference panel including 938 individuals from 53 worldwide populations genotyped over ∼644 000 SNP markers. In the absence of contamination, we expect D_case to be consistent with 0, thus supporting a clade between the whole-genome sequenced Karitiana individual and the Karitiana population, to the exclusion of other H₃ populations. We explored the deviation from this expectation (x-axis in Fig. 9c) as a function of (a) the estimated contamination fraction (y-axis in Fig. 9c and b) D_cont. The latter has the form D (Karitiana, Contaminant; H₃, San), which summarizes the relationship between Karitiana, the contaminant and a given H₃ (color scheme in Fig. 9c). For instance, when the French individual is the contaminant, D_cont is expected to be >0 if H₃ is a Native American or an East Eurasian population, <0 if H₃ is West Eurasian and ∼0 if H₃ is African.

We observed that contamination gave rise to statistically significant deviations from D_case = 0 in both directions: $D_{\mathrm{case}}>$ 0 and $D_{\mathrm{case}}<0$ (significance was assessed through a block-jackknife-based Z-test, where $\left|Z\right|>3$ was regarded as statistically significant; Patterson et al., 2012). When the contaminant was an outgroup to the Karitiana and H₃ ($D_{\mathrm{cont}}>0$), we observed that D_case became significantly positive with contamination as low as 2%, regardless of the contaminant. As expected, D_case increased as a function of (a) the contamination and (b) the length of the branch leading from the common ancestor of H₃ and the Karitiana on the one hand, and the common ancestor of H₃, the Karitiana and the contaminant on the other hand (D_cont) (Patterson et al., 2012). In other words, contamination in Karitiana_cont ‘artificially’ increased allele sharing between the Karitiana and H₃, with the effect being more pronounced when the Karitiana were either closer to H₃ (e.g. the Surui from Brazil) or more distant from the contaminant (e.g. the Yoruba).

Conversely, when the Karitiana were an outgroup to H₃ and the contaminant ($D_{\mathrm{cont}}<$0), larger contamination fractions (>5%) were required to produce significantly negative values of D_case. Intuitively, D_case increased as a function of (a) the contamination and (b) the shared drift between the contaminant and H₃, after their divergence from the Karitiana. In contrast to the scenario above, contamination in Karitiana_cont ‘artificially’ increased allele sharing between Karitiana_cont and H₃, with the effect being larger when H₃ and the contaminant were closer (e.g. the French and the Sardinian).

In practice, ‘conservatively’ set contamination thresholds represent one of the criteria followed for sample exclusion from ancient genomic projects. However, these results illustrate that it is difficult to anticipate the effects of contamination. Indeed, depending on the test, a contamination fraction as low as 2% could result in rejecting a true null hypothesis, while a contamination fraction as large as 10% might not have a substantial effect. As such, we recommend that the potential effect of contamination is assessed for particular analyses, especially when subtle genetic signatures are being dissected or when inferences depend on single samples.

4 Running time

We explored the running time of our method implementation using a machine with 24 2.8 GHz Intel Xeon cores. The data parsing step for 5× X-chromosome datasets was always below 3 min. Following data parsing, the raw contamination estimate is obtained nearly instantaneously. Thus, the step that requires the largest amount of time is the calculation of the standard error. Since we use a jackknife approach this will have a running time of ${\mathcal{O}}^2$ in the number of sites. Therefore, the actual running time will depend on the DoC and the number of polymorphic sites in the reference panel. Using the parameters detailed in Section 3.1, we estimated the contamination fraction in the ∼14× Anzick1 genome (Rasmussen et al., 2014) with a joint running time of ∼3 min for the parsing and estimation steps.

5 Discussion

We present here a new method for efficiently estimating contamination in low depth high-throughput sequencing data based on information from haploid chromosomes. To assess whether our method can be used in challenging situations typical of aDNA research, we tested it through realistic simulations and assess its performance. Note that our simulations involved a single contaminating individual—a realistic assumption in our view. Yet, our method is designed to handle multiple contaminants from Pop_c. Simulations with multiple contaminant improve the performance of our method but we chose to discuss these unfavourable conditions as in practice it is hard to know if contamination is from one or several individuals. Despite the important discrepancy, our simulations suggest that our method can correctly flag highly contaminated samples from male individuals that are unlikely to be useful in evolutionary analyses ($c\ge 25\%$), and outputs an accurate contamination estimate for male samples with lower amounts of contamination ($c<$25%).

Based on the results above, we show that provided one can approximatively guess the contaminant reference population, our estimates will be meaningful even when DoC is as low as 0.2× and essentially unbiased when contamination is below 15%. We also show that our method is easily scalable since the running time is below 5 min for a DoC as high as 10× (on the X-chromosome). Based on these features, we regard our method as an adequate and practical tool for screening large numbers of aDNA male samples and related libraries to get a sense of candidates for follow-up analyses. Indeed, aDNA studies have transitioned to the genomic era with single studies sometimes including whole genomes (Damgaard et al., 2018) or genome-wide SNP data (Olalde et al., 2018) from hundreds of individuals. However, most ancient samples carry low proportions of endogenous DNA and the resulting DoC for a given shotgun experiment is often quite low for laboratories working with a finite budget. Thus, prioritizing resources on promising samples is often a key aspect of human aDNA research.

We have shown that typical sequencing error rates and the genetic distance between the endogenous and contaminant individuals do not affect the accuracy of our estimates. However, we found that mis-specifying the contaminant population leads to underestimation ($\mathit{Bias}<$0.1). In particular, while the method is still able to detect contamination, this issue is more pronounced when contamination is >10%. In practice, our method flags contaminated samples with estimates >10% and we recommend that the user takes a conservative approach in particular when the ancestry of the contaminant population is unknown- and explores several potential contaminant populations reporting the highest estimate. Note that a high error rate could in principle impact the accuracy, but our simulations suggest this would lead to an overestimation of contamination, i.e. our method would be conservative in this case.

Finally, we show that, for human−human contamination, our method outperforms previously published nuclear genome data-based methods ‘One-consensus’ (Rasmussen et al., 2011) and DICE (Racimo et al., 2016). It outperforms them in particular for low depth data (<5×) and when contamination is above 10%. The main difference between the One- and Two-consensus is that for the latter we do not assume that the true endogenous allele is the observed consensus at each site. This assumption is particularly wrong for low-depth data, even when filtering for sites with at least three reads. Since we show the ‘Two-consensus’ method is more accurate across the parameter space we explored, our new method is a better choice. In contrast, DICE can be used for females as well and offers additional functionality by co-estimating contamination, error rates and demography using autosomal data. Thus, while DICE is not useful for screening (or estimating contamination for) low depth samples, an appropriate protocol for male samples would comprise an initial screening using the ‘Two-consensus’ method, followed by further deeper sequencing. If the resulting DoC is >5× DICE could be used to co-estimate contamination and the demography.