The Manipulation of the Internal Hydrophobicity of FraC Nanopores Augments Peptide Capture and Recognition

Abstract

The detection of analytes and the sequencing of DNA using biological nanopores have seen major advances over recent years. The analysis of proteins and peptides with nanopores, however, is complicated by the complex physicochemical structure of polypeptides and the lack of understanding of the mechanism of capture and recognition of polypeptides by nanopores. In this work, we show that introducing aromatic amino acids at precise positions within the lumen of α-helical fragaceatoxin C (FraC) nanopores increased the capture frequency of peptides and largely improved the discrimination among peptides of similar size. Molecular dynamics simulations determined the sensing region of the nanopore, elucidated the microscopic mechanism enabling accurate characterization of the peptides via ionic current blockades in FraC, and characterized the effect of the pore modification on peptide discrimination. This work provides insights to improve the recognition and to augment the capture of peptides by nanopores, which is important for developing a real-time and single-molecule size analyzer for peptide recognition and identification.

Nanopores are potential candidates for developing low-cost and high-throughput portable detectors. Biological nanopores have been shown to be particularly suitable for the detection and discrimination of small molecules based on the current blockade generated when an analyte binds to or translocates through the nanopore.¹⁻⁹ The amplitude of the analyte-induced current signal, however, cannot always be easily predicted. Molecules usually reduce the nanopore current by a value that is proportional to the volume of electrolyte displaced inside the nanopore.¹⁰⁻¹² And for model analytes such as polyethylene glycol (PEG), it has been shown that the nanopore currents can size the polymer in a fashion similar to mass spectrometry.¹³⁻¹⁵ However, many other factors can influence the overall ionic current, such as the conformation of the molecule, its charge or dipole, its position, or its shape.^8,16−20 For more complex polymers such as DNA or proteins, the relationship between analyte mass and signal is more complicated. Most notably, the four DNA nucleotides²¹ or DNA homopolymers^22,23 can induce four different ionic currents that are not related to the mass or the volume of the individual bases.

Recently, we have characterized actinoporin fragaceatoxin C (FraC) for nanopore analysis.²⁴ FraC monomers have a mass of approximately 20 kDa and form nanopores on membrane containing sphingomyelin.²⁵ The crystal structure of wild-type FraC revealed an oligomeric pore formed from eight identical subunits (octameric).²⁶ Compared to the cylindrical shape of β-barrel nanopores commonly used in nanopore analysis, FraC forms a V-shaped α-helical nanopore with a ∼5.5 nm cis entry and a ∼1.5 nm narrow trans exit. In a previous work, we have shown that wild-type FraC (hereafter FraC, see Materials and Methods for the exact sequence) is capable of forming different oligomeric forms—most notably the octameric (T1) and heptameric (T2)—with a distinct pore volume and range of detectable peptides.²⁷ Intriguingly, peptides did not enter the nanopore at physiological pH values. Only when the pH of the solution is lowered to less than 6.5 are peptide blockades observed, reaching optimal capture frequencies at pH values lower than 4.5.²⁸ Although the detailed mechanism responsible for the pH dependence of capture is not understood,²⁹ it is likely that the shape and the highly negatively charged inner constriction of the FraC nanopore play an important role, most likely by influencing the electro-osmotic flow across the nanopore.^9,28,30−36 Importantly, we also demonstrated that at the exact pH of 3.8 and 1 M KCl the current observed from peptide translocation through FraC correlates with the mass of the peptide despite their chemical composition,²⁷ as also observed with α-hemolysin (αHL) nanopores,¹⁵ making FraC a prime target for the development of single-molecule nanopore spectrometry for peptides.

Although several properties of FraC—such as the electro-osmotic flow (EOF), the recognition volume, and the ability to capture peptides^27,28 or DNA²⁴—could be adjusted through protein engineering, the interactions between the nanopore and the analytes and the influence of such interactions on the analyte distinguishability remain poorly characterized. Furthermore, the duration of detectable peptide blockades is rather short [hundreds of microseconds (average dwell time for angiotensin 1 is 0.15 ± 0.04 ms)],²⁷ which implies that a sizable fraction of the translocation events occurs undetected and that some detected events could be inaccurately characterized because of the limited temporal resolution of the ionic current measurement. Previous work with αHL nanopores revealed that a positive surface charge in the nanopore is important for increasing the frequency of DNA capture.^37,38 In this work, we show that the capture and recognition of peptides in α-helical FraC is improved by the introduction of aromatic amino acids near the constriction. This finding enables development of nanopore systems for real-time identification of peptides according to their volume and is crucial for single-molecule sensing where the efficiency of peptide capture is paramount.

Results/Discussion

Fragaceatoxin C Mutant Screening

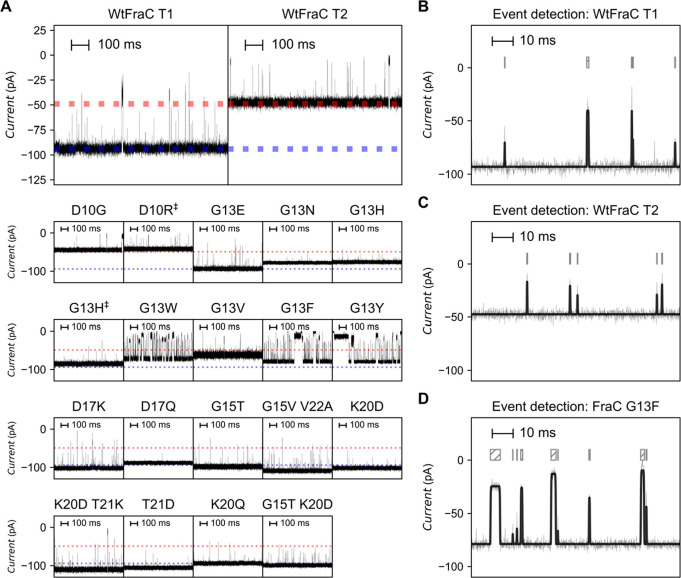
The engineering of α-helical nanopores—such as FraC—is not as straightforward as in the case for β-barrel nanopores—such as α-hemolysin³⁹—because the side chains in the α-helical transmembrane region have a complex interaction with the aqueous and lipid phases. In order to identify the variable region, we aligned the sequence of FraC with other actinoporins (Figure 1A), which have 60–80% common sequence identity.⁴⁰ We identified five nonconserved—lumen facing—positions: D10, G13, G15, D17, and K20 (numbering based on the wild-type FraC sequence, Figure 1B). Notably, the mutation of D10 to arginine (R) in the lumen was reported previously for the preparation of nanopores amenable to DNA analysis.²⁴ We engineered these nonconserved positions into different functionalities. Each of the positions near the presumed recognition site (G13)²⁷ was modified to a residue of a positively (K, R, or H) or negatively (D or E) charged group as well as a neutral (G or Q) or aromatic (W, Y, F, or V) group. In FraC, a glycine residue is positioned at residue 15, while the most common amino acid in other actinoporins is a threonine. We reasoned that the additional methyl group pointing toward the bilayer (Figure 1B) might stabilize the baseline current relative to FraC (Figure 1C). In addition, the aligned sequence (Figure 1A) often contains a pair of opposite charges at positions 20/21; therefore, we constructed two mutants that have the same characteristics: T21D and the double mutant K20D/T21K. For completion, we also included a change of charge on position 20 by introducing a glutamic acid (K20D).

Figure 1.

Actinoporins common sequence alignment and wild-type fragaceatoxin C. (A) Common sequence alignment of known actinoporins. The dots represent the same amino acid as the common sequence; other amino acids are represented by their single-letter code. (B) Artistic model of fragaceatoxin C (PDB: 4TSY) inserted into a lipid bilayer, across which a voltage is applied. Several nonconserved positions are enlarged. (C) Representative traces of the octameric (T1) and heptameric (T2) form of wild-type fragaceatoxin C under an applied potential of −50 mV in 1 M KCl and 50 mM citric acid titrated with bis-tris propane to pH 3.8. Traces were collected at a sampling frequency of 50 kHz, using a 10 kHz Bessel filter and 5 kHz Gaussian filter.

At pH 3.8 and in 1 M KCl solutions, FraC exists in three oligomeric forms, presumably corresponding to octamers, heptamers, and hexamers.²⁷ For initial screening, we only considered octameric pores (or type I pores, T1), with the exception FraC-T2, which corresponds to the heptameric type II pores. Octameric oligomers were identified as the nanopores with the highest conductance. Several mutations significantly reduced the open pore current (I₀) relative to WtFraC-T1 (95 ± 1 pA), some to an extent that the I₀ resembled FraC-T2 (47 ± 3 pA, Supplementary Table 1). Notably, decreased I₀ was observed when residues with a larger volume were introduced, for example, for the aromatic residues (W/F/Y) introduced on position 13 (I₀ = 64 ± 8, 77 ± 4, and 82 ± 3 pA, respectively). Mutations of residues 20 and 21 neither reduced nor increased the I₀, and the introduction of tryptophan residues at positions D10 and D17 resulted in nanopores that did not fold or did not insert into the 1,2-diphytanoyl-sn-glycero-3-phosphocholine planar lipid bilayers under the aforementioned conditions.

The signal-to-noise ratio (I₀/σ(I₀), SNR, Supplementary Table 1) of most mutant pores was similar to that of WtFraC-T1 (35 ± 3, −50 mV), while the introduction of a threonine residue on position 15 showed a 5% increased I₀ (100 ± 3 pA), but showed no significant difference in the SNR (39 ± 6, −50 mV). Replacing the aspartic acid on position 10 by a neutral glycine reduced the SNR (17 ± 2, −50 mV) significantly, as well as introducing a tryptophan residue at position 13 (G13W-FraC-T1, 21 ± 2, −50 mV), a value comparable to FraC-T2 (22 ± 5, −50 mV). However, the introduction of either phenylalanine (G13F-FraC-T1, 31 ± 4, −50 mV) or tyrosine (G13Y-FraC-T1, 36 ± 3, −50 mV) at position 13 did not significantly reduce the SNR compared to WtFraC-T1. Interestingly, we observe a rapid decrease in SNR when a valine residue was introduced on position 13 (G13V-FraC-T1, 5 ± 2, −50 mV).

The observed baseline signals of all aromatic substitutions at position G13 contained current blockades without the presence of added analyte (gating), with an event frequency varying greatly between buffer preparations. These stochastically distributed blockades—with a median dwell time near 0.7 ± 0.4 ms and relative blocked current (excluded current) of 57 ± 10%—reduced to 5 ± 2 events·s^–1 by additional filtering of the buffer solvent using activated charcoal. As this procedure especially reduces the presence of hydrophobic molecules in the final solution, we assume that the gating of these pores is caused by sensitivity toward hydrophobic molecules due to interactions with the hydrophobic patch that was introduced in the recognition area of the pore.

Peptides have different size and chemical properties. Therefore, the predicted range of detectable analytes and frequency of their capture is expected to differ between mutant pores, given their different physicochemical properties. In order to compare between pores, we utilize a mixture of peptides that were generated from the nonspecific tryptic digest of lysozyme (Gallus–Gallus). We used nonspecific trypsin (not purified, containing additional proteases such as chymotrypsin), as it yields a more stochastic peptide mixture with a broad distribution of peptide mass (Supplementary Tables 3 and 4), which is advantageous when sampling nanopores with different chemical compositions. In addition, the mixture has a relatively uniform charge since trypsin cleaves at positively charged amino acids and the pH of the solution is set to 3.8. Therefore, most peptides will have a positive charge next to the zwitterionic charges on the peptide, yielding a positive net charge. All pores were tested with the same proteolytic mixture.

We classify the observed events by quantifying the flat-top shape fitted using a least-squared Levenberg–Marquardt method and a generalized flat-top normal distribution function (see Materials and Methods). In brief, this fit results in a β value that can classify the events as either a spike with β < 1, a normal distribution with β = 1, or flat-top distribution with β > 1. Unless stated otherwise, we report events with β > 1. In addition, for each blockade we determine the excluded current (I_ex%), which is the percentage of the current that is blocked during a translocation event relative to the open pore current [(I_o – I_b)/I_o, where I_b is the average ionic current of the peptide event].

Under an applied potential of −50 mV (+50 mV for D10R-FraC-T1) and in 1 M KCl at pH 3.8, we observe that the capture efficiency of the nonspecific tryptic digest of lysozyme is affected by the mutations near the nanopore constriction (Figure 2A, Supplementary Table 5). When the charge at position 10 or 17 was removed (D10G-FraC-T1 or D17Q-FraC-T1 mutation), the capture frequency was reduced from 13 ± 2 events·s^–1 for WtFraC-T1 to 3.8 ± 0.7 and 1.8 ± 0.5 events·s^–1, respectively. It is important to consider that, even at pH 3.8, about half of the aspartic acid residues retain a negative charge. It has been shown that the EOF is critical for efficient capturing of peptides in the nanopore, and the strength and direction of the EOF are dependent on charges in the constriction site.²⁸ Therefore, the reduced capturing efficiency of peptides with a noncharged constriction can be attributed to the reduced EOF across the nanopore. Replacing the negative charge with a positive charge on these positions (D10R or D17K) significantly changed the behavior of the pore. D10R-FraC-T1 showed a destabilized baseline current under an applied bias of −50 mV, but is stable under +50 mV (Supplementary Figure 1), thereby behaving opposite to FraC. In contrast, D17K-FraC-T1 showed an unstable baseline signal under an applied bias potential of +50 mV, but is stable when −50 mV was applied. Replacing the charge of K20 by introducing an aspartic acid increased the capture frequency only slightly (18.5 ± 0.4 events·s^–1) compared to WtFraC-T1 (13 ± 2 events·s^–1). As expected, the lipid-facing mutation G15T did not significantly change the capture frequency of the pore (12 ± 2 events·s^–1).

Figure 2.

Electrophysiology recordings of (mutant) fragaceatoxin C with trypsin-digested lysozyme. (A) Representative traces of fragaceatoxin C nanopores after addition of an equal concentrations of trypsin-digested lysozyme under an applied potential of −50 mV. The dotted blue line represents the baseline current of the octameric (T1) form of wild-type fragaceatoxin C; the dotted red line represents the baseline current of the heptameric (T2) form of wild-type fragaceatoxin C. (B–D) Representative trace of octameric fragaceatoxin C (T1, B), heptameric fragaceatoxin C (T2, C), and fragaceatoxin C mutant G13F (D). The gray line represents the recorded trace, and the black superimposed line represents the fit after event detection. The block above the trace aligns with the length of the events. Traces were collected in 1 M KCl and 50 mM citric acid titrated with bis-tris propane to pH 3.8 at a sampling frequency of 50 kHz, using a 10 kHz Bessel filter and 5 kHz Gaussian filter.

Interestingly, we find that the introduction of a neutral, hydrophilic asparagine residue on position 13 results in no observed peptide capture, whereas the introduction of an aromatic residue (Y, F, or W) increases the capture frequency to 43 ± 8, 41 ± 4, and 43 ± 9 events·s^–1, respectively, which is significantly different from WtFraC-T1 (13 ± 2 events·s^–1) and FraC-T2 (11 ± 3 events·s^–1). Most of the blockades in pores with an aromatic residue on G13 were flat-top shaped with relatively long dwell times (0.32 ± 0.06, 0.18 ± 0.03, and 0.22 ± 0.06 ms for G13Y-FraC-T1, G13F-FraC-T1, and G13W-FraC-T1, respectively, compared to 0.09 ± 0.06 ms for WtFraC-T1 (Figure 2B) and 0.10 ± 0.01 ms for FraC-T2 (Figure 2C). In contrast, we observe that the substitution of glycine 13 to valine showed little significant difference in capture frequency (17 ± 0.1) or dwell time (0.084 ± 0.002 ms) when compared to WtFraC-T1. The reversal potential of WtFraC-T1 and G13F-FraC-T1 nanopores at pH 3.8 is the same and near zero (Supplementary Table 6), indicating that in both pores the EOF is weak.

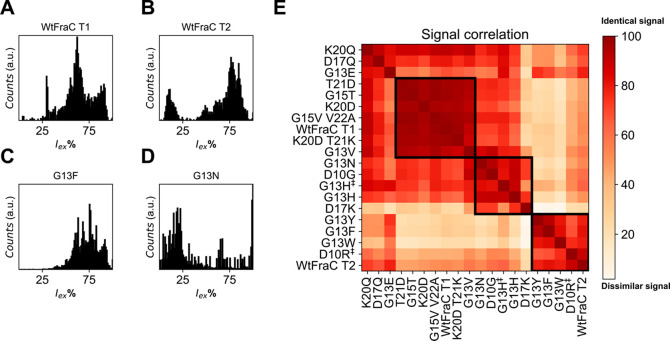
In order to compare the different mutants, we constructed the excluded current spectrum (shown for four pores in Figure 3A–D) by creating a histogram of the excluded currents (I_ex%) using all events with β > 1 (5 kHz Gaussian filter, see Materials and Methods). We normalized the spectra and observe distinct patterns for WtFraC-T1 and T2 (Figure 3A/B) with sharp Gaussian-shaped peaks for G13F-FraC-T1 (Figure 3C), while G13N-FraC-T1 results in a seemingly stochastic spectrum (Figure 3D). We compared the excluded current spectra (Supplementary Figure 3) using a point-to-point spectral matching algorithm, using the excluded current spectrum where 40% < I_ex% < 95% (see Materials and Methods). This range was chosen as events with an I_ex lower than 40% are near the baseline and we are unable to identify them accurately, and events with an I_ex larger than 95% are full blockades that result from the convoluted spectrum of large fragments, which individually do not contribute to the identification of proteins.

Figure 3.

Event counts and signal correlation of (mutant) fragaceatoxin C with trypsin-digested lysozyme. (A–D) Observed excluded current spectra from tryptic digest of lysozyme. (A) Octameric wild-type fragaceatoxin C (T1), (B) heptameric wild-type fragaceatoxin C (T2), (C) fragaceatoxin C mutant G13F, and (D) fragaceatoxin C mutant G13N. (E) Squared first-derivative Euclidean cosine correlation of residual current spectra of (mutant) fragaceatoxin C combined with equal units of trypsin-digested lysozyme. The black boxes surrounding multiple mutants represent similar signals. Traces were collected in 1 M KCl and 50 mM citric acid titrated with bis-tris propane to pH 3.8 at a sampling frequency of 50 kHz, using a 10 kHz Bessel filter and 5 kHz Gaussian filter. The external bias was −50 mV except for D10R^‡ and G13H^‡, which were tested at +50 mV.

To better represent the data, we perform hierarchal clustering using the Ward distance,⁴¹ which revealed three major clusters of nanopores (see Materials and Methods, Figure 3E). The first cluster forms a group of nanopores with high similarity to the octameric WtFraC-T1 (Figure 3A), containing the mutations of T21D, G13V, G15T, K20D, K20D T21K and G15V, V22A. The majority of the mutations on positions 20/21 were included in this cluster, indicating that mutations on these residues did not significantly alter the recognition site of FraC. This observation is in agreement with previous results, where the constriction site was expected to be located between residues 10 and 17.²⁷ The second cluster comprised most of the positive nanopores (e.g., D17K-FraC-T1) and G13N-FraC-T1 (Figure 3D). We believe that the stochastic nature of these spectra is caused by the inability to correctly localize the I_ex% of the events, as most peptides translocate rapidly (faster than 100 μs). The third group of octameric mutant nanopores shared a high similarity to the heptameric form of FraC (Figure 3B). This group includes the aromatic nanopores (G13Y/F/W-FraC-T1) and one positively charged pore (D10R-FraC-T1). Importantly, the D10R mutation prevented efficient capturing of peptides at negative applied potential, but the ability to capture peptides could be restored when a positive potential was applied instead.

Fragaceatoxin C Mutant Characterization

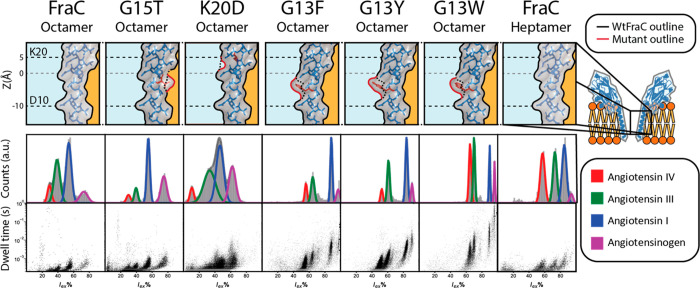
We selected five mutants that show interesting characteristics toward protein detection for further characterization, namely, G15T-FraC-T1, as it is comparable to WtFraC-T1 with a slightly increased I₀, K20D-FraC-T1, as it had one of the higher SNRs and good capture frequency, and the aromatic mutations at G13 (G13Y/F/W-FraC-T1) for their increased dwell times compared to FraC-T2 and capture frequency. For the characterization of these pores we used a mixture of well-defined, chemically similar peptides, in contrast to the unspecific lysozyme digest that was used before. The mixture consisted of four peptides:²⁷ angiotensinogen (DRVYIHPFHLVIHN, 1758.9 Da, charge = +3.96), angiotensin 1 (DRVYIHPFHL, 1296.5 Da, charge = +2.96), angiotensin 3 (RVYIHPF, 931.1 Da, charge = +2.16), and angiotensin 4 (VYIHPF, 774.9 Da, charge = +1.16) abbreviated as Pre-Ang, Ang-I, Ang-III, and Ang-IV, respectively. The resolution of the nanopores was quantified by measuring the separation between peptides using the difference between the peak centers and their mean standard deviation, as shown in eqs 1 and 2.

1

2

where R_s is resolution and μ₁ and μ₂ are the peak centers with standard deviation σ₁ and σ₂, respectively. If R_s < 2, the difference between the peak centers is less than twice the average standard deviation and no baseline separation is achieved. To achieve an overlap of less than 5%, an R_s ≥ 4 is required; that is, the difference between the peak centers is equal to or bigger than 4 times the average standard deviation of the peaks. Thus we can consider them separated. Larger values of R_s indicate a better separation (Table 1).

Table 1. Differences between Peptide Peak Centers (ΔI_ex%) and the Observed Baseline Separation (R_s).

MW: 1759-931	FraC-T1	FraC-T2	K20D- FraC-T1	G15T- WtFraC-T1	G13F-FraC-T1	G13Y- FraC-T1	G13W- FraC-T1
ΔIex% (Ang-IV – Ang-III)	8.8 ± 0.7%	18 ± 3%	14 ± 6%	12 ± 5%	9.2 ± 0.3%	9.1 ± 0.7%	5.0 ± 0.3%
ΔIex% (Ang-III – Ang-I)	17 ± 2%	12.3 ± 0.5%	15 ± 1%	17 ± 2%	24 ± 1%	22 ± 1%	19.9 ± 0.2%
ΔIex% (Ang-I – Pre-Ang)	19.0 ± 0.2%	9.3 ± 0.3%	16.2 ± 0.4%	19.0 ± 0.3%	10 ± 1%	6.1 ± 0.8%	6.4 ± 0.2%
Rs (Ang-IV – Ang-III)	2.1 ± 0.7	4.1 ± 1.2	2.6 ± 1.4	2.0 ± 0.5	4.6 ± 0.5	4.4 ± 1.1	3.6 ± 0.4
Rs (Ang-III – Ang-I)	3.5 ± 0.5	4.2 ± 0.5	2.3 ± 0.2	3.3 ± 0.4	12.1 ± 4.3	11.8 ± 2.9	19.1 ± 1.7
Rs (Ang-I – Pre-Ang)	4.1 ± 0.3	4.0 ± 0.3	3.2 ± 0.5	4.6 ± 0.2	6.1 ± 2.3	4.0 ± 0.7	7.2 ± 1.2

MW:772-556	FraC-T2	FraC-T3	G13F-FraC-T2	G13W-FraC-T2
ΔIex% (Leu-enk – Ang-II(4–8))	N.O.	27.6 ± 0.8%	19.1 ± 0.1%	10.6 ± 0.8%
ΔIex% (Ang-II(4–8) – kemptide)	N.O.	N.O.	6 ± 2%	N.O.
ΔIex% (Leu-enk – Ang-II(4–8))	N.O.	5 ± 1	11 ± 2	3 ± 2
Rs (Ang-II(4–8) – kemptide)	N.O.	N.O.	3 ± 2	N.O.

As observed before from the analysis of the proteolytic digest of lysozyme, both the G15T and K20D mutations did not significantly improve the resolution compared to WtFraC-T1. In fact, the mutation to K20D reduced the resolution by broadening the peaks of all peptides (Table 1). Comparing the dwell times of the peptides measured in FraC-T2 and the aromatic pores shows that the increased retention (Figure 4), which reduces the spread in the residual current, explains the increased resolution. All the aromatic pores revealed a similar trend in the resolution; however, the difference between peak centers is largest for the G13F mutation and lowest for the G13W mutation, while the standard deviation within the residual current follows a reverse trend, resulting in similar observed resolutions.

Figure 4.

Peptide recognition of (mutant) fragaceatoxin C. Mutations are shown in red on the lumen of fragaceatoxin C modeled on PDB: 4TSY. The fit of the residual current is shown for angiotensin IV (VYIHPF), angiotensin III (RVYIHPF), angiotensin I (DRVYIHPFHL), and angiotensinogen (DRVYIHPFHLVIHN) each in 2.5 μM concentration, recorded under an applied potential of −50 mV. Traces were collected in 1 M KCl and 50 mM citric acid titrated with bis-tris propane to pH 3.8 at a sampling frequency of 50 kHz, using a 10 kHz Bessel filter and 5 kHz Gaussian filter. Histograms were created from all events with a dwell time larger than 200 μs, with the exception of G13F, G13Y, and G13W, where the minimal dwell time was set to 1 ms. The dwell time set against the residual current shows all events with a dwell time larger than 200 μs. The marker size of data points in the residual current set against the dwell time is adjusted for visualization.

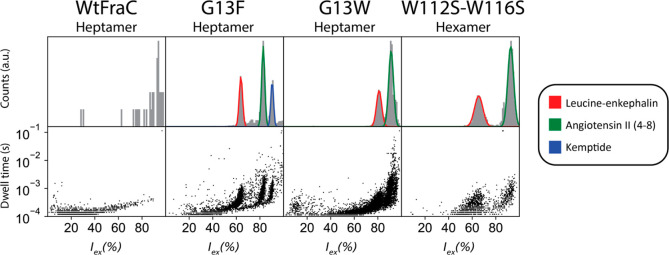
We tested the resolution of aromatic heptameric (T2) nanopores and compared to hexameric (T3) WtFraC-T3 and WtFraC-T2 nanopores using leucine-enkephalin (Leu-enk, YGGFL, 555.6 Da), angiotensin II (4–8) [Ang-II(4–8), YIHPF, 675.8 Da], and kemptide (LRRASLG, 771.9 Da). For WtFraC-T3 we use a FraC version with two altered membrane-interfacing modifications, W112S–W116S, which allowed the formation of hexameric nanopores.²⁷ WtFraC-T2 showed no blockades (Figure 5), suggesting that the majority of peptides translocated through the pore undetected. FraC-T3 and G13W-FraC-T2 showed leucine-enkephalin and angiotensin II (4–8) blockades, while kemptide blockades were not observed. This is surprising, considering kemptide has higher molecular weight than leucine-enkephalin and angiotensin II (4–8). Most likely, the two arginine residues in the kemptide induce a fast electrophoretic translocation across these nanopores. Interestingly, we found that kemptide induced blockades to G13F-FraC-T2. A likely explanation is that cation−π interactions between the aromatic ring of phenyl alanine residues and the two arginine residues are crucial to reduce the residence time of the peptide inside the nanopore.

Figure 5.

Peptide recognition of heptameric and hexameric fragaceatoxin C. The fit of the residual current is shown for leucine-enkephalin (YGGFL), angiotensin II (4–8) (YIHPF), and kemptide (LRRASLG) each in 10 μM concentration, recorded under an applied potential of −70 mV. Traces were collected in 1 M KCl and 50 mM citric acid titrated with bis-tris propane to pH 3.8 at a sampling frequency of 50 kHz, using a 10 kHz Bessel filter and 5 kHz Gaussian filter.

Characterization Using Molecular Dynamics Simulations

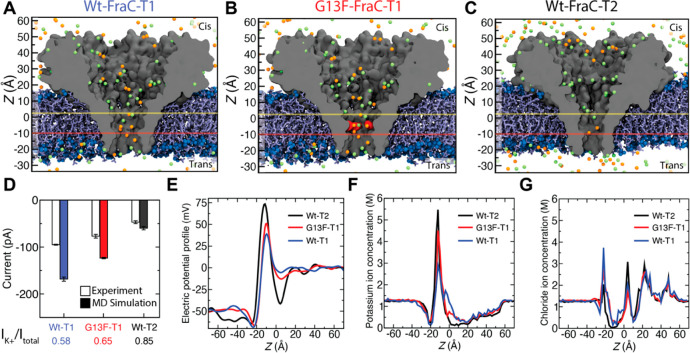
To obtain a molecular level understanding of the ionic current distinguishability, we probed ion and peptide transport through the engineered FraC nanopores using the all-atom molecular dynamics (MD) method. From the experimentally studied FraC pores (Figure 4), we selected three pores, WtFraC-T1, FraC-T2, and G13F-FraC-T1, which had the best distinguishability of the angiotensin peptides (Figure 6A–C). Each system was simulated at the experimental condition with a bias of −50 mV and a solution pH of 3.8 (see Materials and Methods). To compare the current levels with experimental results, the resulting MD currents were scaled by the ratio of the experimental bulk conductivity of 1 M KCl (10.5 S/m) and the simulated bulk conductivity of 1 M KCl (16.6 S/m). The narrowest pore (FraC-T2) showed the lowest MD current value, which was in good quantitative agreement with experiment (Figure 6D). The highest MD current was obtained from the WtFraC-T1 pore, while the G13F-FraC-T1 pore showed an intermediate current value, in qualitative agreement with experiments (Figure 6D). The simulated current values for the T1 pores were higher in the MD simulations than in experiment, which we attribute to possible local changes in the pore structure introduced by the mutations and the approximate treatment of the pH 3.8 conditions in the MD simulations. Although the lumen of the nanopores carries overall high positive charge at pH of 3.8, the nanopore current was found to be carried predominantly by the potassium ions (Figure 6D, SI Figure 6) translocating from the cis to the trans chamber, which agrees with our previous experimental ion selectivity measurements²⁷ and our MD simulations of the FraC nanopore at physiological pH and NaCl electrolyte.⁴² Accordingly, we find the water flux through the FraC nanopores to be directed from the cis to the trans compartment, as to facilitate the capture of neutral peptides, with the flux magnitudes being in the range from 3 to 6 water molecules per nanosecond (SI Figure 6).

Figure 6.

Molecular dynamics simulation of mutant fragaceatoxin C nanopores. (A–C) All-atom models of WtFraC-T1 (A), G13F-FraC-T1 (B), and WtFraC-T2 (C) nanopores. The protein is shown as a gray cutaway surface, embedded in a DPhPC lipid bilayer (blue). The G13F mutation site in panel b is shown in red. All systems contain 1 M KCl solution (potassium in orange and chloride in green, water not shown). The protonation states of the titratable residues are set to reflect the pH of 3.8. The z axis is shown on the left for scale. Yellow and red horizontal lines show the position of the electrostatic minima and maxima, respectively. (D) Experimental and simulated open pore currents at −50 mV for the three systems. The simulated values reflect scaling of the raw MD current with the ratio of the experimental and simulated bulk conductivity of 1 M KCl. The error bars represent the standard error computed by splitting the MD trajectories into 10 ns fragments and considering each fragment as an independent measurement of the current. The contribution of the potassium ion to the MD current is specified at the bottom. (E) Average electrostatic potential along the symmetry axis (z axis) of the three pores. (F, G) Profiles of potassium (F) and chloride (G) ion concentration along the symmetry axis of each nanopore.

The electrostatic potential profile along the symmetry axis of the pores revealed a barrier in the vicinity of the D10 residues, located at z = −10 Å, in our coordinate system (Figure 6E). The barrier was the highest for the FraC-T2 pore, lower for G13F-FraC-T1, and even lower for WtFraC-T1. Just above the barrier, each electrostatic potential profile also exhibits a minimum near residue K20, at z = 4.5, 5, and 5.5 Å for FraC-T2, WtFraC-T1, and the G13F-FraC-T1 pores, respectively. The potential minimum is the deepest for the FraC-T2 pore and is more shallow for G13F-FraC-T1 and even more shallow for WtFraC-T1. The local concentration of potassium ions inside each pore (Figure 6F) has a peak at z = −10 Å with the peak height being the largest for FraC-T2, followed by G13F-FraC-T1 and then by WtFraC-T1, similar to the peak height of the electrostatic potential (Figure 6E). Similarly, the local concentration of chloride ions (Figure 6G) peaks at the location where the local electrostatic potential has a minimum. In our control simulations of WtFraC-T1 at pH 7, the maximum of the electrostatic potential near D10 and the local concentration of potassium ions increased in comparison to the pH 3.8 conditions, reflecting the higher negative charge of the D10 residues, whereas the electrostatic minimum near K20 remained unchanged (SI Figure 7). To summarize, all three pores show similar electrostatic potential profiles, with a minimum near K20 and a maximum near D10, which we attribute to the congregation of chloride and potassium ions, respectively, near those charged residues. This peculiar distribution of the electrostatic potential would favor transient arrest of a positively charged analyte entering the nanopores from the cis side, right before entering the nanopore constriction.

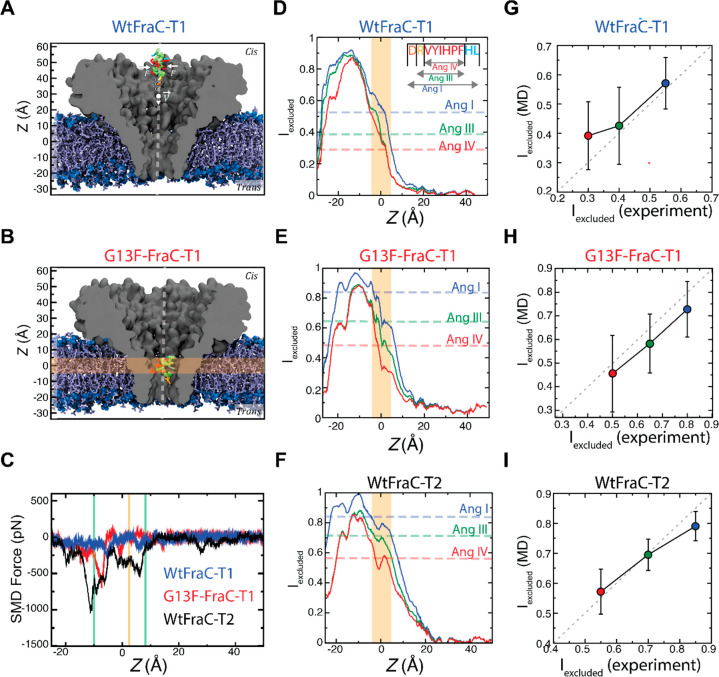
To identify the sensing regions of the FraC nanopore, we modeled the translocation of Ang-I through the three pores (FraC-T1, G13F-FraC-T1, and FraC-T2) using the steered molecular dynamics (SMD) protocol⁴³ (Figure 7A, SI Movies 1–3). As the peptide was pulled through the pore, it experienced a steric barrier when entering the constriction (Figure 7B), followed by another barrier within the constriction, as indicated by the downward spikes in the plots of the SMD force (Figure 7C). The first barrier was of lower magnitude and located around z = 10 Å, near residue E24, whereas the second barrier was more pronounced, originating from the constriction of the pore at z = −10 Å, near residue D10. Both barriers were more pronounced in the FraC-T2 and G13F-FraC-T1 pores, reflecting the smaller constriction of the heptamer and the bulky phenylalanine substitution in the octamer. It is important to note that the electrostatic minima—as calculated from the open pore simulations—is located between the two steric barriers.

Figure 7.

MD simulation of peptide translocation through FraC pores. (A) Steered MD simulation of a peptide translocation through a WtFraC-T1 pore. The pore is shown as a gray cutaway surface embedded in a DPhPC lipid bilayer (blue). Water and ions are not shown for clarity. The Ang-I peptide (DRVYIHPFHL) is placed at the cis-side rim of the pore (backbone shown in green). The peptide is pulled through the pore at a constant velocity v of 1 Å/ns using a spring attached to a template particle. Additional forces F are applied in the x–y plane to constrain the motion of the peptide to the symmetry axis of the pore (white dashed line). (B) Conformation of Ang-I in the sensing region (orange) of the G13F-FraC-T1 pore. (C) Force exerted by the SMD spring (running average, 0.5 Å) vs the z coordinate of Ang-I peptide in the three pores. Green vertical lines show the approximate locations of the two steric barriers; the yellow line shows the location of the electrostatic potential minima (Figure 6E). (D–F) Relative excluded current through the three pores, calculated using SEM (running average, 2 Å), as a function of the center of mass z coordinate of the VYIHPF segment of the three peptides Ang-I, Ang-III, and Ang-IV (sequence in inset). The dashed lines show the average experimental excluded current fraction. The sensing region is highlighted in orange. (G–I) Simulated vs experimental average excluded current fractions for the three peptides (colored as in D–F) in the three pores. The error bars show the standard deviation of I_ex values over the 50 to 60 peptide conformations used to compute each average value.

Using the steric exclusion model (SEM)⁴⁴ and the ensemble of conformations provided by the SMD simulations, we computed the relative excluded current [I_ex = (I_o – I_b)/I_o] as a function of Ang-I location within each of the three pores (Figure 7D-F). As the peptide approaches the constriction of the pores, I_ex values increase rapidly, reaching the value of 1 (complete blockade) when passing through the ring of D10 residues near z = −10 Å. After passing the constriction, I_ex returns to a value close to zero, i.e., the open pore value. From the Ang-I SMD trajectory, we computationally reconstructed conformations of Ang-III and Ang-IV peptides using a previously described protocol.¹Figure 7D–F show the computed excluded current for the three peptides in each pore vs the center of mass z coordinate of the common peptide segment (VYIHPF). For reference, we also plot the experimental I_ex values as dashed horizontal lines in the figures. First, we note that the simulated I_ex values substantially differ among the peptides only in the region where I_ex increases rapidly (around z = 0 Å), being either close to 0 or close to 1 away or when passing through the pore constriction, respectively. Averaging the simulated I_ex values over a 10 Å interval centered at z = 0 Å yielded the excluded current values in close agreement with experiment for the three pores and the three peptides (Figure 7G–I). Interestingly, the computationally derived sensing region, which corresponds well with the sensing region estimated experimentally,²⁷ is located near the electrostatic potential minima and is between the two steric barriers.

The ability of our SEM model to quantitatively describe the experimental blockade current data indicates that the origin of the observed current blockades is steric exclusion, similar to the mechanism enabling amino acid differentiation in the aerolysin nanopore.¹ Compared to the WtFraC-T1 pore, modifications in the G13-FraC-T1 and FraC-T2 pores increase the steric barrier that a peptide needs to overcome to complete the translocation while simultaneously deepening the electrostatic well that keeps the peptides tethered to the entrance of the nanopore constriction in the cis vestibule of FraC. According to our experiments, such tethering is further facilitated through hydrophobic interactions between the peptides and the hydrophobic side chains of FraC introduced through protein engineering.

Conclusions

Nanopores are emerging as powerful single-molecule sensors for DNA and RNA sequencing devices. Recent advances in nanopore analysis revealed that peptides might be recognized by nanopore currents.^{1,15,27,28,42,45−49} Moreover, it has been reported that the size and volume (which relate to the mass) of generic peptides might be measured using nanopores.^15,27 Notably, by lowering the pH of the solution to 3.8, peptides can be captured despite their chemical composition.^15,27,28 Furthermore, it has also been suggested that if a protease–unfoldase pair is coupled directly above the nanopore, the nanopore approach might allow single-molecule protein identification.²⁷

Two of the main challenges in nanopore peptide analysis include the ability to control the speed of peptide translocation, which is often too fast for accurate peptide analysis, and the rate at which the biopolymers are captured by the nanopore. Previous work with DNA revealed that an effective strategy to increase the frequency of polymer capture is to line the nanopore with positive charges in order to increase the electroosmotic flow and augment the electrostatic interactions between the DNA and the nanopore.³⁷ In this work we found that the introduction of either positive or negative charges did not improve peptide retention. Instead, the introduction of aromatic residues near the constriction region of the nanopores enhanced the capture frequency of peptides and improved significantly the discrimination among peptides of similar size. The former is important in proteomic applications where the volume of peptides must be identified with high precision. The latter is important in single-molecule applications, where all peptides or amino acids cleaved by a peptidase must be captured in sequence.

We performed molecular dynamics simulations to better understand how peptides are identified by the nanopore. We found that peptides are trapped between two electrostatic energy barriers near D10 at the constriction and K20 about 1 nm above the constriction. Interestingly, the introduction of aromatic residues at the energy minimum in the middle of the sensing region at position 13 increased both the capture frequency and the dwell time of peptides inside the nanopore. Since the neutral amino acid substitutions did not affect the electroosmotic properties of the nanopore, this effect is likely to be facilitated by a more efficient trapping of peptides transiting the nanopore, which in turn is mediated by cation−π interaction between the nanopore and the positively charged peptides at pH 3.8. Importantly, the MD simulations revealed that the peptide ionic blockades scaled well with the excluded volume of the peptide inside the nanopore, indicating that tour FraC system should be suitable for the development of a nanopore peptide size identifier.

Materials and Methods

Chemicals

Sphingomyelin (porcine brain, ≥99%, CAS# 383907-91-3) and diphytanoyl-sn-glycero-3-phosphocholine (DPhPC, ≥99%, CAS# 207131-40-6) were retrieved from Avanti Polar Lipids. Ni-NTA resin was obtained from Qiagen. Lysozyme (albumin free for tryptic digest, CAS# 12650-88-3), glucose (≥99%, CAS# 50-99-7), sodium chloride (≥99.5%, CAS# 7647-14-5), potassium chloride (≥99%, CAS# 7447-40-7), dithiothreitol (DTT, ≥99.0%, 3483-12-3), Trizma HCl (≥99%, CAS# 1185-53-1), Trizma base (≥99.9%, CAS# 77-86-1), imidazole (≥99%, CAS# 288-32-4), n-dodecyl β-d-maltoside (DDM, ≥99%, CAS# 69227-93-6), hydrochloric acid (1 M, CAS# 7647-01-0), urea (≥99.5%, CAS# 57-13-6), magnesium chloride (≥98.5%, CAS# 7786-30-3), LB broth (Luria/Miller), agar-agar, and 2× YT broth were obtained from Carl Roth. Ampicillin sodium salt (CAS# 69-52-3), isopropyl β-d-1-thiogalactopyranoside (IPTG, ≥99%, CAS# 367-93-1), ethanol (≥99.8%, CAS# 64-17-5), and all enzymes were received from Fisher Scientific. Lysozyme from chicken egg white (for lysis, CAS# 12650-88-3), N,N-dimethyldodecylamine N-oxide (LDAO, ≥99.0%, CAS# 1643-20-5), pentane (≥99%, CAS# 109-66-0), iodoacetamide (IAA, ≥99%, CAS# 144-48-9), and bis-tris propane (≥99.0%, CAS# 64431-96-5) were bought from Sigma-Aldrich. n-Hexadecane (99%, CAS# 544-76-3) and citric acid (99.6%, CAS# 77-92-9) were purchased from Acros. Trypsin (bovine pancreas, CAS# 9002-07-7) was obtained from Alfa Aesar.

Fragaceatoxin C Monomer Expression and Purification

pT7-SC1 vector containing His₆-tagged FraC plasmids (MA-FraC-GSAHHHHHH, hereafter FraC) were electrochemically inserted into E. coli BL21 (DE3) cells and grown overnight at 37 °C on LB agar plates supplemented with 100 mg/L ampicillin and 1% glucose. Colonies were used to inoculate 200 mL of 2× YT medium supplemented with 100 mg/L ampicillin and grown at 37 °C until the optical density at 600 nm (OD₆₀₀) reached 0.6, after which expression was induced using 0.5 mM isopropyl β-d-1-thiogalactopyranoside (IPTG), allowing continued growth overnight at 21 °C. Cell pellets were collected by centrifugation (6000g, 20 min, 4 °C) and stored at −80 °C for at least one hour. The pellets were resuspended in 10 mL of lysis buffer per 50 mL of culture, with a lysis buffer consisting of 150 mM NaCl and 15 mM Tris base solution at pH 7.5 supplemented with 1 mM MgCl₂, 2 M urea, 20 mM imidazole, 0.2 mg/mL lysozyme, and 0.2 units/mL DNase. The solution was mixed for 1 h at room temperature (21 °C) using a rotating mixer at 15 rpm. The cells were fully disrupted by sonification, applying 30 sweeps (duty cycle 30%, output control 3) three times using a Branson Sonifier 450. The lysate was centrifuged at 6000g for 20 min at 4 °C. The supernatant was incubated for 1 h, while under constant rotation (15 rpm), with 100 μL of resuspended Ni-NTA resin (resuspended in 150 mM NaCl and 15 mM Tris base at pH 7.5 supplemented with 20 mM imidazole). The solution was loaded onto a prewashed Micro Bio-Spin column (Bio-Rad). The Ni-NTA beads were extensively washed with 20 mL of WB (150 mM NaCl and 15 mM Tris base at pH 7.5 supplemented with 20 mM imidazole). The column was inserted into a microtube and spin-dried using a centrifuge (13300g, 1 min) in order to remove residual wash buffer. A 150 μL amount of 150 mM NaCl and 15 mM Tris base solution at pH 7.5 supplemented with 300 mM imidazole (EB) was added and left to incubate for 5 min before elution. This step was repeated four times to retrieve four fractions containing FraC monomers. The presence and purity of FraC monomers were estimated using SDS-PAGE. Pure fractions were pooled and stored at 4 °C. The concentration of FraC monomers was estimated using a Nano Drop 2000 UV–vis spectrophotometer (Thermo Scientific) using the elution buffer as blank.

Sphingomyelin-DPhPC Liposome Preparation

Twenty-five milligrams of sphingomyelin (brain, porcine) was mixed with 25 mg of DPhPC and dissolved in 4 mL of pentane containing 0.5 v/v% ethanol. The lipid mixture was evaporated while turning inside a round-bottom flask by application of a hot air stream to create a thin lipid film over the surface of the flask. The film was reconstituted into 10 mL of Sdex buffer (150 mM NaCl and 15 mM tris, pH 7.5) using a sonication bath. The liposome solution (5 mg/mL) was frozen and stored at −20 °C.

Fragaceatoxin C Oligomerization

Liposomes were thawed and added to FraC monomers in a lipid to protein mass ratio of 10:1. The mixture was incubated for 30 min at 37 °C, after which LDAO was added to a final concentration of 0.6 v/v% to dissolve the liposomes. The solution was diluted 10-fold in 150 mM NaCl supplemented with 15 mM Tris (pH 7.5) and 0.02 v/v% DDM. The diluted solution was combined with 100 μL of Ni-NTA, prewashed using WB2 (150 mM NaCl and 15 mM Tris base, pH 7.5 supplemented with 20 mM imidazole and 0.02 v/v% DDM). The mixture was left to incubate for 30 min while mixing under constant rotation (15 rpm). The solution was loaded onto a Micro Bio-Spin column (Bio-Rad), prewashed with 500 μL of WB2. The Ni-NTA beads were washed extensively using 10 mL of WB2. The column was spin-dried in a microtube using a centrifuge (13300g, 1 min) to remove residual wash buffer. A 150 μL amount of elution buffer was added onto the column (150 mM NaCl and 15 mM Tris base supplemented with 1 M imidazole and 0.02 v/v% DDM) and left to stand for 10 min before elution into a clean microtube by centrifugation (13300g, 2 min). The oligomers are stable for several months at 4 °C and can be frozen at −80 °C for long-term storage.

Construction of Fragaceatoxin C Mutants

Fragaceatoxin C mutant DNA was prepared using the MEGAWHOP method.⁵⁰ The megaprimer was constructed using a forward primer synthesized by Integrated DNA Technologies (see Supplementary Table 7) and a T7 reverse primer (5′-GCTAGTTATTGCTCAGCGG-3′). Six reactions were performed per mutation—in order to receive enough DNA for the second PCR—using 25 μL of REDTag ReadyMix PCR reaction mix (Sigma-Aldrich) combined with 22 μL of PCR grade water (Sigma-Aldrich), 1 μL of each forward and reverse primer, and 1 μL of His₆-tagged fragaceatoxin C template DNA. The PCR protocol consisted of a 90 s denaturation step at 95 °C followed by 30 cycles of denaturation at 95 °C (15 s), annealing at 55 °C (15 s), and extension at 72 °C (120 s). The six PCR reactions were combined and purified using a GeneJET PCR purification kit (Thermo Scientific). For the second PCR, 10 μL of 5× Phire buffer (Thermo Scientific) was combined with 1 μL of template DNA, 1 μL of dNTPs (10 mM), 2 μL of megaprimer (first PCR), 35 μL of PCR grade water (Sigma-Aldrich), and 1 μL of Phire II Hot Start DNA polymerase (Thermo Scientific). The PCR protocol consisted of an initial predenaturing step of 98 °C (30 s) followed by 25 cycles of denaturation at 98 °C (5 s) and extension at 72 °C (90 s). A 5.7 μL amount of 5× FD green buffer (Thermo Scientific) and 1 μL of Dpn1 enzyme (Thermo Scientific) were added to the PCR mix and allowed to digest at 37 °C for 1–3 h. A 0.5 μL sample of the digested product was electrochemically transformed into 50 μL of E. cloni 10G (Lucigen) competent cells and grown on LB agar plates containing 100 mg/L ampicillin and 1% glucose. Single colonies were enriched using a GeneJET plasmid miniprep kit (Thermo Scientific), and the sequence was confirmed using the sequencing service of Macrogen Europe.

Protein Sequence of His₆-Tagged Wild Type Fragaceatoxin C

MASADVAGAVIDGAGLGFDVLKTVLEALGNVKRKIAVGIDNESGKTWTAMNTYFRSGTSDIVLPHKVAHGKALLYNGQKNRGPVATGVVGVIAYSMSDGNTLAVLFSVPYDYNWYSNWWNVRVYKGQKRADQRMYEELYYHRSPFRGDNGWHSRGLGYGLKSRGFMNSSGHAILEIHVTKAGSAHHHHHH.

Unspecific Lysozyme Digestion

Lysozyme (Carl Roth, from chicken egg white, free from albumin) was dissolved in 8 M urea supplemented with 15 mM Tris (pH 9.5) to a final concentration of 20 mg/mL and left to denature at 95 °C for 5 min. A 200 μL amount of denatured lysozyme solution was incubated for 30 min at 37 °C with 20 mM DTT, to reduce the cysteine residues. IAA was added to the mixture, to react with reduced cysteines, with a final concentration of 45 mM, and incubated in the dark for 30 min at room temperature. The mixture was diluted 5× with 100 mM Tris (pH 8.5) and trypsin (Alfa Aesar trypsin, bovine pancreas) was added in a ratio of 1:50 (trypsin:protein). The mixture was left to digest overnight (∼18 h) at 37 °C. In order to denature and deactivate any remaining trypsin, the next day, the final mix was denatured at 95 °C for 10 min and HCl was added to lower the pH (approximately pH 4). The mixture was then frozen at −20 °C until use.

Planar Lipid Bilayer Electrophysiological Recordings

The electrophysiology chamber consisted of two compartments separated by a 25 μm thick Teflon (Goodfellow Cambridge Ltd.) membrane (Supplementary Figure 4). The Teflon membrane contained an aperture with a diameter of approximately 100–200 μm. Lipid membranes were formed by first applying 5 μL of 5% hexadecane (Sigma-Aldrich) in pentane (Sigma-Aldrich) to the Teflon membrane, near the aperture. The pentane was left to dry, and 400 μL of buffer (1 M KCl and 50 mM citric acid, titrated with bis-tris propane to pH 3.8) was added to both sides. Twenty microliters of a 6.25 mg/mL solution of DPhPC dissolved in pentane was added on top of the buffer on each side of the chamber. The chamber was left to dry for ∼2 min to allow evaporation of pentane. Silver/silver chloride electrodes were attached to each compartment. The cis compartment was connected to the ground electrode, and the trans was connected to the working electrode. Planar lipid bilayers were created using the Langmuir–Blodgett method described before.⁵¹ The orientation of FraC nanopores was determined by the asymmetry of the current–voltage relationship. A baseline of 2 min was recorded for each of the pores recorded. Analytes were added to the cis compartment of the chamber.

Ion Permeability Measurement

A single channel was obtained in a symmetrical buffer containing 2 M KCl supplemented with 50 mM citric acid titrated to pH 3.8 using bis-tris-propane or 15 mM Tris at pH 7.5. The electrodes were connected via 2.5% agarose salt bridges containing 3 M KCl in the agarose and liquid–solid interface. Upon insertion of a single nanopore, the cis and trans chambers were perfused three times using the 2 M KCl buffer solution, in order to ensure the correct concentration. The electrodes were balanced, and a current–voltage curve (IV curve) was collected to ensure appropriate size and balancing. Afterward, the trans solution was perfused with salt-free buffer to set the final salt concentration to 0.5 M KCl. The salt concentration was ensured by perfusion of the trans solution using 0.5 M KCl buffer and perfusion of the cis solution using 2 M KCl buffer. After equilibrium was reached, IV curves between −100 and +100 mV were recorded with 1 mV steps. The zero current reversal potential (V_r) was determined using second-order polynomial regression over the IV curve. The ion selectivity (P_K⁺/P_Cl^–) was calculated using the Goldman–Hodgkin–Katz equation.

3

where [α_K⁺/Cl^–]_cis/trans are the molar ion activities of K⁺ or Cl^– in cis and trans position as described previously.²⁷V_r is the reversal potential in J·C^–1. F is the Faraday constant in C·mol^–1. R is the gas constant in J·K^–1·mol^–1. T is the temperature in Kelvin.

Data Recording

Recordings of ionic currents were obtained using an Axopatch 200B (Axon Instruments) combined with a Digidata 1550B A/D converter (Axon Instruments), similar to preceding work.^24,27,28,51 The sampling frequency was set at 50 kHz for analyte recordings, and the analogue Bessel filter was set at 10 kHz. Data were recorded using Clampex 10 (Molecular Devices).

Data Analysis

Data were analyzed using Jupyter Notebook (version 5.5.0) running with Python 3.6.5 (64-bit), both within the Anaconda (version 5.2.0) environment. Additional packages were installed from PyPi using pip (version 10.0.1) unless stated otherwise. Axon Binary Format files were loaded and converted into NumPy arrays (NumPy version 1.14.3) using neo (version 0.7.1) and an ad-hoc script; clustering was performed using SciPy (version 1.4.1). The open pore current (I_o) of all traces was determined by calculating the mean current of three independent measurements, bootstrapped for 100 iterations of 10 s snippets for each measurement; similarly so, the standard deviation of the open pore current (σ(I_o)) was calculated. The error displayed in Supplementary Table 1 was calculated over the three resulting values. For event detection, the baseline current and standard error of the recorded traces were determined from a full current histogram of the blank measurement. The value for the baseline was then used to determine the events when analyte was added. All data points above the baseline current and standard error that were separated by at least two times the sampling periods were detected as events. The excluded current (I_ex%) of each event was calculated from the complement to 100% of the event signal divided by the median current of the preceding open pore current.

Impartial Event Detection

We found that short-lived events—with a dwell time near the sampling frequency—tend to form a spike or Gaussian profile due to undersampling and filtering effects, while longer events follow a flat-top shape. Therefore, we introduced a parameter describing the shape of current blockades in order to impartially compare the performance of mutant pores. We assume that the profile of ionic current blockades can be described by a generalized flat-top normal distribution function (gNDF, eq 4). Each observed block was fit to eq 3 using least-squares fitting, due to the nonpolynomial nature of the function.

4

where μ is the events center in the time domain with variance σ² and ΔI_B is the current difference (pA) between the baseline (I_o) and the event maximum. The variable β describes the shape of the function and can take any real number larger than zero (Supplementary Figure 5). If β is less than 1 but larger than 0, the shape of the function is a spike (Supplementary Figure 5a). If β is equal to 1, the function is equal to the normal distribution function. When β is larger than 1, the function starts to follow a rectangular-flat-top profile. Advantageously, the variable β can also be used to assess the quality of individual events in the following way. Events with a β < 1 are mostly events that are too short-lived to accurately measure the ionic current blockade. Therefore, only those events with a β ≥ 1 should be regarded as accurate measurements of peptides. Similarly, we distinguish events with a β ≥ 10, since these events—having a flat-top shape—permit an accurate estimation of the blocked current. The gNDF fit also permits an estimation of the dwell time of an event by taking the full width at half-maximum (fwhm) of the gNDF (eq 5). Estimation of the dwell time using this equation is advantageous, because it allows the treatment of this parameters as continuous rather than discrete, which is the case if the number of data points are counted within the event.

5

where σ equals the square root of the variance (σ², eq 4) and β describes the shape parameter.

Spectral Matching

Several of the residual current spectra we obtain (Supplementary Figure 3) are expected to contain random events induced by factors other than the analyte (gating); so in order to reduce baseline sloping and to maintain high sensitivity, we utilize the squared first-derivative Euclidean cosine correlation (eq 6).⁵² This comparison is sensitive to the position of the peaks observed in the spectra, but not as sensitive to a shifting baseline.

6

where A₁ and A₂ equal the vectors of excluded current counts and A_1,i and A_2,i represent the individual bins of the excluded current spectrum.⁵² In a more detailed description, we set A₁ and A₂ as the vector of counts we observe for each residual current bin (e.g., A_n = counts(40–41%), counts(41–42%), ..., counts(94–95%)). ΔA_n is the derivative of A_n (difference between bins). In the numerator, we multiply each element ΔA_n with the corresponding ΔA_n of the comparing spectrum and take the squared sum of all items. In the denominator, we take the squared sum of each element in ΔA_n and multiply that with the squared sum of each element in the spectrum we want to compare. So, if the two vectors A₁ and A₂ are equal, the correlation is 1; otherwise it is less than 1, and because the derivative of A₁ and A₂ is taken, linear baseline sloping is less impactful.

We perform hierarchal clustering using the Ward distance as implemented in SciPy version 1.4.1 on the resulting correlation coefficients to determine which spectra are most similar.^41,53 In essence, this metric orders the data in such a way that the variance between neighbors is minimal, therefore building a map of similar spectra.

MD Methods

All MD simulations were carried out using NAMD,⁵⁴ a 2 fs integration time step, periodic boundary conditions, and the CHARMM36⁵⁵ force field. SETTLE and RATTLE algorithms were respectively used to fix all water and protein bonds containing hydrogen atoms.⁵⁶ Constant pressure (NPT) simulations used the Nosé–Hoover Langevin piston pressure control.⁵⁷ The temperature in the simulation system was maintained by coupling the non-hydrogen atoms of the lipids to a Langevin thermostat.⁵⁸ Van der Waal forces were calculated with a cutoff of 12 Å and a switching distance of 10 Å. The particle mesh Ewald summation was used for calculating long-range electrostatics over a 1 Å grid.⁵⁹ Multiple time stepping was used to calculate local interactions every 2 fs and the full electrostatics every 4 fs.⁶⁰

All-Atom Model of FraC Nanopores

The initial structural models of WtFraC-T1 and FraC-T2 nanopores were taken from the previous study.²⁷ The WtFraC-T1 is available as PDB ID 4TSY, and the FraC-T2 was created in the previous work from the monomer using Rosetta.⁶¹ The G13F-FraC-T1 variant was created by mutating the 13th residue of each WtFraC-T1 monomer from glycine to phenylalanine, retaining the backbone conformation. Each protein was arranged to have its nanopore axis aligned to the z axis of the simulation system and merged with a 14 nm × 14 nm pre-equilibrated patch of DPhPC lipid bilayer such that the center of mass of residues 4–31 (pore) coincided with that of the bilayer. All lipid and water molecules overlapping with the protein were removed, and the resulting system was solvated with pre-equilibrated TIP3P water,⁶² extending the systems size along the z axis to 16 nm. To emulate the pH 3.8 condition of the experiment, we used the Henderson–Hasselbach equation⁶³ to probabilistically assign fixed protonation states to the following titratable residues of the protein: aspartates (pK_a = 3.8), glutamates (pK_a = 4.5), histidines (pK_a = 6.5), and lysines (pK_a = 10.5). Selecting the locations of titratable groups at random, we protonated 50% of all aspartate residues, 83% of all glutamate residues, and all of the histidines and lysines. Specific to FraC constriction, the D10 and D17 residues of both T1 pores had the following charge states (in the units of proton charge, clockwise, looking down from the cis side): −1, −1, −1, 0, −1, 0, 0 and 0, −1, −1, −1, 0, −1, 0, 0, respectively. The D10 and D17 charge distribution for the T2 pore was −1, 0, −1, −1, 0, −1, −1 and 0, 0, 0, −1, 0, −1, −1, respectively. This initial assignment of the protonation states was maintained throughout the simulation. The total charge of type I and type II FraC nanopores was +177e and +155e, respectively, where e is the charge of a proton. To produce a 1 M KCl solution, Cl^– ions were added first to neutralize the system, followed by the addition of approximately 1500 K⁺ and Cl^– ions. Each final system measured 14 nm × 14 nm × 16 nm and contained about 330 000 atoms.

Each system underwent 1000 steps of energy minimization followed by equilibration in the constant-ratio NPT ensemble at 293 K and 1 atm for 6 ns, which was performed by restraining all non-hydrogen atoms of the protein to their initial coordinates. In the first nanosecond of the equilibration, water molecules were forced out from the interface between the protein and the lipid membrane using a custom tclforces script. During the equilibration, the system’s size was allowed to fluctuate while maintaining the ratio of the unit cell’s dimensions along the x and y axes constant. The final frame of the equilibration simulation was used to initiate electric field simulations, which were performed in the NVT ensemble. A constant electric field, E, was applied normal to the lipid bilayer corresponding to a transmembrane bias of V = −E*L_z,⁶⁵ where L_z is the length of the simulation unit cell along the z axis. The Cα atoms of the nanopore were restrained to their initial coordinates using a harmonic spring with a spring constant of 6.95 pN/nm.

MD Simulation of Angiotensin Peptide Translocation

A model of the Ang-I peptide (sequence: DRVYIHPFHL) was created by mutating an α-helical homopeptide. The aspartate and histidine amino acids were protonated to reflect the 3.8 pH of the solution. The peptide was introduced into each equilibrated FraC nanopore system, placing the peptide at the center of the nanopore, at the level of the FraC’s cis side rim. Water and ions overlapping with the peptide were removed, while keeping the systems electrically neutral. Each system was then equilibrated for 5 ns in the NPT ensemble while restraining all Cα atoms of both the FraC nanopore and the peptide. From the last frame of each equilibration trajectory, an SMD simulation⁴³ was carried out to translocate the Ang-I peptide through the pore. The Cα atoms of the nanopore were kept harmonically restrained using a spring constant of 6.95 pN/nm. The SMD force was applied to the center of mass of all non-hydrogen atoms of the peptide using a spring constant of 4865 pN/nm. The other end of the SMD spring was moved along the nanopore axis with a constant velocity of 1 Å/ns. Additional forces were applied to the peptide using the colvars module of NAMD⁶⁴ to restrain the center of mass of the peptide in the xy plane to the symmetry axis of the pore. A constant electric field was also applied corresponding to a transmembrane potential difference of −50 mV.

SEM Analysis of Peptide Translocation Simulations

For each SMD trajectory, coordinates of all nonsolvent atoms were saved every 0.2 ns and analyzed using the SEM approach⁴⁴ to obtain a nanopore ionic current value for each atomic configuration. The conformations for Ang-III (sequence: RVYIHPF) and Ang-IV (sequence: VYIHPF) were computationally created for each frame of the SMD trajectories by deleting terminal amino acids from the Ang-I peptide. The thereby produced sequence of conformation was analyzed using SEM as described previously.¹

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsnano.0c09958.

• Tables containing the characteristics of FraC mutants including voltage–current dependency, a list of expected peptides from in-silico digestion using low-fidelity trypsin/chymotrypsin, peptides resulting from ESI-MS analysis, capture frequencies, reversal potential, and the primers used for mutagenesis; figures showing the electrical behavior of all FraC mutants, a schematic of the electrophysiology setup, and MD simulated ion transport through FraC nanopores (PDF)

• Movie showing the SMD simulation of peptides translocating FraC nanopores (MP4)

• Movie showing the SMD simulation of peptides translocating FraC nanopores (MP4)

• Movie showing the SMD simulation of peptides translocating FraC nanopores (MP4)

Author Contributions

F.L. and G.M. designed the experiments. G.M. supervised the project. F.L., E.L., DC., and N.H. performed the experiments. K.S. and A.A. designed molecular dynamics simulations. K.S. performed MD simulations and analyzed the data. F.L. performed the experimental data analysis. F.L., R.V., K.S., A.A., and G.M. wrote the manuscript with the input and contribution of all authors.

The authors declare no competing financial interest.