Shared mechanisms underlie the control of working memory and attention

Abstract

Cognitive control guides behavior by controlling what, when, and how information is represented in the brain¹. For example, attention controls sensory processing; top-down signals from prefrontal and parietal cortex strengthen the representation of task-relevant stimuli^2–4. A similar ‘selection’ mechanism is thought to control the representations held ‘in mind’, in working memory^5–10. Here, we show shared neural mechanisms underlie the selection of items from working memory and attention to sensory stimuli. We trained monkeys to switch between two tasks, either selecting one item from a set of items held in working memory or attending to one stimulus from a set of visual stimuli. Neural recordings found similar representations in prefrontal cortex encoded both the control of selection and attention, suggesting prefrontal acts as a domain-general controller. In contrast, attention and selection were independently represented in parietal and visual cortex. Both selection and attention facilitated behavior by enhancing and transforming the representation of the selected memory or attended stimulus. Specifically, during the selection task, memory items were initially represented in independent subspaces of neural activity in prefrontal cortex. Selecting an item caused its representation to transform from its own subspace to a new subspace used to guide behavior. A similar transformation was seen in attention. Together, our results suggest prefrontal cortex controls cognition by dynamically transforming representations to control what and when cognitive computations are engaged.

To study the control of working memory and attention, we trained two monkeys to switch between two tasks. First, a retrospective (‘retro’) task required monkeys to select one of two items held in working memory (Fig. 1a). On each retro trial, the animals remembered the color of two squares (colors drawn randomly from color wheel, see methods). After a memory delay, the animals received a cue indicating whether to report the color of the ‘upper’ or ‘lower’ square (now held in working memory). This cue was followed by a second memory delay, after which the animals reported the color of the cued square by looking at the matching color on a color wheel (which was randomly rotated on each trial to prevent motor planning). Therefore, to perform the task, the animals held two colors in working memory, selected the color of the cued square, and then used it to guide their response.

Figure 1.

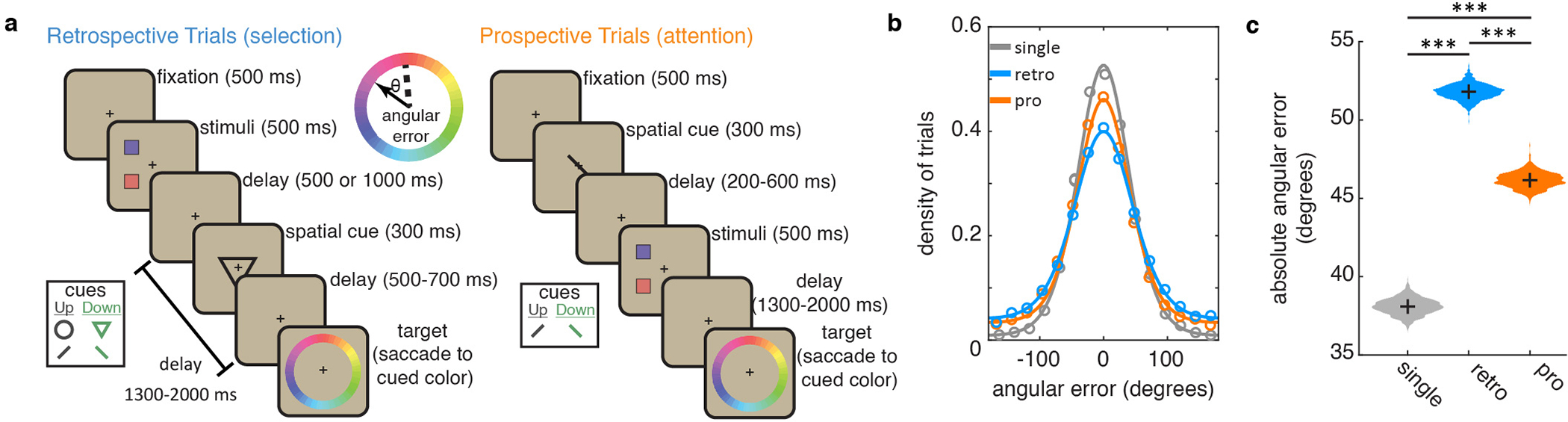
Monkeys use selection and attention to control the contents of working memory. (a) Timecourse of retrospective (‘retro’) and prospective (‘pro’) tasks, as described in main text. Cues (shown in inset) indicated whether the animal should select the ‘upper’ or ‘lower’ item from working memory (retro task) or attend to the upper/lower item (pro task) and report that item after a delay. Reward was graded by error, calculated as the angular deviation between the cued and reported color (dashed and solid lines in inset). On a subset of retro and pro trials, a single item was presented (not shown). (b) Distribution of error (circles) with best-fitting mixture models (lines, see methods) for single item trials (gray), retro trials (blue), and pro trials (orange). As previously shown³⁰, errors reflected both unsystematic error and systematic biases (Extended Data Fig. 1c). (c) Bootstrapped distribution of mean absolute error in the retro, pro, and single-stimulus conditions (N=8620, 8169, and 4207, respectively). All three comparisons were p<0.001 (***) by two-sided uncorrected randomization test.

Monkeys performed the task well; the mean absolute angular error between the presented and reported color was 51.8° (Fig. 1b–c and Extended Data Fig. 1a–b). As expected^11–13, error was reduced when only one item was presented (Fig. 1b–c and Extended Data Fig. 1d; error was 38.1° for 1 item, 51.8° for 2 items, p<0.001, randomization test). The increased error with two items in memory is thought to be due to interference between the items^14–17, which is reduced when an item is selected from working memory^18,19. Consistent with this, error was lower when selection occurred earlier in the trial (Extended Data Fig 1e–f; linear regression, β=4.67°/s ± 1.08 SEM, p<0.001, bootstrap).

In addition, animals performed a prospective (“pro”) task. On pro trials, the cue was presented before the colored squares, allowing the animal to attend to the location of the to-be-reported stimulus (Fig. 1a). Consistent with attention reducing interference between stimuli^20,21 and modulating what enters working memory²², memory reports were more accurate in the pro task than the retro task (Fig. 1b–c and Extended Data Fig 1d; 46.1° vs. 51.8°, p<0.001, randomization test) and increasing the number of stimuli from 1 to 2 led to a smaller increase in error on pro trials (9.01° vs. 13.7° for pro/retro, p<0.001, bootstrap). These results highlight the functional homology between selection and attention, as both forms of control mitigate interference between representations^14,20,23.

Control of Memory and Attention

To understand the neural mechanisms of selection, and their relationship to attention, we simultaneously recorded from four regions involved in working memory and attention (Fig. 2a) – lateral prefrontal cortex (LPFC; 682 neurons), frontal eye fields (FEF; 187 neurons), parietal cortex (7a/b; 331 neurons), and intermediate visual area V4 (341 neurons). Consistent with previous work in humans^9,24,25, neurons in all four regions carried information about which item was selected from working memory (i.e., upper or lower; Extended Data Fig. 2a–b). To quantify this, we trained a logistic regression classifier to decode the location of selection from the firing rates of populations of neurons recorded in each region (Fig. 2b; see methods). The classifier found significant information about the location of selection in all four regions, emerging first in LPFC and then in posterior regions (Fig. 2c; 175 ms post-cue in LPFC, 245 ms in FEF, 285 ms in parietal, and 335 ms in V4). LPFC was significantly earlier than parietal cortex and V4 (p=0.005 and p=0.048, randomization test), but statistically indistinguishable from FEF (p=0.371). These results did not depend on the number of neurons recorded in each region and were not due to differences in neural responsiveness or noise (Extended Data Figs. 2–3 and Table S1). Together, these results suggest control of selection emerges first in prefrontal cortex and propagates to parietal and visual cortex.

Figure 2.

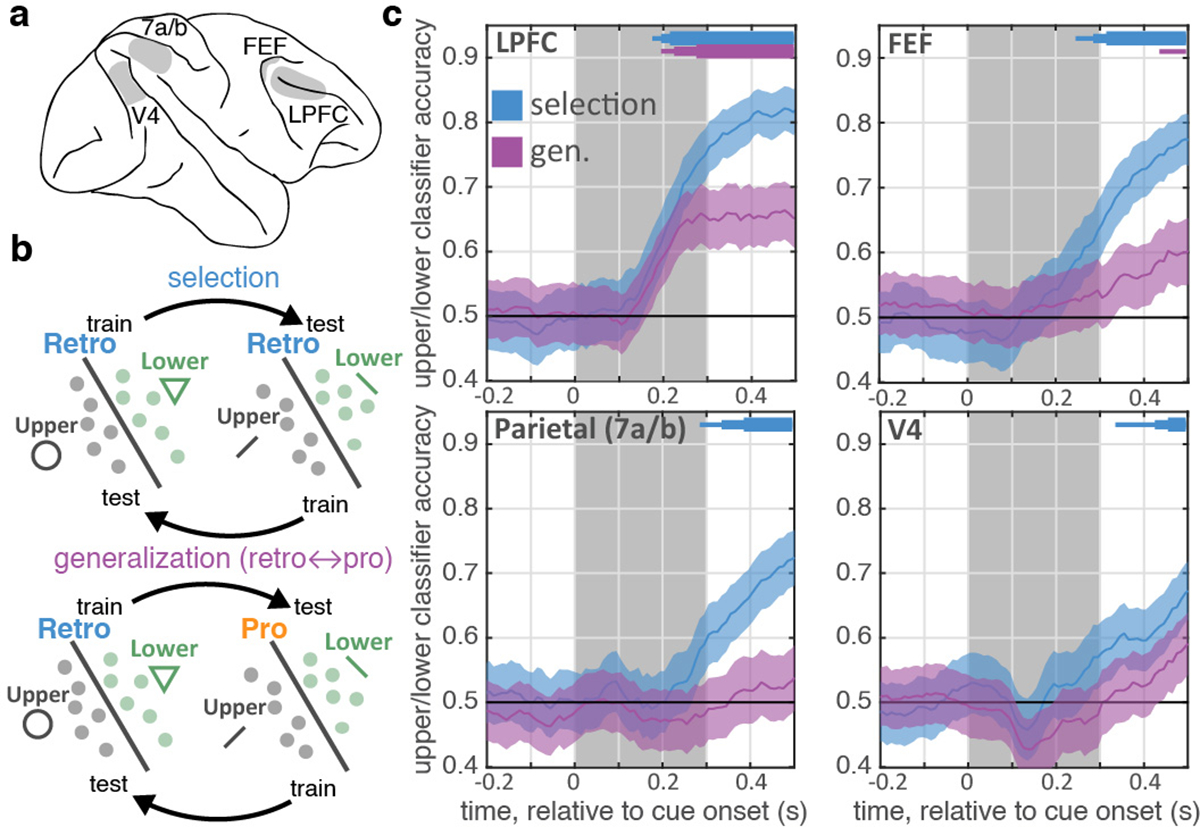
Selection is observed first in prefrontal cortex and shares a population code with attention. (a) Schematic of neural recordings. (b) Schematic of classifiers used to quantify information about whether the upper or lower item was selected from population firing rates (see methods). ‘Selection’ classifier accuracy was measured within retro trials (left) on held-out data. ‘Generalization’ classifier accuracy was measured across retro and pro trials (right). (c) Timecourse of classifier accuracy for each brain region (labeled in upper left). Lines show mean classification accuracy (shaded region is +/− STE), around cue onset, for the selection (blue) and generalization classifiers (purple). Distribution reflects 1,000 iterations of classifiers, trained/tested on N=60 randomly-sampled trials. Horizontal bars indicate above-chance classification: p<0.05, 0.01, and 0.001 for thin, medium, and thick lines, respectively; one-sided uncorrected bootstrap.

Motivated by the functional homology between selection and attention⁵, we tested whether they were encoded in a shared population representation. Specifically, we tested if the classifiers trained to decode the location of selection could generalize to decode the location of attention (and vice versa, Fig. 2b; see methods). Consistent with a shared representation in LPFC, generalization performance in LPFC was significantly above chance and followed the timecourse of the selection classifier (Fig. 2c). Individual LPFC neurons also generalized, representing the location of selection and attention similarly (Extended Data Fig. 4a–c; r(586)=0.09, p=0.036).

In contrast, selection and attention were independently represented in FEF, parietal, and V4. Generalization was weaker in FEF and trended towards being delayed relative to LPFC (Fig. 2c; p=0.12, randomization test). There was no significant generalization in parietal or V4 (Fig. 2c; this was not due to an inability to decode attention, Extended Data Fig. 4d–e). Consistent with different representations, the representation of selection and attention were uncorrelated in FEF, V4, and parietal neurons (Extended Data Fig. 4a–c; FEF: r(169)=0.04, p=0.617; V4: r(318)=−0.04, p=0.513; parietal: r(301)=0.03, p=0.612; although a positive correlation emerged later in FEF).

Together, these results suggest LPFC may act as a ‘domain-general’ controller, with a shared population representation encoding both selection of items from working memory and attention to sensory inputs. This could allow behaviors to generalize across working memory and sensory stimuli. In contrast, the task-specific representations seen in FEF and parietal (and partially in LPFC) could allow for specific control of memories or sensory stimuli. Combining generalized and task-specific representations may balance the need to learn task-specific and generalized behaviors^26,27 (see Supplementary Discussion 1).

Selection & Attention Enhance Memories

Next, we explored how selection and attention affected the neural representation of items in working memory. Single neurons in LPFC, FEF, parietal, and V4 all carried information about the color of the upper or lower item (LPFC: N=387/607 cells; FEF: 114/178; parietal: 181/307; V4: 245/323; all p<0.001, binomial test; see methods and Extended Data Fig. 5a). In all four regions, information about the color of the stimuli emerged during stimulus presentation and was maintained throughout the trial (Fig. 3; see Extended Data Fig. 5b and Supplementary Discussion 2). These memory representations were related to behavior: LPFC and V4 carried more information about the reported color than the presented color (Extended Data Fig. 6a; p<0.001, randomization test).

Figure 3.

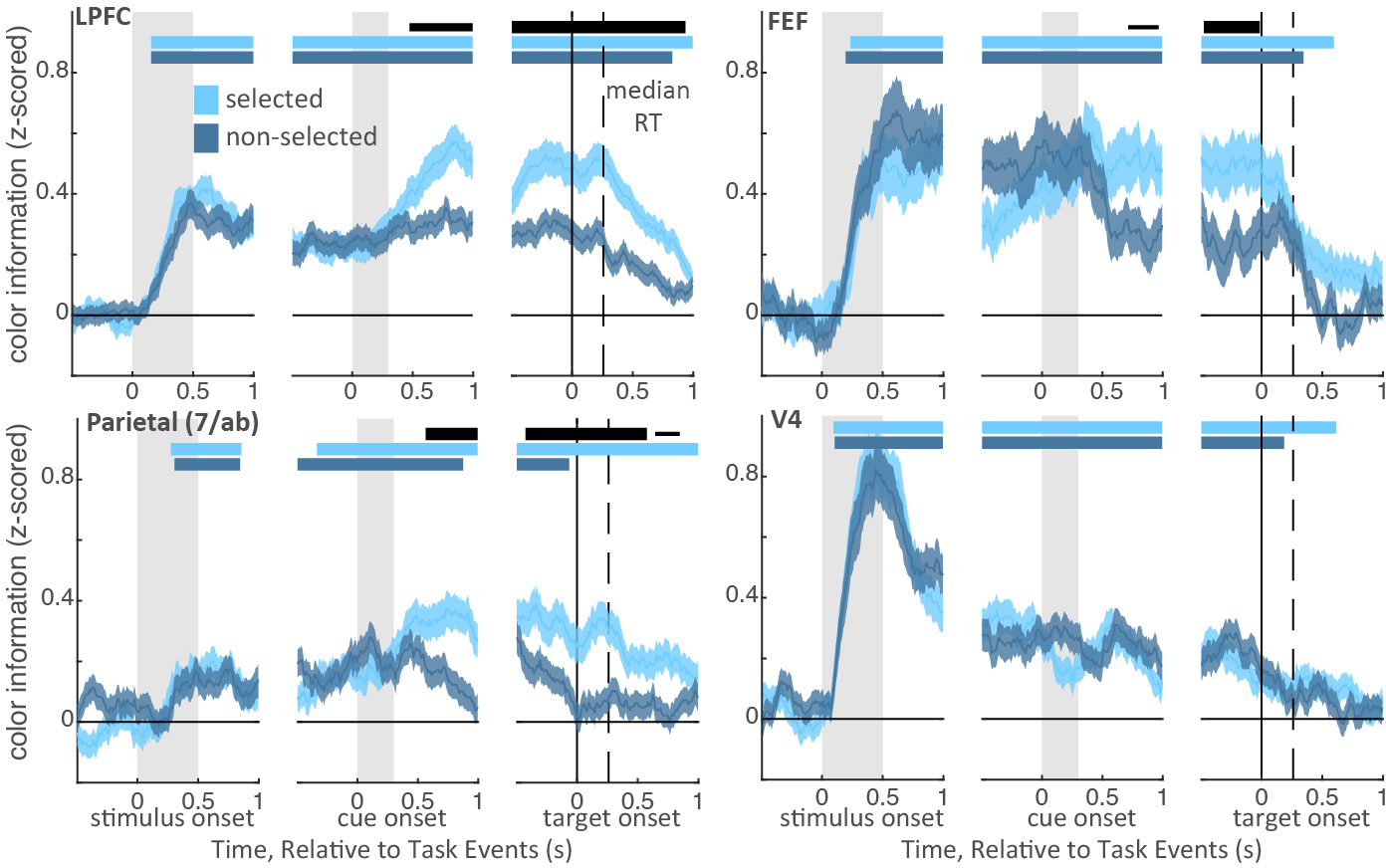
Selection increases color information in working memory. Lines show mean z-scored color information for the selected and non-selected color (light and dark blue, respectively) in each brain region, averaged across neurons (shaded region is +/− STE; LPFC, N=570; FEF, N=163; parietal, N=292; V4, N=311). Information was quantified by circular entropy of each neuron’s response to colors (see methods). Horizontal bars indicate significant information for the selected and non-selected item (light and dark blue) and a significant difference in information about the selected and non-selected items (black). Bar thickness indicates significance: p<0.05, 0.01, and 0.001 for thin, medium, and thick, respectively; two-sided cluster-corrected t-test. Stimulus color information tended to emerge first in V4 (at 85 ms post-stimulus) and flow forward to LPFC (145 ms), FEF (185 ms), and then parietal cortex (275 ms; V4 < parietal, p=0.035; FEF < parietal, p=0.054; randomization tests). In contrast, selection increased color information in LPFC first (see main).

Consistent with previous work in humans^6,8, selection strengthened memories in prefrontal and parietal cortex. In LPFC, color information about the selected memory was greater than the non-selected memory, starting 475 ms after cue onset (Fig. 3; also above pre-cue baseline, Extended Data Fig. 7a). Similar enhancements were seen in FEF and parietal (at 715 and 565 ms, respectively; Fig. 3 and Extended Data Fig. 7a).

The selective enhancement of a memory was related to behavior in all four regions (Extended Data Fig. 7b–c). When memories reports were inaccurate, the effect of selection was absent in LPFC, FEF, and 7a. While selection did not impact memory representations in V4 overall (Fig. 3b), information about the selected item was increased on trials with high memory accuracy and information about the non-selected item was increased on low accuracy trials. Together, these results suggest memory errors occurred when the animal failed to select an item or selected the wrong item.

Similar to selection, attention increased the representation of stimuli, suggesting similar mechanisms strengthen memory/sensory representations in prefrontal and parietal cortex (Extended Data Fig. 6b). However, in contrast with attention^2,28, selection did not reduce information about the non-selected memory in LPFC and parietal cortex (Extended Data Fig. 7a; but information did slightly decrease in FEF), suggesting selection may not engage the competitive mechanisms that suppress unattended stimuli²⁹.

Selection & Attention Transform Memories

Finally, we were interested in how the changing task-demands during retro trials affected memory representations. Early in the trial, before selection, color memories must be maintained in a form that allows the animal to select the cued item (i.e., colors are bound to a location). Later in the trial, after selection, only the color of the selected item is needed to guide the visual search of the color wheel and the animal’s response. Next, we show how selection transformed memory representations to match these changing task demands.

Before selection, the color of each item in memory was represented in separate subspaces in the LPFC neural population. Figure 4a shows the representation of the color of the upper and lower item, before selection (projected into a reduced three-dimensional space, see methods). Color information showed a clear organization; the responses to four categories of color were well-separated and in color order for both the upper and lower item (i.e., neighboring colors in color space had neighboring representations). Color representations for each item were constrained to a ‘color plane’, consistent with a two-dimensional color space (see methods). As seen in Figure 4a, the upper and lower color planes appeared to be independent from one another, suggesting color information about the upper and lower items were separated into two different item-specific subspaces in the LPFC population (before selection).

Figure 4.

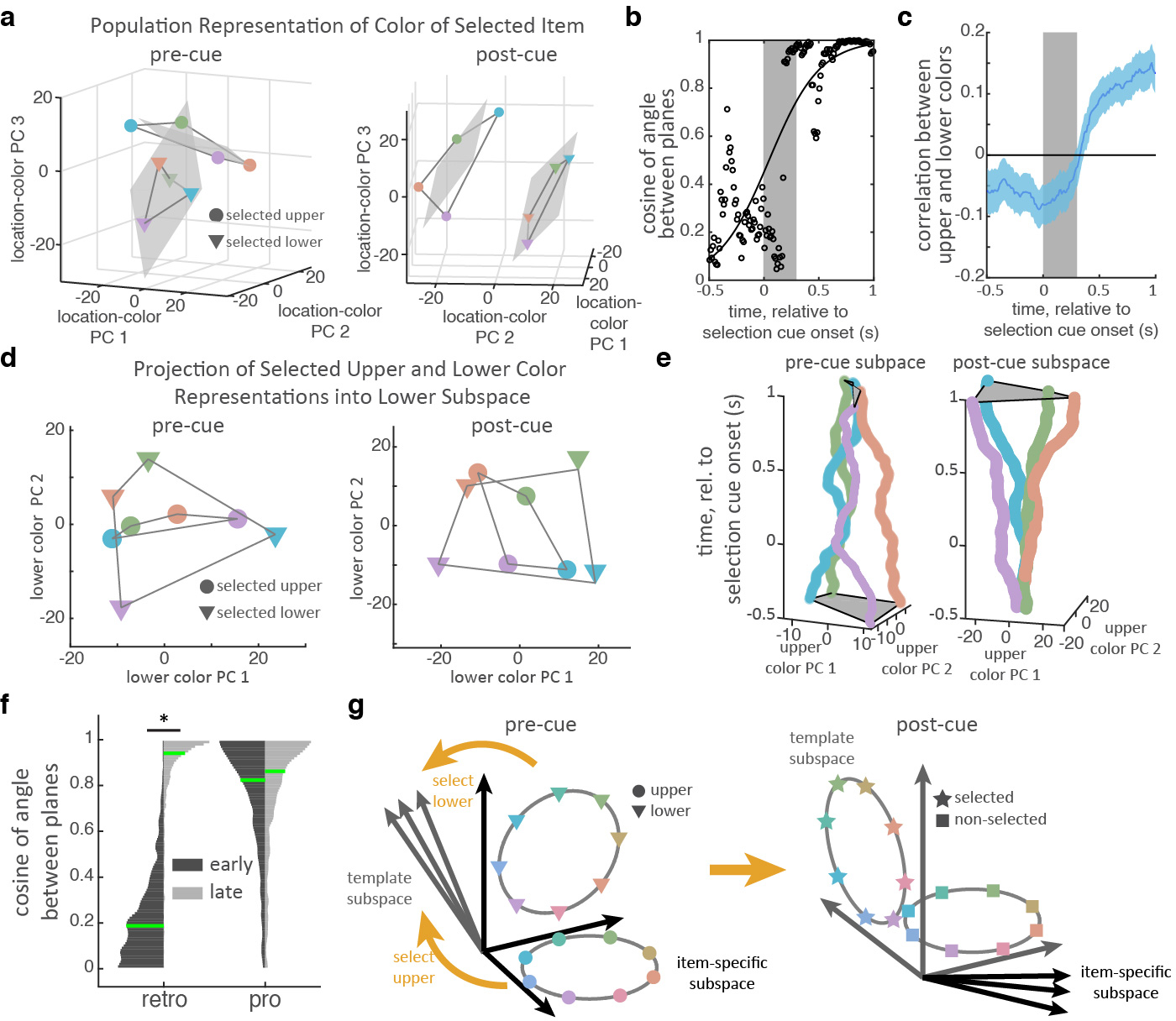
Selection transforms memory information in a task-dependent manner. (a) Population response in LPFC for the color of the selected item (binned into 4 colors indicated by marker color; upper/lower indicated by marker shape). Population response is taken as the vector of mean firing rate of neurons before the cue (pre-cue, left; 400 ms before cue) and after the cue (post-cue, right; before target onset). Responses are projected into a reduced dimensionality subspace defined by the first three principle components (PCs) of all 8 color/location pairs. Grey lines connect adjacent colors on color wheel. Gray shaded region shows best fitting planes to each item. (b) Cosine of the angle between the two color planes (seen in a) over time. Higher numbers reflect better alignment. Black line shows the best-fitting logistic function to N=150 timepoints. (c) Mean correlation between upper and lower color representations in LPFC over time (line and shading show mean +/− STE over N=1000 bootstrap resamples of trials). (d) Color representations in LPFC projected into the ‘lower’ subspace, before (left) and after (right) selection. Timepoints and markers follow panel a. (e) ‘Upper’ color representations in LPFC projected into the ‘upper’ subspace (x-y axes) over time (z-axis, relative to selection). (f) Histograms show distribution of the cosine of the angle between the best-fitting planes for the upper and lower stimuli in an ‘early’ (150–350 ms post-stimulus offset) and ‘late’ (200–0 ms before target onset) time periods for retro (left) and pro (right) tasks (N=1000 bootstrap resamples of trials). Green lines indicate median. Horizontal lines indicate pairwise comparisons. * p=0.016, two-sided uncorrected bootstrap. (g) Schematic of how selection transforms color representations.

Consistent with separate subspaces, the median angle between the upper and lower color planes was 79.1° (Fig. 4b, IQR: 71.4°−85.1°, see methods), suggesting they were almost orthogonal before selection. This was not because the two items were encoded by separate populations of neurons. Rather, representations in LPFC overlapped²⁷, with a significant proportion of neurons encoding both items (31% and 35% of neurons encoding the upper/lower item also encoded the other item; p=1.21e-4, binomial test; Extended Data Fig 8a–b). The color planes were not completely orthogonal, as the representations of the upper and lower items were anti-correlated (Fig. 4c; e.g., the N-neuron population vectors of ‘red upper’ and ‘red lower’ were anti-correlated; mean r=−0.067 for −300 to 0 ms pre-selection, p=0.009, bootstrap). This modest anti-correlation may improve differentiation when the two items have similar colors.

Further supporting independent upper and lower subspaces before selection, color representations of an item were less separated when they were projected onto the other subspace (Fig. 4d; each item’s subspace was defined as the 2D space that maximally captured color information in the full N-dimensional neural space, see methods). To quantify the separability of colors, we measured the area of the quadrilateral defined by the four color representations. This ‘color-area’ was greater when color representations were projected into their own subspace compared to the other subspace (reflecting greater separation in own subspace; 86.1 vs. 35.2 units², p=0.041, bootstrap; all subspaces defined on held-out data).

After selection, memory representations in LPFC were transformed into a different subspace (as previously theorized⁷). Reflecting this, the separation of colors in the pre-selection subspace collapsed by the end of the second memory delay (Fig. 4e, left, and Extended Data Fig. 8c). Accordingly, color-area tended to decrease over time, from 74.1 to 39.4 units² in the pre-selection subspace (Extended Data Fig. 8d; p=0.076, bootstrap). Instead, after selection, colors were represented in a new ‘post-selection’ subspace (Fig. 4e, right, and Extended Data Fig. 8c–d; color-area in post-selection subspace increased from 27.8 to 261.9 units² over time, p<0.001, bootstrap).

While pre-selection subspaces were independent, the post-selection subspaces of the upper and lower were aligned (Fig. 4a). The upper and lower color planes were now parallel (angle between the planes was 20.1°, IQR: 11.6°−29.0°). The cosine of the angle between the upper and lower color planes increased after selection (Fig. 4b, p=0.006, bootstrap test of logistic regression). Furthermore, the representation of the selected item’s color shifted from being anti-correlated before selection to positively correlated after selection (Fig. 4c, mean r=0.139 for −300 to 0 ms prior to target onset, p<0.001 vs zero and vs pre-cue, bootstrap). Finally, color representations of an item were now well separated when they were projected onto the other color subspace (Fig. 4d; color-area increased from 35.2 to 94.0 units² over time, p=0.010, bootstrap). Together, these results suggest selection transformed memories from independent item-specific subspaces to a common subspace that represented the color of the selected item, regardless of its original location. Reflecting the importance of this transformation, the strength of alignment of color spaces in LPFC was correlated with behavior: when memory reports were inaccurate, the cosine of the angle between the two color planes was reduced (Extended Data Fig. 9f, p=0.027, randomization test).

The degree of transformation iteratively decreased in FEF, parietal, and V4 (Extended Data Fig. 9c–d). This may reflect a gradient in the flexibility of neural responses across regions, with dynamic, integrative, representations in prefrontal cortex and more static, localized, representations in visual cortex.

Selection also transformed the non-selected memories in LPFC, although to a lesser degree: the color planes of the non-selected items tended to become aligned (IQR: 61.4°−83.7° to 15.5°−39.7°, p=0.085, bootstrap) but the post-cue representations were not significantly correlated (p=0.202 against zero; Extended Data Fig. 9a–d). Critically, the non-selected item remained nearly orthogonal to the selected item before and after selection (IQR: 80.1°−85.5° to 75.7°−82.4° for pre- and post-cue, p=0.287, bootstrap; Extended Data Fig. 9a,c–d), which could avoid interference between the selected and unselected item. Interestingly, the transformation acting on the selected and non-selected representations partially generalized to the other item, suggesting the transformation had a common component that acted on both items simultaneously (see Extended Data Fig. 9e and Supplementary Discussion 3).

As noted above, the dynamic re-alignment of neural representations reflects the changing task demands during the trial: independently encoding items before selection but aligning items after selection, abstracting over item location. Consistent with the transformation of memories being driven by task demands, memory representations were aligned immediately after stimulus presentation on pro trials. In LPFC, the representations of the upper and lower colors were positively correlated after stimulus offset on pro trials (Extended Data Fig. 10a–d). Additionally, the upper and lower color planes were well-aligned throughout the trial (Fig. 4f and Extended Data Fig 10e; early: median angle=34.5°, IQR: 22.1°−51.4°; late: median angle=30.4°, IQR: 18.5°−46.2°; no change with time, p=0.449; there was a trend towards an interaction between pre/post and pro/retro, p=0.067, bootstrap).

The same aligned subspace seemed to be used in retro and pro trials: there was a weak, but significant, correlation between color representations at the end of the delay on pro and retro trials (Extended Data Fig 10f, mean rho=0.06, p=0.015, bootstrap). This correlation did not exist before selection (mean rho=−0.01, p=0.634) and increased with time (p=0.027, bootstrap).

The task-dependent dynamic transformations we observed may allow for cognitive control of behavior. In the retro task, selection transformed color information from independent item-specific subspaces to a shared ‘template’ subspace (Fig. 4g). From the perspective of a neural circuit decoding information from the template subspace to guide visual search, the transformation abstracts over location and allows the selected item to guide the animal’s response. As the item-specific and non-selected subspaces are orthogonal to the template subspace, this circuit would be unaffected by those representations. In this way, the timing of the transformation determines when this circuit is engaged (e.g., after selection in the retro task or immediately in the pro task). Thus, cognitive control may dynamically transform representations in order to control what and when cognitive computations are engaged.

Methods

Subjects

Two adult male rhesus macaques (Macaca mulatta) participated in the experiment. Monkey 1 (2) weighed 12.1 (8.9) kg. All experimental procedures were approved by the Princeton University Institutional Animal Care and Use Committee and were in accordance with the policies and procedures of the National Institutes of Health.

Subject number was chosen to be consistent with previous work. Both animals performed the same experiments and so no randomization or blinding of animal identity was necessary. As detailed below, conditions within each experiment were chosen randomly and experimenters were blind to experimental condition when pre-processing the data.

Behavioral task

Stimuli were presented on a Dell U2413 LCD monitor positioned at a viewing distance of 58 cm using Psychtoolbox and MATLAB (Mathworks, Natick, MA). The monitor was calibrated using an X-Rite i1Display Pro colorimeter to ensure accurate color rendering. During the experiment, subjects were required to remember the color of either 1 or 2 square stimuli presented at two possible locations. The color of each sample was drawn randomly from 64 evenly spaced points along a photometrically isoluminant circle in CIELAB color space. This circle was centered at (L = 60, a = 6, b = 14) and the radius was 57 units. Colors were independent across locations. The stimuli measured 2° of visual angle (DVA) on each side. Each stimulus could appear at one of two possible spatial locations: 45° clockwise or counterclockwise from the horizontal meridian (in the right hemifield; stimuli are depicted in the left hemifield in Fig. 1 for ease of visualization) with an eccentricity of 5 DVA from fixation. To perform the retrospective task, the animal had to remember which color was at each location (i.e., the ‘upper’ and ‘lower’ colors).

The animals initiated each trial by fixating a cross at the center of the screen. On retrospective (“retro”) trials, after 500 ms of fixation, one (20% of trials) or two (80% of trials) stimuli appeared on the screen. The stimuli were displayed for 500 ms, followed by a memory delay of 500 or 1,000 ms. Next, a symbolic cue was presented at fixation for 300 ms. This cue indicated which sample (upper or lower) the animal should report in order to get juice reward. The location of the selected memory was randomly chosen on each trial. Two sets of cues were used in the experiment to dissociate the meaning of the cue from its physical form. The first set (cue set 1) consisted of lines oriented 45° clockwise and counterclockwise from the horizontal meridian (cueing the lower and upper stimulus, respectively). The second set (cue set 2) consisted of a triangle or a circle (cueing the lower and upper stimulus, respectively). Cues were presented at fixation and subtended 2 degrees of visual angle. After the cue, there was a second memory delay (500–700 ms), after which a response screen appeared. The response screen consisted of a ring 2° thick with an outer radius of 5°. The animals made their response by breaking fixation and saccading to the section of the color wheel corresponding to the color of the selected (cued) memory. Note, in previous work using human subjects, observers are typically free to foveate the color wheel and fine-tune their selection, so differences in performance between monkeys and humans³⁰ may in part reflect task design. Importantly, the color ring was randomly rotated on each trial to prevent motor planning or spatial encoding of memories. The animals received a graded juice reward that depended on the accuracy of their response. The number of drops of juice awarded for a response was determined according a circular normal (von mises) distribution centered at 0° error with a standard deviation of 22°. This distribution was scaled to have a peak amplitude of 12, and non-integer values were rounded up. When response error was greater than 60° for Monkey 1 (40° for Monkey 2), no juice was awarded and the animal experienced a short time-out of 1 to 2 s. Responses had to be made within 8 s, although, in practice, this restriction was unnecessary as response times were on the order of 200–300 ms.

Prospective (“pro”) trials were similar to retro trials, except that the cue was presented 200–600 ms before the stimuli. After the colored squares, a single continuous delay occurred before the onset of responses screen (1300–2000 ms for Monkey 1 and 1000–2000 ms for Monkey 2). For behavioral analyses and all neural analyses around the response epoch, we only analyzed trials with a minimum of delay of 1300 ms to match the total delay range for pro and retro trials.

Condition (retro or pro) and cue set were manipulated in a blocked fashion. Animals transitioned among three different block types: (1) pro trials using cue set 1, (2) retro trials using cue set 1, and (3) retro trials using cue set 2. The sequence of blocks was random. Transitions between blocks occurred after the animal had performed 60 correct trials of block type 1 (pro) or 30 correct trials for block types 2 and 3 (retro), balancing the total number of pro and retro trials. All electrophysiological recordings were done during this task.

In addition, both animals completed a second behavioral experiment (“Experiment 2”) outside of electrophysiological recordings (Extended Data Fig. 1e). In Experiment 2, all trials were a variant of the retrospective load 2 condition, the total stimulus-target delay was fixed to 2,400 ms, and the stimulus-cue delay was randomly selected to be 500, 1000, or 1500 ms. This manipulation allowed us to test if when the retrocue occurred impacted memory accuracy, thereby isolating the effect of selection on the contents of working memory.

The eye position of the animals was continuously monitored at 1 kHz using an Eyelink 1000 Plus eye-tracking system (SR Research, Ottawa, ON). The animals had to maintain their gaze within a 2° circle around the central cross during the entire trial until the response. If they did not maintain fixation, the trial was aborted, and the animal received a brief timeout.

We analyzed all completed trials, defined as any trial on which the animal successfully maintained fixation and made a saccade to the color wheel, regardless of accuracy. Monkey 1 completed 9,865 trials over 10 sessions and Monkey 2 completed 11,131 trials over 13 sessions.

As shown in Extended Data Fig. 1, the behavior of the two animals was qualitatively similar and so we pooled data across animals for all analyses.

Surgical procedures and recordings

Animals were implanted with a titanium headpost to immobilize the head and with two titanium chambers for providing access to the brain. The chambers were positioned using 3D models of the brain and skull obtained from structural MRI scans. Chambers were placed to allow for electrophysiological recording from LPFC, FEF, parietal area 7a/b, and V4.

Epoxy coded tungsten electrodes (FHC Inc, Bowdoin, ME) were used for both recording and microstimulation. Electrodes were lowered using a custom built microdrive assembly that lowered electrodes in pairs from a single screw. Recordings were acute; up to 80 electrodes were lowered through intact dura at the beginning of each recording session and allowed to settle for 2–3 hours before recording. This enabled stable isolation of single units over the session. Broadband activity (sampling frequency = 30 kHz) was recorded from each electrode (Blackrock Microsystems, Salt Lake City, UT). We performed 13 recording sessions in Monkey 2 and 10 sessions in Monkey 1.

After recordings were complete, we confirmed electrode locations by performing structural MRIs after lowering two electrodes in each chamber into cortex. Based on the shadow of these two electrodes, the position of the other electrodes in each chamber could be reconstructed. Electrodes were categorized as falling into LPFC, FEF, parietal area 7a/b, and V4 based on anatomical landmarks.

In separate experiments, we identified which electrodes were located in FEF using electrical microstimulation. Based on previous work³¹, we defined FEF sites as those for which electrical stimulation elicited a saccadic eye movement. Electrical stimulation was delivered in 200 ms trains of anodal-leading bi-phasic pulses with a width of 400 μs and an inter-pulse frequency of 330 Hz. Electrical stimulation was delivered to each electrode in the frontal well of each animal and FEF sites were identified as those sites for which electrical stimulation (<50 μA) consistently evoked a saccade with a stereotyped eye movement vector at least 50% of the time. Untested electrode sites (e.g., from recordings on days with a different offset in the spatial distribution of electrodes) were classified as belonging to FEF if they fell within 1 mm of confirmed stimulation sites and were positioned in the anterior bank of the arcuate sulcus (as confirmed via MRI).

Signal preprocessing

Electrophysiological signals were filtered offline using a 4-pole 300 Hz high-pass Butterworth filter. For Monkey 1, to reduce common noise, the voltage time series x recorded from each electrode was re-referenced to the common median reference³² by subtracting the median voltage across all electrodes in the same recording chamber at each time point.

The spike detection threshold for all recordings was set equal to −4σ_n, where σ_n is an estimate of the standard deviation of the noise distribution:

$${\sigma }_n=median\left(\frac{\left|x\right|}{0.6745}\right)$$

Timepoints at which x crossed this threshold with a negative slope were identified as putative spiking events. Repeated threshold crossings within 32 samples (1.0667 ms) were excluded. Waveforms around each putative spike time were extracted and were manually sorted into single units, multi-unit activity, or noise using Plexon Offline Sorter (Plexon, Dallas, TX).

For all analyses, spike times of single units were converted into smoothed firing rates (sampling interval = 10 ms) by representing each spiking event as a delta function and convolving this time series with a causal half-gaussian kernel (σ = 200 ms).

Statistics and Reproducibility

Experiments were repeated independently in two monkeys and data were combined for subsequent analysis after confirming behavior was similar across animals (Extended Data Figure 1). Tests were not corrected for multiple comparisons unless otherwise specified. Nonparametric tests were performed using 1,000 iterations; therefore, exact p-values are specified when p >= 0.001.

Analyses were performed in MATLAB (Mathworks, Natick, MA).

Mixture modeling of behavioral reports (Extended Data Fig. 1)

Behavioral errors on delayed estimation tasks are thought to be due to at least three sources of errors^12,13: imprecise reports of the cued stimulus, imprecise reports of the uncued stimulus, and random guessing (i.e., from ‘forgotten’ stimuli). To estimate the contribution of each of these sources of error, we used a three-component mixture model to model behavioral reports (Bays et al., 2009):

$$p\left(\widehat{\theta }\right)=\left(1-\gamma -\mathrm{{\rm B}}\right){\varphi }_{\sigma }\left(\widehat{\theta }-\theta \right)+\gamma \frac{1}{2\pi }+\mathrm{{\rm B}}\frac{1}{m}{\varphi }_{\sigma }\left(\widehat{\theta }-{\theta }^{\mathrm{*}}\right)$$

Where θ is the color value of the cued stimulus in radians, $\widehat{\theta }$ is the reported color value, θ^* is the color value of the uncued stimulus, γ is the proportion of trials on which subjects responded randomly (i.e., probability of guessing, p(Guess)), B is the proportion of trials on which subjects reported the color of the uncued stimulus (i.e., probability of ‘swapping’, p(Swap)), and ϕ_𝜎 is a von-mises distribution with a mean of zero and a standard deviation σ (inverse precision). All parameters were estimated using the Analogue Report Toolbox (https://www.paulbays.com/toolbox/index.php). Bootstrapped distributions of the maximum likelihood values of the free parameters γ, B, and σ were generated by fitting the mixture model independently to the behavioral data from each session (N=23) and then resampling the best fitting parameter values with replacement across sessions. In this way, the distribution shows the uncertainty of the mean parameters across sessions.

As noted in the main text, if the animal was able to select an item from memory earlier in the trial, then this reduced the error in the animal’s behavioral response (Extended Data Fig. 1e). Behavioral modeling showed earlier cues improved the precision of memory reports (Extended Data Fig. 1e, β=3.95 ± 1.88 SEM, p=0.012, bootstrap) but did not significantly change the probability of forgetting (i.e. random responses; β=0.03 ± 0.03 STE, p=0.126, bootstrap). Furthermore, we found that memory reports were more accurate in the pro condition than in the retro condition (Fig. 1b–c). Here, behavioral modeling showed the improvement on pro trials was due to an increase in the precision of memory reports and a reduction in forgetting (i.e. fewer random reports; Extended Data Fig. 1d).

Entropy of report distributions (Extended Data Fig. 1)

To quantify whether color reports were more clustered than expected by chance, we used a simple clustering metric³⁰. This metric relies on the fact that entropy is maximized for uniform probability distributions. In contrast, probability distributions with prominent peaks will have lower entropy. Because the target colors are drawn from a circular uniform distribution, the entropy of the targets $H\left(\Theta \right)$ will be relatively high. If responses are clustered, their entropy $H\left(\widehat{\theta }\right)$ will be relatively low. Taking the difference of these two values yields a clustering metric C. Negative values of C indicate greater clustering: $C=H\left(\widehat{\theta }\right)-H\left(\Theta \right)$ where:

$$H\left(x\right)=-\sum _{x=1}^{360}f\left(x\right){log}_{2}f\left(x\right)dx$$

Significance of the clustering metric versus zero was assessed with a bootstrapping process that randomly resampled trials with replacement.

Calculation of cued location d-prime (Extended Data Fig. 2, 4)

We used d-prime to describe how each neuron’s firing rate was modulated by cuing condition (‘upper’ or ‘lower’), defined as:

$$d^{\mathrm{\text{'}}}=\frac{{\mu }_{upper}-{\mu }_{lower}}{\sqrt{\frac{1}{2}\left({\sigma }_{upper}^2+{\sigma }_{lower}^2\right)}}$$

where μ_upper and μ_lower are a neuron’s mean firing rate on trials in which the upper or lower stimulus was cued as task relevant, respectively, and ${\sigma }_{upper}^2$ and ${\sigma }_{lower}^2$ are the variance in firing rate across trials in each condition. D-primes were either computed using trials pooled across all retro trials (Extended Data Fig. 2b) or calculated separately for each of the three block types (Extended Data Fig. 4a, pro with cue set 1, retro with cue set 1, and retro with cue set 2, see above). This analysis included all neurons that were recorded for at least 10 trials per each cued location. The significance of each neuron’s d-prime (Extended Data Fig. 2b) was assessed by comparing to a null distribution of values generated by randomly permuting location labels (upper or lower) across trials (1000 iterations). To test if a region had more significant neurons than expected by chance, the percentage of significant neurons was compared to that expected by chance (the alpha level, 5%).

To understand if cells displayed similar selectivity across cue sets and task conditions, we computed a ‘selection’ correlation, measured as the Pearson’s correlation coefficient between the d-prime to retro cueset 1 and the d-prime to retro cueset 2, and a ‘generalization’ correlation, measured as the Pearson’s correlation coefficient between pro cueset 1 and retro cueset 2 (Extended Data Fig. 4a–c). Significance against zero was tested by randomly resampling cells with replacement.

Classification of cued location (Figure 2 and Extended Data Fig. 4)

We used linear classifiers to quantify the amount of information about the location of the cued stimulus (upper or lower) in the population of neurons recorded from each brain region (Fig. 2b–c). This analysis included all neurons that were recorded during at least 60 trials for each cueing condition (upper or lower) in each block type (pro with cue set 1, retro with cue set 1, and retro with cue set 2, see above). On each of 1000 iterations, 60 trials from each cueing condition and block type were sampled from each neuron with replacement. The firing rate from those trials, locked to cue onset, was assembled into a pseudo-population by combining neurons across sessions such that pseudo-trials matched both block and cue condition. For each timestep, a logistic regression classifier (as implemented by fitclinear.m in MATLAB) with L2 regularization (λ = 1/60) was trained to predict the cueing condition (upper or lower) using pseudo-population data from one block (e.g., retro with cue set 1) and tested on held out data from another block (e.g., retro with cue set 2). Classification accuracy (proportion of correctly classified trials) was averaged across reciprocal tests (e.g., train on retro with cue set 2, test on retro with cue set 1).

We used a randomization test to test for significant differences in the onset time of above-chance classification accuracy between regions. For each pair of regions, we computed the difference in time of first-significance (‘the lag’, p<0.05, using the bootstrap procedure describe above). To generate a null distribution of lags, we randomly permuted individual neurons between the two regions (without changing the size of the population associated with each region) and then repeated the above bootstrap procedure to determine the lag in above-chance classification for each permuted dataset. 1000 random permutations were used for each pair of regions. Significance was assessed by computing the proportion of lags in the null distribution that were greater than the observed lag. Note that this randomization procedure controls for differences in the number of features (neurons) across regions, so differences in the number of neurons recorded across regions cannot explain our results.

To assess the discriminability of the upper and lower pro conditions (Extended Data Fig. 4e), we calculated the 10-fold cross-validated classification accuracy (averaged across folds). To provide an estimate of variability we repeated this analysis 1000 times, each time with a different partition of trials into training and testing sets.

Neuron dropping analyses for classification of cued location (Extended Data Fig. 2)

To further test whether classification performance depended on the number of neurons recorded in each region, we performed ‘neuron dropping’ analyses (as in ³³; Extended Data Fig. 2). To do this, we repeated the classification procedure described above, but limited the analysis to subsets of neurons drawn from the full population of neurons recorded in each region (N = 1,000 iterations per subset size). In the first version of this analysis, the neurons composing each subpopulation were drawn at random (Extended Data Fig. 2c). In the second version of this analysis, the neurons composing each subpopulation were drawn at random, subject to the condition that they displayed a significant evoked response to the presentation of the cue (Extended Data Fig. 2d). Specifically, across trials, neurons with an evoked responses were taken as those with a higher mean firing rate during the 500 ms epoch after the cue compared to the 300 ms epoch before the cue (one-tailed t-test). In the third version of these analysis, neurons were added to the analysis in a fixed order determined by their ability to support classification (Extended Data Fig. 2e–f). For the selection classifier (which was trained to discriminate the cued location on retro cueset 1 trials and tested on retro cueset 2 trials, and vice-versa), neurons entered the analysis based on the magnitude of their d-prime values for both retro cuesets. To quantify this, we projected the d-prime values for the two cuesets onto the identity line (schematized in Extended Data Fig. 2e) and took the absolute value of the resulting vector. Cells with large absolute projection values entered the analysis first. Our ordering procedure for the generalization classifier was the same as for the selection classifier, except that it was based on pro cueset 1 and retro cueset 2 d-prime, as these were the training/testing sets for this classifier.

For each sub-population of neurons in each of these analyses, we measured four statistics:

1. selection classification accuracy after cue onset (300 ms post-cue)

2. generalized classification accuracy after cue onset (300 ms post-cue)

3. time to 55% selection classification accuracy

4. time to 55% generalized classification accuracy

When subpopulations were drawn at random from all neurons in each region or all neurons displaying an evoked response (Extended Data Fig. 2c–d), dropping curves for each of these statistics were well described by two-parameter power functions. Power functions were fit using the Matlab function fit.m and 95% prediction intervals for each statistic at the maximum population size recorded in LPFC were generated using predint.m. The distance of the measured statistic in LPFC from these predicted values (in units of standard error of the prediction interval) were measured and used to calculate p-values.

When subpopulations were drawn in a fixed order (Extended Data Fig. 2e–f), dropping curves for each of these statistics were well described by linear functions. Linear functions were fit using that Matlab function fit.m and 95% confidence intervals for linear fits at each measured value were generated using predint.m. Subpopulations that never reached 55% classification accuracy were excluded from curve-fitting for statistics 3 and 4.

Finally, to assess the discriminability of visual information in each region we trained two classifiers to discriminate either the two ‘upper’ cues or two ‘lower’ cues (on retro trials). Classification accuracy was averaged across 10-fold cross-validated sets (Extended Data Fig. 2g–h). The accuracy of both the upper-cue and lower-cue classifiers were then averaged to estimate the amount of information about low level visual features of the cue while holding other factors constant (e.g., cued location). We then computed neuron dropping curves for (1) accuracy early after cue onset (300 ms post-cue) and (2) time to 55% classification accuracy, as above (Extended Data Fig. 2h).

Signal and noise for classification of cued location (Extended Data Fig. 3)

To assess whether classification performance was driven by increases in signal, decreases in noise, or both, we analyzed the distribution of classifier confidence for ‘upper’ and ‘lower’ test trials (Extended Data Fig. 3a). Classifier confidence was quantified as the probability that a given test trial was an ‘upper’ trial, as estimated by the trained model. Signal was quantified as the distance between the means of the confidence distributions for ‘upper’ and ‘lower trials’ and noise was estimated as the average standard deviation of the confidence distributions. Repeating these calculations for each of the 1,000 resamples yielded bootstrapped distributions of values (Extended Data Fig. 3b).

Noise correlations and variance-to-mean ratio during cue epoch (Extended Data Fig. 3)

To determine whether difference in variance and covariance may be driving differences in classification performance across regions, we calculated variance-to-mean ratios and noise correlations for single neuron firing rates around the time of the selection cue.

Variance-to-mean ratio across trials was calculated by first calculating each neuron’s trial-wise firing rate during the period after cue onset (0–500 ms post-cue). Next, for each trial type (pro cueset 1 upper, pro cueset 1 lower, retro cueset 1 upper, retro cueset 1 lower, pro cueset 2 upper, pro cueset 2 lower), the variance of these firing rates across trials was divided by their mean. Finally, we took the average of these variance-to-mean ratios across the 6 trial types (Extended data Figure 3d).

Calculation of noise correlations also began by first calculating each neuron’s trial-wise firing rate during the period after cue onset (0–500 ms post-cue). Next, for each trial type (pro cueset 1 upper, pro cueset 1 lower, retro cueset 1 upper, retro cueset 1 lower, pro cueset 2 upper, pro cueset 2 lower), each neuron’s pool of firing rates were adjusted to have a mean of zero. Finally, we computed the average correlation between the mean-zeroed firing rates of all pairs of neurons within a region, and then averaged these average correlation values across the 6 trial types (Extended Data Fig. 3c). As expected, given our pseudopopulation approach, noise correlation values were low and did not differ across regions.

Quantification of color information (Fig. 3 and Extended Data Fig. 5–8)

We adapted previous work³⁴ to define a color modulation index (MI_color) that describes how each neuron’s firing rate was modulated by the colors of the remembered stimuli. Critically, this statistic avoids strong assumptions about the structure of tuning curves (e.g., it doesn’t assume unimodal tuning). After dividing color space into N = 8 bins, MI_color is defined as:

$$M{I}_{color}=\frac{{\sum }_{c=1}^N{z}_{c}log\left(N{z}_c\right)}{log\left(N\right)}$$

where z_c is a neuron’s normalized mean firing rate r_c across trials evoked by colors in the c^th bin:

$$z_c=\frac{r_c}{{\sum }_{c=1}^N{r}_c}$$

MI_color is a normalized entropy statistic that is 0 if a neuron’s mean firing rate is identical across all color bins and 1 if a neuron only fires in response to colors from one bin. To control for differences in average firing rate and number of trials across neurons, we z-scored this metric by subtracting the mean and dividing by the standard deviation of a null distribution of MI values. To generate this null distribution, the color bin labels were randomly shuffled across trials and the MI statistic was recomputed (1,000 times per neuron).

Z-scored color modulation indices were computed separately for each time point, trial type (pro or retro), and stimulus type (selected/non-selected/attended/non-attended, Fig. 3b and Extended Data Fig. 6). This analysis included neurons that were recorded for at least 10 trials in each of these conditions. Selectivity for color was computed without respect to the spatial location of the stimulus (upper or lower). Computing selectivity for colors only presented at a neuron’s preferred location did not qualitatively change the results. Z-scored modulation indices were compared to zero or across conditions via t-test (Fig. 3b). We corrected for multiple comparisons over time using a cluster-correction³⁵. Briefly, the significance of contiguous clusters of significant t-tests was computed by comparing their cluster mass (the sum of the t-values) versus what would be expected by chance (randomization test). Additionally, to summarize changes in selected and non-selected color information after cue onset, we averaged color information for each neuron in two time periods (−300 to 0 ms pre-cue and 200 to 500 ms post-cue) and tested the difference of these values (post-pre) against zero by bootstrapping the mean difference in color information across neurons (Extended Data Fig. 7a).

To determine if a neuron displayed significant selectivity for the color at one particular location (upper/lower), we calculated the z-scored information about the cued color at each timepoint over the interval from 0 to 2.5 seconds post-stimulus onset independently for each location. Color selectivity was measured across all conditions, including pro, retro, and single-item trials. As described above, we used a cluster correction to correct for multiple comparisons across time. Neurons with significant color selectivity (p<0.05) at any point during this interval were deemed color selective. Binomial tests compared the proportion of neurons with significant color selectivity for at least one of the two locations to a conservative null proportion of 10% (for two tests with an alpha of 0.05, one test for each location).

To determine if independent populations of LPFC neurons encoded the upper and lower color during the pre-cue period of retro trials, we counted the number of neurons with significant cluster-corrected selectivity during the 500 ms period before cue onset. Of the 607 LPFC neurons entering the analysis, 112 (18.5%) carried information about the upper color and 99 (16.3%) carried information about the lower color. Of these, 35 (5.8%) carried information about both the upper and lower color. A binomial test compared this proportion (5.8%) to that expected by random assignment of top- and bottom-selectivity (i.e., 18.5% x 16.3% ≈ 3.0%). To visualize selectivity in a non-binary manner, we also plotted the distribution of z-scored information about the color of each item for all LPFC neurons, averaged during the 500 ms pre-cue period (Extended Data Fig. 8a).

In addition to the z-scored color modulation index, we also quantified color selectivity using percent explained variance (Extended Data Fig. 5b). As with the z-scored color modulation index, firing rates for each timepoint were binned by the color of the stimulus of interest (selected/non-selected) into 8 color bins. A linear model with a constant term and 8 categorical predictors (1 for each color bin) was then constructed to predict firing rates (using fitlm.m in MATLAB). PEV was then calculated as the r-squared of the fit model x 100. To avoid inflated PEV values due to overfitting, we subtracted the mean PEV during the 200 ms epoch prior to stimulus onset. The resulting traces were analyzed using cluster-corrected t-tests, as described above. Results were similar to those obtained with the color modulation index.

Quantification of reported color information (Figure 3)

To quantify the amount of information each neuron carried about the animal’s reported color, we followed the same approach as for stimulus color, except that responses were binned by the color reported by the animal rather than by the color of the cued or uncued stimulus (Fig. 3).

Modulation of color information by task and behavioral performance (Extended Data Fig. 6–7)

To compare the amount of color information in firing rates across the pro and retro conditions (Extended Data Fig. 6b–c), we computed the z-scored color modulation indices as described above for each of the four conditions of interest (selected, non-selected, attended, and non-attended colors). Trial counts were matched across these four conditions to avoid biases in the color information statistic. To assess relative information about cued (selected and attended) and uncued (non-selected and non-attended) color information, we computed the difference in color information between each pair of conditions, for each neuron. The average difference across all neurons was then tested against zero, using the cluster correction described above to correct for multiple comparisons across time³⁵.

To compare the amount of color information in firing rates when behavioral performance was relatively accurate or inaccurate (Extended Data Fig. S7), we divided retro trials into two groups based on the accuracy of the behavioral report. Trials within each session were split by the median accuracy for that session. Z-scored color modulation indices were computed separately for each split-half of trials. As above, the same number of trials were used for all four conditions (more/less accurate x selected/non-selected). Additionally, to quantify the effect of selection, the difference in color information for selected and non-selected colors was computed for each group of trials separately (more or less accurate). This selected - non-selected difference was then tested against zero to measure the effect of selection and tested between the two groups of trials to measure the effect of behavioral accuracy. Comparisons were done with a t-test across all neurons, with cluster correction to correct for multiple comparisons across time³⁵.

Measuring the angle between upper and lower color planes (Figure 4 and Extended Data Fig. 9–10)

As described in the main text, we were interested in understanding the geometry of mnemonic representations of color across the two possible stimulus locations (upper or lower). To explore this, we examined the response of the population of neurons as a function of the color and location of the stimulus of interest (either cued or uncued). The fidelity of these population representations depended on the behavioral performance of the animal. Therefore, for all principle component analyses, we divided trials based on the accuracy of the behavioral report (median split for each session, as above) and separately analyzed trials with lower angular error (higher accuracy, Figure 4) and higher angular error (lower accuracy, Extended Data Fig. 9f).

Trials were sorted into B = 4 color bins and L = 2 locations (top or bottom), yielding B x L = M, 8 total conditions. To visualize these population representations, we projected the population vector of mean firing rates for each of these 8 conditions into a low-dimensional coding subspace (Fig. 4a and Extended Data Fig. 9a–b, similar to as in previous work³⁶). For each timestep, we defined a population activity matrix X as an M x N matrix, where M is the number of conditions (8) and N is the number of neurons:

$$\mathbf{X}=\left[\begin{array}{c}\mathbf{r}\left(c_{\mathrm{1,1}}\right)-\stackrel{-}{\mathbf{r}}\\ ⋮\\ \mathbf{r}\left(c_{B,L}\right)-\stackrel{-}{\mathbf{r}}\end{array}\right]$$

Here, r(c_B,L) is the mean population vector (across trials) for the condition corresponding to color bin B and location L and $\stackrel{-}{\mathbf{r}}$ is the mean population vector across the M conditions (i.e., the mean of each column is zero).

The principle components of this matrix were identified by decomposing the covariance matrix C of X using singular value decomposition (as implemented by pca.m in MATLAB):

$$\mathbf{C}=\mathbf{P}\mathbf{D}{\mathbf{P}}^{\mathbf{T}}$$

where each column of P is an eigenvector of C and D is a diagonal matrix of corresponding eigenvalues. We constructed a reduced (K = 3) dimensional space whose axes correspond to the first K eigenvectors of C (i.e., columns of P, P_K, assuming eigenvectors are ordered by decreasing explained variance). These first 3 eigenvectors explained an average of 65% of the variance in the mean population response across all examined timepoints. We then projected the population vector for a given condition into this reduced dimensionality space:

$${\mathbf{z}}_K={\mathbf{P}}_K^{\mathit{T}}(\mathbf{r}(c_{B,L})-\stackrel{-}{\mathbf{r}})$$

Where z_K is the new coordinate along axis K in the reduced dimensionality space.

We observed that, when visualized in the reduced dimensionality space, the population representations for each color bin B within a given location L tended to lie on a plane, referred to as the ‘color plane’ in the main manuscript (Fig. 4a). To identify the best fitting plane, we defined a new population activity matrix Y_L for each location L with dimensions B x K:

$${\mathbf{Y}}_L=\left[\begin{array}{c}\mathbf{z}\left(c_{1,L}\right)-{\stackrel{-}{\mathbf{z}}}_L\\ ⋮\\ \mathbf{z}\left(c_{B,L}\right)-{\stackrel{-}{\mathbf{z}}}_L\end{array}\right]$$

where z(c_B,L) is the population vector for the condition corresponding to color bin B and location L in the reduced dimensionality space and ${\stackrel{-}{\mathbf{z}}}_L$ is the mean population vector across color bins for that location (i.e., the mean of each column is zero). The principle components of this matrix were calculated in the same manner as above and the first two principle components were the vectors that defined the plane-of-best-fit to the points defined by the rows of Y_L. These planes explained > 97% of the variance of each set of points in the 3D subspace.

If the vectors defining the plane-of-best-fit for the upper item are v₁ and v₂ and those for the lower item are v₃ and v₄, then the cosine of the angle between these two color planes can be calculated as:

$$\mathit{cos}\left(\mathrm{\theta }\right)=\left({\mathbf{v}}_1\times {\mathbf{v}}_2\right)\cdot \left({\mathbf{v}}_3\times {\mathbf{v}}_4\right)$$

For all analyses, population vectors were based on pseudo-populations of neurons combined across sessions. Pseudo-populations were created by matching trials across sessions according to the color and location of the stimulus of interest (either cued or uncued), as described above (and following previous work²⁷). This analysis only included neurons that were recorded for at least 10 trials for each conjunction of color and location. Confidence intervals of cos(θ) were calculated using a bootstrapping procedure. On each of 1000 iterations, 10 trials from each of the 8 conditions were sampled from each neuron with replacement. The average firing rates across these sampled trials provided the mean population vector for that condition on that iteration. To assess how cos(θ) changed around cue onset (Fig. 4b and Extended Data Fig. 9f), we used a logistic regression model of the form:

$$cos\left(\mathrm{\theta }\right)=\frac{1}{{1+exp(-(\beta }_0+{\beta }_{1}t\left)\right)}$$

where t is time relative to cue onset. This model was fit to values of cos(θ) computed at each timepoint in the interval from 500 ms pre- to 1000 ms post-cue onset on each bootstrap iteration (described above). This yielded a bootstrapped distribution of β₁ estimates which could be compared to zero or across the two groups of trials with more and less accurate behavioral responses (Extended Data Fig 9f).

Defining the color subspaces for the upper and lower items in the full-dimensional space (Figure 4 and Extended Data Fig. 8)

To define the color subspace in the full neuron-dimensional space, we defined B=4 x N mean population activity matrices for each location L in the full space:

$${\mathbf{W}}_L=\left[\begin{array}{c}\mathbf{r}\left(c_{1,L}\right)-{\stackrel{-}{\mathbf{r}}}_L\\ ⋮\\ \mathbf{r}\left(c_{B,L}\right)-{\stackrel{-}{\mathbf{r}}}_L\end{array}\right]$$

The color subspace was defined as the first two principle components of W_L.

These subspaces were used for two analyses. First, we projected the population vectors of color responses from one item into the color subspace for the other item (Fig. 4d). For example, the population vector response to colors of the upper item were projected into the color subspace of the lower item, defined as the first two principal components of W_lower, and vice-versa (Fig. 4d). Second, by defining the color subspace of each item at different timepoints $t_i$, we could examine how color representations evolved during the trial (Fig. 4e and Extended Data Fig. 8c–d).

Measuring separability of colors in a subspace (Figure 4 and Extended Data Fig. 8)

Next, we were interested in quantifying the separability of colors in a given subspace. As seen in Figure 4d–e, the population representation of the four color conditions, projected into the subspace, form the vertices of a quadrilateral with the edges of the quadrilateral connecting adjacent colors on the color wheel (e.g., Fig. 4d). To measure separability of the colors, we computed the area of this quadrilateral (polyarea.m function in MATLAB). Bootstrapped distributions of these area estimates were obtained by resampling trials with replacement from each condition before re-computing W_L.

Similarity of transforms for the upper and lower stimulus (Extended Data Fig. 9e)

We were interested in testing whether the transformation of selected (“cued”) items was the same as non-selected (“uncued”) items (on retro trials). To this end, we examined how the population representation for the color of the selected and non-selected stimulus changed over time. For both a pre-cue (150 to 350 ms post-stimulus offset) and post-cue (−200 to 0 pre-target onset) time epoch, we defined an N x B population activity matrix A where N is the number of neurons, B = 4 color bins, and the elements of the matrix reflect the mean firing rate of each neuron across trials in which the color of the stimulus of interest fell in color bin b.

We computed A_pre and A_post separately for 4 different stimulus types of interest: cued upper stimuli, cued lower stimuli, uncued upper stimuli, and uncued lower stimuli. Then, for each stimulus type, we identified the NxN matrix X that transformed the pre-cue representation to its post-state:

$$A_{post,cued\_upper}=X_{cued\_upper}{A}_{pre,cued\_upper}$$

$$A_{post,cued\_lower}=X_{cued\_lower}{A}_{pre,cued\_lower}$$

$$A_{post,uncued\_upper}=X_{uncued\_upper}{A}_{pre,uncued\_upper}$$

$$A_{post,uncued\_lower}=X_{uncued\_lower}{A}_{pre,uncued\_lower}$$

To assess how similar these transforms were, we applied transforms from one condition (e.g., cued upper) to held out (split half) pre-cue neural data ($A_{pre}^{withheld}$) from a different condition (e.g., cued lower) and compared how similar the predicted post-cue data ($A_{post}^{predicted}$) were to the actual (held-out) post-cue data ($A_{post}^{withheld}$). Reconstruction error was measured as the Euclidean distance between the predicted and actual population vectors ($A_{post}^{withheld}-A_{post}^{predicted}$), averaged across all colors. Low reconstruction error indicates similar transforms.

This procedure allowed us to determine how similar the transforms were across locations and cue types by testing whether the transformation, defined in one condition for one item, generalized to another condition and/or another item. For example, for the “cued upper” condition, the reconstruction error of different forms of generalization were computed as follows:

$$\text{Error}\left(\text{same}\text{condition},\text{same}\text{item}\right)=f(A_{post,cued\_upper}^{witheld}-X_{cued\_upper}{A}_{pre,cued\_upper})$$

$$\text{Error}\left(\text{same}\text{condition},\text{different}\text{item}\right)=f(A_{post,cued\_upper}^{witheld}-X_{uncued\_lower}{A}_{pre,cued\_upper})$$

$$\text{Error}\left(\text{different}\text{condition},\text{same}\text{item}\right)=f(A_{post,cued\_upper}^{witheld}-X_{uncued\_upper}{A}_{pre,cued\_upper})$$

$$\text{Error}\left(\text{different}\text{condition},\text{different}\text{item}\right)=f(A_{post,cued\_upper}^{witheld}-X_{cued\_lower}{A}_{pre,cued\_upper})$$

where f is the mean root sum of squares across columns (i.e., the mean Euclidean distance between the actual and reconstructed population vectors for each color bin b). Similar reconstruction errors were estimated for the other three conditions (e.g., cued-lower, uncued-upper, and uncued-lower).

Applying the estimated transform to held-out data from the same condition and the same item provides a lower bound on reconstruction error due to variance across trials and indicates if the transformations are stable within a condition. Applying transforms to the response to the other item in the same cuing condition (same condition, different location), allows us to test whether the selected and non-selected item are transformed in similar ways by comparing reconstruction error to 1) chance and 2) to the error within condition and within item (same condition, same item). Finally, to control for any similarity in transforms due to a non-condition specific effect of the cue (e.g., time during the task), we can apply transforms based on items in the other cueing condition, either to the same item (different condition, same item) or the other item (different condition, different item).

We computed the four types of reconstruction error by averaging across all four conditions of interest (cued upper, cued lower, uncued upper, uncued lower). To estimate the distribution of reconstruction error, we bootstrapped with replacement across trials. Chance levels of reconstruction error were estimated by repeating the bootstrapping procedure but permuting the condition label (cued upper, cued lower, uncued upper, uncued lower) assigned to each color population vector.

Correlation of color representations (Figure 4, Extended Data Fig. 9–10)

We wanted to understand how similarly color was represented across the upper and lower locations over the course of the trial. To explore this, retro or pro trials were binned based on the color and location of the stimulus of interest (cued or uncued) and then randomly partitioned into two halves. These split halves were used to estimate the degree of noise in the data (Extended Data Fig 10b–d, described below). Specifically, trials were sorted into B = 4 color bins, L = 2 locations (top or bottom), and H = 2 halves, yielding B x L x H = M total conditions. For each of these conditions, at a given timepoint of interest, we computed the average population vector r(c_B,L,H).

We then computed the average correlation between each population vector and the population vectors corresponding to the same color bin at the other location (Figure 4c and Extended Data Figs 9c, 10b–d)

$${\mathrm{\rho }}_{cross}=\frac{1}{B2H}\sum _{i=1}^H\sum _{j=1}^H\sum _{b=1}^{B}corr\left(\mathbf{r}\left(c_{b,1,i}\right)-{〈\mathbf{r}\left(c_{B,1,i}\right)〉}_B,\mathbf{r}\left(c_{b,2,j}\right)-{〈\mathbf{r}\left(c_{B,2,j}\right)〉}_B\right)$$

where ${〈\cdot 〉}_B$ is the average across the set of color bins B. In other words, for each set of B population vectors corresponding to a particular half of the data H and location L, we subtracted the mean across bins to center the vector endpoints around zero. Thus, ρ_cross quantifies to what extent color representations are similarly organized around their mean across the two locations.

To obtain an upper bound on potential values of ρ_cross given the degree of noise in the data, we also computed the average correlation of each population vector with itself across the two halves:

$${\mathrm{\rho }}_{self}=\frac{1}{BL}\sum _{b=1}^B\sum _{l=1}^{L}corr\left(\mathbf{r}\left(c_{b,\mathrm{l},1}\right)-{〈\mathbf{r}\left(c_{B,l,1}\right)〉}_B,\mathbf{r}\left(c_{b,\mathrm{l},2}\right)-{〈\mathbf{r}\left(c_{B,l,2}\right)〉}_B\right)$$

Finally, to understand how similarly color was represented across the two cueing conditions, trials were sorted into B = 4 color bins, L = 2 locations (top or bottom), and C = 2 cuing conditions (pro/retro). For each of these conditions, at a given timepoint of interest, we computed the average population vector r(c_B,L,C). We then computed the average correlation between each population vector and the population vectors corresponding to the same color bin at either the same or different location in the other task (Extended Data Fig. 10f):

$${\mathrm{\rho }}_{att,sel}=\frac{1}{B2L}\sum _{i=1}^L\sum _{j=1}^L\sum _{b=1}^{B}corr\left(\mathbf{r}\left(c_{b,i,1}\right)-{〈\mathbf{r}\left(c_{B,i,1}\right)〉}_B,\mathbf{r}\left(c_{b,j,2}\right)-{〈\mathbf{r}\left(c_{B,j,2}\right)〉}_B\right)$$

To compare the similarity of color representations on retro trials to pre-target pro color representations, we computed this correlation between (1) the response on pro trials, for all timepoints falling within the interval from −300 ms to 0 ms before the onset of the response wheel, and (2) the response on retro trials at two different timepoints: before selection (from −300 to 0 ms before the cue) and after selection (from −300 to 0 ms before the onset of the response wheel). Correlation was measured between each timepoint across windows and then averaged across all pairs of timepoints.

As above, population vectors were pseudo-populations of neurons combined across sessions, where trials across sessions were matched according to color bin and location²⁷. This analysis only included neurons that were recorded for at least 10 trials for each conjunction of color and location. Confidence intervals for ρ_cross, ρ_self, and ρ_att,sel were calculated with a bootstrap. On each of 1000 iterations, and for each neuron and condition (color– location–half conjunction), the entire population of trials in that condition was resampled with replacement. The average firing rates across these sampled trials provided the mean population vector for that condition on that iteration. As with principle components analyses, we divided trials based on the accuracy of the behavioral report (median split of trials for each session) and the presented results reflect analysis of trials with lower angular error, unless otherwise noted.

Data and Code Availability

Data supporting all figures are included with the manuscript. Raw electrophysiological and behavioral data are available from the corresponding author upon reasonable request. The majority of methods used built-in Matlab functions, which are noted in the methods. Custom Matlab analysis functions are either referenced to their original source or available through a repository at github.com/buschman-lab/. Full code is available from the authors upon reasonable request.

Extended Data

Extended Data Figure 1.

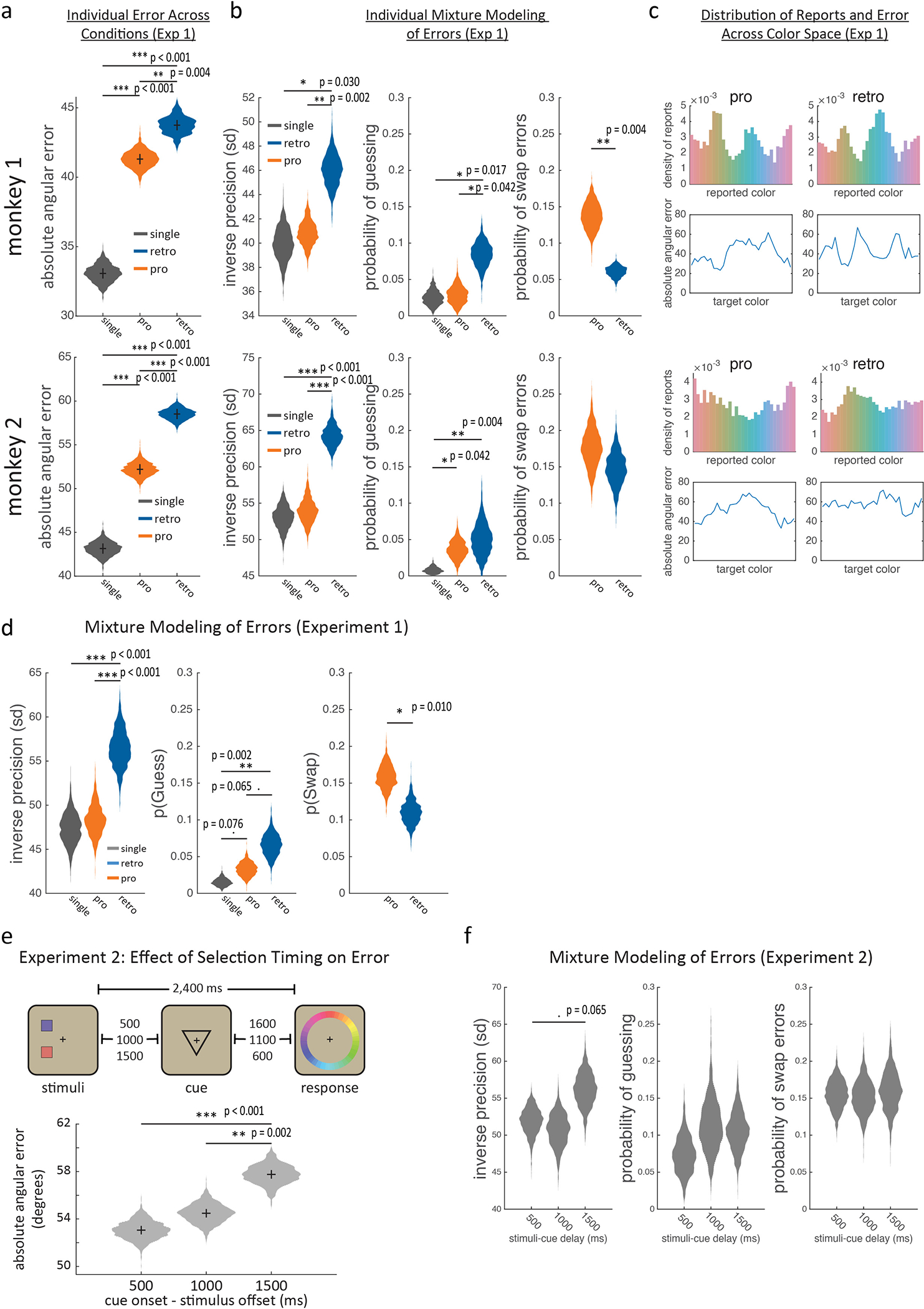
(a) Mean absolute angular error and (b) mean mixture model parameter fits in the main experiment (Experiment 1, Fig. 1a) for each animal (see methods). Violin plots depict bootstrapped distribution across sessions (N=10 for monkey 1 and N=13 for monkey 2). Lines indicate pairwise comparisons. Although monkey 1 displayed slightly better performance than monkey 2, the animals displayed similar patterns of performance across conditions. (c) Distribution of reported colors and absolute angular error as a function of target color in Experiment 1 for each animal for pro and retro trials. The distributions of reported colors for each condition and animal were significantly non-uniform (entropy of report distribution significantly lower than entropy of the target distribution, all p<0.001, bootstrap across N=3,873 pro / 3,943 retro trials for monkey 1 and N=4,440 / 4,769 trials for monkey 2). Details of this behavior have been previously published³⁰. (d) Mixture model parameter fits of behavior pooled across animals for Experiment 1 (bootstrap across N=23 sessions). (e) Top: In a separate behavioral experiment (Experiment 2), we fixed the total memory delay of the retro condition and systematically varied the length of the delay between stimuli offset and cue onset. Bottom: Increasing the time before selection (x-axis), increased mean absolute angular error (53.1°, 54.4°, and 57.8° for 0.5s, 1s, and 1.5s post-stimulus; distributions are 1000 bootstrap resamples across N=3306, 3287, and 3322 trials). (f) Mixture model parameter fits, pooled across animals (1000 bootstrap resamples across N=24 sessions), for Experiment 2. Linear regression showed earlier cues improved the precision of memory reports in Experiment 2 (β=3.95 ± 1.88 SEM, p=0.012, bootstrap) but did not significantly change the probability of forgetting (i.e. random responses; β=0.03 ± 0.03 STE, p=0.126, bootstrap). Bars and asterisks in all panels reflect two-sided uncorrected randomization tests: · p<0.1, * p<0.05, ** p<0.01, *** p<0.001.

Extended Data Figure 2.

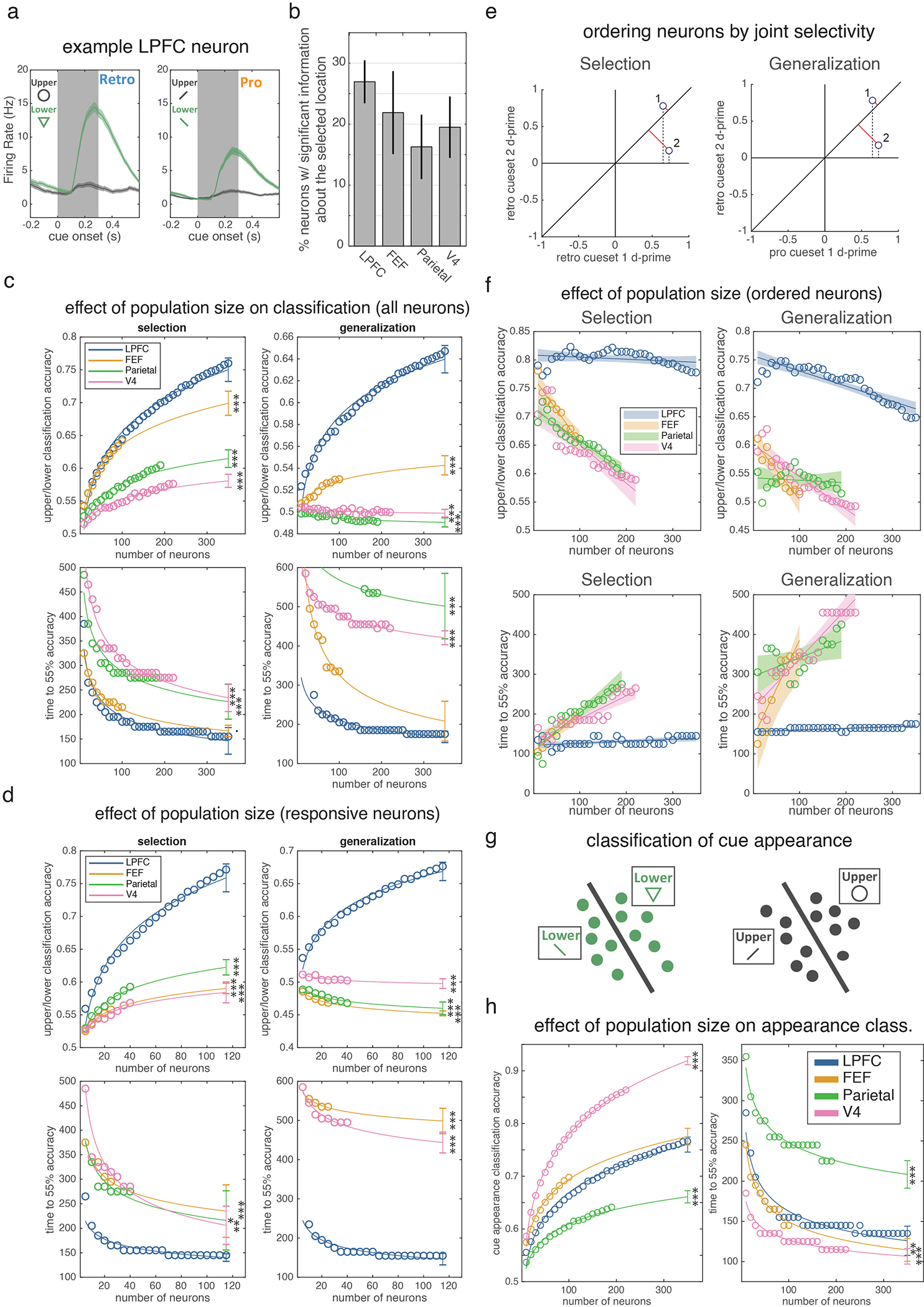
(a) Firing rate of an example LPFC neuron around cue onset when the upper (gray) or lower (green) stimulus was cued in the retro (top) and pro (bottom) conditions. Shaded regions are STE across trials (N = 161 retro upper, 124 retro lower, 150 pro upper, and 121 pro lower trials). Inset shows different cues used for retro and pro trials. (b) Percent of neurons in each region of interest with firing rates that were significantly modulated by the selected location after cue onset on retro trials (trials pooled across cue set 1 and 2). For each neuron, we quantified location selectivity using d-prime (see methods) and compared this value to a null distribution by permuting location labels across trials. All four regions showed strong selectivity: LPFC had 159 out of 590 neurons selective; FEF: 37/169, 7a/b: 49/301, V4: 62/318, all p<0.001 against chance of 5% (two-sided uncorrected binomial test). (c) Mean classification accuracy (top, taken at 300 ms post-cue) and mean time to 55% classification accuracy (bottom) for the selection (left) and generalized (right) classifiers as a function of the number of neurons used for classification. This analysis controls for the total number of neurons recorded in each region. For each subpopulation of a specific size (x-axis), circles reflect average across 1,000 iterations using different randomly selected subpopulations of that size. Lines reflect best-fitting two-parameter power function (see methods). Error bars are 95% prediction intervals. For classifier accuracy (top row): N=35, 10, 19, and 22 unique population sizes for LPFC, FEF, parietal and V4, respectively. For classifier timing (bottom left/right): N=35/32, 10/8, 19/4, and 21/20 for selection/generalization in LPFC, FEF, parietal and V4, respectively. The reduction in number of data points in the bottom plots reflects the fact that, for some neuron counts, classifiers never reached 55% classification accuracy on any iteration. Asterisks indicate significance of projected classification for a given region compared to the measured classification in LPFC at the maximum number of neurons (two-sided z-test, not corrected for multiple comparisons). Selection Classification Accuracy: FEF p=2.18e-10, Parietal p=1e-16, V4 p<1–16. Generalization Classification Accuracy: FEF p<1e-16, Parietal p<1e-16, V4 p<1e-16. Selection Classification Timing: FEF p=0.054, Parietal p=1.02e-4, V4 p<6.94e-8. Generalization Classification Timing: FEF p=0.203, Parietal p=1.11e-13, V4 p<1e-16. (d) Neuron dropping curves as in panel c, except analysis was restricted to neurons with a significant evoked response to cue onset in order to control for potential differences in responsiveness across regions (see methods). For classifier accuracy (top row): N=23, 5, 8, and 8 unique population sizes for LPFC, FEF, parietal and V4, respectively. For classifier timing (bottom left/right): N=23/22, 5/4, 8/0, and 8/8 for selection/generalization in LPFC, FEF, parietal and V4, respectively Selection Classification Accuracy: FEF p<1e-16, Parietal p<1e-16, V4 p<1e-16. Selection Classification Timing: FEF p<1e-16, Parietal p<1e-16, V4 p<1e-16. Generalization Classification Accuracy: FEF p=0.001, Parietal p=0.021, V4 p=0.002. Generalization Classification Timing: FEF p<1e-16, V4 p<1e-16. (e) To determine if there were sub-populations of selective neurons in a region with greater selectivity than the overall population, we ranked neurons in each region by their ability to support the selection (left) or generalized (right) classifier (see methods). Neurons with firing rates that yielded large magnitude (and sign consistent) d-primes for the cued location (upper or lower) across both of the retro cue sets will support selection classifier performance (left). We quantified this by projecting these two d-prime values onto the identity (red lines) and taking the absolute value of the resulting vector. Neuron 1 is ranked higher than neuron 2 because of its larger magnitude projection onto the identity. A similar procedure can be used to rank neurons for generalization from pro to retro trials (right) by repeating the procedure based on selectivity for ‘pro cueset 1’ and ‘retro cueset 2’. (f) Neuron dropping curves (as in c), except that neurons are added to the analysis based on their selectivity/generalization, as described in d. Shaded region is 95% confidence intervals of best linear fit (which fit better than power functions, see methods). Even when selecting ideal subpopulations from each region, no region significantly exceeds PFC performance. Note that performance now decreases as N increases because, due to our ranking procedure, later cells are by-design less able to support performance on withheld cues (whether within selection or across selection/attention). These later neurons may still be weighted heavily by the classifier (due to good performance on the training set) and so negatively impact performance at test. This is exemplified by the projections onto one axis in (d) (dashed lines), showing a greater weighting for neuron 2, despite it not facilitating generalization. For classifier accuracy (top row): N=35, 10, 19, and 22 unique population sizes for LPFC, FEF, parietal and V4, respectively. For classifier timing (bottom left/right): N=35/35, 10/10, 19/18, and 22/22 for selection/generalization in LPFC, FEF, parietal and V4, respectively. (g) To examine ‘bottom-up’ information flow about low-level sensory aspects of the cue, we trained classifiers to discriminate the variants of each cue, using cross validation across subsets of trials (see methods). (h) Neuron dropping curves (as in c) for these ‘cue appearance’ classifiers. Cue appearance classifiers yielded a qualitatively different pattern of performance, with V4 showing superior classification performance at cue offset (left) and faster classification onset (right). Asterisks indicate significance of projected classification for a given region compared to the measured classification in LPFC at the maximum number of neurons (two-sided z-test, not corrected for multiple comparisons). N=35, 10, 19, and 22 unique population sizes for LPFC, FEF, parietal and V4, respectively. Classification Accuracy: FEF p=.282, Parietal p<1e-16, V4 p<1e-16. Classification Timing: FEF p=0.005, Parietal p=4.24e-16, V4 p=2.27e-8. · p<0.1, * p<0.05, ** p<0.01, *** p<0.001 for all panels.

Extended Data Figure 3.

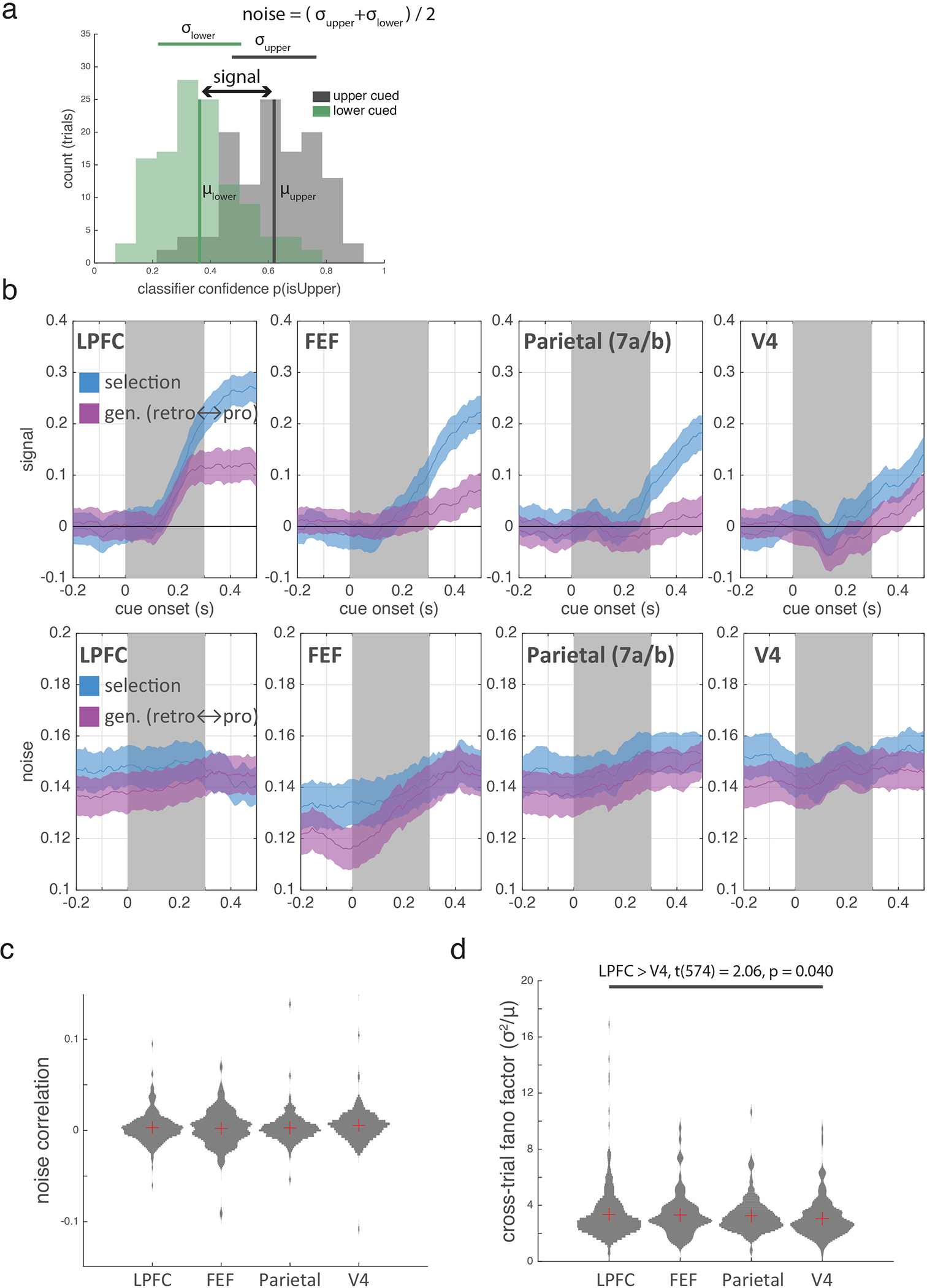
(a) Example histogram of classifier confidence across ‘upper cued’ and ‘lower cued’ trials for the LPFC selection classifier in the 500 ms after cue onset. Classifier confidence measures the distance of neural activity from the hyperplane identified by the classifier. Signal is the difference between the means of the two trial distributions; noise is their average standard deviation. (b) For both the ‘selection’ and ‘generalization’ classifiers, signal (top row) tracks classification performance (Figure 2) much better than noise (bottom row), suggesting classifier performance was due to an increase in signal and not a decrease in noise. Shaded regions is +/− STE. Distributed estimated from 1000 iterations of classifiers trained/tested on random samples of N=60 trials (see methods). (c) Mean noise correlation among neurons entering the ‘selection’ and ‘generalization’ analyses described in Figure 2. Noise correlations were based on mean firing rates over the interval from 0 to 500 ms after the cue. There were no significant differences between regions. Violin plots show distribution of values based on 1000 resamples of N=60 trials (see methods). Red crosses indicate mean. (d) Fano factor (σ²/μ) of single neuron firing rates across trials (averaged from 0 to 500 ms after the cue). Ratio was significantly larger in LPFC than V4 but no other comparisons were significant (horizontal bar; two-sided uncorrected t-test). Violin plots show distribution of values based on 1000 bootstrapped resamples of N=60 trials (see methods). Red crosses indicate mean.

Extended Data Figure 4.

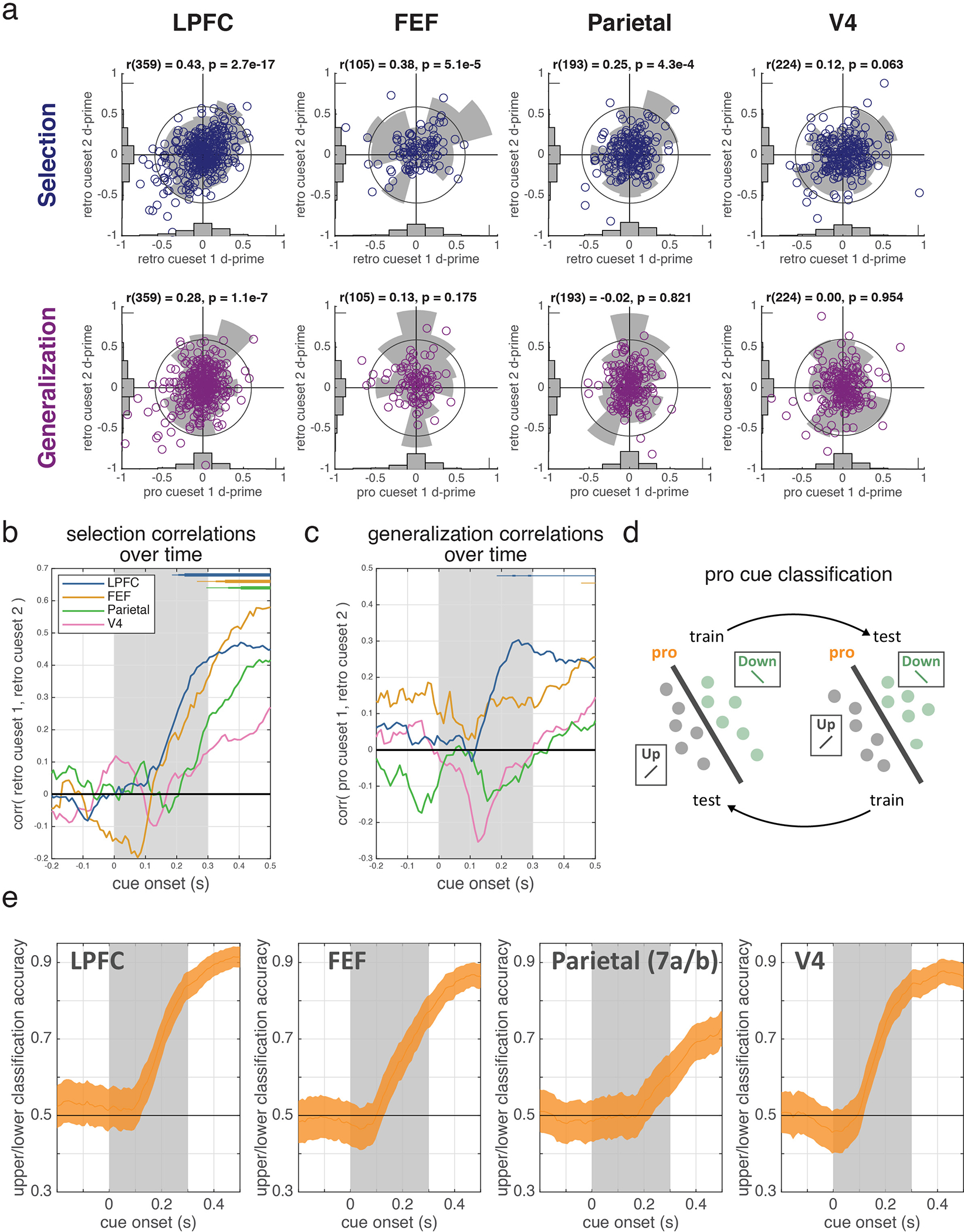
(a) Distribution of selectivity across neurons for the selected location (top row) and for the selected and attended location (bottom row). Selectivity was taken as the normalized difference in firing rate (d-prime) between ‘upper’ and ‘lower’ trials evoked by the two retro cue sets (top row) and by pro cue set 1 and retro cue set 2 (bottom row; see methods). Firing rate was computed at the end of the cue period (300 ms after cue onset). Positive d-primes indicated the neuron was more active when the upper sample was cued. Rose plots in the background show the histogram of neurons binned by angle (gray circle indicates scale; density=.1). Barplots along axes show histogram of marginal distributions (gray ticks on axes indicate scale; density=.2). Statistical tests are Pearson’s r. (b) Selection correlation values (as in panel a) computed over time around cue onset. Bars along top indicate correlations greater than zero: p<0.05, 0.01, and 0.001 for thin, medium, and thick lines, respectively (one-sided uncorrected bootstrap; N=1000 resamples of trials). (c) Generalization correlation values computed over time around cue onset, as in panel b. (d) Schematic of classifier trained to discriminate the neural response to two cue conditions on pro trials. Performance was calculated as the cross-validated classification accuracy (10-fold cross validation on each of 1000 random resamples of trials; see methods). (e) Lines show mean classification accuracy of the pro cues, relative to cue onset, for all four brain regions. Shaded regions reflect STE. Distribution was defined across 1000 random resamples of trials. Note that this analysis captures a mixture of information about the control of attention (up or down) and information about the visual appearance of the cue itself. Importantly, these results show these two conditions are separable in all brain regions, and so any failure in cross-classification performance (Fig. 2d, purple traces) is not due to poor separability of the attention conditions.

Extended Data Figure 5.

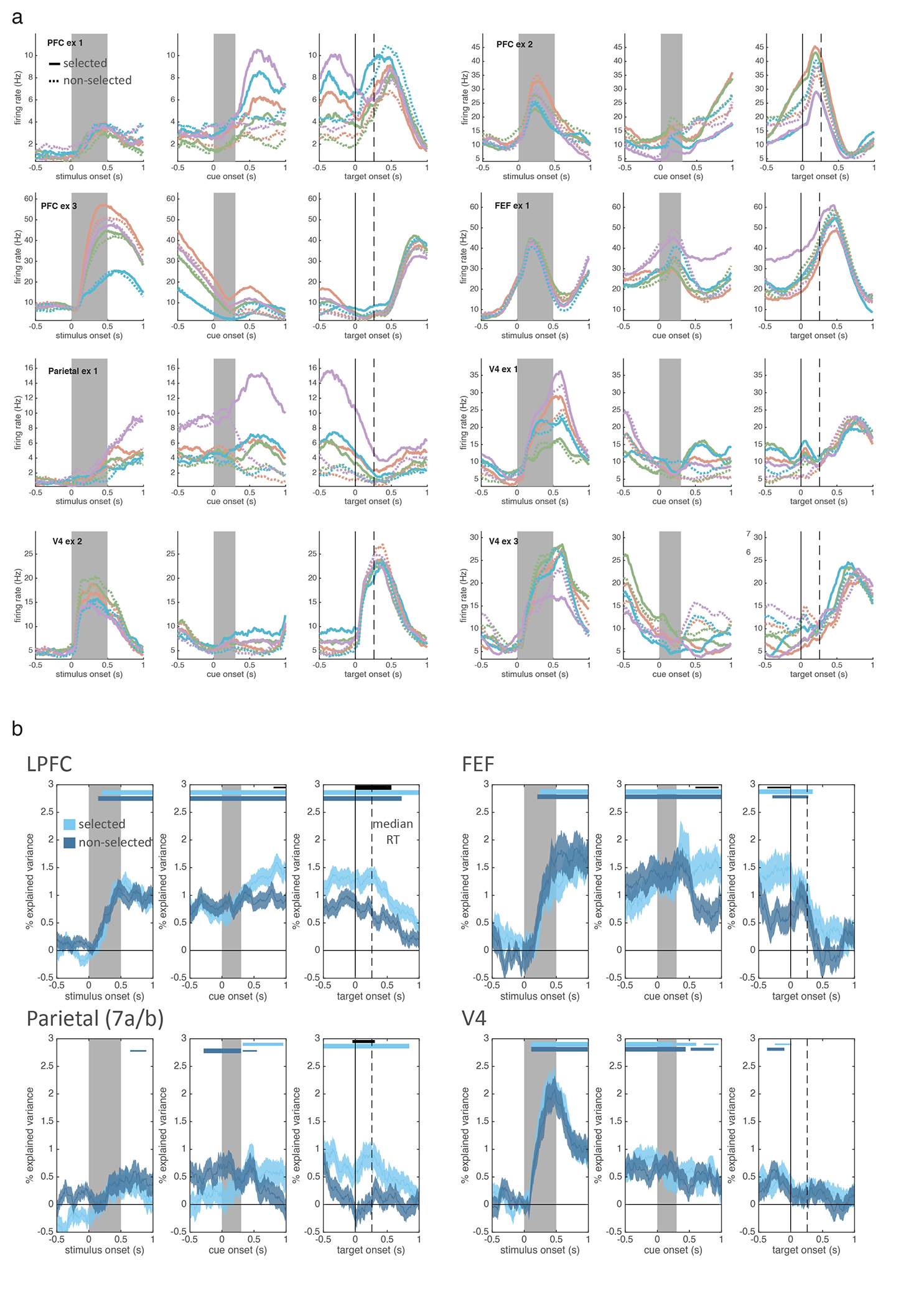
(a) Mean firing rate for example neurons during the retrospective condition, binned by the color (indicated by line color) of the selected (solid) or non-selected (dashed) stimulus. Example neurons are shown for all four brain regions (labeled in upper left). (b) Lines show mean selectivity of neurons in all four regions about the color of the selected and non-selected stimulus (in light and dark blue, respectively) in each brain region, averaged across neurons. Selectivity is measured using a percent explained variance statistics (see methods) and shows similar results as when using a entropy statistic (Figure 3). Shaded regions show STE across neurons (LPFC: 574 neurons, FEF: 163 neurons, Parietal: 292 neurons, V4: 311 neurons). Horizontal bars indicate significant information for the selected item (light blue), the non-selected item (dark blue), and a significant difference in information about the selected and non-selected items (black). Bar width indicates significance: p<0.05, 0.01, and 0.001 for thin, medium, and thick, respectively (two-sided cluster-corrected t-tests).

Extended Data Figure 6.

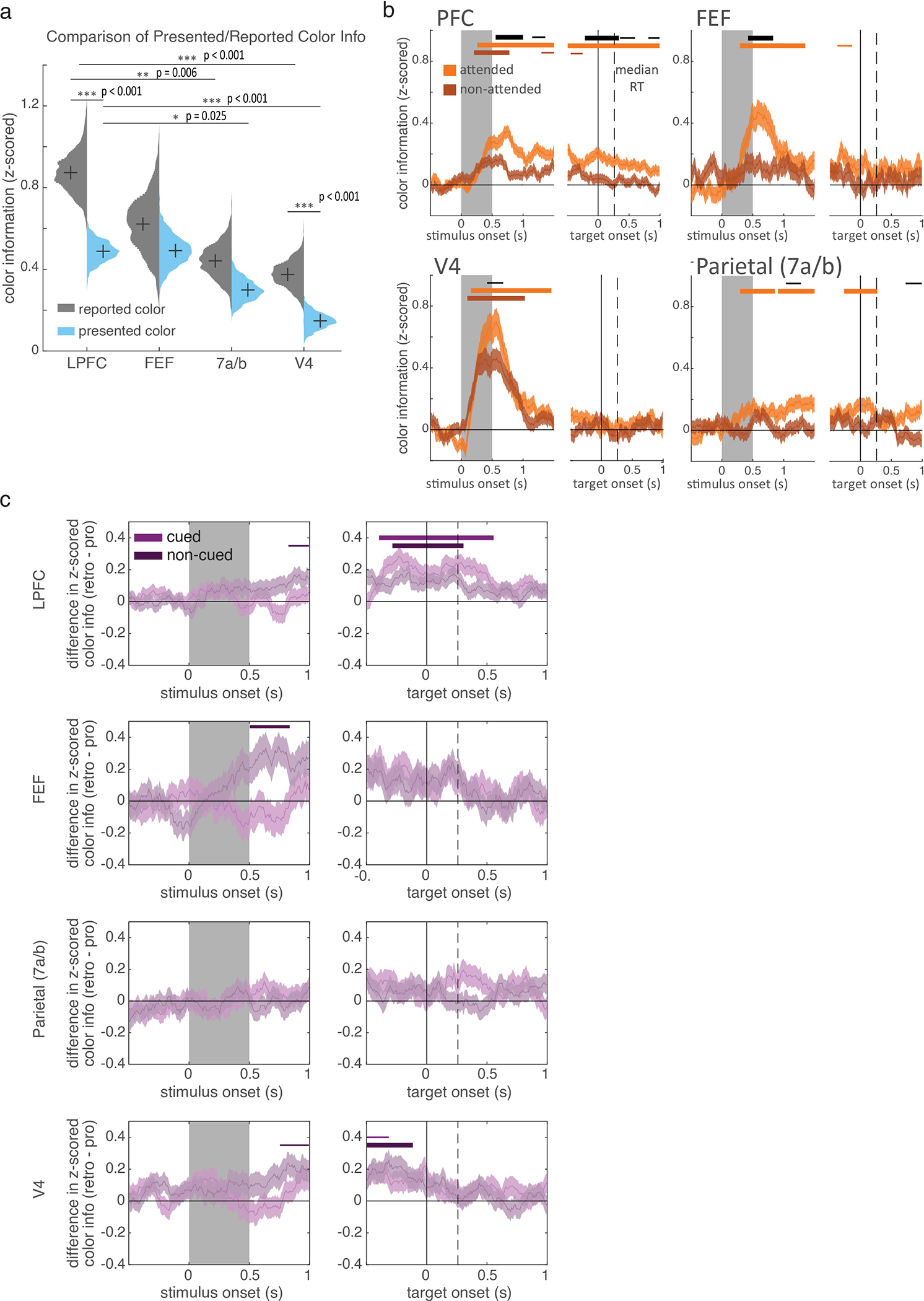
(a) Mean z-scored color information for the reported color (gray) and the color of the presented, selected, item (light blue). Information was calculated on firing rates in a 200 ms window prior to onset of the response color wheel for all neurons. Distributions show bootstrapped estimates of the mean across neurons (LPFC: 570 neurons, FEF: 163 neurons, parietal: 292 neurons, V4: 311 neurons). Horizontal lines indicate pairwise comparisons. * p<0.05, ** p<0.01, *** p<0.001 (two-sided uncorrected randomization tests). (b) Mean z-scored color information for the attended and non-attended color on pro trials. Error bars are STE across neurons (LPFC: 543 neurons, FEF: 160 neurons, parietal: 272 neurons, V4: 300 neurons). Horizontal bars indicate significant information for the attended item (light orange), the non-attended item (dark orange), and significant differences in information about the attended and non-attended items (black). Bar width indicate significance: p<0.05, 0.01, and 0.001 for thin, medium, and thick, respectively (two-sided cluster-corrected t-tests). (c) Difference in z-scored color information between retro and pro trials for the cued item (selected - attended; light purple) and uncued item (non-selected - non-attended; dark purple). Positive values reflect more information about an item on retro trials. Error bars are STE across neurons (LPFC: 511 neurons, FEF: 146 neurons, parietal: 258 neurons, V4: 285 neurons). Horizontal bars indicate significant differences from zero (i.e. differences between retro and pro) for the cued item (light purple) and the non-cued item (dark purple). Bar width indicate significance: p<0.05, 0.01, and 0.001 for thin, medium, and thick, respectively (two-sided cluster-corrected t-tests).

Extended Data Figure 7.

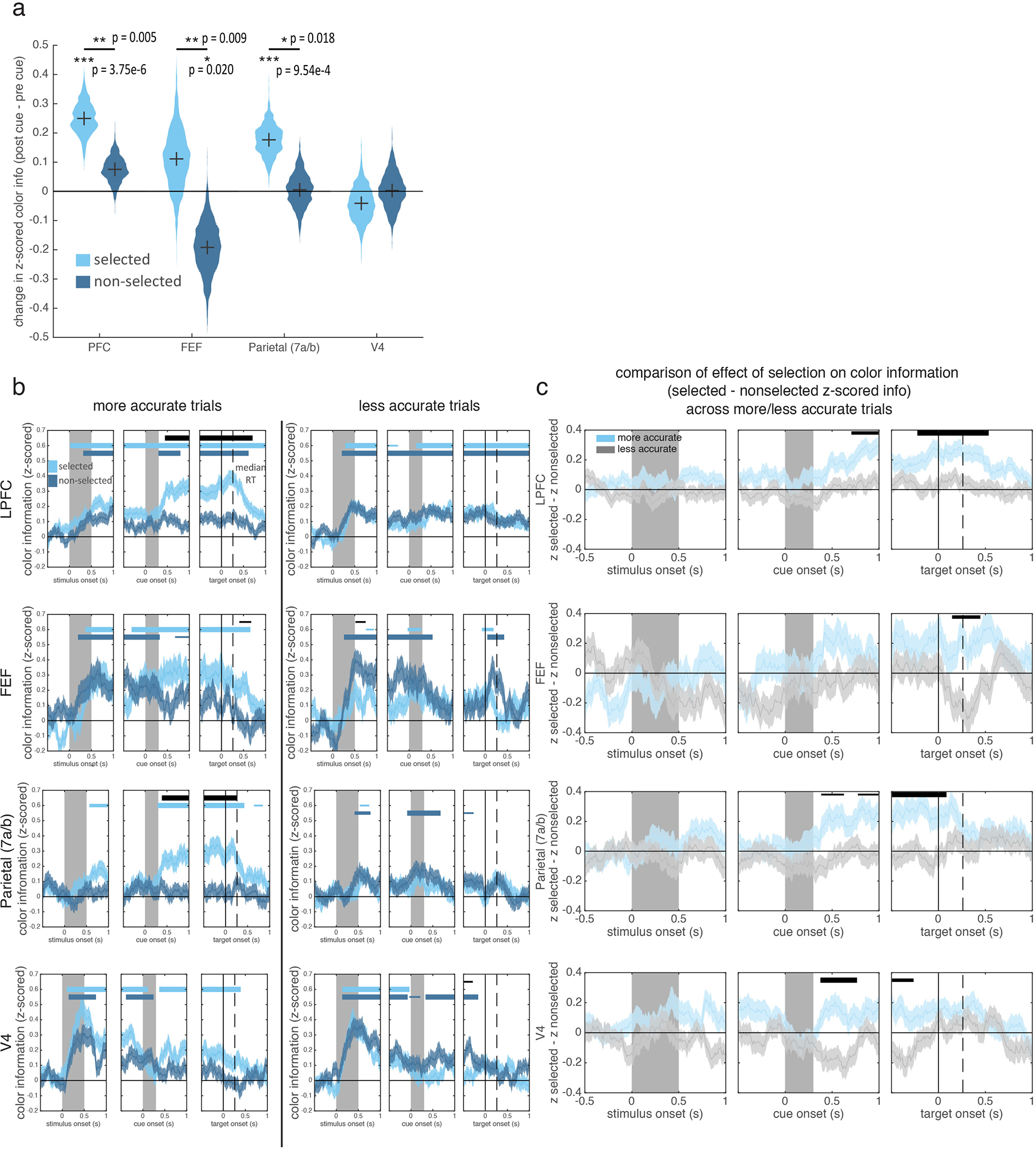
(a) Selection enhanced the representation of the selected item in frontal and parietal regions and reduced the representation of the un-selected item in FEF. Y-axis shows the increase in color information after selection (post-cue period: 200 to 500 ms after cue offset), relative to information before selection (pre-cue period: −300 to 0 ms before cue onset). Violin plots show the distribution of this difference, estimated by 1000 bootstrapped resamples of neurons (LPFC: 577 neurons, FEF: 170 neurons, parietal: 299 neurons, V4: 316 neurons). * p<0.05, ** p<0.01, *** p<0.001 (two-sided uncorrected paired t-tests). (b) Mean z-scored color information for the selected (light blue) and non-selected item (dark blue) on retro trials, for trials with more accurate behavioral responses (left column; error was less than median error) and less accurate behavioral responses (right column; error was greater than median error). Shaded region is STE across neurons (LPFC: 457/472 neurons, FEF: 134/135 neurons, Parietal: 235/241 neurons, V4: 248/267 neurons). Plots follow Figure 3. Horizontal bars indicate significant information for the selected item (light blue), the non-selected item (dark blue), and significant differences in information about the selected and non-selected items (black). Bar width indicate significance: p<0.05, 0.01, and 0.001 for thin, medium, and thick, respectively (two-sided cluster-corrected t-tests). (c) Mean difference in z-scored color information about the selected and non-selected item for more accurate and less accurate trials. Shaded region is STE across neurons (LPFC: 435 neurons, FEF: 125 neurons, Parietal: 221 neurons, V4: 240 neurons). As in panel b, trials were split based on angular error (relative to median error). Positive values reflect more information about the selected item than the non-selected item. Horizontal bars indicate significant differences between more and less accurate trials; width indicates significance: p<0.05, 0.01, and 0.001 for thin, medium, and thick, respectively (two-sided cluster-corrected t-tests).

Extended Data Figure 8.

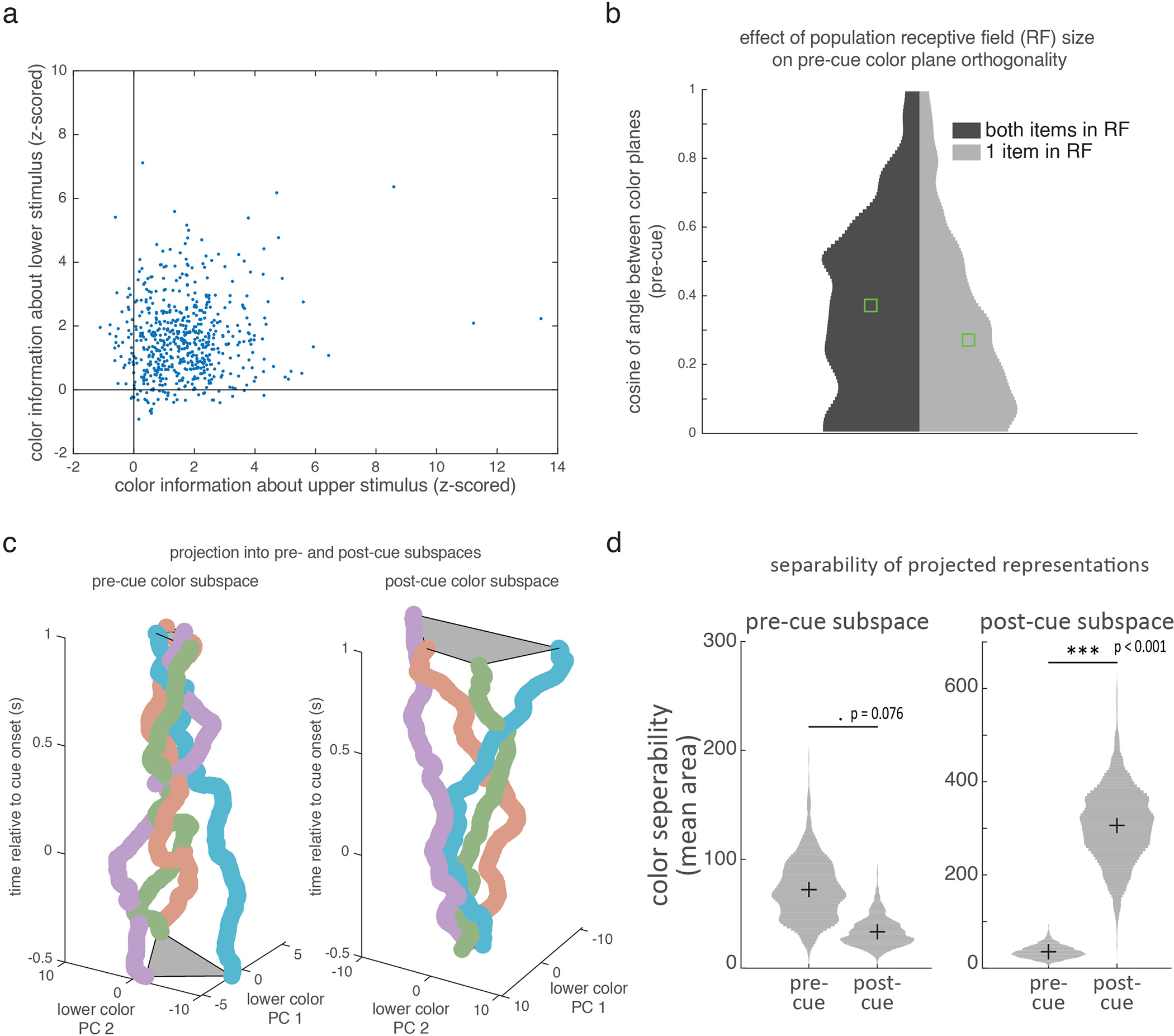
(a) Mean z-scored color information for the upper (x-axis) and lower (y-axis) stimuli immediately prior to selection cue onset (average over −500 to 0 ms before the selection cue) for LPFC (583 neurons). As shown in the scatterplot, most neurons carried some amount of information about both items (i.e., neurons did not lie along the axes). (b) To check if neurons primarily carrying information about just one item were driving the orthogonality between the color planes in LPFC before the selection cue, we re-computed the cosine of the angle between the color planes (see methods) using populations of neurons with significant color information about one item only (“1 item”) or both items (“both”; see methods for description of this test). Histograms show distribution of the cosine of the angle between the best-fitting planes for the upper and lower stimuli during the pre-cue period for these ‘both’ and ‘1 item populations of neurons (with each population subsampled to an equal number of neurons, see methods). Distributions were estimated from 1000 resamples of trials. Green squares indicate median values. While the “both” neurons did display slightly less orthogonality than the “1 item” neurons, this difference was not significant (p > 0.4, two-sided bootstrap of difference). Note that cosine angles are not zero for “1 item” neurons because 1) ‘1 item’ neurons still contain subthreshold information (p > 0.05) about the other item, as seen in panel A, and 2) subsampling cells in this way decreases statistical power, inflating low cosine values. (c) Population trajectories for ‘lower’ colors, over time, as projected into the ‘lower’ color subspace defined either before or after selection (left and right plots, respectively). Follows Fig. 4e. Lower color subspace was defined as a 2D space that maximally explained variance across the four ‘lower’ colors (see methods). As for the ‘upper’ color (shown in Fig. 4e), temporal cross generalization was poor, suggesting the color information was represented in a different subspace before and after the selection cue. (d) Before selection, color representations in LPFC are better separated using the pre-selection subspace. After selection, colors are better separated in the post-selection subspace. Separability was measured as the area of the quadrilateral defined by the responses to colors (shown in panel c and Fig. 4e), projected into either the pre-selection or post-selection subspaces (left and right columns in each plot; area averaged across upper and lower items). Violin plots show distributions estimated from 1000 resamples of trials. * p<0.05, ** p<0.01, *** p<0.001 (two-sided bootstrap of difference).

Extended Data Figure 9.

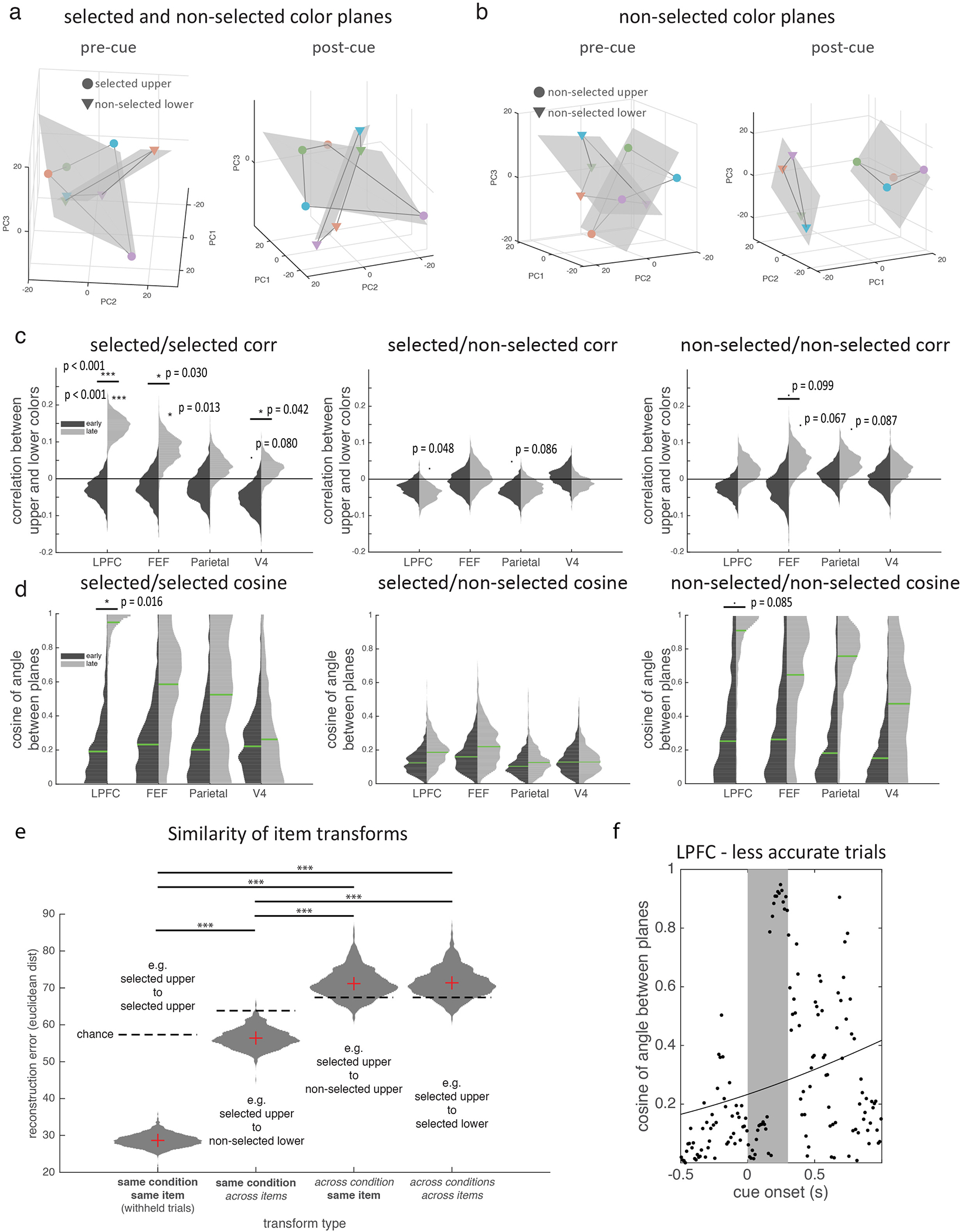
(a) Projected population responses for selected upper and non-selected lower colors, computed as in Figure 4a. Note, the selected and non-selected colors remain orthogonal after the selection cue (see main text for details). (b) Projected population responses for non-selected upper and non-selected lower colors. Like the selected color planes, the non-selected color planes appear parallel after the selection cue. (c) Mean correlation between the population representation of each color in the upper and lower position during retro trials, when both items were selected (left column), one item was selected and another item was non-selected (middle column), and when both items were non-selected (right column). Correlation was measured during an ‘early’ time period during the delay (dark grey; 150–350 ms after the offset of the stimulus) and a ‘late’ time period during the delay (light grey; 200–0 ms before the onset of the color wheel). Correlation was measured after subtracting the mean response at each location (see methods). Violin plots show bootstrapped distributions estimated from 1000 resamples of trials. Horizontal lines indicate pairwise comparisons (two-sided uncorrected bootstrap of difference). Lone asterisks reflect two-sided uncorrected bootstrap vs zero: * p<0.05, ** p<0.01, *** p<0.001. (d) Cosine of the angle between the best-fitting planes for the upper and lower stimuli. Planes were fit to selected and non-selected items during both the early and late time periods (as in panel c). Histograms show full distribution, estimated from 1000 resamples of trials; green lines indicate median values. Horizontal lines indicate pairwise comparisons: * p<0.05, ** p<0.01, *** p<0.001 (two-sided uncorrected bootstrap of difference). (e) To understand if the selection process transformed the cued and non-cued item in similar ways, we estimated the transformation matrices that mapped pre-cue representations of an item onto their post-cue representation (see methods and Supplementary Discussion 3). Then, we tested whether these transformations were able to reconstruct representations on withheld trials. Transformations were tested on the same condition (withheld trials; first column); on the other item in a condition (e.g., applying the transformation of a selected upper item to an non-selected lower item; second column); on the same item, but in a different condition (e.g., applying the transformation of a selected upper item to an non-selected upper item; third column); and on the other item and in a different condition (e.g., applying the transformation of a selected upper item to an selected lower item; fourth column). Violin plots show distributions of these mean reconstruction errors estimated from 1000 resamples of trials. Red crosses indicate the distribution mean, dashed lines show reconstruction error expected by chance (estimated by random shuffle, see methods). The results indicate a common component to the transformation of the selected and non-selected item in the same condition (second column) but there was also an item-specific transformation (reflected in the lower reconstruction error for the same item; first column). Horizontal lines show pairwise comparisons: · all *** p<0.001 by two-sided uncorrected bootstrap of difference. (f) The selected upper and selected lower color planes do not align on inaccurate trials. Figure follows Figure 4b, but shows data for trials in which absolute angular error was greater than the median error. Black markers show the cosine of the angle (y-axis) between the two color planes around the time of cue onset (x-axis) and black line shows best-fitting logistic function.

Extended Data Figure 10.

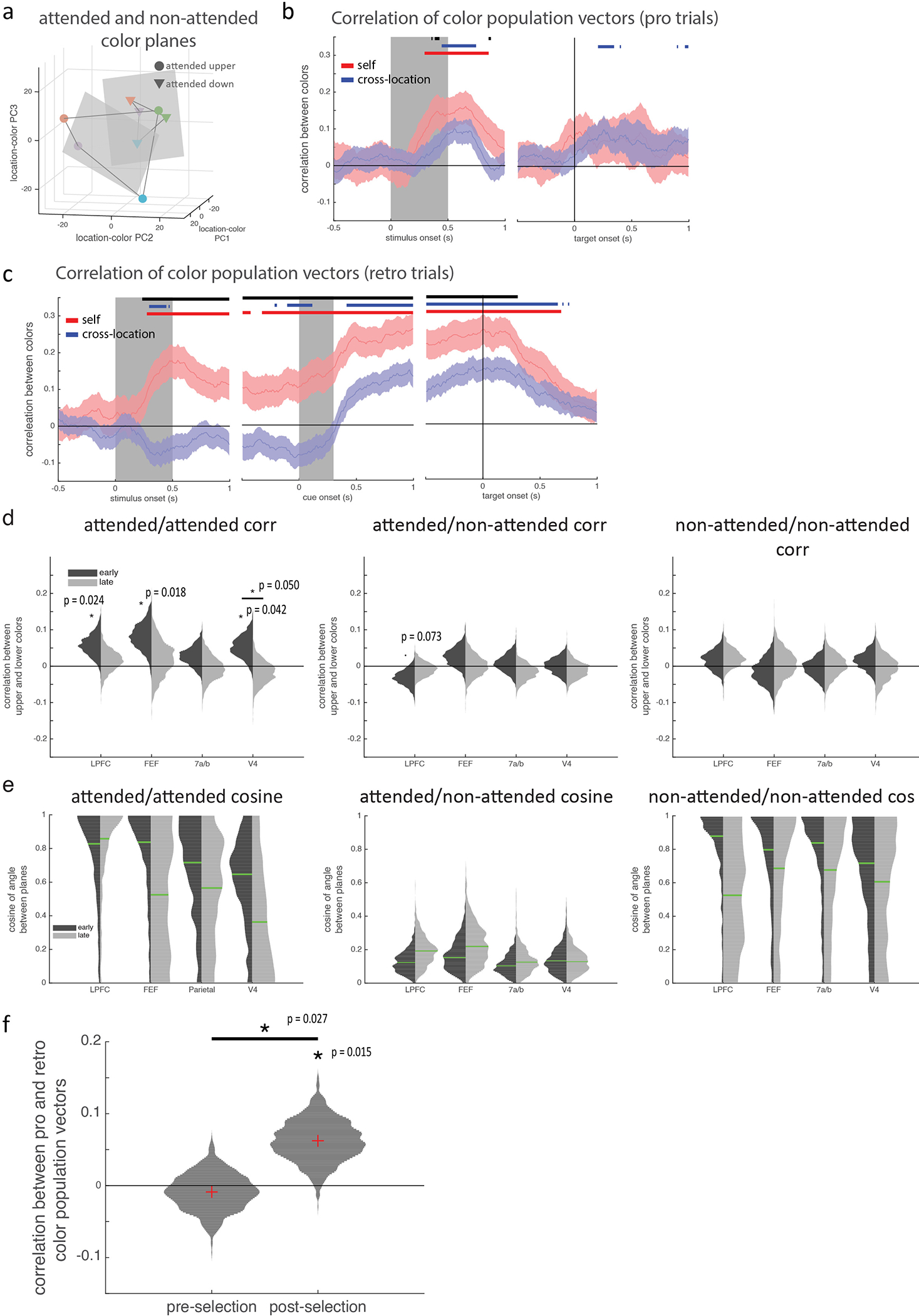
(a) Population responses 200 ms after stimulus offset on pro trials (projected into a reduced subspace for visualization). As in Figure 4a, markers indicate mean position of population activity for each condition (binned by the color and location of the attended item) in a subspace spanned by the first three principle components that explain the most variance across all 8 conditions. (b) Correlation of population vectors representing colors at the same location (self; red line) or between locations (cross-location; blue line) on pro trials. Lines show mean correlation; shaded regions are +/− STE. Correlations were measured after subtracting the mean vector at each location (as in Figure 4c; see methods). Distribution was estimated from 1000 resamples of trials. Self-correlation was computed on held-out trials and provides an upper-bound on the between-location correlation values, given the noise level. Bars reflect uncorrected two-sided bootstrap (p<0.05) for each correlation type against zero (red and blue) and between each other (black). (c) Same as in b, but for retro trials. (d) Mean correlation between the population representation of each color in the upper and lower position during pro trials, when both items were attended (left column), one item was attended and another item was non-attended (middle column), and when both items were non-attended (right column). Correlation was measured during an ‘early’ time period during the delay (dark grey; 150–350 ms after the offset of the stimulus) and a ‘late’ time period during the delay (light grey; 200–0 ms before the onset of the color wheel). Correlation was measured after subtracting the mean response at each location (see methods). Violin plots show distributions, estimated from 1000 resamples of trials. Horizontal lines indicate pairwise comparisons (two-sided uncorrected bootstrap of difference) and lone asterisks reflect two-sided uncorrected bootstrap against zero: * p<0.05, ** p<0.01, *** p<0.001. (e) Cosine of the angle between the best-fitting planes for the upper and lower stimuli. Planes were fit to attended and non-attended items during both the early and late time periods, as in d. Histograms show full distribution, estimated from 1000 resamples of trials; green lines indicate median values. (f) Mean correlation between the population representation for each color during pro trials and the representations during the early or late time periods of retro trials. Correlation was computed between the color representations taken from the 300 ms before the onset of the response wheel on pro trials and the color representations taken from either a pre-selection period (left distribution; −300 to 0 ms pre-cue) or post-selection period (right distribution; −300 to 0 ms before response wheel onset) on retro trials. Correlations were measured after subtracting the mean vector at each location, as in Fig. 4c (see methods). Violin plots reflect the distribution, estimated from 1000 resamples of trials. Horizontal line indicates pairwise comparison (two-sided uncorrected bootstrap of difference) and lone asterisks reflect two-sided bootstrap against zero: * p<0.05, ** p<0.01, *** p<0.001.

Data Availability

Data supporting all figures are included with the manuscript. Raw electrophysiological and behavioral data are available from the corresponding author upon reasonable request.