Joint modelling of longitudinal and survival data in the presence of competing risks with applications to prostate cancer data

Abstract

This research is motivated from the data from a large Selenium and Vitamin E Cancer Prevention Trial (SELECT). The prostate specific antigens (PSAs) were collected longitudinally, and the survival endpoint was the time to low-grade cancer or the time to high-grade cancer (competing risks). In this article, the goal is to model the longitudinal PSA data and the time-to-prostate cancer (PC) due to low- or high-grade. We consider the low-grade and high-grade as two competing causes of developing PC. A joint model for simultaneously analysing longitudinal and time-to-event data in the presence of multiple causes of failure (or competing risk) is proposed within the Bayesian framework. The proposed model allows for handling the missing causes of failure in the SELECT data and implementing an efficient Markov chain Monte Carlo sampling algorithm to sample from the posterior distribution via a novel reparameterization technique. Bayesian criteria, ΔDIC_Surv, and ΔWAIC_Surv, are introduced to quantify the gain in fit in the survival sub-model due to the inclusion of longitudinal data. A simulation study is conducted to examine the empirical performance of the posterior estimates as well as ΔDIC_Surv and ΔWAIC_Surv and a detailed analysis of the SELECT data is also carried out to further demonstrate the proposed methodology.

1. Introduction

In many clinical trials and medical studies, often both longitudinal (repeated measurements of a response) and time-to-event (time until the occurrence of an event of interest) outcomes are collected along with some other baseline covariates. Studies dealing with such outcomes mainly concern to investigate how the change in longitudinal outcome is associated with different covariates and also to determine the relationship among the longitudinal outcome, the survival outcome and other covariates. The traditional random effects model (Laird and Ware, 1982) and Cox proportional hazards model (Cox, 1972) may be considered for analysing the longitudinal and survival outcomes separately. However, a separate analysis of these two outcomes often leads to biased estimates of the model parameters (Hu et al., 2009). It is due to the fact that the longitudinal measurements are often incomplete (missing) and are subject to measurement error (Tsiatis et al., 1995), which may induce informative censoring mechanism for the survival outcome (Wulfsohn and Tsiatis, 1997). Thus, treating longitudinal outcome as a time-dependent covariate in the survival model fails to capture the endogenity of the longitudinal process and may lead us to a wrong interpretation of the model parameters (Prentice, 1982). In such cases, joint modelling of longitudinal and survival outcomes (Faucett and Thomas, 1996; Wulfsohn and Tsiatis, 1997; Henderson et al., 2000; Rizopoulos, 2012) has been widely used in clinical studies.

The standard joint model assumes that the event of interest takes place due to only one cause. However, the event of interest may occur due to one of the many plausible causes under consideration. This study is motivated from the Selenium and Vitamin E Cancer Prevention Trial (SELECT), where the main variable of interest is the time-to-diagnosis of prostate cancer (PC) due to low-grade or high-grade. We consider the two grades of PC as two distinct causes of PC. In the SELECT data, prostate specific antigens (PSAs) of the subjects are collected longitudinally, which is considered to be an important biomarker for the PC. In this study, our goal is to quantify the improvement in the fit of the time-to-PC due to low or high grade after the inclusion of longitudinal PSA in the survival sub-model. We also intend to quantify the cause-specific association between the time-to-PC and longitudinal progression of PSA.

Joint modelling of longitudinal and competing risks survival data has been proposed in the literature. In the joint modelling setting, Elashoff et al. (2007, 2008) extended the cause-specific hazards model and the mixture model by allowing latent variables to adjust for the association between the longitudinal and survival outcomes. However, the development in this area has not been in line under the Bayesian paradigm. A Bayesian extension of the cause-specific hazards models to analyse longitudinal and survival outcomes has been proposed by Huang et al. (2011) and Hu et al. (2009). However, the earlier works do not account for the missing causes of failure, which is common in clinical studies.

In the SELECT data, there are a substantial number of subjects who developed PC without knowing whether PC should be attributed to low-grade or high-grade. This missing cause of PC could happen when subjects reported cancer diagnostics outside the studies home institution. Considering the subjects with unknown causes as missing or ignoring those subjects from the analysis may lead to biased parameter estimates and thus the inference could be misleading (Lu and Tsiatis, 2001). Particularly, when the missing percentage is substantial (e.g., about 26% for SELECT data), the analysis could be erroneous. Within the competing risks setting, multiple imputation technique has been proposed by Lu and Tsiatis (2001), while Gao and Tsiatis (2005) developed an inverse probability weighted complete case estimator. Within the joint modelling framework, the literature to account for the missing causes under the competing risks setting is still sparse. In this study, we propose a shared parameter joint model within the Bayesian framework. Our proposed joint model imputes the missing causes of PC within the Markov chain Monte Carlo (MCMC) sampling algorithm.

In the SELECT data, the substantially large sample size of 32 261 might also impact the performance of the joint model resulting in weak convergence of the variance covariance matrix of the random effects (Zhang et al., 2019). This can also influence the convergence of other parameters that depend on the random effects in MCMC sampling. To deal with this issue, we use the Cholesky factorization of the variance covariance matrix of the random effects similar to Zhang et al. (2019) and propose a novel reparameterization of the regression coefficients associated with the random effects under the survival sub-model, which leads to a convenient but efficient implementation of the MCMC sampling algorithm under the joint model.

One of the main goals of this study is to quantify the improvement in the fit of the competing risks survival data due to the inclusion of the longitudinal PSA. Several measures, for example, Akaike information criterion (AIC), Bayesian information criterion (BIC), widely applicable or Watanabe–Akaike information criterion (WAIC; Watanabe, 2010), deviance information criterion (DIC; Spiegelhalter et al., 2002), etc., have been routinely used to quantify the overall fit of the model under consideration. Under the joint modelling setting, in order to quantify the overall goodness of fit, it is often desirable to assess the separate contribution of each component of the joint model towards the overall fit. Zhang et al. (2014) developed a decomposition of AIC and BIC under the joint model of longitudinal and survival outcomes. A useful SAS macro has been developed by Zhang et al. (2016) that allows to use various flexible models under the joint modelling framework and computes the decomposition of AIC and BIC. Within the Bayesian framework, a novel decomposition of DIC and logarithm of the pseudo-marginal likelihood (LPML; Ibrahim et al., 2001) has been proposed by Zhang et al. (2017). To investigate the performance of our proposed model, we define a BIC, ΔDIC_Surv that quantifies the gain in the performance of joint model due to the inclusion of the longitudinal data. In addition, we extend the idea of Huang et al. (2005) to adjust for the unobserved random effects while calculating DIC under the joint model within the Bayesian framework. We also define ΔWAIC_Surv, and the gain in fit of the SELECT data under the proposed model has been assessed by ΔDIC_Surv and ΔWAIC_Surv. The Bayesian criteria, ΔDIC_Surv and ΔWAIC_Surv, could be related to the association parameters, which are the regression coefficients associated with the random effects (‘covariates’) under the survival sub-model. To assess the change in ΔDIC_Surv and ΔWAIC_Surv due to the change in the association parameters, we carry out a simulation study under the two different scenarios of the association parameters.

The remainder of the article is organized as follows. The description of the SELECT data and some preliminary statistics are presented in Section 2. The development of the proposed methodologies is discussed in Section 3. The Bayesian inference and computation are presented in Section 4. The simulation study design and results are presented in Section 5. A detailed analysis of the SELECT data is carried out in Section 6. We conclude the article with a brief discussion in Section 7. The technical details of MCMC sampling are given in the Supplementary Materials (http://www.statmod.org/smij/archive.html).

2. SELECT data

The dataset for this study is extracted from the SELECT data which was sponsored by National Cancer Institute. Enrolment of the patients into this study started in 2001 and ended in 2004. A total of 35 261 male patients from United States, Puerto Rico and Canada participated in this study. In this study, race, Hispanic status, family history of cancer and smoking status were collected at baseline. Also, height, weight, body mass index (BMI) and PSA were collected longitudinally over the study period. The follow-up process for a patient was terminated when the patient developed PC due to low-grade or high-grade.

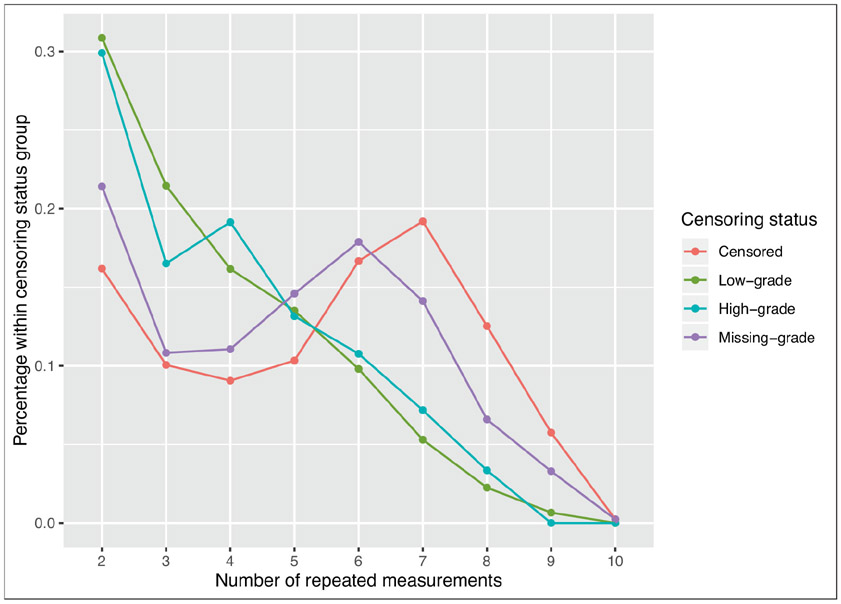
The main variable of interest is the time-to-PC due to low-grade or high-grade (survival outcome), where the low- and high-grades are considered as two different causes of PC. The main objective of this study is to investigate the association between the longitudinal PSA (longitudinal outcome) and the competing risks survival outcome adjusting for other covariates. We include the cases in the analysis, in which the number of follow-up visits is at least two, leading to a total of 22 792 patients. The follow-up visiting times and event times are recorded in years for each patient. For the longitudinal PSAs, the median follow-up times are 4.02 years and 1.95 years, respectively, for the censored and observed patients with an overall median follow-up time of 3.96 years. The observed minimum, median and maximum survival times are 0.003, 8.071 and 14.249 years, respectively. The median number of follow-up visits for the patients is 6 with the minimum and maximum of 2 and 10, respectively. Figure 1 shows the percentage distribution of the number of repeated measurements for different censoring status. We observe that for low-grade and high-grade, the percentage for the patients with less than five repeated measurements is higher compared to those for censored and missing-grade patients.

Figure 1:

Percentage distribution of PSA repeated measurements for different censoring status

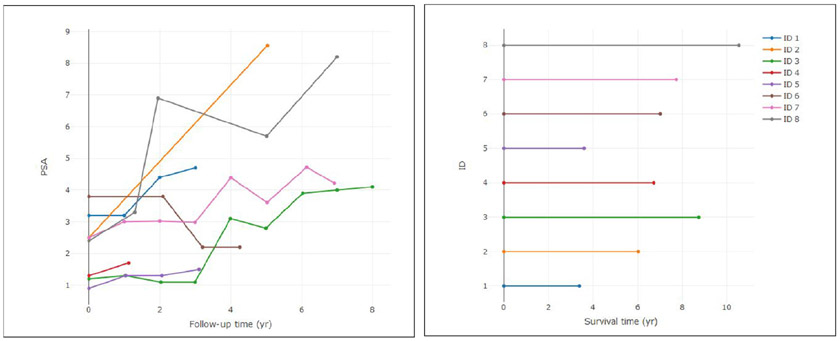
In Table 1, the distribution of PC status and the causes are presented. It is observed that about 7% patients developed cancer among whom for more than 26% patients, the cause of PC is missing. In Figure 2, the longitudinal trajectories and corresponding survival times for eight selected patients are presented. The figure shows that with the increasing PSA trajectory, the survival time tends to be lower compared to those for non-increasing PSA trajectory cases. This motivates us to develop the model to investigate the association between longitudinal PSA measures and the time to PC due to two different causes. Also, the missing cause cases should also be taken care of by imputation in MCMC sampling for carrying out an appropriate inference of the SELECT data.

Table 1:

Distribution of cancer status by cancer grade

PC	Frequency (%)
No	21 194 (92.99)
Yes	1 598 (7.01)
Low-grade	755 (47.25)
High-grade	418 (26.16)
Missing-grade	425 (26.6)

Figure 2:

PSA trajectories and survival times for eight random patients

3. Joint modelling of longitudinal and competing risks survival data

The joint model is comprised of a longitudinal sub-model and a survival sub-model. In the following subsections, the notation and the sub-models are defined under the general setting.

3.1. Longitudinal sub-model

Suppose there are n subjects in the study and for the ith subject, m_i longitudinal measurements are collected for i = 1,…,n. Let y_i(a_ij) denote the longitudinal measurement at time a_ij for j = 1,…,m_i and i = 1,…,n. We assume a mixed effects model (Verbeke and Molenberghs, 2009) for the longitudinal outcome y_i(a_ij) given by

$$y_i(a_{ij})=\mathbf{g}(a_{ij}{)}^{\prime }{\theta }_i+{\mathbf{x}}_i^{\prime }\gamma +{ϵ}_i(a_{ij}),$$ (3.1)

where g(a_ij) is a (q + 1)-dimensional vector of functions of time a_ij, θ_i is a (q + 1)-dimensional vector of the random effects, γ is a p-dimensional vector of regression coefficients corresponding to the p-dimensional covariates x_i and the measurement error ϵ_i(a_ij) is assumed to follow N(0, σ²). We assume that ${\theta }_i=(\theta +{\theta }_i^{\ast })$, where ${\theta }_i^{\ast }\sim N(0,\Omega )$, Ω is a (q + 1) × (q + 1) positive definite variance-covariance matrix, and θ is the vector of overall effects. We further assume that the subject-specific random effects θ_i and the measurement error terms ϵ_i(a_ij)’s are independent. We note that the trajectory function g(a_ij)′θ_i is a linear trajectory if q = 1, g(a_ij)′ = (1, a_ij) and a quadratic trajectory if q = 2, g(a_ij)′ = (1, a_ij, $a_{ij}^2$). The trajectory function captures the unobserved subject-specific progression of the longitudinal outcome, and it is a critical component in the longitudinal sub-model.

This study is motivated from the PC data-SELECT (discussed in Section 2), where PSA measurements are collected longitudinally. The earlier studies (Ferrer et al., 2016) suggest that the logarithm of PSAs can be explained by a linear mixed effects model with a latent linear trajectory function of observation time. In this study, we consider a linear trajectory for the longitudinal sub-model defined in (3.1). Within the Bayesian framework, the posterior estimation of Ω depends on the data only through the random effects ${\theta }_i^{\ast }$’s which results in slow convergence of MCMC sampling (Zhang et al., 2019). To overcome the convergence issue of the covariance matrix of random effects, we consider the Cholesky decomposition of Ω = ΓΓ′ and introduce a novel reparameterization

$${\theta }_i^{\ast }=\Gamma {\theta }_i^R,$$ (3.2)

where ${\theta }_i^R\sim N(0,I_2)$. We redefine the linear mixed effects model using this reparameterization as

$${\mathbf{y}}_i=\mathbf{g}(a_{ij}{)}^{\prime }(\theta +\Gamma {\theta }_i^R)+{\mathbf{x}}_i^{\prime }\gamma +{ϵ}_i,$$ (3.3)

where $\Gamma =\left[\begin{array}{cc}\hfill b_{11}\hfill & \hfill 0\hfill \\ \hfill b_{21}\hfill & \hfill b_{22}\hfill \end{array}\right]$ with b₁₁ > 0 and b₂₂ > 0. This reparameterization will facilitate fast convergence and better mixing of Gibbs sampling from the resulting posterior distribution for the covariance matrix of random effects. More details regarding the posterior computation and estimation are discussed in Section 4.

3.2. Survival sub-model

Let t_i be the event time or censoring time and also let δ_i denote the censoring indicator for the ith subject. The censoring indicator δ_i takes a value of 0 for a censored event and δ_i = k indicates that an event occurred for the ith subject due to the kth cause for k = 1, 2. In this article, we consider the cause-specific hazards model in which, the random effects are included as covariates along with other fixed covariates. The proposed model is defined on the setting when there are two causes of failure and the dimension of the random effects is two. The cause-specific hazards model for the kth observed cause of failure is defined as

$$h_k(t\mid {\mathbf{z}}_i)=h_{k0}(t)\text{exp}({\alpha }_k^{\prime }{\theta }_i^{\ast }+{\mathbf{z}}_i^{\prime }{\beta }_k),k=1,2,$$ (3.4)

where β_k is the vector of the coefficients corresponding to the fixed effects z_i, α_k is the vector of regression coefficients for the random effects ${\theta }_i^{\ast }$ and h_k0(t) is the baseline hazard function for the kth cause of the event at time t. In the survival sub-model, the random effects are linked to the longitudinal sub-model through the association parameter α_k. To account for the missing causes of failure for the uncensored subjects, we propose the following additive hazards model

$$h_{12}(t\mid {\mathbf{z}}_i)=\sum _{k=1}^2{h}_{k0}(t)\text{exp}({\alpha }_k^{\prime }{\theta }_i^{\ast }+{\mathbf{z}}_i^{\prime }{\beta }_k).$$ (3.5)

With the reparameterization of ${\theta }_i^{\ast }=\Gamma {\theta }_i^R$, the random component of the survival sub-model can be expressed as

$${\alpha }_k^{\prime }{\theta }_i^{\ast }=({\alpha }_{k1}{b}_{11}+{\alpha }_{k2}{b}_{21}){\theta }_{i1}^R+({\alpha }_{k2}{b}_{22}){\theta }_{i2}^R={\alpha }_k^{{\ast }^{\prime }}{\theta }_i^R,k=1,2,$$

where

$${\alpha }_{k1}^{\ast }={\alpha }_{k1}{b}_{11}+{\alpha }_{k2}{b}_{21},{\alpha }_{k2}^{\ast }={\alpha }_{k2}{b}_{22}.$$ (3.6)

With this reparameterization, the hazard model (3.4) for the kth cause of event is redefined as

$$h_k(t\mid {\mathbf{z}}_i)=h_{k0}(t)\text{exp}({\alpha }_k^{{\ast }^{\prime }}{\theta }_i^R+{\mathbf{z}}_i^{\prime }{\beta }_k),k=1,2,$$ (3.7)

and the hazard function (3.5) for the unknown cause of failure is redefined as

$$h_{12}(t\mid {\mathbf{z}}_i)=\sum _{k=1}^2{h}_{k0}(t)\text{exp}({\alpha }_k^{{\ast }^{\prime }}{\theta }_i^R+{\mathbf{z}}_i^{\prime }{\beta }_k).$$ (3.8)

We further assume that the baseline hazard function due to the kth cause has a piecewise constant form with G_k partitions of the time axis, 0 = s_k0 < s_k1 < ⋯ < s_kGk = ∞,

$$h_{k0}(t)={\lambda }_{kg},t\in (s_{k,g-1},s_{k,g}],g=1,2,\dots ,G_k,k=1,2.$$ (3.9)

Let [λ_k = (λ_k1, …, λ_kGk), k = 1, 2} denote the vectors of piecewise constants of the baseline hazard functions defined in (3.9). The likelihood function under the proposed joint model is constructed in the following subsection.

3.3. Likelihood construction

Let φ = (φ₁, φ₂), where φ₁ = (θ^R, θ, γ, σ², Γ), φ₂ = (λ₁, λ₂, ${\alpha }_1^{\ast }$, ${\alpha }_2^{\ast }$, β₁, β₂) and ${\theta }^R=({\theta }_1^{R^{\prime }},\dots ,{\theta }_n^{R^{\prime }}{)}^{\prime }$. Let D_obs = (D_Long,obs, D_Surv,obs) denote the observed data, where D_Long,obs = {(y_i, x_i), i = 1,…,n} and D_Surv,obs = {(t_i, δ_i, z_i), i = 1,…,n}. For the ith subject, the censoring indicator δ_i ∈ {0, 1, 2}, where 0 indicates censoring, 1 and 2 indicate two distinct causes of failure. For instance, in the SELECT data, δ_i takes a value of 0 for no PC, 1 for low-grade cancer, and 2 for high-grade cancer. Let u_i take a value of 1 when the ith subject is uncensored due to an unknown cause and takes a value of 0 when the cause of failure for the ith subject is known. In this article, we consider the unobserved random effects as the latent or unknown parameters, conditional on the random effects, the longitudinal data are independent of the survival data. The joint distribution of (y_i, t_i, ${\theta }_i^R$) is written as

$$f({\mathbf{y}}_i,t_i,{\theta }_i^R\mid \phi ,{\delta }_i,{\mathbf{x}}_i,{\mathbf{z}}_i)=f({\mathbf{y}}_i\mid {\theta }_i^R,{\phi }_1,{\mathbf{x}}_i)f(t_i\mid {\delta }_i,{\theta }_i^R,{\phi }_2,{\mathbf{z}}_i)f({\theta }_i^R),$$ (3.10)

where

$$\begin{gathered} f({\mathbf{y}}_i\mid {\theta }_i^R,{\phi }_1,{\mathbf{x}}_i)=\frac{1}{(2\pi {\sigma }^2{)}^{m_i∕2}} \\ \times \text{exp}\left(-\frac{1}{2{\sigma }^2}{\left({\mathbf{y}}_i-\mathbf{g}(a_{ij}{)}^{\prime }(\theta +\Gamma {\theta }_i^R)+{\mathbf{x}}_i^{\prime }\gamma \right)}^{\prime }\left({\mathbf{y}}_i-\mathbf{g}(a_{ij}{)}^{\prime }(\theta +\Gamma {\theta }_i^R)+{\mathbf{x}}_i^{\prime }\gamma \right)\right), \\ f(t_i\mid {\delta }_i,{\theta }_i^R,{\phi }_2,{\mathbf{z}}_i)=\left[\prod _{k=1}^2\{h_{k0}(t_i)\text{exp}({\alpha }_k^{{\ast }^{\prime }}{\theta }_i^R+{\mathbf{z}}_i^{\prime }{\beta }_k){\}}^{I({\delta }_i=k,u_i=0)}\right] \\ \times \text{exp}\left(-\sum _{k=1}^2{H}_{k0}(t_i)\text{exp}({\alpha }_k^{{\ast }^{\prime }}{\theta }_i^R+{\mathbf{z}}_i^{\prime }{\beta }_k)\right) \\ \times {\left[\sum _{k=1}^2{h}_{k0}(t_i)\text{exp}({\alpha }_k^{{\ast }^{\prime }}{\theta }_i^R+{\mathbf{z}}_i^{\prime }{\beta }_k)\right]}^{I({\delta }_i>0,u_i=1)}, \\ f({\theta }_i^R)=\frac{1}{2\pi }\text{exp}(-\frac{1}{2}{\theta }_i^{R^{\prime }}{\theta }_i^R). \end{gathered}$$

In the following Section 4, we present the Bayesian estimation of the parameters under the joint model.

4. Bayesian inference

The Bayesian estimation of the proposed model involves sampling from the full conditional distributions, adaptive rejection sampling (Gilks and Wild, 1992) and Metropolis–Hastings sampling(Metropolis et al., 1953; Hastings, 1970). In the SELECT data, there are a substantial percentage of missing causes of failure. In MCMC sampling from the posterior distribution, we add one additional step to impute the missing causes of failure. Let {${\delta }_i^m$, $i\in {\mathcal{I}}_m$} be the set of censoring indicators with the missing grade, where ${\mathcal{I}}_m$ be the set of patients with missing grade. The occurrence of PC is decided due to low-grade with probability

$$\frac{1}{1+\text{exp}(-\{\log \frac{h_{10}(t_i)}{h_{20}(t_i)}+{\theta }_i^{R^{\prime }}({\alpha }_1^{\ast }-{\alpha }_2^{\ast })+{\mathbf{z}}_i^{\prime }{\beta }_1-{\mathbf{z}}_i^{\prime }{\beta }_2\})},i\in {\mathcal{I}}_m.$$ (4.1)

The probability for high-grade cancer can be calculated similarly. Let {${\delta }_i^o$, $i\in {\mathcal{I}}_o$} be the set of observed censoring status, where ${\mathcal{I}}_o$ denotes the set of subjects with observed causes or censored. We let ${\delta }_i^{\ast }={\delta }_i^m$ if $i\in {\mathcal{I}}_m$ and ${\delta }_i^{\ast }={\delta }_i^o$ if $i\in {\mathcal{I}}_o$, constituting the complete set of censoring status {${\delta }_i^{\ast }$, i = 1,…,n}. With the imputed censoring status, we sample the model parameters from the posterior distribution derived from the augmented likelihood. Particularly, the distribution of the survival time in the augmented likelihood is given by

$$\begin{gathered} f(t_i\mid {\delta }_i^{\ast },{\theta }_i^R,{\phi }_2,{\mathbf{z}}_i)=\left[\prod _{k=1}^2\{h_{k0}(t_i)\text{exp}({\alpha }_k^{{\ast }^{\prime }}{\theta }_i^R+{\mathbf{z}}_i^{\prime }{\beta }_k){\}}^{I({\delta }_i^{\ast }=k)}\right] \\ \times \text{exp}\left(-\sum _{k=1}^2{H}_{k0}(t_i)\text{exp}({\alpha }_k^{{\ast }^{\prime }}{\theta }_i^R+{\mathbf{z}}_i^{\prime }{\beta }_k)\right). \end{gathered}$$ (4.2)

The other components of the augmented likelihood remain the same as defined in (3.10). In the augmented data likelihood, the longitudinal and survival data are independent to each other conditional on the random effects. Thus, the posterior distributions of the longitudinal and survival sub-model parameters depend on the random effects, which are unobserved. We sample the random effects θ^R from the posterior distribution and conditional on the sampled random effects, the survival and longitudinal sub-model parameters are updated in MCMC sampling. Full details regarding the prior and MCMC sampling are presented in the Supplementary Materials (http://www.statmod.org/smij/archive.html). We compute and report the posterior means, the posterior standard deviations and the 95% highest posterior density (HPD) intervals of the model parameters. The convergence of MCMC sampling is investigated via the trace plots of MCMC samples.

4.1. Model assessment: DIC_Surv, ΔDIC_Surv, WAIC_Surv and ΔWAIC_Surv

DIC_Surv:

The (DIC; Spiegelhalter et al., 2002) has been widely used as a Bayesian model assessment measure. In this article, we are mainly interested in the model assessment for the competing risks data and to investigate how much the performance of the model is improved by the inclusion of longitudinal data into the survival model. The DIC for the survival sub-model is defined as

$${\text{DIC}}_{\text{Surv}}={\text{Dev}}_{\text{Surv}}\left(E({\phi }_2\mid D_{\text{Surv,obs}}),E({\theta }^R\mid D_{\text{Surv,obs}})\right)+2P_{D[\text{Surv}]},$$

where P_D[Surv] = E(Dev_Surv(φ₂, θ^R∣D_Surv,obs)) – Dev_Surv (E(φ₂∣D_Surv,obs), E(θ^R∣D_Surv,obs)) is the effective number of model parameters and the deviance function is defined as

$${\text{Dev}}_{\text{Surv}}({\phi }_2,{\theta }^R\mid D_{\text{Surv,obs}})=-2\log L({\phi }_2,{\theta }^R\mid D_{\text{Surv,obs}}).$$

In this article, the random effects θ^R are considered as unknown parameters and the DIC could be influenced by the inappropriate posterior estimate of these unknown parameters. Following Huang et al. (2005), we extend the standard DIC by considering a linear combination of the parameters which is defined as

$${\text{DIC}}_{\text{Surv}}={\text{Dev}}_{\text{Surv}}\left(E(\mathbf{g}({\phi }_2,{\theta }^R)\mid D_{\text{Surv,obs}})\right)+2P_{D[\text{Surv}]},$$ (4.3)

where g(φ₂, θ^R) = (λ₁, λ₂, ${\alpha }_1^{{\ast }^{\prime }}{\theta }^R$, ${\alpha }_2^{{\ast }^{\prime }}{\theta }^R$, β₁, β₂), the effective number of parameters,

$$P_{D[\text{Surv}]}=E\left({\text{Dev}}_{\text{Surv}}\left(\mathbf{g}({\phi }_2,{\theta }^R)\mid D_{\text{Surv,obs}}\right)\right)-{\text{Dev}}_{\text{Surv}}\left(E(\mathbf{g}({\phi }_2,{\theta }^R)\mid D_{\text{Surv,obs}})\right),$$

and the deviance function

$${\text{Dev}}_{\text{Surv}}\left(\mathbf{g}({\phi }_2,{\theta }^R)\mid D_{\text{Surv,obs}}\right)=-2\log L(\mathbf{g}({\phi }_2,{\theta }^R)\mid D_{\text{Surv,obs}}).$$

ΔDIC_Surv:

Another important aspect of the model assessment is to measure the gain in fit due to the inclusion of longitudinal data into the survival model. For this, we fit the survival data alone, that is, considering ${\alpha }_1^{\ast }={\alpha }_2^{\ast }=0$ and the cause-specific hazard function takes the form

$$h_k(t\mid h_{k0},{\alpha }_k^{\ast }=0,{\beta }_k,{\mathbf{z}}_i)=h_{k0}(t)\text{exp}({\mathbf{z}}_i^{\prime }{\beta }_k).$$

The DIC for the survival sub-model with the above consideration

$${\text{DIC}}_{\text{Surv,0}}={\text{Dev}}_{\text{Surv,0}}\left(E({\phi }_2^{\ast }\mid D_{\text{Surv,obs}})\right)+2P_{D[\text{Surv,0}]},$$ (4.4)

where ${\phi }_2^{\ast }=({\lambda }_1,{\lambda }_2,{\beta }_1,{\beta }_2)$, ${\text{Dev}}_{\text{Surv,0}}({\phi }_2^{\ast }\mid D_{\text{Surv,obs}})=-2\log L({\phi }_2^{\ast }\mid D_{\text{Surv,obs}})$ and

$$P_{D[\text{Surv,0}]}=E\left({\text{Dev}}_{\text{Surv},0}({\phi }_2^{\ast }\mid D_{\text{Surv,obs}})\right)-{\text{Dev}}_{\text{Surv,0}}\left(E({\phi }_2^{\ast }\mid D_{\text{Surv,obs}})\right).$$

The following assessment criterion is defined

$$\Delta {\text{DIC}}_{\text{Surv}}={\text{DIC}}_{\text{Surv,0}}-{\text{DIC}}_{\text{Surv}},$$ (4.5)

which quantifies the gain in the fit in the competing risks survival sub-model due to the inclusion of longitudinal data penalizing the additional parameters in the competing survival sub-model.

WAIC_Surv:

The WAIC (Watanabe, 2010) is another known Bayesian criterion for model assessment. The WAIC computes the logarithm of the pointwise posterior predictive density (LPPD) and adds the penalty term to adjust for overfitting (Gelman et al., 2014). LPPD for the survival sub-model is defined as

$${\text{LPPD}}_{\text{Surv}}=\log E\left[L(\mathbf{g}({\phi }_2,{\theta }^R)\mid D_{\text{Surv,obs}})\right].$$

The effective number of parameters is evaluated as

$$P_{\text{WAIC[Surv]}}=2\left(\log E\left[L(\mathbf{g}({\phi }_2,{\theta }^R)\mid D_{\text{Surv,obs}})\right]-E\left[\log L(\mathbf{g}({\phi }_2,{\theta }^R)\mid D_{\text{Surv,obs}})\right]\right).$$

Finally, the WAIC_Surv is defined as

$${\text{WAIC}}_{\text{Surv}}=-2({\text{LPPD}}_{\text{Surv}}-P_{\text{WAIC[Surv]}}).$$ (4.6)

ΔWAIC_Surv:

Similar to the formulation of ΔDIC_Surv, we first define WAIC_Surv,0, which is defined on the parameter vector ${\phi }_2^{\ast }=({\lambda }_1,{\lambda }_2,{\beta }_1,{\beta }_2)$ and setting ${\alpha }_1^{\ast }={\alpha }_2^{\ast }=0$. The WAIC_Surv,0 is given by

$${\text{WAIC}}_{\text{Surv},0}=-2({\text{LPPD}}_{\text{Surv},0}-P_{\text{WAIC[Surv},0]}),$$ (4.7)

where ${\text{LPPD}}_{\text{Surv},0}=\log E\left[L({\phi }_2^{\ast }\mid D_{\text{Surv,obs}})\right]$ and the effective number of parameter, $P_{\text{WAIC[Surv},0]}=2\left(\log E\left[L({\phi }_2^{\ast }\mid D_{\text{Surv,obs}})\right]-E\left[\log L({\phi }_2^{\ast }\mid D_{\text{Surv,obs}})\right]\right)$. Finally, the ΔWAIC_Surv is given by

$$\Delta {\text{WAIC}}_{\text{Surv}}={\text{WAIC}}_{\text{Surv},0}-{\text{WAIC}}_{\text{Surv}}.$$ (4.8)

The interpretation of the ΔWAIC_Surv is similar to ΔDIC_Surv, which again quantifies the gain in fit due to the inclusion of longitudinal outcome in the survival sub-model.

5. A simulation study

5.1. Simulation design

We carry out a simulation study to examine the empirical performance of ΔDIC_Surv and ΔWAIC_Surv under different values of the association parameters α₁ and α₂. We define the sub-models and specify the design values of the parameters using the same notations introduced in Sections 3 and 4. The longitudinal measurements are generated from the following sub-model

$$y_i(a_{ij})=\mathbf{g}(a_{ij}{)}^{\prime }(\theta +\Gamma {\theta }_i^R)+{\mathbf{x}}_i^{\prime }\gamma +{ϵ}_i(a_{ij}),$$ (5.1)

where g(a_ij)′ = (1, a_ij), x_i = (x_1i, x_2i) with x_1i ~ N(0, 1) and x_2i∣x_1i ~ N(0.2x_1i, 1), ϵ_i(a_ij) ~ N(0, σ²), and ${\theta }_i^R=({\theta }_{0i}^R,{\theta }_{1i}^R)\sim N(0,{\mathbf{I}}_2)$. The design values of the parameters are given as θ = (θ₀, θ₁)′ = (0.5, 1)′, $\Gamma =\left(\begin{array}{cc}\hfill b_{11}\hfill & \hfill b_{12}\hfill \\ \hfill b_{21}\hfill & \hfill b_{22}\hfill \end{array}\right)=\left(\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0.5\hfill & \hfill 0.8\hfill \end{array}\right)$, γ = (γ₁, γ₂)′ = (0.15, 0.3)′ and σ² = 0.5.

For the survival sub-model, the same set of covariates is used as for the longitudinal sub-model and set z_i = x_i. The exponential distribution for the baseline hazard functions is considered due to two different causes

$$h_{k0}(t)={\lambda }_{k0},k=1,2,t\in {\mathbf{R}}^{+}.$$

Thus the survival sub-model for the kth cause of failure becomes

$$h_k(t\mid {\lambda }_{k0},{\alpha }_k^{\ast },{\theta }_i^R,{\beta }_k,{\mathbf{z}}_i)={\lambda }_{k0}\text{exp}({\alpha }_k^{{\ast }^{\prime }}{\theta }_i^R+{\mathbf{z}}_i^{\prime }{\beta }_k),k=1,2.$$ (5.2)

We generate the true event time due to the kth cause of failure as follows

$$t_{ik}={\left[-{\lambda }_{k0}\text{exp}({\alpha }_k^{{\ast }^{\prime }}{\theta }_i^R+{\mathbf{z}}_i^{\prime }{\beta }_k)\right]}^{-1}\log (1-U),k=1,2,$$

where $U\sim \mathcal{U}(0,1)$. The censoring times c_i are generated from an exponential distribution with mean 25. Then the observed event time for the ith subject is computed as t_i = min(t_i1, t_i2, c_i). The censoring status for the ith subject is evaluated as δ_i = k if I(t_ik ≤ c_i) for k = 1, 2 and 0 otherwise. To simulate the unknown causes of failure, for each uncensored case, we first generate $v\sim \mathcal{U}(0,1)$, and the cause of failure is then set to be missing if v < 0.1.

The design values of the survival sub-model parameters are given as β₁ = (0.5, 0.6)′, β₂ = (0.2, −0.5)′, λ₁₀ = 0.1 and λ₂₀ = 0.08. For the longitudinal data, we consider a balanced study design with m_i = 20 for i = 1,…,n. The observation times of the longitudinal measurements for the ith subject are evaluated at a_ij = 21 (j – 1)/365, j = 1,…, m_i. We generate the datasets for the following two scenarios with all other parameter values specified as above:

1. True-SPM: In this scenario, we generate the data from the proposed share parameter joint model. In particular, we generate the longitudinal data from the model (5.1) and the survival data from the model (5.2) with ${\alpha }_{11}^{\ast }=0.2$, ${\alpha }_{12}^{\ast }=0.8$, ${\alpha }_{21}^{\ast }=0.5$ and ${\alpha }_{22}^{\ast }=1$.

2. True-Surv: In this scenario, the data are generated from the survival data only model by specifying ${\alpha }_{k1}^{\ast }={\alpha }_{k2}^{\ast }=0$ for k = 1, 2. Thus, the survival sub-model defined in (5.2) becomes

$$h_k(t\mid {\lambda }_{k0},{\beta }_k,{\mathbf{z}}_i)={\lambda }_{k0}\text{exp}({\mathbf{z}}_i^{\prime }{\beta }_k),k=1,2.$$ (5.3)

5.2. Simulation results

We generate two hundred simulated datasets independently with a sample size (n) of 6 000 under each of the scenarios discussed above. The censoring percentages of True-SPM and True-Surv scenarios are about 20% and 17%, respectively. For each of the two scenarios, we fit the data using the proposed joint model and the survival data only model to evaluate ΔDIC_Surv and ΔWAIC_Surv. We take 2 000 burn-in iteration and 5 000 Gibbs samples with five thinned steps for each simulated dataset. For the True-SPM scenario, the simulation results under the proposed joint model and the survival data only model are presented in Tables 2 and 3, respectively. Table 2 shows that the joint model analysis of the simulated data under the True-SPM scenario leads to unbiased and efficient parameter estimates with high coverage probabilities. We also analyse the same simulated data under the True-SPM scenario by the survival data only model and the results are presented in Table 3. Table 3 shows that the biases of the model parameters are higher compared to the joint model analysis and the coverage probabilities are substantially lower. Particularly, the coverage probabilities for λ₁ and λ₂ are zeros. The Bayesian criteria ΔDIC_Surv and ΔWAIC_Surv are evaluated for each simulated data under the True-SPM scenario.

Table 2:

Posterior estimates under the joint model for True-SPM in Section 5.1

Parameter	True	Est.	Bias	SE	SD	Coverage
γ1	0.15	0.150	−0.000	0.011	0.010	0.970
γ2	0.30	0.302	−0.002	0.011	0.012	0.930
σ2	0.50	0.500	0.000	0.002	0.002	0.910
b11	1.00	1.000	0.000	0.009	0.009	0.970
b21	0.50	0.500	0.000	0.012	0.012	0.925
b22	0.80	0.799	0.001	0.008	0.008	0.950
θ1	0.50	0.496	0.004	0.013	0.014	0.905
θ2	1.00	0.990	0.010	0.012	0.013	0.875
${\alpha }_{11}^{\ast }$	0.20	0.202	−0.002	0.023	0.022	0.950
${\alpha }_{12}^{\ast }$	0.80	0.800	0.000	0.023	0.022	0.950
${\alpha }_{21}^{\ast }$	0.50	0.494	0.006	0.027	0.029	0.925
${\alpha }_{22}^{\ast }$	1.00	0.997	0.003	0.026	0.023	0.975
β11	0.50	0.498	0.002	0.021	0.021	0.940
β12	0.60	0.587	0.013	0.023	0.024	0.890
β21	0.20	0.204	−0.004	0.023	0.022	0.960
β22	−0.50	−0.484	−0.016	0.025	0.022	0.950
λ1	0.10	0.099	0.001	0.002	0.002	0.940
λ2	0.08	0.080	−0.000	0.002	0.002	0.955

Table 3:

Posterior estimates under the survival data only model for True-SPM in Section 5.1

Parameter	True	Est.	Bias	SE	SD	Coverage
β11	0.50	0.468	0.032	0.021	0.026	0.650
β12	0.60	0.594	0.006	0.022	0.029	0.845
β21	0.20	0.172	0.028	0.023	0.028	0.705
β22	−0.50	−0.436	−0.064	0.024	0.029	0.310
λ1	0.10	0.079	0.021	0.002	0.002	0.000
λ2	0.08	0.067	0.013	0.002	0.002	0.000

We repeat a similar analysis for the simulated data under the True-Surv scenario. To preserve the space, we present the simulation results under the proposed joint model and the survival data only model in Tables S.1 and S.2, respectively, in the Supplementary Materials (http://www.statmod.org/smij/archive.html). We also evaluate the ΔDIC_Surv and ΔWAIC_Surv for each simulated dataset under the True-Surv scenario to compare with the True-SPM scenario. Table 4 presents the summary statistics of ΔDIC_Surv and ΔWAIC_Surv for the True-Surv and True-SPM scenarios. Under the True-Surv scenario, the median values of ΔDIC_Surv and ΔWAIC_Surv are −4.771 and −4.669, respectively, while under True-SPM scenario, the median values of ΔDIC_Surv and ΔWAIC_Surv are 3793.524 and 3811.183, respectively.

Table 4.

Summary of ΔDIC_Surv and ΔWAIC_Surv for True-SPM and True-Surv

	True-Surv		True-SPM
Criterion	Median	IQR=(Q1, Q3)	Median	IQR=(Q1, Q3)
ΔDICSurv	−4.771	(−6.004, −2.460)	3 793.524	(3 702.444, 3 855.218)
ΔWAICSurv	−4.699	(−5.923, −2.432)	3 811.183	(3 716.918, 3 870.227)

The boxplots of ΔDIC_Surv and ΔWAIC_Surv are shown in Figures 3 and 4, respectively, for the True-Surv and the True-SPM. Figures 3 and 4 show that when there exists no association between the longitudinal and survival data, the gain in fit due to the inclusion of longitudinal data in the survival sub-model is not substantial. In the True-Surv scenario, the inter quartile ranges (IQRs) of ΔDIC_Surv and ΔWAIC_Surv in Table 4 include the value of −4. This indicates that DIC_Surv (4.3) and WAIC_Surv (4.6) penalize more due to the inclusion of four association parameters (α₁, α₂) compared to DIC_Surv,0 (4.4) and WAIC_Surv,0 (4.7). However, the boxplots of ΔDIC_Surv and ΔWAIC_Surv in Figures 3 and 4, respectively, under the True-SPM scenario show a substantial gain in fit. These figures clearly illustrate that our proposed joint model performs better than the survival data only model when there exists an association between the longitudinal and survival data.

Figure 3:

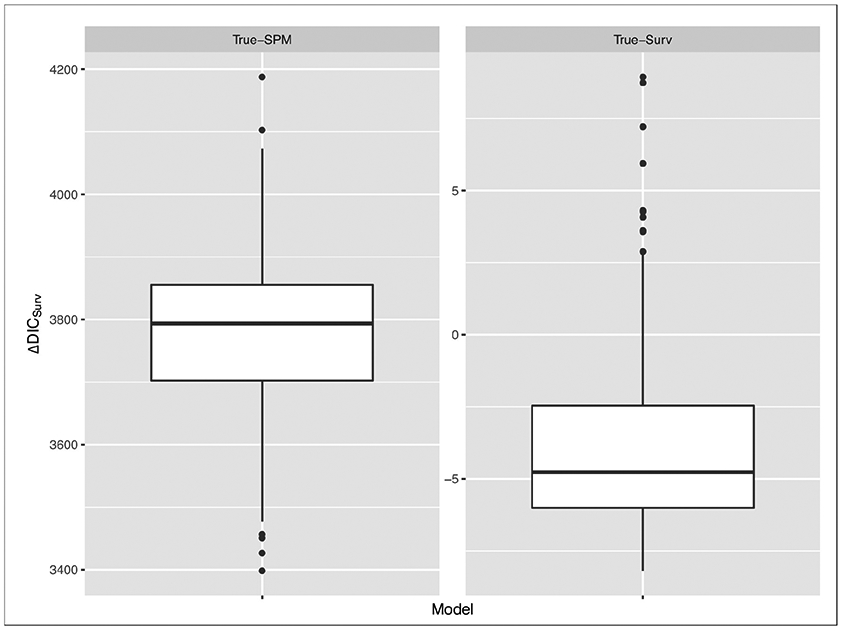
Boxplots of DIC under True-SPM and True-Surv model

Figure 4:

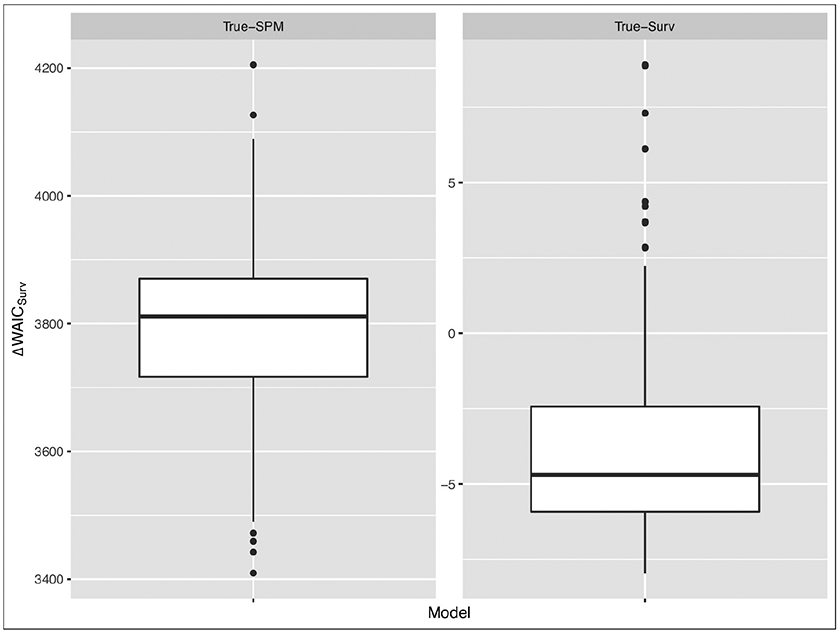
Boxplots of WAIC under True-SPM and True-Surv model

6. Analysis of SELECT data

We carry out an analysis of the SELECT data. The response variable is the time to diagnosis of PC due to low-grade or high-grade. In this analysis, we consider seven covariates, including patients age (in years), BMI in kg/m², Hispanic status (‘Yes’ = 1, ‘No’ = 0), Race (‘African American’ = 1, ‘Others’ = 0), Family history of cancer (‘Yes’ = 1, ‘No’ = 0), current smoking status (‘Yes’ = 1, ‘No’ = 0) and former smoking status (‘Yes’ = 1, ‘No’ = 0). Table 5 shows the summary statistics of the continuous variables. These summary statistics show that the average age of high-grade patients is higher compared to the other groups. The average BMI of high-grade patients is also found to be higher. Table 6 shows the frequency distribution of the patients with respect to the censoring status. Among the patients who developed cancer, missing-grade patients show a higher percentage of Hispanic group compared to the others. From the percentage distribution, we observe that there is no indication of a positive association between smoking status and cancer status. For all three groups of PC, the percentage of family history of cancer was found to be higher compared to the censored group. A similar trend is observed among the African American group indicating a positive association between race and cancer status.

Table 5:

Summary statistics of continuous covariates at baseline by PC

	Mean (SD)
	Censored	Low-grade	High-grade	Missing-grade
Age	62.94 (6.72)	62.95 (6.03)	64.58 (6.24)	62.59 (7.39)
Height	176.64 (7.44)	176.84 (7.29)	176.83 (7.17)	177.09 (7.39)
Weight	89.19 (15.57)	88.11 (14.85)	90.92 (16.23)	89.41 (14.45)
BMI	28.56 (4.55)	28.12 (4.06)	29.08 (4.91)	28.48 (4.15)

Table 6:

Summary statistics of categorical covariates by PC

	Frequency (%)
	Censored	Low grade	High grade	Missing grade
Hispanic
No	20 124 (94.95)	738 (97.75)	405 (96.89)	400 (94.12)
Yes	1 070 (5.05)	17 (2.25)	13 (3.11)	25 (5.88)
Smoking
Current	1 681 (7.93)	51 (6.75)	19 (4.55)	23 (5.41)
Former	10 499 (49.54)	344 (45.56)	193 (46.17)	203 (47.76)
Never	9 014 (42.53)	360 (47.68)	206 (49.28)	199 (46.82)
Family history
No	17 805 (84.01)	533 (70.60)	304 (72.73)	316 (74.35)
Yes	3 389 (15.99)	222 (29.40)	114 (27.27)	109 (25.65)
Race
African American	2 887 (13.62)	108 (14.30)	61 (14.59)	76 (17.88)
Others	18 307 (86.38)	647 (85.70)	357 (85.41)	349 (82.12)

The main goal of this study is to assess the association between the longitudinal PSA and the time-to-PC due to low-grade or high-grade after adjusting for the covariates under consideration. For the longitudinal sub-model, we consider the natural logarithm of PSA as the response variable. For both the longitudinal and survival data, the same seven covariates are used. We consider the shared parameter joint model, in which the random effects are assumed for the longitudinal and survival data. We consider the piecewise constant forms for the baseline hazards functions due to two different causes. To construct the appropriate partitions {s_kl, l = 1,…, G_k, k = 1, 2}, we use DIC_Surv,0 defined in (4.4) to determine the best combination of (G₁, G₂). Table 7 shows the results of DIC_Surv,0 for different combinations of (G₁, G₂) suggesting the piecewise constant hazard function with (G₁ = 70, G₂ = 70) fits the SELECT data best. For the analysis, we used 5 000 burn-ins and 10 000 MCMC samples.

Table 7.

DIC_Surv,0 and dimension penalty for different combinations of G₁ and G₂

G1	G2	DICSurv,0	PD[Surv,0]
60	60	19 137.72	136.06
60	70	19 112.95	146.68
60	80	19 123.86	157.33
60	90	19 137.66	167.99
70	60	19 099.99	146.37
70	70	19 082.67	156.77
70	80	19 094.20	167.72
70	90	19 107.96	178.36
80	60	19 110.30	156.70
80	70	19 093.18	167.19
80	80	19 104.48	178.05
80	90	19 118.93	189.04

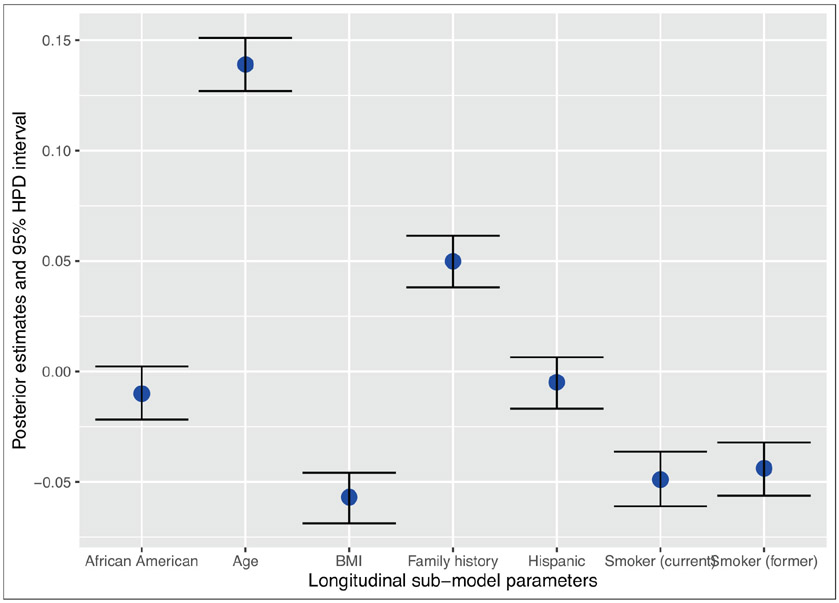
The posterior estimates of γ along with the 95% HPD intervals are presented in Figure 5. The figure suggests that except Hispanic status and race of the patients, all other covariates have significant effects on the longitudinal PSA. In particular, we see that BMI is negatively associated with the PSA, which is consistent with other studies (Hekal and Ibrahiem, 2010). Some studies (Algotar et al., 2011) found there is a positive association between smoking status and PSA. However, the sample size for that study was very small (140 subjects). In our analysis of the SELECT data, we find that smoking status is negatively associated with the PSA. The estimates and the 95% HPD intervals of the association parameters {α_k, k = 1, 2} are presented in Table 8. The results show that both intercept and slope parameters of the longitudinal PSA in the shared parameter joint model have significant effects on both the low-grade cancer and the high-grade cancer. The positive values of the association parameters indicate that there is a positive association between the PSA and the risk of developing low-grade or high-grade cancer. Comparing the risks of the low-grade and high-grade patients, both the intercept parameter and the slope parameter for high-grade are higher compared to those low-grade patients. This indicates that with the increase in the PSA, the risk of developing high-grade cancer is slightly higher compared to the risk of low-grade cancer.

Figure 5.

95% HPD interval of the γ

Table 8.

Posterior estimates and 95% HPD intervals of α₁ and α₂ under the joint model with G₁=70 and G₂ = 70

	Est.	SD	95% HPD interval
α11	1.467	0.057	(1.454, 1.460)
α12	4.333	0.295	(4.291, 4.326)
α21	1.387	0.075	(1.371, 1.380)
α22	6.169	0.349	(6.153, 6.192)
α21 – α11	−0.080	0.096	(−0.108, −0.097)
α22 – α12	1.836	0.457	(1.845, 1.900)

The survival sub-model parameter estimates under the joint model and the survival data only model are presented in Table 9. The results show that age is positively associated with the risk of high-grade cancer and not significantly associated with low-grade cancer, which is found to be consistent under both the joint model and the survival data only model. Both joint model and he survival data only model show that BMI is not associated with the risk of low-grade cancer. Although BMI is significantly positively associated with high-grade cancer under the survival data only model, BMI is not significantly associated with the risk of high-grade cancer under the joint model. Hispanic patients were found to have a lower risk of developing low-grade cancer compared to non-Hispanic patients and Hispanic status is found to be not associated with the risk of developing high-grade cancer. Although race of the patients is a significant factor for the cancer development under the survival data only model, race is not a significant factor associated with the risk of developing low-grade and high-grade cancer under the joint model. We also present the estimates and the 95% HPD intervals of α₂₁ – α₁₁ and α₂₂ – α₁₂ in Table 8. The results in Table 8 indicate that the risk of developing PC due to low grade is higher than high grade at the baseline. The difference in the slope parameters indicates that the risk of developing high grade cancer increases at a faster rate compared to low grade cancer due to increase in PSA.

Table 9.

Posterior estimates, 95% HPD intervals, DIC_Surv, DIC_Surv,0, and ΔDIC_Surv under the joint model and the survival data only model with G₁=70 and G₂ = 70

Variable	Joint model			Survival data only model
	Est.	SD	95% HPD int.	Est.	SD	95% HPD int.
Age	0.028	0.039	(−0.05, 0.103)	0.003	0.034	(−0.063, 0.071)
	0.254	0.05	(0.162, 0.359)	0.234	0.044	(0.15, 0.321)
BMI	−0.153	0.039	(−0.228, −0.075)	−0.096	0.035	(−0.162, −0.025)
	0.044	0.049	(−0.054, 0.138)	0.117	0.043	(0.03, 0.2)
Hispanic	−0.119	0.049	(−0.22, −0.028)	−0.085	0.045	(−0.173, 0)
	−0.073	0.061	(−0.194, 0.041)	−0.048	0.057	(−0.162, 0.058)
African	−0.043	0.039	(−0.12, 0.033)	0.07	0.034	(0.005, 0.138)
American	0.011	0.051	(−0.09, 0.11)	0.139	0.045	(0.052, 0.229)
Family	0.274	0.032	(0.211, 0.335)	0.259	0.027	(0.204, 0.312)
History	0.244	0.044	(0.157, 0.328)	0.231	0.038	(0.156, 0.306)
Currently	−0.086	0.042	(−0.165, −0.003)	−0.066	0.037	(−0.138, 0.008)
Smoker	−0.173	0.066	(−0.304, −0.049)	−0.16	0.063	(−0.286, −0.04)
Former	−0.081	0.039	(−0.155, −0.003)	−0.068	0.035	(−0.138, −0.002)
Smoker	−0.102	0.052	(−0.201, 0)	−0.103	0.047	(−0.196, −0.013)
DICSurv			14 915.091
DICSurv,0						19 082.668
ΔDICSurv			4 167.577
WAICSurv			15 207.596
WAICSurv,0						19 118.526
ΔWAICSurv			3 910.930

The family history of cancer has been an important risk factor associated with the development of low-grade and high-grade cancer. The patients who have family history of cancer tend to have a higher risk of developing low-grade and high-grade cancer compared to the patients who do not have any family history of cancer. This association is observed under both the joint model and the survival data only model. The patients who currently smoke have a lower risk of developing both low-grade and high-grade cancer under the joint model, although under the survival data only model, currently smoking status is not associated with low-grade cancer. The patients who used to smoke before have a lower risk of developing low-grade cancer, however, they do not have a higher risk of high-grade cancer. Finally, we present the Bayesian DIC and WAIC criteria to assess the fit of the models. DIC and WAIC under the survival data only model are DIC_surv,0 = 19082.667 and WAIC_Surv,0 = 19118.526. The DIC_Surv = 14915.091 and WAIC_Surv = 15207.596 under the joint model, which are much lower than the DIC_Surv,0 and WAIC_Surv,0 under the survival data only model. To quantify the gain in fit with the inclusion of longitudinal data in the survival sub-model, we also defined ΔDIC_Surv in (4.5). We found ΔDIC_Surv = 4167.5768, which indicates that we have about 21% gain in fit through the inclusion of the longitudinal PSA in the survival sub-model. In addition to ΔDIC_Surv, we also present the results of ΔWAIC_Surv in Table 9. The ΔWAIC_Surv = 3910.930 indicates that through the shared parameter joint model analysis, we get approximately 20% gain in fit due to the inclusion of longitudinal data compared to the survival data only model. The convergence of the model parameters is checked via the trace plots of MCMC samples of the model parameters. These figures are given in the Supplementary Materials (http://www.statmod.org/smij/archive.html).

7. Discussion

In this article, a joint model for the longitudinal and competing risks survival data is proposed with an applications to SELECT data. Our proposed model is flexible to account for the uncensored subjects with missing causes of failure. We develop a novel reparameterization to facilitate an efficient and convenient implementation of the MCMC sampling algorithm to sample from the posterior distribution. The proposed model is applied to SELECT data and to assess the model fit, we introduce four model assessment criteria, DIC_Surv, ΔDIC_Surv, WAIC_Surv and ΔWAIC_Surv. The Bayesian criteria ΔDIC_Surv and ΔWAIC_Surv measure the gain in fit of the survival sub-model due to the inclusion of longitudinal data. A simulation study is conducted to examine the change in ΔDIC_Surv and ΔWAIC_Surv for different values of the association parameters. Our simulation study shows that when there exists an association between the longitudinal and survival data, our proposed joint model fits the data better compared to the survival data only model. The analysis of the SELECT data shows that there is a significant positive association with PSA and the risk of developing low-grade and high-grade cancer. The performance of the joint model is assessed by ΔDIC_Surv and ΔWIC_Surv that show about the 21% and 20% gain in fit compared to the model with survival data only, respectively. Computer code was written for the FORTRAN 95 compiler, and we used IMSL subroutines with double precision accuracy. The FORTRAN code is available from the authors upon request.