Microstructural design for mechanical–optical multifunctionality in the exoskeleton of the flower beetle Torynorrhina flammea

Significance

In the design of multifunctional materials, harnessing structural and compositional synergies while avoiding unnecessary trade-offs is critical in achieving high performance of all required functions. Biological material systems like the cuticles of many arthropods often fulfill multifunctionality through the intricate design of material structures, simultaneously achieving mechanical, optical, sensory, and other vital functionalities. A better understanding of the structural basis for multifunctionality and the functional synergies and trade-offs in biological materials could thus provide important insights for the design of bioinspired multifunctional materials. In this study, we demonstrate a concerted experimental, theoretical, and computational approach that uncovers the structure–mechanics–optics relationship of the beetle’s cuticle, opening avenues to investigate biological materials and design photonic materials with robust mechanical performance.

Abstract

Biological systems have a remarkable capability of synthesizing multifunctional materials that are adapted for specific physiological and ecological needs. When exploring structure–function relationships related to multifunctionality in nature, it can be a challenging task to address performance synergies, trade-offs, and the relative importance of different functions in biological materials, which, in turn, can hinder our ability to successfully develop their synthetic bioinspired counterparts. Here, we investigate such relationships between the mechanical and optical properties in a multifunctional biological material found in the highly protective yet conspicuously colored exoskeleton of the flower beetle, Torynorrhina flammea. Combining experimental, computational, and theoretical approaches, we demonstrate that a micropillar-reinforced photonic multilayer in the beetle’s exoskeleton simultaneously enhances mechanical robustness and optical appearance, giving rise to optical damage tolerance. Compared with plain multilayer structures, stiffer vertical micropillars increase stiffness and elastic recovery, restrain the formation of shear bands, and enhance delamination resistance. The micropillars also scatter the reflected light at larger polar angles, enhancing the first optical diffraction order, which makes the reflected color visible from a wider range of viewing angles. The synergistic effect of the improved angular reflectivity and damage localization capability contributes to the optical damage tolerance. Our systematic structural analysis of T. flammea’s different color polymorphs and parametric optical and mechanical modeling further suggest that the beetle’s microarchitecture is optimized toward maximizing the first-order optical diffraction rather than its mechanical stiffness. These findings shed light on material-level design strategies utilized in biological systems for achieving multifunctionality and could thus inform bioinspired material innovations.

Natural selection can act on multiple fronts during the diversification and refinement of morphological characters within a given species (1, 2). These evolutionary processes frequently act both independently and synergistically, resulting in characters that exhibit multifunctionality (3–6). While classical characters, particularly those that have been employed for trait-based taxonomic purposes, typically represent macroscale features such as the size and shapes of bird beaks (7), species-specific characters (or phenotypes) also exist at the “material level” as nano- and microstructures (8–12). These micro- and nanoscale architectures have evolved to enable specific and diverse biological functions including, for example, mechanical protection and optical appearance (10, 13–15). As is the case for macroscale characteristics, a specific microscale material morphology is often the basis for multiple concurrent functionalities (4, 16–19). This observation then raises fundamental questions about multifunctional material design in biology: what types of property-related synergies and trade-offs result from function-specific structural constraints? And for specific multifunctional biological materials, which property or set of properties has gained priority in shaping a specific hierarchical material architecture of interest?

Here, we explore functional synergies and trade-offs in a multifunctional biological material system found in the exoskeleton of the flower beetle Torynorrhina flammea. In arthropods, the cuticle forms the hard external “skin” (20), which can simultaneously offer mechanical protection (9, 21), optical signaling (10, 22), water capturing (11), and sensory functions (23). With often incomplete knowledge of the structure–function relationships in biological materials, it is challenging to infer how their microstructures are tailored to fulfill various functional needs, especially considering the fact that this process requires the exploitation of structural synergies and the mitigation of unavoidable compromises in functional performance (3, 24). In all material systems, whether natural or synthetic (4, 25), significant performance trade-offs have to be addressed or accepted when designing for multifunctionality (4, 25–27). As such, the investigation of nature’s strategies for dealing with trade-offs between different properties to achieve multifunctionality is not only of interest to biologists but also to materials scientists and engineers (4–6). Our study of the multifunctional material architecture in the exoskeletons of T. flammea beetles, which enables optical functionality and mechanical robustness simultaneously, provides an example of how to assess functional hierarchy, thereby quantifying the relationship between different material properties in multifunctional material systems. Beyond the analysis of structure–function relationships in biological systems, similar approaches to those described here could also be applied to investigate and optimize the design of engineered multifunctional structural materials.

Results

Structure Characterization: Pillar-Reinforced Photonic Multilayer.

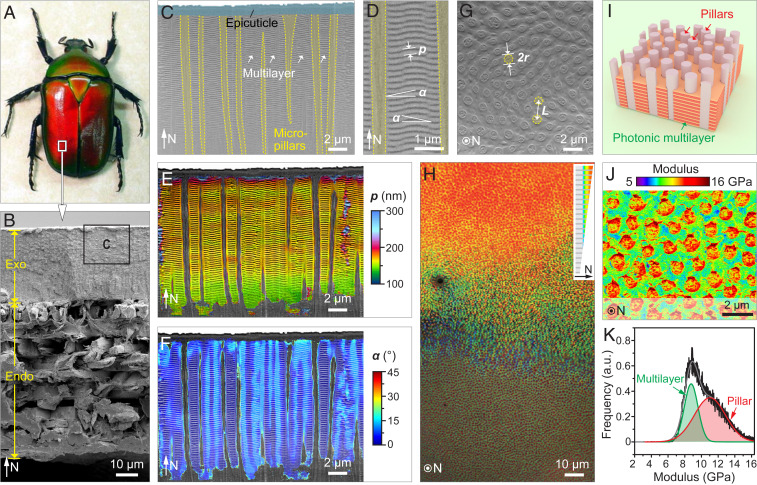
T. flammea belongs to a large family of flower beetles (the Scarabaeidae) native to the tropical rainforests of southeast Asia, including Malaysia, China, and Thailand. T. flammea is known for its extreme variability of color (28), with individuals ranging from purple to blue, green, orange, and red, spanning much of the visible spectrum (29). Fig. 1A shows the morphology and structural coloration of a red-colored T. flammea beetle. Both of its elytra (the hardened wing coverings) exhibit a uniform red color that blueshifts toward the curved edges, a characteristic of its illumination angle– and observation direction–dependent structural color. In the present study, all of our analyses were conducted on the central uniformly colored region of the elytra, which, when viewed as a fractured cross-section, reveals several structural layers in the thickness direction (Fig. 1B). As is the case for many other arthropod exoskeletons (23), the elytra consist of an outer exocuticle (∼30 μm) and an inner endocuticle (∼60 μm) with a distinctive plywood-like structure (Fig. 1B and SI Appendix, Fig. S1). Specifically, the exocuticle layer harbors a photonic structure of ∼15-μm thickness, which is separated from the underlying endocuticle by a region rich in dark pigment (SI Appendix, Fig. S2). This dark-pigmented region provides a black backdrop, which absorbs light transmitted through the photonic structure to enhance the color saturation (i.e., spectral purity) of the reflected light, a feature observed in several other biophotonic systems (30–34).

Fig. 1.

Microstructural characterization of the exoskeleton from the flower beetle, T. flammea. (A) Dorsal view of a red-colored T. flammea beetle. Image credit: Eva Nie (photographer). (B) Cross-sectional SEM image of the beetle’s elytra revealing the exocuticle (Exo) and endocuticle (Endo) layers. N represents the normal direction. (C) SEM image of the photonic structure in the exocuticle layer (boxed region in B). The white arrows mark the multilayer region. (D) The photonic multilayer is characterized by two structural parameters: p, period of the horizontal multilayer, and α, inclination angle. (E and F) False colored map of the multilayer period and orientation based on C. (G) Horizontal SEM image of the exocuticle showing the distribution of vertical micropillars. Two structural parameters are defined: r, the radius of the micropillar, and L, the spacing between adjacent pillars. The methodology for determining r and L is discussed in the Materials and Methods. (H) Low-magnification optical image of the cuticle polished in the horizontal orientation, which shows the upper photonic region and the lower micropillar-only region. Inset depicts the slightly inclined orientation of the polishing. (I) 3D model of the identified photonic microstructure consisting of a photonic multilayer laced with vertical micropillars. (J) Elastic modulus map based on AFM measurements. (K) Statistical analysis of modulus based on J.

Like many photonic architectures found in nature (10), the photonic structure in T. flammea comprises a nanoperiodic multilayer protected by a thin outer homogeneous epicuticle (Fig. 1C). The waxy epicuticle layer enables water repellency and chemical resistance (35) but is not primarily involved in the formation of the structural color. Instead, the beetle’s bright color appearance results from the light interference within the underlying photonic multilayer (∼180 periods), which consists of two alternating material phases, each with distinct optical properties, containing chitin and melanoprotein (36, 37) (Fig. 1D). Using a location-specific Fourier transformation approach to quantitatively map the periodicity, p, and orientation, α, of the multilayer structure (Fig. 1 E and F), we found that the photonic region has an upper zone with a constant periodicity of ∼164 nm, which decreases to ∼144 nm near the bottom of the photonic region (Fig. 1E and SI Appendix, Fig. S3). Moreover, the multilayer normal exhibits local deviations from the global horizontal orientation, with an average tilt angle of 5.6 ± 2.9° (Fig. 1F and SI Appendix, Fig. S4). Embedded within the beetle’s photonic multilayer and spatially distributed with short-range hexagonal order are vertically oriented micropillars (Fig. 1C), which have not been reported previously in other biological multilayer photonic systems (10, 29). For the red-colored beetle, the pillars have an average radius r = 0.36 ± 0.04 μm (n = 283) and an average spacing between adjacent pillars L = 1.23 ± 0.03 μm (n = 1,692), values determined from the analysis of plan-view scanning electron micrographs (SEM, Fig. 1G). The determination of adjacent neighbors and the evaluation of the average adjacent pillar spacing L are based on a Voronoi algorithm (see Computational Methods). Optical images of a close-to-plan-view polished section of the cuticle reveal a gradual transition from a red/orange color to a green/blue hue in the photonic structure (Fig. 1H), which arises from a decrease in layer periodicity toward the base of the multilayer. The micropillars are continuous throughout the entire photonic region and down to the underlying pigment layer, where they subsequently coalesce into discrete bundles (SI Appendix, Fig. S5). This observation suggests that the micropillars may be formed from the same material as the endocuticular microfibers that gradually split into micropillars in the photonic structure. The three-dimensional (3D) illustration in Fig. 1I summarizes our current understanding of the composite photonic structure in T. flammea, consisting of roughly horizontal photonic multilayers laced with vertical micropillars. Atomic force microscopy (AFM)-based quantitative mechanical mapping and statistical analysis further revealed that the micropillars are stiffer than the multilayer matrix (modulus of 11.0 GPa versus 8.8 GPa, Fig. 1 J and K and SI Appendix, Fig. S6).

Mechanical Robustness.

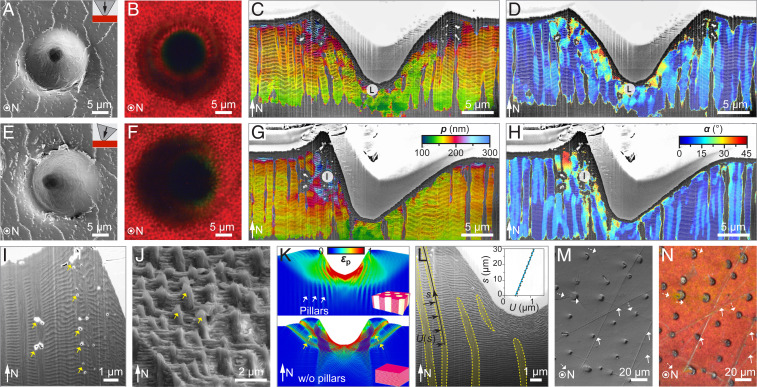
As with other arthropod exoskeletons, the cuticle of T. flammea provides structural support and acts as a protective armor against environmental abrasion and predatory assault. To investigate the cuticle’s mechanical properties, we performed microindentation tests, both parallel to the cuticle’s surface normal and at an inclination angle of 16° (Fig. 2 A and E). The inclined indentation tests likely represent a more biologically relevant condition, since loading from mechanical impacts, either a tooth, beak edge, or hard protrusion during a predatory attack, is unlikely to be normal to the elytral surface. With a conospherical tip of 5-µm radius and 30° half-angle, maximum indentation depths of 14 µm and 18 μm were achieved for normal and inclined indentations at a maximum load of 250 mN, respectively (SI Appendix, Fig. S7). SEM images and the corresponding 3D reconstructions of the residual microindentation impressions (SI Appendix, Fig. S7) illustrate the cuticle’s structural deformation after indentation, which is also apparent in the optical images of indentation craters (Fig. 2 B and F). The optical micrographs show that the red structural color is preserved in the immediate vicinity of the indentation regions, demonstrating that the resulting structural damage remains highly localized.

Fig. 2.

Tough color in the cuticle of T. flammea achieved by damage localization. Top-view (A) SEM and (B) optical images, cross-sectional–view color maps of the multilayer (C) period and (D) orientation across the indentation sites for normal microindentation. (E–H) Corresponding results for inclined microindentation. The maximum load is 250 mN. No radial cracks were observed, and the red photonic color is preserved immediately near the indentation sites. (I) Magnified cross-sectional–view SEM images of the inclined indentation showing the breakage of the vertical micropillars (marked by arrows) due to the tensile stress in the vertical direction. (J) SEM image of a fractured surface in the photonic region shows a microscopically rough surface due to the presence of the vertical micropillars (arrows). (K) FE simulation results of plastic strain, ${\epsilon }_p$, at the maximum load for normal indentations on T. flammea’s photonic structure (Top) and a hypothetical simple multilayer structure (Bottom). Shear bands are formed in the latter case (yellow arrows). (L) Cross-sectional–view high-magnification SEM image of the normal indentation crater, which shows the bending deformation of vertical micropillars (yellow stripes). The inset shows the elastic recovery displacement U(s) of a pillar from simulation. (M) SEM and (N) optical images of a beetle’s cuticle surface directly collected from the field. The arrows mark the cracks in the cuticle. Some scratches (dashed arrow) are seen in the SEM data but hardly observed in the optical image.

Quantitative cross-sectional imaging of the indentation impressions and finite element (FE) simulations allowed us to elucidate the underlying mechanisms for the observed damage localization (see Materials and Methods and SI Appendix, Figs. S8 and S9). The overall subsurface deformation fields for both normal and inclined indentations are color-mapped based on multilayer spacing (Fig. 2 C and G) and orientation (Fig. 2 D and H). These maps reveal that permanent structural damage is localized almost exclusively in the indentation contact area. The multilayer structure directly beneath the indentation tip exhibits densification resulting in smaller periodicities (Fig. 2C), which further leads to the observed blueshifts at the center of the indent (Fig. 2B). Similar damage localization is also observed for inclined indentations, although the entire indentation crater is asymmetric (Fig. 2 G and H). The stiffer micropillars increase the stiffness and hardness of the composite structure in the vertical direction, which further reduces the indentation depth. “Pileup” is observed surrounding the perimeter and the front side of the normal and inclined indents respectively, leading to an increase in multilayer periodicity up to twofold in these pileup regions (Fig. 2 C and G). This increase is due to the tensile stress generated during indentation as revealed by FE simulations (SI Appendix, Figs. S9–S14). Further increase in this stress generates tension-induced voids in the micropillars instead of delamination in the multilayer (38) (Fig. 2I). The fracture surface shown in Fig. 2J clearly illustrates how the vertical micropillars act to restrict catastrophic delamination in the photonic multilayer by the formation of a microscopically tortuous crack propagation path.

Aside from ensuring improved stiffness, hardness, and delamination resistance in the vertical direction, the micropillars can also restrain deformations in the horizontal plane. First, the pillars serve as pinning sites to restrain the build-up of shear deformations in the multilayer and localize the deformation under the indenter. As a result, the formation of shear bands, which readily occur in a multilayer structure without vertical micropillars (39), is largely suppressed in the pillar-laced multilayer architecture (Fig. 2K and SI Appendix, Figs. S10–S13) (40). Second, the micropillars surrounding the indentation crater provide increased elastic recovery. The pillars are stiffer than the surrounding multilayer matrix and bend outwards under indentation, so they can partially restore the original shape after unloading by springing back, further reducing the size of the indentation crater (Fig. 2L and SI Appendix, Figs. S14 and S15). Simulations reveal that the maximum recovery displacement can reach up to 1.2 μm at a maximum indentation depth of 14 µm (Fig. 2 L, Inset). This resistance to widespread structural damage is advantageous for a cuticle that serves as protective armor and simultaneously helps to preserve the visual appearance. Such “tolerance to optical damage” behavior can also be observed in the surface of the collected beetle’s elytra, which usually show scratches that may originate from predatory attacks, abrasion with hard surfaces during locomotion, or specimen handling during collection (Fig. 2M). Nonetheless, the bright color appearance is largely preserved without noticeable degradation outside of the direct damage zones as shown in the corresponding optical image (Fig. 2N).

Consistent Designs in Different Color Polymorphs.

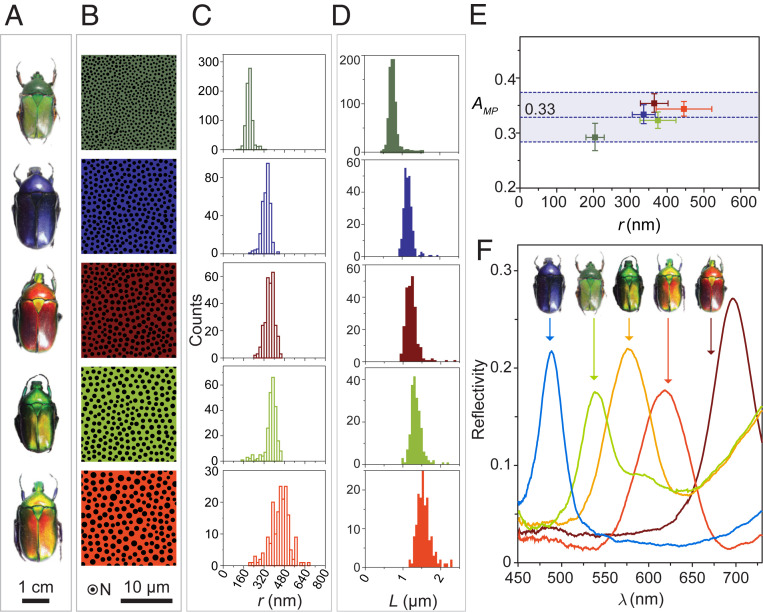
Our structural characterization and mechanical analyses reveal the importance of micropillars in providing increased mechanical robustness to the photonic architecture. The pillars restrict damage propagation and delamination, which is critical for preserving the photonic properties that determine the beetle’s overall appearance. This structural design motif, comprising a micropillar-laced multilayer composite, is found in all inspected T. flammea color polymorphs (41) that span hues from deep blue to green, to yellow-green, to orange and to red (Fig. 3 A–D and SI Appendix, Fig. S16). Quantitative geometric analysis reveals that different colored beetles have evolved different geometric sizes of the micropillar-reinforced multilayer structure. Specifically, for the investigated color polymorphs, the multilayer period ranges from 150 to 220 nm (SI Appendix, Figs. S17 and S18), and the radius of micropillars ranges from 200 to 450 nm (Fig. 3C). The spacing between adjacent pillars varies from 0.76 to 1.56 μm (Fig. 3D and SI Appendix, Figs. S19–S24), and all polymorphs exhibit a short-range–ordered quasihexagonal pillar arrangement (most pillars have six adjacent neighbors as shown in SI Appendix, Fig. S16). Despite the large variation in micropillar size, the areal coverage of micropillars (the fraction of the horizontal plane occupied by the pillars), A_mp, is very similar for all the characterized beetles (i.e., 32.9 ± 2.1%) (Fig. 3E). On one hand, this highly consistent value of A_mp among different color polymorphs may be due to a mass constraint that limits the relative volume fraction of pillars. On the other hand, this consistent A_mp value represents evidence of the compromise between the mechanical and optical performance, since more pillars grant increased mechanical reinforcement, while a larger area coverage with photonic multilayers (i.e., smaller pillar diameters and/or fewer pillars per unit area) provides increased reflectance.

Fig. 3.

Structural analysis and reflection spectra of different colored polymorphs of T. flammea. (A) Photographs of T. flammea with green, deep blue, red, yellow-green, and orange color. (B) Binary images and corresponding size distribution of (C) pillar radius, r, and (D) adjacent pillar spacing, L, based on quantitative analysis from SEM images of horizontal sections. (E) Relationship between the area coverage, A_mp, and the pillar radius, r, for five photonic cuticles with different colors. (F) Reflection spectra of five beetles measured with an integrating sphere. The reflectivity is given in relative intensity compared with a diffusive white surface.

Unique Optical Performance: Scattering Light to Larger Angles.

The total reflectance spectra of the five colored beetle polymorphs were collected with a custom-built integrating sphere and are summarized in Fig. 3F. The spectral location of the observed reflection maxima varies according to the beetles’ corresponding color appearance (i.e., 472 nm, 549 nm, 586 nm, 645 nm, and 690 nm for deep blue, green, yellow-green, orange, and red, respectively). Moreover, unlike a simple multilayer, in which normally incident light only reflects in the same direction, the intensity of the reflected light in T. flammea increases significantly with the increasing light-collection angle, which can be controlled by an objective lens with higher numerical apertures (NA) (SI Appendix, Fig. S25). This observation suggests that the photonic microstructure in T. flammea scatters light to substantially higher polar angles.

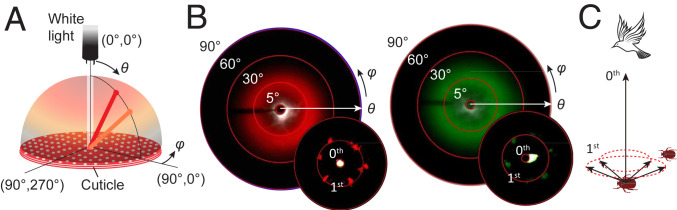
To quantify the light-scattering characteristics in T. flammea, an imaging scatterometer (42) was developed to measure the angular distribution of light reflected by the cuticle in a hemisphere above the sample surface as a function of the polar angle $\theta$ and the azimuthal angle $\phi$ for illumination areas of different sizes (Fig. 4A and SI Appendix, Fig. S26). When light is collected from areas of ∼3 × 10⁴ μm² from the elytra, diffused color rings with large polar angle ranges are apparent for beetles of different hues, which are around 25° to 50° and 20° to 45° for the red and green colors, respectively (Fig. 4B). By contrast, when restricting the collection area to only a few tens of square micrometers, the scattering pattern of the reflected light reveals a pseudohexagonal distribution of brightly colored reflection spots (Fig. 4 B, Insets). This difference in diffraction pattern correlates with the distribution of micropillars that follow a pseudohexagonal pattern locally but do not have a long-range spatial order due to the variations in pillar spacing. This correlation further suggests that the micropillars may function as light redistributors that help to scatter light into a greater polar angle range. Birds are typical predators of flower beetles and thus often observe the beetles from elevated altitudes, viewing the beetle at a much smaller polar angle $\theta$ compared with the beetle’s conspecifics (Fig. 4C). It is conceivable that enhanced scattering of colored light to larger polar angles is advantageous for intraspecies communication (43) while reducing possible detection by visible predators.

Fig. 4.

Diffraction signatures showing the cuticles’ capability of scattering light to larger polar angles. (A) Schematics illustrating the spatial distribution of light reflected from the beetle’s cuticle, which is a function of the polar angle $\theta$ and azimuthal angle $\phi$. (B) Measured diffraction microscopy images for the red and green beetles. The main and the inset diffraction images are collected using an imaging scatterometer with illumination spots of diameter 200 µm and 5 µm, respectively. (C) Schematic illustrating how deviating diffraction efficiency to a larger polar angle could reduce detection by predators and benefit intraspecies communication.

The observed ability of the beetle’s cuticle to scatter light to larger polar angles further motivated us to investigate the diffraction signature of the pillar–multilayer structure theoretically. This was achieved by developing a computational wave optics–based model (44) (SI Appendix, Supplementary Notes and Figs. S27–S29). Consistent with experimental observations, the model shows that introducing the micropillars into the multilayer stack redistributes reflected light to higher polar angle ranges, more specifically into the first diffraction order (SI Appendix, Fig. S30). Moreover, the model successfully predicts the short-range hexagonal first-order scattering patterns and matches the experimentally observed diffuse-color ring patterns, which arise due to variations in micropillar spacing and lattice orientation that appear on length scales of a few pillar distances (SI Appendix, Fig. S31). Our modeling also confirms, consistent with simpler multilayer-only systems, that the thickness of individual layers within the multilayer stack determines the color of the beetle, namely, the spectral range over which light is strongly reflected. The spacing between the micropillars and the orientation of the pillar lattice influence how light is scattered from the photonic architecture, which, in turn, determines the intensity distribution in the polar and azimuthal directions ($\theta$, $\phi$). By contrast, the effect of micropillar size on optical scattering is more complex and is linked to the overall intensity of scattered light integrated over the whole hemisphere as well as to the intensity in a given polar angle range (see detailed discussion in SI Appendix, Supplementary Notes).

Material-Centric Modeling: Functional Synergies and Trade-Offs.

The microstructural–mechanical–optical analysis so far suggests that introducing the vertical micropillars into the multilayer stack offers positive benefits to both mechanical and optical performance: it does this directly by localizing damage and redistributing the reflected light, respectively. Next, we ask the question of whether there is any optimized parameter or performance in this peculiar microstructure of T. flammea. To address this question, we integrated material-centric optical and mechanical models to explore the performance of pillar–multilayer microstructures by varying the pillar size (r) and spacing (L) with an ideal hexagonal pattern (Fig. 5 A–C). Note that the thickness of individual layers within the multilayer stack is calculated for different colored beetles, such that the light reflected from the multilayer–pillar structures exhibits the same peak reflection wavelength as the experimental measurements (Fig. 3F). Moreover, based on the measured diffraction images shown in Fig. 4B, we selected the normalized reflection intensity of the first diffraction order ($R_{photonic}^{1st}$) as the optical property metric and mapped out intensity distributions for different hues (Fig. 5A and SI Appendix, Fig. S32). This approach allowed us to identify the optimal parameters of r and L for a given hue. Surprisingly, the experimentally measured parameters sit very close to the maximum diffraction strength in Fig. 5A.

Fig. 5.

Structural design and functional hierarchy of T. flammea’s pillar–multilayer architecture. (A) Optical and (B) mechanical design spaces mapped by diffraction strength in the first diffraction order ($R_{photonic}^{1st}$) and effective modulus of the composite structure ($E_{beetle}^{eff}/E_{ml}^{eff}$, normalized by the modulus of multilayer), respectively. The data points mark the experimental measurements, and the error bars represent the SDs. C shows the different structural morphology along the dashed arrows in A and B by varying the pillar radius to spacing ratio (r/L). (D) Normalized stiffness (blue curve) and reflectivity of the 0th ($R_{photonic}^{0th}$) and first ($R_{photonic}^{1st}$) order plotted as functions of r/L for the red beetle. This plot demonstrates the trade-offs and synergies between mechanical and optical properties. (Inset) Illustration of the 0th and first-order diffraction. Shaded area: r/L range of the red beetle with the width representing SD. (E) Model-based morphospace analysis. The dashed curve marks the Pareto front obtained by eliminating phenotypes that perform worse in both functions. The arrow indicates a potential shift of the design surface (1 → 2) when accounting for additional metrics. (F) Local heterogeneity surrounding a gland cell pore demonstrated by AFM.

The mechanical performance of a material can be characterized by different material parameters including stiffness, strength, hardness, and toughness. Considering that these different mechanical parameters are typically correlated (27, 45) (for example, strength and hardness are typically proportional to stiffness), here, we selected normalized stiffness of the composite structure as a simplified representative property metric ($E_{beetle}^{eff}/E_{ml}^{eff}$, where $E_{beetle}^{eff}$ is the stiffness of the composite structure and $E_{ml}^{eff}$ is the stiffness of the multilayer stack). The parametric space (Fig. 5B) is then mapped out by a pillar-reinforced biphase layer model (46) (SI Appendix, Supplementary Notes and Figs. S33–S35). Fig. 5B clearly demonstrates that stiffness is not maximized in these systems: instead, we discovered that different beetle polymorphs all possess a similar normalized stiffness relative to the multilayer stack. This result suggests a consistent level of enhancement in structural stiffness for each of the five different colored beetle polymorphs.

The theoretical analysis described above suggests that the pillar–multilayer design observed in T. flammea, while delivering enhanced mechanical resilience, is optimized primarily for optical performance, specifically for increased intensity in the first diffraction order ($R_{photonic}^{1st}$); the optical performance appears to take priority over the stiffness ($E_{beetle}^{eff}$). This point can be further illustrated by evaluating the effective stiffness and reflectivity as a function of the pillar radius to spacing ratio, r/L, where the experimentally measured r/L ratio is very close to the “optimal” value for maximum $R_{photonic}^{1st}$ (Fig. 5D). This plot also reveals the expected reduction in 0th order diffraction in the normal direction ($R_{photonic}^{0th}$) as r/L increases from 0 to 0.35, because the reflected light is redistributed more significantly to the first diffraction order.

To further understand the function-driven architecture of the beetle’s microstructure, we utilized the concept of morphospace and considered the pillar–multilayer structures as phenotypes (with varying r/L) based on four representative structures depicted in Fig. 5C. Fig. 5E depicts the optical–mechanical traits predicted from our theoretical models in which each point on the curve represents a phenotype. Here, to locate a minimum value, the performance is measured in reciprocal form. By eliminating phenotypes that perform worse in both (optical and mechanical) evaluated tasks, we obtain the Pareto front (3), which is shown as a dashed curve in Fig. 5E. Notably, T. flammea occupies a position on the upper end of the Pareto front with maximum optical performance. This result suggests an intriguing question: was optical performance subject to a stronger evolutionary selection pressure than the mechanical stiffness for the beetles’ exocuticle architecture? Unfortunately, this question cannot be fully answered through our findings alone, as we are not able to exclude other factors including additional relevant biological functions (e.g., thermal regulation and sensory properties) and constraints such as mass (flower beetles are flight beetles), developmental processes, and potential evolutionary constraints. Therefore, further systematic studies on other functional performance, formation mechanisms, and the evolutionary history of the flower beetles are required to fully address this complex and intriguing question.

Discussion and Outlook

In this study, we have examined the microstructural design of T. flammea’s multifunctional cuticle. Our results demonstrate that the presence of microsized vertical pillars that are embedded in the photonic multilayer found in the exocuticle of T. flammea’s elytra provides multiple mechanical–optical benefits. Optically, the micropillars help diffract light toward larger polar angles by increasing the light intensity in the first diffraction order, which determines the viewing angles from which the cuticle’s structural colors are most apparent. In terms of mechanical benefits, the micropillars increase the stiffness, strength, and mechanical robustness of the structure by preventing the formation of shear bands, improving the delamination performance, and localizing the damage. Bioinspired strategies gleaned from the beetles’ cuticle architecture to enhance mechanical robustness by reinforcing a laminated composite in the z-direction may thus prove useful in the design of composite materials including laminated glass, capacitors, and electrodes (40, 47, 48). The synergistic effect of the improved reflectivity at larger polar angles and the observed damage-localization capability of the pillar–multilayer structure contribute to the remarkable optical-damage tolerance observed in the beetle’s cuticle. We further note that, while the advantages of the pillar–multilayer structure over a pillar-free multilayer structure are obvious, many photonic structures broadly observed in different plant and animal species, including those associated with many beetles, have multilayer structures without micropillar reinforcements (10, 49). This variation could be due to the extra energy cost required to form the vertical micropillars or the presence of different functional, developmental, and evolutionary constraints.

Besides characterizing the microstructure–optics–mechanics relationship, our results based on material-centric optical and mechanical modeling and Pareto front analysis suggest that the optical performance (first-order diffraction) may present a relatively more important selection pressure over the mechanical performance (stiffness) during the evolution of the material architecture in the exocuticular region of the T. flammea exoskeleton. However, since it is not feasible to model all material properties exclusively and include all potential structural and mass constraints, we cannot exclude other potential factors that affect the evolutionary development of the pillar–multilayer morphology. For example, sensory and thermal regulation functions are also important in the cuticle. In Fig. 5F and SI Appendix, Fig. S36, our AFM image shows that the pillar–multilayer structure adapts locally to accommodate the presence of pores by varying the geometric size and spacing of micropillars. Clearly, this local structural gradient surrounding a gland cell pore sacrifices optical performance but benefits sensing and mechanical reinforcement. Further examinations of the animal behavior, evolutionary history, and ecology of flower beetles are therefore required to confirm whether optical performance indeed takes priority over other material performances. Nonetheless, our approach to consider material microstructures as phenotypes and to combine quantitative experimental characterization, simulation, and theoretical modeling with morphospace analysis, opens up an avenue to gain insights into the relative importance of different functional requirements of biological materials. Moreover, the detailed characterization of functional trade-offs and synergies in the pillar–multilayer structure also provides useful information in the design of multifunctional materials and damage-tolerant photonic devices.

Materials and Methods

Sample Preparation.

T. flammea beetles were purchased from https://www.insect-sale.com. These specimens were collected in Doi Saket, Chiang Mai, Thailand from August to September of 2008. The specimens were stored in dry conditions prior to the experiments. All structural, mechanical, and optical measurements were based on specimens taken from the central part of the elytra, away from any edges.

Microstructural Imaging.

Optical imaging.

The elytra of T. flammea were first carefully removed from the body of the beetle with a pair of scissors. The elytra were then cut with a razor blade into rectangular-shaped specimens of 1-to-5-mm side length for further structural, mechanical, and optical characterizations. Optical imaging was carried out using different instruments depending on the required magnification. To image entire beetles, a wide-zoom stereo microscope was used (Olympus SZX16). High magnification images of the mechanically polished surface (Fig. 1H) and microindentation residues (Fig. 2 B and F) were obtained with a Nikon ECLIPSE L150 microscope with a 100× objective lens (NA = 0.9).

SEM imaging.

For structural observation of the fractured surfaces in the transverse direction, a notch (∼1 mm in length) was first made with a razor blade in the center of a rectangular-shaped piece (2 × 3 mm) of the beetle elytra. The prenotched specimen was then fractured by pulling it apart with tweezers. The fractured samples were mounted on a 45° pretilt SEM holder with conductive silver paste. To obtain high-magnification images of the fracture surface of the photonic microstructure (Fig. 2J), the sample was coated with ultra-thin carbon to reduce charging effects. For low-magnification imaging of the entire cross-section of elytra (Fig. 1B), the samples were coated with Pt/Pd with a sputter coater (Electron Microscopy Sciences, EMS300T). SEM imaging was conducted on a Helios Nanolab 600 Dual Beam (FEI) using an accelerating voltage of 2 to 5 kV, an emission current of 40 to 100 μA, and a nominal working distance of 4 mm. The high- (Figs. 1 C, D, and G and 2 I and L) and low- (Figs. 1B and 2 A and E) magnification SEM images were collected with an immersion mode and a low-angle secondary electron detector. Low-magnification SEM imaging was performed with a Tescan Vega GMU scanning electron microscope.

Cross-sectional imaging.

For structural analysis at two perpendicular orientations shown in Fig. 1 C–G, the precut elytron specimens were first mounted on a 45° pretilt SEM holder with conducting silver paste. For the plan-view cross-section (Fig. 1G), the vertical face of the 45° wedge was facing toward the incoming direction of the ion beam. The sample stage was first tilted by 7° so that the surface of the sample was parallel to the ion-beam direction. The sample was then milled with a Ga ion beam at an acceleration voltage of 30 kV and an emission current of 80 pA. After ion-beam milling, the stage was further tilted to 45° so that the milled surface was normal to the electron beam for SEM imaging. The images were collected under immersion mode at an acceleration voltage of 2 kV and a working distance of 4 mm. For the vertical cross-section (Fig. 1 C and D), the procedure was similar, except that the vertical face of the 45° wedge was facing toward the incoming direction of the ion beam.

Micropillar structural imaging.

The precut elytron specimens (∼2 mm in size) from five beetles with different colors were first placed at the bottom of an epoxy-embedding mold in the horizontal orientation with the photonic side facing downward. The premixed epoxy resin (Epo-Fix, Electron Microscopy Sciences) was then carefully poured into the mold and cured overnight at room temperature. After removing the embedding mold, the sample was polished along the horizontal direction on a polishing wheel (South Bay Technology, Model 920) with aluminum oxide pads stepwise (6, 3, and 1 μm) and, finally, with 50-nm silica nanoparticles on a microcloth (South Bay Technology). The polished sample was coated with ultra-thin carbon prior to SEM imaging on a Helios Nanolab 600 Dual Beam with an immersion mode (acceleration voltage, 2 kV; working distance, 4 mm). Quantitative image analysis of the pillar radius was conducted with ImageJ/Fiji software (50) with the analysis module BioVoxxel and customized MATLAB routines.

Cross-sectional imaging of indentation residue.

For cross-sectional structural analysis of the microindentation residue, specimens after microindentation tests were first coated with Pt/Pd with a thickness of 5 nm prior to imaging with the Helios Nanolab 600 Dual Beam electron microscope. The same system was used to produce the cross-sections of the microindentation residues through the following procedure: the indentation residue region was first coated in situ with a platinum protective layer (thickness, ∼2 μm). One side of the indentation residue was then milled away by focused ion beam (acceleration voltage, 30 kV; emission current, 1.2 nA), revealing the vertical cross-section of the residue (SI Appendix, Fig. S8). The cross-sectional plane was finally polished with low currents (92 pA) at the same acceleration voltage. The cross-sectional SEM images were tilted at a 52° stage angle and imaged with an acceleration voltage of 2 kV in immersion mode.

3D reconstruction of indentation residue.

3D reconstruction of the microindentation residue (SI Appendix, Fig. S7 C and D) was achieved by first taking stereo SEM image pairs with the sample stage tilted at 10° and −10° and then analyzing and rendering with the MountainsMap SEM imaging analysis software.

AFM.

The contact topography measurements were performed with a commercial atomic force microscope (XE7, Park Systems) using a contact mode. An AFM tip (Nanosensors, PPP-Contscr) was used for scanning. The AFM topographies were measured for three different magnifications (field of view) (i.e., 20 × 20 µm², 10 × 10 µm², and 5 × 5 µm²) with a scanning resolution of 512 × 512 pixels. The scan rate per line (512 pixels) was 0.5 Hz, which takes 1,024 s to generate each image. The image processing was performed through commercial software (XEI, Park Systems) to visualize the surface height variation.

Mechanical Characterization.

Microindentation.

Microindentation experiments with loads higher than 10 mN were carried out using a Micro Materials microindenter. The precut rectangular-shaped pieces of elytron samples were first placed on a steel plate and secured with super glue. For inclined microindentation experiments, the elytron samples were placed on a steel plate with an inclined surface (inclination angle, 15.7°). Both normal and inclined tests were carried out with a conospherical indentation tip with a tip radius of 5 μm and a half angle of 30°. The load functions include loading (30 s), holding (10 s), and unloading (30 s), and the maximum loads varied from 45 to 300 mN. The stage drift was calculated automatically when the load was unloaded to 10% of the maximum load and held for 40 s.

Nanoindentation.

Nanoindentation experiments were conducted in ambient conditions using a TriboIndenter (Hysitron, Inc.). The specimens (in vertical orientation) were first embedded in curing epoxy and then sectioned with a diamond saw (IsoMet 5000, Buehler), polished stepwise with aluminum oxide pads (Model 920, South Bay Technology; 15 µm, 5 µm, 3 µm, and 1 µm), and finely polished with 50-nm silica nanoparticles on cloth (MultiTex, South Bay Technology). Load-controlled nanoindentation was performed using a Berkvoich diamond probe tip. The piezoelectric transducer was first equilibrated for 105 s (the last 45 s with digital feedback) and another 40 s for calculating drift automatically prior to each indent. Typical load functions include loading (10 s), holding (20 s), and unloading (10 s), and the maximum load was 1 mN. The standard Oliver–Pharr (O-P) methodology was utilized to quantify material properties (i.e., indentation modulus [E_O-P] and hardness [H_O-P]). The area function A(h_c) of the probe tip (the projected area of the indentation tip as a function of the contact depth h_c) was calibrated before each set of experiments with a fused quartz sample.

AFM-based modulus mapping.

Quantitative nanomechanical mapping was carried out using the PeakForce QNM technique (Quantitative Nanomechanics) on a Bruker Dimension Icon AFM system. The AFM was operated in the PeakForce mode with an oscillation frequency of 1.5 kHz. The vertical motion of the cantilever was controlled by the Z piezo element and relied on the peak force that was preset for feedback. The individual force–depth curves during each tapping cycle were generated and recorded, from which the nanoscale property of the material was determined. The typical oscillation frequency was 2 kHz. The used AFM tip (PDNISP-HS, Bruker) was a nanoindentation tip with a spring constant of 385.0 N/m, tip radius of 26.7 nm (calibrated with a gold calibration sample), and a half-angle of 51°. The deflection sensitivity of the tip was first calibrated by indenting a sapphire surface. Five measurements were carried out, and the average deflection sensitivity was calculated and used for subsequent measurements.

Optical Characterization.

Reflectance measurement.

Spectra and images from samples of the beetle cuticle with varying collection-cone angle were acquired with a modified Olympus BX51 imaging platform that was equipped with a secondary imaging port. This port was used to project light from the specimen into an optical fiber (Ocean Optics), which transmitted the reflected light to a Maya Pro spectrometer (Ocean Optics). The fiber diameter and the microscope objective lens determine the diameter of the area from which light is collected. While a smaller fiber diameter allows the collection of light from a smaller sample area, it also results in less light collection, resulting in a decreased signal-to-noise ratio. The objective, in turn, determines the area of light collection and also defines the width of the illumination cone within which light is incident on the sample and, likewise, the width of the cone of reflected light that is captured for spectroscopy. This is of relevance for photonic architectures that filter light not only spectrally but also control its angular distribution. For the measurements reported in SI Appendix, Fig. S25, we used a 100-µm–wide optical fiber and varied the objective numerical aperture between 0.15 (5× magnification), 0.3 (10×), 0.45 (20×), and 0.75 (50×) using objective lenses from Olympus’ MPLFLN objective series. In other words, the collection-cone apex angle was varied from 18° to 97° with increasing objective numerical aperture and magnification. For each objective, a new reference spectrum was taken from a silver mirror to account for the intensity and spectrum transmitted by the objective from the halogen lamp to the sample.

Diffraction spectrum measurement.

Visualization of the spatial distribution of light scattered to the far field from the beetles’ elytra was achieved using imaging scatterometry (42), the principal component of which is an ellipsoidal mirror. Samples featuring small elytral regions were mounted onto tips of micropipettes, which were then positioned in the mirror’s first focal plane. Forward scattering of light by the sample was focused by the ellipsoidal mirror into its second focal plane and projected by a lens onto its back focal plane. This compressed the far-field scattering pattern into an image that could be captured by charge-coupled devices. SI Appendix, Fig. S26 shows scattergrams for red and green T. flammea specimens showing far-field scattering patterns arising from narrow-beam illumination with decreasing incident spot sizes. Custom-written MATLAB (https://www.mathworks.com/) programs were used to correct each scattergram for geometric aberration. A commercial MgO substrate served as a white standard.

Computational Methods.

Multilayer stack spacing and orientation.

The overall deformation fields for the different indentation directions were visualized by layer spacing maps (SI Appendix, Fig. S3) and angular deviation maps (SI Appendix, Fig. S4). To quantify the local spacing and orientation angle at every pixel position of the SEM images, two-dimensional fast Fourier transform (2D-FFT) was performed using a custom code (MATLAB, MathWorks) on a square sampling area around the pixel position, and a color value corresponding to the calculated spacing or angle was assigned to the pixel. 2D-FFT noises from the irregularity of the local structures were suppressed by averaging the 2D-FFT results from eight different sizes of the sampling area. Generated color-coded maps were then overlaid on the original SEM images (Photoshop, Adobe).

Micropillar distribution.

SEM images of the horizontal cross-sections were first converted to binary images (SI Appendix, Fig. S16) for statistical analysis of the pillar distance. Based on the binary images, the approximately circular-shaped micropillars were identified and fitted to circular disks, defined by two parameters—the radius and the center position of the circular disk. The pillar distances were evaluated based on the center positions of the disks, and three distances, the nearest pillar distance, the adjacent pillar distance, and the average of all pillar distances, were calculated (SI Appendix, Fig. S19). These three definitions were used to characterize the nearest, local, and long-range characteristics of the pillar distance, respectively. Specifically, for the nearest pillar distance ($l_{nearest}^{avg}=\frac{{{\displaystyle \sum }}_1^N{l}_{nearest}^i}{N}$), the distances of each pillar to its nearest neighbor (each pillar has one nearest neighbor) were calculated and averaged. For the adjacent pillar distance ($l_{adj}^{avg}=\frac{{{\displaystyle \sum }}_1^N{\overline{l}}_{adj}^i}{N}$, ${\overline{l}}_{adj}^i$ = $\frac{{{\displaystyle \sum }}_1^n{l}_{adj}^i}{n}$), the average distance of each pillar to its adjacent neighbors was calculated and averaged. The adjacent neighbors of each pillar were determined by a Voronoi cell-division algorithm. The average of all pillar distances in the region of interest ($l_{all}^{avg}=\frac{{{\displaystyle \sum }}_1^M{l}^i}{M}$) was calculated as the average of all center-to-center distances between adjacent micropillars (determined based on the Voronoi method). Following these definitions, the distance analysis was performed for beetles of five different colors on circular areas of diameters of 19 and 9 μm. Here, the calculations based on five smaller circular areas were conducted to compare the variation of the characteristic distances in multiple regions. The results are summarized in SI Appendix, Figs. S20–S24. The nearest distance, $l_{nearest}^{avg}$, measures the averaged smallest distance, which is smaller than $l_{adj}^{avg}$ and $l_{all}^{avg}$. Note that the difference between $l_{adj}^{avg}$ and $l_{all}^{avg}$ for a specific area was within 1%. The average adjacent pillar distance $l_{adj}^{avg}$ was used in the modeling (SI Appendix, Fig. S19C).

FE simulation.

The photonic structure was modeled as a two-phase composite (SI Appendix, Fig. S9), which consisted of a horizontal multilayer structure reinforced by vertical micropillars. The multilayer was a bilayer stack that consisted of alternating hard and soft layers. The micropillars and the hard layers in the multilayer were the hard phase, which had a Young’s modulus of 11.0 GPa and a yield strength of 0.84 GPa. The soft layers of the multilayer structure were composed of the soft phase, which had a Young’s modulus of 8.8 GPa and a yield strength of 0.46 GPa. Here, the material properties of the two components were chosen based on the AFM-based indentation and quantitative nanomechanical mapping results. Note that the relative values between the two components are more important than the absolute values for the FE simulation. The simulation was performed using Abaqus/Standard with the general statics module, and plastic deformation was included in the model. The 2D structural models were constructed based on microscopic characterization. The thicknesses of the soft and hard layers in the multilayer stack were 80 and 140 nm, respectively. The diameter and spacing of the vertical micropillars were 750 and 1,300 nm, respectively. The indentation tip was modeled as an ideal conospherical tip with a radius of 5 µm and a half-angle of 30°. Both normal and inclined indentations were simulated under displacement-controlled conditions. For comparison, simulations were also conducted on a homogeneous material purely made of the stiff phase as well as a multilayer structure without micropillars.

Data Availability

All study data are included in the article and/or SI Appendix.