Estimating genetic nurture with summary statistics of multigenerational genome-wide association studies

Yuchang Wu; Xiaoyuan Zhong; Yunong Lin; Zijie Zhao; Jiawen Chen; Boyan Zheng; James J Li; Jason M Fletcher; Qiongshi Lu

doi:10.1073/pnas.2023184118

. 2021 Jun 15;118(25):e2023184118. doi: 10.1073/pnas.2023184118

Estimating genetic nurture with summary statistics of multigenerational genome-wide association studies

Yuchang Wu ^a,^b, Xiaoyuan Zhong ^a, Yunong Lin ^a,^c, Zijie Zhao ^a, Jiawen Chen ^c,^d, Boyan Zheng ^b,^e, James J Li ^b,^f,^g, Jason M Fletcher ^b,^e,^h, Qiongshi Lu ^a,^b,^c,¹

PMCID: PMC8237646 PMID: 34131076

Significance

It has been shown that human genomes can affect phenotype both directly (through inherited genetic variants) and indirectly (through parents and the family environment they create). Due to the correlation between parental and offspring genotypes, a standard genome-wide association study (GWAS) captures both the direct and indirect genetic effects. In this study, we introduce a statistical framework named DONUTS to estimate direct and indirect effects using summary statistics from GWAS conducted on own and offspring phenotypes. It requires only GWAS summary statistics as input, allows differential paternal and maternal effects, and accounts for sample overlap and assortative mating. DONUTS provides deeper etiological insights for complex traits and has practical guidance on future study designs.

Keywords: genetic nurture, indirect genetic effect, family-based study, GWAS, summary statistics

Abstract

Marginal effect estimates in genome-wide association studies (GWAS) are mixtures of direct and indirect genetic effects. Existing methods to dissect these effects require family-based, individual-level genetic, and phenotypic data with large samples, which is difficult to obtain in practice. Here, we propose a statistical framework to estimate direct and indirect genetic effects using summary statistics from GWAS conducted on own and offspring phenotypes. Applied to birth weight, our method showed nearly identical results with those obtained using individual-level data. We also decomposed direct and indirect genetic effects of educational attainment (EA), which showed distinct patterns of genetic correlations with 45 complex traits. The known genetic correlations between EA and higher height, lower body mass index, less-active smoking behavior, and better health outcomes were mostly explained by the indirect genetic component of EA. In contrast, the consistently identified genetic correlation of autism spectrum disorder (ASD) with higher EA resides in the direct genetic component. A polygenic transmission disequilibrium test showed a significant overtransmission of the direct component of EA from healthy parents to ASD probands. Taken together, we demonstrate that traditional GWAS approaches, in conjunction with offspring phenotypic data collection in existing cohorts, could greatly benefit studies on genetic nurture and shed important light on the interpretation of genetic associations for human complex traits.

Genome-wide association studies (GWAS) have been a great success in the past decade, identifying tens of thousands of associations for numerous complex human traits (1). The standard GWAS approach estimates the marginal association between each single-nucleotide polymorphism (SNP) and a phenotype while assuming that genetic and environmental factors additively affect the phenotype. Despite the simplicity, such an analytical strategy is computationally efficient and statistically robust. However, interpretation of GWAS associations remains a challenge, in part because most identified associations have weak effect sizes and are located in the noncoding regions of the genome (2, 3). Interpretation is especially challenging for behavioral traits since the role of each variant or gene in complex human behavior is difficult to disentangle. Nevertheless, biobank-scale GWAS of complex traits have produced polygenic scores (PGS) that aggregate the effects of many SNPs in the genome to provide robust prediction of trait values (4). These scores are widely used in social genomics research, although our understanding of the underlying mechanism is superficial and incomplete (5).

Recent evidence from family-based studies suggested that a substantial fraction of genetic associations may be mediated by the family environment (6–16). In particular, parental genotypes could affect the family environment through the parents’ educational attainment (EA) (17), personalities (18, 19), behavior (20–24), and socioeconomic status (25), which could subsequently affect the offspring’s phenotypes (26). As a result, a person’s genotypes, which also reside in his or her biological parents, could associate with the person’s phenotype both directly (through inherited genetic variants) and indirectly (through parents and the family environment they create). Due to the correlation between parental and offspring genotypes, GWAS captures both the direct and indirect genetic effects in its estimates, which further complicates the interpretation of GWAS results (13). If the genetic nurture effect (i.e., parental genotypes affecting offspring phenotype) is present for a given trait, downstream analyses based on GWAS associations could be biased and misleading (6, 8, 27).

It is thus crucial to decompose the direct and indirect genetic effects and understand how they jointly affect the phenotype. By leveraging large-scale trio cohorts and regressing the offspring phenotype on two sets of PGS calculated using transmitted and nontransmitted alleles in parents, Kong et al. (6) convincingly demonstrated the existence of genetic nurture effects for multiple traits. In particular, PGS of nontransmitted alleles in parents has an effect size that is about 30% of that by the standard PGS for EA. Using PGS, several other studies (7–12) also identified indirect genetic effects on various phenotypes. Existing methods to detect direct and indirect genetic effects, however, have limitations. First, they require individual-level genotype and phenotype data of a large number of parents–offspring trios or, in some cases, other types of rare samples [e.g., adopted individuals (11, 12)]. Although sample size in GWAS has been steadily increasing, number of trio samples with accessible individual-level data remains moderate even in large biobanks. Second, existing methods quantify genetic nurture using PGS which relies on large GWAS conducted on samples independent from the study. Even when such a GWAS exists, it remains challenging to interrogate the direct and indirect effects of each SNP using designs and data similar to the current GWAS practice, which is critical for functional follow-ups and out-of-sample prediction (13).

Although a simple study design that regresses the phenotypes on both own and parental genotypes should provide estimates for direct and indirect genetic effects of each SNP, such a strategy is most likely underpowered given the limited sample size of trios in existing cohorts. Several recent studies have attempted to solve this challenging problem. Warrington et al. (28) used a structural equation model (SEM) approach to decompose direct genetic effects and indirect maternal effects on birth weight while assuming paternal effects to be 0. This approach only requires summary statistics from a standard GWAS on birth weight and a second GWAS based on maternal genotypes and offspring phenotypes, thus effectively expanding the available sample size. However, the SEM approach was too computationally demanding to be applied to the genome-wide scale, and a “weighted linear model” alternative could not account for sample overlap if individual-level data are unavailable. Another recent approach (14, 15) expands family genotype data by imputing the unobserved parental genotypes using data from other family members. However, this approach still requires a large sample of sibling or parent–offspring pairs. Further, when parental genotypes are imputed from sibling pairs, it is challenging to distinguish paternal and maternal autosomal genotypes. Thus, separate estimation of indirect maternal and paternal effects is unattainable.

Here, we introduce DONUTS (decomposing nature and nurture using GWAS summary statistics), a statistical framework that can estimate direct and indirect genetic effects at the SNP level. It requires GWAS summary statistics as input, allows differential paternal and maternal effects, and accounts for GWAS sample overlap and assortative mating. DONUTS has low computational burden and can complete genome-wide analyses within seconds. Applied to birth weight, our method showed near-identical effect estimates compared to analyses (28) that leveraged individual-level data and improved SE and statistical power after accounting for sample overlap. We also applied our method to dissect the direct and indirect genetic effects of EA. Our results revealed distinct genetic correlations of the direct and indirect genetic components of EA with various traits and shed important light on the complex and heterogenous genetic architecture of EA. Followed up in three independent cohorts of autism spectrum disorder (ASD) proband–parent trios, we identified significant overtransmission of the direct component of EA from healthy parents to ASD probands but not to the healthy siblings.

Results

Method Overview.

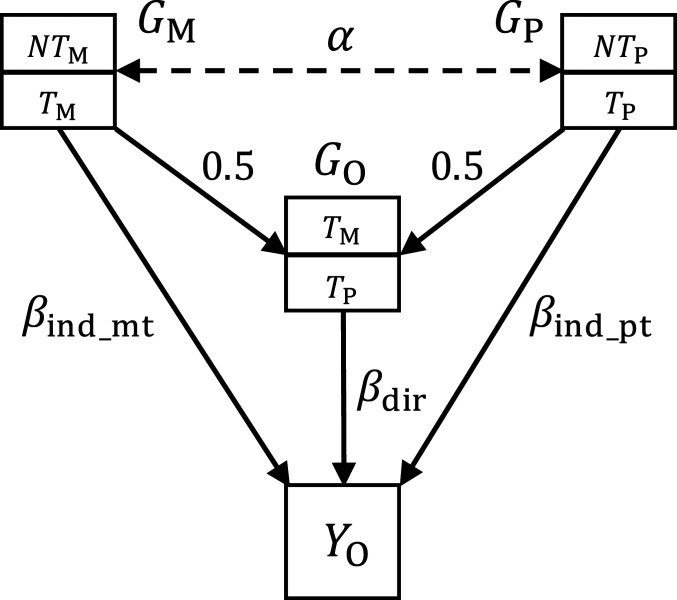
The key idea of our statistical framework is illustrated in Fig. 1. Derivations and statistical details are shown in Methods and SI Appendix. If genetic data are available in a number of parents–offspring trios, by regressing the offspring phenotype values $Y_{O}$ on the offspring, maternal, and paternal genotypes (i.e., $G_{O}$ , $G_{M}$ , and $G_{P}$ ) for a given SNP, the coefficients in the joint regression represent the direct genetic effect $β_{d i r}$ , indirect maternal effect $β_{i n d_m t}$ , and paternal effect $β_{i n d_p t}$ , respectively. We could write the true genetic model as

Y_{O} = β_{d i r} G_{O} + β_{i n d_m t} G_{M} + β_{i n d_p t} G_{P} + ϵ,

[1]

where $ϵ$ is the environmental noise. The total contribution of parental genotypes on offspring phenotype, $(β_{i n d_m t} G_{M} + β_{i n d_p t} G_{P})$ , can be further partitioned into the contribution of transmitted alleles $(β_{i n d_m t} T_{M} + β_{i n d_p t} T_{P})$ and nontransmitted alleles $(β_{i n d_m t} N T_{M} + β_{i n d_p t} N T_{P})$ . In our framework, we define the indirect genetic effect $β_{i n d}$ as the effect of a person’s genotype on the phenotype via the indirect pathway that goes through biological parents and the family environment. The component of parental indirect contribution that can be affected by $G_{O}$ is $(β_{i n d_m t} T_{M} + β_{i n d_p t} T_{P})$ . Regressing it on $G_{O}$ , we find that the indirect genetic effect $β_{i n d} = (β_{i n d_m t} + β_{i n d_p t}) / 2$ . Unsurprisingly, the indirect effect size is the average of the indirect maternal and paternal effects since each parent contributes half of the offspring’s genotype. A key question we aim to investigate in this paper is whether it is possible to estimate the direct and indirect effect sizes (i.e., $β_{d i r}$ , $β_{i n d}$ , $β_{i n d_m t}$ , and $β_{i n d_p t}$ ) from marginal GWAS association statistics via proper study designs.

Fig. 1. — Schematic diagram of direct and indirect genetic effects. $G_{M}, G_{P}, G_{O}$ represents the maternal, paternal, and offspring genotypes, respectively. $α = Corr (G_{M}, G_{P})$ is the correlation between spousal genotypes at a locus. Effect size 0.5 is due to the fact that half of the parent’s genome is randomly transmitted to the offspring $G_{O}$ . $Y_{O}$ is the offspring’s phenotype. $T$ and $N T$ represent transmitted and nontransmitted alleles from a parent to the offspring. In general, both offspring and parental genotypes could affect the offspring’s phenotype with effect sizes of $β_{d i r}, β_{i n d_m t,}$ and $β_{i n d_p t}$ , respectively.

Instead of focusing on a joint regression based on trio data, we describe three separate GWASs. We refer to the marginal regressions of own phenotype $Y_{O}$ on own genotype $G_{O}$ as GWAS-O. GWAS-M and GWAS-P denote the marginal analyses that regress offspring phenotype on maternal genotype $G_{M}$ and paternal genotype $G_{P}$ , respectively. $β_{O}$ , $β_{M}$ , and $β_{P}$ denote the expectation of marginal effect estimates obtained from these three analyses, respectively. It can be shown that $β_{d i r}$ and $β_{i n d}$ of a given SNP are linear combinations of $β_{O}$ , $β_{M}$ , and $β_{P}$ (Methods and SI Appendix):

β_{d i r} = (2 + α) β_{O} - β_{M} - β_{P},

[2]

β_{i n d} = \frac{2 + α}{2 + 2 α} [β_{M} + β_{P} - (1 + α) β_{O}],

[3]

where $α = Corr (G_{M}, G_{P})$ is the correlation between spousal genotypes at the locus, which quantifies the degree of assortative mating. Plugging in the ordinary least square estimates ${\hat{β}}_{O}$ , ${\hat{β}}_{M}$ , and ${\hat{β}}_{P}$ from the three marginal GWASs described above, we obtain the unbiased estimates for the direct and indirect effects of each SNP. Importantly, we do not require $G_{O}, G_{M},$ and $G_{P}$ to be obtained from actual trios. In fact, samples in the three GWAS could be independent or partially overlapped. From the Eqs. 2 and 3, we also found that

β_{d i r} + (1 + \frac{α}{2 + α}) β_{i n d} = β_{O},

[4]

which clearly shows that the effect size from a typical GWAS is the combination of both direct and indirect effects and is also affected by assortative mating (13).

Besides direct and indirect effects (i.e., $β_{d i r}$ and $β_{i n d}$ ), we could also derive the expressions for indirect maternal and indirect paternal effects (i.e., $β_{i n d_m t}$ and $β_{i n d_p t}$ ), which makes it possible to infer the parent-of-origin of genetic nurture. The results are summarized in Table 1. Case i is the most general scenario, in which we use summary statistics from GWAS-O, GWAS-M, and GWAS-P to estimate $β_{d i r}$ , $β_{i n d}$ , $β_{i n d_m t}$ , and $β_{i n d_p t}$ . Case ii illustrates that it is not always necessary to have separate paternal and maternal GWASs. If paternal and maternal effects are identical $(β_{i n d_m t} = β_{i n t_p t})$ or if there are equal numbers of mothers and fathers $(n_{M} = n_{P})$ in a parental GWAS (referred to as GWAS-MP in which fathers and mothers from different families are pooled together in the GWAS), the corresponding effect size $β_{M P} = (n_{M} β_{M} + n_{P} β_{P}) / (n_{M} + n_{P})$ can be used to estimate $β_{d i r}$ and $β_{i n d}$ . Case iii illustrates a special case in which only maternal genotype has an indirect effect while the indirect paternal effect is zero (SI Appendix, Fig. S1A). If we further assume random mating $(α = 0)$ , then our model gives identical estimates for direct effect, $β_{d i r}$ , and maternal effect, $β_{i n d_m t}$ ,compared to previous work on birth weight (28). The results for the case with only indirect paternal effects are similar.

Table 1.

Estimating direct and indirect genetic effects from multigenerational GWAS summary statistics

Input GWAS	$β_{d i r}$	$β_{i n d} = (β_{i n d_m t} + β_{i n d_p t}) / 2$	$β_{i n d_m t}$ and $β_{i n d_p t}$
(i) GWAS-O, GWAS-M, and GWAS-P	$(2 + α) β_{O} - β_{M} - β_{P}$	$\frac{2 + α}{2 + 2 α} [β_{M} + β_{P} - (1 + α) β_{O}]$	$β_{i n d_m t} = \frac{3 - α^{2}}{2 (1 - α^{2})} β_{M} + \frac{1 - 2 α - α^{2}}{2 (1 - α^{2})} β_{P} - \frac{2 + α}{2} β_{O} β_{i n d_p t} = \frac{3 - α^{2}}{2 (1 - α^{2})} β_{P} + \frac{1 - 2 α - α^{2}}{2 (1 - α^{2})} β_{M} - \frac{2 + α}{2} β_{O}$
(ii) GWAS-O and GWAS-MP (when parents contribute equally $β_{i n d_m t} = β_{i n d_p t}$ or have equal sample size $n_{M} = n_{P}$ in GWAS-MP)	$(2 + α) β_{O} - 2 β_{M P}$	$\frac{2 + α}{2 + 2 α} [2 β_{M P} - (1 + α) β_{O}]$	$β_{i n d_m t} = β_{i n d_p t} = β_{i n d}$ (when $β_{i n d_m t} = β_{i n d_p t}$ )
(iii) GWAS-O and GWAS-M (when only the maternal effect contributes, [i.e., $β_{i n d_p t} = 0$ ])	$\frac{2}{3 - α^{2}} [(2 + α) β_{O} - (1 + α) β_{M}]$	$\frac{2 + α}{3 - α^{2}} (β_{M} - \frac{1 + α}{2} β_{O})$	$β_{i n d_m t} = \frac{2 + α}{3 - α^{2}} [2 β_{M} - (1 + α) β_{O}]$

Open in a new tab

We illustrate the direct and indirect effect sizes under three different settings. Case i is the general case in which GWAS-O, GWAS-M, and GWAS-P are used as input. In case ii, GWAS-O and GWAS-MP are used. This is valid only when $β_{i n d_m t} = β_{i n d_p t}$ or $n_{M} = n_{P}$ . If we only know $n_{M} = n_{P}$ , we cannot obtain separate estimates for the indirect maternal and paternal effects. Case iii is when the indirect paternal effect size is 0. $β_{O}, β_{M}, β_{P}, and β_{M P}$ are the expected effect sizes in GWAS-O, GWAS-M, GWAS-P, and GWAS-MP, respectively. In all the cases, we always have $β_{d i r} + [1 + α / (2 + α)] β_{i n d} = β_{O}$ and $β_{i n d} = (β_{i n d_m t} + β_{i n d_p t}) / 2$ .

Calculations of the variances of estimated direct and indirect effects are straightforward when the input GWASs are independent. However, it is possible for a subset of individuals to be involved in both the GWAS of their own phenotype and the GWAS of their children’s phenotype (SI Appendix, Fig. S1B), which causes technical correlations among ${\hat{β}}_{O}$ , ${\hat{β}}_{M}$ , and ${\hat{β}}_{P}$ . We show that the correlations can be estimated using the intercept term from linkage disequilibrium score (LDSC) regression (29) (SI Appendix), thereby correcting the sample overlap bias in SE estimates.

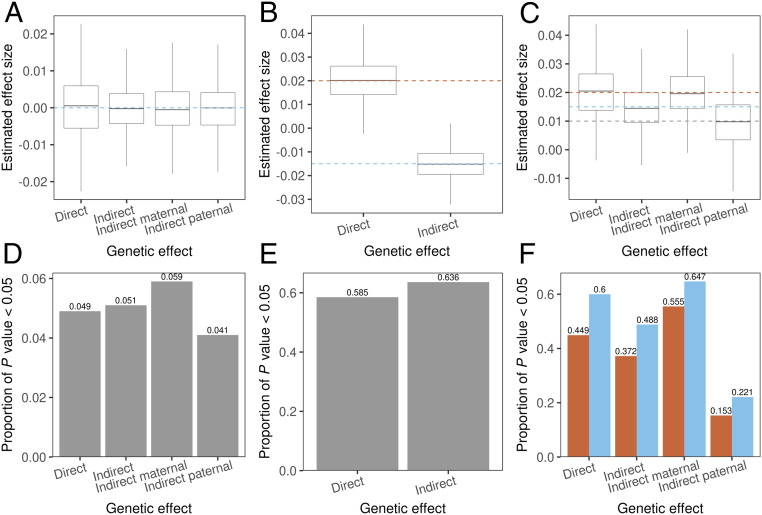
Simulation Results.

We performed extensive simulations to demonstrate that our method provides unbiased estimates for direct and indirect effects, shows well-controlled type-I error, and properly accounts for sample overlap (Methods and SI Appendix, Fig. S2). The results are summarized in Fig. 2 and SI Appendix, Figs. S3–S5. Fig. 2 A and C describe results for case i in Table 1 in which three sets of GWAS summary statistics are used. The estimates for direct, indirect, indirect maternal, and indirect paternal effect sizes were all unbiased. When only GWAS-O and GWAS-MP are available (case ii in Table 1), we could not distinguish indirect maternal and paternal effects but could still estimate the indirect genetic effect (Fig. 2B). Here, despite the difference between indirect maternal and paternal effect sizes, estimation of the indirect genetic effects remained unbiased when equal number of fathers and mothers were used in GWAS-MP.

Fig. 2. — Simulation results. Box plots of direct and indirect effect size estimates (A–C) and the proportion (numbers shown at the top of each bar) of P values smaller than 0.05 (D–F) from 1,000 repeats. Each column shows results for the same simulation setting. Red and blue dashed lines indicate true values of direct and indirect genetic effects, and gray dashed lines are the true indirect maternal and indirect paternal effect sizes. The direct, indirect maternal, and indirect paternal effect sizes are (0, 0, 0), (0.02, −0.02, −0.01), and (0.02, 0.02, 0.01) for *A–C*, respectively. A and C describe results for case i in Table 1 in which three input GWAS are used. B describes case ii in which GWAS-O and GWAS-MP are used as input. There are no sample overlaps in A and B and a complete overlap in C (i.e., all samples in GWAS-M and GWAS-P are also in GWAS-O). In F, blue and red bars show the statistical power with and without sample overlap correction, respectively. $n_{O} = n_{M} = n_{P} = 30 K$ in A and B. $n_{O} = n_{M} + n_{P} = 60 K, n_{M} = n_{P} = 30 K$ in C.

Sample overlap in input GWASs will not affect effect size estimation. However, it will affect their SEs due to the introduced correlations among ${\hat{β}}_{O}$ , ${\hat{β}}_{M}$ , and ${\hat{β}}_{P}$ . In Fig. 2 C and F, there were overlapping samples between GWAS-O and parental GWAS. Since the phenotypic correlation among the overlapping samples (i.e., correlation between parental and offspring phenotypes) would most likely be positive, the covariance between effect size estimates is positive. As a result, correcting for sample overlap reduces SE and increases power. Simulations under diverse settings all showed consistent results (SI Appendix, Figs. S3–S5).

Direct and Maternal Effects on Birth Weight.

To assess the performance of our framework, we applied DONUTS to dissect the direct genetic effect and indirect maternal genetic effect on birth weight. Following a previous study by Warrington et al. (28), we assumed random mating and absent indirect paternal effect on offspring birth weight, which reduces the problem to a special case in our framework (case iii in Table 1 and SI Appendix, Fig. S1A). Using summary statistics from GWAS-O and GWAS-M (n = 298,142 and 210,267, respectively; Methods), we estimated the direct and indirect maternal effects of each SNP. Both estimates were highly concordant with previous reports (Pearson correlations = 0.976 and 0.982, respectively; SI Appendix, Fig. S6). The genetic correlations among these effects were very close to those reported in previous work (Datasets S1 and S2).

Of note, Warrington et al.’s results were based on a meta-analysis of UK Biobank (UKB) (30) and many other smaller cohorts. UKB was a main cohort used in both GWAS-O and GWAS-M of birth weight, which caused a substantial sample overlap. Warrington et al. (28) addressed sample overlap within UKB by creating two linearly transformed, orthogonal phenotypes for each individual who reported both her own birth weight and her first child’s birth weight. GWAS were then performed on the two phenotypes. This approach requires individual-level genotype and phenotype data to identify the overlapping samples and perform phenotype transformations, which is not easily applicable to other studies where only summary statistics are available. In fact, their post hoc analysis (28) found that there were about several thousand overlapping samples between UKB and other cohorts used in the meta-analysis. These overlapping samples were not accounted for in their analysis since it was difficult to identify the exact samples that were shared across cohorts. Therefore, compared with our results, the SEs given by the paper showed a mild inflation (SI Appendix, Fig. S6).

To further demonstrate that our method could effectively account for sample overlap, we conducted GWAS-O and GWAS-M using 75,711 independent female samples of European ancestry in the UKB who reported birth weights of themselves and of their oldest child (Methods). Using these two sets of summary statistics with a complete sample overlap, we estimated the direct and indirect maternal effects of each SNP. For comparison (Fig. 3), we followed Warrington et al. (28) to run two separate GWAS on the orthogonal phenotypes representing the direct and maternal components of birth weight constructed using individual-level data. Results from these two approaches were nearly identical (Pearson correlation = 1.00 for both the direct and indirect effect estimates). Not properly accounting for sample overlap did not affect the effect size estimates but substantially inflated SEs which led to reduced statistical power (Fig. 3). In addition, removing genetic principal components (PCs) from the regression and performing GWAS using a linear mixed model (Methods) both obtained highly consistent results for direct and indirect maternal effects (Dataset S3 and SI Appendix, Figs. S7 and S8), showcasing robustness of these results to population stratification.

Fig. 3. — Comparison of DONUTS and analyses based on individual-level data. We estimated direct and indirect maternal genetic effects on birth weight using independent female samples of European ancestry in the UKB who reported both their own birth weight and their first child’s birth weight (n = 75,711). The x-axis of each panel shows results based on DONUTS, and the y-axis shows results based on the phenotype transformation approach. Each data point represents an SNP. A total of 7,080,935 imputed SNPs were included in the analysis. The first row is for the direct genetic effect, and the second row is for the indirect maternal effect. Two methods gave almost identical estimates for effect sizes (first column) and SEs (second column). The SEs showed inflation if sample overlap was not accounted for (third column). The diagonal line is highlighted in each panel.

Partitioning Direct and Indirect Genetic Effects on EA.

Next, we conducted a GWAS on offspring EA using a total of 15,277 individuals from the UKB, Wisconsin Longitudinal Study (WLS), and Health and Retirement Study (HRS) while adjusting for year of birth, sex, PCs, and cohort-specific covariates (Methods). Due to the limited sample size, balanced sex ratio, and previous reports on comparable maternal and paternal effects on EA (6), we pooled fathers and mothers together to perform a parental GWAS (i.e., GWAS-MP). Combining results in GWAS-MP with a meta-analyzed GWAS-O that does not contain full sibling pairs in the UKB (n = 680,881), we estimated the direct and indirect effects on EA. Further, we applied software SNIPar (15) (https://github.com/AlexTISYoung/SNIPar) to impute the parental genotypes of full sibling pairs in the UKB and estimated direct and indirect effects with linear mixed models (Methods). We meta-analyzed two sets of analyses to obtain the final partitioned direct and indirect genetic effects on EA (effective n = 24,434 and 37,081 for direct and indirect effects, respectively). The flowchart of the analysis is illustrated in SI Appendix, Fig. S9. No loci reached genome-wide significance at the current sample size (SI Appendix, Fig. S10). We assumed random mating in the main analysis, but the results were highly robust to assortative mating (SI Appendix, Fig. S11).

We estimated genetic correlations of the direct and indirect EA effects with 45 other complex traits using LDSC (Fig. 4 and Datasets S4–S7). As a comparison, an alternative approach [i.e., software GNOVA (31)] also showed consistent results (SI Appendix, Fig. S12 and Dataset S8). At a false discovery rate cutoff of 0.05, we identified 18 significant genetic correlations, 4 of which were with the direct effect and 14 were with the indirect effect, which highlighted the substantial contribution of genetic nurture on the etiologic sharing among complex traits. We also estimated genetic correlations based on a standard EA GWAS (i.e., GWAS-O; SI Appendix, Fig. S13).

Three traits (i.e., cognitive performance [ $P = 1.53 \times 10^{- 7}$ and $2.51 \times 10^{- 6}$ ], age at first birth [ $P = 1.02 \times 10^{- 5}$ and $3.64 \times 10^{- 5}$ ], and smoking cessation [ $P = 3.97 \times 10^{- 3}$ and $3.05 \times 10^{- 3}$ ]) were significantly correlated with both direct and indirect components of EA. Across four traits for smoking behavior, we observed a consistent pattern that higher EA, especially its indirect component, was correlated with reduced smoking activity. Among neurological traits, attention-deficit/hyperactivity disorder ( $P = 1.77 \times 10^{- 3}$ ), major depressive disorder ( $P = 2.27 \times 10^{- 3}$ ), and neuroticism ( $P = 3.87 \times 10^{- 3}$ ) showed significant negative correlations with the indirect EA effect, while ASD ( $P = 3.91 \times 10^{- 3}$ ) was positively correlated with the direct effect. Notably, several diseases and anthropometric traits known to genetically correlate with EA (e.g., rheumatoid arthritis $[P = 2.23 \times 10^{- 3}]$ , height $[P = 2.77 \times 10^{- 4}]$ , and body mass index [BMI; $P = 1.85 \times 10^{- 5}$ ]) were only correlated with the indirect component of EA in our analysis. Such a pattern was also observed for type-2 diabetes, coronary artery disease, and various lipid traits despite not reaching statistical significance.

Next, we assessed the predictive performance of PGS of direct and indirect effects on EA. We generated bioinformatically fine-tuned PGS (32) for direct and indirect components of EA using UKB participants (Methods and Dataset S10). Overlapping UKB samples were removed from the input GWAS when necessary (Methods). SI Appendix, Fig. S14 shows the predictive performance on 15,580 full sibling pairs and 370,308 independent UKB samples. Both direct and indirect PGS were significantly associated with EA in independent samples ( $P = 4.63 \times 10^{- 8}$ and $1.46 \times 10^{- 9}$ ) with similar effect sizes (regression coefficient = $8.7 \times 10^{- 3}$ and $9.6 \times 10^{- 3}$ ). Direct-effect PGS was positively associated with the EA in full sibling pairs with an effect size comparable to that in the population (regression coefficient = 0.013). The indirect PGS was negatively correlated with EA in full siblings. However, due to a limited sample size, neither direct nor indirect PGS reached statistical significance in sibling pairs (P = 0.16 and 0.52). The effect sizes of these PGS were also substantially weaker compared to the standard EA PGS based on population GWAS (17).

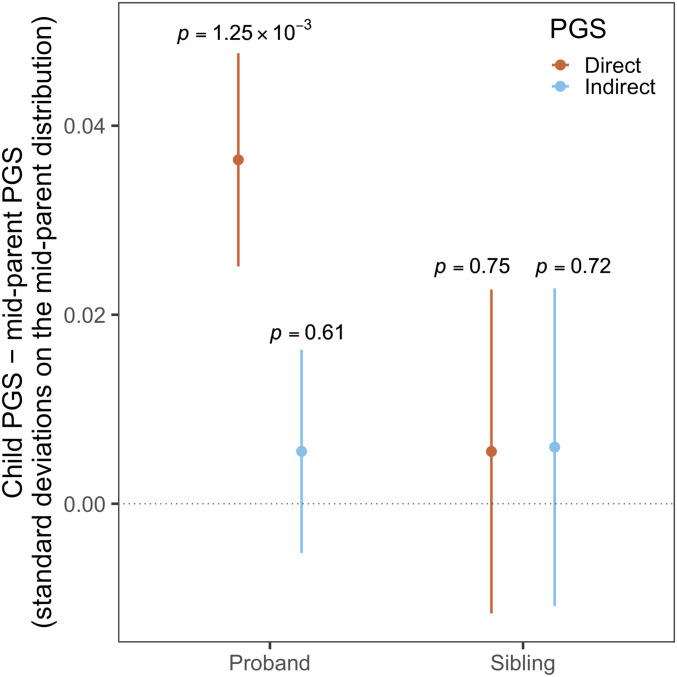
We found that the somewhat surprising yet consistently replicated genetic correlation between ASD and higher EA (33, 34) is mainly driven by the direct genetic component of EA (Fig. 4). We followed up this finding in 7,804 ASD proband–parent trios from three cohorts (Methods), including the Autism Genome Project (AGP), Simons Simplex Collection (SSC), and Simons Foundation Powering Autism Research for Knowledge (SPARK). We performed polygenic transmission disequilibrium test (35) (pTDT) to quantify the deviation of ASD probands’ EA PGS from the parents’ PGS (Methods). We identified a significant $(P = 1.25 \times 10^{- 3})$ overtransmission of the direct-effect EA PGS from healthy parents to ASD probands (Fig. 5 and Dataset S11). We did not identify a significant overtransmission of the indirect EA PGS $(P = 0.61)$ . Neither PGS showed any significant deviation from transmission equilibrium in healthy sibling controls.

Fig. 5. — pTDT results for direct and indirect EA PGS in 7,804 ASD probands and 3,242 healthy siblings. Dots are the mean difference between child PGS and midparent PGS and intervals indicate the SE.

Discussion

GWAS has identified more than 60,000 genetic associations for thousands of human diseases and traits, yet our understanding toward their etiology remains incomplete (36). Recent advances in family-based studies (6–9, 14, 15, 28, 37) have convincingly demonstrated genetic nurture effects on a variety of behavioral traits as well as health-related outcomes. These results also shed important light on the limitations of current GWAS approaches. Accurate dissection of direct and indirect genetic effects is critical for advancing the interpretation of genetic associations and may fundamentally change the current practice of genetic prediction and its clinical applications.

In this paper, we introduced a statistical framework that uses summary statistics from multigenerational GWAS to decompose the direct and indirect genetic effects for a given trait. Compared to existing methods, our approach does not require access to individual-level data, has minimal computational burden, and accounts for GWAS sample overlap and assortative mating. In addition, when results from GWAS-M and GWAS-P are available, our method can partition the contribution of maternal and paternal genetic effects, thereby inferring the parent-of-origin of genetic nurture. Even when only a combined parental GWAS (i.e., GWAS-MP) is available, statistical inference of direct and indirect effects remain valid under weak assumptions. Importantly, due to these methodological advances, our approach does not require drastic changes to the current GWAS practice. All it needs is collecting offspring phenotype data (but not genotypes) in GWAS cohorts, which is substantially more economical and practical compared to collecting both genotypes and phenotypes from a large number of families. We note that even when individual-level data are available, our method will not have substantially lower power, especially for traits with higher heritability. We compared the effective sample sizes between our study design and a trio-based design (SI Appendix) and found that the effective sample size of two approaches converge (SI Appendix, Fig. S15).

EA is an important and highly complex trait that correlate with many health and social outcomes (17). Kong et al. (6) quantitatively demonstrated the existence of indirect genetic effects on EA. It is thus of great interest to understand the etiologic relevance of its direct and indirect components and how they affect other genetically correlated phenotypes. Using a PGS approach, Willoughby et al. (9) found that the indirect effect of EA may work through the family socioeconomic status. The genetic relationships of the direct and indirect effect of EA with other traits, however, are still unknown. We dissected the genetic effects of EA at the SNP level using our approach. The direct and indirect components of EA showed distinct genetic correlations with other complex traits. The known genetic correlations between EA and higher height, lower BMI, less-active smoking behavior, and better health outcomes were mostly explained by the indirect genetic component of EA. One exception that stood out in our analysis was ASD, a clinically heterogenous neurodevelopmental disorder that has been consistently identified to genetically correlate with higher cognitive ability (33, 34). We found that the positive ASD–EA genetic correlation mostly resides in the direct component of EA. We also note that these results are unlikely confounded by population stratification due to robustness of the LDSC approach (29, 38). Although exceptions exist where bivariate LDSC fails to provide robust estimates for genetic correlations (39, 40) when unadjusted confounding is correlated with LD in both input GWAS (38, 41), we did not observe strong unadjusted population stratification nor its correlation with LD in our results. Followed up in three independent cohorts of ASD proband–parent trios, we identified significant overtransmission of the direct component of EA from healthy parents to ASD probands but not to the healthy siblings. These results added value to the recent advances in understanding common genetic variations’ roles in ASD etiology (33, 35, 42, 43) and provided critical insights into the shared genetic basis of ASD and cognitive ability. These results also call for extreme caution in human genome editing and embryo screening (44). Beyond the ethical issues, elevating the PGS of EA may have limited direct protective effects on health outcomes and could lead to deleterious consequences such as increased ASD risk.

Our study has several limitations. First, we assumed that population stratification is properly controlled in each input GWAS. Unadjusted confounding in GWAS may lead to biased effect size estimates in DONUTS (SI Appendix). In addition, applications involving PGS may be particularly susceptible to such population stratification when weak, but systematic bias is aggregated across many SNPs (39, 40). We have used birth weight GWAS to demonstrate the robustness of our approach to confounding. Nevertheless, we emphasize that the quality of DONUTS estimates will depend on the data quality of input GWAS. It is always a good practice to remove as much confounding as possible from input GWAS, and results should be interpreted with caution. A related issue is that direct and indirect effect size may be heterogeneous across birth cohorts. However, in reality, each input GWAS may contain individuals from diverse age groups. If the true genetic effects are different across age groups, the effect estimate from a GWAS meta-analysis will be a weighted average of the effects from different generations. As a result, DONUTS results will also be the averaged effects across multiple generations. It is crucial to take this into consideration when interpreting the results.

Second, assortative mating is another crucial factor that may bias inference in DONUTS (45, 46). In our main framework, we only considered assortative mating in the parent generation. We also provide a principled approach to account for assortative mating in the grandparent generation (SI Appendix). However, it is not compatible with the Hardy–Weinberg equilibrium (HWE) assumption in our model, although the deviation from HWE may be small in practice (46). Practically, it is difficult to leverage heterogenous $α$ in real data analysis since the degree and pattern of assortative mating could be very different across diverse geographic locations and age groups. Our sensitivity analysis showed that the effect of assortative mating at the SNP level is small and will not substantially impact our results for EA or birth weight (SI Appendix, Fig. S11). Still, consolidating these different sources of technical biases through a unified framework remains a challenge.

Third, accurate estimation of direct and indirect effects requires all input GWAS to be sufficiently large with comparable sample sizes. Otherwise, the estimation performance will be limited by the least-powered GWAS. This is because the GWAS with a smaller sample size will tend to have noisier effect estimates and larger SEs. Since our direct and indirect effect estimators are linear combinations of input GWAS associations (Table 1), GWAS with the smallest sample size would dominate final results by introducing substantial noise. The current sample size in our EA analyses was not sufficient for significant association mapping or calculating well-powered PGS of direct and indirect EA effects.

Fourth, we did not account for potential indirect sibling effects in our model. Although evidence has suggested that the indirect effects from siblings are negligible compared to direct effects and parental effects (15, 16), it may be important to account for sibling effects in certain applications (47).

Fifth, summary statistics of the 45 complex traits used in our genetic correlation analyses are mixtures of direct and indirect effects. Genetic correlations of direct/indirect effects on both traits included in the pairwise correlation analysis will provide a deeper and clearer understanding about the shared genetic architectures across these traits. However, direct and indirect effect summary statistics are not currently available for most traits, mostly due to limited sample size that reported children’s phenotype. Therefore, careful dissection of genetic correlation into direct and indirect components remains to be implemented in the future.

Finally, our method provides unbiased effect size estimates but will introduce a negative technical correlation between the direct and indirect effect estimates, which we discuss in detail in SI Appendix. This is not a unique issue in our approach and was also observed in analyses based on individual-level data (15, 28). Similarly, the indirect maternal and indirect paternal effect estimates will also become positively correlated due to this technical artifact. When sample size is limited, such technical correlations will shade the true genetic effects and hinder the interpretation of associations.

Taken together, our method has made important technical advancements in partitioning complex traits’ direct and indirect genetic effects. It provides statistically rigorous and computationally efficient estimates based on summary statistics from multigenerational GWAS, which provide a clear guidance on future study designs. If large genetic cohorts with multigenerational phenotypic information becomes the convention in the field, our method will have broad applications and can facilitate our understanding of the genetic basis of numerous human traits.

Methods

Method Details.

We assume the true genetic model for the offspring phenotype $Y_{O}$ in a family to be

Y_{O} = G_{O} β_{d i r} + G_{M} β_{i n d_m t} + G_{P} β_{i n d_p t} + ϵ = G_{O} β_{d i r} + (T_{M} β_{i n d_m t} + T_{P} β_{i n d_p t}) + (N T_{M} β_{i n d_m t} + N T_{P} β_{i n d_p t}) + ϵ,

where $G_{O} = T_{M} + T_{P}, G_{M} = T_{M} + N T_{M}$ , and $G_{P} = T_{P} + N T_{P}$ are the offspring, maternal, and paternal genotypes in a family, respectively. $T$ and $N T$ represent the transmitted and nontransmitted alleles, respectively. $β_{d i r}, β_{i n d_m t}$ , and $β_{i n d_p t}$ are the true direct, indirect maternal, and indirect paternal effect sizes, respectively. $ϵ$ is the noise term. Without loss of generality, we assume $Y_{O}$ , $G_{O}, G_{M},$ and $G_{P}$ are all centered at 0. We also assume the transmitted and nontransmitted alleles to be independent. That is, $T_{M}$ and $N T_{M}$ are independent; $T_{P}$ and $N T_{P}$ are also independent. Due to assortative mating between parents, maternal and paternal genotypes may be correlated, and we denote their correlation at a locus to be $Corr (G_{M}, G_{P}) = α$ to quantify the degree of assortative mating. We also assume the variance of parental genotypes to be $Var (G_{M}) = Var (G_{P}) = 2 p (1 - p)$ , where $p$ is the minor allele frequency (MAF).

We define indirect genetic effect $β_{i n d}$ as the effect of a person’s genotype on his or her phenotype via the indirect pathway that goes through biological parents and the family environment. Equivalently, $β_{i n d}$ is the projection of $T_{M} β_{i n d_m t} + T_{P} β_{i n d_p t}$ on $G_{O}$ which can be denoted as

β_{i n d} = (β_{i n d_m t} + β_{i n d_p t}) / 2 .

If genetic data are available in a number of parents–offspring trios, by regressing $Y_{O}$ on the offspring, maternal, and paternal genotypes, the coefficients in the joint regression estimate the direct, indirect maternal, and indirect paternal genetic effects, respectively. If instead we have data of own phenotype and own genotype and perform GWAS-O that regresses $Y_{O}$ on $G_{O}$ (which is the standard GWAS), the effect size estimate is given by ${\hat{β}}_{O} = {(G_{O}^{T} G_{O})}^{- 1} G_{O}^{T} Y_{O} = {(G_{O}^{T} G_{O})}^{- 1} G_{O}^{T} (β_{d i r} G_{O} + β_{i n d_m t} G_{M} + β_{i n d_p t} G_{P} + ϵ)$ . It can be found that (SI Appendix) $Cov (G_{O}, G_{M}) = Cov (G_{O}, G_{P}) = p (1 - p) (1 + α)$ . Then, we can express $β_{O}$ in terms of the direct and indirect effect sizes. Similarly, we can also perform GWAS-M (regress $Y_{O}$ on $G_{M}$ ) and GWAS-P (regress $Y_{O}$ on $G_{P}$ ) with effect size $β_{M}$ and $β_{P}$ , respectively. The expressions for $β_{M}$ and $β_{P}$ can also be derived. Then, using three equations, we can solve for the direct and indirect genetic effects analytically:

β_{d i r} = (2 + α) β_{O} - β_{M} - β_{P}, β_{i n d_m t} = \frac{3 - α^{2}}{2 (1 - α^{2})} β_{M} + \frac{1 - 2 α - α^{2}}{2 (1 - α^{2})} β_{P} - (1 + \frac{α}{2}) β_{O}, β_{i n d_p t} = \frac{3 - α^{2}}{2 (1 - α^{2})} β_{P} + \frac{1 - 2 α - α^{2}}{2 (1 - α^{2})} β_{M} - (1 + \frac{α}{2}) β_{O}, β_{i n d} = \frac{β_{i n d_m t} + β_{i n d_p t}}{2} = \frac{2 + α}{2 + 2 α} [β_{M} + β_{P} - (1 + α) β_{O}] .

Our framework could also be naturally extended to the PGS level (SI Appendix). Another technical note is that the covariance between ${\hat{β}}_{d i r}$ and ${\hat{β}}_{i n d}$ are always negative. We discuss this in detail in SI Appendix.

Simulation.

We randomly selected 1,000 independent SNPs in the UKB genotyped data as causal variants and sampled their true effect sizes from a normal distribution with mean 0 and variance of ${0.01}^{2}$ , which gives us realistic values of effect sizes. As a comparison, the effect size in EA summary statistics (17) ranges from about −0.05 to 0.05 with a variance of about ${0.005}^{2}$ . We first simulated three sets of trios (sets 1 through 3). Each set consisted of 30,000 trios. In each trio, parental genotypes were independently simulated under binomial distributions using each SNP’s MAF. The offspring genotypes were generated from parental data following Mendelian inheritance. The offspring phenotype was computed as a weighted sum of these 1,000 SNPs plus a normal error term $y_{O} = \sum_{i = 1}^{1000} G_{O, i} β_{d i r, i} + G_{M, i} β_{i n d_m t, i} + G_{P, i} β_{i n d_p t, i} + ε$ . We used these three sets to run GWAS-O, GWAS-M, and GWAS-P, respectively. To simulate overlapping samples, we generated two additional sets (sets 4 and 5) of multigenerational families. In each family, we simulated data for three generations: two grandparents, two parents, and one child. Thus, these parents can be used as overlapping samples since we can compute both their own and their children’s phenotypes (SI Appendix, Figs. S1B and S2). When simulating the phenotypes for the overlapping samples, we set the errors for computing own phenotypes and those for computing offspring’s phenotypes to be correlated since they share similar family environment. We set the correlation to be 0.3. $Var (ε)$ was set to be 0.04 so that it accounted for ∼30% of the phenotypic variance.

We simulated three different scenarios: 1) GWAS-O, GWAS-M, and GWAS-P as inputs in which all the samples in these three GWASs were independent; 2) GWAS-O and GWAS-MP as inputs in which these two GWASs also used independent samples; 3) GWAS-O, GWAS-M, and GWAS-P as inputs in which GWAS-M and GWAS-P used independent samples; however, all samples in GWAS-M and GWAS-P were also present in GWAS-O (SI Appendix, Fig. S2). That is, for scenario 3, we used the parents in sets 4 and 5 to conduct GWAS-O, GWAS-M, and GWAS-P.

Among the 1,000 causal SNPs, we focused on one SNP with a MAF of 0.23. We used different settings for its true effect sizes: $(β_{d i r}, β_{i n d_m t}, β_{i n d_p t})$ = (0, 0, 0), (0, 0.02, 0.01), (0.02, 0, 0.01), (0.02, 0.02, 0), (0.02, 0.01, 0.01), (0.02, 0.02, 0.01), and (0.02, −0.02, −0.01) to cover the null, positive direct and positive indirect, and positive direct and negative indirect effects combinations. For each setting, we repeated the simulation 1,000 times. For each repeat, we applied our method to estimate the direct and indirect effects. We also tested two other SNPs with MAF = 0.01 and 0.48.

In order to assess the effects of assortative mating on birth weight and EA (SI Appendix, Fig. S11), we simulated $α \sim N (0, {0.025}^{2})$ to have comparable values with those obtained from real couples reported in Guo et al. (48) Since assortative mating would most likely be positive, we also investigated the scenario in which we set the $α$ to be its absolute value if it is negative. Our simulation generates $α$ approximately within the range of estimates in a previous study (48).

UKB Data Processing.

We used UKB data to conduct GWASs on birth weight and EA and perform PGS regression analyses. We excluded the participants that are recommended by UKB to be excluded from analysis (data field 22010 in the UKB), those with conflicting genetically inferred (data field 22001) and self-reported sex (data field 31), and those who withdrew from the study. UKB samples with European ancestry were identified from PC analysis (data field 22006). We used software KING (49) to infer the pairwise family kinship. We identified 154 pairs of monozygotic twins, 242 pairs of fraternal twins, 19,136 full sibling pairs, and 5,336 parent–offspring pairs among 408,921 individuals with European ancestry in the UKB. PCs were computed using flashPCA2 (50) on genotyped data for each in-house GWAS using UKB samples. In each GWAS, we kept only the SNPs with missing call rate $\leq 0.01$ , MAF $\geq 0.01$ , and with HWE test P value $\geq 10^{- 6}$ .

Birth Weight GWAS Analysis.

The own (n = 298,142) and maternal (n = 210,267) GWAS summary statistics reported in Warrington et al. (28) were downloaded from the Early Growth Genetics Consortium website (https://egg-consortium.org/birth-weight-2019.html). We removed duplicated SNPs in each file, took SNP intersections between these two sets of summary statistics, and flipped the sign of effect size estimates when necessary, such that the effect alleles were matched between the two input GWASs. We also downloaded the summary statistics for the inferred direct and indirect maternal genetic effects to compare with our results (SI Appendix, Fig. S6). To have a fair comparison, we used the SNPs whose sample sizes and effect allele frequencies reported in the paper’s direct and indirect maternal effect summary statistics that are consistent with those reported in their GWAS-O and GWAS-M summary statistics and heterogeneity P value > 0.05. More than 8 million SNPs were used in the comparative analysis.

The UKB collected participants’ birth weight (data field 20022). Women who had at least one child were also asked for the birth weight of their first child (data field 2744). We also constructed two orthogonal phenotypes representing the direct and indirect components of birth weight following Warrington et al. (28) The two phenotypes were defined as the following: $2 (2 B W_{own} - B W_{offpring}) / 3$ and $2 (2 B W_{offspring} - B W_{own}) / 3$ , where $B W_{own}$ is own birth weight and $B W_{offspring}$ is the offspring’s birth weight.

We conducted GWASs for these four phenotypes (i.e., own and offspring birth weights and the two orthogonal phenotypes) on 75,711 independent individuals of European ancestry who had both own and first child’s birth weights available. To compare, this number was 101,541 in Warrington et al. (28), which included both Europeans and non-European samples. Birth weight was constructed following Warrington et al. (28) Year of birth, genotyping array, and top 20 PCs were used as covariates. The results on own and first child’s birth weight were used as input in our framework to estimate the direct and maternal effects while the GWASs on orthogonal phenotypes were used as comparison. To investigate the robustness of our approach to population stratification, we also performed GWAS-O and GWAS-M without PCs as covariates and using linear mixed models implemented in the software BOLT-LMM (51).

GWAS on Offspring EA.

We identified 5,336 parent–offspring pairs among the UKB European ancestry samples. Following Lee et al. (17), we used the “qualification” (data field 6138) to compute the years of schooling as the EA phenotype. Year of birth, sex, genotyping array, and top 20 PCs were used as covariates. We used parents from independent parent–offspring pairs with offspring EA phenotype and covariates information as GWAS samples. If both parents’ genotype data were available, we only included one of them in the analysis. The GWAS sample size was n = 4,181 (2,619 females and 1,562 males).

In the HRS cohort, the respondent’s oldest child’s EA phenotype was constructed following Okbay et al. (52) We kept only the independent [inferred by KING (49)] European parents (self-identified as “white/caucasian”) in our analyses. Year of birth, sex, and top 10 PCs were used as covariates. GWAS sample size was n = 6,324 (3,780 females and 2,544 males).

In the WLS cohort, the oldest child’s education information was given by variables “z_rd01001”, “z_gd01001”, and “z_gd21001” corresponding to different rounds of collection. We used the maximum value whenever there was any inconsistency among different rounds. The EA phenotype was constructed following Lee et al. (17) We required the GWAS samples to be of European ancestry (variable “z_ie008re”), independent [inferred by KING (49)], that the oldest child was a biological offspring (“z_rd00401” and “z_gd00401”), that the offspring’s EA was measured when the child was at least 30 y old, and that parent was at least 15 y older than the child. Year of birth, sex, and top 10 PCs were used as covariates. GWAS sample size was n = 4,772 (2,513 females and 2,259 males).

Software PLINK (53) version 1.9 was used to perform all GWASs. Finally, we meta-analyzed these three offspring EA GWASs using the inverse variance based approach in METAL (54) to obtain the GWAS-MP as the input for our framework.

We also compared results given by our framework and SNIPar (15) with a same set of data in UKB. Using the full siblings (n = 35,243 samples from 17,136 families) of European ancestries in UKB identified by KING (49) (here, we only used the full siblings whose parents are not in the UKB), SNIPar imputed their expected average parental genotype. With the sum of imputed parental genotype and the observed offspring’s genotype jointly in the model, SNIPar computed the direct and indirect effects on EA with a linear mixed model (n = 34,956 samples from 17,135 unique families with nonmissing EA phenotype). Using the same full sibling data, we performed GWAS-O using the observed siblings (n = 17,135 independent samples with phenotype and covariates available). Using the imputed sum of parental genotype, we ran GWAS-MP. Then our framework could also compute the direct and indirect effects using the two summary statistics, and the comparison results are shown in SI Appendix, Fig. S16. Year of birth, sex, genotyping array, and top 20 PCs were used as covariates in GWAS-O. In GWAS-MP, the offspring’s year of birth, genotyping array, and top 20 PCs were used as covariates in which the PCs were computed using the imputed parental genotype by flashPCA2 (50).

GWAS on Own EA in UKB.

We conducted GWAS-O (n = 356,719) using independent European samples in the UKB, excluding the full sibling samples (n = 35,243) that were used by SNIPar. The EA phenotypes were constructed following Lee et al. (17). Year of birth, sex, genotyping array, and top 20 PCs were used as covariates. We then meta-analyzed with EA3 summary statistics that excluded UKB samples. The reason for excluding the full siblings was because later we would do meta-analysis with SNIPar results which used the full sibling data.

Genetic Correlation Analysis.

We used both LDSC (29) and GNOVA (31) to compute genetic covariances and genetic correlations for any given pair of traits using their GWAS summary statistics. The results based on two approaches were comparable. The genetic correlation results shown in the main text were from LDSC. Details of the 45 traits used in the analysis and LDSC and GNOVA results are shown in Datasets S6–S8.

PGS Calculation and Regression Analysis.

We performed PGS analysis on two sets of UKB samples with European ancestry: the first set was 16,580 pairs of full siblings, and the second was 370,308 independent individuals. For each sample, two EA PGSs based on direct and indirect effect estimates were computed. To maximize the power and avoid overfitting, we used different input summary statistics to compute the direct and indirect effects. For the full sibling pairs, we first excluded full sibling pairs from the UKB samples, then used KING (49) to identify a subset of independent individuals (n = 356,719) and ran an EA GWAS following Lee et al. (17) We used METAL (54) to meta-analyze it with EA3 GWAS that excluded 23andMe and UKB samples (n = 324,162). Together with the offspring EA GWAS as inputs, we computed the direct and indirect effect summary statistics which were used to compute the PGSs for the full sibling pairs in UKB. For the second set, we used the EA3 GWAS that excluded 23andMe and UKB samples and the offspring EA GWAS as input to estimate the direct and indirect effects.

To compute PGS, we first clumped the summary statistics in PLINK (53) version 1.9 using the Northern Europeans from Utah (CEU) samples in 1000 Genome Project Phase III cohort (55) as the LD reference panel. We applied an LD window size of 1 Mb and a pairwise r2 threshold of 0.1. Then, we computed PGS using software PRSice-2 (56) with a fine-tuned P value cutoff given by software PUMAS (32). PUMAS uses GWAS summary statistics as input and output and an optimal P value cutoff that gives the highest $R^{2}$ for the PGS regression analysis. Since the PGS will use only the SNPs that are present in the target samples, we used only the SNPs that are present in the summary statistics, LD reference panel, and the target samples when running PUMAS.

We used software R (57) version 3.5.1 to run linear regression of EA on PGSs. Both the EA phenotype and PGS were standardized. For full sibling pairs, we regressed EA difference between siblings on PGS differences. For independent samples, we used year of birth, sex, genotyping array, assessment center, and top 10 PCs as covariates. $R^{2}$ was computed as the ratio of sum squares by PGS to the total sum of squares.

pTDT Analysis.

Three ASD cohorts were used in the pTDT analysis: AGP (n = 2,188 trios), SSC (1,794 proband trios and 1,430 sibling trios), and SPARK (3,822 proband trios and 1,812 sibling trios). Details of data processing in these cohorts have been described previously (42). To compute PGS, we first used PLINK (53) version 1.9 to clump the direct and indirect effect summary statistics using the CEU samples in 1000 Genome Project Phase III cohort (55) as the LD reference panel. We applied an LD window size of 1 Mb and a pairwise r2 threshold of 0.1. PGSs were computed using PRSice-2⁵⁶ with optimal P value cutoffs estimated by PUMAS (32). We performed pTDT (35) to measure the transmission disequilibrium in EA polygenic risks for ASD probands and siblings. The pTDT details were described in Weiner et al. (35) Briefly, it first scales every PGS by subtracting the parental average PGS and then dividing the parental PGS SD. Then, the scaled PGS deviation values are used to test whether the children’s PGS are significantly different from the parental average.

Supplementary Material

Supplementary File

pnas.2023184118.sapp.pdf^{(3.4MB, pdf)}

Supplementary File

pnas.2023184118.sd01.xlsx^{(10.3KB, xlsx)}

Supplementary File

pnas.2023184118.sd02.xlsx^{(10.5KB, xlsx)}

Supplementary File

pnas.2023184118.sd03.xlsx^{(11.1KB, xlsx)}

Supplementary File

pnas.2023184118.sd04.xlsx^{(12.2KB, xlsx)}

Supplementary File

pnas.2023184118.sd05.xlsx^{(12.2KB, xlsx)}

Supplementary File

pnas.2023184118.sd06.xlsx^{(14.2KB, xlsx)}

Supplementary File

pnas.2023184118.sd07.xlsx^{(17.9KB, xlsx)}

Supplementary File

pnas.2023184118.sd08.xlsx^{(21.9KB, xlsx)}

Supplementary File

pnas.2023184118.sd10.xlsx^{(11.2KB, xlsx)}

Supplementary File

pnas.2023184118.sd11.xlsx^{(11.5KB, xlsx)}

Supplementary File

pnas.2023184118.sd09.xlsx^{(9.5KB, xlsx)}

Acknowledgments

This project was supported by the Clinical and Translational Science Award program, through the NIH National Center for Advancing Translational Sciences, Grant UL1TR000427. We also acknowledge research support from the University of Wisconsin–Madison Office of the Chancellor and the Vice Chancellor for Research and Graduate Education with funding from the Wisconsin Alumni Research Foundation and the Waisman Center pilot grant program at the University of Wisconsin–Madison. We are grateful to all the families participating in the AGP, the SSC, and SPARK study. We thank Dr. Aysu Okbay for providing the EA meta-analysis results with UKB data removed. We thank Drs. Jan Greenberg and Marsha Mailick for their assistance in WLS data collection and processing.

Footnotes

The authors declare no competing interest.

This article is a PNAS Direct Submission.

See online for related content such as Commentaries.

This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2023184118/-/DCSupplemental.

Data Availability

Previously published data were used for this work: 1) Ref. 30, 2) Ref. 28, 3) WLS: https://www.ssc.wisc.edu/wlsresearch/, 4) HRS: https://hrs.isr.umich.edu/about, 5) AGP Consortium: https://www.ncbi.nlm.nih.gov/projects/gap/cgi-bin/study.cgi?study_id=phs000267.v5.p2, 6) SSC: https://www.sfari.org/resource/simons-simplex-collection/, and 7) SPARK: https://www.sfari.org/resource/spark/. The DONUTS package is available in GitHub at https://github.com/qlu-lab/DONUTS. All summary statistics generated in this study are freely accessible from the Q.L. laboratory (http://qlu-lab.org/data.html) or at the GWAS Catalog:

http://ftp.ebi.ac.uk/pub/databases/gwas/summary_statistics/GCST90017001-GCST90018000/GCST90017139/, http://ftp.ebi.ac.uk/pub/databases/gwas/summary_statistics/GCST90017001-GCST90018000/GCST90017140/, http://ftp.ebi.ac.uk/pub/databases/gwas/summary_statistics/GCST90017001-GCST90018000/GCST90017141/, and http://ftp.ebi.ac.uk/pub/databases/gwas/summary_statistics/GCST90017001-GCST90018000/GCST90017142/.

References

1.Visscher P. M., et al., 10 years of GWAS discovery: Biology, function, and translation. Am. J. Hum. Genet. 101, 5–22 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
2.Manolio T. A., et al., Finding the missing heritability of complex diseases. Nature 461, 747–753 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
3.Hindorff L. A., et al., Potential etiologic and functional implications of genome-wide association loci for human diseases and traits. Proc. Natl. Acad. Sci. U.S.A. 106, 9362–9367 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
4.Chatterjee N., Shi J., García-Closas M., Developing and evaluating polygenic risk prediction models for stratified disease prevention. Nat. Rev. Genet. 17, 392–406 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
5.Harden K. P., Koellinger P. D., Using genetics for social science. Nat. Hum. Behav. 4, 567–576 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
6.Kong A., et al., The nature of nurture: Effects of parental genotypes. Science 359, 424–428 (2018). [DOI] [PubMed] [Google Scholar]
7.Bates T. C., et al., The nature of nurture: Using a virtual-parent design to test parenting effects on children’s educational attainment in genotyped families. Twin Res. Hum. Genet. 21, 73–83 (2018). [DOI] [PubMed] [Google Scholar]
8.Trejo S., Domingue B. W., Genetic nature or genetic nurture? Introducing social genetic parameters to quantify bias in polygenic score analyses. Biodemogr. Soc. Biol. 64, 187–215 (2018). [DOI] [PubMed] [Google Scholar]
9.Willoughby E. A., McGue M., Iacono W. G., Rustichini A., Lee J. J., The role of parental genotype in predicting offspring years of education: Evidence for genetic nurture. Mol. Psychiatry, 10.1038/s41380-019-0494-1 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
10.de Zeeuw E. L., et al., Intergenerational transmission of education and ADHD: Effects of parental genotypes. Behav. Genet. 50, 221–232 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
11.Cheesman R., et al., Comparison of adopted and nonadopted individuals reveals gene–environment interplay for education in the UK Biobank. Psychol. Sci. 31, 582–591 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
12.Domingue B. W., Fletcher J., Separating measured genetic and environmental effects: Evidence linking parental genotype and adopted child outcomes. Behav. Genet. 50, 301–309 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
13.Young A. I., Benonisdottir S., Przeworski M., Kong A., Deconstructing the sources of genotype-phenotype associations in humans. Science 365, 1396–1400 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
14.Hwang L.-D., et al., Estimating indirect parental genetic effects on offspring phenotypes using virtual parental genotypes derived from sibling and half sibling pairs. bioRxiv [Preprint] (2020). 10.1101/2020.02.21.959114 (Accessed 17 April 2020). [DOI] [PMC free article] [PubMed]
15.Young A. I., et al., Mendelian imputation of parental genotypes for genome-wide estimation of direct and indirect genetic effects. bioRxiv [Preprint] (2020). 10.1101/2020.07.02.185199 (Accessed 15 July 2020). [DOI]
16.Kong A., Benonisdottir S., Young A. I., Family analysis with Mendelian imputations. bioRxiv [Preprint] (2020). 10.1101/2020.07.02.185181 (Accessed 15 July 2020). [DOI]
17.Lee J. J.et al.; 23andMe Research Team; COGENT (Cognitive Genomics Consortium); Social Science Genetic Association Consortium , Gene discovery and polygenic prediction from a genome-wide association study of educational attainment in 1.1 million individuals. Nat. Genet. 50, 1112–1121 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
18.Okbay A.et al.; LifeLines Cohort Study , Genetic variants associated with subjective well-being, depressive symptoms, and neuroticism identified through genome-wide analyses. Nat. Genet. 48, 624–633 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
19.Day F. R., Ong K. K., Perry J. R. B., Elucidating the genetic basis of social interaction and isolation. Nat. Commun. 9, 2457 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
20.Pappa I., et al., A genome-wide approach to children’s aggressive behavior: The EAGLE consortium. Am. J. Med. Genet. B. Neuropsychiatr. Genet. 171, 562–572 (2016). [DOI] [PubMed] [Google Scholar]
21.Tielbeek J. J.et al.; Broad Antisocial Behavior Consortium collaborators , Genome-wide association studies of a broad spectrum of antisocial behavior. JAMA Psychiatry 74, 1242–1250 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
22.Erlangsen A., et al., Genetics of suicide attempts in individuals with and without mental disorders: A population-based genome-wide association study. Mol. Psychiatry 25, 2410–2421 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
23.Karlsson Linnér R.et al.; 23and Me Research Team; eQTLgen Consortium; International Cannabis Consortium; Social Science Genetic Association Consortium , Genome-wide association analyses of risk tolerance and risky behaviors in over 1 million individuals identify hundreds of loci and shared genetic influences. Nat. Genet. 51, 245–257 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
24.Liu M.et al.; 23andMe Research Team; HUNT All-In Psychiatry , Association studies of up to 1.2 million individuals yield new insights into the genetic etiology of tobacco and alcohol use. Nat. Genet. 51, 237–244 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
25.Krapohl E., Plomin R., Genetic link between family socioeconomic status and children’s educational achievement estimated from genome-wide SNPs. Mol. Psychiatry 21, 437–443 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
26.Belsky D. W., et al., Genetic analysis of social-class mobility in five longitudinal studies. Proc. Natl. Acad. Sci. U.S.A. 115, E7275–E7284 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
27.Tubbs J. D., Zhang Y. D., Sham P. C., Intermediate confounding in trio relationships: The importance of complete data in effect size estimation. Genet. Epidemiol. 44, 395–399 (2020). [DOI] [PubMed] [Google Scholar]
28.Warrington N. M.et al.; EGG Consortium , Maternal and fetal genetic effects on birth weight and their relevance to cardio-metabolic risk factors. Nat. Genet. 51, 804–814 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
29.Bulik-Sullivan B.et al.; ReproGen Consortium; Psychiatric Genomics Consortium; Genetic Consortium for Anorexia Nervosa of the Wellcome Trust Case Control Consortium 3 , An atlas of genetic correlations across human diseases and traits. Nat. Genet. 47, 1236–1241 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
30.Bycroft C., et al., The UK Biobank resource with deep phenotyping and genomic data. Nature 562, 203–209 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
31.Lu Q., et al., A powerful approach to estimating annotation-stratified genetic covariance via GWAS summary statistics. Am. J. Hum. Genet. 101, 939–964 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
32.Zhao Z., et al., Fine-tuning polygenic risk scores with GWAS summary statistics. bioRxiv [Preprint] (2019). 10.1101/810713 (Accessed 28 March 2020). [DOI]
33.Grove J.et al.; Autism Spectrum Disorder Working Group of the Psychiatric Genomics Consortium; BUPGEN; Major Depressive Disorder Working Group of the Psychiatric Genomics Consortium; 23andMe Research Team , Identification of common genetic risk variants for autism spectrum disorder. Nat. Genet. 51, 431–444 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
34.Anttila V.et al.; Brainstorm Consortium , Analysis of shared heritability in common disorders of the brain. Science 360, eaap8757 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
35.Weiner D. J.et al.; iPSYCH-Broad Autism Group; Psychiatric Genomics Consortium Autism Group , Polygenic transmission disequilibrium confirms that common and rare variation act additively to create risk for autism spectrum disorders. Nat. Genet. 49, 978–985 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
36.Claussnitzer M., et al., A brief history of human disease genetics. Nature 577, 179–189 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
37.Young A. I., et al., Relatedness disequilibrium regression estimates heritability without environmental bias. Nat. Genet. 50, 1304–1310 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
38.Gao B., Yang C., Liu J., Zhou X., Accurate genetic and environmental covariance estimation with composite likelihood in genome-wide association studies. PLoS Genet. 17, e1009293 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
39.Sohail M., et al., Polygenic adaptation on height is overestimated due to uncorrected stratification in genome-wide association studies. eLife 8, e39702 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
40.Berg J. J., et al., Reduced signal for polygenic adaptation of height in UK Biobank. eLife 8, e39725 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
41.Yengo L., Yang J., Visscher P. M., Expectation of the intercept from bivariate LD score regression in the presence of population stratification. bioRxiv [Preprint] (2018). 10.1101/310565 (Accessed 5 November 2020). [DOI]
42.Huang K., et al., Transcriptome-wide transmission disequilibrium analysis identifies novel risk genes for autism spectrum disorder. PLoS Genet. 17, e1009309 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
43.Zhang Y., et al., Local genetic correlation analysis reveals heterogeneous etiologic sharing of complex traits. bioRxiv [Preprint] (2020). 10.1101/2020.05.08.084475 (Accessed 5 November 2020). [DOI] [PMC free article] [PubMed]
44.Karavani E., et al., Screening human embryos for polygenic traits has limited utility. Cell 179, 1424–1435.e8 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
45.Crow J. F., Kimura M., An Introduction to Population Genetics Theory (Harper & Row, New York, 1970). [Google Scholar]
46.Yengo L., et al., Imprint of assortative mating on the human genome. Nat. Hum. Behav. 2, 948–954 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
47.Fletcher J. M., Wu Y., Zhao Z., Lu Q., The production of within-family inequality: Insights and implications of integrating genetic data. bioRxiv [Preprint] (2020). 10.1101/2020.06.06.137778 (Accessed 15 July 2020). [DOI] [PMC free article] [PubMed]
48.Guo G., Wang L., Liu H., Randall T., Genomic assortative mating in marriages in the United States. PLoS One 9, e112322 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
49.Manichaikul A., et al., Robust relationship inference in genome-wide association studies. Bioinformatics 26, 2867–2873 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
50.Abraham G., Qiu Y., Inouye M., FlashPCA2: Principal component analysis of biobank-scale genotype datasets. Bioinformatics 33, 2776–2778 (2017). [DOI] [PubMed] [Google Scholar]
51.Loh P.-R., et al., Efficient Bayesian mixed-model analysis increases association power in large cohorts. Nat. Genet. 47, 284–290 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
52.Okbay A.et al.; LifeLines Cohort Study , Genome-wide association study identifies 74 loci associated with educational attainment. Nature 533, 539–542 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
53.Purcell S., et al., PLINK: A tool set for whole-genome association and population-based linkage analyses. Am. J. Hum. Genet. 81, 559–575 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
54.Willer C. J., Li Y., Abecasis G. R., METAL: Fast and efficient meta-analysis of genomewide association scans. Bioinformatics 26, 2190–2191 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
55.Auton A.; The 1000 Genomes Project Consortium , A global reference for human genetic variation. Nature 526, 68–74 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
56.Choi S. W., O’Reilly P. F., PRSice-2: Polygenic Risk Score software for biobank-scale data. Gigascience 8, giz082 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
57.R Core Team , R: A Language and Environment for Statistical Computing (R Core Team, 2020). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary File

pnas.2023184118.sapp.pdf^{(3.4MB, pdf)}

Supplementary File

pnas.2023184118.sd01.xlsx^{(10.3KB, xlsx)}

Supplementary File

pnas.2023184118.sd02.xlsx^{(10.5KB, xlsx)}

Supplementary File

pnas.2023184118.sd03.xlsx^{(11.1KB, xlsx)}

Supplementary File

pnas.2023184118.sd04.xlsx^{(12.2KB, xlsx)}

Supplementary File

pnas.2023184118.sd05.xlsx^{(12.2KB, xlsx)}

Supplementary File

pnas.2023184118.sd06.xlsx^{(14.2KB, xlsx)}

Supplementary File

pnas.2023184118.sd07.xlsx^{(17.9KB, xlsx)}

Supplementary File

pnas.2023184118.sd08.xlsx^{(21.9KB, xlsx)}

Supplementary File

pnas.2023184118.sd10.xlsx^{(11.2KB, xlsx)}

Supplementary File

pnas.2023184118.sd11.xlsx^{(11.5KB, xlsx)}

Supplementary File

pnas.2023184118.sd09.xlsx^{(9.5KB, xlsx)}

Data Availability Statement

[r1] 1.Visscher P. M., et al., 10 years of GWAS discovery: Biology, function, and translation. Am. J. Hum. Genet. 101, 5–22 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]

[r2] 2.Manolio T. A., et al., Finding the missing heritability of complex diseases. Nature 461, 747–753 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]

[r3] 3.Hindorff L. A., et al., Potential etiologic and functional implications of genome-wide association loci for human diseases and traits. Proc. Natl. Acad. Sci. U.S.A. 106, 9362–9367 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]

[r4] 4.Chatterjee N., Shi J., García-Closas M., Developing and evaluating polygenic risk prediction models for stratified disease prevention. Nat. Rev. Genet. 17, 392–406 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]

[r5] 5.Harden K. P., Koellinger P. D., Using genetics for social science. Nat. Hum. Behav. 4, 567–576 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]

[r6] 6.Kong A., et al., The nature of nurture: Effects of parental genotypes. Science 359, 424–428 (2018). [DOI] [PubMed] [Google Scholar]

[r7] 7.Bates T. C., et al., The nature of nurture: Using a virtual-parent design to test parenting effects on children’s educational attainment in genotyped families. Twin Res. Hum. Genet. 21, 73–83 (2018). [DOI] [PubMed] [Google Scholar]

[r8] 8.Trejo S., Domingue B. W., Genetic nature or genetic nurture? Introducing social genetic parameters to quantify bias in polygenic score analyses. Biodemogr. Soc. Biol. 64, 187–215 (2018). [DOI] [PubMed] [Google Scholar]

[r9] 9.Willoughby E. A., McGue M., Iacono W. G., Rustichini A., Lee J. J., The role of parental genotype in predicting offspring years of education: Evidence for genetic nurture. Mol. Psychiatry, 10.1038/s41380-019-0494-1 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]

[r10] 10.de Zeeuw E. L., et al., Intergenerational transmission of education and ADHD: Effects of parental genotypes. Behav. Genet. 50, 221–232 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]

[r11] 11.Cheesman R., et al., Comparison of adopted and nonadopted individuals reveals gene–environment interplay for education in the UK Biobank. Psychol. Sci. 31, 582–591 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]

[r12] 12.Domingue B. W., Fletcher J., Separating measured genetic and environmental effects: Evidence linking parental genotype and adopted child outcomes. Behav. Genet. 50, 301–309 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]

[r13] 13.Young A. I., Benonisdottir S., Przeworski M., Kong A., Deconstructing the sources of genotype-phenotype associations in humans. Science 365, 1396–1400 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]

[r14] 14.Hwang L.-D., et al., Estimating indirect parental genetic effects on offspring phenotypes using virtual parental genotypes derived from sibling and half sibling pairs. bioRxiv [Preprint] (2020). 10.1101/2020.02.21.959114 (Accessed 17 April 2020). [DOI] [PMC free article] [PubMed]

[r15] 15.Young A. I., et al., Mendelian imputation of parental genotypes for genome-wide estimation of direct and indirect genetic effects. bioRxiv [Preprint] (2020). 10.1101/2020.07.02.185199 (Accessed 15 July 2020). [DOI]

[r16] 16.Kong A., Benonisdottir S., Young A. I., Family analysis with Mendelian imputations. bioRxiv [Preprint] (2020). 10.1101/2020.07.02.185181 (Accessed 15 July 2020). [DOI]

[r17] 17.Lee J. J.et al.; 23andMe Research Team; COGENT (Cognitive Genomics Consortium); Social Science Genetic Association Consortium , Gene discovery and polygenic prediction from a genome-wide association study of educational attainment in 1.1 million individuals. Nat. Genet. 50, 1112–1121 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]

[r18] 18.Okbay A.et al.; LifeLines Cohort Study , Genetic variants associated with subjective well-being, depressive symptoms, and neuroticism identified through genome-wide analyses. Nat. Genet. 48, 624–633 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]

[r19] 19.Day F. R., Ong K. K., Perry J. R. B., Elucidating the genetic basis of social interaction and isolation. Nat. Commun. 9, 2457 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]

[r20] 20.Pappa I., et al., A genome-wide approach to children’s aggressive behavior: The EAGLE consortium. Am. J. Med. Genet. B. Neuropsychiatr. Genet. 171, 562–572 (2016). [DOI] [PubMed] [Google Scholar]

[r21] 21.Tielbeek J. J.et al.; Broad Antisocial Behavior Consortium collaborators , Genome-wide association studies of a broad spectrum of antisocial behavior. JAMA Psychiatry 74, 1242–1250 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]

[r22] 22.Erlangsen A., et al., Genetics of suicide attempts in individuals with and without mental disorders: A population-based genome-wide association study. Mol. Psychiatry 25, 2410–2421 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]

[r23] 23.Karlsson Linnér R.et al.; 23and Me Research Team; eQTLgen Consortium; International Cannabis Consortium; Social Science Genetic Association Consortium , Genome-wide association analyses of risk tolerance and risky behaviors in over 1 million individuals identify hundreds of loci and shared genetic influences. Nat. Genet. 51, 245–257 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]

[r24] 24.Liu M.et al.; 23andMe Research Team; HUNT All-In Psychiatry , Association studies of up to 1.2 million individuals yield new insights into the genetic etiology of tobacco and alcohol use. Nat. Genet. 51, 237–244 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]

[r25] 25.Krapohl E., Plomin R., Genetic link between family socioeconomic status and children’s educational achievement estimated from genome-wide SNPs. Mol. Psychiatry 21, 437–443 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]

[r26] 26.Belsky D. W., et al., Genetic analysis of social-class mobility in five longitudinal studies. Proc. Natl. Acad. Sci. U.S.A. 115, E7275–E7284 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]

[r27] 27.Tubbs J. D., Zhang Y. D., Sham P. C., Intermediate confounding in trio relationships: The importance of complete data in effect size estimation. Genet. Epidemiol. 44, 395–399 (2020). [DOI] [PubMed] [Google Scholar]

[r28] 28.Warrington N. M.et al.; EGG Consortium , Maternal and fetal genetic effects on birth weight and their relevance to cardio-metabolic risk factors. Nat. Genet. 51, 804–814 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]

[r29] 29.Bulik-Sullivan B.et al.; ReproGen Consortium; Psychiatric Genomics Consortium; Genetic Consortium for Anorexia Nervosa of the Wellcome Trust Case Control Consortium 3 , An atlas of genetic correlations across human diseases and traits. Nat. Genet. 47, 1236–1241 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]

[r30] 30.Bycroft C., et al., The UK Biobank resource with deep phenotyping and genomic data. Nature 562, 203–209 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]

[r31] 31.Lu Q., et al., A powerful approach to estimating annotation-stratified genetic covariance via GWAS summary statistics. Am. J. Hum. Genet. 101, 939–964 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]

[r32] 32.Zhao Z., et al., Fine-tuning polygenic risk scores with GWAS summary statistics. bioRxiv [Preprint] (2019). 10.1101/810713 (Accessed 28 March 2020). [DOI]

[r33] 33.Grove J.et al.; Autism Spectrum Disorder Working Group of the Psychiatric Genomics Consortium; BUPGEN; Major Depressive Disorder Working Group of the Psychiatric Genomics Consortium; 23andMe Research Team , Identification of common genetic risk variants for autism spectrum disorder. Nat. Genet. 51, 431–444 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]

[r34] 34.Anttila V.et al.; Brainstorm Consortium , Analysis of shared heritability in common disorders of the brain. Science 360, eaap8757 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]

[r35] 35.Weiner D. J.et al.; iPSYCH-Broad Autism Group; Psychiatric Genomics Consortium Autism Group , Polygenic transmission disequilibrium confirms that common and rare variation act additively to create risk for autism spectrum disorders. Nat. Genet. 49, 978–985 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]

[r36] 36.Claussnitzer M., et al., A brief history of human disease genetics. Nature 577, 179–189 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]

[r37] 37.Young A. I., et al., Relatedness disequilibrium regression estimates heritability without environmental bias. Nat. Genet. 50, 1304–1310 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]

[r38] 38.Gao B., Yang C., Liu J., Zhou X., Accurate genetic and environmental covariance estimation with composite likelihood in genome-wide association studies. PLoS Genet. 17, e1009293 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]

[r39] 39.Sohail M., et al., Polygenic adaptation on height is overestimated due to uncorrected stratification in genome-wide association studies. eLife 8, e39702 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]

[r40] 40.Berg J. J., et al., Reduced signal for polygenic adaptation of height in UK Biobank. eLife 8, e39725 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]

[r41] 41.Yengo L., Yang J., Visscher P. M., Expectation of the intercept from bivariate LD score regression in the presence of population stratification. bioRxiv [Preprint] (2018). 10.1101/310565 (Accessed 5 November 2020). [DOI]

[r42] 42.Huang K., et al., Transcriptome-wide transmission disequilibrium analysis identifies novel risk genes for autism spectrum disorder. PLoS Genet. 17, e1009309 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]

[r43] 43.Zhang Y., et al., Local genetic correlation analysis reveals heterogeneous etiologic sharing of complex traits. bioRxiv [Preprint] (2020). 10.1101/2020.05.08.084475 (Accessed 5 November 2020). [DOI] [PMC free article] [PubMed]

[r44] 44.Karavani E., et al., Screening human embryos for polygenic traits has limited utility. Cell 179, 1424–1435.e8 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]

[r45] 45.Crow J. F., Kimura M., An Introduction to Population Genetics Theory (Harper & Row, New York, 1970). [Google Scholar]

[r46] 46.Yengo L., et al., Imprint of assortative mating on the human genome. Nat. Hum. Behav. 2, 948–954 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]

[r47] 47.Fletcher J. M., Wu Y., Zhao Z., Lu Q., The production of within-family inequality: Insights and implications of integrating genetic data. bioRxiv [Preprint] (2020). 10.1101/2020.06.06.137778 (Accessed 15 July 2020). [DOI] [PMC free article] [PubMed]

[r48] 48.Guo G., Wang L., Liu H., Randall T., Genomic assortative mating in marriages in the United States. PLoS One 9, e112322 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]

[r49] 49.Manichaikul A., et al., Robust relationship inference in genome-wide association studies. Bioinformatics 26, 2867–2873 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]

[r50] 50.Abraham G., Qiu Y., Inouye M., FlashPCA2: Principal component analysis of biobank-scale genotype datasets. Bioinformatics 33, 2776–2778 (2017). [DOI] [PubMed] [Google Scholar]

[r51] 51.Loh P.-R., et al., Efficient Bayesian mixed-model analysis increases association power in large cohorts. Nat. Genet. 47, 284–290 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]

[r52] 52.Okbay A.et al.; LifeLines Cohort Study , Genome-wide association study identifies 74 loci associated with educational attainment. Nature 533, 539–542 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]

[r53] 53.Purcell S., et al., PLINK: A tool set for whole-genome association and population-based linkage analyses. Am. J. Hum. Genet. 81, 559–575 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]

[r54] 54.Willer C. J., Li Y., Abecasis G. R., METAL: Fast and efficient meta-analysis of genomewide association scans. Bioinformatics 26, 2190–2191 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]

[r55] 55.Auton A.; The 1000 Genomes Project Consortium , A global reference for human genetic variation. Nature 526, 68–74 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]

[r56] 56.Choi S. W., O’Reilly P. F., PRSice-2: Polygenic Risk Score software for biobank-scale data. Gigascience 8, giz082 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]

[r57] 57.R Core Team , R: A Language and Environment for Statistical Computing (R Core Team, 2020). [Google Scholar]

PERMALINK

Estimating genetic nurture with summary statistics of multigenerational genome-wide association studies

Yuchang Wu

Xiaoyuan Zhong

Yunong Lin

Zijie Zhao

Jiawen Chen

Boyan Zheng

James J Li

Jason M Fletcher

Qiongshi Lu

Series information

Significance

Abstract

Results

Method Overview.

Fig. 1.

Table 1.

Simulation Results.

Fig. 2.

Direct and Maternal Effects on Birth Weight.

Fig. 3.

Partitioning Direct and Indirect Genetic Effects on EA.

Fig. 4.

Fig. 5.

Discussion

Methods

Method Details.

Simulation.

UKB Data Processing.

Birth Weight GWAS Analysis.

GWAS on Offspring EA.

GWAS on Own EA in UKB.

Genetic Correlation Analysis.

PGS Calculation and Regression Analysis.

pTDT Analysis.

Supplementary Material

Acknowledgments

Footnotes

Data Availability

References

Associated Data

Supplementary Materials

Data Availability Statement

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases