Significance
In tumors, tissue oxygen heterogeneity leading to the appearance of hypoxic regions is linked to poor prognosis and reduces the efficiency of therapeutic treatment. Following previous reports that vessel compression, caused by the tumor, leads to tumor tissue oxygen heterogeneity, we formulate a computational model to investigate the mechanism whereby vessel compression affects tissue oxygenation. Our results show that compressed vessels lead to an abnormal partitioning of red blood cells at vascular bifurcations and therefore heterogeneity in oxygen transport to tissue. This work uncovers a biomechanical causal link between vessel compression and tumor tissue oxygen heterogeneity, furthering our understanding of the tumor microenvironment and contributing to an emergent theory of biotransport in tumors that can underpin future therapeutic approaches.
Keywords: tumor vasculature, vessel compression, hematocrit dynamics, oxygen heterogeneity, mathematical modeling
Abstract
The tumor microenvironment is abnormal and associated with tumor tissue hypoxia, immunosuppression, and poor response to treatment. One important abnormality present in tumors is vessel compression. Vessel decompression has been shown to increase survival rates in animal models via enhanced and more homogeneous oxygenation. However, our knowledge of the biophysical mechanisms linking tumor decompression to improved tumor oxygenation is limited. In this study, we propose a computational model to investigate the impact of vessel compression on red blood cell (RBC) dynamics in tumor vascular networks. Our results demonstrate that vessel compression can alter RBC partitioning at bifurcations in a hematocrit-dependent and flow rate–independent manner. We identify RBC focusing due to cross-streamline migration as the mechanism responsible and characterize the spatiotemporal recovery dynamics controlling downstream partitioning. Based on this knowledge, we formulate a reduced-order model that will help future research to elucidate how these effects propagate at a whole vascular network level. These findings contribute to the mechanistic understanding of hemodilution in tumor vascular networks and oxygen homogenization following pharmacological solid tumor decompression.
The tumor microenvironment (TME) is abnormal and associated with tumor tissue hypoxia (1), which is a known biomarker for poor prognosis (2). In addition, tumor hypoxia is a source of immunosuppression (3) and constitutes a barrier to the success of recent promising immunotherapeutic approaches (3, 4). As such, researchers have proposed normalizing the TME to improve oxygenation and overcome these limitations (3). One of the abnormalities of the TME is vessel compression (5, 6), which is a consequence of the proliferation of cells within a solid tumor and the growth of the tumor against its surroundings (7). Fang et al. (8) showed that the presence of compressed microvessels in tumor tissue is a promising prognosis predictor in non–small-cell lung cancer patients. Furthermore, Chauhan et al. (9) demonstrated that normalizing the TME through decompressing solid tumors leads to increased survival rate in animal models, when combined with chemotherapy, as well as increased tumor tissue oxygenation and homogeneity. However, our knowledge of the biophysical mechanisms linking tumor decompression to increased tumor oxygenation is limited.
Oxygen binds to hemoglobin in red blood cells (RBCs) and is transported through the vasculature with the RBCs. Early investigations demonstrated that hematocrit (the volume fraction of RBCs in total blood) can vary between child branches of a vascular bifurcation as a function of hemodynamic and geometrical vessel properties (see ref. 10 for a review). Our recent work has shown that vascular development works to avoid vessel segments with rare or transient RBC flow through them (11). However, the abnormal TME is associated with marked heterogeneity in hematocrit (12), including reports of plasma-only channels (13). We recently identified reduced interbifurcation distance as a source of hematocrit variation via its impact on RBC partitioning at bifurcations (14). However, the impact that other tumor vascular phenotypes such as vessel compression have on this process is not known.
In vitro work has provided some evidence of how RBC suspensions behave in the presence of a compression in single, straight, channels. At low hematocrits (5%), the narrowing of a channel leads to a focusing of the RBCs toward the center of the channel (15, 16). Fujiwara et al. (17) performed a similar experiment in an asymmetric geometry at higher hematocrits (20%) and similarly saw a focusing of the RBCs toward the channel center. They observed that this is more pronounced at lower hematocrits (17). The focusing of RBCs is identified to be due to an increased shear rate within the compressed section of the channel (15, 17). However, whether the narrowing in RBC cross-sectional distribution postcompression is permanent or not is unclear, nor is it clear how the narrowing of the RBCs toward the channel center has an impact on RBC partitioning at a downstream bifurcation.
Investigating the transport dynamics of oxygen and other blood-borne solutes in realistic tumor networks is challenging due to the limited experimental tools available. Several groups have proposed the use of mathematical modeling to bridge this gap (18–21). In this work, we propose a computational model to study how vessel compression impacts the partitioning of RBCs at a downstream bifurcation. We report the finding that, below a critical hematocrit threshold, vessel compression alters the partitioning of RBCs at the downstream bifurcation due to a change in the cross-sectional distribution of the RBCs induced by the compression. Furthermore, we show that this is independent of flow rate and compression asymmetry. In addition, we report the mechanism and length scale for the cross-sectional distributions of RBCs to return to their precompression configuration. Finally, we propose a reduced-order model to calculate RBC partitioning at a bifurcation downstream of a compression in a computationally efficient manner. Future investigations can use this reduced-order model to link vessel compression to tumor tissue oxygen heterogeneity on a whole vascular network level.
Taken together, our findings suggest that 1) protection against abnormal partitioning at bifurcations due to naturally occurring morphological variations in vessel cross-section can be achieved during development by homogenizing and increasing the average hematocrit in networks, 2) increased perfusion (in terms of total flow rate through the network) is not sufficient to reverse the anomalous RBC partitioning due to vessel compression, and 3) the link between solid stress and oxygen heterogeneity in tumors, and its reported reversal via stress alleviation, can be partially explained via anomalous RBC partitioning at bifurcations due to compressed vessels.
Results
At 10% Hematocrit, Vessel Compression Alters RBC Partitioning at a Downstream Bifurcation.
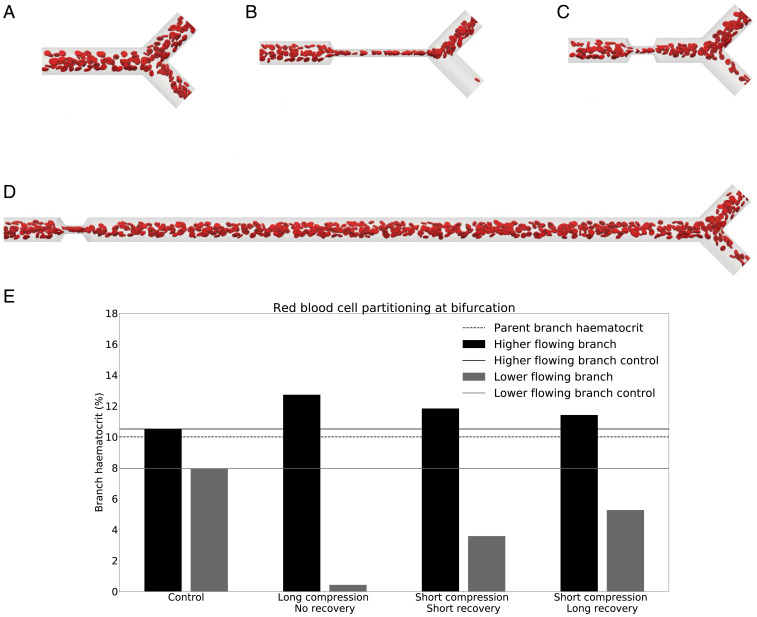
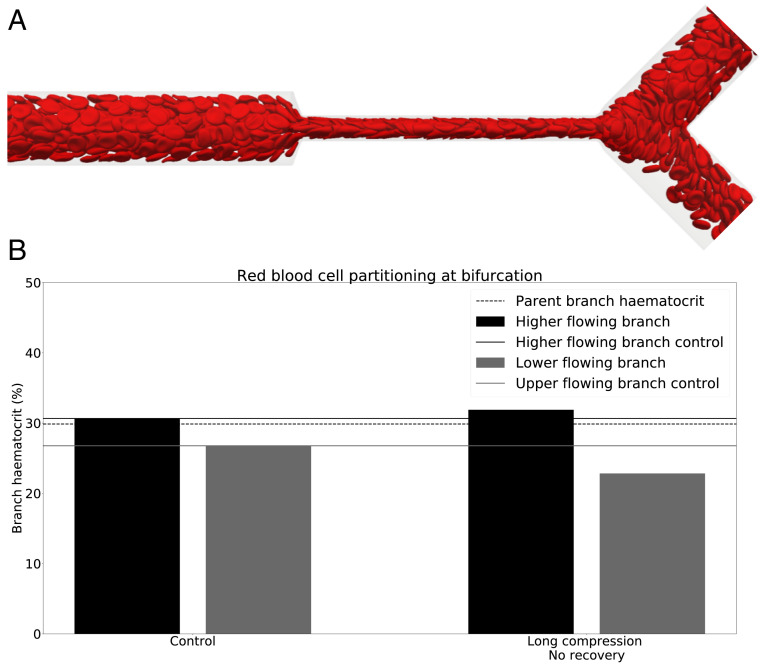
We start by investigating whether vessel compression has an impact on RBC partitioning at a downstream bifurcation. Simulation results for a long compression at 10% hematocrit (Fig. 1B) reveal that the RBC split at the bifurcation is strongly affected by the compression. Fig. 1E shows that, for a long compression, the child branch with the lower flow rate is almost depleted of RBCs and has approximately 0.5% hematocrit, whereas the control simulation indicates that the same branch has 8% hematocrit in the absence of a compression. The control simulation is in agreement with the standard plasma skimming model (SI Appendix, Fig. S1).
Fig. 1.
Phase separation in child branches after a bifurcation at . (A–D) Snapshots of the control (A); long compression, no recovery (B); short compression, short recovery (C); and short compression, long recovery (D), respectively. (E) The hematocrit in the child branches for these four cases. Black/gray indicates the higher/lower-flowing child branch, respectively. Solid lines are the control discharge hematocrits. The dotted line illustrates the discharge hematocrit of the parent branch.
The short compression, short recovery geometry (Fig. 1C) shows a smaller impact on the RBC split than the long compression. With hematocrit in the child branch with the lower flow rate, this is still less than half of the hematocrit in the control simulation.
To test whether the symmetry of the compression has an effect on the partitioning of the RBCs at the downstream bifurcation, we investigated an asymmetric compression (SI Appendix, Fig. S2). The simulation results are similar to those obtained with a symmetric compression. Thus, we infer that, under the present conditions, the asymmetry of the compression does not have an important effect on the downstream partitioning of RBCs.
We also investigated the effect of flow rate on RBC partitioning. By changing the flow rate, we change the capillary number, which quantifies the deformation of the RBCs. We performed two additional simulations at a capillary number of 0.02 and 0.5, to cover the RBC tumbling and tank-treading regimes and the range of flow rates typical for the tumor microvasculature (12). SI Appendix, Fig. S3 shows that the RBC partitioning does not change with capillary number, which implies that the flow rate and capillary number are not important parameters for RBC partitioning in the presence of a compression within the studied range of flow rates.
Narrowing of Cell Distribution Alters Partitioning of RBCs.
Next, we investigated which mechanism leads to the observed changes in partitioning and why the different geometries have different effects.
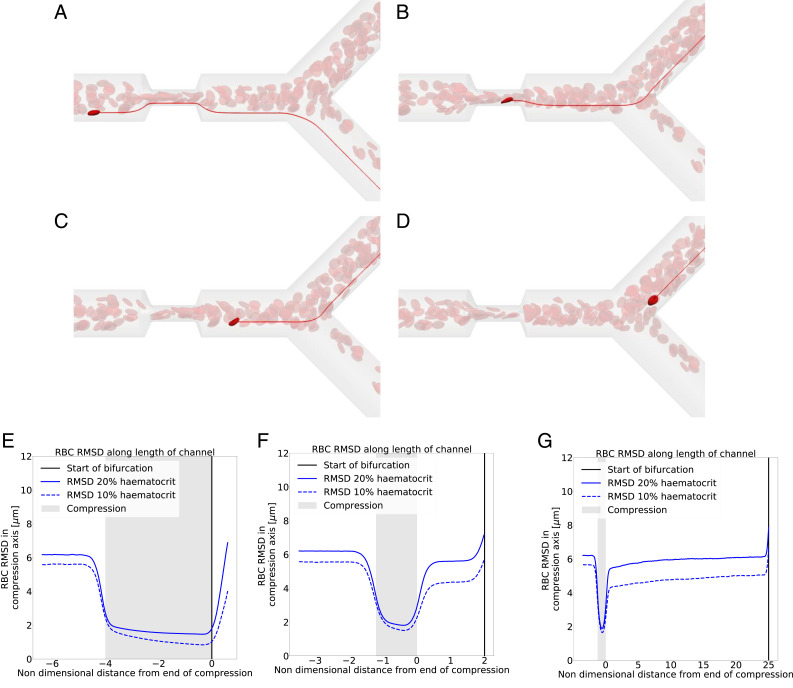
As blood flows through the compression, the shear rate increases since 1) the fluid velocity within the compression is larger due to mass conservation and 2) the width of the channel along the compression axis is reduced. Our simulations show that RBCs situated close to the wall prior to the compression migrate across streamlines toward the channel center. After leaving the compression, RBCs do not immediately migrate back toward the wall. As a consequence, the RBC distribution downstream of the compression is narrower than that upstream of the compression. This explanation is in line with prior findings from experimentalists (17). Fig. 2 A–D illustrates this mechanism.
Fig. 2.
Narrowing of RBC distribution in compression. (A–D) In red are the streamlines of the underlying fluid. In bright red is an RBC of interest. (A) An RBC situated prior to the compression near the vessel wall. (B) The same RBC after it has crossed streamlines within the compression. (C) The RBC exits the compression on a more central streamline than the one on which it entered the compression. (D) The RBC goes to a different branch than the precompression streamline it was on. (E–G) RBC RMSD along the vessel length, solid line at and dashed line at . Blue line is the RMSD, black vertical line is the point of bifurcation, and shaded gray zone is the compression area. Geometries are (E) long compression, no recovery; (F) short compression, short recovery; and (G) short compression, long recovery. The child branch flow ratio is 4:1 in all cases.
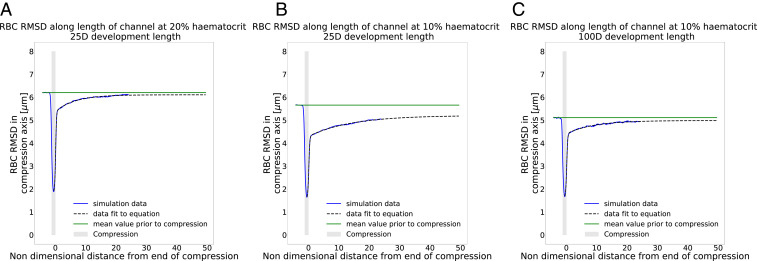
To quantify the narrowing of the RBC distribution, we plot the root-mean-squared distance (RMSD) of the RBC centers of mass along the compression axis. Fig. 2 E–G shows that, for all geometries, there is a narrowing of the distribution of cells in and after the compression compared to that in the region before the compression. However, in the short recovery geometries (Fig. 2 F and G), the RBC distribution partially recovers before the cells reach the bifurcation. This explains why the RBC partitioning is more affected when there is no recovery length between compression and bifurcation (Fig. 2E). Previous studies report an increase of the cell-free layer (CFL) postcompression compared to the CFL thickness precompression, here seen as a narrowing of the RBC distribution, which leads to a partitioning bias of RBCs toward the higher-flowing branch (22).
To investigate the behavior of the RBC distribution after the compression, we increased the distance between the compression and the bifurcation from to (Fig. 1D). Fig. 2G shows a gradual recovery of the RBC distribution between the compression and bifurcation, although 25 channel diameters are not sufficient to reach the same RMSD as before the compression.
While our data imply that a mechanism exists that leads to the recovery of the RBC distribution, it is not clear a priori what the underlying mechanism is. We assume that, given enough channel length after the compression, the RBC distribution will fully recover eventually. Katanov et al. (23) demonstrated that, from an initially uniform distribution of RBCs in a channel, the formation of a stable CFL is governed by the shear-rate time scale and takes a length of about 25 vessel diameters to form, independently of flow rate, hematocrit, or vessel diameter. Our data suggest that the opposite effect, the recovery of an initially heterogeneous RBC distribution where most of the RBCs are close to the channel center, cannot be described in the same way since a length of 25 channel diameters is not sufficient for recovery. The shear rate is lower and cells move faster near the channel centerline, which should lead to a weaker shear-induced recovery of the cell distribution along a distance of . We hypothesize that cell–cell interactions are the dominant driver for the recovery.
Abnormal Partitioning Is Present in a Large Range of Flow Ratios.
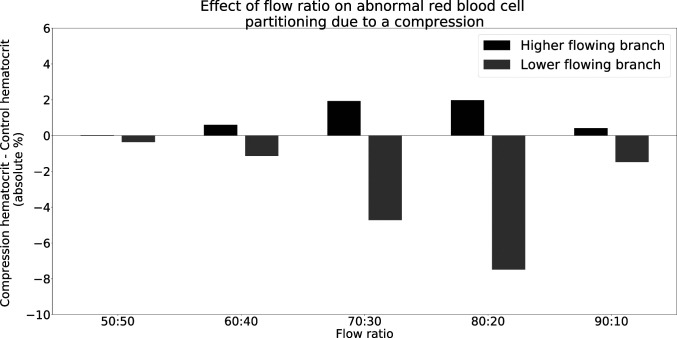
We next investigate the effect of the flow ratio on the abnormal partitioning of RBCs downstream of the compression. We varied the flow ratio from 50:50 to 90:10 in five steps and measured the difference between the compression geometry and the control geometry. Fig. 3 reveals that abnormal partitioning is present over a wide range of flow ratios, except for the 50:50 case. Since the compression is symmetric (Fig. 2) and both downstream branches behave identically in the 50:50 case, the overall symmetry is retained and an equal number of RBCs enter both branches. Therefore, the 50:50 split does not lead to abnormal partitioning. The presence of a small difference between the compression and the control for the 50:50 case in Fig. 3 is attributable to the finite number of RBCs in the simulations.
Fig. 3.
Effect of flow ratio on phase separation of blood downstream of a compression at . The difference between the control geometry (Fig. 1A) and the compression geometry (Fig. 1B) is an absolute hematocrit value. A positive value denotes a hematocrit enrichment compared to the control geometry, and a negative value denotes a hematocrit reduction compared to the control geometry. Note that the flow ratios X:Y and Y:X would give the same results due to the symmetry of the geometry.
We also observe that the degree of abnormal partitioning is largest for the 80:20 case and sharply decreases for the 90:10 case. When the flow ratio in a bifurcation increases, the low-flow branch has a decreasing discharge hematocrit, until the branch eventually becomes a pure plasma branch (10), even in uncompressed geometries. Therefore, in the 90:10 case, the discharge hematocrit in the low-flow branch is already small, and any change due to abnormal partitioning will also be small. Eventually, when the flow ratio is sufficiently high, there will be no difference between the compression and control geometries.
Increasing Hematocrit Reduces Bias in RBC Partitioning.
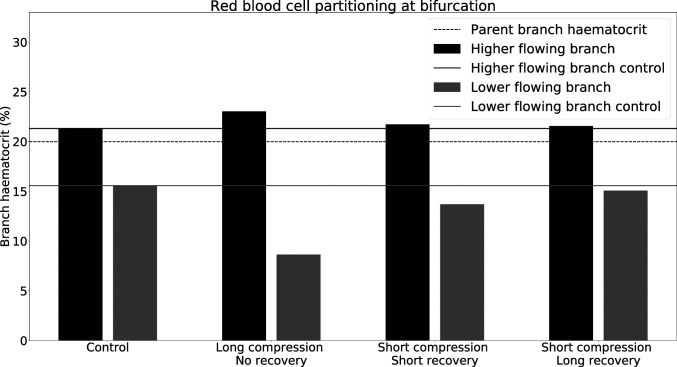
To test the hypothesis that cell–cell interactions drive the recovery of the distorted RBC distribution, we investigate blood flow at an increased hematocrit of 20%. Fig. 4 shows that the long compression, no recovery geometry still leads to a deviation from the control simulation. However, the deviation is smaller than at 10% hematocrit (Fig. 1). This observation can be explained by Fig. 2 E–G, which reveals that the narrowing of the RBC distribution is less pronounced at higher hematocrit compared to lower hematocrit. We conclude that, as the hematocrit increases, hydrodynamic cell–cell interactions become more relevant, leading to a smaller narrowing of the cell distribution by the compression as well as a faster decay of the narrowed RBC distribution after the compression.
Fig. 4.
Phase separation in child branches after a bifurcation at . Black/gray indicates the hematocrit in the higher/lower-flowing child branch, respectively. Solid lines are the control discharge hematocrits. The dotted line illustrates the discharge hematocrit of the parent branch. The child branch flow ratio is 4:1 in all cases.
For the short compression, long recovery geometry, the deviation from the control is almost nonexistent at (Fig. 4). While the control simulation shows hematocrit in the lower-flowing child branch, the compression merely alters that value to . As can be seen from Fig. 2F, not only is the narrowing of the RBC distribution in the compression smaller, but also after exiting the compression the RBC distribution is much closer to its precompression counterpart.
We also investigated the role of the distance between the short compression and the bifurcation by increasing it from to . Fig. 2G shows that the RBC distribution with eventually recovers and goes back to its precompression level, contrary to the simulation at 10% hematocrit.
The decreasing effect of the constriction on the RBC distribution at increasing hematocrit raises the question of whether there is a critical hematocrit above which the RBC partitioning is not modified by the presence of an upstream constriction. To that end, we increased the hematocrit in the parent branch to 30% and revisited the long compression geometry that has no recovery length between compression and bifurcation. Fig. 5 shows that there is no significant difference in RBC split when compared to the control without compression. We conclude that the critical hematocrit value lies near 30%.
Fig. 5.
Phase separation in child branches after a long bifurcation at . (A) The snapshot of the simulation in the long compression. The child branch flow ratio is 4:1. (B) The hematocrit of the child branches. Black/gray indicates the higher/lower-flowing child branch, respectively. Solid lines are the control discharge hematocrits. The dotted line illustrates the discharge hematocrit of the parent branch.
Reduced-Order Model.
A challenge in the theoretical study of RBC transport in networks is computational expense (24–26). For this reason, several authors have proposed the use of reduced-order models to quantify the partitioning of RBCs at bifurcations, which is key for tissue oxygenation modeling due to the RBC’s role as oxygen carrier. The most common model existing for partitioning of RBCs is that presented by Pries et al. (27, 28), although others exist (29).
We have demonstrated that vessel compression indeed has an impact on the partitioning of RBCs at a downstream bifurcation and that this is not captured by a state-of-the-art reduced-order model. To investigate how this effect propagates on a network level, we propose a reduced-order model that captures this phenomenon. We make four main assumptions for the reduced-order model:
-
1)
An RBC’s center of mass will go to the same child branch as its underlying streamline. This assumption relies on the low Reynolds number of the system, which is true for the microcirculation, where the Reynolds number is (10). Similar to reports of RBCs crossing the separatrix prior to a bifurcation (22, 30, 31), in our simulations we observed of RBCs near the separatrix crossing streamlines. Due to this small fraction, we deem the assumption appropriate.
-
2)
A curved separatrix independent of the diameter ratio between the child and parent branch and independent of Reynolds number is used, whereas the curvature of the separatrix generally depends on both parameters (31, 32). Since blood flow in the microvasculature is in the low-Reynolds regime, a small change in Reynolds number has a negligible effect on the separatrix. The diameter ratio has been shown to have a more significant impact, even at a Reynolds number of 0 (32). However, the impact on the curvature of the separatrix is higher toward the vessel walls, where there are fewer or no RBCs due to the existence of the CFL. Considering the difficulty of parameterizing a curved separatrix as a function of diameter ratios, a curved separatrix for a diameter ratio of 1 is used at the expense of a small but acceptable modeling error.
-
3)
The cross-sectional distribution of RBC centers of mass can be approximated by a step function, whereas the distribution profile of RBCs tends to quickly, but not instantaneously, reduce at the edge of the RBC distribution as is often reported (33, 34) and indeed observed in our simulations. The step function, however, is a good fit and simplifies the model considerably. We assume the step function to take the shape of an ellipse on any given cross-section of the channel (Fig. 6 A–C). The fraction of RBCs ending up in the top and the bottom child branch is and , respectively, defined by the areas and above and below the separatrix. Since the separatrix is a consequence of the geometry and flow ratio to each child branch, our model is applicable to all cases for which the separatrix is known.
-
4)
The cross-section that determines which child branch an RBC enters is located about upstream of the bifurcation. Our simulations show that this is the upstream perturbation length after which the streamlines start to curve to enter the child branches. The length is similar to that found in other studies (31). Therefore, the reduced-order model needs to be able to predict the cross-sectional distribution of the RBCs up to a point upstream of the bifurcation.
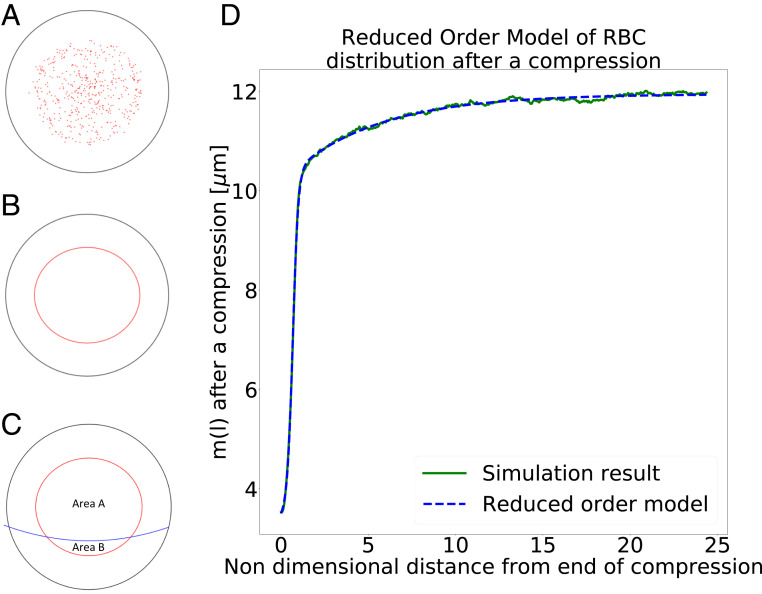
Fig. 6.
Reduced-order model. (A) The RBCs’ centers of mass are shown on a cross-section. (B) An ellipse is used to represent the distribution of the RBCs. (C) The curved separatrix is added. Any RBC above the separatrix is assumed to go to the top branch and any RBC below it to go to the bottom branch. (D) from the reduced-order model in Eq. 1 with parameters from Table 1 for 20% hematocrit compared to simulation data.
The step function that approximates the RBC distribution in a channel cross-section has the form of an ellipse. Therefore, the major and minor semiaxes of this ellipse, and , need to be defined. We found that the best results are obtained when
-
1)
the aspect ratio of the ellipse is determined by the ratio of the RMSD along the width and height directions (where the height direction is the axis of the compression) and
-
2)
the ellipse encloses 90% of the RBCs’ centers of mass.
Next, we propose a function that describes the development of the radius , along the compression axis, of the step function along the channel length between the end of the compression (defined as ) and the point upstream of the bifurcation. The area of the ellipse is given by , where and are the major and the minor semiaxis of the ellipse for the step function. Once the minor axis , which is , and the aspect ratio are known, the model can predict the number of RBCs entering either child branch.
Our simulations show that there are three key mechanisms governing the lateral RBC distribution when entering and leaving the compression. The first one is that the RBC distribution is suddenly narrowed by the compression. Second, upon exiting the compression, the RBC distribution sees a quick but only partial lateral recovery due to the expansion of the streamlines. Finally, cell–cell interactions lead to a slow recovery of the RBC distribution to its precompression distribution via cross-streamline migration if given sufficient length. We model the flow expansion of the RBC distribution with a logistic term and the cross-streamline recovery with an exponential decay:
| [1] |
For , at the downstream end of the compression, the equation returns the ellipse radius inside the compression, which is within 5% of , due to the second term becoming very small when , but not vanishing. is the change in RBC distribution due to the flow expansion, which occurs over a length scale . The length determines the steepness of the slope. is the change in RBC distribution due to cell–cell interaction, which occurs over a longer length scale . For long distances, , we have , which is the width of the fully recovered RBC distribution and the width of the unperturbed RBC distribution before the compression. If is not sufficiently large, the RBC distribution is still affected by the compression, and the RBC split in the bifurcation tends to be biased accordingly. Although it may be possible to construct a reduced-order model with fewer parameters, the advantage of Eq. 1 is that all parameters have a physical meaning and can potentially be predicted by separate models.
We obtained the numerical values of the parameters in the reduced-order model by fitting to the simulation data for 10 and 20% hematocrit, respectively. The parameters are listed in Table 1, and Fig. 1D shows an excellent agreement between and the simulation data at . In particular, we find that , independently of the chosen hematocrit. This value corresponds to the characteristic length that describes the streamline recovery after a distortion. We find that the cross-streamline recovery length reduces by a factor of about 2 when the hematocrit is increased from 10 to 20%. This is in line with literature reporting that shear-induced diffusion is directly proportional to the particle concentration (35).
Table 1.
Parameter values for Eq. 1 obtained by fitting the reduced-order model to simulation data
| Hematocrit, % | , m | , m | , m | |||
| 10 | ||||||
| 20 |
With the reduced-order model being calibrated, we can now predict the RBC partitioning at the downstream bifurcation and compare these results with actual RBC simulation data. We apply the separatrix model to the cross-sectional RBC distribution predicted by the reduced-order model at the length that marks the distance between the compression and the point of bifurcation.
Table 2 compares the absolute difference in discharge hematocrit obtained from the HemeLB simulations and the reduced-order model. We find that the reduced-order model accurately predicts the impact of the compression on the RBC partitioning at the downstream bifurcation within 1% on average. Notwithstanding the assumptions underlying the reduced-order model, the relative error is low. Our approach, therefore, provides a means of modeling the disturbance caused by a compressed vessel in network simulations, which has not been possible using established empirical models (27, 29). Despite this success, further simulations are necessary to extend the applicability of the reduced-order model to a larger parameter space.
Table 2.
Absolute differences of the discharge hematocrit in both child branches between the results of the HemeLB simulations and the predictions of the reduced-order model
 |
In each cell, the top left is the difference for the higher-flowing child branch, whereas the bottom right is the difference for the lower-flowing child branch. See Fig. 1 A–D for the respective geometries.
At 10% Hematocrit, a Converged Suspension of RBCs Requires a Long Development Length.
We observed that, at 20% hematocrit, the RMSD of the RBCs after downstream of the compression has recovered to 98% of its original value prior to the compression (Fig. 7A). However, at 10% hematocrit in the same geometry, the RMSD recovery is incomplete after . In fact, the reduced-order model predicts a partial recovery of the RMSD at to only 91% of its precompression value (Fig. 7B).
Fig. 7.
Recovery of RBC distribution after short compression. (A) Simulation at . (B and C) Simulations at . A and B are simulations with the cells inserted after of initialization length. C is a simulation with cells inserted after an initialization length of . The blue line is the simulation data, the black dashed line is the prediction of the reduced-order model, and the green line is the mean value of the RMSD prior to the compression.
Given the results in Fig. 7B, we hypothesize that, at 10% hematocrit, details of the RBC initialization in the simulation play a role. An inconsistent RBC distribution upstream of the compression might affect the overall outcome of the simulation. To confirm this, we increased the length of the periodic tube that is used to generate the RBC distribution fed into the compression geometry from (Fig. 7B) to (Fig. 7C). We observed that the longer tube leads to a narrowing in the precompression distribution of the RBCs (Fig. 7C). At 10% hematocrit, when the initialization length is , we can assume that the RBC distribution has reached a steady state. In fact, Fig. 7C shows that after the RMSD of the RBCs has recovered to 98% of its precompression value. Despite the sensitivity of the precompression distribution on the cell initialization strategy at , we found that the RBC dynamics after the compression are quantitatively and qualitatively similar for both RBC initialization lengths used.
Discussion
The tumor microvasculature is abnormal and linked to tumor tissue hypoxia (1), which is a known biomarker for poor prognosis (2) and a barrier to recent promising immunotherapeutic approaches (3). One such abnormality is vessel compression (5). Previous studies have shown that decompressing tumor vessels leads to increased survival rates (8) via increased perfusion (1, 8) and oxygen homogenization (9). However, the mechanism linking tumor decompression to increased oxygen homogeneity is unclear. Oxygen binds to hemoglobin in RBCs and is transported through the vasculature with the RBCs. We recently identified the reduced interbifurcation distance associated with the proangiogenic tumor environment as a source of oxygen heterogeneity via its impact on RBC splitting at bifurcations (14). However, the impact that other tumor vascular phenotypes, such as vessel compression, has on this process is not known.
Motivated by the limitations on experimental methods available to query this process, we propose a computational model to elucidate the link between vessel compression and abnormal RBC partitioning at bifurcations. Our numerical simulations show that a vessel compression enhances the disproportional partitioning of RBCs at a downstream bifurcation in favor of the higher flow-rate child branch, occurring over a wide range of flow ratios. This is a consequence of the previously identified narrowing of the RBC distribution within the vessel cross-section (17).
Similar to previous studies (15, 17), we identify the mechanism leading to this narrowing as RBC cross-streamline migration toward the vessel center due to an increased shear rate within the compression. Once the RBCs leave the compression, their cross-sectional distribution gradually goes back to their precompression configuration in a hematocrit-dependent manner. This process is significantly slower at 10% hematocrit, where the dynamics occur over a length of vessel diameters. However, at 20% hematocrit, there is an almost instantaneous recovery, and after 2 vessel diameters in length, the difference in RBC partitioning compared to a control simulation is negligible. Furthermore, we show that at 30% hematocrit, the difference between the compressed and control simulations is negligible. This suggests the presence of a critical hematocrit above which vessel compression no longer alters the partitioning of RBCs at a bifurcation. We hypothesize that the different dynamics at 10, 20, and 30% hematocrit are caused by cell–cell interaction, which increases with hematocrit. We also show that an asymmetric compression does not lead to a measurable difference in the partitioning of RBCs compared to a symmetric compression. Likewise, a reduction and increase in flow rate by a factor of 5, respectively, do not significantly change the RBC partitioning.
Our study focuses on a single vessel diameter of 33 m. As the abnormal partitioning of RBCs is attributed to a narrowing of the cross-sectional distribution of RBCs in the vessel, it follows that for single-file RBC flow in the microvasculature, the abnormal partitioning will be reduced or negligible. Therefore, we expect the abnormal distribution to be of significance in channels with diameter larger than around 8 m, the diameter of an RBC.
We propose a reduced-order model to approximate the partitioning of RBCs at a bifurcation downstream of a compression, which we show has an error of 1% compared to our fully resolved numerical simulations, in the range of parameters studied. This model has the potential to overcome the computational tractability limitations associated with simulating RBC flow in large computational domains. The reduced-order model will help to understand the network effects arising from the abnormal partitioning of RBCs, such as hematocrit heterogeneity at a network level and compensatory mechanisms due to changes in vessel resistance with hematocrit. This will contribute to unraveling the dynamics of oxygen transport in large vascular tumor networks.
The implications of our findings are multiple. First, our results show that the effect of vessel compression on the downstream partitioning of RBCs is apparent only when discharge hematocrit and the distance between the compression and the bifurcation are sufficiently low. Another study by our group showed that two consecutive bifurcations within a short distance can also alter the partitioning of RBCs at the downstream bifurcation (14). Furthermore, we showed that interbifurcation distances are much reduced in the tumor microenvironment, and Kamoun et al. (12) showed that hemodiluted vessels are more common and are present across a larger range of diameters in tumor networks than in controls. Taken together, this suggests that healthy vascular networks are structurally adapted to protect themselves from mechanisms leading to RBC transport heterogeneity and that this may be compromised in diseased networks.
Second, previous studies have shown that decompressing tumor vessels leads to increased survival rates (8, 9). This effect has been attributed to 1) increased tumor perfusion due to reduced vessel resistance (1, 8) and 2) reduced hypoxia fraction and increased oxygen homogeneity (9). Our results of anomalous RBC partitioning being unaffected by increases in flow rate support the view that increasing total perfusion through the network may not be sufficient to homogenize oxygenation if it is not accompanied by vessel decompression (or other forms of structural remodeling normalizing RBC partitioning). This finding is further supported by recent work demonstrating that hematocrit plays a more important role in the delivery of oxygen to tissue than the speed of the RBCs (36), indicating that hematocrit normalization can play a more critical role than increased perfusion for improved tissue oxygenation.
Third, Kamoun et al. (12) found that up to 29% of tumor vessels in an animal model of glioma experience hemodilution (defined as having hematocrits below 5%) and proposed a mechanism whereby extravasated plasma from leaky vessels would be reabsorbed by other vessels and lead to hemodilution. Along similar lines, recent studies have reported findings of tissue hypoxia near perfused vessels (2). Our results demonstrate that, in the presence of vessel compression and uneven flow split at bifurcations, hematocrit can decrease from 20% to nearly 0% following two consecutive bifurcations without contributions from interstitial fluid. Our present findings, therefore, provide an alternative explanation of the occurrence of hemodilution in tumor networks. Future work should elucidate the relative importance of these two mechanisms.
Finally, we identified that, in the semidilute regime of 10% hematocrit, achieving convergence in an RBC suspension that has been disturbed requires longer distances than previously thought. Katanov et al. (23) reported that it takes a length of 25 diameters for the CFL of a randomly initialized suspension in a straight channel to converge. However, our data suggest that up to of length is required for an initially compacted RBC distribution to expand and reach a steady distribution when the hematocrit is 10%. This finding supports the view that the cross-sectional distribution of RBCs at low in vivo hematocrits may be away from equilibrium not only in diseased vascular networks, as we previously showed in tumors (14), but also under physiological conditions where interbifurcation lengths average fewer than . Further research into the network-level dynamics arising from our results is warranted.
As a final comment, our results should be considered for in vitro experiments that need to carefully consider the design of microfluidic devices if full convergence of RBC suspensions is required in the semidilute regime. It is also an additional challenge for in silico studies with open boundary conditions, where not only the insertion of cells needs to be considered (37), but also their cross-sectional distribution.
In this work we have demonstrated that vessel compression can alter RBC partitioning at a downstream bifurcation. Interestingly, this happens in a hematocrit-dependent and flow rate–independent manner. We argue that these findings contribute to the mechanistic understanding of hemodilution in tumor vascular networks and oxygen homogenization following pharmacological solid tumor decompression. Furthermore, we have formulated a reduced-order model that will help future research elucidate how these effects propagate at a whole network level. Unraveling the causal relationship between tumor vascular structure and tissue oxygenation will pave the way for the development of improved therapeutic strategies.
Materials and Methods
Physical Model.
We model blood flow as a suspension of deformable RBC particles in a continuous plasma phase. The plasma is treated, to leading-order effect within the range of shear rates considered (38), as a continuous Newtonian fluid, with the non-Newtonian properties of blood arising from the presence of the deformable RBCs. The model for the RBC membrane is hyperelastic, isotropic, and homogeneous. We characterize the RBC deformability with the capillary number
| [2] |
where is the fluid dynamic viscosity, is a characteristic shear rate, is a characteristic length (the RBC radius), and s is the strain modulus of the RBCs. The capillary number is set to 0.1, unless stated otherwise.
The numerical algorithm is implemented in the software HemeLB (https://github.com/hemelb-codes/hemelb) (39), and the simulations have been run on the ARCHER supercomputer. The results of the simulations are available online (40). Further information on the model and the numerical implementation is available in SI Appendix.
Geometry.
We produced four geometries representing a vessel with diameter and a downstream bifurcation. The first geometry is a control (no compression, Fig. 1A), while the remaining three geometries feature a single compression upstream of the bifurcation. The first compression model (Fig. 1B) contains a long compression without a recovery length between compression and bifurcation. In the second compression model (Fig. 1C), the compression is short, and there is a short recovery length between compression and bifurcation. The last geometry (Fig. 1D) features a short compression followed by a long recovery segment. The relevant geometrical parameters of all four geometries are summarized in Table 3.
Table 3.
Dimensions of the geometry ( is channel diameter)
| Geometry name | Compression length | Distance between compression and bifurcation |
| Control | N/A | N/A |
| Long compression, no recovery | 0 | |
| Short compression, short recovery | ||
| Short compression, long recovery |
N/A, not applicable.
We set the channel diameter to m, a typical value for the tumor microvasculature (12). We assume the cross-section of the channel to be circular, except for the section that is compressed, where it takes an elliptical form. We assume the perimeter of the cross-section to be constant along the channel, setting the ellipse perimeter to the same value as the uncompressed circular cross-section. The segment with elliptical cross-section has an aspect ratio of 4.26 (8). The assumption of an elliptical cross-section within the compression is in line with observations from tumor histological slices where vessel compression is commonly reported as the aspect ratio of the elliptical shape of the vessel cross-sections (8, 41–43).
Our aim is to focus on the effect of the compression. Therefore, we remove any effect from the slope leading to the compression by having a steep transition to and from the compression. We also remove the effect of a bifurcation asymmetry by having both child branches at the same diameter and angle from the parent branch.
Inlet and Outlet Boundary Conditions.
We set the outflow boundary conditions at the child branches as a Poiseuille velocity profile with an imposed maximum velocity and control the ratio of these velocities such that one child branch receives 80% of the flow and the other child branch 20%. Unless specified otherwise, the inlet branch has an average velocity of 600 m/s, a typical value for the tumor microvasculature (12).
The inlet boundary condition is an arbitrary pressure value that has no impact on the simulation result. To reduce any memory effects and establish a quasi–steady-state distribution of RBCs, the cells flow through a straight tube with a length of 25 tube diameters before entering the compression (23); we call this length the initialization length.
We vary the value of hematocrit within our system from 10 to 30%, covering a wide range that is physiologically present within the tumor microvasculature (12).
The physical Reynolds number of the system is 0.04. Therefore, viscous forces dominate and the system is in the Stokes flow regime. For computational tractability we set the numerical Reynolds number to 1, where inertial forces still do not play a significant role.
Processing Results.
All hematocrits reported are discharge hematocrits. We calculate the discharge hematocrit, , by calculating the fraction of RBC flow to total blood flow at any channel cross-section normal to the direction of flow,
| [3] |
where is the volumetric flow rate of RBCs and is the volumetric flow rate of blood, i.e., plasma and RBCs. The flow rate of RBCs is calculated by counting the RBCs crossing a plane normal to the direction of flow over a given period, . Knowing the volume of an RBC, , one can calculate the RBC flow rate,
| [4] |
where is the number of cells that have crossed the plane.
To quantify the distribution of the RBCs in a cross-section, we measure the RMSD of the RBC centers of mass with respect to the channel centerline,
| [5] |
where is the ith RBC position, and is the channel center, both taken on a cross-section normal to the direction of flow at points of interest. SI Appendix, Fig. S4 illustrates how we obtain the positions in practice.
We nondimensionalize length by the vessel diameter , unless stated otherwise. By definition, we set the downstream end of the compression as the reference point with an axial position of 0. Axial positions are positive in the downstream direction () and negative in the upstream direction ().
The separatrix is an imaginary surface separating fluid particles going to one child branch from those going to the other child branch. It is an important tool for the investigation of RBC partitioning at a bifurcation (31). We determine the separatrix by completing a simulation without RBCs to obtain streamlines unperturbed by RBCs (see SI Appendix, Fig. S5 for details).
Supplementary Material
Acknowledgments
We acknowledge the contributions of the HemeLB development team. Software development was supported by the Engineering and Physical Sciences Research Council (EPSRC) (Grant eCSE-001-010). Supercomputing time on the ARCHER UK National Supercomputing Service (http://www.archer.ac.uk) was provided by the “UK Consortium on Mesoscale Engineering Sciences” under the EPSRC Grant EP/R029598/1. R.E. is funded by The University of Edinburgh through a Chancellor’s Fellow PhD studentship. D.H. is supported by the European Union’s Horizon 2020 research and innovation program under Grant 801423. M.O.B. is supported by grants from EPSRC (EP/R021600/1, EP/R029598/1), Fondation Leducq (17 CVD 03), and the European Union’s Horizon 2020 research and innovation program under Grant 801423. T.K. and M.O.B. are supported by EPSRC Grant EP/T008806/1.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2025236118/-/DCSupplemental.
Data Availability
HemeLB vessel compression simulation data have been deposited in Edinburgh DataShare (https://doi.org/10.7488/ds/3035) (40).
References
- 1.Jain R. K., Martin J. D., Stylianopoulos T., The role of mechanical forces in tumor growth and therapy. Annu. Rev. Biomed. Eng. 16, 321–346 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Michiels C., Tellier C., Feron O., Cycling hypoxia: A key feature of the tumor microenvironment. Biochim. Biophys. Acta Rev. Canc 1866, 76–86 (2016). [DOI] [PubMed] [Google Scholar]
- 3.Martin J. D., Cabral H., Stylianopoulos T., Jain R. K., Improving cancer immunotherapy using nanomedicines: Progress, opportunities and challenges. Nat. Rev. Clin. Oncol. 17, 251–266 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Munn L. L., Jain R. K., Vascular regulation of antitumor immunity. Science 365, 544–545 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Padera T., et al. , Cancer cells compress intratumour vessels. Nature 427, 695 (2004). [DOI] [PubMed] [Google Scholar]
- 6.Nia H. T., Munn L. L., Jain R. K., Physical traits of cancer. Science 370, eaaz0868 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Stylianopoulos T., et al. , Causes, consequences, and remedies for growth-induced solid stress in murine and human tumors. Proc. Natl. Acad. Sci. U.S.A. 109, 15101–15108 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Fang L., et al. , Flattened microvessel independently predicts poor prognosis of patients with non-small cell lung cancer. Oncotarget 8, 30092–30099 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Chauhan V. P., et al. , Angiotensin inhibition enhances drug delivery and potentiates chemotherapy by decompressing tumour blood vessels. Nat. Commun. 4, 2516 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Secomb T. W., Blood flow in the microcirculation. Annu. Rev. Fluid Mech. 49, 443–461 (2017). [Google Scholar]
- 11.Zhou Q., et al. , Association between erythrocyte dynamics and vessel remodelling in developmental vascular networks. J. R. Soc. Interface, in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kamoun W. S., et al. , Simultaneous measurement of RBC velocity, flux, hematocrit and shear rate in vascular networks. Nat. Methods 7, 655–660 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Dewhirst M. W., et al. , Microvascular studies on the origins of perfusion-limited hypoxia. Br. J. Canc. 74, 247–251 (1996). [PMC free article] [PubMed] [Google Scholar]
- 14.Bernabeu M. O., et al. , Abnormal morphology biases haematocrit distribution in tumour vasculature and contributes to heterogeneity in tissue oxygenation. Proc. Natl. Acad. Sci. U.S.A. 117, 27811–27819 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Faivre M., Abkarian M., Bickraj K., Stone H. A., Geometrical focusing of cells in a microfluidic device: An approach to separate blood plasma. Biorheology 43, 147–159 (2006). [PubMed] [Google Scholar]
- 16.Abay A., Recktenwald S. M., John T., Kaestner L., Wagner C., Cross-sectional focusing of red blood cells in a constricted microfluidic channel. Soft Matter 16, 534–543 (2020). [DOI] [PubMed] [Google Scholar]
- 17.Fujiwara H., et al. , Red blood cell motions in high-hematocrit blood flowing through a stenosed microchannel. J. Biomech. 42, 838–843 (2009). [DOI] [PubMed] [Google Scholar]
- 18.Grimes D. R., et al. , Estimating oxygen distribution from vasculature in three-dimensional tumor tissue. J. R. Soc. Interface 13, 20160070 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.D’Esposito A., et al. , Computational fluid dynamics with imaging of cleared tissue and of in vivo perfusion predicts drug uptake and treatment responses in tumours. Nat. Biomed. Eng. 2, 773–787 (2018). [DOI] [PubMed] [Google Scholar]
- 20.Arvanitis C. D., et al. , Mechanisms of enhanced drug delivery in brain metastases with focused ultrasound-induced blood–tumor barrier disruption. Proc. Natl. Acad. Sci. U.S.A. 115, E8717–E8726 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Stylianopoulos T., Munn L. L., Jain R. K., Reengineering the physical microenvironment of tumors to improve drug delivery and efficacy: From mathematical modeling to bench to bedside. Trends Canc. 4, 292–319 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Barber J. O., Alberding J. P., Restrepo J. M., Secomb T. W., Simulated two-dimensional red blood cell motion, deformation, and partitioning in microvessel bifurcations. Ann. Biomed. Eng. 36, 1690–1698 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Katanov D., Gompper G., Fedosov D. A., Microvascular blood flow resistance: Role of red blood cell migration and dispersion. Microvasc. Res. 99, 57–66 (2015). [DOI] [PubMed] [Google Scholar]
- 24.Balogh P., Bagchi P., The cell-free layer in simulated microvascular networks. J. Fluid Mech. 864, 768–806 (2019). [Google Scholar]
- 25.Krüger T., Varnik F., Raabe D., Efficient and accurate simulations of deformable particles immersed in a fluid using a combined immersed boundary lattice Boltzmann finite element method. Comput. Math. Appl. 61, 3485–3505 (2011). [Google Scholar]
- 26.Závodszky G., Van Rooij B., Azizi V., Hoekstra A., Cellular level in-silico modeling of blood rheology with an improved material model for red blood cells. Front. Physiol. 8, 8 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Pries A., Ley K., Classen M., Gaehtgens P., Red cell distribution at microvascular. Microvasc. Res. 38, 81–101 (1989). [DOI] [PubMed] [Google Scholar]
- 28.Pries A. R., Secomb T. W., Microvascular blood viscosity in vivo and the endothelial surface layer. Am. J. Physiol. Heart Circ. Physiol. 289, 2657–2664 (2005). [DOI] [PubMed] [Google Scholar]
- 29.Gould I. G., Linninger A. A., Hematocrit distribution and tissue oxygenation in large microcirculatory networks. Microcirculation 22, 1–18 (2015). [DOI] [PubMed] [Google Scholar]
- 30.Doyeux V., Podgorski T., Peponas S., Ismail M., Coupier G., Spheres in the vicinity of a bifurcation: Elucidating the Zweifach-Fung effect. J. Fluid Mech. 674, 359–388 (2011). [Google Scholar]
- 31.Wang Z., Sui Y., Salsac A. V., Barthès-Biesel D., Wang W., Motion of a spherical capsule in branched tube flow with finite inertia. J. Fluid Mech. 806, 603–626 (2016). [Google Scholar]
- 32.Enden G., Popel A. S., A numerical study of the shape of the surface separating flow into branches in microvascular bifurcations. J. Biomech. Eng. 114, 398–405 (1992). [DOI] [PubMed] [Google Scholar]
- 33.Shen Z., et al. , Inversion of hematocrit partition at microfluidic bifurcations. Microvasc. Res. 105, 40–46 (2016). [DOI] [PubMed] [Google Scholar]
- 34.Sherwood J. M., Holmes D., Kaliviotis E., Balabani S., Spatial distributions of red blood cells significantly alter local haemodynamics. PloS One 9, e100473 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Grandchamp X., Coupier G., Srivastav A., Minetti C., Podgorski T., Lift and down-gradient shear-induced diffusion in red blood cell suspensions. Phys. Rev. Lett. 110, 1–5 (2013). [DOI] [PubMed] [Google Scholar]
- 36.Lücker A., Secomb T. W., Weber B., Jenny P., The relative influence of hematocrit and red blood cell velocity on oxygen transport from capillaries to tissue. Microcirculation 24, 1–12 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Lykov K., Li X., Lei H., Pivkin I. V., Karniadakis G. E., Inflow/outflow boundary conditions for particle-based blood flow simulations: Application to arterial bifurcations and trees. PLoS Comput. Biol. 11, e1004410 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Varchanis S., Dimakopoulos Y., Wagner C., Tsamopoulos J., How viscoelastic is human blood plasma? Soft Matter 14, 4238–4251 (2018). [DOI] [PubMed] [Google Scholar]
- 39.Mazzeo M. D., Coveney P. V., HemeLB: A high performance parallel lattice-Boltzmann code for large scale fluid flow in complex geometries. Comput. Phys. Commun. 178, 894–914 (2008). [Google Scholar]
- 40.Enjalbert R., Hardman D., Krüger T., Bernabeu M. O., HemeLB vessel compression simulation data. DataShare Edinburgh. 10.7488/ds/3035. Deposited 11 May 2021. [DOI] [Google Scholar]
- 41.Hagendoorn J., et al. , Onset of abnormal blood and lymphatic vessel function and interstitial hypertension in early stages of carcinogenesis. Canc. Res. 66, 3360–3364 (2006). [DOI] [PubMed] [Google Scholar]
- 42.Aromando R. F., et al. , Angiogenesis in potentially malignant lesions and carcinomas during experimental oral carcinogenesis: A preliminary study in the hamster cheek pouch. Anticancer Res. 34, 6381–6388 (2014). [PubMed] [Google Scholar]
- 43.Tadeo I., et al. , Vascular patterns provide therapeutic targets in aggressive neuroblastic tumors. Oncotarget 7, 19935–19947 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
HemeLB vessel compression simulation data have been deposited in Edinburgh DataShare (https://doi.org/10.7488/ds/3035) (40).