Performance of Regression Models as a Function of Experiment Noise

Abstract

Background:

A challenge in developing machine learning regression models is that it is difficult to know whether maximal performance has been reached on the test dataset, or whether further model improvement is possible. In biology, this problem is particularly pronounced as sample labels (response variables) are typically obtained through experiments and therefore have experiment noise associated with them. Such label noise puts a fundamental limit to the metrics of performance attainable by regression models on the test dataset.

Results:

We address this challenge by deriving an expected upper bound for the coefficient of determination (R²) for regression models when tested on the holdout dataset. This upper bound depends only on the noise associated with the response variable in a dataset as well as its variance. The upper bound estimate was validated via Monte Carlo simulations and then used as a tool to bootstrap performance of regression models trained on biological datasets, including protein sequence data, transcriptomic data, and genomic data.

Conclusions:

The new method for estimating upper bounds for model performance on test data should aid researchers in developing ML regression models that reach their maximum potential. Although we study biological datasets in this work, the new upper bound estimates will hold true for regression models from any research field or application area where response variables have associated noise.

Background

Machine learning (ML) based regression analysis, which is used to discover complex relationships between sample features and labels (supervised learning), is frequently applied in diverse biological fields including metabolic engineering, ¹ protein engineering, ² and systems biology.^3-5 A key question when developing these supervised ML models is whether there is sufficient information in the available data to accurately predict sample labels. For a given dataset, the performance of the best possible function for mapping input features to sample labels should thus be estimated to serve as a benchmark in ML model development. This level of performance is typically referred to as Bayes optimal error for classification problems. ⁶ In many classical ML problems—such as image classification, handwriting recognition and speech recognition—human-level performance at the task is very high and can therefore be used as a heuristic to estimate maximal performance.^7,8 However, for biological multi-dimensional data, human-level performance is low and is therefore not a good performance estimate. On the contrary, in biology one often seeks to train ML models for the explicit purpose of recognizing patterns and gaining insights that were obscured from the human intellect.^9,10 Therefore, without a clear performance benchmark against which to bootstrap biological regression models, it is difficult to know whether further model development is worth-while and when the performance limit has been reached.

When testing the performance of trained ML regression models on holdout data, the discrepancy between predicted labels and observed labels in a test dataset is evaluated using metrics such as the mean squared error (MSE) and the coefficient of determination (R²). ¹¹ Sample labels used in regression analysis of biological systems are typically real numbers obtained through measurements in a set of laboratory experiments. Such measurements inextricably have experimental noise and measurement error associated with them,^12-14 thus affecting the quality of the sample labels. Because of such label noise a ML model with an MSE of 0 or R² of 1 (perfect prediction) cannot be achieved; there is an upper bound that cannot be surpassed. Methods to estimate this upper bound are underdeveloped, although some progress has been made recently.^15,16 Moreover, the resources invested into model development have diminishing returns on model performance as one approaches the upper bound. Knowing the best expected MSE or R² (i.e. the upper bounds) of a specific regression problem and dataset enables the discrepancy between current and potential model performance to be quantified, thus giving researchers a means to assess the cost-benefit trade-off of further model development.

In the present study, we mathematically derive a method to estimate upper bounds for the regression model performance metrics MSE and R² on holdout data directly from the experimental noise associated with response variables in a dataset and independently of their predictors. Using Monte Carlo simulations, we show that this method is highly accurate and outperforms existing ones. Furthermore, by applying the method to real biological modeling problems and datasets, including protein sequence data, transcriptomics data and genomics data, we demonstrate how the new upper bound estimates can inform model development.

Methods

Enzyme catalytic temperature optima dataset

We first collected T_opt of 5675 enzymes with known protein sequences from BRENDA. ¹⁷ Of these 3096 enzymes were successfully mapped to a microbial optimal growth temperature (OGT) database. ¹⁸ To obtain a clean dataset with less noise we carried out several steps: (1) Enzymes for which the T_opt entry contained “assay at” in the BRENDA “comments” field were removed from the raw dataset. (2) If a subset of all enzymes from a specific organism had the same EC number and exactly the same T_opt, then these were removed. This was done to address an issue with non-perfect matching between experimental data from the literature and Uniprot identifiers (186 enzymes). (3) Enzymes with multiple T_opt values having standard deviations greater than 5 were removed (96 enzymes). After these steps, 1902 enzymes remained in the cleaned dataset, of which 1232 were with known OGT. In both raw and cleaned datasets, any sequences shorter than 30 residues or containing letters that are not in 20 standard amino acids were discarded and for enzymes still with multiple T_opt values the average value was used. Estimation of label noise: For enzymes with multiple T_opt values in BRENDA, the variance for each enzyme was calculated. Subsequently, the average variance for all those enzymes was calculated and used as the estimation of experimental noise $\overline{{\sigma }_y^2}$ of the dataset. For the cleaned dataset the label noise was estimated at step (2) in the paragraph above, before samples with high standard deviation were removed.

Protein transcription level dataset

Genomic data including open reading frame (ORF) boundaries of Saccharomyces cerevisiae C288 was obtained from the Saccharomyces Genome Database (https://www.yeastgenome.org/)^19,20 and published data.^21,22 Coding regions were extracted based on ORF boundaries and codon frequencies were normalized to probabilities. Processed raw RNA sequencing Star counts were obtained from the Digital Expression Explorer V2 database (http://dee2.io/index.html) ²³ and filtered for experiments that passed quality control. Raw mRNA data were transformed to transcripts per million (TPM) counts ²⁴ and genes with zero mRNA output (TPM < 5) were removed. Prior to modeling, the mRNA counts were Box-Cox transformed. ²⁵

Yeast pangenome and quantitative traits dataset

The gene presence/absence (P/A) encoding of S. cerevisiae pan genome were obtained from Li et al. ²⁶ The 35 quantitative traits were obtained from Peter et al. ²⁷

Monte Carlo simulations on expected $R^2$ score

Given the true functions between features and labels $f(x)$ :

1. Randomly generate 1000 samples from $N(0,1)$ as $x$ . Then true values are $y=f(x)$ ;

2. Randomly generate a noise vector ${\epsilon }_y$ . Each ${\epsilon }_{y,i}$ is randomly sampled from $N(0,{\sigma }_{y,i}^2)$ , where ${\sigma }_{y,i}^2$ is randomly sampled from ${\chi }^2(1)$ ;

3. $y_{obs}=y+{\epsilon }_y$ ;

4. Add noise to $x_{obs}=x+{\epsilon }_x$ , in which ${\epsilon }_x$ is sampled from a normal distribution with zero-mean and variance of ${\sigma }_x^2$ (varying from 0 to 1);

5. Calculate $R_{ML}^2$ by performing a 2-fold cross-validation on dataset $\{x_{obs,i},y_{obs,i}\}$ with support vector machine regression model (another inner 2-fold cross-validation for hyper-parameter optimization);

6. Calculate upper bound for $R^2$ with ${〈R^2〉}_{LG}=\frac{{\sigma }_{obs}^2-\overline{{\sigma }_y^2}}{{\sigma }_{obs}^2}$ and ${〈R^2〉}_{FP}=\frac{{\sigma }_{obs}^2-2\overline{{\sigma }_y^2}}{{\sigma }_{obs}^2}$ , where ${\sigma }_{obs}^2$ is the variance of $y_{obs}$ and $\overline{{\sigma }_y^2}$ is the average value of randomly generated ${\sigma }_{y,i}^2$ .

7. Repeat steps 1 to 6 for 1000 times.

A linear function $f(x)=2x+1$ and a nonlinear function $f(x)=2sin(x)+1$ were tested, respectively.

Monte Carlo simulations on data cleaning

Define a linear function $f\left(x\right)={\displaystyle \sum }_{i=1}^{10}{x}_i$ as the true function to map 10 features to a target $y$ . Each feature follows a standard normal distribution.

1. Randomly generate feature of 1000 samples as $X$ . Calculate real target values $y$ ;

2. Randomly generate a noise vector ${\epsilon }_y$ . Each ${\epsilon }_{y,i}$ is randomly sampled from $N(0,{\sigma }_{y,i}^2)$ , where ${\sigma }_{y,i}^2$ is randomly sampled from ${\chi }^2(5)$ ;

3. Calculate observed target values via $y_{obs}=y+{\epsilon }_y$ , and resulted a dataset $\{X,y_{obs}\}$ ;

4. Assume we only know the first $n$ features $(n=2,4,6,8,10)$ , Sort all samples based on ${\sigma }_{y,i}^2$ values, gradually remove the samples with the highest ${\sigma }_{y,i}^2$ values, calculate $R^2$ score of a linear function via a 2-fold cross validation on such a dataset with only a subset of features.

5. Repeat steps 1 through 4 for a total of 100 times.

Feature extraction for enzymes in T_opt dataset

The 5494 features from iFeature were broken up into 20 sub-feature sets according to their types, and their predictive power was evaluated using 5 different regression models (linear, elastic net, Bayesian ridge, decision tree and random forest regressors).

A total of 20 different sets of protein features were extracted with iFeature ²⁸ using default settings: amino acid composition (AAC, 20 features), dipeptide composition (DPC, 400), composition of k-spaced amino acid pairs (CKSAAP, 2400), dipeptide deviation from expected mean (DDE, 400), grouped amino acid composition (GAAC, 5), composition of k-spaced amino acid group pairs (CKSAAGP, 150), grouped dipeptide composition (GDPC, 25), grouped tripeptide composition (GTPC, 125), Moran autocorrelation (Moran, 240), Geary autocorrelation (Geary, 240), normalized Moreau-Broto (NMBroto, 240), composition-transition-distribution (CTDC, 39; CTDT, 39; CTDD, 195), conjoint triad (CTriad, 343), conjoint k-spaced triad (KSCTriad, 343), pseudo-amino acid composition (PAAC, 50), amphiphilic PAAC (APAAC, 80), sequence-order-coupling number (SOCNumber, 60) and quasi-sequence-order descriptors (QSOrder, 100). In total, we obtained 5494 features from iFeature. Furthermore, we additionally obtained features in the form of sequence embedding representations encoded by a deep learning model UniRep, ²⁹ which is a Multiplicative Long-Short-Term-Memory (mLSTM) Recurrent Neural Networks (RNNs) that was trained on the UniRef50 dataset. ³⁰ A total of 1900 $\mathrm{\times }$ 3 features were extracted for each protein sequence using UniRep.

Supervised classical ML methods

Input features were first scaled to a standard normal distribution by $x_{N,i}=\frac{x_i-u_i}{{\sigma }_i}$ , where $x_i$ is the values of feature i of all samples, $u_i$ and ${\sigma }_i$ are the mean and standard deviation of $x_i$ , respectively. Two linear regression algorithms BayesianRidge and Elastic Net as well as three non-nonlinear algorithms Decision Tree, Random Forest and Support Vector Machine ⁶ were evaluated on each feature set (iFeatures and UniRep). The evaluation was conducted via a nested cross-validation approach: an inner 3-fold cross validation was used for the hyper-parameter optimization via a grid-search strategy and an outer 5-fold cross-validation was used to estimate the model performance (see Table S2 for hyper-parameter values). With the transcriptomics data, linear regression was the only algorithm used, as it was previously found to outperform all other algorithms with a similar dataset. ⁵ For genomics datasets, only the random forest regression was tested. All ML analysis was performed with scikit-learn (v0.20.3) ³¹ using default settings and Python v3.6.7.

Supervised deep ML methods

To test the performance of a deep neural networks on the prediction of enzyme T_opt, architectures were tested that comprised up to 9 convolutional neural network (CNN) layers ³² followed by 2 fully connected (FC) layers. ³³ Batch normalization ³⁴ and weight dropout ³⁵ were applied after all layers and max-pooling ³⁶ after CNN layers. The Adam optimizer ³⁷ with MSE loss function and ReLU activation function ³⁸ with uniform ⁷ weight initialization were used. In total, 26 hyper-parameters were optimized over a predefined parameter space (Table S3) using a tree-structured Parzen estimators approach ³⁹ at default settings for 1000 iterations.^40,41 The Keras v2.2 and Tensorflow v1.10 software packages were used.

Prediction of T_opt for enzymes from BRENDA and CAZy

Sequences and associated OGT values for the BRENDA database was obtained from Li et al. ⁴² For the CAZy database, enzyme information including protein name, EC number, Organism, GenBank id, Uniprot id, PDB id and CAZy family id were obtained from http://www.cazy.org/. ⁴³ 1 346 471 proteins with unique GenBank identifiers were obtained. Protein sequences were first downloaded from NCBI ftp site: https://ftp.ncbi.nih.gov/ncbi-asn1/protein_fasta/. Then only those sequences that were present in the CAZy dataset were kept by matching GenBank identifier. 924 642 sequences could be mapped to an OGT value by cross-referencing the source organism name and an OGT dataset. ¹⁸ Only the species names were checked, ignoring strain designations, for instance S. cerevisiae S288 C was considered as S. cerevisiae. For T_opt prediction on the BRENDA and CAZy data, the model with the best performance was selected, which in this case was the random forest model trained only on amino acid frequencies and OGT. The model was then trained on all samples in the training dataset. For the prediction, (1) the 20 amino acid frequencies were extracted with iFeature ²⁸ and OGT values of their source organisms were mapped; (2) all these 21 features were normalized by subtracting the mean and then divided by the standard deviation obtained from the training dataset; and (3) these data were used as input of the model for the prediction of the T_opt values.

Theoretical Analysis

Starting from first principles, we mathematically derived a method to estimate upper bounds of model performance on holdout data in terms of R² and benchmarked the upper bound estimates against existing methods.

Estimating the theoretical upper bound of regression model performance

Given a set of samples with experimentally determined labels $\left\{y_{obs,i}\right\}$ and corresponding unknown real labels $\left\{y_i\right\}$ , we assume a normally distributed experimental noise ${\epsilon }_{y,i}\sim N(0,{\sigma }_{y,i})$ : $y_{obs,i}=y_i+{\epsilon }_{y,i}$ ( $y_i\in R$ ), and that a complete set of features is known as $x_i\in R^k$ for each sample. This complete set of features can be used to calculate the real value of label $y_i$ with $y=f(x)$ for all samples. The performance of this real function $f(x)$ on the dataset $\{x_i,y_{obs,i}\}$ gives an upper bound for the expected performance of any ML model. The coefficient of determination ( $R^2$ ) is a common metric to assess model performance and thus the $R^2$ of the model in the above argument is given by

$$R^2=1-\frac{{{\displaystyle \sum }}_{i=1}^m{\left(y_{obs,i}-{\hat{y}}_{obs,i}\right)}^2}{{{\displaystyle \sum }}_{i=1}^m{\left(y_{obs,i}-{\overline{y}}_{obs}\right)}^2}=1-\frac{{{\displaystyle \sum }}_{i=1}^m{\left(y_{obs,i}-f\left(x_i\right)\right)}^2}{{{\displaystyle \sum }}_{i=1}^m{\left(y_{obs,i}-{\overline{y}}_{obs}\right)}^2}$$ (1)

where $m$ is the number of samples. Although it is not possible to obtain an exact value from the above equation, since the real values $f(x_i)$ are unknown, we can instead obtain the expectation of $R^2$ (Note S1), which is given by

$$〈R^2〉=1-〈\frac{{{\displaystyle \sum }}_{i=1}^m{\left(y_{obs,i}-f\left(x_i\right)\right)}^2}{{{\displaystyle \sum }}_{i=1}^m{\left(y_{obs,i}-{\overline{y}}_{obs}\right)}^2}〉=1-\frac{m}{m-3}\frac{\underset{\_}{{\sigma }_y^2}}{{\sigma }_{obs}^2}$$ (2)

and in which $\overline{{\sigma }_y^2}=\frac{1}{m}{\displaystyle \sum }_{i=1}^m{\sigma }_{y,i}^2$ . As the number of examples in ML is usually very large (m >> 1), we can approximate the final equation for upper bound estimation as

$$〈R^2〉\approx 1-\frac{\overline{{\sigma }_y^2}}{{\sigma }_{obs}^2}=\frac{{\sigma }_{obs}^2-\overline{{\sigma }_y^2}}{{\sigma }_{obs}^2}$$ (3)

We refer to this upper bound estimate as ${〈R^2〉}_{LG}$ hereafter. It has a variance of $\frac{2m\left(m-2\right)}{{\left(m-3\right)}^2\left(m-5\right)}\frac{\overline{{\sigma }_y^4}}{{\sigma }_{obs}^4}$ (Note S1). Similarly, the best MSE that one can expect is given as $〈MSE〉=\overline{{\sigma }_y^2}$ with a variance of $\frac{2\overline{{\sigma }_y^4}}{m}$ (Note S2). ${〈R^2〉}_{LG}$ gives a measure of the best R² one can expect when testing an ML model on a held out dataset.

The new upper bound estimate ${〈R^2〉}_{LG}$ , which is the $R^2$ expectation of the best possible ML model on holdout data, solely depends on 2 properties of the dataset: (1) the true variance of the observed response values $({\sigma }_{obs}^2)$ and (2) the average variance of experimental noise of all samples $(\overline{{\sigma }_y^2})$ . In practice, ${\sigma }_{obs}^2$ and $\overline{{\sigma }_y^2}$ are unknown and have to be approximated from the dataset. ${\sigma }_{y,i}$ can be approximated with the standard error (SE) of n replicates, which represent the standard error of the mean, and ${\sigma }_{obs}^2$ can be approximated as the variance of the target values (Figure 1). Since the resulting ${〈R^2〉}_{LG}$ is an expectation and relies on approximated values, it does not strictly represent an upper bound for the $R^2$ of regression models and the real value may be slightly higher or lower. In this way the ${〈R^2〉}_{LG}$ estimate is analogous to using human-level performance to approximate upper bounds in image classification applications.^44-47

Figure 1.

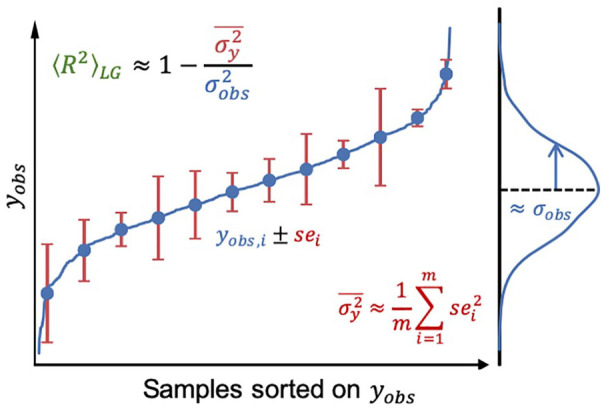
Schematic diagram depicting the estimation of the upper bound of model performance ${〈R^2〉}_{LG}$ based on experimental label noise. $\underset{\_}{{\sigma }_y^2}$ can be approximated from the standard errors (se) of samples in the dataset, and ${\sigma }_{obs}^2$ can be approximated as the variance of the target values. Data shown were randomly generated, se_i denotes standard error of sample i. ${〈R^2〉}_{LG}$ is the expected upper bound for the coefficient of determination $R^2$ derived in this study (see section “Estimating the theoretical upper bound of regression model performance”).

${〈R^2〉}_{LG}$ upper bound estimates outperform existing methods

In recent publications it has been proposed that, given a set of experimentally measured values $y_{obs,i}$ , the best possible model is $y=x$ in which $x$ are the values collected from another set of experiments conducted at identical conditions.^15,16 Under this assumption, the expectation of the upper bound for MSE is $2\overline{{\sigma }_y^2}$ and $R^2$ is $\frac{{\sigma }_{DB}^2-\overline{{\sigma }_y^2}}{{\sigma }_{DB}^2+\overline{{\sigma }_y^2}}$ , where $\overline{{\sigma }_y^2}$ is the average variance of all sample noise and ${\sigma }_{DB}^2$ is the variance of the real values (without noise). Since ${\sigma }_{DB}^2+\overline{{\sigma }_y^2}\approx {\sigma }_{obs}^2$ , the upper bound for $〈R^2〉$ becomes $\frac{{\sigma }_{obs}^2-2\overline{{\sigma }_y^2}}{{\sigma }_{obs}^2}$ , and we refer to this upper bound as ${〈R^2〉}_{FP}$ hereafter. Despite claims that no ML model could perform better than this upper bound,^15,16 by comparing the equations for ${〈R^2〉}_{LG}$ and ${〈R^2〉}_{FP}$ , it is clear that ${〈R^2〉}_{FP}$ estimates are lower than both ${〈R^2〉}_{LG}$ estimates as well as achieved ML model performance.

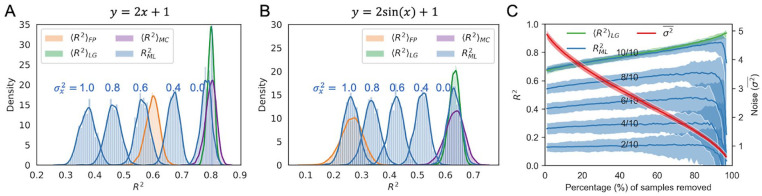
To directly compare ${〈R^2〉}_{FP}$ and ${〈R^2〉}_{LG}$ , we performed Monte Carlo simulations. Briefly, a random dataset $\left\{x_i,y_{obs,i}\right\}$ was generated from a known real function $f\left(x\right)$ with added experimental noise ${\sigma }_{y,i}$ (see section “Monte Carlo simulations on expected $R^2$ score”). For this dataset, ${〈R^2〉}_{FP}$ and ${〈R^2〉}_{LG}$ were calculated, and then the $R^2$ of a support vector machine regression model ⁴⁸ trained on the data was calculated via a 2-fold cross validation approach ( $R_{ML}^2$ ). This process was repeated for 1000 iterations. A linear (Figure 2A) and nonlinear real function (Figure 2B) were used in two separate simulations (see observed data distributions in Figure S1). Furthermore, to evaluate the effects of feature noise on regression model performance, we generated noise-free features ( ${\sigma }_x^2=0.0$ ), as well as features with different levels of noise associated with them ( ${\sigma }_x^2=0.2$ , ${\sigma }_x^2=0.4$ , ${\sigma }_x^2=0.6$ , ${\sigma }_x^2=0.8$ , ${\sigma }_x^2=1.0$ ). The simulations illustrated three key points. First, in both linear and nonlinear cases, $R_{ML}^2$ is always smaller than or close to ${〈R^2〉}_{LG}$ , which confirms that ${〈R^2〉}_{LG}$ gives a good estimation of the model performance upper bound. Second, the simulations show that there are ML models with $R_{ML}^2$ higher than ${〈R^2〉}_{FP}$ , which is contrary to the expectation if ${〈R^2〉}_{FP}$ is a true upper bound.^15,16 Third, as ${\sigma }_x^2$ increases, the ML model performance falls short of the $R^2$ upper bound, eventually falling below ${〈R^2〉}_{FP}$ . This shows that ${〈R^2〉}_{LG}$ gives a more accurate estimation of the upper bound for the performance of ML models at any condition, including cases with or without noisy features. ${〈R^2〉}_{FP}$ is however useful as an estimate of the reproducibility of experiments, in accordance with the assumptions in the original papers.^15,16

Figure 2.

Monte Carlo simulations of the upper bound of $R^2$ assuming different levels of feature noise. ${〈R^2〉}_{FP}$ and ${〈R^2〉}_{LG}$ are expected upper bounds for the coefficient of determination $R^2$ with equations derived by Benevenuta and Fariselli et al ¹⁵ and this study, respectively. ${〈R^2〉}_{MC}$ is the expected upper bound for $R^2$ obtained by Monte Carlo simulation as described in the “Results” section. $R_{ML}^2$ is the $R^2$ obtained via a 2-fold cross-validation with a support vector machine. Two real functions were tested; (A) linear and (B) nonlinear. ${\sigma }_x^2$ is the variance of noise added to feature vector $x$ , with examples of the observed data distributions depicted in Figure S1. (C) Monte Carlo simulation on data cleaning via gradually removing the samples with the largest ${\sigma }_{y,i}$ . n/10 indicates that n features out of a complete set of 10 features were used to train and validate the model. Noise values are given as the average variance of all samples $(\overline{{\sigma }^2})$ .

Since $x$ is normally distributed in the simulations (Figure 2B), $2sin(x)+1+ϵ$ gives a non-normal distribution for $y_{obs}$ values. While ${〈R^2〉}_{LG}$ was derived under the assumption that $y_{obs}$ is normally distributed, the Monte Carlo simulations indicate that ${〈R^2〉}_{LG}$ is accurate also when applied to non-normal distributions (Figure 2B). Since it is challenging to prove this mathematically, we devised an additional simulation strategy to further test whether ${〈R^2〉}_{LG}$ can be applied to a given dataset with non-normal distributed $y_{obs}$ values given the experimental noise. Following the same notations as “Estimating the theoretical upper bound of regression model performance,” we can get $y_i=y_{obs,i}-{\epsilon }_{y,i}$ , in which ${\epsilon }_{y,i}\sim N(0,{\sigma }_{y,i})$ . We can randomly draw a $y_i$ as an estimation of $y_i$ in this equation. The $R^2$ resulting from using $\left\{y_i\right\}$ as the prediction of $\left\{y_{obs,i}\right\}$ is an independent estimation of the best achievable $R^2$ . By repeating this step, a list of $R^2$ scores can be calculated and the average $R^2$ gives an estimation of the expectation of the best $R^2$ we can get (referred to as ${〈R^2〉}_{MC}$ ). Since ${〈R^2〉}_{MC}$ does not rely on the normality assumption of $y_{obs}$ values, it can be applied to any distribution. As shown in Figure 2A and B, ${〈R^2〉}_{LG}$ gives a consistent estimation of ${〈R^2〉}_{MC}$ , at least in the 2 tested cases (Figure 2A and B). With a dataset with non-normal distributed $y_{obs}$ values, one can use this simulation strategy to obtain a ${〈R^2〉}_{MC}$ to check if ${〈R^2〉}_{LG}$ gives a correct estimation.

In the above analysis, idealized conditions were used in that all features were known. Conversely, in real-world ML applications, typically only an incomplete set of features is known. To more accurately simulate this real-world situation, we performed Monte Carlo simulations using incomplete feature sets (see section “Monte Carlo simulations on data cleaning”). We also evaluated how ML model performance is affected by removal of the most noisy sample labels (Figure 2C). As anticipated, models trained with the full feature set (10/10) outperformed those trained with a subset of features, with the model containing all 10 features reaching the ${〈R^2〉}_{LG}$ (Figure 2C). Furthermore, model performance generally improved as noisy samples were removed. However, an interesting observation is that the degree to which the models improve upon removal of noisy samples depends on how many features were used to train them. For instance, if only a small fraction of relevant features were used (2/10 in Figure 2C), the removal of the most noisy samples did not improve model performance. In contrast, when a majority of the relevant features were known (8/10 and 10/10 in Figure 2C), the removal of noisy samples significantly improved the model performance in terms of $R^2$ . These results indicate that when $R_{ML}^2$ is very far from the ${〈R^2〉}_{LG}$ upper bound, model performance can be most readily improved by obtaining additional or more relevant features, as opposed to performing data cleaning to reduce sample noise.

Experimental Case Studies

We next explored the applicability of ${〈R^2〉}_{LG}$ to inform ML model development on real-world data that included enzyme optimal temperatures, transcriptomic and genomic datasets.

Using the theoretical upper bound to inform modeling

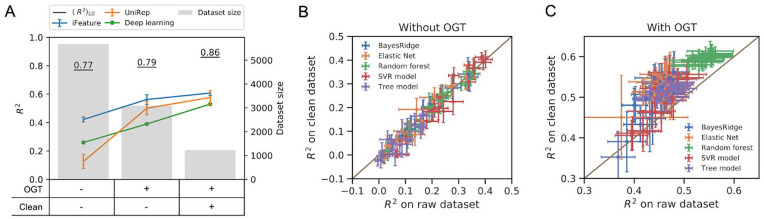
We first tackled the problem of obtaining models to accurately predict enzyme optimal catalytic temperatures (T_opt) using features extracted from their protein primary structures. A dataset comprising the T_opt of 5343 individual enzymes was collected from the BRENDA ¹⁷ database. Here, using enzymes for which T_opt values had been measured in multiple experiments, the experimental noise $\overline{{\sigma }_y^2}$ was estimated as $(7.84°C){}^2$ and ${\sigma }_{obs}^2$ was $(16.32°C){}^2$ , giving an ${〈R^2〉}_{LG}$ upper bound of 0.77. Moreover, an estimated ${〈R^2〉}_{MC}$ of 0.77 confirmed that ${〈R^2〉}_{LG}$ could be applied on this dataset with non-normally distributed T_opt values (Figure S2). To provide features for ML model training (see section “Supervised classical ML methods”), two established feature extraction methods were applied to the protein primary structures, one based on domain knowledge (iFeature, ²⁸ 5494 features) and the other based on embeddings obtained from unsupervised deep learning (UniRep, ²⁹ 5700 features). Despite testing six different types of regression algorithms to predict enzyme T_opt using the two feature sets, even the best achieved $R^2$ of 0.42 (average over 5-fold cross-validations, Figure 3A) was only 55% of the estimated ${〈R^2〉}_{LG}$ upper bound, indicating that the model could be further improved. Such improvement might be achieved through either feature engineering or noise reduction, as seen in the Monte Carlo simulations (Figure 2C).

Figure 3.

Development of machine learning models for the prediction of enzyme optimal temperature (T_opt). (A) Performance of classical models using iFeatures ²⁸ and UniRep encoding ²⁹ feature sets as well as a deep neural networks with one-hot encoded protein sequence as input. (B, C) Comparison of model performance on raw and clean dataset (B) with; and (C) without optimal growth temperature (OGT) as one of the features. The features calculated by iFeature were grouped into 20 sub-feature sets as described in the “Methods” section. Error bars show the standard deviation of $R^2$ scores obtained in 5-fold cross validation. ${〈R^2〉}_{LG}$ is the expected upper bound for the coefficient of determination $R^2$ derived in this study (see section “Estimating the theoretical upper bound of regression model performance”).

First, we performed feature engineering by including the OGT of the organism, from which the enzyme was derived, as an additional feature into the iFeature and UniRep feature sets. Consequently, the dataset size decreased to 2917 enzymes, as 55% of the samples were omitted due to unknown OGT values of their source organisms. This led to models improved by 33% and 384%, respectively (Figure 3A), and the best resulting $R^2$ (0.56) achieved 71% of the estimated ${〈R^2〉}_{LG}$ (0.79). These results are consistent with our previous work, ⁴² where it was shown that prediction of enzyme T_opt was significantly improved when including OGT as a feature. We then tested whether a deep convolutional neural network (Figure S3, see section “Supervised deep ML methods”) could discover additional features in the enzyme primary structures^5,40 and provide better predictive models (with/without OGT as an additional feature). This did not, however, lead to models that outperformed the classical ones trained on iFeatures (Figure 3A). Next, we considered reducing the noise $(\overline{{\sigma }_y^2})$ in T_opt values as a means to further improve model performance and used the information from the “comment” field associated with each enzyme in the BRENDA database to remove values that were deemed less likely to represent true catalytic optima (see section “Enzyme catalytic temperature optima dataset”). Despite dramatically reducing the number of samples in the dataset (1902 enzymes of which 1232 with known OGT), the experimental noise $\overline{{\sigma }_y^2}$ was reduced from $(7.84°C){}^2$ to $(7.22°C){}^2$ and the calculated ${〈R^2〉}_{LG}$ increased from 0.79 to 0.85 ( ${〈R^2〉}_{MC}$ was 0.85). Accordingly, the best model obtained with this dataset achieved an improved $R^2$ of 0.61, which again was around 71% of ${〈R^2〉}_{LG}$ . Here, in accordance with the expectation that large training datasets are required for optimal deep learning performance, ⁴⁰ the convolutional network displayed a reduced $R^2$ score (Figure 3A). Finally, further in-depth analysis to explore how different sub-features of the iFeature set contributed to predictive accuracy (20 sub-feature sets used, see section “Feature extraction for enzymes in T_opt dataset”) showed that each sub-feature set only improved model performance when OGT was included as an additional feature (Figures 3B, C and S4, 5). This is consistent with Monte Carlo simulation results showing that noise reduction is mainly beneficial with more complete feature sets (Figure 2C).

As a side note, we used the improved model (a random forest trained on amino acid composition and OGT) to update T_opt annotation of BRENDA enzymes in the Tome package ⁴² and also extended it to carbohydrate-active (CAZy) enzymes ⁴³ (Figure S6) (https://github.com/EngqvistLab/Tome).

Further analyses of ${〈R^2〉}_{LG}$ in relation to experimental noise

We next explored how the amount of experimental noise in the response variables can affect the ${〈R^2〉}_{LG}$ and model performance. A suitable problem for this was the prediction of intrinsic gene expression levels in S. cerevisiae, since thousands of RNAseq experiments across multiple conditions are available for this species. ²³ For a given gene, the intrinsic expression level was defined as the average mRNA level across the different experiments and conditions. ⁵ The noise level could then be adjusted by increasing or decreasing the number of sampled data points (i.e. replicates) (Figure 4 inset), where the corresponding standard deviation was used to quantify the amount of noise present within the intrinsic expression levels (see section “Protein transcription level dataset”). Apart from estimating the ${〈R^2〉}_{LG}$ upper bounds, the achievable predictive performance was explored by building linear regression models using DNA sequence features (codon usage)^5,49 as input. We observed a strong effect of the amount of experimental noise on the theoretical upper bound, especially with a smaller number of data replicates (Figures 4 and S7). Similarly, the variability of the ${〈R^2〉}_{LG}$ upper bound also markedly decreased with an increasing number of replicates. Therefore, with an insufficient amount of replicates, apart from a lower confidence in the estimated upper bound, the variability of the data was found to also drastically affect the predictive performance and accuracy of the models. This suggests that for data that are inherently noisy, such as those obtained from transcriptomics, the ${〈R^2〉}_{LG}$ upper bound, as well as the overall ML performance, can both be improved by increasing the number of experimental replicates generated for downstream computational analysis. ⁵⁰ For accurate condition-specific or cross-condition modeling, the number of replicates of at least 100, with most reliable results above 1000, should be used (Figures 4 and S6). Such dataset sizes are nowadays highly feasible, especially in the case of genomics, transcriptomics and proteomics data, as resources that comprise thousands of experiments are readily available for each model organism.^23,26,27

Figure 4.

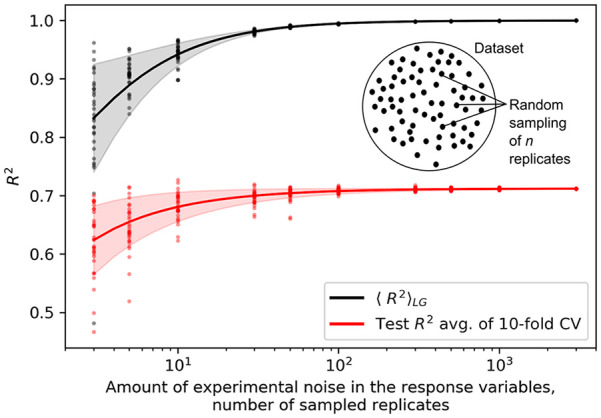
Amount of experimental noise affects estimates of ${〈R^2〉}_{LG}$ and model performance. Analysis of the effect of experimental noise in the response variables on the ${〈R^2〉}_{LG}$ upper bound estimates (black) and predictive performance of ML models (red) with the case of a large yeast multi-experiment transcriptomics dataset. ²³ The noise level was varied by adjusting the number of data replicates with random sampling (inset figure). Lines and shaded areas depict means and standard deviations of the 30 measurements per each n replicates, depicted as points. ${〈R^2〉}_{LG}$ is the expected upper bound for the coefficient of determination $R^2$ derived in this study (see section “Estimating the theoretical upper bound of regression model performance”), CV denotes cross validations.

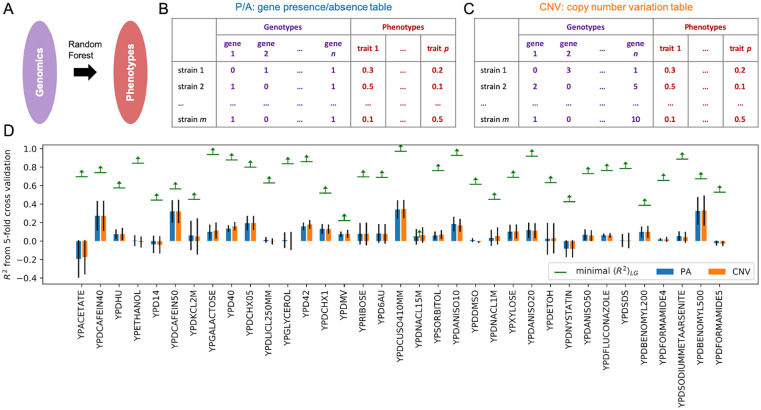
Finally, for some datasets it may not be feasible to estimate the experimental noise, for instance, if the values for replicates in an experiment are not available. We thus analyzed how ${〈R^2〉}_{LG}$ can be used to define the predictive potential of biological regression analysis even in the absence of direct experimental noise estimates. Since ${〈R^2〉}_{LG}$ is an upper bound estimate, $R_{ML}^2\le {〈R^2〉}_{LG}$ holds true, from which we obtain that $\overline{{\sigma }_y^2}\le (1-R_{ML}^2)\times {\sigma }_{obs}^2$ . If multiple datasets with the same level of (unknown) experimental noise are available, the inequality holds for all datasets, meaning that $\overline{{\sigma }_y^2}\le min(\{(1-R_{ML,i}^2)\times {\sigma }_{obs,i}^2|i=1,··,s\})$ , in which $s$ is the number of the datasets. In this way it is possible to estimate the maximal level of experimental noise based on the ML results, and then further use it to obtain the minimal value of ${〈R^2〉}_{LG}$ , where ${〈R^2〉}_{LG}$ could be any value between ${〈R^2〉}_{LG,min}$ and 1.0. This idea was applied on a problem to predict yeast phenotypes directly from genomes ⁵¹ (Figure 5A) using a dataset of growth profiles of 971 sequenced S. cerevisiae isolates under 35 stress conditions, ²⁷ where experimental noise was not reported nor replicate data provided (see section “Yeast pangenome and quantitative traits dataset”). To analyze these data we made use of a published S. cerevisiae pan-genome ²⁶ that included all protein-coding genes across 971 isolates with measured phenotypes. Here, the pan-genome was represented as either a gene presence/absence table (P/A, Figure 5B), or copy number variation table (CNV) which contains additional information to P/A (Figure 5C). Using these features we could estimate ${〈R^2〉}_{LG,min}$ for each condition by training a random forest regressor on the 35 different quantitative traits. P/A and CNV showed a similar predictive power and could explain at most 30% of the variance (Figure 5D: R² was ~0.3) for some traits like the growth profile under the YPD medium enriched with 40 mM of caffeine (YPDCAFEIN40). Furthermore, with $R_{ML}^2$ s for these 35 datasets, the maximal experimental noise were estimated as $\overline{{\sigma }_y^2}\le {0.076}^2$ , based on which we could finally estimate the ${〈R^2〉}_{LG,min}\approx 1-\frac{{0.076}^2}{{\sigma }_{obs,i}^2}$ for each condition (Figure 5C). Since most of the traits did not follow a normal distribution (Figure S8), ${〈R^2〉}_{MC}$ was obtained by Monte Carlo simulation with $\overline{{\sigma }_y^2}$ of ${0.076}^2$ for each dataset and was used to cross-check the ${〈R^2〉}_{LG}$ values, indicating that breaking the normality assumption did not adversely affect the $R^2$ estimate (Figure S9 $:{〈R^2〉}_{MC}$ was consistent with ${〈R^2〉}_{LG}$ ). Despite that for a small number of traits (e.g. YPDNACL15M) the low ${〈R^2〉}_{LG,min}$ was too low to be useful (Figure 5D), in most cases it was higher than the current predictive performance of our models (e.g. > 0.97 with YPDCUSO410MM). Thus, for most of the conditions, the estimated upper bounds showed great potential for further improvement of model performance (Figure 5D), demonstrating the applicability and usefulness of ${〈R^2〉}_{LG}$ even in case the experimental noise is unknown.

Figure 5.

${〈R^2〉}_{LG}$ is applicable even in case the experimental noise is unknown. Analysis of 34 quantitative traits of S. cerevisiae from its pan-genome composition. (A) A random forest model applied to predict yeast phenotypes from genomics features. Genomes are represented as (B) gene presence/absence table and (C) copy number variance table in the pangenome. ²⁶ (D) Obtained R² score for 35 different phenotypes. Experimental trait values were taken from Peter et al. ²⁷ Detailed label description can be found in Table S2 of Peter et al. ²⁷ Error bars show the standard deviation of $R^2$ scores obtained in 5-fold cross validation. ${〈R^2〉}_{LG}$ is the expected upper bound for the coefficient of determination $R^2$ derived in this study (see section “Estimating the theoretical upper bound of regression model performance”).

Discussion

In the present study, we establish a method to estimate an upper bound for expected ML regression model performance on holdout data. This addresses an important need in the ML field as human performance on multi-dimensional data is poor and cannot be used to bootstrap regression model performance,^9,10 an approach that is common when developing ML systems for image analysis.^7,8 The coefficient of determination upper bound (model performance) for regression analysis is: ${〈R^2〉}_{LG}\approx 1-\frac{\overline{{\sigma }_y^2}}{{\sigma }_{obs}^2}$ , and depends only on the experimental noise $\overline{{\sigma }_y^2}$ and the variance of observed labels ${\sigma }_{obs}^2$ (Figure 1), under the assumptions that observed label values $\left\{y_{obs,i}\right\}$ are normally distributed and that each $y_{obs,i}$ has a normally distributed experimental noise with 0 mean. With non-normally distributed $\left\{y_{obs,i}\right\}$ , we provide a Monte Carlo based approach ( ${〈R^2〉}_{MC}$ ) to estimate ${〈R^2〉}_{LG}$ . In all tested cases, ${〈R^2〉}_{LG}$ gives results consistent with ${〈R^2〉}_{MC}$ , indicating that even though it was derived under the normality assumption of $\left\{y_{obs,i}\right\}$ , it can also be applied to data with other distributions (Figures 2A and B and S8). ${〈R^2〉}_{LG}$ is thus confirmed using Monte-Carlo simulations and also shown to outperform existing measures ¹⁵ (Figure 2A and B).

Our case studies demonstrate how calculating the ${〈R^2〉}_{LG}$ upper bound estimate for experimental data yields a more realistic modeling objective than naively assuming that an $R^2$ of 1.0 is possible. For instance, in the prediction of enzyme optimal temperature, ${〈R^2〉}_{LG}$ was estimated at 0.86 for a specific dataset (Figure 3A), and one should not expect to obtain ML models with $R^2$ scores on holdout data above this value. Moreover, achieving upper bound performance is only possible when a complete set of noise-free features relevant for the predicted labels are used for model training and prediction (Figure 2A to C). When noisy features are used, the performance attainable by ML algorithms will be lower than ${〈R^2〉}_{LG}$ , and thus for classical ML models relying on engineered features, models with holdout data $R^2$ close to their upper bound are not easily achieved in practice (Figures 3A, 4 and 5D). On the other hand, if the estimated ${〈R^2〉}_{LG}$ upper bound for a specific problem and dataset is low (label values are noisy compared to the label variance, $\overline{{\sigma }_y^2}$ is close to ${\sigma }_{obs}^2$ ), it may not be worthwhile to attempt modeling at all, at least not before collecting additional data (more replicates). An example of this is the prediction of melting temperatures of human proteins (Table S1) using the dataset from Leuenberger et al. ⁵² The sample labels for human proteins in this dataset have a large level of noise ( $\overline{{\sigma }_y^2}$ , 5.49) ² compared to the label variance ( ${\sigma }_{obs}^2$ , 6.57) ² and the calculated ${〈R^2〉}_{LG}$ was therefore correspondingly low at approximately 0.30 (using equation (3), see section “Estimating the theoretical upper bound of regression model performance”). Even if a ML model with upper bound performance could be developed for these data, it would have little predictive value. In contrast, for three other, non-human, organisms in the Leuenberger dataset the calculated ${〈R^2〉}_{LG}$ was above 0.90, indicating that the development of predictive ML models may be worthwhile (Table S1).

To conclude, our method for estimating upper bounds for model performance on holdout data should aid researchers from diverse fields in developing ML regression models that reach their maximum potential.