Mapping the multiscale structure of biological systems

Abstract

Biological systems are by nature multiscale, consisting of subsystems that factor into progressively smaller units in a deeply hierarchical structure. At any level of the hierarchy, an ever-increasing diversity of technologies can be applied to characterize the corresponding biological units and their relations, resulting in large networks of physical or functional proximities – e.g. proximities of amino acids within a protein, of proteins within a complex, or of cell types within a tissue. Here, we review general concepts and progress in using network proximity measures as a basis for creation of multiscale hierarchical maps of biological systems. We discuss the functionalization of these maps to create predictive models, including those useful in translation of genotype to phenotype; strategies for model visualization; and challenges faced by multiscale modeling in the near future. Collectively, these approaches enable a unified hierarchical approach to biological data, with application from the molecular to the macroscopic.

Introduction

Biological structure is fundamentally multiscale (Simon, 1991). Atoms make up amino acids which, in turn, are the building blocks of proteins; proteins interact to form protein complexes; and protein complexes interrelate within cellular components such as organelles. The hierarchy can be expanded further to consider interactions among cell types to form tissues, among different tissues in an organ, or among organs in an organism. Determining this multiscale structural hierarchy, as well as its relation to biological function, is one of the ultimate goals of the biological sciences (Box 1).

Box 1: What is Scale?

Many different studies have been described variously as “multiscale,” “large-scale” or “genome-scale”, motivating an important question of what exactly is meant by “scale” in these efforts. In many contexts including this article, scale is used to describe the physical size of the entities under study. Entities of interest in the biological sciences range from single atoms with diameters measured in angstroms, to amino acid residues on the order of a nanometer, to proteins and protein complexes of tens to hundreds of nanometers, to organelles and whole cells several microns in diameter, to tissues, organs and individuals measured in fractions of meters. In this sense, a “multiscale” model is one that includes entities at more than one of these size ranges, along with defined relationships between the entities at different scales (e.g., containment of two proteins within a protein complex; trafficking of a protein complex between the nucleus and cytoplasm). Some contexts measure scale using mass rather than size, especially molecular characterizations by mass spectrometry or centrifugation which typically measure units in Daltons.

The biological entities characterized by an analysis can be described by upper and lower limits in size or mass, determined by the experimental method used to generate the data. The lower limit of scale is known as the resolution, or the ability to distinguish between two entities. The upper limit of scale is called the field of view (FOV), originally based on the literal two-dimensional field of view of a light microscope but applicable to many technologies. For example, a multiscale model of a protein complex generated using cryo-EM analysis typically has near-atomic resolution and a field of view equal to the overall complex size, and thus the scale spans from approximately 0.1 – 10.0 nm. Standard proteomic and genomic analyses on a single cell type result in a field of view at the cellular level, whereas single-cell RNA-sequencing analyses extend the field of view to the tissue level when clustering is performed to form a hierarchy of cell types.

In contrast to these definitions, the phrase “genome-scale” has a very different connotation in that it refers to studies that include measurements for nearly all instances of a single type of entity, the gene. Similarly, proteome-scale analysis refers to studies at the level of the whole proteome in terms of the number of proteins analyzed. Despite these monikers, genome-and proteome-scale analyses are typically narrow in scale as they focus on measurement of a single type of biological entity – genes or proteins.

Various biological studies excel at different aspects of encapsulating both a comprehensive analysis (i.e., examining all genes, proteins or other entities) and multiscale dimensionality regarding resolution and field of view (Box 1 Figure). An ideal model of biological structure of a tissue would perhaps be one that captures both the breadth of proteins (i.e. proteome-wide) as well as encapsulates the many different sizes of subsystems (i.e. deeply multiscale).

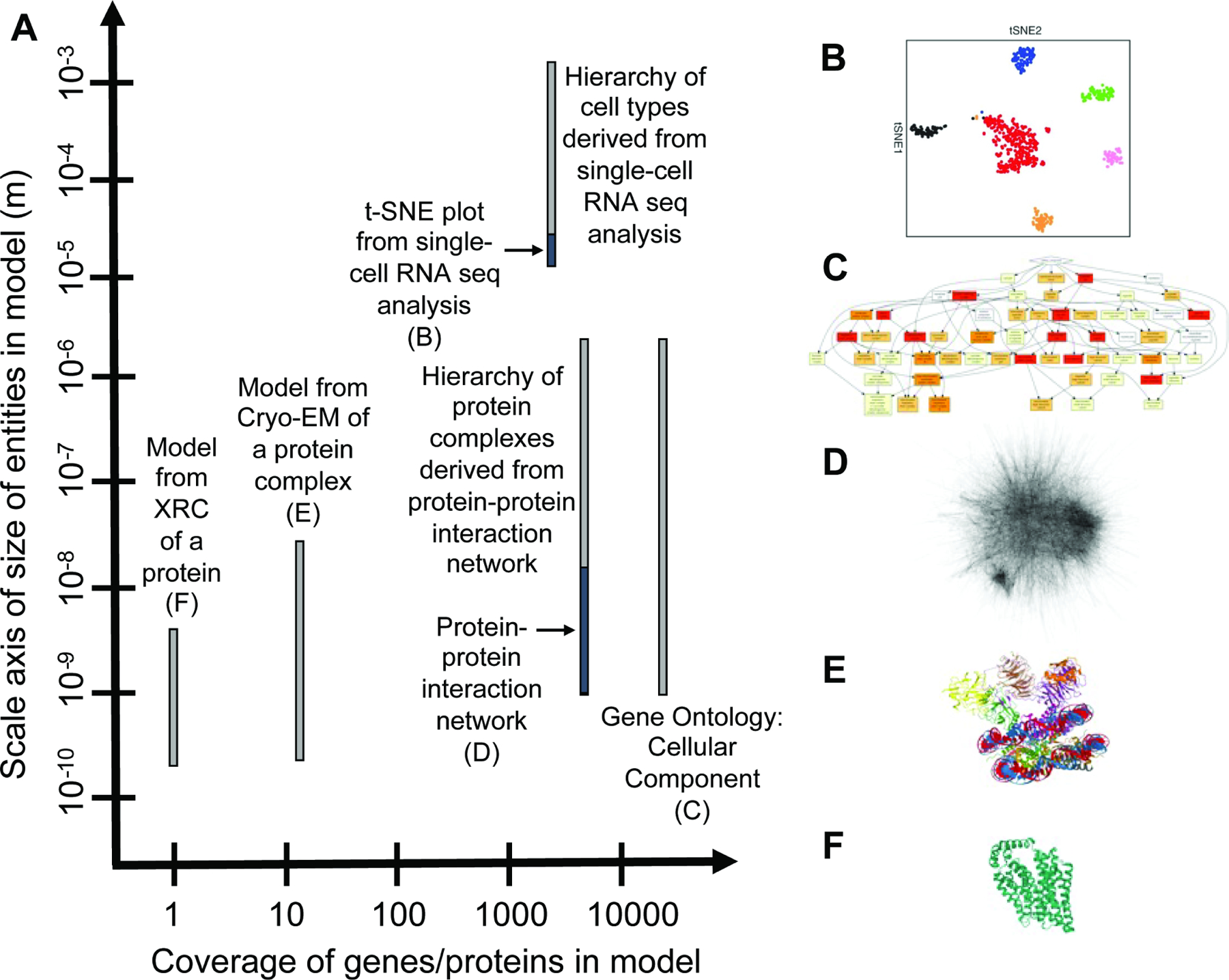
Box 1 Figure. Scale and coverage of common biological analyses.

(A) Various biological analyses result in models with different coverage of the human proteome (x-axis) that span multiple scales to varying degrees (y-axis). (B) t-SNE plot from single-cell RNA sequencing data of malignant cells. Distinct communities of cells (colored points) are visible in the plot area, with each community containing 1 to 100 cells measuring in the 10^–4 to 10^–5 m range for a human cell with nominal radius 10^–5 m. From Tirosh, I., Izar, B., Prakadan, S.M., Wadsworth, M.H., 2nd, Treacy, D., Trombetta, J.J., Rotem, A., Rodman, C., Lian, C., Murphy, G., et al. (2016). Dissecting the multicellular ecosystem of metastatic melanoma by single-cell RNA-seq. Science 352, 189–196. Reprinted with permission from AAAS. (C) Enriched Cellular Component GO terms for list of genes present in MitoCarta 2.0 database (Calvo et al., 2016) visualized with GOrilla (Eden et al., 2009). Color coding shows the degree of enrichment for each GO term. (D) Protein interaction network from BioPlex AP-MS data of HEK293 cells (Huttlin et al., 2015). Reprinted with permission from Elsevier. (E) Model of MLL1-ubNCP complex from cryo-EM analysis. Image from the RCSB PDB (rcsb.org) of PDB entry 6KIW (Xue et al., 2019). (F) Model of human glucose transporter GLUT1 from x-ray crystallography. Image from the RCSB PDB (rcsb.org) of PDB entry 4PYP (Deng et al., 2014).

There has been much recent interest in the challenge of multiscale modeling within the field of “integrative” structural biology, whereby data from different measurement approaches are combined to generate a unified, superior model of a biological structure (Alber et al., 2008; Faini et al., 2016; Lasker et al., 2010; Rout and Sali, 2019; Russel et al., 2012; Ward et al., 2013). A core concept is that complementary measurement techniques are not only beneficial in general, but they may ultimately be necessary to gain a full understanding of biological structure across multiple scales. For instance, such an approach was applied to the challenging problem of determining the 552-protein nuclear pore structure in yeast at sub-nanometer precision, illustrating the power of integrating multiple experimental approaches (Kim et al., 2018).

Many of the same principles and analysis frameworks important for modeling the structure of proteins and protein complexes are now emerging in the analysis of larger biological systems – scales usually considered to be in the realm of “systems”, rather than structural, biology (Singla et al., 2018). For instance, gene and protein expression, interaction, and other ‘omics profiles are routinely integrated to elucidate multiscale hierarchies of cellular processes (Jaimovich et al., 2010; Kramer et al., 2017; Ryan et al., 2012; Vaske et al., 2010). At a larger scale still, single-cell RNA sequencing data are now often used to infer multiscale maps of cell types comprising an anatomical tissue along with their developmental trajectories (Durruthy-Durruthy et al., 2014; Farrell et al., 2018; Wagner et al., 2018; Zeisel et al., 2015; Zhong et al., 2018).

Importantly, many of the measurement techniques underlying structural, systems, and developmental biology are based on observations of pairwise proximity, which are naturally represented by biological “proximity” networks. In each of these cases, measurements focus on a particular type of biological entity – atoms, nucleic or amino acids, DNA fragments, peptides, proteins, cells, tissues, and so on – with the goal of determining which groups of entities are in close physical contact or are otherwise related by a high degree of functional similarity. In the representation of these data, the entities are treated as network “nodes”, and proximal or similar entities are connected by network “edges” (connecting pairs of biological entities) or “hyperedges” (used to interconnect larger groups greater than two) (Berge, 1984). Edges may be assigned weights, expressing quantitative proximity relationships, or they may be present/absent, in which they simply mark the entities determined to be physically or functionally close to one another. Thus, networks provide a core foundation for representing many types of experimental evidence – across many different scales – in the inference of biological structure and function.

Here, we explore the extent to which proximity networks and their analysis can provide a general, unifying framework to map the hierarchical structures and functions that make up an organism. In what follows, we survey the specific network proximity measurements most commonly used to characterize biological systems at different size scales. We then review general methods by which multiscale hierarchical maps can be assembled from network proximity measures, and we discuss the similarities and differences between these assembled maps and biological ontologies. Next, we explore the functionalization and visualization of multiscale maps and models. Finally, we explore current challenges facing the field along with potential solutions. Collectively, these techniques provide the opportunity to create unified hierarchical models across multiple relevant biological scales, from the very small (angstroms) to the very large (meters).

Proximity networks as a general data structure across scales

While examples of proximity networks abound at every scale of biology, perhaps the largest diversity of biological network research has been in proteomics, where nodes represent proteins and edges represent physical proximity of a protein pair. Such protein interaction networks are produced by a variety of methods including affinity purification mass spectrometry (AP-MS) (Gordon et al., 2020; Huttlin et al., 2015, 2017), co-elution mass spectrometry (Bludau et al., 2020; Havugimana et al., 2012; Salas et al., 2020), peptide crosslinking (Liu and Heck, 2015; Vasilescu et al., 2004), yeast two-hybrid assays (Luck et al., 2020; Rolland et al., 2014; Stelzl et al., 2005), and proximity labeling (Go et al., 2019; Lobingier et al., 2017; Roux et al., 2012). Protein interactions of these various types are documented in online databases such as BioGRID (Stark et al., 2006) and STRING (Szklarczyk et al., 2018). The PrePPI database documents protein-protein interactions predicted using high resolution structural data as well as functional, evolutionary, and expression data (Zhang et al., 2012b).

Closely related to physical protein interactions are so-called “genetic” interactions, which indicate a close functional, rather than physical, relationship among pairs of genes. A genetic interaction occurs when mutations to two genes produce a phenotype that is unexpected from mutations to each gene individually (Dixon et al., 2009). Large genetic interaction screens, in which panels of genes are mutated or otherwise perturbed in combination, were originally reserved for model species (Bandyopadhyay et al., 2010; Costanzo et al., 2010; van Leeuwen et al., 2016; Tong et al., 2001) but are increasingly applied to humans using combinatorial CRISPR techniques (Behan et al., 2019; Han et al., 2017; Shen et al., 2017). The phenotype of each combination can be measured using static growth assays to characterize fitness (Byrne et al., 2007; Luo et al., 2008; Tsherniak et al., 2017) or more complex or dynamic readouts (Díaz-Mejía et al., 2018; Gonatopoulos-Pournatzis et al., 2020; Jaffe et al., 2019; Norman et al., 2019; Tsherniak et al., 2017). Although genes with similar genetic interaction profiles can encode proteins in close physical proximity, this does not always have to be the case, as genetic interactions can also be observed among genes participating in distinct parallel biological pathways (Gonatopoulos-Pournatzis et al., 2020).

Beyond genes and proteins, networks are convenient data structures for representing relations among entities at many other levels of biological hierarchy (Figure 1). At the atomic scale, electron density images generated by x-ray crystallography (Adams et al., 2002; Kleywegt et al., 2004; Yang et al., 2016) or cryo-electron microscopy (cryo-EM) (Chen et al., 2016; Frenz et al., 2017; Hryc et al., 2017) produce proximity constraints that can be represented as networks of atoms (nodes) linked to other atoms determined to be in close spatial proximity (edges). Moving from atoms to residues, cross-linking MS has recently been very successful in generating networks of proximal amino acids in a protein, or between proteins in a protein complex (Holding, 2015). In these networks, amino acid residues (nodes) are interconnected to others within a certain distance of one another (edges), where this maximum interresidue distance depends on the length of the cross-linker utilized. Such amino-acid proximity networks, whether experimentally generated or inferred, are central to many efforts to model protein structure. They are also central to protein structure prediction. For instance, AlphaFold, a recent major achievement in protein folding prediction (Senior et al., 2019, 2020), uses a deep neural network to generate (initial AlphaFold version) and/or interpret (most recent implementation) the amino-acid proximity network as a central data structure. Here, proximity can be due to either covalent bonds that link atoms or weaker chemical interactions (including hydrogen bonds, hydrophobic interactions, and steric occlusion), which are typically the relevant ones for biological systems.

Figure 1. Biological entities and proximity measures ranging in scale from angstroms to meters.

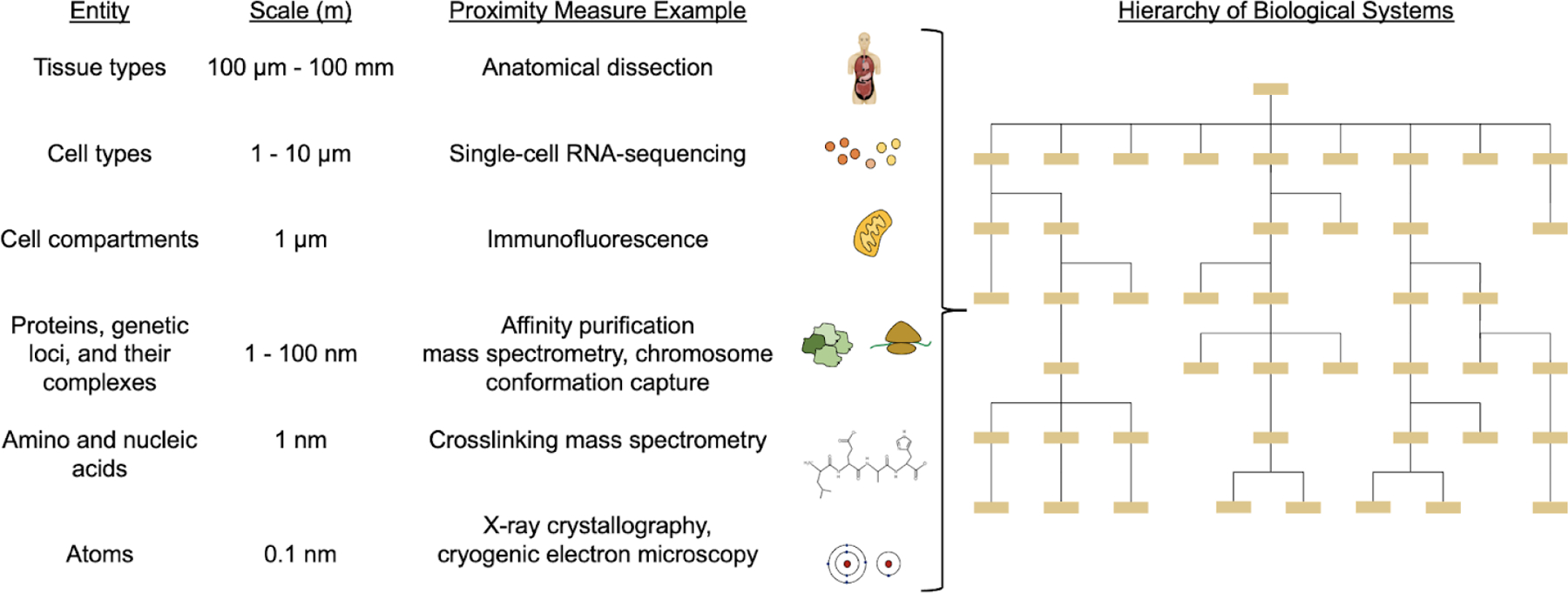
A wide range of analytical methods provide proximity or distance measurements among entities at successive layers of biological structure. A unified hierarchy of biological systems would ideally span all scales of biological structure and function within an organism.

Moving from proteins to DNA, the family of techniques known as chromosome conformation capture, including 3C (Dekker et al., 2002) and Hi-C (Lieberman-Aiden et al., 2009), record pairs of genomic loci that are at close proximity. In Hi-C studies, certain pairs of loci emerge at close proximity in three dimensions although some of these loci are separated at large nucleotide distances along the linear chromosome; such linkages can implicate regulatory interactions among enhancers, promoters, and gene bodies. Similar to how atomic or amino-acid distances are used in determination of protein structure, HiC networks can be used to reconstruct the 3D structure of chromatin and its spatial distribution within the nucleus (Varoquaux et al., 2014).

Above the level of individual proteins and genomic loci, many recent studies use the technique of single-cell RNA sequencing to generate cell-cell networks, in which nodes represent the RNA expression state of an individual cell, and edges connect pairs of cells that are highly similar (Bendall et al., 2014; Trapnell et al., 2014). Edges are typically determined by drawing the shortest cell-cell Euclidean distances from a reduced representation of the RNA expression data, such as a t-Distributed Stochastic Neighbor Embedding (t-SNE) (van der Maaten and Hinton, 2008) or Uniform Manifold Approximation and Projection (UMAP) (Becht et al., 2018). The resulting cell-cell similarity network can then be analyzed to track cell developmental trajectories over time (Farrell et al., 2018; Wagner et al., 2018; Zhong et al., 2018) or to recognize groups of cells forming a distinct cell type or tissue (Jaitin et al., 2014; Zeisel et al., 2015). Finally, at the highest level in the structural hierarchy of an organism, results from anatomical dissection can be thought of as generating a network of tissue types interrelated to one another by physical or functional proximity. This concept can be extended even further to consider interactions at and above the level of organisms, such as social networks interconnecting individuals of a species (Sah et al., 2019), or host-pathogen (Gordon et al., 2020; Penn et al., 2018) or symbiotic interactions interconnecting different species within an ecosystem (Pringle and Tarnita, 2017; Widder et al., 2016). These examples portray how different methods result in networks of biological entities at different levels of biological hierarchy, from angstroms to meters.

Inferring multiscale hierarchical maps from proximity networks

Developing a multiscale representation requires analyzing communities in biological networks at more than one scale. Communities (clusters of highly interconnected nodes) are first defined and identified at each of multiple scales; subsequently, communities that are contained within other communities, in whole or in part, can be traced to infer a hierarchical map (Figure 2) (Dotan-Cohen et al., 2009; Jaimovich et al., 2010; Kelley and Ideker, 2005; Park and Bader, 2011; Ravasz et al., 2002; Tanay et al., 2004). Such a community hierarchy is also a type of network (formally, a directed acyclic graph or DAG) (Thulasiraman and Swamy, 1992) in which hierarchy nodes represent communities and directed edges in the hierarchy (A → B) represent containment or partial containment of one community (A) by another (B). An example containment relation would be a set of protein subunits (A₁, A₂, …) contained by a multimeric protein complex B. Note that in the hierarchical DAG structure, a system can be assigned (receive edges from) multiple subsystems, and it can participate in (have edges to) multiple overarching supersystems.

Figure 2. Community detection in a biological network.

Community detection algorithms define communities (different color circle nodes) in a biological network. Subsequently, communities that are contained within other communities (boxes around circle nodes) can be determined to create a multiscale hierarchical map, where hierarchy nodes (square nodes) represent communities and directed edges in the hierarchy (A → B) represent containment or partial containment of one community (A) by another (B).

In network science, the clustering process that generates the hierarchy is known as community detection, for which a great many algorithms have been developed (Newman, 2018). Specific methods include modularity-based clustering (Newman, 2004), clique percolation (Palla et al., 2005), Louvain clustering (Blondel et al., 2008), Infomap (Rosvall and Bergstrom, 2008, 2011), Order Statistics Local Optimization Method (OSLOM) (Lancichinetti et al., 2011), Clique eXtracted Ontologies (CliXO) (Kramer et al., 2014), HiDef (Zheng et al., 2021), and many others. The Community Detection APplication and Service (CDAPS) (Singhal et al., 2020) integrates end-to-end hierarchical analysis of network communities in the Cytoscape biological network analysis tool (Shannon et al., 2003; Smoot et al., 2011). Functionality includes detection of hierarchical communities with a selection of methods; annotation by alignment with a known ontology such as the Gene Ontology (GO) (Ashburner et al., 2000); visualization of the hierarchical structure; and analysis of the resulting hierarchical communities.

The community detection approach was well illustrated in recent analyses of protein-protein interaction networks in yeast (Dutkowski et al., 2013) and human (Huttlin et al., 2015). In the human study, the authors first performed clique percolation to determine high-level protein communities; subsequently, they ran modularity-based clustering to further subdivide these communities into more granular subsystems, resulting in a multi-layer hierarchical structure (Figure 3A). One of the large communities following clique percolation corresponded to the proteasome, which modularity-based clustering was able to further divide into catalytic and regulatory subunits alongside a cluster of kinetochore components. The result of this data analysis was a multiscale model of the proteasome, including entities such as the protein complex as a whole, subunits of the complex, and individual proteins in each subunit. A very similar hierarchical structure was reported in the corresponding study in yeast (Dutkowski et al., 2013).

Figure 3. Analyzing biological networks to reveal a hierarchy of communities.

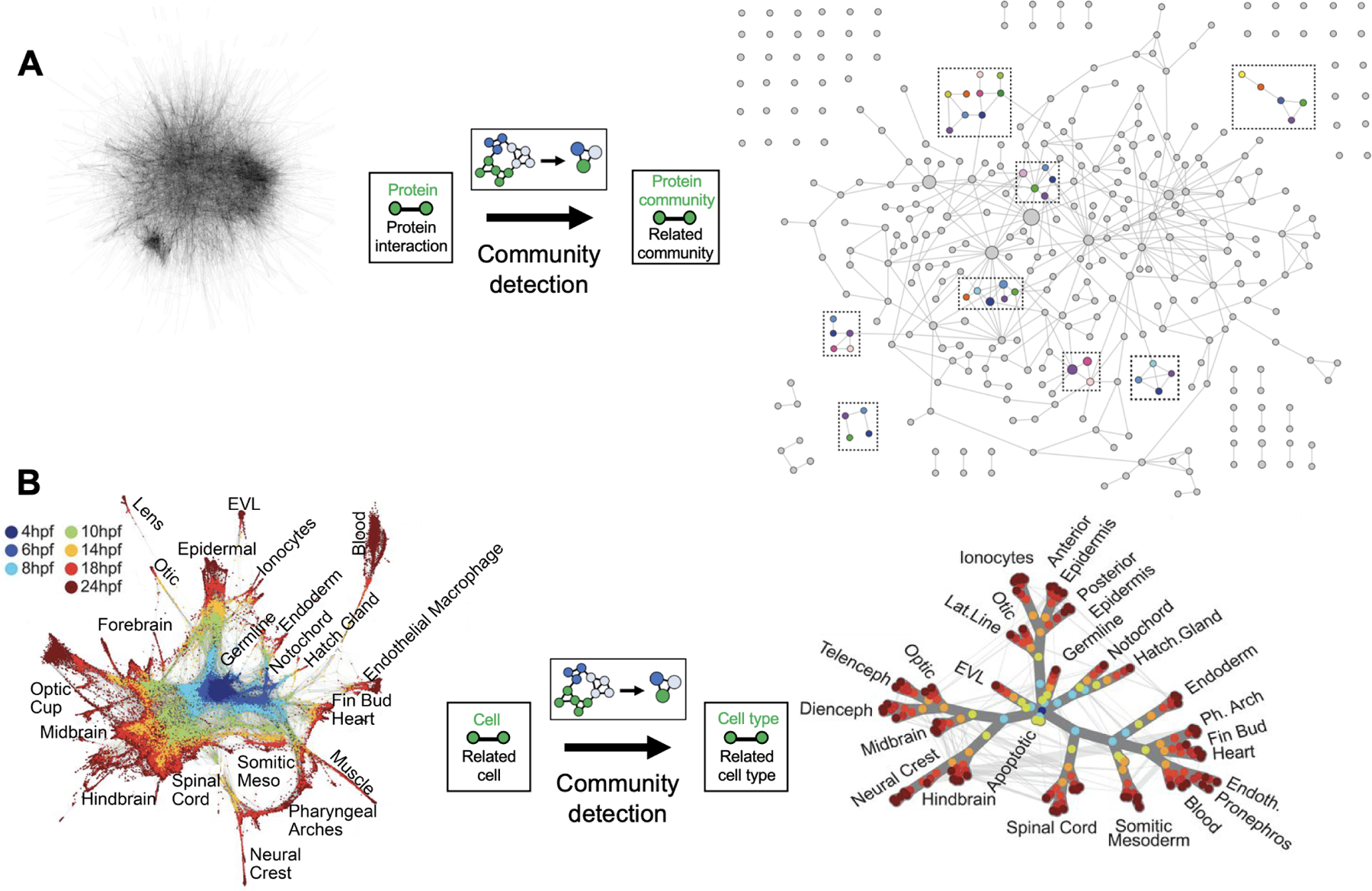
(A) The BioPlex resource uses affinity purification mass spectrometry (AP-MS) experiments to define a large network of interacting pairs of proteins. In the raw network data (left), nodes are proteins; edges are measured protein interactions. Community detection is applied to subdivide communities into increasingly smaller units. In the resulting multiscale model (right), the dotted boxes highlight modules of multiple protein communities, and nodes represent protein communities consisting of proteins; edges run between communities that share a protein or that were subdivided using modularity-based clustering. Figure 3A adapted from Huttlin, E.L., Ting, L., Bruckner, R.J., Gebreab, F., Gygi, M.P., Szpyt, J., Tam, S., Zarraga, G., Colby, G., Baltier, K., et al. (2015). The BioPlex Network: A Systematic Exploration of the Human Interactome. Cell 162, 425–440. Reprinted with permission from Elsevier. (B) Single-cell network from single-cell RNA sequencing analysis of zebrafish embryo development at different hours post fertilization (hpf). In the raw network data (left), nodes represent single cells colored by time of collection; edges represent pairs of cells that are neighbors in a low-dimensional projection of RNA expression data. Community detection is applied to determine a hierarchy of cell types. In the resulting multiscale model, nodes are cell types (consisting of clusters of cells), and edges are weighted based on the number of original single-cell edges. Figure 3B adapted from Wagner, D.E., Weinreb, C., Collins, Z.M., Briggs, J.A., Megason, S.G., and Klein, A.M. (2018). Single-cell mapping of gene expression landscapes and lineage in the zebrafish embryo. Science 360, 981–987. Reprinted with permission from AAAS.

As another example, Costanzo et al. assembled a hierarchy of biological processes using data from a large scale screen of genetic interactions, which examined cell growth for most double mutants of yeast genes, identifying ~1 million genetic interactions (Costanzo et al., 2016, 2019). The lower levels of the hierarchy contained many small but highly related communities of genes, representing focused biological processes and protein complexes. In contrast, the top levels contained a small number of large gene communities with weakly similar profiles, representing pathways and whole organelles. In another recent study, similarities between mutational profiles were converted into an upper bound on distance between mutational residues to create multiscale models of protein complex structures (Braberg et al., 2020). This approach was used to determine the structure of the yeast histone H3-H4 complex by crossing 350 mutations in histones H3 and H4 against 1370 gene deletions.

Moving to higher scales in the biological hierarchy, conceptually similar methods were recently used to build a compelling multiscale map of zebrafish embryo cell types from single-cell RNA sequencing data (Figure 3B) (Wagner et al., 2018). A cell-cell similarity network was constructed using a k-nearest-neighbor graph, where each node represents a cell and edges connect cells to their k nearest neighbors based on their RNA expression profiles. A hierarchy of cell types was constructed from this network: nodes annotated to the same tSNE density cluster were grouped into cell type nodes; edges between cell type nodes were weighted based on the number of edges between grouped single-cell nodes in the original k-nearest-neighbor graph. The result was a hierarchical model of the zebrafish embryo cell types, containing clusters of single cells, with weighted edges connecting similar cell types (either within or between time points). In this example, the scale of the hierarchy is in the time dimension as opposed to physical space, under the assumption that cells related in developmental lineage will have similar expression profiles; it is a challenge in single-cell analyses to deconvolve the relationship between cell type and time, resulting in the development of a diversity of algorithms to infer the trajectory of cell differentiation across time (Saelens et al., 2019). These examples illustrate a process by which biological networks provide the starting points towards building multiscale hierarchical models (Bechtel, 2017, 2020).

Generating multiscale models from multiple network datasets requires combining information from different data types. One approach is to treat the multiple datasets as different “features” annotated to each edge in a single unified network; these multiple features are combined to estimate a single interaction likelihood score for each node pair using supervised machine learning (Kramer et al., 2017) or Bayesian inference (Franceschini et al., 2013; Wong et al., 2004). In a related method, the Mashup algorithm analyzes the topology of each network separately and learns a single weighted network representation that best explains the topological patterns observed across all networks (Cho et al., 2016). Once the data have been combined into a unified network, community detection algorithms may then be run on this network to build hierarchical maps as described above.

Interplay of data-driven hierarchies and literature curated ontologies

There is a notable relation of the multiscale hierarchies described above and biological ontologies, in which a biological entity or concept is recursively factored into a set of subconcepts, sub-subconcepts, and so on (Gruber, 1995). The Gene Ontology (GO) (Ashburner et al., 2000), Cell Ontology (CL) (Bard et al., 2005; Diehl et al., 2016), Human Phenotype Ontology (HPO) (Robinson et al., 2008) and related projects provide a set of widely used, manually curated ontologies that attempt to hierarchically factor entities such as biological processes, components and functions (GO), cell types (CL), and human phenotypes (HPO) into progressively more specific subunits. These ontologies are therefore prime examples of multiscale maps, albeit ones that are manually curated rather than data-driven. Conversely, hierarchical maps generated from proximity networks can be thought of as a type of ontology, as demonstrated in the NeXO project (Dutkowski et al., 2013), albeit one that is driven by direct data analysis rather than manual curation of literature. Regardless, in both cases, entities are interrelated by nested relationships in a hierarchical structure.

The existence of a curated hierarchy of cellular systems like GO greatly facilitates analysis of data-driven maps, by identifying systems in the data-driven hierarchy that correspond to well-known biological components and processes documented in GO. Conversely, systems not found in GO may correspond to novel discoveries. For instance, the multiscale models of cellular components constructed by the NeXO and Mashup efforts (see above) found that the majority of cellular components catalogued in GO could be recovered from hierarchical detection of communities in protein network data (Cho et al., 2016; Dutkowski et al., 2013). Likewise, hierarchies of cell communities inferred from single-cell RNA seq data are typically compared to the CL to determine which communities correspond to known versus novel cell types (Bernstein et al., 2021; Hou et al., 2019). For this purpose, the area known as ”ontology alignment” seeks to address the challenge of determining entities in different hierarchies that represent the same concept, including how to handle multiple overlapping entities and differences in ontology organization. Aligning biological ontologies is also computationally challenging due to their complexity and large size; the GO catalogs tens of thousands of entities for example. Methods for alignment of hierarchies and ontologies are under active research in computer science, including the evaluation of various algorithms for their performance (Ehrig, 2006; Mohammadi and Rezaei, 2020; Otero-Cerdeira et al., 2015). Many of these ontology alignment algorithms may turn out to have useful application in biology, provided the equivalence between multiscale analyses of data and biological ontologies is fully realized.

Functionalization and application of multiscale models

Multiscale models have great potential for the applications of understanding function and predicting outcomes in biological systems, since knowledge of the higher-order protein assemblies in which proteins participate provides evidence for their function and relevance to particular diseases. One important motivation for multiscale biological modeling is to provide a framework for understanding the complex mechanisms by which genotype is expressed as phenotype, including states of health and disease. Entities at very different scales can have significant functional effects on a phenotype under study (Figure 4A). For example, genetic mutations in a genotype may exert their effects at the level of the gene, the protein complex, or the broader pathway or organelle; determining the relevant scale in the biological hierarchy can enable accurate prediction of phenotype, revealing the importance of multiple scales in modeling biological function.

Figure 4. Functionalization of multiscale hierarchies.

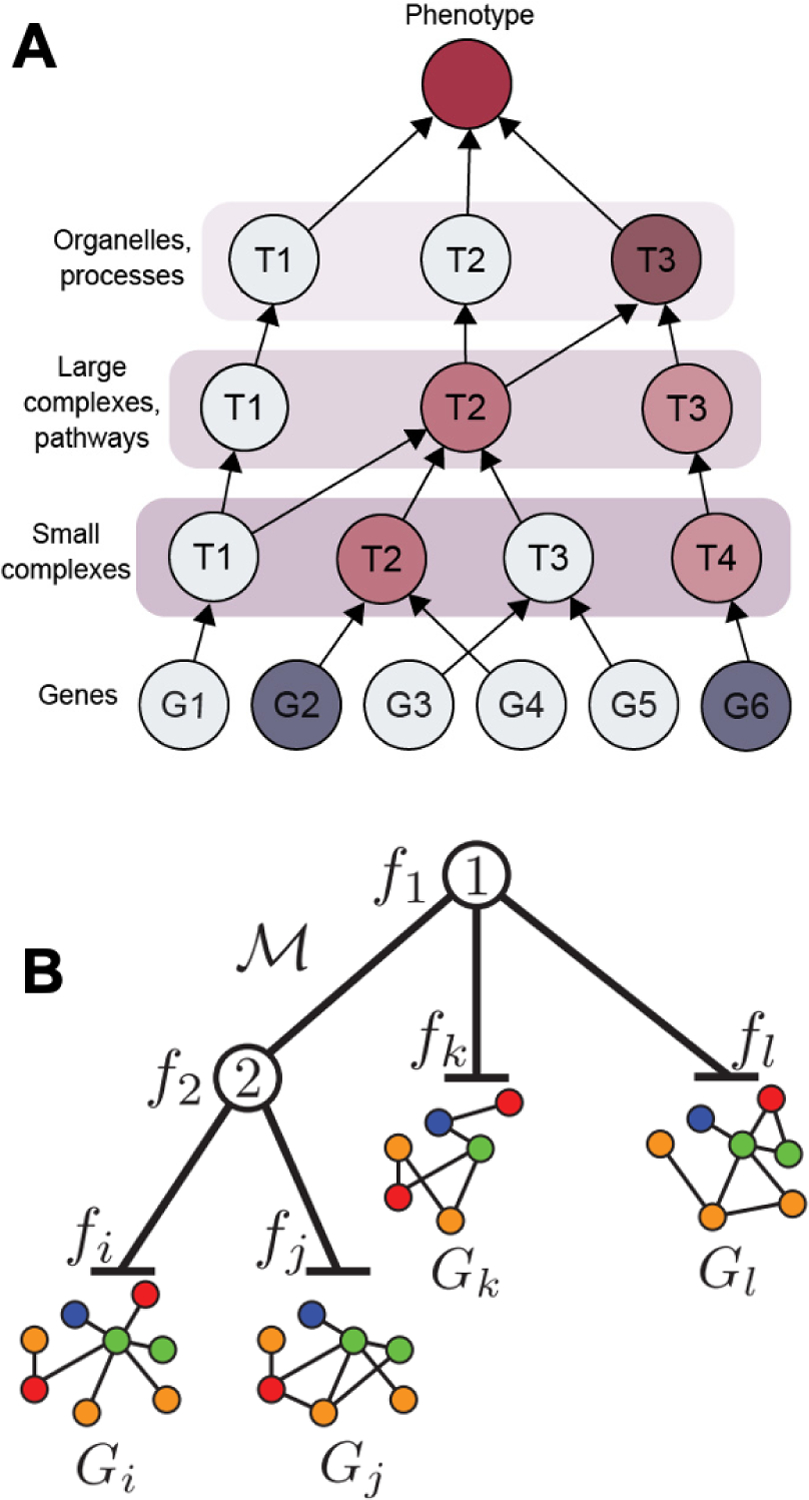
(A) Translation of genotype to phenotype through a hierarchy of subcellular systems. Gene deletions are represented by dark blue. Resulting changes in state for affected systems are shown in red, with darker colors representing effects that are larger or more likely. (B) The OhmNet algorithm learns tissue-specific interactions in a multi-layer network by taking into account tissue hierarchy. OhmNet learns function f_i given tissue-specific network graphs G_i in hierarchical model M. Figure 4B reprinted from Zitnik, M., and Leskovec, J. (2017). Predicting multicellular function through multi-layer tissue networks. Bioinformatics 33, i190–i198, by permission of Oxford University Press.

An explicit hierarchical approach for translation of genotype to phenotype was proposed by (Yu et al., 2016), in which mutations were propagated upward through a hierarchy of cellular components and processes. The mutation states of these entities (i.e. entities containing mutated genes) were then used as features to explain phenotype, enabling the appropriate scale in the cell to be used for accurate prediction. This hierarchical approach was used to accurately predict yeast growth phenotypes from pairwise deletions of non-essential yeast genes, determining affected areas in the hierarchy. For example, many genetic interactions were predicted within the oxidative phosphorylation subsystem; negative interactions (worse than expected growth) occurred between the two subsystems of electron and protein transport, whereas positive interactions (better than expected growth) occurred solely within electron transport.

Even with a multiscale model, the translation of genotype to phenotype can be complex, and the use of standard “black-box” machine learning algorithms prevents a straightforward biological interpretation (Rudin, 2019). In this respect, recent work has shown that using a biological hierarchy to guide the machine learning model can help with interpretability (Ma et al., 2018). In this study, the structure of a deep neural network (i.e. configuration of artificial neurons) was constrained to mirror the hierarchy of cellular components recorded by GO or, alternatively, a multiscale map of cellular components derived from molecular interaction data. This model, called DCell, was able to learn not only to translate genotype to phenotype, but also to capture the functional state of cell subsystems throughout the hierarchy. This thread was recently extended through the development of DrugCell, an interpretable deep learning model of cancer cell proliferation (Kuenzi et al., 2020). Here, the model was trained on the response of tumor cell lines to a large panel of drugs, combining genotype and drug structure to predict the drug response along with the specific cellular subsystems mediating that response. In a related study, Gaudelet et al. modeled a neural network structure on the multiscale functional organization of a cell by integrating gene-pathway annotations in the Reactome database; their model was able to accurately determine patient diagnoses based on gene expression data. Importantly, the trained neural network enabled extraction of biological knowledge by determining novel disease-pathway and disease-gene associations (Gaudelet et al., 2020). The concept of interpretable neural networks has also been applied to determine how genotype governs brain phenotypes, by embedding a regulatory network into a multilayer neural network model including intermediate phenotypes (such as gene expression), gene groupings, and observed traits such as psychiatric disorders (Wang et al., 2018). Related work has used neural networks to perform interpretable deep learning on biological networks to differentiate cell types and determine regulatory differences in single cell RNA sequencing data (Fortelny and Bock, 2020). Here, the authors describe their neural networks as “knowledge-primed”: each neuron is a protein or gene and each edge is an annotated regulatory relationship, with regulated gene expression levels as input neurons (measured by single-cell RNA-seq), signaling protein and transcription factors as hidden neurons, and receptors as output neurons to reflect the cell type phenotype. The use of multiscale maps to guide machine learning systems has potential applications outside of biology (Lipton, 2018), for example in business or finance in which interpretable machine learning systems are necessary to ensure unbiased predictions, meet regulatory requirements, and increase confidence in the model.

Multiscale maps have also facilitated determination of novel gene functions. For example, Gaudelet et al. modeled pairwise protein interactions, complexes, and pathways as multiscale hypernetworks; analysis of these hypergraphs resulted in determining protein function for many uncharacterized genes (Gaudelet et al., 2018). Another study generated a multiscale hierarchical map from a co-expression network of a pathogenic fungus; this map was used to identify clusters in the hierarchy associated with plant cell infection, determining genes not previously reported to function in these pathways (Ames, 2017). The Ohmnet algorithm was developed to perform hierarchy-aware unsupervised feature learning in multi-layer networks, with a focus on the hierarchical relationship between different tissues (e.g. cell types within tissues; organs within organ systems) (Zitnik and Leskovec, 2017). Each layer in the multi-layer protein interaction network represents interactions between proteins in a different human tissue (Figure 4B); the tissue hierarchical relationships were determined by the BRENDA Tissue Ontology (Gremse et al., 2011). This multiscale approach at the level of biological tissues enabled prediction of tissue-specific cellular functions for different proteins, outperforming competing methods which did not account for the multiscale hierarchical organization of tissues. DeepGO used features from protein sequences and interactions to predict protein function; the features were used to build a hierarchical neural network classifier based on GO, so that predictions and features could be refined at each level of the biological hierarchy, resulting in a model optimized for function prediction (Kulmanov et al., 2018). Finally, Knowledge- and Context-driven Machine Learning (KCML) is a recently developed strategy for using a hierarchical approach to predict gene functions from high-throughput gene perturbation screening (Sailem et al., 2020). In this approach, a support vector machine (SVM) classifier for each GO biological process learned to distinguish between phenotypic profiles of genes annotated to that process versus random subsets of other genes. The study found examples where genes annotated to the same higher-scale process perform different functions at lower scales, reflecting the hierarchical organization of cellular subsystems.

Visualization of multiscale models

A critical aspect of model construction is visualization, which enables researchers to determine biological subsystems of interest and perform further exploration or validation. While many applications of clustering and community detection show the detected communities as a flat list or network (Figure 3A), visualization of results as a hierarchy (Figure 5A) communicates the hierarchical relationships among subsystems across multiple levels. Visualization of hierarchical structures is challenging if the containment relations among communities cannot be well-described by a tree but have the aforementioned directed acyclic graph (DAG) structure, i.e. with each system potentially having not only multiple subsystems but also multiple supersystems that contain it. As a result, attempts to visualize the hierarchy can take on the appearance of an uninterpretable “hairball”, with many edges crossing one another (Di Battista et al., 1999). In this common case, there is an important tradeoff between conveying the complete information represented in the hierarchy while avoiding a graphic that is too complex to interpret or investigate.

Figure 5. Visualization of multiscale models as a hierarchy.

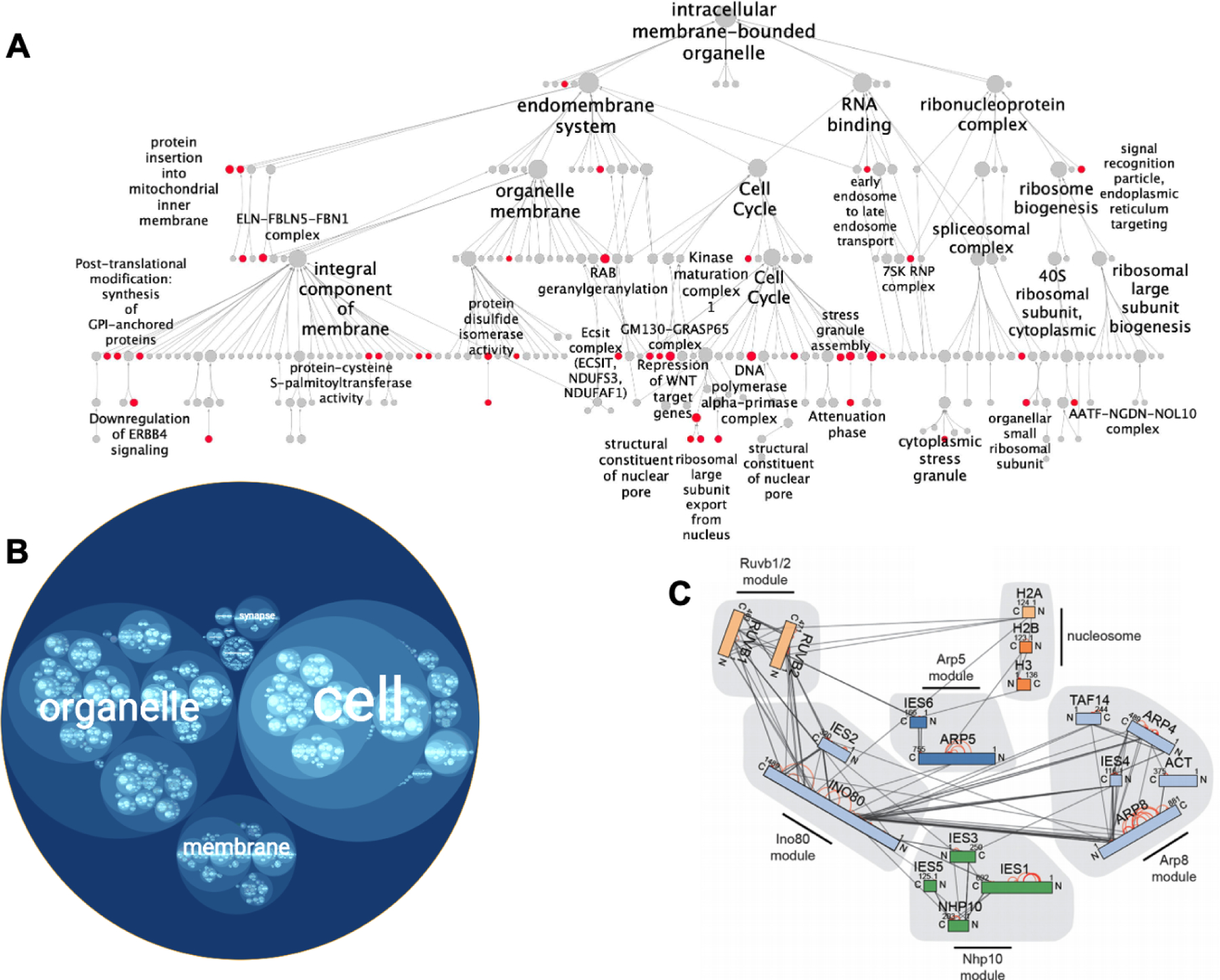
(A) Node-link hierarchy of human protein assemblies interacting with SARS-CoV-2. Red communities are enriched for human proteins that interact with SARS-CoV-2 viral proteins. Figure 5A adapted from Zheng, F., Zhang, S., Churas, C., Pratt, D., Bahar, I., and Ideker, T. (2021). HiDeF: identifying persistent structures in multiscale ‘omics data. Genome Biol. 22, 21., with permission (https://creativecommons.org/licenses/by/4.0/). (B) Circle-packing diagram showing an alternative visualization of the same SARS-CoV-2 hierarchy, generated with HiView. Protein assemblies are represented as circles, with hierarchical containment of one assembly by another represented as nesting of one circle inside another. (C) Hierarchy of protein complexes involving INO80 and the nucleosome, assembled using data from peptide cross-linking analysis. Protein complex modules are highlighted in grey. Rectangle nodes represent proteins, and edges represent crosslinks. Figure 5C reprinted from Grimm, M., Zimniak, T., Kahraman, A., and Herzog, F. (2015). xVis: a web server for the schematic visualization and interpretation of crosslink-derived spatial restraints. Nucleic Acids Res. 43, W362–W369, by permission of Oxford University Press.

Biological ontologies are large hierarchies which also have a DAG structure; as such, existing tools for visualizing ontologies can also have direct application to data-driven multiscale models (Binns et al., 2009; Eden et al., 2009; Sealfon et al., 2006; Supek et al., 2011; Zhu et al., 2019). For example, the Augmented Exploration of GO with Interactive Simulations (AEGIS) platform implements a focus-and-context framework, where a focus graph shows the structure of a selected sub-hierarchy, and a context view is color-coded to show the overall number of nodes related to the sub-hierarchy (Zhu et al., 2019). NaviGO uses an interactive visualization of the hierarchy named GO Visualizer (Khan et al., 2015), allowing users to expand GO terms in the hierarchy and change the view. Similarly, VisANT uses a metagraph (Hu et al., 2004, 2007) to display hierarchies, containing metanodes that can be collapsed or expanded to show subnodes (Hu et al., 2009). HiVis clusters biological networks; to simplify visualization, nodes are only visible in the current level and the next level of the hierarchy (Qiang et al., 2018). The HiView web application contains different options for transforming a DAG hierarchy into a tree (Figure 5A); in each method, a tradeoff exists between information included and the size (Yu et al., 2019). In HiView, the hierarchy can also be visualized as a “circle-packing” diagram (Wang et al., 2006), where subsystems lower in the hierarchy are represented as circles within larger circles (systems) higher in the hierarchy (Figure 5B).

A separate consideration in the visualization of hierarchical models is how to integrate geometric and spatial localization information when it is available. Visualization methods that attend only to the containment relations within the system, as described above, do not necessarily capture spatial subcellular localizations or the number, shape, or positions of subcellular systems, which are important geometric aspects of cellular suborganization. On the other hand, the hierarchical multiscale representations have the major advantages of generality across analytical methods (and their scales) and a comprehensive scope (genome-wide, see Box 1). One strategy for integrating hierarchical maps with spatial organization is to overlay the localization coordinates of each entity in 2D or 3D. For example, programs have been developed to analyze and visualize cross-linking data as a network of amino acid nodes, where edges represent a detected cross-link (Combe et al., 2015; Courcelles et al., 2017; Grimm et al., 2015; Riffle et al., 2016); organizing clusters of nodes spatially according to subunit is one approach that has been applied in these networks (Figure 5C). At a larger scale, studies have integrated protein-protein interaction networks with subcellular organization by partitioning a network into subnetworks according to subcellular location (Barsky et al., 2007; Heberle et al., 2017; Nagasaki et al., 2011; Ofran et al., 2006; Zhang et al., 2012a). A complementary multiscale visualization strategy is to integrate 3D structural information with associated nodes in a hierarchy; software tools have been developed that display available 3D structural data for selected proteins and physical pairwise interactions in protein-protein interaction networks (Morris et al., 2007; Mosca et al., 2013; Nepomnyachiy et al., 2015).

Outstanding Challenges in Multiscale Modeling

There are still many challenges related to the construction and application of multiscale models as they seek to accurately capture biological structure and exhibit high predictive power. First, multiscale modeling carries with it all of the challenges of general community detection, including determining the optimal number of communities, since this number is typically not known in biological analysis. Community detection algorithms such as Louvain (Blondel et al., 2008) or Newman Girvan (Girvan and Newman, 2002) determine the approximate number of communities by optimizing modularity, or the density of links within communities versus links between communities. When performing community detection at multiple scales to develop a hierarchy, there is the additional challenge of determining a suitable number of levels for the hierarchy, as this number is also typically not known beforehand. Another well-known problem in community detection is the tradeoff between quality control and completeness, since not all biological entities of interest may be detected or meet a quality threshold due to experimental challenges. Clustering analysis of networks is sensitive to network noise (Stacey et al., 2020), and biochemical experimental challenges as well as cell-to-cell variation can contribute to this issue. One way this issue may be addressed is through fuzzy or overlapping communities, where nodes can belong to more than one (Yazdanparast et al., 2020).

A second open question regards the best way to evaluate multiscale models, a question that is also vital to optimization of the number of communities and levels. One way to evaluate multiscale models is to align hierarchies with known gold-standard ontologies and determine how many known cellular subsystems are recovered. As discussed above, however, alignment of hierarchies has its own set of challenges. Another option is to determine how many communities in the hierarchy can be validated with experimental evidence from another data set, with the caveat that comprehensive datasets may not exist for the biological contexts or conditions under study.

A third set of challenges relates to integrating diverse modalities of data, such as protein interaction networks with single cell sequencing. How to actually connect communities across these broader scales to generate a single unified hierarchy is an open question to be explored. Some approaches have used machine learning to integrate pairwise distance measurements at different scales (Qin et al., 2020) or to integrate single cell data with context-independent data to create cell-type specific interactomes (Mohammadi et al., 2019). In integrative structural biology, data from multiple methods are collected and translated to spatial restraints, which are used in scoring sampled structures (Rout and Sali, 2019); this type of wholly integrative constraints-based approach may also prove useful when constructing broader multiscale models.

A fourth challenge relates to the capture of dynamics. While many of the multiscale models that have been described herein are presented as a static snapshot of biological structure, cellular processes are highly dynamic, involving transient regulatory interactions and control of protein interactions via post-translational modifications. Limiting one’s study to a static snapshot of protein interactions may limit predictive power for determining biological consequences of chemical drugs or genetic variations, as the resulting variations may be context dependent. An important strategy moving forward will be to determine hierarchical models for each context under study, then implement hierarchy or ontology alignment algorithms to compare the various context-dependent hierarchies.

Finally, many networks and subsequent multiscale models have a one gene-per-node representation, when in reality protein diversity (including sequence isoforms and post-translational modifications) controls interactions between proteins and individual protein function (Aebersold et al., 2018). Additionally, small molecular interactions are critical for biological regulation in both intracellular processes and cell-to-cell communications, up to the even broader coordination between organs in an organism (Schreiber, 2005). Thus, significantly broadening the set of biological entities included in a modeling project is a significant future direction.

Conclusions

Biological structure can be effectively modeled as a hierarchy of subsystems that, collectively, span scales of at least ten orders of magnitude, from angstroms to meters. Various experimental data types and analytical methods generate networks of proximity between biological entities at different levels of the hierarchy and thus at different scales. With ongoing technological developments in data collection and analytical methodology, we expect biological networks and the resulting multiscale models to vastly improve in both scope (field of view) and level of detail (resolution), towards ever-larger and more complete hierarchical models that enable unprecedented understanding of biological function.

In this review, Schaffer and Ideker discuss concepts and progress towards the goal of creating unified multiscale models of biological structure and function. Many experimental technologies measure physical proximity or functional similarity among biological entities at different scales– including amino acids within a protein, proteins within an enzymatic complex, and cells within a tissue. This review discusses use of these proximity networks to create multiscale models, along with major applications, visualization techniques, and current challenges.