Separating Algorithms From Questions and Causal Inference With Unmeasured Exposures: An Application to Birth Cohort Studies of Early Body Mass Index Rebound

Abstract

Observational studies reporting on adjusted associations between childhood body mass index (BMI; weight (kg)/height (m)²) rebound and subsequent cardiometabolic outcomes have often not paid explicit attention to causal inference, including definition of a target causal effect and assumptions for unbiased estimation of that effect. Using data from 649 children in a Boston, Massachusetts–area cohort recruited in 1999–2002, we considered effects of stochastic interventions on a chosen subset of modifiable yet unmeasured exposures expected to be associated with early (<age 4 years) BMI rebound (a proxy measure) on adolescent cardiometabolic outcomes. We considered assumptions under which these effects might be identified with available data. This leads to an analysis where the proxy, rather than the exposure, acts as the exposure in the algorithm. We applied targeted maximum likelihood estimation, a doubly robust approach that naturally incorporates machine learning for nuisance parameters (e.g., propensity score). We found a protective effect of an intervention that assigns modifiable exposures according to the distribution in the observational study of persons without (vs. with) early BMI rebound for fat mass index (fat mass (kg)/ height (m)²; −1.39 units, 95% confidence interval: −1.63, −0.72) but weaker or no effects for other cardiometabolic outcomes. Our results clarify distinctions between algorithms and causal questions, encouraging explicit thinking in causal inference with complex exposures.

Abbreviations

BMI

body mass index

CI

confidence interval

DBP

diastolic blood pressure

FMI

fat mass index

HOMA-IR

homeostasis model assessment of insulin resistance

IPW

inverse probability weighting

SBP

systolic blood pressure

SD

standard deviation

TMLE

targeted maximum likelihood estimation

Typically, body mass index (BMI; calculated as weight (kg)/height (m)²) increases during the first year of life and decreases to a nadir during childhood, before finally rising again (1). This second rise in BMI in childhood, known as the BMI rebound, typically occurs between 4 and 6 years of age (2, 3). Observational studies have shown strong associations between an early BMI rebound in childhood (i.e., before 4 years of age) and obesity, type 2 diabetes, and the metabolic syndrome in adolescence and adulthood (4–8). Despite adjustment for covariates, these studies have not explicitly considered causal inference, including causal-effect definitions and assumptions sufficient for unbiasedly estimating that effect with available data. An “effect of early BMI rebound,” with “early BMI rebound” being the ostensible “exposure” (“treatment”), is not sufficiently well-defined (9, 10) and may not be the effect of interest. Early BMI rebound may result from many underlying processes, including modifiable (e.g., diet, physical activity (11–13)) and nonmodifiable (e.g., genetics (14)) factors. Investigators reporting “adjusted associations” between early BMI rebound and health outcomes may in fact be interested in reporting effects of interventions on 1 or more of these processes that may not fully control early BMI rebound. In many cases, data on even modifiable processes are limited and difficult to measure in existing data sets.

Here we consider the problem of using existing observational data to estimate effects of particular stochastic interventions (which assign from a specified distribution) on 1 or more unmeasured yet modifiable exposures (e.g., diet and physical activity) on mean adiposity, blood pressure, insulin resistance, and global metabolic risk in early adolescence. These interventions do not guarantee control of early BMI rebound, a proxy for exposure. We consider a set of assumptions under which these effects may still be identified when the proxy is measured but the exposures are not. We rely on the “usual” consistency, exchangeability, and positivity assumptions for stochastic interventions defined with respect to the unmeasured exposures. Failure to measure exposure also comes with the price of requiring an additional strong assumption that the proxy is a particular coarsening of the exposures. Under this proxy separation assumption, the proxy acts as the exposure in the analytical procedure even though it is not the conceptual exposure. This provides an alternative interpretation of effect estimates from such an analysis to effects of interventions on the “versions of treatment” (15). Our alternative formulation is similar to this latter interpretation, including reliance on a coarsening assumption, with the distinction of emphasis that the proxy is not a treatment but a measured variable to be leveraged for identification.

We illustrate these ideas using data from Project Viva, a prebirth cohort study. To obtain effect estimates, we applied targeted maximum likelihood estimation (TMLE) (16), a doubly robust approach that naturally incorporates machine learning for nuisance parameters (e.g., the propensity score) in order to mitigate reliance on parametric models (17).

METHODS

The observational study: Project Viva

Project Viva is an ongoing study of pre- and perinatal influences on maternal, fetal, and child health (18). Briefly, we recruited eligible pregnant women from obstetrical practices at Atrius Harvard Vanguard Medical Associates in eastern Massachusetts during their first prenatal appointment between April 1999 and November 2002. Mothers provided written informed consent at enrollment and follow-up visits, and children provided verbal assent at midchildhood (ages 7–10 years) and early adolescent (ages 12–16 years) research visits. The Institutional Review Board of Harvard Pilgrim Health Care Institute (Boston, Massachusetts) approved the project in line with ethical standards established by the Declaration of Helsinki.

The analytical cohort and BMI rebound

Previous studies have defined early BMI rebound as a rise in BMI that happens before 4 years of age, after an initial decline from infancy (4–7). Given that few children had 3 or more measurements of BMI during this early period, we restricted the study population to children with BMI measurements indicating a decline of at least 0.1 BMI units between infancy (ages 6–12 months) and early childhood (ages 2–3.9 years). We defined BMI rebound as an increase of at least 0.1 units between early childhood and midchildhood (ages 4–8 years), following previous studies (19, 20). Below we refer to this as an indicator of “early” BMI rebound, and in the Discussion we explicitly consider the error associated with this interval measure of BMI rebound timing and tradeoffs with latent class modeling.

We also restricted the analytical cohort to children with complete data on baseline covariates (see Table 1 and below). We have previously described the methods of measurement of these covariates (21–23). Of 2,128 live singleton births, 1,183 children had BMI measurements in infancy (median age, 6.2 months; range, 5.0–11.2) and early childhood (median age, 37.5 months; range, 24.0–47.8) indicating a BMI decline after infancy. Of these children, 1,002 had complete data on baseline covariates and 649 had a subsequent BMI measurement at age 48 months (4 years) or later (median age, 49.0 months; range, 48.0–94.9). We obtained measures of weight and length/height at research visits during infancy, early childhood, and midchildhood and from medical records, where pediatric clinics recorded weight and length/height at each well-child visit (21–23). We used both research and clinical measures of weight and length/height to calculate BMI.

Table 1.

Baseline Covariates Used for Confounding Adjustment in a Study of Effects of Stochastic Interventions on a Chosen Subset of Modifiable yet Unmeasured Exposures Expected to Be Associated With Early Body Mass Index Rebound on Adolescent Cardiometabolic Outcomes, Project Viva, Boston, Massachusetts, 1999–2002

Covariate	Cardiometabolic Outcome
	Fat Mass Index a	Blood Pressure z Score	HOMA-IR	Metabolic Risk Score
Continuous variables
Maternal prepregnancy BMIb	Y	Y	Y	Y
Gestational weight gain	Y	Y	N	N
Paternal BMI	Y	N	Y	Y
Birth weight for gestational age	Y	Y	N	N
Gestational age at delivery	N	Y	N	N
BMI in early childhoodc	Y	Y	Y	Y
Categorical variables
Maternal educational level (non–college-educated vs. college-educated)	Y	Y	Y	Y
Smoking history (never smoked vs. smoked before pregnancy vs. smoked during pregnancy)	Y	Y	Y	Y
Glucose tolerance (normal vs. abnormal)	N	N	Y	Y
Pregnancy hypertension (no vs. yes)	N	Y	N	N
Paternal educational level (non–college-educated vs. college-educated)	Y	N	Y	Y
Breastfeeding initiation (no vs. yes)	Y	N	N	N
Child’s sex (male vs. female)	Y	N	Y	N
Child’s race/ethnicity (White vs. non-White)	Y	Y	Y	Y

Abbreviations: BMI, body mass index; HOMA-IR, homeostasis model assessment of insulin resistance; N, no; Y, yes.

^a Fat mass (kg)/height (m)².

^b Weight (kg)/height (m)².

^c Early childhood was the baseline measure.

Adolescent adiposity and cardiometabolic outcomes

In early adolescence (median age, 12.9 years; interquartile range, 12.5–13.6), trained research assistants measured waist circumference using a nonstretchable tape, measured fat mass using foot-to-foot bioimpedance, and measured systolic blood pressure (SBP) and diastolic blood pressure (DBP) using calibrated automated oscillometric monitors according to standardized protocols (21). We calculated fat mass index (FMI) as fat mass (in kilograms) divided by squared height (in meters). We derived age-, sex-, and height-specific SBP and DBP z scores according to the American Academy of Pediatrics reference values for children and adolescents (24). Trained technicians also collected fasting blood specimens, which were used to measure fasting glucose, insulin, high-density lipoprotein cholesterol, and triglyceride levels according to standard protocols. Following previous studies, we calculated insulin resistance using homeostasis model assessment of insulin resistance (HOMA-IR) (8, 21). We used external references to calculate age- and sex-specific z scores for waist circumference, SBP, HOMA-IR, triglycerides, and high-density lipoprotein cholesterol (24–27). Subsequently, we derived a metabolic risk score as the average of z scores for waist circumference, HOMA-IR, triglycerides, high-density lipoprotein cholesterol (scaled inversely), and SBP.

The causal question and target trial

Consider the causal effect on an adolescent outcome (Y) of implementing 2 different interventions in the study population of children with measured BMI decline between the ages of 6 and 11.9 months (<1 year). Beginning at the time of this measurement (baseline) and ending approximately 4 years later, define intervention 1 for a given individual i in this population as follows: On each day k = 0, …, K of this intervention period, assign individual i values of a selected set of modifiable characteristics (minutes of physical activity and screen time (television only) and servings of sugar-sweetened beverages) by randomly assigning these values from a particular distribution. No intervention is made beyond day K = 4 × 365.

For R, an indicator of not experiencing BMI rebound by the end of the intervention period (the “early” period), we will choose this intervention distribution to be the distribution of exposures on day k (denoted by a vector A_k containing values for physical activity, screen time, and sugar-sweetened beverage consumption on that day) among Project Viva participants meeting study-population criteria who did not experience BMI rebound during this period (R = 1) and who have the same values of the measured baseline covariates (L) and, for k > 0, exposure history (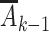) as subject i. We define intervention 2 in the same way, but with the assignment distribution instead defined by children with BMI rebound (R = 0). We will refer to these interventions as proxy representative interventions. The proxy serves only to define the intervention distributions; there is no guarantee or intent of intervention on the proxy. Similar interventions have been previously considered (15, 28–30). (Also see Web Appendix 1, available at https://doi.org/10.1093/aje/kwab029.)

Ideally, we would conduct a trial to estimate this causal effect. This target trial (31) would recruit a large random sample of children at the time at which they met the criteria for the study population and randomize them to either intervention 1 or intervention 2. In an ideal execution of this trial, with perfect adherence to the daily assigned exposure values and no loss to follow-up, an unbiased estimate of this effect could be made by calculating the difference between outcome means in each study arm. These interventions are complicated by the fact that the distribution of the exposure assignment is unknown. However, in principle, it could be estimated prior to the trial in an observational study that measured the covariates L and these daily exposures during this early period in a comparable population and treatment assigned in the trial using these estimates.

Our choice of these particular interventions is convenient in that, as discussed below, we may achieve or approximately achieve identification of these intervention effects even when the data available for estimating them do not include measures of the true exposure(s) of interest for any individual. This provides a way forward under explicit reasoning in such settings that may be common to many social and life-course epidemiologic studies. It will also help shed additional light on the interpretation of common approaches to data analysis in these settings. Also driven by convenience is our choice to define the intervention rules to be dependent only on a single proxy measure (an indicator of BMI rebound anywhere in this “early” period) and baseline covariates because time-updated measures in this period were not available in our study. In Web Appendix 1, we consider more general extensions.

Estimating the effect of proxy representative interventions in observational studies when exposure is measured

We now consider assumptions that allow unbiased estimation of this causal effect in an observational study when the variables L, 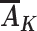 , R, and Y are measured, with 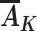being the vector of time-varying exposures. Under the untestable assumptions discussed below, the following function of these variables,

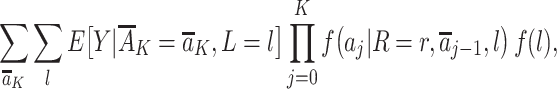(1)

identifies the outcome mean value that would have been present had all individuals followed a proxy representative intervention from the target trial on the exposures 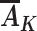, where 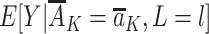denotes the mean of Y within a particular level of the exposures and covariates, denotes the probability of having exposure level A_j = a_j among children with proxy status R = r and in a particular exposure and baseline covariate stratum, and 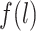denotes the probability of having covariate level L = l. For simplicity, equation 1 considers discrete variables. More generally, the summation symbols 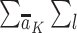over all levels of exposure and covariates can be replaced with integrals. The difference between equation 1 indexed by r = 1 and equation 1 indexed by r = 0, in turn, identifies the causal effect of the proxy representative interventions defined above. The function shown in equation 1 is an example of Robins’ g-formula (32), characterized by a particular stochastic intervention (30, 33, 34). Assumptions that equate the g-formula with the outcome mean under this intervention include the particular versions of exchangeability that are conditional on L (the assumed measured “confounders”), positivity, and consistency, which are reviewed in Web Appendix 1 (30, 32).

The second term in equation 1 quantifies the exposure distribution conditional on the assumed measured confounders but under the intervention. For a proxy representative intervention, this coincides with 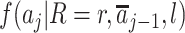being equal to the exposure distribution among children with R = r for a level of the measured confounders in the observational study. The first term in equation 1, 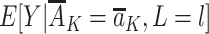, quantifies the outcome mean conditional on exposure and measured confounders. This term is not conditioned on R, because we assume that this postexposure variable is not needed to ensure exchangeability (also see Web Appendix 1).

This exchangeability assumption will hold under a counterfactual causal model represented by a causal directed acyclic graph in which there are no unblocked backdoor paths between each A_k and Y conditional on past exposure and baseline covariates only (and is therefore quite strong) (35, 36). The causal directed acyclic graph in Figure 1 represents a simplified assumption on the data-generating process where A_k contains 2 exposures and K = 2. U₀ represents an unmeasured baseline characteristic (e.g., genes) and U₁ an interim characteristic (e.g., interim weight change). Exchangeability would hold under the absence of any arrows from U₀ or U₁ to any exposure but fails with the presence of the dotted arrows. In Web Appendix 1, we formally review these identifying conditions and generalize ideas in the main text to the case where time-varying covariates such as U₁ are measured. In our application, these covariates were not measured (e.g., the majority of children had, at most, 1 measure of weight during the exposure period of interest).

Figure 1.

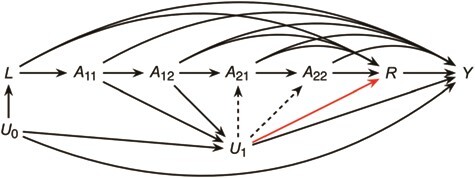
Causal directed acyclic graph representing a data-generating assumption relating a time-varying exposure A, a proxy measure R, an outcome Y, and other covariates U, Project Viva, Boston, Massachusetts, 1999–2002. With all solid arrows present, exchangeability requires dashed arrows to be absent. With all solid black arrows present, proxy separation may fail by the presence of the red arrow.

Positivity requires that for both intervention 1 and intervention 2, there are no levels of L in the observational study for which a level of 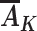possible under intervention is impossible in the observational study. Effects of stochastic interventions in general are less susceptible to positivity violations than deterministic interventions (30). Finally, the consistency assumption in this setting is reasonable as long as there are not multiple versions of exposure or these versions do not affect the outcome (9, 10). Because we have defined exposure only in terms of modifiable characteristics, this assumption may be reasonable.

WHEN EXPOSURE IS NOT MEASURED

Even if the exchangeability, consistency, and positivity conditions hold with respect to proxy representative interventions, the quantity in equation 1 clearly cannot be estimated when exposure is not measured without additional assumptions. Let 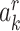denote any value of A_k possibly occurring in the study population had A_k been assigned according to a proxy representative intervention indexed by a level of R = r and consider the following assumption:

Proxy separation: Within each covariate level L = l, if 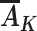 =  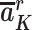, then R = r.

To understand how this assumption could be violated, suppose that A_k includes only daily screen time and some children in the Project Viva study population who experienced early BMI rebound watched 6 hours of television each day in a particular stratum of baseline covariates L (Table 1). Proxy separation would be violated if there were also some children in this stratum who watched 6 hours of television each day and did not experience early BMI rebound. Under proxy separation, the quantity calculated in equation 1 equals

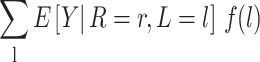(2)

(see Web Appendix 1 for proof).

If 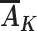were measured, proxy separation could be evaluated in the data. However, paradoxically, in that case it would not be needed because the quantity in equation 1 could be estimated directly. Exchangeability, consistency, and positivity, coupled with proxy separation, are strong assumptions and, at best, hold approximately. When they do, the quantity in equation 2 equals the outcome mean under a proxy representative intervention from the target trial indexed by proxy level r (15). We would expect proxy separation to be more reasonable with increasing dimensions of exposure A_k (provided that additional components are causes, or even only proxies of causes, of BMI rebound; see Web Figures 1–3 in Web Appendix 1) but at the cost of stronger exchangeability and positivity assumptions to still interpret the quantity derived by equation 2 in terms of proxy representative interventions on this higher-dimensional set of exposures.

In Web Appendix 1 we consider extensions that rely on measured time-varying proxies and time-varying confounders. Note that the positivity condition needed for equation 1, coupled with proxy separation, implies the more familiar positivity condition that P(R = r|L) > 0 for any possible level of L.

In practice, even the quantity in equation 2 is not possible to estimate without additional assumptions given missing data on L, R, and Y. In the next section, we consider the computationally straightforward estimator of

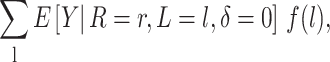(3)

where all terms of equation 3 are implicitly restricted to individuals with complete data on L and R and δ is an indicator of censoring due to missing Y.

The function in equation 3 is equal to that in equation 2 when missing data are absent. When missing data are present, a contrast in equation 3 identifies the effect of interest from the target trial where all interventions include an additional intervention, “eliminate censoring,” under additional exchangeability, positivity, and consistency assumptions with respect to 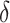and also under the assumption that the functions 1 and 2 in the original target population equal that in the subpopulation with complete data on L and R. Less restrictive assumptions in this case may be considered with respect to missing data but admitting more complex identifying functions and estimation procedures that incorporate measured time-varying covariates when they are available.

Statistical analysis

Several methods may be used to estimate the quantity in equation 3 with this sample, including inverse probability weighting (IPW) (37), parametric g-computation (32, 38), and TMLE (16). Even though the proxy R is not the exposure, the above results allow that an implementation of any of these methods for estimating the effect of a time-fixed static deterministic intervention on a binary exposure can be used to estimate the quantity in equation 3 by algorithmically treating R as this exposure (15, 29, 39). For our primary analysis, we applied TMLE, an approach to estimation of the function in equation 3 that begins with an initial estimate of E(Y|R = r, L, δ = 0), followed by a “targeting” step that updates this initial estimate with a weight that depends on estimates of P(R = r|L) and P(δ = 0|R = r, L) (16, 40). The algorithm is implemented in the R package tmle (R Foundation for Statistical Computing, Vienna, Austria) (41). We review details of the estimation procedure in Web Appendix 2.

This approach is doubly robust in that it consistently estimates the quantity in equation 3 if either E(Y|R = r, L, δ = 0) or both P(R = r|L) and P(δ = 0|R = r, L) are consistently estimated, all implicitly restricted here to children with complete data on R and L. Note that P(R = r|L) can be operationally referred to as a “propensity score” even though R is not “treatment” (42). Estimates of both sets of nuisance parameters may be easily computed using standard parametric models (e.g., linear or logistic regression). However, to avoid reliance on a parametric model for either set, we used SuperLearner (R, version 3.6.1), which generates estimates on the basis of a weighted combination of algorithms selected by cross-validation (43). We selected algorithms used in prior studies that cover a broad range: additive generalized linear models, generalized linear models with interactions, stepwise models, penalized regression models (i.e., the least absolute shrinkage and selection operator (LASSO)), and Bayesian additive regression trees (44, 45).

To assess robustness to the choice of estimation method, we alternatively implemented TMLE with parametric models for nuisance parameters. We also estimated the quantity in equation 3 using parametric g-computation and IPW (see details in Web Appendix 2). For all methods, we used a nonparametric bootstrap with 1,000 bootstrap samples to obtain 95% confidence intervals. For all analyses, we used STATA 16 (StataCorp LLC, College Station, Texas) and R, version 3.6.1 (the tmle and SuperLearner packages). Software code is provided in Web Appendices 3–8.

Data availability

All data described in this article are available from the authors upon request.

RESULTS

Of the 649 children in the analysis sample, the 406 children without early BMI rebound (R = 1) were more likely to have mothers (BMI 24.4 vs. 25.6) or fathers (BMI 26.0 vs. 27.4) with lower BMI, were more likely to be male (56% vs. 46%), had higher birth weight-for-gestational-age z scores (0.3 standard deviation (SD) units vs. 0.2 SD units), and had higher BMI in early childhood (BMI 16.5 vs. 16.1) than the 243 children with early BMI rebound (R = 0) (Table 2). In Web Table 1, we present empirical comparisons of the characteristics of children excluded from the analytical cohort with those of the included children. The distribution of the stabilized weights for all approaches in estimating the weight denominator showed no evidence of positivity violations (Web Table 2).

Table 2.

Characteristics of Children Classified as Having Early Body Mass Index Rebound Versus Those Without Early Body Mass Index Rebound, Project Viva, Boston, Massachusetts, 1999–2002

Characteristic	Early Rebound   (n = 243)		No Early Rebound   (n = 406)
	%	Mean (SD)	%	Mean (SD)
Maternal factors
Prepregnancy BMIa		25.6 (5.6)		24.4 (4.8)
College education	68		73
Smoking history
Never smoked	71		73
Smoked before pregnancy	19		21
Smoked during pregnancy	9		6
Gestational weight gain, kg		15.5 (5.9)		15.4 (5.3)
Abnormal glucose tolerance (IH, GIGT, GDM)	18		17
Pregnancy hypertension (GH, PE, CH)	10		9
Paternal BMI		27.4 (4.4)		26.0 (3.7)
Paternal college education	65		67
Child factors
Birth weight-for-gestational-age z score, SD units		0.2 (0.9)		0.3 (1.0)
Gestational age at delivery, weeks		39.5 (1.6)		39.6 (1.6)
No breastfeeding initiation	10		11
Male sex	46		56
White race/ethnicity	67		68
Age in early childhood, months		36.8 (5.5)		37.5 (3.9)
BMI in early childhood		16.1 (1.3)		16.5 (1.2)

Abbreviations: BMI, body mass index; CH, chronic hypertension; GDM, gestational diabetes mellitus; GH, gestational hypertension; GIGT, gestational impaired glucose tolerance; IH, isolated hyperglycemia; PE, preeclampsia; SD, standard deviation.

^a Weight (kg)/height (m)².

Using TMLE with SuperLearner for nuisance parameter estimation, our estimates of the effects of a proxy representative intervention indexed by R = 1 (a stochastic intervention that assigns individual values for daily physical activity, screen time, and sugar-sweetened beverage consumption from the joint distribution in Project Viva among children who did not experience BMI rebound with that individual’s baseline confounder values) versus R = 0 (the same values but taken from the distribution among those who did experience BMI rebound) were −1.39 units (95% confidence interval (CI): −1.63, −0.72) for FMI, 0.07 SD units (95% CI: −0.09, 0.21) for SBP z score, 0.08 SD units (95% CI: −0.07, 0.17) for DBP z score, −0.09 units (95% CI: −0.20, 0.06) for HOMA-IR, and −0.06 SD units (95% CI: −0.15, 0.04) for metabolic risk score (Table 3).

Table 3.

Effect Estimates for Proxy Representative Interventions Indexed by R = 1 Versus R = 0 Using Different Methods to Estimate the Quantity in Equation 3, Project Viva, Boston, Massachusetts, 1999–2002

Estimation Method	Fat Mass Index a , b   (n = 500)		SBP z Score c ,SD units (n = 498)		DBP z Score c ,SD units (n = 498)		HOMA-IR d ,units (n = 306)		Metabolic Risk Score e ,SD units (n = 302)
	β	95% CI	β	95% CI	β	95% CI	β	95% CI	β	95% CI
Unadjusted results	−1.72	−2.26, −1.18	0.10	−0.04, 0.24	0.08	−0.03, 0.19	−0.14	−0.28, 0.00	−0.06	−0.15, 0.03
Least-squares regressionf	−1.29	−1.75, −0.84	0.10	−0.05, 0.24	0.09	−0.02, 0.21	−0.09	−0.22, 0.05	−0.06	−0.16, 0.03
TMLE
Parametric modelg	−1.41	−1.86, −0.94	0.05	−0.12, 0.23	0.07	−0.04, 0.22	−0.08	−0.21, 0.06	−0.07	−0.16, 0.05
SuperLearner
Version 1h	−1.44	−1.71, −0.72	0.05	−0.12, 0.21	0.08	−0.08, 0.17	−0.09	−0.22, 0.07	−0.06	−0.16, 0.05
Version 2i	−1.39	−1.63, −0.72	0.07	−0.09, 0.21	0.08	−0.07, 0.17	−0.09	−0.20, 0.06	−0.06	−0.15, 0.04
G-computation
Parametric model	−1.31	−1.75, −0.86	0.07	−0.08, 0.22	0.11	−0.01, 0.24	−0.07	−0.20, 0.06	−0.06	−0.15, 0.05
SuperLearner
Version 1	−1.25	−1.59, −0.73	0.07	−0.13, 0.22	0.10	−0.06, 0.21	−0.09	−0.22, 0.04	−0.06	−0.16, 0.05
Version 2	−1.21	−1.56, −0.69	0.07	−0.08, 0.21	0.07	−0.03, 0.20	−0.08	−0.21, 0.05	−0.05	−0.14, 0.05
Stabilized IPW
Parametric model	−1.34	−1.88, −0.84	0.06	−0.11, 0.22	0.09	−0.04, 0.22	−0.09	−0.23, 0.05	−0.06	−0.17, 0.05
SuperLearner
Version 1	−1.43	−1.75, −0.81	0.07	−0.08, 0.23	0.08	−0.05, 0.20	−0.09	−0.20, 0.06	−0.06	−0.14, 0.06
Version 2	−1.45	−1.79, −0.86	0.07	−0.08, 0.24	0.09	−0.04, 0.20	−0.09	−0.21, 0.05	−0.06	−0.15, 0.04

Abbreviations: BMI, body mass index; CI, confidence interval; DBP, diastolic blood pressure; HOMA-IR, homeostasis model assessment of insulin resistance; IPW, inverse probability weighting; SBP, systolic blood pressure; SD, standard deviation; TMLE, targeted maximum likelihood estimation.

^a Fat mass (kg)/height (m)².

^b Adjusted for maternal smoking status, educational level, BMI (weight (kg)/height (m)²), paternal educational level, paternal BMI, total gestational weight gain, birth weight for gestational age, breastfeeding initiation, child’s sex, child’s race/ethnicity, and BMI in early childhood.

^c Adjusted for maternal smoking status, educational level, BMI, pregnancy hypertension, total gestational weight gain, birth weight for gestational age, gestational age, child’s race/ethnicity, and BMI in early childhood.

^d Adjusted for maternal smoking status, educational level, BMI, glucose tolerance, paternal educational level, paternal BMI, child’s sex, child’s race/ethnicity, and BMI in early childhood.

^e Adjusted for maternal smoking status, educational level, BMI, glucose tolerance, paternal educational level, paternal BMI, child’s race/ethnicity, and BMI in early childhood.

^f Parametric model with no interaction terms for nuisance parameters.

^g SuperLearner with prediction algorithms for generalized linear models, interaction terms, and stepwise modeling for nuisance parameters.

^h SuperLearner with prediction algorithms for generalized linear models, interaction terms, stepwise modeling, penalized regression models, Bayesian additive regression trees, and generalized additive models for nuisance parameters.

ⁱ Estimates of the regression coefficient on R from a linear regression model where the outcome (Y) is regressed on the proxy R and covariates L.

When using parametric models for nuisance parameter estimation using TMLE, the estimates were −1.41 (95% CI: −1.86, −0.94) for FMI, 0.05 SD units (95% CI: −0.12, 0.23) for SBP z score, 0.07 SD units (95% CI: −0.04, 0.22) for DBP z score, −0.08 units (95% CI: −0.21, 0.06) for HOMA-IR, and −0.07 SD units (95% CI: −0.16, 0.05) for metabolic risk score. Results were not substantively different when using parametric g-computation or IPW approaches, with either parametric estimation of nuisance parameters or SuperLearner (Table 3). We also conducted a simple IPW sensitivity analysis wherein individuals were censored upon missing R, with weights incorporating these censoring weights as a function of L. Results were not substantially different (Web Table 3).

DISCUSSION

We considered assumptions under which causal effects of interventions on a set of unmeasured exposures can be estimated in observational studies when only a proxy is measured. We illustrated these ideas in a study where early BMI rebound was used as a proxy for modifiable exposures (screen time, physical activity, and features of diet). Using TMLE with SuperLearner, we estimated a protective effect on FMI of interventions that assign these exposures to an individual according to their factual distribution in the study population among children without (vs. with) early BMI rebound and the same past exposure and covariates. Effect estimates were weaker for other outcomes. The use of non–doubly robust methods (i.e., parametric g-computation and IPW) and/or parametric estimates of nuisance parameters did not substantively change our conclusions.

Effect estimates were much stronger for FMI (−1.39 units) than for other cardiometabolic markers such as SBP z score (0.07 SD units) and metabolic risk score (−0.06 SD units). To put these estimates on the same scale, a change in FMI of 1.39 units is equivalent to a change of 0.40 SD units, which is thus reasonably stronger than estimates for other cardiometabolic markers. This finding is consistent with previous studies that have found a higher rate of fat gain and disproportionately high increases in fat mass among children with an early rebound than in those with a late rebound (46, 47). It is possible that interventions on modifiable behaviors associated with early BMI rebound might have a stronger and more direct influence on true adiposity-related outcomes (e.g., FMI) than on other cardiometabolic markers (e.g., SBP), which has been suggested by previous studies (13, 48). Further, their influence on other cardiometabolic markers, such as insulin resistance, may require more time to develop, since insulin resistance is primarily driven by visceral fat accumulation (49).

Researchers in several studies have estimated associations between early BMI rebound and later cardiometabolic risk using latent class regression methods with adjustment for covariates (4–8). These studies have relied heavily on parametric regression models and have also avoided explicit attention to causal inference. Recently some authors have interpreted the target effect of latent class models as an effect of an assumed latent class variable (50, 51). Drawbacks of this conceptual framework include the facts that a latent class variable may not exist or cannot be articulated, interventions on such a variable are not well-defined (particularly when the variable does not exist), and, in turn, effect estimates can never (even in principle) be confirmed in a real-world trial. However, the assumption of a latent class model allows the derivation of BMI trajectories such that rebound timing can be “known” even when only interval measures of BMI changes are available. This is at the expense of model misspecification bias. By avoiding these assumptions, we relied on a probably mismeasured indicator of BMI rebound such that children classified as having an “early” rebound may indeed have had this rebound sometime after age 4 years. A possible source of bias due to this mismeasurement is violation of the proxy separation assumption.

In contrast to interventions on unknown latent class variables, effects of proxy representative interventions can, in principle, be studied in a real-world trial. Further, formal sensitivity analyses of both the proxy separation assumption and the exchangeability assumption can be developed for particular choices of exposure. Finally, motivating estimators from an explicit causal question rather than a parametric regression model allowed the use of modern, robust estimation procedures.

Our application relied on several strong assumptions, with limitations discussed throughout. Beyond this, our findings may not be generalizable to other populations from different settings, since a majority of mothers in our study were White and college-educated. However, our approach allowed explicit definition of a target effect coinciding with effects of sustained interventions on modifiable exposures of key interest to obesity researchers. Our results highlight the crucial distinctions between questions, assumptions, and statistical algorithms in causal inference with observational data. Articulating clearly what we hope to estimate with an analysis allows explicit reasoning about assumptions, open debate about question value and assumption viability, and ultimately improved design of future studies.